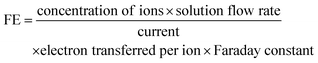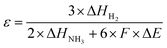Alkaline ammonia electrolysis in a membrane electrode assembly cell: parameter optimization and dynamic operation

Abstract

Hydrogen could potentially play an important role in decarbonizing hard-to-abate sectors where electrification is not viable. Due to lower density, storing and transporting hydrogen in its pure form as compressed gas or liquid poses significant challenges. Ammonia is considered a potentially viable solution as a hydrogen carrier due to its higher volumetric energy/hydrogen density and mature infrastructure. It can act as a medium to store and transport hydrogen. However, extracting hydrogen from ammonia currently relies on energy-intensive thermal cracking. While ammonia electrolysis, based on thermodynamics, may offer a more energy-efficient alternative to thermal cracking, catalyst-related challenges such as high overpotential and poisoning still hamper its prospects. This study explores the prospects of ammonia electrolysis through optimization of cell design and operational parameters, and the use of dynamic operation protocols for long-term operation. In specific, the work highlights the promise of the membrane electrode assembly (MEA) cell design for ammonia electrolysis: operational parameters of flow rate, electrolyte composition including ammonia concentration, pH, and cation identity are studied to evaluate their impact on MEA performance. Their optimization led to a peak current density of over 600 mA cm⁻² at RT and higher at elevated temperature. Furthermore, a pulsed electrolysis approach addresses catalyst poisoning issues, allowing the MEA cell to operate continuously for over 100 hours. These findings lay the groundwork for efficient ammonia electrolysis systems, supporting the broader adoption of ammonia as a viable hydrogen carrier to support a future and more sustainable hydrogen economy.

---

Broader context

Hydrogen is crucial to decarbonizing sectors that are difficult to electrify; yet its storage and transport remain major challenges. Ammonia is a promising hydrogen carrier because it is easier to liquefy, safer to handle, and compatible with existing infrastructure. Conventional hydrogen extraction from ammonia relies on thermal cracking, a catalytic process requiring temperatures above 500 °C, which is energy-intensive and difficult to decentralize. As a lower-temperature and potentially more efficient alternative, this study investigates ammonia electrolysis, which directly converts ammonia into nitrogen and hydrogen using electricity. The research focuses on two barriers that have limited ammonia electrolysis: severe catalyst poisoning and insufficient reaction rates and efficiency at practical current densities. Using the membrane electrode assembly cell, we systematically optimize operating parameters and achieve record current densities at room temperature. To address deactivation, we introduce pulsed electrolysis, enabling long-term operation while maintaining high faradaic and energy efficiency. These advances highlight the potential of MEA-based ammonia electrolysis as a viable alternative to thermal cracking, laying the groundwork for efficient ammonia-to-hydrogen systems powered by renewable electricity. Beyond improved performance, this approach links hydrogen release to intermittent renewable power, enables decentralized supply chains, and reduces the carbon footprint associated with high-temperature processes.

Introduction

Green hydrogen holds promise as a low-carbon energy carrier for the future, because it can be produced from water with renewable electricity from solar, hydro or wind energy. Also, when consumed, water is the only product of hydrogen oxidation. For the hydrogen economy to become a reality, challenges related to hydrogen storage and transportation need to be addressed.¹ During the liquefaction and compression process of hydrogen transportation and storage, 30–40% of the energy content is lost. Furthermore, safety issues such as flammability and hydrogen embrittlement need to be taken into account.² In this context, ammonia is proposed to substitute hydrogen as a hydrogen carrier.^2–4 In contrast to hydrogen, ammonia liquefies easily at room temperature (∼10 bar,⁵ similar to LPG; vs. ∼700 bar for H₂^6,7) or under atmospheric pressure (−33 °C,⁸ vs. −252 °C for H₂⁹). Ammonia is less flammable than hydrogen, and ammonia possesses 50% higher energy density in volume than liquefied hydrogen.^2,10 One drawback is that ammonia is highly toxic and would require appropriate safety measures for handling. Part of this can be managed using current industry practices, as it has been handled for years, and a part needs to be developed for new applications. Ammonia production (Haber–Bosch process) is well established, making use of ammonia as a hydrogen carrier even more practical. Advances in ammonia electro-synthesis may substitute for Haber–Bosch, achieving green ammonia production.³ On the user end, when converting ammonia back to hydrogen, only benign nitrogen and hydrogen are formed, while also reducing emission of CO₂ and SO₂, pollutants associated with the use of hydrocarbon-based energy carriers.¹¹

The large-scale commercial utilization of ammonia as a hydrogen carrier will still require significant technological advances to reduce cost and energy losses. While the theoretical energy requirement for ammonia decomposition is only 46 kJ mol_NH3⁻¹, current technology primarily relies on thermal catalytic ammonia decomposition at high temperatures (typically at >500 °C,^12,13 though thermodynamically feasible at 400 °C¹⁴) to produce hydrogen. This approach is energy-intensive, with an energy efficiency of only 61.0–68.5%.² Nearly half of the energy losses arise from the need to continuously heat the process.² Additionally, hydrogen purification systems are necessary, for example, to prevent poisoning of proton-exchange membrane fuel cells (PEMFCs) by unreacted ammonia traces,¹⁵ further increasing costs.

Ammonia electrolysis has been proposed as a promising alternative for thermal cracking.^2–4,16 Ammonia electrolysis is expected to be achievable at significantly lower temperature (close to room temperature) compared to thermal cracking, while holding promise to achieve a higher power-fuel-power efficiency.² During ammonia electrolysis, a process that can be driven by renewable electricity, e.g., from solar or wind, the electrolyzer decomposes ammonia to nitrogen on the anode (ammonia oxidation reaction, AOR; eqn (1)), while water is reduced to hydrogen on the cathode (hydrogen evolution reaction, HER; eqn (2)). The overall reaction (eqn (3)) only produces benign nitrogen and hydrogen.¹⁷ Notably, the theoretical minimum applied cell potential for this reaction is only 0.06 V. Thus, ammonia electrolysis is significantly less energy intense than water electrolysis, requiring a minimum of 1.23 V.¹⁸

Anode: NH₃ + 3OH⁻ → 1/2N₂ + 3H₂O + 3e⁻

E^θ = −0.77 V vs. SHE (1)

Cathode: 3H₂O + 3e⁻ → 3/2H₂ + 3OH⁻

E^θ = −0.83 V vs. SHE (2)

Overall: NH₃ → 1/2N₂ + 3/2H₂

E_cell = −0.06 V (3)

The ammonia oxidation reaction and ammonia electrolysis are gradually gaining more attention as topics of research. In particular, ammonia oxidation is of significant interest not only for hydrogen production and storage,^2–5,19,20 but also for its potential in wastewater treatment through simultaneous energy recovery and nitrogen removal.^21–26 To date, the majority of studies primarily have focused on catalyst design, with an emphasis on addressing issues of high overpotential and, most critically, catalyst poisoning.^{13,17,20,27–36} Notably, most studies to date employ H-type or batch electrochemical cells, which provide controlled testing environments but are limited in terms of providing scalability insights.

Among the various catalysts evaluated, platinum (Pt) remains the most active single-metal catalyst for AOR, as demonstrated in both experimental studies and Sabatier principle-based theoretical analyses.^{32,33,37–40} While alternative non-platinum catalysts typically require applied cell potentials exceeding 1.2 V vs. RHE,²⁰ severely limiting their practical use, Pt exhibits significantly lower overpotential and favorable activity.²⁰ State-of-the-art performance for AOR on Pt shows that the applied cell potential at peak current density exceeds 0.6 V, and the peak current density is below 150 mA cm⁻² (scan rate 5 mV s⁻¹, 1 M NH₃(aq) and 1 M KOH, at RT).^17,20,33 Poisoning of the Pt catalyst surface, however, severely limits long-term performance.^41,42 Although the desired pathway of ammonia oxidation on Pt leads to the desorption of nitrogen gas on the surface, the undesired path, which has not been well characterized, includes the reaction of ammonia and hydroxide ions and leads to the production of N* and NO_x* species. These species combine strongly with active sites, effectively blocking them. Occupation of all active sites by N*/NO_x* renders the electrode nonreactive toward ammonia oxidation.^{20,30,39,43–46}

Beyond AOR catalysts, several research efforts have been carried out on the ammonia electrolysis process.^{15,16,47–50} For example, Zhang et al. developed a hydroxide exchange membrane ammonia electrolyzer (HEMAE) featuring a zero-gap design.¹⁶ The device achieved a current density of 100 mA cm⁻² at an applied cell potential varying between 0.4 and 0.6 V using 3 M NH₃(aq) and 3 M KOH, with a 5 mg cm⁻² PtIr/C anode at 90 °C, demonstrating 317 hours of stable operation. This result represents the best performance and durability reported for ammonia electrolysis in alkaline media to date. Recently, Gecgel et al. developed a 3000 cm² bipolar ammonia electrolyzer for simultaneous hydrogen production and ammonia remediation in wastewater treatment.⁵¹ Operating at 60 °C with 0.5 M NaOH and 1250 ppm N-NH₃ (nitrogen in the form of ammonia), the system achieved an average current density of 48.3 mA cm⁻² at 0.75 V per cell using a 0.5 mg cm⁻² Pt₃Ir/C anode and maintained a faradaic efficiency of 72.6% over 260 minutes. To date, this represents the largest reported ammonia electrolyzer, operating at a cell voltage of 0.75 V, thereby confirming its scalability for practical deployment.

A recent perspective by Babar and Botte indicated that more research is needed to transition ammonia electrolysis from the laboratory scale to industrial application.²⁷ They highlight critical challenges including sluggish ammonia oxidation kinetics, catalyst degradation, and limited system durability as still hindering scalability. Overcoming these challenges will require advances in both electrocatalyst development and system-level optimization.

In summary, two challenges stand in the way of developing ammonia electrolysis as a viable process for ammonia decomposition. First, the catalyst poisoning issues significantly influence its stability and electrolyzer durability during ammonia electrolysis. This catalyst-poisoning effect has been widely observed for Pt group catalysts in the presence of ammonia under operating conditions.⁴² Second, achieving acceptable overall energy efficiency limits the maximum cell potential that can be applied for ammonia electrolysis. However, achieving economic viability of the overall process will require a reasonable hydrogen production rate (current density). To surpass the thermal cracking process in terms of energy efficiency, we calculated (see Methods, “Calculation of Applied Cell Potential Requirement”) that the applied cell potential for ammonia electrolysis cannot exceed 0.73–0.96 V, depending on the energy intensity of other parts of the ammonia synthesis and decomposition process.² Based on comparison with water electrolysis, most closely related to ammonia electrolysis, we pose that hydrogen production rates corresponding to a current density approaching 1 A cm⁻² will be necessary to achieve economic viability.⁵²

This study aims to address both challenges. First, to meet the potential and current density targets necessary to compete with thermal cracking and enable viable hydrogen extraction, we investigate how cell configuration influences performance and scalability by comparing batch, flow, and MEA cells, while also examining the factors underlying their differences. Analysis of MEA cell performance under a range of influencing factors further highlights its potential to meet target performance metrics. Second, to tackle the challenge of catalyst poisoning, we evaluate the MEA cell using electrochemical methods combined with product detection to better understand the effects of poisoning on MEA cell operation. To address the drop in performance due to poisoning in practice, we apply and optimize a pulsed potential operational method, thus achieving long-term stable MEA cell operation.

Results and discussion

Cell configurations and performance comparison

In this study, we explored three types of electrochemical cells: a batch cell, a flow cell and a membrane electrode assembly (MEA) cell (Fig. 1a–c). All anodes and cathodes are comprised of Pt nanoparticles deposited on carbon paper substrates (gas diffusion electrodes). To ensure reproducibility, all experimental measurements were repeated two to three times under the same conditions, and representative results are shown.

Fig. 1 Cell configurations for ammonia electrolysis: (a) batch cell, (b) flow cell, and (c) MEA cell. (d) Cyclic voltammetry (5 mV s⁻¹, without iR compensation) of 1 M NH₃(aq) and 1 M KOH at room temperature (RT) for these three cell configurations. (e) Nyquist plots of the potentiostatic EIS measurements of all cells in 1 M NH₃(aq) and 1 M KOH at an applied cell potential of 0.7 V. In the flow and MEA cells, solution flow rates are set to 4 mL min⁻¹.

In the three-electrode cell (batch cell; Fig. 1a and Fig. S1), all electrodes are placed in a single glass compartment without agitation. In contrast, the flowing liquid electrolyte cell (flow cell; Fig. 1b and Fig. S2) allows the solution to flow through the electrolyte chamber improving mass transport. In flow cells, both electrodes are positioned with one side exposed to a gas chamber, facilitating the use of gaseous feed as well as the removal of gaseous products. The membrane electrode assembly cell (MEA cell; Fig. 1c and Fig. S3) consists of a MEA, a solid electrolyte membrane, sandwiched between anode and cathode electrodes. The anode is exposed to a solution chamber and the cathode to a gas chamber. Compared to the flow cell, the MEA cell is easier to scale, as the presence of the membrane minimizes the need for product/feed separation.⁵³ A polymer membrane (Sustainion X37-50 Grade RT) serving as the electrolyte increases the complexity of the cell, introducing additional factors that need to be considered when seeking to optimize MEA cell performance.

To explore effective cell designs for ammonia electrolysis, CVs were recorded in a standard 1 M NH₃(aq) and 1 M KOH electrolyte at a scan rate of 5 mV s⁻¹ over an anodic potential range from 0.05 to 1.0 V (vs. RHE), as shown in Fig. 1d. All three CVs exhibit a peak for ammonia oxidation at an anode potential of 0.6 V or higher. The small feature at 0.25 V is associated with NH₃ adsorption on the Pt electrode surface.^54,55 In the MEA cell, the current fluctuation observed between 0.7 and 0.9 V, which is attributed to the oxidation of the Pt surface monolayer, superimposed with the AOR current,^42,56 which can lead to dynamic surface restructuring and thus current fluctuation. This potential region (0.7–0.9 V) coincides with the Pt surface oxidation peak observed in the blank CV without ammonia (Fig. S4a), supporting the hypothesis for the origin of the fluctuation. To confirm that ammonia oxidation indeed occurs within the cells we performed control experiments with the same electrolyte in the absence of ammonia under the same conditions (Fig. S5). Table 1 summarizes key information obtained from the CVs in the different cells: the MEA cell possesses the lowest onset potential (0.41 V), the lowest peak potential (0.63 V), and the highest peak current density (171 mA cm⁻²), with the peak current density being more than four times higher than that observed for the flow and batch cells. The minor fluctuation of the peak potential and current density in the MEA cell data is due to the inherent sensitivity of MEA-based configurations to membrane state and assembly-induced variability, which influence local transport and interfacial properties.^57–64

Table 1 Summary of electrochemical parameters obtained from cyclic voltammetry and potentiostatic electrochemical impedance spectroscopy (PEIS) of ammonia oxidation (1 M NH₃(aq) and 1 M KOH) in batch, flow, and MEA cells at room temperature. Reported values include onset and peak potential, peak current density, Ohmic resistance (R_Ohm), and charge-transfer resistance (R_ct, at 0.7 V). In the flow and MEA cells, solution flow rates are set to 4 mL min⁻¹

	Onset potential (V vs. RHE)	Peak potential (V vs. RHE)	Peak current density (mA cm^−2)	ROhm (Ohm)	Rct, anode (Ohm)	Rct, cathode (Ohm)
Batch cell	0.43 ± 0.00	0.82 ± 0.00	21.5 ± 0.8	3.5 ± 0.2	7.2 ± 0.4	4.3 ± 0.2
Flow cell	0.41 ± 0.00	0.90 ± 0.01	40.4 ± 1.8	10.5 ± 0.3	6.5 ± 0.4	0.1 ± 0.0
MEA cell	0.41 ± 0.01	0.63 ± 0.03	171 ± 6	0.2 ± 0.0	1.4 ± 0.1	0.4 ± 0.0

---

The same trends are observed when performing these CVs with iR compensation (Fig. S6a), highlighting the benefit of utilizing MEA cells (low cell resistance) for ammonia electrolysis. From the CV results, the peak potentials for ammonia oxidation (AOR) in both the batch cell and the flow cell are significantly higher than that observed in the MEA cell. This difference can be attributed primarily to differences in solution resistance, as further confirmed by electrochemical impedance spectroscopy (EIS) analysis (Table 1, vide infra). Additionally, the broader peak widths observed in the batch and flow cells compared to the MEA cell can be partially explained by diffusion limitations in the batch cell and slower anodic electron transfer in the flow cell, as confirmed by EIS (Table 1), due to the absence of direct interfacial contact between the anode and the membrane.^65–67 Even after applying iR compensation, the peak potentials in the batch and flow cells shift to lower values but remain higher than those in the MEA cell, indicating that intrinsic differences in mass transport and interfacial kinetics also contribute to the observed shift.

To identify the factors causing the outstanding performance of the MEA cell under ammonia electrolysis operational conditions, the potentiostatic electrochemical impedance spectroscopy (PEIS) of all cells in 1 M NH₃(aq) and 1 M KOH at an applied cell potential of 0.7 V was measured, over a range of 100 kHz to 0.1 Hz, with an amplitude of 10 mV. The MEA cell possesses the lowest solution resistance and charge transfer resistance (Fig. 1e). The Nyquist plots were fitted to a “two series circuit and solution resistance” model as an equivalent circuit⁶⁸ (see Methods, “Electrochemical Reactor Operation and Analysis – Electrochemical Impedance Spectroscopy”, Fig. S7). The resulting resistances, phase elements, and exponents are summarized in Table 1 and Table S1. The relative values of the decoupled resistances based on the equivalent circuit reveal that the MEA cell exhibits the lowest solution resistance (0.2 Ohm), the lowest anodic charge transfer resistance (1.4 Ohm), and, like the flow cell, a low cathodic charge transfer resistance (0.4 Ohm). This finding explains the lower overpotential and higher peak current density observed for the MEA cell. In an MEA cell the thin membrane yields a low Ohmic resistance, and the catalyst–electrolyte–membrane interface provides effective physical contact and ion transport pathways. This enables ions to efficiently reach the active sites and participate in interfacial charge transfer reactions, which contributes to a low anodic charge transfer resistance and facilitates ammonia oxidation. Furthermore, continuous flow of the anolyte minimizes mass transport limitations in MEA cells. The lower cathodic charge-transfer resistance observed in the flow cell compared to the MEA cell can be attributed to the direct contact of the electrode with the liquid electrolyte and the resulting improved wettability, rather than to the lack of sufficient water at the cathode interface in the MEA cell. Enhanced humidification in future designs may improve the interfacial wetting and thereby reduce the cathodic resistance of the MEA configuration.

The PEIS data also highlight the improved charge transfer in the flow cell relative to the batch cell. Significant iR losses become apparent in the flow cell when applying iR compensation (Fig. S6a), a finding corroborated by PEIS analysis (Table 1). The high Ohmic resistance originates from the placement of the reference electrode between the electrodes, which increases the thickness of the solution compartment and reduces the effective ionic conduction area in the middle region. Even though reducing the solution chamber thickness will decrease solution resistance in a flow cell, the observed differences in solution resistance highlight the importance of minimizing iR losses in cells to be used for electrolysis processes at scale. Overall, the MEA cell design, due to its low Ohmic and charge transfer resistances (and the resulting high current density and low iR losses), is the most suitable option for ammonia electrolysis.

MEA cell performance

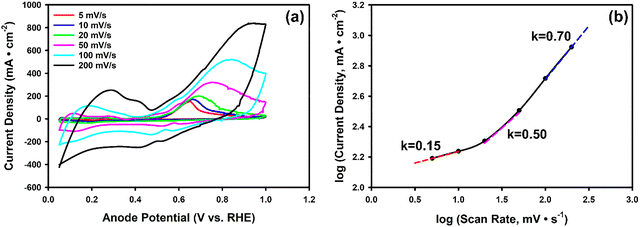
The above comparison of different cell configurations revealed that the MEA cell is the most effective option for ammonia electrolysis. Now, we first report on the electrochemical characterization of the MEA cell for ammonia electrolysis. Then we report on the systematic study of four key parameters: (i) feed solution flow rate, (ii) [NH₃], (iii) [KOH], and (iv) electrolyte composition.

Fig. 2a shows the anode CVs of AOR with 1 M NH₃(aq) and 1 M KOH for different scan rates in the MEA cell. A positive shift in the peak potential of AOR with increasing scan rate was observed in the MEA cell, consistent with previous reports.³⁸ This shift is not solely governed by intrinsic reaction kinetics but is also influenced by the surface coverage of adsorbed species such as OH/O* and N*, as well as by mass transport limitations. At high scan rates, the CV curves appeared more rounded, with a higher non-faradaic (capacitive) current. The peaks also became broader and less symmetrical, which can be attributed to kinetic limitations and the restricted development of the diffusion layer within the shortened timescale of fast scans.^65,66 To visualize the nature of the limiting phenomena, we plotted the measured peak current densities and scan rates using a log plot (Fig. 2b).³⁸ The slope in the log plot indicates the nature of the limiting process in the reaction: in the kinetic limit, k = 1; in the poisoning limit, k = 0; and in the mass transport limit, k = 0.5.^65,66,69 In our experiments, the slope increased from 0.15 to 0.7 upon increasing the scan rate. Under quasi steady-state conditions (scan rate of 5 mV s⁻¹), the slope is 0.15, indicating that catalyst poisoning is the primary limiting factor. In contrast, during transient operation (scan rate of 200 mV s⁻¹) the slope reaches 0.7, indicating that reaction kinetics has become the main limiting factor, but mass transport and poisoning limitations cannot be fully excluded.

Fig. 2 (a) Cyclic voltammetry of 1 M NH₃(aq) and 1 M KOH at RT as a function of scan rate. The flow rate is set to 4 mL min⁻¹. (b) Plot of log(current density) vs. log(scan rate) to visualize the nature of the limiting phenomena: for reference, in the kinetic limit, k = 1; in the poisoning limit, k = 0; and in the mass transport limit, k = 0.5.

Next, we performed chrono-amperometry (CA) experiments with 1 M NH₃(aq) and 1 M KOH. Fig. 3a presents CA data both at the half-peak anode potential from CV (scan rate of 5 mV s⁻¹) and at an applied cell potential of 0.7 V. The anode CA is noisier than the cell CA, possibly because the anode potential is controlled relative to the reference electrode, which may be disturbed by local bubble formation (e.g., nitrogen), leading to fluctuations in the measured anode current. The results indicate that maintaining these half-peak and cell anode potentials leads to a rapid decay of current density over time. This rapid decrease in current during continuous AOR is caused by catalyst poisoning; reaction intermediates strongly bind to the catalyst, significantly reducing performance over time.^{38,40,45,55,70–73} In addition, CA testing at half-peak anode potential (Fig. S8a) indicates that ammonia electrolysis can be performed at a measurable current density within an applied cell potential range of 0.6 to 0.8 V. Moreover, CA testing at an applied cell potential of 0.7 V shows that the anode potential falls within the region of the AOR peak in CV (Fig. S8b). These experiments demonstrate that an applied cell potential of 0.6–0.8 V corresponds to an anode potential in the AOR peak region in CV, and the reverse relationship also holds true. This relationship is also illustrated in Fig. S6b, which shows the range of applied cell potentials associated with AOR during anodic CV.

Fig. 3 (a) Chronoamperometry of 1 M NH₃(aq) and 1 M KOH at half-peak anode potential and at an applied cell potential of 0.7 V at RT. (b) Chronopotentiometry of 1 M NH₃(aq) and 1 M KOH at 80 mA cm⁻² at RT. During the first 2 minutes (region 1), ammonia oxidation to nitrogen takes place, but after that, poisoning hampers ammonia oxidation, leading to the oxygen evolution reaction and the conversion of ammonia to nitrate starting to dominate (region 2). The flow rate for all experiments is set to 4 mL min⁻¹.

A chrono-potentiometry (CP) experiment (Fig. 3b) conducted with 1 M NH₃(aq) and 1 M KOH at a current density of 80 mA cm⁻², approximately half of the peak current density observed in cyclic voltammetry (CV), reveals a leap in cell voltage after 2 minutes, indicating two distinct stages, probably indicative of two distinct electrochemical processes. To analyze the processes occurring during these two stages, we used an online gas chromatograph (GC) system to identify and quantify the products from the ammonia electrolyzer. The ionic byproducts present in the solution were evaluated using a spectroscopic approach. Scheme S1 provides a diagram illustrating our approach to analyzing the products formed at the anode and the cathode. The products observed during the two stages of the reaction are summarized in Table 2. In the first stage, lasting the initial 2 minutes, only nitrogen was detected, indicating the occurrence of ammonia oxidation to nitrogen. However, after around 3 minutes, in addition to some nitrogen, a substantial amount of oxygen and nitrate was detected. This shift suggests that poisoning inhibits ammonia oxidation, causing the oxygen evolution reaction and the conversion of ammonia to nitrate to become dominant in the second stage. We also found that during the transition from the first to the second stage, the cathode potential exhibited a noticeable fluctuation between approximately 1.5 and 3.5 minutes, indicating transient instability in the cathodic environment. A possible explanation is a gradual increase in catalyst poisoning at the anode during this time span. As intermediates accumulate, part of the anodic current is diverted to side reactions that no longer produce water in a stoichiometric ratio with electron transfer.⁷⁴ This affects local water generation and induces temporary instability in water transport across the membrane, resulting in short-term variations in water availability at the cathode for HER.^75–77 Once the anodic process becomes dominated by oxygen evolution, water transport stabilizes, and the cathode potential returns to a relatively steady state. Up to this point, CA and CP have demonstrated two different effects of poisoning on ammonia electrolysis in an MEA cell: (i) under constant voltage, the current density significantly drops over time (lower AOR rate); and (ii) under constant current, not only the voltage dramatically increases, but also side-reactions occur once certain applied cell potentials are reached: the oxygen evolution reaction and ammonia oxidation to nitrate. To avoid operating the cell under high voltage, resulting in undesired byproduct formation, it is necessary to mitigate the effects of catalyst poisoning.

Table 2 Faradaic efficiencies for different products of two stages in chronopotentiometry of 1 M NH₃(aq) and 1 M KOH at 80 mA cm⁻²

Stage	FE (N2)	FE (O2)	FE (NO2^−)	FE (NO3^−)	Overall
a Not detected or below the detection limit.
1	99.3 ± 2.8%	—^a	—	—	99.3 ± 2.8%
2	15.5 ± 0.4%	65.3 ± 0.9%	—	13.5 ± 0.0%	94.3 ± 1.0%

---

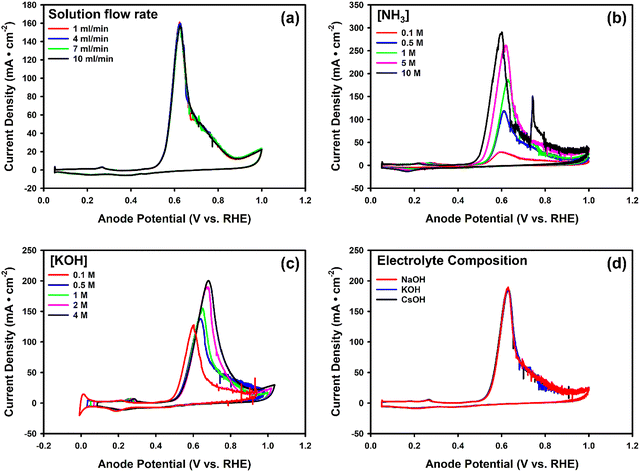
To evaluate the effect of operating conditions, we systematically studied four key parameters: (i) feed solution flow rate, (ii) [NH₃], (iii) [KOH], and (iv) electrolyte composition. Fig. 4a displays the CVs for 1 M NH₃(aq) and 1 M KOH at a scan rate of 5 mV s⁻¹, with flow rates ranging from 1 to 10 mL min⁻¹. All experiments demonstrated similar performance. This observation suggests that, within this range, mass transport in the solution chamber is not limiting. While a flow rate of 1 mL min⁻¹ is probably adequate for MEA cell experiments, we decided to use 4 mL min⁻¹ for all the following experiments.

Fig. 4 Cyclic voltammetry (5 mV s⁻¹) at RT as a function of (a) solution flow rate, (b) NH₃ concentration, (c) KOH concentration, and (d) supporting electrolyte composition. Unless otherwise varied, NH₃ concentration, KOH concentration, and flow rate are fixed at 1 M, 1 M, and 4 mL min⁻¹, respectively. Higher flow rates reduce gas bubble accumulation and lead to more stable CVs, although they may also make the peristaltic pump's mechanical pulsation more apparent, introducing minor baseline fluctuations.

Subsequently, we varied [NH₃]. Fig. 4b shows representative results of the CVs for [NH₃(aq)] ranging from 0.1 to 10 M in a 1 M KOH solution. Each experiment was repeated 2 to 3 times to ensure reproducibility. In the figure, we observed that the AOR peak potential initially shifts positively and then reverses to a negative shift as the ammonia concentration increases. As reported by Li et al., at concentrations below 1 M, the reaction is limited by reaction kinetics, diffusion of reaction products, local pH change, as well as possible surface poisoning, leading to a positive shift in peak potential with increasing concentration.³⁸ However, at higher ammonia concentrations, faster surface poisoning by strongly adsorbed species such as N* and NO* can significantly saturate the active sites, which may shift the peak potential in the negative direction.⁴² The sharp peaks (spikes) observed in Fig. 4b after 0.7 V are attributed to bubble formation, typically occurring in high-concentration ammonia solutions under high current density and low scan rates, as consistently seen in subsequent experiments. These peaks usually appear after the ammonia oxidation reaction (AOR) peak (0.5–0.7 V), but unlike the AOR peak, they do not occur at a consistent potential. Their occurrence coincides with visible gas bubbles at the outlet, further supporting bubble formation as their origin. Increasing the ammonia concentration from 1 M to 10 M leads to a significant increase in peak current density. 10 M NH₃(aq) achieved a current density of 289 ± 6 mA cm⁻². Minor fluctuations in the signal may arise from a combination of small bubble formation and mechanical disturbances caused by the peristaltic pump.

Fig. 4c presents the CVs for KOH concentrations from 0.1 to 4 M with a constant 1 M NH₃(aq) concentration. In this case, a higher concentration of KOH, corresponding to a higher pH, also resulted in an increased peak current density. At 4 M KOH, the current density reaches 202 ± 6 mA cm⁻². The beneficial effect, i.e., high current density, of higher ammonia and hydroxide ion (OH⁻) concentrations originates from both serving as reactants in the anodic ammonia oxidation reaction. We also observed that with increasing KOH concentration, the AOR peak potential shifts positively in CV. This may be caused by the following: (1) in MEA systems, local pH deviates from the bulk, causing a positive shift when converting to the RHE scale;^78,79 (2) a high concentration of hydroxide can adsorb onto Pt surfaces, occupying active sites and suppressing the adsorption of NH_x intermediates, causing higher overpotentials;^74,80 and (3) higher hydroxide concentrations facilitate the accumulation of poisoning intermediates, requiring higher overpotentials to sustain the reaction, thus shifting the peak potential.^74,81

We also studied whether the cation of the hydroxide has an effect on ammonia electrolysis. Fig. 4d illustrates the CVs for various supporting electrolyte compositions (CsOH/KOH/NaOH) while maintaining 1 M NH₃(aq) and 1 M OH⁻. All experiments demonstrated similar performance. This observation, in connection with the findings related to OH⁻ concentration, suggests that only the concentration of OH⁻ matters, while the type of cation does not appear to have an impact.

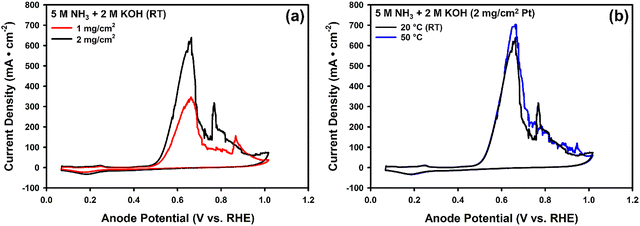
To further understand how concentrations influence current density, we also explored the possible effect of changes in solution resistance. The solution resistances are measured using PEIS at open circuit potential (OCP) (Fig. S9). Although described here as ‘solution resistance’, the measured values primarily reflect the ionic resistance of the membrane acting as a solid electrolyte under operating conditions, rather than the bulk resistance of the flowing solution. The solution resistance for various concentrations of NH₃(aq) (with 1 M KOH) is relatively constant, ranging from 0.19 to 0.22 Ohm (Fig. 5a). This stability in resistance does not account for the observed increase in current density with varying ammonia concentrations. Fig. 5a demonstrates the non-linear relationship between peak current density and ammonia concentration, showing a sharp rise in current density at low ammonia concentrations followed by a plateau as the concentration increases. At low ammonia concentrations (<1 M), the steep rise in current density suggests that the reaction rate is strongly influenced by ammonia availability, while at higher concentrations (>1 M), the curve levels off, indicating a diminishing effect on current density with increasing ammonia concentration. This plateau can be attributed to factors such as the kinetic limitations of the catalyst surface saturation, where active sites on the electrode become fully occupied by reactants or intermediates. This effect is confirmed through experiments where we increased the anode catalyst loading from 1 mg cm⁻² to 2 mg cm⁻² Pt. The electrochemically active surface area (ECSA) of the 2 mg cm⁻² Pt sample (57 m² g⁻¹) is similar to that of the 1 mg cm⁻² (55 m² g⁻¹) Pt sample (Fig. S4a). 2 mg cm⁻² Pt showed a higher peak current density of 308 ± 5 mA cm⁻² (Fig. S4b) in 1 M NH₃(aq) and 1 M KOH and 568 ± 3 mA cm⁻² (Fig. S4c) in 10 M NH₃(aq) and 1 M KOH, which is 1.7–1.9 times that of 1 mg cm⁻² Pt (171 mA cm⁻² and 289 mA cm⁻²). Moreover, an ammonia concentration of 5 M yielded 261 ± 1 mA cm⁻², only 10% less than the current density observed at 10 M (289 mA cm⁻²). The marginal rise in current density at ammonia concentrations exceeding 5 M does not justify the use of more concentrated feeds.

Fig. 5 (a) Peak current density and solution resistance at different NH₃ concentrations with 1 M KOH at RT. (b) Peak current density and solution resistance at different KOH concentrations with 1 M NH₃(aq) at RT. Error bars represent standard errors from 2 to 3 repeats.

Fig. 5b shows the relationship between solution resistance and KOH concentration (with 1 M NH₃(aq)), demonstrating a decreasing trend in solution resistance as the KOH concentration increases. At low concentrations of KOH (<1 M), the solution resistance decreases rapidly, indicating a significant increase in ionic conductivity due to the introduction of more dissociated ions into the solution. However, at higher concentrations (>1 M), the decline in resistance slows down.⁸² Fig. 5b depicts the non-linear relationship between peak current density and KOH concentration, revealing that current density increases with KOH concentration, similar to the case with NH₃, with a steep rise at lower concentrations and plateauing at higher concentrations. At low KOH concentrations (<2 M), the current density increases rapidly due to significant improvement in either or both ionic conductivity and the kinetics. Beyond 2 M, the current density levels off, indicating that reaction kinetics rather than solution conductivity becomes the primary constraint. This plateau can also be attributed to the saturation of the catalyst surface, as increasing the anode catalyst loading from 1 mg cm⁻² to 2 mg cm⁻² Pt resulted in a higher peak current density of 351 ± 3 mA cm⁻² (Fig. S4d) in 1 M NH₃(aq) and 4 M KOH, increasing by 1.8 times (compared to 202 mA cm⁻² of 1 mg cm⁻² Pt). In addition, a KOH concentration of 2 M yields a current density of 189 ± 1 mA cm⁻², only 5% less than the current density at 4 M (202 mA cm⁻²). Increases in KOH concentration beyond 4 M provide minimal additional benefit. Additionally, since the measurements were not performed in the lower concentration range (<0.1 M, not of interest in this study), the reaction order with respect to [NH₃] or [KOH] may not be conclusively determined from the current data.³⁸

Both NH₃(aq) and KOH concentrations have been shown to influence current density positively. Individually, 5 M NH₃(aq) and 2 M KOH each resulted in a greater increase in current density compared to 1 M NH₃(aq) and 1 M KOH. To evaluate whether simultaneously increasing both concentrations would result in a greater enhancement, the MEA cell was tested in 5 M NH₃(aq) and 2 M KOH. The resulting peak current density is 352 ± 4 mA cm⁻² (Fig. 6a). Furthermore, we increased the anode catalyst loading from 1 mg cm⁻² to 2 mg cm⁻² and observed a peak current density of 633 ± 2 mA cm⁻² (1.8 times) at less than 0.7 V (Fig. 6a), marking the highest reported value at room temperature using Pt as the catalyst. Increasing the temperature from room temperature (20 °C) to 50 °C – below the boiling point of 5 M NH₃ solution (∼70 °C^83–85) – can further enhance the reaction kinetics, leading to a higher peak current density of 702 ± 4 mA cm⁻² (Fig. 6b). This finding demonstrates a synergistic effect between ammonia and hydroxide concentrations and highlights additional opportunities to optimize reaction conditions.

Fig. 6 (a) Cyclic voltammetry (5 mV s⁻¹) of 5 M NH₃(aq) and 2 M KOH at RT using 1 mg cm⁻² or 2 mg cm⁻² Pt. (b) Cyclic voltammetry (5 mV s⁻¹) of 5 M NH₃(aq) and 2 M KOH at room temperature (20 °C) and 50 °C using 2 mg cm⁻² Pt. The flow rate is set to 4 mL min⁻¹.

Overcoming poisoning: pulsed electrolysis

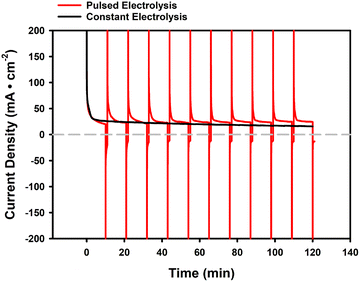
Poisoning during ammonia oxidation is primarily caused by strongly adsorbed overoxidized nitrogen species, such as N* or NO*, that block active catalytic sites.^20,43 Inspired by prior work,¹⁰ we presumed that a pulsed electrolysis approach could mitigate some of the observed catalyst poisoning issues, by electrochemically removing adsorbed species that accumulate on the catalyst surface during sustained operation.⁴² We tested this presumption in the MEA cell by applying an applied cell potential pulse of −0.7 V to a solution of 1 M NH₃(aq) and 1 M KOH for 1 minute after every 10 minutes (10 cycles) at an applied cell potential of +0.7 V. Compared to holding the applied cell potential at +0.7 V for 120 minutes, with an average current density of 21.1 mA cm⁻², applying a pulse of opposite potential allows the current to return to a high current density close to the initial level (Fig. 7), resulting in a higher average current density (including the regeneration time) of 26.7 mA cm⁻². This confirms the hypothesis that the application of periodic pulses allows for recovery of ammonia oxidation performance in the MEA cell. XPS analysis (Fig. S10) of MEA anodes under three operating conditions—before ammonia oxidation (pre-AOR), after constant electrolysis, and after pulsed electrolysis—revealed a clear trend associated with Pt poisoning and regeneration. The pre-AOR sample showed no detectable N 1s signal, while a distinct nitrogen peak appeared after constant electrolysis, indicating the accumulation of N-containing poisoning species.⁸⁶ After pulsed electrolysis, the N signal nearly disappeared, confirming the effective removal of nitrogen-bound species and the alleviation of Pt poisoning under dynamic operation.

Fig. 7 Chronoamperometric profiles of pulsed (red) and constant (black) electrolysis of a 1 M NH₃ and 1 M KOH solution in an MEA cell at RT. Compared to electrolysis at a constant potential of +0.7 V, pulsed electrolysis was performed by applying a ‘pulse’ of −0.7 V for 1 min after every 10 min at +0.7 V. The flow rate is set to 4 mL min⁻¹.

Next, we conducted long-term testing using a slightly modified pulsed electrolysis method. Instead of applying a pulse after a specific time of operation (fixed ‘working’ phase), we set a threshold for the current density. In specific, we maintained the applied cell potential at +0.7 V (the same for all following instances) during the working phase and applied a regenerating pulse of −0.7 V (the same for all following instances) for 1 minute once the current density dropped to the threshold of 20 mA cm⁻². Setting the threshold is intended to prevent the current density from dropping to a level that is impractical for application.

We also conducted this and the subsequent experiments using 10 M NH₃(aq) and 1 M KOH by recirculating the solution (a total of 1 liter) to simulate possible industrial operation conditions. A high NH₃ concentration not only enables higher current density, as discussed in the previous section, but it also more closely resembles a practical operation condition, and ensures a more stable concentration over time, which is beneficial for continuously recirculating operation. Moreover, recirculation of the solution would facilitate the observation of possible minor byproducts, as they would accumulate.

In practice, the current density threshold inducing the regeneration pulse was reached approximately every 60 minutes. We ran this experiment for 100 cycles. The entire process exceeded 100 hours, demonstrating the durability of the cell using the pulsed electrolysis method. Fig. 8a illustrates the application of potential over time for the middle five working/regeneration cycles (48–52 pulses). Fig. 8b presents the measured current density over time for the middle five working/regeneration cycles (48–52 pulses). Fig. S11a indicates that the duration of the working phase increases with the number of cycles during the first 20 cycles, a direct result of the gradual conditioning of the MEA, but the working phase decreases afterward, presumably due to persistent poisoning effects.

Fig. 8 The pulsed operation method applied to a 10 M NH₃(aq) and 1 M KOH solution (flow rate: 4 mL min⁻¹, RT) (working phase: hold at +0.7 V until a threshold of 20 mA cm⁻² is reached; regeneration phase: hold at −0.7 V for 1 minute). (a) Repeated application of the pulse sequence over time for cycles 48–52 out of a total of 100 pulses and (b) the measured current density over time for the same set of working/regeneration cycles.

During the working phase at a cell voltage of +0.7 V, the average anode potential was 0.63 V with an average current density of 34.7 mA cm⁻² (Table 3). Nitrogen gas was the only product detected at the anode, with a faradaic efficiency close to 100% (99.8 ± 1.6%). Meanwhile, oxygen and other nitrogen species (NO₂⁻ and NO₃⁻) were below the detection limit (0.23 mg L⁻¹ NO₃-N and 0.015 mg L⁻¹ NO₂-N). On the cathode side, hydrogen was the only product observed, also showing a faradaic efficiency near 100% (101.5 ± 1.4%), at an average hydrogen production rate of 1.31 × 10⁻³ g cm⁻² h⁻¹ (see Methods, “Product Analysis and Calculation of Faradaic Efficiency – Calculation of Hydrogen Production Rate”). Thus, the ratio of H₂ to N₂ is 3.05 ± 0.06, as expected. These findings confirm that ammonia oxidation to nitrogen occurred exclusively in the MEA cell, with minimal or no production of NO_x, oxygen, or other byproducts. The total charge consumed during the working phase (1.28 × 10⁴ C cm⁻²) far exceeds the total charge used for regeneration (−5.46 × 10² C cm⁻²) (Table 3), demonstrating that the majority of energy (96%) is directed towards ammonia electrolysis rather than the regeneration process. During the process, ammonia crossover from the anode side to the cathode side occurs at a rate of 0.042 mmol min⁻¹ (detected by GC), which accounts for the loss of only 0.26 mol (compared to 10 mol) of ammonia over the process.

Table 3 Average potentials, current densities, total time, and charge per unit area of working and regeneration phases in the long-term testing of 10 M NH₃(aq) and 1 M KOH with pulsed electrolysis at ±0.7 V (1 min regeneration, 20 mA cm⁻² threshold)

	Average anode potential (V vs. RHE)	Average cathode potential (V vs. RHE)	Average current density (mA cm^−2)	Total time (h)	Total charge per unit area (C cm^−2)
Working	0.63	−0.07	34.7	102.8	1.28 × 10^4
Regeneration	−0.09	0.61	−91.0	1.7	−5.46 × 10^2

---

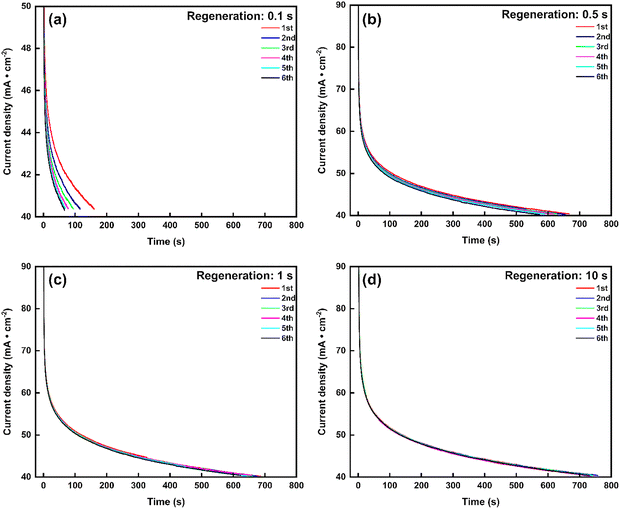
To minimize energy loss during the regeneration phase and to increase the average current density of the overall process, we (i) examined whether we could reduce the regeneration time and (ii) explored the effects of increasing the threshold to 40 mA cm⁻² or 60 mA cm⁻². In the first set of experiments, we adjusted the regeneration time, varying it from 1 minute to 0.1 seconds (with a threshold of 40 mA cm⁻² during the working phase) (partial in Fig. 9, complete in Fig. S12). Each experiment was conducted over six cycles with 10 M NH₃(aq) and 1 M KOH to assess whether the successive cycles overlap or not. Overlapping cycles would indicate a sufficiently long regeneration time. As shown in Fig. 9 and Fig. S12, when the regeneration time exceeds 1 second, the catalyst is effectively reactivated, performing nearly as well as in its initial state. In addition, longer regeneration times (>1 s) slightly prolong the period before the current density reaches the threshold, indicating better recovery of active sites and enhanced electrolyzer durability. In contrast, a regeneration time of 0.5 s leads to a noticeable decline in working time (before reaching the threshold) across cycles. Further reducing the regeneration time to 0.1 s causes the working time to drop significantly to less than 200 s, with a rapid decline evident in subsequent cycles. These findings suggest that a regeneration time exceeding 1 s is necessary for effective catalyst reactivation in pulsed electrolysis operation. Table S2 compares the average current density and charge ratio (working charge over total charge) over six cycles, highlighting that a regeneration time of less than 5 seconds ensures that more than 98% of the charge and energy are utilized for the working phase. We conclude that for the experimental conditions tested, a regeneration time of 1 s guarantees both catalyst reactivation and energy efficiency.

Fig. 9 Chronoamperometric profiles of pulsed electrolysis with varying regeneration durations: (a) 0.1 s, (b) 0.5 s, (c) 1 s, and (d) 10 s. Each condition was tested over six cycles in 10 M NH₃(aq) and 1 M KOH at RT, with a threshold current density of 40 mA cm⁻² during the working phase. The flow rate is set to 4 mL min⁻¹. Representative results are presented; the full dataset is shown in Fig. S12.

In the second set of experiments, we focused on increasing the current density threshold during the working phase, aiming to enhance the average current density. In the first set of experiments, we had already confirmed that with a threshold of 40 mA cm⁻², the average current density was higher compared to a threshold of 20 mA cm⁻². Ultimately, we raised the threshold for the working phase to 60 mA cm⁻² (at an applied cell potential of +0.7 V) and set the regeneration time to 1 second (at an applied cell potential of −0.7 V). Using the pulsing operation method, we conducted long-term testing for 100 cycles with a 10 M NH₃(aq) and 1 M KOH solution. The regeneration pulse occurred approximately every 10 minutes. Fig. 10a illustrates the application of applied cell potential and the measured current density over time (48–52 pulses). Fig. S11b indicates the duration of the working phase. As in our prior experiments, nitrogen and hydrogen were the only products on each side with faradaic efficiency close to 100% (N₂: 98.7 ± 1.9%, H₂: 97.6 ± 1.6%), indicating the occurrence of ammonia electrolysis exclusively, yielding nitrogen and hydrogen (H₂:N₂ = 2.97 ± 0.08). During the working phase, the average current density is 68.2 mA cm⁻², accounting for 99.7% of the total 10.6 hours, while only 0.3% was allocated to the regeneration phase (Table S3). This average current density corresponds to a hydrogen production rate of 2.57 × 10⁻³ g cm⁻² h⁻¹. Most of the charge and energy (98.3%) was allocated to the working phase of ammonia electrolysis rather than the regeneration process, resulting in an overall energy efficiency of 68.5%, which is comparable to the energy efficiency reported for the thermal cracking process (61.0–68.5%).² From the EIS results at 0.7 V (Table 1) and the observed anode potential during pulsed electrolysis (Table 3), we infer that the major energy losses originate from anode resistance-related overpotentials, providing a clear direction for further efficiency improvement through enhanced anode design and catalytic activity. This ammonia electrolysis performance at +0.7 V that we report here, with room for further optimization, demonstrates the promise of this method to replace the thermal cracking process in converting ammonia to hydrogen. Compared to the MEA cell developed by Zhang et al., which operated at 90 °C with a high anode loading of 5 mg cm⁻² PtIr/C and achieved an average current density of 100 mA cm⁻²,¹⁶ our MEA system reaches a comparable current density of 68 mA cm⁻² under significantly milder conditions—room temperature and a lower catalyst loading of 1 mg cm⁻² Pt. While there remains room for catalyst optimization, these results highlight the efficiency of our design and operational conditions. Meanwhile, Gecgel et al. demonstrated the scalability of a 3000 cm² bipolar ammonia electrolyzer for wastewater treatment, although their device operated at highly diluted ammonia concentrations representative of wastewater, with a faradaic efficiency of ∼70% over 260 minutes.⁵¹ By comparison, our MEA system sustains a higher current density over a much longer duration (more than 10 hours) and employs ammonia concentrations representative of industrial hydrogen production, achieving nearly 100% faradaic efficiency during the working phase.

Fig. 10 (a) The pulsed potential method in 10 M NH₃(aq) and 1 M KOH (flow rate: 4 mL min⁻¹, RT) (working phase: hold at +0.7 V until the threshold of 60 mA cm⁻² is reached; regeneration phase: hold at −0.7 V for 1 s): measurement of current density over time (48–52 pulses). (b) Simulation of the achievable average current density and working charge ratio over 100 cycles as a function of current density threshold.

To establish the optimum current density threshold during the working phase, we conducted simulations of 100 cycles at various current density thresholds, based on the results of the previous pulsing experiment (working potential of +0.7 V with varied thresholds and regeneration potential of −0.7 V for 1 s). We hypothesized that the regeneration phase would remain unchanged while varying the working thresholds above 60 mA cm⁻². We then calculated the average current density and the working charge ratio, defined as the proportion of charge applied during working phases as a fraction of the total charge applied, for each condition over 100 pulse cycles. Although higher thresholds generally result in greater average current densities, they also reduce the working charge ratio (Fig. 10b). The plot of these simulation results shows that the working charge ratio decreases with increasing threshold. This simulation data now can provide guidance for achieving certain performance levels in terms of working charge ratio: by following the blue and red arrows in Fig. 10b, one can see that to maintain a working charge ratio above 90% (meaning that over 90% of the charge is used during working phases) a threshold at or just below 75 mA cm⁻² (average current density of 90 mA cm⁻²) is required. To resemble a typical 10 MW water electrolyzer, consuming approximately 50 kWh of energy to produce 1 kg of hydrogen,⁸⁷ the MEA-based ammonia electrolyzer with an average of 90 mA cm⁻² (achievable performance based on data in Fig. 10b) under pulsed operation would require a total electrode area of approximately 5900 m². This area could be realized by configuring 60 stacks, each containing 200 cells with an active area of 0.49 m² per cell. This scaling analysis serves as a feasibility illustration, and further improvements in catalyst activity and operating conditions would proportionally reduce the required electrode area and stack number.

Conclusions

This study compared three cell designs for ammonia electrolysis, identifying the MEA cell as an optimal cell configuration due to its reduced Ohmic/charge transfer resistance and enhanced mass transport. However, the performance of MEA cells for ammonia electrolysis remains constrained by sluggish kinetics and catalyst poisoning - two central challenges to the viability of ammonia electrolysis. CA and CP experiments confirmed the occurrence of poisoning: under constant cell voltage operation, the current density drops over time, while constant current operation results in a leap in cell voltage and byproduct formation.

To address these challenges, two strategies were employed to improve MEA cell performance. First, parameter optimization demonstrated that solution flow rate (1–10 mL min⁻¹) and hydroxide cation type (Na⁺/K⁺/Cs⁺) had negligible impacts, while higher NH₃(aq) and KOH concentrations boosted the current density for ammonia oxidation. A peak current density exceeding 600 mA cm⁻² was achieved with 5 M NH₃(aq) and 2 M KOH—the highest reported value for Pt-catalyzed ammonia electrolysis at room temperature, even higher than current densities reported previously when operating at 60 °C (at less than 0.7 V vs. RHE).⁴¹ Second, we demonstrated that a pulsed potential operation method mitigated poisoning, enabling stable operation of the MEA electrolysis cell over more than 100 hours. Pulse optimization (a minimal regeneration time of 1 second at −0.7 V; setting a current density of 60 mA cm⁻² as the threshold to induce the regeneration pulse, when operating the cell at a working potential of +0.7 V) achieves an average current density of 68 mA cm⁻². Indeed, catalyst activity is restored upon applying a negative pulse for just 1 second. This set of operation conditions and the resulting average current density correspond to high efficiency in charge utilization (>98%) during ammonia electrolysis, while achieving an overall energy efficiency of 68.5%, which is comparable to the energy efficiency reported for the thermal cracking process (61.0–68.5%).² This approach exclusively produced N₂ and H₂ during the working phases (N₂-FE: 99 ± 2%, H₂-FE: 98 ± 2%) at the expected ratio of 1 to 3. These results suggest that both major barriers to ammonia electrolysis, insufficient performance and catalyst poisoning, can be effectively mitigated through appropriate cell design and operation. Thus, MEA-based ammonia electrolysis may hold promise to be further developed as a possible alternative to conventional thermal cracking. Furthermore, the pulsed ammonia electrolysis process occurs at ambient temperature with electricity as the sole energy input. This differs from thermal ammonia cracking, which operates at higher temperatures and needs continuous thermal energy. In contrast, the low-temperature operation of ammonia electrolysis implies benefits in system integration and decentralized deployment.

The scalability of this system is inherently favorable because the MEA configuration can be directly adapted to stack designs similar to commercial water electrolyzers. The optimized operating condition identified in this study (5 M NH₃ and 2 M KOH at RT) is mild and industrially practical, and the demonstrated dynamic operation strategy can be readily implemented in larger systems through electronic control.

It is worth emphasizing that the performance achieved in this work, exceeding 600 mA cm⁻² at room temperature, is among the highest reported for MEA-based ammonia electrolysis employing platinum catalysts at moderate loadings (1–2 mg cm⁻²).^20,33 Although comparable current densities have been reported using greater catalyst loadings or multi-metal alloys at elevated temperatures, the present study demonstrates that similar or even superior performance and long-term durability can be realized using moderate loading of only monometallic Pt through optimized reactor design and dynamic operation at even room temperature, which is particularly desirable for practical applications. Furthermore, this work establishes a systematic methodological framework that integrates reactor configuration, parameter optimization, and dynamic control strategies to simultaneously achieve high current density, extended durability, and high energy efficiency. This framework also implies that, by applying the same design principles, even higher performance and durability could be achieved when employing more poison-resistant catalysts under higher temperature and loading conditions. This integrated approach offers not only a practical performance advance but also a generalizable pathway for the rational design of next-generation ammonia electrolysis systems.

Insights from this work, as well as from prior work, suggest several directions for future study. First, future work could investigate whether the use of other AOR catalysts with lower overpotentials and/or greater resistance to poisoning,^{28,32–36,73,88–90} such as PtIr, PtRh alloys⁹¹ and Pt/TiO₂⁸⁶ reported in recent studies, when applied in MEA cells operated with the here-introduced pulsed electrolysis method, could further improve performance, while reducing the total precious metal content. Second, a more systematic approach, such as design of experiments (DOE), response surface methodology (RSM), or AI-guided optimization, could be employed to further refine the operational parameters, identify optimal concentration ratios, pulsing potentials, and working current thresholds, and ultimately mitigate poisoning effects and prolong stable operation. Third, evaluating the feasibility of using ammonia gas, whether anhydrous or humidified, as a direct feedstock in MEA cells might hold promise. This strategy would remove the need to dissolve ammonia in water prior to electrolysis, simplifying the overall process. Fourth, system-level aspects should be considered for further performance improvements. These include addressing ammonia crossover from the anode to the cathode, as it compromises hydrogen purity and may poison downstream fuel cells; studying long-term operation at varying (elevated) temperatures to gain insight into durability and associated degradation mechanisms; and scaling single MEA cells to large-area, multi-cell stacks.

All these aspects will be of importance to transition ammonia electrolysis concepts for deployment at large scale. Progress in these research areas will pave the way for the broader adoption of green ammonia as a renewable energy carrier, speeding up its role in the transition to sustainable energy systems.

Experimental

Preparation of electrolytes

All electrolyte solutions of ammonia and KOH were prepared by dissolving KOH (85%, Sigma Aldrich) in Barnstead E-pure water (>18 MΩ cm) and mixing with ammonium hydroxide (28–30% NH₃ in water, 14.8 M, VMR). In the electrolyte composition analysis, we replaced KOH with NaOH (97%, Sigma Aldrich) and CsOH (99.5%, Sigma Aldrich).

Preparation of electrodes

The anode and cathode gas diffusion electrodes (GDEs) (Fig. S13) were prepared by spraying the catalyst ink on carbon paper using an ultrasonic coating system (ExactaCoat, Sono-Tek). Gas diffusion electrodes consist of two main layers: a catalyst layer, where reactions occur on the catalyst's surface, and a gas diffusion layer (carbon paper), which allows gas and liquid to diffuse from one side to the other. The carbon paper without the microporous layer (MPL) (AvCarb, MGL280, Fuel Cell Store) was used for the anodes of the batch cell, the cathode of the batch cell, and the anode of the MEA cell for better transportation of solution. The carbon paper with a microporous layer (AvCarb, GDS5130, Fuel Cell Store) was used for the anode of the flow cell, the cathode of the flow cell, and the cathode of the MEA cell for better water management and prevention of flooding issues.⁶¹ The two carbon paper substrates are very similar in all key physical and electrical properties, including thickness, porosity, and conductivity,^92,93 except for the presence or absence of an MPL. However, for electrodes operating without an MPL, the electrolyte tended to penetrate through the carbon paper from one side to the other, resulting in flooding. The MPL effectively suppresses such crossover due to its hydrophobicity and fine-pore structure, which increases capillary pressure and acts as a physical barrier against liquid penetration.⁹⁴ Therefore, the selection of MPL-coated or non-MPL carbon paper varied slightly among cell configurations to ensure stable and optimal operation. The observed operational differences should primarily originate from wettability and interfacial contact, rather than from differences in conductivity or bulk physical properties of the carbon paper substrates.

We used commercially available Pt NPs (high surface area, 5–8 nm, Fuel Cell Store) as catalysts for both the anode and cathode, and the target catalyst loading was 1 mg cm⁻². Catalyst inks were prepared from a 1 : 1 mixture of isopropyl alcohol (IPA) and DI water with Sustainion® XA-9 (5% in ethanol, Dioxide Materials) as the binder and the catalyst powder. The catalyst-to-binder weight ratio was 10 : 1. The inks were sonicated in a water bath for one hour to ensure uniform dispersion, and then sprayed onto respective carbon papers with a geometric area of 8 × 8 cm², which were then cut into shapes according to their use for different cells. The actual catalyst loading was determined by weighing the carbon paper before and after deposition. The final catalyst loadings were all 1 ± 0.05 mg cm⁻² unless specified otherwise.

Assembly of cells

Batch cell. GDEs are clipped by PTFE replaceable titanium electrode holders (Dek Research), with a 1 cm² active area immersed in water alongside the reference electrode, all placed in a single 50 mL glass bottle without any rotation (Fig. S1).

Flow cell. The home-built flow cell (1 cm² active area) was a modified version of a gas diffusion flow cell (Dek Research). The anode and cathode electrodes were positioned on two purpose-built Ti plates as current collectors, sandwiching the solution chamber (1 cm thick) with the inserted reference electrode. Both the anode and cathode gas chambers were placed next to the Ti plates to allow the gas products to escape (Fig. S2). All chambers in the flow cell and also in the following MEA cell were made of PEEK to prevent ammonia-induced corrosion and sealed by PEEK end plates. PTFE and silicone gaskets were used to seal the cell.

MEA cell. The home-built MEA cell (1 cm² active area) was also modified based on a gas diffusion flow cell (Dek Research). It was assembled by placing the anode and cathode catalyst electrodes prepared above on Ti plates. A Sustainion® X37-50 Grade RT (Dioxide Materials) anion exchange membrane (soaked in 1 M KOH for 24 h) was placed between the anode and cathode electrodes to form the MEA. The MEA was situated between the anode solution chamber (1 cm thick) and the cathode gas chamber. End plates sealed all chambers (Fig. S3).

Electrochemical reactor operation and analysis

All electrochemical experiments were performed under room temperature (20 °C) and atmosphere pressure. All GDEs for experiments were 1 cm². A peristaltic pump (BG600LC-S, Chonry) was used to pump the electrolyte through the solution chamber for both flow and MEA cells at a desired flow rate of 4 mL min⁻¹, except for the study on the effect of solution flow rate. Flow controllers (MC-100SCCM, Alicat Scientific) are used in all the cells to control inert gas (Ar/He) for various purposes: (1) batch cell: argon flows over the top of the glass bottle to prevent air from entering; (2) flow cell: argon and helium flow separately on the cathode and anode gas chambers to prevent air from entering; and (3) MEA cell: argon flows through the water trap for the MEA-GC system to carry out the anode gas product for analysis, while helium flows through the cathode gas chamber to blow out the cathode gas product for analysis, also serving to prevent air from entering the gas chamber. Ammonia electrolysis experiments, including CV, EIS, CA, CP, and pulsed electrolysis, were carried out by using a potentiostat (Interface 5000E, Gamry). A Hg/HgO electrode (filled with 1 M KOH) was used as the reference. All electrode potentials were converted to the reversible hydrogen electrode (RHE) by using the Nernst equation: E (vs. RHE) = E (vs. Hg|HgO) + 0.098 V + 0.059 V × pH. During testing, current densities and potentials exhibited minor fluctuations due to gas bubble evolution (spikes) and the periodic motion of the peristaltic pump (within ±3% of the peak current density), particularly at high current densities with concentrated NH₃(aq). However, these fluctuations did not influence the overall trends or alter the positions and magnitudes of the peaks. Therefore, the data presented are considered reliable and representative, and the minor fluctuations do not influence the interpretation of electrochemical behavior.

Cyclic voltammetry. Unless specified otherwise, cyclic voltammetry (CV) was recorded in a 1 M NH₃(aq) and 1 M KOH electrolyte at a scan rate of 5 mV s⁻¹ over an anodic potential range from 0.05 to 1.0 V (vs. RHE). In the flow and MEA cells, the solution flow rates are set to 4 mL min⁻¹. In this study, onset potentials are defined as the crossover potential that occurs after the ammonia adsorption peak (0.2–0.4 V) during the anodic sweeps of the CVs for both the experimental group (KOH only) and the control group (NH₃(aq) and KOH). Applied cell potentials during the CVs of the anode are recorded using a Digital Multimeter (365B, Hantek). Where necessary, iR compensation was performed with the software associated with the potentiostat (Gamry Echem Analyst) using the Post-Run iR correction method. Anode potentials were adjusted based on the solution resistance between the anode and reference electrode, measured using potentiostatic EIS (PEIS) at open circuit potential (OCP) (batch cell: 1.6 Ohm, flow cell: 5.0 Ohm, MEA cell: 0.1 Ohm).

Electrochemical impedance spectroscopy. EIS was performed using the potentiostat's EIS module. The spectra were recorded in potentiostatic mode (PEIS) at OCP and at an applied cell potential of 0.7 V. Ten points per decade were scanned in the range from 10 kHz to 0.1 Hz. A single sine wave with an amplitude of 10 mV RMS for PEIS was used for the sweep.

The Nyquist plots obtained in this study were fitted to a “two series circuits and solution resistance” model as an equivalent circuit⁶⁸ using the Gamry Echem Analyst module. The model is shown in Fig. S7. R.E. stands for the reference electrode, W.E. stands for the working electrode, R1 represents the solution resistance (resistance of the membrane), R2 is the anodic charge transfer resistance, R3 is the cathodic charge transfer resistance, Yo4 is a constant phase element (to model the non-ideal behavior of the EDL) for the anode side, and a5 is the exponent associated with Yo4. Similarly, Yo6 is a constant phase element for the cathode side and a7 is the exponent associated with Yo6.

Chronoamperometry and chronopotentiometry. Chronoamperometry of the MEA cell was measured with 1 M NH₃(aq) and 1 M KOH, flowing at 4 mL min⁻¹, at half-peak anode potential in the CV and at an applied cell potential of 0.7 V. Chronopotentiometry of the MEA cell was measured with 1 M NH₃ and 1 M KOH, flowing at 4 mL min⁻¹ at 80 mA cm⁻², which is around the half-peak current density in the CV. During the chronoamperometry of the anode, applied cell potentials are recorded using a digital multimeter. In the chronoamperometry of the cell and chronopotentiometry, we used a potentiostat to measure the potentials of both the anode and cathode simultaneously.

Pulsed electrolysis. The cycling series includes both the working and regeneration phases. During the working phase, we maintained the applied cell potential at +0.7 V. During the regeneration phase, we applied a regenerating pulse of −0.7 V for a specific duration once the current density dropped to a certain threshold. Product analysis was conducted throughout the working phase. While maintaining the applied cell potential, the potentiostat measured both the current density and the potentials of both electrodes if necessary at the same time.

Characterization of materials

Scanning electron microscopy (SEM) was performed on untreated and catalyst-coated carbon papers using a Thermo Fisher Axia ChemiSEM and a JEOL JCM-7000 NeoScope benchtop SEM. For the XPS analysis, the operation for the electrode remained the same as in the standard test, while the binder was replaced with Nafion D521 (5 wt%, Ion Power) and the membrane was substituted with alkaline-treated Nafion 212 (Ion Power) to avoid interference from nitrogen signals originating from the binder and membrane. After electrolysis, the catalyst surface was rinsed with DI water and dried under Ar flow. The sample was then transferred into the XPS vacuum chamber. High-resolution spectra were collected in the N 1s region and fitted using CasaXPS v2.3.26.

Product analysis and calculation of faradaic efficiency

Products from the MEA cell were analyzed by using an online gas chromatograph (8890 GC System, Agilent Technologies) equipped with a thermal conductivity detector, using helium (for O₂/N₂ detection) and argon (for H₂ detection) as the carrier gas. During operation, a water trap was utilized to separate the gas produced on the anode side from the solution. The GC subsequently analyzed the gas products on each side using packed columns (Molesieve 5Å, 80/100 mesh, 6′ length, 1/8″ diameter, Agilent). Crossover ammonia was also analyzed by GC using a capillary column (CP-Volamine, fused silica, 60 m length, 0.32 mm ID, Agilent). The ionic byproducts in the solution, including nitrate and nitrite, were analyzed using a Nitrate and Nitrite TNTplus Vial Test Kit (detection limit: 0.23 mg L⁻¹ NO₃-N and 0.015 mg L⁻¹ NO₂-N, Hach) with a commercial spectrophotometer (DR3900, Hach). A schematic diagram showing the simultaneous MEA-GC analysis is shown in Scheme S1.

Calculation of gas product faradaic efficiency

The gas product ratio in the carrier gas was measured using gas chromatography (GC). The carrier gas flow rates were controlled by using mass flow controllers. The number of electrons transferred per H₂ molecule is 2, and per N₂ molecule is 6. Additionally, the current was calculated by averaging the working phase during pulsed electrolysis.

Calculation of ionic product faradaic efficiency

The concentration of ions in the solution was measured using the Vial Test Kit in the commercial spectrophotometer. The solution flow rate was controlled by using the peristaltic pump (BG600LC-S, Chonry). The number of electrons transferred per NO₂⁻ ion is 6, and per NO₃⁻ ion is 8. Additionally, the current was calculated by averaging the working phase during pulsed electrolysis.

Calculation of hydrogen production rate

The hydrogen ratio in the carrier gas was measured using gas chromatography (GC). The carrier gas flow rates were controlled by using mass flow controllers. M_H2 is the molar mass of H₂, which is 2 g mol⁻¹.

Calculation of ammonia crossover rate

The ammonia ratio in the carrier gas was measured using gas chromatography (GC). The carrier gas flow rates were controlled by using mass flow controllers.

Table S4 provides the raw data, specifically GC and spectrophotometer product data for the anode and the cathode channels for different runs.

Calculation of applied cell potential requirement

The current status of the energy efficiency of the NH₃-to-H₂ conversion process (%) based on the thermal cracking method is 61.0–68.5%.² To compete with thermal cracking as a more efficient cracking technique, ammonia electrolysis must achieve at least the same level of energy efficiency. The ammonia electrolytic cell efficiency was expressed using the following equation:
where ΔH_H2 is the lower heating value of H₂ (242.7 kJ mol⁻¹), ΔH_NH3 is the lower heating value of NH₃ (320.1 kJ mol⁻¹), F is Faraday's constant (26.8 Ah mol⁻¹) and ΔE is the applied cell potential.¹² Assume ε to be 61.0–68.5%, ΔE is calculated as 0.730–0.956 V.

Author contributions

H. L. performed most of the experiments, including cell assembly, electrochemical testing, product detection, and data analysis. C. Y. S. assisted with cell design development and the setup of the gas chromatography system. A. P. contributed to data interpretation, while T. C. assisted with data collection and analysis. J. K. G., M. A. R., Y. J. S., and K. Z. provided industrial insights, resources, and technical advice. A. A. G. contributed to the mechanistic understanding and supervised parts of the electrochemical study. P. J. A. K. and A. A. G. conceived the project and supervised the overall research direction. All authors contributed to the writing. H. L. and P. J. A. K. were the primary authors of the paper and were chiefly responsible for experimental design, data analysis, and manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: details on cell configurations (Fig. S1–S3), electrochemical methods and measurements (Fig. S4–S9), XPS Data (Fig, S10), pulsed electrolysis data (Fig. S11 and S12), SEM data (Fig. S13), schematic diagram for product detection (Scheme S1), EIS data (Table S1), pulsed electrolysis data (Tables S2 and S3), and summary of faradaic efficiencies (Table S4). See DOI: https://doi.org/10.1039/d5ey00324e.

Acknowledgements

The authors gratefully acknowledge the Energy & Biosciences Institute-Shell research program for funding this work. The authors acknowledge the School of Chemical Sciences Machine Shop for manufacturing cell parts. SEM and XPS analysis of electrodes was carried out in the Materials Research Laboratory Central Research Facilities, University of Illinois. The authors also acknowledge Minjun Choi, Sukhwa Hong, and Jeff Xu for the advice.

References

1. M. M. Rampai, C. B. Mtshali, N. S. Seroka and L. Khotseng, RSC Adv., 2024, 14, 6699–6718.
2. S. Chatterjee, R. K. Parsapur and K.-W. Huang, ACS Energy Lett., 2021, 6, 4390–4394.
3. D. R. MacFarlane, P. V. Cherepanov, J. Choi, B. H. R. Suryanto, R. Y. Hodgetts, J. M. Bakker, F. M. Ferrero Vallana and A. N. Simonov, Joule, 2020, 4, 1186–1205.
4. E. Spatolisano, L. A. Pellegrini, A. R. de Angelis, S. Cattaneo and E. Roccaro, Ind. Eng. Chem. Res., 2023, 62, 10813–10827.
5. S. Giddey, S. P. S. Badwal, A. Kulkarni and C. Munnings, ACS Sustain. Chem. Eng., 2017, 5, 10231–10239.
6. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
7. P. Preuster, A. Alekseev and P. Wasserscheid, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 445–471.
8. A. Valera-Medina, H. Xiao, M. Owen-Jones, W. I. F. David and P. J. Bowen, Prog. Energy Combust. Sci., 2018, 69, 63–102.
9. A. Züttel, Mater. Today, 2003, 6, 24–33.
10. F. Vitse, M. Cooper and G. G. Botte, J. Power Sources, 2005, 142, 18–26.
11. M. Aziz, A. T. Wijayanta and A. B. D. Nandiyanto, Energies, 2020, 13, 3062.
12. M. Muthuvel and G. G. Botte, Mod. Asp. Electrochem., 2009, 45, 207–245.
13. D. T. Tran, T. H. Nguyen, H. Jeong, P. K. L. Tran, D. Malhotra, K. U. Jeong, N. H. Kim and J. H. Lee, Nano Energy, 2022, 94, 106929.
14. T. V. Choudhary, C. Sivadinarayana and D. W. Goodman, Catal. Lett., 2001, 72, 197–201.
15. B. K. Boggs and G. G. Botte, J. Power Sources, 2009, 192, 573–581.
16. K. Zhang, Y. Han, Y. Zhao, T. Wei, J. Fu, Z. Ren, X. Xu, L. Zhou and Z. Shao, Cell Rep. Phys. Sci., 2024, 5, 102171.
17. N. M. Adli, H. Zhang, S. Mukherjee and G. Wu, J. Electrochem. Soc., 2018, 165, J3130–J3147.
18. F. Chang, W. Gao, J. Guo and P. Chen, Adv. Mater., 2021, 33, 2005721.
19. D. Lim, J. A. Moon, C. W. Yoon and H. Lim, Green Chem., 2023, 25, 3888–3895.
20. X. Xi, Y. Fan, K. Zhang, Y. Liu, F. Nie, H. Guan and J. Wu, Chem. Eng. J., 2022, 435, 134818.
21. L. Marinčić and F. Leitz, J. Appl. Electrochem., 1978, 8, 333–345.
22. K. W. Kim, Y. J. Kim, I. T. Kim, G. I. Park and E. H. Lee, Water Res., 2006, 40, 1431–1441.
23. W. T. Mook, M. H. Chakrabarti, M. K. Aroua, G. M. A. Khan, B. S. Ali, M. S. Islam and M. A. Abu Hassan, Desalination, 2012, 285, 1–13.
24. J. Yao, M. Zhou, D. Wen, Q. Xue and J. Wang, J. Electroanal. Chem., 2016, 776, 53–58.
25. A. M. Pourrahimi, R. L. Andersson, K. Tjus, V. Ström, A. Björk and R. T. Olsson, Sustain. Energy Fuels, 2019, 3, 2111–2124.
26. G. Zhang, J. Ruan and T. Du, ACS ES&T Eng., 2020, 1, 310–325.
27. P. Babar and G. G. Botte, ACS Sustain. Chem. Eng., 2024, 12, 13030–13047.
28. H. Kim, S. Hong, H. Kim, Y. Jun, S. Y. Kim and S. H. Ahn, Appl. Mater. Today, 2022, 29, 101640.
29. R. Perez, Y. Huang, H. S. Pillai and H. Xin, ACS ES&T Eng., 2023, 4, 269–276.
30. K. Siddharth, Y. Chan, L. Wang and M. Shao, Curr. Opin. Electrochem., 2018, 9, 151–157.
31. C. Zhong, W. B. Hu and Y. F. Cheng, J. Mater. Chem. A, 2013, 1, 3216–3238.
32. Z.-H. Lyu, J. Fu, T. Tang, J. Zhang and J.-S. Hu, EnergyChem, 2023, 5, 100093.
33. Y. Tian, Z. Mao, L. Wang and J. Liang, Small Struct., 2023, 4, 2200266.
34. X. Ding, Y. Ji, H. Huang, J. Huang, S. Chen, C. Yang, F. Li and M. Luo, Chem. Catal., 2024, 4, 100932.
35. Y. Ji, A. Ozden, S. Chen, C. Yang and M. Luo, J. Mater. Chem. A, 2025, 13, 20176–20199.
36. N. S. Hassan, A. A. Jalil, R. Saravanan, N. M. Izzuddin, M. B. Bahari, D. Prasetyoko and R. E. Nugraha, J. Mater. Chem. A, 2024, 12, 23202–23217.
37. J. A. Herron, P. Ferrin and M. Mavrikakis, J. Phys. Chem. C, 2015, 119, 14692–14701.
38. Z.-F. Li, Y. Wang and G. G. Botte, Electrochim. Acta, 2017, 228, 351–360.
39. A. C. A. de Vooys, M. T. M. Koper, R. A. van Santen and J. A. R. van Veen, J. Electroanal. Chem., 2001, 506, 127–137.
40. X. Ding, Y. Ji, H. Huang, J. Huang, S. Chen, C. Yang, F. Li and M. Luo, Chem Catal., 2024, 4, 100932.
41. Y. Yang, J. Kim, H. Jo, A. Seong, M. Lee, H.-K. Min, M.-G. Seo, Y. Choi and G. Kim, J. Mater. Chem. A, 2021, 9, 11571–11579.
42. H. Kim, W. Yang, W. H. Lee, M. H. Han, J. Moon, C. Jeon, D. Kim, S. G. Ji, K. H. Chae, K.-S. Lee, J. Seo, H.-S. Oh, H. Kim and C. H. Choi, ACS Catal., 2020, 10, 11674–11684.
43. T. Matsui, S. Suzuki, Y. Katayama, K. Yamauchi, T. Okanishi, H. Muroyama and K. Eguchi, Langmuir, 2015, 31, 11717–11723.
44. J.-Y. Ye, J.-L. Lin, Z.-Y. Zhou, Y.-H. Hong, T. Sheng, M. Rauf and S.-G. Sun, J. Electroanal. Chem., 2018, 819, 495–501.
45. H. Kim, M. W. Chung and C. H. Choi, Electrochem. Commun., 2018, 94, 31–35.
46. H. Gerischer and A. Mauerer, J. Electroanal. Chem. Interfacial Electrochem., 1970, 25, 421–433.
47. E. Latvytė, X. Zhu, L. Wu, R. Lan, P. Vale and J. E. Graves, Int. J. Hydrogen Energy, 2024, 52, 265–282.
48. D. Yoon, S. Chung, M. Choi, E. Yang and J. Lee, J. Energy Chem., 2024, 93, 352–360.
49. Z. Liu, G. Zhang, H. Lan, H. Liu and J. Qu, Environ. Sci. Technol., 2021, 55, 12596–12606.
50. H. Shin, S.-M. Jung, Y. J. Lim, O.-J. Yim, B.-J. Lee, K.-S. Kim, I.-H. Baek, J. Baek, J. Lee and Y.-T. Kim, Adv. Sci., 2025, 12, 2500579.
51. O. Gecgel, C. E. Alvarez-Pugliese, J. Solis and G. G. Botte, Int. J. Hydrogen Energy, 2025, 141, 1349–1358.
52. Q. Xu, L. Zhang, J. Zhang, J. Wang, Y. Hu, H. Jiang and C. Li, EnergyChem, 2022, 4, 100087.
53. Y. Yang and F. Li, Curr. Opin. Green Sustain. Chem., 2021, 27, 100419.
54. I. Katsounaros, T. Chen, A. A. Gewirth, N. M. Markovic and M. T. Koper, J. Phys. Chem. Lett., 2016, 7, 387–392.
55. V. Rosca and M. T. Koper, Phys. Chem. Chem. Phys., 2006, 8, 2513–2524.
56. H. Imai, K. Izumi, M. Matsumoto, Y. Kubo, K. Kato and Y. Imai, J. Am. Chem. Soc., 2009, 131, 6293–6300.
57. B. Hu, S. He, X. Su, L. Xu and D. Zhu, Int. J. Hydrogen Energy, 2023, 48, 35050–35063.
58. C.-Y. Chen and S.-C. Su, Energy, 2018, 159, 440–447.
59. X.-Z. Yuan, J. C. Sun, H. Wang and H. Li, J. Power Sources, 2012, 205, 340–344.
60. G. A. Lindquist, S. Z. Oener, R. Krivina, A. R. Motz, A. Keane, C. Capuano, K. E. Ayers and S. W. Boettcher, ACS Appl. Mater. Interfaces, 2021, 13, 51917–51924.
61. N. Schwartz, J. Harrington, K. J. Ziegler and P. Cox, ACS Omega, 2022, 7, 29832–29839.
62. M. Wang, J. H. Park, S. Kabir, K. C. Neyerlin, N. N. Kariuki, H. Lv, V. R. Stamenkovic, D. J. Myers, M. Ulsh and S. A. Mauger, ACS Appl. Energy Mater., 2019, 2, 6417–6427.
63. J. Zhao, S. Shahgaldi, A. Ozden, I. E. Alaefour, X. Li and F. Hamdullahpur, Appl. Energy, 2019, 255, 113802.
64. M. B. Sassin, Y. Garsany, B. D. Gould and K. E. Swider-Lyons, Anal. Chem., 2017, 89, 511–518.
65. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical methods: fundamentals and applications, John Wiley & Sons, 2022.
66. R. G. Compton and C. E. Banks, Understanding voltammetry, World Scientific, 2007.
67. R. G. Kelly, J. R. Scully, D. Shoesmith and R. G. Buchheit, Electrochemical techniques in corrosion science and engineering, CRC Press, 2002.
68. M. E. Orazem and B. Tribollet, Electrochemical Impedance Spectroscopy, Wiley, 2011.
69. P. Zanello, C. Nervi and F. F. De Biani, Inorganic electrochemistry: theory, practice and application, Royal Society of Chemistry, 2019.
70. W. Peng, L. Xiao, B. Huang, L. Zhuang and J. Lu, J. Phys. Chem. C, 2011, 115, 23050–23056.
71. S. Le Vot, L. Roué and D. Bélanger, J. Electroanal. Chem., 2013, 691, 18–27.
72. R. Acevedo, C. M. Poventud-Estrada, C. Morales-Navas, R. A. Martínez-Rodríguez, E. Ortiz-Quiles, F. J. Vidal-Iglesias, J. Sollá-Gullón, E. Nicolau, J. M. Feliu, L. Echegoyen and C. R. Cabrera, Microgravity Sci. Technol., 2017, 29, 253–261.
73. H. S. Pillai, Y. Li, S. H. Wang, N. Omidvar, Q. Mu, L. E. K. Achenie, F. Abild-Pedersen, J. Yang, G. Wu and H. Xin, Nat. Commun., 2023, 14, 792.
74. I. Katsounaros, M. C. Figueiredo, F. Calle-Vallejo, H. Li, A. A. Gewirth, N. M. Markovic and M. T. M. Koper, J. Catal., 2018, 359, 82–91.
75. V. M. Truong, N. B. Duong, C. L. Wang and H. Yang, Materials, 2019, 12, 2048.
76. N. Mahmood, Y. Yao, J.-W. Zhang, L. Pan, X. Zhang and J.-J. Zou, Adv. Sci., 2018, 5, 1700464.
77. S. Wang, A. Lu and C. J. Zhong, Nano Converg., 2021, 8, 4.
78. L. M. Baumgartner, A. Kahn, M. Hoogland, J. Bleeker, W. F. Jager and D. A. Vermaas, ACS Sustain. Chem. Eng., 2023, 11, 10430–10440.
79. E. L. Clark, J. Resasco, A. Landers, J. Lin, L.-T. Chung, A. Walton, C. Hahn, T. F. Jaramillo and A. T. Bell, ACS Catal., 2018, 8, 6560–6570.
80. N. Aligholizadeh, A. Reddy, E. A. Monyoncho and E. A. Baranova, Ind. Chem. Mater., 2023, 1, 542–552.
81. H. S. Pillai and H. Xin, Ind. Eng. Chem. Res., 2019, 58, 10819–10828.
82. X. Luo, D. I. Kushner and A. Kusoglu, J. Membr. Sci., 2023, 685, 121945.
83. J. A. Dean, Lange's handbook of chemistry, 1999.
84. K. Thomsen and P. Rasmussen, Chem. Eng. Sci., 1999, 54, 1787–1802.
85. U. Göppert and G. Maurer, Fluid Phase Equilib., 1988, 41, 153–185.
86. A. Paliwal, B. Li, H. Long, L. Assaf, R. T. Haasch, J. K. Gupta, M. A. Reynolds, Y. J. Son, K. Zhang, S. Ye, P. J. A. Kenis and A. A. Gewirth, ACS Catal., 2025, 15, 10856–10867.
87. E. N. Aminaho, N. S. Aminaho and F. Aminaho, Appl. Energy, 2025, 399, 126515.
88. J. H. Jang, S. Y. Park, D. H. Youn and Y. J. Jang, Catalysts, 2023, 13, 803.
89. C. Machado Fernandes, E. M. Rodrigues, O. C. Alves, F. Garcia, Y. Xing, M. C. dos Santos and J. C. M. Silva, Appl. Catal. O: Open, 2025, 205, 207052.
90. R. Zhang, Y. Li, X. Zhou, A. Yu, Q. Huang, T. Xu, L. Zhu, P. Peng, S. Song, L. Echegoyen and F.-F. Li, Nat. Commun., 2023, 14, 2460.
91. A. Paliwal, L. Assaf, H. Long, R. T. Haasch, J. K. Gupta, M. A. Reynolds, Y. J. Son, K. Zhang, P. J. A. Kenis and A. A. Gewirth, ACS Appl. Mater. Interfaces, 2025, 17, 3383–3392.
92. Gas Diffusion Layers (GDL) Product Information, https://www.avcarb.com/products/gas-diffusion-layers-gdl/.
93. Molded Graphite Laminates (MGL) Product Data Sheet, https://www.avcarb.com/products/molded-graphite-laminates-mgl/.
94. J. Zhang, B. Wang, J. Jin, S. Yang and G. Li, Renew. Sustain. Energy Rev., 2022, 156, 111998.

---