Open Access Article
Open Access ArticleSolvation effects in liquid-phase esterification reactions catalyzed by hydrogen-form ion exchange resins
Mackenzie R.
Todd
a,
Jaeryul
Park
b,
Mara
Kuenen
a,
Griffin
Drake
a,
Mohammed
Al-Gharrawi
a,
Luke T.
Roling
 b and
Thomas J.
Schwartz
b and
Thomas J.
Schwartz
 *a
*a
aDepartment of Chemical & Biomedical Engineering Forest Bioproducts Research Institute, University of Maine, Orono, ME 04469, USA. E-mail: thomas.schwartz@maine.edu
bDepartment of Chemical and Biological Engineering, Iowa State University, Ames, IA 50011, USA
First published on 18th November 2025
Abstract
Renewable carbon resources, such as biomass or CO2, are crucial for replacing unsustainable fossil-based carbon in fuels, chemicals, and materials. However, valorization of these resources is often impeded by high oxygen content, which must be reduced, and low molecular weight, which often must be increased. Solid-acid-catalyzed reactions are critical for this valorization, and the reactions often occur in solution. The well-defined structure of crystalline solid acids, such as zeolites, makes them amenable for study, while other materials, such as the AmberlystTM family of polymeric resin catalyst, are harder to characterize. Here, we apply rigorous reaction kinetics measurements coupled with density functional theory (DFT) calculations to elucidate the influence of solvation on the esterification of butyric acid with n-butanol, used as a model reaction. We find surprising kinetic behavior, whereby the reaction is first-order with respect to both butyric acid and n-butanol when toluene is used as a nonpolar solvent, but the rate both decreases and becomes zero-order with respect to both butyric acid and n-butanol when tetrahydrofuran (THF) is used as a polar, aprotic solvent. DFT calculations reveal strong binding of THF to the sulfonate active sites on AmberlystTM, which partially explains the decrease in rate, while strong hydrogen bonding of the reactants with the solvent lead to an overall decrease in entropy in the bulk phase, thereby improving the thermodynamics for adsorption of the reactants to the catalyst and causing the observed shift in reaction order.
Broader contextThe transition from a fossil-based to a sustainable chemical economy requires developing processes to convert renewable carbon resources into useful products. Unlike fossil resources, renewable carbon, such as biomass or captured CO2, is highly oxygenated. This presents a significant challenge, as converting such molecules into fuels and chemicals often requires liquid phase processing, in contrast to the traditional vapor-phase refining used for most petroleum-derived products. The performance of conventional catalysts is often poorly understood. Here, we combine experimental and computational studies to investigate how the choice of reaction solvent impacts complex reactions. We show that the solvent can fundamentally alter the underlying reaction mechanism, which can impact process efficiency. The molecular-level insight developed in this work is crucial for the rational design of new catalytic systems thereby enabling the efficient production of sustainable fuels, chemicals, and materials. |
1. Introduction
Increases in global temperature have inspired a range of climate change mitigation strategies that focus on reducing the amount of CO2 released into the atmosphere by human activities.1–4 One way to reduce net CO2 emissions is to shift reliance away from fossil resources and toward biomass resources for fuel and chemical production.2–6 For example, organic materials obtained from forest residues are derived from carbon dioxide removed from the atmosphere via photosynthesis.1–3 Therefore, the use of forest products in fuel and chemical production opens a window for nearly carbon-neutral lifecycles for societally important materials.2,3An important challenge in this regard is that organic products derived from woody biomass have high oxygen contents, which can make them less stable or of lesser value to existing fossil-based industry and infrastructure.2,5,7,8 To reduce oxygen content, one class of reactions of interest to the field of biomass upgrading is dehydration condensation.3–5,7 Condensation reactions remove oxygen in the form of water, which maintains high carbon yields, as shown for Fischer esterification in Scheme 1.
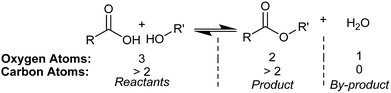 | ||
| Scheme 1 Fischer esterification decreases the oxygen content of organic products via dehydration condensation. | ||
Esters are industrially relevant as solvents and specialty chemicals, and the mechanism of Fischer esterification has been well studied.9–11 Of specific interest in biomass conversion are reactions that are catalyzed by heterogeneous Brønsted acid catalysts, such as sulfonate resins. An example of a known mechanism for acid catalyzed esterification has been proposed by Vafaeezadeh and Fattahi,12 shown in Scheme 2. In this mechanism, the carboxylic acid first coordinates to the Brønsted acidic proton of the sulfonate group on the acid catalyst, with the alcohol hydroxyl associated with a sulfonate oxygen. A C–O bond is formed between the alcohol hydroxyl (R2OH) and the carbonyl carbon of the acid (R1COOH) in a rate-limiting transition state, followed by rearrangement and elimination of a water in a second, kinetically insignificant transition state. Product desorption regenerates the sulfonate site.
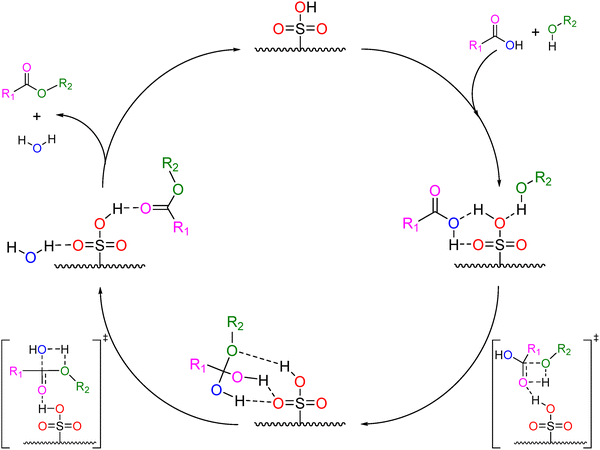 | ||
| Scheme 2 Proposed reaction mechanism for esterification catalyzed by a heterogeneous Brønsted acid catalyst, as presented by Vafaeezadeh et al.12 | ||
Santhanakrishnan et al.9 and Teo et al.13 also agree that acid catalyzed esterification begins with the protonation of the carboxylic acid followed by a nucleophilic attack of the protonated carboxylic acid by the alcohol. They describe this nucleophilic attack as being the rate-limiting transition state.9 Lee et al.10 and Dange et al.11 both report Langmuir–Hinshelwood kinetic models as being the best match to data from the esterification of n-butanol with C3 and C1 alcohols, respectively, catalyzed by AmberlystTM 70. Over AmberlystTM 15, Ali et al.14 found that a modified Eley–Rideal model was most accurate for fitting data from esterification of propionic acid with 1-propanol. However, with this exception, there appears to be more support in the literature for a Langmurian mechanism for various esterification reactions catalyzed by acidic resins.10,11,13
In this work, we evaluated acidic AmberlystTM resins because they are well-studied polymer catalysts with Brønsted acid sites that are also stable at typical reaction conditions.7,15–20 We consider especially the impact of solvation on the reaction mechanism, as AmberlystTM 15 is often described as being “much less sensitive to the nature of the solvent than the conventional resin.”17 While information about the reaction rate and mechanism of esterification is available, there are few studies that provide insight into the impact of solvent polarity on the reaction rate of acid-catalyzed esterification, yet solvent effects are clearly important for understanding catalysis in these systems.9–11 The AmberlystTM family of catalysts are composed of functionalized styrene-divinylbenzene polymer backbones, with AmberlystTM 15 (A15) having a higher acid site density and differing degrees of backbone crosslinking than AmberlystTM 46 (A46).17–19 If the polarity of acid sites impacts the way the nonpolar catalyst backbone interacts with solvents of different polarities, then the extent of stabilization of reaction intermediates may be different for those solvents. We probe these potential effects using A15- and A46-catalyzed esterification of butanol with butyric acid as a model reaction, comparing reactivity in toluene (nonpolar solvent) with that in THF (polar solvent). We couple these reactivity measurements with density functional theory (DFT) calculations to propose a potential reaction mechanism that can reconcile the diverse effects observed in the literature.
2. Methods
2.1 Materials
1-Butanol (Sigma Aldrich or Acros Organics, both >99.4% purity), n-butyric acid (Sigma Aldrich or Acros Organics, both >99% purity), toluene (Acros, 99.85% purity, extra-dry), and tetrahydrofuran (Fisher, containing butylated hydroxytoluene as an inhibitor) were all used as received. A15 and A46 were purchased from Sigma Aldrich. The catalyst resin beads were soaked in ultrapure water (18 MΩ) overnight, then filtered and washed with ultrapure water three times. The resin beads were then dried under vacuum at 313 K and crushed and sieved to between 50–100 mesh.2.2 Catalyst characterization
Based on the procedure used by Akkaramonakolporn et al.,21 0.10 grams of washed, crushed, and dried catalyst were added to a flask with 25 mL of a 2 N solution of sodium chloride. The slurry was left to equilibrate for 3 hours, stirring occasionally. The slurry was then titrated with a 1 N solution of sodium hydroxide, with pH measured by a digital pH probe (Fisher Scientific, Acumet AE150). The titration data were fit with cubic spline interpolation using MATLAB. The endpoint of the titration was determined from the inflection point of the spline curve. The endpoint was then used to determine the ion exchange capacity as described by eqn (1),21 where C is the concentration of NaOH solution (mol H+ L−1), V is volume of NaOH solution added at titration endpoint (mL), and W is the mass of catalyst (g).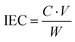 | (1) |
The bulk density of the resin was measured by adding 0.4 grams of crushed, washed, and dried catalyst to a small graduated cylinder. 5 mL of solvent were then added to the cylinder. The slurry was left to equilibrate for at least eight hours, stirring periodically. Before stirring, the volume of the resin bed and the volume of solution were measured. Changes in resin bed volume were measured over time to determine effective bulk densities (corresponding to the extent of resin swelling) in toluene, THF, and water.
2.3 Reaction kinetics measurements and analysis
10 mL batch reactors (Alltech, thick-walled glass, Teflon liners in phenolic caps) with triangular stir bars were used to measure reaction rates. A Fisher Isotemp stirring hotplate was used with a silicon oil bath to maintain constant temperature (373 K) and stirring (250 rpm) throughout the reactions. The reactors were operated at autogenic pressure. The concentrations of butanol and butyric acid were varied among reaction experiments. For each reaction experiment, six batch reactors were prepared with the same feed composition. In general, the initial liquid volume was ca. 5 mL (comprising 4 g liquid and 0.05 g catalyst). When removing reactors from the oil bath (after 20, 40, 60, 80, 100, and 120 minutes each), the reactors were quenched in an ice bath to stop the progression of the reaction. Short reaction times were used to maintain reaction conversion less than 25%. Initial rates were determined from a plot of concentration vs. reaction time, using only points over which the plot was linear. The concentrations of reactants and products were measured by gas chromatography with flame ionization detection (Shimadzu GC2010, Agilent DB-624 UI column).Initial production rates of butyl butyrate were calculated from initial slopes of plots of the amount of butyl butyrate produced per mass of catalyst over time. Calculations were performed using Microsoft Excel and MATLAB. Reaction orders were calculated from the slopes of log–log plots of reaction rate vs. initial reactant concentration.
The Weisz–Prater criterion was used to confirm that all reactions were conducted in a kinetically controlled regime. The Weisz parameter, as described by Levenspiel,22 is given by eqn (2), where Mw is the Weisz parameter, n is the reaction order, 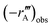 is the measured volumetric reaction rate (per-volume-of-catalyst), L is the characteristic dimension of the catalyst particles (one third of the radius in this case), Deff is the effective diffusivity of species A inside the catalyst particle, and CAs is the concentration of species A at the catalyst surface, which can be approximated by the concentration of species A in the bulk phase where stirring rates are sufficiently high.23
is the measured volumetric reaction rate (per-volume-of-catalyst), L is the characteristic dimension of the catalyst particles (one third of the radius in this case), Deff is the effective diffusivity of species A inside the catalyst particle, and CAs is the concentration of species A at the catalyst surface, which can be approximated by the concentration of species A in the bulk phase where stirring rates are sufficiently high.23
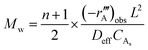 | (2) |
To evaluate eqn (2), the reaction order and observed reaction rate were determined experimentally. In the case of both solvents, the maximum measured reaction rates were used to provide a worst-case scenario. A catalyst density of 1.513 g mL−1 was used (the “true skeletal density” according to Kunin et al.16) to convert specific rates to per-volume reaction rates. A range of catalyst particle sizes was used (50–100 mesh), so eqn (2) was evaluated at the extremes. The minimum particle radius was 0.00745 cm, and the maximum particle radius was 0.014895 cm. The effective diffusivity was approximated as 0.0138 cm2 s−1, calculated by Yu et al. for methyl acrylate production catalyzed by A15.24 Because the rate of stirring for all reactions was high, the reactant concentration on the catalyst surface can be approximated by the reactant concentration in the bulk solution.
2.4 Density functional theory calculations
DFT calculations were performed using the Gaussian 09 simulation package25 with the B3LYP26,27 functional and the 6-311++G(d,p) basis set.28,29 The polarizable continuum model (PCM30) with SMD variation31 was used to implicitly model the presence of solvents. Geometry optimizations were performed with “verytight” convergence criteria. Transition states were identified using the QST3 algorithm and verified to contain only one imaginary vibrational mode. For simplicity, the catalyst surface was represented as a benzenesulfonic acid molecule. All atoms were fully relaxed in simulations.The implicit solvation model calculates entropies in the same fashion as for gas-phase species, leading to overestimation of entropies for liquid-phase species. As it would be prohibitively computationally expensive to obtain more detailed estimates for these entropies, we as a first approximation corrected the DFT-calculated entropies of 1-butanol and butanoic acid by the difference between gas- and liquid-phase entropies of the pure species tabulated in the NIST WebBook.32 We note that the tabulated corrections are for the respective pure species, not for solvation in toluene or THF. As the percentage of gas-phase entropy retained in liquid 1-butanol (62%) and butanoic acid (64%) was similar, we corrected the entropy of the ester product by setting the liquid entropy as 63% of the DFT-computed gas-phase value. We further computed the entropy of the water product in toluene or THF as 63% of the DFT-computed gas-phase value; although explicit values are available for pure liquid and gas water entropies, the entropy retained by liquid water relative to gas-phase water (37%) is likely much smaller due to the strong hydrogen bonding in liquid water. The use of an implicit solvation model, while necessary to limit the scope and complexity of the calculations in this study, introduces some error due to neglecting explicit interactions such as hydrogen bonds between solvents, surface models, and adsorbed species. In an absolute sense, the resulting solvation energies obtained by the SMD method are sometimes weakly correlated with those calculated by explicit models, depending particularly on solvent polarity.33 While the absolute energies calculated using our model will include some error resulting from this phenomenon, we anticipate that some level of error reduction for given elementary steps will occur by comparing relative energies of similar systems, such that the uncertainty estimates discussed in our kinetics analysis (±0.3 eV) will capture such deviations.
2.5 Maximum rate analysis
Based on Gibbs free energies of reactive intermediates and transition states, obtained from DFT calculations as described above, a separate reaction rate equation was derived assuming each transition state corresponded to an irreversible rate determining step with all other steps assumed to be quasi-equilibrated. For each equation, equilibrium and rate constants were calculated from eqn (3) and (4), respectively. These rate equations were then used to predict reaction rates corresponding to each mechanism, which were plotted over a range of thermodynamic activities corresponding to the experimental data collected as described above. In this analysis, the mechanism with the highest predicted rate that also matches the kinetic trends in the experimental data can be assumed to be the operative mechanism.34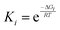 | (3) |
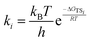 | (4) |
3. Results and discussion
3.1 Catalyst characterization
The number of Brønsted acid sites present on each catalyst sample was estimated from the ion-exchange capacity, determined by aqueous phase titration with sodium hydroxide, following the method of Akkaramonakolporn et al.21 The SO3H groups were first ion-exchanged with NaCl to form SO3Na and H3O+, which in turn was titrated with NaOH. For both catalysts, the initial pH of the solution following ion exchange was below 4, indicating successful deprotonation of the sulfonate groups on each material. Fig. 1 depicts the resulting titration curves, including fits used to determine the ion exchange capacity of each catalyst. The ion exchange capacities of both catalysts were extracted from the titration data and are outlined in Table 1. As shown in Table 1, these capacities are consistent with the published values from DuPont.| Solvent | Change in resin density (%) | |
|---|---|---|
| A15 | A46 | |
| Water | −3.2 | 6.7 |
| Toluene | −4.2 | 5.9 |
| Tetrahydrofuran | −28 | −5.6 |
Results of the swelling experiments are shown as the percent change in density of the resin bed after each experiment. Swelling (i.e., increased bed volume) is indicated by decreases in density, or negative percent changes in density. As shown in Table 1, both catalysts swell to a similar extent in both toluene and water. In tetrahydrofuran, however, both catalysts swell to a greater degree relative to their respective swelling in water, with A15 swelling significantly more than A46.
3.2 Reaction kinetics measurements
Before analyzing the reaction kinetics for esterification, we verified that our data were collected in a kinetically controlled regime, free of mass transfer limitations. To evaluate the potential for mass transfer limitations, we calculated the Weisz–Prater number for the worst-case scenario (i.e., the condition which gave the highest specific rate) for both solvents and for the maximum and minimum radii of catalyst particles. The calculation results are presented in Table 2. In all cases, the Weisz–Prater number is much less than 0.15, which corresponds to an effectiveness factor close to unity.23 We also calculated the Thiele modulus and effectiveness factor directly for one reaction condition, by comparing rates measured using two different particle sizes (see derivation in the SI). For the A15 catalyst using THF as a solvent, we find an effectiveness factor of 0.94, consistent with our Weisz–Prater calculations. Therefore, we conclude that, at all conditions studied here the reaction rate is slower than the diffusion rate, and the data were collected in a kinetically controlled regime.| N WP | ||
|---|---|---|
| Toluene solvent | THF solvent | |
| Minimum particle radius | 6.4 × 10−6 | 6.1 × 10−7 |
| Maximum particle radius | 2.6 × 10−5 | 2.5 × 10−6 |
TOFs normalized to the number of acid sites were calculated using initial rates extracted from batch reaction data. These initial TOFs were measured at fractional conversions below 25% and then normalized by the overall approach to equilibrium to obtain forward reaction rates (TOFf), as described by eqn (5).35 To account for the effect of variations in the excess reactant activity (i.e., the thermodynamic activity of species B when measuring the reaction order with respect to species A in an A + B reaction36,37), these forward rates were normalized again by the activity of the excess reactant (i.e., species B), as described by eqn (6). In eqn (5) and (6), TOF0 is the initial TOF, Keq is the overall equilibrium constant calculated from NIST data,32aj is the thermodynamic activity of species j, νj is the stoichiometric coefficient for species j, where nj is the reaction order with respect to species j, and kf is the forward rate constant. Thermodynamic activities were calculated from measured concentrations and UNIFAC activity coefficients.38,39
 | (5) |
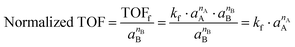 | (6) |
The reaction orders, nj, used in eqn (6) were determined iteratively, based on estimations from log–log plots of normalized rate data. These kinetics measurements are shown in Fig. 2, with the converged reaction orders presented in Table 3. Fig. 2 compares the TOFs obtained in THF with those obtained in toluene, and the reaction orders are listed in Table 3. In this case, the reaction order for esterification decreases from close to unity (with toluene solvent) to close to zero (with THF solvent), concomitant with a dramatic decrease in reaction rate, clearly indicating an impact of solvent identity on the reaction.
 | ||
Fig. 2 Esterification of n-butanol (BuOH) with butyric acid (HBu) with varying catalyst and solvent, plotted in terms of thermodynamic activity. Open circles: A46 catalyst, toluene solvent. Closed circles: A15 catalyst, toluene solvent. Closed squares: A15 catalyst, THF solvent. Reaction orders were determined with respect to BuOH (a) and butyric acid HBu (b). Initial TOFs were normalized by the thermodynamic activity of HBu (a) or BuOH (b) raised to the appropriate reaction order (see eqn (5) and (6)). Reaction conditions: T = 373 K, cat![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) feed = 1 feed = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 250 rpm stirring, initial concentrations varied from 0.2 to 85 mmol L−1, conversion of limiting reactant <25%. 80, 250 rpm stirring, initial concentrations varied from 0.2 to 85 mmol L−1, conversion of limiting reactant <25%. | ||
| Limiting reactant | Catalyst | Solvent | Reaction rate order |
|---|---|---|---|
| BuOH | A15 | Toluene | 0.64 ± 0.09 |
| HBu | A15 | Toluene | 0.88 ± 0.07 |
| BuOH | A46 | Toluene | 0.82 ± 0.09 |
| HBu | A46 | Toluene | 0.79 ± 0.04 |
| BuOH | A15 | THF | −0.3 ± 0.7 |
| HBu | A15 | THF | 0.2 ± 0.2 |
In the case of the dramatic decrease in reactivity observed when using THF, rather than toluene, as a solvent, it is likely that THF adsorbs to the SO3H sites, competing with butanol and butyric acid for free sites. That THF binds to acid sites is not without precedent. Halawy et al.40 used THF as a mildly basic probe molecule for Lewis acid sites and Li et al.41 used THF as a reactant with a Brønsted acidic zeolite active site. As shown in Table 4, our DFT calculations for binding energies of butanol, butyric acid, THF, and toluene indicate that THF binds 0.44 eV more strongly to an SO3H site than does toluene. Indeed, THF is predicted to have a similar binding energy to that for butanol, and both THF and butanol have higher binding energies than butyric acid.
| Adsorbate | Adsorption energy on sulfonate (eV) | |
|---|---|---|
| THF solvent | Toluene solvent | |
| Solvent (THF or toluene) | −0.47 | −0.03 |
| Butanol | −0.42 | −0.47 |
| Butyric acid | −0.24 | −0.23 |
3.3 Reaction kinetics analysis
The decrease in reaction order from ca. 1 to ca. 0 when switching from toluene to THF can be attributed to the impacts of hydrogen bonding on the stabilization of the reacting system. To arrive at this conclusion, we follow the same general mechanism proposed by Vafaeezadeh et al.,12 including an additional rearrangement on the catalyst surface to correctly orient the surface species for the second transition state. The reaction sequence is as follows:1. BuOH + HBu + * → Ads*
2. Ads* → IA*
3. IA* → IB*
4. IB* → IC*
5. IC* → FS*
6. FS* → BuBu + H2O + *
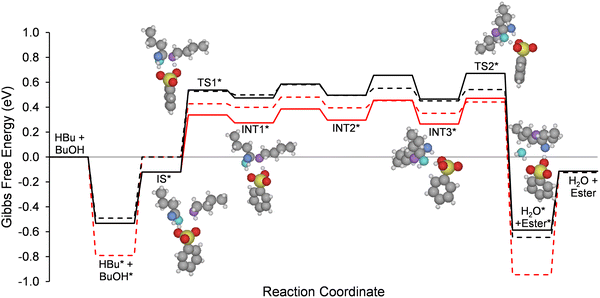
The reaction free energy diagram for this mechanism is shown in Fig. 3 along with structures of the intermediate species. It should be noted that the DFT calculations used to estimate free energies and transition states have a typically accepted uncertainty of ± 0.1 eV. In this case there is additional uncertainty in the free energies due to the entropic corrections associated with the liquid phase system,42 especially with respect to hydrogen bonding and the use of implicit solvation models (cf., Section 2.4). We therefore use a maximum rate analysis to examine the effects of an uncertainty of up to ±0.3 eV applied to the free energies of the liquid phase initial states (i.e., the sum of BuOH + HBu) in this network (Fig. 4a); we note that this perturbation influences only the absolute binding strength of the reactants and that the energies of intermediate and transition states relative to the initial adsorbed state are unchanged. We separately considered uncertainties of up to ±0.2 eV in the energies of intermediate and transition states when conducting reaction mechanism analyses (Fig. 4b). Importantly, while it is tempting to think of these modifications as ΔΔGsol values, that is not quite the case here, as the enthalpic contribution to ΔG has already been accounted for via the SMD model used in the DFT calculations. There is likely to be some compensation effect between enthalpic and entropic contributions to the Gibbs free energy in this system, as hydrogen bonding is likely to provide enthalpic stabilization but entropic destabilization ultimately leading to ΔΔG values comparable to those found via rigorous simulation of solvent molecule interactions.43
From the reaction coordinate diagrams in Fig. 4 it is evident that, because formation of the C–O bond requires the highest intrinsic barrier, it may be the rate-determining step in the esterification reaction. A rate equation can be derived for the forward reaction rate assuming this step is rate-determining with all other steps assumed to be quasi-equilibrated. Eqn (7) corresponds to the forward rate equation for this case, which we evaluate for its potential to reproduce our kinetic trends.
 | (7) |
The term KsolCsol in the denominator of eqn (7) accounts for competitive binding of the solvent (i.e., THF or toluene). To evaluate the applicability of this reaction rate equation and the underlying DFT-derived energetics, we conducted a maximum rate analysis using two fitting parameters: K1 (equilibrium forming IS* from liquid-phase HBu and BUOH), and k2 (forming TS1* from IS*), which were determined according to eqn (3) and (4), respectively. These parameters can be fit using the DFT-derived energetics as a starting point, modifying the parameter values within the expected uncertainty of ca. 0.3 eV. To illustrate the potential effects of such modifications, we show in Fig. 4 the potential energy surface corresponding to stabilization/destabilization of the initial liquid phase (Fig. 4a) by ±0.3 eV (maintaining the reference state at 0 eV) and stabilization/destabilization of transition states and surface intermediates (Fig. 4b) by ±0.2 eV (also maintaining the reference state).
Importantly, while an uncertainty of ±0.3 eV in the sum of two adsorbate free energies is relatively small, it can lead to significant variations in apparent reaction order. Fig. 5 shows the maximum rate for each of these modifications, with rates predicted viaeqn (7). These plots show the impact of K1 on the reaction rate as ΔG1 is adjusted within ±0.30 eV. The reaction rate orders vary from ca. 0 to ca. 1, depending on the correction made to the value of K1. At lower values of ΔG1, the reaction orders with respect to both reactants approach unity, aligning with the data collected in toluene solvent. At higher values of ΔG1, the reaction orders with respect to both reactants approach 0, aligning with the data collected in THF solvent.
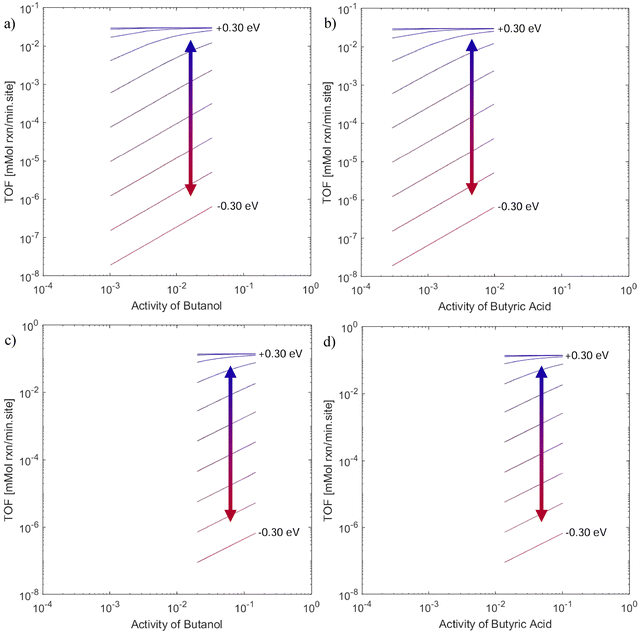 | ||
| Fig. 5 Predicted reaction rate data based on eqn (7) and changes to K1 by varying ΔG1. Plots (a) and (b) consider toluene as a solvent, and plots (c) and (d) consider THF as a solvent. The slopes of plots (a) and (c) represent the predicted reaction order with respect to butanol. The slopes of plots (b) and (d) represent the predicted reaction order with respect to butyric acid. Positive values (blue) correspond to destabilization of the initial liquid state. Negative values (red) correspond to stabilization of the initial liquid state. | ||
In the case of toluene, the DFT-calculated energetics accurately describe the kinetic trends without meaningful modification (i.e., within the expected uncertainty of ±0.1 eV for DFT). For data collected in THF solvent, however, the model requires a ca. 0.3 eV correction to ΔG1 to capture the same kinetic trends. We attribute the large correction to solvent participation in hydrogen bonding, which is not accurately captured by the implicit solvent model. Hydrogen bonding between solvent molecules should decrease the entropy of the liquid mixture by inducing order in the solvent, which would in turn increase the Gibbs free energy. In this case, a correction of 0.30 eV is reasonable given the magnitude of such bond energies (∼0.05–0.2 eV per bond,44 with several such bonds likely). Indeed, for studies of solvated reactions carried out in zeolites, hydrogen bonding in solvent networks often leads to variations in entropy between 50–100 J mol−1 K−1, which at 373 K leads to changes in Gibbs free energy of ca. 0.2–0.3 eV,45–47 further justifying the modifications suggested here. The data collected in the presence of THF can be accurately predicted within this range of uncertainty.
The sensitivity of k2 to uncertainty was evaluated by the same strategy, varying the activation energy by ±0.20 eV (see Fig. 4b). Again, eqn (7) was used to estimate rates as a function of activation energies ranging from ±0.2 eV. The resulting kinetic trends are shown in Fig. 6, where increases in activation energy (i.e., by destabilizing the transition state for step 2) correspond to decreases in reaction rate. Likewise, stabilizing the transition state (i.e., decreasing the activation barrier) increases the overall rate of reaction. In both cases, the reaction rate order with respect to either reactant does not change.
 | ||
| Fig. 6 Predicted reaction rate data based on eqn (7) and changes to k2 by varying ΔG2. Plots (a) and (b) consider toluene as a solvent, and plots (c) and (d) consider THF as a solvent. The slopes of plots (a) and (c) represent the predicted reaction order with respect to butanol. The slopes of plots (b) and (d) represent the predicted reaction order with respect to butyric acid. Positive values (blue) correspond to destabilization of the transition state. Negative values (red) correspond to stabilization of the transition state. | ||
Finally, the relative rates of reaction in the presence of toluene and in the presence of THF were compared to those of the experimental data. The reaction rate equation given in eqn (7) can predict, within uncertainty, the difference in reaction rate when the reaction is conducted in toluene rather than THF. To wit, the trends shown in Fig. 7 correspond to taking the upper limit of activation energies for THF and the lower limit of activation energies for toluene. Fig. 2 shows that the reaction rate in the presence of THF is about 2 orders of magnitude lower than the reaction rate in the presence of toluene, an effect which is captured in Fig. 7 when the activation energy for reactions carried out in THF is increased by 0.16–0.20 eV and decreased by 0.16–0.20 eV for reactions carried out in toluene. The red curves in Fig. 3 show the reaction coordinate diagrams after correcting the energies of the initial states, final states, and activation energies as described.
 | ||
| Fig. 7 Reaction rates (expressed as normalized TOFs) calculated using eqn (7) after adjusting the values of K1 and k2 to fit experimental reaction order plots with respect to BuOH (a) and HBu (b). Circles correspond to reactions with toluene as a solvent. Squares correspond to reactions with THF as a solvent. Positive values (blue) correspond to increases in activation energy (in eV) relative to the initially calculated value using DFT. Negative values (maroon) correspond to decreases in activation energy (in eV) relative to the initially calculated value using DFT. | ||
As shown in Fig. 3, the adjustments made during parameter fitting to experimental data essentially resulted in deepening the energy well of adsorbed reactants and products in presence of THF solvent relative to the reaction in the presence of the toluene solvent. These adjustments are attributed to relatively low entropy of reactive species in the polar THF solvent, relative to those in toluene, with potential solvent molecule organization due to hydrogen bonding interactions. Such interactions are not expected when toluene is used as a solvent, and in turn we do not require a deepening of the well to explain reactivity in toluene. All adjustments, however, were made within the range of expected error for the initial DFT calculations, showing that our proposed reaction mechanism and derived reaction rate equation can be used to describe this esterification reaction in the presence of either solvent, and that the use of DFT calculations was sufficient to give us an accurate starting point for rate and equilibrium constant determination.
4. Conclusions
Experimental data showed that the form of power-law reaction rate equations for esterification of butanol and butyric acid depend on solvent polarity. With a nonpolar solvent, the reaction is ca. first order with respect to both reactants. With a polar aprotic THF solvent, the reaction is ca. zero order with respect to both reactants, and the magnitude of the TOF for reactions carried out in THF is much lower than that for reactions carried out in toluene. DFT calculations were used to propose a reaction mechanism and estimate Gibbs free energies of all reactive species in the two different solvents. The rate equation derived from the proposed mechanism required adjustments to DFT-estimated parameters of ±0.30 eV to the free energies of the reactants in the bulk solvent and ±0.20 eV of activation energy for C–O bond formation. For reactions where H-bonding is significant (i.e., those in THF), the required adjustments were larger than for those without H-bonding (i.e., those in toluene), consistent with the inability of implicit solvation models to account for H-bonding effects. However, our results show that calculations can be reconciled with experiments via simple parameter adjustment within accepted levels of calculation uncertainty.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included in the article text and supplementary information (SI). Supplementary information is available, which includes a description of the Thiele modulus calculations. See DOI: https://doi.org/10.1039/d5ey00230c.Acknowledgements
The authors acknowledge Profs M. Clayton Wheeler, Brian G. Frederick, and Adriaan van Heiningen for helpful discussions. This work was funded by the US Department of Energy (DOE) under award DE-EE0008479 as part of the Co-Optimization of Fuels & Engines (Co-Optima) project sponsored by the DOE Office of Energy Efficiency and Renewable Energy (EERE) Bioenergy Technologies Office (BETO). MK and GD acknowledge support through the National Science Foundation REU Site: Explore It! Building the Next Generation of Sustainable Forest Bioproduct Researchers, Grant Number EEC-1461116. LTR acknowledges support from the Jack R. and Carol A. Johnson Faculty Fellowship.References
- J. Artz, T. E. Müller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Chem. Rev., 2018, 118, 434–504 CrossRef CAS PubMed.
- A. Corma, S. Iborra and A. Velty, Chem. Rev., 2007, 107, 2411–2502 CrossRef CAS.
- G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044–4098 CrossRef CAS.
- L. Petrus and M. A. Noordermeer, Green Chem., 2006, 8, 861–867 RSC.
- G. W. Huber, J. N. Chheda, C. J. Barrett and J. A. Dumesic, Science, 2005, 308, 1446–1450 CrossRef CAS PubMed.
- A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick, J. P. Hallett, D. J. Leak, C. L. Liotta, J. R. Mielenz, R. Murphy, R. Templer and T. Tschaplinski, Science, 2006, 311, 484–489 CrossRef CAS PubMed.
- T. J. Schwartz, B. J. O'Neill, B. H. Shanks and J. A. Dumesic, ACS Catal., 2014, 4, 2060–2069 CrossRef CAS.
- T. J. Schwartz, B. H. Shanks and J. A. Dumesic, Curr. Opin. Biotechnol, 2016, 38, 54–62 CrossRef CAS PubMed.
- A. Santhanakrishnan, A. Shannon, L. Peereboom, C. T. Lira and D. J. Miller, Ind. Eng. Chem. Res., 2012, 52, 1845–1853 CrossRef.
- M.-J. Lee, J.-Y. Chiu and H.-M. Lin, Ind. Eng. Chem. Res., 2002, 41, 2882–2887 CrossRef CAS.
- P. N. Dange, A. Sharma and V. K. Rathod, Catal. Lett., 2014, 144, 1537–1546 CrossRef CAS.
- M. Vafaeezadeh and A. Fattahi, Comput. Theor. Chem., 2015, 1071, 27–32 CrossRef CAS.
- H. T. R. Teo and B. Saha, J. Catal., 2004, 228, 174–182 CrossRef CAS.
- S. H. Ali, A. Tarakmah, S. Q. Merchant and T. Al-Sahhaf, Chem. Eng. Sci., 2007, 62, 3197–3217 CrossRef CAS.
- N. Bothe, F. Döscher, J. Klein and H. Widdecke, Polymer, 1979, 20, 850–854 CrossRef CAS.
- R. Kunin, E. Meitzner and N. Bortnick, J. Am. Chem. Soc., 1962, 84, 305–306 CrossRef CAS.
- R. Kunin, E. A. Meitzner, J. A. Oline, S. A. Fisher and N. Frisch, I&EC Product Res. Dev., 1962, 1, 140–144 Search PubMed.
- M. Ahmed, M. A. Malik, S. Pervez and M. Raffiq, Eur. Polym. J., 2004, 40, 1609–1613 CrossRef CAS.
- O. Ilgen, Fuel Process. Technol., 2014, 124, 134–139 CrossRef CAS.
- E. I. Gurbuz, S. G. Wettstein and J. A. Dumesic, ChemSusChem, 2012, 5, 383–387 CrossRef PubMed.
- P. Akkaramongkolporn, T. Ngawhirunpat and P. Opanasopit, AAPS PharmSciTech, 2009, 10, 641–648 CrossRef CAS.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley and Sons, Inc., New York, 3rd edn, 1999 Search PubMed.
- M. A. Vannice, Kinetics of Catalytic Reactions, Springer, New York, NY, 2005 Search PubMed.
- W. Yu, K. Hidajat and A. K. Ray, Appl. Catal., A, 2004, 260, 191–205 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, 2009.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- NIST Chemistry WebBook, https://webbook.nist.gov/chemistry.
- J. Zhang, H. Zhang, T. Wu, Q. Wang and D. van der Spoel, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS.
- C. A. Farberow, J. A. Dumesic and M. Mavrikakis, ACS Catal., 2014, 4, 3307–3319 CrossRef CAS.
- N. K. Razdan, T. C. Lin and A. Bhan, Chem. Rev., 2023, 123, 2950–3006 CrossRef CAS.
- T. J. Schwartz and J. Q. Bond, J. Catal., 2021, 404, 687–705 CrossRef CAS.
- T. J. Schwartz and J. Q. Bond, Chem. Commun., 2017, 53, 8148–8151 RSC.
- J. M. Smith, H. C. Van Ness and M. M. Abbott, Introduction to Chemical Engineering Thermodynamics, McGraw-Hill, New York, NY, 7th edn, 2005 Search PubMed.
- H. K. Hansen, P. Rasmussen, A. Fredenslund, M. Schiller and J. Gmehling, Ind. Eng. Chem. Res., 1991, 30, 2352–2355 CrossRef CAS.
- S. A. Halawy, A. I. Osman, A. Abdelkader, M. Nasr and D. W. Rooney, ChemistryOpen, 2022, 11, e202200021 CrossRef CAS PubMed.
- S. Li, O. A. Abdelrahman, G. Kumar, M. Tsapatsis, D. G. Vlachos, S. Caratzoulas and P. J. Dauenhauer, ACS Catal., 2019, 9, 10279–10293 CrossRef CAS.
- R. J. Madon and E. Iglesia, J. Mol. Catal. A: Chem., 2000, 163, 189–204 CrossRef CAS.
- A. K. Chew, T. W. Walker, Z. Shen, B. Demir, L. Witteman, J. Euclide, G. W. Huber, J. A. Dumesic and R. C. Van Lehn, ACS Catal., 2020, 10, 1679–1691 CrossRef CAS.
- V. V. Neklyudov, N. R. Khafizov, I. A. Sedov and A. M. Dimiev, Phys. Chem. Chem. Phys., 2017, 19, 17000–17008 RSC.
- N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Nat. Commun., 2020, 11, 1060 CrossRef CAS.
- N. Pfriem, P. H. Hintermeier, S. Eckstein, S. Kim, Q. Liu, H. Shi, L. Milakovic, Y. Liu, G. L. Haller, E. Baráth, Y. Liu and J. A. Lercher, Science, 2021, 372, 952–957 CrossRef CAS PubMed.
- D. S. Potts, J. K. Komar, M. A. Jacobson, H. Locht and D. W. Flaherty, JACS Au, 2024, 4, 3501–3518 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |