 Open Access Article
Open Access ArticleStructure–activity relationship in Co–N–C catalysts for multiple H2O2-related electrochemical reactions
Jie
Yang
 ab,
Lifang
Chen
ab,
Lifang
Chen
 *a,
Xuya
Zhu
c,
Wenwen
Shi
*a,
Xuya
Zhu
c,
Wenwen
Shi
 a,
Mengxue
Huang
a,
Mengxue
Huang
 ab,
Chang
Liu
ab,
Chang
Liu
 ab,
Ruimin
Ding
ab,
Ruimin
Ding
 *a,
Lin
Gan
*a,
Lin
Gan
 *c and
Xi
Yin
*c and
Xi
Yin
 *a
*a
aState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, Shanxi 030001, China. E-mail: chenlifang@sxicc.ac.cn; dingrm@sxicc.ac.cn; xiyin@sxicc.ac.cn
bSchool of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, China
cTsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, 518055, China. E-mail: lgan@sz.tsinghua.edu.cn
First published on 21st August 2025
Abstract
H2O2-related electrochemical reactions, including the two-electron oxygen reduction reaction (2e-ORR), H2O2 oxidation reaction (HPOR), and H2O2 reduction reaction (HPRR), have received significant attention for the electrosynthesis of H2O2 and energy storage. Understanding the complex structure–activity relationships among 2e-ORR/HPOR/HPRR and their connections is crucial for further developing highly efficient catalysts and working systems. Herein, we unveil these intricacies by employing model Co–N–C catalysts with a well-defined active site configuration (Co–N4-pyrrolic and Co–N4-pyridinic) in a combined experimental and computational approach. We report the higher 2e-ORR/HPOR but lower HPRR activity of the CoN4-pyrrolic site than the CoN4-pyridinic site based on their reaction free energy landscapes remodeled considering the chemisorption steps of O2 and H2O2. The results reveal that the binding free energy of *OOH (ΔG*OOH) can only be utilized as a reliable descriptor for 2e-ORR/HPOR activity, but not indicative of HPRR activity, regardless of the scaling relationship of the common reaction intermediates (*OOH or *OH). The HPRR activity of CoN4 sites strongly depends on the H2O2 adsorption strength and configuration. These findings provide valuable insights into the design of catalysts for H2O2-related electrochemical energy conversion and storage systems.
Broader contextHydrogen peroxide (H2O2)-mediated electrochemical reactions—including two-electron oxygen reduction (2e−-ORR), H2O2 oxidation (HPOR), and reduction (HPRR)—are pivotal for sustainable energy technologies, such as electrosynthesis of H2O2 (a green oxidant and energy carrier), direct H2O2 fuel cells, and regenerative energy storage systems. However, the efficiency of these interconnected reactions is fundamentally limited by the lack of universal activity descriptors and catalysts that can selectively drive target pathways while suppressing competing side reactions. Here, we decouple the structure–activity relationships of Co–N4 single-atom catalysts with defined coordination environments (pyrrolic vs. pyridinic) for all three H2O2-related reactions. We demonstrate that the conventional descriptor (ΔG*OOH) fails to predict HPRR activity, which is governed by H2O2 adsorption configurations and dissociation kinetics instead. This work provides design principles for on-demand catalysts tailored to specific H2O2 energy applications—enabling efficient H2O2 electrosynthesis, high-power fuel cells, and closed-loop H2O2-based energy storage. |
1. Introduction
Hydrogen peroxide (H2O2)-related electrochemical reactions, including two-electron oxygen reduction reaction (2e-ORR), H2O2 oxidation reaction (HPOR), and H2O2 reduction reaction (HPRR), have received significant attention due to their key roles in H2O2 electrosynthesis,1–5 fuel cells,6–10 and energy storage systems.11–14 These reactions often couple with each other positively or negatively, depending on their specific applications (Scheme 1). For instance, at the 2e-ORR electrode for H2O2 electrosynthesis, the undesired HPRR often occurs and consumes the valuable product.15,16 Conversely, in the cathode of hydrogen fuel cells, the HPRR can convert harmful H2O2 into water, thereby enhancing stability and efficiency.17,18 The 2e-ORR and its reverse reaction, HPOR, facilitate the electrochemical cycle of H2O2, offering potential applications in energy and hydrogen storage.11 In the case of an H2O2 electrolyzer for power-to-H2 conversion, the coupling of HPRR with HPOR at the anode reduces the H2O2 utilization and energy efficiency of the system.13,14 Furthermore, HPOR and HPRR can be employed in driving direct-H2O2 fuel cells at the anode and cathode, respectively.6–10 To date, the mechanistic studies of 2e-ORR,2,19,20 HPOR,11,14,21,22 and HPRR23–26 are often conducted independently rather than being fully integrated. Given the significance of these reactions and their intricate relationships in various applications, understanding their comprehensive connections is imperative for the advancement of highly efficient catalysts and operational systems.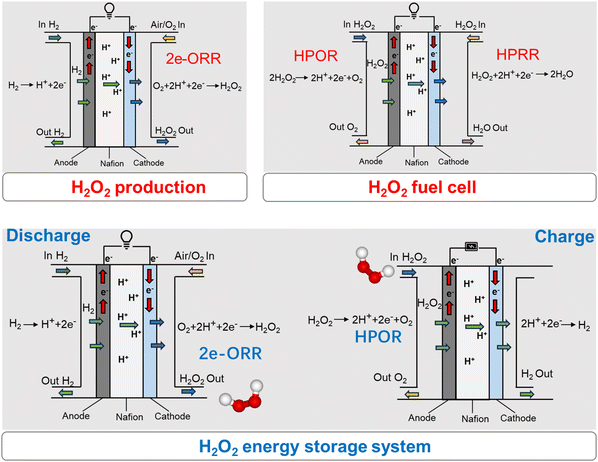 | ||
| Scheme 1 Critical roles of H2O2-related electrochemical reactions, including 2e-ORR, HPOR, and HPRR, for various applications. | ||
Among these reactions, 2e-ORR and HPOR share the same intermediate of adsorbed hydroperoxyl (*OOH, where * denotes the catalytic site), and the HPRR involves an intermediate of adsorbed hydroxyl (*OH).2,13,27–30 The binding free energies of these intermediates, namely ΔG*OOH and ΔG*OH, have been proposed as the thermodynamic activity descriptors for the above reactions.31–34 Considering the established scaling relationship between ΔG*OOH and ΔG*OH for various catalyst types (ΔG*OOH = ΔG*OH + 3.2 ± 0.2 eV), there may be an intrinsic correlation among the 2e-ORR, HPOR, and HPRR (2e-ORR/HPOR/HPRR) processes.
Cobalt and nitrogen-doped carbon (Co–N–C), specifically those with nitrogen-coordinated cobalt (CoNx) sites, have demonstrated activities across all three H2O2-related reactions.11,15,35 For instance, Dodelet et al. observed that Co–N–C is a remarkable catalyst for both HPOR and HPRR,35 and Strasser et al. found that Co–N–C exhibits high 2e-ORR selectivity and low HPRR activity, contributing significantly to H2O2 productivity.15 However, there is a discrepancy in the HPRR activity of the Co–N–C catalyst between these findings, possibly due to differences in the coordination environment around the Co ions. A recent study combining theoretical simulation and experiments identified that pyrrolic-type CoN4 (CoN4-pyrrolic) is mainly responsible for the 2e-ORR, while pyridinic-type CoN4 (CoN4-pyridinic) catalyzes the 4e-ORR.36 This highlights the significance of the coordination environment around Co ions for its catalytic properties. Through precise control of the coordination environment of Co, we could gain fundamental insights into the structure–activity relationship between CoN4 and 2e-ORR/HPOR/HPRR, opening opportunities to find a correlation among these reactions.
Herein, we employ Co–N–C catalysts with CoN4-pyridinic and CoN4-pyrrolic sites to establish the structure–activity relationships for 2e-ORR/HPOR/HPRR, examining the underlying connections among these reactions. The catalyst characterization and performance evaluation confirm that the CoN4-pyrrolic site exhibits higher 2e-ORR and HPOR activity but lower HPRR activity compared to the CoN4-pyridinic site. The results from density functional theory (DFT) calculations predict the same active site structural dependency for these reactions. The chemical process involving H2O2 determines the HPRR activity, while ΔG*OOH determines the 2e-ORR/HPRR activity. The activity of 2e-ORR and HPOR can be accurately predicted using a single thermodynamic descriptor. While HPRR follows chemical–electrochemical mechanisms, predicting its activity requires an in-depth analysis of the reaction pathway. This work advances the field by providing the first systematic investigation of three distinct H2O2 reaction pathways across differently coordinated CoN4 motifs, while rigorously evaluating the universality of conventional activity descriptors through both theoretical and experimental validation. These valuable insights into the H2O2-related reactions can guide the development of high-performance catalysts for various H2O2-based energy applications.
2. Experimental section
2.1 Materials
Cobalt chloride (CoCl2, 99.7%, anhydrous, Aladdin Biochemical Technology Co.), cobalt(II) acetate tetrahydrate (Co(CH3COO)2·4H2O, 98%, Sigma Aldrich), zinc acetate dihydrate (Zn(CH3COO)2·2H2O, analytical reagent grade, Aladdin Biochemical Technology Co.), aniline (98%, Sigma-Aldrich), hydrogen peroxide (H2O2, 30 wt%, Alfa Aesar), 2-methylimidazole (2-MIM, C4H6N2, 98%, Aladdin Biochemical Technology Co.), tannic acid (TA, analytical reagent grade, Aladdin Biochemical Technology Co.), hydrochloric acid (HCl, 36–38 wt%, analytical reagent grade, SCR, China), nitric acid (HNO3, 65–68 wt%, analytical reagent grade, SCR, China), sulfuric acid (H2SO4, 95–98 wt%, analytical reagent grade, SCR, China), APS (98%, Sigma-Aldrich), isopropanol (IPA, >99.7%, analytical reagent grade; Kermel, SCR, China), methanol (CH3OH, analytical reagent grade, SCR, China), deionized water (DI-water, Milli-Q, 18.2 MΩ cm at 25 °C), ultrapure N2 (99.999%), ultrapure O2 (99.999%), carbon black (BlackPearl 2000, Cabot Co.), 20 wt% Pt/C (Hispec3000, Johnson Matthey Co.) and a D521 Nafion dispersion (5 wt%, EW = 1100, Chemours) were utilized as received.2.2 Preparation of catalysts
The Co–N–C catalyst, featuring CoN4-pyrrolic dominated coordination (CoNpyrrC), was prepared by heating a precursor mixture containing CoCl2, polymerized aniline, and oxidized carbon black (OCB). Aniline (1.024 g, 8.11 mmol) was added to 200 mL of 1 M HCl under continuous magnetic stirring to form a monomer solution. Separately, a second solution was prepared by adding 1.246 g of 30 wt% H2O2 solution (11 mmol H2O2) and 7.141 g of CoCl2 (55 mmol) to 200 mL of 1 M HCl. This second solution was then introduced into the aniline solution to initiate the polymerization process. The resulting mixture was maintained at room temperature with constant magnetic stirring at 60 rpm for 4 h. Concurrently, a dispersion of OCB was prepared by sonicating 0.20 g of OCB in a mixture of 100 mL of H2O and 10 mL of IPA. The OCB dispersion was then added to the polymer dispersion under stirring at 600 rpm. After 24 h, the combined dispersion was heated to 80 °C and concentrated under continuous stirring at 600 rpm to yield a dark slurry. Then, the slurry was loaded into an alumina combustion boat and heat-treated at 900 °C in a tube furnace in N2 under ambient pressure. The ramping rate was 30 °C min−1, and the holding time at 900 °C was 1 h. Finally, the pyrolyzed material was ground into a fine powder using an agate mortar and pestle and treated with a 12 N HCl solution for 24 h to remove spectator Co-rich phases. The acid-leached sample was washed with DI water and dried under vacuum at 60 °C. The final product was obtained after the second heat treatment at 900 °C for 3 h in flowing N2 with a ramping rate of 30 °C min−1.NpyrrC refers to the blank N-doped carbon matrices that replicate the morphological features of CoNpyrrC but are intentionally devoid of CoN4 coordination sites. Its synthesis follows a similar procedure to that of CoNpyrrC but without adding CoCl2.
The Co–N–C catalyst, featuring CoN4-pyridinic dominated coordination (CoNpyC), was synthesized by heat treatment of the ZIF-67 material obtained by reacting acetate with 2-MIM. First, Zn(CH3COO)2·2H2O (1 mmol) and Co(CH3COO)2·4H2O (1 mmol) were dissolved in 5 mL of H2O to form a clear pink solution, which was subsequently added to 5 mL of H2O containing 2-MIM (13.6 mmol) under stirring at room temperature. The resulting mixture turned purple after a few seconds and was left undisturbed at room temperature for 4 h, then washed three times with DI water to obtain ZIF-67. Then, the prepared ZIF-67 was etched with 50 mL of TA solution (5 mg mL−1) while stirring for 20 min. The products were washed with water and methanol and then dried in an oven at 80 °C. Finally, the dried powder was loaded into an alumina combustion boat and heat-treated at 900 °C (5 °C min−1) in a tube furnace in N2 at ambient pressure. The holding time at 900 °C was 2 h.
NpyC refers to the blank N-doped carbon matrices that mimic the morphological features of CoNpyC but lack CoN4 coordination sites. Its synthesis is similar to that of CoNpyC but without the incorporation of Co(CH3COO)2·4H2O.
2.3 Physical characterization
The Co–N–C catalysts were characterized using a scanning electron microscope (SEM, JSM-7001F, Japan) operated at an accelerating voltage of 80 kV and a high-resolution transmission electron microscope (TEM, JEM-2100F, JEOL, Japan). Powder X-ray diffraction (XRD, D8 ADVANCE A25, Bruker Co., USA) patterns were recorded using a Bruker D8-Advance-A25 diffractometer with Cu Kα radiation over a 2θ range from 5° to 90°. Raman spectra were recorded using a LabRAM HR Evolution (HORIBA Scientific, France) using a 514 nm laser as the excitation source. X-ray photoelectron spectroscopy (XPS, Axis Ultra DLD, Kratos Analytical Ltd, UK) was performed using a monochromatic Al Kα source at 150 W without charge compensation. Cobalt K-edge X-ray Co K-edge X-ray absorption spectroscopy (XAS) was measured at the XRD station of the 4B9A beamline of the Beijing Synchrotron Radiation Facility (BSRF) in the transmission or fluorescence mode.2.4 Electrochemical measurements
The electrochemical activities of 2e-ORR were measured at ambient temperature (25 ± 2 °C) in a five-necked electrochemical cell filled with a 0.5 M H2SO4 electrolyte employing a bipotentiostat (CHI 760E; CH Instruments, Inc.). A rotating ring-disc electrode (RRDE, Pine Research Instrumentation) with a glassy carbon disk (Φ = 5.50 mm, area = 0.2375 cm2) and a Pt ring was employed as the working electrode, whereas a graphite rod and reversible hydrogen electrode (RHE) were employed as the counter and reference electrodes, respectively. Catalyst ink was prepared by dispersing 5 mg of the catalyst powder in 500 μL of DI water. Subsequently, 500 μL of IPA was added, followed by the addition of 12 μL of Nafion D521 dispersion. The mixture was then sonicated in an ice-water bath for 1 h to ensure homogeneity. Subsequently, to prepare the electrodes, 4.7 μL of the ink was deposited onto the GCE, resulting in a catalyst loading of 0.1 mg cm−2. Uniform catalyst coating on the GCE was achieved by slow drying under rotation.Their cyclic voltammograms (CVs) were recorded from 0 to 1.0 V vs. RHE in an N2-saturated 0.5 M H2SO4 solution at a scan rate of 50 mV s−1. The 2e-ORR performance was measured in O2-saturated 0.5 M H2SO4 (O2 purged for ≥30 min) under steady-state conditions by polarizing the working electrode from 1.0 to 0 V vs. RHE employing 20 mV potential steps and a hold time of 20 s at each step. The rotation rate was 900 rpm. The ring current was measured at a ring potential of 1.3 V vs. RHE, and the current collection coefficient of the ring electrode (N) was 0.38. The electrochemical surface areas (ECSA) of the catalyst were calculated from the equation:
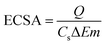 | (1) |
Electron transfer number (n) and H2O2 yield (YH2O2) were calculated using the following equations:
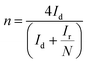 | (2) |
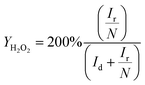 | (3) |
The electrochemical activities of HPOR/HPRR were measured by a bipotentiostat (CHI 760E) in an H-type electrolysis cell. A proton exchange membrane (Nafion® NR211) was used to separate the two compartments of the H-cell. A glassy carbon rotating disk electrode (RDE) (Φ = 5.00 mm, area = 0.1963 cm2) and an Ag/AgCl (KCl, 3 M) reference electrode were placed in one cell compartment, which was filled with 0.5 M H2SO4 and 0.5 M H2O2. At the same time, a graphite rod counter electrode was positioned in the other compartment that was filled with 0.5 M H2SO4. Catalysts loaded at 0.1 mg cm−2 were prepared by depositing 3.9 μL of ink onto the GCE. CVs were recorded from 0.4 to 1.0 V vs. RHE in an N2-saturated 0.5 M H2SO4 and 0.5 M H2O2 solution at a scan rate of 50 mV s−1. The rotation rate was 900 rpm.
The kinetically limited current density (jk) was determined using the Koutecký–Levich equation:
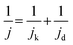 | (4) |
The diffusion-limited current density is governed by the equation:
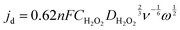 | (5) |
The logarithm of the current density (jk) was plotted against the potential to obtain a semilogarithmic polarization curve, also known as a Tafel plot. The linear part of this curve was fitted using the equation:
η = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) jk jk | (6) |
Mass activity (MA) and specific activity (SA) were quantified through the following equations:
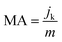 | (7) |
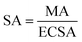 | (8) |
2.5 Computational details
All spin-polarized density functional theory (DFT) calculations were performed using the GGA-PBE functional in the VASP 5.4.4 code.37–39 The core–valence interactions were described using the projector augmented wave (PAW) pseudopotential,40,41 with a plane-wave basis set truncated at a cut-off energy of 400 eV. The van der Waals (vdW) interactions were incorporated through the empirical Grimme's DFT-D3 method.42 The k-point grids were set to be 4 × 4 × 1 by the Monkhorst–Pack method. Geometric optimizations employed the conjugate gradient algorithm, with force and energy convergence criteria set to 0.01 eV Å−1 and 10−5 eV, respectively. A 15 Å vacuum layer was set to avoid interactions.The chemical potential of the H+/e− pair is equal to half of the gas-phase H2 at standard hydrogen electrode (SHE) conditions from the computational hydrogen electrode (CHE).43 All free energies were calculated relative to H2O(l) and H2(g).
The free energy (G) for each reaction intermediate was calculated as:
| G = EDFT + ZPE − TS + Esol | (9) |
The adsorption free energies of *OOH, *OH, and *O were defined as follows:
| ΔG(*OOH) = G(*OOH) − G(*) − 2G(H2O) + 3/2G(H2) | (10) |
 | (11) |
| ΔG(*O) = G(*O) − G(*) − G(H2O) + G(H2) | (12) |
3. Results and discussion
3.1 Co–N–C catalysts with CoN4-pyrrolic and CoN4-pyridinic active sites
We synthesized Co–N–C catalysts with dominant CoN4-pyrrolic sites (CoNpyrrC catalyst) and CoN4-pyridinic sites (CoNpyC catalyst) using separate methods (Fig. 1a).45,46 Briefly, the CoNpyrrC catalyst was prepared by heat-treatment of a precursor mixture containing cobalt(II) chloride, polyaniline (PANI), and oxidized carbon black (OCB).45 The CoNpyC catalyst was synthesized by heat-treatment of the ZIF-67 material obtained by reacting cobalt(II) acetate with 2-methylimidazole (2-MIM).46The structural and elemental analysis results indicate that both catalysts are primarily carbon matrices doped with dispersed Co and N elements. Specifically, XRD patterns of both catalysts display a graphite-type phase, evident by two distinct characteristic peaks at 26.54° and 43.28°, corresponding to the (002) and (101) planes of graphite (PDF #75–1621), respectively (Fig. S1a). No peaks indicative of cobalt-rich phases were observed. Their Raman spectra (Fig. S1b) share a similar ratio of the D-band (disordered carbon, at ca. 1350 cm−1) to the G-band (graphitic carbon, at ca. 1580 cm−1) with ID![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IG ratios of 1.07 and 1.08, respectively, indicating comparable disordered graphitic structures. SEM and TEM (Fig. 1b, c and Fig. S1c, d) micrographs show that the CoNpyrrC catalyst exhibits an amorphous carbon particle morphology, while the CoNpyC catalyst displays a hollow dodecahedral structure with a concave shell. EDS elemental mapping (Fig. 1d and e) indicates the distinguishable signals of C, N, and Co, revealing uniform dispersion of Co within the carbon matrix. HAADF-STEM images show bright and isolated spots (Fig. 1f and g), indicative of atomically dispersed Co sites in both catalysts.
IG ratios of 1.07 and 1.08, respectively, indicating comparable disordered graphitic structures. SEM and TEM (Fig. 1b, c and Fig. S1c, d) micrographs show that the CoNpyrrC catalyst exhibits an amorphous carbon particle morphology, while the CoNpyC catalyst displays a hollow dodecahedral structure with a concave shell. EDS elemental mapping (Fig. 1d and e) indicates the distinguishable signals of C, N, and Co, revealing uniform dispersion of Co within the carbon matrix. HAADF-STEM images show bright and isolated spots (Fig. 1f and g), indicative of atomically dispersed Co sites in both catalysts.
The N 1s XPS spectra of CoNpyrrC and CoNpyC (Fig. 2a) can be fitted with four main types of N species, including pyridinic-N (398.6 eV), pyrrolic-N (400.3 eV), graphitic-N (401.3 eV), and oxidized-N (403.2 eV) species.36,47,48 The fitting results (Fig. 2b and Table S1) show that the CoNpyrrC catalyst has a higher proportion of pyrrolic-N (ca. 45 at%) compared to pyridinic-N (ca. 22 at%). Conversely, CoNpyC predominantly contains pyridinic-N species (ca. 52 at%) with a low fraction of pyrrolic-N (ca. 14 at%). Assuming that atomically dispersed Co is randomly coordinated with pyridinic- or pyrrolic-N sites, and considering their favorable thermodynamic formation energies,36,49 the probability of CoN4 sites in CoN4-pyrrolic or CoN4-pyridinic configurations is 67% vs. 33% in CoNpyrrC, and 79% vs. 21% in the CoNpyC catalyst.
To further investigate the oxidation state and local coordination environment of the Co ions at the atomic level, Co K-edge XAS measurements were conducted. For comparative purposes, Co foil and cobalt phthalocyanine (CoPc) were also analyzed. We acknowledge the lack of a well-defined pyridinic-CoN4 reference material for direct XAS comparison. The Co K-edge X-ray absorption near-edge structure (XANES) spectra (Fig. 2c) show that both CoNpyrrC and CoNpyC exhibit a higher pre-edge adsorption energy at the energy half of the edge maximum intensity compared to Co foil, indicating a positive valency of Co in the catalysts.36,50,51 The XANES spectrum of CoPc shows a sharp pre-edge peak at 7712 eV (peak B), indicative of the square-planar symmetry (D4h) of the CoN4 structure (Fig. 2c).45,47,52
In contrast, CoNpyrrC and CoNpyC lack peak B, but instead, feature a peak at 7706 eV (peak A), attributable to the distorted local structures of atomically dispersed CoN4 sites. The presence of peak A confirms the existence of the CoN4 site structure within the CoNpyrrC and CoNpyC catalysts.
The Fourier-transform (FT) of Co K-edge extended X-ray absorption fine structure (FT-EXAFS) spectra (Fig. 2d) confirms the absence of Co–Co bonds (2.17 Å) in CoNpyrrC and CoNpyC, consistent with the HAADF-STEM images. The prominent peaks at 1.44 Å for CoNpyrrC and CoPc point to the CoN4-pyrrolic structure, whereas the prominent peak at 1.33 Å for CoNpyC aligns well with the CoN4 structures featuring a pyridinic-N configuration reported in the literature.36,53 To further confirm this analysis, we performed a least-square curve fitting analysis for the first coordination shell of Co (Fig. S2–S5). The fitted coordination numbers for CoNpyrrC and CoNpyC are 3.99 and 4.02 (Table S2), respectively, and the fitted bond lengths of Co–N in CoNpyrrC and CoNpyC are 2.02 Å and 1.90 Å, respectively. These bond-length trends align with those reported by others and those from our DFT modeling (Fig. S8), validating the CoN4-pyrrolic and CoN4-pyridinic in the Co–N–C catalysts.53,54
The wavelet-transform (WT) of EXAFS analysis further elucidates the differences in the coordination environments across the samples, as illustrated in Fig. 2e. CoNpyrrC exhibits a maximum intensity around ca. 3.8 Å−1, closely aligned with the Co–N path in CoPc. In contrast, CoNpyC displays a maximum intensity at 3.6 Å−1, reflecting its different coordination environment compared to CoNPyrrC.53 Summarizing the above results, we have experimentally obtained the Co–N–C catalysts with CoN4-pyridinic and CoN4-pyrrolic sites. These samples serve as model catalysts to explore the structure–activity relationship between the Co–N coordination structure and the ORR/HPOR/HPRR and to investigate the connections among these reactions.
3.2 2e-ORR/HPOR/HPRR on Co–N–C with CoN4-pyridinic and CoN4-pyrrolic sites
The Co–N–C catalysts with CoN4-pyridinic and CoN4-pyrrolic coordination exhibit distinct catalytic properties. In Fig. S6, the CV reveals comparable capacitive currents for both catalysts, corresponding to similar electrochemically active surface areas of 360.3 m2 g−1 for CoNpyrrC and 379.8 m2 g−1 for CoNpyC. This surface area equivalence establishes a controlled baseline for subsequent performance comparisons, eliminating morphological factors as primary contributors to catalytic differences. The steady-state polarization curves in Fig. 3a highlights that CoNpyrrC exhibits significantly higher 2e-ORR activity than CoNpyC, with an onset potential (Eonset) of 0.71 V vs. RHE, closer to the thermodynamic theoretical potential (0.695 V vs. RHE). The limiting current density (jL) of CoNpyrrC is 2.10 mA cm−2, closer to the theoretical jL value for 2e-ORR, while that of CoNpyC is 4.02 mA cm−2. Fig. 3b compares the YH2O2 and n for these two structures. The maximum YH2O2 for CoNpyrrC is ca. 66.5% at 0.6 V vs. RHE, corresponding to n around 2.6. The YH2O2 for CoNpyC is below 12% over the wide voltage range (0–0.6 V vs. RHE), with n close to 4. This result implies that the CoN4-pyrrolic coordination is more favorable for 2e-ORR than CoN4-pyridinic coordination.The polarization curves of the two catalysts in an N2-saturated solution containing 0.5 M H2O2 and 0.5 M H2SO4 electrolyte are presented in Fig. 3c. The anodic current at high potential represents the HPOR-dominated process, and the cathodic current at low potential represents the HPRR. When the anode and cathode processes are in equilibrium, the net current becomes zero at the mixing potential (Umix).11,14 For an ideal HPOR catalyst, the Umix should be close to the thermodynamic equilibrium potential (0.704 V, reversible cell voltage in 0.5 M H2SO4 and 0.5 M H2O2 anolyte) to achieve high efficiency in HPOR. As displayed in Fig. 3c, CoNpyrrC and CoNpyC show a Umix of ca. 0.66 and 0.75 V vs. RHE. At 1.0 V vs. RHE, these catalysts achieve maximum current densities of ca. 300 and 130 mA cm−2, respectively. Corresponding MA and SA at this potential, detailed in Table S3, are 5440 A g−1 and a SA of 1.51 mA cm−2 for CoNpyrrC versus 1617 A g−1 and 0.43 mA cm−2 for CoNpyC. Furthermore, the calculated Tafel slopes are 94 and 337 mV dec−1 for CoNpyrrC and CoNpyC, respectively, based on the Tafel equation (eqn (6)) (Fig. 3d). CoNpyrrC exhibits significantly higher HPOR activity compared to CoNpyC. We assume that the CoN4-pyrrolic is the active site for the HPOR process.
For the HPRR process, CoNpyC exhibits significantly higher activity than the CoNpyrrC catalyst. At 0.4 V vs. RHE, the CoNpyC catalyst achieves a current density of ca. 62 mA cm−2, much higher than that of CoNpyrrC (ca. 10 mA cm−2). This enhanced activity is reflected in the MA and SA values at 0.4 V vs. RHE. CoNpyC achieves a markedly higher MA of 675 A g−1 and SA of 0.18 mA cm−2, while CoNpyrrC displays an MA of 119.8 A g−1 and SA of 0.03 mA cm−2 (Table S3). Despite this superior activity, CoNpyC displays a larger Tafel slope (305 mV dec−1) compared to CoNpyrrC (231 mV dec−1). It is noteworthy that both CoNpyC and CoNpyrrC catalysts exhibit large Tafel slopes for the HPRR. Tafel slopes larger than 120 mV dec−1 are typically associated with a chemical–electrochemical mechanism in which the chemical step is rate-determining.23 Overall, the CoN4-pyrrolic coordination shows high activity for 2e-ORR/HPOR, whereas CoN4-pyridinic coordination exhibits preferred HPRR. Critical control experiments with negligible ORR/HPOR/HPRR activity for NpyrrC and NpyC blank N-doped carbon matrices (Fig. S7) further confirm that the catalytic activity difference is predominantly due to the variation in CoN4 coordination environment rather than morphological features or residual metals.
Table S4 provides a benchmark comparison of our CoNpyC and CoNpyrrC catalysts with selected CoN4-based catalysts reported in prior studies.15,35,55,56 It appears that the high 2e-ORR is accompanied by high HPOR and low HPRR, while when 4e-ORR occurs, it is typically accompanied by acceptable HPOR and HPRR. Subsequent DFT calculations will provide further insight into the correlation among these reactions.
3.3 Theoretical calculation on 2e-ORR/HPOR/HPRR
DFT calculations were performed to understand the structure–activity relationship between CoN4 catalysts with CoN4-pyridinic and CoN4-pyrrolic coordination and the 2e-ORR/HPOR/HPRR. We built the CoN4-pyrrolic and CoN4-pyridinic models and optimized their structures. The optimized lattice parameters and Co–N bond length are shown in Fig. S8. The detailed calculation data for all species are displayed in Table S5.For 2e-ORR, the generally accepted pathway in acid is as follows:34,57
| * + O2 + H+ + e− → *OOH | (13) |
| *OOH + H+ + e− → * + H2O2 | (14) |
This pathway is composed of two consecutive proton-coupled electron transfer (PCET) steps, involving a single intermediate, *OOH. However, the chemisorption of oxygen (* + O2 → *O2) and the desorption of H2O2 are not considered in this pathway, and the reason is not well documented.32 Therefore, we first remodeled the 2e-ORR pathways on the CoN4-pyrrolic and CoN4-pyridinic surfaces by considering the O2-adsorption and H2O2-desorption steps and compared the results with the conventional 2e-ORR pathway model. The remodeled pathway is as follows:
| * + O2 → *O2 | (15) |
| *O2 + H+ + e− → *OOH | (16) |
| *OOH + H+ + e− → *H2O2 | (17) |
| *H2O2 → H2O2 + * | (18) |
Fig. 4a shows the reaction free energy diagrams of these pathways at U = 0.695 V. The optimized structures of the intermediates are shown in Fig. S9. We found that the strong binding of *O2 at the CoN4-pyridinic site creates a high barrier for the next reduction step of *O2 to *OOH, which would negatively affect both 4e-ORR and 2e-ORR activity (dashed line in Fig. 4a), while the slightly weak binding of *O2 at the CoN4-pyrrolic site can be easily overcome. However, this prediction is not consistent with the observed high 4e-ORR activity of the CoNpyC catalyst in our experiment. Alternatively, considering the O2 gas, dissolved O2, and *O2 are at equilibrium (0.695 V) and therefore have the same chemical potential, the free energy *O2 at equilibrium (rather than at the O2 coverage used in the DFT model) can be replaced with that of free O2. With this treatment, the conventional pathway model predicts higher 2e-ORR activity of CoN4-pyrrolic than CoN4-pyridinic (solid line in Fig. 4a). In this case, the removal of *OOH is slightly uphill, and it serves as the rate-determining step (RDS) for both CoN4-pyrrolic and CoN4-pyridinic. The CoN4-pyrrolic exhibits a lower thermodynamic onset overpotential (η, η2e-ORR = 0.06 V) compared to the CoN4-pyridinic (η2e-ORR = 0.25 V), indicating that the CoN4-pyrrolic has a higher 2e-ORR activity than CoN4-pyridinic.
Fig. 4b shows the volcano-type relationship between the thermodynamic limiting potential (UL) and the binding free energy of *OOH (ΔG*OOH) and the predicted values for CoN4-pyrrolic and CoN4-pyridinic. The left region of the plot represents the strong binding of *OOH, while the right downhill part in the volcano plot corresponds to the weak binding of *OOH. The volcano reaches its peak at the equilibrium potential at 0.695 V with the optimal ΔG*OOH of 4.225 eV. The CoN4-pyrrolic shows ΔG*OOH of 4.16 eV, which is close to the optimal value, indicating that CoN4-pyrrolic prefers the 2e-ORR process. This prediction agrees with the observed low Eonset of 2e-ORR for the CoNpyrrC catalyst in Fig. 3a. Furthermore, we also investigated the electron transfer between the *OOH intermediate and these two types of CoN4 sites by Bader charge analysis, which determines the binding strength of the *OOH intermediate. As shown in Fig. S10, the CoN4-pyrrolic site transfers less charge (0.28e) to the *OOH intermediate than the CoN4-pyridinic site (0.35e), which leads to the weaker binding of *OOH at the CoN4-pyrrolic site. The good agreement between the experimental and theoretical results indicates that ΔG*OOH is a suitable activity descriptor for 2e-ORR at these CoN4 sites. Therefore, deliberate engineering of CoN4-pyrrolic sites, guided by the ΔG*OOH descriptor, provides a strategic pathway to design highly active catalysts for H2O2 production.
On the other hand, the HPOR is the reverse 2e-ORR process involving the same intermediate, and its pathway is as follows:
| * + H2O2 → *OOH + H+ + e− | (19) |
| *OOH → * + O2 + H+ + e− | (20) |
Fig. 4a shows the calculated reaction free energy diagrams of the HPOR (inverse process of 2e-ORR) at 0.695 V. In the conventional pathway model, without considering the *O2 and *H2O2, the RDS of HPOR for both CoN4-pyrrolic and CoN4-pyridinic is the removal of *OOH, due to the uphill energy required for converting *OOH to O2. The CoN4-pyrrolic exhibits ηHPOR of 0.06 V, lower than 0.25 V predicted for the CoN4-pyridinic, indicating its higher HPOR than the CoN4-pyridinic. If considering the *O2 and *H2O2 states, the model predicts O2 desorption as the RDS for HPOR at CoN4-pyridinic and its lower activity than CoN4-pyrrolic.
Fig. 4b shows the relationship between the UL of the HPOR and ΔG*OOH. An optimal HPOR catalyst should have a ΔG*OOH of 4.225 eV, and the corresponding UL should be close to the equilibrium potential (0.695 V) with minimized overpotential. The CoN4-pyrrolic demonstrates a ΔG*OOH of 4.16 eV with a UL of 0.76 V, which is near the theoretical equilibrium potential. While the CoN4-pyridinic has a ΔG*OOH of 3.97 eV, and the corresponding UL is 0.95 V. These results are consistent with the higher HPOR activity of CoNpyrrC than CoNpyC (Fig. 3c). Consequently, ΔG*OOH serves as a thermodynamic activity descriptor for both the HPOR and 2e-ORR at CoN4 sites. The superior HPOR and 2e-ORR demonstrated by CoN4-pyrrolic sites enable an efficient electrochemical cycle of H2O2, offering potential applications in energy and hydrogen storage.11,13,14
For HPRR, no general pathway has been proposed so far. The Tafel slopes observed in our results and reported for various catalysts exceed 120 mV dec−1, which are very large and typical for chemical–electrochemical mechanisms.23,58,59 Therefore, we propose the following possible chemical–electrochemical HPRR pathways on the CoN4-pyrrolic and CoN4-pyridinic. On the CoN4-pyrrolic, the HPRR is as follows:
| * + H2O2 → *H2O2 | (21) |
| *H2O2 → *OH + *OH | (22) |
| *OH + *OH + H+ + e− → *OH + H2O | (23) |
| *OH + H+ + e− → H2O | (24) |
The HPRR on the CoN4-pyridinic is as follows:
| * + H2O2 → *O + H2O | (25) |
| *O + H+ + e− → *OH | (26) |
| *OH + H+ + e− → H2O | (27) |
Fig. 4c and d shows the complete HPRR pathways and calculated reaction free energy diagram at U = 0.695 V for both CoN4-pyrrolic and CoN4-pyridinic (Fig. S11 for U = 0 V). On the CoN4-pyrrolic, H2O2 adsorbs on top of the Co atom via the O atom (Fig. S12), and then dissociates to two *OH via HO–OH scission, which is an endothermic chemical reaction. Subsequently, these two *OH combine with two (H+ + e−) pairs to form two H2O molecules, which is characterized by significant exothermicity. The RDS of this pathway is the HO–OH scission step, with an energy barrier exceeding 0.25 eV, in line with the chemical–electrochemical mechanism suggested by Tafel slope analyses (Fig. 3d). In contrast, H2O2 undergoes spontaneous dissociation on the CoN4-pyridinic (Fig. S13), resulting in the formation of *O and H2O. The *O combines with one (H+ + e−) pair, forming *OH, followed by a second (H+ + e−) pair and forming H2O. This pathway is entirely exothermic, with the RDS being the electrochemical removal of *OH. Consequently, at U = 0.695 V, the HPRR activity on the CoN4-pyridinic is thermodynamically more favorable than that on the CoN4-pyrrolic surface, which aligns well with the observed activity order in Fig. 3c. Furthermore, the simple electrochemical process involving only the *OH intermediate is also calculated to compare the HPRR activity (Fig. S14). Therefore, DFT calculations and Tafel slope analysis validate the chemical–electrochemical mechanism for the HPRR on both CoN4-pyrrolic and CoN4-pyridinic. This leads to the conclusion that the ΔG*OH cannot serve as a reliable descriptor for HPRR. As the first atomistic-level elucidation of HPRR pathways on CoN4 catalysts, this work provides fundamental insights for designing cathode catalysts in direct H2O2 fuel cells.6–10
It is important to note that the free energy diagram indicates that CoN4-pyrrolic and CoN4-pyridinic exhibit lower overpotentials (ηHPRR < 0.5 V) for HPRR, which deviates from the experimental results (ηHPRR ≈ 1 V). This discrepancy arises from the limitations of computational methods like DFT, which focus on thermodynamics but overlook kinetic barriers crucial for reaction rates, such as proton–electron transfer. Additionally, DFT may not accurately represent realistic surface coverages of reactants or intermediates, affecting the energetics of key reaction steps. Thus, while DFT and experimental data agree on the trend that HPRR is thermodynamically favorable on CoN4-pyridinic surfaces, factors like reaction kinetics and surface coverage lead to higher observed overpotentials than predicted by DFT.
Our detailed theoretical investigation on CoN4-pyrrolic and CoN4-pyridinic elucidates the critical role of the *OOH intermediate as a descriptor for both the 2e-ORR and HPOR activities. The CoN4-pyrrolic type structure exhibits higher 2e-ORR/HPOR activity than the CoN4-pyridinic type structure due to its more optimal ΔG*OOH. The HPRR pathway analysis offers insights that the oversimplified use of ΔG*OH as a descriptor might fail to depict chemical–electrochemical mechanisms accurately. The significant differences in HPRR pathways on CoN4-pyrrolic and CoN4-pyridinic originate from H2O2 adsorption and thermodynamic energies. The CoN4-pyrrolic type structure demonstrates inferior catalytic activity in HPRR compared to the CoN4-pyridinic type structure, attributable to a higher chemical dissociation barrier of H2O2, while H2O2 spontaneously dissociates on the CoN4-pyridinic. Thus, ΔG*OOH can serve as a descriptor for 2e-ORR/HPOR activities, but not for the HPRR, which requires a more detailed consideration of the chemical reaction steps involved. For electrochemical H2O2 synthesis, we propose targeting CoN4-pyrrolic sites while tuning ΔG*OOH toward optimal values (4.225 eV) through coordination engineering. Conversely, for H2O2 fuel cell cathodes requiring efficient HPRR, catalyst design should prioritize CoN4-pyridinic configurations that facilitate spontaneous H2O2 dissociation and optimize *OH binding energetics. These site-specific design principles enable the rational development of integrated systems where H2O2 serves as both an energy carrier (in production) and a fuel (in consumption).
4. Conclusion
We explored the intrinsic relationship between 2e-ORR/HPOR/HPRR using two model Co–N–C catalysts with CoN4 sites in different coordination environments. The Co–N–C catalyst with CoN4-pyrrolic sites exhibits higher 2e-ORR and HPOR activity than that with CoN4-pyridinic sites, while the latter shows higher HPRR activity. Computational results indicate that the superior 2e-ORR/HPOR activity of the CoN4-pyrrolic site originates from its more optimal ΔG*OOH value. The HPRR activity of the CoN4 sites is determined by the chemical adsorption step of H2O2. The CoN4-pyrrolic exhibits a high H2O2 dissociation barrier that hinders HPRR, whereas H2O2 spontaneously dissociates on CoN4-pyridinic, leading to higher HPRR activity. These results suggest that ΔG*OOH can serve as a descriptor for 2e-ORR/HPOR activities, but not for the HPRR, which needs to take the chemical reaction steps into consideration. These results can provide valuable insights into the H2O2-related reactions and guide the development of high-performance catalysts for various H2O2-based energy conversion and storage applications.Author contributions
Jie Yang: writing – original draft, methodology, investigation, and visualization. Lifang Chen: methodology, investigation, visualization, and supervision. Xuya Zhu: investigation and visualization. Wenwen Shi: investigation and visualization. Mengxue Huang: investigation and visualization. Chang Liu: investigation and visualization. Ruimin Ding: writing – review & editing, supervision, and funding acquisition. Lin Gan: writing – review & editing, supervision, and funding acquisition. Xi Yin: conceptualization, methodology, writing – review & editing, supervision, and funding acquisition.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The data supporting this article have been included as part of the SI. See DOI: https://doi.org/10.1039/d5ey00224a.Acknowledgements
This study was financially supported by the National Key Research and Development Program of China grant (Grant No. 2021YFB4001203), the Shanxi Province grant (Grant No. 202203021212007) and the Autonomous Research Project of SKLCC (Grant No. SCJC-HN-2023-16 and SCJC-HN-2023-17). The authors wish to thank the facility's support for the 4B9A beamline of the Beijing Synchrotron Radiation Facility (BSRF) and the BL14W1 beamline of the Shanghai Institute of Applied Physics (SINAP).References
- C. Xia, Y. Xia, P. Zhu, L. Fan and H. Wang, Science, 2019, 366, 226–231 CrossRef CAS PubMed.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, Nat. Catal., 2018, 1, 156–162 CrossRef CAS.
- H. Kim, M. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. McCloskey, Nat. Catal., 2018, 1, 282–290 CrossRef.
- J. Qi, Y. Du, Q. Yang, N. Jiang, J. Li, Y. Ma, Y. Ma, X. Zhao and J. Qiu, Nat. Commun., 2023, 14, 6263 CrossRef CAS.
- L. Jing, W. Wang, Q. Tian, Y. Kong, X. Ye, H. Yang, Q. Hu and C. He, Angew. Chem., Int. Ed., 2024, 63, e202403023 CrossRef CAS.
- C. J. McDonnell-Worth and D. R. MacFarlane, Aust. J. Chem., 2018, 71, 781–788 CrossRef CAS.
- Y. Yang, R. Dong, Y. Zhu, H. Li, H. Zhang, X. Fan and H. Chang, Chem. Eng. J., 2020, 381, 122749 CrossRef CAS.
- F. Yang, K. Cheng, X. Liu, S. Chang, J. Yin, C. Du, L. Du, G. Wang and D. Cao, J. Power Sources, 2012, 217, 569–573 CrossRef CAS.
- A. E. Sanli and A. Aytaç, Int. J. Hydrogen Energy, 2011, 36, 869–875 CrossRef CAS.
- L. An, T. Zhao, X. Yan, X. Zhou and P. Tan, Sci. Bull., 2015, 60, 55–64 CrossRef CAS.
- J. Yang, R. Ding, C. Liu, S. Liu, Q. Xu, L. Chen, J. Chen, J. Li and X. Yin, J. Power Sources, 2022, 545, 231948 CrossRef CAS.
- R. Disselkamp, Int. J. Hydrogen Energy, 2010, 35, 1049–1053 CrossRef CAS.
- J. Yang, R. Ding, C. Liu, L. Chen, Q. Wang, S. Liu, Q. Xu and X. Yin, Green Chem., 2024, 26, 7769–7778 RSC.
- C. Liu, R. Ding, J. Yang, S. Liu, L. Chen, Q. Xu, J. Li and X. Yin, ACS Sustainable Chem. Eng., 2023, 11, 2599–2606 CrossRef CAS.
- Y. Sun, L. Silvioli, N. R. Sahraie, W. Ju, J. Li, A. Zitolo, S. Li, A. Bagger, L. Arnarson, X. Wang, T. Moeller, D. Bernsmeier, J. Rossmeisl, F. Jaouen and P. Strasser, J. Am. Chem. Soc., 2019, 141, 12372–12381 CrossRef CAS.
- Y. Sun, S. Li, Z. P. Jovanov, D. Bernsmeier, H. Wang, B. Paul, X. Wang, S. Kuhl and P. Strasser, ChemSusChem, 2018, 11, 3388–3395 CrossRef CAS.
- C. H. Choi, H. Lim, M. Chung, G. Chon, N. Ranjbar, A. Altin, M. Sougrati, L. Stievano, H. Oh, E. Park, F. Luo, P. Strasser, G. Drazic, K. Mayrhofer, H. Kim and F. Jaouen, Energy Environ. Sci., 2018, 11, 3176–3182 RSC.
- J. Wu, X. Yuan, J. Martin, H. Wang, J. Zhang, J. Shen, S. Wu and W. Merida, J. Power Sources, 2008, 184, 104–119 CrossRef CAS.
- S. Siahrostami, A. Verdaguer, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero, E. Paoli, R. Frydendal, T. Hansen, I. Chorkendorff, I. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- J. Lim, Y. Sa and S. Joo, Cell Rep. Phys. Sci., 2022, 3, 100987 CrossRef CAS.
- J. Lee, B. Lee, Y. Lee, A. Kim, D. Lee, H. Lim and H. Song, Small, 2023, 19, 2303263 CrossRef CAS.
- K. Deng, W. Wang, Q. Mao, H. Yu, Z. Wang, Y. Xu, X. Li, H. Wang and L. Wang, Small, 2022, 18, 2203020 CrossRef CAS.
- K. Stewart and A. Gewirth, Langmuir, 2007, 23, 9911–9918 CrossRef CAS PubMed.
- V. Briega, E. Herrero and J. Feliu, Chin. J. Catal., 2020, 41, 732–738 CrossRef.
- I. Katsounaros, W. Schneider, J. Meier, U. Benedikt, P. Biedermann, A. Auer and K. Mayrhofer, Phys. Chem. Chem. Phys., 2012, 14, 7384–7391 RSC.
- R. Rizo, J. Feliu and E. Herrero, Chin. J. Catal., 2021, 398, 123–132 CrossRef CAS.
- S. Deshpande, J. Kitchin and V. Viswanathan, ACS Catal., 2016, 6, 5251–5259 CrossRef CAS.
- G. Luque, M. Rojas, G. Rivas and E. Leiva, Electrochim. Acta, 2010, 56, 523–530 CrossRef CAS.
- S. Shi, J. Yang, L. Chen, M. Huang, C. Liu, R. Ding and X. Yin, J. Electrochem. Soc., 2024, 171, 046504 CrossRef CAS.
- X. Li, D. Heryadi and A. Gewirth, Langmuir, 2005, 21, 9251–9259 CrossRef CAS.
- F. Calle, J. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643 RSC.
- A. Kulkarni, S. Siahrostami, A. Patel and J. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS.
- K. Exner, Chem. Catal., 2021, 1, 258–271 CAS.
- Z. Seh, J. Kibsgaard, C. Dickens, I. Chorkendorff, J. Nørskov and T. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- F. Jaouen and J. Dodelet, J. Phy. Chem. C, 2009, 113, 15422–15432 CrossRef CAS.
- S. Chen, T. Luo, X. Li, K. Chen, J. Fu, K. Liu, C. Cai, Q. Wang, H. Li, Y. Chen, C. Ma, L. Zhu, Y. Lu, T. Chan, M. Zhu, E. Cortes and M. Liu, J. Am. Chem. Soc., 2022, 144, 14505–14516 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- J. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- F. Calle-Vallejo, J. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643 RSC.
- X. Yin, H. Chung, U. Martinez, L. Lin, K. Artyushkova and P. Zelenay, J. Electrochem. Soc., 2019, 166, F3240 CrossRef CAS.
- X. Ao, Y. Ding, G. Nam, L. Soule, P. Jing, B. Zhao, J. Hwang, J. Jang, C. Wang and M. Liu, Small, 2022, 18, 2203326 CrossRef CAS.
- K. Artyushkova, B. Kiefer, B. Halevi, A. Knop-Gericke, R. Schlogl and P. Atanassov, Chem. Commun., 2013, 49, 2539–2541 RSC.
- J. Wang, Y. Huang, Y. Wang, H. Deng, Y. Shi, D. Wei, M. Li, C. Dong, H. Jin, S. Mao and S. Shen, ACS Catal., 2023, 13, 2374–2385 CrossRef CAS.
- Y. Tian, M. Li, Z. Wu, Q. Sun, D. Yuan, B. Johannessen, L. Xu, Y. Wang, Y. Dou, H. Zhao and S. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202213296 Search PubMed.
- Y. He, H. Guo, S. Hwang, X. Yang, Z. He, J. Braaten, S. Karakalos, W. Shan, M. Wang, H. Zhou, Z. Feng, K. L. More, G. Wang, D. Su, D. A. Cullen, L. Fei, S. Litster and G. Wu, Adv. Mater., 2020, 32, 2003577 Search PubMed.
- Y. Han, Y.-G. Wang, W. Chen, R. Xu, L. Zheng, J. Zhang, J. Luo, R.-A. Shen, Y. Zhu, W.-C. Cheong, C. Chen, Q. Peng, D. Wang and Y. Li, J. Am. Chem. Soc., 2017, 139, 17269–17272 CrossRef CAS.
- Y. Sa, S. Park, G. Jung, T. Shin, H. Jeong, S. Kwak and S. Joo, ACS Catal., 2019, 9, 83–97 Search PubMed.
- H. Zhuang, T. Zhang, H. Xiao, F. Zhang, P. Han, H. Gu, J. Jiao, W. Chen and Q. Gao, Appl. Catal., B, 2024, 340, 123273 Search PubMed.
- Y. Cheng, J. Peng, G. Lai, X. Yue, F. Li, Q. Wang, L. Chen and J. Gu, ACS Catal., 2024, 14, 8446–8455 CrossRef CAS.
- J. Lee, B. Lee, Y. Lee, A. Kim, D. Lee, H. Lim and H.-K. Song, Small, 2023, 19, 2303263 CrossRef CAS.
- J. Gao, H. Yang, X. Huang, S.-F. Hung, W. Cai, C. Jia, S. Miao, H. Chen, X. Yang, Y. Huang, T. Zhang and B. Liu, Chem, 2020, 6, 658–674 CAS.
- X. Sun, K. Li, C. Yin, Y. Wang, M. Jiao, F. He, X. Bai, H. Tang and Z. Wu, Carbon, 2016, 108, 541–550 CrossRef CAS.
- P. Balbuena, S. Calvo, E. Lamas, P. Salazar and J. Seminario, J. Phys. Chem. B, 2006, 110, 17452–17459 CrossRef CAS.
- M. Eslamibidgoli and M. Eikerling, ACS Catal., 2015, 5, 6090–6098 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |




