Photovoltaic drives 100× carbon reduction and albedo-driven cooling exceeding forestation in climate mitigation

Abstract

Large-scale photovoltaic (PV) systems and anthropogenic forestation are increasingly used to fight climate change. However, their distinct mechanisms regarding albedo and carbon management pose a challenge to quantify their climate mitigation effectiveness, a gap rooted in systemic neglect of PV's albedo-mediated synergy. Our 0.5° × 0.5° grid-cell region analysis (n = 1465) demonstrates PV's dual advantage, with achieving synergy between carbon gains and Earth's surface energy balance in 96% of regions through 100-fold higher emission reductions than CO₂ absorption of forestation (15 vs. 0.09 kgC per m² per year) and albedo-driven solar radiative cooling that amplifies with carbon gains (Δα/ΔC = 0.008 ± 0.0007). Conversely, anthropogenic forestation requires tradeoff in 54.8% of cases, where albedo decline with carbon gains (Δα/ΔC = −0.004 ± 0.0007) generates solar radiative warming equivalent to six times of their CO₂ absorption benefit. Mechanistically, a change in PV's effective albedo (accounting for PV solar-to-electricity conversion) relative to the original land steeply responds to the aridity index (slope = −0.007 vs. forestation's −0.001), enabling >0.5 synergy probability in wider ranges of original surface albedo regions (α < 0.25) versus forestation's limited climate mitigation efficacy in humid regions (aridity index >1.47, synergy probability <0.5). Our synergy probability modeling framework emphasizes the previously underappreciated carbon gains and regulating solar radiation energy within PV systems, helping formulate more effective climate mitigation strategies by optimizing the spatial arrangement of PV plants in actual environmental conditions.

---

Broader context

Amidst the pressing efforts to combat climate change, the rapid expansion of photovoltaic (PV) systems has brought about a significant challenge: the competition for land resources between these emerging green energy infrastructures and traditional forest ecosystems. While PV's carbon-reduction capabilities are well-known, its influence on surface energy balance (direct climate effects) has received relatively little attention, leading to a continued policy preference for afforestation despite its limited climate mitigation effectiveness in many countries. This study compares the climate feedback mechanisms of PV plants and nearby forests across various aridity regions. We reveal PV systems can achieve a notable synergy between carbon emission reduction and albedo-driven cooling accounting for PV solar-to-electricity conversion, which differs from the carbon-albedo trade-off in forestation. By considering environmental aspects like background albedo and aridity, we offer a fresh perspective on optimizing PV plant deployment. Our synergy probability modeling framework can assist policymakers in formulating more informed strategies to balance energy production and direct climate regulation, potentially contributing to a more harmonious coexistence between green energy development and the traditional land-based carbon management approaches.

1. Introduction

Since the Industrial Revolution, fossil fuels formed over millions of years have been consumed at rates tens of thousands of times faster, driving unprecedented greenhouse gas emissions. The Global Carbon Project reports atmospheric CO₂ concentrations reached a record 37.4 billion tons in 2024.¹ While long-practiced anthropogenic forestation (fixing atmospheric CO₂ in biomass and soils by afforestation/reforestation) and expanding solar photovoltaic (PV) power plants both serve as alternative solutions to fight climate change,^2,3 the former's 20% contribution to emission reductions over the past decade has failed to offset accelerating fossil fuel emissions.¹ This paradox reveals a critical limitation that end-of-pipe atmospheric CO₂ sequestration cannot keep pace with rapid emissions at source. We thus face a pivotal choice prioritizing fossil fuel emission cessation.

Current research predominantly adopts a “green vs. green” dilemma perspective, favoring forest carbon sinks for their established multifunctionality over PV infrastructure.^4,5 However, properly deployed renewable energy systems demonstrate comparable climate mitigation potential through technological advances.^6,7 Crucially, both strategies modify the Earth's surface energy balance, producing climate feedbacks through direct radiative forcing (RF) that impact their carbon-related benefits.^8,9 Yet existing studies evaluate PV and forestation separately, leaving a key question unresolved: how do PV-induced radiative forcing effects compare with those of forestation in shaping their respective climate mitigation efficiencies?

The climate impacts of these solutions stem from their distinct carbon-energy interaction mechanisms. Forest CO₂ absorption exhibits low light-use efficiency (<1% photosynthetically active radiation).¹⁰ The CO₂ absorption capacity of forests is jointly regulated by the regional dominant vegetation functional groups and water resource availability. It directly reflects the long-term biological removal of atmospheric CO₂ by forest ecosystems.^4,11 Dark-canopied forests reduce the albedo to around 0.1, enhancing the absorption of shortwave radiation and leading to warming. However, field observations indicate that evapotranspiration-mediated cooling can partially offset this warming through reduced upwelling longwave radiation (ULR),¹² with the degree of offset depending on aridity.¹³ In contrast, the carbon benefit of PV systems arises from avoided fossil fuel emissions rather than direct CO₂ absorption. PV systems can achieve 23.5% photon-to-electron conversion efficiency, which contributes to the annual yield of renewable energy.¹⁴ Its carbon reduction efficiency is also determined by the regional solar radiation resource availability and meteorological factors such as temperature. Although PV panels also decrease the albedo and even suppress evapotranspiration, which may in turn induce a local warming effect, they transform a part of the absorbed solar radiation into electrical energy instead of merely converting it all into heat.^8,15 In observational studies, ultimately, PV systems ultimately generates complex energy balance effects. Existing research on PV surface temperatures report contradictions, with cooling in some regions¹⁶ and warming in others,¹⁷ suggesting diverse climatic consequences. These disparities may stem from both solar radiation regulation (PV's “effective albedo”, a parameter integrating panel reflection and radiation-to-electricity conversion to adjust the actual solar radiation input into the local surface energy budget¹⁸) and local moisture conditions,⁸ challenging the conventional assumption that albedo reduction in natural ecosystem universally leads to warming.¹² When deployed on low-albedo land covers, PV's energy diversion may outweigh its actual changes in reduction, potentially creating negative radiative forcing that synergizes with benefits of carbon emission reduction. Given that aridity influences the climate patterns related to forest albedo-evapotranspiration, and the effective albedo and energy balance of PV is dependent on the land cover, we hypothesize that the climate mitigation advantage of PV compared to forestation is likely to be contingent upon the regional aridity and the pre-existing land cover.

To meet the requirements of the Paris Agreement and support initiatives such as the Bonn Challenge, China has made remarkable progress in forestation and PV plants from 2001–2020. A series of ecological restoration projects led to a 6.2% (59.2 Mha) increase in forest cover.¹⁹ Meanwhile, since the 2009 Golden Sun project, China's PV industry has experienced explosive growth, with its cumulative PV plants total installed capacity rising exponentially from 2010–2022.²⁰ This real-world development not only underscores China's commitment to climate action but also provides an ideal scenario for our research. By analyzing 1465 independent 0.5° × 0.5° grid cells across mainland China's diverse aridity gradients (Fig. S1), which cover regions where both PV and forestation coexist under similar regional climatic conditions, we aim to bridge the knowledge gap in understanding the climate impacts of these two mitigation strategies. First, we use long-term observational data to reveal the contrasting amplification or offset relationships between surface energy budgets and carbon benefits (carbon-energy) of PV and forestation, demonstrating their asymmetric climate mitigation efficiency. Then, we examine how land cover and aridity impact key climate attributes (CO₂ absorption/reduction rates, albedo changes, and ULR changes) of both solutions, highlighting their external environmental responses. Next, we clarify the internal coupling between energy and carbon. Finally, we develop probability modeling to identify the optimal deployment zones that are delineated by the background environmental conditions of aridity and albedo, providing practical and actionable guidance for maximizing the benefits of climate mitigation under constrained land use.

2. Method

2.1 Quantifying radiative forcing

2.1.1 Energy-budget-induced direct radiative forcing. The radiative forcing induced by PV systems and anthropogenic forestation through modification of Earth's surface energy balance can be expressed as eqn (1):

The radiative forcing induced by surface energy changes is denoted as R_Fr. The albedo change, represented as Δα, is calculated as α_original − α_modified, where α is the actual surface albedo calculated as the ratio of reflected to incoming shortwave radiation. Here, α_original and α_modified correspond to the albedo of original land-cover surfaces and PV systems/forestation-covered surfaces, respectively. A positive Δα indicates a darker modified surface that enhances energy absorption (positive radiative forcing). The surface incoming shortwave radiation, denoted as R_g, is measured in W m⁻² and encompasses both direct and diffuse components. The difference in upwelling longwave radiation (ULR, W m⁻²) between modified and original land surfaces (i.e., ULR_modified − ULR_original) is quantified as ΔULR. A positive ΔULR reflects a warmer modified surface that transfers more longwave radiation upwelling through the atmosphere. While a fraction of this ULR escapes to space (represented by factor 0.1), the majority interacts with atmospheric components (e.g., greenhouse gases or aerosols), amplifying near-surface energy retention and constituting a positive feedback.²¹ These fluxes are normalized by Earth's total surface area (denoted as A_E, equal to 5.1 × 10¹⁴ m²) to derive global mean radiative forcing (W m⁻²), which enables direct comparison with CO₂-induced radiative forcing.²²

According to the Stefan–Boltzmann law, ULR is determined by the surface temperature and effective emissivity. Specifically, it is calculated as eqn (2):

ULR = εσT⁴ (2)

The Stefan–Boltzmann constant is denoted as σ, with a value of 5.67 × 10⁻⁸ W m⁻²·K⁻⁴; the ε represents the surface emissivity, and T is the land surface temperature in Kelvin (K).

PV systems across different regions, a portion of incoming solar radiation is converted to electricity. This electricity generation process does not contribute to radiative forcing through energy budget changes.¹⁸ It removes energy from the local surface budget (thus reducing heat available for local radiative forcing) but is dissipated elsewhere, differing physically from reflected radiation which directly escapes the atmospheric system. Therefore, when assessing PV-induced radiative forcing impacts on the energy budget, the albedo change should be adjusted by subtracting the PV conversion efficiency, representing how electricity generation mitigates radiative forcing through energy diversion, as expressed in eqn (3).

PV_eff = EP_a/GTI_opta (3)

The photovoltaic conversion efficiency for electricity production is denoted as PV_eff. The annual cumulative total solar irradiance (kWh m⁻²) incident on optimally tilted PV panels, incorporating both direct and diffuse radiation components, is represented as GTI_opta. The annual electricity production (kWh m⁻²), denoted as EP_a, is calculated from the specific energy yield (PV_out, kWh/kWp), the PV system's actual power generation (PV_power, kW), and the total panel area (A_PV, m²),^23,24 following eqn (4):

The specific energy yield, denoted as PV_out, integrates multiple factors affecting photovoltaic conversion efficiency, including regional solar irradiance and temperature conditions, system configuration (module type, capacity, orientation, and spacing), and component performance (module temperature effects and DC-to-AC conversion losses). These parameters collectively determine the annual energy production per unit area (denoted as EP_a), excluding impacts from operational maintenance or power transmission losses.²⁴

The effective albedo of PV is derived by summing the PV panel's actual albedo and PV_eff. This adjustment is grounded in matching the surface energy balance (local radiation input minus non-heat losses, eqn (5)) and separating local energy diversion from global radiation escape.

R_g = (α_actualR_g + ULR) + (PV_effR_g) + (H + LE + G) (5)

According to the surface energy balance, the surface incoming shortwave radiation of the PV system constitutes reflected radiation (α_actualR_g + ULR), electricity (PV_effR_g), and available Energy (H + LE + G). We directly isolate the fraction of R_g that does not contribute to surface warming. At the top-of-atmosphere (TOA) scale, reflected radiation contributes to TOA flux, while electricity does not. However, our study focuses on surface-driven direct radiative forcing. Within this physically grounded justification, the effective albedo of PV is a valid metric. We found that the correlations between the PV panel's actual albedo, effective albedo and their ULR are consistent (R = − 0.36, Fig. S4), verifying the rationality of effective albedo and accounting for energy diverted to electricity rather than heat.

We further verify the robustness of effective albedo change across practical engineering scenarios by conducting a sensitivity analysis focusing on PV tilt angles, a key parameter that directly influences irradiance capture and conversion efficiency in actual PV project design (Table S1). The results showed that the relative sensitivity of effective albedo change to tilt angles was significantly lower than that of global irradiation in 15° and 30° tilt groups. This indicates that even when tilt angles vary within practical engineering ranges, the effective albedo remains stable. Notably, constrained by the limitations of the current dataset, subsequent studies should incorporate panel type-specific data and orientation information. Such supplementary data integration will facilitate the validation of the metric's adaptability across a broader range of engineering scenarios.

2.1.2 CO₂-induced indirect radiative forcing. We quantified CO₂-induced radiative forcing from PV systems and forestation by adopting the improved parameterization method follows eqn (6) proposed by Etminan, et al.,²⁵ which is developed based on Myhre, et al.²⁶ and Betts²⁷ formulations, enabling direct carbon-climate impact comparisons.

R_Fc = [a₁(C − C₀)² + b₁|C − C₀ |+ c₁N̄ + 5.36]ln C/C₀ (6)

The radiative forcing (W m⁻²) induced by PV emission reduction and forestation CO₂ absorption is denoted as R_Fc. The coefficients in the formula (6) are defined as follows: a₁ = −2.4 × 10⁻⁷ W m⁻² ppm⁻¹, b₁ = 7.2 × 10⁻⁴ W m⁻² ppm⁻¹, and c₁ = −2.1 × 10⁻⁴ W m⁻² ppb⁻¹.

The 15-year average background atmospheric concentrations (from 2010 to 2024, since PV installation) of CO₂ and N₂O are represented by C₀ and N̄,²⁸ respectively, with measured values of 405.17 ppm and 330.18 ppb. The new atmospheric CO₂ concentration resulting from PV emission reduction or forestation CO₂ absorption is denoted as C, which is calculated as C₀ + ΔC, and the ΔC is calculated as eqn (7).

ΔC = CES × AF/k (7)

The change in CO₂ concentration (ppm) resulting from PV systems or forestation is denoted as ΔC. The carbon emission reduction rate for PV systems or CO₂ absorption rate for forestation (kgC per m² per year) is represented by CES. The conversion factor, denoted as k with a value of 2.16 × 10¹², is used to convert units of kgC to ppm.²⁹ The airborne fraction (with a value of 0.46) is denoted as AF. It accounts for the partitioning of CO₂ among atmospheric, terrestrial, and oceanic reservoirs, where only 46% of the emitted or sequestered carbon ultimately affects atmospheric concentrations.¹

For the carbon emission reduction rate from PV (CES_PV), we accounted for both the carbon content of displaced fossil-fuel electricity (emission factor) and the life-cycle carbon cost of PV systems. Using China's latest fossil energy power emission factor (EF_E = 0.2298 kgC per kWh⁻¹) in 2021 (ref. 30) and accounting for PV life-cycle emissions (EF_LCA = 0.01008 kgC kWh⁻¹) from manufacturing, installation to decommissioning in 2023,³¹ the CES_PV is calculated as eqn (8):

CES_PV = EP_a(EF_E − EF_LCA) (8)

Vegetation sequesters CO₂ through two primary pathways: (1) direct atmospheric CO₂ uptake via biomass accumulation (e.g., tree growth, foliage expansion), serving as an active carbon sink that immediately reduces atmospheric CO₂ levels, and (2) long-term carbon storage through decomposition of plant residues (e.g., leaf litter, deadwood) into soil organic matter, while critical for retaining previously absorbed carbon, this pathway does not directly enhance current atmospheric CO₂ absorption rates.¹¹

To enable robust, contextually comparison between forestation CO₂ absorption and PV's carbon emission reductions, we adopted 23-year (2001–2023) average annual ecosystem CO₂ absorption rates (CES_eco, kgC per m² ·per year).³² Instead of short-term vegetation growth dynamics and interannual disturbances, this CES_eco accounts for net ecosystem productivity after deducting respiratory losses, disturbances (deforestation, land-use changes), and demographic processes (e.g., vegetation growth/mortality), ensuring that the quantified carbon absorption rate reflects stable. For blue carbon ecosystems and data-limited regions (e.g., the Tibetan Plateau, arid northwest China), we integrated long-term eddy covariance flux tower site data^33–40 to ensure spatial consistency of the annual, per-unit-area CES_eco values and minimize uncertainties from short-term vegetation growth variations.

2.2 Data analysis

We analyzed 30 023 Chinese PV plants (2010–2022) from Chen, et al.,²⁰ extracting their construction timelines and original land covers. A 0.5° × 0.5° gridding system was used to generate 1465 independent PV-forestation comparison units. The 0.5° grid resolution was selected primarily for its advantage in balancing data availability and macro-pattern identification. On one hand, this resolution enables spatial matching and integration of PV plant with forest data, avoiding the issue of low regional sample proportion and minimize biases from local land-use changes. On the other hand, the 0.5° scale adequately captures China's diverse aridity gradients, which is critical for underpinning cross-regional analysis of the “climate-energy-forest” nexus. This spatial design ensures that our subsequent assessments of PV and forestation's climate mitigation effects are both data-driven and regionally comprehensive. Beyond spatial consistency, we further justify comparing PV and forestation in the same metric. We note both metrics reflect annual impact on atmospheric CO₂ per unit land, aligning their climate effect dimension. For factors altering interpretation, 23-year forest data smoothing short-term growth fluctuations and 13-year PV data capturing mature operational stability ensure annual flux stability.

2.2.1 Remote sensing data processing. We integrated GLC_FCS30D (30 m)⁴¹ and MODIS (500 m) datasets to quantify spatiotemporal dynamics of land cover and the variation characteristics of solar radiation. For each sample grid, we computed: (i) the pixel areas corresponding to quinary (5-year interval) tree cover changes (2001–2024) were identified as the prominent patch regions of anthropogenic forestation, (ii) pre-/post-PV albedo (MCD43A3/A2) and ULR (MOD11A1) differences after excluding pixels with QA flags indicating clouds/snow, and (iii) shortwave radiation means (MCD18A1). The MCD43A3 product provides black-sky albedo (α_{black_sky}) and white-sky albedo (α_{white_sky}) in the shortwave spectrum. Using model calculations and solar zenith angles (θ) from the MCD43A2 product for quality control,^42,43 we derived the actual surface (blue-sky) albedo (α_{blue_sky}) for PV and forestation expansion areas through the following eqn (9) and (10):

r = 0.122 + 0.85 exp(−4.8cos θ) (9)

α_{blue_sky} = (1 − r)α_{black_sky} + r × α_{white_sky} (10)

The diffuse skylight fraction (r) was calculated using high-quality pixels filtered from the MCD43A3 product with quality control (QC) flags equal to 0 (indicating best-quality data) and solar zenith angles below the 70° threshold. All remote sensing data processing is completed on Google Earth Engine.

2.2.2 External environmental impact analysis. We employed linear regression models to quantify the responses of carbon gain, ULR, and albedo changes to aridity index (AI, which is the ratio of annual average precipitation to annual average reference evapotranspiration⁴⁴) for both PV systems and forestation. The slope coefficients from these models represent the sensitivity of each climate attribute to increasing AI. Additionally, we used Wilcoxon rank-sum tests to compare differences in climate attributes between PV systems and forestation within each aridity class.

2.2.3 Internal carbon-energy coupling mechanism. To quantify the relationship between carbon gains and energy budget in PV and forestation, we employed linear mixed-effects models (LMMs) with AI as a random effect. The models were structured as eqn (11):

Energy_budget = β₁(carbon_gain) + (1|AI) (11)

In this model, Energy_budget represents either Δα or ΔULR, and carbon_gain refers to the normalized CES for PV systems or forestation. Normalization was performed to eliminate magnitude differences between carbon_gain values of PV and forestation, thereby enabling direct comparison of effect sizes. The fixed effect coefficient (β₁) quantifies the magnitude and direction of energy budget change per unit carbon gain, with 95% confidence intervals calculated to assess statistical significance. This approach accounts for spatial autocorrelation within aridity gradients while enabling comparison of carbon-energy coupling mechanisms between different land-use strategies. All analyses were conducted using the ‘lme4’ package in R.

2.2.4 Carbon-energy synergy probability modeling framework. To predict the probability of carbon-energy synergy for PV systems and forestation across different environmental conditions, we employed binary logistic regression models. The synergy status (synergy vs. trade-off) was modeled as a function of AI and background albedo (pre-existing land cover before PV/forestation), including their interaction term. The models were formulated as eqn (12):

logit(P_synergy) = β₀ + β₁(AI) + β₂(α) + β₃(AI × α) (12)

In this model, P_synergy represents the probability of achieving carbon-energy synergy. Model coefficients were estimated using maximum likelihood estimation. All analyses were performed in R using the 'stats' package for logistic regression modeling and the ‘dplyr’ package for data manipulation.

3. Results and discussion

3.1 Climate mitigation efficiency

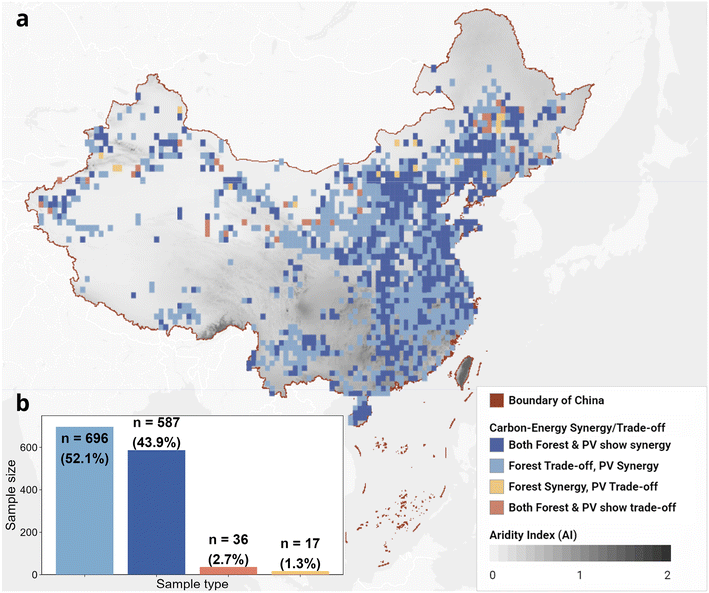
PV systems demonstrated carbon-energy synergy for climate mitigation in 96% of grid regions (n = 1283), while forestation faced carbon-energy tradeoff in 54.8% of cases (n = 732), highlighting their distinct climate mitigation performance patterns. Geographically, PV tradeoff regions clustered in northern China's arid zones (mean AI = 0.21), whereas forestation tradeoff occurred across a wider range of aridity gradients (mean AI = 0.57), implying distinct aridity-response between PV systems and forestation.

Specifically, the distinct climate mitigation performance patterns are further highlighted by their markedly different radiative forcing components (Fig. S2). The CO₂-induced radiative forcing (R_Fc) mitigation from PV systems averaged [−4.17 ± 0.9] × 10⁻¹⁴ W m⁻², approximately 160 times higher than that of forestation [−0.026 ± 0.02] × 10⁻¹⁴ W m⁻². For energy-budget-induced radiative forcing (R_Fr), PV-mediated climate mitigation [-1.15 ± 0.96] × 10⁻¹⁴ W m⁻² was roughly 50 times greater than forestation's near-climate-neutral effect [0.02 ± 0.35]×10⁻¹⁴ W m⁻². Notably, in the forestation involving carbon-energy tradeoff, the R_Fr generated was equivalent to six times the magnitude of R_Fc, indicating the energy budget significantly offsets the benefits of CO₂ absorption by plant.^9,45

3.2 Response to external environments

Contrary to our initial hypothesis, 70.2% of PV grid regions achieved carbon-energy synergy across diverse land cover types (Fig. 2). In contrast, 29.8% of forestation cases faced carbon-energy tradeoffs, validating the role of pre-existing land cover in shaping forestry's climate mitigation outcomes. Notably, PV systems occupied some land cover types unutilized by forestation (i.e., grasslands, woodlands, and coastal zones), yet retained high synergy proportions across diverse landscapes, demonstrating both broader siting adaptability and robust climate co-benefits.

While forestation enhanced CO₂ absorption with increasing AI (slope = 0.046, Fig. 3), its absolute absorption rates were two orders of magnitude lower than PV's emission reduction rates across all aridity levels (0.09 ± 0.07 vs. 15.00 ± 3.21 kgC per m² per year, Fig. 3a and Table S2). PV systems sustained strong emission reductions despite a slight decline with increasing AI (slope = −0.017), highlighting their drought-resilient carbon benefits. Notably, PV increased ΔULR (positive values denote climate amplification, see method) with the increase of AI more strongly than forestation (slope = 0.479 vs. 0.350, Fig. 3b), surpassing neutral levels (ΔULR = 0) in humid zones (AI > 0.8). Conversely, PV's effective albedo change (Δα = original land cover albedo – PV effective albedo), where negative values indicate albedo increase relative to the original surface, intensified more rapidly decreased with increasing AI (slope = −0.007 vs. −0.001, Fig. 3c). The PV's shortwave component of RFr is consistently lower than the longwave component (Fig. S3b), leading to net climate mitigation associated with negative Δα. This indicates that PV counteracts warming through albedo-mediated energy conversion. In contrast, forestation's minimal albedo-longwave fluctuations suggest it primarily stabilizes the surface energy budget, maintaining pre-existing energy states (Fig. 3b and c and S3b). The findings validate our hypothesis regarding the differential climate attribute responses of PV and forestation to aridity. They fundamentally redefine their roles: the reduction of albedo in PV synergizes with a high emission reduction rate to actively regulate the climate, whereas forestation only passively stabilizes the surface energy budget, mainly through the widely-recognized mechanism of “cooling via evapotranspiration”.⁴⁶ However, future drought-induced reductions in evapotranspiration and the tradeoffs associated with water demand further diminish the viability of large-scale forestation.⁴⁷

3.3 Internal energy-carbon coupling

Our results from mixed-effects models, isolating the influence of external environment aridity, reveal divergent intrinsic couplings between normalized carbon gains and energy budget responses (Fig. 4). Notably, PV systems exhibit albedo-mediated co-benefits, with each unit of carbon emission reduction correlating with enhanced effective albedo (Δα/ΔC = +0.008 ± 0.0007, Fig. 4b) and reduced ULR (ΔULR/ΔC = −8.53, Fig. 4a). The finding confirms the albedo-carbon synergy that actively regulates the climate (Fig. 3). In contrast, forestation shows each CO₂ absorption unit exhibits albedo decline (Δα/ΔC = −0.004 ± 0.0007) without significant ΔULR reduction. The decoupling indicates the anticipated climate mitigation from forest carbon sequestration is often counteracted by albedo-induced warming, leading to climate change amplification.⁴⁸ However, the divergent PV effect challenges this long-held view that a reduction in albedo universally offsets the benefits of carbon mitigation.

3.4 Optimal zone identification

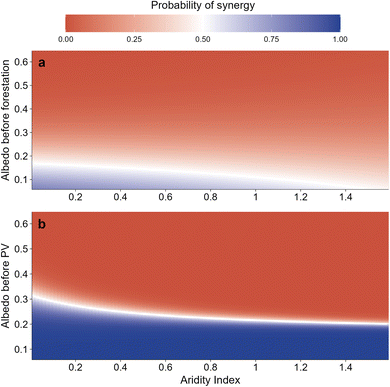
Our probability model pinpoints actionable landscape thresholds for optimizing climate mitigation. PV systems have a greater than 0.5 probability of attaining carbon-energy synergy when the average background albedo is less than 0.25. The thresholds for a synergy probability greater than 0.5 span from 0.31 (with an AI of 0.01) to 0.20 (with an AI of 1.58, Fig. 5). In contrast, anthropogenic forestation shows constrained synergy efficacy. The synergy probability greater than 0.5 of forestation only occurs at extremely low albedo values (less than 0.17) and is ineffective in humid zones (AI greater than 1.47, probability less than 0.5). These thresholds for a synergy probability greater than 0.5 underscore the geographical versatility of PV systems in balancing emission reduction and surface energy regulation across aridity gradients.

In this study, a grid resolution of 0.5° was adopted as the analytical base, which may introduce a local smoothing effect that impacts the accuracy of carbon sequestration and energy balance estimates. Although we employed 23-year average forest ecosystem carbon absorption rates instead of short-term data to mitigate uncertainties in forest age, a single 0.5° grid cell can still encompass sub-pixel heterogeneity in the forest structure. For instance, the coexistence of high-density plantations and open forests. Such structural differences may drive variability in evapotranspiration-mediated cooling, leading to within-grid fluctuations in ΔULR even under the same aridity conditions.⁴⁹ Crucially, our results indicate that 54.8% of forestation zones exhibit a carbon-energy trade-off, with the R_Fr in these trade-off zones being six times the magnitude of R_Fc (Fig. 1 and S2). Additionally, the carbon emission reduction rate of PV systems is 100-fold higher than the CO₂ absorption rate of afforestation (Fig. 3c). Thus, sub-pixel heterogeneity in forests does not alter the macroscopic conclusion that PV systems outperform afforestation in terms of climate mitigation effectiveness.

Fig. 1 Spatial distribution of the synergy-tradeoff relationship between carbon gains and Earth's surface energy balance in the feedback of anthropogenic forestation or solar photovoltaic (PV) power plants to climate change. (a) Spatial distribution of sample grids with synergy or tradeoff in feedback to climate change. The gray-scale background indicates the aridity index (AI, which is the ratio of annual average precipitation to annual average reference evapotranspiration). (b) Sample sizes (n) of different types of synergy or tradeoff grids. The value in parentheses is the percentage of the total sample size.

Fig. 2 The synergy-tradeoff relationship effectiveness of carbon gains and Earth's surface energy balance of forestation and PV systems under different land cover types in terms of climate mitigation. The percentage of total sample size is shown in parentheses.

Fig. 3 Climate attribute responses of forestation and PV systems to AI. (a) Forestation's CO₂ absorption and PV's emission reduction relative to original land cover versus AI, with the ordinate (vertical axis) being logarithmized on a base of 10 (log 10). (b) Upwelling longwave radiation anomalies (ΔULR = forestation/PV − original surface). (c) Forestation or PV's actual albedo and PV's effective albedo changes accounting for energy diversion (Δα = original surface − forestation/PV). Positive values of ΔULR signify the climate amplification effect, while negative values of Δα represent the climate mitigation benefit. Linear fits (least-squares) show slope significance, where “**” indicates p < 0.01, “***” indicates p < 0.001, and “ns” indicates not significant. AI classification: Hyper Arid (<0.03), Arid (0.03–0.2), Semi-Arid (0.2–0.5), Dry Sub-Humid (0.5–0.65), Humid (>0.65). Boxes show the interquartile range (25th–75th percentiles) of climate attributes across AI classification, with central lines marking medians, whiskers extend to ±1.5× IQR. n is the sample size.

Fig. 4 Intrinsic coupling between normalized carbon gains and energy budget responses for forestation and PV. (a) Forestation or PV's ULR versus normalized carbon gains. (b) Forestation or PV's actual albedo and PV's effective albedo versus carbon gains. All carbon metrics are normalized by z-scoring. Blue shaded background indicates climate mitigation benefit (ULR < 0 or α > 0 per unit carbon gain), while red shaded background indicates climate amplification effect (ULR > 0 or α < 0 per unit carbon gain). The slopes of linear mixed-effects models, presented with 95% confidence interval (CI) error bars, serve to quantify the intrinsic couplings (see method). Here, “***” indicates p < 0.001, while “ns” indicates not significant.

Fig. 5 Probability of achieving carbon-energy synergy for climate mitigation, mapped against regional aridity and background albedo. (a) Forestation exhibits limited synergy potential (probability less than 0.5). (b) PV shows robust synergy (probability greater than 0.5).

Forests provide irreplaceable multifunctional ecosystem services beyond carbon sequestration. Their role as critical habitats for maintaining global biodiversity, regulating water cycles, and supporting local livelihoods dependent on ecological stability.⁵⁰ Although our findings question the overestimated climate mitigation efficiency of anthropogenic forestation, contrasting with the IPCC AR6's designation of forestation as a cornerstone climate solution,⁵¹ we do not dismiss the intrinsic and ecological value of forests. Instead, these results aim to refine our understanding of forestation's specific role in climate mitigation, while strongly emphasizing that the value of sustainable forest management practices, particularly those centered on biodiversity conservation, remains indispensable. Such practices are crucial for preserving existing carbon stocks and enhancing climate resilience.^4,52 Our focus on PV's carbon-albedo synergy is intended to complement, rather than compete with, efforts to protect and sustainably manage forest ecosystems.⁵³ As the positive ecological benefits of PV systems are gaining recognition,⁵⁴ we emphasize the need for careful assessment of deployment scale in arid (AI < 1.47) and high-albedo regions to ensure carbon gains outweigh the potential climate costs associated with altered surface energy budgets. In humid regions (AI > 1.47) with intense land-use competition, given the carbon-energy tradeoffs of forestation versus PV's synergistic advantages, protecting natural forests from degradation should be prioritized while promoting PV-based integrated land-use models. Overall, we underscore that PV outperforms forestation as a more efficient climate mitigation strategy.

4. Conclusion

As large-scale PV systems are increasingly covering the Earth's surface as a novel land-use infrastructure, the choice between PV and traditional forestation for climate change mitigation within limited land resources has become a key challenge in climate policy. Our study, which compared the direct and indirect climate mitigation feedbacks of PV systems and forest vegetation across different environmental regions, yielded significant findings. First, PV systems show a strong carbon-energy synergy, reducing emissions at a rate 100 times higher than the CO₂ absorption of forestation. Additionally, their albedo-driven solar radiative cooling effect increases as they reduce more carbon emission. In contrast, anthropogenic forestation encounters a carbon-albedo trade-off; the decrease in albedo due to carbon sequestration generates solar radiative warming six times greater than the benefit from CO₂ absorption. Crucially, we found that in regions with diverse aridity levels, controlling the albedo of the areas where PV systems are installed can create a more effective climate mitigation strategy than traditional afforestation. This research reveals the overlooked potential of PV systems in combining carbon emission reduction and solar radiation regulation, offering a scientific foundation for optimizing PV placement to boost climate mitigation effectiveness. Future studies can deepen the understanding of PV system's cooling effects beyond shortwave radiation regulation by exploring additional mechanisms associated with longwave/heat fluxes and displaced fossil fuel generation and developing enhanced energy balance models and integrating complex power system analyses.

Author contributions

Q. Y. conceived the study; Q. Y., and H. Q. G. collected remote sensing data and flux site data; Q. Y. performed the analysis and generated figures with support from B. Z.; Q. Y. and B. Z. jointly drafted the paper. All authors contributed to the interpretation of the results.

Conflicts of interest

The authors declare no competing interests.

Data availability

The data in this study are publicly available, transparently sourced, and derived from published datasets. It can be easily found and replicated according to our description in the Method section.

Supplementary information is available. See DOI: https://doi.org/10.1039/d5el00093a.

Acknowledgements

This research was supported by the National Key Research and Development Project of China (grant number: 2022YFC3105402), the National Natural Science Foundation of China (grant number: 32371621), and Ministry of Education Key Laboratory for Biodiversity Science and Ecological Engineering (grant number: Z202402).

References

1. P. Friedlingstein, M. O'Sullivan, M. W. Jones, R. M. Andrew, J. Hauck, P. Landschützer, C. Le Quéré, H. Li, I. T. Luijkx and A. Olsen, Global carbon budget 2024, Earth Syst. Sci. Data Discuss., 2025, 17, 965–1039,  DOI:10.5194/essd-17-965-2025.
2. J.-F. Bastin, Y. Finegold, C. Garcia, D. Mollicone, M. Rezende, D. Routh, C. M. Zohner and T. W. Crowther, The global tree restoration potential, Science, 2019, 365, 76–79,  DOI:10.1126/science.aax0848.
3. IEA, Renewables 2022, International Energy Agency, 2022, 2022,.
4. L. Augusto, R. Borelle, A. Boča, L. Bon, C. Orazio, A. Arias-González, M. Bakker, N. Gartzia-Bengoetxea, H. Auge and F. Bernier, Widespread slow growth of acquisitive tree species, Nature, 2025, 640, 395–401,  DOI:10.1038/s41586-025-08692-x.
5. S. Chiquier, P. Patrizio, M. Bui, N. Sunny and N. Mac Dowell, A comparative analysis of the efficiency, timing, and permanence of CO₂ removal pathways, Energy Environ. Sci., 2022, 15, 4389–4403,  10.1039/D2EE01021F.
6. S. Dunnett, R. A. Holland, G. Taylor and F. Eigenbrod, Predicted wind and solar energy expansion has minimal overlap with multiple conservation priorities across global regions, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2104764119,  DOI:10.1073/pnas.2104764119.
7. B. Tan, L.-S. Sheng, Q. Yuan, D.-F. Xu, Y.-Y. Hao, S.-Q. Zhou and B. Zhao, Chinese adapting land policy is guiding “photovoltaic plus” as a nature-based solution towards future, Nat. Based Solut., 2024, 6, 100201,  DOI:10.1016/j.nbsj.2024.100201.
8. S. Wei, A. D. Ziegler, Y. Qin, D. Wang, Y. Chen, J. Yan and Z. Zeng, Small reduction in land surface albedo due to solar panel expansion worldwide, Commun. Earth Environ., 2024, 5, 474,  DOI:10.1038/s43247-024-01619-w.
9. J. Weber, J. A. King, N. L. Abraham, D. P. Grosvenor, C. J. Smith, Y. M. Shin, P. Lawrence, S. Roe, D. J. Beerling and M. V. Martin, Chemistry-albedo feedbacks offset up to a third of forestation's CO2 removal benefits, Science, 2024, 383, 860–864,  DOI:10.1126/science.adg6196.
10. R. E. Blankenship, D. M. Tiede, J. Barber, G. W. Brudvig, G. Fleming, M. Ghirardi, M. Gunner, W. Junge, D. M. Kramer and A. Melis, Comparing photosynthetic and photovoltaic efficiencies and recognizing the potential for improvement, Science, 2011, 332, 805–809,  DOI:10.1126/science.1200165.
11. Y. M. Bar-On, X. Li, M. O'Sullivan, J.-P. Wigneron, S. Sitch, P. Ciais, C. Frankenberg and W. W. Fischer, Recent gains in global terrestrial carbon stocks are mostly stored in nonliving pools, Science, 2025, 387, 1291–1295,  DOI:10.1073/pnas.2104764119.
12. R. Alkama and A. Cescatti, Biophysical climate impacts of recent changes in global forest cover, Science, 2016, 351, 600–604,  DOI:10.1126/science.aac8083.
13. Z. Yu, M. Shao, W. Ma, C. Wang and J. Yang, Satellite-driven evidence of forest-induced temperature variability and its biophysical and biogeochemical pathways across latitudes, Ecol. Indic., 2025, 175, 113545,  DOI:10.1016/j.ecolind.2025.113545.
14. J. Bao, X. Li, T. Yu, L. Jiang, J. Zhang, F. Song and W. Xu, Are Regions Conducive to Photovoltaic Power Generation Demonstrating Significant Potential for Harnessing Solar Energy via Photovoltaic Systems?, Sustainability, 2024, 16, 3281,  DOI:10.3390/en13236224.
15. E. Skoplaki and J. A. Palyvos, Operating temperature of photovoltaic modules: A survey of pertinent correlations, Renewable energy, 2009, 34, 23–29,  DOI:10.1016/j.renene.2008.04.009.
16. Z. Xu, Y. Li, Y. Qin and E. Bach, A global assessment of the effects of solar farms on albedo, vegetation, and land surface temperature using remote sensing, Sol. Energy, 2024, 268, 112198,  DOI:10.1016/j.solener.2023.112198.
17. G. A. Barron-Gafford, R. L. Minor, N. A. Allen, A. D. Cronin, A. E. Brooks and M. A. Pavao-Zuckerman, The Photovoltaic Heat Island Effect: Larger solar power plants increase local temperatures, Sci. Rep., 2016, 6, 35070,  DOI:10.1038/srep35070.
18. R. Stern, J. D. Muller, E. Rotenberg, M. Amer, L. Segev and D. Yakir, Photovoltaic fields largely outperform afforestation efficiency in global climate change mitigation strategies, PNAS nexus, 2023, 2, pgad352,  DOI:10.1093/pnasnexus/pgad352.
19. Z. Liao, C. Yue, B. He, K. Zhao, P. Ciais, R. Alkama, G. Grassi, S. Sitch, R. Chen and X. Quan, Growing biomass carbon stock in China driven by expansion and conservation of woody areas, Nat. Geosci., 2024, 17, 1127–1134,  DOI:10.1038/s41561-024-01569-0.
20. Y. Chen, J. Zhou, Y. Ge and J. Dong, Uncovering the rapid expansion of photovoltaic power plants in China from 2010 to 2022 using satellite data and deep learning, Rem. Sens. Environ., 2024, 305, 114100,  DOI:10.1016/j.rse.2024.114100.
21. K. E. Trenberth, J. T. Fasullo and J. Kiehl, Earth's global energy budget, Bull. Am. Meteorol. Soc., 2009, 90, 311–324,  DOI:10.1175/2008BAMS2634.1.
22. G. F. Nemet, Net radiative forcing from widespread deployment of photovoltaics, Environ. Sci. Technol., 2009, 43, 2173–2178,  DOI:10.1021/es801747c.
23. S. Dunnett, A. Sorichetta, G. Taylor and F. Eigenbrod, Harmonised global datasets of wind and solar farm locations and power, Sci. Data, 2020, 7, 130,  DOI:10.1038/s41597-020-0469-8.
24. Solargis, Global Solar Atlas 2.0, https://globalsolaratlas.info/.
25. M. Etminan, G. Myhre, E. J. Highwood and K. P. Shine, Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing, Geophys. Res. Lett., 2016, 43(12), 614–612,  DOI:10.1002/2016GL071930.
26. G. Myhre, E. J. Highwood, K. P. Shine and F. Stordal, New estimates of radiative forcing due to well mixed greenhouse gases, Geophys. Res. Lett., 1998, 25, 2715–2718,  DOI:10.1029/98GL01908.
27. R. A. Betts, Offset of the potential carbon sink from boreal forestation by decreases in surface albedo, Nature, 2000, 408, 187–190,  DOI:10.1038/35041545.
28. N. G. M. Laboratory, Trends in Atmospheric, CO₂, N₂O, https://gml.noaa.gov/ccgg/trends/.
29. S. Rohatyn, D. Yakir, E. Rotenberg and Y. Carmel, Limited climate change mitigation potential through forestation of the vast dryland regions, Science, 2022, 377, 1436–1439,  DOI:10.1126/science.abm9684.
30. MoEaEnvironment and NBO Statistics, Statistics on the Release of the Carbon Dioxide Emission Factor of Electricity in 2021, People's Republic of China, China, 2024.
31. D. C. a. Envision., Photovoltaic Modules-Carbon Footprint and Low-Carbon Development Report, Deloitte China, China, 2024.
32. N. L. Harris, D. A. Gibbs, A. Baccini, R. A. Birdsey, S. De Bruin, M. Farina, L. Fatoyinbo, M. C. Hansen, M. Herold and R. A. Houghton, Global maps of twenty-first century forest carbon fluxes, Nat. Clim. Change, 2021, 11, 234–240,  DOI:10.1038/s41558-020-00976-6.
33. W. Xufeng, C. Tao, X. Jingfeng, W. Tonghong, J. Tan, Y. Zhang, Z. Ren, L. Geng, H. Wang, Z. Xu., S. Liu and X. Li, A post-processed carbon flux dataset for 34 eddy covariance flux sites across the Heihe River Basin, China, National Tibetan Plateau Data Center, 2025.
34. H. Guo, B. Zhao, J. Chen, Y. Yan, B. Li and J. Chen, Seasonal changes of energy fluxes in an estuarine wetland of Shanghai, China, Chin. Geogr. Sci., 2010, 20, 23–29,  DOI:10.1007/s11769-010-0023-2.
35. R. Gou, J. Chi, J. Liu, Y. Luo, A. Shekhar, L. Mo and G. Lin, Atmospheric water demand constrains net ecosystem production in subtropical mangrove forests, J. Hydrol., 2024, 630, 130651,  DOI:10.1016/j.jhydrol.2024.130651.
36. J. Liu and D. Y. Lai, Subtropical mangrove wetland is a stronger carbon dioxide sink in the dry than wet seasons, Agric. For. Meteorol., 2019, 278, 107644,  DOI:10.1016/j.agrformet.2019.107644.
37. C. Wang, X. Zhao, X. Chen, C. Xiao, X. Fan, C. Shen, M. Sun, Z. Shen and Q. Zhang, Variations in CO₂ and CH₄ exchange in response to multiple biophysical factors from a mangrove wetland park in southeastern China, Atmosphere, 2023, 14, 805,  DOI:10.3390/atmos14050805.
38. G. Han, F. Wang, J. Ma, L. Xiao, X. Chu and M. Zhao, Blue carbon sink function, formation mechanism and sequestration potential of coastal salt marshes, Chin. J. Plant Ecol., 2022, 46, 373–382,  DOI:10.17521/cjpe.2021.0264.
39. X. Zhu, J. Chen, L. Li, M. Li, T. Li, Z. Qin, F. Wang and X. Zhao, Asynchronous methane and carbon dioxide fluxes drive temporal variability of mangrove blue carbon sequestration, Geophys. Res. Lett., 2024, 51, e2023GL107235,  DOI:10.1029/2023GL107235.
40. D. Wei, Y. Qi, Y. Ma, X. Wang, W. Ma, T. Gao, L. Huang, H. Zhao, J. Zhang and X. Wang, Plant uptake of CO₂ outpaces losses from permafrost and plant respiration on the Tibetan Plateau, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2015283118,  DOI:10.1073/pnas.2015283118.
41. X. Zhang, T. Zhao, H. Xu, W. Liu, J. Wang, X. Chen and L. Liu, GLC_FCS30D: the first global 30 m land-cover dynamics monitoring product with a fine classification system for the period from 1985 to 2022 generated using dense-time-series Landsat imagery and the continuous change-detection method, Earth Syst. Sci. Data, 2024, 16, 1353–1381,  DOI:10.5194/essd-16-1353-2024.
42. J. Liu, C. Schaaf, A. Strahler, Z. Jiao, Y. Shuai, Q. Zhang, M. Roman, J. A. Augustine and E. G. Dutton, Validation of Moderate Resolution Imaging Spectroradiometer (MODIS) albedo retrieval algorithm: Dependence of albedo on solar zenith angle, J. Geophys. Res.:Atmos., 2009, 114(D1), D01106,  DOI:10.1029/2008JD009969.
43. M. O. Román, C. B. Schaaf, P. Lewis, F. Gao, G. P. Anderson, J. L. Privette, A. H. Strahler, C. E. Woodcock and M. Barnsley, Assessing the coupling between surface albedo derived from MODIS and the fraction of diffuse skylight over spatially-characterized landscapes, Rem. Sens. Environ., 2010, 114, 738–760,  DOI:10.1016/j.rse.2009.11.014.
44. R. J. Zomer, J. Xu and A. Trabucco, Version 3 of the global aridity index and potential evapotranspiration database, Sci. Data, 2022, 9, 409,  DOI:10.1038/s41597-022-01493-1.
45. S. Liang, A. D. Ziegler, P. B. Reich, K. Zhu, D. Wang, X. Jiang, D. Chen, P. Ciais and Z. Zeng, Climate mitigation potential for targeted forestation after considering climate change, fires, and albedo, Sci. Adv., 2025, 11, eadn7915,  DOI:10.1126/sciadv.adn7915.
46. G. B. Bonan, Forests and climate change: forcings, feedbacks, and the climate benefits of forests, Science, 2008, 320, 1444–1449,  DOI:10.1126/science.1155121.
47. R. Alkama, G. Forzieri, G. Duveiller, G. Grassi, S. Liang and A. Cescatti, Vegetation-based climate mitigation in a warmer and greener World, Nat. Commun., 2022, 13, 606,  DOI:10.1038/s41467-022-28305-9.
48. N. Hasler, C. A. Williams, V. C. Denney, P. W. Ellis, S. Shrestha, D. E. Terasaki Hart, N. H. Wolff, S. Yeo, T. W. Crowther and L. K. Werden, Accounting for albedo change to identify climate-positive tree cover restoration, Nat. Commun., 2024, 15, 2275,  DOI:10.1038/s41467-024-46577-1.
49. Y. Su, C. Zhang, P. Ciais, Z. Zeng, A. Cescatti, J. Shang, J. M. Chen, J. Liu, Y.-P. Wang and W. Yuan, Asymmetric influence of forest cover gain and loss on land surface temperature, Nat. Clim. Change, 2023, 13, 823–831,  DOI:10.1038/s41558-023-01757-7.
50. P. Manning, F. Van Der Plas, S. Soliveres, E. Allan, F. T. Maestre, G. Mace, M. J. Whittingham and M. Fischer, Redefining ecosystem multifunctionality, Nat. Ecol. Evol., 2018, 2, 427–436,  DOI:10.1038/s41559-017-0461-7.
51. IPCC, Climate Change 2023: Synthesis Report. A Report of the Intergovernmental Panel on Climate Change. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, IPCC, 2023.
52. Y. Feng, B. Schmid, M. Loreau, D. I. Forrester, S. Fei, J. Zhu, Z. Tang, J. Zhu, P. Hong, C. Ji, Y. Shi, H. Su, X. Xiong, J. Xiao, S. Wang and J. Fang, Multispecies forest plantations outyield monocultures across a broad range of conditions, Science, 2022, 376, 865–868,  DOI:10.1126/science.abm6363.
53. C. Wu, H. Liu, L. Wei, Y. Yu, W. Zhao, L. Guo, Z. He, O. Yetemen and D. Yang, Diverse vegetation responses to solar farm installation are also driven by climate change, Commun. Earth Environ., 2025, 6, 118,  DOI:10.1038/s43247-025-02121-7.
54. M. A. Sturchio, A. Gallaher and S. M. Grodsky, Ecologically informed solar enables a sustainable energy transition in US croplands, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2501605122,  DOI:10.1073/pnas.2501605122.

---