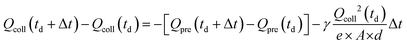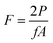Charge recombination in polythiophene: non-fullerene acceptor solar cells with IE offsets exceeding 1 eV

Abstract

In organic solar cells the energetic landscape of the donor–acceptor heterojunction determines the efficiency of charge generation and charge recombination processes, and thereby the device performance. Here, we present a study on a series of 15 donor–acceptor bulk heterojunctions (BHJs) consisting of either the donor polymer poly(3-hexylthiophene) (P3HT) or poly[2,5-bis(3-tetradecylthiophen-2-yl)thieno[3,2-b]thiophene] (pBTTT-C14) and selected non-fullerene acceptors (NFAs), spanning a wide range of interfacial energetics. We demonstrate that the internal quantum efficiency (IQE) is limited by geminate and non-geminate recombination processes and, importantly, decreases with the energy difference between the donor's ionization energy (IE) and the acceptor's electron affinity (EA), in other words, the diagonal bandgap, specifically if less than 1 eV, regardless of the interfacial IE offset. The dependence of charge recombination on the diagonal bandgap can be explained in the framework of the energy gap law. Our results provide further insight into the importance and impact of interfacial energetics in donor:NFA blends with large IE offsets.

---

Broader context

Photovoltaic (PV) technology is a clean and renewable energy source that has recently surpassed the TW scale. It plays a critical role in the urgently required transition from fossil fuel-based energy production to sustainable and green energy generation. Among the many different PV materials and device concepts, organic semiconductors offer appealing properties for applications where low-weight, non-toxic, solution-processable, and flexible materials are required. However, device performance and stability still limit their application. The photoactive layer of such cells is composed of two blended components, and understanding their interactions and interface energetics is critical for the design and development of further optimized material systems. Our study shows that large energy offsets between those two components facilitate charge recombination, severely limiting device performance, a key factor in materials design and combination.

Introduction

The power conversion efficiency (PCE) of organic solar cells (OSCs) has recently surpassed 20%, primarily due to the development of novel non-fullerene acceptors.¹ However, limited (photo)stability and reductions in device efficiency when upscaling to larger cell areas, as well as the use of expensive materials and hazardous (co)solvents during thin film deposition still hamper commercialization.^2,3 In fact, the current state-of-the-art efficiencies are only possible when using sophisticated electron donor and acceptor materials, which are costly due to their complex synthesis and thus may not gain commercial relevance.^4,5 Hence, simpler, cost-effective and scalable materials are of importance. In this regard, regioregular poly(3-hexylthiophene) (P3HT) and poly[2,5-bis(3-tetradecylthiophen-2-yl)thieno[3,2-b]thiophene] (pBTTT-C14) are two of the most considered conjugated donor polymers, and promising candidates for upscaling, since they can be synthesized in large quantities at affordable cost.^6,7 Recent work has highlighted polymer donor:non-fullerene acceptor (NFA) systems as the most promising for upscaling and commercialization, with ongoing efforts to simplify synthetic routes and make NFA synthesis more cost-effective.⁸ However, efficiencies of P3HT and pBTTT:NFA based solar cells lag behind the current state-of-the-art achieved with highly engineered organic semiconductors.^9–11

In general, the efficiency of a solar cell is determined by three figures of merit: the device's short circuit current density (J_SC), the open circuit voltage (V_OC), and the fill factor (FF). The photocurrent generation J_SC can be optimized through variation of the donor and acceptor bandgaps, aiming for absorption of light in complementary spectral parts, thereby increasing the maximum theoretical photocurrent of the blend-based cell. Similarly, a lot of effort has gone into optimizing the energetic landscape of the blends, specifically at the interface between the donor and acceptor, mainly to enhance the V_OC, while maintaining high quantum efficiencies in OSCs.^12–15

The photophysics of OSCs differs substantially from that of conventional inorganic solar cells and hybrid organic–inorganic perovskite solar cells since the primary photoexcitation in organic semiconductors is a coulombically bound Frenkel-type exciton.^16,17 Following photogeneration, the exciton must first be converted into free charges, which is mediated by interfacial charge transfer (CT) states and driven by the energy offsets at the donor:acceptor heterojunction interface. The offset between the ionization energy (IE) of the donor and that of the acceptor drives the hole transfer (HT) process, similarly, the offset between the donor's and acceptor's electron affinity (EA) drives the electron transfer (ET) process, and the energetic landscape at the interface facilitates charge separation and transport away from the interface towards the bulk. However, the offsets required to drive charge transfer and separation can add to the energetic losses that ultimately determine the device's V_OC.^13,18

The minimum offset required to ensure efficient (near unity) exciton-to-charge conversion has been a matter of debate.^19–23 We have recently demonstrated that sizeable IE offsets (ΔIE) of about 0.5 eV as measured by ultraviolet photoelectron spectroscopy (UPS) and photoelectron yield spectroscopy in air (PESA) on the pristine materials are required to ensure near-unity photon-to-charge conversion in donor/low-bandgap NFA systems. In fact, inefficient acceptor exciton quenching occurs in low IE offset systems due to interfacial energy level bending, as a consequence of the interfacial energetic landscape influenced by the acceptors’ quadrupole moments.²⁴ Consequently, sizeable IE offsets are needed to ensure complete exciton quenching, with many of the current donor:NFA couples matching this condition.²⁴ In this regard, regioregular P3HT and pBTTT are promising materials, since they have the lowest IEs among common donor polymers used in OSCs.²⁵ However, using donors with a low IE can result in small diagonal bandgaps (i.e., the energy difference between IE of the donor, IE_D, and EA of the acceptor, EA_A), which causes low V_OC¹³ and potentially increased non-radiative losses.^26–28

To explore this IE offset regime, in this work, we compare the photovoltaic performance of BHJ solar cells using P3HT and pBTTT as donor polymers in binary blends with different NFAs, spanning a range of IE offsets from 0.79 eV to as much as 1.56 eV, and diagonal bandgaps, IE_D-EA_A, from as low as 0.50 eV to about 1.06 eV. The corresponding OSCs yield moderate PCEs in the range of 0.4–8% at best, with P3HT:ZY-4Cl exhibiting the highest device performance. To gain more insight into the processes that cause the low J_SC and moderate device performance, we focused in particular on the donor polymer P3HT and conducted an in-depth study on various P3HT:NFA-based devices. We reveal the photophysical processes through a combination of steady-state and transient optical and electro-optical spectroscopies.

Interestingly, we observed that not only the V_OC but also the J_SC decreased when the diagonal bandgap was reduced. Hence, we examined the origin of the low internal quantum efficiency (IQE), that is, the conversion of photons absorbed by the photoactive layer into charge carriers ultimately extracted from the device. We observed that the IQE decreases with decreasing diagonal bandgap. However, time-resolved photoluminescence (TRPL) measurements revealed efficient and near-unity photoluminescence quenching efficiency (PLQE) in all blends, indicating that exciton quenching is not an efficiency-limiting factor; unlike in lower IE offset systems,²⁴ the IQE did not closely follow the PLQE. This lack of a direct correlation between PLQE and IQE indicates the presence of additional loss channels besides the exciton-to-CT state conversion process, further reducing the efficiency of P3HT:NFA devices.²¹

The central aim of this work is to unravel why P3HT-based devices underperform compared to devices based on other state-of-the-art donor polymers. We demonstrate that this limitation originates from its low IE, which results in small diagonal bandgaps when combined with common NFAs. The small diagonal bandgap promotes charge carrier recombination. One potential strategy to overcome this challenge is to use NFAs with lower EA, thereby increasing the diagonal bandgap energy, while maintaining efficient exciton quenching and charge generation. Such an approach could also mitigate bi-molecular recombination, ultimately improving device performance, as demonstrated for P3HT:ZY-4Cl and P3HT:O-IDTBR, both also examined in our study. Such molecular design strategies can be supported by computational material design approaches, as highlighted in a recent report.²⁹

We examined the origin of the reduced IQE using an optical-pump electronic-probe technique (i.e., time-delayed collection field, TDCF) to reveal the dominant recombination mechanisms responsible for these losses. We identified significant bi-molecular recombination as an efficiency-limiting process in small diagonal bandgap blends, particularly in P3HT:IT-4F, which has the lowest diagonal bandgap (with only 0.51 eV). Our results show that bi-molecular recombination decreases with increasing the diagonal bandgap as suggested by the energy gap law.^26–28 Overall, the results obtained from transient absorption (TA), TRPL, and TDCF spectroscopies suggest that both geminate and non-geminate recombination decrease with increasing diagonal bandgap. Importantly, we found that the energy gap law influences not only the energy losses and photocurrent generation in fullerene acceptor (FA) based solar cells, as previously reported,^26,27 but it also contributes to recombination and photocurrent losses in NFA-based systems.

Results and discussion

Impact of energy levels on photocurrent generation efficiency

P3HT and pBTTT-C14 were combined with different NFAs encompassing in total 15 different binary bulk heterojunctions of increasingly large IE offset. Fig. 1a shows the chemical structures of the donor polymers, namely, regio-regular P3HT and pBTTT-C14 and the NFAs IEICO, IEICO-4Cl, IEICO-4F, IDT-2Br, ZY-4Cl, Y6, O-IDTBR, BT-CIC, IT-4F, ICC6, and FBR, by order of increasing IE offset (see Fig. 1b). Generally, the IEs of the NFAs are all significantly larger than that of P3HT and pBTTT, leading to large IE offsets in donor:NFA blends, which are expected to drive efficient hole transfer at the donor/acceptor heterojunction. Energy levels were determined by UPS and LE-IPES (low-energy inverse photoelectron spectroscopy), and the spectra shown in Fig. S1 SI are for the P3HT, IEICO-4Cl, IDT-2Br, and ZY-4Cl. Energy levels of other NFAs were used as measured and reported in our previous works^24,30 (Y6 values were updated).³⁰ For comparison, we also used photoelectron yield spectroscopy in air (PESA) to determine the IE, see Fig. S2 (SI), and observed that the values were in good agreement with those from UPS measurements.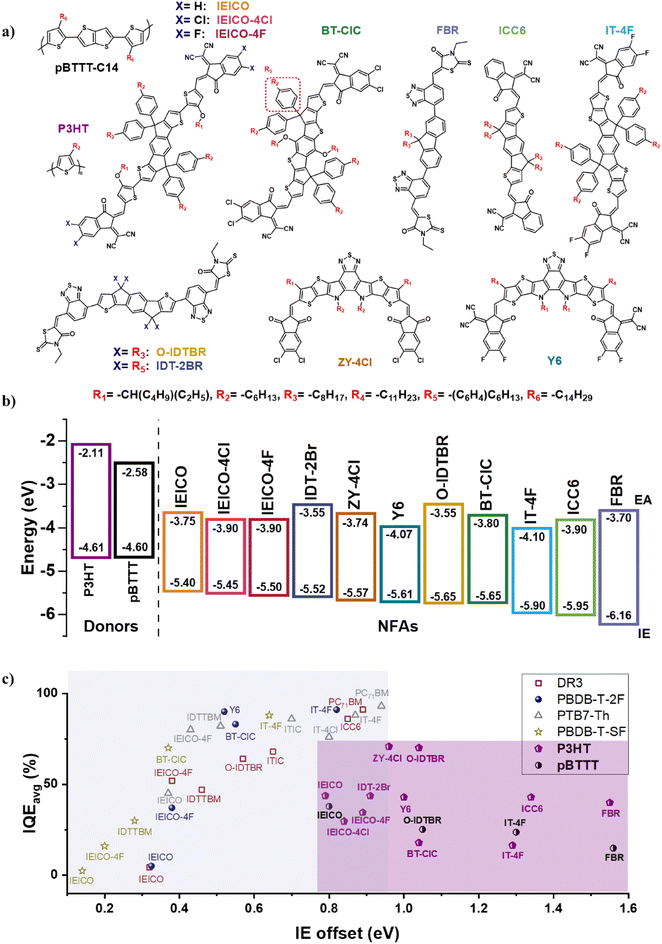

Fig. 1 Role of large IE offset on the average internal quantum efficiency, IQE_Avg, in P3HT:NFA and pBTTT:NFA based devices. (a) Chemical structures of the donor polymers P3HT and pBTTT-C14 and the NFAs. (b) IE and EA of the investigated materials measured by UPS and LE-IPES, respectively. (c) Averaged IQE (IQE_Avg) of optimized BHJ donor-NFA devices from our previous study²⁴ (grey shaded area), P3HT:NFA, and pBTTT:NFA based devices (purple shaded area) versus the IE offset (ΔIE) of the photoactive blends.

Next, we evaluated the spectrally-averaged internal quantum efficiency (IQE_Avg) of the devices as a function of the ΔIE to reveal the impact of ΔIE > 0.9 eV on the IQE. Fig. 1c displays the IQE_Avg in relation to ΔIE ranging from 0.1 eV to as much as 1.55 eV. Note that the data includes in total 39 donor:acceptor pairs, providing a comprehensive assessment of the impact of ΔIE on the device IQE. The IQEs and ΔIE provided for DR3, PBDB-T-2F, PTB7-Th, and PBDB-T-SF donor based systems (grey shaded area) are from our previous study,²⁴ whereas the P3HT:NFA and pBTTT:NFA based systems (purple shaded area) were all investigated in this work. Generally, for the systems with ΔIE up to 0.5–0.9 eV, an increase in IQE was observed upon increasing ΔIE.²⁴ However, for P3HT and pBTTT systems with offsets exceeding 0.9 eV, this trend no longer persisted, as not only were lower IQE_Avg values observed, but they also no longer correlated with ΔIE, suggesting other processes became the limiting factors of the charge generation efficiency and device performance.

The IQE spectra were determined from the measured EQE spectra (Fig. 2b–d) using the relationship IQE = EQE/(1 − reflectance − parasitic absorption).³¹ The corresponding reflectance spectra were collected in an integrating sphere, while the parasitic absorption was obtained from transfer matrix modelling using refractive indexes (n) and extinction coefficients (k) of the representative systems obtained by spectroscopic ellipsometry measurements (see Fig. S3 and S4 for n and k data and the reflectance spectra, respectively, SI). The resulting IQE spectra are shown in Fig. S5 (SI). All systems exhibited relatively flat IQE spectra, with P3HT:ZY-4Cl and P3HT:O-IDTBR exhibiting the highest IQE values. The values of the IQE_Avg and the spectral range (λ_Avg) used for estimating the IQE_Avg are shown in Table S1 (SI).

Fig. 2 Device performance of optimized P3HT:NFA and pBTTT:NFA based blends. (a) J–V characteristics of P3HT:NFA based solar cells. (b) EQE spectra of P3HT:NFA devices. (c) J–V characteristics of pBTTT:NFA based solar cells. (d) EQE spectra of pBTTT:NFA OSCs.

Since the IE offset is not the only efficiency-determining parameter in P3HT-based and pBTTT-based systems, we also investigated the impact of the electron affinity offset (ΔEA) and of the diagonal bandgap (IE_D-EA_A) on the IQE_Avg (Fig. S6, SI). Interestingly, the IQE_Avg appears to increase with the diagonal bandgap of the heterojunction. A possible explanation is increased charge recombination at low diagonal bandgap, hampering the (re)-dissociation of CT states and/or the generation and extraction of free charges.^26–28 This is in line with the energy gap law,^26–28 which predicts an exponential increase of the rate of internal conversion processes between two electronic states (here the CT and ground state) when decreasing the energy difference between the two states due to stronger Franck Condon coupling to vibrational states. This increases non-radiative recombination, possibly explaining the decreased IQE observed in many of the P3HT:NFA and pBTTT:NFA systems. In fact, the diagonal bandgaps are mostly below 1 eV. However, at the interface local shifts of the energy levels caused by the interactions of the charges with the surrounding acceptor's quadrupole moments might change the energetics. To understand the reasons behind the low IQE observed in this study, we investigated which of the devices’ figures of merit most significantly limited the performance.

Absorption and device performance

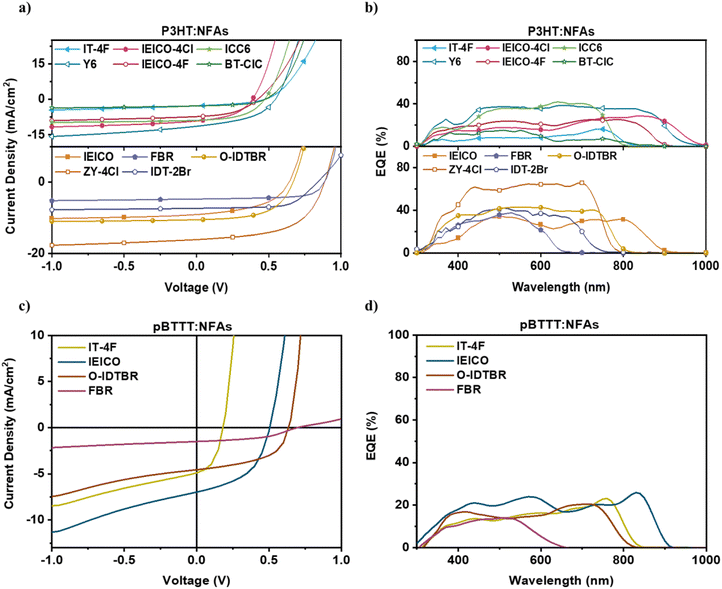
Steady-state optical characterization was carried out by UV-Vis-NIR spectrophotometry and photoluminescence (PL) spectroscopy. The UV-Vis-NIR spectra of the neat materials are presented in Fig. S7a and b (SI). P3HT and pBTTT generally absorb from 350 to 650 nm (see Fig. S7a and b, SI). The corresponding blend absorption coefficients (α_abs) were determined (Fig. S7e and f, SI) where two absorption peaks were observed, from the donor (∼500 nm) and NFA absorption, respectively. The studied NFAs include low bandgap near-infrared (NIR) absorbers (BT-CIC, ICC6, Y6, IEICO-4F, and IEICO-4Cl), intermediate bandgap NFAs, whose absorption partially overlaps with that of the donor (O-IDTBR, IDT-2Br, ZY-4Cl, IT-4F, and IEICO), and a high bandgap NFA (FBR) with a 2.46 eV bandgap energy (E_g) exhibiting no complementarity in absorption to P3HT while little complementary absorption to pBTTT. The corresponding optical bandgap (E_opt) energy of the films was calculated from the intersection of the normalized absorption and photoluminescence (PL) emission spectra of the neat materials (Fig. S8, SI).

The preparation protocol for optimized devices is given in the Experimental section (Table S2, SI). The current–voltage (J–V) characteristics are presented in Fig. 2a and c. The highest PCE (∼8%) was achieved for P3HT:ZY-4Cl devices, with figures-of-merit given in Table 1, and they are consistent with previously reported efficiencies for that specific molecular weight (17 kDa) of P3HT.^32,33 The photo-current of P3HT-based devices was lowest for IT-4F (2.75 mA cm⁻²) and highest for ZY-4Cl (16.14 mA cm⁻²).

Table 1 Figures-of-merit of optimized donor:NFA devices, J_SC,int is the integrated current density calculated from the EQE of the devices assuming AM1.5G illumination. The diagonal bandgap is determined by IE_D-EA_A, here IE_D is the IE of donor (P3HT/pBTTT), and EA_A is the EA of the respective NFA

Donor:NFAs	V OC (V)	J SC (mA cm^−2)	FF (%)	PCE (%)	J SC,int (mA cm^−2)	IED-EAA (eV)
P3HT:IT-4F	0.47	2.75	40	0.52	2.67	0.51
P3HT:Y6	0.54	11.39	44.8	2.79	11.74	0.54
P3HT:IECO-4Cl	0.38	9.13	45.6	1.61	8.65	0.71
P3HT:IEICO-4F	0.42	7.30	45.6	1.41	7.07	0.71
P3HT:ICC6	0.47	8.86	50.2	2.10	8.59	0.71
P3HT:BT-CIC	0.47	2.79	49.6	0.70	2.67	0.81
P3HT:IEICO	0.64	9.12	48.4	2.84	9.08	0.86
P3HT:ZY-4Cl	0.88	16.14	56.3	8.07	14.20	0.87
P3HT:FBR	0.88	4.78	67.2	2.85	4.42	0.91
P3HT:IDT-2Br	0.83	7.39	64.8	4.01	7.39	1.05
P3HT:O-IDTBR	0.66	10.57	56.6	4.00	9.98	1.06
pBTTT:IT-4F	0.18	4.88	46.7	0.42	4.43	0.5
pBTTT:IEICO	0.50	6.97	48.8	1.72	6.57	0.85
pBTTT: FBR	0.69	1.51	46.1	0.48	1.54	0.9
pBTTT:O-IDTBR	0.63	4.54	52.2	1.51	4.22	1.05

---

In general, pBTTT-based devices exhibited a lower PCE compared to P3HT-based devices, with PCE values ranging from 0.42% for pBTTT:IT-4F to 1.72% for pBTTT:IEICO. The pBTTT:PC₇₀BM blend performed well when a ratio of 1 : 4 was used, because fullerene molecules intercalate with the pBTTT side chains forming a well-defined cocrystal phase, while the excess fullerene creates fullerene clusters.³⁴ This arrangement is known to facilitate efficient charge separation while also reducing geminate recombination.³⁴ In contrast, NFAs cannot intercalate between the side chains of pBTTT, because of their different chemical structure, leading to lower device performance as observed in this study.

The solar cells’ external quantum efficiency (EQE) spectra are presented in Fig. 2b and d with the corresponding integrated short current densities (J_SC,int) under AM1.5G conditions shown in Table 1. The integrated current densities match the measured J_SC. The acquired EQE spectra match the photoactive blends’ absorption spectra. The donor absorption covers the spectral range up to 600 nm, whilst the longer wavelength range, up to 1000 nm, is covered by the respective NFAs. The values of the EQEs are generally lower than 45% with the exception of P3HT:ZY-4Cl, reaching almost 60%. The moderate EQE values are in line with the moderate J_SC obtained from devices. In particular, P3HT:IEICO-4Cl based devices absorb photons up into the near-infrared spectral range, yet fail to convert them into photocurrent. P3HT:IT-4F based devices exhibit the highest absorption coefficient, yet they have the lowest EQE. ZY-4Cl based devices yield substantially higher EQE, which translates into higher photocurrent and thus PCE. Interestingly, P3HT:O-IDTBR based devices exhibited the second highest IQE, while the EQE was significantly lower. Calculating the maximum achievable photocurrent (J_SC,sim) by assuming unity IQE and using transfer matrix simulations (Fig. S9, SI) reveals that optimal P3HT:O-IDTBR cells have significantly lower thicknesses than the thickness at which absorption is maximized. This suggests that non-geminate recombination sets a ceiling to the further increase of the photoactive layer's thickness as charge extraction can no longer compete with carrier recombination. The FFs of the devices varied from 67.2% for P3HT:FBR based devices to about 40% for P3HT:IT-4F based cells. Low FFs are often an indication of either field-assisted charge separation, charge extraction competing with non-geminate carrier recombination due to low carrier mobility, or a combination of both.³⁵

In this study, pBTTT was included as another donor with low IE alongside P3HT to support the generality of the effects of large IE offsets in donor:NFA systems and its impact on the quantum efficiency of the solar cells. In the following, the characterization and discussion of the photophysics will focus on the P3HT:NFA-based photoactive blends and differences to the pBTTT:NFA based blends will be addressed if important for the discussion.

Photoexcited state energy transfer

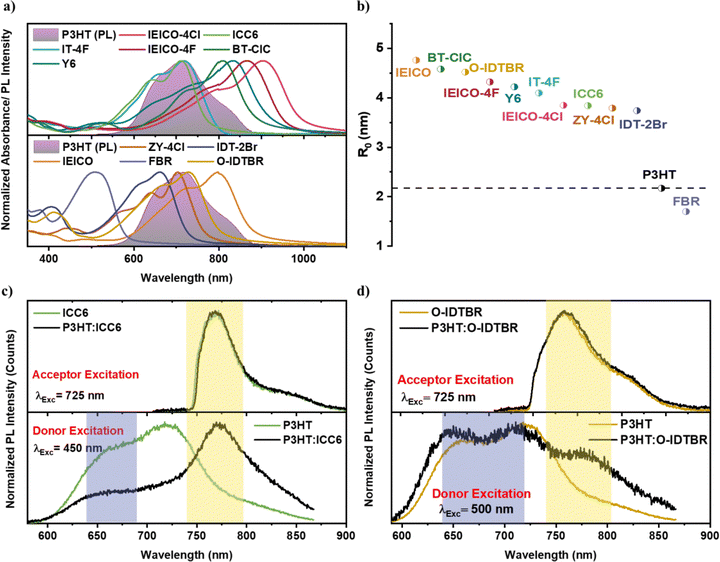
In principle, both IE and EA offsets determine the charge generation process and its efficiency depending on the nature of the charge transfer process, namely, photoinduced hole or electron transfer. However, based on recent studies on donor:NFA blends by us and others,²⁴ we expect that fast Förster resonant energy transfer (FRET) from the large-bandgap donor (P3HT) to the low-bandgap acceptor (NFA) followed by hole (back) transfer from the acceptor to the donor, dominates the charge generation process in the investigated systems. Consequently, the IE offset provides the driving force for the hole (back) transfer process. However, the IQE of the P3HT-based devices does not exhibit a strict dependence on the IE offset as can be seen in Fig. 1C. Energy transfer efficiencies compared to the previously reported systems could be different and thus, we calculated the FRET radii from the spectral overlap of the steady-state PL emission of P3HT and the absorption of the different NFAs (Fig. 3a).

Fig. 3 FRET radii and time-resolved photoluminescence spectra of P3HT:NFA blends. (a) Normalized absorption spectra of the NFAs (solid line) and the PL of P3HT (shaded area). (b) FRET radii of P3HT:NFA based blends with the donor phase (the data are ordered by decreasing the radii R₀). (c) and (d) Normalized time-resolved PL spectra for a selection of neat materials and blends at different excitation wavelengths (time range ∼0–2 ns for neat films and ∼0–0.2 ns for blend films). The purple shaded area represents the emission region of the donor and the yellow shaded area represents the NFA emission region. Long-pass filters (725 and 750 nm) were used for the 725 nm excitation to block scattered excitation light.

Fig. 3b presents calculated FRET radii for all donor–acceptor blends and for comparison also for P3HT:P3HT. Details of the calculation are provided in the SI in Table S3. P3HT:NFA blends show FRET radii of 3–4 nm, larger than the 2.17 nm for P3HT:P3HT, except P3HT:FBR (1.7 nm) due to limited spectral overlap (see Fig. S11, SI). This suggests that in most blends, FRET from P3HT to the NFAs competes with exciton diffusion to the D:A interface and subsequent electron transfer.²⁴ Our calculations of the FRET rates (∼10¹² s⁻¹) indicate that donor–acceptor energy transfer dominates when excitons are within ∼1 nm of the donor:acceptor interface.³⁶

Consequently, efficient energy transfer from P3HT to most of the non-fullerene acceptors studied here can be anticipated, with the only exception of P3HT:FBR. TRPL strongly suggests energy transfer in the P3HT:ICC6 blend (Fig. 3c), where the acceptor emission dominated for either donor or acceptor excitation, indicating rapid donor–acceptor energy transfer. Although we cannot entirely exclude that PL originates from direct ICC6 photoexcitation (in spite of the very low absorption coefficient of ICC6 at that wavelength (see Fig. S11, SI)). In contrast, the P3HT:O-IDTBR blend (Fig. 3d) exhibited less pronounced energy transfer, as evidenced by significant donor emission when P3HT was excited, suggesting less efficient energy transfer.

FRET causes excitons to be funneled to the acceptor after donor photoexcitation and the subsequent hole (back) transfer from the acceptor to the donor is determined by the IE offset since it provides the necessary driving force for the charge transfer process.²⁴ However, in contrast to our earlier work, it appears that in P3HT:NFA systems, the IE offset and the exciton-to-CT state conversion is not the limiting factor for the IQE, rather other loss channels determine the device performance. Thus, we further investigated the charge carrier separation and charge carrier extraction efficiencies.

Charge generation

To determine the charge generation efficiency, we first measured the exciton quenching efficiency (PLQE) by TRPL measurements on neat NFA films and P3HT:NFA blends. Here, we selectively photoexcited the acceptor of the blends (see excitation wavelengths in Fig. S13 and S14, SI). The PL dynamics were fitted at the respective NFAs’ PL peak positions with a sum of two exponentials to determine the intensity-weighted decay times of the PL for neat NFAs [τ_neat(NFA)] and blends (τ_blend) as described in the SI. The fitting parameters extracted from fits to the data are given in Table S4 (SI).

The PL spectra of the blend films measured after donor photoexcitation are red-shifted in most systems^32,36,37 (Fig. S15 and S16, SI) compared to those of P3HT films prepared under the same conditions. This indicated that both acceptor and donor are excited and/or the presence of donor/acceptor energy transfer. The parameters extracted from the two-exponential fits to the TRPL dynamics for the neat P3HT [τ_neat(P3HT)] films and the blends are shown in Table S5 (SI).

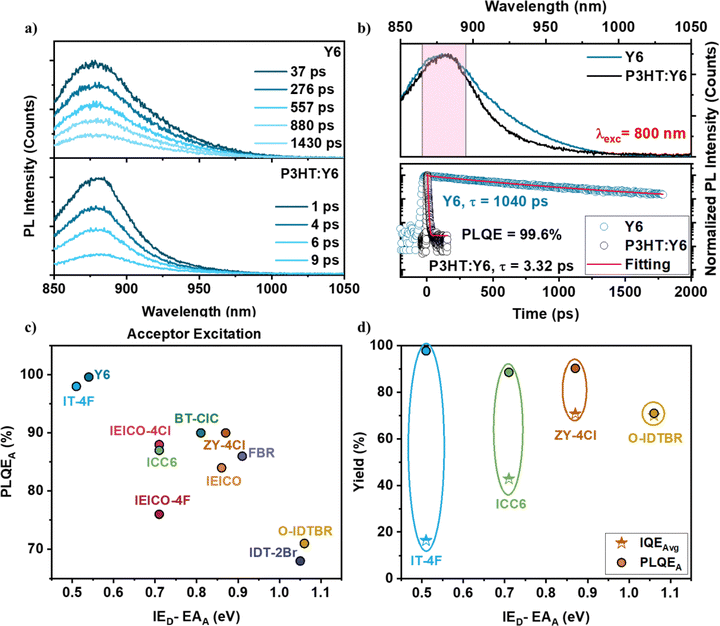
We determined the exciton decay time on neat NFAs [τ_neat(NFA)] and neat P3HT [τ_neat(P3HT)] films (intensity-average of the PL decay components, see the SI), and the photoluminescence quenching efficiency (PLQE) was calculated using the relationship PLQE = 1-τ_blend/τ_neat. The values are provided in Table S6. Fig. 4a and b show the highest PLQE we observed among the systems studied, reaching near-unity for P3HT:Y6. Interestingly, following acceptor photoexcitation, we observe efficient exciton quenching in all systems (PLQE∼84–99%), except for P3HT:IDT-2Br and P3HT:O-IDTBR, which exhibited less efficient exciton quenching of ∼68% and ∼71%, respectively, for reasons not fully understood.^33,37,38 Furthermore, for donor photoexcitation, we observe higher PLQE compared to acceptor photoexcitation, except for P3HT:ZY-4Cl, which exhibits lower PLQE (∼71%) when the donor was photoexcited compared to acceptor photoexcitation (∼90%) (see Table S6).

Fig. 4 PL decay times and PL quenching efficiencies from TRPL spectroscopy. (a) Shows TRPL spectra at different time ranges upon optical excitations at 800 nm of neat Y6 (top panel) and photoactive blend, P3HT:Y6 (bottom panel). (b) Normalized PL kinetics (bottom panel) tracked at the respective PL peak positions (shadowed in top panel) of the neat and blend thin films and fits to the data (solid pink lines) using bi-exponential tail fit. For neat NFAs τ_neat(NFA), and τ_blends of the photoactive blends along with the estimated PLQE. (c) The photoluminescence quenching efficiency with acceptor excitation (PLQE_A) versus diagonal bandgap. (d) IQE_Avg (stars) and PLQE_A (circles) as a function of the diagonal bandgap for a selection of systems.

In previously studied NFAs,²⁴ the exciton quenching was associated with an efficient charge generation, separation and transport, resulting in IQE closely matching the PLQE. Here, however, we observe a strong mismatch between those two efficiencies (Fig. 4d), pointing to the presence of (an) additional loss channel(s), which becomes more significant when reducing the diagonal bandgap. Moreover, we find the PLQE decreases with the diagonal bandgap, while the IQE roughly follows the opposite trend. Hole transfer from the acceptor to the donor remains efficient and increases with the IE offset, in good agreement with the systems we studied and reported previously,²⁴ even for those with very large IE offsets (∼1.55 eV). We noticed the same trend when photoexciting the donor (see Fig. S17, SI). Hence, the variation of the photocurrent (determined by the IQE) is not due to a variation of the charge transfer efficiency (determined by the PLQE).

In fact, the PLQE is high for all systems and does not correlate with the IE offset, indicating that charge transfer is not impeded by a large IE offset, as could be expected for a Marcus-inverted charge transfer regime.³⁹ The absence of a Marcus-inverted regime can be explained when assuming that higher energy charge-transfer states can be accessed from the primary photoexcited state, thus, with increasing IE offset, charge transfer occupies electronically higher excited CT states or higher vibrational states, followed by fast vibrational cooling and dissipation of energy in the charge separation process.

Charge separation and recombination

Light intensity-dependent current–voltage (J–V) measurements were performed to gain more insight into the recombination processes, i.e., to distinguish between trap-assisted recombination (V_OC) and non-geminate recombination limiting the device J_SC. Fig. S18a and b show the J_SC and V_OC measured for increasing light intensity. J_SC depends on light intensity I according to J_SC ∝ I^α, with α smaller than 1 (∼0.85 to 1 for polymer/fullerene-based solar cells) implying non-geminate charge recombination.^9,16 However, we note that α = 1 is not conclusive, as non-geminate recombination can occur between dark (injected) carriers and photogenerated carriers,⁴⁰ also causing a linear dependence of photocurrent on light intensity. Furthermore, the slope (m) of the V_OCvs. light-intensity dependence plotted in a semi-log plot (Fig. S18b, SI) is typically interpreted by m = n_Ik_BT/q with n_I being the ideality factor, k_B the Boltzmann constant, T the absolute temperature, and q the elementary charge. Here, n_I close to 1 implies that trap-free recombination dominates while n_I close to 2 points to trap-assisted recombination.^17,41–45

The slope of the J_SCvs. I dependence and n_I calculated from the slope of V_OCvs. I dependence are shown in Fig. S18c and d, respectively (SI). We observed that most of the systems exhibit some non-geminate recombination even in short circuit conditions (i.e. α < 1), in particular P3HT:IT-4F and P3HT:IEICO-4Cl, which showed the largest fraction of non-geminate recombination, explaining in part their moderate photocurrents. Generally, non-geminate charge recombination competes with charge extraction, reducing the device photocurrent and fill factor.

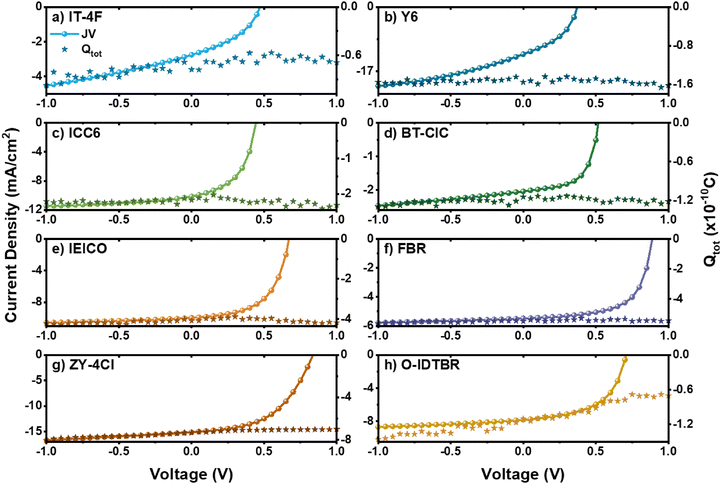
Apart from non-geminate recombination, the FF can be affected by field-dependent interfacial CT-state dissociation. Interfacial charge separation can be facilitated by the external electric field, in turn reducing geminate charge recombination.⁴⁶ This process can be probed by pre-bias-dependent time-delayed collection field (TDCF) measurements as previously exemplified on many donor–acceptor systems by Neher's group.^47–53Fig. 5 shows the evolution of the total extracted charge (Q_tot) as a function of the bias potential applied during photoexcitation, along with the photocurrent density of the devices. Fig. S19 (SI) shows that the photoexcitation was indeed in the linear response regime, limiting non-geminate charge recombination prior to charge extraction.⁵⁴

Fig. 5 Field dependence of free charge generation from TDCF measurements. (a)–(h) Current density (left axes) and collected charges (Q_tot) (right axes), measured by time-delayed collection field (TDCF) for various pre-bias voltages for P3HT:NFA based systems. The photoexcitation was performed at 532 nm, using a variety of low pulse fluences ranging from 0.03 to 0.2 µJ cm⁻².

The TDCF measurements indicate a weak field-dependence of free charge generation in all systems investigated in this study, except P3HT:IT-4F and P3HT:O-IDTBR, which both exhibited a more pronounced field-dependent charge generation. Here, the slope of the field-dependence of charge generation resembles the devices’ J–V curves, indicating that in both systems the fill factor is primarily limited by field-dependent charge generation, competing with geminate charge pair recombination.⁵⁵ For the other six systems, we observe field-independent charge generation indicating that non-geminate recombination increases between the maximum power point (MPP) and the device V_OC due to the increased dwell time (slower drift) of charges at small external electric fields. The comparably weak field-dependence that we observe in these systems suggests that interfacial charge transfer states dissociate, which results in larger photocurrents;⁵⁴ see Fig. S20b (SI) for better comparability across systems. However, our results also demonstrate that the weak field-dependence of charge generation cannot entirely explain the low FF we observe in most of these systems, precisely 39%–50%. Hence, charge extraction competing with non-geminate charge recombination appears to further limit the device FF.

To quantify the charge separation efficiency, we compared the charge density determined by TDCF measurements to the incident photon density, a quantity previously defined as external charge generation efficiency (EGE_TDCF):

Here, e is the elementary charge, A is the device area, d is the active layer thickness, and I is the incident fluence, equivalent to the energy density per excitation pulse, calculated as the incident laser power divided by the laser's repetition rate and divided by the beam area (assuming a uniform beam profile), and E_φ is the energy of a 532 nm photon as used in the measurement (3.74 × 10⁻¹⁹ J). Similarly, we calculate IGE_TDCF, i.e., the internal charge generation efficiency, that is, the number of extracted charges per absorbed photons, as the EGE_TDCF divided by the active layer's absorptance. The IGE_TDCF is the product of the charge generation yield (exciton-to-charge conversion), the yield of separation of the charge pairs bound at the interface into free charges, and the charge extraction efficiency. Presumably, if applying a sufficiently high external bias, all interfacial charge pairs dissociate. The resulting quantum efficiencies are shown in Fig. S21a (SI) as a function of the applied pre-bias voltage V_pre.

Weak or no field-dependence observed in TDCF measurements is often interpreted as the absence of geminate recombination, in other words, separation of all interfacial CT states. In the absence of geminate recombination, we expect that all excitons quenched in the blend are converted into free charges. However, the IGE_TDCF is lower than the PLQE obtained from TRPL experiments, even if the IGE_TDCF is probed using a strong pre-bias (−1 V). This suggests that either the excitons are quenched, but do not generate charges, or charge transfer occurs, but charges are not separated in the range of the applied pre-biases (from −1 to 1 V).^56,57 This is particularly important for low diagonal bandgap systems, leading to low interfacial CT energies, where charges could remain trapped. One possible explanation is that during the charge transfer process the system returns to the ground state via a conical intersection, which has been observed to limit the charge generation efficiency in small molecular donor–acceptor systems.³⁹

To address this question, we used broadband transient absorption (TA) pump–probe spectroscopy to probe charge formation without the need to separate charge carriers and extract them.

Exciton and charge carrier dynamics from transient absorption

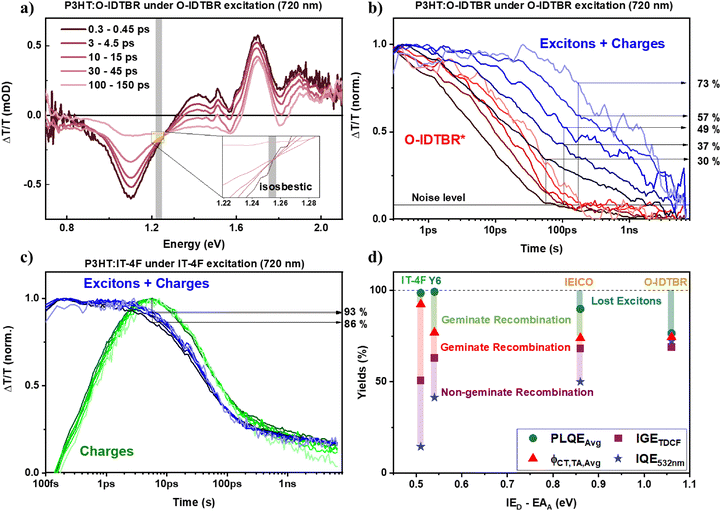
Here, we employed transient absorption (TA) spectroscopy as an all-optical (contactless) probe to monitor charge generation and recombination processes. We selected a set of representative systems, coded P3HT:IT-4F, P3HT:Y6, P3HT:IEICO, and P3HT:O-IDTBR, and estimated the charge transfer efficiency Φ_CT,TA by determining the fraction of the total population that remained at the point in time where all excitons had either decayed or been converted into charge carriers, according to:
To estimate the total density of excited states, we evaluated the dynamics at the isosbestic points observed in all system studied except one (see below). At the isosbestic point, the charge carrier-induced absorption cross section equals the exciton-induced absorption cross section, thus, the signal amplitude at that wavelength is a measure of the total density of excited states, which does not change if only exciton-to-charge conversion occurs.⁵⁸ We determined the fraction of the signal remaining after exciton-to-charge conversion was completed, including the decay of excitons to the ground state. However, in P3HT:Y6 blends following acceptor (Y6) excitation, we could not observe an isosbestic point and thus could not determine Φ_CT,TA.

We approximated the time of completion of the exciton-to-charge conversion either when the exciton-induced absorption signal became negligible (IT-4F, Y6, IEICO) or at the time at which the charge-induced absorption signal reached its maximum (IEICO, IT-4F upon acceptor excitation, see Fig. 6c), depending on which state could be probed independently. In the case of P3HT:O-IDTBR, neither excitons nor charges exhibited a spectral range where they could be tracked separately and thus, multivariate curve resolution was used to separate the component contributions (see Fig. S24, SI).^59–62

Fig. 6 Exciton dissociation and charge generation probed by transient absorption spectroscopy. (a) The excited state spectra exhibit an isosbestic point, allowing monitoring of the overall excitation (excitons + charges) density, here exemplified for P3HT:O-IDTBR upon excitation with a fluence of 1.6 µJ cm⁻² (see other systems in Fig. S23, SI). (b) In P3HT:O-IDTBR, up to 73% of the initial excitation remains after excitons decayed (level of the exciton + charge signal at the time the exciton-only signal reaches the noise level). Different shades represent different excitation densities (from 2.5 × 10¹⁷ cm⁻³ to 3 × 10¹⁸ cm⁻³) with the lowest fluences represented by the lightest colors. Exciton + charge population is probed at the isosbestic point (1.255–1.265 eV) and the exciton decay is extracted by multivariate curve resolution (see the SI for other examples). (c) In P3HT:IT-4F, up to 93% of the initial excitation is still present by the time the charge generation is concluded. The spectral shape of excited states exhibits virtually no evolution, indicating that all photoexcitations have been converted to charges (Fig. S23(a)). (d) Comparison of charge generation as estimated from TRPL (PLQE), TA (Φ_CT,TA), and TDCF (IGE), with the IQE measured at 532 nm (to be compared to TDCF). As detailed in the main text, Φ_CT,TA is taken from the lowest fluence measured (see examples in panels b and c), and is possibly underestimating the charge generation when using the exciton signal (all cases except IT-4F and IEICO under acceptor excitation), or overestimating when using the charge signal (IT-4F and IEICO under acceptor excitation).

We note that charge recombination could have started prior to the completion of exciton-to-charge conversion. In that case, some charges are not counted towards the charge generation yield, which makes Φ_CT,TA prone to underestimate the actual charge generation efficiency Φ_CT, which is thus at least Φ_CT,TA.

Despite this shortcoming, and as shown in Fig. 6d, Φ_CT,TA is generally larger than IGE_TDCF. This indicates that some charges are generated, which cannot be extracted in the TDCF experiment in the range of applied pre-biases, possibly due to their low energy at the interface, due to the small diagonal bandgap.^58–62 The average charge generation yield Φ_CT,TA,Avg (determined by donor- and acceptor-excitation, see Fig. S25c, SI) ranges between 73 and 94%, and thus is close to the PLQE_TRPL. Φ_CT,TA is, however, still less than the PLQE. The discrepancy indicates that low IGE_TDCF in small diagonal bandgap systems (i.e. IT-4F, Y6) arises from inefficient charge separation at the interface rather than inefficient charge transfer, as the applied pre-bias is insufficient to dissociate the interfacial CT states. For IT-4F, most charges recombined geminately within tens of picoseconds (fluence-independent decay, Fig. 6c), preventing separation by the electric field.⁵⁷

Larger diagonal bandgap systems for instance P3HT:IEICO and P3HT:O-IDTBR exhibited similar Φ_CT,TA,Avg, IGE_TDCF, and PLQE, indicating efficient charge separation. In the case of O-IDTBR, this results in a higher PCE compared to the other three systems. Lastly, we note that in some systems including P3HT:IT-4F and P3HT:Y6, a difference between the charge generation efficiency determined from TDCF (IGE_TDCF) and the internal quantum efficiency (IQE) remained. This implies that a significant fraction of the excited state population is consumed by non-geminate charge recombination following charge separation but prior to charge extraction.

Non-geminate recombination dynamics

To understand further how the diagonal bandgap influences the charge recombination process, we determined the non-geminate recombination rates γ by TDCF measurements. Fig. 7 shows the amount of charge extracted during the application of the pre-bias (Q_pre), the collection bias (Q_coll), and their sum (Q_tot) as a function of the delay time t_d between photoexcitation and the onset of charge extraction. A constant collection field was used (here V_coll = −4 V) and a pre-bias (V_pre) close to the open circuit voltage V_OC to avoid charges being extracted instead of recombining prior to t_d. Consequently, the total extracted charge Q_tot decreased with delay time due to charge recombination. However, Q_pre is non-zero implying that some charge is still extracted during the application of the pre-bias, in part due to the decrease of V_OC upon charge recombination. The decrease of Q_coll between two successive time delays (t_d and t_d + Δt_d) is thus corrected for Q_pre before fitting a bimolecular decay to extract γ:

Fig. 7 Charge recombination in P3HT:NFA devices measured by time-delayed collection field experiments. (a) P3HT:IT-4F, (b) P3HT:Y6, (c) P3HT:ICC6, (d) P3HT:BT-CIC, (e) P3HT:IEICO, (f) P3HT:FBR, (g) P3HT:ZY-4Cl, and (h) P3HT:O-IDTBR. Where, (Q_pre) is the amount of charge extracted during pre-bias, and (Q_coll) is the amount of charge extracted during collection bias (V_coll = −4 V) and their fits as a function of delay time between excitation and the beginning of extraction yields the bi-molecular recombination rate (γ). Thus, the total extracted charges Q_tot = Q_pre + Q_coll.

Here, A is the active area of the device, d is the film thickness, and γ is the (strictly) bi-molecular recombination rate constant.⁶³

The evolution of the collected charge Q_coll, i.e., the charge escaping recombination and undergoing extraction, as a function of the delay time t_d is presented in Fig. S26 (SI). The obtained bi-molecular recombination rates are on the higher end of those typically observed in organic semiconductors, where γ ranges from 10⁻¹⁴ cm³ s⁻¹ to 10⁻¹⁰ cm³ s⁻¹.^{32,55,64–71} In P3HT:IT-4F, P3HT:Y6, and P3HT:O-IDTBR, the large bi-molecular recombination rate explains the low FFs of these systems ranging from 39% to 50%, as non-geminate recombination competes efficiently with charge extraction, especially when the bias approaches V_OC. Reciprocally, P3HT:FBR, which exhibits the lowest recombination rate constant of 1.15 × 10⁻¹¹ cm³ s⁻¹ among the investigated systems, shows the highest FF of 67% in devices.

In Fig. 8a (top panel), the bi-molecular recombination rates obtained from TDCF are plotted against the diagonal bandgap. Except for P3HT:O-IDTBR, γ appears to decrease steadily with increasing diagonal bandgap. This can be understood in the framework of the energy gap law:^26–28 the non-radiative recombination rate of excited states increases exponentially when the energy difference between the ground state and the excited state reduces. In the case of donor–acceptor blends, the CT state energy can be approximated from the diagonal bandgap (Fig. 8b), and non-geminate charge recombination proceeds through CT states as intermediates, as only they are coupled to the system's ground state, implying that faster CT state recombination (via non-radiative processes) limits the probability of the CT state to re-dissociate into free charge carriers. Indeed, a fit of the dependence of the non-geminate recombination rate on the diagonal bandgap according to γ = Ae^{−(IE_D-EA_A)/E_vib} yields an E_vib of about 160 meV, in good agreement with the energy of the carbon–carbon double bond vibration of P3HT, which is considered the dominant mode responsible for energy dissipation during internal conversion processes.^72–74 Here we hypothesize that the geminate recombination rate of the initially generated CT states follows the same trend, however, likely with a larger pre-factor A due to the closer proximity of the electron and hole at the interface. This explains why geminate recombination dominates over charge separation in systems with low energy offsets, as observed from the comparison of the yield of generation of separated charges (IGE_TDCF) and the overall charge generation efficiency (PLQE or φ_CT,TA,A), shown in Fig. 6d.

Fig. 8 Impact of diagonal bandgap on non-geminate recombination rates. (a) Bi-molecular recombination rate constant (γ) as a function of the diagonal bandgap (IE_D-EA_A) (top panel) and the evolution of PLQE_A, IGE at 0 V, and IQE at 532 nm of the diagonal bandgap (bottom panel). (b) Schematic representation of the diagonal bandgap (IE_D-EA_A) at the interfacial landscape between the donor and the acceptor. (c) IQE_Avg as a function of diagonal bandgap, based on six different donors paired with various NFAs and a Fullerene acceptor (FA) (PCBM) across 25 systems (IQE_Avg of P3HT and pBTTT was obtained from this study, while the other donors were obtained from our previous work²⁴).

However, P3HT:O-IDTBR seems to contradict this trend for reasons not entirely clear. P3HT:O-IDTBR exhibits field-dependent charge separation and a large bi-molecular recombination rate, indicating both geminate and non-geminate recombination rates limit the device performance. In our recent work, we linked the exciton-to-CT state conversion and subsequent dissociation to the quadrupole moment of the NFA, and the density functional theory (DFT) calculations indeed suggest that a large quadrupole moment facilitates efficient CT state dissociation.⁷⁵ This can explain the strong field dependence we observe in P3HT:O-IDTBR, since the quadrupole moment of O-IDTBR is smaller compared to that of the other NFAs.⁷⁵ Moreover, it explains the larger bi-molecular recombination rate of this system, which is also in line with a recent study.⁷⁶ Based on our analysis, we conclude that exciton-to-CT-state conversion is still possible in the investigated P3HT:NFA blends, as indicated by the high PLQE observed. Furthermore, CT states dissociate as indicated by the field-independent charge generation. Consequently, both geminate and non-geminate recombination compete with charge extraction severely limiting the efficiency of these systems.

Fig. 8a (bottom panel) shows that for the systems with low diagonal bandgaps, the high non-radiative recombination results in geminate recombination outcompeting charge separation. In systems with intermediate diagonal bandgaps, charge separation kinetically outcompetes geminate recombination. However, the energy gap law also determines non-geminate recombination as discussed above, which competes with charge extraction, particularly in blends with low charge carrier mobility. As a result, significant losses in photocurrent and fill factor are observed. Ultimately, only the blends with large diagonal bandgaps partially overcome these efficiency-limiting processes. In that respect, we note that P3HT:O-IDTBR has demonstrated high internal quantum efficiency, while P3HT:FBR exhibits a high fill factor. However, these systems are limited in terms of charge separation and extraction. In fact, only P3HT:ZY-4Cl appears to combine a high charge generation efficiency with good charge extraction, leading to the highest PCE in the series of P3HT:NFA blends.

Fig. 8c illustrates the evolution of the IQE_Avg in relation to the diagonal bandgap across 25 systems, which includes six donors and various NFAs and FAs (PCBM). We ensured that these systems are not limited by energy offsets, with IE offsets all exceeding 0.65 eV. This observation supports our finding of the relationship between the diagonal bandgap and the energy gap law. Additionally, it elucidates the low IQE observed in P3HT and pBTTT, demonstrating that the energy gap law can be applied to other donor materials as well and is not limited to P3HT as the donor polymer.

In our previous work (Karuthedath et al.²⁴), we focused on exciton-to-CT conversion, emphasizing the importance of the IE offset. In systems with large IE offsets (>0.65 eV), efficient exciton-to-CT conversion is always observed; however, CT state to free charge conversion can still be limiting the IQE. This conclusion is supported by a report from Hinrichsen et al.,⁷⁷ providing a mechanistic understanding in the framework of the energy gap law. For instance, the energy gap law considerably increases non-radiative recombination in systems with low CT state energies, in line with their results. They point out that the long-lived nature of the CT state is of critical importance; nevertheless, if significant non-radiative recombination occurs, facilitated by low CT energies and the energy gap law, the CT state can be short-lived, resulting in decreased (re)-dissociation efficiency. This scenario highlights that the energy gap law sets a limit to the photocurrent in systems with low CT state energies, where charge generation is no longer limited by the system's energetics but by the kinetic competition between charge transport and extraction and interfacial charge recombination as discussed in the next section.

Charge extraction versus recombination

To obtain further information about the charge transport properties of the P3HT:NFA blends, we determined their electron and hole mobilities using space charge-limited current (SCLC) measurements on electron-only and hole-only devices. The SCLC experiments demonstrated that IT-4F and IEICO-based systems exhibit low electron and hole mobilities (Table S8 and Fig. S27, SI), making extraction less efficient. The BT-CIC-based systems exhibit higher carrier mobility, and consequently their charge extraction is faster and less non-geminate charge recombination occurs, yet their charge separation efficiency is lower, in turn leading to an overall lower IQE. Similarly, O-IDTBR blends exhibit moderate charge carrier mobility in line with their better device efficiency, exceeding most of the other P3HT:NFA blends, while being limited by their large non-geminate recombination rate γ.

With the charge carrier mobility and bi-molecular recombination coefficients in hand, we can gain a deeper understanding of the competition between charge carrier extraction and recombination by calculating the parameters α and θ introduced by Neher et al.,^78–80 which quantify the balance between charge recombination and extraction in organic solar cells. While they share a conceptual foundation, they differ in their specific definitions and applications.

α is derived from an analytical expression of the current–voltage (J–V) characteristics of organic solar cells, reflecting charge carrier mobility, recombination, and transport properties.⁷⁸θ represents the ratio of recombination to the extraction rates, including effects of charge mobility, recombination, light intensity (carrier concentration), energy levels (energetic landscape), and photoactive-layer thickness.⁷⁹ Fig. S28a and b (SI) illustrate the relationship between the FF and the two parameters α and θ. In Fig. S28a (SI), the experimental data (excluding FBR) aligns well with the analytical model proposed by Neher et al.,⁷⁸ where α > 1 and the low FF suggests transport-limited photocurrent.⁷⁸ Fig. S28b (SI) shows that all systems (except FBR) follow the simulated FF versus θ curve as demonstrated by Neher et al.⁷⁹ High FFs indicate low recombination rates versus extraction rate ratios, with FF decreasing exponentially as charge recombination increases, eventually plateauing at low FFs when recombination dominates.⁷⁹

Further analysis was conducted to calculate the diffusion length (l_dif) and drift length (l_dr) derived from α and θ, respectively.⁸⁰ Fig. S28c (SI) shows the FF versus l_dif/d alongside Neher's analytical model (V_OC = 0.6 V to 1.1 V), showing good agreement except for FBR. As l_dif approaches the device thickness (d), α nears unity, indicating a transition to a Shockley-type solar cell.^78,81 A Shockley-type cell can be defined by l_dif/d ≥ 1. Fig. S28d (SI) shows the relationship between the efficiency of charge extraction at short circuit (J_SC/J_G) and l_dr/d. Simulations from Neher et al.⁸⁰ and our data using J_sat(−1 V) as an approximation for J_G (generation current density) confirm current loss when l_dr is less than the device thickness. The Hecht model was used for comparison.⁸⁰ Some systems show l_dr > d, implying minimal loss under short-circuit conditions, while others with shorter drift lengths show significant losses. The figures of merit can be found in Table S9 (SI).

It is clear that all P3HT:NFA systems align with the analytical models and simulated data concerning the figures of merit, supporting the determined mobility values and recombination rates. However, P3HT:FBR does not follow the same trend. This discrepancy arises because the models and equations used are valid for systems with balanced mobility, while P3HT:FBR has strongly imbalanced mobility (see Table S8, SI), which explains its different characteristics. It is worth noting that not all other P3HT:NFA systems exhibit balanced mobility and thus with some minor variation follow closely the analytical model.

Although P3HT:NFA systems have lower charge mobility and higher recombination rates compared to P3HT:PCBM, most of the NFAs, in particular ZY4-Cl, outperform PCBM. However, some NFAs investigated in this study show worse performance than P3HT:PCBM. This discrepancy can be explained by the energy gap law. PCBM exhibits a large diagonal bandgap with most donors, while many NFAs have a smaller diagonal bandgap (see Fig. 8c). Additionally, the unique micro-morphology of fullerenes, in particular the aggregation of PCBM, is known to reduce recombination losses.⁸² The increased crystallinity and domain purity enable charge carriers to be delocalized over larger areas.⁸² This delocalization enhances the dissociation of charge-transfer states formed between electrons and holes. Therefore, the focus should be on increased molecular order, crystallinity, and domain purity. This is particularly important for devices based on NFAs, where minimizing the recombination rates is crucial due to the low carrier mobilities.⁸²

Donor:acceptor blend morphology and topography

We performed atomic force microscopy (AFM) on P3HT:IT-4F and P3HT:ZY-4Cl blends, and representative images are presented in Fig. S29 (SI). We observed a smooth surface in the former, while the latter exhibited crystal-like structures. However, since AFM probes only the blends’ topography, we also conducted transmission electron microscopy (TEM) and electron energy loss spectroscopy (EELS) analysis to create maps of the donor–acceptor separation and to investigate the degree of component demixing in P3HT:IT-4F and P3HT:ZY-4Cl (small and large diagonal bandgap systems) as shown in Fig. S30 (SI). EELS can be used to map abundant elements in one of the components either in the donor or the acceptor. For example, when scanning for chlorine and nitrogen in P3HT:ZY-4Cl, one can differentiate between acceptor and donor-rich regions of the film. The TEM results effectively show that the donor and acceptor are thoroughly mixed in the P3HT:IT-4F system, which explains its high PLQE (∼96%). However, this is not the case for P3HT:ZY-4Cl, which exhibits crystal-like features. This difference can explain the lower PLQE (∼70%) observed in this system, while all other systems exhibit a PLQE exceeding 90%. Generally, we anticipate intimate mixing of P3HT and also the other NFAs, similar to that of P3HT:IT-4F, based on the blends’ high PLQE values. This suggests that morphological differences are not the root cause of the performance differences in these devices.

Outdoor stability

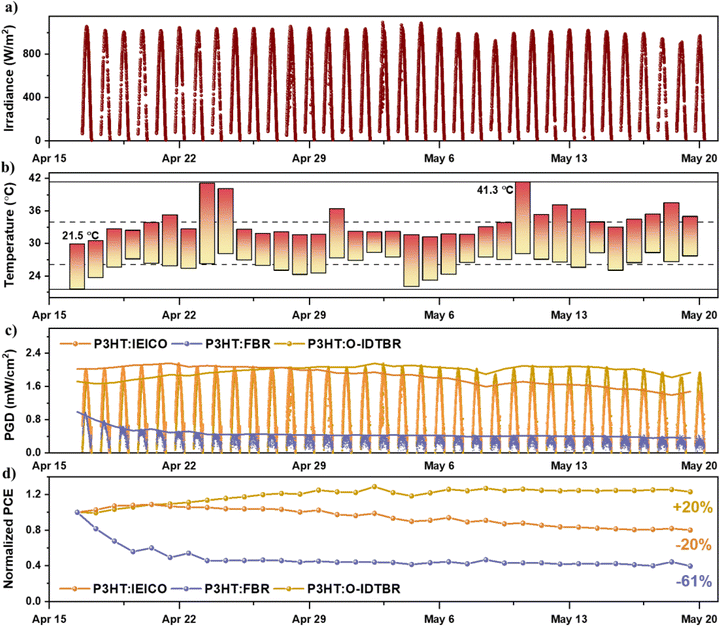
In addition to investigating the photophysical processes that determine the device IQE, we employed outdoor stability measurements to assess how the studied material systems perform under operationally relevant conditions, thereby linking the photophysics to long-term device robustness. Here, we investigated the outdoor stability of three P3HT:NFA systems, namely, P3HT:IEICO, P3HT:FBR, and P3HT:O-IDTBR. Fig. 9 displays outdoor performance measurements conducted in the extremely hot and harsh weather conditions at KAUST, Thuwal, Saudi Arabia; see also the SI for experimental details. This location experiences high irradiance and temperatures; in fact, the irradiance reached as high as 1093.8 Wm⁻² at noon (Fig. 9a), as measured by a calibrated pyranometer. Fig. 9b illustrates the air temperature during the stability measurements, with a maximum of 41.3 °C and a minimum of 21.5 °C. The figures of merit for encapsulated devices (P3HT:IEICO, P3HT:FBR, and P3HT:O-IDTBR) are shown in Fig. 9c. The devices were measured every 10 minutes over 34 days. The power generation density (PGD) increased from sunrise, peaked at noon, and subsequently decreased from noon to sunset. Fig. 9d shows the normalized PCE at noon (accounting for the irradiance at 12:00 pm) to track outdoor degradation.

Fig. 9 Impact of outdoor irradiance on the stability of P3HT:NFA based devices. (a) Solar irradiance. (b) Outdoor temperature during stability measurements (34 days). (c) Power generation density (PGD) of the encapsulated P3HT:IEICO, P3HT:FBR, and P3HT:O-IDTBR. (d) The corresponding normalized encapsulated devices at noon (∼12:00 p.m). The outdoor stability measurements were carried out in KAUST, Thuwal, Kingdom of Saudi Arabia from April 17th to May 20th. J–V curves were measured every 10 minutes.

Surprisingly, P3HT:NFAs exhibit excellent outdoor stability, despite their lower performance compared to state-of-the-art OPV material systems. Both P3HT:O-IDTBR and P3HT:IEICO exhibit remarkable stability over a 34-day period. In fact, the efficiency of P3HT:O-IDTBR, which has the largest diagonal bandgap, increased by 20% compared to its initial performance. This improvement can be attributed to several factors, such as light soaking, which often leads to processes like trap state filling, ion migration, or structural reorganization within the photoactive layer.⁸³ These processes can enhance charge transport and reduce recombination losses. Additionally, temperature effects can play a role; elevated outdoor temperatures can enhance charge carrier mobility or activate morphological changes not triggered during lower irradiance indoor tests.⁷ P3HT:IEICO experienced a 20% decrease in performance, which is among the best outdoor stability reported for third-generation PV devices.^84–87 However, P3HT:FBR exhibited severe degradation of about 80%, in conjunction with low device performance observed after encapsulation.

Conclusion

To conclude, we investigated the effect of large IE offsets exceeding 1 eV on device IQE and overall device performance by studying 15 bulk heterojunctions in organic solar cells incorporating P3HT and pBTTT as donor polymers blended with non-fullerene acceptors. We focused on the efficiency-limiting mechanisms in P3HT:NFA BHJ solar cells. In contrast to other donor:NFA systems, where the IQE primarily depends on the exciton-to-CT state conversion efficiency, we observe efficient PL quenching in all P3HT:NFA systems as a consequence of large interfacial energy offsets, while the IQE appears to be limited by subsequent geminate and non-geminate recombination processes, its extent varying depending on the specific NFA used. Interestingly, we found that the IQE_Avg gradually decreased with decreasing diagonal bandgap, while the exciton-to-charge conversion efficiency remained high. The IQE and device performance decrease can be understood in the framework of the energy gap law due to increased interfacial carrier recombination. Overall, our findings indicate that the efficiencies of P3HT:NFA-based OSCs are primarily limited by charge recombination, incomplete charge separation, and limited charge extraction, unlike many other donor:NFA systems. Hence, in addition to maintaining sufficiently large IE offsets, the diagonal bandgap between the donor and the NFA can substantially limit device performance and thus must be considered when designing bulk heterojunction blends for OSCs.

Experimental

Materials availability

O-IDTBR, IT-4F, Y6, and IEICO-4F were purchased from Solarmer Materials Inc. IEICO-4Cl, ICC6 (IDIC), BT-CIC, and IEICO were purchased from 1-Material Inc. P3HT with M_w = 17 kDa, Poly[2,5-bis(3-tetradecylthiophen-2-yl)thieno[3,2-b]thiophene] (pBTTT-C14), ZY-4Cl, IDT-2Br, and PEDOT:PSS were purchased from Sigma-Aldrich. FBR was synthesized at KAUST. PFN-Br was purchased from Organtec Ltd. Chlorobenzene anhydrous 99.8%, anisole anhydrous ≥99%, tetrahydrofuran anhydrous ≥99% and 1,8-diiiodooctane 98% were purchased from Sigma-Aldrich, chloroform from VWR, 1-chloronaphtalene from Fluka and dimethydisulfde 99% from Alfa Aesar. All materials were used as received.

OPV devices

Bulk heterojunction solar cells were fabricated with both device architecture, inverted (glass/ITO/ZnO/Donor:NFA/MoO_x/Ag), and normal device architecture (glass/ITO/PEDOT:PSS/Donor:NFA/PFN-Br/Ag). Glass substrates with pre-patterned indium tin oxide (ITO) were cleaned by sonication in diluted Hellmanex, deionized water, acetone, and isopropanol, followed by oxygen plasma treatment. For the inverted structure: a ZnO layer (30–40 nm) was deposited by spin-coating the ZnO precursor, which was prepared by dissolving Zn(OAc)₂ in monoethanolamine (60 µL) and 2-methoxyethanol (2 mL), followed by annealing at 150 °C for 10 minutes. Active layers were deposited using different concentrations and solvents (Table S2), followed by annealing at 140–160 °C for 10–15 minutes inside the glovebox. MoO_x (10 nm) and Ag (100 nm) layers were deposited by evaporation through a shadow mask yielding active areas of 0.1 cm² in each device. For the normal structure, a PEDOT:PSS layer was spin-coated on the ITO at 4000 rpm to function as the hole transporting layer (HTL), and PFN-Br was deposited on top of the active layer by spin-coating at 2000 rpm to function as the electron transporting layer (ETL).

Device characterization

J–V measurements of solar cells were performed in a N₂ filled glovebox using a Keithley 2400 source meter and an Oriel Sol3A Class AAA solar simulator calibrated to 1 sun, AM1.5G, with a KG-5 silicon reference cell certified by Newport.

The External Quantum Efficiency (EQE) was characterized using a specially designed EQE system (PV Measurement Inc.). The measurements were performed at zero bias by illuminating the device with monochromatic light supplied by a Xenon arc lamp in combination with a dual-grating monochromator. The number of photons incident on the sample was calculated for each wavelength by using a silicon photodiode calibrated by NIST.

The Internal Quantum Efficiency (IQE) spectra were calculated from EQE spectra using the relationship: IQE = EQE/(1 − Reflectance − Parasitic Absorption). The reflectance spectra were collected with an integrating sphere while the parasitic absorption spectra were obtained from transfer matrix modelling.³¹

UV-Vis and PL spectroscopy

Steady-state absorption measurements were conducted using a Cary 5000 UV-visible spectrometer (Agilent Technologies), and the PL was measured using the Horiba Fluorolog- Modular PL spectrometer. Films were prepared on glass substrates, long-pass filters were used to remove strong scattering at the excitation wavelength, and the measurements were conducted in air.

FRET radii and rates

To calculate the extinction coefficients, transmittance and reflectance spectra (to obtain absorptance) were obtained using a PerkinElmer LAMBDA 950 UV-vis/near-infrared spectrophotometer equipped with a 150-mm InGaAs integrating sphere. For more information on the FRET radii calculations, please refer to the SI.

Ultraviolet photoelectron (UPS) and low-energy inverse photoelectron (IPES) spectroscopy

UPS measurements were conducted using a vacuum UV He (1) discharge line with an energy of 21.22 eV (focus) and a Sphera II EAC 125 7-channeltron electron analyzer. The sample was positioned at 0° relative to the analyzer-to-sample plane. Fermi level calibration was performed by using an Ar⁺ sputtered clean metallic Ag foil in electrical contact with the manipulator holding the sample in contact with the electron analyzer. A bias of −10 V was applied during UPS to observe the secondary electron cut-off. To prevent surface charging, subsequent measurements were carried out in electrical contact with thin films. UPS scans were performed from low to high kinetic energy at a constant analyzer pass energy of 10 eV, and careful monitoring was conducted to detect any beam-induced degradation or evidence of charging in subsequent scans.

An in-house ultra-high vacuum LE–IPES setup was used for this study. The setup operates in the Bremsstrahlung isochromatic mode. An incident electron beam (with a dispersion of 0.25–0.5 eV) is directed at 0° relative to the sample plane, and the electron energy is slowly swept. To collect the outgoing light from the surface, an external focusing lens and an internal vacuum collimating lens were placed, along with a detector and shielding to prevent stray light. For this experiment, a low-energy electron source (Staib) was used, operating at an energy range of 20–30 eV (using a BaO cathode Heatwaves), and a retarding bias of +20 V was applied to the sample, ensuring good electrical contact. The photons were collected outside of the vacuum by a solid-state PMT detector (Hamamatsu R585) using a narrow wavelength window defined by a 280 nm bandpass filter (Semrock) with a width of 10 nm. The measurement was performed consecutively, without exposing the surface to the ambient atmosphere. The measurements were conducted in a base pressure of 10⁻⁹ mbar to ensure accurate integration with UPS spectra. The photoactive solutions were prepared by dissolving 5 mg mL⁻¹ of the materials in CF and preparing the films on gold-coated substrates.

Photoelectron spectroscopy in air (PESA)

Thin films were prepared on glass substrates, and the PESA measurements were performed using a Riken Keiki PESA spectrometer (Model AC-2) with a power setting of 10 nW, and a power number of 0.33, in air.

Time-resolved photoluminescence spectroscopy (TRPL)

Time-resolved photoluminescence measurements of the films spin coated on quartz were performed in a vacuum chamber at different fluences (from 6.8 pJ cm⁻² to 94.6 nJ cm⁻² – but only plotted here at fluences at which no fluence dependence was observed). For these measurements, we used the output of a modelocked Ti:Sa (Chameleon Ultra I from Coherent) fs laser operating at 80 MHz repetition rate, at 400, 450 and 500 nm (SHG pumped at 800, 900 and 1000 nm, respectively), and at 690, 700, 725 and 800 nm through a Chameleon Compact OPO-VIS, as stated in the manuscript to selectively excite the different donors and acceptors studied as stated along the manuscript. The PL of the samples was collected by an optical telescope (consisting of two plano-convex lenses), focused on the slit of a spectrograph (Princeton Instrument Spectra Pro SP2300) and detected with a Streak Camera (Hamamatsu C10910) system, with an appropriate long-pass filter (namely 458, 700, 715 and 830 nm) used when needed. Each measurement was taken until at least 10 k counts at maximum emission wavelength were reached. Each material system was measured ∼9–38 times to investigate time, fluence, and excitation dependence, as well as other spectral regions, and different time ranges and account for sample variability. The instrument response function was acquired for each set of measurements with both films and substrates. The data were acquired in photon counting mode using the Streak Camera software (HPDTA) and exported to Origin for further analysis. The presented data are not corrected for spectral sensitivity. The TRPL decays were fitted with a sum of exponentials, and the intensity-averaged lifetime was calculated, the reason being that the emission is the time derivative of the exciton density. The exciton density is thus obtained by integrating the TRPL transients. Averaging the signal intensity (∼amplitude × duration) corresponds to this integration (see the SI). The PL quenching efficiency was then calculated according to the previously reported procedure. Please refer to the SI (TRPL).

Light intensity dependent current voltage (LID-IV)

Current–voltage characteristics under different illumination conditions were measured by PAIOS (Platform for all-in-one characterization of solar cells and (O)LEDs by Fluxim AG), (Electrical and Optical Characterization of LEDs and Solar Cells) setup from FLUXIM. As a light source, an LED lamp that has 1 sun intensity is used. The J–V measurements of the solar cells were performed as a function of the illumination intensity (up to 1 sun), and the measurements were carried out inside the glove box under a nitrogen environment.

Time-delayed collection field spectroscopy (TDCF)

The home-built TDCF setup uses the second harmonic (532 nm) of an actively Q-switched sub-ns Nd:YVO₄ laser, specifically the INNOLAS piccolo AOT model, which operates at 5 kHz, as the source of excitation. To ensure a minimal resistor-capacitor response time, a small device area of 1 mm² is utilized. To prevent any degradation, the samples were measured under dynamic vacuum conditions. The pre-bias and extraction bias were provided by a Keysight S1160A function generator, while the current response of the device was measured using a four-channel digital oscilloscope also manufactured by Keysight.

Transient absorption spectroscopy (TA)

Transient absorption (TA) spectroscopy was carried out using a home-built pump–probe setup. The output of a Ti:sapphire amplifier (Coherent LEGEND DUO, 800 nm, 4.5 mJ, 3 kHz, 100 fs) was split into four beams (2 mJ, 1 mJ, 1 mJ, and 0.5 mJ). Three of them were used to separately pump three optical parametric amplifiers (OPA; Light Conversion TOPAS Prime). One of the 1 mJ TOPAS was used to generate wavelength-tuneable pump pulses (240–2600 nm, using Light Conversion NIRUVIS extension). A fraction of the 0.5 mJ output of the Ti:sapphire amplifier was focused into a c-cut 3 mm thick sapphire window, thereby generating a white light supercontinuum from 500 to 1800 nm. For picosecond-nanosecond TA, the pump–probe delay time was achieved by varying the probe path length using a broadband retroreflector mounted on a 600 mm automated mechanical delay stage (Thorlabs optical delay line ODL600/M), generating delays from −500 ps to 7.5 ns. Excitation pulses were mechanically chopped to 1.5 kHz to provide the pump-on and pump-off signals.

For nanosecond-microsecond TA, the excitation pulse was provided by an actively Q-switched Nd:YVO₄ laser (InnoLas Picolo-AOT 1-MOPA, 1064 nm, 2.5 W, 5 kHz, <0.8 ps) frequency-doubled, providing pulses at 532 nm. The pump laser was triggered by an electronic delay generator (Stanford Research Systems DG535) itself triggered by the transistor–transistor logic sync from the Legend DUO, allowing control of the delay between pump and probe with a jitter of roughly 100 ps. The trigger frequency from the Legend DUO was reduced by 2 to give the excitation pulse repetition rate of 1.5 kHz to obtain the pump-on and pump-off signals.

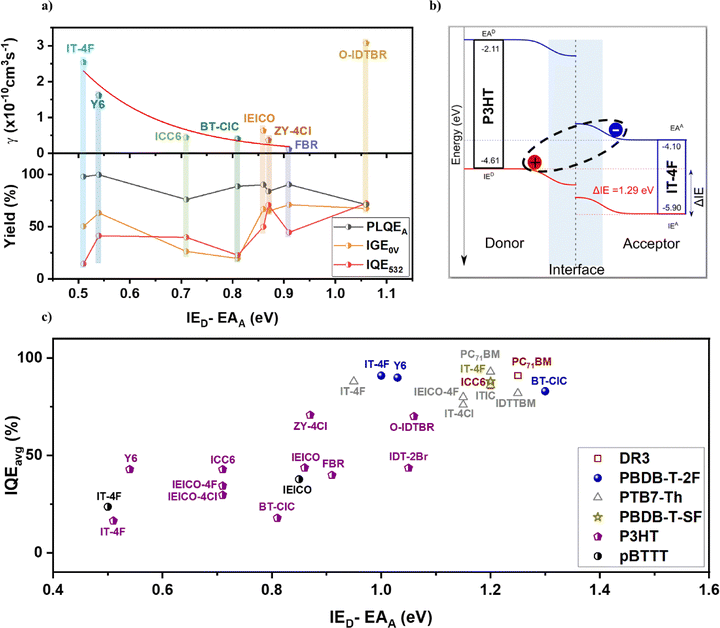
Pump and probe beams were focused on the sample to spot sizes of ∼1.0–2.0 mm (varied depending on wavelength) and <0.06 mm diameter, respectively (from a Gaussian fit at 86.5% intensity), as measured using a beam profiler (Coherent LaserCam-HR II). From the corresponding pump beam surface area (A), its average power (P), and the repetition rate, we calculated the excitation energy density per pulse (fluence) as

This corresponds to the fluence at the maximum of the Gaussian shaped pump beam, which is the region through which we send the probe beam.

The samples were kept under a dynamic vacuum of <10⁻⁵ mbar, and pump and probe beams were incident on the film-side of the sample. The transmitted fraction of the white light was guided to a custom-made prism spectrograph (Entwicklungsbüro Stresing) where it was dispersed by a prism onto a 512-pixel CMOS linear image sensor (Hamamatsu G11608-512A). The detector array was read out at 3 kHz, corresponding to the probe repetition rate. Adjacent diode readings corresponding to the transmission of the sample after excitation and in the absence of an excitation pulse were used to calculate ΔT/T. Measurements were averaged over several thousand shots to obtain a good signal-to-noise.

Transmission electron microscope (TEM) and electron energy loss spectroscopy (EELS)

TEM imaging and STEM-EELS spectrum imaging were performed on a Thermo Fischer Titan Themis Z TEM operated at 300 kV. For TEM investigation the samples were prepared by spin-coating the P3HT:NFA solution on a silicon wafer using PEDOT:PSS as the sacrificial layer. The sacrificial layer was dissolved in DI water and the floating film was picked-up on lacey carbon copper TEM grids. TEM images were acquired using a Gatan One View camera and EELS spectrum imaging were acquired in STEM mode with a Gatan Imaging Filter (GIF) Quantum 966 spectrometer.

Author contributions

W. A. optimized the devices, carried out the steady state spectroscopy, device characterization and analysis, TDCF measurements and analysis, TRPL samples and analysis, FRET calculation, AFM measurements and samples for TEM, provided samples for all characterization measurements and prepared the first draft of the MS. J. G. assisted with TA analysis and supervised the project, C. S. P. D. C. assisted with steady state PL measurements, and performed TRPL measurements/analysis as well as TA analysis. J. I. K. conducted TRPL measurements. C. P. conducted TA measurements and analysis. S. A. performed the light-intensity dependence measurements and analyzed the data. O. M. performed the PLQY measurements. Y. H. helped with control experiments. G. T. H. performed UPS/LE-IPES measurements for P3HT, IEICO-4Cl, and IDT-2Br. A. S. performed UPS/LE-IPES measurements for ZY-4Cl. W. Z. provided synthesized FBR. V. M. conducted the TEM-EELS measurements. J. P. J. and M. M. assisted with outdoor stability measurements. D. B., S. D. W. and S. F. supervised the photoemission measurements. I. M. supervised the synthesis of FBR. F. L. supervised the project. All authors contributed to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ee05059f.

Acknowledgements

This publication is based upon work supported by the King Abdullah University of Science and Technology (KAUST) Office of Research Administration (ORA) under Award No. OSR-CARF/CCF-3079 and Award No. ORFS-CRG11-2022-5045. C. E. P. acknowledges support from King Abdullah University of Science and Technology (KAUST) Global Fellowship Program under Award No. ORA-2022-5002. W. A. acknowledges the core labs at King Abdullah University of Science and Technology (KAUST).

References

1. J. Wang, et al., Tandem organic solar cells with 20.6% efficiency enabled by reduced voltage losses, Natl. Sci. Rev., 2023, 10, nwad085 , ISSN2095-5138.
2. R. Xue, J. Zhang, Y. Li and Y. Li, Organic Solar Cell Materials toward Commercialization, Small, 2018, 14, 1801793.
3. F. Yang, Y. Huang, Y. Li and Y. Li, Large-area flexible organic solar cells, npj Flexible Electron., 2021, 5, 2397–4621,  DOI:10.1038/s41528-021-00128-6.
4. F. Zhao, et al., Single-Junction Binary-Blend Nonfullerene Polymer Solar Cells with 12.1% Efficiency, Adv. Mater., 2017, 29, 1700144.
5. W. Zhao, et al., Molecular Optimization Enables over 13% Efficiency in Organic Solar Cells, J. Am. Chem. Soc., 2017, 139, 7148–7151.
6. G. Li, et al., High-efficiency solution processable polymer photovoltaic cells by self-organization of polymer blends, Nat. Mater., 2005, 4, 864–868.
7. Y. Kim, et al., A strong regioregularity effect in self-organizing conjugated polymer films and high-efficiency polythiophene:fullerene solar cells, Nat. Mater., 2006, 5, 197–203.
8. H. Tang, et al., Elucidating the optimal material combinations of organic photovoltaics for maximum industrial viability, Joule, 2024, 8, 2208–2219,  DOI:10.1016/j.joule.2024.06.022.
9. C. Yang, et al., Achieving over 10% Efficiency in Poly(3-hexylthiophene)-Based Organic Solar Cells via Solid Additives, ChemSusChem, 2021, 14, 3607–3613.
10. J. Yuan, et al., Single-Junction Organic Solar Cell with over 15% Efficiency Using Fused-Ring Acceptor with Electron-Deficient Core, Joule, 2019, 3, 1140–1151.
11. P. Bi, et al., Reduced non-radiative charge recombination enables organic photovoltaic cell approaching 19% efficiency, Joule, 2021, 5, 2408–2419.
12. Y. Zhong, A. Tada, S. Izawa, K. Hashimoto and K. Tajima, Enhancement of VOC without loss of JSC in organic solar cells by modification of donor/acceptor interfaces, Adv. Energy Mater., 2014, 4, 1301–1332.
13. J. Gorenflot, et al., Increasing the Ionization Energy Offset to Increase the Quantum Efficiency in Non-Fullerene Acceptor-Based Organic Solar Cells: How Far Can We Go?, Adv. Mater. Interfaces, 2023, 10, 2202515.
14. Q. Wu, et al., High-performance organic photovoltaic modules using eco-friendly solvents for various indoor application scenarios, Joule, 2022, 6, 2138–2151.
15. I. Burgués-Ceballos, et al., Transparent organic photovoltaics: A strategic niche to advance commercialization, Joule, 2021, 5, 2261–2272,  DOI:10.1016/j.joule.2021.07.004.
16. S. M. Menke, N. A. Ran, G. C. Bazan and R. H. Friend, Understanding Energy Loss in Organic Solar Cells: Toward a New Efficiency Regime, Joule, 2018, 2, 25–35,  DOI:10.1016/j.joule.2017.09.020.
17. A. M. Andermann and L. G. C. Rego, Energetics of the charge generation in organic donor-acceptor interfaces, J. Chem. Phys., 2022, 156, 024104 , ISSN0021-9606.
18. S. U. Z. Khan, et al., Quantifying the effect of energetic disorder on organic solar cell energy loss, Joule, 2022, 6, 2821–2834.
19. C. Yang, et al., Effects of energy-level offset between a donor and acceptor on the photovoltaic performance of non-fullerene organic solar cells, J. Mater. Chem. A, 2019, 7, 18889–18897.
20. J. Zhang, et al., Accurate Determination of the Minimum HOMO Offset for Efficient Charge Generation using Organic Semiconducting Alloys, Adv. Energy Mater., 2020, 10, 1903298.
21. M. C. Scharber, et al., Design rules for donors in bulk-heterojunction solar cells - Towards 10% energy-conversion efficiency, Adv. Mater., 2006, 18, 789–794.
22. S. Chen, et al., Efficient Nonfullerene Organic Solar Cells with Small Driving Forces for Both Hole and Electron Transfer, Adv. Mater., 2018, 30, 1804215.
23. F. Jin, et al., Improved Charge Generation via Ultrafast Effective Hole-Transfer in All-Polymer Photovoltaic Blends with Large Highest Occupied Molecular Orbital (HOMO) Energy Offset and Proper Crystal Orientation, Adv. Funct. Mater., 2018, 28, 1801611.
24. S. Karuthedath, et al., Intrinsic efficiency limits in low-bandgap non-fullerene acceptor organic solar cells, Nat. Mater., 2021, 20, 378–384.
25. G. D’Avino, et al., Energetics of electron-hole separation at P3HT/PCBM heterojunctions, J. Phys. Chem. C, 2013, 117, 12981–12990.
26. J. Benduhn, et al., Intrinsic non-radiative voltage losses in fullerene-based organic solar cells, Nat. Energy, 2017, 2, 17053 , ISSN2058-7546.
27. E. Collado-Fregoso, et al., Energy-Gap Law for Photocurrent Generation in Fullerene-Based Organic Solar Cells: The Case of Low-Donor-Content Blends, J. Am. Chem. Soc., 2019, 141, 2329–2341.
28. A. Rana, N. Vashistha, A. Kumar, M. Kumar and R. K. Singh, Charge Carrier Formation following Energy Gap Law in Photo-Activated Organic Materials for Efficient Solar Cells, Energies, 2024, 17, 2114 , ISSN1996-1073.
29. A. Markina, et al., Chemical Design Rules for Non-Fullerene Acceptors in Organic Solar Cells, Adv. Energy Mater., 2021, 11, 2102363.
30. J. Bertrandie, et al., The Energy Level Conundrum of Organic Semiconductors in Solar Cells, Adv. Mater., 2022, 34, 2202575.
31. G. F. Burkhard, E. T. Hoke and M. D. McGehee, Accounting for interference, scattering, and electrode absorption to make accurate internal quantum efficiency measurements in organic and other thin solar cells, Adv. Mater., 2010, 22, 3293–3297.
32. J. I. Khan, et al., P3HT Molecular Weight Determines the Performance of P3HT:O-IDTBR Solar Cells, Sol. RRL, 2019, 3, 1900023.
33. A. Wadsworth, et al., Progress in Poly (3-Hexylthiophene) Organic Solar Cells and the Influence of Its Molecular Weight on Device Performance, Adv. Energy Mater., 2018, 8, 1801001.
34. D. W. Gehrig, et al., The impact of donor-acceptor phase separation on the charge carrier dynamics in pBTTT:PCBM photovoltaic blends, Macromol. Rapid Commun., 2015, 36, 1054–1060.
35. A. Yin, et al., Mediated Non-geminate Recombination in Ternary Organic Solar Cells Through a Liquid Crystal Guest Donor, Front Chem, 2020, 8, 21 , ISSN2296-2646.
36. A. Karki, et al., Unifying Charge Generation, Recombination, and Extraction in Low-Offset Non-Fullerene Acceptor Organic Solar Cells, Adv. Energy Mater., 2020, 10, 2001203.
37. E. Pascual-San-José, et al., Blade coated P3HT:non-fullerene acceptor solar cells: A high-throughput parameter study with a focus on up-scalability, J. Mater. Chem. A, 2019, 7, 20369–20382.
38. Y. Wu, et al., A planar electron acceptor for efficient polymer solar cells, Energy Environ. Sci., 2015, 8, 3215–3221.
39. Y. Zhong, et al., Sub-picosecond charge-transfer at near-zero driving force in polymer:non-fullerene acceptor blends and bilayers, Nat. Commun., 2020, 11, 833 , ISSN2041-1723.
40. U. Würfel, et al., Recombination between Photogenerated and Electrode-Induced Charges Dominates the Fill Factor Losses in Optimized Organic Solar Cells, J. Phys. Chem. Lett., 2019, 10, 3473–3480.
41. IEEE Electron Devices Society, Annual IEEE Computer Conference, IEEE Photovoltaic Specialists Conference 35 2010.06.20-25 Honolulu, H. & PVSC 35 2010.06.20-25 Honolulu, H. 35th IEEE Photovoltaic Specialists Conference (PVSC), 2010 20-25 June 2010, Honolulu, Hawaii; Conference Proceedings.
42. C. M. Proctor, M. Kuik and T. Q. Nguyen, Charge carrier recombination in organic solar cells, Prog. Polym. Sci., 2013, 38, 1941–1960,  DOI:10.1016/j.progpolymsci.2013.08.008.
43. W. Siiocklev and A. W. T. Read, A SOLUBLE PROBLEM IN ENERGY HANDS Statistics of the Recombinations of Holes and Electrons, Phys. Rev., 1952, 835.
44. S. Zeiske, et al., Direct observation of trap-assisted recombination in organic photovoltaic devices, Nat. Commun., 2021, 12, 3603 , ISSN2041-1723.
45. A. K. K. Kyaw, et al., Intensity dependence of current-voltage characteristics and recombination in high-efficiency solution-processed small-molecule solar cells, ACS Nano, 2013, 7, 4569–4577.
46. C. M. Proctor, S. Albrecht, M. Kuik, D. Neher and T. Q. Nguyen, Overcoming geminate recombination and enhancing extraction in solution-processed small molecule solar cells, Adv. Energy Mater., 2014, 4, 1400230.
47. J. Kniepert, M. Schubert, J. C. Blakesley and D. Neher, Photogeneration and recombination in P3HT/PCBM solar cells probed by time-delayed collection field experiments, J. Phys. Chem. Lett., 2011, 2, 700–705.
48. J. Kurpiers and D. Neher, Dispersive Non-Geminate Recombination in an Amorphous Polymer:Fullerene Blend, Sci. Rep., 2016, 6, 26832 , ISSN2045-2322.
49. M. Pranav, et al., Anticorrelated photoluminescence and free charge generation proves field-assisted exciton dissociation in low-offset PM6:Y5 organic solar cells, APL Mater., 2023, 11, 061111 , ISSN061-111.
50. S. Shoaee, et al., What We have Learnt from PM6:Y6, Adv. Mater., 2024, 36, 2302005,  DOI:10.1002/adma.202302005 , ISSN0935-9648.
51. G. He, et al., Performance-Limiting Factors in Ultralow-Bandgap PTB7-Th:COTIC-4F-Based Organic Solar Cells, ACS Energy Lett., 2023, 8, 3980–3988.
52. N. Tokmoldin, et al., Elucidating How Low Energy Offset Matters to Performance of Nonfullerene Acceptor-Based Solar Cells, ACS Energy Lett., 2023, 8, 2552–2560.
53. B. Sun, et al., Toward More Efficient Organic Solar Cells: A Detailed Study of Loss Pathway and Its Impact on Overall Device Performance in Low-Offset Organic Solar Cells, Adv. Energy Mater. 13, 2023, 2300980 , ISSN1614-6832.
54. Y. Firdaus, et al., Charge Photogeneration and Recombination in Mesostructured CuSCN-Nanowire/PC70BM Solar Cells, Sol. RRL, 2018, 2, 1800095 , ISSN2367-198.
55. A. H. Balawi, et al., Quantification of Photophysical Processes in All-Polymer Bulk Heterojunction Solar Cells, Sol. RRL, 2020, 4, 2000181.
56. M. Mingebach, S. Walter, V. Dyakonov and C. Deibel, Direct and charge transfer state mediated photogeneration in polymer-fullerene bulk heterojunction solar cells, Appl. Phys. Lett., 2012, 100, 193302 , ISSN0003-6951.
57. J. Kern, S. Schwab, C. Deibel and V. Dyakonov, Binding energy of singlet excitons and charge transfer complexes in MDMO-PPV: PCBM solar cells, Phys. Status Solidi RRL, 2011, 5, 364–366.
58. I. A. Howard, R. Mauer, M. Meister and F. Laquai, Effect of morphology on ultrafast free carrier generation in polythiophene:fullerene organic solar cells, J. Am. Chem. Soc., 2010, 132, 14866–14876.
59. J. Jaumot, R. Gargallo, A. De Juan and R. Tauler, A graphical user-friendly interface for MCR-ALS: A new tool for multivariate curve resolution in MATLAB, Chemom. Intell. Lab. Syst., 2005, 76, 101–110.
60. J. Jaumot, A. de Juan and R. Tauler, MCR-ALS GUI 2.0: New features and applications, Chemom. Intell. Lab. Syst., 2015, 140, 1–12.
61. A. de Juan and R. Tauler, Multivariate Curve Resolution-Alternating Least Squares for Spectroscopic Data, Data Handling in Science and Technology, Elsevier Ltd, vol. 30, 2016, pp. 5–51.
62. I. A. Howard, H. Mangold, F. Etzold, D. Gehrig and F. Laquai, Transient Absorption Data Analysis By Soft-Modelling, Ultrafast Dynamics in Molecules, Nanostructures and Interfaces, 2014, pp. 53–78.
63. J. Kniepert, I. Lange, N. J. Van Der Kaap, L. J. A. Koster and D. Neher, A Conclusive view on charge generation, recombination, and extraction in as-prepared and annealed P3HT:PCBM Blends: Combined experimental and simulation work, Adv. Energy Mater., 2014, 4, 1301401 , ISSN1614-6832.
64. S. M. Hosseini, et al., Impact of Bimolecular Recombination on the Fill Factor of Fullerene and Nonfullerene-Based Solar Cells: A Comparative Study of Charge Generation and Extraction, J. Phys. Chem. C, 2019, 123, 6823–6830.
65. G. Lakhwani, A. Rao and R. H. Friend, Bimolecular recombination in organic photovoltaics, Annu. Rev. Phys. Chem., 2014, 65, 557–581.
66. S. Shoaee, et al., Decoding Charge Recombination through Charge Generation in Organic Solar Cells, Sol. RRL, 2019, 3, 1900184.
67. J. Gorenflot, et al., From Recombination Dynamics to Device Performance: Quantifying the Efficiency of Exciton Dissociation, Charge Separation, and Extraction in Bulk Heterojunction Solar Cells with Fluorine-Substituted Polymer Donors, Adv. Energy Mater., 2018, 8, 1701678 , ISSN1614-6832.
68. S. Karuthedath, et al., Buildup of Triplet-State Population in Operating TQ1:PC71BM Devices Does Not Limit Their Performance, J. Phys. Chem. Lett., 2020, 11, 2838–2845.
69. O. Alqahtani, et al., Mixed Domains Enhance Charge Generation and Extraction in Bulk-Heterojunction Solar Cells with Small-Molecule Donors, Adv. Energy Mater., 2018, 8, 1702941 , ISSN1614-6832.
70. J. I. Khan, et al., Thienyl Sidechain Substitution and Backbone Fluorination of Benzodithiophene-Based Donor Polymers Concertedly Minimize Carrier Losses in ITIC-Based Organic Solar Cells, J. Phys. Chem. C, 2020, 124, 10420–10429.
71. H. Xu, et al., Dissecting the structure-stability relationship of Y-series electron acceptors for real-world solar cell applications, Joule, 2023, 7, 2135–2151.
72. F. C. Spano, Modeling disorder in polymer aggregates: The optical spectroscopy of regioregular poly(3-hexylthiophene) thin films, J. Chem. Phys., 2005, 122, 234701 , ISSN0021-9606.
73. J. Clark, J. F. Chang, F. C. Spano, R. H. Friend and C. Silva, Determining exciton bandwidth and film microstructure in polythiophene films using linear absorption spectroscopy, Appl. Phys. Lett., 2009, 94, 163306 , ISSN0003-6951.
74. J. F. Gorenflot Optical Study of the Excited States in the Semiconducting Polymer Poly(3-Hexylthiophene) for Photovoltaic Applications.( 2015).
75. J. I. Khan, et al., Impact of Acceptor Quadrupole Moment on Charge Generation and Recombination in Blends of IDT-Based Non-Fullerene Acceptors with PCE10 as Donor Polymer, Adv. Energy Mater., 2021, 11, 2100839 , ISSN1614-6832.
76. Y. Wu, et al., Reduced bimolecular charge recombination in efficient organic solar cells comprising non-fullerene acceptors, Sci. Rep., 2023, 13, 4717 , ISSN2045-2322.
77. T. F. Hinrichsen, et al., Long-lived and disorder-free charge transfer states enable endothermic charge separation in efficient non-fullerene organic solar cells, Nat. Commun., 2020, 11, 5617 , ISSN2041-1723.
78. D. Neher, J. Kniepert, A. Elimelech and L. J. A. Koster, A New Figure of Merit for Organic Solar Cells with Transport-limited Photocurrents, Sci. Rep., 2016, 6, 24861 , ISSN2045-2322.
79. D. Bartesaghi, et al., Competition between recombination and extraction of free charges determines the fill factor of organic solar cells, Nat. Commun., 2015, 6, 7083 , ISSN2041-1723.
80. N. Tokmoldin, et al., Explaining the Fill-Factor and Photocurrent Losses of Nonfullerene Acceptor-Based Solar Cells by Probing the Long-Range Charge Carrier Diffusion and Drift Lengths, Adv. Energy Mater., 2021, 11, 2100804 , ISSN1614-6832.
81. A. Armin, et al., A Shockley-Type Polymer: Fullerene Solar Cell, Adv. Energy Mater., 2018, 8, 1701450 , ISSN1614-6832.
82. S. Wilken, et al., How to Reduce Charge Recombination in Organic Solar Cells: There are Still Lessons to Learn from P3HT:PCBM, Adv. Electron. Mater., 2021, 7, 2001056 , ISSN2199-160.
83. E. Spiliarotis, et al., Long-term outdoor performance of a solar farm enabled by graphene-perovskite panels: investigating degradation mechanisms, dark storage recovery, and visual defects., EES Solar, 2025, 295–309,  10.1039/D5EL00042D.
84. H. Tang, et al., Rationale for highly efficient and outdoor-stable terpolymer solar cells, Energy Environ. Sci., 2023, 2056–2067,  10.1039/d3ee00350g.
85. J. Liu, et al., 28.2%-efficient, outdoor-stable perovskite/silicon tandem solar cell, Joule, 2021, 5, 3169–3186.
86. M. Babics, et al., Unleashing the Full Power of Perovskite/Silicon Tandem Modules with Solar Trackers, ACS Energy Lett., 2022, 7, 1604–1610.
87. M. De Bastiani, et al., Toward Stable Monolithic Perovskite/Silicon Tandem Photovoltaics: A Six-Month Outdoor Performance Study in a Hot and Humid Climate, ACS Energy Lett., 2021, 6, 2944–2951.

---

Footnote

† Present Address: J.I.K: University of Hull, Department of Physics, HU6 7RX, Hull, UK.

---