Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Improved calculation framework for Prussian Blue analogues as a battery material
Sebastian
Baumgart
 *a,
Mohsen
Sotoudeh
*a,
Mohsen
Sotoudeh
 acd,
Ivano E.
Castelli
acd,
Ivano E.
Castelli
 b and
Axel
Groß
b and
Axel
Groß
 *ad
*ad
aInstitute of Theoretical Chemistry, Ulm University, Oberberghof 7, 89081 Ulm, Germany. E-mail: sebastian.baumgart@uni-ulm.de; axel.gross@uni-ulm.de
bDepartment of Energy Conversion and Storage, Technical University of Denmark, Agnes Nielsens Vej 301, DK-2800 Kongens Lyngby, Denmark
cKarlsruhe Institute of Technology (KIT), 76021 Karlsruhe, Germany
dHelmholtz Institute Ulm (HIU) for Electrochemical Energy Storage, Helmholtzstraße 11, 89081 Ulm, Germany
First published on 8th December 2025
Abstract
Prussian Blue analogues are promising, low-cost cathodes for sodium-ion batteries, yet their complex mixed-valent and polymorphic nature challenges predictive modeling. This study provides a transferable density functional theory calculation framework for Prussian Blue analogues in sodium-ion battery applications by systematically benchmarking six representative exchange–correlation functionals across three sodiation states and two structural modifications (cubic and rhombohedral). We evaluate structural and electronic properties, open-circuit voltages, and the sodium ion transport via two prominent migration mechanisms. Additionally, we highlight the differing computational requirements for modeling Prussian Blue analogues either as half-filled, mixed-valent compounds with a strong focus on the electronic structure or as high-grade functional battery materials, where an accurate prediction of the phase stability and the ion transport is essential. Our results establish practical recommendations for reliable density functional theory studies of Prussian Blue analogues, warn of pitfalls to be avoided and lay the groundwork for high-throughput screening of sustainable sodium-ion battery materials.
Broader contextThe global transition toward sustainable and cost-effective energy storage has brought sodium-ion batteries to the forefront of large-scale grid applications. Among their potential cathode materials, Prussian Blue analogues (PBAs) stand out for their earth abundance, high ionic conductivity, and long cycle life. However, despite extensive research and widespread computational modeling, the commonly used density functional theory framework for PBAs has not been systematically re-evaluated since its introduction in 2008. This study provides a comprehensive benchmark of six exchange–correlation functionals across multiple sodiation states and structural phases, revealing how functional choice critically influences the accuracy of predicted structural, electronic, and ionic transport properties. The resulting recommendations establish a validated, transferable computational workflow that enhances the reliability of density functional theory in modeling PBAs. By improving predictive accuracy and reproducibility, this work supports the rational design and high-throughput screening of sustainable cathode materials, contributing directly to the advancement of sodium-ion batteries for large-scale energy storage applications. |
Introduction
As science enters its fourth paradigm – “(Big) data driven science”1 – the central challenge transforms from the absence of data to an overwhelming abundance of it, making manual analysis challenging. This shift has led to the emergence of the field of data science, which focuses on the correct handling of generated data, including the preparation of meta-data and data analysis. Yet, this evolution introduces new complications: datasets often contain undetected biases, originate from heterogeneous sources, and exhibit inconsistencies, dependencies, or poorly quantified uncertainties.2,3 Even the moderation or curation of data can introduce ambiguity or subjectivity, further complicating the data analysis. In the field of battery materials, the development of standardized computational frameworks has advanced considerably; however, no such framework yet exists for accurately simulating Prussian Blue analogues. Their complex and correlated structural and electronic interactions render accurate predictions of key battery properties highly nuanced and sensitive to the choice of computational methods.Prussian blue type materials (A0–2Fe[Fe(CN)6]) are crystalline double-perovskite materials with cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) symmetry.4 The structure can be derived by replacing the oxygen anions of a typical (double) perovskite structure by (C
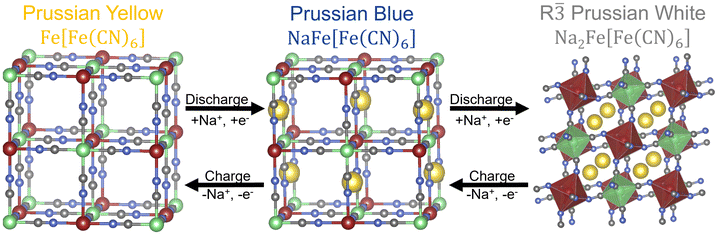
m) symmetry.4 The structure can be derived by replacing the oxygen anions of a typical (double) perovskite structure by (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N)− anions.5 This results in the structural motive of cyanide-interconnected high spin (FeC6) and low spin (FeN6) iron octahedra, which are alternating along all three crystal axis. Further complexity arises from the intercalation of sodium ions into the 24d Wyckoff positions, which offer a high number of available positions relative to the number of intercalating ions, resulting in a partially occupied sublattice.6 This breaks the structural symmetry and greatly increases the number of possible charge carrier configurations. Structures in which any one of the iron atoms is substituted with a different transition metal are typically called Prussian blue analogues (PBAs, A0–2B[B′(CN)6]), the most common representative being Na2Mn[Fe(CN)6]. The thermodynamically stable degrees of sodiation of this material are nowadays named after the color they exhibit: the fully desodiated compound being called Prussian Yellow (PY), the half sodiated Prussian Blue (PB) and the fully sodiated material is called Prussian White (PW).7 Additionally, a configuration of the fully sodiated structure exhibiting R
N)− anions.5 This results in the structural motive of cyanide-interconnected high spin (FeC6) and low spin (FeN6) iron octahedra, which are alternating along all three crystal axis. Further complexity arises from the intercalation of sodium ions into the 24d Wyckoff positions, which offer a high number of available positions relative to the number of intercalating ions, resulting in a partially occupied sublattice.6 This breaks the structural symmetry and greatly increases the number of possible charge carrier configurations. Structures in which any one of the iron atoms is substituted with a different transition metal are typically called Prussian blue analogues (PBAs, A0–2B[B′(CN)6]), the most common representative being Na2Mn[Fe(CN)6]. The thermodynamically stable degrees of sodiation of this material are nowadays named after the color they exhibit: the fully desodiated compound being called Prussian Yellow (PY), the half sodiated Prussian Blue (PB) and the fully sodiated material is called Prussian White (PW).7 Additionally, a configuration of the fully sodiated structure exhibiting R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry is often called rhombohedral Prussian white (R-PW).8,9 The structure of R-PW was included in this work due to its importance as a cathode material in battery applications.
symmetry is often called rhombohedral Prussian white (R-PW).8,9 The structure of R-PW was included in this work due to its importance as a cathode material in battery applications.
The calculation of Prussian blue type materials via electronic structure methods is especially challenging due to the complex electronic structure which itself is strongly correlated to the geometry of the material. The fact that a correct description of the electronic structure is essential to the accurate description of the geometry is well known and thoroughly explored for PB as prototypical mixed-valent material.10–17 This is complicated further when talking about battery materials, as PY and PW are – contrary to PB – neither mixed-valent, nor semi-conducting. This complexity poses great challenges for the first-principles electronic structure treatment of these materials. All three degrees of sodiation have to be described properly, if relevant properties for batteries, such as the Open circuit voltage (OCV), are to be calculated accurately. However, current first-principles methods typically fail to reproduce measured trends in the properties of PB type materials, as even the calculated trend in lattice constants between PY/PB/PW18,19 is already in disagreement with experiment.20 Furthermore, with respect to the DFT+U approach, widely used to describe strongly correlated materials, it was found in a previous study21 that utilizing the standard approach of Wojdeł13 with U-parameters of 3 and 7 eV for FeC and FeN, respectively, does not allow for a consistent calculation of the OCV and the energy barrier of charge carrier migration. Even in the limit of low sodium concentrations, the estimation of the energy barrier fails due to artifacts that are introduced during the calculation of the transition state energy via Nudged elastic band (NEB) calculations. These artifacts most likely occur due to an unphysical overlocalization of the transition metal d-electrons – which is caused by the high U values needed for correctly describing the band gap of Prussian blue. This might also be the reason for the low number of published studies on this material class despite being pushed into focus of battery researches since 2015. The only report on the migration barriers of charge carriers in the Prussian blue framework that is known to the authors is published by Peng et al.,22 as well as the afore mentioned previous study by the authors of this work.21 Guo et al.23 briefly explored a similar benchmark for NaxMn[Fe(CN)6], but this aspect received only limited attention in their report. Moreover, their study did not propose any novel approaches to address the challenges associated with functional selection, nor did it systematically report the performance of each exchange–correlation functional.
In this paper, we present the reader with a detailed guideline for performing electronic structure calculations on Prussian Blue and its analogues, focusing on the accuracy and applicability of widely used exchange–correlation functionals. Specifically, we investigate the performance of the standard PBE functional, the commonly employed PBE+U approach as proposed by Wojdeł et al.,13 the recently developed SCAN and r2SCAN meta-GGA functionals, as well as the well-established hybrid functionals PBE0 and HSE06. By systematically comparing their ability to capture structural, electronic, and ion transport properties, we identify the most appropriate functional(s) for targeted applications. These findings not only provide a practical reference for computational researchers but also contribute to accelerating the design of PBA materials with improved electrochemical performance and sustainability for grid-scale energy storage, if incorporated into materials design pipelines.
Computational details
Density functional theory (DFT)24–26 calculations were performed with the plane-wave method based code Vienna Ab initio Simulation Package (VASP)27,28 in version 6.2.1. The projector augmented wave (PAW) approach was utilized to represent the interactions between the electrons and the core.28,29 In all calculations a Gaussian smearing with a width of 0.1 eV was used. The plane-wave cutoff was set to 550 eV. The atomic structures were optimized until the energy difference in the electronic self-consistent field (SCF) fell below 10−6 eV, and the force convergence criteria was fixed to 10−2 eV Å−1. The Brillouin zone was sampled with an automatically generated, gamma-centered k-point grid of 5 × 5 × 5 and 5 × 5 × 3 in all non-hybrid calculations of the cubic and rhombohedral structures, respectively. To minimize computational cost, hybrid functional calculations were performed using gamma-point-only structural optimizations, followed by electronic structure evaluations on a 2 × 2 × 2 k-point grid. To ensure convergence to the correct high-spin-low-spin spin state, the total excess majority spin electrons were held constant. To assess the accuracy towards a correct description of the atomic and electronic structure of the Prussian blue material class, we have tested a range of different functionals. We start with the generalized gradient approximation (GGA) represented by the widely used PBE functional proposed by Perdew, Burke and Ernzerhof.30 To address the known issue of overdelocalization associated with GGA functionals, we have employed the PBE functional with the addition of Hubbard U-correction to the iron d-states, as suggested by Dudarev et al.31 The chosen U-values follow the methodology established by Wojdeł et al.,13 who systematically tested a range of U-parameters for both iron sites and evaluated their influence on key properties, including lattice constants, total energy differences between magnetic configurations and band gap variations in Prussian Blue. Their results demonstrated that PBAs are best represented using two distinct U-values – 3 eV for the d-states of the low-spin iron in FeC6 octahedra and 7 eV for the high-spin iron in FeN6 octahedra – values that were subsequently adopted and validated in more recent studies.21 The level of meta-GGA functionals is exemplified by the inclusion of the SCAN32 and r2SCAN33 functionals. As representatives of hybrid functionals PBE034–36 and HSE0637 were chosen. The structure of all cubic geometries was adapted from the Crystallography Open Database,38–40 COD ID 4100931. This structure corresponds to the conventional unit cell for Prussian Blue, exhibiting Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry and containing four formula units of Na0–2Fe[Fe(CN)6] (56–64 atoms depending on state of charge). The initial structure for R-PW, containing three formula units of Na0–2Fe[Fe(CN)6] (42–48 atoms depending on state of charge) and exhibiting R
m symmetry and containing four formula units of Na0–2Fe[Fe(CN)6] (56–64 atoms depending on state of charge). The initial structure for R-PW, containing three formula units of Na0–2Fe[Fe(CN)6] (42–48 atoms depending on state of charge) and exhibiting R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry was adapted from the structural parameters published by Wang et al.41
symmetry was adapted from the structural parameters published by Wang et al.41
The NEB calculations42,43 have been carried out with the help of PerQueue.44 PerQueue is a data-passing and persistence framework that utilizes the MyQueue45 package to submit jobs to a chosen scheduler. The NEB calculations utilize a single climbing-image in a charge-neutral fashion to estimate the Na-ion migration transition state energy. Single-image NEB calculations are commonly regarded as inadequate due to their limited resolution of complex migration pathways. However, in cases where the migration path is already known or not the focus of the study, utilizing a single NEB image becomes a suitable approximation. The use of the climbing-image method enhances both the feasibility and reliability of this approach. Recent literature confirms that, under such conditions, single-image NEB can achieve substantial computational efficiency without compromising the accuracy of transition state energy predictions.46–48 This efficiency is especially advantageous in comparative studies, such as the present investigation, that include computationally intensive hybrid functionals, for which the use of traditional multi-image NEBs would be prohibitively expensive. To benchmark the single-image NEB approach used here, we compare its performance against the standard multi-image NEB method for a high-vacancy/Prussian Yellow reference system using the computationally inexpensive PBE functional. The full comparison is provided in the SI (Fig. S1). The reported structure was determined to be sufficiently large to ensure a negligible interaction between the periodic images of the migrating sodium ions. All structures were fully relaxed until the forces on the atoms were converged within 10−2 eV Å−1.
Reasonable migration pathways were estimated prior to the performance of the NEB calculations via a bond valence sum (BVS) mismatch utilizing pyAbstantia.49 The bond valence sum (BVS) method computes the valence Vi of an ion i by summing over the empirical bond valences sij to all adjacent ions j of opposite charge.50,51
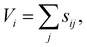 | (1) |
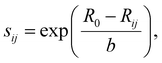 | (2) |
The BVS approach allows for a rapid identification of chemically plausible intercalation sites where the calculated valence matches the formal oxidation state (Videal) of the ion. By mapping the deviation of the BVS (|ΔV|) between the calculated valence and the formal oxidation state, a bond valence sum mismatch plot highlights regions of low mismatch, which correspond to energetically favorable pathways for ion migration.51,53
| |ΔV| = |Vi − Videal| | (3) |
In practice, one generates a three-dimensional grid of BVS values across the unit cell, and the isosurfaces of minimal |ΔV| delineate likely migration channels without the need for exhaustive atomistic simulations.51,54 We utilized a grid with a step length of 0.1 Å to calculate the BVS mismatch and visualize the resulting isosurfaces at a value of 0.5.
Results and discussion
Sodium iron hexacyanoferrate, Na0–2Fe[Fe(CN)6]
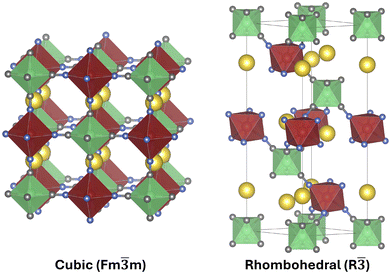
Prussian Blue exists in two different modifications, cubic (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, 225) and rhombohedral (R
m, 225) and rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , 148). The PBE optimized geometries for both systems are presented in Fig. 1, while a simplified presentation of the complete sodiation process and the name of the different compounds are represented in Fig. 2.
, 148). The PBE optimized geometries for both systems are presented in Fig. 1, while a simplified presentation of the complete sodiation process and the name of the different compounds are represented in Fig. 2.
The cubic structure consists of iron octahedra interconnected with cyanide ligands – where the low-spin FeC6 and high-spin FeN6 octahedra are ordered in an alternating fashion in all three spatial directions. When sodium is intercalated, it prefers to occupy the 24d Wyckoff position. The cubic modification is relevant specifically for a sodium content below 1 sodium atom per f.u. The framework is stable without any intercalated cations and the missing charge is compensated by all irons being oxidized to +3. Upon sodiation, the FeC6 centers are selectively reduced to +2 until the half-sodiated state is reached. In this state the sodium ions are arranged in a tetragonal fashion.
When the material is further sodiated above 1 Na per f.u., the phase changes from the cubic to the rhombohedral modification. The new structure – exhibiting R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry – is formed by a cooperative out-of-phase rotation of the iron octahedra. While this phase transition still allows for straight C
symmetry – is formed by a cooperative out-of-phase rotation of the iron octahedra. While this phase transition still allows for straight C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds, the shift is accompanied by a shift of the sodium atoms along the [111] axis of the cubic cell, moving them out of the 24d position into layers (along the c-axis) of FeN6 octahedra to fully optimize the sodium–nitrogen interactions. While the fully sodiated cubic compound is not stable with regard to the rhombohedral phase, it is included in this study for comparison's sake. Please note further, that the complete floating-point data underlying all figures and graphs presented in the following sections “Structural analysis” and “Electronic analysis” are provided in the SI – Tables S5–S16.
N bonds, the shift is accompanied by a shift of the sodium atoms along the [111] axis of the cubic cell, moving them out of the 24d position into layers (along the c-axis) of FeN6 octahedra to fully optimize the sodium–nitrogen interactions. While the fully sodiated cubic compound is not stable with regard to the rhombohedral phase, it is included in this study for comparison's sake. Please note further, that the complete floating-point data underlying all figures and graphs presented in the following sections “Structural analysis” and “Electronic analysis” are provided in the SI – Tables S5–S16.
 | ||
| Fig. 3 Lattice constant in dependence on the functional. The left hand graph depicts the lattice constants of cubic Prussian Yellow, Prussian Blue and Prussian White (grey). The right hand graph depicts the lattice constants for the fully sodiated, rhombohedral system. The a and b lattice constants are depicted in dark red, while the c lattice constant is represented in light red. Horizontal lines represent the experimental results20,55 and match in color with the respective data representation. Please also note the difference in y-axis range between both panels. | ||
The lattice constants in Prussian Yellow are calculated to be larger than experimentally measured ones for GGA functionals (PBE, PBE+U), though meta-GGA (SCAN, r2SCAN) and hybrid (PBE0, HSE06) functionals match experimental values well. Contrary, for Prussian Blue the results of the GGA functionals agree with the experimental literature, while meta-GGA and hybrid functionals underestimate the lattice constant. For Prussian White, PBE and the hybrid functionals match best, while the meta-GGA functionals underestimate the lattice constant. The only functional to overestimate the volume expansion is PBE+U. Regarding the volume expansion during sodium intercalation, a linear trend is observed in the experiments of Wu et al. While the change in lattice constant from Prussian Yellow to Prussian Blue is positive for the non-hybrid functionals, the trend is by far not a linear one. Prussian Yellow and Prussian Blue exhibit almost the same lattice constants, while most of the lattice expansion is attributed to the sodiation step from Prussian Blue to Prussian White. The hybrid functionals even predict the lattice constant of Prussian Blue to be smaller than that of Prussian Yellow, qualitatively mismatching the experimentally observed trend.
For rhombohedral Prussian White there are slight variations in the lattice constants when comparing functionals, though no significant outliers are to be reported. All functionals fit the experimental data reasonably well. Notably, during the full duration of the study we were not able to converge the rhombohedral Prussian White system with the HSE06 functional. Whether this is due to the specific setup of the computation cluster and software, or due to a more fundamental reason is currently under further investigation. Therefore, in this and all following comparisons, the data for the rhombohedral Prussian White structure calculated with the HSE06 functional are omitted.
In Fig. 4 the upper panel depicts the Fe–N and Fe–C bond length, while the C–N bond length is represented in the lower panel. This separation is necessary due to the markedly shorter C–N bonds relative to the metal–ligand bonds. Further, a more narrow y-axis scale is used in the lower panel to improve clarity and avoid overlapping data lines. The experimental values for Prussian blue are taken from an early report of Buser et al.,56 while the values for rhombohedral Prussian White are extracted from the atomic structure reconstructed from the published Rietveld parameters of Brant et al.55 The variations in bond lengths mirrors the behavior observed in the lattice constants, indicating a consistent structural response across different measured properties.
 | ||
| Fig. 4 Representation of the bond length in dependence on the functional for all four compounds. The Fe–N bonds are represented with dots, Fe–C bonds with squares and C–N bonds with diamonds. The compounds are color coded: Prussian Yellow (yellow), Prussian Blue (blue), cubic Prussian White (grey) and rhombohedral Prussian White (red). Experimental references are given by the dotted lines for cubic Prussian Blue56 and rhombohedral Prussian White55 in the compounds respective color. | ||
The Fe–N bond length exhibits the highest sensitivity to changes in both the exchange–correlation functional and the degree of sodiation. Consistent with the behavior of the lattice constants, the Fe–N bond length shows minimal variation between Prussian Yellow and Prussian Blue, with Prussian Blue generally displaying slightly expanded bond lengths. A significant increase is observed when transitioning to the fully sodiated cubic and rhombohedral phases. These two structures, representing the same sodiation level, show comparable lattice constants, with the rhombohedral variant being marginally larger. This difference is attributed to the elongation of bonds induced by octahedral tilting and distortion in the rhombohedral lattice. In contrast to the flexible Fe–N bond, the Fe–C bond is considerably more rigid. Across all degrees of sodiation, it shows only a minor contraction, confirming its structural stability. The C–N bond is even more invariant, with almost no measurable changes as the sodium content increases. This stability can be attributed to the strong covalent nature of the carbon–nitrogen bond. Any slight elongation detected in the C–N bond follows a predictable trend of marginal lengthening with increased sodiation, which is slightly more pronounced upon transitioning to the rhombohedral structure due to associated lattice distortions.
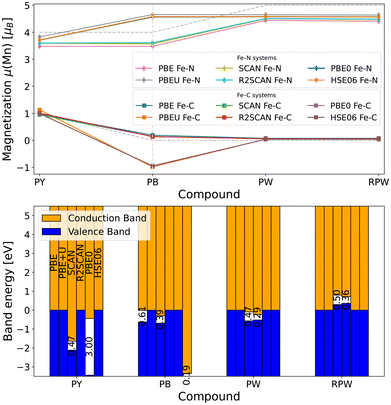
The average magnetization of the carbon- and nitrogen-coordinated iron centers can be used to represent the selective oxidation of the iron atoms during sodiation. First, the low-spin Fe–C6 center is selectively oxidized, then the Fe–N6 centers. The currently not oxidized iron centers stays relatively constant in their magnetization. While there are slight differences in the magnetization of the iron centers between the fully sodiated cubic and rhombohedral modification, these do not change the ordering in results for the functionals, just the split between the functionals is larger for RPW than PW. The values for the carbon-coordinated iron atoms are relatively stable between the functionals and also match the formally expected number of unpaired electrons. For the nitrogen-coordinated iron atom on the other hand, all functionals predict lower values than the number of formally unpaired electrons. The PBE functional predicts the lowest magnetization for the high-spin iron centers, as it most strongly delocalizes the electrons, a phenomenon known as overdelocalization, well known in this type of functional. The meta-GGA functionals show an increase in the localization of the electrons around the iron atoms, though not as pronounced as for the hybrid functionals. The highest magnetization is predicted by the PBE+U functional, representing the ability for the Hubbard U-parameter to more strongly localize the electrons, while keeping the computational cost low in using a GGA functional. The trend of functionals perfectly matches the localization degree of the functionals – showing the influence of the localization onto the local magnetization. Further, this trend is consistent for all compounds and inversely true for the Fe–C6 centers as well.
The second, maybe even more important, electronic property is the band gap of a material. Experimentally, Prussian Yellow, as well as cubic and rhombohedral Prussian White are poor metallic conductors,57–59 while Prussian Blue is a semiconductor with a band gap of ∼1.75 eV.60 The general trend for functionals in this regard is that GGA functionals significantly underestimate the band gap of most materials, again due to the strong electron delocalization of the functionals. Meta-GGA functionals improve upon the accuracy of the GGA functionals in exchange for an increase in computational time. They normally still underestimate the band gap of materials, but are closer to experimental values than pure GGA calculations. Hybrid functionals on the other hand tend to overestimate the band gap slightly to significantly, though they are seen as the best choice for calculating electronic properties for materials without prior knowledge. The GGA+U approach again tries to rectify the underestimation of the band gap with as little as possible additional computational effort by including a simple correction term. The U-values used here are even adapted from a study13 on Prussian Blue, that screened the U-values to best reproduce the band gap of the original Prussian Blue material with potassium ions intercalated into the 8c position, which report a band gap of 1.73 eV – in perfect agreement with the experimental reports.60
The results for Prussian Yellow align with expectations: GGA and meta-GGA functionals predict metallic behavior, while hybrid functionals incorrectly open a band gap. For Prussian Blue, the functional dependence continues to reflect anticipated trends, although PBE+U anomalously predicts metallic behavior. Interestingly, when sodium is placed in the 8c position, PBE+U yields a band gap of 1.813 eV – closely matching experimental values. However, when sodium is shifted to the 24d site, the band gap collapses as electronic states begin to cross the Fermi level. This behavior may be attributed to the broken symmetry arising from sodium occupying a lower-symmetry sublattice. A complete set of results for all exchange–correlation functionals applied to the Prussian Blue model system, with sodium intercalated into the 8c Wyckoff position, is available in the SI – Fig. S3 and Tables S1, S2.
The electronic structure predictions for Prussian White exhibit notable discrepancies with the established literature,58,59 particularly in the absence of the metallic character. The computed band gaps show a clear dependence on the degree of electron localization inherent to each exchange–correlation functional. The GGA functional PBE yields the smallest gap at 0.42 eV, while meta-GGA functionals produce values just under 1 eV. In contrast, the highly localized functionals PBE+U, PBE0, and HSE06 result in significantly larger gaps exceeding 3 eV. Again, when sodium is placed at the 8c Wyckoff site, both GGA and meta-GGA functionals predict a metallic state, aligning with expectations, whereas hybrid functionals still maintain band gaps – although reduced to 2.27–2.97 eV – suggesting a partial recovery of the expected electronic structure. Again, the complete data for the model Prussian White system used for comparison is available in the SI – Fig. S3 and Tables S3, S4.
For the rhombohedral modification again, similar to the Prussian Yellow system, everything seems to be in order. GGA and meta-GGA accurately predict metallic behavior while the PBE0 functional opens up a very large band gap of 4.34 eV.
Sodium manganese hexacyanoferrate, Na0–2Mn[Fe(CN)6]
The upcoming sections explore the effects of substituting the nitrogen-coordinated iron center in the Prussian Blue framework with manganese, chosen for its demonstrated potential in cathode applications. This substitution allows for a test of the transferability of the previously employed exchange–correlation functionals to other types of PBAs. Additionally, the structural and electronic properties of the material shall be explored, as well as how they are affected relative to the original iron-based compound.The improved energy density of the manganese-based Prussian Blue analogue, achieved through a higher operating voltage (3.45 V vs. Na/Na+), represents the primary advantage of this substitution.9,61,62 Beyond this electrochemical advantage, manganese hexacyanoferrate (MnHCF) retains key benefits such as the exclusive use of earth-abundant, low-cost, and nontoxic elements, ensuring sustainability and cost-effectiveness comparable to FeHCF-based cathodes.62,63 Despite these strengths, MnHCF faces critical challenges, especially due to the Jahn–Teller distortions caused by the manganese atoms in a +3 oxidation state. These distortions induce severe structural degradation, transforming the lattice into a monoclinic phase at low sodium concentrations.61,64 The phase transition undermines the structural integrity, leading to diminished reversible capacity, lower cycling stability, and reduced initial coulombic efficiency.62,65 Furthermore, similar to FeHCF, MnHCF suffers from lattice defects, interstitial water incorporation, and limited electronic conductivity, all of which restrict rate performance. Another major concern is the disproportionation of surface Mn3+ ions, which promotes compositional dissolution and accelerates capacity fading.61,62
Several strategies have been developed to address these challenges. Efforts to finely control the crystal structure aim to reduce the impact of lattice distortions, intrinsic defects, and interstitial water.62 In parallel, conductive polymer coatings are employed to enhance the inherently low electronic conductivity and improve rate capability. Furthermore, heterostructured coatings using other Prussian Blue analogues have emerged as an effective approach to enhancing the overall structural stability of the material during cycling.
Overall, the challenges hindering the practical application of MnHCF as a battery material closely mirror those of its iron-based counterpart. However, the introduction of the Jahn–Teller effect presents a new and significant obstacle. The resulting lattice distortion intensifies the pre-existing issue of phase transitions within the electrochemical operating window, thereby posing additional difficulties for maintaining structural and cycling stability during operation.
As manganese-hexacyanoferrate (MnHCF) is derived from its iron-based analogue by simply substituting the nitrogen-coordinated iron with manganese, the underlying crystal framework is preserved. The structure remains composed of alternating FeC6 and MnN6 octahedra interconnected via cyanide ligands. In the fully desodiated state (Na0MnHCF), the material exhibits minor deviations from cubic symmetry due to the Jahn–Teller distortion associated with the presence of Mn3+. However, the half-sodiated compound (Na1MnHCF) retains a cubic structure. Upon further sodiation beyond 1 Na per formula unit, the structure transitions into a rhombohedral configuration, a behavior consistent with the well-established structural evolution observed in the original iron-based Prussian Blue compound. Consequently, the fully sodiated MnHCF (Na2MnHCF) also adopts the rhombohedral structure. Please note, that the complete floating-point data underlying all figures and graphs presented in the following sections “Structural analysis” and “Electronic analysis” are provided in the SI – Tables S17–S28.
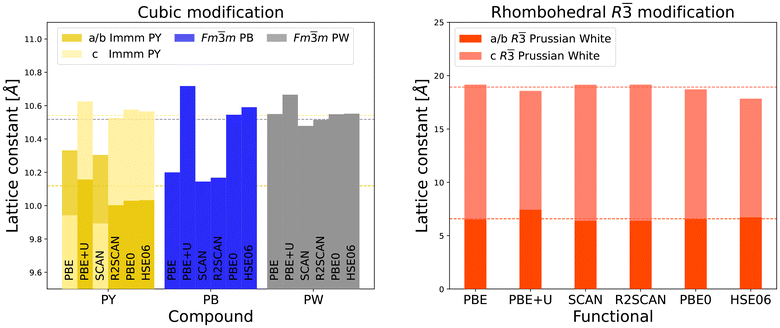 | ||
| Fig. 6 MnHCF lattice constants in dependence on the functional. The left hand graph depicts the lattice constants of cubic Prussian Yellow, Prussian Blue and Prussian White (grey). The right hand graph depicts the lattice constants for the fully sodiated, rhombohedral system. For the non-cubic systems the a and b lattice constants are depicted in dark hues, while the c lattice constant is represented in light ones. Horizontal lines represent the experimental results9 and match in color with the respective data representation. Please also note the difference in y-axis range between both panels. | ||
The predicted elongation direction of the lattice constants in Prussian Yellow varies depending on the functional, although the tetragonal symmetry (a = b ≠ c) is preserved in all cases. This can be visually identified in the figure by a shift in the hue of the yellow color. Overall, the Jahn–Teller-induced changes in lattice parameters are minor and smaller than those caused by the choice of exchange–correlation functional.
For both manganese-based Prussian Blue and Prussian White, the choice of exchange–correlation functional has a negligible effect on the computed lattice constants. A consistent trend is observed where the lattice constant increases with sodium content, again dominated by the transition from Prussian Blue to Prussian White. The calculated lattice parameters for the rhombohedral Prussian White phase show good agreement with experimental data across all tested functionals. The PBE+U functional stands out, as it predicts a noticeable expansion along the a and b axes and a slight compression along the c axis when compared to standard PBE.
Substituting iron with manganese in the FeHCF system leads to a contraction of the Prussian Blue lattice constant, while cubic Prussian White shows a slight expansion. Across all tested functionals, the rhombohedral lattice constants decrease marginally with manganese substitution.
The bond lengths in MnHCF compounds are shown in Fig. 7. Overall trends closely resemble those observed in FeHCF, as the substitution does not significantly alter the bonding character. Mn–N and C–N bond lengths increase with sodium content, while Fe–C bonds contract. Among them, Mn–N bonds are the most flexible, exhibiting the largest variation, whereas Fe–C bonds remain relatively rigid. C–N bonds again show the lowest variation of the bonds present in the Prussian Blue framework.
 | ||
| Fig. 7 Representation of the bond length in dependence on the functional for all four compounds. Color code: Prussian Yellow (yellow), Prussian Blue (blue), cubic Prussian White (grey) and rhombohedral Prussian White (red). The Mn–N bonds are represented with dots, Fe–C bonds with squares and C–N bonds with diamonds. Experimental references for cubic and rhombohedral Prussian White,9 taken from the published atomic coordinates of the Rietveld refinement, are given by the dotted lines in the compounds respective color. | ||
A notable anomaly is the sharp increase in lattice constants between Prussian Yellow and Prussian Blue when employing the PBE+U functional. This behavior stands in contrast to all other tested functionals, which distribute structural expansion more gradually across intermediate sodiation states. Additionally, the r2SCAN functional shows an uncommon inversion in the Mn–N bond length trends between Prussian Yellow and Prussian Blue, diverging from the expected behavior. When comparing the two material systems, MnHCF consistently displays longer Mn–N and Fe–C bonds than the corresponding Fe–N and Fe–C bonds in FeHCF.
The magnetization trends in MnHCF mirror those in FeHCF, with Mn–N centers adopting a high-spin state and Fe–C centers remaining in a low-spin configuration. Due to manganese contributing one fewer electron than iron, the Fe–C center transitions from one to zero unpaired electrons during the first sodium intercalation step. Meanwhile, the Mn–N center remains unchanged initially, and increase from four to five unpaired electrons during the second sodium intercalation.
For Prussian Yellow and both the cubic and rhombohedral forms of the Prussian White analogue, all functionals yield consistent results that align with the formally expected electronic structures. In contrast, for the half-intercalated manganese Prussian Blue analogue, PBE, SCAN and r2SCAN accurately capture the expected trend in the electronic structure. PBE+U, PBE0 and HSE06 predict an unexpected and counterintuitive electronic configuration, including the emergence of antiferromagnetic ordering and the premature reduction of the Fe–N center. This result deviates from both experimental observations and chemical intuition. The nonphysical electronic states are likely caused by excessive localization, as only functionals with strong localization tendencies produce these anomalies. While hybrid functionals have fixed localization strength, the PBE+U framework offers tunability and could, in principle, be adjusted to recover the correct electronic trends. However, this also highlights the risk of indiscriminately transferring Hubbard U values to systems that differ even slightly from their original benchmarking context.
The calculated band gaps for the MnHCF system vary significantly depending on the choice of exchange–correlation functional, and no clear trend can be established. SCAN consistently predicts small band gaps across all compounds, ranging from 0.39 to 0.50 eV. In contrast, PBE0 attributes the largest band gap to the Prussian Yellow analogue. PBE yields a moderate band gap of 0.61 eV for the Prussian Blue analogue, while r2SCAN identifies both Prussian White analogues as semiconducting, with gaps of approximately 0.3 eV. Interestingly, both PBE+U and HSE06 predict metallic behavior in all systems studied.
Stability considerations
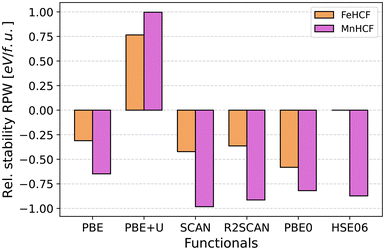
In this section we like to explore some stability considerations of the presented compounds. It is known from experiment that the rhombohedral modification of Prussian Blue/White is preferably formed for >1 Na per f.u. in systems with low water content and low defect density. The conditions of low (or no) water content and low (or no) defect density are easily fulfilled when doing theoretical calculations by simply setting up the system in a pristine state. Therefore, one can easily evaluate the relative stability of these compounds by comparing the total energy per formula unit of the system. The energetic comparison of the cubic and rhombohedral Prussian White modifications for the original FeHCF compound and its manganese-substituted counterpart are shown in Fig. 9.While the absolute value of stabilization slightly varies between functionals, these differences in themselves are not noteworthy. The difference in the two modifications is always, for all functionals, more pronounced for MnHCF than FeHCF. What is most noteworthy, is that only PBE+U predicts a larger stability for the cubic modification, completely inverting the trend seen with every other functional, curiously for FeHCF and MnHCF. We propose that the unexpected trend reversal associated with the PBE+U functional stems from the use of U-values that were originally calibrated for a significantly different reference system. Specifically, these values were derived for a cubic, mixed-valent Prussian Blue compound with a finite band gap and potassium occupying the 8c Wyckoff position. In contrast, the rhombohedral system is a non-cubic, non-mixed-valent, metallic system with sodium located in the 24d site. Most likely, the cubic system is relatively well described, but the stability of the rhombohedral system is severely underestimated due to the non-transferable nature of U-values. We still expect that employing distinct U-values for iron centers in chemically distinct environments remains advantageous. Problematically though, system-specific re-optimization of the U-values would compromise the comparability, leading to a conundrum that has to be carefully evaluated when utilizing the Hubbard U-correction for multiple state of charges in any battery material. Nonetheless, further studies are warranted to investigate the observed anomaly more systematically and increase the certainty of the hypothesis.
All exchange–correlation functionals consistently predict that sodium prefers the 24d Wyckoff site in the cubic modification – regardless of the transition metal species or sodium concentration. Further comparison reveals significant anomalies in the results obtained using the PBE+U functional. Specifically, two sodium configurations display an unusual increase in site preference of approximately 300%. A more detailed discussion of this behavior is provided in the SI – Fig. S4.
The previously discussed stability considerations directly impact one of the key battery properties derived from DFT calculations: the open-circuit voltage. We computed OCV curves for a purely cubic model and for a system incorporating both cubic and rhombohedral Prussian Blue structures, considering various exchange–correlation functionals, as shown in Fig. 10. The included structures correspond to the thermodynamically stable structures obtained in our earlier convex-hull study.6 As metastable configurations do not contribute to the OCV, the OCV profile is considered complete with regards to the number of intercalated sodium atoms x. Further, please note that the possibility of phase transitions occurring during the charge/discharge process is inherently captured in this figure. Between x = 0 and x = 1, the stable structure remains cubic (dark-colored curves). Beyond this point, two branches are available: retention of cubic symmetry (dark curves) or a transition to the rhombohedral phase (light curves). At each composition, the branch yielding the higher voltage corresponds to the lower Gibbs free energy and is therefore selected as the thermodynamically stable path. This representation enables a direct comparison of how functional choice influences both the predicted voltage and the stability landscape across the sodiation range.
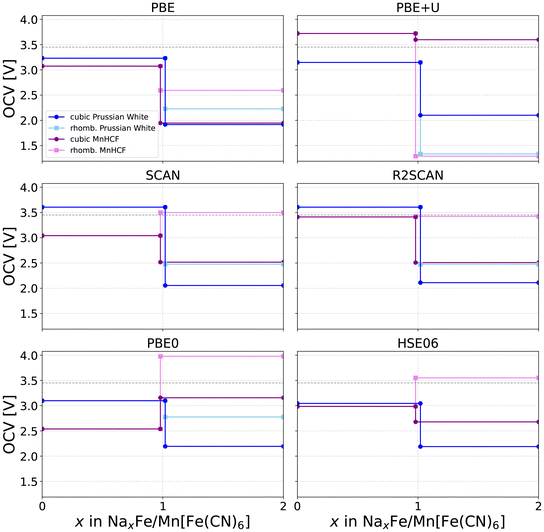 | ||
| Fig. 10 Plot of the calculated open circuit voltage curves for the purely cubic and cubic/rhomb Prussian Blue systems calculated with all functionals. Plotted is the voltage vs. the sodium concentration x. The voltages curves for FeHCF systems are displayed in blue hues, while the values for the MnHCF system are displayed in purple hues. Dark colors were utilized for purely cubic model systems, while the experimentally observed switch from cubic to rhombohedral modification is included by taking into account the light colored curves. The dark grey dotted line represents an approximate experimental reference voltage of 3.45 V, included as a visual guide reflecting reported measurements for both transition metal systems between 3.3 V and 3.6 V across various studies.8,9,66 | ||
Across all functionals, the rhombohedral phase generally yields higher voltages than the cubic counterpart, regardless of the transition metal used. The only exception is PBE+U, where the artificial stabilization of the cubic phase leads to a significantly lower predicted voltage for the rhombohedral structure. In some instances, such as the MnHCF system calculated with PBE0, the reported potential from the half-sodiated to the fully sodiated state is higher than that from the desodiated to the half-sodiated state. In practice, the potential should never increase with further sodiation, as the Gibbs free energy must decrease monotonically. This behavior therefore wrongly suggests that the half-sodiated phase is thermodynamically unstable and will disproportionate into a mixture of the fully desodiated and fully sodiated phases. However, both prior computational studies and experimental observations confirm that the half-sodiated Prussian Blue phase is thermodynamically stable. The observed behavior is thus best interpreted as an artifact arising from discrete total-energy differences rather than a genuine thermodynamic instability. Finally, a comparison of the two transition metal systems reveals that substituting iron with manganese increases the OCV in all cases, consistent with experimental observations,9 except under the PBE+U-rhombohedral model.
Migration barrier calculation
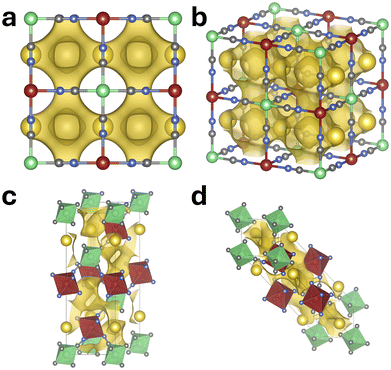
Migration barrier calculations were limited to the FeHCF system due to the high computational cost, especially when using hybrid functionals. To manage the computational cost, an initial estimate of likely migration pathways was obtained using bond valence sum mismatch analysis, which served to guide the subsequent NEB (nudged elastic band) calculations. The generated isosurfaces depicting the sodium ion migration pathways are shown in Fig. 11, with panels a and b illustrating the cubic system, and panels c and d corresponding to the rhombohedral structure.The isosurface for the cubic system reveals a three-dimensional migration framework aligned with the crystallographic axes, with ion motion revolving around adjacent CN bonds and circumventing the large central cavities. This result agrees well with and visually illustrates the ladder-like diffusion mechanism previously described by Nordstrand et al.67,68 In the rhombohedral system, the basic migration topology remains similar, but the structural distortions characteristic of this phase lead to a pronounced asymmetry in the migration channels. The corresponding visualizations highlight this deformation and match well with prior findings.21
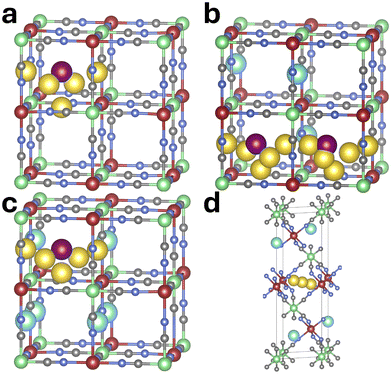
The migration barriers were calculated along the BVS-identified pathways for all four FeHCF compounds, using each of the six exchange–correlation functionals. Fig. 12 shows PBE-calculated transition states of the elementary migration steps along these pathways, indicated by the string of yellow-colored sodium atoms. Panel a illustrates the migration process in the high-vacancy limit, with only the diffusing charge carrier present in the conventional unit cell. Panels b and c depict the half-sodiated and low-vacancy cubic phase, respectively. For each cubic configuration, two single-image NEB calculations were performed to explore the ladder-like migration mechanism between sodium ions occupying minimum-energy 24d Wyckoff sites. In the half-sodiated system, this path was further extended by mirroring to complete a full round-trip trajectory, allowing the path to return to its original, energetically favored configuration.
Additionally, diffusion across the large central void (Wyckoff 8c site) was evaluated within the cubic modification using a single-image NEB calculation. The transition state of this alternative pathway – sharing the same initial and final configurations as the standard route – is shown in purple in Fig. 12. In addition, panel d presents a visualization of the migration event studied within the rhombohedral low-vacancy limit. This pathway was also modeled using a single-image NEB approach. For clarity, sodium ions not involved in the migration process are shown in cyan, allowing easy identification of the diffusing species.
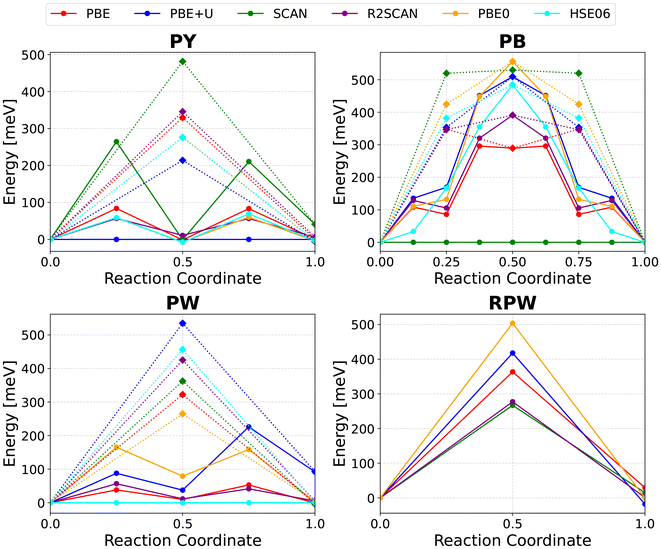
The calculated migration barriers for each state of sodiation and exchange–correlation functional are shown in Fig. 13 for comparative analysis. The assessment of migration barriers begins with the high-vacancy system, chosen for its simplicity and idealized conditions. Due to the degeneracy of available sodium sites and the absence of neighboring ions, it provides a reference scenario without site-specific interactions. Most exchange–correlation functionals yield a migration energy of approximately 60–80 meV for the ladder-like diffusion pathway, with SCAN as the notable exception at ∼250 meV. Although these values are lower than those previously reported, they align with the high site accessibility and well-documented fast ion transport in Prussian Blue. In comparison, migration through the central void is energetically less favorable across all functionals, with calculated barriers between 200–350 meV and a maximum of 450 meV for SCAN. This route also shows greater sensitivity to the choice of functional than the ladder-like mechanism.
The half-sodiated Prussian Blue system is special due to its notable stabilization of a tetragonal sodium ion configuration within the framework, making it a uniquely stable intermediate phase between the fully desodiated and fully sodiated structures. While this structural ordering is energetically favorable, it introduces complications for migration barrier calculations. Specifically, the combination of a strongly preferred sodium configuration and otherwise low migration barriers leads to a situation where the energy landscape is overwhelmingly influenced by configurational contributions rather than actual ion migration energetics.69 This effect is consistently observed across all tested exchange–correlation functionals. The shape and hight of the NEB energy profile, as well as the position of the transition state is further consistent with a recent publication of Ito et al.70 Only PBE predicts a residual barrier of ∼60 meV, though only in the case of a migration through the unfavorable 8c site. In all other cases, the configuration after two completed ladder-like diffusion events is considered the highest energy structure. In real-world conditions, thermal fluctuations in the sodium ion configuration are expected to enhance ion mobility, by disrupting the rigid tetragonal ordering and flattening the migration energy landscape. This is expected to result in a migration profile more consistent with those of Prussian Yellow or Prussian White, a hypothesis further supported by the similarity of 8c site diffusion barriers across all three sodium concentrations, especially in both PBE and HSE06 calculations. This is also well in line with results of 70 meV for the migration barrier of sodium in PB from AI-MD simulations as reported by Ito et al.70
The migration barriers in the low-vacancy limit of Prussian Blue systems – i.e., charge carrier diffusion in cubic Prussian White – closely resemble those in Prussian Yellow. However, a slight overall increase in barrier height is observed, which can be attributed to a greater influence of the surrounding sodium environment on ion migration pathways. This environmental sensitivity manifests differently across functionals: for instance, SCAN predicts a reduction in the barrier, whereas PBE+U, PBE0, and HSE06 yield higher values. Other functionals produce similar results, without establishing a consistent trend. As in the Prussian Yellow case, diffusion through the 8c site remains energetically unfavorable, reinforcing the notion that this site is generally avoided during sodium migration.
Ion diffusion in the rhombohedral modification of Prussian Blue exhibits a strong sensitivity to the chosen exchange–correlation functional, with migration barriers ranging from approximately 250 meV (SCAN and r2SCAN) to as high as 500 meV (PBE0).
Across all studied systems, there is a modest increase in migration barriers with rising sodium concentration, likely due to increasing electrostatic constraints imposed by the surrounding sodium environment. However, this trend does not fundamentally govern the overall diffusion behavior in Prussian Blue analogues. The PBE+U functional typically yields higher migration barriers than standard PBE. This anomaly may suggest that the inclusion of the Hubbard U parameter amplifies the environmental influence on ion migration. Complete numerical data for all migration barriers calculated with various functionals is provided in the SI – Tables S29–S35.
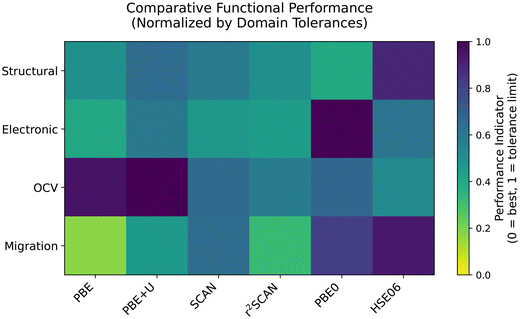
Conclusion
The present study employs density functional theory to benchmark six widely used exchange–correlation functionals, selected to represent three rungs of Jacob's ladder, in their ability to accurately capture key battery-relevant properties. These include structural, electronic, and sodium ion transport characteristics of the cubic modification of Prussian Yellow and Prussian Blue and the cubic and rhombohedral modification of Prussian White. Our results provide critical insights into the influence of functional choice on the predictive reliability of computational battery materials screening. The functional-dependent performance across the four evaluated domains: structural accuracy, electronic property calculation, OCV prediction and ion migration barrier estimation are concisely summarized in the heatmap shown in Fig. 14. The structural domain considers the percentage deviations of lattice constants and bond lengths; the electronic domain evaluates the number of unpaired electrons on the high-spin and low-spin Fe sites as well as the band gap of the half-sodiated compound; the OCV domain measures the deviation from the experimentally reported open-circuit voltage of 3.45 V; and the migration domain captures the deviation from the average calculated migration barrier as an indicator of ion-transport accuracy. Unless otherwise specified, all quantities were computed for the four relevant structural models: cubic Prussian Yellow, Prussian Blue, Prussian White, and rhombohedral Prussian White. To facilitate comparison, these metrics were averaged into a single performance score for each functional and normalized – capped by a tolerance limit. Tolerance limits are set to 3.5% for the structural domain, 1 in arbitrary units for the electronic domain, 1 V for the OCV domain and 150 meV for the migration domain. A performance indicator of 0 indicates no deviation from the reference values, while a performance indicator of 1 means that the tolerance limit was matched or exceeded. This score serves as a heuristic, qualitative representation that complements the detailed discussion provided above and is not intended to convey quantitative precision.The PBE functional reliably reproduces the structural and ion transport properties of Prussian Blue, provided the total magnetic moment of the unit cell is fixed to the formally expected value. However, it still severely underestimates the OCV and electronic band gaps, as commonly observed. Our findings reveal that the widely used approach to utilize the Hubbard U correction with PBE, can produce unphysical predictions in complex systems such as Prussian Blue analogues when sodium content varies. This reinforces the necessity for rigorous benchmarking of U-values tailored to the exact use case. This is particularly evident in the treatment of rhombohedral distortions, which play a crucial role in stabilizing high sodium content phases. While all other functionals accurately capture the stabilization effect and its impact on the calculated open-circuit voltage (OCV), PBE+U fails to do so, thus compromising its reliability for battery-relevant predictions.
Meta-GGA functionals, such as SCAN and r2SCAN, provide enhanced accuracy in describing the electronic structure of Prussian Blue analogues, particularly by partially correcting the underestimated band gaps often observed with lower-rung functionals. Despite this, the provided improvement on key battery-related properties – such as open circuit voltage and ion migration barriers – is limited. Given the considerable computational demand of meta-GGAs, the benefits must be weighed against the cost. In this regard, r2SCAN demonstrates clear advantages over SCAN, offering slightly improved accuracy with significantly better computational performance.
Hybrid functionals offer high accuracy but are computationally intensive. While effective for single-point electronic structure calculations, they are unsuitable for more demanding simulations such as NEB. Moreover, they tend to significantly overestimate band gaps – comparable in magnitude to the underestimation seen with meta-GGAs. It is also important to note that the HSE06 hybrid functional failed to converge during structural relaxation of the rhombohedral system, although single-point calculations with this functional were successful.
In conclusion, for studies focused solely on half-intercalated, mixed-valent Prussian Blue, the widely adopted approach proposed by Wojdeł, which utilizes a U-value of 3 and 7 eV for the carbon-coordinated and nitrogen-coordinated iron, respectively, offers the best compromise between accuracy and computational cost. However, in the context of practical battery applications, where a wide range of properties must be simultaneously captured – including the prediction of open-circuit voltages, and sodium migration behavior – this approach is insufficient. The use of fixed U-values leads to incorrect energetic trends, particularly for the stability of the rhombohedral phase. As such, we advise employing a more adaptable functional scheme.
For the best balance between accuracy and computational efficiency, we recommend using the PBE functional with a fixed total magnetization, supplemented by hybrid single-point calculations for the electronic structure and OCV calculations, when necessary. If unrestricted magnetization is preferred, pure meta-GGA calculations offer a valid alternative. Although they tend to underestimate band gaps, their predictions still align with experimentally observed trends. In this case, r2SCAN is preferable to SCAN due to its enhanced computational efficiency and higher accuracy for Prussian Blue systems.
Single-image climbing NEB calculations provided an efficient and sufficiently accurate method for estimating migration barriers. The results exhibit functional-dependent yet systematic trends across sodium concentrations and structural phases. Overall, the ladder-like diffusion pathway, as proposed by Nordstrand et al., is consistently favored, showing activation energies that are typically 3–6 times lower than those for diffusion through the large void (Wyckoff 8c site).
Overall, this work establishes a transferable, high-fidelity computational workflow for evaluating Prussian Blue analogues and underlines the importance of functional choice in capturing the nuanced physics of these systems. We anticipate that the computational strategies and results outlined in this study will contribute meaningfully to the rational design of sustainable and economically viable materials tailored for long-duration, grid-scale energy storage systems. Incorporating these theoretical insights into materials design pipelines has the potential to significantly shorten development cycles and guide researchers toward PBA systems with enhanced cycling stability, higher energy density, and greater compatibility with sustainable, large-scale energy storage.
Author contributions
S. B. performed all DFT simulations and the data analysis, and he prepared the figures and drafted the initial version of the manuscript. M. S. provided methodological guidance, contributed to the interpretation of the results, and revised the manuscript. I. E. C. supervised the project, with particular responsibility during the abroad stay at DTU (Denmark), and together with A. G. provided overall conceptual and strategic guidance during the project. All authors reviewed the manuscript and have granted their approval for the final version.Conflicts of interest
There are no conflicts of interest to declare.Data availability
Full input and output data for this article are available at NOMAD under: https://www.doi.org/10.17172/NOMAD/2025.11.18-1.Further data supporting this article have been included as part of the Supplementary Information. Supplementary information: Comparison of single- and multi-image NEB approach; Procedure for linear interpolation of experimental lattice constants; Visualizations and numerical data for the cubic model system with sodium intercalated into the Wyckoff 8c position; Complete numerical data for all plots regarding the FeHCF and MnHCF systems, including for the migration-barrier evaluations within the FeHCF system. See DOI: https://doi.org/10.1039/d5eb00211g.
Acknowledgements
This work contributes to the research performed at CELEST (Center for Electrochemical Energy Storage Ulm-Karlsruhe) and was funded by the German Research Foundation (DFG) under Project ID 390874152 (POLiS Cluster of Excellence). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 cluster). Financial support by the Dr Barbara Mez-Starck Foundation is gratefully acknowledged. We acknowledge support from the Novo Nordisk Foundation Data Science Research Infrastructure 2022 Grant: A high-performance computing infrastructure for data-driven research on sustainable energy materials, Grant No. NNF22OC0078009. S. B. expresses his heartfelt gratitude to Dr Benjamin Heckscher Sjølin for not only introducing him to PerQueue, but also for his patient and ongoing guidance during the learning process. Dr. Sjølin's support was instrumental in overcoming the challenges associated with adopting a new computational tool.References
- T. Hey, S. Tansley, K. Tolle and J. Gray, The Fourth Paradigm: Data-Intensive Scientific Discovery, Microsoft Research, 2009 Search PubMed.
- A. Agrawal and A. Choudhary, Perspective: Materials informatics and big data: Realization of the of science in materials science, APL Mater., 2016, 4, 053208 CrossRef.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys Mater., 2019, 2, 032001 CrossRef CAS.
- V. D. Ivanov, Four decades of electrochemical investigation of Prussian blue, Ionics, 2020, 26, 531–547 CrossRef CAS.
- H. L. Boström and W. R. Brant, Octahedral tilting in Prussian blue analogues, J. Mater. Chem. C, 2022, 10, 13690–13699 RSC.
- S. Baumgart, A. Groß and M. Sotoudeh, Data-Driven Site Occupancy Statistics in Cubic Prussian Blue, ACS Phys. Chem. Au, 2025, 5, 346–355 CrossRef CAS PubMed.
- A. Kraft, Some considerations on the structure, composition, and properties of Prussian blue: A contribution to the current discussion, Ionics, 2021, 27, 2289–2305 CrossRef CAS.
- L. Wang, J. Song, R. Qiao, L. A. Wray, M. A. Hossain, Y.-D. Chuang, W. Yang, Y. Lu, D. Evans and J.-J. Lee, et al., Rhombohedral Prussian white as cathode for rechargeable sodium-ion batteries, J. Am. Chem. Soc., 2015, 137, 2548–2554 CrossRef CAS PubMed.
- J. Song, L. Wang, Y. Lu, J. Liu, B. Guo, P. Xiao, J.-J. Lee, X.-Q. Yang, G. Henkelman and J. B. Goodenough, Removal of interstitial H2O in hexacyanometallates for a superior cathode of a sodium-ion battery, J. Am. Chem. Soc., 2015, 137, 2658–2664 CrossRef CAS PubMed.
- J. C. Wojdeł and S. T. Bromley, Efficient calculation of the structural and electronic properties of mixed valence materials: application to Prussian Blue analogues, Chem. Phys. Lett., 2004, 397, 154–159 CrossRef.
- J. C. Wojdeł and S. T. Bromley, From cluster calculations to molecular materials: a mixed pseudopotential approach to modeling mixed-valence systems, J. Mol. Model., 2005, 11, 288–292 CrossRef.
- J. C. Wojdeł and S. T. Bromley, Band gap variation in prussian blue via cation-induced structural distortion, J. Phys. Chem. B, 2006, 110, 24294–24298 CrossRef PubMed.
- J. C. Wojdeł, I. de P. R. Moreira, S. T. Bromley and F. Illas, On the prediction of the crystal and electronic structure of mixed-valence materials by periodic density functional calculations: The case of Prussian Blue, J. Chem. Phys., 2008, 128, 044713 CrossRef PubMed.
- J. C. Wojdeł, First principles calculations on the influence of water-filled cavities on the electronic structure of Prussian Blue, J. Mol. Model., 2009, 15, 567–572 CrossRef PubMed.
- J. C. Wojdeł, I. d. P. R. Moreira and F. Illas, Periodic density functional theory study of spin crossover in the cesium iron hexacyanochromate prussian blue analog, J. Chem. Phys., 2009, 130, 014702 CrossRef PubMed.
- J. C. Wojdeł, I. de P. R. Moreira, S. T. Bromley and F. Illas, Prediction of half-metallic conductivity in Prussian Blue derivatives, J. Mater. Chem., 2009, 19, 2032–2036 RSC.
- D. S. Middlemiss and C. C. Wilson, Ferromagnetism and spin transitions in prussian blue: A solid-state hybrid functional study, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155129 CrossRef.
- C. Ling, J. Chen and F. Mizuno, First-principles study of alkali and alkaline earth ion intercalation in iron hexacyanoferrate: the important role of ionic radius, J. Phys. Chem. C, 2013, 117, 21158–21165 CrossRef CAS.
- F. S. Hegner, J. R. Galán-Mascarós and N. López, A database of the structural and electronic properties of Prussian blue, Prussian white, and Berlin green compounds through density functional theory, Inorg. Chem., 2016, 55, 12851–12862 CrossRef CAS PubMed.
- X. Wu, W. Deng, J. Qian, Y. Cao, X. Ai and H. Yang, Single-crystal FeFe (CN) 6 nanoparticles: a high capacity and high rate cathode for Na-ion batteries, J. Mater. Chem. A, 2013, 1, 10130–10134 RSC.
- S. Baumgart, M. Sotoudeh and A. Groß, Rhombohedral (R
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) Prussian White as Cathode Material: An Ab initio Study, Batteries Supercaps, 2023, 6, e202300294 CrossRef CAS.
) Prussian White as Cathode Material: An Ab initio Study, Batteries Supercaps, 2023, 6, e202300294 CrossRef CAS. - J. Peng, J. Wang, H. Yi, W. Hu, Y. Yu, J. Yin, Y. Shen, Y. Liu, J. Luo and Y. Xu, et al., A dual-insertion type sodium-ion full cell based on high-quality ternary-metal Prussian blue analogs, Adv. Energy Mater., 2018, 8, 1702856 CrossRef.
- X. Guo, Z. Wang, Z. Deng, X. Li, B. Wang, X. Chen and S. P. Ong, Water contributes to higher energy density and cycling stability of Prussian blue analogue cathodes for aqueous sodium-ion batteries, Chem. Mater., 2019, 31, 5933–5942 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- H. Euchner and A. Groß, Atomistic modeling of Li- and post-Li-ion batteries, Phys. Rev. Mater., 2022, 6, 040302 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, Accurate and numerically efficient r2SCAN meta-generalized gradient approximation, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- S. Gražulis, D. Chateigner, R. T. Downs, A. F. T. Yokochi, M. Quirós, L. Lutterotti, E. Manakova, J. Butkus, P. Moeck and A. Le Bail, Crystallography Open Database – an open-access collection of crystal structures, J. Appl. Crystallogr., 2009, 42, 726–729 CrossRef PubMed.
- S. Gražulis, A. Daškevič, A. Merkys, D. Chateigner, L. Lutterotti, M. Quirós, N. R. Serebryanaya, P. Moeck, R. T. Downs and A. Le Bail, Crystallography Open Database (COD): an open-access collection of crystal structures and platform for world-wide collaboration, Nucleic Acids Res., 2011, 40, D420–D427 CrossRef.
- A. Vaitkus, A. Merkys, T. Sander, M. Quirós, P. A. Thiessen, E. E. Bolton and S. Gražulis, A workflow for deriving chemical entities from crystallographic data and its application to the Crystallography Open Database, J. Cheminf., 2023, 15, 123 Search PubMed.
- W. Wang, Y. Gang, Z. Hu, Z. Yan, W. Li, Y. Li, Q.-F. Gu, Z. Wang, S.-L. Chou and H.-K. Liu, et al., Reversible structural evolution of sodium-rich rhombohedral Prussian blue for sodium-ion batteries, Nat. Commun., 2020, 11, 980 CrossRef CAS PubMed.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- B. H. Sjølin, W. S. Hansen, A. A. Morin-Martinez, M. H. Petersen, L. H. Rieger, T. Vegge, J. M. García-Lastra and I. E. Castelli, PerQueue: managing complex and dynamic workflows, Digital Discovery, 2024, 3, 1832–1841 RSC.
- J. J. Mortensen, M. Gjerding and K. S. Thygesen, MyQueue: Task and workflow scheduling system, J. Open Source Softw., 2020, 5, 1844 CrossRef.
- J. Klimeš, D. R. Bowler and A. Michaelides, A critical assessment of theoretical methods for finding reaction pathways and transitionstates of surface processes, J. Phys.: Condens. Matter, 2010, 22, 074203 CrossRef.
- A. Golov and J. Carrasco, Enhancing first-principles simulations of complex solid-state ion conductors using topological analysis of procrystal electron density, npj Comput. Mater., 2022, 8, 187 CrossRef CAS.
- G. K. Nayak, D. Holec and M. Zelenỳ, Impact of d-states on transition metal impurity diffusion in TiN, Sci. Rep., 2023, 13, 8244 CrossRef CAS PubMed.
- S. Nishimura , PyAbstantia 0.7c Documentation, 2017, https://shinichinishimura.github.io/pyabst/#, (cited 2025 May 15).
- S. Adams and R. P. Rao, High power lithium ion battery materials by computational design, Phys. Status Solidi A, 2011, 208, 1746–1753 CrossRef CAS.
- I. D. Brown, Recent developments in the methods and applications of the bond valence model, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- H. Chen and S. Adams, Bond softness sensitive bond-valence parameters for crystal structure plausibility tests, IUCrJ, 2017, 4, 614–625 CrossRef CAS PubMed.
- S. Adams and R. Rao, et al., Modelling of ion transport in solids with a general bond valence based force-field, At. Indones., 2010, 36, 95–104 Search PubMed.
- F. Hesse, I. da Silva and J.-W. G. Bos, Insights into Oxygen Migration in LaBaCo2O6−δ Perovskites from In Situ Neutron Powder Diffraction and Bond Valence Site Energy Calculations, Chem. Mater., 2022, 34, 1191–1202 CrossRef CAS PubMed.
- W. R. Brant, R. Mogensen, S. Colbin, D. O. Ojwang, S. Schmid, L. Haggstrom, T. Ericsson, A. Jaworski, A. J. Pell and R. Younesi, Selective control of composition in Prussian white for enhanced material properties, Chem. Mater., 2019, 31, 7203–7211 CrossRef CAS.
- H. Buser, D. Schwarzenbach, W. Petter and A. Ludi, The crystal structure of Prussian blue: Fe4 Fe (CN) 6. 3. xH2O, Inorg. Chem., 1977, 16, 2704–2710 CrossRef CAS.
- D. M. Pajerowski, T. Watanabe, T. Yamamoto and Y. Einaga, Electronic conductivity in Berlin green and Prussian blue, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 153202 CrossRef.
- A. Xidis and V. D. Neff, On the electronic conduction in dry thin films of prussian blue, prussian yellow, and everitt's salt, J. Electrochem. Soc., 1991, 138, 3637 CrossRef CAS.
- R. Huggins, Mixed-conductors with either cation or anion insertion, Ionics, 1997, 3, 379–389 CrossRef CAS.
- M. B. Robin, The color and electronic configurations of Prussian blue, Inorg. Chem., 1962, 1, 337–342 CrossRef CAS.
- Y. Shang, B. Ren, R. Wu, J. Lin, X. Li, J. Shen, D. Yan and H. Y. Yang, Building Robust Manganese Hexacyanoferrate Cathode for Long-Cycle-Life Sodium-Ion Batteries, Small, 2024, 2408018 Search PubMed.
- Z. Zhou, Y. Qian, X. Chen, J. Chen, X. Zhou, W. Kuang, X. Shi, X. Wu, L. Li and J. Wang, et al., Challenges and Strategies toward Manganese Hexacyanoferrate for High-Performance Sodium-Ion Batteries, Adv. Funct. Mater., 2024, 34, 2404938 CrossRef CAS.
- Y. Moritomo, S. Urase and T. Shibata, Enhanced battery performance in manganese hexacyanoferrate by partial substitution, Electrochim. Acta, 2016, 210, 963–969 CrossRef CAS.
- Y. Moritomo, K. Wakaume, M. Takachi, X. Zhu and H. Kamioka, Li+ intercalation of manganese ferrocyanide as investigated by in situ valence-differential absorption spectroscopy, J. Phys. Soc. Jpn., 2013, 82, 094710 CrossRef.
- Y. Tang, W. Li, P. Feng, M. Zhou, K. Wang, Y. Wang, K. Zaghib and K. Jiang, High-performance manganese hexacyanoferrate with cubic structure as superior cathode material for sodium-ion batteries, Adv. Funct. Mater., 2020, 30, 1908754 CrossRef CAS.
- D. O. Ojwang, M. Svensson, C. Njel, R. Mogensen, A. S. Menon, T. Ericsson, L. Haggstrom, J. Maibach and W. R. Brant, Moisture-driven degradation pathways in Prussian white cathode material for sodium-ion batteries, ACS Appl. Mater. Interfaces, 2021, 13, 10054–10063 CrossRef CAS PubMed.
- J. Nordstrand, E. Toledo-Carrillo, S. Vafakhah, L. Guo, H. Y. Yang, L. Kloo and J. Dutta, Ladder mechanisms of ion transport in Prussian blue analogues, ACS Appl. Mater. Interfaces, 2021, 14, 1102–1113 CrossRef PubMed.
- J. Nordstrand, E. Toledo-Carrillo, L. Kloo and J. Dutta, Sodium to cesium ions: a general ladder mechanism of ion diffusion in prussian blue analogs, Phys. Chem. Chem. Phys., 2022, 24, 12374–12382 RSC.
- M. Sotoudeh, S. Baumgart, M. Dillenz, J. Döhn, K. Forster-Tonigold, K. Helmbrecht, D. Stottmeister and A. Groß, Ion mobility in crystalline battery materials, Adv. Energy Mater., 2024, 14, 2302550 CrossRef CAS.
- D. Ito, S.-H. Jang, H. Ando, T. Momma and Y. Tateyama, Dissimilar Diffusion Mechanisms of Li+, Na+, and K+ Ions in Anhydrous Fe-Based Prussian Blue Cathode, J. Am. Chem. Soc., 2025, 147, 25441–25453 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |