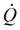Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heat generation behavior of high-voltage spinel LiNi0.5Mn1.5O4 cathodes under varying cycling conditions and material configurations
Kevin Böhm *a,
Aleksandr Kondrakov
*a,
Aleksandr Kondrakov b,
Torsten Markus
b,
Torsten Markus a and
David Henriques
a and
David Henriques *a
*a
aTechnische Hochschule Mannheim, Institute for Materials Science and Engineering (IMaSE), Paul-Wittsack-Straße 10, 68163 Mannheim, Germany. E-mail: k.boehm@doktoranden.th-mannheim.de; d.henriques@th-mannheim.de
bBASF SE, Carl-Bosch-Straße 38, 67056 Ludwigshafen, Germany
First published on 5th January 2026
Abstract
The temperature of lithium-ion batteries significantly impacts cell performance, cycle life, and safety. Effective thermal management and cooling systems require a detailed understanding of heat generation within battery cells, which strongly depends on the specific materials used. Particularly, lithium–nickel–manganese–oxide (LNMO) is a promising cathode candidate for next-generation lithium-ion batteries, because of its cobalt-free composition and high operating voltage (∼4.7 V vs. Li/Li). This study systematically investigates various factors influencing heat generation in LNMO cathodes. Initially, the impact of charging and discharging currents on heat generation was examined, revealing that heat generation during charging is lower than during discharging. As a result, charging currents 1.58 times higher than the discharging currents can be achieved while maintaining similar maximum heat fluxes. Subsequently, the effects of material additives and temperature variations were investigated. The results show that an optimization of the material combination can reduce the maximum heat flux peaks of LNMO cathodes by approximately 30% at 25 °C and about 20% at 45 °C. Furthermore, the analysis demonstrates that 35–55% of the total heat is generated at State of Charge (SoC) below 20%, highlighting a significant potential for thermal improvement in LNMO cathodes particularly within the low SoC range.
Broader contextHigh-voltage spinel LiNi0.5Mn1.5O4 (LNMO) cathodes offer a cobalt-free and energy-dense alternative for next-generation lithium-ion batteries. However, their limited stability at elevated temperatures and the pronounced heat generation during cycling remain key challenges for safety and thermal management. A detailed understanding of their heat generation behavior is therefore essential for optimizing cooling strategies and battery management systems. This study systematically investigates the thermal response of LNMO-based half-cells under varying current rates, temperatures, and material configurations using calorimetric analysis. It shows that, at C-rates ≤1 h−1, distinct heat flux features can be clearly separated, whereas at higher C-rates these merge into a single, broader feature, leading to a significant increase in maximum heat release. Charging generally produces less heat than discharging, allowing higher charging currents without exceeding thermal limits. The results further suggest that specific combinations of surface coatings and electrolyte additives may mitigate irreversible heat generation, possibly by improving interfacial stability. A large fraction of the total heat—up to about 55%—is generated at states of charge below 20%, emphasizing the critical role of the low-SoC region in the thermal design of fast-charging cells. These insights support the development of thermally robust and fast-charging energy-storage systems. |
1. Introduction
Lithium-ion batteries have become a key technology for a sustainable future,1 driven by the increasing demand for electric mobility and stationary energy storage.2 A central performance criterion in both applications is the energy density, as higher energy densities enable the development of electric vehicles with extended ranges and more compact energy storage systems without compromising the amount of stored energy. Since the energy density scales with the operating voltage, lithium–nickel–manganese–oxide (LNMO) has attracted considerable attention as a cathode material, particularly in the stoichiometry LiNi0.5Mn1.5O4. Owing to the high redox potential of the Ni species at 4.7 V vs. Li/Li+, an energy density of over 650 Wh kg−1 can be achieved.3–6 Furthermore, LNMO does not contain cobalt, which is both cost-intensive and associated with critical social and environmental concerns.7However, its high operation potential leads to poor cycling stability,8 especially at elevated temperatures.9–11 To mitigate these effects, surface coatings (e.g., borate7 or manganese phosphate12) and electrolyte additives (e.g., ferrocene hexafluorophosphate,13 tris(pentafluorophenyl)silane,14 or sulfone-based solvents15) have been widely applied. Among these approaches, aluminium–oxide surface coatings have been shown to improve capacity retention and coulombic efficiency while reducing transition-metal dissolution,16–18 whereas the decomposition of the functional additive tris(trimethylsilyl) phosphate (TMSP) forms a stabilizing cathode–electrolyte interphase (CEI) and lowers the HF content in the electrolyte.19–21 While the electrochemical benefits of such modifications are well documented, their influence on heat generation during cycling remains largely unexplored.
The heat generation during cell cycling significantly affects the ability of the thermal management system to maintain the cell within the optimal temperature range of 20–40 °C,22,23 while ensuring a homogeneous temperature distribution across the battery pack (ΔT < 5 K).24
Several studies have examined heat generation in LNMO-based cells under various conditions:
Sayah et al.25 investigated the impact of the electrolyte additives fluoroethylene carbonate (FEC), hexafluorocyclotriphosphazene (HFPZ), ethoxypentafluorocyclotriphosphazene (EtPFPZ) and phenoxycyclotriphosphazene (PhPZ) on the cycling of LNMO-cathodes. During the first two cycles two heat flux peaks were obtained during a complete cycle while the first peak reduces significantly after the first cycle, indicating surface modifications during the first cycle. The cells with only FEC and the combination of EtPFPZ and FEC showed the lowest heat generation. Moreover for the combination of PhPZ and FEC a constant heat generation while no applied current is obtained, indicating an oxidation of the electrolyte. Baazizi et al.26 showed that the electrolyte additives FEC and succinonitrile (SN) significantly reduce the heat during cycling by a factor of about 4 during charge and discharge. Moreover, they showed the increase in heat generation with increasing C-rate. However, due to short CC-Phases during charging at C-rates >1 h−1 the impact on heat generation on charge is limited in interpretation. Mao et al.27 determined the entropy coefficient of disordered LNMO and calculated the reversible heat generation during cycling. The results lead to the prediction that the change in entropy leads to a reduction in heat generation during charge and an increase during discharge. Our previous study28 confirmed similar trends and additionally considered the influence of internal resistance on the total heat generation. Kinetic limitations at low states of charge were identified as the origin of pronounced thermal peaks, whereas diffusion-limited processes during the Ni2+/4+ redox transition resulted in lower but more evenly distributed heat generation. Furthermore, endothermic behavior was observed during charging at low C-rates (1/10 h−1), underscoring the relevance of reversible entropic contributions under near-equilibrium conditions.
Despite these recent advances, a systematic understanding of the heat generation behavior of LNMO-based cells under realistic cycling conditions is still lacking. In particular, the combined influence of C-rate, temperature, and material modifications on the thermal response during charge and discharge remains insufficiently explored. Moreover, the extent to which parasitic heat generation contributes to the overall thermal behavior and whether such processes manifest as distinct thermal features is not yet fully understood.
To address these gaps, the present study investigates the heat generation characteristics of LNMO cathodes under various operating conditions. First, the influence of different C-rates at 25 °C is examined to assess the rate dependence of the heat generation. Second, the thermal behavior of LNMO cells is systematically analyzed for four material configurations: with and without an aluminium–oxide surface modification, each combined with either a standard electrolyte or an electrolyte containing the functional additive TMSP. All configurations are evaluated at 25 °C and 45 °C to capture temperature-dependent effects. This approach aims to clarify how cycling conditions and material adaptations influence heat generation during battery operation and whether parasitic reactions leave measurable thermal signatures.
2. Materials and methods
This study comprises two main experimental campaigns: (i) the impact of the current rate and (ii) the influence of material combinations and temperature. The following section is divided into two parts: section 2.2 provides a general description of the applied measurement techniques, while section 2.3 details the specific experimental parameters used in each campaign.To provide a structured overview, Table 1 summarizes the key experimental methods used in each campaign. These include cell assembly (CA), cell initialization and capacity check (Init/CapC), heat flux measurement (Calo), and incremental capacity analysis (ICA). The selection of methods was tailored to the specific objectives of each series.
| Method | (i) | (ii) |
|---|---|---|
| CA | x | x |
| Init/CapC | x | |
| Calo | x | x |
| ICA | x |
2.1. Cell assembly
Two different cathode materials, two different electrolytes, separators and 2032 coin cell cases were provided by BASF SE (Ludwigshafen, Germany) for this study. The cathode materials differ in their surface modification, and the electrolytes vary in composition. For clarity, the cathode materials are referred to as CI (improved, aluminium–oxide-coated) and CS (standard), and the electrolytes as EI (improved, LP40 containing TMSP) and ES (standard, LP40).The supplied LiNi0.5Mn1.5O4 cathode sheets were coated on aluminum foil and featured an areal capacity of 2 mAh cm−2 according to the supplier. Electrodes with a diameter of 15 mm were punched from these sheets inside an argon-filled glovebox, where O2 and H2O concentrations were maintained below 0.5 ppm.
Whatman GF/D separators with a diameter of 17 mm were used, and 100 μl of electrolyte was added per cell. Lithium metal with a diameter of 13 mm and a thickness of 0.5 mm (Nanografi Nano Technology, Ankara, Türkiye) served as the counter electrode.
2.2. Measurement procedures
The cells were charged with a constant current (CC) at a C-rate of 0.1 h−1 up to an upper voltage limit of 4.8 V, followed by a constant voltage (CV) phase lasting 30 min or until the cut-off current of 0.035 mA was reached. This step is referred to as initialization.
For the capacity checks, a CC-CV protocol was applied. The cells were discharged and charged at a C-rate of 0.1 h−1 within a voltage window of 3.5 V to 4.8 V. The CV phase was limited by either a maximum duration of 30 min or a cut-off current of 0.035 mA.
In this study, the C-rate refers to an areal capacity of 2 mAh cm−2.
To charge and discharge the cells, a VMP 300 potentiostat (BioLogic, Seyssinet-Pariset, France) is connected. When the sample is cycled, the difference between the signals of the two heat flux sensors is calculated, yielding the heat flux absorbed or released by the electrode.
For quantitative heat flux evaluation, the calorimeter was calibrated in both temperature and heat flux according to the manufacturer's specifications, using the known melting points and enthalpies of gallium, indium, tin, and bismuth. Since gallium has a melting point closest to the cell operating temperature, the calibration was verified using gallium.
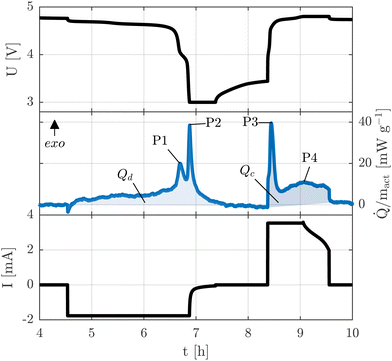
During the entire operation, the calorimeter was placed inside a cooling incubator KB 240 E6 (BINDER GmbH, Germany), set to 5 °C with a fan speed of 40%. Fig. 1 shows an example of a heat flux measurement normalized to the mass of the active material mact covering one discharge and charge cycle.
The total heat
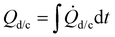 | (1) |
Moreover, four peaks observed during each full cycle of LNMO cathodes are labeled as P1, P2, P3, and P4. Peaks P1, P2, and P3 are associated with an increase in transfer resistance, while P4 corresponds to the transition between the constant current (CC) and constant voltage (CV) phases during charging.28
In this study, the calorimeter baseline was shifted to zero using a fitted curve. The baseline was determined from heat flux data points recorded at zero current. These baseline points were fitted using a second-order exponential function of the form
| f(t) = aebt + cedt | (2) |
As a result of this baseline-shift, a positive heat flux indicates exothermic heat generation, whereas a negative heat flux represents endothermic heat absorption.
In this study, the SoC was defined separately for discharge and charge processes, based on the maximum charge qmax transferred during each respective step. During discharge, the SoC was calculated as
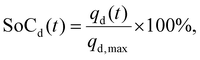 | (3) |
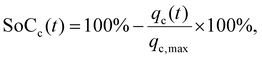 | (4) |
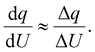 | (5) |
Peaks in the ICA curve indicate distinct reaction steps during cycling. The area under each peak corresponds to the amount of charge transferred during that particular reaction step and thus provides insight into the extent of each electrochemical process.
ICA measurements were conducted inside an IPP55plus temperature chamber using a BCS-805 battery cycler. The cells were maintained at a constant temperature according to the respective test protocol and rested for 3 h prior to measurement. To cover the full voltage window from 3.5 V to 4.8 V, the cells were initially charged to 4.8 V using a CC at a rate of 0.05 h−1. Upon reaching the upper voltage limit, the cells were discharged and subsequently charged again at the same rate (0.05 h−1) without any rest period between the two steps.
The ICA was then calculated over the entire discharge and charge cycle. Unlike all other measurements in this study, the C-rate applied during ICA does not refer to the nominal areal capacity of 2 mAh cm−2, but instead to the individual capacity determined during the initial capacity check of each respective cell.
2.3. Experimental campaigns
Subsequently, the cells were initialized by charging them with a CC at a C-rate of 1/10 h−1 up to an upper voltage limit of 4.8 V, followed by a CV phase lasting 30 min or until the cut-off current of 0.035 mA was reached.
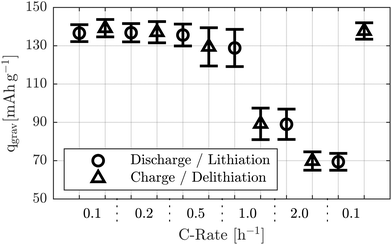
After this initial charge, the measurement protocol was started. It consisted of multiple discharge and charge steps, beginning with a discharge. All cycles were conducted within a voltage window of 3.5 V to 4.8 V. Each charge and discharge step was performed using a CC followed by a CV phase, with the same time limits and cut-off current as during initialization. Table 2 presents the capacities of the individual cells during the first 0.1 h−1 cycle, indicating consistent performance across all cells.
| Cell | Material combination | Test temp. [°C] | q0 [mAh] | q0, area [mAh cm−2] | q0, grav [mAh g−1] |
|---|---|---|---|---|---|
| 1 | CIEI | 25 | 4.09 | 2.31 | 132.99 |
| 2 | CIEI | 25 | 4.21 | 2.38 | 141.37 |
| 3 | CIEI | 25 | 4.14 | 2.34 | 135.19 |
After each charge, the applied current was increased stepwise, starting at 0.1 h−1 and continuing with 0.2 h−1, 0.5 h−1, 1.0 h−1, and 2.0 h−1. To assess aging effects, the final discharge and charge steps were repeated at 0.1 h−1. The used C-rates all correspond to an areal capacity of 2 mAh cm−2.
To clearly distinguish the individual heat flux contributions from each charge or discharge step, an open-circuit voltage (OCV) phase of 30 min was applied after the current was switched off.
The error bars and shaded bands shown in the following results represent the cell-to-cell variation, quantified as the estimated standard deviation (ESD) of the three independently assembled cells. For the SoC-dependent heat flux curves, the ESD was calculated at each SoC value. Consequently, the ESD increases in regions with steep voltage slopes, because small shifts in the peak positions, originating from resistance and capacity differences between the cells, lead to larger deviations when mapped onto the SoC axis. This effect becomes more pronounced at elevated C-rates.
For transparency, the individual heat flux uncertainties for each cell and for the three-cell group are reported in SI Table S1.
To ensure a minimal statistical basis, three cells were assembled for each material and temperature combination. As only one cell could be measured calorimetrically at a time, all cells were fabricated on separate days to avoid differences in storage duration and to exclude calendar aging effects.
The experimental procedure was as follows: after cell assembly, all cells underwent an initialization and capacity check under identical conditions at 25 °C. The resulting capacities are listed in Table 3. Subsequently, the cells were placed in the calorimeter, where measurements were conducted at the designated test temperature of either 25 °C or 45 °C.
| Cell | Cathode | Elektrolyte | Test temp. [°C] | q0 [mAh] | q0, area [mAh cm−2] | q0, grav [mAh g−1] | ||
|---|---|---|---|---|---|---|---|---|
| CI | CS | EI | ES | |||||
| 4 | x | x | 25 | 4.00 | 2.26 | 129.81 | ||
| 5 | x | x | 25 | 3.94 | 2.23 | 130.86 | ||
| 6 | x | x | 25 | 4.02 | 2.27 | 133.52 | ||
| 7 | x | x | 25 | 3.90 | 2.21 | 126.93 | ||
| 8 | x | x | 25 | 3.96 | 2.24 | 128.61 | ||
| 9 | x | x | 25 | 3.90 | 2.21 | 127.49 | ||
| 10 | x | x | 25 | 3.17 | 1.80 | 129.58 | ||
| 11 | x | x | 25 | 3.39 | 1.92 | 131.90 | ||
| 12 | x | x | 25 | 3.32 | 1.88 | 132.14 | ||
| 13 | x | x | 25 | 3.33 | 1.89 | 127.47 | ||
| 14 | x | x | 25 | 3.35 | 1.90 | 128.85 | ||
| 15 | x | x | 25 | 3.36 | 1.90 | 127.29 | ||
| 16 | x | x | 45 | 3.99 | 2.26 | 132.09 | ||
| 17 | x | x | 45 | 4.08 | 2.31 | 128.37 | ||
| 18 | x | x | 45 | 3.96 | 2.24 | 128.79 | ||
| 19 | x | x | 45 | 3.74 | 2.12 | 134.69 | ||
| 20 | x | x | 45 | 3.90 | 2.21 | 132.63 | ||
| 21 | x | x | 45 | 3.89 | 2.20 | 130.09 | ||
| 22 | x | x | 45 | 3.31 | 1.87 | 127.32 | ||
| 23 | x | x | 45 | 3.30 | 1.87 | 132.61 | ||
| 24 | x | x | 45 | 3.26 | 1.85 | 128.85 | ||
| 25 | x | x | 45 | 3.44 | 1.95 | 131.35 | ||
| 26 | x | x | 45 | 3.41 | 1.93 | 134.39 | ||
| 27 | x | x | 45 | 3.29 | 1.86 | 131.62 | ||
Each calorimetric experiment consisted of a sequence of three cycles, beginning with a discharge. A CCCV protocol was applied with a discharge C-rate of 0.5 h−1 and a charge C-rate of 1.0 h−1, reflecting the typical use case in practical applications where charging currents are generally higher than discharging currents. The voltage window was set to 3.5 V to 4.8 V. The CV phase was limited to 30 min or terminated earlier if the current dropped below 0.035 mA. All C-rates were referenced to an areal capacity of 2 mAh cm−2.
Following the calorimetric measurement, ICA was performed at the respective test temperature. Finally, the capacity was measured again at 25 °C to assess possible capacity changes. For the cells tested at 25 °C, this capacity check was conducted immediately after the ICA. In contrast, the cells previously tested at 45 °C were given an additional rest period of 3 h after being transferred to the 25 °C temperature chamber to allow for thermal equilibration.
As in the previous section, all results are shown as the mean of three independently assembled cells, and the error bars represent the cell-to-cell variation (ESD), as defined in section 2.3.1. Detailed uncertainty values for each cell and group are given in SI Table S1.
3. Results and discussion
3.1. Influence of current rate
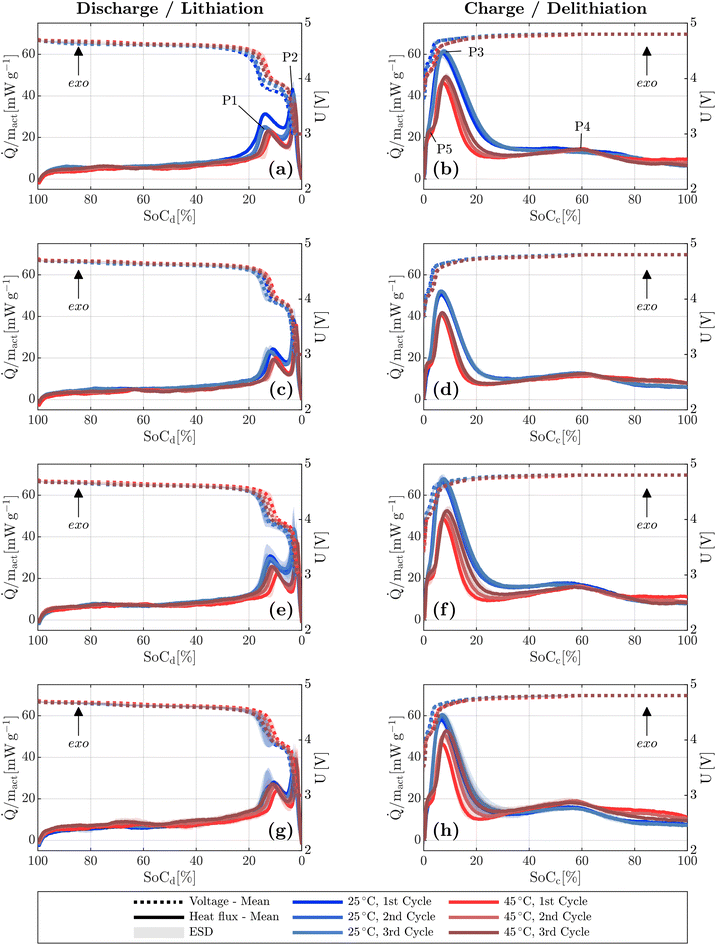
Fig. 2 displays the SoC dependent heat generation (a, b) along with magnified views (c, d), and the corresponding voltage profiles (e, f) at various C-rates. During discharge, two distinct exothermic peaks P1 and P2 are observed. With increasing C-rate, these peaks shift progressively toward lower SoC values and begin to merge. At a C-rate of 2.0 h−1, the individual peaks are no longer clearly distinguishable and appear as a single broad peak P1/2. This behavior is consistent with the observations reported by Baazizi et al.,26 who described a further development of this effect at C-rates up to 4.0 h−1, where the flat region becomes part of the overall peak.During charging, a single dominant peak P3 is typically observed at SoC values below 20% SoCc. At low C-rates of 0.1 and 0.2 h−1, the short initial heat flux peak is also visible. For a C-rate of 2.0 h−1, a constantly decreasing heat flux follows this initial peak, whereas for C-rates of 1.0 h−1 and below, a local minimum is observed. This minimum is endothermic for C-rates below 0.2 h−1. The minimum is followed by a continuous increase in exothermic heat flux. From approximately 50% SoCc onward, all C-rates exhibit a net exothermic heat release.
The evolution of the individual peaks is assumed to be related to an increase in charge transfer resistance associated with the transition between electrochemical reaction steps.28
The endothermic contribution during charging is attributed to entropy changes within the electrode.28 However, at higher C-rates, this effect becomes increasingly dominated by irreversible heat generation.29,30
The shift of the peaks toward higher SoC values can be attributed to a decrease in the inserted charge with increasing C-rate. As displayed in Fig. 3, a capacity loss of approximately 40% is observed at a C-rate of 1.0 h−1. The reduction mainly occurs during the charging step, as the coulombic efficiency consistently remained above 97% (SI Fig. S6), despite the use of a lower C-rate for charging.
Further evidence is provided by the final 0.1 h−1 cycle, during which the charge capacity fully recovers and matches that of the initial 0.1 h−1 cycle. The underlying reason is the time limitation of the CV phase. At higher current rates, polarization effects are more pronounced, requiring a longer CV phase to insert the same amount of charge. This behavior is also visible in Fig. 2f, where the CV phase stretches over an increasingly wide SoCc range with an increase in C-rate.
A further consequence appears during the second 0.1 h−1 discharge step: the manganese-related reaction plateau becomes more pronounced in the SoCd region, and one of the two nickel-related reaction steps is no longer visible (Fig. 2e). The correlation between the peak positions and the transitions between reaction steps becomes evident, as a corresponding shift in the heat flux peaks is observed in Fig. 2c, mirroring the voltage profile in Fig. 2e. No such shift is observed during the discharge step, where the capacities match again.
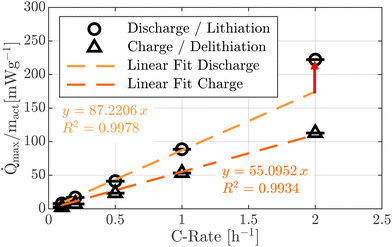
Fig. 4 displays the maximum heat flux observed during discharge and charge. A continuous increase in the peak values for both processes is evident. Furthermore, the maximum heat flux during discharge is consistently higher than during charge.
For both discharge and charge, a linear relationship between the C-rate and the maximum heat flux can be assumed in the lower current range. Nevertheless, the increase is more pronounced for discharge. For instance, to reach a maximum heat flux of approximately 50 mW g−1, a C-rate of around 0.57 h−1 is required during discharge, compared to about 0.91 h−1 during charge. This indicates that the charge C-rate can be roughly 1.58 times higher than the discharge C-rate while generating a comparable maximum heat flux.
However, this linear trend appears to be valid only up to 1.0 h−1 (discharge), as the maximum heat flux measured at 2.0 h−1 deviates from the linear fit of the lower C-rates. One possible explanation is that, at 2.0 h−1, the two individual discharge-related heat flux peaks begin to merge, as illustrated in Fig. 2a. This superposition leads to an increased combined peak value. Since no such overlapping is observed for the charge process, the charge-related maximum heat flux continues to follow the linear relation. Alternatively, the deviation may be attributed to increasing contributions from mixing-related heat effects at higher C-rates, caused by more pronounced charge gradients within the electrode.31,32 This increase likely contributes to a further rise of the previously calculated factor of 1.58 at higher C-rates, though this remains a hypothesis based on the current data.
Another aspect considered is the total heat generated. As displayed in Fig. 2(c and d), a large portion of the heat generation at C-rates below 0.5 h−1 is close to zero. The noise level of the calorimeter was determined from the heat flux signal during the final OCV period of the current-variation experiment, resulting in σnoise = 0.35 mW g−1 (see SI Fig. S3). The signal-to-noise ratio (SNR) is shown in SI Fig. S4. While all maximum heat flux peaks satisfy SNR > 5, most of the heat flux signal at C-rates below 0.5 h−1 lies below this threshold. For this reason, only the integrals for C-rates of 0.5, 1.0, and 2.0 h−1 are evaluated and presented in Fig. 5.
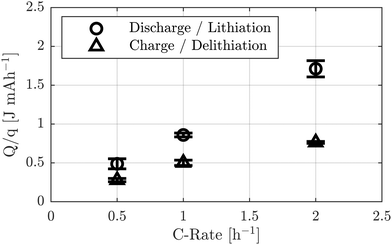 | ||
| Fig. 5 Charge-normalized heat during discharge and charge for different C-rates. Due to the poor signal-to-noise ratio, only data for C-rates above 0.5 h−1 are displayed. | ||
Since the heat integral strongly depends on the duration of the charge and discharge steps, the heat is normalized to the corresponding charged or discharged capacity.
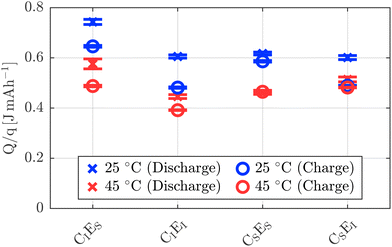
Similar to the maximum heat flux, the total heat increases with increasing C-rate. The ratio of heat generated during discharge to that during charge shows that at 0.5 h−1, the heat released during discharge is approximately 1.77 ± 0.25 times higher than during charge. This trend continues with increasing current, reaching a factor of 2.43 ± 0.34 at 2.0 h−1. These findings coincide with the observations of the heat flux maxima and indicate the possibility of increasing charge currents while maintaining comparable total heat generation during charge and discharge.
Existing literature on other cathode materials provides useful context for interpreting the distinctive thermal behaviour of LNMO. For NCM, Liang et al.33 reported a relatively flat heat flux during lithiation and delithiation with a final exothermic peak at the end of lithiation, whereas He et al.34 observed a gradually increasing heat flux during delithiation. LFP, in contrast, shows a plateau-like heat flux that reflects its flat voltage profile, accompanied by a single exothermic peak at the end of both lithiation and delithiation.35 Despite some discrepancies between studies, both NCM and LFP share the absence of an additional low-SoC exothermic peak, highlighting that the pronounced low SoC heat flux feature is specific to LNMO.
In full cells, the thermal response is further shaped by the graphite anode, whose SoC-dependent heat generation often dominates the cell-level behaviour at low C-rates.36,37 Graphite exhibits a characteristic sequence of thermal events: an initial endothermic peak followed by an extended exothermic regime during lithiation,33,38 and renewed endothermic behaviour during early and mid-SoC delithiation.33 In a full cell, these graphite-derived contributions might overlap with those of the LNMO cathode. As a consequence, the exothermic LNMO peak during discharge would coincide with the exothermic heat release of graphite, potentially increasing the maximum heat flux, whereas during charge the endothermic behaviour of graphite may partially offset the LNMO heat generation. This coupling effect indicates that the maximum heat flux in LNMO/graphite full cells may differ from LNMO half-cell results and requires dedicated investigation in future thermal studies.
3.2. Influence of material combination and temperature
| Mat. | Process | q-Check 1 [mAh g−1] | q-Check 2 [mAh g−1] | Relative capacity loss [%] |
|---|---|---|---|---|
| CIES | Discharge | 127.68 ± 0.85 | 131.11 ± 2.58 | 2.69 ± 2.28 |
| Charge | 135.95 ± 2.69 | 133.37 ± 2.66 | −1.68 ± 2.20 | |
| CIEI | Discharge | 131.40 ± 1.92 | 133.14 ± 1.44 | 1.33 ± 0.73 |
| Charge | 136.58 ± 1.50 | 134.29 ± 1.69 | −1.68 ± 0.71 | |
| CSES | Discharge | 132.46 ± 1.68 | 132.74 ± 0.36 | 0.22 ± 0.96 |
| Charge | 138.97 ± 1.67 | 136.00 ± 1.60 | −2.14 ± 0.13 | |
| CSEI | Discharge | 129.59 ± 2.73 | 131.85 ± 3.10 | 1.74 ± 3.72 |
| Charge | 135.86 ± 3.49 | 133.82 ± 3.30 | −1.50 ± 3.67 |
| Mat. | Process | q-Check 1 [mAh g−1] | q-Check 2 [mAh g−1] | Relative capacity loss [%] |
|---|---|---|---|---|
| CIES | Discharge | 127.87 ± 0.86 | 64.06 ± 13.59 | −49.76 ± 11.57 |
| Charge | 134.16 ± 1.49 | 27.42 ± 7.30 | −79.49 ± 6.26 | |
| CIEI | Discharge | 131.21 ± 1.42 | 132.20 ± 2.95 | 0.76 ± 2.41 |
| Charge | 136.03 ± 0.93 | 132.01 ± 1.58 | −2.95 ± 1.80 | |
| CSES | Discharge | 132.46 ± 2.28 | 122.72 ± 8.32 | −7.36 ± 6.07 |
| Charge | 139.02 ± 1.89 | 114.02 ± 12.21 | −18.00 ± 8.68 | |
| CSEI | Discharge | 129.75 ± 2.04 | 132.48 ± 1.20 | 2.11 ± 1.20 |
| Charge | 137.64 ± 2.42 | 129.05 ± 1.85 | −6.24 ± 0.51 |
At 25 °C, no significant capacity loss is observed for either discharge or charge, indicating stable cycling behavior across all material combinations over a limited number of cycles.
At 45 °C, however, clear differences between the material combinations become evident. CIEI still shows stable cycling behavior with no significant losses in either discharge or charge. The second material combination containing the improved electrolyte, CSEI, exhibits the second-lowest capacity fade. While the increase in discharge capacity may be attributed to the lower current used during the ICA measurement, a capacity loss of approximately 6.2% is observed during charge.
Among the combinations using the standard electrolyte, CIES shows rapid capacity degradation, with a loss of approximately 50% during discharge and 80% during charge. CSES also exhibits a notable capacity fade, with around 7% loss during discharge and 18% during charge.
The differences in capacity are also reflected in the ICA measurements (Fig. 6).
In ICA analysis, a shift of the peak along the x-axis correlates with changes in internal resistance.39 A shift to lower voltages during discharge and to higher voltages during charge indicates an increase in resistance. Conversely, shifts in the opposite direction suggest a reduction in internal resistance. A second observable effect is the loss of active material, which manifests as a reduction in the area beneath the corresponding peaks.40 Since half-cells with lithium counter electrodes are used, a loss of lithium inventory cannot be detected in this setup.40
Consistent with the observed capacity changes, no significant differences are detected in the ICA measurements for CIEI. Only a slight shift toward lower voltages during charge and higher voltages during discharge is observed, indicating a reduced internal resistance at elevated temperature. This can be attributed to improved interfacial kinetics at the electrode surface and a reduction in electrolyte viscosity.41,42
In contrast, a clear decrease in peak height is observed for the other material combinations, indicating a loss of active material. Among them, CIES shows the most pronounced reduction, suggesting the highest degree of active material loss. Since the ratio of charge transferred during the individual peaks remains nearly unchanged despite aging, it can be concluded that both redox processes are affected to a similar extent. This suggests that temperature-induced degradation does not preferentially impact one of the two reactions.
Additionally, all cells (with the exception of CIEI) exhibit a shift of the peaks along the x-axis, with higher voltages during charge and lower voltages during discharge. This indicates an increase in internal resistance. Although elevated temperatures generally improve electrolyte viscosity and interfacial kinetics. This effect is most pronounced for CIES. The assumption of enhanced CEI formation at elevated temperatures is consistent with aging studies conducted by Maiti et al.10 and Nisar et al.,7 who attributed the observed shift of ICA peaks and the associated capacity fading of LNMO cathodes to a progressive growth of the CEI layer. This interpretation is further supported by previous studies reporting a continuous thickening of the CEI during LNMO aging,43,44 as well as by works demonstrating that the extent of the CEI depend on the choice of electrolyte additives.45 Such CEI growth has been linked to increased resistance,45,46 consistent with the trends observed in the present study.
When comparing the two capacity check measurements, it must be noted that both include a time-limited CV phase. As a result, particularly in the case of CIES, the increased resistance, alongside the loss of active material, further limits the achievable capacity during charging. This highlights that, in addition to active material loss, the rise in cell resistance has a compounding negative effect on the performance.
Overall, it is evident that cells containing the improved electrolyte (EI) exhibited superior cycling performance compared to their counterparts. This effect may be attributed to the presence of functional electrolyte additive TMSP, which is known to promote the formation of a more stable CEI layer and thereby mitigate interfacial degradation.19–21
For the improved electrode with aluminium–oxide surface treatment (CI), no consistent trend in cycling performance can be observed. While its combination with EI resulted in enhanced cycling stability, the pairing with the standard electrolyte (ES) led to a deterioration in performance. A possible explanation is the formation of pitting structures within the surface layer, which may locally accelerate degradation processes along active conduction paths.47 The TMSP may contribute to a stabilization of the CEI and mitigate such effects.
However, a comprehensive understanding of the underlying mechanisms requires further investigation and is beyond the scope of this study, which focuses primarily on heat generation behavior.
Independent of the material combination, a similar heat flux profile is observed across all measurements. With an increase in temperature from 25 °C to 45 °C, the overall heat flux tends to decrease, particularly at low SoC values below 20% SoCd and 30% SoCc. During charging at 45 °C, an additional step P5 appears at very low SoCc values (<5%), which could be attributed to a more pronounced Mn3+/4+ redox reaction around 4 V due to enhanced kinetics.
Among the investigated material combinations, CIEI exhibits the lowest overall heat release (Fig. 8) and the lowest individual heat flux peaks (Fig. 9) at both 25 °C and 45 °C. The corresponding data for subsequent cycles are provided in the SI (Fig. S8 and S9).
The low amplitudes of peaks P1, P2, and P3 suggest superior kinetics and the lowest transfer resistance among the tested combinations, which could indicate a thinner CEI.
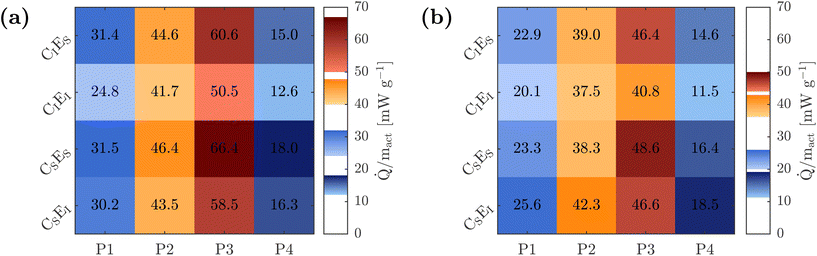
In contrast, the highest heat release and the most pronounced peaks are observed for CSES. For example, at 25 °C, the heat release at the most intense peak P3 exceeds that of CIEI by approximately 31%, and by about 19% at 45 °C.
In the first calorimetric cycle, a smaller difference between CIEI and CSES is observed at 45 °C compared to 25 °C. If the measured heat were primarily caused by exothermic electrolyte decomposition, a larger difference between the thermally stable CIEI and the less stable CSES would be expected at elevated temperature, since such decomposition reactions are typically exothermic.48 This, however, is not reflected in the measurements.
Moreover, in the third cycle at 45 °C, the peak value of P3 reaches approximately 41.9 mW g−1 for CIEI, corresponding to an increase of about 3%, while CSES reaches 53.0 mW g−1, an increase of approximately 9%. This indicates that the increase in P3 is about three times greater for CSES than for CIEI, resulting in a relative difference of around 26% after three cycles. This trend suggests that the observed increase in heat release is not primarily caused by direct electrolyte decomposition but rather by secondary effects. In particular, the progressive formation of the CEI likely contributes to an increase in charge transfer resistance, thereby enhancing irreversible heat generation at later stages of cycling. Interestingly, CIES does not exhibit a pronounced SoC shift, although this might be expected based on the observed capacity fade and ICA results.
While P3 is mainly caused by kinetic limitations,28 the heat flux for SoC values above 20% SoCd/c do not show such distinct changes due to a change of temperature or aging, indicating that the diffusion limited heat fluxes are less affected by the temperature and aging.
Finally, the distribution of the released heat as a function of the SoC is considered. Since the material combination CIEI exhibited the best stability, the following analysis is limited to this configuration. Table 6 presents the percentage of heat released below 20% SoCd and 20% SoCc. The corresponding absolute values are reported in SI Table S4, while the individual cell values, including the geometrical drift-corrected heat contributions, are provided in SI Tables S2 and S3. The magnitude of the geometrical correction remained below 4% for all cells.
| Temperature | Phase | Cycle 1 [%] | Cycle 2 [%] | Cycle 3 [%] |
|---|---|---|---|---|
| 25 °C | Discharge | 54.5 ± 8.9 | 54.4 ± 4.7 | 55.0 ± 4.3 |
| Charge | 41.3 ± 2.5 | 41.9 ± 1.7 | 41.9 ± 1.3 | |
| 45 °C | Discharge | 55.6 ± 12.6 | 53.4 ± 3.9 | 52.2 ± 2.8 |
| Charge | 34.5 ± 1.5 | 36.8 ± 2.1 | 37.6 ± 1.9 |
It is evident that approximately 50–55% of the total heat generated during discharge is released within the last 20% of the SoCd range. During charge, this share decreases to about 35–42%.
This behavior is attributed to strong kinetic limitations in the low-SoC region,28 leading to an increase in charge-transfer resistance. The charge-transfer resistance Rct is inversely proportional to the concentration of electroactive species.49 Consequently Rct rises, when the number of accessible Ni or Mn redox centers is strongly reduced, reflected by the steep voltage change in this regime (see Fig. 2(e) and (f)). A similar increase in charge-transfer resistance at low lithiation has also been reported for disordered LNMO by Amin et al.50 The elevated Rct amplifies the polarization losses and thereby enhances the irreversible heat generation in this SoC range.
Furthermore, the proportion is consistently higher at 25 °C than at 45 °C, with the exception of cycle 1 discharge where the large ESD obscures this trend. This behavior is consistent with the previously observed temperature dependence of the P3 peak. However, it appears counterintuitive that the relative share during discharging at 45 °C decreases with increasing cycle number. This effect is likely caused by a broadening of the peaks, which leads to a shift of the heat generation toward higher SoC values and consequently reduces the relative contribution within the defined low SoC range.
4. Conclusions
With increasing current rates, the heat released by LNMO cathodes also increases. At higher currents, individual heat flux peaks begin to merge, indicating overlapping electrochemical processes.From a thermal management perspective, elevated current rates are of particular relevance. The analysis of heat flux profiles and total heat generation reveals that the heat released during discharge consistently exceeds that during charge. As a result the charge current can be increased by a factor of about 1.58 while maintaining similar maximum heat fluxes as during discharging at 25 °C. Moreover, the results indicate that this factor might increase, due to a nonlinear increase of the maximum heat flux during discharging for C-rates >1.0 h−1. This observation supports the design of thermal systems that allow for higher charging currents than discharging currents under identical cooling capacity, which is particularly advantageous for fast-charging applications.
The second part of this study examined the influence of temperature and material configuration on both thermal behavior and capacity retention. While all cells showed comparable performance at 25 °C, pronounced material-dependent differences emerged at 45 °C. The combination of surface coating and electrolyte modification CIEI resulted in the most stable cycling behavior, with a capacity loss of only about 3%. In contrast, pairing the coated cathode with the standard electrolyte led to rapid capacity degradation of approximately 80%, likely due to localized breakdown of active transport pathways.47
A similar trend was observed in the heat flux profiles. The configuration CIEI exhibited the lowest total heat generation, the most uniform thermal behavior, and the smallest increase in irreversible heat release over cycling. In contrast, material combinations with pronounced aging showed increasing heat release, particularly in the low SoC region, which is likely attributable to the progressive formation of the CEI layer and the resulting increase in interfacial resistance. Diffusion-limited processes, however, appeared less sensitive to temperature and degradation.
Furthermore, heat generation in LNMO cathodes was found to be highly localized in the low SoC region. For CIEI, approximately 50–55% of the discharge heat and 35–42% of the charge heat was generated below 20% SoCd/c.
These findings illustrate how current rate, operating temperature, and material selection jointly influence the thermal behavior of LNMO-based cells. The reduced heat generation during charging under equal current conditions, enables the application of higher charging rates without surpassing thermal limits. Moreover, appropriately adapted charge/discharge protocols could allow increased currents at SoC values above 20%, provided that thermal management systems are optimized for the dominant heat peaks occurring at low SoC.
Furthermore, this study demonstrates that the combination of two complementary material modifications can significantly enhance cycling stability and thermal performance, even though each strategy alone resulted in reduced stability. This highlights the importance of synergy between electrode and electrolyte design in the development of next-generation high-voltage cathode systems.
It should be noted that additional modifications such as the aluminium–oxide surface coating and the use of TMSP as functional additive inherently increase production complexity and material costs for LNMO-based electrodes. Consequently, part of the intrinsic cost advantage of cobalt-free LNMO over NCM cathodes may be reduced. However, the overall economic impact will strongly depend on long-term cobalt price trends, large-scale manufacturing efficiencies, and supply-chain developments.
Finally, the results indicate that severe degradation during cycling does not lead to additional heat flux peaks that could be directly linked to parasitic side reactions. Instead, changes in the heat flux signals are attributed to secondary effects of such reactions, such as the increase in interfacial resistance due to CEI formation.
Author contributions
Conceptualization, K. B.; methodology, K. B.; software, K. B.; validation, K. B.; formal analysis, K. B.; investigation, K. B.; resources, K. B., A. K., T. M. and D. H.; data curation, K. B.; writing—original draft preparation, K. B.; writing—review and editing, K. B., A. K., T. M. and D. H.; visualization, K. B.; supervision, T. M. and D. H.; project administration, A. K. and D. H.; funding acquisition, D. H. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The datasets supporting this article are available within the article and the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5eb00203f.Acknowledgements
The authors gratefully acknowledge the support of the junior research group Kems4Bats by the German Federal Ministry of Research, Technology and Space (BMFTR) and by industry and science sponsors (Netzsch-Gerätebau GmbH, Comsol Multiphysics GmbH, MAHLE GmbH, Volkswagen AG, BASF SE, GHS Vakuumtechnik GmbH, Pfeiffer Vacuum GmbH, BorgWarner Inc., CHARISMA, Verfasste Studierendenschaft Technische Hochschule Mannheim).The authors would like to acknowledge the use of OpenAI's ChatGPT for assistance in grammar, spelling, and sentence structure checks, as well as for support in developing MATLAB scripts used for data visualization presented in this paper.
References
- A. Nekahi, A. K. Madikere Raghunatha Reddy, X. Li, S. Deng and K. Zaghib, Electrochem. Energy Rev., 2025, 8, 1 CrossRef CAS.
- A. Singh, V. Jately, P. Kala and Y. Yang, J. Energy Storage, 2025, 110, 115274 CrossRef.
- G. Liang, V. K. Peterson, K. W. See, Z. Guo and W. K. Pang, J. Mater. Chem. A, 2020, 8, 15373–15398 RSC.
- J. Cen, B. Zhu, S. R. Kavanagh, A. G. Squires and D. O. Scanlon, J. Mater. Chem. A, 2023, 11, 13353–13370 RSC.
- M. Fehse, N. Etxebarria, L. Otaegui, M. Cabello, S. Martin-Fuentes, M. A. Cabanero, I. Monterrubio, C. F. Elkjaer, O. Fabelo, N. A. Enkubari, J. M. Lopez Del Amo, M. Casas-Cabanas and M. Reynaud, Chem. Mater., 2022, 34, 6529–6540 CrossRef CAS PubMed.
- X. Zhu, A. Huang, I. Martens, N. Vostrov, Y. Sun, M. I. Richard, T. U. Schulli and L. Wang, Adv. Mater., 2024, 36, e2403482 CrossRef PubMed.
- U. Nisar, J. Bansmann, M. Hebel, B. Reichel, M. Mancini, M. Wohlfahrt-Mehrens, M. Hölzle and P. Axmann, Chem. Eng. J., 2024, 493, 152416 CrossRef CAS.
- D. Versaci, R. Colombo, G. Montinaro, M. Buga, N. Cortes Felix, G. Evans, F. Bella, J. Amici, C. Francia and S. Bodoardo, J. Power Sources, 2024, 613, 234955 CrossRef CAS.
- M. T. Nguyen, H. Q. Pham, J. A. Berrocal, I. Gunkel and U. Steiner, J. Mater. Chem. A, 2023, 11, 7670–7678 RSC.
- S. Maiti, H. Sclar, J. Grinblat, M. Talianker, Y. Elias, X. Wu, A. Kondrakov and D. Aurbach, Small Methods, 2022, 6, 2200674 CrossRef CAS PubMed.
- D. S. Lu, L. B. Yuan, J. L. Li, R. Q. Huang, J. H. Guo and Y. P. Cai, J. Electroanal. Chem., 2015, 758, 33–38 CrossRef CAS.
- J. Yan, M. Yuan, S. Xie, T. Wang, J. Liu, Z. Li and J. Peng, J. Mater. Res., 2023, 38, 1293–1303 CrossRef CAS.
- Z. Yao, T. Fu, T. Pan, C. Luo, M. Pang, S. Xiong, Q. Guo, Y. Li, S. Liu, C. Zheng and W. Sun, Nat. Commun., 2025, 16, 2791 CrossRef CAS PubMed.
- T. J. Lee, J. B. Lee, T. Yoon, D. Kim, O. B. Chae, J. Jung, J. Soon, J. H. Ryu, J. J. Kim and S. M. Oh, J. Electrochem. Soc., 2016, 163, A898–A903 CrossRef CAS.
- Z. Wang, Z. Wang, Y. Zheng, L. Zhang, X. Zhou, X. Shen, T. Zhang, T. Qian, J. Liu and C. Yan, ACS Appl. Energy Mater., 2025, 8, 4784–4792 CrossRef CAS.
- J. Kim, H. Kim and K. Kang, J. Korean Ceram. Soc., 2018, 55, 21–35 CrossRef CAS.
- Y. Han, Y. Xue, Y.-F. Xia, J.-N. Zhang, F.-D. Yu, D.-M. Gu and Z.-B. Wang, Ionics, 2018, 25, 2459–2468 CrossRef.
- Z. A. Qureshi, M. E. S. Ali, R. A. Shakoor, S. AlQaradawi and R. Kahraman, Ceram. Int., 2024, 50, 17818–17835 CrossRef CAS.
- G. Xu, C. Pang, B. Chen, J. Ma, X. Wang, J. Chai, Q. Wang, W. An, X. Zhou, G. Cui and L. Chen, Adv. Energy Mater., 2017, 8, 1701398 CrossRef.
- J. Mu, A. Wei, X. Li, R. He, L. Sun, P. Liu, X. Bai, L. Zhang, X. Zhang, Z. Liu and J. Gao, J. Power Sources, 2024, 611, 234707 CrossRef CAS.
- T. Kim, H. Oh, S. Yang and H. J. Lee, ACS Appl. Energy Mater., 2025, 8, 13155–13178 CrossRef CAS.
- A. M. Fathimathul Faseena and A. Sreekumar, J. Energy Storage, 2025, 113, 115644 CrossRef.
- K. Chen, Y. Chen, Z. Li, F. Yuan and S. Wang, Int. J. Heat Mass Transfer, 2018, 127, 393–401 CrossRef.
- A. A. Pesaran, J. Power Sources, 2002, 110, 377–382 CrossRef CAS.
- S. Sayah, M. Baazizi, M. Karbak, J. Jacquemin and F. Ghamouss, Energy Technol., 2023, 11, 2201446 CrossRef CAS.
- M. Baazizi, S. Sayah, M. Karbak, O. Hajjaj, M. Aqil, M. Dahbi and F. Ghamouss, Batteries Supercaps, 2023, 6, e202300151 CrossRef CAS.
- J. Mao, P. Zhang, X. Liu, Y. Liu, G. Shao and K. Dai, ACS Omega, 2020, 5, 4109–4114 CrossRef CAS PubMed.
- K. Böhm, A. Kondrakov, T. Markus and D. Henriques, Batteries, 2025, 11, 357 CrossRef.
- Y. Tan, Y. Li, Y. Gu, W. Liu, J. Fang and C. Pan, Energies, 2023, 17, 178 CrossRef.
- A. Nazari and S. Farhad, Appl. Therm. Eng., 2017, 125, 1501–1517 CrossRef CAS.
- R. Mehta and A. Gupta, Electrochim. Acta, 2024, 475, 143509 CrossRef CAS.
- D. Chalise, W. Lu, V. Srinivasan and R. Prasher, J. Electrochem. Soc., 2020, 167, 090560 CrossRef.
- C. Liang, L. Jiang, S. Ye, Z. Wang, Z. Wei, Q. Wang and J. Sun, J. Energy Chem., 2021, 54, 332–341 CrossRef CAS.
- W. He, W. Shen, J. Zhang, M. Zhong and S. Guo, J. Energy Storage, 2025, 134, 118079 CrossRef.
- L. Song, X. Li, Z. Wang, H. Guo, Z. Xiao, F. Zhang and S. Peng, Electrochim. Acta, 2013, 90, 461–467 CrossRef CAS.
- K. Chen, G. Unsworth and X. Li, J. Power Sources, 2014, 261, 28–37 CrossRef CAS.
- V. V. Viswanathan, D. Choi, D. Wang, W. Xu, S. Towne, R. E. Williford, J.-G. Zhang, J. Liu and Z. Yang, J. Power Sources, 2010, 195, 3720–3729 CrossRef CAS.
- A. Kunz, C. Berg, F. Friedrich, H. A. Gasteiger and A. Jossen, J. Electrochem. Soc., 2022, 169, 080513 CrossRef CAS.
- L. Spitthoff, P. J. S. Vie, M. S. Wahl, J. Wind and O. S. Burheim, J. Electroanal. Chem., 2023, 944, 117627 CrossRef CAS.
- S. Casino, T. Beuse, V. Küpers, M. Börner, T. Gallasch, M. Winter and P. Niehoff, J. Energy Storage, 2021, 41, 102812 CrossRef.
- A. Hu, F. Li, W. Chen, T. Lei, Y. Li, Y. Fan, M. He, F. Wang, M. Zhou, Y. Hu, Y. Yan, B. Chen, J. Zhu, J. Long, X. Wang and J. Xiong, Adv. Energy Mater., 2022, 12, 2202432 CrossRef CAS.
- E. R. Logan, E. M. Tonita, K. L. Gering, J. Li, X. Ma, L. Y. Beaulieau and J. R. Dahn, J. Electrochem. Soc., 2018, 165, A21–A30 CrossRef CAS.
- W. Bao, W. Yao, Y. Li, B. Sayahpour, B. Han, G. Raghavendran, R. Shimizu, A. Cronk, M. Zhang, W. Li and Y. S. Meng, Energy Environ. Sci., 2024, 17, 4263–4272 RSC.
- M. Börner, P. Niehoff, B. Vortmann, S. Nowak, M. Winter and F. M. Schappacher, Energy Technol., 2016, 4, 1631–1640 CrossRef.
- Y. Dong, B. T. Young, Y. Zhang, T. Yoon, D. R. Heskett, Y. Hu and B. L. Lucht, ACS Appl. Mater. Interfaces, 2017, 9, 20467–20475 CrossRef CAS PubMed.
- N. Zhang, B. Wang, F. Jin, Y. Chen, Y. Jiang, C. Bao, J. Tian, J. Wang, R. Xu, Y. Li, Q. Lv, H. Ren, D. Wang, H. Liu, S. Dou and X. Hong, Cell Rep. Phys. Sci., 2022, 3(12), 101197 CrossRef CAS.
- E. R. Ostli, Y. Tesfamhret, S. Wenner, M. J. Lacey, D. Brandell, A. M. Svensson, S. M. Selbach and N. P. Wagner, ACS Omega, 2021, 6, 30644–30655 CrossRef PubMed.
- Y. Dai and A. Panahi, Next Energy, 2025, 6, 100186 CrossRef.
- A. C. Lazanas and M. I. Prodromidis, ACS Meas. Sci. Au, 2023, 3, 162–193 CrossRef CAS PubMed.
- R. Amin and I. Belharouak, J. Power Sources, 2017, 348, 318–325 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |