From polyamines to nanogels: a supramolecular approach for boosting relaxivity of [Gd(DOTP)]⁵⁻

Abstract

Supramolecular chemistry has played a central role in advancing the development of more effective contrast agents (CAs) for magnetic resonance imaging (MRI). By incorporating Gd(III) complexes into larger supramolecular architectures, host–guest interactions can be exploited to enhance both performance and targeting. Optimizing these interactions has the potential to substantially increase relaxivity (r₁), thereby improving MRI signal enhancement and enabling lower administered doses without compromising image quality. In this work, we investigated the formation of ion pairs between the anionic complex [Gd(DOTP)]⁵⁻, which lacks an inner-sphere water molecule, and cationic polyamine substrates such as cyclen, octaazacryptand, and low-molecular-weight polyethyleneimine. Our approach combines ¹H NMR relaxometric techniques with DFT calculations. Relaxometric titrations of dilute [Gd(DOTP)]⁵⁻ solutions with increasing amounts of the cationic substrates allow determination of the ion-pair binding constants as well as the relaxivity of the resulting supramolecular adducts. The strength of these interactions increases with the number of positive charges on the polyamine and depends strongly on pH, reflecting the optimal balance of charges between anion and cation. A further and remarkable enhancement in relaxivity is observed when the metal complex is confined within nanogels. Analysis of the corresponding NMRD (Nuclear Magnetic Relaxation Dispersion) profiles highlights the essential contribution of well-organized second-sphere water molecules with restricted mobility, which are responsible for the unusually high relaxivity values at magnetic fields relevant for MRI.

---

Introduction

Supramolecular chemistry serves as a foundational pillar for many cutting-edge developments in modern inorganic chemistry and materials science. It explores molecular organization beyond traditional covalent bonding, focusing on the assembly of components via a wide range of weak, non-covalent interactions. These forces, operating over relatively long distances (typically 200–400 picometers), play a key role in dictating molecular architecture and behavior.¹ The strength of supramolecular chemistry lies in its ability to exert precise control over such interactions, enabling the rational design and synthesis of functional molecular systems. This level of control is essential for advanced processes like molecular recognition, which underlies highly selective sensing, catalytic activity, and specific binding-functions central to both biological systems and material technologies. Examples of supramolecular inorganic systems include coordination cages and capsules,² metal–organic frameworks (MOFs),³ polyoxometalates,⁴ self-assembled monolayers,⁵ and molecular machines.⁶ These architectures demonstrate how supramolecular strategies can be leveraged to construct complex systems with finely tuned chemical and physical properties. Supramolecular chemistry strategies have also been effectively employed to enhance the performance and efficacy of paramagnetic ion complexes used as diagnostic probes in Magnetic Resonance Imaging (MRI).^7–9 Today, more than 40% of MRI procedures involve the use of paramagnetic compounds, commonly referred to as contrast agents (CAs). These agents improve image quality by shortening the relaxation times of nearby water protons. Among the available contrast agents, gadolinium(III) chelates are by far the most commonly used.^10–12 This dominance is largely due to the favourable magnetic properties of the Gd(III) ion: it possesses seven unpaired electrons (S = 7/2), which confer high paramagnetism, along with relatively long electronic relaxation times.¹³ These features enable Gd(III) to efficiently reduce the longitudinal relaxation time (T₁) of surrounding water protons, resulting in increased signal intensity and enhanced contrast in T₁-weighted MR images.¹³ The efficiency of a contrast agent in enhancing proton relaxation per unit concentration of Gd(III) is quantified by its relaxivity (r₁).^13,14 For Gd(III)-based agents, relaxivity primarily arises from two distinct mechanisms involving interactions with water molecules: inner-sphere (IS) and outer-sphere (OS) contributions.¹³ While both mechanisms contribute, the inner-sphere process is typically the dominant determinant of r₁. Several key parameters govern inner-sphere relaxivity:^13,14

- Hydration number (q): the number of water molecules directly coordinated to the Gd(III) ion. A higher q generally provides more efficient relaxation pathways.

- Water residence lifetime (τ_M): the average time a water molecule remains bound in the inner coordination sphere before exchanging with bulk water.

- Correlation time (τ_C): the effective timescale over which electron–nucleus dipolar interactions fluctuate. Its value depends on several factors, including electronic relaxation times (T_1e, T_2e) and the rotational correlation time (τ_R) of the complex.

- Rotational correlation time (τ_R): this component of τ_C reflects how fast the entire contrast agent tumbles in solution. At clinically relevant magnetic fields (1.5–3.0 T), τ_R is often the primary limiting factor for r₁, as small, fast-tumbling complexes typically relax too quickly to maximize dipolar interactions. Consequently, strategies to increase τ_R (e.g., by increasing molecular size or restricting mobility) are key to enhancing relaxivity for clinical applications.

To enhance the performance of Gd(III)-based contrast agents at clinical magnetic field strengths, researchers have pursued several strategies to increase the τ_R value.¹⁵ These include enlarging the molecular structure through conjugation to macromolecules¹⁶ or introducing rigid elements that slow molecular rotation,¹⁷ all while maintaining biocompatibility and ensuring efficient clearance from the body. Another effective strategy involves exploiting non-covalent interactions between appropriately functionalized Gd(III) complexes and slowly rotating substrates. A notable early example is the reversible association between hydrophobically modified Gd-complexes and poly-β-cyclodextrins.^18–20 These supramolecular assemblies – particularly those involving trisubstituted Gd(III) complexes and β-cyclodextrins multimers – form tightly bound adducts that exhibit longitudinal relaxivity values exceeding those of conventional extracellular clinical agents by more than an order of magnitude.²¹ By leveraging similar supramolecular interaction mechanisms, nanocapsules constructed from β-cyclodextrins units linked by disulfide bonds were effectively loaded with [Gd(Bn-AAZTA)(H₂O)₂]⁻ embodying a pendant aromatic group (Bn-AAZTA = 6-amino-6-benzylperhydro-1,4-diazepine-N,N′,N″,N″-tetraacetic acid).²² The robust binding interaction between these chelates and the β-cyclodextrins units facilitated their efficient encapsulation within the nanoparticles during the assembly process. The resulting Gd-loaded nanocapsules exhibited high r₁ values, particularly at high magnetic fields.²² This enhanced relaxivity is attributed to the significantly reduced rotational mobility of the encapsulated chelates and the favourable water permeability through the polymeric shell. Among the many reported examples, notable cases include a binuclear Gd(III) complex based on an AAZTA chelator functionalized with an adamantyl moiety and a [Gd(DOTA)]⁻ derivative incorporating a hydrophobic biphenyl group (H₄DOTA = 2,2′,2″,2‴-(1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrayl)tetraacetic acid).²³ Both complexes interact with the hydrophobic binding sites of human serum albumin. This interaction significantly enhances r₁ while also extending the circulation time in the bloodstream of the Gd(III)-chelates. Additional examples in the literature highlight supramolecular adducts stabilized by electrostatic interactions between anionic Gd(III) complexes and cationic substrates.^24–27 A particularly illustrative case is [Gd(DOTP)]⁵⁻ (H₄DOTP = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrakis(methylenephosphonic acid)), which is derived from the well-known macrocyclic complex [Gd(DOTA)(H₂O)]⁻ by replacing carboxylate groups with phosphonate moieties.²⁷ This substitution imparts a net charge of −5 at near-neutral pH. Unlike [Gd(DOTA)(H₂O)]⁻, which has one coordinated water molecule (q = 1), [Gd(DOTP)]⁵⁻ is non-hydrated (q = 0) and thus lacks a direct IS contribution to relaxivity. However, at clinically relevant magnetic field strengths, the r₁ values of the two complexes are surprisingly similar. This apparent paradox is explained by the presence of structured solvent molecules in the second coordination sphere (SS).²⁸ These water molecules form relatively strong and long-lived hydrogen bonds with the phosphonate groups. When the residence time of these interactions is sufficiently long, the dipolar coupling between the Gd(III) ion and SS water molecules becomes modulated by molecular tumbling, contributing significantly to the observed relaxivity.^29,30 A number of studies have examined the interactions between the highly anionic [Gd(DOTP)]⁵⁻ complex and a variety of positively charged substrates.^24–27 These substrates, ranging in molecular weight and chemical complexity, have notably included functionalized cyclodextrins,²⁶ strategically used as model systems to mimic the positively charged side chains of proteins. In such cases, the observed enhancement in r₁ relaxivity relative to the free chelate has been primarily attributed to one or both of the following mechanisms: an increase in the average number of second-sphere water molecules effectively confined within the resulting supramolecular adducts, and a reduction in the tumbling rate of these second-sphere water molecules due to their entrapment via ion-pair interactions. Importantly, both key parameters, the number and effective correlation time of second-sphere water molecules, can be finely tuned by modifying the substrate or substituting it with alternative compounds. This concept is robustly supported by a recently published study, which describes the fabrication of a nanogel structure resulting from the interaction between chitosan chains and [Gd(DOTP)]⁵⁻ chelates.³¹ The resulting nanoparticles displayed exceptionally high relaxivity values (r₁ = 78.0 mM⁻¹ s⁻¹ at 0.5 T and 298 K), representing an approximate twenty-fold increase over the isolated chelate. Subsequent detailed analysis of the relaxation data revealed the pivotal role of second-sphere water molecules, which participate in robust and prolonged hydrogen bonding interactions with the complex. Building on these insights, the present study undertakes a systematic investigation to clarify the role of second-sphere water molecules in modulating r₁ relaxivity across a series of supramolecular adducts. We began by examining a simple system formed via the interaction between the highly anionic [Gd(DOTP)]⁵⁻ and the cationic tetraazacyclododecane (cyclen; 2) macrocycle (Fig. 1).

Fig. 1 Chemical structure of [Gd(DOTP)]⁵⁻ (1) and the cationic polyamines cyclen (2), octaazacryptand (3) and PEI (4).

This was followed by the analysis of more complex assemblies involving the cryptand 1,4,7,10,13,16,21,24-octaaza bicyclo[8.8.8]hexacosane (octaazacryptand; 3) and low molecular weight polyethyleneimine (PEI; 4) (Fig. 1). To extend this framework, we also synthesized a nanogel incorporating both PEI and [Gd(DOTP)]⁵⁻, enabling a broader assessment of SS contributions in a more constrained environment. All systems, including the small-molecule adducts and the nanogel, were comprehensively characterized using a multidisciplinary approach combining high resolution NMR spectroscopy, field-dependent ¹H relaxometry, and DFT calculations.

Experimental

Chemical and materials

All chemicals were purchased from Merck/Sigma-Aldrich (St Louis, MO, USA), Thermo Fisher Scientific (Waltham, MA, USA) or BLD Pharm (Karlsruhe, Germany) and used without further purification.

Synthetic procedures

Na₅[Gd(DOTP)]. 1.0 g (1.70 mmol) of DOTP (BLD Pharm, CAS. No. 91987-74-5) was dissolved in 20 mL of Milli-Q water in a round-bottom flask, and the pH was adjusted to 7.0 by the addition of 1 M NaOH. In parallel, an aqueous solution of GdCl₃·6H₂O (Sigma Aldrich, 13450-84-5, 632 mg, 1.70 mmol in 5 mL of water) was prepared and gradually added to the DOTP solution under continuous stirring. The pH was maintained at 7.0 by the addition of 1 M NaOH, while the mixture was kept at 60 °C. Near the point of stoichiometric equivalence, a notable precipitate developed, which dissolved again upon raising the pH beyond 8.0. To compensate for a possible excess of the metal ion, a small amount of ligand (0.4%) was added. The solvent was then removed under reduced pressure, yielding a white solid. MS ESI⁻ (m/z) = 702.2 [M]⁻; calculated C₁₄H₂₈GdN₄O₁₂P₄ = 701.4 g mol⁻¹.

Octaazacryptand (3). 1,4,7,10,13,16,21,24-Octaazabicyclo[8.8.8]hexacosane has been prepared in two steps by: (1) condensation of tris(2-aminoethylamine) (“tren”) with glyoxal, with a slight modification of the procedure reported in ref. 32 (the condensation was run at −18 °C); (2) reduction of the intermediate hexaimine by NaBH₄, with a minor modification of the procedure reported in ref. 33 (the product was recrystallized by water and dried in vacuo). ¹H-NMR (CDCl₃, 400.2 MHz) δ = 3.43 (bs, 6H), 2.80 (s, 12H), 2.76 (bt, 12H, J ∼ 5.4 Hz), 2.52 (bt, 12H, J ∼ 5.4 Hz) ppm. ¹³C-NMR (CDCl₃, 100.6 MHz) δ = 51.0 [CH₂], 49.3 [CH₂], 46.4 [CH₂] ppm. ESI-MS: calcd for C₁₈H₄₂N₄: 370.4, found: 371.4 (MH⁺).

[Gd(DOTP)]^5−/4−/polyamine adducts

[Gd(DOTP)]⁵⁻/cyclen adduct. 8.5 mg of cyclen (Sigma Aldrich, 339652-250MG) were added to 1 mL of Gd(DOTP) (1.0 mM). The pH was fixed to 9.0 with HCl solution (0.5 mM).

[Gd(HDOTP)]⁴⁻/octaazacryptand adduct. 18.6 mg of octaazacryptand were added to 1 mL of Gd(DOTP) (1.0 mM) and the pH was corrected to 7.1 with HCl 0.5 M.

[Gd(HDOTP)]⁴⁻/PEI adduct. 2.0 mg of PEI (Thermo Fisher Scientific, 9002-98-6, molecular weight: 2 kDa) were added to 1 mL of a 1.0 mM solution of Gd(DOTP) at pH 7.2.

Synthesis of NG-PEI

NG-PEI was prepared by modifying a procedure already described in the literature.³¹ 11.25 mg of PEI (Thermo Fisher Scientific, 9002-98-6, molecular weight: 2 kDa) was dissolved in 18 mL of acetic acid solution (10 wt%). In a second fask, 11.4 mg of sodium tripolyphosphate (TPP, Alfa Aesar 13440), 8.0 mg of sodium hyaluronate (Hya, Alfa Aesar J66993, molecular weight greater than 1 MDa), and 21 mg of the previously prepared Na₅[Gd(DOTP)] (0.025 mmol) were solubilized in 9.0 mL of ultrapure water. The concentration of [Gd(DOTP)]⁵⁻ was 0.9 mM. After 30 min, the second solution was added dropwise to the first one, and the reaction was stirred for 30 min at 298 K (pH = 3.0), promoting the activation of the gelation process. The obtained white suspension was purified by dialysis using a membrane with a cut-off of 14 kDa in pure water. The purification procedure was repeated for 3 days in order to remove the unreacted compounds. The pH of the NG suspensions changed from 3.0 to 7.5 during the dialysis purification.

Characterization techniques

NMR experiments. ¹H and ¹³C NMR spectra were recorded at 298 K using a Bruker AVANCE III 500 spectrometer equipped with a wide bore 11.7 Tesla magnet and a Bruker BVT 3200 control unit. The addition of a capillary containing D₂O allowed for the lock during the measurement. The metal ion concentration in aqueous solution was determined by ¹H NMR measurements using the Bulk Magnetic Susceptibility (BMS) method, considering a μ_eff = 7.92 B.M. for Gd(III).³⁴ The ¹³C longitudinal relaxation rates (1/T₁) of cyclen, both in the absence and in the presence of [Gd(DOTP)]⁵⁻ complex (pH 9.0), were measured using standard inversion recovery sequences. A sealed capillary with D₂O was inserted in the NMR tube for frequency lock. These values can be plotted linearly as a function of the molar ratio between [Gd(III)] and the total substrate concentration (ρ) (eqn (2), Results and discussion section).²⁵ The paramagnetic contribution (1/T_1C) to the relaxation rate can then be expressed by the Solomon–Bloembergen equation, considering a dipolar interaction between the paramagnetic probe and the substrate (eqn (3)), Results and discussion section).³⁵

Relaxometric characterization. 1/T₁ ¹H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles were recorded on a Fast-Field Cycling (FFC) Stelar SmarTracer Relaxometer from 0.00024 to 0.25 T (0.01–10 MHz proton Larmor Frequencies). This relaxometer operates under computer control with a ±1% uncertainty in the relaxation rate. The proton relaxation in the 20–120 MHz frequency range was investigated with a High Field Relaxometer (Stelar), equipped with a HTS-110 3T Metrology Cryogen-free Superconducting Magnet. The temperature during the measurements was controlled trough a Stelar VTC-91 airflow heater equipped with a copper-constantan thermocouple (uncertainty of ±0.1% °C). The effective temperature at the sample level in the probe head was further monitored with a Fluke 52k/j digital thermometer (Fluke, Zürich, Switzerland). Data were collected using the standard inversion recovery sequence (16 experiments, 3 scans) with a typical 90° pulse width of 3.5 μs, and a reproducibility of the data within ±0.5%. The diamagnetic contribution was measured by collecting ¹H NMRD profiles of the corresponding diamagnetic solution (in absence of the paramagnetic complex), at different temperatures. Relaxivity values (r₁, mM⁻¹ s⁻¹) at different magnetic fields and temperatures were obtained by measuring the longitudinal relaxation rates of the sample solutions and subtracting the corresponding diamagnetic contribution depending on the measurement conditions, and by dividing this value by the mM concentration of Gd(III).

The interaction of [Gd(DOTP)]⁵⁻ complex with the different substrates was studied by relaxometric titrations. In the case of direct titration, the longitudinal relaxation rate at 32 MHz and 298 K of a 1.0 mM solution of the complex was measured as a function of increasing additions of substrate. The pH value was maintained at the desired value by small addiction of HCl 1 M. The so obtained titration curve was then fitted following the procedures reported in the literature.^13,36

For the investigation of the [Gd(HDOTP)]⁴⁻–PEI interaction, a reverse titration was also performed. In this experiment, a solution containing a fixed concentration of PEI (0.625 mM) was prepared and increasing amounts of the [Gd(HDOTP)]⁴⁻ complex were added. After each incremental addition of the complex, the longitudinal relaxation rate was measured at 32 MHz and 298 K. The pH was kept constant by adding small aliquots of 1 M HCl. Data from reverse titration were plotted in the form of a Scatchard plot according to eqn (1):^13,37

where r is the molar ratio between the concentration of the complex in the adduct and the total amount of substrate, [GdL]_Free is the concentration of the free complex, K is the binding constant and n is the number of equivalent binding sites of the substrate.

DLS and Z-potential. Dynamic light scattering and Z-potential experiments were carried out on a small amount of solution at 298 K by using a Malvern Zetasizer Nano ZS operating in a particle size range from 0.6 nm to 6 mm and equipped with a He–Ne laser with λ = 633 nm.

Computational analysis. All calculations were performed at the DFT level using the GAUSSIAN 16 (Rev. C.01) quantum-chemistry package,³⁸ and the hybrid PBE0 functional.³⁹ The Grimme D3 dispersion correction was also used.⁴⁰ For interaction energies, geometry optimizations and vibrational frequency analysis (no imaginary frequencies were found), the aug-pcseg-1 basis set of Jensen (superior to the aug-cc-pVDZ) of double-ζ-quality and optimized for DFT calculations,⁴¹ was used for all atoms except for gadolinium. For the latter, the def2-SV(P) basis set was employed together with the corresponding relativistically contracted effective core potential, which replaces 28 core electrons on the gadolinium center.⁴² The counterpoise correction was applied when interaction energies were computed (see the “Interaction energies” section of the SI for numerical details).⁴³ To stabilize the ionic electronic structures, geometry optimizations were performed using the default optimization criteria in the presence of a continuum aqueous solvent, defined via the scrf command in GAUSSIAN.⁴⁴ Electron densities were used as the starting point for further analysis including NCI,⁴⁵ and employing the Multiwfn (version 3.8) software.⁴⁶ For the NCI and Molecular Electrostatic Potential (MEP) analysis a grid with an ultra-high resolution of 5 pm was employed. The VMD (version 1.9.4) software was used for visualization purposes.⁴⁷

Results and discussion

Relaxometric properties of [Gd(DOTP)]⁵⁻

The key properties of this complex were first investigated nearly thirty years ago.²⁸ These earlier findings are briefly revisited here to provide context for the new data concerning the formation of host–guest adducts. The relaxivity of a paramagnetic complex does not remain constant but rather exhibits a characteristic dependence on the magnetic field strength. This behaviour is specific to each metal complex and reflects how its efficiency in enhancing water proton relaxation varies with the applied magnetic field (or, equivalently, with the proton Larmor frequency). The variation of relaxivity with magnetic field strength, typically explored in the 0–3 T range, is described by Nuclear Magnetic Relaxation Dispersion (NMRD) profiles.¹³

These curves are generated using specialized instruments known as fast field-cycling relaxometers. The NMRD profile of [Gd(DOTP)]⁵⁻ displays a characteristic shape: a low-field plateau (0–2 MHz) where r₁ remains nearly constant, followed by a sharp dispersion near 4 MHz, and finally a second plateau emerging beyond ∼10 MHz. As shown in Fig. 2, this profile can be fully interpreted in terms of the two dominant relaxation mechanisms: outer-sphere (OS) and second sphere (SS) interactions. The SS contribution, in particular, plays a crucial role.⁴⁸ It is governed by three key factors: the number of water molecules hydrogen-bonded to the phosphonate groups (q^ss), their Gd–H distance from the Gd(III) centre (^ssr_Gd–H), and their residence lifetime within the second coordination sphere (^ssτ_M). In this case, the best fit of the data yields a set of parameters that accurately reproduces the experimental results. The second-sphere contribution corresponds to that expected from four second-sphere water molecules, with a Gd–H distance of 3.5 Å, a residence lifetime of 1 ns, and a global rotational correlation time (^ssτ_R) of 40 ps.

Fig. 2 The ¹H NMRD profile of [Gd(DOTP)]⁵⁻ recorded at 298 K and pH = 7.5. The lower dotted curves represent the calculated outer- (blue) and second sphere (green) contributions. The red dashed curve at the top represents the NMRD profile of [Gd(DOTA)(H₂O)]⁻, under the same experimental conditions for comparison.

Adducts of [Gd(DOTP)]⁵⁻ with polyamines

Since the relaxivity contribution arising from the SS mechanism depends on the ^ssτ_R value of the SS water molecules, an enhancement of relaxivity can be pursued through the formation of host–guest interactions or ion pairs between the anionic complex and suitable cations. The resulting increase in molecular size and the promotion of a more extensive hydrogen-bond network at the anion–cation interface are expected to lead to a significant increase in r₁. For this reason, we investigated the influence of forming larger and more structurally complex ion pairs on the relaxivity of [Gd(DOTP)]⁵⁻. By increasing the overall size and fine-tuning the ionic interactions within these supramolecular assemblies, our goal was to modulate key parameters governing relaxivity, namely, rotational dynamics, hydration state, and intermolecular interactions. To this end, we selected both cyclic and acyclic polyamines, which are positively charged within the pH range of 7.0–9.0, to interact with the negatively charged sites of [Gd(DOTP)]⁵⁻ located on the upper square plane of its antiprismatic structure. Specifically, we examined interactions with cyclen (2), octaazacryptand (3), and low molecular weight polyethyleneimines (4; Fig. 1). The relaxivity enhancement exhibited by the resulting adducts is expected to display a pH-dependent trend, governed by the balance between the increasing anionic character of the metal complex and the progressively diminishing positive charge of the cation as the pH rises.

For this reason, the initial investigation focused on measuring the longitudinal relaxation rate (R₁) as a function of pH for a dilute solution of complex 1 in the presence of an excess of polyamine, at 32 MHz and 298 K. The relaxivity of a 1.0 mM [Gd(DOTP)]⁵⁻ solution (4.3 mM⁻¹ s⁻¹ at 32 MHz and 298 K) increases significantly in the presence of a large excess of cyclen substrate (50 mM), exhibiting a pronounced pH dependence. Relaxivity gradually increases from about pH 4.5, reaching a maximum around pH 9.0, and then decreases again at higher pH values, though it never returns to the initial value corresponding to the free complex. This trend reflects the pH dependence of the supramolecular interaction, governed by the protonation state and charge balance between the negatively charged Gd-chelate guest and the positively charged host. Around pH 9.0, the optimal balance is achieved between the diprotonated form of the cyclen²⁵ and the pentaanionic form of the Gd(III) complex,⁴⁹ as shown in Fig. 3. With a large excess of octaazacryptand (50 mM) and an equimolar amount of PEI (1 mM), the highest r₁ enhancement is observed at neutral pH (Fig. 3). In the case of the octaazacryptand 3 (50 mM), the behaviour is quite different. The variation of relaxivity with pH displays a pronounced bell-shaped profile, with a distinct maximum around pH 7.0. Under these conditions, the polyamine 3 exists predominantly in its triprotonated form,⁵⁰ while the Gd(III) complex is mainly tetra-anionic, resulting in an almost ideal charge balance between the two species. The increase in r₁ relative to the free complex is remarkable, nearly a fivefold enhancement, and significantly greater than that observed in the previous case (Fig. 3). Finally, the interaction with 4 (1 mM) results in an additional increase in relaxivity. The observed pH dependence closely resembles that measured with 3, showing a maximum near the point of neutrality. The maximum relaxivity value corresponds to an overall increase of approximately six-fold compared to that of the free complex. This enhancement is entirely analogous to that measured in the case of monohydrated complexes anchored to nanoscale substrates. This result clearly indicates the significant contribution of the SS relaxation mechanism to the overall relaxivity, demonstrating a contribution fully comparable to that associated with a single coordinated water molecule (q = 1) to the Gd(III) ion.

Fig. 3 Relaxivity dependence on pH for an aqueous solution of [Gd(DOTP)]⁵⁻ (1.0 mM) in the presence of 2 (, 50.0 mM), 3 (, 50.0 mM), and 4 (, 1.0 mM) measured at 298 K and 32 MHz.

¹H NMR relaxometric titrations

To investigate the formation of ion pairs between [Gd(DOTP)]⁵⁻ and the polyamines, and to determine the association constant of the resulting supramolecular adducts, we performed relaxometric titrations. These experiments involved monitoring the changes in the longitudinal relaxation rate of a dilute Gd(III) complex solution as the concentration of the cationic substrate was gradually increased, at a fixed frequency of 32 MHz and a temperature of 298 K. The measurements were conducted at the pH corresponding to the maximum relaxivity (Fig. 3). Data analysis yielded the binding constant (K), the average number of metal complexes per substrate unit (n) in the supramolecular adduct, and the relaxivity of the bound complex (r₁^b). As expected, R₁ increases markedly upon the progressive addition of the substrate, then gradually levels off to a plateau value depending on the relaxivity of the resulting supramolecular adduct. In the case of cyclen, the shape of the binding curve deviates from that expected for a simple monoexponential process. A much better fit is obtained by assuming a sequential binding model in which a 1 : 1 adduct, characterized by the association constant K₁ (K₁ = 82.8 ± 1.1 M⁻¹), forms initially and predominates at low substrate concentrations. At higher cyclen concentrations, a second equilibrium leading to the formation of a 1 : 2 adduct (constant K₂ = 40.5 ± 1.0 M⁻¹) becomes dominant.

This behaviour is reminiscent of that previously observed for ion-pair formation between oppositely charged complexes.³⁶ The relaxivity of the first adduct is 7.3 mM⁻¹ s⁻¹, while that of the second increases to 9.0 mM⁻¹ s⁻¹. The final value of n equals 0.5, indicating that the resulting adduct consists of one [Gd(DOTP)]⁵⁻ complex interacting with two units of the cationic species 2 (Fig. 4A and Table 1).

Fig. 4 R₁ dependence of [Gd(DOTP)]⁵⁻ (1.0 mM) on increasing concentration of the substrates: (A) cyclen (; pH 9.0) and octaazacryptand (; pH 7.1); (B) PEI (; pH 7.2) recorded at 298 K and 32 MHz. Solid lines represent the fit of the data, with parameters reported in Table 1.

Table 1 Best-fit binding parameters resulting from the ¹H NMR relaxometric titrations at 32 MHz and 298 K of Gd(III)-complex 1 with polyamines 2–4

	2	3	4
a β2 (M^−2).b β1 (M^−1).c Fixed during the analysis.
Binding constant K	3.3 (±0.2) × 10^3 ^a	111 ± 5^b	1.8 (±0.2) × 10^4 ^b
n	0.5^c	1^c	6.4 ± 0.1
r1^b/mM^−1 s^−1	9.0 ± 0.3	25.6 ± 0.3	27.0 ± 0.1

---

The titration curve of the [Gd(HDOTP)]⁴⁻ solution with substrate 3 differs from the previous one both in its steeper initial slope and in the plateau R₁ value, which is significantly higher – indicating a notably larger r₁^b value. The binding constant K is also substantially greater than K₁ in the case of cyclen. This points to a stronger degree of interaction, as clearly shown by the trend of the curves in Fig. 4A and as one would logically expect. The much higher value of r₁^b, on the other hand, suggests the presence of an optimized host–guest interaction geometry and possibly the formation of larger aggregates. In this case, the data are well fitted by a 1 : 1 binding model between the anionic and cationic species, consistent with their relative sizes and overall charge balance.

The titration curve with compound 4 reveals a significantly stronger interaction than that observed with the previous polyamines. The flexibility of the cationic polymer chain likely allows it to better adapt to the anionic complex, forming more compact supramolecular adducts. Data analysis indicates an average of six equivalent binding sites (n = 6.4) on the polycation, consistent with the formation of a complex and extended supramolecular structure. The binding constant (K = 1.8 (±0.2) × 10⁴ M⁻¹) is about two orders of magnitude higher than in the earlier cases and comparable to that reported for interactions with amine-functionalized cyclodextrins.²⁶ A Scatchard plot, obtained by titrating a fixed-concentration solution of 4 (0.625 mM) with complex 1, reveals both strong primary and weaker secondary binding interactions, highlighting the intricate nature of the association between these two species (Fig. S1). The resulting adduct exhibits a relaxivity of 27.0 mM⁻¹ s⁻¹, slightly higher than that of the host–guest complex with compound 3.

DFT calculations

In the case of the interaction between [Gd(DOTP)]^5−/4− and the cationic polyamines 2 and 3, the best fit between the experimental data and the binding parameters is consistent with the formation of 1 : 2 and 1 : 1 adducts, respectively. To verify the plausibility and reliability of this conclusion, we performed DFT calculations. Geometry optimization of the isolated [Gd(DOTP)]⁵⁻ complex proved unfeasible, most likely because of its very high negative charge. Even at the earliest stages of the optimization, the system undergoes proton loss, bond cleavage, and extensive fragmentation. Successful geometry optimization was achieved only in the presence of appropriate counter-cations, such as four protons, yielding the [GdH₄(DOTP)]⁻ complex. In this case, the optimized structure closely resembles that obtained for the complex interacting with the substrates. For the cyclen system, the results indicate a significantly greater energetic stability for the 1 : 2 adduct compared to the 1 : 1 species, when four hydration water molecules are included, each bridging two phosphonate groups of the complex (Fig. S2). The choice of including four explicit water molecules, on top of the implicit solvation model is motivated by the fact that it increases the reliability of our model, approaching what is likely to be found in solution.²⁸ This enhanced stability of the 1 : 2 adduct is maintained even in the presence of two protonated cyclen cations (see SI for details). In such highly charged systems, the dominant interaction mode arises from electrostatic forces. The molecular electrostatic potential (MEP) map, a powerful tool to visualize these interactions, highlights distinct regions of positive and negative charge density corresponding to the main interaction sites (Fig. 5A). As expected, positively charged regions are located primarily on the upper portions of the cations, while negatively charged regions are concentrated on the upper part of the anion, ensuring overall charge balance. The areas of negative charge density are mainly associated with the phosphate groups, hydration water molecules, and unprotonated amine groups within the cations. Overall, the geometry of the [Gd(DOTP)]⁵⁻ anions does not change when complexed with 2 or 3, nonetheless, due to the higher positive charge of 3 compared to a single 2 cation, we observe higher (more positive and more negative) electrostatic potential areas in the complex of [Gd(HDOTP)]⁴⁻ with 3. In addition to the MEP analysis, an NCI (Non-Covalent Interaction) analysis was performed to further characterize the interaction pattern (Fig. S3).⁵¹ The NCI results clearly reveal hydrogen-bonding networks among the water molecules and phosphate groups, as well as a hydrogen bond between a phosphate group and a protonated amine on one of the cyclen molecules.

Fig. 5 Molecular electrostatic potential ESP (PBE0 aug-pcseg1 D3), plotted on the 0.001 au contour of the electron density, of the supramolecular complexes of complex 1 with: (A) two cyclen units, and (B) octaazacryptand. Colour code: grey = C, white = H, red = O, blue = N, orange = P, light blue = Gd.

This combined computational evidence strongly supports the formation and enhanced stability of the 1 : 2 adduct, consistent with the experimental findings. In the energy-minimized structure of the adduct, DFT calculations estimate a minimum Gd–C distance of 5.76 Å. This distance value can be independently verified by ¹³C NMR relaxation measurements.²⁵ In this approach, Gd–C distances (r_C) are derived by monitoring the changes in the ¹³C T₁ relaxation times of the equivalent carbon nuclei in cyclen (δ = 43.1 ppm) as a function of increasing [Gd(DOTP)]⁵⁻ concentration in aqueous solution (eqn (2), Fig. 6).

1/T₁ = ρ(m/T_1C) + 1/T_1d (2)

Fig. 6 ¹³C NMR relaxation rate (1/T₁) of cyclen as a function of [Gd³⁺]/[cyclen] molar ratio (pH 9.0, D₂O, 298 K, 125 MHz).

Here, 1/T₁ and 1/T_1d denote the observed relaxation rates in the presence and absence of the paramagnetic complex, respectively; m represents the number of substrate molecules bound per paramagnetic centre and ρ is the molar ratio of [Gd(DOTP)]⁵⁻ to 2. The paramagnetic contribution to the ¹³C longitudinal relaxation rates (T_1C) of compound 2 can be analysed using the Solomon–Bloembergen equation, which describes the nuclear–electron dipolar interaction (eqn (3)):^25,35

where S is the electron spin for Gd(III), g is the electron factor, β is the Bohr magneton, γ is the gyromagnetic ratio and τ_C corresponds to the overall correlation time, which at the experimental magnetic field strength of 11.7 T can be reasonably approximated to τ_R.

The model also assumes that relaxation occurs under a fast-exchange regime (T_1C ≫ τ_M). To obtain an accurate evaluation of the distance, it is essential to have a reliable estimate of τ_R. At high magnetic fields, it is well established that the relaxivity values of small Gd(III) complexes exhibit an approximately linear dependence on molecular weight. Assuming an adduct composed of one [Gd(DOTP)]⁵⁻ molecule and two cyclen molecules, as indicated by both NMR titration and DFT calculations, the corresponding value of τ_R can be derived from the relaxivity versus molecular weight plot (τ_R = 148 ps; Fig. S4). From the 1/T_1C value obtained from the slope of the line in Fig. 5, the Gd–C distance can finally be calculated as r_C = 5.49 Å ± 0.2, which agrees remarkably well with the DFT-derived value (5.76 Å), thus providing strong validation for the proposed binding model. Regarding the [Gd(HDOTP)]⁴⁻/3 ion pair, the titration data are consistent with a 1 : 1 binding model. Based on the observed behaviour, we can hypothesize that the cavity of polyamine 3 is geometrically well suited to accommodate the upper plane of the square antiprismatic structure in which the negative charges of [Gd(HDOTP)]⁴⁻ are distributed. This hypothesis is also strongly supported by DFT calculations (Fig. 5B). As in the previous case, the dominant binding mode arises primarily from electrostatic interactions, clearly illustrated by the MEP map in Fig. 5B. Similar considerations to those made for the cyclen complex apply here, since the final adduct exhibits a comparable electrostatic character. The NCI analysis of this adduct (Fig. S5) further reveals an intricate network of hydrogen bonds and van der Waals interactions involving [Gd(HDOTP)]⁴⁻, water molecules, and the cationic species 3.

¹H 1/T₁ NMRD profiles

Additional insight into the nature of the species present in solution, and into the mechanism responsible for the observed relaxivity enhancement, can be gained from the measurement and analysis of ¹H NMRD profiles of the adducts over a broad frequency range and at different temperatures. As discussed above, a measurable second-sphere relaxation contribution requires that the hydrogen-bonded water molecules have residence lifetimes longer than the translational diffusion correlation time (τ_D). This condition ensures that the water molecules remain near the paramagnetic centre long enough to undergo efficient dipolar interactions, that is, to experience molecular reorientation. Such behaviour occurs only when the water molecules are stabilized through strong hydrogen bonds within roughly 4 Å of the Gd(III) ion. In the systems examined here, these water molecules are likely to be positioned between the anionic complex and the protonated polyamines, forming a network of bridging interactions that enhances relaxivity.

The ¹H NMRD profile of [Gd(DOTP)]⁵⁻ was discussed previously and analysed using the Solomon–Bloembergen–Morgan^52–54 and Freed equations⁵⁵ to account for the second- and outer-sphere contributions to relaxation. The key best-fit parameters are reported in Table 2. Regarding the outer-sphere contribution, in this and all subsequent analyses the distance of closest approach (a_Gd–H) between the paramagnetic centre and the freely diffusing water molecules, as well as the relative diffusion coefficient of solute and solvent (D), were fixed to their standard values of 4.0 Å and 2.24 × 10⁻⁵ cm² s⁻¹, respectively. The NMRD profile of the [Gd(DOTP)]⁵⁻/2 adduct (Fig. 7, green) shows clear differences in both shape and amplitude compared to the free complex. Relaxivity values are approximately twice as high across most of the investigated frequency range. Moreover, in the intermediate-to-high field region (>10 MHz), the profile exhibits the onset of a broad shoulder, a feature typically associated with a slowing of the molecular reorientation rate, corresponding to rotational correlation times (τ_R) exceeding about 100 ps. This behaviour suggests that the electrostatic anion–cation interaction involves several water molecules located in the interfacial region, which become strongly bound and therefore share a rotational correlation time comparable to that of the entire molecular assembly. Indeed, the experimental data are well reproduced by assuming the presence of four SS water molecules characterized by ^SSτ_R = 150 ps, in perfect agreement with the estimated value from the r₁ vs. M.W. plot (Fig. S4), at 3.5 Å from Gd(III) and a mean residence lifetime of 1 ns.

Fig. 7 Comparison of ¹H NMRD profiles of [Gd(DOTP)]⁵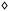⁻ () and its adducts with cyclen (), octaazacryptand () and PEI () at 298 K. Solid lines represent the fit of the data, with parameters reported in Table 2.

Table 2 Best-fit parameters (298 K) obtained from the analysis of ¹H NMRD profiles of [Gd(DOTP)]⁵⁻ (1) and its adducts with polyamines 2–4

	[Gd(DOTP)]^5−	1/2	1/3	1/4
a Fixed during the analysis.
^SSτRL/ps	—	—	135 ± 10	202 ± 15
^SSτRG/ns	0.04 ± 0.002	0.150 ± 0.003	3.5 ± 0.6	6.0 ± 0.8
S^2	—	—	0.16 ± 0.01	0.22 ± 0.01
^SSτM/ns	1.0 ± 0.1	1.0 ± 0.2	6.0 ± 0.9	1.9 ± 0.2
q^SS	4^a	3.9 ± 0.1	4.0 ± 0.1	4.1 ± 0.2
^SSrGd–H/Å	3.5^a	3.5^a	3.5^a	3.5^a

---

Naturally, the parameters q^SS, ^SSτ_R, and ^SSr_Gd–H are strongly interdependent, so there is no unique set of fitting values consistent with the NMRD profile. Rather, this analysis provides plausible estimates of the key parameters, allowing the role of the second-sphere mechanism in the observed relaxivity enhancement to be properly appreciated. Moreover, the possible contribution of a prototropic exchange mechanism involving the protonated nitrogen atoms of cyclen cannot be entirely ruled out, as it could be catalysed under the basic experimental conditions (pH = 9.0). However, based on the estimated Gd–C distance (5.49–5.76 Å) in the adduct, it appears unlikely that the protons of the –NH groups are located sufficiently close (<∼4 Å) to the metal centre to have a significant impact on relaxation. The NMRD profiles of the adducts with 3 and 4 (Fig. 7, blue and orange respectively) are quite similar to each other and display much more pronounced changes compared to the previous case. The most striking feature is the presence of a relaxivity peak centred around 30 MHz, with values that decrease rapidly at higher frequencies. Both adducts exhibit a maximum r₁ of approximately 26 mM⁻¹ s⁻¹ at 30 MHz and 298 K, nearly six times higher than that of the free complex. This behaviour is typical of nanosized systems, where the overall size and mass substantially slow down molecular tumbling, effectively increasing τ_R. While such behaviour is expected for the [Gd(HDOTP)]⁴⁻/4 adducts, it is somewhat surprising in the case of [Gd(HDOTP)]⁴⁻/3. In the latter, the shape of the NMRD profile suggest the formation of larger aggregates in solution, despite maintaining a 1 : 1 host–guest stoichiometry. During the fitting procedure, it was necessary to account for the rotational dynamics of the second-sphere water molecules involved in the supramolecular adduct by applying the Lipari–Szabo model-free approach.^56,57 This formalism allows one to distinguish between a local rotational correlation time ^SSτ_RL, which is faster, and the overall molecular reorientation time ^SSτ_RG, with the degree of coupling between these two motions described by the order parameter S² (0 < S² < 1).^56,57 In the fitting procedure, the value of ^SSτ_RG was found to be 3.5 and 6 ns for the interaction of [Gd(HDOTP)]⁴⁻ with 3 and 4 respectively, in good agreement with their hydrodynamic diameters of approximately 1–1.5 nm, as determined by DLS analysis (Fig. S6), and consistent with values reported for paramagnetic micelles of comparable size.⁵⁸ The temperature dependence of the NMRD profiles indicates that all systems operate in the fast-exchange regime; therefore, the water residence time does not represent a limiting factor for relaxivity (Fig. S7). Assuming four SS water molecules ^SSq = 4, but allowing their number to vary during fitting, the best agreement with the experimental data was obtained with a ^SSτ_RL value of 135 ps and 202 ps for the adducts with 3 and 4, respectively (Table 2). The corresponding order parameters are relatively small (S² = 0.16 for 3 and 0.22 for 4), consistent with a weak coupling between the global motion of the adduct and the local reorientation of the SS water molecules. Furthermore, an increase in ^SSτ_M is observed, from 1 ns for [Gd(DOTP)]⁵⁻/2 to 6.0 ns and 1.9 ns for [Gd(HDOTP)]⁴⁻/3 and [Gd(HDOTP)]⁴⁻/4, respectively. Taken together, these results indicate that, moving from the supramolecular adducts of [Gd(DOTP)]⁵⁻ with 2 to those with 3 and 4, stronger interactions, larger adduct size, and greater compactness are achieved. These factors collectively slow down the rotational dynamics, increase rotational anisotropy, and ultimately enhance relaxation efficiency.

Nanogel based on [Gd(DOTP)]⁵⁻

Electrostatic interactions with polycations and the presence of structured water molecules near the paramagnetic centre also occur in the case of paramagnetic metal ion complexes encapsulated within nanosystems, particularly in physically crosslinked nanogels (NGs). The formation of chitosan-based nanogels incorporating [Gd(DOTP)]⁵⁻ has recently been the subject of extensive investigation.³¹

To further explore the relaxivity enhancement resulting from the confinement of this q = 0 complex within similar systems, we developed a highly organized nanosystem through ionotropic gelation of PEI with sodium tripolyphosphate (TPP) and sodium hyaluronate, in the presence of [Gd(DOTP)]⁵⁻, adapting a synthetic procedure previously reported in the literature.³¹ Details regarding reagent quantities and experimental conditions are provided in the Experimental section. The resulting nanogel (NG/[Gd(DOTP)]⁵⁻) was purified by dialysis to remove unreacted species and any unincorporated complex. The water content retained within the matrix, determined by a gravimetric method,⁵⁹ exceeds 90%. The sample contains 31.4 mg of Gd(III) per gram of material. The aqueous suspension at physiological pH (7.4) is stable and homogeneous, showing no sedimentation or nanoparticle aggregation. Dynamic light scattering (DLS) analysis of the aqueous suspension ([Gd(III)] = 0.36 mM) reveals a hydrodynamic diameter centred at 2 nm, with a polydispersity index (PDI) of 0.04, indicating a highly uniform particle size distribution (Fig. 8A). At 32 MHz and 298 K, the r₁ relaxivity of NG/[Gd(DOTP)]⁵⁻ reaches the remarkable value of 42.4 mM⁻¹ s⁻¹, which is approximately 60% higher than that of the supramolecular adduct [Gd(HDOTP)]⁴⁻/4 and ten times greater than that of the free metal complex. It is worth noting that such a relaxivity value is fully comparable to, or even exceeds, that observed for Gd(III) complexes covalently anchored to macromolecular substrates. More detailed information can be obtained from the analysis of the ¹H NMRD profiles, recorded at three different temperatures (283, 298, and 310 K, Fig. 8B). The data show that the relaxivity values decrease with increasing temperature over the entire frequency range investigated (0.01–120 MHz), a typical feature of systems operating under a fast-exchange regime. In the case of these NGs, the exchange processes involve both the hydrogen-bonded water molecules associated with the complex and those residing within the nanoparticle matrix, as well as the exchange between internal and external water molecules of the nanogel. Data analysis yields a water residence lifetime on the order of nanoseconds (^SSτ_M = 2.9 ns), which is of the same magnitude as that estimated for the supramolecular adducts previously discussed (Tables 3 and S1). From a qualitative standpoint, the relaxometric profiles exhibit a shape closely resembling that observed for the [Gd(HDOTP)]⁴⁻ adducts with polyamines 3 and 4, whose main feature is a distinct relaxivity peak centred around 30 MHz.

Fig. 8 (A) DLS analysis of NG/[Gd(DOTP)]⁵⁻; (B) ¹H NMRD profiles of NG/[Gd(DOTP)]⁵⁻ recorded at pH 7.4 and at different temperatures ( = 283 K, = 298 K, = 310 K) ([Gd(III)] = 0.36 mM). The ¹H NMRD of [Gd(DOTP)]⁵⁻ at 298 K () is reported for comparison.

Table 3 Best-fit parameters (298 K) obtained from the analysis of ¹H NMRD profiles of NG/[Gd(DOTP)]⁵⁻

	[Gd(DOTP)]^5−	NG/[Gd(DOTP)]^5−
a Fixed during the analysis.
τRL^SS/ps	—	610 ± 34
τRG^SS /ns	0.040 ± 0.002	10.0 ± 0.9
S^2	—	0.30 ± 0.02
τM^SS/ns	1.0 ± 0.1	2.9 ± 1.7
q^SS	4^a	3.1 ± 0.3
^SSrGd–H/Å	3.5^a	3.5^a

---

As noted previously, this feature indicates a significant restriction in rotational dynamics. Such behaviour is entirely consistent with that reported for other paramagnetic nanogels described in the literature^31,59–61 and, more generally, for Gd(III)-based nanoscale systems.¹⁵ As in the previous cases, the quantitative analysis of the relaxometric profiles was carried out using the model-free Lipari–Szabo approach to describe the rotational dynamics. The best-fit analysis yields the set of parameters reported in Table 3, highlighting significantly longer values for both the global (^SSτ_RG = 10 ns) and local (^SSτ_RL = 0.61 ns) rotational correlation times. The ^SSτ_RG value, approximately twice that of the [Gd(HDOTP)]⁴⁻/4 adduct, reflects the larger molecular dimensions of the nanogel system, whereas the ^SSτ_RL value indicates a marked restriction of local rotational motion for the SS water molecules. Using the same parameters for the outer-sphere contribution and the average Gd–H distance as before, the number of SS water molecules responsible for the observed relaxivity enhancement was found to be 3.1, in excellent agreement with that determined for chitosan-based nanogels.³¹ This result further underscores the crucial role of SS water molecules, suggesting that the dominant factor governing relaxivity is not merely their number, but rather the degree of restriction of their rotational mobility within the polymeric matrix.

Conclusions

The ¹H NMR relaxometric data collected for aqueous solutions of [Gd(DOTP)]⁵⁻ in the presence of various polyamines, as well as when confined within the polymeric matrix of a nanogel, demonstrate the remarkable and somewhat unexpected degree of relaxivity enhancement that can be achieved even when the Gd(III) ion lacks inner-sphere water molecules in its coordination environment. The key lies in the rational design of the ligand, which must feature efficient hydrogen-bond acceptor groups capable of engaging a sufficient number of water molecules in strong interactions at short distances (typically < ∼4 Å). In such cases, the second-sphere relaxation mechanism plays a dominant role. This contribution can be effectively optimized not merely by increasing the number of second-sphere water molecules or reducing their distance from the metal centre, but more importantly by restricting their local rotational mobility. This principle emerges clearly from the study of supramolecular adducts formed between [Gd(DOTP)]⁵⁻ and cyclen, octaazacryptand, and low-molecular-weight polyethyleneimines, which collectively emphasize the pivotal role of elongated rotational correlation times in driving the observed relaxivity enhancement. These findings are further supported by the relaxometric behaviour of nanogels incorporating [Gd(DOTP)]⁵⁻, offering deeper insight into the mechanisms underlying their unusually high relaxivity values. In conclusion, these results demonstrate the possibility of achieving more than a tenfold increase in relaxivity, and consequently in in vitro efficacy, approaching the theoretical maximum, even for complexes that lack directly coordinated inner-sphere water molecules. To this end, it is essential to confine water molecules sufficiently close to the metal centre, foster strong hydrogen-bonding interactions, and limit molecular tumbling. Additionally, the occurrence of prototropic exchange processes could further enhance relaxation efficiency. The interactions between [Gd(DOTP)]⁵⁻ and diverse cationic substrates highlight the potential to achieve high relaxivity while preserving maximal kinetic inertness, effectively shielding the metal centre from direct water coordination. Importantly, this effect is not limited to Gd(III) complexes but may also be extended to other paramagnetic metal ions, such as Fe(III). Finally, non-covalent supramolecular interactions offer intrinsic reversibility and adaptability, enabling the possible design of a wide variety of nanostructures capable of encapsulating MRI probes while permitting their gradual degradation and renal clearance. However, the dynamic nature of these interactions generally results in lower stability of the nanosystems compared to covalently bound systems. Therefore, further efforts are needed to enhance their robustness under physiological conditions.

Author contributions

M. B., F. C. and M. R. designed the experimental method. G. B. G. performed the chemical synthesis. M. R. performed the experiments. M. S. realized the computational analysis. F. C. and M. B analysed the results. The manuscript was written by F. C, M. B and M. S. and revised by all authors.

Conflicts of interest

The authors declare no competing interests.

Data availability

The authors declare that all data in this work are available within the article and supplementary information (SI) files and from the corresponding author on request.

Supplementary information: the results include Scatchard plot of the [Gd(DOTP)]⁵⁻ and PEI interaction, molecular electrostatic potential, isosurface maps, computed coordinates, DLS and NMRD profiles of the adducts. See DOI: https://doi.org/10.1039/d5dt02799c.

Acknowledgements

This publication is part of the project NODES which has received funding from the MUR – M4C2 1.5 of PNRR with grant agreement no. ECS00000036.

References

1. J. M. Lehn, Eur. Rev., 2009, 17, 263–280.
2. J. T. C. Cox, J. Hale, P. Molinska and J. E. M. Lewis, Chem. Soc. Rev., 2024, 53, 10380–10408.
3. E. Miguel-Casañ, G. R. F. Orton, D. E. Schier and N. R. Champness, Adv. Mater., 2025, 2414509–2414528.
4. C.-L. Liu, G. Kalandia, J. N. H. Reek and T. N. Parac-Vogt, Chem. – Eur. J., 2025, 31, e202403856–e202403863.
5. M. T. Campos, L. S. Pires, F. D. Magalhães, M. J. Oliveira and A. M. Pinto, Nanoscale, 2025, 17, 5526–5570.
6. I. Aprahamian, ACS Cent. Sci., 2020, 6, 347–358.
7. J. W. Fredy, J. Scelle, B. Hasenknopf, E. Toth, G. Vives and C. S. Bonnet, Inorg. Chim. Acta, 2026, 589, 122947–122956.
8. Y. A. Mondjinou, B. P. Loren, C. J. Collins, S.-H. Hyun, A. Demoret, J. Skulsky, C. Chaplain, V. Badwaik and D. H. Thompson, Bioconjugate Chem., 2018, 29, 3550–3560.
9. Z. Zhou, Y. Mondjinou, S.-H. Hyun, A. Kulkarni, Z.-R. Lu and D. H. Thompson, ACS Appl. Mater. Interfaces, 2015, 7, 22272–22276.
10. J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chem. Rev., 2019, 119, 957–1057.
11. M. Le Fur and P. Caravan, Metallomics, 2019, 11, 240–254.
12. H. Li and T. J. Meade, J. Am. Chem. Soc., 2019, 141, 17025–17041.
13. L. Helm, J. R. Morrow, C. J. Bond, F. Carniato, M. Botta, M. Braun, Z. Baranyai, R. Pujales-Paradela, M. Regueiro-Figueroa, D. Esteban-Gómez, C. Platas-Iglesias and T. J. Scholl, in New Developments in NMR, ed. V. C. Pierre and M. J. Allen, Royal Society of Chemistry, 2017, pp. 121–242.
14. S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Mol. Phys., 2019, 117, 898–909.
15. M. Botta and L. Tei, Eur. J. Inorg. Chem., 2012, 1945–1960.
16. M. Ricci, F. Carniato, L. Tei, S. Camorali, G. Ferrauto and M. Botta, Eur. J. Inorg. Chem., 2024, 27, e202300675–e202300684.
17. K. B. Maier, L. N. Rust, F. Carniato, M. Botta and M. Woods, Chem. Commun., 2024, 60, 2898–2901.
18. S. Aime, M. Botta, L. Frullano, S. G. Crich, G. B. Giovenzana, R. Pagliarin, G. Palmisano and M. Sisti, Chem. – Eur. J., 1999, 5, 1253–1260.
19. E. Battistini, E. Gianolio, R. Gref, P. Couvreur, S. Fuzerova, M. Othman, S. Aime, B. Badet and P. Durand, Chem. – Eur. J., 2008, 14, 4551–4561.
20. S. Aime, M. Botta, M. Panero, M. Grandi and F. Uggeri, Magn. Reson. Chem., 1991, 29, 923–927.
21. S. Aime, M. Botta, F. Fedeli, E. Gianolio, E. Terreno and P. Anelli, Chem. – Eur. J., 2001, 7, 5261–5269.
22. J. Martinelli, M. Fekete, L. Tei and M. Botta, Chem. Commun., 2011, 47, 3144–3146.
23. G. Gambino, S. De Pinto, L. Tei, C. Cassino, F. Arena, E. Gianolio and M. Botta, J. Biol. Inorg. Chem., 2014, 19, 133–143.
24. S. Aime, M. Botta, S. Geninatti Crich, E. Terreno, P. L. Anelli and F. Uggeri, Chem. – Eur. J., 1999, 5, 1261–1266.
25. R. A. Carvalho, J. A. Peters and C. F. G. C. Geraldes, Inorg. Chim. Acta, 1997, 262, 167–176.
26. G. A. Pereira, J. A. Peters, E. Terreno, D. Delli Castelli, S. Aime, S. Laurent, L. Vander Elst, R. N. Muller and C. F. G. C. Geraldes, Eur. J. Inorg. Chem., 2012, 2087–2098.
27. X. Wu, A. C. Dawsey, B. N. Siriwardena-Mahanama, M. J. Allen and T. J. Williams, J. Fluorine Chem., 2014, 168, 177–183.
28. S. Aime, M. Botta, E. Terreno, P. L. Anelli and F. Uggeri, Magn. Reson. Med., 1993, 30, 583–591.
29. D. A. Fulton, E. M. Elemento, S. Aime, L. Chaabane, M. Botta and D. Parker, Chem. Commun., 2006, 1064–1066.
30. D. A. Fulton, M. O'Halloran, D. Parker, K. Senanayake, M. Botta and S. Aime, Chem. Commun., 2005, 474–476.
31. F. Carniato, M. Ricci, L. Tei, F. Garello, E. Terreno, E. Ravera, G. Parigi, C. Luchinat and M. Botta, Inorg. Chem., 2022, 61, 5380–5387.
32. M. Y. Redko, R. Huang, J. L. Dye and J. E. Jackson, Synthesis, 2006, 759–761.
33. Y. P. H. Smith, M. E. Barr, J. R. Brainard, D. K. Ford, H. Frieser, S. Muralidharan, S. D. Reilly, R. R. Ryan, L. A. Silks III and H. W. Yu, J. Org. Chem., 1993, 58, 7939.
34. D. F. Evans, J. Chem. Soc., 1959, 2003–2005.
35. R. A. Dwek, NMR in Biochemistry, Oxford University Press, Oxford, 1973.
36. D. M. Corsi, H. van Bekkum and J. A. Peters, Inorg. Chem., 2000, 39, 4802–4808.
37. G. Scatchard, Ann. N. Y. Acad. Sci., 1949, 51, 660–672.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
39. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154109.
41. F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085.
42. M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734.
43. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
44. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
45. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
46. T. Lu, J. Chem. Phys., 2024, 161, 082503.
47. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
48. M. Botta, Eur. J. Inorg. Chem., 2000, 399–407.
49. A. D. Sherry, J. Ren, J. Huskens, E. Brucher, E. Toth, C. F. C. G. Geraldes, M. M. C. A. Castro and W. P. Cacheris, Inorg. Chem., 1996, 35, 4604–4612.
50. B. Dietrich, B. Dilworth, J.-M. Lehn, J.-P. Sonchez, M. Cesario, J. Guilhem and C. Pascard, Helv. Chim. Acta, 1996, 79, 569–587.
51. M. Petroselli, M. Saccone and M. Cametti, ChemPhysChem, 2023, 24, e202200883–e202200892.
52. I. Solomon, Phys. Rev., 1955, 99, 559–565.
53. N. Bloembergen, J. Chem. Phys., 1957, 27, 572–573.
54. N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842–850.
55. J. H. Freed, J. Chem. Phys., 1978, 68, 4034–4037.
56. G. Lipari and S. Szabo, J. Am. Chem. Soc., 1982, 104, 4546–4559.
57. G. Lipari and S. Szabo, J. Am. Chem. Soc., 1982, 104, 4559–4570.
58. S. Torres, J. A. Martins, J. P. André, C. F. G. C. Geraldes, A. E. Merbach and É. Tóth, Chem. – Eur. J., 2006, 12, 940–948.
59. F. Carniato, L. Tei, M. Botta, E. Ravera, M. Fragai, G. Parigi and C. Luchinat, ACS Appl. Bio Mater., 2020, 3, 9065–9072.
60. M. Callewaert, V. G. Roullin, C. Cadiou, E. Millart, L. Van Gulik, M. C. Andry, C. Portefaix, C. Hoeffel, S. Laurent, L. Vander Elst, R. Muller, M. Molinari and F. Chuburu, J. Mater. Chem. B, 2014, 2, 6397–6405.
61. T. Courant, V. G. Roullin, C. Cadiou, M. Callewaert, M. C. Andry, C. Portefaix, C. Hoeffel, M. C. de Goltstein, M. Port, S. Laurent, L. Vander Elst, R. Muller, M. Molinari and F. Chuburu, Angew. Chem., Int. Ed., 2012, 51, 9119–9122.

---