Mononuclear Fe^II and heterobinuclear Fe^IINi^II thiolate complexes derived from a compartmental hexaazadithiophenolato ligand: synthesis, structure and properties

Abstract

Compartmental macrocycles have proven to be very successful for the synthesis of heterobinuclear transition metal complexes. We obtained a mixed-ligand FeNi thiolate complex, [FeNiL(µ-OAc)]ClO₄ (3), where L²⁻ represents a 24-membered hexaaza-dithiophenolato ligand, by metalation of either the mononuclear [Fe^II(H₂L)](ClO₄)₂ (1) or [Ni^II(H₂L)](ClO₄)₂ (2) complex with Ni^II or Fe^II salts in good to moderate yields. However, the homobinuclear [Fe₂L(µ-OAc)]ClO₄ (4), or [Ni₂L(µ-OAc)]ClO₄ (5), complexes are invariably formed as byproducts (≈12–15%). The metal atoms in 3 are bridged at a distance of 3.4588(5) Å by two thiolate residues and one external μ_1,3-acetato ligand to give a bioctahedral N₃Fe^II(μ-(SR)₂(µ-OAc)Ni^IIN₃) core structure. Magnetic susceptibility measurements for 3 show the presence of a high-spin Fe^II (S = 2) ion, which is antiferromagnetically coupled to the Ni^II (S = 1) ion to give a S_total = 1 ground state. Broken symmetry DFT calculations revealed J = −6.88 cm⁻¹ (H = −JS₁S₂). The integrity and robust nature of complex 3 is maintained in solution as confirmed by ESI mass spectrometry and UV-vis-NIR spectroscopy. Cyclic voltammetry measurements for 3 in MeCN show two electrochemically quasi-reversible redox waves which are assigned to sequential oxidations of Fe^II and Ni^II, respectively (E(Fe^II/III) = +0.30 V, E(Ni^II/III) = +1.29 V vs. SCE). The [Fe^II(H₂L)]²⁺ complex was isolated as a pale-yellow, paramagnetic (μ_eff = 5.41μ_B) perchlorate salt. It comprises a five-coordinated Fe^II ion in a distorted square-pyramidal N₃S₂ coordination environment, and a system of intramolecular N⁺–H⋯S⁻ hydrogen bonds in the free pocket of the compartmental macrocycle.

---

1. Introduction

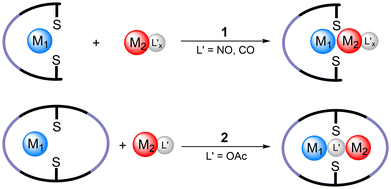
In the past few decades, many heterobinuclear complexes have been investigated because of their specific chemical and physicochemical properties arising from the proximity of the two disparate metal centers.^1–3 Understanding the structural, electronic, and reactivity features of such complexes is of importance in the field of cooperative catalysis,^4–11 sensing, imaging,^12,13 and molecular magnetism.^14–16 Heterobinuclear complexes of first-row transition metal ions have also attracted much interest as structural mimics of the active site of certain metalloenzymes.^17–22 Compartmental macrocyclic ligands are popular for construction of heterobinuclear complexes due to their high binding selectivity and the macrocyclic effect that can lead to a higher thermodynamic stability of the complexes.^23–26 This is especially the case when combinations of labile 3d block metal ions are targeted.²⁷

Heterobinuclear complexes derived from symmetrical phenol-based compartmental macrocycles have been known since the 1980s,^28,29 and their electrochemical and magnetic properties were extensively studied.^30–32 More recently, the catalytic activity of some heterobinuclear complexes has been reported.^33–38 Several synthetic procedures have been developed to access heterobinuclear complexes based on phenolate-containing macrocycles. In a comparably straightforward approach, the compartmental ligand can be generated in situ by templation with the desired metal-ions, M₁ and M₂ (Scheme 1, method 1). Accordingly, binuclear transition metal complexes are obtained, however, preferably of homobinuclear nature.³⁹ Thus, stepwise approaches aiming the complexation of one metal ion at the time are the better choice. Of great success for asymmetric complexes are pre-organized ligands which already coordinated one of the metal ions. Final cyclization then occurs in situ with complexation of the final M₂ (Scheme 1, method 2).⁴⁰ Furthermore, the exchange of labile coordinated metal-ions in the second binding pocket, such as Pb^II, may be of advantage. The addition of M₂ sulfates leads to the precipitation of PbSO₄ and concomitant incorporation of M₂ (Scheme 1, method 3).^41–43 A particularly versatile approach targets the mononuclear M₁ complexes (Scheme 1, method 4), through metalation of the free ligand⁴⁴ or exchange with a templating agent like Mg^II.⁴⁵ In the final step, the second metal ion can easily be inserted.

Scheme 1 Four approaches to generate heterobimetallic complexes supported by phenolate-based compartmental macrocycles. 1: A ‘one-pot’ template-directed synthesis yields the compartmental complex. 2: Final cyclization of pre-organized M₁ complex occurs along with insertion of M₂. 3: Transmetallation of labile coordinated Pb^II ion accelerates insertion of M₂. 4: Metal ions like Mg^II may aid the ligand synthesis by directed template condensation reaction or the ligand is available with free binding pockets. With the mononuclear M₁ complex, the second free binding pocket is available for M₂ insertion.

Inspired by the abundance of catalytically active thiolate complexes in metalloenzymes and their synthetic models, we have synthesized and characterized several thiolato-bridged transition metal complexes supported by acyclic and macrocyclic polyaza–thiophenolato ligands.^46–48 A coordinatively-saturated [Fe^IINi^IIL′]⁺ complex supported by a compartmental N₆S₃ tripod ligand is a representative example (Fig. 1).⁴⁹ It should be noted that the above methods developed for phenolato-based macrocycles are of little synthetic value for the synthesis of such ligands. We have been successful by utilizing metal-free protocols using protected thioether precursor derivatives to access such ligands.

Fig. 1 Heterobinuclear Fe^IINi^II complexes supported by compartmental amino-thiophenolato ligands. The [Fe^IINi^IIL′]⁺ complex has been reported previously.⁴⁹

We have now been able to synthesize a bioctahedral FeNi complex with an active coordination site, namely [FeNiL(µ-OAc)]ClO₄ (3), by utilizing a related macrocyclic amino-thiophenolato ligand H₂L with an N₆S₂ donor set. The active coordination site in 3 is occupied by the acetato ligand. A stepwise approach comprising metalation reactions of mononuclear Fe^IIN₃S₂ (or Ni^IIN₃S₂) metalloligands (1, 2) was devised to synthesize such a complex. The formation of intramolecular hydrogen bonds blocks one of the coordination sites allowing for the isolation of the mononuclear intermediate complexes 1 and 2. Herein, we report on the synthesis, structure, and physicochemical properties of this new heterobinuclear Fe^IINi^II complex. The synthesis and characterization of the new complex [Fe(H₂L)](ClO₄)₂ (1) is also reported. To our knowledge, only few heterobinuclear FeNi complexes derived from macrocyclic ligands are reported in literature. The complex [NiFeL]²⁺ supported by a Py₂N₄S₂ macrocycle is an example.⁵⁰

2. Results and discussion

Syntheses of the complexes [Fe(H₂L)](ClO₄)₂ (1) and [FeNiL(µ-OAc)](ClO₄) (3)

The macrocyclic ligand H₂L is known to form mono- as well as binuclear complexes with various 3d block metal ions.^51,52 A mononuclear Fe^II complex has not been reported previously and was considered as a precursor for a heterobinuclear Fe^IINi^II complex. Thusly, Fe(ClO₄)₂·6 H₂O, NEt₃, and H₂L·6HCl were reacted in a 1 : 6 : 1 stoichiometric ratio in MeOH under N₂ (Scheme 2) for 24 h to afford a pale-yellow solution, from which an off-white, air-sensitive, paramagnetic perchlorate salt of composition [Fe(H₂L)](ClO₄)₂ (1) was isolated in 69% yield. Once the Fe^II complex 1 was synthesized, its metalation with Ni^II salts was attempted. When a solution of [Fe(H₂L)](ClO₄)₂1 in MeOH/MeCN was treated with Ni(OAc)₂·4H₂O and NEt₃ as a base for 4 d at room temperature, a yellow solution formed, from which a golden-orange, paramagnetic, mixed-ligand [Fe^IINi^IIL(µ-OAc)]⁺ complex could be reproducibly isolated as a perchlorate salt (3) albeit in moderate yield (42%) and invariably contaminated by the known homobinuclear [Fe₂L(µ-OAc)]ClO₄ (4) and [Ni₂L(µ-OAc)]ClO₄ (5) complexes. The total amount of the byproducts was estimated to be ≈12% on the basis of a mass spectrometric analysis (see the SI). Complex 3 could also be obtained in good yield (80%) by reaction of the Ni^II complex 2 with anhydrous Fe(OAc)₂ and NEt₃ in MeOH/MeCN, but again contaminated with 4 and 5. All attempts to separate 3 from 4 and 5 have failed so far.

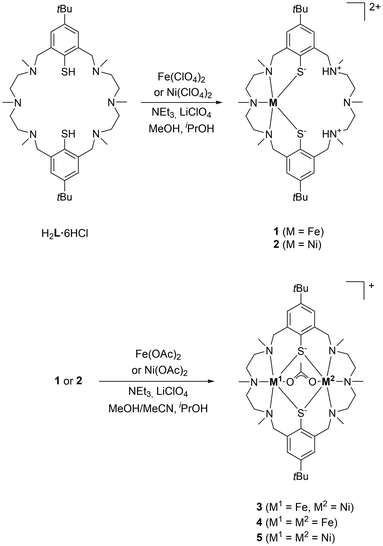Scheme 2 Synthesis of complexes 1–5 as ClO₄ salts; salt metathesis to the BPh₄ salts yielded 3′, 4′ and 5′.

We performed control experiments to examine whether metal scrambling occurs in the complex 3 in the solution state. Therefore, a 1 : 1 mixture of genuine samples of the homobinuclear complexes 4 and 5 was left to stir for several days at room temperature, as indicated in eqn (1). According to mass spectrometric analysis, the initial 1 : 1 ratio of the two complexes 4 and 5 remained unchanged. A similar experiment was conducted with complex 3, which was contaminated with 4 and 5. Again no changes in the stoichiometric composition could be detected after stirring for several days. The absence of metal scrambling was further confirmed by UV/vis spectroscopy and cyclic voltammetry (vide infra). It can be concluded that the integrity of complex 3 is maintained in solution state and that the byproducts 4 and 5 form during complexation reactions of the mononuclear species 1 and 2.

The two new compounds have been characterized by elemental analysis, mass spectrometry, UV-vis-NIR and FTIR spectroscopy, variable-temperature magnetic susceptibility measurements, cyclic voltammetry (for 3), X-ray crystallography, X-ray powder diffraction (for 1) and SEM-EDX (for 3′). The synthesis and characterization of compounds 2, 4, and 5 has been reported previously.^53,54 As demonstrated in these earlier studies, the choice of counter-ion has a negligible effect on their spectroscopic and electronic properties. Therefore, unless otherwise noted, all compounds are discussed in their ClO₄⁻ salt form.

Crystallographic characterization of the complexes [Fe(H₂L)](ClO₄)₂ (1) and [FeNiL(µ-OAc)]BPh₄ (3′)

Single-crystals of the perchlorate salt 1·MeOH suitable for X-ray crystallographic analysis were obtained by slow diffusion of Et₂O into a concentrated MeOH solution. The title compound crystallizes in the monoclinic space group P2₁/n. The asymmetric unit contains one independent complex dication, two ClO₄⁻ anions, and one MeOH solvent molecule. Fig. 2 displays a perspective view of the molecular structure of the [Fe(H₂L)]²⁺ dication, as well as a ball and stick model of the immediate coordination environment of the Fe atom. Selected bond lengths and angles are given in the Figure caption (see the SI for a full list of crystallographic and metrical data).

Fig. 2 Left: Ellipsoid representation of the molecular structure of the [Fe^II(H₂L)]²⁺ dication in crystals of [Fe(H₂L)](ClO₄)₂·MeOH (1·MeOH) (CCDC 2392032). Thermal ellipsoids drawn at 30% probability level. Hydrogen atoms (except H4 and H6) were omitted for clarity. Dashed lines refer to intramolecular NH⋯S hydrogen bonding interactions. Right: The coordination polyhedron of the Fe atom in complex 1. Selected interatomic distances and bond angles: N4⋯S1 3.777(2), N4⋯S2 3.230(2), N6⋯S1 3.111(1), N4⋯N6 5.420(3), N6⋯N5 2.874(3), Fe–S1 2.3291(6), Fe–S2 2.3511(6), Fe–N1 2.269(2), Fe–N2 2.150(2), Fe–N3 2.305(2) Å; N1–Fe–N3 157.29(6)°.

The Fe atom in 1 is five-coordinated by three nitrogen and two thiophenolato–sulphur atoms. The coordination sphere is best described as distorted square pyramidal, as manifested by the τ value of 0.36.⁵⁵ A similar value was found for the isostructural [Ni(H₂L)](ClO₄)₂ complex (2, τ = 0.29).⁵³ The average Fe–S and Fe–N bond lengths at 2.3401(8) Å and 2.241(2) Å, respectively, show no unusual features and match well with those of other five-coordinated FeN₃S₂ complexes.^56–58 For instance, in the distorted trigonal bipyramidal complex [Fe^IIS₂N₃(Pr,Pr)]⁵⁶ (S₂N₃(Pr,Pr) = 1,2-dimethyl-3,7,1-triazatridecane-1,13-dithiolate) the average Fe–S and Fe–N bonds are of length 2.353(1) and 2.177(6) Å.

The two hydrogen atoms bonded to N4 and N6 are involved in intramolecular hydrogen bonding interactions as illustrated in Fig. 2. According to Bondi's van der Waals radii criterion (N⋯S ≤ 3.35 Å, N⋯N ≤ 3.10 Å),⁵⁹ one direct (N4⋯S2, 3.23 Å) and one three-centred, or bifurcated, hydrogen bond (N6⋯S1/N5, 3.11, 2.87 Å) are present. The latter involves two acceptor atoms – specifically, a sulphur and a nitrogen atom. Bifurcated hydrogen bonds are comparably rare. In the mixed ligand complex [Ni(nmp)(S-o-babt)]⁺ (nmp = the deprotonated form of N-2 (mercaptoethyl)picolinamide, S-o-babt = thiolate of o-benzoylaminobenzene thiol) a bifurcated hydrogen bond is present, the corresponding N⋯S distances being 2.954 and 3.308 Å.⁶⁰

In general, hydrogen bond donor acceptor distances, especially in bifurcated hydrogen bonds, can exceed the sum of van der Waals radii.⁶¹ The presence (or absence) of such weak hydrogen bonding interactions may be more reliably determined by means of theoretical calculations.⁶² Thus, we performed corresponding density functional theory (DFT) calculation at the B3LYP level of theory and the def2-SVP and def2-TZVP basis set followed by non-covalent interaction index (NCI) calculations,⁶³ in order to study the hydrogen bonding interactions in 1. The NCI index determines the strength of the hydrogen bonds based on the associated electron density and its reduced density gradient.^63,64Fig. 3 shows a representative NCI plot involving the two S and three N atoms in 1. This plot clearly shows the presence of two bifurcated hydrogen bonds (N4⋯S1/S2 and N6⋯S1/N5). From the NCI fingerprint plot, the strength of the hydrogen bonds can be estimated.⁶⁵ Importantly, negative values correspond to attractive interactions with hydrogen bonds at higher density values (−0.01 < p < −0.06 au) and positive values show repulsive forces.^66,67 Therefore, the strongest interactions in 1 occur between N6–H⋯S1/N5 and N4–H⋯S2 with −0.027/−0.017 and −0.017 au respectively. The N6–H⋯N5 interaction is with −0.011 au the weakest. In contrast to the proposed hydrogen bonding based on the van der Waals radii criterion (N⋯S ≤ 3.35 Å, N⋯N ≤ 3.10 Å),⁵⁹ the NCI plot analysis supports the presence of two bifurcated hydrogen bonds instead of just one.

Fig. 3 NCI plot showing the presence of bifurcated N4⋯S1/S2 and N6⋯S1/N5 hydrogen-bonding interactions (dotted lines) in 1. Gradient isosurfaces (s = 0.3 au) coloured on an RGB-inspired scale according to the sign(λ₂)ρ values over the range of −0.06 to 0.06 au. Blue surfaces indicate hydrogen bonds and green surfaces van der Waals interactions. Hydrogen atoms except those bound to N4 and N6 were omitted for clarity. Additional weak C–H⋯S1 hydrogen interactions are visible as smaller blue surfaces and not subject to further investigation.

Single crystals of [Fe^IINi^IIL(µ-OAc)]BPh₄·MeCN (3′·MeCN) suitable for X-ray crystallography were obtained by slow evaporation of a mixed MeCN/EtOH solution of 3 (contaminated by 4 and 5) to which NaBPh₄ had been added. The structure comprises binuclear [Fe^IINi^IIL(µ-OAc)]⁺ complex (Fig. 4), BPh₄⁻ anions and MeCN solvate molecules. There is only one complex cation per asymmetric unit, with the Fe^II and Ni^II atoms statistically distributed (50 : 50) about the two metal binding sites. Thus, this crystal structure can only serve to confirm the atom connectivity of the [Fe^IINi^IIL(µ-OAc)]⁺ cation.

Fig. 4 Left: Molecular structure of the [Fe^IINi^IIL(µ-OAc)]⁺ cation in crystals of 3′·MeCN (CCDC 2392031). Right: The coordination polyhedron of the metal ions. Thermal ellipsoids drawn at 30% probability level. All hydrogen atoms were omitted for clarity. The Fe and Ni atoms (M) are statistically distributed (50 : 50) about the two metal binding sites.

The Fe^IINi^II complex is isostructural with the corresponding Fe₂ (4) and Ni₂ complexes (5), with the metal atoms surrounded by three N and two S atoms from the macrocycle and one O atom from the bridging acetato ligand in a distorted octahedral fashion. The M⋯M distance in 3′ (3.4588(5) Å) is intermediate between that in 4′ (Fe⋯Fe 3.421(1) Å) and 5′ (Ni⋯Ni 3.483(1) Å), in agreement with the presence of two metal ions with different ionic radii (Fe^II 0.83, Ni^II 0.92 Å).^68,69 The same applies to the corresponding M–S and M–N distances. The long metal–ligand bonds in 3′ are indicative of a high-spin configuration for the Fe^II ion. Relative to the five-coordinated Fe^II in 1, the average metal–S and metal–N distances in 3′ increase by 0.16 and 0.03 Å, respectively (see SI). To assess the distribution of Fe^II and Ni^II within a single crystal as well as among a mixture of crystals, SEM–EDX analyses were carried out with 3′·MeCN. The measurements indicate a largely homogeneous elemental distribution (see SI).

Spectroscopic characterization

FTIR spectroscopic measurements were carried out on complex 1 to probe potential N–H⋯S hydrogen bonding. However, for reasons unclear, no NH stretching bands could be detected in the characteristic range (3400–2500 cm⁻¹). Similar behavior was already noted for the isostructural [Ni(H₂L)](ClO₄)₂ (2) and [Zn(H₂L)](ClO₄)₂ (6) complexes. So, the presence of these NH⋯S bonds relies solely on the basis of the distance criteria for NH⋯S bonding and the DFT calculations. The FTIR spectrum (Fig. S5) of 3 reveals two characteristic vibrations at 1592 and 1425 cm⁻¹ attributed to the symmetric and asymmetric carboxylate stretches. The separation of the two modes is large (v˜_asym − v˜_sym = 167 cm⁻¹) and consistent with a µ_1,3-bridging acetato group as in 4 and 5. The IR spectra of 3, 4, and 5 can be superimposed on one another. The three complexes could not be clearly resolved with the available spectral resolution.

The electronic absorption spectrum of complex 1, recorded in MeCN solution, is presented in Fig. 5, with the corresponding data compiled in Table 1 alongside those of the isostructural Ni^II and Zn^II complexes 2 and 6. Since complex 6 does not exhibit charge-transfer or d–d transitions, its spectral profile is dominated by two intense π–π* absorptions in the UV region, both with extinction coefficients above 15 000 M⁻¹ cm⁻¹, and a shoulder ≈313 nm. On this basis, the analogous features observed for complex 1 are likewise assigned to π–π* transitions. Additional shoulders around 298 and 328 cm⁻¹ are discernible for complex 1, which are tentatively attributed to ligand-to-metal charge transfer (LMCT). Comparable LMCT transitions of similar energy have previously been described for related five-coordinate Fe^II aryloxide complexes⁷⁰ and are also observed for 2. The spectrum further reveals a weak d–d transition at ≈800 nm with an extinction coefficient below 50 M⁻¹ cm⁻¹. A second d–d transition is expected above 2000 nm, which could not be detected with our experimental setup. The (two) d–d transitions are assigned to the B₁(d_x²−y²) and A₁(d_z²) states (in pure, square-pyramidal (C_4v) geometry) as observed for other five-coordinated Fe^II complexes with the normal, doubly occupied d_xy ground state ((d_xy)²(d_xz)¹(d_yz)¹(d_z²)¹(d_x²−y²)¹).^71–74

Fig. 5 Electronic absorption spectrum of the mononuclear Fe^II (1) complex in black (400–1200 nm, c = 10^–3 M, MeCN, 295 K). The inset shows the UV region 190–400 nm (c = 10^–5 M, MeCN, 295 K); spectra of 2 and 6 are shown for comparison.

Table 1 Electronic absorption spectral data for 1 (λ_max/nm; ε/M⁻¹ cm⁻¹). The data for 2 and 6 are included for comparison

	[Fe^II(H2L)](ClO4)2 (1)	[Ni^II(H2L)](ClO4)2 (2)	[Zn^II(H2L)] (ClO4)2 (6)
π–π*	208(37 400), 266(18 800)	209(35 200), 250(sh), 280(14 900)	211(34 500), 266(25 700), 306(sh)
LMCT	298(10 500), 328(sh)	343(sh), 425 (900), 504(1200)	—
d–d transitions	806(33)	684(66)	—

---

Fig. 6 displays the electronic absorption spectrum of the Fe^IINi^II complex 3 in the vis-NIR region (600–1400 nm). The spectra of the homobinuclear complexes 4 and 5 are shown for comparison. The spectrum of 3 differs significantly from those of 4 and 5, as one might expect for a heterobinuclear Fe^IINi^II species. This is particularly evident from the position and intensity of the characteristic d–d transition (ν₂, ³T_1g ← ³A_2g designation in pure O_h symmetry) for the six- coordinated Ni^II (d⁸, S = 1) ion. This transition is significantly red-shifted from 648 in 5 to 660 nm in 3. Likewise, the extinction coefficient decreases from 28 to 17 M⁻¹ cm⁻¹. For a 50%/50% mixture of 4 and 5 no red-shift would be expected. Two further weak absorptions at λ_max = 907 (shoulder) and 1188 nm are clearly discernible in the NIR region for complex 3. A deconvolution analysis of the spectrum reveals three ligand-field based transitions for six-coordinated Fe^II ions (885 and 1275 nm) and Ni^II (1164 nm) ions, as illustrated in Fig. 6. The former transitions can be assigned to the components of the ⁵E ← ⁵T₂ absorption of a high-spin Fe^II (d⁶, S = 2) ion, split by a dynamic Jahn–Teller effect in the excited ⁵E state which is typical for high-spin Fe^II compounds.⁷⁵ The remaining absorption at 1164 nm is then readily assigned to the ν₁ (³T_2g(F) ← ³A_2g) ligand field transition of a six-coordinated Ni^II (S = 1) ion. Again, these values are different from those seen for the homobinuclear complexes (937(14), 1239(36) for 4, 1134(55) for 5).^54,76 The third d–d transition of the Ni²⁺ ion, ν₃ expected at ≈400 nm, is obscured by intense bands arising from thiolate-to-M²⁺ charge transfer transitions (λ_max = 395 nm, ε = 2640 M⁻¹ cm⁻¹).⁷⁷ Overall, the electronic absorption spectrum suggests that complex 3 exists as a stable heterobinuclear Fe^IINi^II complex comprising a six-coordinated high-spin Fe^II (S = 2) and a six-coordinated Ni^II (S = 1) ion. The ligand field strength in the N₃S₂O compartment is thus surprisingly low, comparable to a ligand field produced by six oxygen (aqua) donors. This is in contrast to the complex [Fe^IINi^IIL′]⁺ which comprises a low-spin Fe^II centre.⁴⁹

Fig. 6 Top: vis-NIR spectra for complexes 3–5 in MeCN (c ≈ 10^–3 M, 295 K). The absorption marked with an asterisk is related to the spectrometer. Bottom: Deconvolution of the absorptions of 3 in the 800–1600 nm range.

Variable temperature magnetic susceptibility measurements

In order to confirm oxidation and spin states, variable temperature magnetic susceptibility measurements were carried out in an applied magnetic field of 0.05 T over a temperature range of 2–300 K for complex 1 and of 0.5 T for complex 3. Fig. 7 shows the effective magnetic moment µ_eff (per mononuclear Fe^II complex 1) versus T.

Fig. 7 Temperature dependence of the µ_eff value for the mononuclear complex 1 at 0.05 T.

The effective magnetic moment at room temperature of 5.41µ_B decreases steadily to 60 K (5.27µ_B) and then rapidly to 4.44µ_B at 2 K, which may be due to zero-field splitting effects and intermolecular exchange interactions. Nevertheless, the room temperature value is clearly comparable to other five-coordinated high-spin Fe^II (d⁶, S = 2) complexes with µ_eff being close to the spin-only value of 4.90µ_B.^78,79Fig. 8 shows the temperature dependence of the effective magnetic moment µ_eff (per binuclear complex) for the (impure) Fe^IINi^II complex 3. The data for complexes 4 and 5 are displayed for comparison.⁵⁴ The susceptibility data of complex 3 was recorded for a powdered sample between 2 and 300 K in an applied external magnetic field of B = 0.5 T. The effective magnetic moment at room temperature (6.30µ_B) is much higher than expected for two non-interacting high-spin Fe^II (d⁶, S = 2) and Ni^II (d⁸, S = 1) ions with g = 2.0 (5.66µ_B). With decreasing temperature, the magnetic moment decreases steadily to 1.83µ_B at 2 K. This behavior is indicative of a weak antiferromagnetic superexchange interaction. However, the expected maximum in the χ_mvs. T plot (SI) is not observed at low temperatures. This can be traced to the small amounts of the paramagnetic impurities 4 and 5 in the sample.

Fig. 8 Blue curve: measured temperature dependence of the effective magnetic moment μ_eff (at 0.5 T) for 3. Due to contaminations, a fit of the data was omitted. Black curves: the effective magnetic moments μ_eff (at 0.2 T) for 4 and 5 with solid lines corresponding to the best fit.⁵⁴

Due to the homobinuclear impurities, no reasonable fits of the magnetic susceptibility data could be obtained for complex 3. Consequently, broken symmetry DFT calculations (PBE0/def2-TZVP level of theory) were performed. These calculations confirmed an antiferromagnetic exchange interaction. The exchange coupling parameter J = −6.88 cm⁻¹ (H = −JS₁S₂) was calculated.⁸⁰ The antiferromagnetic exchange interaction in 3 is somewhat weaker than in the Fe^II complex 4 (J = −11.97 (DFT), −10.63 (experiment)⁵⁴ cm⁻¹). This may be traced to the decrease of exchange interactions of the t_2g ↔ e_g type (expected to be antiferromagnetic in nature) although other effects cannot be ruled out.^81a To gain deeper insight into the pathways mediating the interaction between the paramagnetic Fe^II and Ni^II sites, we examined the direct and differential overlap of the corresponding orbital pairs obtained from the Broken symmetry density functional theory solutions for 3, as done for other triply bridged Cr^III complexes.^81b,c The results of the corresponding orbital transformations are shown in Fig. S9. The small overlap integrals for the corresponding orbital pairs (0.063, 0.042 for the orbitals 222, and 223, respectively), suggest that direct metal–metal through-space interactions are not significant in the present complex.

The BS-DFT calculations further reveals that the two magnetic orbitals in 3 resemble the Fe^II d_xz and d_yz orbitals as well as the Ni^II d_z² and d_x²−y² orbitals. In the case of these orbital pairs, overlap occurs over the bridging ligands.^81b BS-DFT calculations on truncated model complex 3″ (with the carboxylate bridge removed) have also been performed to study the individual contributions of the carboxylate ligands and thiolato bridges to the overall magnetic behaviour. This approach has previously proven to be a powerful tool to unravel the contributions of the individual bridges in Ni complexes supported by (L)²⁻.^81b,c The results imply that a dominant “antiferromagnetic” contribution (−17.11 cm⁻¹ (3″) Table S8) through the bridging thiolates is counterbalanced by a ferromagnetic interaction by the carboxylato bridge (Fig. 9).

Fig. 9 Exchange interactions by ferromagnetic (F) or antiferromagnetic (AF) coupling for the Fe^IINi^II complex.

Cyclic voltammetry

Despite small impurities, the distinctive properties of complex 3 can still be evaluated by means of cyclovoltammetry. The cyclic voltammogram (CV) recorded in MeCN containing 0.1 M nBu₄NPF₆ as the supporting electrolyte at 298 K shows two electrochemically quasi-reversible redox waves at E_1/2 = +0.30 V vs. SCE (ΔE_p = 90 mV) and at +1.29 V (ΔE_p = 93 mV), respectively. The CV of 3 clearly differs from those of 4 and 5. The two redox waves can be assigned to sequential one-electron oxidations to the formal Fe^IIINi^II and Fe^IIINi^III redox states, respectively, by comparison with the CVs of 4 and 5 (Fig. 10). Not many redox-active Fe^IINi^II thiolate complexes have been reported.^82,83 The [FeNiL′]⁺ complex supported by the tripodal N₆S₃ ligand,⁴⁹ is oxidized at much more cathodic potentials (−0.43 V, +0.45 V vs. SCE). The shifts of +0.73 V and +0.84 V for the two oxidations of 3 relative to those in [FeNiL′]⁺ are consistent with the much weaker ligand field in 3. Stronger donors in [FeNiL′]⁺ that lie on the right-hand side in the spectrochemical series (primary and secondary amine) are replaced by weak field donors in 3 that are further to the left (tertiary amine, carboxylate) to destabilize the divalent oxidation states, thereby causing the shifts in the redox potential.

Fig. 10 Cyclic voltammograms for 3–5 in MeCN (10⁻³ M, 0.1 M nBu₄PF₆), Pt-disk working electrode, Pt-wire counter electrode, Ag wire reference electrode, scan rate = 100 mV s⁻¹.

3. Conclusion

Several synthetic routes for preparing heterobinuclear complexes have been developed. Considerable success has been achieved in case of NiFe complexes using the cis-thiolate strategy, with significant contributions reported by Darensbourg et al. (Scheme 3, common approach 1). The approach relies on coupling pre-formed MN₂S₂ metallodithiolato synthons with reactive M(CO)_x or M(NO)_x units, allowing both structural variability and the formation of various heterobimetallic FeNi complexes. This approach does not lead to homobinuclear byproducts.¹⁹

Scheme 3 Comparison of approaches to generate heterobimetallic complexes supported by thiophenolato-based ligands; 1. the approach by Darensbourg et al. based on the reaction of a M₁N₂S₂ synthon with M₂(CO)_x or M₂(NO)_x fragments; 2. the stepwise strategy utilizing macrocyclic compartments presented herein.

A newly prepared mononuclear Fe^II complex with a N₃S₂ coordination sphere is presented and fully characterized by UV-vis-NIR and ATR-FTIR spectroscopy, single crystal X-ray crystallography, and SQUID magnetometry. Additionally, the complex exhibits advantageous N⁺–H⋯S⁻ hydrogen bonding, which facilitates the synthesis of heterobinuclear complexes. The presence of this interaction was confirmed through NCI plot analysis.

The main findings of this paper are as follows: an air-stable heterobimetallic Fe^IINi^II complex featuring an active coordination site was successfully synthesized using a macrocyclic N₆S₂ ligand. While the isolated product contained a minor proportion (≈12–15%) of homobinuclear complexes 4 and 5, its preparation nonetheless demonstrates the feasibility of forming the desired heterometallic species. Because the intermediate mononuclear and homobinuclear complexes were independently obtained and fully characterized in pure form, the properties of the target heterobinuclear complex could be evaluated in a comprehensive and well-supported manner.

In the molecular crystal structure of the heterobinuclear complex, 3′, the metal ions are bridged by an acetate group with a M–M distance of 3.4588(5) Å, which is intermediate of the Fe–Fe and Ni–Ni distances in the homobinuclear complexes 4′ and 5′. The UV-vis-NIR spectra differ significantly from those in the homobinculear species which speaks in favour of a heterobimetallic complex, instead of a 50/50% mixture of the homobinuclear complexes. This is further supported by magnetic susceptibility measurements which imply antiferromagnetic coupling of a high spin Fe^II (S = 2) with Ni^II (S = 1) to produce an overall S_total = 1. The coupling constant of J = −6.88 cm⁻¹ (H = −JS₁S₂) was determined by DFT calculations. Finally, the redox potential of Fe^II/III is with +0.30 V much lower than that of Ni^II/III with 1.29 V vs. SCE in MeCN.

Future advances target the issue of metal scrambling. Separation of the hetero- from the homobinuclear complexes may be realized by either exploiting the different redox potentials of complex 3, 4 and 5 or take advantage of different chemical reactivity. Alternatively, the formation of homobinuclear complexes may be impeded by utilizing the corresponding deprotonated complex of compounds 1 or 2 for better integration of the second metal ion.

Of major interest is the binding mode of the coordination site in complex 3. For instance, exchanging the acetato ligand with a hydride ion could ease the understanding of functionality in several enzymes.^17–22

4. Experimental

Materials and methods

All reagents were purchased from commercial sources unless otherwise specified. Anhydrous methanol was prepared by refluxing over magnesium, distilled and stored over N₂. Mass spectra were recorded with ESI(+) ionization on a Bruker Daltronics Esquire 3000 Plus ITMS or Impact II UHR Qq-TOF instrument. Isotope patterns were simulated using MestReNova 11.0, the estimation of contamination with homobinuclear species was established by systems of linear equations. Infrared spectra (4000–400 cm⁻¹) were recorded at 2 cm⁻¹ resolution and measured with 32 scans on a Bruker-Vertex 80 V FTIR spectrometer using a diamond-ATR unit or the Bruker Tensor 27 spectrometer. Spectra of complexes 1 and 3 were collected at room temperature on a Jasco V-670 UV-vis-NIR spectrophotometer, equipped with a photomultiplier and a PbS photoconductive cell. The spectrum was collected in the 190–1600 nm range with a resolution of 2 nm.

Caution! Perchlorate salts of transition-metal complexes are hazardous and may explode. Only small quantities should be prepared and great care should be taken.

[Fe(H₂L)](ClO₄)₂ (1). To a solution of Fe(ClO₄)₂·6 H₂O (60 mg, 0.17 mmol, 0.95 eq.) and H₂L·6 HCl (156 mg, 0.18 mmol, 1 eq.) in anhydrous MeOH (50 mL) was added a 1 M solution of NEt₃ in MeOH (1.05 mL, 1.05 mmol, 6 eq.) was added. The solution turned pale yellow. The reaction was stirred for 1 d. Then, a solution of LiClO₄·3H₂O (281 mg, 1.7 mmol, 10 eq.) in ⁱPrOH (10 mL) was added. The mixture was concentrated under reduced pressure to give a white solid, which was filtered, washed with cold ⁱPrOH and dried in vacuum. Further purification was done by slow diffusion of Et₂O into a concentrated MeOH solution, to obtain a fine crystalline product. Yield: 112 mg (69%), off-white powder. UV/Vis (CH₃CN): λ_max (ε) = 208 (37 355), 266 (18 743), 298 (10 501), 328 (sh), 806 (33) nm. IR (KBr, 22°) = 2962 (m), 2913 (m), 2905 (m), 2869 (m), 1630 (w), 1466 (s), 1365 (w), 1301 (w), 1230 (w), 1153 (m), 11 212 (s), 1108 (s), 1096 (s), 1014 (w), 890 (w), 844 (w), 819 (w), 636 (w), 624 (s) cm⁻¹. ESI-MS (MeCN): m/z 363.19 [M–2ClO₄]²⁺, 725.38 [M–H–2ClO₄]⁺, 825.33 [M–ClO₄]⁺. Elemental analysis calc (%) for C₃₉H₇₂Cl₂FeN₆O₁₀S₂ (1·MeOH·H₂O, 974.35): C 48.00, H 7.44, N 8.61; found: C 48.03, H 7.34, N 8.02. Based on the PXRD data recorded for 1·MeOH, the compound can be identified as phase-pure with respect to crystallinity with an amorphous component due to sample preparation. Further details are provided in the SI.

[FeNiL(µ-OAc)]ClO₄ (3). Method A: A solution of [Fe(H₂L)](ClO₄)₂ (67 mg, 0.072 mmol, 1.00 eq.), Ni(OAc)₂·4H₂O (18 mg, 0.72 mmol, 1.00 eq.), and NEt₃ (15 µL, 0.14 mmol, 2 eq.) in MeOH/MeCN (40 mL (1 : 1)) was stirred for 4 d. Then, a solution of LiClO₄·3H₂O (58 mg, 0.861 mmol, 5 eq.) in ⁱPrOH (5 mL) was added. The mixture was concentrated under reduced pressure to give an orange-brown solid, which was filtered, washed with cold ⁱPrOH and dried in vacuum. The crude product was purified by recrystallization from MeCN/EtOH. Yield: 29 mg (42%), brown-orange, microcrystalline solid. UV/Vis (CH₃CN): λ_max (log ε) = 193 (4.76), 308 (4.15), 476 (sh), 659 (1.20), 910 (sh), 1184 (1.67) nm. IR (KBr): v˜ = 3441 (br, w), 3022 (w), 2956 (m), 2905 (m), 2867 (m), 1630 (w), 1584 (s), 1552 (w), 1464 (s), 1424 (s), 1394 (w), 1367 (w), 1343 (w), 1302 (w), 1278 (w), 1228 (m), 1094 (br, s), 1016 (m), 971 (w), 929 (w), 911 (w), 896 (m), 852 (w), 819 (w), 792 (w), 759 (w), 742 (w), 656 (w), 624 (s), 599 (w), 537 (w), 478 (w), 455 (w) cm⁻¹. ESI-MS (MeCN): m/z 841.35 [M–ClO₄]⁻. Elemental analysis calc (%) for C₄₀H₇₁ClFeN₆NiO₈S₂ (3·2H₂O, 978.15): C 49.12, H 7.32, N 8.59; found: C 49.58, H 6.94, N 8.63. Byproducts of [Fe₂L(µ-OAc)]ClO₄ (4) and [Ni₂L(µ-OAc)]ClO₄ (5) were determined with 12.5% by mass spectrometry.

Method B: A solution of [Ni(H₂L)](ClO₄)₂ (2) (100 mg, 0.11 mmol, 1 eq.), Fe(OAc)₂ (23 mg, 0.13 mmol, 1.2 eq.), and NEt₃ (31 µL, 0.22 mmol, 2 eq.) in MeOH (30 mL) was stirred for 3 d. Then a solution LiClO₄·3H₂O (35 mg 0.22 mmol, 2 eq.) in EtOH (25 mL) was added. The solvent was concentrated under reduced pressure to give an orange-brown solid, which was filtered, washed with cold EtOH and dried in vacuum. The crude product was purified by recrystallization from MeCN/EtOH. Yield: 81 mg (80%), orange-brown, microcrystalline solid. The analytical data for this material is identical with that prepared by method A. Byproducts of [Fe₂L(µ-OAc)]ClO₄ (4) and [Ni₂L(µ-OAc)]ClO₄ (5) were determined with 15.7% by mass spectrometry.

Magnetic measurements

The magnetic susceptibility measurements were performed with a MPMS 7XL SQUID magnetometer (quantum design). Respective data were collected in the temperature range of 2 to 300 K for an applied dc field of 0.05 T for complex 1 and of 0.5 T for complex 3. The polycrystalline samples were grounded and were prepared in a gelatine capsule. The measured susceptibility data were corrected for the underlying diamagnetism, which was estimated using Pascal constants. The data were processed with the DAVE.⁸⁴

Cyclic voltammetry

Cyclic voltammetry measurements were carried out at room temperature with an Autolab PGSTAT12 potentiostat/galvanostat. The cell contained a Pt disk working electrode, a Pt wire auxiliary electrode, and a Ag wire as reference electrode. Concentrations of sample solutions were 10⁻³ M in a 0.1 M supporting electrolyte (tetrabutylammonium hexafluorophosphate in MeCN). The scan rate was 100 mV s⁻¹. Ferrocene was used as internal standard. All potentials were converted to the SCE reference using tabulated values.⁸⁵

X-ray crystallography

Suitable single crystals of [Fe(H₂L)](ClO₄)₂·MeOH (1·MeOH) and [NiFeL(µ-O₂CMe)]BPh₄·MeCN (3′·MeCN) were selected and mounted on the tip of a polyimide loop using perfluoropolyether oil. The data set for 1·MeOH was collected using a Stoe Stadivari diffractometer equipped with a Cu-K_α X-ray microsource (λ = 1.54178 Å) with a graded multilayer mirror monochromator and a Dectris Pilatus 300K detector. The data set for 3′·MeCN was collected at 180(2) K using a STOE IPDS-2T image plate diffractometer system equipped with a sealed Mo X-ray tube (λ(Mo-K_α) = 0.71073 Å) and a graphite monochromator crystal. Reflection data was processed using the X-area package.⁸⁶ The structure was solved by dual-space methods⁸⁷ and refined by full-matrix least-squares techniques on the basis of all data using SHELXL-2018/3⁸⁸ and Olex2.⁸⁹ Platon was used to search for higher symmetry.⁹⁰ All non-hydrogen atoms were refined anisotropically. Graphics were produced with Diamond 4.6.8 by Crystal Impact GbR.⁹¹ The parameter τ was calculated according to eqn (2).⁵⁵

Crystallographic data for 1·MeOH

C₃₉H₇₀FeN₆S₂Cl₂O₉, M_r = 957.80 g mol⁻¹, monoclinic group P2₁/n, a = 14.1064(3) Å, b = 17.0368(4) Å, c = 19.4289(4) Å, α = 90°, β = 92.671(2)°, γ = 90°, V = 4664.23(18) ų, Z = 4, ρ_calcd = 1.364 g cm⁻³, T = 180 K, μ(Cu K_α) = 4.952 mm⁻¹ (λ = 1.54186 Å), 30 056 reflections measured, 8768 unique, 7827 with I > 2σ(I). Final R₁ = 0.0364, wR₂ = 0.0962 (I > 2σ(I)), 613 parameters/149 restraints, min./max. residual electron density = −0.34/0.47 e⁻ Å⁻³. Due to free rotation, the ClO₄⁻ anions as well as the methanol solvent molecule were found to be disordered over two and three positions, respectively. These disorders were successfully modeled with a split atom model using SADI instructions implemented in SHELXL.

Crystallographic data for 3′·MeCN

C₆₆H₉₀BFeN₇NiO₂S₂, M_r = 1202.93 g mol⁻¹, triclinic space group P1̄, a = 13.3261(6) Å, b = 15.6750(8) Å, c = 16.9825(7) Å, α = 108.791(4)°, β = 92.255(4)°, γ = 107.496(3)°, V = 3166.3(3) ų, Z = 2, ρ_calcd = 1.262 g cm⁻³, T = 180(2) K, μ(Mo K_α) = 0.641 mm⁻¹ (λ = 0.71073 Å), 22 706 reflections measured, 12 366 unique, 8827 with I > 2σ(I). Final R₁ = 0.0428, wR₂ = 0.1003 (I > 2σ(I)), 797 parameters/24 restraints, min./max. residual electron density = 0.53/−0.57 e⁻ Å⁻³. It has not been possible to assign the Fe and Ni atoms to the two coordination pockets. A refinement with full site occupancy factors led to R values of 0.0463 and 0.0473 for the two options. In both models the Fe and Ni bond lengths are within experimental error identical, suggesting that the metals are statistically distributed over the two coordination pockets. The refinements were therefore carried out with 50%/50% occupancy factors using EXYZ and EADP instructions implemented in SHELX. The tBu groups were found to be disordered over two positions. This disorder was successfully modelled with a split atom model using SADI instructions implemented in SHELXL.

Computational details

The calculations were done using density functional theory (DFT) within the broken symmetry approach.^92–94 The hybrid functional of Perdew, Burke and Ernzerhof (PBE0)^95,96 and Ahlrichs triple-zeta valence basis set (TZV(P))⁹⁷ as implemented in the ORCA^98,99 program package (revision 4.2.0) were used for all calculations. The geometry of all considered structures were taken from the crystal structures and were fixed during the calculations. All calculations make use of the resolution of identity (Split-RI-J) approach for the Coulomb term in combination with the chain-of-spheres approximation for the exchange term (COSX) as implemented in ORCA.^100,101 Grimme's empirical dispersion correction D3(BJ) was employed.^102,103 All calculations were performed using increased iteration grids (GRID5 NOFINALGRID).

The calculation of J included the following steps: definition of the geometry of the molecule from X-ray analysis; calculation of the total energy for the high-spin (HS) state (S = 2); calculation of the total energy for the broken-symmetry (BS) state (S = 0); calculation of the J value within the following scheme:

where ^HSE, ^HS〈S²〉 ^HSE, ^HS〈S²〉 – correspond to the total energy and total spin angular momentum for the high-spin state (HS), ^BSE and ^BS〈S²〉 to the total energy and total spin angular momentum for the broken-symmetry state (BS). This scheme is valid over the whole coupling strength regime.⁸⁰ For the DFT calculations required for the NCI plot,^92–94,104 the hybrid functional B3LYP¹⁰⁰ was used in combination with the def2-TZVP¹⁰⁵ basis set as implemented in ORCA 5.0.4^106–108

Non-covalent-interaction plot analysis

NCI plots were computed with the NCIPLOT program using the electron density derived from DFT calculations.¹⁰⁹ For computing the NCI plots, we defined a cube with a side length of 3 Å with the midpoint between the two sulphur atoms at the cube center, in which the electron density (ρ) and the reduced density gradient (s) was computed. The representation of s versus sign(λ₂)ρ shows representative peaks at low density values in the presence of non-covalent interactions due to the annihilation of the reduced density gradient at these points.¹¹⁰ To distinguish between attractive and repulsive interactions, the NCI approach considers the accumulation or depletion of density in the plane perpendicular to the interaction, which is mainly characterized by the second eigenvalue λ₂ of the electron-density Hessian matrix.¹¹¹

A very important feature is the visualization of the reduced density gradient isosurfaces in real space using ChimeraX.¹¹² The isosurfaces at s = 0.3 a.u. are colored according to their relative strength using the value of the sign(λ₂)ρ from the generated fingerprint plot. An RGB-inspired color scale (red-green-violet) is used, where red isosurfaces represent repulsive interactions, green very weak van der Waals interactions and violet attractive interactions.

X-ray powder diffraction

PXRD measurements were carried out on a STOE STADI-P diffractometer (Stoe & Cie. GmbH, Darmstadt, Germany) equipped with a sealed Cu X-ray tube, a germanium (111) monochromator crystal (λ(Cu-K_α1) = 154.060 pm) and a DECTRIS Mythen 1K detector (Baden, Switzerland). The sample was ground, filled in a glass capillary (Hilgenberg, outer diameter 0.3 mm) and measured in the Debye–Scherrer mode. Data analysis was done by STOE WinXPOW software Version 3.11. Theoretical powder diffraction from the single crystal structure (CIF file) was calculated using the WinXPOW software. The data were plotted using Origin 2019.

Scanning electron microscopy with energy-dispersive X-ray spectroscopy

SEM was performed on a leo gemini device with 20 kV acceleration voltage equipped with an Oxford Instruments 7426 EDX detector. Samples were drop coated in ⁱPrOH to a sample holder with carbon pad and were dried at air. Samples were covered with carbon using a carbon evaporator. All images were obtained using the Everhart–Thornley detector. All EDX mappings were measured for 1 h due to the limited thickness of the crystals.

Author contributions

Vanessa Stephan: writing – original draft, visualization, validation, investigation, formal analysis. Christian Zocher: writing – review & editing, investigation, formal analysis. Martin Börner: writing – review & editing, investigation, formal analysis. Jennifer Klose: writing – review & editing. Daniel Fuhrmann: review & editing, investigation, formal analysis. Berthold Kersting: writing – review & editing, writing – original draft, supervision, resources, project administration, funding acquisition.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

All experimental data supporting the findings of this study are provided in the supplementary information (SI). Supplementary information: additional raw data, including mass spectrometry spectra, spectroscopic files, additional crystallographic and DFT calculated structural data, and magnetic data. See DOI: https://doi.org/10.1039/d5dt02350e.

CCDC 2392031 (3) and 2392032 (1) contain the supplementary crystallographic data for this paper.^113a,b

Acknowledgements

We are thankful to Prof. Dr H. Krautscheid for providing facilities for X-ray crystallographic measurements and to Prof. Dr O. Oeckler for providing facilities for SEM-EDX measurements. This project was co-financed by the European Union and tax revenues on the basis of the budget adopted by the Saxon State Parliament. This work was funded in part by the German Research Foundation (DFG) within the CRC Transregio TRR 386 – B1 (514664767). We also thank the DFG for an FTIR spectrometer (Project number 448298270). Computations for this work were done (in part) using resources of the Leipzig University Computing Center.

References

1. J. Klingele, S. Dechert and F. Meyer, Coord. Chem. Rev., 2009, 253, 2698–2741.
2. R. Robson, Aust. J. Chem., 1970, 23, 2217–2224.
3. A. L. Gavrilova and B. Bosnich, Chem. Rev., 2004, 104, 349–384.
4. B. G. Cooper, J. W. Napoline and C. M. Thomas, Catal. Rev., 2012, 54, 1–40.
5. S. Maggini, Coord. Chem. Rev., 2009, 253, 1793–1832.
6. V. Ritleng and M. J. Chetcuti, Chem. Rev., 2007, 107, 797–858.
7. R. C. Cammarota, L. J. Clouston and C. C. Lu, Coord. Chem. Rev., 2017, 334, 100–111.
8. P. Buchwalter, J. Rosé and P. Braunstein, Chem. Rev., 2015, 115, 28–126.
9. M. R. Halvagar, B. Neisen and W. B. Tolman, Inorg. Chem., 2013, 52, 793–799.
10. S. Gu, D. Xu and W. Chen, Dalton Trans., 2011, 40, 1576–1583.
11. S. Deolka, O. Rivada-Wheelaghan, S. L. Aristizábal, R. R. Fayzullin, S. Pal, K. Nozaki, E. Khaskin and J. R. Khusnutdinova, Chem. Sci., 2020, 11, 5494–5502.
12. W. Guan, S. Yamabe and S. Sakaki, Dalton Trans., 2013, 42, 8717–8728.
13. C.-F. Chow, M. H. W. Lam and W.-Y. Wong, Anal. Chem., 2013, 85, 8246–8253.
14. M. Ostrowska, I. O. Fritsky, E. Gumienna-Kontecka and A. V. Pavlishchuk, Coord. Chem. Rev., 2016, 327–328, 304–332.
15. Y. Peng and A. K. Powell, Coord. Chem. Rev., 2021, 426, 213490.
16. K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289–290, 74–122.
17. W. Lubitz, H. Ogata, O. Rüdiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148.
18. Y. Ohki and K. Tatsumi, Eur. J. Inorg. Chem., 2011, 2011, 973–985.
19. J. A. Denny and M. Y. Darensbourg, Chem. Rev., 2015, 115, 5248–5273.
20. C. Pathak, S. K. Gupta, M. K. Gangwar, A. P. Prakasham and P. Ghosh, ACS Omega, 2017, 2, 4737–4750.
21. C. Wombwell, C. A. Caputo and E. Reisner, Acc. Chem. Res., 2015, 48, 2858–2865.
22. (a) C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245–2274; (b) D. Brazzolotto, L. Wang, H. Tang, M. Gennari, N. Queyriaux, C. Philouze, S. Demeshko, F. Meyer, M. Orio, V. Artero, M. B. Hall and C. Duboc, ACS Catal., 2018, 8(11), 10658–10667; (c) H. Tang and M. B. Hall, J. Am. Chem. Soc., 2017, 139(49), 18065–18070; (d) H. Tai, Y. Higuchi and S. Hirota, Dalton Trans., 2018, 47, 4408–4423.
23. H. Ōkawa, H. Furutachi and D. E. Fenton, Coord. Chem. Rev., 1998, 174, 51–75.
24. D. E. Fenton, Chem. Soc. Rev., 1999, 28, 159–168.
25. A. J. Atkins, D. Black, A. J. Blake, A. Marin-Becerra, S. Parsons, L. Ruiz-Ramirez and M. Schröder, Chem. Commun., 1996, 457–464.
26. P. Zanello, S. Tamburini, P. A. Vigato and G. A. Mazzocchin, Coord. Chem. Rev., 1987, 77, 165–273.
27. D. Huang and R. H. Holm, J. Am. Chem. Soc., 2010, 132, 4693–4701.
28. R. R. Gagne, C. L. Spiro, T. J. Smith, C. A. Hamann, W. R. Thies and A. D. Shiemke, J. Am. Chem. Soc., 1981, 103, 4073–4081.
29. R. R. Gagne and C. L. Spiro, J. Am. Chem. Soc., 1980, 102, 1443–1444.
30. M. Tadokoro, H. Ōkawa, N. Matsumoto, M. Koikawa and S. Kida, J. Chem. Soc., Dalton Trans., 1991, 1657–1663.
31. A. Hori, Y. Mitsuka, M. Ohba and H. Ōkawa, Inorg. Chim. Acta, 2002, 337, 113–121.
32. E. J. Larson and V. L. Pecoraro, J. Am. Chem. Soc., 1991, 113, 7809–7810.
33. J. A. Garden, P. K. Saini and C. K. Williams, J. Am. Chem. Soc., 2015, 137, 15078–15081.
34. P. K. Saini, C. Romain and C. K. Williams, Chem. Commun., 2014, 50, 4164–4167.
35. A. C. Deacy, C. B. Durr and C. K. Williams, Dalton Trans., 2020, 49, 223–231.
36. G. Trott, J. A. Garden and C. K. Williams, Chem. Sci., 2019, 10, 4618–4627.
37. K. Wang, T. J. Prior and C. Redshaw, Chem. Commun., 2019, 55, 11279–11282.
38. O. Santoro and C. Redshaw, Catalysts, 2020, 10, 210.
39. P. Zanello, S. Tamburini, P. A. Vigato and G. A. Mazzocchin, Coord. Chem. Rev., 1987, 77, 165–273.
40. A. J. Atkins, D. Black, A. J. Blake, A. Marin-Becerra and S. Parsons, Chem. Commun., 1996, 457–464.
41. H. Ōkawa, H. Furutachi and D. E. Fenton, Coord. Chem. Rev., 1998, 174, 51–75.
42. M. Tadokoro, H. Ōkawa, N. Matsumoto, M. Koikawa and S. Kida, J. Chem. Soc., Dalton Trans., 1991, 1657–1663.
43. J. Nishio, H. Ōkawa, S. Ohtsuka and M. Tomono, Inorg. Chim. Acta, 1994, 218, 27–32.
44. D. Huang and R. H. Holm, J. Am. Chem. Soc., 2010, 132, 4693–4701.
45. S. Mohanta, S. Baitalik, S. K. Dutta and B. Adhikary, Polyhedron, 1998, 17, 2669–2677.
46. B. Kersting and G. Steinfeld, Chem. Commun., 2001, 1376–1377.
47. (a) Y. Journaux, V. Lozan, J. Klingele and B. Kersting, Chem. Commun., 2006, 83–84; (b) S. Brooker, Coord. Chem. Rev., 2001, 222(1), 33–56; (c) A. Christensen, C. Mayer, F. Jensen, A. D. Bond and C. J. McKenzie, Dalton Trans., 2006, 108–120.
48. M. Börner, D. Fuhrmann, J. Klose, H. Krautscheid and B. Kersting, Inorg. Chem., 2021, 60, 13517–13527.
49. G. Steinfeld and B. Kersting, Chem. Commun., 2000, 205–206.
50. C. Núñez, R. Bastida, A. Macías, L. Valencia, J. Ribas, J. L. Capelo and C. Lodeiro, Dalton Trans., 2010, 39, 7673–7683.
51. M. Gressenbuch and B. Kersting, Z. Anorg. Allg. Chem., 2016, 642, 719–723.
52. V. Lozan, C. Loose, J. Kortus and B. Kersting, Coord. Chem. Rev., 2009, 253, 2244–2260.
53. T. Fritz, G. Steinfeld, S. Käss and B. Kersting, Dalton Trans., 2006, 3812–3821.
54. Y. Journaux, T. Glaser, G. Steinfeld, V. Lozan and B. Kersting, Dalton Trans., 2006, 1738–1748.
55. A. W. Addison, T. Nageswara Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
56. S. C. Shoner, A. M. Nienstedt, J. J. Ellison, I. Y. Kung, D. Barnhart and J. A. Kovacs, Inorg. Chem., 1998, 37, 5721–5726.
57. T. Komuro, T. Matsuo, H. Kawaguchi and K. Tatsumi, Inorg. Chem., 2003, 42, 5340–5347.
58. C.-Y. Chiang, M. L. Miller, J. H. Reibenspies and M. Y. Darensbourg, J. Am. Chem. Soc., 2004, 126, 10867–10874.
59. M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812.
60. E. M. Gale, B. S. Narendrapurapu, A. C. Simmonett, H. F. I. Schaefer and T. C. Harrop, Inorg. Chem., 2010, 49, 7080–7096.
61. S. J. Grabowski, Understanding Hydrogen Bonds, The Royal Society Of Chemistry, 2020.
62. L. A. H. van Bergen, M. Alonso, A. Palló, L. Nilsson, F. De Proft and J. Messens, Sci. Rep., 2016, 6, 30369.
63. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
64. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
65. L. A. H. van Bergen, M. Alonso, A. Palló, L. Nilsson, F. De Proft and J. Messens, Sci. Rep., 2016, 6, 30369.
66. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266.
67. J. Contreras-García, W. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983–12990.
68. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B, 1969, 25, 925–946.
69. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
70. S. A. Cantalupo, H. E. Ferreira, E. Bataineh, A. J. King, M. V. Petersen, T. Wojtasiewicz, A. G. DiPasquale, A. L. Rheingold and L. H. Doerrer, Inorg. Chem., 2011, 50, 6584–6596.
71. D. H. Busch, P. H. Merrell, V. L. Goedken and J. A. Stone, J. Am. Chem. Soc., 1970, 92, 7590–7591.
72. C. Hu, B. C. Noll, C. E. Schulz and W. R. Scheidt, Inorg. Chem., 2010, 49, 10984–10991.
73. M. Ciampolini and G. P. Speroni, Inorg. Chem., 1966, 5, 45–49.
74. M. Ciampolini and N. Nardi, Inorg. Chem., 1966, 5, 41–44.
75. F. A. Cotton and M. D. Meyers, J. Am. Chem. Soc., 1960, 82, 5023–5026.
76. B. Kersting, Angew. Chem., Int. Ed., 2001, 40, 3987–3990.
77. J. Hausmann, S. Käss, S. Klod, E. Kleinpeter and B. Kersting, Eur. J. Inorg. Chem., 2004, 2004, 4402–4411.
78. X. Zhu, X.-Y. Wang, B.-L. Li, J. Wang and S. Gao, Polyhedron, 2012, 31, 77–81.
79. O. K. Medhi, S. Mazumdar and S. Mitra, Inorg. Chem., 1989, 28, 3243–3248.
80. T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230.
81. (a) O. Kahn, Molecular Magnetism, VCH Publishers, New York NY, 1993; (b) D. A. Pantazis, J. Chem. Theory Comput., 2019, 15, 938–948; (c) D. E. Bolster, P. Gütlich, W. E. Hatfield, S. Kremer, E. W. Müller and K. Wieghardt, Inorg. Chem., 1983, 22, 1725–1729.
82. T. Glaser, F. Kesting, T. Beissel, E. Bill, T. Weyhermüller, W. Meyer-Klaucke and K. Wieghardt, Inorg. Chem., 1999, 38, 722–732.
83. T. Glaser, T. Beissel, E. Bill, T. Weyhermüller, V. Schünemann, W. Meyer-Klaucke, A. X. Trautwein and K. Wieghardt, J. Am. Chem. Soc., 1999, 121, 2193–2208.
84. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358.
85. N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877–910.
86. Stoe & Cie, X-AREA and X-RED 32; V1.35, Stoe & Cie: Darmstadt, 2006.
87. G. M. Sheldrick, Crystal Structure Refinement with SHELXL, Acta Crystallogr., 2015, C71, 3–8.
88. G. M. Sheldrick, SHELXT Integrated Space-Group and Crystal Structure Determination, Acta Crystallogr., 2015, C71, 3–8.
89. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and K. H. Puschmann, OLEX2: A Complete Structure Solution, Refinement and Analysis Program, J. Appl. Crystallogr., 2009, 42, 339–341.
90. A. L. Spek, PLATON - A Multipurpose Crystallographic Tool; Utrecht University, Utrecht, The Netherlands, 2000.
91. K. Brandenburg, Diamond, Crystal Impact GbR, Bonn, Germany, 1999.
92. L. Noodleman, C. Y. Peng, D. A. Case and J.-M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244.
93. L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143.
94. L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743.
95. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
96. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
97. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
98. F. Neese, Int. J. Quantum Chem., 2001, 83, 104–114.
99. F. Neese, J. Chem. Phys., 2003, 119, 9428–9443.
100. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
101. R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105.
102. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
103. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
104. F. Neese, Chem. Phys. Lett., 2000, 325, 93–98.
105. D. Bykov, T. Petrenko, R. Izsák, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113, 1961–1977.
106. “Software update: The ORCA program system—Version 5.0 - Neese - 2022 - WIREs Computational Molecular Science - Wiley Online Library”, can be found under https://wires.onlinelibrary.wiley.com/doi/10.1002/wcms.1606.
107. F. Neese, J. Comput. Chem., 2023, 44, 381–396.
108. G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562.
109. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
110. R. A. Boto, J. Contreras-García, J. Tierny and J.-P. Piquemal, Mol. Phys., 2016, 114, 1406–1414.
111. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
112. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
113. (a) CCDC 2392031: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2l939b; (b) CCDC 2392032: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2l93bc.

---