Open Access Article
Open Access ArticleCationic beryllium–group 13 heterobimetallic dimetallocenes with a donor–acceptor bond
Fathima Thanha
Thazhe Namboorikandy
 and
Pattiyil
Parameswaran
and
Pattiyil
Parameswaran
 *
*
Department of Chemistry, National Institute of Technology Calicut, Kozhikode, Kerala 673601, India. E-mail: param@nitc.ac.in
First published on 20th November 2025
Abstract
A comprehensive geometrical and bonding analysis of heterobimetallic dimetallocenes of the form [Cp–Be–M–Cp]+, where M represents group 13 elements (B, Al, Ga, In, Tl), is presented. The equilibrium geometry of dimetallocenes indicates a collinear geometry along the centre of the two Cp rings, the Be centre and the group 13 element, except for the Tl complex. Optimised geometries reveal that Be–C bond distances decrease when the group 13 element changes from B to Tl. The molecular orbital and NBO analyses show a Be–M σ-bond formed by the overlap of the 2s orbital of Be with the spn hybrid orbital of the group 13 element. The percentage of s character in the spn hybrid orbital increases as the group 13 element changes from B to Tl. However, the natural population analysis (NPA) indicates a significant charge polarisation with a low value of the Wiberg bond index. Energy decomposition analysis with natural orbitals for chemical valence (EDA-NOCV) reveals that the Be–M σ bond can be represented by a donor–acceptor interaction (Cp–Be+ ← M–Cp). Apart from the σ bonding interaction, there exists a slight π bonding interaction arising from hyperconjugative donation from the [BeCp]+ bonding molecular orbital to the [BCp] antibonding molecular orbital. Even though the strength of the Be–M bond decreases, the percentage of covalent interaction increases when the group 13 element changes from B to Tl.
Introduction
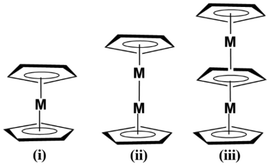
The revolutionary discovery of ferrocene by Kealy and Pauson1 in 1951 led to the origin of a novel class of compounds in organometallic chemistry, metallocenes, also called ‘sandwich compounds’(Scheme 1(i)). Two cyclopentadienyl rings (Cp) sandwich a metal centre to form a metallocene.2–4 Derivatives of metallocenes with the general formula (Cp)2M (where Cp is cyclopentadienyl and M is the metal centre) have been reported for many elements in the periodic table over the years.5–7 The discovery and isolation of the [Cp3Fe2]+ (ref. 8) and Cp3Ni+ (ref. 9 and 10) cations, where the metal atom is stacked between three cyclopentadienyl rings, marked a major step in multi-decker metallocenes11–13 (Scheme 1(ii and iii)). Metallocenes have a wide range of applications in various fields, including catalysis,14–16 biomedicine,17–19 cathodic batteries,20–22 and sensor design.23–25The unexpected discovery of decamethyldizincocene (Cp*–Zn–Zn–Cp*, Cp* = C5Me5)26 by Carmona and coworkers in 2004 opened a new dimension in metallocene chemistry. In this D5h symmetric compound, a pair of Zn atoms is sandwiched between two Cp* rings, and the Zn–Zn bond is aligned collinearly with the C5 axes of the Cp* rings. Carmona also synthesised a similar dizincozene, Zn2(η5-C5Me4Et)2,27 with a substituted cyclopentadienyl ring. Kress28–32 confirmed from the electronic structural studies that the Zn atom has a +1 oxidation state rather than the usual +2 oxidation state for group 12 metals. Later, theoretical studies by many scientists concluded that the Zn–Zn bond is a single σ bond supported by weak π-type d–d and p–p interactions.33,34 Later, other bimetallic metallocenes of group-12 elements, including Zn,35,36 Cd37,38 and Hg,39 were also theoretically predicted (Scheme 1(ii)).
The discovery of transition metal dimetallocenes paved the way for main-group dimetallocenes. Schaefer and co-workers40 theoretically predicted the existence of homobimetallic dimetallocenes of alkaline-earth metals based on the view that both Zn and alkaline-earth metals possess an ns2 valence shell electronic configuration. Similarly, the electronic structure of stable binuclear metallocenes of group 2 metals has also been studied.41 Frenking and coworkers subsequently studied multimetallocenes with Be, Mg, Ca, and Zn.42 These studies showed that Cp2Be2 (or Cp*2Be2) is more stable than Cp*2Zn2. This led to the groundbreaking discovery of unusual metal–metal bonding among the main-group homobimetallic dimetallocenes. Boronski, Aldridge, and co-workers experimentally characterised a diberyllocene with a Be–Be single bond.43 They also isolated complexes with the first Be–Zn, Be–Al,44 Be–In and Be–Ga45 bonds. Later, many other complexes with homobimetallic46 and heterobimetallic47 bonding involving Be and alkaline earth metals have been reported. The metal–metal bonding in homonuclear dimetallocenes of Be, Mg, and Ca has been investigated in a theoretical study of A2N-MM′-NA2 (A = H, Li, Na)48 complexes. However, dimetallocenes of p-block elements are still unknown. Despite numerous attempts to isolate a silicon dimetallocene, all of them failed, as the alleged decamethyldisilicocene disproportionates into silicon(0) and decamethylsilicocene (Cp*2Si).49,50 Main-group bis-element sandwiches formed by donor–acceptor interactions of MCp and ECp (M = Li, Na, K; E = B, Al, Ga) have been studied by Timoshkin and Schaefer.51 Previous theoretical work52 and recent experimental studies53 have shown that heterobimetallic dimetallocenes with donor–acceptor interactions can preferentially adopt double-decker structures, such as [CpBe⋯CpE]+, rather than the conventional dimetallocene form [CpBe ← ECp]+. Recently, a lithium–aluminium dimetallocene with a highly polar Li–Al bond was isolated by Schafer in 2024.54 It is significantly reinforced by dispersion interactions, which arise between the two highly substituted Cp ligands. Li and co-workers elucidated the bonding characteristics in (η5-C5H5)2M2 complexes through computational analysis.55 Meanwhile, Gosch and Wilson56 expanded this understanding by examining related heterobimetallic systems, thereby providing a comparative perspective on metal–metal and metal–ligand interactions across main-group and transition metals.
Unlike classical transition metal metallocenes, such as Cp2Fe, which exhibit significant covalent bonding due to d-orbital participation, metallocenes of alkaline earth metals, like Cp2Ba, are predominantly ionic, reflecting pronounced differences in bonding nature and reactivity. However, the bonding in heterobimetallic dimetallocenes incorporating both beryllium and group 13 elements remains largely unexplored. At the same time, similar systems with two of the same metals or with group 1 and group 13 metals have been studied. Notably, beryllium is expected to favour electrostatic interactions, whereas group 13 metals are known for electron sharing and multicenter bonding. This research gap leaves open the question of how these differing bonding tendencies interact within a single molecule. We hypothesise that such systems may exhibit unique donor–acceptor interactions, offering new insights into bonding beyond the established electrostatic and covalent paradigms in metallocene chemistry.
Results and discussion
The optimised geometries of dimetallocenes [Cp–Be–M–Cp]+ (M = B–Tl), along with important structural parameters such as Be–Cp, Be–M, and M–Cp bond distances, are shown in Fig. 1. The centres of the two η5-C5H5 groups and the two metal atoms are collinear in all dimetallocenes, except for the Tl dimetallocene. The cyclopentadienyl rings deviate slightly from an ideal eclipsed conformation, exhibiting a minor variation in their relative orientation.The Be–C bond distances decrease as the group 13 element changes from B to Tl. This can be attributed to the donation of electrons from the bonding molecular orbital corresponding to Cp and Be interactions in [CpBe]+ to the antibonding molecular orbital corresponding to Cp and M interactions in [MCp] (vide infra). All metal–metal interactions can be considered as single bonds, where these distances are slightly shorter than single bond covalent radii proposed by Pyykkö and Atsumi, with values of 1.02 Å (Be), 0.85 Å (B), 1.26 Å (Al), 1.24 Å (Ga), 1.42 Å (In), and 1.44 Å (Tl).57 Although certain values are derived from a limited sample size (notably for Be), they provide a valuable comparison of metal–metal bonding. The Be–M (M = Al, Ga, In) bond distances observed in our complexes were compared with experimentally reported values. The experimentally known Be–Al bond lengths are 2.474 Å and 2.432 Å,44 while the calculated Be–Al distance in [Cp–Be–Al–Cp]+ is 2.279 Å. The calculated value closely matches the expected value for a typical single covalent bond. The Be–Ga (2.206 Å)44 and Be–In (2.358 Å)45 bond lengths determined experimentally align well with our calculated values of 2.213 Å and 2.364 Å, respectively.
Except for the Be–Tl dimetallocene, all other dimetallocenes have almost similar metal–ring (M–C) bond distances, which suggests that the hapticity of the cyclopentadienyl ring is 5. Cp–Be–Tl–Cp has one shorter Tl–C bond of 2.373 Å, two Tl–C bonds of 2.555 Å and two longer bonds of 2.791 Å. Therefore, the geometrical parameters suggest the bonding possibilities of η1–η3.
Our primary focus is to study the nature of metal–metal bonding in heterobimetallic dimetallocenes of Be. Molecular orbital analysis indicates that all dimetallocenes have occupied the Be–M σ-bonding orbital, viz HOMO−2 for [Cp–Be–B–Cp]+ and [Cp–Be–Al–Cp]+ and HOMO−4 for other dimetallocenes (Fig. 2). The molecular orbitals corresponding to Be–M π bonds are vacant. However, the valence p orbitals of Be and group 13 elements are involved in bonding interaction with π-molecular orbitals of the cyclopentadienyl ring, as indicated by the frontier occupied molecular orbitals of the system. All the MOs of the five dimetallocenes of Be are given in the SI. All the molecules exhibit a significant HOMO–LUMO energy gap, indicating their greater stability. The aforementioned bonding description is corroborated by the numerical data obtained from the natural bond orbital (NBO) analysis (Table 1). The Be atom in all dimetallocenes shows a positive value, which lies in the range of 1.27–1.53e. The positive charge on Be is moreover consistent with the electronegativity of the attached group 13 element, where the Be atom shows the highest positive charge in [Cp–Be–B–Cp]+. The charge analysis suggests that Be is electrophilic. However, it should be noted that previously reported beryllium–aluminyl complexes by Boronski and Aldridge44 suggested a nucleophilic Be(δ−)–Al(δ+) bond. This variation is attributed to the difference in the electronegativity of the atom/group attached to Al. The atoms/groups coordinated to aluminium in the beryllium–aluminyl complex are two N atoms and one O atom, whereas the atom/group attached to Al in [Cp–Be–Al–Cp]+ is a C atom. The charge of the Cp ring is negative except for that of the Cp ring attached to B. This indicates a significant electrostatic interaction between Be and the group 13 element, as indicated by the relative contribution of the orbital towards the Be–M bond (Table 2). The Wiberg bond index (WBI) values are less than one, indicating charge polarisation in the Be–M bond. The charge difference between Be and group 13 elements is in the order of Be–B (1.78e) ≫ Be–Tl (0.77e) > Be–Ga (0.74e) > Be–In (0.71e) > Be–Al (0.50e). The calculated WBI values are correlated with the above-mentioned charge differences. The Be–M σ-bond is formed by the overlap of the 2s orbital of Be (90.37%–94.20%) with the spn hybrid orbital of the group 13 element, M. The percentage of s character in the spn hybrid orbital increases as the group 13 element changes from B (55.78%) to In (84.7%). Therefore, the orbital overlap increases as the group 13 element changes from B to Tl in [Cp–Be–M–Cp]+. The NBO calculation reveals a lone pair on Tl, with a major contribution from the 6s orbital (94.2%), having an occupancy of 1.72e (Table 2). The η1 to η3 hapticity of the Cp ring connected to Tl can be attributed to the larger atomic size as well as the predominant relativistic effect of the 6s orbital of Tl.58
 | ||
| Fig. 2 Important frontier molecular orbitals of dimetallocenes at the M06/def2-TZVPP//BP86/def2-TZVP level of theory; eigenvalues are given in eV in parentheses; isosurface value = 0.03. | ||
| [Cp–Be–M–Cp]+ | Wiberg bond index (Be–M) | q Cp (attached to Be) | q Be | q M | q Cp (attached to M) |
|---|---|---|---|---|---|
| [Cp–Be–B–Cp]+ | 0.475 | −0.41 | 1.531 | −0.245 | +0.14 |
| [Cp–Be–Al–Cp]+ | 0.710 | −0.71 | 1.271 | 0.764 | −0.33 |
| [Cp–Be–Ga–Cp]+ | 0.613 | −0.70 | 1.352 | 0.614 | −0.27 |
| [Cp–Be–In–Cp]+ | 0.592 | −0.71 | 1.354 | 0.639 | −0.29 |
| [Cp–Be–Tl–Cp]+ | 0.588 | −0.71 | 1.364 | 0.591 | −0.25 |
| Be–M | Occupancy | Contribution from Be | Contribution from M | Relative contribution (Be![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M) M) |
||
|---|---|---|---|---|---|---|
| s-Orbital contribution | p-Orbital contribution | s-Orbital contribution | p-Orbital contribution | |||
| Be–B | 1.99 | 94.20% | 5.79% | 5.79% | 44.07% | 15.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84.6 84.6 |
| Be–Al | 1.99 | 91.64% | 8.14% | 8.14% | 24.45% | 25.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74.1 74.1 |
| Be–Ga | 2.00 | 90.37% | 9.54% | 9.54% | 16.25% | 20.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79.1 79.1 |
| Be–In | 2.00 | 90.51% | 9.21% | 9.21% | 15.12% | 19.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80.0 80.0 |
| Be–Tl | — | — | — | — | — | — |
To understand the quantitative nature of the above-mentioned bonding description, we have performed an energy decomposition analysis coupled with natural orbital for chemical valence (EDA-NOCV) for all heterobimetallic dimetallocenes [Cp–Be–M–Cp]+. The choice of electronic states for the fragments is crucial in the EDA-NOCV analysis. Two different intuitive bonding possibilities have been considered for each dimetallocene (1–5, Scheme 2 and Table 3). The bonding representation A shows a donor–acceptor interaction with [CpBe]+ and [CpM] fragments. The bonding possibility B is an electron-sharing interaction with [CpBe] and [CpM]+. The best bonding situation has the lowest numerical value for the orbital interaction term, ΔEorb. The lowest orbital interaction energy, ΔEorb, indicates how closely the electronic states of the fragments match with those in the molecule.59 Since the ΔEorb value for bonding representation A is relatively low compared to that of B for all dimetallocenes, the former representation can be considered as the best bonding representation. It is noteworthy that the ΔEPauli for the bonding representation B is much higher than that in bonding representation A. The preparation energy (ΔEprep) for bonding possibility A is lower than for the other possibilities studied. Hence, bonding possibility A is considered for further analysis. The ΔEint can be considered as the measure of the strength of the Be–M bond, which increases as the group 13 element changes from B to Tl. The ΔEint correlates well with the dissociation energy of the Be–M bond as well. The electrostatic interaction energy, ΔEelect, increases and Pauli's repulsion energy, ΔEPauli, decreases as M changes from B to Tl. On the other hand, the variation in orbital stabilisation energy, ΔEorb, is minimal. Among the attractive components of interaction energy, the percentage of orbital stabilisation energy, ΔEorb, increases (38.64 to 90.16%) and the percentage of electrostatic energy, ΔEelect, decreases (61.35% to 9.83%) when the group 13 element moves down the group (Fig. 3). The Be–M σ-bond is formed by the donation of a lone pair of electrons from the spn hybrid orbital of the group 13 element to the vacant 2s orbital of Be (Fig. 4). The charge difference between [CpBe]+ and [MCp] and the electronegativity difference between Be and the group 13 element, M, is of the order Be–B ≫ Be–Ga > Be–In > Be–Tl > Be–Al, which accounts for the increased covalent character as the group 13 element changes from B to Tl, except for [Cp–Be–Al–Cp]+.
 | ||
| Fig. 4 Orbital interaction diagram of the [Cp–Be–B–Cp]+ dimetallocene showing frontier valence MOs. The fragments are [CpBe]+ (left side) and [BCp]0 (right side). | ||
| Be–B | Be–Al | Be–Ga | Be–In | Be–Tl | Be–B | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | A | B | A | B | A | A | B | |
| a Values in parentheses give the percentage contribution to ΔEorb + ΔEelect. b Percentage contribution to ΔEorb. c ΔErest = ΔEorb − (ΔEσ + ΔEπ⊥ + ΔEπ∥). d Dissociation energy (De). | ||||||||||||
| ΔEint | −120.45 | −146.43 | −78.78 | −121.80 | −66.69 | −150.68 | −59.05 | −134.28 | −49.46 | −105.90 | −120.45 | −146.43 |
ΔEelect![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−101.67 (61.35%) | −101.40 (24.20%) | −35.69 (35.48%) | −80.70 (25.60%) | −25.30 (29.89%) | −114.28 (30.66%) | −15.32 (20.74%) | −124.42 (35.80%) | −6.08 (9.83%) | −147.39 (43.29%) | −101.67 (61.35%) | −101.40 (24.20%) |
| ΔEPauli | 50.35 | 277.60 | 26.08 | 197.70 | 22.54 | 226.54 | 19.60 | 217.97 | 17.67 | 239.80 | 50.35 | 277.60 |
ΔEorb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−64.03 (38.64%) | −317.52 (75.79%) | −64.89 (64.51%) | −234.53 (74.39%) | −59.34 (70.10%) | −258.35 (69.33%) | −58.53 (79.25%) | −223.03 (64.19%) | −55.75 (90.16%) | −193.02 (56.70%) | −64.03 (38.64%) | −317.52 (75.79%) |
| ΔEdisp | −5.10 | −5.10 | −4.28 | −4.28 | −4.59 | −4.59 | −4.80 | −4.80 | −5.30 | −5.30 | −5.10 | −5.10 |
ΔEσ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−49.17 (76.79%) | −259.81 (81.82%) | −57.81 (89.08%) | −186.14 (79.36%) | −50.97 (85.89%) | −129.96 (50.30%) | −50.54 (86.34%) | −122.41 (54.88%) | −47.76 (85.66%) | −60.56 (31.37%) | −49.17 (76.79%) | −259.81 (81.82%) |
ΔEπ⊥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−3.99 (6.23%) | −31.33 (9.86%) | −1.83 (2.82%) | −34.08 (14.53%) | −2.65 (4.46%) | −90.44 (35.01%) | −2.43 (4.15%) | −61.94 (27.77%) | −2.66 (4.77%) | −93.58 (48.48%) | −3.99 (6.23%) | −31.33 (9.86%) |
ΔEπ∥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
−3.99 (6.23%) | −10.35 (3.25%) | −1.83 (2.82%) | −2.65 (1.12%) | −2.65 (4.46%) | −20.98 (8.12%) | −2.43 (4.15%) | −26.08 (11.69%) | −2.11 (3.78%) | −11.85 (6.13%) | −3.99 (6.23%) | −10.35 (3.25%) |
ΔErest![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
−6.88 (10.74%) | −16.03 (5.04%) | −3.42 (5.27%) | −11.66 (4.97%) | −3.07 (5.17%) | −16.97 (6.56%) | −3.13 (5.34%) | −12.60 (5.64%) | −3.22 (5.77%) | −27.08 (14.02%) | −6.88 (10.74%) | −16.03 (5.04%) |
| ΔEprep | 11.93 | 37.91 | 11.29 | 54.31 | 26.96 | 110.95 | 18.91 | 94.14 | 11.05 | 67.49 | 11.93 | 37.91 |
−De![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
−108.52 | −108.52 | −67.49 | −67.49 | −39.73 | −39.73 | −40.14 | −40.14 | −38.41 | −38.41 | −108.52 | −108.52 |
The orbital stabilisation energy (ΔEorb) can be categorised into three symmetry-adapted components: one σ-interaction and two π-interactions (π∥ and π⊥). The σ bonding energy (ΔEσ) is the primary component of orbital interactions in all dimetallocenes. This arises from the donation of a lone pair of electrons from [CpM] to an empty spn hybrid orbital of [CpBe]+. The deformation densities Δρ1 in Fig. 5 represent this σ-bonding interaction. Hence, the σ-bonding interaction in dimetallocenes can be best described by a donor–acceptor (Be ← M) bond, with a significant contribution from electrostatic interaction (61.35%) (HOMO−2, Fig. 2, and Δρ1, Fig. 5). It is notable that the percentage of electrostatic interactions is lower than that of orbital interactions for all other heavier group 13 compounds. The donor fragment orbital of BCp is an spn hybrid orbital on B, with the back lobe strongly bonding with all in-phase π-molecular orbitals of the Cp ring (Fig. 4). As a result, there is a net charge transfer from the Cp ring to B. Since the electronegativity of heavier group 13 elements is much lower than that of B, electrostatic interactions between Cp and these heavier elements are more dominant. Consequently, the Cp ring carries a slight positive charge, while the group 13 element bears a slight negative charge in [Cp–Be–B–Cp]+. An opposite trend is observed in the heavier group 13 analogues. It is to be noted that the previously reported heterobimetallic dimetallocenes show significant ionic character for the Al–Li bond, which can be attributed to the difference in the electronegativity of Al and Li compared to Be and group-13 elements.54,55
ΔEπ∥ and ΔEπ⊥ correspond to pseudo-π bonding interactions resulting from donation of electrons from the bonding molecular orbital corresponding to Cp and Be interactions in [CpBe]+ to the antibonding molecular orbital corresponding to Cp and M interactions in [MCp]. Accordingly, these pseudo-π-interactions can be considered as hyperconjugative interactions. However, these pseudo-π-bonding interactions also show significant polarisation of electron density from the Cp ring to the M centre as well. This can be attributed to the high positive charge in the [BeCp]+ fragment. The sum of ΔEπ∥ and ΔEπ⊥ increases in the following order: Be–B (−7.98 kcal mol−1) < Be–Ga (−5.30 kcal mol−1) < Be–In (−4.86 kcal mol−1) < Be–Tl (−4.77 kcal mol−1) < Be–Al (−3.66 kcal mol−1). This can be correlated with the decrease in Be–C bond distances as the group 13 element changes from B to Tl, except for [Cp–Be–Al–Cp]+. Note that these second-order interactions are more efficient when the Be–M bond has more covalent character, which is the highest in [Cp–Be–Al–Cp]+. The deformation densities Δρ2 and Δρ3 in Fig. 5 represent the above-discussed pseudo π-bonding interaction. Since hyperconjugative interactions are of secondary type, energy stabilisation is found to be much less across all dimetallocenes. The dispersive interactions (ΔEdisp) stabilize and the extent of stabilization is similar in all dimetallocenes (−4.28 to −5.30 kcal mol−1). Hence, it is proposed that the substituted Cp rings, which could stabilize dimetallocenes more effectively through dispersive interactions, can be potential synthetic targets.
Conclusions
This study provides a systematic computational quantum mechanical analysis of heterobimetallic dimetallocenes of the type [Cp–Be–M–Cp]+, where M represents the group 13 elements (B–Tl). The dimetallocenes investigated in this work are cationic species, carrying a +1 charge and exhibiting a closed-shell electronic configuration. The equilibrium geometries of [Cp–Be–M–Cp]+ dimetallocenes (M – group 13 element, B–Tl) are collinear along the Cp–Be–M–Cp axis, except for the Tl complex, with optimised structures showing a shortening of Be–C bond lengths as M changes from B to Tl. The overlap between the 2s orbital of Be and the spn hybrid orbital of group 13 elements results in the formation of the Be–M σ-bond, which was confirmed by MO and NBO analysis. Furthermore, lower Wiberg bond indices indicate a significant charge polarisation of the Be–M bond. The EDA-NOCV analysis shows that the Be–M σ bond is a donor–acceptor interaction (Cp–Be+ ← M–Cp), where the lone pair of electrons from the filled orbital of M is donated to the vacant orbital of Be. In addition to the σ bonding interaction, a minor π bonding interaction occurs due to hyperconjugative transfer from the [CpBe]+ bonding molecular orbital to the [MCp] antibonding molecular orbital. In summary, the percentage of covalent interaction increases and electrostatic interaction decreases as M changes from B to Tl. The results lay a foundation for future experimental and theoretical research on the reactivity and potential uses of these types of organometallic systems, especially for compounds with very high M–M bond dissociation energies, such as [Cp–Be–B–Cp]+.Computational methodology
All calculations were carried out using Gaussian 0960 and the Amsterdam modelling suite program.61 All geometries were optimised using the generalised gradient approximation (GGA) with Becke's exchange functional incorporated with the correlation functional of Perdew(BP86).62 The basis set has triple ζ-quality, augmented with a single polarisation function (def2-TZVP).63 This is denoted as BP86/def2-TZVP. The nature of the minimum was characterised by calculating the Hessian matrix analytically. NBO analysis was performed using the NBO6.064 program package at the M06/def2-TZVPP//BP86/def2-TZVP level of theory. The energy decomposition analysis65 coupled with natural orbital for chemical valence66 (EDA NOCV) was carried out at the BP86/TZ2P level of theory using ADF 2024.1. The ZORA67 (Zeroth Order Regular Approximation) method was used for scalar relativistic correction, and the core electrons were treated with the frozen-core approximation.EDA considers the interactions between fragments A0 and B0 in their electronic and geometric ground states ψ0A and ψ0B with energies E0A and E0B,68 resulting in the formation of a molecule A–B with the corresponding wave function ψAB and energy EAB. The initial step involves distorting the fragments A0 and B0 from their equilibrium geometries and wave functions ψ0A and ψ0B to the electronic states and geometries ψA and ψB (with energies EA and EB) that they have in the molecule A–B. The preparation energy ΔEprep (eqn (1)) is the total energy required to electrically excite and distort all fragments to this state:
| ΔEprep = EA − E0A + EB − E0B | (1) |
The intrinsic interaction energy (ΔEint), which is the difference between the energy of the molecule EAB and the energies of the prepared fragments EA and EB (eqn (2)), is calculated in EDA:
| ΔEint = EAB − EA − EB | (2) |
The bond dissociation energy De (by definition with the opposite sign) is the sum of the instantaneous interaction energy ΔEint and ΔEprep (eqn (3))
| −De = ΔEint + ΔEprep | (3) |
The instantaneous interaction energy of a bond A–B, which is an indicator of the bond strength, is partitioned into chemically meaningful components. Within the EDA scheme, this partitioning is as follows.
| ΔEint = ΔEelect + ΔEPauli + ΔEorb + ΔEdisp |
The term ΔEelect refers to the quasi-classical electrostatic interactions, wherein the frozen electron density distribution of the fragments in the molecular geometry is computed using quantum mechanics, while the interaction between the nuclei and electrons is determined by classical rules. This is an appealing component that provides an estimate of electrostatic interactions not accounted for in the orbital-based analysis. It is important to remember that ΔEPauli denotes the repulsive interactions between fragments of a similar spin as they approach each other, not ionic bonding. It is computed using the antisymmetrization and renormalisation of the Kohn–Sham determinant of the orbitals. ΔEb is the energy associated with the stability of orbitals during bond formation and constitutes an attractive component.
It encompasses the impacts of charge transfer, relaxation, and polarisation resulting from the alteration of the charge distribution of the fragments during bond formation.
In the EDA-NOCV framework, the ΔEorb term can be further decomposed into contributions from each irreducible representation within the point group of the interacting system. Developed by Mitoraj and Michalak, the natural orbitals for chemical valence (NOCV) offer insight into each orbital interaction between the fragments and the contribution of each pair of interacting orbitals (ψ−n/ψn) to the total bond energy.
The EDA-NOCV system expresses ΔEorb in terms of NOCVs as follows:
The Kohn–Sham matrix elements  and
and  are defined over NOCV pairs with eigenvalues −vn and vn, respectively, with respect to the transition-state density. The density of the transition state is the intermediate density between that of the molecule and the superimposed fragments. Orbitals with a negative value exhibit antibonding properties, while those with a positive value exhibit bonding properties. It is equivalent to the percentage of electron density that is transmitted between NOCV pairs during the formation of the molecule from the frozen fragments. The strength of pairwise orbital interactions can be quantitatively estimated, and the resulting change in charge density is visualised using deformation densities.
are defined over NOCV pairs with eigenvalues −vn and vn, respectively, with respect to the transition-state density. The density of the transition state is the intermediate density between that of the molecule and the superimposed fragments. Orbitals with a negative value exhibit antibonding properties, while those with a positive value exhibit bonding properties. It is equivalent to the percentage of electron density that is transmitted between NOCV pairs during the formation of the molecule from the frozen fragments. The strength of pairwise orbital interactions can be quantitatively estimated, and the resulting change in charge density is visualised using deformation densities.
Author contributions
The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: molecular orbitals of 1–5, orbital interaction diagrams, NOCV orbitals, NOCV deformation density plots and bond orbital occupancy. See DOI: https://doi.org/10.1039/d5dt02345a.Acknowledgements
PP and FT thank the Centre for Computational Modelling and Simulation (CCMS) and the Central Computer Center (CCC) at NITC for the computational facilities. PP acknowledges the SERB, India, for financial support.References
- T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039–1040 CrossRef CAS.
- S. A. Miller, J. A. Tebboth and J. F. Tremaine, J. Chem. Soc. (Resumed), 1952, 632 RSC.
- G. Wilkinson, M. Rosenblum, M. C. Whiting and R. B. Woodward, J. Am. Chem. Soc., 1952, 74, 2125–2126 CrossRef CAS.
- R. K. Bohn and A. Haaland, J. Organomet. Chem., 1966, 5, 470–476 CrossRef CAS.
- M. Green and I. R. Butler, The Royal Society of Chemistry eBooks, Royal Society of Chemistry, Cambridge, 2001, pp. 442–478 Search PubMed.
- S. Baguli, S. Mondal, C. Mandal, S. Goswami and D. Mukherjee, Chem. – Asian J., 2022, 17, e202100962 CrossRef CAS.
- J. Rausch, C. Apostolidis, O. Walter, V. Lorenz, C. G. Hrib, L. Hilfert, M. Kühling, S. Busse and F. T. Edelmann, New J. Chem., 2015, 39, 7656–7666 RSC.
- S. M. Schildcrout, J. Am. Chem. Soc., 1973, 95, 3846–3849 CrossRef CAS.
- H. Werner and A. Salzer, Synth. React. Inorg. Met.-Org. Chem., 1972, 2, 239–248 CrossRef CAS.
- A. Salzer and H. Werner, Angew. Chem., Int. Ed. Engl., 1972, 11, 930–932 CrossRef.
- S. Nagao, A. Kato, A. Nakajima and K. Kaya, J. Am. Chem. Soc., 2000, 122, 4221–4222 CrossRef.
- C. Morari, H. Allmaier, F. Beiuşeanu, T. Jurcuţ and L. Chioncel, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 085413 CrossRef.
- F. Huttmann, N. Schleheck, N. Atodiresei and T. Michely, J. Am. Chem. Soc., 2017, 139, 9895–9900 CrossRef PubMed.
- K. Foo, E. Sella, I. Thomé, M. D. Eastgate and P. S. Baran, J. Am. Chem. Soc., 2014, 136, 5279–5282 CrossRef PubMed.
- K. P. Fitzpatrick, C. B. Schwamb, C. T. Check, K.-P. Jang, D. N. Barsoum and K. A. Scheidt, Organometallics, 2020, 39, 2705–2712 CrossRef.
- L. Cunningham, A. Benson and P. J. Guiry, Org. Biomol. Chem., 2020, 18, 9329–9370 RSC.
- C. Ornelas, New J. Chem., 2011, 35, 1973 RSC.
- V. Raičević, N. Radulović and L. Jovanović, Eur. J. Inorg. Chem., 2022, 1666–1676 Search PubMed.
- M. Bouché, C. Hognon, S. Grandemange, A. Monari and P. C. Gros, Dalton Trans., 2020, 49, 11451–11466 Search PubMed.
- C. Su, L. Ji, L. Xu, X. Zhu, H. He, Y. Lv, M. Ouyang and C. Zhang, RSC Adv., 2015, 5, 14053–14060 Search PubMed.
- S. M. Beladi-Mousavi, S. Sadaf, L. Walder, M. Gallei, C. Rüttiger, S. Eigler and C. E. Halbig, Adv. Energy Mater., 2016, 6, 1600108 Search PubMed.
- S. M. Beladi-Mousavi and L. Walder, Polymer, 2022, 245, 124658 Search PubMed.
- L. Yan, X. Yan, H. Li, X. Zhang, M. Wang, S. Fu, G. Zhang, C. Qian, H. Yang, J. Han and F. Xiao, Microchem. J., 2020, 157, 105016 Search PubMed.
- S. Dewangan, T. Barik, B. Halder, A. Mishra, R. Dhiman, T. Sasamori and S. Chatterjee, J. Organomet. Chem., 2021, 948, 121922 CrossRef.
- R. Hein, P. D. Beer and J. J. Davis, Chem. Rev., 2020, 120, 1888–1935 CrossRef PubMed.
- I. Resa, E. Carmona, E. Gutierrez-Puebla and A. Monge, Science, 2004, 305, 1136–1138 CrossRef PubMed.
- A. Grirrane, I. Resa, A. Rodriguez, E. Carmona, E. Alvarez, E. Gutierrez-Puebla, A. Monge, A. Galindo, D. del Río and R. A. Andersen, J. Am. Chem. Soc., 2006, 129, 693–703 CrossRef PubMed.
- D. del Río, A. Galindo, I. Resa and E. Carmona, Angew. Chem., Int. Ed., 2005, 44, 1244–1247 CrossRef PubMed.
- S. L. Richardson, T. Baruah and M. R. Pederson, Chem. Phys. Lett., 2005, 415, 141–145 Search PubMed.
- M. R. Philpott and Y. Kawazoe, Chem. Phys., 2006, 327, 283–290 CrossRef.
- Y. Kan, J. Mol. Struct.:THEOCHEM, 2006, 805, 127–132 CrossRef.
- J. W. Kress, J. Phys. Chem. A, 2005, 109, 7757–7763 CrossRef PubMed.
- Z.-Z. Xie and W.-H. Fang, Chem. Phys. Lett., 2005, 404, 212–216 Search PubMed.
- M. R. Philpott and Y. Kawazoe, J. Mol. Struct.:THEOCHEM, 2006, 773, 43–52 CrossRef.
- Z. Zhu, R. J. Wright, M. M. Olmstead, E. Rivard, M. Brynda and P. P. Power, Angew. Chem., Int. Ed., 2006, 45, 5807–5810 CrossRef PubMed.
- A. Grirrane, I. Resa, A. Rodriguez, E. Carmona, E. Alvarez, E. Gutierrez-Puebla, A. Monge, A. Galindo, D. del Río and R. A. Andersen, J. Am. Chem. Soc., 2006, 129, 693–703 CrossRef PubMed.
- Z. Zhu, R. C. Fischer, J. C. Fettinger, E. Rivard, M. Brynda and P. P. Power, J. Am. Chem. Soc., 2006, 128, 15068–15069 CrossRef.
- Z. Liu, W. Q. Tian, J. Feng, G. Zhang, W. Li, Y. Cui and C. Sun, Eur. J. Inorg. Chem., 2006, 2006, 2808–2818 CrossRef.
- A. Grirrane, I. Resa, D. del Río, A. Rodríguez, E. Álvarez, K. Mereiter and E. Carmona, Inorg. Chem., 2007, 46, 4667–4676 CrossRef PubMed.
- A. Y. Timoshkin and H. F. Schaefer, Organometallics, 2005, 24, 3343–3345 CrossRef.
- Y. Xie, H. F. Schaefer and E. D. Jemmis, Chem. Phys. Lett., 2005, 402, 414–421 CrossRef.
- A. Velazquez, I. Fernández, G. Frenking and G. Merino, Organometallics, 2007, 26, 4731–4736 CrossRef.
- J. T. Boronski, A. E. Crumpton, L. L. Wales and S. Aldridge, Science, 2023, 380, 1147–1149 CrossRef PubMed.
- J. T. Boronski, L. R. Thomas-Hargreaves, M. A. Ellwanger, A. E. Crumpton, J. Hicks, D. F. Bekiş, S. Aldridge and M. R. Buchner, J. Am. Chem. Soc., 2023, 145, 4408–4413 CrossRef PubMed.
- J. T. Boronski, L. P. Griffin, C. Conder, A. E. Crumpton, L. L. Wales and S. Aldridge, Chem. Sci., 2024, 15, 15377–15384 RSC.
- J. T. Boronski, A. E. Crumpton, A. F. Roper and S. Aldridge, Nat. Chem., 2024, 16, 1295–1300 CrossRef PubMed.
- L. P. Griffin and J. T. Boronski, Dalton Trans., 2025, 54, 13020–13029 RSC.
- P. Banerjee and P. K. Nandi, Phys. Chem. Chem. Phys., 2016, 18, 12505–12520 RSC.
- P. Jutzi, Chem. – Eur. J., 2014, 20, 9192–9207 CrossRef PubMed.
- P. Jutzi, A. Klipp, A. Mix, B. Neumann and H.-G. Stammler, Silicon Chem., 2006, 3, 151–156 CrossRef.
- A. Y. Timoshkin and H. F. Schaefer, Organometallics, 2005, 24, 3343–3345 CrossRef.
- N. He, H.-B. Xie and Y.-H. Ding, Organometallics, 2007, 26, 6839–6843 CrossRef.
- I.-A. Bischoff, B. Morgenstern, M. Zimmer and A. Schäfer, Angew. Chem., Int. Ed., 2025, 64, e202419688 CrossRef.
- I.-A. Bischoff, S. Danés, P. Thoni, B. Morgenstern, D. M. Andrada, C. Müller, J. Lambert, E. C. J. Gießelmann, M. Zimmer and A. Schäfer, Nat. Chem., 2024, 16, 1093–1100 CrossRef PubMed.
- X. Li, S. Huo, Y. Zeng, Z. Sun, S. Zheng and L. Meng, Organometallics, 2013, 32, 1060–1066 CrossRef.
- M. A. Gosch and D. J. D. Wilson, Organometallics, 2023, 42, 2185–2196 CrossRef.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2008, 15, 186–197 CrossRef PubMed.
- N. Parvin, N. Sen, S. Tothadi, S. Muhammed, P. Parameswaran and S. Khan, Organometallics, 2021, 40, 1626–1632 CrossRef.
- (a) Á.M Pendás and E. Francisco, Nat. Commun., 2022, 13, 3327 CrossRef PubMed; (b) M. Gimferrer, S. Danés, E. Vos, C. B. Yildiz, I. Corral, A. Jana, P. Salvador and D. M. Andrada, Chem. Sci., 2022, 13, 6583–6591 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven Jr, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- (a) SCM, SCM – Accelerate your chemistry & materials research, https://www.scm.com/; (b) G. T. Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef PubMed; (b) J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed; (c) J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef.
- (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef; (b) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef; (c) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565 CrossRef; (d) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48–63 CrossRef.
- (a) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef; (b) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580 CrossRef; (c) M. Mitoraj and A. Michalak, J. Mol. Model., 2006, 13, 347–355 Search PubMed; (d) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681–687 Search PubMed.
- (a) E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef; (b) J.-L. Heully, I. Lindgren, E. Lindroth, S. Lundqvist and A.-M. Martensson-Pendrill, J. Phys. B:At., Mol. Opt. Phys., 1986, 19, 2799–2815 CrossRef; (c) E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 Search PubMed; (d) E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 Search PubMed.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |