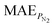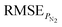Open Access Article
Open Access ArticlePolyRL: reinforcement learning-guided polymer generation for multi-objective polymer discovery
Wentao
Li†
a,
Yijun
Li†
ab,
Qi
Lei†
a,
Zemeng
Wang
a and
Xiaonan
Wang
 *a
*a
aState Key Laboratory of Chemical Engineering and Low-carbon Technology, Department of Chemical Engineering, Tsinghua University, Beijing 100084, China. E-mail: wangxiaonan@tsinghua.edu.cn
bTanwei College, Tsinghua University, Beijing 100084, China
First published on 25th November 2025
Abstract
Designing high-performance polymers remains a critical challenge due to the vast design space. While machine learning and generative models have advanced polymer informatics, most approaches lack directional optimization capabilities and fail to close the loop between design and physical validation. Here we introduce PolyRL, a closed-loop reinforcement learning (RL) framework for the inverse design of gas separation polymers. By integrating reward model training, generative model pre-training, RL fine-tuning, and theoretical validation, PolyRL achieves multi-objective optimization under data-scarce conditions. We demonstrate that PolyRL is capable of efficiently generating polymer candidates with enhanced gas separation performance, as substantiated by detailed molecular simulation analyses. Additionally, we establish a standardized benchmark for RL-based polymer generation, providing a foundation for future research. This work showcases the power of reinforcement learning in polymer design and advances AI-driven materials discovery toward closed-loop, goal-directed paradigms.
1 Introduction
Polymers have emerged as versatile and economically viable platforms for addressing global challenges such as climate change mitigation and environmental sustainability owing to their inherent flexibility, ease of processing, and scalable production. They play a crucial role in various industrial separation processes when used in membranes, including gas purification, oxygen enrichment, biogas upgrading, and carbon capture applications.1–4 Due to the vast design space of polymers, obtaining polymer materials with better performance has always been a challenging issue.Traditional approaches for developing high-performance polymers have largely relied on trial-and-error methods guided by experimental intuition and incremental optimization of chemical structures. Although computational techniques, such as Density Functional Theory (DFT) calculations, molecular dynamics (MD) and Monte Carlo (MC) simulations, offer effective property predictions, their computational intensity restricts exploration to limited chemical spaces.5–7 Machine learning (ML) has emerged as a promising alternative, employing large-scale data-driven models, such as Random Forest (RF), Deep Neural Networks (DNNs), Graph Convolutional Networks (GCNs) and Transformer, to predict polymer properties directly from chemical structures8–13 and discover the relationship between microscopic features and macroscopic properties.14–16 However, this train-and-predict paradigm is inherently constrained by existing datasets or predefined candidate polymer materials, limiting exhaustive exploration of the vast design space and preventing the targeted optimization of material properties.
With the rise of generative models and inverse design methods, an increasing number of researchers are using deep generative algorithms to explore the chemical space of compounds, especially in the fields of drug and inorganic material discovery.17,18 In polymer informatics, researchers use deep generative algorithms to generate polymers with specified properties. For example, Batra et al.19 combined syntax-directed variational autoencoders (VAEs) and Gaussian process regression (GPR) to identify robust polymers suitable for extreme conditions. Liu et al.20 employed an invertible graph generative model focused on discovering high-temperature polymer dielectrics. Gurnani et al.21 proposed an inverse design method named PolyG2G, aiming to discover better polymer dielectric materials. Basdogan et al.22 customized the fitness of gas separation polymer materials and used genetic algorithms to generate high-performance gas separation polymer materials. However, most of the research on the inverse design of gas separation polymer materials remains at the data-driven model level and has not completed the closed-loop discovery process from AI models to theoretical calculations or experimental verification. Additionally, the conditional generation methods for materials cannot directionally optimize specific properties, and genetic algorithms face problems of large sample sizes and low efficiency in directional optimization.
Reinforcement learning (RL), an alternative paradigm distinct from conventional generative and genetic algorithms, has demonstrated notable potential for inverse design and directional optimization of material properties. RL systematically explores chemical spaces through autonomous and sequential decision-making strategies, effectively balancing exploration and exploitation to efficiently identify optimal candidates. Its inherent ability to directly optimize specific properties through goal-oriented reward mechanisms enables RL to overcome limitations associated with existing generative models and genetic algorithms, such as inefficient sampling and weak directional control. Reinforcement learning based generative methods have been used in drug discovery,23–25 crystal material optimization26 and functional material design.27,28
However, RL-based generative approaches have not yet been thoroughly explored for polymer materials, particularly in the context of gas separation polymers. In this work, we introduce the PolyRL framework (Polymer Reinforcement Learning) and specifically target its application to gas separation polymers, aiming to address the existing gap in RL-driven material design for this critical domain.
The main contributions of this study can be summarized as follows.
(1) This work presents the first reinforcement learning-based framework for the generation of gas separation polymers, establishing a closed-loop system that integrates reward model training, generative model pre-training, reinforcement learning fine-tuning, and theoretical validation. Our results demonstrate the feasibility of our reinforcement learning approach and the effectiveness of the generated polymer candidates. This study provides a foundational exploration into the utility of reinforcement learning in the field of polymer informatics.
(2) Multi-objective optimization has remained a challenging task in the conditional generation of materials. This work addressed this issue through custom-defined reward functions, achieving multi-objective optimization of gas separation polymer materials in targeted properties.
(3) A comprehensive benchmark for reinforcement learning-driven gas separation polymer generation is developed, including evaluations of the reinforcement learning algorithm, pre-trained generative model, and the size of pre-training dataset. This benchmark will facilitate future research in developing more advanced algorithmic frameworks for gas separation polymer and membrane design.
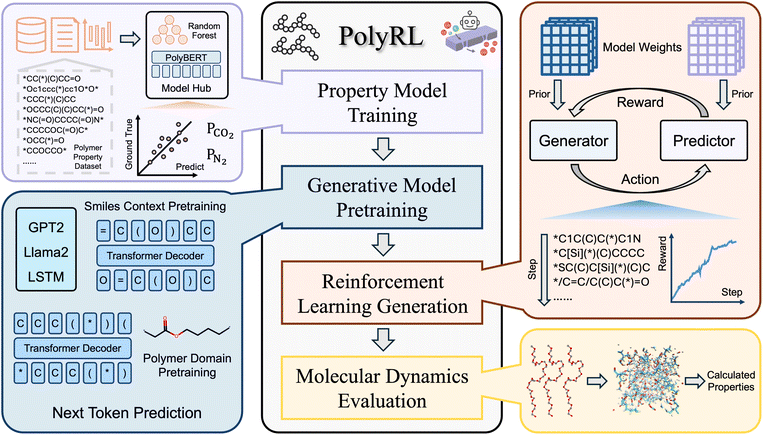
2 The overall PolyRL framework
The overall PolyRL framework is composed of five main parts: data acquisition, property prediction models, deep generative models, reinforcement learning, and high throughput calculation pipeline. The overall framework of PolyRL is illustrated in Fig. 1.2.1 Task definition
The primary objective of the PolyRL framework is to optimize gas separation polymer materials used in membrane for enhanced gas permeability and selectivity. Specifically, the target is to achieve high selectivity for CO2 over N2, ensuring efficient separation by maximizing permeability for CO2 while maintaining low permeability for N2.2.2 Data acquisition
To obtain a diverse and representative dataset for training the property prediction model, we collected a wide range of gas separation polymer materials from literature. The dataset of gas separation polymer materials from Yang et al.9 was used as a basic dataset. After data cleaning, we obtained a dataset containing 353 gas separation polymer materials. To enhance the polymer generation model's understanding of polymer semantics, we selected 1 million hypothetical polymers mentioned in the paper by Yang et al.9 as the pre-training dataset. More detailed statistical information about the dataset is provided in part 2.1 of the SI.All polymer material data are represented using polymer simplified molecular input line representation (P-SMILES) strings. P-SMILES is a special string representation that is used to describe the chemical structure of polymers. These strings play an important role in data-driven tasks related to polymer discovery, design, or prediction. In the representation of homopolymers, P-SMILES contains two asterisks (linear homopolymers) ([*] or *) or four asterisks (ladder polymers) in the string. These asterisks represent the endpoints of the polymer repeat units, effectively marking the boundaries of the repeating segments in the polymer chain.
2.3 Deep generative models
Deep generative models learn the distribution of existing data and generate new data through sampling, achieving significant progress in both image and text domains. In the field of material generation, most research focuses on generating one-dimensional (SMILES sequences), two-dimensional (graph), and three-dimensional (geometric coordinates) material representations. The one-dimensional SMILES representation method can succinctly and thoroughly represent material information. Moreover, with the success of the transformer architecture and pre-training paradigm, chemical language models trained on a large SMILES corpus have become powerful tools for one-dimensional SMILES generation.P-SMILES and SMILES are fundamentally similar in form. Throughout the entire PolyRL framework, we need to obtain a pre-trained chemical language model as a prior model. This model can generate valid P-SMILES strings and will be directionally optimized through reinforcement learning fine-tuning to produce high-performance polymers. The model architectures considered include traditional GRU29 and LSTM30 as well as the latest GPT2 (ref. 31) and LLaMA2 (ref. 32) architectures. All chemical language models are pre-trained through the “next-token prediction” paradigm on the hypothetical dataset of 1 million polymers, enabling them to learn the semantic information inherent in P-SMILES and generate valid polymers. This training process is detailed in eqn (1). Specifically, given a SMILES sequence x = x1x2⋯xn, the models are trained to maximize the probability P(xi|x1, x2, …, xi−1; θ), where each xi represents the i-th token in the sequence, and θ denotes all parameters of the language model. The hyperparameters of the pre-trained chemical language model and details of the training performance evaluation are provided in part 2.3 of the SI. After the pre-training is completed, we load the pre-trained chemical language models to directionally generate polymer materials with better performance in the reinforcement learning process.
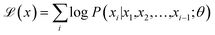 | (1) |
2.4 Property prediction models
Machine learning-driven chemical property prediction models map material features to predicted properties. Due to the efficiency of machine learning, these models often serve as surrogate models for experiments or theoretical calculations, enabling high-throughput screening of materials. In the reinforcement learning framework, the property prediction model acts as a reward model, providing scores for the currently generated samples to the generative model, thereby achieving optimization for specific properties.We selected methods for property prediction that combine molecular descriptors or molecular fingerprints with traditional machine learning models, including Random Forest (RF) combined with molecular fingerprints and Support Vector Regression (SVR) combined with molecular fingerprints. Additionally, in alignment with the emergence of large-scale pre-training methods, we also integrated polymer material pre-training models based on the transformer architecture like PolyBERT10 and general large language models such as GPT-3.5-turbo. These pre-trained models directly use P-SMILES as input for property prediction. The evaluation of the prediction models was conducted on the gas separation polymer material dataset we constructed.
2.5 Reinforcement learning algorithm
In the context of gas separation polymer material generation, the reinforcement learning task can be framed as a sequential decision-making process, where a polymer is incrementally constructed through successive actions. Formally, this task can be defined using Markov Decision Processes (MDPs), characterized by the tuple 〈S, A, P, R, ρ0〉. Here, S denotes the state space representing partially constructed polymers, and A denotes the action space comprising modifications or extensions to the polymer structure encoded in the SMILES or P-SMILES representation.The transition dynamics 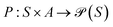 determine the probability distribution of transitioning from a current polymer configuration (state) st to a subsequent configuration st+1 given a polymer-building action at. The reward function
determine the probability distribution of transitioning from a current polymer configuration (state) st to a subsequent configuration st+1 given a polymer-building action at. The reward function 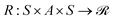 assigns numerical feedback based on performance metrics such as gas permeability and selectivity, encouraging the generation of materials with enhanced desired properties. ρ0 signifies the initial state distribution.
assigns numerical feedback based on performance metrics such as gas permeability and selectivity, encouraging the generation of materials with enhanced desired properties. ρ0 signifies the initial state distribution.
To optimize policy performance, we define the expected cumulative return in eqn (2),
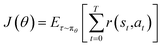 | (2) |
In eqn (2), πθ denotes the policy parameterized by θ, and the trajectory τ = (s0, a0, s1, a1, …, sT, aT) represents the complete molecular generation process. The immediate reward r(st, at) corresponds to the gain obtained by executing action at at state st. In this study, r(st, at) is not computed step by step but assigned based on the final performance score R(x) of the generated molecule. This scalar reward is uniformly distributed to all steps in the trajectory, allowing the final molecular performance to directly influence the policy optimization.
In policy gradient methods, the gradient of the objective function is typically expressed in eqn (3).
∇θJ(θ) = E(s,a)∼πθ[∇θlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πθ(a|s)·Qπθ(s,a)] πθ(a|s)·Qπθ(s,a)] | (3) |
In eqn (3), ∇θlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πθ(a|s) measures the sensitivity of the policy to action selection, and Qπθ(s,a) denotes the expected return after taking action a in state s under policy π. As Qπθ(s,a) depends on the cumulative rewards from future state-action sequences, its exact value is often intractable.
πθ(a|s) measures the sensitivity of the policy to action selection, and Qπθ(s,a) denotes the expected return after taking action a in state s under policy π. As Qπθ(s,a) depends on the cumulative rewards from future state-action sequences, its exact value is often intractable.
To address this issue, reinforcement learning methods generally fall into two categories: the first retains the original policy gradient form and employs various strategies to estimate Qπθ(s,a) (e.g., REINFORCE,33 A2C,34 PPO35). All three methods satisfy the form of eqn (3). The second bypasses the direct use of this gradient expression and instead defines surrogate objectives that approximate or transform the optimization process to steer the policy toward high-reward regions (e.g., REINVENT,36 AHC,37 DPO38).
Despite differences in implementation, all approaches share the common objective of maximizing the expected cumulative return by minimizing an appropriately defined loss function. The basic principles of each reinforcement learning algorithm in PolyRL framework are detailed in part 2.4 of the SI.
Subsequently, we utilize the Robeson upper bound as a benchmark which is commonly used for evaluating gas separation performance, defining a shifted reward in eqn (4).
R(x) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S − (a − b × log S − (a − b × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCO2) + 2 PCO2) + 2 | (4) |
In eqn (4), log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 denotes the logarithm of CO2 permeability. log
CO2 denotes the logarithm of CO2 permeability. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S represents the logarithm of the ratio of CO2 to N2 permeability, also called selectivity. The constants a and b are parameters obtained from Robeson's upper bound correlation, specifically a = 2.595 and b = 0.3464 for the CO2/N2 separation. Eqn (4) is expanded and written in the form of eqn (5).
S represents the logarithm of the ratio of CO2 to N2 permeability, also called selectivity. The constants a and b are parameters obtained from Robeson's upper bound correlation, specifically a = 2.595 and b = 0.3464 for the CO2/N2 separation. Eqn (4) is expanded and written in the form of eqn (5).
R(x) = (b + 1)log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PCO2 − log PCO2 − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PN2 − a + 2 PN2 − a + 2 | (5) |
2.6 Feature attribution and model interpretation
SHAP (SHapley Additive exPlanations) is a model interpretability framework based on cooperative game theory that decomposes a single-sample prediction into the sum of the contribution values of all input features.39 Its core idea is to sequentially add features to the model and compute each feature's average marginal gain across all possible feature combinations, thereby quantifying its contribution to the final prediction. SHAP results satisfy additivity and consistency: the sum of all feature contributions equals the difference between the sample prediction and the baseline prediction, and when the impact of a feature on the model output increases, its SHAP value increases monotonically. This analysis enables us to identify which structural fragments enhance or reduce CO2 permeability and CO2/N2 selectivity (i.e., the contribution of structural features to performance), and to measure the overall importance of each feature across the entire dataset by calculating the mean absolute SHAP values. The detailed SHAP calculation procedure and results are provided in Part 3.2 of the SI.2.7 High throughput calculation pipeline
Molecular dynamics (MD) simulation is a precise approach to calculate the transport properties and structural characteristics of the gas separation polymer materials. In the MD procedure, polymer structures were initially generated from repeating unit representations and converted into polymer models with periodic boundary conditions to simulate infinite polymeric chains. A series of preparatory simulation steps, including energy minimization, thermal annealing, and equilibration under controlled temperature and pressure conditions, were employed to stabilize the polymer configurations.Thermal annealing procedures were applied systematically, decreasing the temperature stepwise to identify transitions in the material properties indicative of the glass transition temperature (Tg). Gas molecules were introduced into the equilibrated polymer structures at dilute conditions to evaluate fundamental transport properties, such as solubility and diffusivity. Production simulations under steady-state conditions were then conducted to quantify these properties. The key characteristics of gas separation polymers, including gas permeability, were computed from simulated solubility and diffusivity data. The detailed calculation parameters are provided in Part 3.3 of the SI.
3 Results and discussion
3.1 Generative model performance
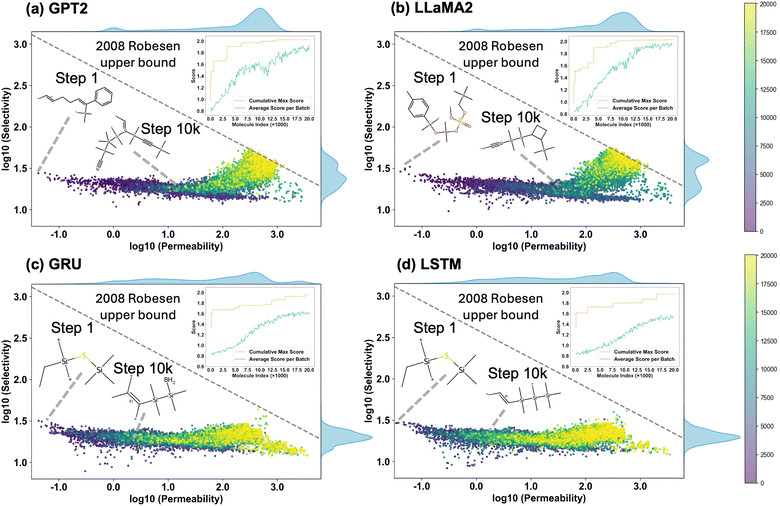
Four autoregressive models were first pre-trained for the next-token prediction task on a P-SMILES dataset containing 1 million entries. We observed that, due to the simplicity of the semantic information in P-SMILES, the massive pre-training dataset was redundant for the models to comprehend the semantics of P-SMILES. Both GPT-2 and LLaMA-2 converged within 1–2 epochs during pre-training. We utilized the validity of molecules generated by the models as an indicator of model training performance, specifically the proportion of valid molecules among 128 molecules generated by each model. The results are presented in Table 1.| Model | GRU | LSTM | GPT2 | LLaMA2 |
|---|---|---|---|---|
| Validity | 100% | 98.44% | 94.53% | 100% |
3.2 Prediction model performance
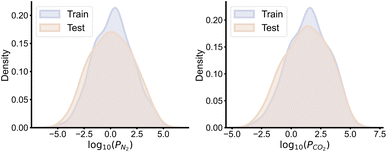
A dataset for gas separation polymer was first constructed using data from literature, comprising a total of 353 entries. The dataset was split into training and test sets in a 282![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 71 ratio. The distribution of the gas separation properties is illustrated in Fig. 2. Two traditional machine learning models (RF and SVR) and one pre-trained polymer language model (PolyBERT) were trained for this task. Furthermore, the large language model GPT-3.5-turbo was fine-tuned to assess its capability on this dataset. The Mean Absolute Error (MAE), Root Mean Square Error (RMSE) and inference time on the test set of all the three methods are summarized in Table 2.
71 ratio. The distribution of the gas separation properties is illustrated in Fig. 2. Two traditional machine learning models (RF and SVR) and one pre-trained polymer language model (PolyBERT) were trained for this task. Furthermore, the large language model GPT-3.5-turbo was fine-tuned to assess its capability on this dataset. The Mean Absolute Error (MAE), Root Mean Square Error (RMSE) and inference time on the test set of all the three methods are summarized in Table 2.
The two traditional machine learning models, RF and SVR, achieve faster inference speeds. While GPT-3.5-turbo outperforms other models owing to its large-scale pretraining and strong semantic understanding, its slow inference renders it impractical as a surrogate model for reinforcement learning. In particular, RF as a traditional machine learning model outperforms the pre-trained PolyBERT in accuracy. To further investigate the difference of model performance, a sample-by-sample comparison was conducted among the RF, SVR, PolyBERT and GPT-3.5-turbo. The results of this comparison are presented in Fig. 3. From the error scatter plots, the predictions of RF present a higher accuracy, with fewer outliers in the test set, suggesting that the model is more robust and can providereliable predictions for unseen samples.
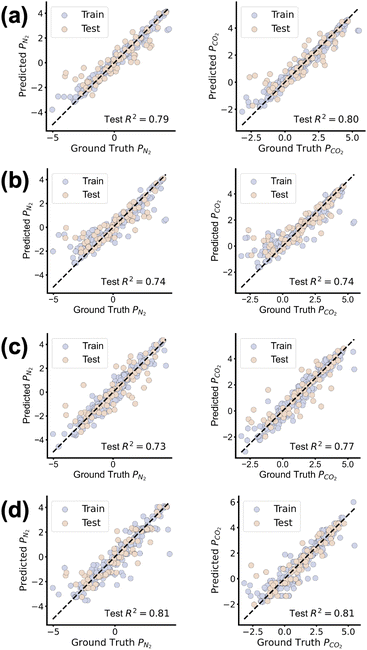 | ||
| Fig. 3 Error scatter plot of (a) RF, (b) SVR (c) PolyBERT and (d) GPT-3.5-turbo in gas permeability tasks. | ||
3.3 Reinforcement learning performance
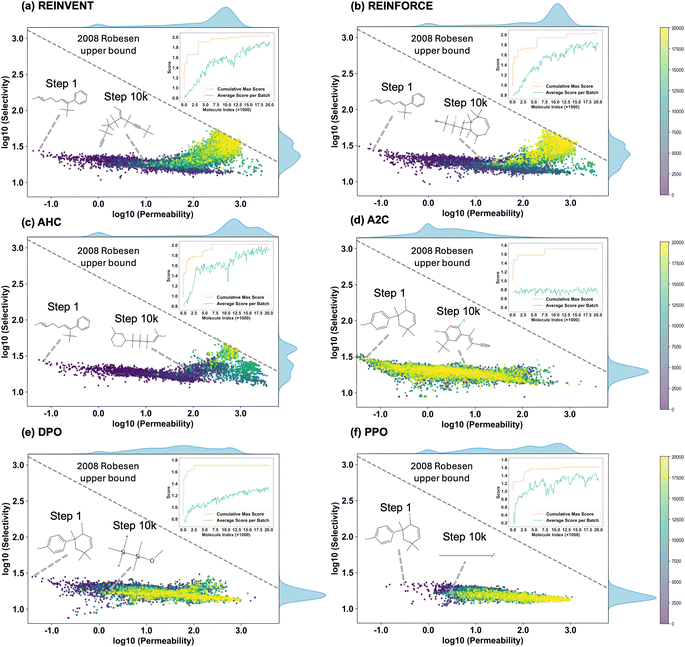
REINVENT and REINFORCE demonstrate superior capability in multi-objective molecular generation, successfully discovering candidates that surpass the Robeson upper bound. In contrast, although algorithms such as A2C and PPO exhibit improvements in CO2 permeability, they fail to yield further enhancement in selectivity, limiting their effectiveness in achieving a balanced optimization of both objectives.
REINVENT and REINFORCE are categorized as policy gradient methods, typically comprising a single actor model. In contrast, A2C and PPO adopt an actor-critic architecture, incorporating both actor and critic components. The critic estimates the value function, providing feedback that guides the actor's policy updates. However, inaccuracies in the critic's value estimations can introduce bias, potentially steering the policy updates toward suboptimal solutions. As depicted in Fig. 4d, the A2C algorithm's average score per batch converges prematurely, highlighting the tendency of actor-critic methods to settle into local optima during polymer generation tasks.
As training progresses, the gas separation polymers generated by REINVENT, REINFORCE, and AHC exhibit a two-phase optimization trend, initially improving permeability, followed by an enhancement in selectivity. This behavior can be attributed to the reward formulation in eqn (3). Specifically, the reward function assigns a greater weight to the permeability of CO2, making the early stages of optimization favor an increase in CO2 permeability to maximize the overall reward. However, due to the predictive model's boundary limitations, further improving CO2 permeability becomes increasingly difficult in later iterations. Consequently, the optimization process shifts toward reducing N2 permeability, thereby improving selectivity. This results in the observed progression: an initial rise in CO2 permeability followed by a subsequent enhancement in CO2/N2 selectivity.
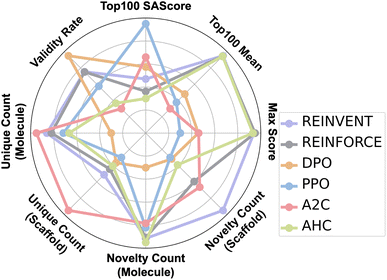
We evaluated the performance of molecular generation algorithms using eight comprehensive metrics. Max score denotes the highest score among all generated molecules based on a predefined scoring function that considers properties such as chemical stability, reflecting the algorithm's optimal generation capability. Top100 mean is the average score of the top 100 highest-scoring molecules, indicating the algorithm's ability to consistently generate high-quality candidates. Top100 SAscore measures the synthetic accessibility of these top molecules, with lower scores suggesting greater ease of synthesis and higher practical feasibility. Validity rate represents the proportion of chemically valid molecules that comply with valence and structural rules, assessing structural correctness. Unique Count (molecule) quantifies the number of distinct molecules generated, indicating structural diversity. Unique Count (scaffold) captures the diversity at the scaffold level, reflecting the algorithm's ability to explore different core structures. Novelty Count (molecule) and Novelty Count (scaffold) measure the number of novel molecules and scaffolds not present in the training data, respectively, highlighting the model's capacity for structural innovation, which is crucial for de novo molecule design.
As shown in Fig. 5, REINVENT, REINFORCE, and AHC achieved higher scores and more novel molecules relative to the training set, with lower synthetic complexity. PPO and A2C generated molecules with higher synthetic complexity, but the uniqueness of the molecules generated during the process was greater. In summary, REINVENT performs best in the task of generating polymers for gas separation.
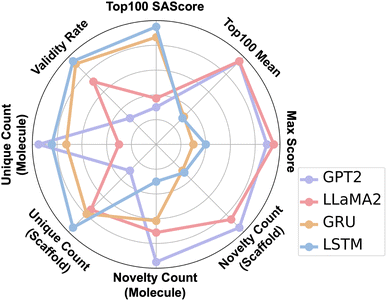
Fig. 6 shows the trends in gas selectivity and CO2 permeability of molecules generated by four generative models as the number of reinforcement learning iterations increases. It can be seen that GPT-2 and LLaMA-2 are able to obtain molecules with higher selectivity and permeability in the later stages of iteration, while the LSTM and GRU models only optimized primarily for CO2 permeability, and the selectivity of the generated molecules did not improve significantly. Fig. 7 reflects eight comprehensive indicators of the generation performance of the four models. Notably, GPT2 and LLaMA2 achieved the best results in the Top100 scores and max scores, and both also had the highest novelty in molecules and scaffolds. This reflects that models based on the transformer global attention mechanism can better focus on specific substructure information and explore the space of gas-separation polymers more comprehensively, thereby achieving improvements in both novelty and score.
The generation metrics for gas separation polymers are shown in Fig. 8. We can see that as the amount of pre-training data increases, the average score of the molecules, uniqueness, and novelty all improve significantly, but this is accompanied by an increase in synthetic complexity. This aligns with intuition: with more high-scoring polymers in the training set, the model learns a larger search space, generating more diverse and complex molecules. At the same time, there is no significant improvement in the average molecular score between 500 k and 750 k data points. These results suggest that selecting a sufficiently large pre-training dataset is important for polymer generation via reinforcement learning, and that a balance between synthetic complexity and diversity needs to be considered.
3.4 Molecular dynamics evaluation and chemical interpretation
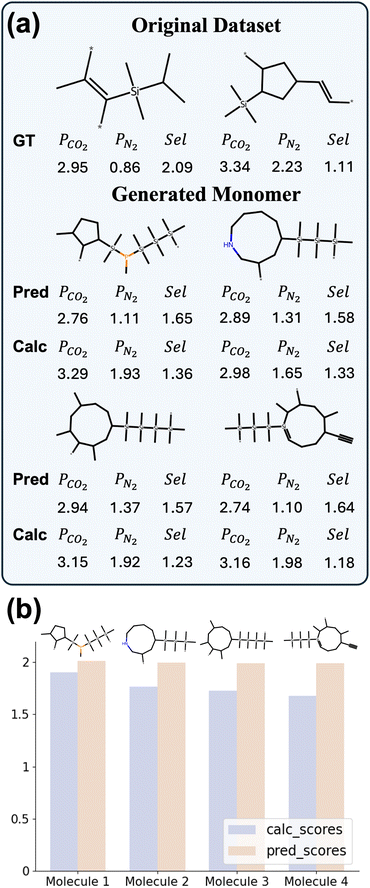
We selected the top 20 gas separation polymers recommended by the optimal combination of GPT-2 + REINVENT + RF, which exhibit similar predicted scores and chemical structures. To obtain more reliable performance evaluations, we conducted molecular dynamics (MD) simulations on these candidate polymers. Fig. 9 presents both the reward scores predicted by the RF model and those obtained from MD calculations across four categories of generated gas separation polymers.As shown in Fig. 9a, the GPT-2 + REINVENT + RF framework tends to generate monomers containing silicon (Si) atoms and large ring structures. This trend is consistent with observations from the original labeled dataset, where polymers containing Si atoms and cyclic backbones often exhibit both high CO2 permeability and high CO2/N2 selectivity. Consequently, the RF reward model shows a bias toward overestimating the performance of polymers with Si-containing moieties and cyclic structures, thereby guiding the generation process toward such motifs.
From a chemical perspective, Si-containing groups are bulky and fan-shaped, occupying substantial spatial volume. This steric hindrance disrupts close packing of polymer chains and significantly enhances the free volume and fractional free volume of the resulting polymer. The SHAP analysis results further corroborate this point. For the high-scoring molecules, the fingerprint features with the highest SHAP values are associated with Si-containing structural regions, indicating that these Si-based groups make significant contributions to the final score, with details provided in Section 3.2 of the SI. Additionally, cyclic backbones restrict the rotational freedom of the polymer chains, contributing to the preservation of high free volume. These structural features promote the formation of microporous domains, which favor the adsorption of highly condensable gases such as CO2, thereby improving the solubility selectivity. As a result, these polymers demonstrate a desirable combination of high permeability and reasonable selectivity.
In terms of model error, the RF prediction model exhibits a mean absolute error (MAE) of approximately 0.6. For the recommended gas separation polymers, the deviations between predicted scores and MD-calculated scores mostly fall within this error margin, supporting the reliability of the model's overall predictions. In Fig. 9b, we compare the reward scores predicted by the RF model with those obtained from MD simulations. Although the MD-derived scores are generally lower, indicating a tendency of the RF model to overestimate performance, the highest MD score reaches 1.90, closely approaching to the predicted score of 2.01. This consistency between the top-performing predictions and the simulation results underscores the practical relevance of the PolyRL framework in guiding the discovery of high-performance gas separation materials.
4 Conclusions
In this study, we introduced PolyRL, the first reinforcement learning (RL) framework specifically designed for the inverse design of high-performance gas separation polymers. PolyRL effectively addresses the long-standing challenge of multi-objective optimization in polymer design by integrating generative model pre-training, property prediction, and RL fine-tuning into a unified, closed-loop system. Our extensive evaluations demonstrate that RL algorithms, particularly REINVENT and REINFORCE, effectively generate polymer candidates that surpass traditional design boundaries. Furthermore, the integration of transformer-based generative models, notably GPT-2 and LLaMA-2, significantly enhanced the quality and novelty of the generated polymers.Through molecular dynamics validation, we confirmed that polymers recommended by the PolyRL framework exhibit superior performance, aligning closely with predicted results. Chemically, our analysis revealed that polymers containing silicon atoms and cyclic structures provide optimal permeability and selectivity due to their structural properties enhancing free volume and microporous domain formation.
In summary, this work establishes a robust benchmark for RL-driven polymer generation, facilitating future research into algorithmic advancements and data efficiency. Ultimately, PolyRL represents a significant stride toward AI-driven, goal-oriented polymer discovery, highlighting the potential of reinforcement learning to accelerate the development of advanced materials for critical applications in gas separation.
Author contributions
Wentao Li: conceptualization, methodology, writing original draft, review and editing; Yijun Li: conceptualization, methodology, writing original draft; Qi Lei: methodology; Zemeng Wang: review and editing; Xiaonan Wang: conceptualization, review and editing, supervision.Conflicts of interest
There are no conflicts to declare.Data availability
All code and data supporting the findings of this study are openly available.The PolyRL framework, including data, source code for polymer generation, reward function design, and reinforcement learning optimization, is available at Zenodo. The DOI for both the latest version and archived version is currently: 10.5281/zenodo.17498383. It can be accessed via the following link: https://doi.org/10.5281/zenodo.17498383.
The code and data for PolyRL can also be found at the GitHub repository: https://github.com/Knitua/PolyRL. The README.md file in the repository provides detailed instructions to reproduce the results.
The representative dataset used in this study, which includes polymer SMILES strings for training the generator and predictor, has been uploaded to Zenodo. The dataset DOI is: 10.5281/zenodo.17498407. It can be accessed via the following link: https://doi.org/10.5281/zenodo.17498407.
Supplementary information: the additional details of the methods, datasets, model training, and extended results supporting this study. See DOI: https://doi.org/10.1039/d5dd00272a.
Acknowledgements
This work is supported by the National Key R&D Program of China (No. 2022ZD0117501), the Scientific Research Innovation Capability Support Project for Young Faculty (ZYGXQNJSKYCXNLZCXM-E7), Carbon Neutrality and Energy System Transformation (CNEST) Program led by Tsinghua University and the Tsinghua University Initiative Scientific Research Program.Notes and references
- S. Zhao, P. H. Feron, L. Deng, E. Favre, E. Chabanon, S. Yan, J. Hou, V. Chen and H. Qi, J. Membr. Sci., 2016, 511, 180–206 CrossRef CAS.
- B. von Vacano, H. Mangold, G. W. Vandermeulen, G. Battagliarin, M. Hofmann, J. Bean and A. Künkel, Angew. Chem., Int. Ed., 2023, 62, e202210823 CrossRef CAS PubMed.
- A. K. Mohanty, F. Wu, R. Mincheva, M. Hakkarainen, J.-M. Raquez, D. F. Mielewski, R. Narayan, A. N. Netravali and M. Misra, Nat. Rev. Methods Primers, 2022, 2, 46 CrossRef CAS.
- G. Zhang, X. Fu, D. Zhou, R. Hu, A. Qin and B. Z. Tang, Smart Mol., 2023, 1, e20220008 CrossRef PubMed.
- R. C. Dutta and S. K. Bhatia, ACS Appl. Polym. Mater., 2019, 1, 1359–1371 CrossRef CAS.
- A. Tardy, N. Gil, C. M. Plummer, C. Zhu, S. Harrisson, D. Siri, J. Nicolas, D. Gigmes, Y. Guillaneuf and C. Lefay, Polym. Chem., 2020, 11, 7159–7169 RSC.
- D. T. Umeta, S. N. Asfaw, S. H. Didu, C. G. Feyisa and D. K. Feyisa, Adv. Polym. Technol., 2022, 2022, 6707429 CrossRef.
- J. W. Barnett, C. R. Bilchak, Y. Wang, B. C. Benicewicz, L. A. Murdock, T. Bereau and S. K. Kumar, Sci. Adv., 2020, 6, eaaz4301 CrossRef CAS PubMed.
- J. Yang, L. Tao, J. He, J. R. McCutcheon and Y. Li, Sci. Adv., 2022, 8, eabn9545 CrossRef CAS PubMed.
- C. Kuenneth and R. Ramprasad, Nat. Commun., 2023, 14, 4099 CrossRef CAS PubMed.
- C. Xu, Y. Wang and A. Barati Farimani, npj Comput. Mater., 2023, 9, 64 CrossRef.
- O. Queen, G. A. McCarver, S. Thatigotla, B. P. Abolins, C. L. Brown, V. Maroulas and K. D. Vogiatzis, npj Comput. Mater., 2023, 9, 90 CrossRef.
- J. Park, Y. Shim, F. Lee, A. Rammohan, S. Goyal, M. Shim, C. Jeong and D. S. Kim, ACS Polym. Au, 2022, 2, 213–222 CrossRef CAS.
- X. Huang, S. Ma, C. Zhao, H. Wang and S. Ju, npj Comput. Mater., 2023, 9, 191 CrossRef.
- W. Li, Z. Wang, M. Zhao, J. Pei, Y. Hu, R. Yang and X. Wang, J. Mater. Inf., 2025, 5, N–A Search PubMed.
- Y. Zhao, Q. Liu, J. Du, Q. Meng and L. Zhang, Smart Mol., 2023, 1, e20230012 CrossRef.
- Y. Du, A. R. Jamasb, J. Guo, T. Fu, C. Harris, Y. Wang, C. Duan, P. Liò, P. Schwaller and T. L. Blundell, Nat. Mach. Intell., 2024, 6, 589–604 CrossRef.
- H. Park, Z. Li and A. Walsh, Matter, 2024, 7, 2355–2367 CrossRef CAS.
- R. Batra, H. Dai, T. D. Huan, L. Chen, C. Kim, W. R. Gutekunst, L. Song and R. Ramprasad, Chem. Mater., 2020, 32, 10489–10500 CrossRef CAS.
- D.-F. Liu, Y.-X. Zhang, W.-Z. Dong, Q.-K. Feng, S.-L. Zhong and Z.-M. Dang, J. Chem. Inf. Model., 2023, 63, 7669–7675 CrossRef CAS.
- R. Gurnani, D. Kamal, H. Tran, H. Sahu, K. Scharm, U. Ashraf and R. Ramprasad, Chem. Mater., 2021, 33, 7008–7016 CrossRef CAS.
- Y. Basdogan, D. R. Pollard, T. Shastry, M. R. Carbone, S. K. Kumar and Z.-G. Wang, J. Membr. Sci., 2024, 712, 123169 CrossRef CAS.
- X. Hu, G. Liu, Y. Zhao and H. Zhang, Adv. Neural Inf. Process. Syst., 2023, 36, 7405–7418 Search PubMed.
- A. Bou, M. Thomas, S. Dittert, C. Navarro, M. Majewski, Y. Wang, S. Patel, G. Tresadern, M. Ahmad and V. Moens, et al. , J. Chem. Inf. Model., 2024, 64, 5900–5911 CrossRef CAS.
- A. Zholus, M. Kuznetsov, R. Schutski, R. Shayakhmetov, D. Polykovskiy, S. Chandar and A. Zhavoronkov, Proc. AAAI Conf. Artif. Intell., 2025, 26083–26091 Search PubMed.
- Z. Cao and L. Wang, arXiv, 2025, preprint, arXiv:2504.02367, DOI:10.48550/arXiv.2504.02367.
- J. Qiu, H. H. Lam, X. Hu, W. Li, S. Fu, F. Zeng, H. Zhang and X. Wang, arXiv, 2025, preprint, arXiv:2503.23766, DOI:10.48550/arXiv.2503.23766.
- B. Zheng, Z. Zheng and G. X. Gu, npj Comput. Mater., 2022, 8, 225 CrossRef.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, arXiv, 2014, preprint, arXiv:1412.3555, DOI:10.48550/arXiv.1412.3555.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS.
- A. Radford, J. Wu, R. Child, D. Luan, D. Amodei and I. Sutskever, et al. , OpenAI blog, 2019, 1, 9 Search PubMed.
- H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava and S. Bhosaleet al., arXiv, 2023, preprint, arXiv:2307.09288, DOI:10.48550/arXiv.2307.09288.
- R. J. Williams, Mach. Learn., 1992, 8, 229–256 CrossRef.
- V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap, T. Harley, D. Silver and K. Kavukcuoglu, International conference on machine learning, 2016, pp. 1928–1937 Search PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, preprint, arXiv:1707.06347, DOI:10.48550/arXiv.1707.06347.
- T. Blaschke, J. Arús-Pous, H. Chen, C. Margreitter, C. Tyrchan, O. Engkvist, K. Papadopoulos and A. Patronov, J. Chem. Inf. Model., 2020, 60, 5918–5922 CrossRef CAS PubMed.
- M. Thomas, N. M. O'Boyle, A. Bender and C. De Graaf, J. Cheminf., 2022, 14, 68 Search PubMed.
- R. Rafailov, A. Sharma, E. Mitchell, C. D. Manning, S. Ermon and C. Finn, Adv. Neural Inf. Process. Syst., 2023, 36, 53728–53741 Search PubMed.
- S. M. Lundberg and S.-I. Lee, Adv. Neural Inf. Process. Syst., 2017, 30, 4768–4777 Search PubMed.
Footnote |
| † These authors contribute equally. |
| This journal is © The Royal Society of Chemistry 2026 |