Advanced solar-driven CO2 photothermal–electrocatalytic co-reduction system design and research
Jintao
Song
a,
Jiaxin
Du
b,
Fuqiang
Wang
 *ab,
Guoliang
Zhang
a,
Yaping
Fan
b,
Hongliang
Yi
a,
Yong
Shuai
*ab,
Guoliang
Zhang
a,
Yaping
Fan
b,
Hongliang
Yi
a,
Yong
Shuai
 a,
Dong
Li
c and
Liwu
Fan
a,
Dong
Li
c and
Liwu
Fan
 d
d
aSchool of Energy Science and Engineering, Harbin Institute of Technology, 92, West Dazhi Street, Harbin 150001, PR China. E-mail: Wangfuqiang@hitwh.edu.cn
bSchool of New Energy, Harbin Institute of TechnologyWeihai, 2, West Wenhua Road, Weihai 264209, PR China
cSchool of Civil and Architectural Engineering, Northeast Petroleum University, 99 Xuefu Street, Longfeng District, Daqing 163000, PR China
dState Key Laboratory of Clean Energy Utilization, Zhejiang University, 38 Zheda Road, Hangzhou 310027, PR China
First published on 21st November 2025
Abstract
The efficient reduction of CO2 is significant for achieving carbon neutrality and renewable fuel synthesis. However, CO2 thermostatic systems are limited by energy utilization efficiency, while high-temperature electrocatalysis is limited by the need for inlet preheating of the material. Considering the existence of high-grade thermal energy at the outlet of thermostatic CO2 not utilized, the article proposes a combined thermal–electrocatalytic CO2 reduction system, which can utilize high-temperature products of thermostatic CO2 reduction for further electrocatalytic co-electrolysis of H2O as well as CO2, and at the same time solves the problems of lower efficiency of thermostatic reduction as well as the need of pre-heating for electrocatalytic reduction. Mathematical models of the two subsystems were developed, and thermodynamic analyses were performed. The results show that the efficiency of the thermostatic reduction part could be optimized by designing the reaction parameters, and the maximum efficiency could reach 25.42%, while the electrolytic efficiency of the electrocatalytic part could reach 99.21%. The electrocatalytic efficiency of the coupled system can be increased by 24.84% to 95.80%. And when the two systems are coupled to catalyze CO2, the overall efficiency of the system can be increased by 29.00%.
1 Introduction
The rapid development of human production has significantly increased global carbon emissions, resulting in a severe climate crisis.1–3 According to the UK Meteorological Office, the global average CO2 concentration in the atmosphere is expected to peak at 429.6 ± 0.6 ppm in May 2025, far surpassing the ecological safety threshold of 350 ppm.4–6 As the world's largest carbon-emitting economy, China urgently needs to develop advanced carbon conversion technologies to reduce CO2 emissions.7,8 In this context, CO2 reduction and conversion technologies have become essential for achieving carbon neutrality and establishing a new energy system, due to their clean and low-carbon characteristics.9–11In the field of CO2 thermochemical reduction, researchers have primarily focused on two technologies: hydrothermal catalysis and solar photothermal catalysis.12,13 The thermal catalysis of CO2, using hydrogen-containing media, can reduce the reaction temperature, thereby enhancing the CO2 conversion efficiency.14–16 Solar photothermal catalysis, on the other hand, harnesses high-flux solar irradiation to drive CO2 reduction, overcoming the reliance of traditional thermal catalysis on high-pressure conditions and enabling efficient CO2 conversion under atmospheric pressure.17–19 Notably, the reverse water gas shift (rWGS) reaction acts as a key precursor step for converting CO2 to CO, which is essential for producing high-value-added products such as synthetic fuels or other chemical building blocks.19–21 However, the current rWGS systems still face challenges, including low conversion rates at atmospheric pressure and the lack of available waste heat, necessitating technological breakthroughs through innovative strategies like photothermal co-catalysis.
Electrocatalytic reduction technology has shown distinct advantages due to its cost-effectiveness, enabling the direct conversion of CO2 and H2O into various high-value-added energy sources at room temperature and atmospheric pressure.22–24 Thanks to advancements in in situ characterization and computational simulations, several selective electrocatalysts have been developed in recent years.25–27 However, the low CO2 conversion rate of this technology still limits its large-scale industrial applications. To address this issue, high-temperature electrocatalytic reduction of CO2 (solid oxide cells) has attracted significant attention. By raising the operating temperature, the energy required for CO2 activation and the equilibrium potential of the electrochemical reaction can be significantly reduced, thereby improving reaction rates and energy efficiency.28–30 However, pure CO2 electrolysis can cause catalyst deactivation due to carbon accumulation, which reduces the conversion rate.31 Recent studies have shown that CO2/H2O co-electrolysis can effectively balance the dual goals of preventing carbon buildup and enhancing conversion efficiency, offering a promising approach for optimizing high-temperature electrolysis systems.32
The above literature review shows that thermostatic CO2 reduction has a problem of low efficiency, while electrocatalytic CO2 has a problem of high temperature preheating. It is considered to couple thermocatalysis and electrocatalysis to form a new system of co-catalysis, which can utilize the high temperature products of thermostatic CO2 reduction for further electrocatalytic co-electrolysis of H2O and CO2, and at the same time, solve the problems of low efficiency of thermocatalysis and need of preheating of electrocatalysis, and provide a behaviorally effective way for efficient catalytic reduction of CO2. At the same time, the low efficiency of thermocatalysis and the problem of preheating of electrocatalysis can be solved to provide a behavioral and effective way for the efficient catalytic reduction of CO2.
2 Simulation and analysis methods
2.1 Mathematical model
| CO2 + H2 ⇒ CO + H2O ΔH0298K = +41 kJ mol−1 | (1) |
The kinetic parameters are shown below:33,34
The mass conservation equation is as follows:11
∇·(ρf![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) ) = 0 ) = 0 | (2) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is the velocity and ρf is the density of gas.
is the velocity and ρf is the density of gas.
The equation for conservation of momentum is shown below:11
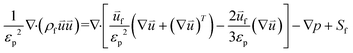 | (3) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) f and S are the dynamic viscosity and source terms, respectively.
f and S are the dynamic viscosity and source terms, respectively.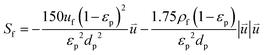 | (4) |
The energy equation is as follows:35
Solid:
| 0 = ∇·(λeff,s∇Ts) + hv(Tf − Ts) + SZ | (5) |
Fluid:
∇·(ρfCp,f![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Tf) = ∇·hv(λeff,f∇Tf) + hv(Ts − Tf) + Schem Tf) = ∇·hv(λeff,f∇Tf) + hv(Ts − Tf) + Schem | (6) |
The intensity distribution of solar radiation absorbed by the porous medium is:36
| SZ = q(r)kee−kez | (7) |
The total solar power is defined as:35
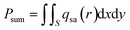 | (8) |
| ∇(−σion∇Vion) = Sion | (9) |
| ∇(−σel∇Vel) = Sel | (10) |
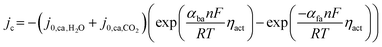 | (11) |
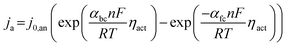 | (12) |
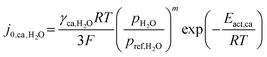 | (13) |
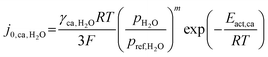 | (14) |
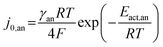 | (15) |
The required potential applied to the SOEC is:40
| V = E + ηact,an + ηact,ca + ηohmic | (16) |
The E is calculated by the following formula:41
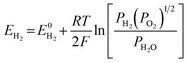 | (17) |
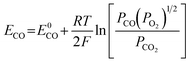 | (18) |
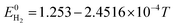 | (19) |
| E0CO = 1.46713 − 4.527 × 10−4T | (20) |
 | (21) |
The efficiency of solar-to-fuel chemical energy conversion without considering the inlet heat as well as when considering the inlet heat is:43
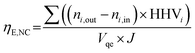 | (22) |
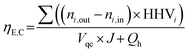 | (23) |
2.2 Initial conditions and assumptions
The research proposes a coupled CO2 reduction system based on thermocatalysis as well as electrocatalysis for photo-heating. The system parameters of the study on thermal catalysis are shown in Table 1 and those of electrocatalysis are shown in Tables 2 and 3.| Parameter | Unit | Value |
|---|---|---|
| Solar power | W | 1000 |
| Porous media diameter | mm | 30 |
| Porous media pore size | mm | 3 |
| Porous media length | mm | 30 |
| Porous media porosity | % | 80 |
| CO2 to H2 mole fraction ratio | — | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| CO2 flow rate | m s−1 | 15 |
| Parameter | Unit | Value |
|---|---|---|
| Channel length | mm | 50 |
| Channel width | mm | 0.5 |
| Channel height | mm | 0.5 |
| Thickness of the cathode | mm | 0.5 |
| Thickness of the anode | mm | 0.1 |
| Thickness of the electrolyte | μm | 15 |
| Gas composition of the anode | — | 21.00 vol% O2 |
| 79.00 vol% N2 | ||
| Gas composition of the cathode | — | 25.25 vol% H2O |
| 25.25 vol% CO | ||
| 24.75 vol% CO2 | ||
| 24.75 vol% H2 | ||
| Inlet temperature | K | 940 |
| Pressure | atm | 1 |
| Stoichiometric ratio of the anode | — | 1.33 |
| Parameter | Unit | Value |
|---|---|---|
| Anode activation energy (CO2)44 | J mol−1 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Anode activation energy (H2O)45 | J mol−1 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Cathode activation energy | J mol−1 | 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| The ionic conductivity of electrolytes | S m−1 | 3.34 × 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−10 exp(−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300/T) 300/T) |
| Anode conductivity | S m−1 | 4.2 × 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1150/T) exp(−1150/T) |
| Electrical conductivity of the gas diffusion layer | S m−1 | 3.27 × 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1165.3/T) exp(−1165.3/T) |
| Electrolyte thermal conductivity | W m−1 K−1 | 2.7 |
| Anode thermal conductivity | W m−1 K−1 | 11 |
| Cathode thermal conductivity | W m−1 K−1 | 6 |
| Electrolyte heat capacity | J kg−1 K−1 | 300 |
| Anode heat capacity | J kg−1 K−1 | 430 |
| Cathode heat capacity | J kg −1 K−1 | 420 |
| Porous electrode porosity | — | 0.36 |
| Porous electrode tortuosity | — | 3 |
To simplify the calculations, some reasonable assumptions are made as follows:
(1) Thermal catalytic system.5
1) The system operates at steady state;
2) Viscous dissipation but not considered;
3) The effect of gravity is not taken into account.
(2) Electrocatalytic system.37
1) All the gas species are ideal gases;
2) Operates in a steady state;
3) Permeability of gases and electrons in the electrolyte is neglected;
4) The effect of gravity is neglected;
5) The inlet material of the electrocatalytic system is the outlet material of the thermal catalytic system, with no heat loss occurring in between.
3 System description and model verification
Fig. 1A shows the conceptual diagram of the combined photothermal–electrical catalytic carbon dioxide reduction system. The left side of Fig. 1A shows a system for photothermal reduction of CO2, where the reaction mixture enters the reactor from the front end and flows along the flow path into the porous media reactor for the reaction. The quartz window at the front of the reactor allows light reflected from the solar collector to enter the reaction system, and the porous medium absorbs the incident light to raise the temperature, providing heat as well as a catalytic environment for CO2 reduction. The porous media is surrounded by a ceramic insulation layer for thermal insulation, and the ceramic insulation layer is protected by a stainless-steel shell. The system has a high-temperature co-electrolysis device on the right side, which receives the high-temperature tail gas (mainly composed of CO2 and H2O) from the co-reforming reaction and performs reduction treatment in the electrolytic cell. Under the combined action of an applied direct current electric field and high-temperature thermal energy, the SOEC achieves simultaneous electrochemical reduction of CO2 and H2O. This process further converts unconverted reactants into syngas components, thereby enhancing the overall system's carbon conversion rate and energy utilization efficiency. Simultaneously, oxygen by-products can be directly vented or recycled, improving the system's sustainability. | ||
| Fig. 1 (A) System schematic; (B) incident energy distribution verification; (C) Faraday efficiency verification; (D) mesh independence verification. | ||
Fig. 1B shows the contrast between the light intensity test data and the simulated data; the maximum error between the two data is 5.06%. Fig. 1C shows the electrocatalytic simulation data compared to the ref. 46 data, where the maximum error of both data is within 2.00%. The data in both Fig. 1B and C show the high accuracy of the model developed.
From Fig. 1D, the mesh independence verification results for both systems show that the efficiency variation of the reforming system and the co-electrolysis system under different mesh numbers remains within 1.00%. Therefore, a model with a moderate number of mesh points was selected for calculations in this study. Regarding mesh refinement, in the thermal catalytic system, refinement primarily targets the porous medium region of the reactor, while in the co-electrolysis system, refinement is applied to both the cathode and anode regions.
4 Results and discussion
The study analyzes the performance of CO2 thermal reduction under different operating conditions from the CO2 solar thermal reduction part. The discussion sections are shown in the following sections.4.1 Thermal catalytic system
From Fig. 2A, the inlet temperature of different inlet materials can directly affect the outlet temperature, which directly affects the inlet temperature in the electrocatalytic carbon dioxide system. Combined with Fig. 2B, when the inlet temperature rises to about 400 K, the average temperature of the outlet can rise close to 50 K. From Fig. 2C, when the temperature of the inlet temperature rises, the radiation regulation ability of the system has risen, which makes the front porous medium transfer more radiation energy to the internal porous medium.
Fig. 2D shows the percentage of carbon dioxide at the exit of the system and the ratio of carbon dioxide to water vapor as a mole fraction. The molar ratio of CO2 to water vapor can reflect the material conditions at the outlet of the thermal reduction system, which is also the inlet of the electric reduction system. From the results in the figure, the ratio of the molar fraction of carbon dioxide to water vapor is greater than in the range of 0.9–1.1, which means that the molar fractions of hydrogen and water entering into the electric reduction system are almost the same.
Fig. 2E shows the concentration of CO2 inside the reactor for both inlet temperature conditions. From the figure, the CO2 at both inlet temperatures reacted intensely in the front part of the porous media, and the concentration decreased rapidly, and the reactor with higher inlet temperature showed a flow field in the middle of the reactor with a lower concentration part.
Fig. 2F shows the conversion of the system at different inlet temperatures as well as the solar-fuel efficiency, and from the results in the figure, it can be seen that the CO2 conversion is around 45% and the solar-fuel efficiency is around 20%. With the increase of temperature, both efficiencies show an increasing trend, of which the main reason is that the internal energy of the imported material is not considered in the efficiency calculation process. When the inlet temperature increases, the reaction temperature increases accordingly, favoring the reaction in the positive direction.
From Fig. 3A, when the porosity of the porous medium is increased, the temperature level inside the reactor shows a tendency to decrease. Observing the outlet temperature in Fig. 3B, the change in outlet temperature is not linear with the change in porosity. When the pore size decreases to a certain extent, the outlet temperature first increases and then decreases with increasing porosity. Fig. 3C shows the CO2 concentration inside the reactor at different porosities. The figure shows that increasing porosity reduces the degree of reaction.
Fig. 3D is a graph of the mole fraction of CO2 at the outlet under different pore sizes and porosities. The graph shows that when the porosity is constant, the CO2 at the outlet gradually decreases with decreasing pore size, indicating that more CO2 is reacted. With a constant pore size, the mole fraction of CO2 at the outlet gradually increases with increasing porosity. Comparing the mole fraction of CO2 at the outlet with the temperature field results shows that a higher temperature field is conducive to the occurrence of the CO2 reduction reaction. Fig. 3E shows the reaction rate along the flow direction of the reactor. The graph shows that the reaction rate decreases along the flow direction, but there is also a region where the rate gradually increases in the initially rapidly reacting area.
Fig. 3F is a graph of the CO2 conversion rate with pore size and porosity. As porosity increases, the conversion first rises and then decreases, which is similar to this with the change of outlet temperature with the change of porosity. However, the conversion rate decreases with the increase of pore size, which is opposite to this with the change of outlet temperature with porosity. Fig. 3G shows the molar fraction ratio of CO2 to H2O at the outlet. From the figure, as the porosity increases, the mole fraction ratio first increases and then decreases, which is also similar to the variation of outlet temperature with porosity. Moreover, the molar ratio increases gradually with increasing pore size.
Fig. 3H shows the variation of solar-fuel efficiency with pore size and porosity, and from the information in the figure, it can be seen that when the pore size is large, the efficiency of the system shows a monotonically decreasing trend as the porosity increases. When the pore size is small, the efficiency of the system shows a trend of increasing and then decreasing. And when the porosity is certain, the efficiency decreases with the increase of pore size. Summarizing the above results, the porous media of the system should be designed with smaller porosity, and the efficiency of solar thermal reduction of carbon dioxide can be maintained at a high level when a medium level of porosity is selected.
Fig. 4A shows the absorption of optical radiation intensity by the porous medium. As the incident power of the system increases, the power absorbed by the porous medium also increases significantly. This behavior suggests that higher incident power results in a greater heat input into the system, leading to an increase in the temperature of the porous medium, which enhances the CO2 reduction reaction.
From Fig. 4B and C, the outlet temperature increases with the increase in power, and when the power is 667 W, the outlet temperature is about 796.56 K. When the power is increased to 1333 W, the outlet temperature can be increased to 1053.35 K. The increase of the power by 667 W increases the outlet temperature by 256.79 K. This indicates a direct relationship between incident power and temperature, suggesting that as more power is supplied, the heat generation in the system increases, leading to a higher thermal environment that could promote more endothermic reactions or faster reaction rates.
As shown in Fig. 4D, the concentration of CO2 at the inlet of the porous medium decreases very much when the incident power increases, and the reaction is strong. When the power is 667 W, the reaction is less and the CO2 concentration in the reactor is around 14 mol m−3, and when the power is increased to 1333 W, the CO2 concentration in the reactor is reduced to around 5 mol m−3. Fig. 4D shows the CO2 export percentage and the molar fraction ratio of CO2 to H2O, where both show a rapid decreasing trend. The rapid decrease in CO2 export percentage could be due to the enhanced reaction rates at higher power inputs, where more CO2 is being converted, reducing the remaining CO2 available for export. The change in the CO2 to H2O ratio reflects the shift in the reaction dynamics as more CO2 is reduced, and by-products like water are formed in the process.
Fig. 4F shows the CO2 conversion rate and the efficiency; with the increase of the feed power, the conversion rate is increased significantly, from 11.35% at 667 W to 60.46% at 1333 W, while the efficiency changes first increase and then decrease, where the highest value of the efficiency is 21.45% when the incident power is 1000 W.
Fig. 5A shows the CO2 molar concentration plots at different inlet flow rates. When the inlet flow rate of the system increased, the CO2 concentration increased significantly and a section of low concentration zone appeared in the center of the porous medium at high flow rates, indicating that the temperature in this region was higher and more CO2 was reacted. Fig. 5B shows the variation of outlet temperature with the flow rate. As seen in this figure, although the outlet temperature varies with the flow rate, the variation is within 10 K, which is a narrow range. This indicates that the heat generated in the system is relatively stable despite changes in flow, which can be attributed to the efficient heat exchange or the system's thermal capacity to absorb small changes in inlet conditions.
Fig. 5C shows the CO2 export percentage and the ratio of the CO2 to H2O molar fraction, where both show a decreasing and then increasing trend. Fig. 5D shows the CO2 conversion rate as well as the efficiency; with the increase of the inlet flow rate, the conversion first decreases and then increases, while the change of the efficiency is gradually increasing, but the increase of the efficiency is gradually regionally flat, and finally the efficiency can reach 25.42% in the case of the inlet rate of 30 m s−1. It is highly likely that the increased flow rate may not allow sufficient reaction of the carbon dioxide.
As shown in Fig. 5E, the CO2 molar concentration is plotted for different inlet molar fractions. Fig. 5F shows the variation of the outlet temperature with the inlet CO2 molar fraction, from which it can be seen that although the outlet temperature varies with the inlet molar fraction, it varies within 8 K, which is a very small range of variation. Fig. 5G shows the percentage of CO2 export and the ratio of molar fraction of CO2 to H2O, in which the percentage of CO2 export gradually decreases, while the ratio of the molar fraction of CO2 to H2O gradually increases. Fig. 5H shows the CO2 conversion ratio and efficiency. The conversion rate gradually increases with the increase of inlet flow rate. And the efficiency changes with the increase of molar fraction first increase and then decrease, and tend to the maximum value of efficiency at the molar fraction of 0.5; the maximum value is 21.45%.
4.2 Electrocatalytic system
As shown in Fig. 6A, the temperature inside the CO2 electrocatalytic electrolyser varied considerably when the inlet temperature varied, and when the inlet temperature is 800 K, the overall electrocatalytic temperature of the system is at around 800 K without significant change. When the inlet temperature is around 950 K, the electrolyser temperature shows some decrease along the flow direction, where the outlet temperature is 939.54 K.
Fig. 6B shows the power of a single electrolyser at different inlet temperatures, from which it can be found that the power of the electrolyser has a large increase as the inlet temperature increases. The increase in electrolytic power due to elevated temperatures provides more favorable conversion conditions for reactants. At the same operating current, total losses decrease, enabling higher current output and thereby boosting electrolytic power. Additionally, higher temperatures enhance the migration rates of electrons and ions, contributing to stronger electrochemical reaction driving forces. Consequently, the figure shows a positive correlation between power and temperature.
Fig. 6C shows the boundary current of the electrolyser at different inlet temperatures; similar to the power case in Fig. 6B, with the increase of inlet temperature, the boundary current of the electrolyser also increases. Among the reasons mainly considered are the faster reaction rate due to increase in temperature, decrease in activation energy, increase in ionic conductivity and enhancement of the mass transfer process. Fig. 6C analyzes the CO2 concentration at different inlet temperatures. As shown in the figure, when the inlet temperature is 800 K, the CO2 concentration hardly changes. As the temperature increases, the catalytic conversion of CO2 increases, and the concentration decreases significantly.
Fig. 6E shows the conversion rates of CO2 as well as H2O. From the figure, the electrolysis of H2O increases with the increase of temperature, and when the temperature is at 800 K, there is also a certain conversion rate of H2O. However, although the conversion rate of CO2 has a high increase with the increase of temperature, there is a negative conversion rate at 800 K. This is because at 800 K, CO2 is almost not electrolyzed; instead, the CO produced by the electrolysis of water reacts with water to produce CO2, which gives rise to a negative conversion rate. When the temperature rises, however, the efficiency of CO2 electrolysis rises rapidly, and when the inlet temperature reaches 950 K, more than 80% CO2 conversion rate can be achieved.
Fig. 6F shows the electrolysis efficiency as the inlet temperature transforms. The electrolytic efficiency of the system is 88.53% when the inlet temperature is 800 K. The efficiency increases to 99.59% when the inlet temperature is 950 K, which is an increase of 11.06%. Mechanistically, elevated temperatures cause the reaction rate constant to increase rapidly according to the Arrhenius relationship, meaning that the same input electrical energy can be converted into more products. Simultaneously, elevated temperatures reduce reaction overpotentials and ohmic losses, increasing the number of chemical reactions per unit electrical energy input. Consequently, as temperature rises, more input electrical energy is effectively utilized (higher Faraday efficiency), significantly boosting overall system efficiency. Particularly above 600 °C, accelerated reaction kinetics and lower polarization losses cause efficiency to approach saturation.
 | ||
| Fig. 7 (A) Temperature of the electrocatalytic system; (B) electrolysis power; (C) boundary current; (D) changes in reactant mole fraction; (E) reactant conversion rate; (F) electrolysis efficiency. | ||
The temperature variation of the system at a high H2O/CO2/CO inlet mole fraction is shown in Fig. 7A, respectively. At a high CO2 inlet molar fraction, the temperature of the system undergoes a decrease of about 30 K. The main reason for this is water vapor electrolysis: ΔH ≈ ΔG (thermo-neutral), low heat uptake demand, and temperature stabilization. Carbon dioxide electrolysis, ΔH ≫ ΔG (strong heat absorption), requires a large amount of ambient heat, and the temperature is prone to drop. Also, the reason for the lower temperature change in the inlet state for high concentrations of CO is that there are fewer reactions.
Fig. 7B shows the variation of electrolysis power for the three inlet mole fractions, from which it can be seen that the power of the electrolyser increases when the mole fraction of CO2 as well as water increases. In contrast, the electrolytic power decreases when the molar fraction of CO increases, and when the molar fraction of CO increases to a certain level, the electrolytic power decreases to close to zero, i.e., the reaction does not occur. As the molar fraction of H2O increases, the system's electrical energy consumption rises almost linearly, indicating that more charge is required to electrolyze additional water vapor. Conversely, when the molar fraction of CO2 increases, the rise in energy consumption is smaller, suggesting that CO2 electrolysis contributes relatively less to the overall reaction activity compared to water vapor. At the same total feed rate, a high H2O content implies greater H2 production, thus requiring higher current. Although high CO2 also consumes energy, CO2 typically possesses a higher reduction potential than H2O. Consequently, at the same potential, the actual electrolytic intensity does not increase as linearly as it does for H2O. In summary, the variation in energy consumption reflects the differing contributions of each component to the electrolytic reaction rate.
Fig. 7C shows the variation of boundary currents for the three inlet molar fractions, which is similar to the results of Fig. 7B.
From the above analysis, it can be seen that the reaction hardly occurs after the molar fraction of CO is increased to a certain level, so we investigated the change of its molar fraction at high CO2 as well as high H2O molar fraction, and the results are shown in Fig. 7D. The results in the figure show that at high H2O molar fraction, the system can electrolyze more CO2, and its molar fraction change is more drastic, in which the H2O decreases from 95.00% in the inlet to 16.68%, while the CO2 decreases from 95.00% in the inlet to 48.82%. Fig. 7E shows the conversion rates of the two substances with different inlet molar fractions, and it can be seen that the conversion rates of the two substances show an increasing and then decreasing trend with the increase of their inlet molar fractions.
Fig. 7F shows the electrolysis efficiency with different inlet molar fractions. From the figure, the electrolysis efficiency of the system decreases with the increase in the inlet molar fraction of CO as well as H2O, and increases with the increase in the inlet molar fraction of CO2, where the electrolysis efficiency reaches 99.21% when the inlet molar fraction of CO2 is 95.00%.
4.3 Coupled system
The final effect of the coupling system should be reflected in the comprehensive efficiency; the study analysed the efficiency improvement of the electrocatalytic part of the coupling system as well as the total efficiency improvement of the coupling system, and the results of the study are shown in Fig. 8.Fig. 8A shows the efficiencies at different inlet temperatures, considering the heat of the inlet material and without considering the heat of the inlet material. As can be seen from the data in the figure, there is a large gap between the two efficiencies with and without heat, where the maximum gap between the two efficiencies is 55.13%, and the gap between the two efficiencies is 24.84% at the highest efficiency. Fig. 8B and C show the variation of the two efficiencies with different CO2 inlet molar fractions and H2O inlet molar fractions, respectively, and it can be seen that the trend of the two efficiencies is the same as in the case of with and without heat.
The improvement of the coupled system for the two systems individually is also analysed, where the original parameter case, the high-efficiency pore/aperture case, and the high-efficiency flow rate case are selected for analysis. As can be seen in Fig. 8D, the coupled system has an efficiency enhancement of 24.84% for the electrocatalytic system and 16.98% for the whole system. The values of enhancement in Fig. 8E are 24.41% and 17.24%, respectively, whereas the values for the high flow rate case are 27.84% and 29.00%, respectively. The increase in efficiency is mainly due to the increase in the efficiency of electrocatalysis, which consumes more power than photothermal catalysis, thus resulting in an overall increase in efficiency.
When the electricity supplied to SOEC comes from renewable energy sources such as photovoltaics or wind power, then this electricity is essentially derived from primary energy sources such as solar energy. For example, we can assume a photovoltaic conversion efficiency of 20%. When taking into account both solar thermal and photovoltaic conversion, the overall “solar-to-electrolysis” efficiency would be lower than the current value.
5 Conclusion
Considering that solar photothermal-driven reverse water gas shift reactions can consume carbon dioxide for carbon emission reduction, while the tail gas contains high-quality heat that remains unused, we propose a solar-heated combined thermal–electrical catalytic CO2 reduction system. This system integrates solar photothermal CO2 reduction with an electrocatalytic CO2 reduction system, utilizing the high-temperature tail gas from the solar photothermal process to provide high-temperature reaction materials for the electrocatalytic reduction of CO2. The conclusions for the coupled system are as follows:(1) For the thermostatic reduction part, the reactor can achieve high solar-chemical energy efficiency under the reaction conditions of high porosity and low pore size, medium power, high inlet flow rate, high inlet temperature and the same inlet mole fraction, where the highest efficiency can reach 25.42%.
(2) For the electrocatalytic part, the electrolytic efficiency of co-electrolysis decreases with increasing molar fractions of H2O as well as CO and increases with an increasing molar fraction of CO2. The electrolysis efficiency of the system can reach 99.21% when the inlet CO2 molar fraction is 95.00%.
(3) The coupled system effectively improves the efficiency of the system, and the electrocatalytic efficiency of the system can be improved by 24.84% to 95.80% when there is waste heat available in the electrocatalytic part. And the efficiency of the system can be improved by 29.00% when the two systems are coupled to catalyze CO2.
In summary, this solar-thermal-electric coupling system fully exploits the potential for reusing waste gas thermal energy and reactant resources, demonstrating significant efficiency advantages and synergistic enhancement capabilities. This research provides technical guidance for designing multi-source synergistic utilization systems driven by solar energy, while offering theoretical support and technical references for achieving efficient carbon resource conversion and carbon neutrality goals.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The datasets supporting this article have been uploaded as part of the supplementary information (SI).Supplementary information is available. See DOI: https://doi.org/10.1039/d5cy00892a.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 52436008), the Heilongjiang Province's Key Research and Development Project: “Leading the Charge with Open Competition” (No. 2023ZXJ06A04) and the State Key Laboratory of Clean Energy Utilization (No. ZJUCEU2024007).Notes and references
- W. C. Satyro, C. M. V. B. de Almeida, M. J. A. Pinto Jr., J. C. Contador, B. F. Giannetti, A. F. de Lima and M. A. Fragomeni, Industry 4.0 implementation: The relevance of sustainability and the potential social impact in a developing country, J. Cleaner Prod., 2022, 337, 130456 CrossRef.
- T. Zhou, T. Zhou, Z. Li, K. B. Aviso and R. R. Tan, Multi-objective optimization of straw-based bio-natural gas supply chains considering cost, CO2 emission, and safety, J. Cleaner Prod., 2024, 449, 141759 CrossRef CAS.
- R. Zhou, M. Jin, Z. Li, Y. Xiao, D. McCollum and A. Li, Techno-economic analysis and network design for CO2 conversion to jet fuels in the United States, J. Cleaner Prod., 2025, 210, 115191 CAS.
- H. Lund, P. A. Østergaard, M. Yuan, P. Sorknæs and J. Z. Thellufsen, Energy balancing and storage in climate-neutral smart energy systems, Renewable Sustainable Energy Rev., 2025, 209, 115141 CrossRef.
- X. Wang, X. Wei and H. Dai, Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge, J. Energy Storage, 2019, 21, 618–631 CrossRef.
- https://www.metoffice.gov.uk/research/climate/seasonal-to-decadal/long-range/forecasts/co2-forecast-for-2025 .
- Z. Cheng, H. Han, F. Wang, Y. Yan, X. Shi and H. Liang, et al., Efficient radiative cooling coating with biomimetic human skin wrinkle structure, Nano Energy, 2021, 89, 106377 CrossRef CAS.
- J. Janmontree, H. Zadek and K. Ransikarbum, Analyzing solar location for green hydrogen using multi-criteria decision analysis, Renewable Sustainable Energy Rev., 2025, 209, 115102 CrossRef CAS.
- Y. Zhang, Y. Li, Y. Xu, F. Wang, Z. Wei and Y. Fang, et al., CaO/CaCO3 thermochemical energy storage performance of MgO/ZnO co-doped CaO honeycomb in cycles, J. Energy Storage, 2023, 66, 107447 CrossRef.
- Z. Cheng, F. Wang, D. Gong, H. Liang and Y. Shuai, Low-cost radiative cooling blade coating with ultrahigh visible light transmittance and emission within an “atmospheric window”, Sol. Energy Mater. Sol. Cells, 2020, 213, 110563 CrossRef CAS.
- X. Shi, J. Song, Z. Cheng, H. Liang, Y. Dong and F. Wang, et al., Radiative intensity regulation to match energy conversion on demand in solar methane dry reforming to improve solar to fuel conversion efficiency, Renewable Energy, 2023, 207, 436–446 CrossRef.
- J. Xiong, J. Ji, Q. Lei, X. Yang, Y. Bai and X. Zhang, et al., Synergetic energy coupled thermal catalytic systems for CO2 reduction, eScience, 2024, 100306 Search PubMed.
- J. Song, Y. Fan, Z. Cheng, F. Wang, X. Shi and J. Xu, et al., Biomimetic low carbonization efficient solar-driven thermochemical energy storage reactor design inspired by the diatoms' superior photosynthesis capacity, Energy Convers. Manage., 2025, 323, 119224 CrossRef CAS.
- J. Sun and J. Wu, Modeling Thermocatalytic Systems for CO2 Hydrogenation to Methanol, Chem. Sci., 2025,(17), 7477–7488 RSC.
- S. Wang, A. A. Tountas, W. Pan, J. Zhao, L. He and W. Sun, et al., CO2 Footprint of Thermal Versus Photothermal CO2 Catalysis, Small, 2021, 17, 2007025 CrossRef CAS.
- H. Liang, F. Wang, D. Zhang, Z. Cheng, C. Zhang and B. Lin, et al., Experimental investigation of cost-effective ZnO nanofluids based spectral splitting CPV/T system, Energy, 2020, 194, 116913 CrossRef CAS.
- X. Ding, W. Liu, J. Zhao, L. Wang and Z. Zou, Photothermal CO2 Catalysis toward the Synthesis of Solar Fuel: From Material and Reactor Engineering to Techno-Economic Analysis, Adv. Mater., 2024, 37, 38683953 Search PubMed.
- R. Fiorenza, M. Bellardita, S. A. Balsamo, L. Spitaleri, A. Gulinoet and M. Condorelli, et al., A solar photothermocatalytic approach for the CO2 conversion: Investigation of different synergisms on CoO-CuO/brookite TiO2-CeO2 catalysts, Chem. Eng. J., 2022, 428, 131249 CrossRef CAS.
- F. Sun, X. Xing and H. Hong, Comment on “CO2 Footprint of Thermal Versus Photothermal CO2 Catalysis”, Small, 2022, 19, 2203647 CrossRef.
- M. F. Santos, A. E. Bresciani, N. L. Ferreira, G. S. Bassani and R. M. B. Alves, Carbon dioxide conversion via reverse water-gas shift reaction: Reactor design, J. Environ. Manage., 2023, 345, 118822 CrossRef CAS PubMed.
- Z. Wu, J. Shen, C. Li, C. Zhang, K. Feng and Z. Wang, et al., Mo2TiC2 MXene-Supported Ru Clusters for Efficient Photothermal Reverse Water–Gas Shift, ACS Nano, 2022, 17, 1550–1559 CrossRef PubMed.
- B. Chang, Z. Min, N. Liu, N. Wang, M. Fan and J. Fan, et al., Electrocatalytic CO2 reduction to syngas, Green Energy Environ., 2024, 9, 1085–1100 CrossRef CAS.
- D. Xu, K. Li, B. Jia, W. Sun, W. Zhang and X. Liu, et al., Electrocatalytic CO2 reduction towards industrial applications, Carbon Energy, 2022, 5, e230 CrossRef.
- Z. Zhu, W. Tang, J. Wang, L. Zhao, Y. Lin and Z. Li, et al., Insights into Operating Conditions on Electrocatalytic CO2 Reduction, Adv. Energy Mater., 2025, 2405768 CrossRef CAS.
- B. Deng, M. Huang, X. Zhao, S. Mou and F. Dong, et al., Interfacial Electrolyte Effects on Electrocatalytic CO2 Reduction, ACS Catal., 2021, 12, 331–362 CrossRef.
- Y. Pei, H. Zhong and F. Jin, A brief review of electrocatalytic reduction of CO2—Materials, reaction conditions, and devices, Energy Sci. Eng., 2021, 9, 1012–1032 CrossRef CAS.
- Y. Li, L. Zhang, B. Yu, J. Zhu and C. Wu, CO2 High-Temperature Electrolysis Technology Toward Carbon Neutralization in the Chemical Industry, Engineering, 2023, 21, 101–114 CrossRef CAS.
- G. Xiang-Kui, J. S. A. Carneiro and E. Nikolla, First-Principles Study of High Temperature CO2 Electrolysis on Transition Metal Electrocatalysts, Ind. Eng. Chem. Res., 2017, 56, 6155–6163 CrossRef.
- Z. Nan, W. Zhang Wenyu, W. R. Mengyu, Y. Gong and H. Wang, et al., Entropy-engineered perovskite cathodes: A novel approach for efficient and durable CO2 electrolysis, J. Colloid Interface Sci., 2025, 682, 70–79 CrossRef PubMed.
- Y. Zhang, C. Yu, X. Song, X. Tan, W. Li and S. Liu, et al., Defect-enabled local high-temperature field within carbon to promote in-plane integration of an electrocatalyst for CO2-to-CO conversion, Energy Environ. Sci., 2025, 18, 1331–1342 RSC.
- S. Hu, B. Pang, L. Zhang, Z. Cao, P. Zhang and Y. Ding, et al., Mapping a thermodynamic stability window to prevent detrimental reactions during CO2 electrolysis in solid oxide electrolysis cells, Appl. Catal. B: Environ., 2023, 324, 122239 CrossRef CAS.
- H. Qi, J. Zhang, B. Tu, Y. Yin, T. Zhang and D. Liu, et al., Extreme management strategy and thermodynamic analysis of high temperature H2O/CO2 co-electrolysis for energy conversion, Renewable Energy, 2022, 183, 229–241 CrossRef CAS.
- N. Gokon, Y. Osawa, D. Nakazawa and T. Kodama, Kinetics of CO2 reforming of methane by catalytically activated metallic foam absorber for solar receiver-reactors, Int. J. Hydrogen Energy, 2009, 34, 1787–1800 CrossRef CAS.
- H. Zheng, Z. Zhang, K. Xu, S. Wang, B. Yu and T. Xie, Analysis of structure-induced performance in photothermal methane dry reforming reactor with coupled optics-CFD modeling, Chem. Eng. J., 2022, 428, 131441 CrossRef CAS.
- J. Song, Z. Cheng, Y. Fan, F. Wang, X. Shi and J. Xu, et al., Human ear inspired solar thermochemical reactor for steam methane reforming with the consideration of minimum Gibbs free energy principle, J. Energy Storage, 2023, 72, 108172 CrossRef.
- J. R. Howell, M. Pinar Mengüc, K. Daun and R. Siegel, Thermal Radiation Heat Transfer, 2020, vol. 1040 Search PubMed.
- Y. Du, Y. Qin, G. Zhang, Y. Yin, K. Jiao and Q. Du, Modelling of effect of pressure on co-electrolysis of water and carbon dioxide in solid oxide electrolysis cell, Int. J. Hydrogen Energy, 2019, 44, 3456–3469 CrossRef CAS.
- P. Costamagna, P. Costa and V. Antoucci, Micro-modelling of solid oxide fuel cell electrodes, Electrochim. Acta, 1998, 43, 375–394 CrossRef CAS.
- J. Park, P. Li and J. Bae, Analysis of chemical, electrochemical reactions and thermo-fluid flow in methane-feed internal reforming SOFCs: Part I – Modeling and effect of gas concentrations, Int. J. Hydrogen Energy, 2012, 37, 8512–8531 CrossRef CAS.
- M. Ni, An electrochemical model for syngas production by co-electrolysis of H2O and CO2, J. Power Sources, 2012, 202, 209–216 CrossRef CAS.
- G. Cinti, A. Baldinelli, A. D. Michele and U. Desideri, Integration of Solid Oxide Electrolyzer and Fischer-Tropsch: A sustainable pathway for synthetic fuel, Appl. Energy, 2016, 162, 308–320 CrossRef CAS.
- M. Ni, 2D thermal modeling of a solid oxide electrolyzer cell (SOEC) for syngas production by H2O/CO2 co-electrolysis, Int. J. Hydrogen Energy, 2012, 37, 6389–6399 CrossRef CAS.
- Z. Pan, Q. Liu, L. Zhang, J. Zhou, C. Zhang and S. H. Chan, et al., Experimental and thermodynamic study on the performance of water electrolysis by solid oxide electrolyzer cells with Nb-doped Co-based perovskite anode, Appl. Energy, 2017, 191, 559–567 CrossRef CAS.
- S. Afroze, N. S. B. Sofri and M. S. Reza, et al., Solar-Powered Water Electrolysis Using Hybrid Solid Oxide Electrolyzer Cell (SOEC) for Green Hydrogen—A Review, Energies, 2023, 16, 7794–7816 CrossRef CAS.
- F. R. Bianchi, A. Baldinelli and L. Barelli, et al., Multiscale Model-ing for Reversible Solid Oxide Cell Operation, Energies, 2020, 13, 5058–5074 CrossRef CAS.
- F. R. Bianchi, A. Baldinelli, L. Barelli, G. Cinti, E. Audasso and B. Bosio, Multiscale Modeling for Reversible Solid Oxide Cell Operation, Energies, 2020, 13, 5058–5074 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |