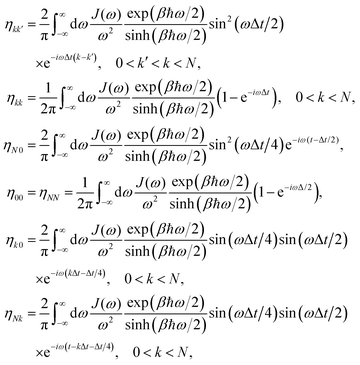DOI:
10.1039/D5CS00948K
(Review Article)
Chem. Soc. Rev., 2026, Advance Article
Quantum coherent dynamics in photosynthetic protein complexes
Received
10th August 2025
First published on 23rd December 2025
Abstract
Since the birth of quantum mechanics, there has been a long fascination of the role of quantum effects in the evolution of biological systems, which has inspired decoding quantum coherence effects in photosynthetic systems. In photosynthetic complexes, the pigments do not exist in isolation; they interact with their surrounding protein environment. However, the strength of this system–bath coupling can vary, and one must be careful in characterizing it (with many complexes actually in an intermediate coupling regime). This review will summarize the studies toward unraveling excitonic energy transfer in photosynthetic systems, examining the influence of electronic and vibronic coherence and system–bath interactions on transfer efficiency in photosynthetic protein complexes. The review first examines the absorption properties of chlorophylls and the structural organization of protein complexes, highlighting their role in facilitating ultrafast-energy and charge-transfer processes. It also introduces the principles of multidimensional coherent spectroscopy (a nonlinear four-wave-mixing technique) and related ultrafast spectroscopic methods, which provide key insights into these processes. We also discuss theoretical approaches and models (quantum master equations and other quantum dissipative models) used to simulate the evolution of electronic coherence in photosynthetic systems. Additionally, the review considers recent advancements in both natural and artificial photosynthetic systems, focusing on the critical role of system–bath interactions and dissipation in protein environments. These dynamics are shown to direct energy transfer effectively, overcoming the fragility of quantum coherence under physiological conditions.
 Ajay Jha | Ajay Jha completed his undergraduate degree in chemistry at Sri Venkateswara College, University of Delhi in 2007, followed by a master's degree in organic chemistry in 2009. He then pursued a PhD at TIFR, Mumbai, under Prof Jyotishman Dasgupta, focusing on ultrafast electron transfer in solutions and at interfaces. In 2015, he joined the Max Planck Institute in Hamburg, where he used multidimensional spectroscopy to study energy and electron transfer in photosynthetic systems. He moved to the Rosalind Franklin Institute in 2020 and became an Associate Investigator in 2023, developing light-activated strategies to map biomolecular dynamics and interactions. |
 Michael Thorwart | Michael Thorwart studied physics at the Universität Tübingen and completed his Diploma thesis at the University of Urbana–Champaign in 1996. He earned his doctorate in 2000 under Prof. Peter Hänggi at the Universität Augsburg. Between 2001 and 2003, he was a postdoctoral researcher at TU Delft, then served as a scientific assistant to Prof. Reinhold Egger at the Universität Düsseldorf, completing his Habilitation in 2006. He later led a junior research group in Freiburg before becoming a professor at the Universität Hamburg in 2010. His work explores nonequilibrium dynamics in diverse open quantum systems. |
 R. J. Dwayne Miller | R. J. Dwayne Miller's research has focused on diffractive optics based nonlinear spectroscopy, notably the work on 2D photon echo methods, that contributed to the reviewed work. These studies have been complemented by his group's development of ultrabright electron sources to light up atomic motions at the fundamental spatial-temporal resolution to imaging chemistry. His research accomplishments have been recognized with numerous awards including the ACS E. Bright Wilson Award, the EPS Laser Science Prize, and the APS Earl K Plyler Prize for atomically resolved dynamics. He is a Fellow of the Royal Society of Canada and Royal Society of London. |
 Hong-Guang Duan | Hong-Guang Duan completed his physics degree at Sichuan Normal University in 2009, then pursued postgraduate studies in theoretical physics at Ningbo University from 2009 to 2012. He continued his academic development at the University of Hamburg, earning his doctoral degree in 2018. He subsequently held postdoctoral positions at the Max Planck Institute in Hamburg and the European XFEL until 2021. Upon returning to China, he founded his independent research group at Ningbo University in November 2021. His team develops advanced 2D electronic spectroscopy and ultrafast electron diffraction methods to study energy transfer, quantum coherence, and wave-packet dynamics in photosynthetic proteins. |
1 Introduction
The relevance of quantum effects in the evolution of biological systems has long fascinated scientists since the inception of quantum physics.1–3 Among these, quantum coherence, the maintenance of phase relationships between quantum states, has been a focal point of research due to its potential implications for understanding and optimizing natural processes.4 The ability of living systems to employ these quantum coherences efficiently in the challenge of environmental noise poses fascinating questions about the extent to which coherent quantum effects can persist and influence biological functions. These insights are not only of fundamental interest but also hold transformative implications for quantum technologies.5
Quantum systems in biology are inherently open systems, interacting continuously with their surroundings in what is known as the system–bath framework.6 While these interactions enable processes such as energy dissipation and thermal equilibration, they simultaneously drive decoherence, limiting the longevity of quantum interference effects to direct biological processes.7 Nonetheless, it has been hypothesized that nature may have optimized these interactions to constructively exploit quantum phase effects, especially in crucial biological processes.8,9 Exploring this hypothesis has the potential to yield insights that could bridge biology with disciplines such as quantum computing and quantum information science, where decoherence remains a significant challenge.10
Photosynthetic systems provide an ideal platform for investigating quantum coherence in biological settings. Photosynthesis, one of the most fundamental processes sustaining life on Earth, involves the efficient capture, transfer, and conversion of solar energy into chemical energy.11,12 Within the pigment–protein complexes of photosynthetic systems, energy transfer processes occur with near-perfect efficiency, facilitated by the interplay of electronic and vibrational dynamics. The Fenna–Matthews–Olson (FMO) protein complex, a light-harvesting assembly found in green sulphur bacteria, has served as a model system for probing these dynamics due to its relatively simple structure and well-characterized properties. The advent of pulsed laser technologies and advanced ultrafast spectroscopic tools has enabled the measurement of delicate quantum coherent dynamics in matter on ultrashort timescales.13,14 This progress has opened new avenues for investigating nontrivial quantum effects during the initial stages of biological processes, contributing to the establishment of quantum biology as a scientific field.4,8,15 Notably, two-dimensional electronic spectroscopy (2DES) has played a pivotal role in these investigations by providing a powerful method to explore quantum coherence within these complex systems.16,17 The initial discovery of oscillatory signals in the FMO complex was interpreted as evidence of long-lived electronic quantum coherence, suggesting a functional role in enhancing energy transfer efficiency.18 The observed long-lived quantum coherence was proposed to speed up the transfer of excitation energy in protein complexes, even at physiological temperature.19–21 This observation catalyzed widespread interest, laying the foundation for quantum biology as a discipline. However, subsequent studies have called this interpretation into question, offering alternative explanations such as vibrational coherence or ground-state dynamics for the observed oscillations. The debate highlights the complexity of disentangling quantum coherence from other phenomena in biological systems.
Experimental and theoretical studies have illustrated the transient nature of electronic coherence in photosynthetic complexes. The lifetime of electronic coherence, heavily influenced by system–bath interactions, is typically much shorter than the energy transfer timescale under physiological conditions. For instance, ultrafast transient absorption experiments at cryogenic temperatures have measured electronic dephasing lifetimes on the order of 140–180 femtoseconds (fs) in the FMO complex,22 while room temperature studies observe even shorter lifetimes. These findings imply that electronic coherence is unlikely to directly mediate energy transfer in natural environments. Instead, nature appears to employ strong system–bath coupling to ensure robust, efficient energy transport via classical mechanisms such as Förster resonance energy transfer (FRET).23 While the role of electronic coherence remains contentious, the interplay between electronic and vibrational dynamics has emerged as a promising area of study.24 Vibronic coupling, the interaction between electronic states and molecular vibrations, has been proposed to extend the coherence lifetime and potentially facilitate energy transfer. Recent studies have explored the concept of vibrationally enhanced electronic coherence, where specific vibrational modes are resonantly coupled to electronic transitions.25 These modes, often delocalized and anticorrelated, may persist for picoseconds, significantly longer than electronic coherence. However, the extent to which such mechanisms contribute to energy transfer efficiency in physiological conditions remains still an open question. Recent experimental work has revisited the FMO complex and other photosynthetic systems to address these uncertainties. The energy transfer and coherent dynamics of the FMO complex have been revisited by Duan et al. at room temperature.26 In contrast to the long-lived electronic coherence, they reported a rather short lifetime for the electronic coherence (60 fs), which is significantly shorter than the timescale of energy transfer at physiological temperature (several ps). By systematically varying temperature and controlling system–bath interactions, researchers have clarified the relationship between coherence and energy transfer. The 2DES measurements and analyzed results showed that the lifetime of electronic dephasing is shorter than 170 fs at 77 K.27 The long-lived oscillatory dynamics observed in 2DES has been found to originate from the ground state bleach. Theoretical models have been instrumental in interpreting those studies and elucidating the mechanisms underlying energy transfer.
The entire issue eventually reduces to the decisive question of how long a quantum matter wave can keep its coherence and thus its required coherence and thus its wave-like characteristics. This is determined by the magnitude of the system bath interaction and distribution by which the biological chromophores are coupled to a noisy, warm, and wet biological environment under biological conditions. Theoretical simulations of dynamical processes in photosynthetic systems require preliminary knowledge of electronic properties of the target systems, such as the excitation energies of the pigments, the excitonic coupling between the pigments, and the system–bath interactions. The electronic structure of a molecule is affected by its surroundings. The stronger the ‘system–bath coupling’, the stronger the electronic coupling between chromophores must be in order to overcome the random energy fluctuations and phase shifts in the induced polarization between the resonantly interacting molecules, as part of the spatial transport of energy. In the limit of strong interactions of the chromophores with their surroundings, these random changes in phase reduce the interaction to an incoherent, or Förster mechanism, of energy transport, which can be understood classically through dipole–dipole interactions, or classical limit. It all comes down to most accurately determining the system–bath coupling in terms of a parameter known as the reorganization energy in the system–bath framework.
Early theoretical analyses used relatively small reorganization energy values derived from the frequency difference between the absorption and emission spectra peaks. Based on the very accurate spectral density of the bath modes, which include vibrational fluctuations of the protein and the pigments for an experimentally determined fluctuation spectrum,28 the system–bath coupling could be determined to define the limitations to quantum coherence effects. Numerically exact path integral simulations for the quantum coherent energy transfer in the FMO aggregate under realistic physiological conditions were reported in 2011.29 Coherence times shorter than those originally assigned to exciton coherence were found. Based on these assumptions, Shi et al. applied 2DES calculations and found shorter electronic coherence lifetimes than those interpreted experimentally.30 To address this discrepancy, ab initio calculations were conducted to capture site-dependent reorganization energies in pigment–protein complexes such as the FMO complex and reaction centers.31 These calculations confirmed significantly larger reorganization energy values, approximately an order of magnitude higher than previously estimated, highlighting the critical role of environmental coupling in shaping coherence dynamics within these systems. These findings suggest that the lifetime of electronic coherence observed experimentally require accurate realistic theoretical models and calculations. Furthermore, other studies have demonstrated that the optimal efficiency of energy transfer in pigment–protein complexes, even in thermal environments, can be achieved through purely incoherent hopping processes. This mechanism, driven by downhill energy gradients, highlights the role of robust, classical pathways in ensuring efficient energy transfer without reliance on sustained quantum coherence effects, highly sensitive to noise cancellation.32,33 With this solid experimental and theoretical work on the short lived coherence, the collective view of the researchers involved in this critical evaluation, was that the electronic coherence is too fragile to enhance energy transfer in photosynthetic protein complexes under physiological conditions.34
The field of quantum biology has still been motivated by theoretical models suggesting various models for system–bath interactions that might enhance quantum coherence in energy transfer. These concepts often invoke exotic interactions to create correlated noise, yet systematic experiments are necessary to validate such effects. Temperature dependent studies provide a straightforward way to modulate the system–bath coupling to reveal this relationship to the quantum decoherence timescales. At ultra-low temperatures of 20 K, quantum coherent transport is observed by Duan et al., but coherence diminishes rapidly with increasing temperature, demonstrating its negligible role in the biological function at physiological conditions.35 Rigorous analysis of temperature-dependent 2D spectra shows the long-lived coherent oscillations ascribed previously to coherent exciton states are instead vibrational oscillations in the ground state. This study's observation of ultrafast coherence decay is consistent with a memory-less (Markovian) description of energy transfer on its intrinsic timescale; however, further calculations including disorder to reproduce these timescales are needed. In addition, coherent dynamics in energy and charge transfer processes within reaction centers have been investigated using 2DES. Optical measurements conducted at 20 K reveal distinct coherence lifetimes in the PSII reaction center compared to the FMO complex, attributed to variations in pigment arrangement and excitonic coupling.36 Notably, the strong exciton interactions in the radical pair produce clear evidence of electronic coherence persisting for over 600 fs albeit at low temperature. These findings underscore the importance of temperature-dependent measurements in determining the nature of observed coherences and assessing their potential functional roles in energy transfer processes within photosynthetic systems.
The exploration of quantum coherence in photosynthetic systems highlights the value of an interdisciplinary approach that combines experimental techniques, theoretical modeling, and computational simulations to unravel the dynamics of complex biological systems. This review summarizes the key recent findings, offering a detailed analysis of energy transfer mechanisms in photosynthetic systems, with a particular emphasis on the impact of quantum coherence. By integrating the latest experimental and theoretical developments, this review seeks to advance the understanding of how quantum dynamics contribute to the efficiency of energy transfer in natural and potentially artificial systems. We begin by offering a general introduction to energy transfer mechanisms, contrasting classical Förster energy transfer with coherent energy transfer models. A theoretical framework for system–bath interactions will be developed, highlighting the interplay between coherence, decoherence, and dissipation. An introduction to photosynthetic complexes to put this work in context is provided. Additionally, this review will include an overview of the multidimensional electronic spectroscopic methods used to study energy transfer pathways, discuss various theoretical approaches to model experimental data, and summarize significant 2DES findings that shed light on system–bath interactions and the evaluation of the role of quantum coherences. Finally, it discusses open questions and future directions, emphasizing the broader relevance of the fundamental understanding gained from these studies in bridging fundamental science with applied technologies. Through this comprehensive analysis, the review aims to provide a detailed understanding of quantum coherences and energy dissipation during energy transfer processes in nature.
2 Energy transfer: coherent vs. incoherent
Energy transfer is a fundamental process that governs a wide range of physical, chemical, and biological phenomena. It plays a crucial role in molecular excitations, facilitating energy migration in materials, and is central to charge and exciton transport in semiconductors. Moreover, it is a key process in quantum optics and photonic materials, influencing the design and function of optoelectronic devices and energy-harvesting systems. The ability to control and optimize energy transfer mechanisms is vital for technological advancements in fields such as materials science, nanotechnology, and biological energy conversion. Depending on the role of quantum coherence and environmental interactions, energy transfer is broadly classified into two regimes: coherent and incoherent energy transfer. The distinction between these two mechanisms is significant, as it influences the overall efficiency, speed, and effectiveness of energy migration in complex molecular and nanoscale systems. The delineating factor between the two regimes is the degree of electronic coupling between chromophores relative to the system–bath coupling. Most photosynthetic complexes fall in the intermediate coupling regime, where electronic couplings (tens to a couple hundred cm−1) are comparable to or somewhat larger than reorganization energies (tens to 100 cm−1).37
Coherent energy transfer occurs when an excitation remains delocalized over multiple sites, behaving as a quantum wavefunction rather than undergoing a sequential hopping process (as depicted in Fig. 1). In this regime, quantum superposition and phase coherence significantly impact the energy transfer process, leading to interference effects and wave-like propagation of excitations. The persistence of coherence is determined by factors such as strong electronic coupling between sites and weak interactions with the surrounding environment, both of which help suppress decoherence. When the system maintains coherence over extended time scales, energy can propagate efficiently over long distances with minimal losses. This behavior is commonly observed in engineered quantum systems, superconducting circuits, and certain condensed-phase materials, where coherent transport has been shown to enhance energy transfer efficiency beyond what is expected from purely classical models.
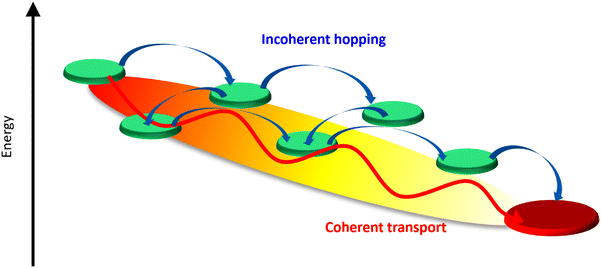 |
| | Fig. 1 Comparison of coherent and incoherent energy transfer mechanisms in a photosynthetic protein complex. The red pathway illustrates coherent transport, where excitation energy flows smoothly through quantum coherence. In contrast, the blue arrows represent incoherent hopping, characterized by random, thermally driven transitions between chromophores. The energy landscape (color gradient) highlights the variation in site energies that influence both mechanisms. | |
Unlike coherent transfer, where quantum effects enable wave-like motion, incoherent transfer is better described using rate equations that follow classical probabilistic dynamics. A well-known mechanism for incoherent energy transfer is Förster resonance energy transfer (FRET), in which energy is transferred through dipole–dipole interactions between chromophores. Förster's theory, while yielding a rate expression reminiscent of classical kinetics, is fundamentally derived from quantum mechanical perturbation theory, specifically Fermi's golden rule. The efficiency of this process is highly dependent on factors such as the donor–acceptor separation, molecular orientation, and surrounding solvent dynamics. This mechanism is particularly relevant in biological and soft-matter systems, where interactions with a dynamic and complex environment strongly influence energy transport.
When comparing the two mechanisms, a key difference lies in their dependence on environmental conditions. Coherent energy transfer is highly sensitive to external perturbations, and any interaction with the environment that induces dephasing can disrupt quantum coherence, causing the system to transition toward incoherent behavior. In contrast, incoherent energy transfer is more robust in thermally fluctuating environments, as it relies on localized hopping and differences in site energies to create energy gradients to direct the transport energetically downhill, exploiting dissipation, rather than extended quantum coherence over the relevant length scale. Another important distinction is in their efficiency and speed: while coherent transfer can, under ideal conditions, allow for faster and loss-minimized energy transport, incoherent transfer provides a more predictable and stable mechanism, especially in complex, disordered systems such as biological membranes and organic molecular assemblies. In the classical limit, the difference in site energies can be minimized to correspondingly minimize energy loss while still providing sufficient direction to unerringly direct the energy transport. It must be noted that the Förster and Redfield theories represent extreme limits. Generalised Förster or modified Redfield theoretical methods have also been employed to study light-harvesting dynamics that account for simultaneous coherent delocalization and incoherent dissipation.38,39
In the following sections, we provide a detailed discussion of the theoretical frameworks governing both energy transfer mechanisms followed by the introduction to system–bath interactions. By examining these processes in various systems, we aim to clarify their roles in energy transport and explore how different conditions favor one mechanism over the other.
2.1 Förster resonance energy transfer
Förster resonance energy transfer is applicable for the energy transfer between molecules at relatively longer distance and weaker couplings. The mechanism was firstly proposed by Theodor Förster in the 1940's.40–42 It describes a nonradiative resonance transfer process between two pigments, which are usually separated by several Angstroms with the associated electronic transitions. The energy transfer between two pigments occurs primarily via a Coulomb coupling. Based on ref. 41, the rate of energy transfer can be written aswhere ke denotes the first-order rate constant for energy transfer from the donor to the acceptor, while kf represents the rate constant for donor fluorescence. R refers to the distance between the donor and acceptor. R0 is the critical distance at which there is a 50% probability of energy transfer occurring within the donor's excited-state lifetime, which is given by the relation| | |
R06 = 8.79 × 10−5Jκ2n−4 Å.
| (2) |
n is the refractive index, κ2 is an orientation factor and J is an energy overlap factor, which can be written as| |
 | (3) |
where ε(λ) refers to the molar extinction coefficient of the acceptor. FD(λ) represents the normalized emission spectrum of the donor. The parameter J indicates the overlap area of absorption of the donor and emission spectrum of the acceptor. The physical underpinnings of this spectral overlap parameter is the degree of similarity of energy scales between donor and acceptor, which is required by the conservation of total energy of the system before and after the transfer. This process requires both molecules to share a common energy state and have spectral transitions at the same wavelength. Although overlap between donor fluorescence and acceptor absorption is necessary, FRET does not involve photon emission and reabsorption, a common misconception. Actually, it is not the case. The Förster resonance energy transfer is a nonradiative process without photon emission or absorption involved in the process. Some developments, such as multi-chromophoric FRET and mixed quantum-classical methods, extend the original theory's applicability by incorporating partial coherence effects.43–45
2.2 Coherent energy transfer
Exciton energy transfer is a key mechanism for energy migration over short distances, particularly when strong excitonic coupling is present. This type of transfer is most effective when molecules are in close proximity, typically within 10 Å,46 allowing for significant electronic interactions between them. The strength of excitonic coupling plays a crucial role in determining the efficiency and nature of energy transfer, often facilitating coherent energy transfer by enabling the formation of delocalized excitonic states. In such cases, the excitonic wave functions span multiple molecular sites, allowing energy to propagate efficiently without discrete hopping, distinguishing it from classical incoherent mechanisms. Here, we consider a dimer of two electronically coupled pigments and the treatment can be further extended to several numbers of the interacting pigments. The associated absorption spectra show a splitting of peaks reflecting the excitonic coupling and circular dichroism (CD) is observed. The magnitude of the splitting and the intensity of the two transitions is strongly related to the distance between two pigments and also the relative orientations of the transition dipole moments. The molecular wave functions of the dimer are given as| |
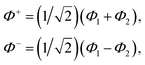 | (4) |
where Φ+ and Φ− are the wave functions of the excited dimer (in exciton basis) and Φ1 and Φ2 are the wave functions for the two monomeric pigments (site basis).
2.3 System–bath interactions and the reorganization energy
In photosynthetic protein complexes, the molecular system is typically modeled in terms of its electronic degrees of freedom and the optical transitions occurring between the ground state and electronically excited states. During photoexcitation, the transition probability associated with electronic excitation exhibits time-dependent fluctuations. These fluctuations mediate interactions between the excited electronic states and the surrounding protein environment, notably through couplings to molecular vibrations and solvent dynamical modes. The primary interactions between the electronic system and its environment arise from the coupling of transition charge densities to vibrational motions of the pigment or cofactor molecules embedded within the protein matrix. These interactions are generally governed by scattering processes. Recent research has highlighted that vibrational modes, in conjunction with appropriately scaled Huang–Rhys factors, play a critical role in defining the reaction coordinates for both energy and charge transfer processes. In addition to pigment-related vibrations, system–bath coupling also includes contributions from interactions between the electronic wave packet and vibrational and polarization modes of the solvent. These solvent vibrations possess distinct frequency distributions, which influence the relaxation dynamics of the excited-state wave packet. Typically, this results in rapid energy dissipation toward lower-energy excitonic states within the complex. The frequency distribution of solvent vibrations is characterized by the spectral density function, J(ω), which quantifies how different vibrational modes couple to the electronic system. It is formally defined as:  , where mi, ωi are the mass and frequency of ith mode. Ci is the coupling strength between system and ith mode. Normally, the Ohmic form with an exponential or a Lorentzian type of cutoff is employed in the calculations. They show the form J(ω) = ηω
, where mi, ωi are the mass and frequency of ith mode. Ci is the coupling strength between system and ith mode. Normally, the Ohmic form with an exponential or a Lorentzian type of cutoff is employed in the calculations. They show the form J(ω) = ηω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ω/ωc) and
exp(−ω/ωc) and  . Here η, ωc are the coupling constant and cutoff frequency of the spectral density, the λ and γ are the reorganization energy and cutoff frequency in the Lorentzian type of the spectral density. A more detailed discussion of these spectral forms and their implications is provided in the subsequent section.
. Here η, ωc are the coupling constant and cutoff frequency of the spectral density, the λ and γ are the reorganization energy and cutoff frequency in the Lorentzian type of the spectral density. A more detailed discussion of these spectral forms and their implications is provided in the subsequent section.
From a detailed perspective of system–environment interactions, solvent molecules in close proximity to the molecular system play a pivotal role in shaping the excited-state dynamics and the associated relaxation processes. These nearby solvent molecules exert a significant influence due to their strong coupling with the electronic states of the system. Furthermore, the bulk solvent exhibits a broad, highdensity spectrum of vibrational frequencies, contributing to rapid and efficient deactivation of the excited-state wave packet. This vibrational coupling facilitates energy dissipation and relaxation toward lower-energy states. A key parameter used to quantify the extent of this system–solvent interaction is the reorganization energy, denoted by λ. This parameter captures the total coupling strength between the optical transitions, from the ground to the electronically excited states, and the dynamic response of the surrounding solvent. As such, λ serves as a fundamental descriptor of how environmental fluctuations influence the photoinduced processes in molecular systems.
3 Photosynthetic protein complexes
The structural and functional understanding of photosynthetic systems has evolved remarkably since the 1970s, driven by advances in biochemical isolation and structural biology techniques. Early studies of the Fenna–Matthews–Olson (FMO) complex from green sulfur bacteria set the stage for high-resolution characterization of photosynthetic complexes.47,48 This pioneering work revealed the precise spatial arrangement of pigment molecules, which are intricately organized to enable highly efficient excitation energy transfer within these systems.
The elucidation of bacterial antenna complexes, such as LH1 and LH2, further highlighted the sophistication of photosynthetic architectures.49 Using X-ray crystallography, researchers demonstrated that these systems exhibit densely packed arrangements of chlorophyll and bacteriochlorophyll molecules, organized to promote rapid energy migration. These structures minimize energy losses through competing pathways, showcasing an evolutionary design optimized for solar energy capture and conversion. Similarly, in plants, the detailed architecture of light-harvesting complex II (LHCII) revealed the cooperative interactions between chlorophylls and carotenoids embedded within protein matrices.50 These pigments work synergistically to broaden the absorption spectrum and protect against oxidative damage.
The recognition of modular organization within PSII supercomplexes marked another significant advance.51–53 These supercomplexes, comprising inner antennae such as CP43 and CP47 and outer light-harvesting complexes, display remarkable adaptability to environmental conditions. The ability of these modules to reorganize allows the system to optimize light capture under varying light intensities while protecting against photodamage. For example, during high light conditions, the dissipation of excess energy via non-photochemical quenching mechanisms prevents oxidative damage to the photosynthetic machinery.
This modularity also reflects the evolutionary refinement of photosynthetic systems.54 Adaptations in pigment–protein complexes and their spatial arrangements have enabled photosynthetic organisms to thrive across diverse ecological niches, from deep-sea hydrothermal vents to sunlit terrestrial habitats. By maintaining efficiency while responding to environmental stresses, the modular design underscores the resilience and flexibility inherent in photosynthetic systems. These structural and functional revelations not only deepened our understanding of the fundamental processes of photosynthesis but also provided a blueprint for bioinspired designs in artificial energy systems. The following section provides an in-depth examination of the structural and functional characteristics of photosynthetic protein complexes, laying the foundation for a subsequent discussion on their roles in energy and charge transfer dynamics.
3.1 Protein complexes: structure and functions
The structure of a protein is intimately linked to its biological function. This section discusses the structural features and functional roles of the FMO protein complex, which is named after Roger Fenna, Brian Matthews (firstly elucidated its structure) and John Olson (originally discovered the protein). The FMO complex serves as a critical component in the energy transfer process of photosynthetic bacteria. It is situated between the light-harvesting antenna complex (chromophores) and the reaction center, facilitating the transfer of captured solar energy. Structurally, the FMO complex forms a trimer, composed of three identical subunits. Each subunit contains seven bacteriochlorophyll (BChl) molecules, amounting to 21 pigments in total.55,56 Recent studies have identified an additional, eighth pigment located at the interface between subunits, increasing the total pigment count to 24.57,58 The overall molecular configuration of the FMO complex is illustrated in Fig. 2(a). Specifically, Fig. 2(a) depicts the spatial arrangement of the BChl pigments within the protein matrix; the eighth pigment is not shown, as it is often lost during the crystallization process used for structural analysis.59 Fig. 2(a) also shows the labeling of individual BChl molecules. Functionally, solar energy absorbed by the BChl pigments is funneled through excitonic energy transfer to a specific pigment with the lowest site energy, typically the third BChl molecule, located in close proximity to the reaction center. This strategic positioning facilitates the initiation of charge separation in the photosynthetic process.
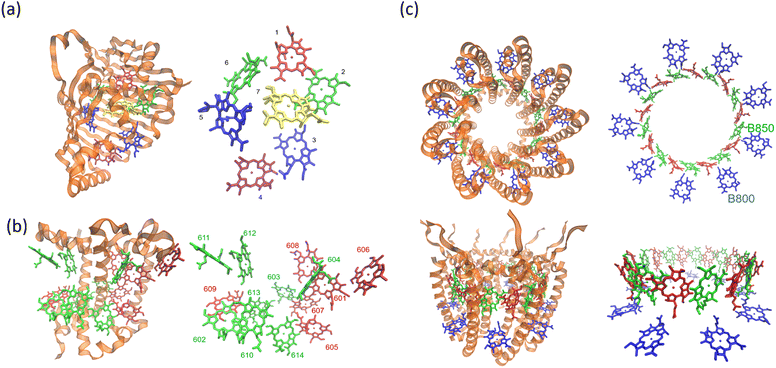 |
| | Fig. 2 (a) The Fenna–Matthews–Olson (FMO) complex from Chlorobium tepidum (PDB ID: 3ENI), showing bacteriochlorophyll a (BChl a) pigments enclosed by a beta-sheet-rich protein scaffold (left). The right panel presents a detailed arrangement of the seven BChl a molecules. (b) The trimeric light-harvesting complex II (LHCII) monomer viewed from the stromal side (PDB ID: 2BHW), with BChl a pigments highlighted: carotenoids are omitted fro clarity. (c) Top-down and side perspectives of the LH2 complex from (Rbi. acidophilus), highlighting the pigment rings: B850 (or B820) in blue, B850 (or B820) in green, and B800 in red. Visualizations were produced using VMD.60 | |
For comparison, the LHCII is a crucial pigment–protein complex involved in the capture and transfer of solar energy in higher plants and marine algae. As one of the most abundant light-harvesting systems in nature, LHCII plays a central role in photosynthetic light capture and exhibits near-unity efficiency in transferring excitation energy to the photosystem II reaction center. In higher plants, LHCII is the primary site for photon absorption within photosystem II. Structurally, LHCII forms a trimer, composed of three homologous monomeric subunits.61 Each monomer houses a suite of pigment molecules, including chlorophyll a (Chl a), chlorophyll b (Chl b), and carotenoids such as lutein. Carotenoids, particularly effective in the blue-green spectral region, complement the absorption capabilities of chlorophylls, which primarily absorb light in the 600–700 nm range. These pigments are intricately embedded within the protein scaffold of the LHCII complex. The structural elucidation of LHCII was initially achieved through a combination of electron microscopy and electron crystallography,62 followed by high-resolution X-ray crystallography.50 As an integral membrane protein complex, LHCII serves as a peripheral antenna system, transferring excitation energy to the core complexes of photosystem II. The crystal structure of LHCII, illustrated in Fig. 2(b), reveals the presence of three transmembrane helices per monomer, coordinating seven chlorophyll molecules (both Chl a and Chl b) and two lutein molecules. The luteins adopt an “X”-shaped conformation, believed to stabilize the trimeric complex. Fig. 2(b) depicts the detailed arrangement of protein helices and pigments, while Fig. 2(b) identifies and labels the 14 distinct pigments within the protein matrix, differentiated by color and numerical labels corresponding to their pigment types. Upon photon absorption, the resulting exciton is efficiently funneled through a cascade of excitonic states, ultimately reaching the reaction center where charge separation initiates the photosynthetic electron transport chain.
Another essential component of the photosynthetic apparatus is the LH2, a visually striking and structurally elegant pigment–protein complex found in purple photosynthetic bacteria. These organisms possess two major types of light-harvesting complexes, LH1 and LH2, each contributing to the overall efficiency of photosynthesis.63 LH2 functions as a peripheral antenna complex and is classified as an integral membrane protein. The structural organization of LH2 has been elucidated using X-ray diffraction techniques,64 and its arrangement within the native membrane environment has been visualized through atomic force microscopy.65 The LH2 complex is composed of repeating heterodimeric subunits, each formed by two polypeptides, designated as the α and β chains, accompanied by three carotenoid molecules per heterodimer. One of the defining features of LH2 is its characteristic ring-like architecture, consisting of two concentric circular aggregates of BChl a molecules, nine in the inner ring and eighteen in the outer ring. This unique arrangement facilitates efficient excitonic coupling and energy transfer within the complex. Fig. 2(c) illustrates both the top and side views of the LH2 complex, highlighting the spatial configuration of its protein subunits and associated cofactors.
Next, we examine the protein architecture and pigment arrangement of the PSII reaction center, as illustrated in Fig. 3(a). PSII is a remarkable biological complex, uniquely capable of driving the oxidation of water to molecular oxygen using solar energy. The molecular structure of the PSII reaction center, comprising the core proteins D1, D2, and cytochrome b559 (Cyt b559), has been thoroughly characterized through X-ray crystallography.66 Within the PSII reaction center, eight key cofactors are embedded in the protein matrix. The structure of PSII reaction center includes two primary chlorophyll molecules (PD1 and PD2), accompanied by additional accessory (ChlD1 and ChlD2) and peripheral chlorophylls (ChlzD1 and ChlzD2), as well as pheophytin molecules (PheoD1 and PheoD2). These components are organized in a pseudo-symmetrical layout, forming two parallel branches known as D1 and D2, which reflect the underlying protein subunits that coordinate them. However, recent research has demonstrated that only the D1 branch plays an active role in the initial steps of charge separation, initiating the photochemical reactions leading to oxygen evolution.67
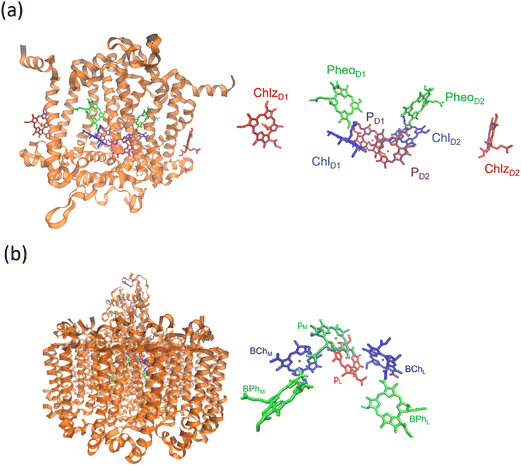 |
| | Fig. 3 Structural organization of reaction centers in photosynthetic systems. (a) Structure of the photosystem II (PSII) reaction center, highlighting the transmembrane protein scaffold (left) and the spatial arrangement of key pigments (right), including chlorophylls (ChlD1, ChlD2, ChlzD1, ChlzD2), pheophytins (PheoD1, PheoD2), and the special pair (PD1 and PD2). (b) Structure of the bacterial reaction center, with the protein complex shown on the left and the configuration of associated pigments on the right, including bacteriochlorophylls (BChlL, BChlM), bacteriopheophytins (BPhL, BPhM, and the special pair (PL, PM). The 3ARC.pdb file has been used to generate the figure. | |
In comparison, the bacterial reaction center (BRC) is another structurally symmetric protein complex responsible for charge separation and electron transfer in purple photosynthetic bacteria. The BRC exhibits a high degree of symmetry along its central axis, and recent studies have shown that charge separation occurs with near-unity quantum efficiency along the so-called “A” branch.68 The BRC contains a strongly coupled special pair of bacteriochlorophyll a (BChl a) molecules, as well as two additional BChl molecules (designated BA and BB) and two bacteriopheophytins (HA and HB). These pigments are spatially organized according to their respective positions along the A and B branches. Compared to the PSII reaction center, the BRC displays distinctive absorption characteristics in the Qy region, allowing for high-resolution investigation of ultrafast energy transfer and charge separation dynamics. The molecular configuration and pigment distribution within the BRC are depicted in Fig. 3(b).
4 Spectroscopic methods for characterizing dynamics
4.1 Femtosecond transient absorption and emission spectroscopy
The development of femtosecond spectroscopy in the 1990s marked a significant leap in experimental capabilities.69,70 Ultrafast spectroscopy techniques, particularly transient absorption and fluorescence measurements, revolutionized our understanding of energy and charge transfer in photosynthetic systems.71–76 Femtosecond transient absorption (TA) spectroscopy uses optical interactions to probe ultrafast dynamics in molecular systems. A pump pulse excites the sample, creating an initial excited-state population. The subsequent probe measures changes in transmission that arise from a combination of ground-state bleaching, stimulated emission, and excited-state absorption pathways. This enables detailed insights into population dynamics, energy relaxation, and coherent phenomena, making it a powerful tool for studying energy transfer and reaction mechanisms in complex systems. This technique has been pivotal in studying bacterial light-harvesting systems like LH1 and LH2. Energy transfer between B800 and B850 pigment rings, for instance, was shown to occur in less than 1 ps, confirming theoretical predictions of rapid exciton hopping.77,78 In PSII, transient absorption studies revealed the interplay between energy transfer and charge separation.79 The reaction center's primary donor, P680, initiates charge separation, transferring an electron to pheophytin and subsequently to plastoquinone. Measurements showed that excitation energy is funneled efficiently from peripheral antennae to P680, facilitated by bridging chlorophyll molecules strategically positioned within the protein matrix.
Time-resolved fluorescence spectroscopy80 complements TA spectroscopy by capturing emission lifetimes of excited states. This method had been crucial for mapping energy transfer pathways in complex photosynthetic systems.81–86 Studies demonstrated that chlorophyll fluorescence lifetimes are shortened when energy transfer is efficient, reflecting the system's ability to minimize energy losses during migration toward reaction centers. Fluorescence anisotropy measurements further revealed details about energy migration dynamics.87 By monitoring the depolarization of emitted light, researchers inferred the orientation and coupling strength of chromophores within light-harvesting complexes. These findings emphasized the role of pigment–protein interactions in dictating the efficiency of energy transfer.
The vast datasets generated by TA and fluorescence studies necessitate sophisticated analysis techniques. Global analysis, a powerful tool for deconvoluting overlapping spectral features, has been instrumental in resolving the kinetics of energy transfer and charge separation.88–90 This approach employs kinetic models to extract rate constants and species-associated spectra, providing a quantitative understanding of photosynthetic dynamics. Target analysis, often used in tandem, applies predefined kinetic schemes to identify specific pathways and intermediate states. For example, in PSII, this method clarified the sequential steps of electron transfer, from P680 to quinone acceptors QA and QB.89 The application of sophisticated data analysis techniques alongside ultrafast spectroscopy has significantly enhanced our understanding of energy flow in photosynthesis. High-resolution structures inform the placement and orientation of pigments, while spectroscopic data validate dynamic models.
In the 1990s, the experiments demonstrated a role for coherent nuclear motions in the TA signals. Studies on bacterial light-harvesting complexes revealed oscillatory features linked to vibrational coherences, with prominent modes at 110 cm−1 and minor contributions from others, showcasing a coupling between electronic and nuclear degrees of freedom.91,92 By the mid-1990s, transient absorption experiments on bacterial reaction centers captured coherent vibrational motions persisting for over 1 ps, challenging the assumption of rapid vibrational dephasing prior to electron transfer. These studies demonstrated that vibrational coherence significantly influences energy transfer dynamics.92 In the late 1990s, investigations into light-harvesting complex II (LHC-II) utilized three-pulse photon echo and transient absorption techniques to identify oscillations at 60 cm−1, linked to coherent nuclear dynamics during energy transfer from Chl-b to Chl-a molecules. These experiments revealed distinct time scales for coherence between exciton states of a single complex and coherence between ground and excited state populations.93 Entering the 2000s, the focus shifted to understanding the role of quantum coherence in photosynthetic energy transfer. Long-lived vibrational coherences lasting on the order of a picosecond were detected in bacterial and plant light-harvesting complexes. For instance, in LH1 and LH2 systems, oscillatory features associated with excitonic states and low-frequency vibrational modes were observed, persisting even at room temperature.94,95 The evolution of TA studies highlighted the growing sophistication in monitoring and interpreting coherence signals, underscoring their importance in photosynthetic energy transfer dynamics.
4.2 Multidimensional coherent spectroscopy
Before discussing multidimensional spectroscopy, we note that pigments in photosynthetic complexes have electronic excited states coupled to vibrational modes of the pigments and protein; this electron-vibrational coupling means that both purely electronic and mixed vibronic coherences can influence the transient spectroscopic signals. Multidimensional spectroscopy has revolutionized the exploration of ultrafast energy dynamics in photosynthetic complexes by disentangling some of these coherent features. Traditional spectroscopic techniques, such as TA spectroscopy, often faced challenges in resolving the complex pathways and dynamics of energy transfer due to spectral congestion. To address these limitations, multidimensional spectroscopic methods were conceptualized in the 1990s. This approach, inspired by nuclear magnetic resonance (NMR) techniques, was later adapted to the optical regime, paving the way for studies on photosynthetic complexes.96,97 Two-dimensional electronic spectroscopy (2DES) has emerged as a groundbreaking technique. As an extension of nonlinear optical methods, 2DES enables detailed investigation of coherence and population transfer processes at femtosecond timescales. As illustrated in Fig. 4, a 2D spectrum is obtained by plotting the signal as a function of excitation and detection frequencies. It provides a powerful tool for disentangling complex spectral overlaps, offering insights into both electronic and vibrational couplings in photosynthetic systems. The versatility and precision of 2DES have also extended its applications beyond photosynthesis, facilitating studies of energy and charge transfer dynamics in conjugated polymers,89,98–101 organic semiconductors,102,103 hybrid perovskites,104–107 and quantum materials108 and their topological properties.109
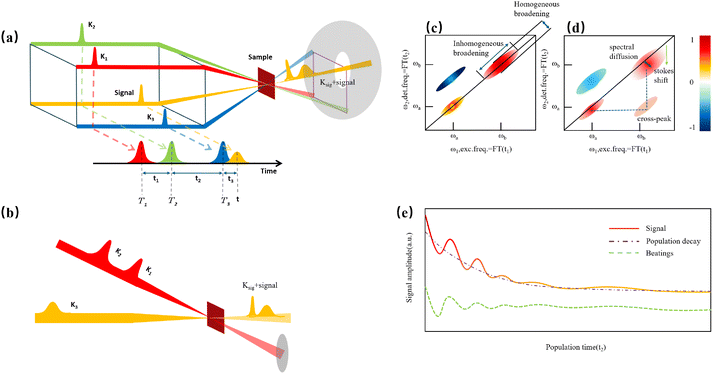 |
| | Fig. 4 (a) Pulse sequence for 2DES, showing the interaction of three pulses with wavevectors k1, k2 and k3 with the sample, and the resulting signal emission along ksig. The time delays t1, t2 and t3 between pulses define the experimental timeline. (b) Experimental BOXCAR geometry illustrating spatial separation of the laser pulses and the signal detection path. (c) and (d) Representations of the 2D spectra: (c) demonstrates homogeneous versus inhomogeneous broadening along diagonal and antidiagonal directions; (d) highlights spectral features such as cross-peaks, Stokes shifts and spectral diffusion. (e) Time-resolved signal trace for a selected peak as a function of population time t2, decomposed into kinetic (purple) and quantum beating (green) components. | |
Numerous reviews have documented the development and evolution of 2DES, highlighting both its theoretical foundations and its diverse applications.97,110–115 These reviews provide valuable insights into the method's transformative role in understanding ultrafast dynamics across various systems. The principle of 2DES is rooted in the interaction between three ultrafast laser pulses and the sample, which induces a third-order nonlinear polarization within the system. This polarization, generated by the interaction of the incident pulses, emits a coherent third-order polarization, which is measured via heterodyne detection of the emitted signal. This detection method captures both the amplitude and phase of the signal, ensuring high-resolution spectral and temporal information. The 2DES involves two key time intervals: t1 (the coherence time) and t2 (the waiting time). During t1, coherence is established between the ground and excited states of the system, allowing quantum superpositions to evolve. Following the second pulse, the system evolves during the waiting time t2, during which population relaxation and other dynamics (such as energy transfer or decoherence) occur. By performing a Fourier transform over t1 and t3 (the detection time), a two-dimensional spectrum is generated. This spectrum is plotted with excitation frequency (ω1) on one axis and detection frequency (ω3) on the other, offering a detailed view of the coupling and dynamics between different states within the sample. The pulse sequence and photon echo (PE) signal are shown in Fig. 4(a).
Two primary geometries are employed in 2DES setups: the noncollinear BOXCARS geometry and the partially collinear pump–probe geometry, which are shown in detail in Fig. 4(b) and (c). The BOXCARS geometry uses four noncollinear beams arranged in a rectangular pattern, offering precise phase-matching conditions that isolate the signal from undesired background contributions to achieve better signal-to-noise.116,117 However, its complexity makes alignment and implementation technically demanding. Conversely, the partially collinear pump–probe geometry is simpler and more robust, as it uses overlapping beams in a collinear arrangement.118 While this geometry requires meticulous calibration to maintain phase stability and data reliability, its ease of use makes it a popular choice for many experimental setups. 2D spectra are typically plotted with one frequency axis for excitation (ω1) and another for detection (ω3); either axis can be assigned to excitation or detection, and both conventions (ω1 on x-axis vs. y-axis) are used in literature.
The 2DES offers significant advantages over one-dimensional techniques like transient absorption or fluorescence spectroscopy by addressing the limitations posed by spectral congestion. In one-dimensional techniques, overlapping spectral features often obscure distinct contributions from different chromophores or energy states. In a 2D spectrum, diagonal features (peaks along the ω1 = ω3 line) indicate populations or zero-quantum coherences (absorptive peaks without energy change), whereas off-diagonal cross-peaks reveal correlations between different transitions, indicating coupling or energy transfer between excitonic states. This enhanced resolution enables the identification of individual transitions and their interactions, even in complex systems like photosynthetic complexes or organic materials. A key feature of 2DES is its ability to separate contributions from homogeneous and inhomogeneous broadening. Homogeneous broadening arises from the intrinsic dynamics of a chromophore, such as interactions with its immediate environment or decay processes. Inhomogeneous broadening, on the other hand, reflects static disorder in the system, such as variations in chromophore environments or structural heterogeneity. In the limit of fast modulation (motional narrowing), homogeneous broadening approaches a Lorentzian lineshape, whereas in the static limit of slow modulation, inhomogeneous broadening can often be approximated by a Gaussian. In practice, lineshapes may be Voigt or intermediate depending on the regime. The ability to distinguish these contributions is crucial for understanding how local environments affect chromophore properties, energy transfer efficiencies, and photophysical behaviors. In 2DES spectra, this separation is achieved by examining diagonal and off-diagonal (cross-peak) features. Diagonal peaks are often dominated by inhomogeneous broadening, while off-diagonal peaks reflect couplings and energy transfer between states.
The presence of cross-peaks in 2DES spectra is particularly revealing. These features indicate interactions or energy transfer between coupled chromophores. The intensity, shape, and temporal evolution of cross-peaks provide quantitative information about coupling strengths, transfer rates, and the efficiency of energy migration. For example, in photosynthetic light-harvesting complexes, 2DES can resolve energy flow between pigments and reveal how structural or environmental factors modulate these pathways. Temporal changes in cross-peaks can be analysed to extract quantum coherence lifetimes, which are critical for understanding how long coherent superpositions persist in biological or material systems. The details of 2DES with resolved main and cross peaks, the time-resolved trace of selected peak are presented in Fig. 4(d)–(f).
5 Theoretical methods
5.1 Response-function formalism vs. phase-matching approach
In this section, we compare two computational frameworks for simulating multidimensional spectra: (i) the response function formalism14 and (ii) the phase-matching approach.119 We consider these two theoretical formalisms for calculating third-order nonlinear optical signals. The response function formalism uses an integral (convolution) representation of four-wave mixing via double-sided Feynman diagrams (the traditional Liouville-space approach). In contrast, the phase-matching time-domain approach uses real-time propagation of the density matrix under specific phase-matching conditions (a time-domain kinetic equation approach).
5.1.1 Spectroscopic calculations based on response function. In the regime of weak electromagnetic field-matter interaction, perturbation theory provides a fundamental framework for analyzing a wide range of physical observables encountered in both linear and nonlinear optical spectroscopy. Within this approach, the system's optical response is described through correlation functions involving transition dipole moments, capturing the underlying dynamics of light-induced processes.14 The two-dimensional spectra is a third-order optical response signal and the electronic polarization P can be written as| |
 | (5) |
Here, N refers to the number of the molecules and r represents the wave vector of electric field. R(3) is the third-order optical response function and it shows the form| |
 | (6) |
where ρ0 refers to the system density operator at initial time, μ(t) = eiHmoltμe−iHmolt. Here, μ and Hmol is the transition dipole moment and molecular Hamiltonian, respectively. The Liouville space super-operators ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (t) are defined as
(t) are defined as ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ρ = [μ,ρ] and
ρ = [μ,ρ] and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (t)ρ = e−iHmoltρeiHmolt, respectively. Moreover, the time intervals t1, t2 and t3 are denoted in Fig. 4(a).
(t)ρ = e−iHmoltρeiHmolt, respectively. Moreover, the time intervals t1, t2 and t3 are denoted in Fig. 4(a).In the 2D spectroscopic measurement, a sequence of three laser pulses, characterized by wave vectors k1, k2, and k3 sequentially interacts with the sample. The resulting third-order nonlinear signal emerges along a specific phase-matching direction, denoted as ksig. Under the rotating wave approximation, the overall signal response can be decomposed into two distinct contributions: the rephasing component kI = −k1 + k2 + k3 and the non-rephasing component kII = −k1 − k2 + k3. The total signal can be obtained as: R(3)(t3,t2,t1) = Rrp(t3,t2,t1) + Rnr(t3,t2,t1). The rephasing and non-rephasing parts can be written as
| |
 | (7) |
where
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ±ρ
±ρ = [
μ±,
ρ],

, and

.
a†m and
am are the creation and annihilation operators. The transition dipole moment can be written as
| |
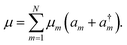 | (8) |
With expansion of the commutators, we have the Rrp and Rnr with forms
| |
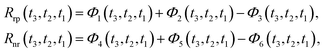 | (9) |
where the response functions (
Φ1 −
Φ6) are defined by the following expressions:
| |
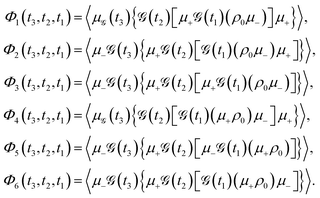 | (10) |
The components
Φ1 to
Φ6 correspond to distinct pathways in Liouville space, each represented by double-sided Feynman diagrams illustrated in
Fig. 5. These pathways contribute to the third-order optical response and are typically categorized into ground state bleaching (GSB), stimulated emission from the excited state (ESE), and excited state absorption (ESA).
14 The connection between the terms
Φ1 −
Φ6 and the four third-order response functions,
14 R1–
R4 is also depicted in
Fig. 5. For completeness,
Fig. 5 illustrates various Liouville-space pathways, including the double quantum coherence (DQC) pathway (involving two-exciton states). Although two-exciton (double-excitation) levels are not a focus of this review, we include DQC to show the full third-order response picture; in practice, our discussions and the experiments reviewed do not excite or probe the two-exciton manifold in detail.
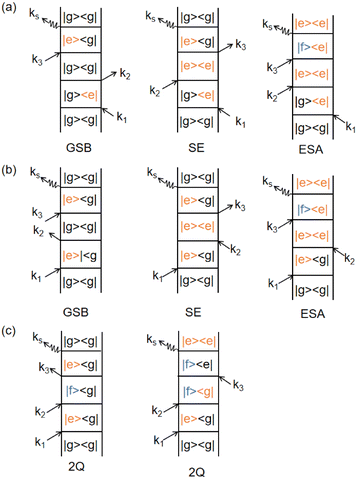 |
| | Fig. 5 Feynman diagrams representing different signal pathways in two-dimensional electronic spectroscopy. (a) Rephasing (photon echo) pathways showing ground state bleaching (GSB), stimulated emission (SE) and excited state absorption (ESA). (b) Non-rephasing pathways for the same three processes: GSB, SE and ESA. (c) Double quantum coherence (2Q) pathways invovling coherences between the ground, single-exciton and double-exciton states. Each diagram shows the sequence of light–matter interactions with wavevectors k1, k2, k3 and the emitted signal ksig with quantum state evolution indicated at each step. | |
Under the impulsive excitation approximation, the absorptive component of the two-dimensional spectrum is obtained by taking the real part of the combined double Fourier–Laplace transforms of the rephasing, Rrp and non-rephasing, Rnr with respect to the first and third time variables, t1 and t3:
| |
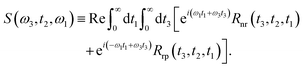 | (11) |
In the response function formalism, finite laser pulse durations and shapes are included via convolution integrals of the impulsive response with the pulse temporal profile (often Gaussian). This convolution effectively accounts for the pulse bandwidth without explicitly including the pulse in the system Hamiltonian.
5.1.2 Phase matching approach. We now focus on the phase-matching (time-domain) approach (sometimes referred to as the ‘photon echo’ method in the context of nonlinear spectroscopy). Photon echo transient grating often simply called the photon echo technique is a specific phase-matched four-wave mixing experiment in the phase matching approach (PMA), the evolution of the system density matrix is simulated up to the desired detection time, and the induced polarization is evaluated at that time for given t1 and t2 delays by evolving three auxiliary density matrices, denoted as ρ1, ρ2, and ρ3.119 This formalism incorporates the rotating wave approximation to simplify the treatment of light–matter interaction. The corresponding equations governing their time evolution are presented here:| |
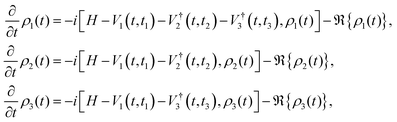 | (12) |
here, Vα = XEα(t − tα)eiωt and Eα(t − tα) = exp[−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2(t − tα)2/τp2], τp is the pulse duration. H is the system Hamiltonian, X is the transition dipole coordinate and ℜ is the dissipative superoperator. The calculation of the third-order 2D response involves evaluating the polarization component that propagates along the specified phase-matching direction, as formulated below:
2(t − tα)2/τp2], τp is the pulse duration. H is the system Hamiltonian, X is the transition dipole coordinate and ℜ is the dissipative superoperator. The calculation of the third-order 2D response involves evaluating the polarization component that propagates along the specified phase-matching direction, as formulated below:| | |
PPE(t1,t2,t3) = eiksig·r〈X[ρ1(t) − ρ2(t) − ρ3(t)]〉 + c.c.,
| (13) |
here, the bracket 〈…〉 denotes the expectation value of operator. Experimentally, the Gaussian pulses can be given as| |
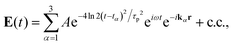 | (14) |
here, A denotes the pulse amplitude, tα represents the central time of the pulse envelope, kα is the associated wave vector, τp specifies the pulse duration, and ω corresponds to its frequency. A relatively weak magnitude (A, comparing to the molecular Hamiltonian HS) of the laser pulses has been employed to obtain a reasonable scale of 2D spectra.While the previous section dealt with calculating both rephasing (photo echo) and non-rephasing contributions via response functions, this section describes an alternative approach focusing on simulating the photon echo signal directly in the time domain. Using the phase-matching approach, one can simulate the time-domain photon echo signal directly by including the laser pulse interactions in the propagation. A Fourier transform of this time-domain signal (along appropriate axes) then produces the corresponding 2D spectrum. In the response function method, arbitrary pulse shapes can be incorporated via convolution integrals; in the phase-matching approach, they are included by explicitly applying the time-dependent fields during propagation. Thus, both frameworks can handle shaped or chirped pulses and even be used for pulse optimization studies (such as coherent control). Both the response function and phase-matching calculations can be paralleled. In the response function method, independent Liouville-space pathways or frequency points can be computed in parallel, while in the time-domain approach, different ensemble members or pulse delay conditions can be paralleled. Modern implementations use multi-CPU and GPU computing to accelerate these calculations.
The response function formalism is well-suited for deriving analytical expressions and separating contributions (e.g., rephasing vs. non-rephasing) and has been the traditional approach for spectra calculations. The phase-matching time-domain approach, on the other hand, can be more convenient for incorporating detailed experimental conditions (pulse shapes, specific phase sequences) and for simulating time-domain signals directly. Each approach provides similar results when applied to the same problem, and choice of method can depend on the specific computational or conceptual convenience. It should be noted that the conventional response function approach typically employs the rotating wave approximation (RWA) and assumes that each light–matter interaction changes the excitation quantum by one (no AC Stark or strong-driving effects included), and it treats dissipation independently of the driving field (dissipative dynamics are not altered by the instantaneous presence of the laser field). These approximations, while usually valid for weak laser fields, mean that certain phenomena (e.g., dynamic Stark shifts or pulse-driven modifications of decoherence) are not captured in that framework. A real-time propagation approach could, in principle, include such effects by not invoking RWA or by coupling the field into the system–bath interaction if needed.
5.2 Quantum dissipative systems and open-system dynamics
In this section, we present the quantum dissipative system and introduce the corresponding system–bath Hamiltonian. In addition, we outline several distinct formulations of master equations employed in its description. We begin with the coherent modified Redfield theory, an approach that extends standard Redfield to include certain coherence effects. It is a second-order perturbation theory in the system–bath coupling that can incorporate non-Markovian effects (here non-Markovian or time-nonlocal dynamics means that the future evolution of the system depends on its history, i.e., the equation of motion involves an integral over past times – a memory kernel).120 We discuss several theoretical formalisms for open quantum dynamics: (1) perturbative density-matrix approaches (e.g., Redfield and its variants, including coherent modified Redfield), which assume weak system–bath coupling; (2) Förster resonance energy transfer (FRET) and modified-FRET methods, which are applicable in the incoherent (hopping) regime; (3) hierarchical equations of motion (HEOM), a numerically exact method for system–bath dynamics; (4) quantum path-integral methods such as QUAPI; and (5) hybrid quantum-classical (QM/MM) simulations, which combine quantum chemistry with molecular dynamics. Each approach has its regime of validity and strengths, as described below.
5.2.1 Quantum dissipative systems. A molecular system with electronic degrees of freedom (DOFs) interacting with a thermal bath can be considered as a quantum dissipative system. The total Hamiltonian is given as| | |
Htot = HS + HB + HSB,
| (15) |
where HS describes the electronic DOFs, which shows| |
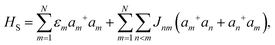 | (16) |
In this formulation, εm denotes the transition energy localized on site m, while Jnm represents the coupling between molecules n and m. HB corresponds to the nuclear phonon degrees of freedom. The model assumes that the electronic excitation on molecule m interacts exclusively with its own independent harmonic bath, such that| |
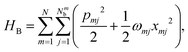 | (17) |
Here, Nmb denotes the total number of bath modes interacting with molecule m. The quantities xmj and pmj represent the mass-weighted coordinate and momentum, respectively, of the j-th harmonic oscillator bath mode with frequency ωmj. The electron–phonon interaction term, HSB, is considered to induce only site-specific fluctuations in the electronic energy, with no correlations between different chromophores. HSB is assumed to be linear in the bath coordinates, then, we have| |
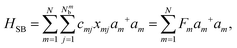 | (18) |
where the collective bath coordinate Fm is defined as 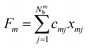 with cmj being the coupling strength between the excitation of molecule m and the j-th mode. The correlation function of the collective bath coordinate Fm is then given by
with cmj being the coupling strength between the excitation of molecule m and the j-th mode. The correlation function of the collective bath coordinate Fm is then given by| |
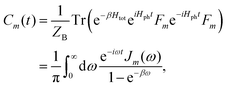 | (19) |
where ZB is the partition function, β = 1/(kBT), and Jm(ω) is the spectral density, which describes the frequency distribution of harmonic oscillators in the bath and their coupling to the molecule. The definition of the spectral density is| |
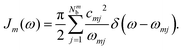 | (20) |
For the light–matter interaction, we employ the dipole approximation of the molecule in the visible range and the Hamiltonian can be written as| | |
H(t) = Htot − μ·E(t),
| (21) |
where E(t) is the classical electromagnetic field and μ is the dipole operator. The total dipole operator μ has been defined in eqn (8).
5.2.2 Quantum master equation: Redfield vs. coherent modified Redfield equation. The population dynamics of the molecular system and their interactions with light and the bath can be calculated by quantum master equations.121 The Nakajima–Zwanzig equation can be directly derived from the total Hamiltonian with the projection operators. With the second-order approximation of system–bath interaction, the typical form of Redfield equation can be derived with Markovian approximation. The evolution of the system is characterized through its reduced density matrix, derived by performing a trace over the bath degrees of freedom in the total density matrix, ρtot(t),| | |
ρS(t) = trB{ρtot(t)}.
| (22) |
The formal expression for the time evolution of the reduced density matrix, ρS(t), is provided by the Nakajima–Zwanzig equation (here ħ = 1)| |
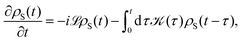 | (23) |
where the kernel of the integro-differential equation is defined by| |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (τ) = trB{ (τ) = trB{![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBe−i SBe−i![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (1−P)τ (1−P)τ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBρB}. SBρB}.
| (24) |
Here, the Liouville-space superoperator notation is employed, such that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρ = [H,ρ], and related forms. The projection operator P is specified as:where ρB is the equilibrium density matrix of the bath
ρ = [H,ρ], and related forms. The projection operator P is specified as:where ρB is the equilibrium density matrix of the bath| |
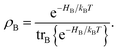 | (26) |
For convenience, it has been assumed that the system–bath interaction fulfillsThe initial state is taken to be separable, such that ρtot(t = 0) = ρS(t = 0)ρB. The Nakajima–Zwanzig eqn (23) is formally exact. However, the kernel (24) is hard to obtain. Thus, the Nakajima–Zwanzig equation is of little practical use. Here, we need to include two approximations: (i) the memory kernel (24) is expanded up to the second order in HSB (Born approximation)
| |
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (τ) ≃ trB{ (τ) ≃ trB{![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBe−i( SBe−i(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) S+ S+![[script L]](https://www.rsc.org/images/entities/char_e144.gif) B)τ B)τ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBρB}. SBρB}.
| (28) |
(ii) The reduced density matrix ρS(t − τ) in the integral is expressed by
| |
ρS(t − τ) ≃ ei![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SτρS(t), SτρS(t),
| (29) |
here, we need to neglect the interaction with bath. Because the integro-differential equation is local in time, the second step presented here relates to the Markov approximation. In this context the non-local and local equations of motion relate to a chronological or partial time ordering,
122 respectively.
With the two approximations (28) and (29), a local-in-time equation of motion for the reduced density matrix can be written as
| |
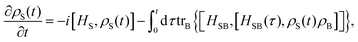 | (30) |
where we have defined
| | |
HSB(τ) = e−i(HS+HB)τHSBei(HS+HB)τ.
| (31) |
Introducing, furthermore, the energy eigenstates of the system
the original form of the Redfield equation is obtained,
| |
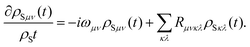 | (33) |
Here,
ρSμν(
t) = 〈
μ|
ρS(
t)|
ν〉 indicates the matrix elements of the reduced density matrix in the eigen-representation and
ωμν =
Eμ −
Eν. In this subsection, we assume the
μ is the index of the electronic state, which should not be mixed with the definition of transition dipole moment in the last sections. As the same description as in
eqn (23), the first term on the right-hand side of
eqn (33) accounts for the isolated-system dynamics, the dissipation due to the interaction to the thermal bath is accounted by the Redfield tensor
Rμνκλ. The explicit expression for
Rμνκλ is derived from
eqn (30) and it can be written as
| |
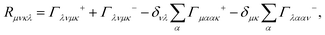 | (34) |
with
| |
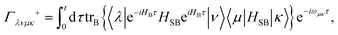 | (35) |
| |
 | (36) |
The accuracy of the approximation can be improved by the coherent modified Redfield equation (CMRT), in which the non-Markovian effect can be included with the time-dependent correlation functions. The CMRT can be derived from the Nakajima–Zwanzig equation123 using a scheme for the separation of the total Hamiltonian,124 it can be expressed as
| |
 | (37) |
where |
μ〉 are eigenstates of
HS and
H′ is the off-diagonal term of the system–bath interaction part in the exciton basis. In this exciton basis,
H0 is diagonal and it shows
| | |
〈μ|H0|μ〉 = εμ − λμμμμ + HB(μ),
| (38) |
where
εμ is the
μ-th excitonic energy of the system Hamiltonian and
| |
 | (39) |
is the weighted reorganization energy. Here,
Km is the
m-th element of the system–bath interaction term, which denotes the coupling elements between system and bath. Moreover,
| |
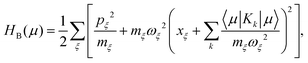 | (40) |
describes a bath of harmonic oscillators with mass
mξ, frequency
ωξ, and momentum
pξ.
Moreover, we need to define the new projection operator for CMRT method. Different from Redfield master equation, here, we define only projections on the diagonal part of the system density matrix in the eigenstate basis. We have
| |
 | (41) |
where
Pμ is the projector onto the
μ-th excitonic state and
Rμeq = exp[−
βHB(
μ)]/
Zμeq is the equilibrium density matrix of the bath when the system is in the excitonic state |
μ〉. Also,
Zμeq = tr
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp[−
βHB(
μ)] with
β = 1/(
kBT).
T is the temperature.
With these defined variables, one obtains the equation of motion for the populations in the form (determining H′ to second order and invoking the time-dependent population transfer rate)
| |
 | (42) |
with the population transfer rates
125| |
 | (43) |
Here,
ωμν =
εμ −
εν. The lineshape function
gμνμ′ν′(
t) can be expressed as two-time-integral of the bath correlation functions, which shows
| |
 | (44) |
with

. With these equations, we obtain the absorption lineshape in the CMRT framework as
| |
 | (45) |
Up to this point, eqn (42) constitutes the modified Redfield theory, as developed and applied in ref. 125–131. Based on the population transfer term in eqn (42), we could extend the quantum master equation by including the time-dependent terms and the resulting coherent modified Redfield quantum master equation can be written as132
| |
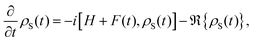 | (46) |
where
F(
t) is the time-dependent system–field interaction term.
The diagonal and off-diagonal terms are also included in the relaxation and dephasing operator ℜ{ρS(t)} and the diagonal part of the relaxation operator, which was described in ref. 121, can be written as the following after the secular approximation
| |
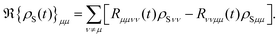 | (47) |
The off-diagonal terms ℜ{
ρS(
t)}
μν describe the decoherence of the excited states and electronic dephasing between the ground and excited states. Moreover, the transfer rate can be effectively determined by

, where
T2 is the transverse relaxation time,
T1,

are the longitudinal relaxation time and pure dephasing time, respectively. For more specificity,
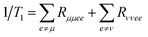
and
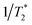
is given by the first derivative of the lineshape function
gμμνν(
t). Thus, the off-diagonal terms of the excited states and the relaxation between ground and excited states are
| |
 | (48) |
The extension of the quantum master equation has also been developed in ref.
133.
5.2.3 Time local vs. non-local quantum master equation. Apart from the Redfield and CMRT approaches, several other quantum master equation formulations exist that are derived under the second-order approximation for system–bath interactions. These perturbative schemes are generally categorized into two types: time-local (TL) and time-nonlocal (TNL), which are based on the Nakajima–Zwanzig projection formalism and the Hashitsume–Shibata–Takahashi identity, respectively. In the TL quantum master equation (QME), the system's evolution depends solely on its instantaneous state, whereas the TNL QME additionally incorporates the influence of its past dynamics. In this section, our primary focus is on the TL framework, though comparisons with the TNL formalism are also provided.The TL formalism originates from the Hashitsume–Shibata–Takahashi identity and is also referred to in the literature as the time-convolutionless method,134 the partial time-ordering prescription,135 or the Tokuyama–Mori approach.136 This framework can be derived via a second-order cumulant expansion of the time-ordered exponential, leading to a resummed form of the resulting expression.135 In some studies, it is alternatively described as the time-dependent Redfield theory.137 Gzyl138 demonstrated that the time-convolutionless formulation developed by Shibata et al.139 is equivalent to an earlier formulation proposed by Fuliński and Kramarczyk.140,141 By applying the Hashitsume–Shibata–Takahashi identity, the TL equation can be obtained to second order in the system–bath interaction.142
| |
 | (49) |
where
| |
 | (50) |
| |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) effS = [HS + Hren, •], effS = [HS + Hren, •], ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k− = −i[Kk, •], k− = −i[Kk, •], ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k+ = [Kk, •]+, k+ = [Kk, •]+,
| (51) |
where
Kk is the
k-th element of system–bath coupling term, the free time evolution superoperator of the relevant system can be written as
| |
 | (52) |
here,
T+ is the time-ordering operator. Here, we do not consider the initial correlation between system and bath, thus, we have
ρS(
t = 0) =
ρ(
t = 0)
ρeqB. By making the approximation substitution,
137 we could obtain the formula as
| |
ρS(t′) = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) †S(t,t′)ρS(t), †S(t,t′)ρS(t),
| (53) |
in the form of TNL equation. Here, we neglect the influence of dissipation on the time propagation of the density matrix within the integral. Employing the real and imaginary parts of the correlation function and carrying out the commutators
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k−
k− and
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k+
k+, we define the following operators
| |
 | (54) |
| |
 | (55) |
and
| | |
Λk(t) = Λrk(t) − iΛik(t).
| (56) |
With these defined identities, the EOM for the reduced density matrix can be obtained as:
| |
 | (57) |
these equations will be used in the following discussion of time-dependent and time-independent cases.
In its classical definition, a master equation is considered Markovian when it lacks any time-convolution terms, as exemplified by the TL approach. In the present context, however, the term “non-Markovian” is used in a different sense than in some prior works. Within the TNL framework, non-Markovian behavior generally refers to deviations from the standard Markov approximation. This approximation typically involves two steps:143,144 first, reformulating the equations such that the density matrix does not depend on the integration variable; and second, extending the upper integration limit to infinity, thereby fixing the integral to a constant value. In this treatment, the system Hamiltonian is taken to be time-independent, enabling the use of an energy eigenbasis without further approximations. In this representation, Greek indices will refer to energy eigenstates and eigenenergies, e.g., Eμ and |μ〉. For a time-independent Hamiltonian, the matrix elements of operators Λk can be evaluated in this basis, with the corresponding transition frequencies ωμν. The desired expression can then be obtained by decomposing the spectral density and applying a change of integration variables,137,145 leading to the following form:
| |
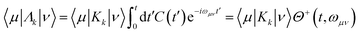 | (58) |
in which the complex function
Θ+(
t,
ωμν) is given by
| |
 | (59) |
here, the notation of ref.
146 is adopted for
Θ+(
t,
ωμν), together with the use of correlation functions. For the non-Markovian case,
Θ+(
t,
ωμν) must be computed at every time step, in contrast to the Markovian limit where it is evaluated only once. In the Markovian approximation, the expressions are readily obtained by extending the upper integration limit in
eqn (58) to infinity.
144 Regardless of whether the dynamics are Markovian or non-Markovian, the computation of the electronic matrix elements in
eqn (59) does not require any explicit time integration.
We now consider the scenario of a time-dependent Hamiltonian, where the eigenstate representation can no longer be employed as a straightforward means of solving the problem. Even performing instantaneous diagonalization at each time step is insufficient, as it necessitates corrections for the time dependence of the basis functions. A viable approach to address this challenge involves the introduction of auxiliary quantities, a strategy originally proposed by Meier and Tannor for the TNL-QME framework.147 Within the TL formalism, however, auxiliary operators are defined in place of auxiliary density matrices,148 taking the following form:
| |
 | (60) |
| |
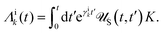 | (61) |
With these operators, the TL-QME can be written as
| |
 | (62) |
Taking the time derivative of Λrk(t) and Λik(t), the following differential equations can be written as
| |
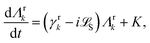 | (63) |
| |
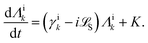 | (64) |
The formulation is independent of the chosen representation and remains applicable to any general time-dependent system Hamiltonian, including scenarios such as light–matter interactions or strong laser driving. The coupled differential equations given in eqn (62)–(64) can be numerically integrated using a Runge–Kutta algorithm. In related work, Yan and collaborators149,150 proposed an analogous method derived from a correlation function framework, which takes the form:
| |
 | (65) |
| |
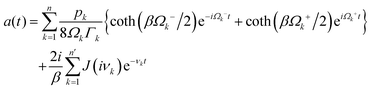 | (66) |
| |
 | (67) |
In numerical studies, the TNL variant of the quantum master equation has been widely utilized, as it explicitly incorporates non-Markovian interactions between the system and its environment. Within the framework of a second-order treatment of system–bath coupling, the kernel function, which is responsible for encoding the memory effects, can be reformulated into a set of coupled equations through the introduction of auxiliary density operators. This formulation is referred to as the TNL quantum master equation.147,151 The temporal evolution of the full density matrix, ρtot, is then described by the Liouville–von Neumann equation ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
| |
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) tot = −i[Htot, ρtot] = tot = −i[Htot, ρtot] = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρtot. ρtot.
| (68) |
The total Hamiltonian, Htot = HS + HB + λHSB + λ2Hren, comprises the system Hamiltonian, bath Hamiltonian, system–bath interaction term, and the corresponding renormalization term, as previously outlined. The interaction is expressed as 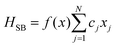 , where f(·) is a real-valued function. Following the Nakajima–Zwanzig projection formalism,152 the dynamics are partitioned into system and bath contributions. The thermal bath is described by the canonical density operator ρeqb = exp(−βHb)/Zb at temperature T, with Zb denoting the bath partition function. The exact formal quantum master equation for the reduced density operator ρS(t) is obtained by applying the projection operator P = ρeqb, trb, with trbρeqb = 1, and its complement Q = 1 − P,147 yielding:
, where f(·) is a real-valued function. Following the Nakajima–Zwanzig projection formalism,152 the dynamics are partitioned into system and bath contributions. The thermal bath is described by the canonical density operator ρeqb = exp(−βHb)/Zb at temperature T, with Zb denoting the bath partition function. The exact formal quantum master equation for the reduced density operator ρS(t) is obtained by applying the projection operator P = ρeqb, trb, with trbρeqb = 1, and its complement Q = 1 − P,147 yielding:
| |
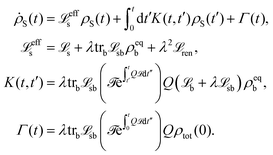 | (69) |
In this context, ρtot(0) denotes the total density operator at the initial time t = 0. The Liouville superoperators ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) s,
s, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sb, and
sb, and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ren correspond to the system, the system–bath interaction, and the reorganization energy contributions, respectively. The effective system Liouvillian is given by
ren correspond to the system, the system–bath interaction, and the reorganization energy contributions, respectively. The effective system Liouvillian is given by ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) effs = −i[HS + Hren, •], while Γ(t) represents the inhomogeneous term arising from the initial density configuration. By performing a first-order expansion of the correlated thermal equilibrium state with respect to the overall coupling strength λ, the expression can be reformulated as:
effs = −i[HS + Hren, •], while Γ(t) represents the inhomogeneous term arising from the initial density configuration. By performing a first-order expansion of the correlated thermal equilibrium state with respect to the overall coupling strength λ, the expression can be reformulated as:
| |
 | (70) |
here, the partition functions are
Ztot = Tr
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
βHtot),
Zb = Tr
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
βHb) and
Zs = Tr
S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
βHS). We take the trace over the system part and we can write
| |
 | (71) |
where
χ = (1/
Zs)tr
s[
f(
x)e
−βHS]. The well-known bath correlation function can be separated into real
a(
t) and imaginary parts
b(
t). After inserting
eqn (70) and (71) into
eqn (69), we can write the last three terms of
eqn (69) by
a(
t) and
b(
t), then, we obtain
| |
 | (72) |
with
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −
− = −
i[
HSB, •] and
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) +
+ = [
HSB, •]
+ − 2
χ.
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
is the time-ordering operator
153 and
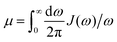
.
In order to obtain an analytic form of the bath correlation function, the actual spectral density can be expanded into a sum of artificial forms of spectral density in the form
| |
 | (73) |
where
pk,
Ωk and
Γk are the spectral amplitude, frequency and width follows from the expansion of the original function in terms of Lorentzian functions. After inserting the expanded form of
J(
ω) in
eqn (71), we obtain
| |
 | (74) |
with the Matsubara frequencies
νk = 2π
k/
β. Then, we rewrite the correlation functions as

and
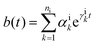
with
ni = 2
n,
nr = 2
n +
n′ (
n′ is the number of Matsubara frequencies). We then define a new set of auxiliary density matrices
| |
 | (75) |
The time-retarded term of eqn (69) can be deconvoluted into a set of coupled first-order equations, which shows the form
| |
 | (76) |
5.2.4 Hierarchy equation of motion and recent progress. Different from Redfield and time non-local quantum master equations, the hierarchy equation of motion (HEOM) includes the full order of system–bath couplings and yields numerically exact results. The HEOM has been constructed by Tanimura154–158 and it has been further extended by other research groups.30,159–162 Here, we start from the bath correlation function as described before| |
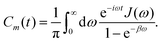 | (77) |
The Lorentzian spectral density with a Drude type of cutoff is  . The bath correlation function Cm(t) in eqn (77) can be written as a sum of exponentially decaying functions, which shows the form
. The bath correlation function Cm(t) in eqn (77) can be written as a sum of exponentially decaying functions, which shows the form
| |
 | (78) |
with
ν0 =
γ and
νk are the Matsubara frequencies, as introduced before. The coefficients are
| |
 | (79) |
and
| |
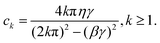 | (80) |
Here,
η is the coupling strength contained in the spectral density. The initial state can be expressed as a direct product between the reduced density matrix and the bath at equilibrium. The formula of HEOM can be written as
| |
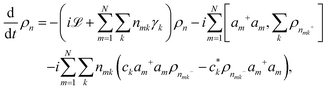 | (81) |
where
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρ
ρ = [
HS,
ρ] and
HS is the system Hamiltonian with electronic DoFs. The subscript
n denotes the set of indices
n = {
n1,
n2, …,
nN} = {{
n10,
n11, …}, …, {
nN0,
nN1, …}}. The index of
nmk± differs from
n only by changing the specified
nmk to
nmk ± 1. The
ρ0 with
0 = {{0, 0, …}, …,{0, 0, …}} is the real system reduced density operator and the other
ρn are the auxiliary density operators (ADOs). The ADOs shows in the hierarchy levels of coupled differential equations and contain the information of collective bath modes and also their interaction with the system part. The schematic diagram of reduced and auxiliary density operators is shown in
Fig. 6.
 |
| | Fig. 6 Hierarchical structure of reduced density matrices and auxiliary density operators. The diagram illustrates the hierarchical equation of motion (HEOM) framework, where the top node represents the primary reduced density matrix of the system, ρ(0). Lower levels include auxiliary density operators ρ(1), ρ(2), ρ(3), etc., which account for successive orders of system–bath coupling. Dashed lines denote the coupling between different hierarchy levels, with the depth N defining the extent of the hierarchy in the simulation. | |
Starting from the non-Markovian quantum state diffusion framework, Eisfeld and Strunz et al. developed a hierarchy of stochastic differential equations for pure states.163 This hierarchy of pure states (HOPS) method can include non-Markovian dynamics in open quantum systems from the ensemble average over a bunch of quantum trajectories. It has been shown that the equation of motion for the reduced density matrix obtained via HOPS is formally equivalent to that of the HEOM method (hierarchical equations of motion), meaning HOPS can reproduce HEOM's results for a given spectral density when converged to the same level of accuracy.164 Recently the matrix product states have been combined with the HOPS method, significantly reducing the complexity of HOPS for increasing system size.165–168 Raccordi et al. have recently developed an adaptive HOPS scheme, extending the application of HOPS to larger (mesoscopic) photosynthetic systems.169,170 These developments have enabled HOPS to simulate systems of previously intractable size by dynamically adjusting the number of trajectories or basis elements in the method.
Different to aforementioned methods where the bath DOFs are typically traced out to produce the dynamics for the system of interest, Zhao's research group has been developing a wave function based method by combining the Davydov trial states with the time-dependent variational principle, which can treat both the system and bath DOFs explicitly.171,172 Thanks to its excellent accuracy-efficiency balance and high adaptability to broad parameter regimes, this method has been widely applied to simulate the coupled exciton–phonon dynamics173–176 and spectroscopy of light-harvesting complexes.177,178 Recently the exciton diffusion dynamics in nanoarrays containing more than one hundred B850 rings (>1600 pigments) has been successfully simulated with the GPU implementation of this method.176 Numerically exact results also can be obtained within this framework using a superposition of the Davydov trial states.171,172
5.3 Quasi-adiabatic path integral
The quasi-adiabatic path integral (QUAPI) method is another approach to calculate the population dynamics of system–bath model. This method was developed by Makri's research group179–183 and further extended by others.184–186 It is different from the quantum master equation, since it employs an iteration procedure to propagate and account the influence of the bath by an influence functional. With a proper account of the memory effect in a specific system, QUAPI is able to yield numerically exact results. Different from HEOM, the QUAPI produces the results without limitation on the form of the spectral density. It is well known that the HEOM is suitable for Lorentzian types of spectral densities. We include a brief note on the QUAPI (quasi-adiabatic path integral) method, which is a numerically exact open-system technique. In the context of photosynthetic energy transfer, QUAPI has been used to investigate the example of the exciton dynamics in the FMO complex, providing benchmarks for other approximate treatments. We restrict our discussion to such energy-transfer-related findings, referring the reader to dedicated reviews for the general QUAPI methodology.
More recently, Makri et al.187 recently proposed the small matrix decomposition of the path integral (SMatPI), a method designed to overcome the substantial memory demands of the iterative QUAPI algorithm. This approach works by progressively distributing the temporal entanglement across extended path segments, thereby diminishing its overall contribution. As the entangled component becomes sufficiently small, the reduced density matrix can be propagated iteratively through simple multiplication of matrices whose dimensions match those of the isolated system. Furthermore, Makri demonstrated that certain additional long-range influence functional terms can be incorporated into the SMatPI framework without incurring notable computational overhead, resulting in the extended SMatPI (x-SMatPI) method.188
A related advancement involves reformulating the QUAPI path summation within a tensor network framework, as introduced by Strathearn et al.189 In this formulation, the time-evolving matrix product operator (TEMPO) method performs the QUAPI calculation by contracting a tensor network, thereby significantly enhancing the method's efficiency and applicability. This tensor network representation enables highly accurate treatment of otherwise challenging bath spectral densities, such as those found in sub-Ohmic environments.190
In this section, we briefly review the QUAPI method. We assume that the interaction between the system and the bath is turn on at t = 0. Thus, we can write the initial density matrix in the form
Then, we can write the evolution of the system part of the reduced density matrix as the evolution of coordinates in the discrete variable representation (DVR) |
s〉, which shows the form
| | |
ρS(s″,s′,t) = trB〈s″|e−iHt/ħρ(0)eiHt/ħ|s′〉
| (83) |
, and which is given by
| |
 | (84) |
where the time-discretized influence functional is given as
| |
 | (85) |
These terms have been obtained in ref.
180 and
181. The influence functional can be written with the bath temperature (
kBβ)
−1,
| |
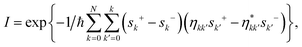 | (86) |
The parameters
ηkk′,

are
| |
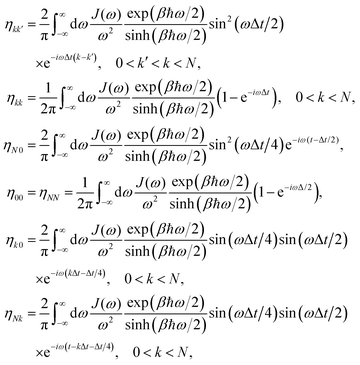 | (87) |
and have been taken from ref.
180 and
181. The time propagation of QUAPI is performed by the reduced density tensor
| T(2Δkmax)(sk±,sk+1±,…,sk+2Δkmax−1±) |
and the propagator matrix
AΔkmax. Both are given by
| |
 | (88) |
and by
| |
 | (89) |
The reduced density tensor at t = 0 is given as
| | |
A(Δkmax) (s0±,s1±,…,sΔkmax±;0) = 〈s0+|ρs(0)|s0−〉.
| (90) |
Then, one determines the time-resolved density matrix of the system by the iteration process. The finite memory of the system is included by the memory time
τ = Δ
kmaxΔ
t. The reduced density matrix at time
t =
NΔ
t can be expressed as
| | |
ρs(sN±;NΔt) = A(Δkmax) (sN±,sN+1± = ⋯ = sN+Δkmax−1± = 0;NΔt)I0(sN±).
| (91) |
The calculation of the time-evolved reduced density operator requires to consider the proper timescale of non-Markovian effects in a particular system. The calculations have to be performed with an initial test of the memory of the system by varying Δkmax and Δt. The converged results can be obtained by evaluating the special state of a density operator. The detailed procedures have been described in the ref. 185. The time propagation of tensor and reduced density operators are shown in Fig. 7.
 |
| | Fig. 7 Iterative time propagation of the reduced density matrix using a time-evolution tensor. The diagram illustrates the stepwise time propagation of the reduced density matrix through successive applications of the time-evolution superoperator R, defining at discrete time intervals. | |
More recent improvement of the full iterative QUAPI sum have been introduced as SMatPI187 and its extended version x-SMatPI.188 We refer to the original literature for further details. Furthermore, we mention that the tensor network approach TEMPO has been used recently to calculate two-dimensional spectra191 and transient X-ray absorption spectra.192
5.4 Quantum dynamics based on atomistic modeling
It is challenging to treat the whole system (molecule + environment) fully quantum mechanically. Combining molecular mechanics (MM) simulations with quantum mechanics (QM) calculations provides a compromise solution for this problem.193–199 The environment of the molecules is simulated using molecular dynamics (MD) while the molecules of interest are treated quantum mechanically. This forms the basis of the QM/MM approach. This partition is chosen for computational efficiency and does not necessarily align with a physical division into system vs. bath in the sense used in our open-system discussions above. This first-principles approach yields detailed structural and energetic information (e.g., time series of site energies and couplings), but it does not directly give spectral lineshapes because no open-system averaging is performed; line shapes must be obtained by further analysis of the QM/MM trajectory (e.g., via Fourier transforming correlation functions or using ensemble averages). In other words, QM/MM provides parameters and dynamical trajectories rather than a closed-form description of decoherence or relaxation.
In practice, one often uses MD simulations to generate an ensemble (or trajectory) of chromophore configurations within the protein. Electronic structure calculations (quantum chemistry) are then performed on snapshots from this ensemble to obtain distributions of excitation energies and couplings. This approach captures how thermal fluctuations influence electronic properties over time. In order to consider the environmental effects on the electronic structures of the molecule, for each frame, the surrounding atoms within a radius of a target molecule can be included in the single point calculations via various treatment, such as point charges. Reliable electronic structures are evaluated from the ensemble average over all the snapshots.
Beyond the pioneer application to the LH2 complex,194 this methodology has been extensively applied to investigate the electronic structures of the various photosynthetic complexes.200–206 Kleinekathöfer and co-workers have further studied the effects of the surrounding protein atoms and QM methods on the excitation energies of the pigments in LH2,207 FMO,208 LHCII,209 and photosystem II.210–212 Zhao et al. constructed the excitonic model for the 8-site FMO complex200 and a bacterial RC system.201 With the excitation energies for all the frames, not only can the average site energy be obtained, but also the pigment–environment coupling strength can be evaluated by calculating auto-correlation functions of excitation energy fluctuations. Apart from QM/MM, fully quantum dynamic methods like the multi-configuration time-dependent Hartree (MCTDH) approach have been applied to model energy transfer in light-harvesting complexes,213,214 providing detailed insight into vibronic coherence (see, e.g., the work of Kühn and co-workers).
6 Energy transfer in photosynthetic protein complexes
In this section, we review four illustrative cases in which coherence and energy transfer have been investigated: (6.1) a synthetic dimer as a basic model system, (6.2) and (6.3) two natural light-harvesting complexes (examples), and (6.4) Physical principles of energy transfer under dissipation. Each subsection will describe the system, the key findings about coherence, and the implications for the energy transfer efficiency.
Natural photosynthetic protein complexes exhibit non-trivial electronic excited-state behavior, largely due to the intricate coupling between electronic degrees of freedom (DoFs) and molecular vibrations. This coupling presents a significant challenge in unambiguously identifying the origins of quantum coherence observed in these systems. We begin with a synthetic heterodimer, which, being a minimal two-chromophore system, serves as a baseline for testing quantum coherence effects. This system was designed with two chromophores at a fixed separation resulting in a measurable excitonic coupling, providing a controlled environment to observe electronic coherence without the complexity of larger complexes.215–217
6.1 Energy transfer in an artificial dimer system
To elucidate the origin of long-lived coherence, Miller and colleagues employed 2DES to study a synthetically designed dimer composed of two identical indocarbocyanine (cyanine) dye molecules linked by butyl chains.218,219 The two chromophores are separated by approximately 10 Å, resulting in strong excitonic interactions (given their transition dipole moments, this geometry corresponds to a substantial Coulombic coupling between them), with ab initio calculations indicating a coupling energy of approximately 800 cm−1 between the monomers. The refined molecular structure of the dye dimer is presented in Fig. 8(a). Experimental absorption spectra reveal clear vibrational progressions, indicative of strong electronic-vibrational coupling in the cyanine dye system, as shown in Fig. 8(b). These interactions make the system particularly well-suited for resolving and distinguishing between electronic and vibrational coherences via 2DES. The real and total parts of the measured and simulated 2D spectra are shown in Fig. 8(c) and (d), respectively. Distinct and well-resolved diagonal and cross peaks in the spectra provide direct evidence of significant excitonic and vibronic couplings within the dimer. Oscillations observed in the dimer's 2D spectra were attributed to vibronic coherence – a coherent superposition between an electronic excited state and a vibrationally excited level of another electronic state (as defined earlier in Section 4.2). In contrast, purely electronic coherence (superposition of exciton states) was either not observed or damped quickly. The presence of these well-separated spectral features enables a clear distinction between pure electronic coherence and vibrational coherence components. Theoretical analysis, employing a vibronic dimer model alongside time non-local methods, was used to fit the experimental data. These calculations indicate that electronic coherence in the system persists for less than 120 fs at room temperature, whereas vibrational coherence can endure for >1 ps. The time-resolved trace and associated Fourier transform are shown in Fig. 8(e). The extracted reorganization energy of 250 cm−1 is significantly higher than values typically observed in natural photosynthetic protein complexes. While this synthetic dimer system offers a valuable framework for dissecting the respective contributions of electronic and vibrational coherence, the presence of both strong excitonic coupling and pronounced system–bath interactions (as reflected in the large reorganization energy) limits the direct comparison of its energy and charge transfer dynamics to those occurring in natural photosynthetic complexes. The main point of this paper is that the decoherence time could be directly determined from the antidiagonal corresponding to the homogeneous linewidth. The decay in the off diagonal peak corresponding to excitonic coupling are intrinsically related. Further, the magnitude of the excitonic cross peak is also the square of the corresponding dipole moments such that this signal contribution should be on the order of 25% of the peak amplitude on the diagnal, not the much small amplitude previously assigned to excitonic features.18 This latter connection allows a simple way to distinguish vibronic terms from impulsive Raman contributions from ground state coherences.
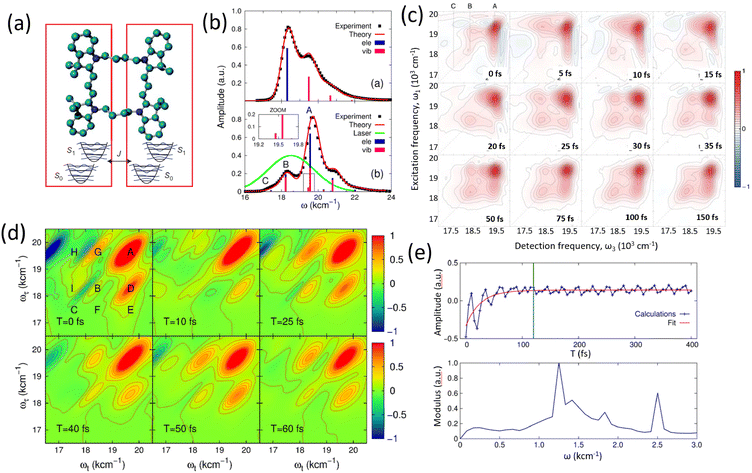 |
| | Fig. 8 Optical response and coherent dynamics in a dye dimer system. (a) Molecular structure of the dye dimer, showing the coupling between the two monomer units. Adapted from ref. 218 with permission from Springer Nature Limited,218 copyright © 2014. (b) Experimental and theoretical absorption spectra for the monomer (top) and dimer (bottom), with electronic and vibronic contributions indicated. A zoom-in inset highlights fine spectral features near peak A. (c) Experimental 2DES of the dye dimer at various population times, revealing dynamic spectral evolution. (d) Simulated 2DES at selected waiting times, capturing the progression of peak features and coherence patterns. (e) Real part of the signal trace for a selected spectral feature (top) and its Fourier transform (bottom), showing oscillatory components and their frequencies. Adapted from ref. 219 with permission from IOP Publishing Ltd and Deutsche Physikalische Gesellschaft,219 copyright © 2015. | |
The nature and origin of quantum coherence in photosynthetic systems have also been explored extensively by van Grondelle's research group220 using 2DES. Their investigations focused on the B820 bacteriochlorophyll dimer, aiming to differentiate between electronic, vibrational, and vibronic coherences. Theoretical simulations of the 2DES spectra showed strong agreement with experimental data, thereby validating the employed models and parameter sets. However, the presence of prominent ground-state bleach signals in the spectra posed a challenge in isolating purely electronic coherence from vibrational contributions. In response to these complexities, a growing body of theoretical work has emerged, seeking to more precisely resolve the underlying mechanisms of coherence in such systems.221–226 Notably, Plenio and collaborators24 investigated the influence of vibrational coherence on electronically coupled dimers. Their findings suggest that long-lived oscillatory features in 2DES can be interpreted as arising from an enhancement of vibronic coherence, particularly when vibrational modes resonate with the energy gap between two electronic excited states. In contrast, alternative explanations have been proposed by the research groups of Tiwari and Thorwart.25,227 Tiwari et al. developed a vibronic dimer model that incorporates anti-correlated vibrational modes in both the ground and excited electronic states to account for the experimentally observed long-lived coherences.25 Their work underscores the role of nonadiabatic couplings in facilitating energy transfer in photosynthetic antenna complexes. Further insights into the coupling between electronic and vibrational degrees of freedom were provided by Engel and co-workers,228 who argued that electronic coherence lifetimes can be extended when vibrational modes resonate with electronic energy gaps, particularly under weak system–bath coupling conditions. However, this interpretation has been critically evaluated by Duan et al.,227 who employed a projection technique that maps wave packet dynamics in the excited-state manifold onto key reaction coordinates. Their results suggest that under conditions of strong system–bath coupling, the proposed enhancement of electronic coherence by resonant vibrations is significantly diminished. Consequently, their findings challenge the notion that vibrational resonance alone can sustain long-lived electronic coherence in biological systems. The associated molecular dimer structures, measured 2DES and modeling are shown in Fig. 9.
 |
| | Fig. 9 Coherent dynamics in a coupled chromophore dimer system. (a) Structural model of a dimeric protein complex with associated energy levels, including the ground state, two exciton states and a higher excited state. (b) Experimentally measured two-dimensional electronic spectra (real part of the rephasing component) at selected population times, showing evolution of spectral features over time. Adapted from ref. 220 with permission from Royal Society of Chemistry,220 copyright © 2014. (c) Schematic illustration of light harvesting, where a photon excites a pigment–protein complex, generating excitonic states. Reproduced from ref. 24 with permission from Springer Nature Limited,24 copyright © 2013. (d) Theoretical model of two coupled chromophores interacting via excitonic coupling, incorporating both electronic and vibrational relaxation pathways. (e) Time-domain oscillatory signals from different experimental conditions, compared with theoretical fits, highlighting long-lived vibronic and electronic coherences. (f) Simulated 2DES spectra, revealing vibronically induced quantum beat signatures consistent with experimental data. Adapted from ref. 228 with permission from National Academy of Sciences,228 copyright © 2019. | |
Extensive investigations utilizing 2DES have been conducted with the goal of disentangling the intricate interplay between electronic and vibrational coherence. Studies involving artificial dye dimers and other synthetic molecular dimer systems have provided valuable insights. However, the preponderance of experimental evidence indicates the absence of long-lived electronic coherence under typical conditions. This absence has been largely attributed to strong system–bath interactions, which significantly suppress electronic coherence lifetimes, particularly at room temperature. Similarly, studies on photosynthetic protein complexes containing two pigment molecules have encountered challenges in isolating electronic coherence. The presence of dominant GSB signals in the 2DES spectra limits the effectiveness of distinguishing purely electronic contributions from ground state and excited state vibrational dynamics superimposed on the spectral changes. Furthermore, theoretical models have yielded varying conclusions regarding the potential enhancement of electronic coherence, depending on whether the system–environment coupling is in the weak or strong coupling regime. These findings underscore the nuanced and context-dependent nature of coherence phenomena in excitonic systems.
6.2 Energy transfer in natural antenna complexes (FMO, LHCII and LH2)
Studies on artificial dimer systems have revealed that purely electronic coherence typically persists for less than 120 fs at room temperature. In contrast, molecular vibrational coherence has been shown to endure for durations exceeding 1 ps. The synthetic molecular dimer examined by Miller and colleagues exhibited both strong excitonic coupling and significant system–bath interactions, resulting in a relatively large reorganization energy. In photosynthetic protein complexes, pigments are embedded within a protein matrix and surrounded by a solvent environment. The structural rigidity imposed by the protein scaffold, along with the specific binding of pigments, contributes to a more stable configuration, leading to weaker system–bath coupling and a correspondingly smaller reorganization energy. 2DES was initially employed to study excitonic energy transfer in these biological systems. In 2005, Brixner et al. conducted pioneering 2DES measurements on the FMO complex,229 where the appearance of cross peaks in the 2D spectra provided evidence for delocalized excitonic states and coherent energy transfer across pigment sites. Subsequent studies in 2007 reported long-lived oscillatory dynamics18 (data are shown in Fig. 10(a)), sparking widespread interest in the potential role of quantum coherence in biological energy transfer.
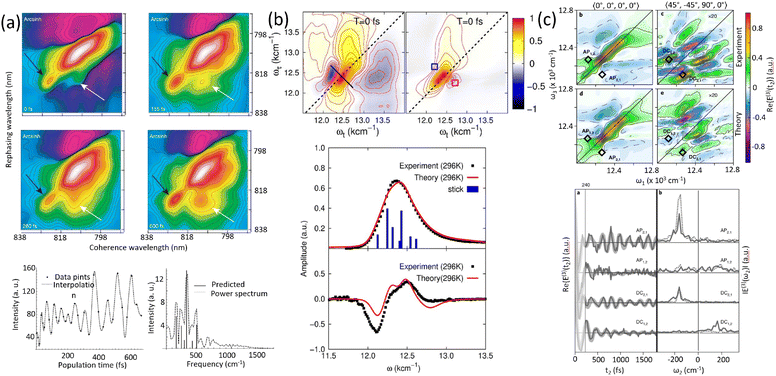 |
| | Fig. 10 2DES of the FMO complex under different conditions. (a) Experimental 2DES maps of the FMO complex at 77 K from the Fleming group at various population times, along with corresponding time-domain traces and Fourier analysis revealing coherent oscillations and their spectral components. Reproduced from ref. 18 with permission from Springer Nature Limited,18 copyright © 2007. (b) Comparison of experimental (left) and theoretical (right) 2DES at room temperature (296 K), with additional plots showing absorption and circular dichroism (CD) spectra and their theoretical fits. Adapted from ref. 26 with permission from National Academy of Sciences,26 copyright © 2017. (c) Experimental 2DES results at 77 K from the Zigmantas group under different polarization configurations, along with theoretical simulations. Bottom panel: extracted time traces and their Fourier transforms for selected cross-peaks, revealing electronic and vibronic coherent dynamics. Adapted from ref. 27 with permission from Springer Nature Limited,27 copyright © 2018. | |
Building on this, Duan et al. revisited the ultrafast excitonic dynamics and associated electronic coherence in the FMO complex using diffractive-optics-based 2DES at physiological temperature (296 K).26 Fig. 10(b) presents the experimentally measured real component of the 2D spectra. The authors developed an advanced theoretical model and extracted optimal parameters by fitting both absorption and CD spectra. The excellent agreement between the measured and simulated 2DES confirmed the robustness of the model. To further investigate electronic coherence lifetimes, the anti-diagonal spectral profile of the primary peak was analyzed and is shown as a black solid line in Fig. 10(b). A Lorentzian lineshape function was used to extract the spectral bandwidth, from which an electronic dephasing time of approximately 60 fs was determined, which is substantially shorter than the timescale of energy transfer within the FMO complex. Additionally, time-resolved traces of selected main and cross peaks in the 2DES revealed electronic coherence lifetimes consistent with this dephasing time, reinforcing the conclusion that electronic coherence decays on a timescale shorter than energy transfer. This coherence-dephasing equivalence is valid within the Markovian regime. Notably, instead of the conventionally assumed reorganization energy of ∼35 cm−1, a larger value of ∼100 cm−1 was required to accurately reproduce both linear and nonlinear spectroscopic features in the system. Further investigations by Duan et al. extended this work to low temperatures,35 where temperature-dependent 2DES measurements on the FMO complex enabled the separation of electronic coherence from vibrational contributions. The 2D spectra recorded at 20 K, shown in Fig. 11 at various waiting times (30, 50, 510, and 1005 fs), allowed for precise characterization of electronic dephasing and decoherence lifetimes across different thermal conditions.
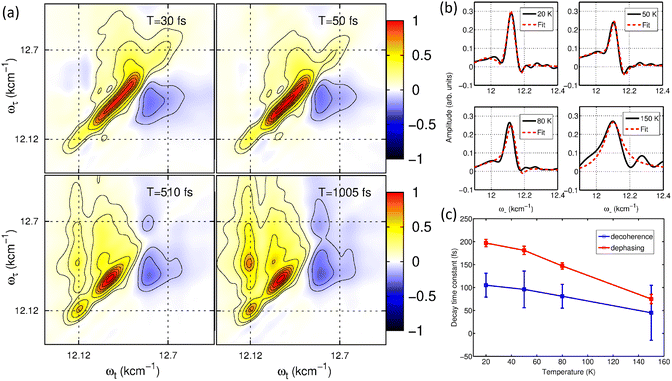 |
| | Fig. 11 Temperature-dependent coherence dynamics in the FMO complex. (a) Real part of the 2DES of the FMO complex measured at 20 K, shown at selected population times: 30 fs, 50 fs, 510 fs and 1005 fs, illustrating the evolution of spectral features over time. (b) Spectral line shapes from antidiagonal cuts through the lowest-energy excitonic peak at different temperature (20 K, 50 K, 80 K and 150 K), with experimental data (black) and corresponding fits (red dashed). (c) Extracted decay time constants for coherence dynamics at a function of temperature: red squares represent electronic dephasing between ground and excited states, while blue circles show decoherence lifetimes between excited states. Adapted from ref. 35 with permission from National Academy of Sciences,35 copyright © 2022. | |
In addition, the excitonic energy transfer and quantum coherence dynamics within the FMO complex have been investigated by the Zigmantas research group.27 Utilizing polarization-selective 2DES at cryogenic temperatures, the study aimed to differentiate between electronic and vibrational coherences. The extracted coherence lifetimes revealed that electronic coherence remains short-lived, even at 77 K (details in Fig. 10(c)). These results are consistent with the timescales reported by Duan et al.,35 further reinforcing the conclusion that electronic coherence in the FMO complex decays rapidly.
The LHCII system has been the focus of extensive ultrafast spectroscopic investigations due to its central role in photosynthetic energy transfer. In 2009, 2DES was first applied to probe energy transfer dynamics within LHCII,230 with subsequent studies examining coherent behavior at cryogenic temperatures. These efforts were later extended to physiological conditions,231 where rapid electronic dephasing and persistent vibrational coherence were observed during the energy transfer process. Theoretical modeling was employed to reproduce the experimental results and elucidate the underlying dynamics. Advancements in multidimensional spectroscopy, particularly through the use of multi-pulse configurations, led to the development of three-dimensional (3D) electronic spectroscopy,232 which was successfully applied to study LHCII. This innovative approach enabled the resolution of coherent energy transfer pathways and the identification of the origins of coherence without the need for complex theoretical frameworks. Further progress was achieved through the implementation of multi-color 2DES and two-dimensional electronic-vibrational (2DEV) spectroscopy.233 These techniques allowed for the selective detection of electronic and vibrational coherences, revealing the intricate interplay of vibronic and vibrational contributions to the energy transfer process in LHCII. The representative results of 2DES and 2DEV are shown in Fig. 12. Additionally, Weng, Shi, and collaborators employed 2DES to further explore coherent energy transfer in LHCII.234
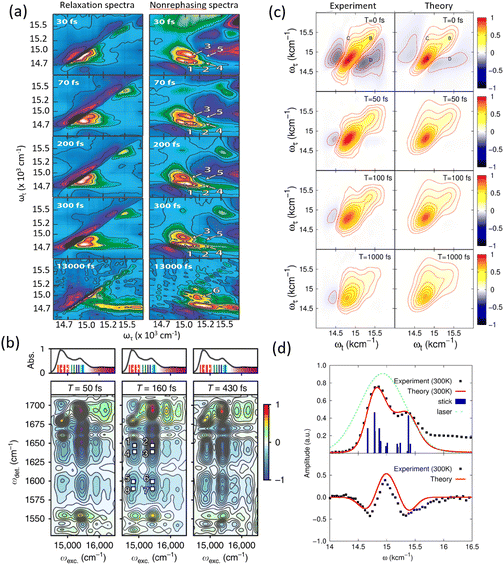 |
| | Fig. 12 Two-dimensional spectroscopy studies of the LHCII complex. (a) Relaxation (left) and non-rephasing (right) 2D electronic spectra measured at various population times, from 30 fs to 1300 fs, revealing spectral evolution and peak assignments over time. Adapted from ref. 230 with permission from American Chemical Society,230 copyright © 2009. (b) Time-resolved 2D spectra at selected waiting times (T = 50 fs, 160 fs, and 430 fs), showing vibronic coherences signatures. Absorption spectra and transition markers are provided above each panel for reference. (c) Comparison of experimental and theoretical 2D spectra at four time points (T = 0 fs, 50 fs, 100 fs and 1000 fs), highlighting the temporal dynamics and model accuracy. (d) Absorption (top) and circular dichroism (CD) spectra (bottom) at 300 K: experimental results are compared with theoretical simulations, laser profiles and stick spectra to resolve vibronic structure. Adapted from ref. 231 with permission from American Chemical Society,231 copyright © 2015. | |
Parallel developments have occurred in the study of the LH2 complex, another essential photosynthetic assembly involved in light energy transport. In 2006, ultrafast energy transfer dynamics in LH2 were investigated using 2DES, with particular focus on the excitonic coupling and energy transfer between the B800 and B820 bands.235 Technological advancements subsequently enabled single-shot detection and the use of ultrabroadband pulses for enhanced temporal and spectral resolution.236,237 Engel and colleagues later reported evidence of long-lived electronic coherence in LH2, suggesting that coherence may facilitate efficient energy transfer within the complex.238 Cerullo and co-workers further contributed by developing multicolor coherent spectroscopy,239 which utilized varying excitation and detection wavelengths to resolve population transfer pathways from higher-energy Qx to lower-energy Qy states of two ring structures of LH1. Importantly, 2DES has also been employed to study energy transfer in vivo, revealing that the timescales of excitonic transport in native photosynthetic membranes closely resemble those observed in isolated LH2 complexes.240 Complementary to this, Ogilvie and Jansen introduced fluorescence-detected 2DES,241 which exhibited enhanced signal clarity through reduced ground-state bleaching, enabling the observation of strong cross peaks. They proposed using time-resolved fluorescence-detected 2D spectroscopy to investigate state-resolved exciton–exciton annihilation. Furthermore, van Grondelle and colleagues explored hidden dark states in LH2,242 while the effects of static and dynamic disorder were examined in subsequent studies.243 Their simulations revealed that accurately modeling the frequency distribution of the protein environment requires incorporating temperature-dependent factors. The representative results of 2DES of LH2 complex are shown in Fig. 13.
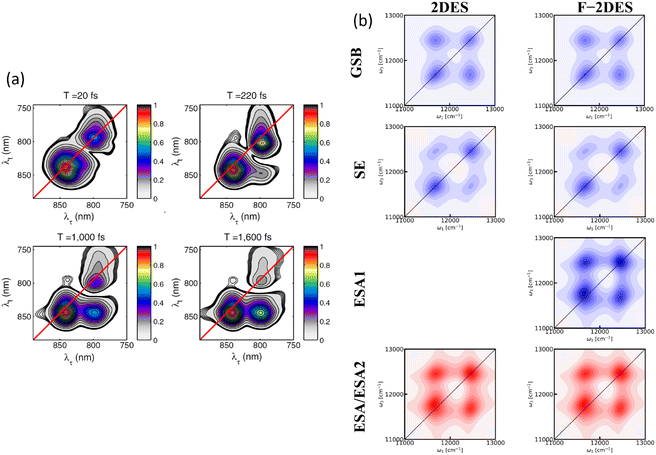 |
| | Fig. 13 Conventional and fluorescence-detected 2DES of the LH2 complex. (a) Experimental 2DES of the LH2 complex at various population times (T = 20 fs, 220 fs, 1000 fs and 1600 fs), showing the evolution of spectral features. Adapted from ref. 238 with permission from National Academy of Sciences,238 copyright © 2012. (b) Comparison of simulated conventional 2DES (left column) and fluorescence-detected 2DES (right column), decomposed into GSB, SE and two contributions from excited-state absorption (ESA1 and ESA2), highlighting difference in signal pathways between detection methods. Adapted from ref. 241 with permission from American Chemical Society,241 copyright © 2018. | |
6.3 Energy transfer in PSII reaction center and bacteria reaction center
The PSII RC complex plays a crucial role in facilitating both excitonic and charge transfer processes within natural photosynthetic protein assemblies. Early insights into the ultrafast timescales governing population transfer were obtained through transient absorption spectroscopy, which later evolved into more advanced studies using 2DES. The first 2DES experiment on a photosynthetic reaction center was conducted by Ogilvie and colleagues in 2010,244 revealing critical information about the dynamics and pathways of population transfer. To interpret these experimental findings, a theoretical framework was developed using a quantum master equation approach, specifically the Redfield equation.131 Subsequently, a tight-binding model was proposed, with parameters refined through fitting to the absorption spectra, enabling the incorporation of charge-transfer states and their associated dynamics.127 Building upon these models, Novoderezhkin and collaborators245–248 introduced a comprehensive excitonic model incorporating charge-transfer states. Their model parameters, including system–bath coupling constants, were robustly constrained through simultaneous fitting of multiple linear spectroscopic measurements: absorption, CD and fluorescence emission. Further 2DES investigations by Ogilvie's group249 revealed long-lived oscillatory signals, attributed to coherent dynamics associated with energy and charge transfer in the reaction center. The measured data is shown in Fig. 14(a) and (b). Independently, van Grondelle and co-workers9 independently reported similar findings. Both studies highlighted strong vibronic coupling between electronic excited states and nuclear vibrational modes. Complementary theoretical analyses confirmed the presence of vibronic quantum coherence during the photoexcitation process. More recently, a multi-color 2DES approach was developed to probe coherent dynamics and charge separation in the PSII reaction center250 (see Fig. 14(d)). This technique, with its broadband detection window, enabled simultaneous observation of excitonic states and dark charge-transfer states. In 2024, Jha et al. revisited the energy and charge transfer dynamics in PSII using 2DES at cryogenic temperatures (20 K).36 The resulted data are shown in Fig. 14(c). Their analysis and theoretical modeling indicated an absence of strong electronic coherence, while vibrational coherence was observed to persist for over 1 ps. The study also revealed that electronic coherence lifetimes are highly sensitive to the magnitude of excitonic couplings between pigment molecules. Additionally, a novel type of PSII reaction center capable of absorbing far-red light was recently purified and investigated using 2DES.251 This study reported the formation of a radical pair within ∼3 ps, assigned to the state ChlD1−PD1+. These findings suggest that, in far-red PSII, primary charge separation occurs between ChlD1 and PD1, highlighting a potentially underappreciated role of the PD1/PD2 pair in the initial stages of PSII charge separation.
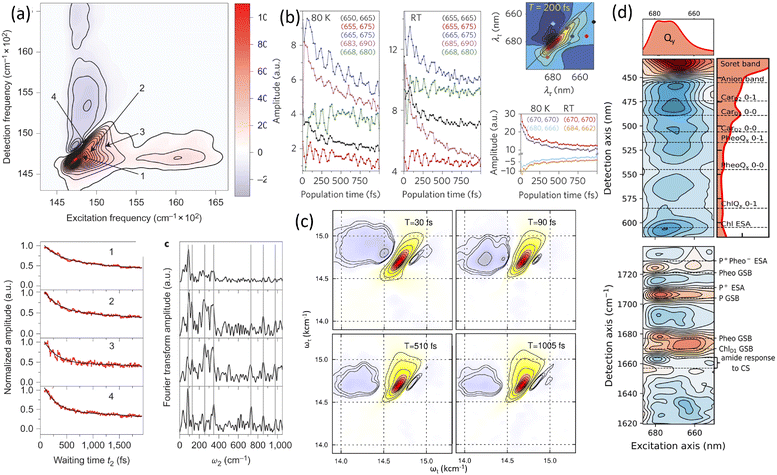 |
| | Fig. 14 2DES of the PSII reaction center and its coherent dynamics. (a) Experimental 2DES map of the PSII reaction center showing four key spectral frequares and their associated coherence decay profiles (left), with Fourier transforms of oscillatory components (right). Reproduced from ref. 249 with permission from Springer Nature Limited,249 copyright © 2014. (b) Population dynamics at 80 K and room temperature (RT) for different spectral regions, along with corresponding 2D spectra and decay traces, as reported by Grondelle's group. Reproduced from ref. 9 with permission from Springer Nature Limited,9 copyright © 2014. (c) Time evolution of 2DES spectra at selected waiting times (30 fs to 1000 fs), illustrating changes in peak structure and coherence lifetimes. Adapted from ref. 36 with permission from The American Association for the Advancement of Science,36 copyright © 2024. (d) High-resolution 2DES data collected at 20 K, revealing detailed spectral assignments including Qy, Soret and anion bands, as well as excitonic and charge-separated (CS) state features. (e) Reported 2DES measured using a milticolor pulse configuration, enabling broader spectral coverage and enhanced resolution of overlapping transitions. Adapted from ref. 250 with permission from The American Association for the Advancement of Science,250 copyright © 2023. | |
The bacteria reaction center is another unique protein complex in nature. The measured absorption spectrum of bacteria reaction center shows less congested spectral features compared to the spectrum of the PSII reaction center, which indicates strong excitonic couplings between different pigments in the bacteria reaction center. This feature of well-separated cross peaks is well resolved in 2DES. This separation of the excitation and the detection windows of 2DES becomes an valuable tool to disentangle the origins of electronic and vibrational coherence. Zigmantas et al. employed 2DES and studied the energy and charge transfer dynamics in bacteria reaction center complex.252 The measured 2DES and 2D vibrational maps are shown in Fig. 15. They claimed the vibronic coherence was observed after photoexcitation. Moreover, the primary energy and charge transfer processes were probed by 2DES.253 The detailed pathways of population transfer were revealed by applying a global fit and the resulted data show the detailed timescales of charge transfer in bacteria reaction centers. In addition, the coherent dynamics during the charge transfer process in bacteria reaction center has been further investigated by 2DES.254 Moreover, the electronic and vibrational coherence in the bacteria reaction center have also been studied by van Grondelle and coworkers.255 They reported that the electronic and vibrational coherences were involved during the processes of energy and charge transfers. In addition, the electronic couplings between different regions of pigments were studied by multi-color 2DES.256 Pumping in the visible region and probing in the near IR allows one to track in detail the population transfer and charge-associated dynamics in bacteria reaction center.
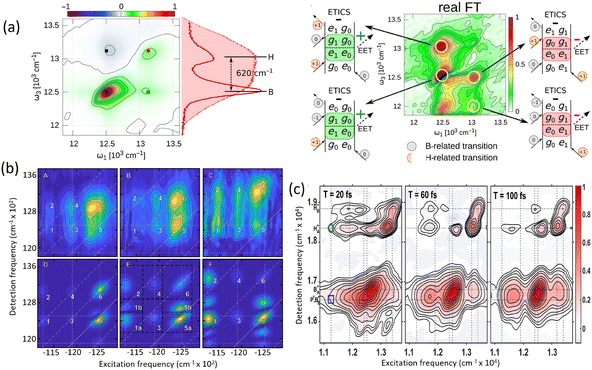 |
| | Fig. 15 Coherent dynamics and vibronic structure in BRC revealed by multidimensional spectroscopy. (a) Left: 2DES of the BRC, highlighting distinct coherence features. The absorption spectrum (in red) identifies vibronic transitions with an energy spacing of ∼620 cm−1. Right: Real part of the Fourier-transformed 2D Map showing coherence pathways involving B and H states, interpreted through electronic-transition-induced coherence shifting diagrams. Vibrational and vibronic coherence patterns resolved from 2D vibrational maps derived via Fourier transformation of residuals from experimental data, with individual peaks labeled. Adapted from ref. 252 with permission from The American Association for the Advancement of Science,252 copyright © 2017. (b) Comparison between measured and simulated 2D vibrational maps at early times (T = 20 fs) with associated energy-level diagrams and pathway assignments for GSB and ESA. Adapted from ref. 254 with permission from The American Association for the Advancement of Science,254 copyright © 2022. (c) Experimental 2DES obtained using a multi-color pulse scheme at various waiting times (T = 20 fs, 60 fs and 100 fs), illustrating the temporal evolution of photoinduced coherence and population dynamics. Adapted from ref. 256 with permission from American Chemical Society,256 copyright © 2018. | |
The BRC represents another highly specialized protein complex within natural photosynthetic systems. Compared to the PSII reaction center, the absorption spectrum of the BRC displays fewer congested spectral features, suggesting stronger excitonic coupling among its constituent pigments. This characteristic leads to well-resolved and clearly distinguishable cross peaks in 2DES, making BRC an ideal system for disentangling the contributions of electronic and vibrational coherences through spectral separation in the excitation and detection windows. Zigmantas and collaborators252 applied 2DES to investigate the energy and charge transfer dynamics within the BRC. Their study provided compelling evidence for the presence of vibronic coherence following photoexcitation. Additionally, the primary energy and charge transfer events were examined in greater detail through 2DES.253 By employing global fitting procedures, they were able to extract specific population transfer pathways and associated timescales for charge separation processes in the BRC. Further investigations into coherent dynamics during charge transfer in the BRC have reinforced the presence of quantum coherence, vibronic coherences in particular, on short time scales.254 van Grondelle and co-workers255 also explored this system, reporting the concurrent involvement of both electronic and vibrational coherences in mediating energy and charge transfer processes. Moreover, multi-color 2DES techniques have been employed to probe electronic couplings between distinct pigment domains within the BRC.256 By selectively pumping in the visible spectral region and probing in the near-infrared, it was possible to track the detailed progression of population transfer and charge-associated dynamics with high temporal and spectral resolution.
6.4 Physical principles of energy transfer under dissipation
In the investigation of energy and charge transfer dynamics within natural photosynthetic protein complexes, it has become evident that the system–bath coupling and reorganization energies are generally weaker than those observed in photoactive molecules directly exposed to solvent environments. For instance, studies by Miller, Thorwart, and colleagues on synthetic dye dimers reported reorganization energies associated with solvent vibrational modes in the range of 250–300 cm−1.218,219 In contrast, more recent analyses of natural antenna complexes, such as the FMO complex, have suggested considerably lower reorganization energies, on the order of 100 cm−1, albeit significantly higher than the previously estimated value of 35 cm−1, which was originally inferred from the Stokes shift between absorption and emission peaks in linear spectra. However, advanced spectroscopic measurements and refined theoretical modeling have since demonstrated that the earlier estimate of 35 cm−1 substantially underrepresents the actual system–bath interaction in FMO. A critical factor influencing this interaction is the protein environment. When pigments are embedded within a protein matrix, rather than directly solvated, they experience structural shielding and increased rigidity. These features attenuate the influence of the environment by reducing the effective reorganization energy. This feature will lead to lower energy losses in directing the energy transport and should not be taken as evolutionary optimization to increase electronic coherence time scales, which all occur with smaller system–bath couplings. In this regard, recent studies on charge separation in the PSII reaction center36 have shown that the magnitude of excitonic coupling between pigments significantly influences the persistence of electronic quantum coherence. Strong electronic coupling, such as that found in the radical pair intermediates within the PSII reaction center, can support relatively long-lived electronic coherence even at room temperature. In contrast, antenna complexes, where the average inter-pigment distance is greater, tend to exhibit weaker or intermediate excitonic coupling. As a result, these systems are less likely to sustain observable electronic coherence, even under cryogenic conditions. Moreover, we have listed the lifetimes of electronic coherence of the studied photosynthetic systems, which is shown in the table below:
| Artificial dimer |
45 fs |
| FMO protein complex |
60 fs |
| LHCII protein complex |
65 fs |
| PSII reaction center |
56 fs |
An intriguing aspect of photosynthetic antenna complexes is that the typical energy gap between pigment sites is approximately 100 cm−1, a value comparable to the thermal energy scale at room temperature. Notably, the strongest electronic coupling values facilitating excitonic energy transfer are also on the order of 100 cm−1. This energetic proximity plays a critical role in determining the lifetime of electronic coherence within these systems. Duan and colleagues conducted temperature-dependent 2DES studies on the FMO complex, extending measurements down to cryogenic temperatures (20 K). This experimental design enabled them to systematically investigate how electronic coherence lifetimes evolve with temperature. Their findings revealed that even at 20 K, the lifetime of purely electronic coherence does not exceed 1 ps. Instead, it decays rapidly on the same timescale as electronic dephasing between the ground and excited states, confirming that electronic coherence in the FMO complex is inherently short-lived, even under low-temperature conditions. These decay constants include inhomogeneous dephasing due to static site disorder, detailed modeling is required to separate pure dephasing from ensemble-averaged contributions.257–260
Particularly compelling are recent investigations into ultrafast energy and charge transfer dynamics in the reaction center complex, as reported in ref. 36. 2DES measurements revealed a congested spectral region characterized by vibrational progression features. Detailed analysis of the data identified long-lived oscillatory dynamics following photoexcitation, suggestive of coherent interactions. By applying fitting procedures and theoretical modeling to the measured 2DES, it was possible to quantify the coupling between electronic degrees of freedom and environmental vibrational modes. The resulting calculations indicated a system–bath coupling strength corresponding to a reorganization energy of ∼120 cm−1, signifying a relatively strong interaction between the electronic system and its environment. Importantly, the analysis also suggested the presence of long-lived electronic coherence within the radical pair persisting even at room temperature. However, recent theoretical studies by Renger and co-workers261–263 challenge the interpretation of this radical pair as the initial site for charge separation. Their findings suggest that the PD1 and PD2 pair is not the primary origin of charge transfer in the reaction center. Consequently, while a long-lived electronic coherence between these two pigments may be observed, it does not directly correlate with the initiation of charge separation. Instead, the strong orbital overlap and interaction within the radical pair likely facilitate charge delocalization during photoexcitation but are not sufficient to account for the full charge-transfer pathway.
A recent study by Weng and colleagues264 applied 2DES to the allophycocyanin (APC) photosynthetic protein complex. Rather than observing electronic coherence, the authors reported long-lived vibrationally assisted quantum coherence during the energy transfer process. Their findings were compared between dimeric and monomeric APC systems. The notable differences in the spectroscopic signatures, particularly the absence of narrow anti-diagonal peaks and well-resolved cross peaks in the dimer, were attributed to distinct excited-state absorption characteristics rather than coherent excitonic features. These observations closely resemble earlier results obtained from artificial dimer systems. In the APC dimer, a substantial excitonic energy gap (∼800 cm−1) exists between monomers, while the inter-monomer excitonic coupling was relatively weak (∼150 cm−1). Such a parameter regime falls within what is generally defined as the weak coupling limit, which is known to support only short-lived electronic coherence, particularly at room temperature. In this regime, the large energy gap combined with moderate coupling strength leads to rapid electronic decoherence, and vibrational coherence alone is insufficient to sustain or enhance quantum coherence in the electronic system. In this review, we emphasize that while energy and charge transfer in photosynthetic protein complexes can be understood within the framework of excitonic energy transfer, the dynamics largely fall outside the domain of coherent quantum transport. The relatively strong system–bath interactions and the correspondingly large reorganization energies characteristic of these biological systems limit the persistence of electronic coherence, even under cryogenic conditions. The protein environment imposes a smaller reorganisation energy (50–100 cm−1) than a polar solvent might, thus incurring lower energy loss per transfer step.37 Nature appears to favor a thermally driven, dissipative mechanism for energy transfer, wherein energy cascades from higher to lower excited states via robust, environmentally stabilized pathways. It is notable that the collective difference in site energies is on the order of 100 cm−1, the minimum required to thermally prevent back transfer on the relevant time scale and ensure the energy transport process is unidirectional. The evolutionary optimization then is on engineering of the difference in site energies to be as small as possible while still directing energy transport energetically downhill. These dissipative channels ensures efficient and reliable energy transfer in natural photosynthetic systems. The schematic diagrams are shown in Fig. 16.
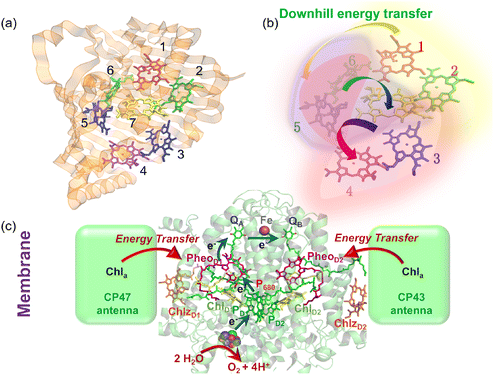 |
| | Fig. 16 Concluding perspective on energy flow in photosynthetic complexes. (a and b) The FMO protein illustrates a structured energy landscape that promotes robust downhill excitation transfer, where site energetics and couplings guide relaxation while limiting long-lived quantum coherences. (c) In PSII, antenna–reaction center organization similarly favors efficient energy funneling toward charge separation over coherence preservation. | |
7 Future perspectives
Cutting-edge ab initio and hybrid quantum-classical computational methods, accelerated by GPU-based computing, have made it possible to accurately estimate site energies, excitonic couplings, and system–bath interactions. These developments enable not only refined modeling of bright and dark exciton states but also the decoding of quantum coherence and dissipation pathways during energy and charge transfer. Despite increased understanding of excitonic energy transfer mechanisms, there is a growing consensus that in typical biological conditions, the combination of relatively strong system–bath interactions (i.e., on the order of electronic splittings) due fundamentally to large reorganization energies tend to suppress any long-lived electronic coherence. As demonstrated in FMO, LH2, LHCII, and PSII complexes, coherence lifetimes are typically on the order of tens to hundreds of fs, shorter than the energy transfer timescales. This suggests that natural photosynthesis operates primarily in a dissipative regime, where thermally driven relaxation through well-organized pigment networks ensures robust and efficient energy transport, even in fluctuating environments. Nevertheless, the idea of leveraging transient coherence as a functional tool—rather than expecting it to be sustained indefinitely—opens up new avenues for research and technology. While long-lived electronic coherence is unlikely to dominate under physiological conditions, the transient coherence observed during early excitation may still enhance energy transport under specific conditions. In this view, coherence is not seen as a long-term phenomenon, but rather as a transient mechanism that can momentarily stabilize or guide excitonic energy flow. However, strong dissipation typically limits its practical impact in natural systems. The precise assignment of these coherences in complex biological systems, along with their direct functional implications for population dynamics, remains an unresolved issue. Emerging experimental and theoretical advances, particularly those employing varied pulse sequences265–268 and probing distinct frequency regimes,269–271 hold promise for further unraveling the complexities inherent in 2DES.
Looking forward, artificial enhancement of coherence offers a transformative opportunity. Emerging strategies include: plasmon-enhanced energy transfer and cavity quantum electrodynamics (cavity-QED). In plasmon-enhancement, by coupling photosynthetic complexes to metal nanostructures, intense near-field optical fields can modulate the system's Hamiltonian. These interactions can act as auxiliary energy states or coherent control tools, accelerating energy transfer and modulating excitonic interactions. Such light–matter hybridization platforms offer external control over quantum states and may enable engineered initial wavefunctions for targeted energy flow.272 In cavity-QED, embedding pigment–protein complexes into optical cavities allows the formation of polariton states through strong light–matter coupling. Initial measurements show promising evidence that these hybrid states can reshape population dynamics and enhance excitonic transport efficiency.273–277 This field opens the door to quantum control over biological function, enabling programmable coherence lifetimes and transfer pathways. Together, these advancements suggest a future where natural energy transfer principles are not merely understood but engineered, combining biological inspiration with quantum optical technologies. The intersection of quantum photonics, synthetic biology, and computational chemistry may lead to the development of next-generation light-harvesting systems, both as platforms to study the fundamental limits of coherence in complex systems and as templates for high-efficiency, bio-inspired energy technologies.
8 Conclusions
In this review, we have summarized recent experimental and theoretical advances concerning coherent energy and charge transfer in photosynthetic protein complexes. Early interpretations, particularly those based on original interpretations of 2DES, supported the idea that quantum coherence, especially electronic and vibronic coherence, could play a functional role in mediating energy transfer between pigments. However, accumulating evidence from more recent studies has challenged this view, indicating that the efficiency of energy and charge transport in natural photosynthetic systems does not depend significantly on the persistence of such coherences. Temperature-dependent 2DES experiments have been especially instrumental in probing the lifetimes of coherence under biologically relevant conditions. These studies reveal that electronic coherence, when observable, decays rapidly, particularly at physiological temperatures. Moreover, refined 2DES methodologies combined with advanced data analysis have demonstrated that the previously suggested vibrationally enhanced electronic coherence lacks strong empirical support. Collectively, these findings, bolstered by complementary theoretical models, indicate that energy transfer in photosynthetic complexes can proceed with high efficiency in the absence of long-lived electronic or vibronic coherence.
Our assessment, consistent with results from other leading groups, points to excitonic couplings in these systems being in the weak to intermediate regime. Under such coupling strengths, excitonic delocalization is typically limited to small pigment clusters, often two or three chromophores, as exemplified by the FMO complex. This limited delocalization, if not dominating spatial transport, still contributes to the efficient and high-fidelity population transfer, maintaining near-unity energy transport efficiency. Importantly, strong system–bath interactions intrinsic to the protein and solvent environment lead to rapid electronic decoherence. These interactions are not detrimental; rather, they appear to be functionally advantageous. Nature seems to have optimized photosynthetic energy transfer by exploiting such dissipative dynamics, allowing energy to be funneled reliably through thermally activated and environmentally robust pathways. Overall, our review indicates that while oscillatory coherent phenomena can be observed in certain photosynthetic systems, they are not required for a high efficiency of the energy transfer. Instead, efficient transport appears to arise from a combination of controlled excitonic coupling and environmental interactions (dissipation and static disorder) that funnel energy rapidly and irreversibly to reaction centers. Coherence might play a transient role under special circumstances (e.g., unusually weak decoherence or very strong electronic coupling), but these cases are exceptions rather than the rule. In general, nature's light-harvesting complexes seem to exploit dissipation across all relevant time and length scales to ensure robust energy transport, rather than relying on long-lived quantum coherence as a design principle. Of course, in reality these systems have evolved with electronic and vibrational degrees of freedom tuned together to maximize function; our use of terms like ‘dissipation’ simply categorizes the physical mechanism by which these natural systems achieve robust transport.
Author contributions
H. G. D. and A. J. wrote the initial draft with contribution from F. Z. on the HEOM method. H. G. D. and A. J. prepared the figures with the help of Z. L. All authors read, revised and approved the manuscript.
Conflicts of interest
The authors declare that they have no competing financial interests.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.
Acknowledgements
We thank Jing Yang, Junhua Zhou to help refining the figures. This work was supported by National Key Research and Development Program of China (Grant No. 2024YFA1409800), NSFC Grant with No. 12274247 and 12504279, Yongjiang talents program with No. 2022A-094-G and 2023A-158-G, Ningbo International Science and Technology Cooperation with No. 2023H009, ‘Lixue+’ Innovation Leading Project and the foundation of national excellent young scientist. The Next Generation Chemistry theme at the Rosalind Franklin Institute is supported by the EPSRC (V011359/1 (P))(AJ). Natural Sciences and Engineering Research Council of Canada (RJDM). S. M. gratefully acknowledges the support of NSF grant CHE-2246379.
Notes and references
- E. Schrödinger, What is life?: With mind and matter and autobiographical sketches, Cambridge University Press, 1992 Search PubMed.
- P. Jordan, Die Physik und das Geheimnis des organischen Lebens, Die Wissenschaft, 1941 Search PubMed.
- J. McFadden and J. Al-Khalili, The origins of quantum biology, Proc. R. Soc. A, 2018, 474, 20180674 CrossRef.
- N. Lambert, et al., Quantum biology, Nat. Phys., 2013, 9, 10–18, DOI:10.1038/nphys2474.
- A. G. J. MacFarlane, J. P. Dowling and G. J. Milburn, Quantum technology: the second quantum revolution, Philos. Trans. R. Soc. London, Ser. A, 2003, 361, 1655–1674, DOI:10.1098/rsta.2003.1227.
- A. M. Kelley, Condensed-Phase Molecular Spectroscopy and Photophysics, John Wiley & Sons, Inc. ©, 2023, pp. 103–126 Search PubMed.
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, 2007 Search PubMed.
- G. D. Scholes, et al., Using coherence to enhance function in chemical and biophysical systems, Nature, 2017, 543, 647–656, DOI:10.1038/nature21425.
- E. Romero, et al., Quantum coherence in photosynthesis for efficient solar-energy conversion, Nat. Phys., 2014, 10, 676–682, DOI:10.1038/nphys3017.
- A. Marais, et al., The future of quantum biology, J. R.Soc., Interface, 2018, 15, 20180640, DOI:10.1098/rsif.2018.0640.
- R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, 2021 Search PubMed.
- R. Croce, R. Van Grondelle, H. Van Amerongen and I. Van Stokkum, Light harvesting in photosynthesis, CRC Press, 2018 Search PubMed.
- U. Keller and R. Paschotta, Ultrafast lasers, Springer, 2021 Search PubMed.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995 Search PubMed.
- R. Hildner, D. Brinks, J. B. Nieder, R. J. Cogdell and N. F. van Hulst, Quantum Coherent Energy Transfer over Varying Pathways in Single Light-Harvesting Complexes, Science, 2013, 340, 1448–1451, DOI:10.1126/science.1235820.
- J. Kim, S. Mukamel and G. D. Scholes, Two-Dimensional Electronic Double-Quantum Coherence Spectroscopy, Acc. Chem. Res., 2009, 42, 1375–1384, DOI:10.1021/ar9000795.
- Y.-C. Cheng and G. R. Fleming, Coherence Quantum Beats in Two-Dimensional Electronic Spectroscopy, J. Phys. Chem. A, 2008, 112, 4254–4260, DOI:10.1021/jp7107889.
- G. S. Engel, et al., Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems, Nature, 2007, 446, 782–786, DOI:10.1038/nature05678.
- G. Panitchayangkoon, et al., Long-lived quantum coherence in photosynthetic complexes at physiological temperature, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12766–12770, DOI:10.1073/pnas.1005484107.
- H. Lee, Y.-C. Cheng and G. R. Fleming, Coherence Dynamics in Photosynthesis: Protein Protection of Excitonic Coherence, Science, 2007, 316, 1462–1465, DOI:10.1126/science.1142188.
- G. S. Schlau-Cohen, et al., Elucidation of the timescales and origins of quantum electronic coherence in LHCII, Nat. Chem., 2012, 4, 389–395, DOI:10.1038/nchem.1303.
- S. Savikhin, D. R. Buck and W. S. Struve, Oscillating anisotropies in a bacteriochlorophyll protein: Evidence for quantum beating between exciton levels, Chem. Phys., 1997, 223, 303–312, DOI:10.1016/S0301-0104(97)00223-1.
- T. H. Förster in Comprehensive Biochemistry, ed. M. Florkin and E. H. Stotz, Elsevier, 1967, vol. 22, pp. 61–80 Search PubMed.
- A. W. Chin, et al., The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes, Nat. Phys., 2013, 9, 113–118, DOI:10.1038/nphys2515.
- V. Tiwari, W. K. Peters and D. M. Jonas, Electronic resonance with anti-correlated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208, DOI:10.1073/pnas.1211157110.
- H.-G. Duan, et al., Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8493–8498, DOI:10.1073/pnas.1702261114.
- E. Thyrhaug, et al., Identification and characterization of diverse coherences in the Fenna–Matthews–Olson complex, Nat. Chem., 2018, 10, 780–786, DOI:10.1038/s41557-018-0060-5.
- J. Adolphs and T. Renger, How Proteins Trigger Excitation Energy Transfer in the FMO Complex of Green Sulfur Bacteria, Biophys. J., 2006, 91, 2778–2797, DOI:10.1529/biophysj.105.079483.
- P. Nalbach, D. Braun and M. Thorwart, Exciton transfer dynamics and quantumness of energy transfer in the Fenna-Matthews-Olson complex, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041926 Search PubMed.
- L. Chen, R. Zheng, Y. Jing and Q. Shi, Simulation of the two-dimensional electronic spectra of the Fenna-Matthews-Olson complex using the hierarchical equations of motion method, J. Chem. Phys., 2011, 134, 194508, DOI:10.1063/1.3589982.
- D. J. Cole, A. W. Chin, N. D. M. Hine, P. D. Haynes and M. C. Payne, Toward Ab Initio Optical Spectroscopy of the Fenna-Matthews-Olson Complex, J. Phys. Chem. Lett., 2013, 4, 4206–4212, DOI:10.1021/jz402000c.
- J. Wu, F. Liu, J. Ma, R. J. Silbey and J. Cao, Efficient energy transfer in light-harvesting systems: Quantum-classical comparison, flux network, and robustness analysis, J. Chem. Phys., 2012, 137, 174111, DOI:10.1063/1.4762839.
- J. Moix, J. Wu, P. Huo, D. Coker and J. Cao, Efficient Energy Transfer in Light-Harvesting Systems, III: The Influence of the Eighth Bacteriochlorophyll on the Dynamics and Efficiency in FMO, J. Phys. Chem. Lett., 2011, 2, 3045–3052, DOI:10.1021/jz201259v.
- J. Cao, et al., Quantum biology revisited, Sci. Adv., 2020, 6, eaaz4888, DOI:10.1126/sciadv.aaz4888.
- H.-G. Duan, et al., Quantum coherent energy transport in the Fenna-Matthews-Olson complex at low temperature, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2212630119, DOI:10.1073/pnas.2212630119.
- A. Jha, et al., Unraveling quantum coherences mediating primary charge transfer processes in photosystem II reaction center, Sci. Adv., 2024, 10, eadk1312, DOI:10.1126/sciadv.adk1312.
- M. K. Lee, P. Huo and D. F. Coker, Semiclassical Path Integral Dynamics: Photosynthetic Energy Transfer with Realistic Environment Interactions, Annu. Rev. Phys. Chem., 2016, 67, 639 CrossRef CAS PubMed.
- S. J. Jang and B. Mennucci, Delocalized excitons in natural light-harvesting complexes, Rev. Mod. Phys., 2018, 90, 035003 CrossRef CAS.
- J. D. Schultz, et al., Coherence in Chemistry: Foundations and Frontiers, Chem. Rev., 2024, 124, 11641 CrossRef CAS.
- T. Förster, Zwischenmolekulare Energiewanderung und Fluoreszenz, Ann. Phys., 1948, 2, 55–75, DOI:10.1002/andp.19484370105.
- T. Förster, Delocalized excitation and excitation transfer, in Modern Quantum Chemistry, Section III B, Action of Light and Organic Crystals, ed. O. Sinanoglu, Academic Press, New York, 1965, pp. 93–137 Search PubMed.
- B. R. Masters, Paths to Förster's resonance energy transfer (FRET) theory, Eur. Phys. J. H, 2014, 39, 87–139, DOI:10.1140/epjh/e2013-40007-9.
- S. Jang, et al., Nonequilibrium generalization of Förster–Dexter theory for excitation energy transfer, Chem. Phys., 2002, 275, 319 CrossRef.
- S. Jang, Generalization of the Förster resonance energy transfer theory for quantum mechanical modulation of the donor-acceptor coupling, J. Chem. Phys., 2007, 127, 147710 CrossRef.
- S. Jang, et al., Multichromophoric Förster Resonance Energy Transfer, Phys. Rev. Lett., 2004, 92, 218301 CrossRef PubMed.
- H. van Amerongen, Photosynthetic Excitons, World Scientific Press, 2000 DOI:10.1142/3609.
- R. Fenna and B. Matthews, Chlorophyll arrangement in a bacteriochlorophyll protein from Chlorobium limicola, Nature, 1975, 258, 573–577, DOI:10.1038/258573a0.
- B. W. Matthews, R. E. Fenna, M. Bolognesi, M. Schmid and J. M. Olson, Structure of a bacteriochlorophyll a-protein
from the green photosynthetic bacterium Prosthecochloris aestuarii, J. Mol. Biol., 1979, 131, 259–285, DOI:10.1016/0022-2836(79)90076-7.
- J. Koepke, X. Hu, C. Muenke, K. Schulten and H. Michel, The crystal structure of the light-harvesting complex II (B800–850) from Rhodospirillum molischianum, Structure, 1996, 4, 581–597, DOI:10.1016/S0969-2126(96)00063-9.
- Z. Liu, et al., Crystal structure of spinach major light-harvesting complex at 2.72 A resolution, Nature, 2004, 428, 287–292, DOI:10.1038/nature02373.
- N. Kamiya and J.-R. Shen, Crystal structure of oxygen-evolving photosystem II from Thermosynechococcus vulcanus at 3.7 A resolution, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 98–103, DOI:10.1073/pnas.0135651100.
- X. Su, et al., Structure and assembly mechanism of plant C-type PSII-LHCII supercomplex, Science, 2017, 357, 815–820, DOI:10.1126/science.aan0327.
- J. Gao, H. Wang, Q. Yuan and Y. Feng, Structure and Function of the Photosystem Supercomplexes, Front. Plant Sci., 2018, 9 DOI:10.3389/fpls.2018.00357.
- T. Cardona, A fresh look at the evolution and diversification of photochemical reaction centers, Photosynth. Res., 2015, 126, 111–134, DOI:10.1007/s11120-014-0065-x.
- B. W. Matthews and R. E. Fenna, Structure of a green bacteriochlorophyll protein, Acc. Chem. Res., 1980, 13, 309–317, DOI:10.1021/ar50153a003.
- Y. F. Li, W. L. Zhou, R. E. Blankenship and J. P. Allen, Crystal structure of the bacteriochlorophyll a protein from Chlorobium tepidum, J. Mol. Biol., 1997, 271, 456–471, DOI:10.1006/jmbi.1997.1189.
- J. Wen, H. Zhang, M. L. Gross and R. E. Bankenship, Membrane orientation of the FMO antenna protein from Chlorobaculum tepidum as determined by mass spectrometry-based footprinting, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16134–16139, DOI:10.1073/pnas.0901691106.
- J. Wen, H. Zhang, M. L. Gross and R. E. Blankenship, Native electrospray mass spectrometry reveals the nature and stoichiometry of pigments in the FMO antenna protein, Biochemistry, 2011, 50, 3502–3511, DOI:10.1021/bi200239k.
- E. L. Read, G. S. Schlau-Cohen, G. S. Engel, J. Z. Wen, R. E. Blankenship and G. R. Fleming, Visualization of excitonic structure in the Fenna-Matthews-Olson photosynthetic complex by polarization-dependent two-dimensional electronic spectroscopy, Biophys. J., 2008, 95, 847–856, DOI:10.1529/biophysj.107.128199.
- W. F. Humphrey, A. Dalke and K. Schulten, VMD – Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38, DOI:10.1016/0263-7855(96)00018-5.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Lessons from nature about solar light harvesting, Nat. Chem., 2011, 3, 763–774, DOI:10.1038/nchem.1145.
- W. Kühlbrandt, D. N. Wang and Y. Fujiyoshi, Atomic model of plant light-harvesting complex by electron crystallography, Nature, 1994, 367, 614–621, DOI:10.1038/367614a0.
- R. J. Cogdell, A. Gall and J. Köhler, The architecture and function of the light-harvesting apparatus of purple bacteria: from single molecules to in vivo membranes, Q. Rev. Biophys., 2006, 39, 227–324, DOI:10.1017/S0033583506004434.
- G. McDermott, S. Prince and A. Freer, et al., Crystal-Structure of an Integral Membrane light-harvesting complex from photosynthetic bacteria, Nature, 1995, 374, 517–521, DOI:10.1038/374517a0.
- S. Bahatyrova, R. Frese and C. Siebert, et al., The native architecture of a photosynthetic membrane, Nature, 2004, 430, 1058–1062, DOI:10.1038/nature02823.
- Y. Umena, K. Kawakami, J. R. Shen and N. Kamiya, Crystal structure of oxygen-evolving Photosystem II at a resolution of 1.9 Å, Nature, 2011, 473, 55–60, DOI:10.1038/nature09913.
- B. A. Diner and F. Rappaport, Structure, dynamics, and energetics of the
primary photochemistry of Photosystem II of oxygenic photosynthesis, Annu. Rev. Plant Biol., 2002, 53, 551–580, DOI:10.1146/annurev.arplant.53.100301.135238.
- C. Kirmaier, D. Holten and W. W. Parson, Picosecond-photodichroism studies of the transient states in Rhodopseudomonas sphaeroides reaction centers at 5 K. Effects of electron transfer on the six bacteriochlorin pigments, Biochim. Biophys. Acta, Bioenerg., 1985, 810, 49–61, DOI:10.1016/0005-2728(85)90205-1.
- N. Tamai and H. Miyasaka, Ultrafast Dynamics of Photochromic Systems, Chem. Rev., 2000, 100, 1875–1890, DOI:10.1021/cr9800816.
- A. H. Zewail, Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond Using Ultrafast Lasers (Nobel Lecture), Angew. Chem., Int. Ed., 2000, 39, 2586–2631, DOI:10.1002/1521-3773(20000804)39:15<2586::AID-ANIE2586>3.0.CO;2-O.
- G. R. Fleming and R. V. Grondelle, Femtosecond spectroscopy of photosynthetic light-harvesting systems, Curr. Opin. Struct. Biol., 1997, 7, 738–748, DOI:10.1016/S0959-440X(97)80086-3.
- R. Berera, R. van Grondelle and J. T. M. Kennis, Ultrafast transient absorption spectroscopy: principles and application to photosynthetic systems, Photosynth. Res., 2009, 101, 105–118, DOI:10.1007/s11120-009-9454-y.
- D. Zigmantas, T. Polívka, P. Persson and V. Sundström, Ultrafast laser spectroscopy uncovers mechanisms of light energy conversion in photosynthesis and sustainable energy materials, Chem. Phys. Rev., 2022, 3, 041303, DOI:10.1063/5.0092864.
- R. van Grondelle and V. I. Novoderezhkin, Energy transfer in photosynthesis: experimental insights and quantitative models, Phys. Chem. Chem. Phys., 2006, 8, 793–807, 10.1039/B514032C.
- M. H. Vos and J.-L. Martin, Femtosecond processes in proteins, Biochim. Biophys. Acta, Bioenerg., 1999, 1411, 1–20, DOI:10.1016/S0005-2728(99)00035-3.
- H. van Amerongen and R. Croce, Light harvesting in photosystem II, Photosynth. Res., 2013, 116, 251–263, DOI:10.1007/s11120-013-9824-3.
- S. Hess, E. Akesson, R. Cogdell, T. Pullerits and V. Sundström, Energy transfer in spectrally inhomogeneous light-harvesting pigment-protein complexes of purple bacteria, Biophys. J., 1995, 69, 2211–2225, DOI:10.1016/S0006-3495(95)80137-2.
- J. L. Herek, et al., B800 lightarrow B850 Energy Transfer Mechanism in Bacterial LH2 Complexes Investigated by B800 Pigment Exchange, Biophys. J., 2000, 78, 2590–2596, DOI:10.1016/S0006-3495(00)76803-2.
- S. Vasil'ev, P. Orth, A. Zouni, T. G. Owens and D. Bruce, Excited-state dynamics in photosystem II: Insights from the x-ray crystal structure, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 8602–8607, DOI:10.1073/pnas.141239598.
- J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer, 2006 Search PubMed.
- A. J. Campillo and S. L. Shapiro, Picosecond fluorescence studies of exciton migration and annihilation in photosynthetic systems. a review, Photochem. Photobiol., 1978, 28, 975–989, DOI:10.1111/j.1751-1097.1978.tb07736.x.
- C. E. Swenberg, N. E. Geacintov and J. Breton, Laser pulse excitation studies of the fluorescence of chloroplasts, Photochem. Photobiol., 1978, 28, 999–1006, DOI:10.1111/j.1751-1097.1978.tb07738.x.
- V. U. Chukhutsina, A. R. Holzwarth and R. Croce, Time-resolved fluorescence measurements on leaves: principles and recent developments, Photosynth. Res., 2019, 140, 355–369, DOI:10.1007/s11120-018-0607-8.
- S. Vasil'ev, S. Wiebe and D. Bruce, Non-photochemical quenching of chlorophyll fluorescence in photosynthesis. 5-Hydroxy-1,4-naphthoquinone in spinach thylakoids as a model for antenna based quenching mechanisms, Biochim. Biophys. Acta, Bioenerg., 1998, 1363, 147–156, DOI:10.1016/S0005-2728(97)00096-0.
- C. D. van der Weij-de Wit, J. A. Ihalainen, R. van Grondelle and J. P. Dekker, Excitation energy transfer in native and unstacked thylakoid membranes studied by low temperature and ultrafast fluorescence spectroscopy, Photosynth. Res., 2007, 93, 173–182, DOI:10.1007/s11120-007-9157-1.
- B. Gobets and R. van Grondelle, Energy transfer and trapping in photosystem I, Biochim. Biophys. Acta, Bioenerg., 2001, 1507, 80–99, DOI:10.1016/S0005-2728(01)00203-1.
- R. van Grondelle, Excitation energy transfer, trapping and annihilation in photosynthetic systems, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 147–195, DOI:10.1016/0304-4173(85)90017-5.
- C. Ruckebusch, M. Sliwa, P. Pernot, A. de Juan and R. Tauler, Comprehensive data analysis of femtosecond transient absorption spectra: A review, J. Photochem. Photobiol., C, 2012, 13, 1–27, DOI:10.1016/j.jphotochemrev.2011.10.002.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Global and target analysis of time-resolved spectra, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104, DOI:10.1016/j.bbabio.2004.04.011.
- A. R. Holzwarth in Biophysical Techniques in Photosynthesis, ed. J. Amesz and A. J. Hoff, Springer, Netherlands, 1996, pp. 75–92 Search PubMed.
- M. Chachisvilis, T. Pullerits, M. R. Jones, C. N. Hunter and V. Sundström, Vibrational dynamics in the light-harvesting complexes of the photosynthetic bacterium Rhodobacter sphaeroides, Chem. Phys. Lett., 1994, 224, 345–354, DOI:10.1016/0009-2614(94)00560-5.
- M. H. Vos, M. R. Jones, C. N. Hunter, J. Breton and J. L. Martin, Coherent nuclear dynamics at room temperature in bacterial reaction centers, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12701–12705, DOI:10.1073/pnas.91.26.12701.
- R. Agarwal, et al., Ultrafast Energy Transfer in LHC-II Revealed by Three-Pulse Photon Echo Peak Shift Measurements, J. Phys. Chem. B, 2000, 104, 2908–2918, DOI:10.1021/jp9915578.
- V. Novoderezhkin, R. Monshouwer and R. van Grondelle, Electronic and Vibrational Coherence in the Core Light-Harvesting Antenna of Rhodopseudomonas viridis, J. Phys. Chem. B, 2000, 104, 12056–12071, DOI:10.1021/jp001881z.
- V. I. Novoderezhkin, et al., Coherent nuclear and electronic dynamics in primary charge separation in Photosynethetic reaction centers: A Redfield theory approach, J. Phys. Chem. B, 2004, 108, 7445–7457, DOI:10.1021/jp0373346.
- G. R. Fleming and G. D. Scholes, The development and applications of multidimensional biomolecular spectroscopy illustrated by photosynthetic light harvesting, Q. Rev. Biophys., 2024, 57, e11, DOI:10.1017/S003358352400009X.
- D. M. Jonas, Two-Dimensional Femtosecond Spectroscopy, Annu. Rev. Phys. Chem., 2003, 54, 425–463, DOI:10.1146/annurev.physchem.54.011002.103907.
- A. Jha, H.-G. Duan, V. Tiwari, M. Thorwart and R. J. D. Miller, Origin of poor doping efficiency in solution processed organic semiconductors, Chem. Sci., 2018, 9, 4468–4476, 10.1039/c8sc00758f.
- V. Tiwari, et al., Multitype Electronic Interactions in Precursor Solutions of Molecular Doped P3HT Polymer, J. Phys. Chem. B, 2024, 128, 3249–3257, DOI:10.1021/acs.jpcb.4c00584.
- E. Collini and G. D. Scholes, Coherent Intrachain Energy Migration in a Conjugated Polymer at Room Temperature, Science, 2009, 323, 369–373, DOI:10.1126/science.add8943.
- Y. Song, S. N. Clafton, R. D. Pensack, T. W. Kee and G. D. Scholes, Vibrational coherence probes the mechanism of ultrafast electron transfer in polymer–fullerene blends, Nat. Commun., 2014, 5, 4933, DOI:10.1038/ncomms5933.
- A. A. Bakulin, et al., Real-time observation of multiexcitonic states in ultrafast singlet fission using coherent 2D electronic spectroscopy, Nat. Chem., 2016, 8, 16–23, DOI:10.1038/nchem.2371.
- H.-G. Duan, et al., Intermolecular vibrations mediate ultrafast singlet fission, Sci. Adv., 2020, 6, eabb0052, DOI:10.1126/sciadv.abb0052.
- J. M. Richter, et al., Ultrafast carrier thermalization in lead iodide perovskite probed with two-dimensional electronic spectroscopy, Nat. Commun., 2017, 8, 376, DOI:10.1038/s41467-017-00546-z.
- A. Jha, et al., Direct Observation of Ultrafast Exciton Dissociation in Lead Iodide Perovskite by 2D Electronic Spectroscopy, ACS Photonics, 2018, 5, 852–860, DOI:10.1021/acsphotonics.7b01025.
- H.-G. Duan, et al., Photoinduced Vibrations Drive Ultrafast Structural Distortion in Lead Halide Perovskite, J. Am. Chem. Soc., 2020, 142, 16569–16578, DOI:10.1021/jacs.0c03970.
- H. Seiler, et al., Two-dimensional electronic spectroscopy
reveals liquid-like lineshape dynamics in CsPbI3 perovskite nanocrystals, Nat. Commun., 2019, 10, 4962, DOI:10.1038/s41467-019-12830-1.
- F. Novelli, J. O. Tollerud, D. Prabhakaran and J. A. Davis, Persistent coherence of quantum superpositions in an optimally doped cuprate revealed by 2D spectroscopy, Sci. Adv., 2020, 6, eaaw9932, DOI:10.1126/sciadv.aaw9932.
- F. Gerken, T. Posske, S. Mukamel and M. Thorwart, Unique Signatures of Topological Phases in Two-Dimensional THz Spectroscopy, Phys. Rev. Lett., 2022, 129, 017401 CrossRef CAS.
- F. D. Fuller and J. P. Ogilvie, Experimental Implementations of Two-Dimensional Fourier Transform Electronic Spectroscopy, Annu. Rev. Phys. Chem., 2015, 66, 667–690, DOI:10.1146/annurev-physchem-040513-103623.
- S. Biswas, J. Kim, X. Zhang and G. D. Scholes, Coherent Two-Dimensional and Broadband Electronic Spectroscopies, Chem. Rev., 2022, 122, 4257–4321, DOI:10.1021/acs.chemrev.1c00623.
- M. Cho, Coherent Two-Dimensional Optical Spectroscopy, Chem. Rev., 2008, 108, 1331–1418, DOI:10.1021/cr078377b.
- E. Fresch, et al., Two-dimensional electronic spectroscopy, Nat. Rev. Methods Primers, 2023, 3, 84, DOI:10.1038/s43586-023-00277-0.
- F. Milota, J. Sperling, A. Nemeth, T. Mančal and H. F. Kauffmann, Two-Dimensional Electronic Spectroscopy of Molecular Excitons, Acc. Chem. Res., 2009, 42, 1364–1374, DOI:10.1021/ar800282e.
- V. I. Prokhorenko, A. Halpin and R. J. D. Miller, Coherently-controlled two-dimensional photon echo electronic spectroscopy, Opt. Express, 2009, 17, 9764–9779, DOI:10.1364/OE.17.009764.
- M. L. Cowan, J. P. Ogilvie and R. J. D. Miller, Two-dimensional spectroscopy using diffractive optics based phased-locked photon echoes, Chem. Phys. Lett., 2004, 386, 184–189, DOI:10.1016/j.cplett.2004.01.027.
- F. D. Fuller, D. E. Wilcox and J. P. Ogilvie, Pulse shaping based two-dimensional electronic spectroscopy in a background free geometry, Opt. Express, 2014, 22, 1018–1027, DOI:10.1364/OE.22.001018.
- P. Hamm and M. Zanni, Concepts and methods of 2D infrared spectroscopy, Cambridge University Press, 2011 Search PubMed.
- M. F. Gelin, D. Egorova and W. Domcke, Efficient method for the calculation of time- and frequency-resolved four-wave mixing signals and its application to photon-echo spectroscopy, J. Chem. Phys., 2005, 123, 164112, DOI:10.1063/1.2062188.
- J. Cerrillo and J. Cao, Non-Markovian dynamical maps: numerical processing of open quantum trajectories, Phys. Rev. Lett., 2014, 112, 110401 CrossRef PubMed.
- V. May and O. Kuhn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH Press, Weinheim, 2011 Search PubMed.
- V. Chernyak, W. M. Zhang and S. Mukamel, Multidimensional femtosecond spectroscopies of molecular aggregates and semiconductor nanostructures: The nonlinear exciton equations Available, J. Chem. Phys., 1998, 109, 9587 CrossRef.
- M. Schroder, U. Kleinekathofer and M. Schreiber, Calculation of absorption spectra for light-harvesting systems using non-Markovian approaches as well as modified Redfield theory, J. Chem. Phys., 2006, 124, 084903, DOI:10.1063/1.2171188.
- A. Ishizaki and G. R. Fleming, Unified treatment of quantum coherent and incoherent hopping dynamics in electronic energy transfer: Reduced hierarchy equation approach, J. Chem. Phys., 2009, 130, 234110, DOI:10.1063/1.3155372.
- W. M. Zhang, T. Meier, V. Chernyak and S. Mukamel, Exciton-migration and three-pulse femtosecond optical spectroscopies of photosynthetic antenna complexes, J. Chem. Phys., 1998, 108, 7763, DOI:10.1063/1.476212.
- M. Yang and G. R. Fleming, Influence of phonons on exciton transfer dynamics: comparison of the Redfield, Förster, and modified Redfield equations, Chem. Phys., 2002, 275, 355–372, DOI:10.1016/S0301-0104(01)00540-7.
- A. Gelzinis, L. Valkunas, F. D. Fuller, J. P. Ogilvie, S. Mukamel and D. Abramavicius, Tight-binding model of the photosystem
II reaction center: application to two-dimensional electronic spectroscopy, New J. Phys., 2013, 15, 075013 CrossRef.
- V. I. Novoderezhkin, A. G. Yakovlev, R. van Grondelle and V. A. Shuvalov, Coherent Nuclear and Electronic Dynamics in Primary Charge Separation in Photosynthetic Reaction Centers: A Redfield Theory Approach, J. Phys. Chem. B, 2004, 108, 7445, DOI:10.1021/jp0373346.
- Q. Ai, T.-C. Yen, B.-Y. Jin and Y.-C. Cheng, Clustered Geometries Exploiting Quantum Coherence Effects for Efficient Energy Transfer in Light Harvesting, J. Phys. Chem. Lett., 2013, 4, 2577–2584, DOI:10.1021/jz4011477.
- M. Cho, et al., Exciton Analysis in 2D Electronic SpectroscopyCl, J. Phys. Chem. B, 2005, 109, 10542–10556, DOI:10.1021/jp050788d.
- K. L. M. Lewis, F. D. Fuller, J. A. Myers, C. F. Yocum, S. Mukamel, D. Abramavicius and J. P. Ogilvie, Simulations of the Two-Dimensional Electronic Spectroscopy of the Photosystem II Reaction Center, J. Phys. Chem. A, 2013, 117, 34, DOI:10.1021/jp3081707.
- M. Schroder, M. Schreiber and U. Kleinekathofer, A time-dependent modified Redfield theory for absorption spectra applied to light-harvesting systems, J. Lumin., 2007, 125, 126–132, DOI:10.1016/j.jlumin.2006.08.086.
- Y.-H. Hwang-Fu, W. Chen and Y.-C. Cheng, A coherent modified Redfield theory for excitation energy transfer in molecular aggregates, Chem. Phys., 2015, 447, 46 CrossRef.
- H.-P. Breuer, B. Kappler and F. Petruccione, Stochastic wave-function method for non-Markovian quantum master equations, Phys. Rev. A:At., Mol., Opt. Phys., 1999, 59, 1633–1643, DOI:10.1103/PhysRevA.59.1633.
- Y. Yan, Quantum Fokker-Planck theory in a non-Gaussian-Markovian medium, Phys. Rev. A:At., Mol., Opt. Phys., 1998, 58, 2721–2732, DOI:10.1103/PhysRevA.58.2721.
- V. Čápek, Interplay of exciton or electron transfer and relaxation: II. Tokuyama-Mori approach, Phys. A, 1994, 203, 520–532, DOI:10.1016/0378-4371(94)90013-2.
- D. Egorova, M. Thoss, W. Domcke and H. Wang, Modeling of ultrafast electron-transfer processes: Validity of multilevel Redfield theory, J. Chem. Phys., 2003, 119, 2761–2773, DOI:10.1063/1.1587121.
- H. Gzyl, On the equivalence of some exact master equations, J. Stat. Phys., 1981, 26, 803–805, DOI:10.1007/BF01010941.
- F. Shibata, Y. Takahashi and N. Hashitsume, A generalized stochastic liouville equation. Non-Markovian versus memoryless master equations, J. Stat. Phys., 1977, 17, 171–187, DOI:10.1007/BF01040100.
- A. Fuliński, Master equations without time convolution, Phys. Lett. A, 1967, 25, 13–14, DOI:10.1016/0375-9601(67)90312-X.
- A. Fuliński and W. J. Kramarczyk, On the exact master equations, Physica, 1968, 39, 575–592, DOI:10.1016/0031-8914(68)90033-5.
- M. Tokuyama and H. Mori, Statistical-Mechanical Theory of Random Frequency Modulations and Generalized Brownian Motions, Prog. Theor. Phys., 1976, 55, 411–429, DOI:10.1143/PTP.55.411.
- K. Blum, Density Matrix Theory and Applications, Plenum Press, New York, 2nd edn, 1996 Search PubMed.
- V. May and O. Kuhn, Charge and Energy Transfer in Molecular Systems, Wiley-VCH, Berlin, 2nd edn, 2004 Search PubMed.
- U. Kleinekathöfer, Non-Markovian theories based on a decomposition of the spectral density, J. Chem. Phys., 2004, 121, 2505–2514, DOI:10.1063/1.1770619.
- W. T. Pollard and R. A. Friesner, Solution of the Redfield equation for the dissipative quantum dynamics of multilevel systems, J. Chem. Phys., 1994, 100, 5054–5065, DOI:10.1063/1.467222.
- C. Meier and D. J. Tannor, Non-Markovian evolution of the density operator in the presence of strong laser fields, J. Chem. Phys., 1999, 111, 3365–3376, DOI:10.1063/1.479669.
- S. Welack, M. Schreiber and U. Kleinekathöfer, The influence of ultrafast laser pulses on electron transfer in molecular wires studied by a non-Markovian density-matrix approach, J. Chem. Phys., 2006, 124, 044712, DOI:10.1063/1.2162537.
- R. Xu and Y. J. Yan, Theory of open quantum systems, J. Chem. Phys., 2002, 116, 9196–9206, DOI:10.1063/1.1474579.
- Y. J. Yan and R. X. Xu, Quantum mechanics of dissipative systems, Annu. Rev. Phys. Chem., 2005, 56, 187–219, DOI:10.1146/annurev.physchem.55.091602.094425.
- U. Kleinekathofer, Non-Markovian theories based on a decomposition of the spectral density, J. Chem. Phys., 2004, 121, 2505–2514, DOI:10.1063/1.1770619.
- R. Zwanzig, in Statistical mechanics of irreversibility. Lectures in Theoretical Physics (Boulder), ed. W. E. Britten, B. W. Downs and J. Downs, Interscience, New York, 1961, vol. 3, pp. 106–141 Search PubMed.
- M. Morillo and R. I. Cukier, Controlling low-temperature tunneling dynamics with external fields, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 13962–13973, DOI:10.1103/PhysRevB.54.13962.
- Y. Tanimura and R. Kubo, Time Evolution of a Quantum System in Contact with a Nearly Gaussian-Markoffian Noise Bath, J. Phys. Soc. Jpn., 1989, 58, 101–114, DOI:10.1143/JPSJ.58.101.
- A. Ishizaki and Y. Tanimura, Quantum Dynamics of System Strongly Coupled to Low-Temperature Colored Noise Bath: Reduced Hierarchy Equations Approach, J. Phys. Soc. Jpn., 2005, 74, 3131–3134, DOI:10.1143/JPSJ.74.3131.
- M. Tanaka and Y. Tanimura, Quantum Dissipative Dynamics of Electron Transfer Reaction System: Nonperturbative Hierarchy Equations Approach, J. Phys. Soc. Jpn., 2009, 78, 073802, DOI:10.1143/JPSJ.78.073802.
- Y. Tanimura, Reduced hierarchy equations of motion approach with Drude plus brownian spectral distribution: probing electron transfer processes by means of two-dimensional correlation spectroscopy, J. Chem. Phys., 2012, 137, 22A550, DOI:10.1063/1.4766931.
- G. R. Fleming, V. Y. Chernyak and A. Ishizaki, Tribute to Yoshitaka Tanimura, J. Phys. Chem. B, 2021, 125, 11785–11786, DOI:10.1021/acs.jpcb.1c08551.
- A. Ishizaki and G. R. Fleming, Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17255–17260, DOI:10.1073/pnas.0908989106.
- L. Chen, R. Zheng, Q. Shi and Y. Yan, Two-dimensional electronic spectra from the hierarchical equations of motion method: Application to model dimers, J. Chem. Phys., 2010, 132, 024505, DOI:10.1063/1.3293039.
- D. Hou, R. Wang, X. Zheng, N. Tong, J. Wei and Y. J. Yan, Hierarchical Equations of Motion for an Impurity Solver in Dynamical Mean-Field Theory, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 045141, DOI:10.1103/PhysRevB.90.045141.
- Q. Shi, L. Chen, G. Nan, R.-X. Xu and Y. J. Yan, Efficient hierarchical Liouville space propagator to quantum dissipative dynamics, J. Chem. Phys., 2009, 130, 084105, DOI:10.1063/1.3077918.
- D. Suess, A. Eisfeld and W. T. Strunz, Hierarchy of Stochastic Pure States for Open Quantum System Dynamics, Phys. Rev. Lett., 2014, 113, 150403, DOI:10.1103/PhysRevLett.113.150403.
- D. Suess, W. T. Strunz and A. Eisfeld, Hierarchical Equations for Open System Dynamics in Fermionic and Bosonic Environments, J. Stat. Phys., 2015, 159, 1408–1423, DOI:10.1007/s10955-015-1236-7.
- X. Gao, J. Ren, A. Eisfeld and Z. Shuai, Non-Markovian stochastic Schrödinger equation: Matrix-product-state approach to the hierarchy of pure states, Phys. Rev. A, 2022, 105, L030202, DOI:10.1103/PhysRevA.105.L030202.
- S. Flannigan, F. Damanet and A. J. Daley, Many-Body Quantum State Diffusion for Non-Markovian Dynamics in Strongly Interacting Systems, Phys. Rev. Lett., 2022, 128, 063601, DOI:10.1103/PhysRevLett.128.063601.
- J. M. Moix and J. Cao, A hybrid stochastic hierarchy equations of motion approach to treat the low temperature dynamics of non-Markovian open quantum systems, J. Chem. Phys., 2013, 139, 134106 CrossRef PubMed.
- C. Hsieh and J. Cao, A unified stochastic formulation of dissipative quantum dynamics. I. Generalized hierarchical equations, J. Chem. Phys., 2018, 148, 014103 CrossRef.
- L. Varvelo, J. K. Lynd and D. I. G. Bennett, Formally exact simulations of mesoscale exciton dynamics in molecular materials, Chem. Sci., 2021, 12, 9704–9711, 10.1039/D1SC01448J.
- L. Varvelo, J. K. Lynd, B. Citty, O. Kühn and D. I. G. B. Raccah, Formally Exact Simulations of Mesoscale Exciton Diffusion in a Light-Harvesting 2 Antenna Nanoarray, J. Phys. Chem. Lett., 2023, 14, 3077–3083, DOI:10.1021/acs.jpclett.3c00086.
- Y. Zhao, The hierarchy of Davydov's Ansaetze: from guesswork to numerically “exact” many-body wave functions, J. Chem. Phys., 2023, 158, 080901, DOI:10.1063/5.0140002.
- Y. Zhao, K. Sun, L. Chen and M. Gelin, The hierarchy of Davydov's Ansaetze and its applications, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1589, DOI:10.1002/wcms.1589.
- J. Ye, K. Sun, Y. Zhao, Y. Yu, C. K. Lee and J. Cao, Excitonic energy transfer in light-harvesting complexes in purple bacteria, J. Chem. Phys., 2012, 136, 245104, DOI:10.1063/1.4729786.
- K. Sun, Y. Yu and Y. Zhao, Path induced coherent energy transfer in light-harvesting complexes in purple bacteria, J. Chem. Phys., 2014, 141, 124103, DOI:10.1063/1.4895791.
- A. Somoza, L. Chen, K. Sun and Y. Zhao, Probing ultrafast excitation energy transfer of the chlorosome with exciton-phonon variational dynamics, Phys. Chem. Chem. Phys., 2016, 18, 20298–20311, 10.1039/C5CP06491K.
- F. Zheng, L. Chen, J. Gao and Y. Zhao, Fully Quantum Modeling of Exciton Diffusion in Mesoscale Light Harvesting Systems, Materials, 2021, 14, 3291, DOI:10.3390/ma14123291.
- L. Chen, M. Gelin, W. Domcke and Y. Zhao, Theory of femtosecond coherent double-pump single-molecule spectroscopy: application to light harvesting complexes, J. Chem. Phys., 2015, 142, 164106, DOI:10.1063/1.4919240.
- L. Chen, M. Gelin, W. Domcke and Y. Zhao, Simulation of Femtosecond Phase-Locked Double-Pump Signals of Individual Light-Harvesting Complexes LH2, J. Phys. Chem. Lett., 2018, 9, 4488, DOI:10.1021/acs.jpclett.8b01887.
- N. Makri, Improved Feynman propagators on a grid and nonadiabatic corrections within the path integral framework, Chem. Phys. Lett., 1992, 193, 435–444, DOI:10.1016/0009-2614(92)85654-S.
- N. Makri and D. E. Makarov, Tensor propagator for iterative quantum time evolution of reduced density matrices. I. Theory, J. Chem. Phys., 1995, 102, 4600–4610, DOI:10.1063/1.469508.
- N. Makri and D. E. Makarov, Tensor propagator for iterative quantum time evolution of reduced density matrices. II. Numerical methodology, J. Chem. Phys., 1995, 102, 4611–4618, DOI:10.1063/1.469509.
- J. Shao and N. Makri, Iterative path integral formulation of equilibrium correlation functions for quantum dissipative systems, J. Chem. Phys., 2002, 116, 507–514, DOI:10.1063/1.1423936.
- J. Shao and N. Makri, Iterative path integral calculation of quantum correlation functions for dissipative systems, Chem. Phys., 2001, 268, 1–10, DOI:10.1016/S0301-0104(01)00286-5.
- J. Eckel, J. H. Reina and M. Thorwart, Coherent control of an effective two-level system in a non-Markovian biomolecular environment, New J. Phys., 2009, 11, 085001 CrossRef.
- M. Thorwart, P. Reimann and P. Hänggi, Iterative algorithm versus analytic solutions of the parametrically driven dissipative quantum harmonic oscillator, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5808, DOI:10.1103/PhysRevE.62.5808.
- H.-G. Duan, A. G. Dijkstra, P. Hänggi and M. Thorwart, Efficient tool to calculate two-dimensional optical spectra for photoactive molecular complexes, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042708, DOI:10.1103/PhysRevE.92.042708.
- N. Makri, Small matrix disentanglement of the path integral: Overcoming the ex-ponential tensor scaling with memory length, J. Chem. Phys., 2020, 152, 041104 CrossRef CAS PubMed.
- N. Makri, Small Matrix Path Integral with Extended Memory, J. Chem. Theory Comput., 2021, 17, 1–6 CrossRef CAS PubMed.
- A. Strathearn, P. Kirton, D. Kilda, J. Keeling and B. W. Lovett, Efficient non-Markovian quantum dynamics using time-evolving matrix product operators, Nat. Commun., 2018, 9, 3322 CrossRef CAS PubMed.
- F. Otterpohl, P. Nalbach and M. Thorwart, Hidden phase of the spin-boson model, Phys. Rev. Lett., 2022, 129, 120406 CrossRef CAS PubMed.
- R. de Wit, J. Keeling, B. W. Lovett and A. W. Chin, Phys. Rev. Res., 2025, 7, 013209 CrossRef CAS.
- F. Otterpohl, D. Keefer, S. Mukamel and M. Thorwart, Coherent ultrafast stimulated x-ray Raman spectroscopy of dissipative conical intersections, Phys. Rev. Lett., 2024, 133, 098001 CrossRef CAS.
- E. Cignoni, V. Slama, L. Cupellini and B. Mennucci, The Atomistic Modeling of Light-Harvesting Complexes from the Physical Models to the Computational Protocol, J. Chem. Phys., 2022, 156, 120901, DOI:10.1063/5.0086275.
- A. Damjanović, I. Kosztin, U. Kleinekathöfer and K. Schulten, Excitons in a photosynthetic light-harvesting system: a combined molecular dynamics, quantum chemistry, and polaron model study, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031919, DOI:10.1103/PhysRevE.65.031919.
- S. Maity and U. Kleinekathöfer, Recent Progress in Atomistic Modeling of Light-Harvesting Complexes: A Mini Review, Photosynth. Res., 2023, 156, 147–162, DOI:10.1007/s11120-022-00969-w.
- J. Moix, J. Wu, P. Huo, D. Coker and J. Cao, Efficient energy transfer in light-harvesting systems, III: The influence of the eighth bacteriochlorophyll on the dynamics and efficiency in FMO, J. Phys. Chem. Lett., 2011, 2, 3045–3052 CrossRef CAS.
- P. Huo and D. F. Coker, Communication: Partial linearized density matrix dynamics for dissipative, non-adiabatic quantum evolution, J. Chem. Phys., 2011, 135, 201101 Search PubMed.
- M. K. Lee, P. Huo and D. F. Coker, Semiclassical path integral dynamics: Photosynthetic energy transfer with realistic environment interactions, Annu. Rev. Phys. Chem., 2016, 67, 639 CrossRef CAS PubMed.
- P. Huo and D. F. Coker, Iterative linearized density matrix propagation for modeling coherent excitation energy transfer in photosynthetic light harvesting, J. Chem. Phys., 2010, 133, 184108 CrossRef CAS.
- J. Gao, W. J. Shi, J. Ye, X. Wang, H. Hirao and Y. Zhao, QM/MM Modeling of Environmental Effects on Electronic Transitions of the FMO Complex, J. Phys. Chem. B, 2013, 117, 3488–3495, DOI:10.1021/jp3109418.
- F. Zheng, M. Jin, T. Mancal and Y. Zhao, Study of Electronic Structures and Pigments-Protein Interactions in the Reaction Center of Thermochromatium Tepidum with a Dynamic Environment, J. Phys. Chem. B, 2016, 120, 10046–10058, DOI:10.1021/acs.jpcb.6b06628.
- F. Müh, D. Lindorfer, M. Schmidt Am Busch and T. Renger, Towards a structure-based exciton Hamiltonian for the CP29 antenna of photosystem II, Phys. Chem. Chem. Phys., 2014, 16, 11848–11863, 10.1039/C3CP55166K.
- F. Segatta, L. Cupellini, S. Jurinovich, S. Mukamel, M. Dapor, S. Taioli, M. Garavelli and B. Mennucci, A Quantum Chemical Interpretation of Two-Dimensional Electronic Spectroscopy of Light-Harvesting Complexes, J. Am. Chem. Soc., 2017, 139, 7558–7567, DOI:10.1021/jacs.7b02130.
- M. K. Lee and D. F. Coker, Modeling Electronic-Nuclear Interactions for Excitation Energy Transfer Processes in Light-Harvesting Complexes, J. Phys. Chem. Lett., 2016, 7, 3171–3178, DOI:10.1021/acs.jpclett.6b01440.
- M. K. Lee, K. B. Bravaya and D. F. Coker, First-Principles Models for Biological Light-Harvesting: Phycobiliprotein Complexes from Cryptophyte Algae, J. Am. Chem. Soc., 2017, 139, 7803 Search PubMed.
- X. Wang, G. Ritschel, S. Wuster and A. Eisfeld, Open quantum system parameters for light harvesting complexes from molecular dynamics, Phys. Chem. Chem. Phys., 2015, 17, 25629–25641, 10.1039/C5CP03891J.
- C. Olbrich and U. Kleinekathöfer, Time-Dependent Atomistic View on the Electronic Relaxation in Light-Harvesting System II, J. Phys. Chem. B, 2010, 114, 12427–12437, DOI:10.1021/jp106542v.
- S. Maity, B. M. Bold, J. D. Prajapati, M. Sokolov, T. Kubar, M. Elstner and U. Kleinekathöfer, DFTB/MM Molecular Dynamics Simulations of the FMO Light-Harvesting Complex, J. Phys. Chem. Lett., 2020, 11, 8660–8667, DOI:10.1021/acs.jpclett.0c02526.
- S. Maity, V. Daskalakis, M. Elstner and U. Kleinekathöfer, Multiscale QM/MM Molecular Dynamics Simulations of the Trimeric Major Light-Harvesting Complex II, Phys. Chem. Chem. Phys., 2021, 23, 7407–7417, 10.1039/D1CP01011E.
- S. Maity, P. Sarngadharan, V. Daskalakis and U. Kleinekathöfer, Time-Dependent Atomistic Simulations of the CP29 Light-Harvesting Complex, J. Chem. Phys., 2021, 155, 055103, DOI:10.1063/5.0053259.
- P. Sarngadharan, S. Maity and U. Kleinekathöfer, Spectral Densities and Absorption Spectra of the Core Antenna Complex CP43 from Photosystem II, J. Chem. Phys., 2022, 156, 215101, DOI:10.1063/5.0091005.
- P. Sarngadharan, Y. Holtkamp and U. Kleinekathöfer, Protein Effects on the Excitation Energies and Exciton Dynamics of the CP24 Antenna Complex, J. Phys. Chem. B, 2024, 128, 5201–5217, DOI:10.1021/acs.jpcb.4c01637.
- J. Schulze and O. Kühn, Explicit Correlated Exciton-Vibrational Dynamics of the FMO Complex, J. Phys. Chem. B, 2015, 119, 6211 CrossRef.
- M. F. Shibl, J. Jan Schulze, M. Al-Marri and O. Kühn, Multilayer-MCTDH approach to the energy transfer dynamics in the LH2 antenna complex, J. Phys. B:At., Mol. Opt. Phys., 2017, 50, 184001 CrossRef.
- A. Eisfeld and J. S. Briggs, The J-and H-bands of organic dye aggregates, Chem. Phys., 2006, 324, 376–384 CrossRef.
- A. Eisfeld, L. Braun, W. T. Strunz, J. S. Briggs, J. Beck and V. Engel, Vibronic energies and spectra of molecular dimers, J. Chem. Phys., 2005, 122, 134103 CrossRef PubMed.
- P. Kjellberg, B. Brüggemann and T. Pullerits, Two-dimensional electronic spectroscopy of an excitonically coupled dimer, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 74, 024303 CrossRef.
- A. Halpin, P. Johnson and R. Tempelaar, et al., Two-dimensional spectroscopy of a molecular dimer unveils the effects of vibronic coupling on exciton coherences, Nat. Chem., 2014, 6, 196–201, DOI:10.1038/nchem.1834.
- H.-G. Duan, P. Nalbach, V. I. Prokhorenko, S. Mukamel and M. Thorwart, On the origin of oscillations in two-dimensional spectra of excitonically-coupled molecular systems, New J. Phys., 2015, 17, 072002 CrossRef.
- M. Ferretti, V. I. Novoderezhkin, E. Romero, R. Augulis, A. Pandit, D. Zigmantas and R. van Grondelle, The nature of coherences in the B820 bacteriochlorophyll dimer revealed by two-dimensional electronic spectroscopy, Phys. Chem. Chem. Phys., 2014, 16, 9930–9939, 10.1039/C3CP54634A.
- P. Kjellberg, B. Brüggemann and T. Pullerits, Two-dimensional electronic spectroscopy of an excitonically coupled dimer, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 74, 024303, DOI:10.1103/PhysRevB.74.024303.
- C. Kreisbeck and T. Kramer, Long-Lived Electronic Coherence in Dissipative Exciton Dynamics of Light-Harvesting Complexes, J. Phys. Chem. Lett., 2012, 3, 2828–2833, DOI:10.1021/jz3012029.
- A. Chenu, N. Christensson and H. Kauffmann, et al., Enhancement of Vibronic and Ground-State Vibrational Coherences in 2D Spectra of Photosynthetic Complexes, Sci. Rep., 2013, 3, 2029, DOI:10.1038/srep02029.
- R. Tempelaar, T. I. Jansen and J. Knoester, Vibrational beatings conceal evidence of electronic coherence in the FMO light-harvesting complex, J. Phys. Chem. B, 2014, 118, 12865–12872, DOI:10.1021/jp510074q.
- J. Xu, H.-D. Zhang, R.-X. Xu and Y. Yan, Correlated driving and dissipation in two-dimensional spectroscopy, J. Chem. Phys., 2013, 138, 024106, DOI:10.1063/1.4773472.
- M. B. Plenio, J. Almeida and S. F. Huelga, Origin of long-lived oscillations in 2D-spectra of a quantum vibronic model: Electronic versus vibrational coherence, J. Chem. Phys., 2013, 139, 235102, DOI:10.1063/1.4846275.
- H.-G. Duan, M. Thorwart and R. J. D. Miller, Does electronic coherence enhance anticorrelated pigment vibrations under realistic conditions?, J. Chem. Phys., 2019, 151, 114115, DOI:10.1063/1.5119248.
- S. Yeh, R. D. Hoehn, M. A. Allodi, G. S. Engel and S. Kais, Elucidation of near-resonance vibronic coherence lifetimes by nonadiabatic electronic-vibrational state character mixing, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18263–18268, DOI:10.1073/pnas.1701390115.
- T. Brixner, J. Stenger and H. Vaswani, et al., Two-dimensional spectroscopy of electronic couplings in photosynthesis, Nature, 2005, 434, 625–628, DOI:10.1038/nature03429.
- G. S. Schlau-Cohen, T. R. Calhoun, G. S. Engel, E. L. Read, N. S. Ginsberg, D. Zigmantas, R. Bassi and G. R. Fleming, Pathways of Energy Flow in LHCII from Two-Dimensional Electronic Spectroscopy, J. Phys. Chem. B, 2009, 113, 15352 CrossRef PubMed.
- H.-G. Duan, A. L. Stevens, P. Nalbach, M. Thorwart, V. I. Prokhorenko and R. J. D. Miller, Two-dimensional Electronic Spectroscopy of Light Harvesting Complex II at Ambient Temperature: A Joint Experimental and Theoretical Study, J. Phys. Chem. B, 2015, 119, 12017–12027, DOI:10.1021/acs.jpcb.5b05592.
- Z. Zhang, P. Lambrev and K. Wells, et al., Direct observation of multistep energy transfer in LHCII with fifth-order 3D electronic spectroscopy, Nat. Commun., 2015, 6, 7914, DOI:10.1038/ncomms8914.
- E. A. Arsenault, Y. Yoneda and M. Iwai, et al., Vibronic mixing enables ultrafast energy flow in light-harvesting complex II, Nat. Commun., 2020, 11, 1460, DOI:10.1038/s41467-020-14970-1.
- X. Leng, Y.-M. Yan, R.-D. Zhu, K. Song, Y.-X. Weng and Q. Shi, Simulation of the Two-Dimensional Electronic Spectroscopy and Energy Transfer Dynamics of Light-Harvesting Complex II at Ambient Temperature, J. Phys. Chem. B, 2018, 122, 4642–4652, DOI:10.1021/acs.jpcb.8b00674.
- D. Zigmantas, E. L. Read, T. Mančal, T. Brixner, A. T. Gardiner, R. J. Cogdell and G. R. Fleming, Two-dimensional electronic spectroscopy of the B800–B820 light-harvesting complex, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12672–12677, DOI:10.1073/pnas.0602961103.
- E. Harel, P. D. Long and G. S. Engel, Single-shot ultrabroadband two-dimensional electronic spectroscopy of the light-harvesting complex LH2, Opt. Lett., 2011, 36, 1665–1667, DOI:10.1364/OL.36.001665.
- R. Hildner, D. Brinks, J. B. Nieder, R. J. Cogdell and N. F. van Hulst, Quantum Coherent Energy Transfer over Varying Pathways in Single Light-Harvesting Complexes, Science, 2013, 340, 1448–1451, DOI:10.1126/science.1235820.
- E. Harel and G. S. Engel, Quantum coherence spectroscopy reveals complex dynamics in bacterial light-harvesting complex 2 (LH2), Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 706–711 CrossRef PubMed.
- M. Maiuri, et al., Ultra-broadband 2D electronic spectroscopy of carotenoid-bacteriochlorophyll interactions in the LH1 complex of a purple bacterium, J. Chem. Phys., 2015, 142, 212433, DOI:10.1063/1.4919056.
- P. D. Dahlberg, A. F. Fidler, J. R. Caram, P. D. Long and G. S. Engel, Energy Transfer Observed in Live Cells Using Two-Dimensional Electronic Spectroscopy, J. Phys. Chem. Lett., 2013, 4, 3636–3640, DOI:10.1021/jz401944q.
- T. Kunsel, V. Tiwari, Y. A. Matutes, A. T. Gardiner, R. J. Cogdell, J. P. Ogilvie and T. L.
C. Jansen, Simulating Fluorescence-Detected Two-Dimensional Electronic Spectroscopy of Multichromophoric System, J. Phys. Chem. B, 2019, 123, 394–406, DOI:10.1021/acs.jpcb.8b10176.
- M. Ferretti, R. Hendrikx and E. Romero, et al., Dark States in the Light-Harvesting complex 2 Revealed by Two-dimensional Electronic Spectroscopy, Sci. Rep., 2016, 6, 20834, DOI:10.1038/srep20834.
- O. Rancova and D. Abramavicius, Static and Dynamic Disorder in Bacterial Light-Harvesting Complex LH2: A 2DES Simulation Study, J. Phys. Chem. B, 2014, 118, 7533–7540, DOI:10.1021/jp5043156.
- J. A. Myers, K. L. M. Lewis, F. D. Fuller, P. F. Tekavec, C. F. Yocum and J. P. Ogilvie, Two dimensional electronic spectroscopy of the D1-D2-cytb559 photosystem II reaction center complex, J. Phys. Chem. Lett., 2010, 1, 2774, DOI:10.1021/jz100972z.
- V. I. Novoderezhkin, E. Romero and R. van Grondelle, How exciton-vibrational coherences control charge separation in the photosystem II reaction center, Phys. Chem. Chem. Phys., 2015, 17, 30828–30841, 10.1039/C5CP00582E.
- V. I. Novoderezhkin, E. G. Andrizhiyevskaya, J. P. Dekker and R. van Grondelle, Pathways and timescales of primary charge separation in the photosystem II reaction center as revealed by a simultaneous fit of time-resolved fluorescence and transient absorption, Biophys. J., 2005, 89, 1464–1481, DOI:10.1529/biophysj.105.060020.
- V. I. Novoderezhkin, J. P. Dekker and R. van Grondelle, Mixing of Exciton and Charge-Transfer States in Photosystem II Reaction Centers: Modeling of Stark Spectra with Modified Redfield Theory, Biophys. J., 2007, 93, 1293–1311, DOI:10.1529/biophysj.106.096867.
- E. Romero, I. H. M. van Stokkum, V. I. Novoderezhkin, J. P. Dekker and R. van Grondelle, Two different charge separation pathways in photosystem II, Biochemistry, 2010, 49, 4300–4307, DOI:10.1021/bi1003926.
- F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavicius and J. P. Ogilvie, Vibronic coherence in oxygenic photosynthesis, Nat. Chem., 2014, 6, 706–711, DOI:10.1038/nchem.2005.
- H. H. Nguyen, et al., Charge separation in the photosystem II reaction center resolved by multispectral two-dimensional electronic spectroscopy, Sci. Adv., 2023, 9, eade7190, DOI:10.1126/sciadv.ade7190.
- Y. Silori, R. Willow, H. H. Nguyen, G. Shen, Y. Song, C. J. Gisriel, G. W. Brudvig, D. A. Bryant and J. P. Ogilvie, Two-Dimensional Electronic Spectroscopy of the Far-Red-Light Photosystem II Reaction Center, J. Phys. Chem. Lett., 2023, 14, 10300–10308, DOI:10.1021/acs.jpclett.3c02604.
- D. Paleček, et al., Quantum coherence as a witness of vibronically hot energy transfer in bacterial reaction center, Sci. Adv., 2017, 3, e1603141, DOI:10.1126/sciadv.1603141.
- A. Niedringhaus, V. R. Policht, R. Sechrist, A. Konar, P. D. Laible, D. F. Bocian, D. Holten, C. Kirmaier and J. P. Ogilvie, Primary processes in the bacterial reaction center probed by two-dimensional electronic spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3563–3568, DOI:10.1073/pnas.1721927115.
- V. R. Policht, et al., Hidden vibronic and excitonic structure and vibronic coherence transfer in the bacterial reaction center, Sci. Adv., 2022, 8, eabk0953, DOI:10.1126/sciadv.abk0953.
- F. Ma, E. Romero and M. R. Jones, et al., Both electronic and vibrational coherences are involved in primary electron transfer in bacterial reaction center, Nat. Commun., 2019, 10, 933, DOI:10.1038/s41467-019-08751-8.
- A. Konar, et al., Electronic interactions in the bacterial reaction center revealed by two-color 2D electronic spectroscopy, J. Phys. Chem. Lett., 2018, 9, 5219–5225, DOI:10.1021/acs.jpclett.8b02394.
- K. M. Pelzer, et al., Inhomogeneous dephasing masks coherence lifetimes in ensemble measurements, J. Chem. Phys., 2012, 136, 164508 CrossRef PubMed.
- L. Wang, et al., Quantum
coherences reveal excited-state dynamics in biophysical systems, Nat. Rev. Chem., 2019, 3, 477 CrossRef.
- F. Milota, et al., Two-Dimensional Electronic Spectroscopy of Molecular Excitons, Acc. Chem. Res., 2009, 42, 1364 CrossRef CAS PubMed.
- A. Ishizaki and Y. Tanimura, Nonperturbative non-Markovian quantum master equation: Validity and limitation to calculate nonlinear response functions, Chem. Phys., 2008, 347, 185 CrossRef CAS.
- D. Lindorfer, F. Müh, R. Purchase, E. Krausz and T. Renger, Non-conservative circular dichroism of photosystem II reaction centers: Is there an enhancement by a coupling with charge transfer states?, J. Photochem. Photobiol., A, 2021, 404, 112883, DOI:10.1016/j.jphotochem.2020.112883.
- D. Abramavicius and S. Mukamel, Energy-transfer and charge-separation pathways in the reaction center of photosystem II revealed by coherent two-dimensional optical spectroscopy, J. Chem. Phys., 2010, 133, 184501, DOI:10.1063/1.3493580.
- M. Groot, F. van Mourik, C. Eijckelhoff, I. H. M. van Stokkum, J. P. Dekker and R. van Grondelle, Charge separation in the reaction center of photosystem II studied as a function of temperature, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 4389–4394, DOI:10.1073/pnas.94.9.4389.
- R. Zhu, W. Li and Z. Zhen, et al., Quantum phase synchronization via exciton-vibrational energy dissipation sustains long-lived coherence in photosynthetic antennas, Nat. Commun., 2024, 15, 3171, DOI:10.1038/s41467-024-47560-6.
- J.-H. Choi, et al., Quadrupole contribution to the third-order optical activity spectroscopy, J. Chem. Phys., 2007, 127, 024507, DOI:10.1063/1.2750342.
- Z. Liu, et al., Transient chiral dynamics revealed by two-dimensional circular dichroism spectroscopy, Phys. Rev. E, 2023, 107, 054119, DOI:10.1103/PhysRevE.107.054119.
- Z. Liu, et al., Transient Chiral Dynamics in the Fenna–Matthews–Olson Complex Revealed by Two-Dimensional Circular Dichroism Spectroscopy, J. Phys. Chem. Lett., 2024, 15, 6550–6559, DOI:10.1021/acs.jpclett.4c01179.
- Y. Yang, et al., Diverse Transient Chiral Dynamics in Evolutionary Distinct Photosynthetic Reaction Centers, J. Chem. Theory Comput., 2025, 21, 321–332, DOI:10.1021/acs.jctc.4c01469.
- M. Cho, et al., Two-Dimensional Electronic–Vibrational Spectroscopy Reveals Cross-Correlation between Solvation Dynamics and Vibrational Spectral Diffusion, J. Phys. Chem. B, 2020, 124, 11222–11235, DOI:10.1021/acs.jpcb.0c08959.
- T. A. A. Oliver, et al., Correlating the motion of electrons and nuclei with two-dimensional electronic–vibrational spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10061–10066, DOI:10.1073/pnas.1409207111.
- X. Zhang, et al., Disentangling the complexity of coupled vibrations by two-dimensional electronic-vibrational spectroscopy, J. Phys. B: At., Mol. Opt. Phys., 2023, 56, 145001, DOI:10.1088/1361-6455/ace1bb.
- A. Tsargorodska, et al., Strong Coupling of Localized Surface Plasmons to Excitons in Light-Harvesting Complexes, Nano Lett., 2016, 16, 6850–6856, DOI:10.1021/acs.nanolett.6b02661.
- L. E. H. Rodríguez, A. Sindhu, K. J. R. Espinosa and A. A. Kananenka, Cavity-Mediated Enhancement of the Energy Transfer in the Reduced Fenna-Matthews-Olson Complex, J. Chem. Theory Comput., 2024, 20, 7393–7403, DOI:10.1021/acs.jctc.4c00626.
- R. Sáez-Blázquez, et al., Cavity-Modified Exciton Dynamics in Photosynthetic Units, J. Phys. Chem. Lett., 2019, 10, 4252–4258, DOI:10.1021/acs.jpclett.9b01495.
- F. Caruso, et al., Probing biological light-harvesting phenomena by optical cavities, Phys. Rev. A:At., Mol., Opt. Phys., 2012, 85, 125424 CrossRef.
- F. Wu, et al., Optical cavity-mediated exciton dynamics in photosynthetic light harvesting 2 complexes, Nat. Commun., 2022, 13, 6864 CrossRef CAS PubMed.
- A. Debnath, et al., Entangled Biphoton Enhanced Double Quantum Coherence Signal as a Probe for Cavity Polariton Correlations in Presence of Phonon Induced Dephasing, Front. Phys., 2022, 10, 879113 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Fulu Zhengc,
Zihui Liuc,
Shaul Mukameld,
Michael Thorwart
*e,
R. J. Dwayne Miller
*ab,
Fulu Zhengc,
Zihui Liuc,
Shaul Mukameld,
Michael Thorwart
*e,
R. J. Dwayne Miller
 *f and
Hong-Guang Duan
*c
*f and
Hong-Guang Duan
*c

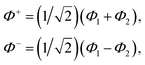
 , where mi, ωi are the mass and frequency of ith mode. Ci is the coupling strength between system and ith mode. Normally, the Ohmic form with an exponential or a Lorentzian type of cutoff is employed in the calculations. They show the form J(ω) = ηω
, where mi, ωi are the mass and frequency of ith mode. Ci is the coupling strength between system and ith mode. Normally, the Ohmic form with an exponential or a Lorentzian type of cutoff is employed in the calculations. They show the form J(ω) = ηω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ω/ωc) and
exp(−ω/ωc) and  . Here η, ωc are the coupling constant and cutoff frequency of the spectral density, the λ and γ are the reorganization energy and cutoff frequency in the Lorentzian type of the spectral density. A more detailed discussion of these spectral forms and their implications is provided in the subsequent section.
. Here η, ωc are the coupling constant and cutoff frequency of the spectral density, the λ and γ are the reorganization energy and cutoff frequency in the Lorentzian type of the spectral density. A more detailed discussion of these spectral forms and their implications is provided in the subsequent section.



![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (t) are defined as
(t) are defined as ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ρ = [μ,ρ] and
ρ = [μ,ρ] and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (t)ρ = e−iHmoltρeiHmolt, respectively. Moreover, the time intervals t1, t2 and t3 are denoted in Fig. 4(a).
(t)ρ = e−iHmoltρeiHmolt, respectively. Moreover, the time intervals t1, t2 and t3 are denoted in Fig. 4(a).
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ±ρ = [μ±,ρ],
±ρ = [μ±,ρ],  , and
, and  . a†m and am are the creation and annihilation operators. The transition dipole moment can be written as
. a†m and am are the creation and annihilation operators. The transition dipole moment can be written as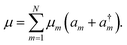
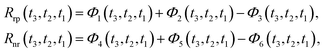
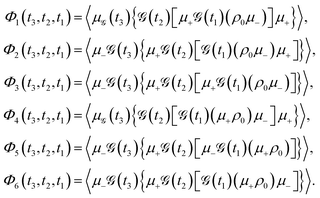
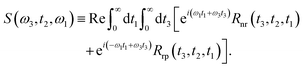
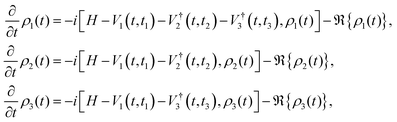
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2(t − tα)2/τp2], τp is the pulse duration. H is the system Hamiltonian, X is the transition dipole coordinate and ℜ is the dissipative superoperator. The calculation of the third-order 2D response involves evaluating the polarization component that propagates along the specified phase-matching direction, as formulated below:
2(t − tα)2/τp2], τp is the pulse duration. H is the system Hamiltonian, X is the transition dipole coordinate and ℜ is the dissipative superoperator. The calculation of the third-order 2D response involves evaluating the polarization component that propagates along the specified phase-matching direction, as formulated below: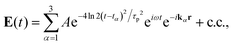
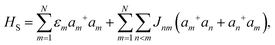
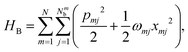
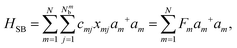
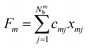 with cmj being the coupling strength between the excitation of molecule m and the j-th mode. The correlation function of the collective bath coordinate Fm is then given by
with cmj being the coupling strength between the excitation of molecule m and the j-th mode. The correlation function of the collective bath coordinate Fm is then given by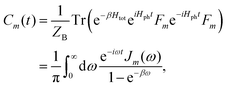
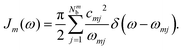
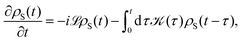
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (τ) = trB{
(τ) = trB{![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBe−i
SBe−i![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (1−P)τ
(1−P)τ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBρB}.
SBρB}.
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρ = [H,ρ], and related forms. The projection operator P is specified as:
ρ = [H,ρ], and related forms. The projection operator P is specified as: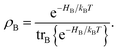
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (τ) ≃ trB{
(τ) ≃ trB{![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBe−i(
SBe−i(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) S+
S+![[script L]](https://www.rsc.org/images/entities/char_e144.gif) B)τ
B)τ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SBρB}.
SBρB}.
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) SτρS(t),
SτρS(t),
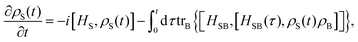
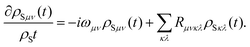
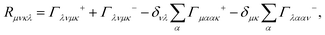
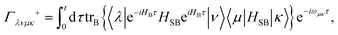



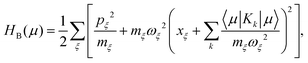

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−βHB(μ)] with β = 1/(kBT). T is the temperature.
exp[−βHB(μ)] with β = 1/(kBT). T is the temperature.



 . With these equations, we obtain the absorption lineshape in the CMRT framework as
. With these equations, we obtain the absorption lineshape in the CMRT framework as
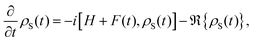
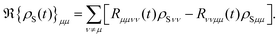
 , where T2 is the transverse relaxation time, T1,
, where T2 is the transverse relaxation time, T1,  are the longitudinal relaxation time and pure dephasing time, respectively. For more specificity,
are the longitudinal relaxation time and pure dephasing time, respectively. For more specificity, 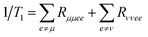 and
and 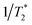 is given by the first derivative of the lineshape function gμμνν(t). Thus, the off-diagonal terms of the excited states and the relaxation between ground and excited states are
is given by the first derivative of the lineshape function gμμνν(t). Thus, the off-diagonal terms of the excited states and the relaxation between ground and excited states are


![[script L]](https://www.rsc.org/images/entities/char_e144.gif) effS = [HS + Hren, •],
effS = [HS + Hren, •], ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k− = −i[Kk, •],
k− = −i[Kk, •], ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k+ = [Kk, •]+,
k+ = [Kk, •]+,

![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) †S(t,t′)ρS(t),
†S(t,t′)ρS(t),
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k− and
k− and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) k+, we define the following operators
k+, we define the following operators


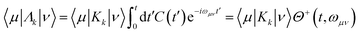


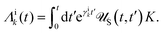

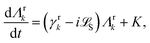
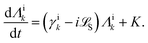

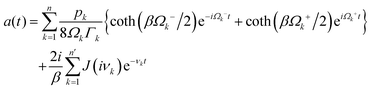

![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) tot = −i[Htot, ρtot] =
tot = −i[Htot, ρtot] = ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρtot.
ρtot.
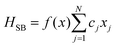 , where f(·) is a real-valued function. Following the Nakajima–Zwanzig projection formalism,152 the dynamics are partitioned into system and bath contributions. The thermal bath is described by the canonical density operator ρeqb = exp(−βHb)/Zb at temperature T, with Zb denoting the bath partition function. The exact formal quantum master equation for the reduced density operator ρS(t) is obtained by applying the projection operator P = ρeqb, trb, with trbρeqb = 1, and its complement Q = 1 − P,147 yielding:
, where f(·) is a real-valued function. Following the Nakajima–Zwanzig projection formalism,152 the dynamics are partitioned into system and bath contributions. The thermal bath is described by the canonical density operator ρeqb = exp(−βHb)/Zb at temperature T, with Zb denoting the bath partition function. The exact formal quantum master equation for the reduced density operator ρS(t) is obtained by applying the projection operator P = ρeqb, trb, with trbρeqb = 1, and its complement Q = 1 − P,147 yielding: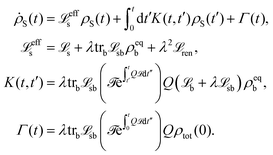
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) s,
s, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sb, and
sb, and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ren correspond to the system, the system–bath interaction, and the reorganization energy contributions, respectively. The effective system Liouvillian is given by
ren correspond to the system, the system–bath interaction, and the reorganization energy contributions, respectively. The effective system Liouvillian is given by ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) effs = −i[HS + Hren, •], while Γ(t) represents the inhomogeneous term arising from the initial density configuration. By performing a first-order expansion of the correlated thermal equilibrium state with respect to the overall coupling strength λ, the expression can be reformulated as:
effs = −i[HS + Hren, •], while Γ(t) represents the inhomogeneous term arising from the initial density configuration. By performing a first-order expansion of the correlated thermal equilibrium state with respect to the overall coupling strength λ, the expression can be reformulated as:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βHtot), Zb = TrB
exp(−βHtot), Zb = TrB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βHb) and Zs = TrS
exp(−βHb) and Zs = TrS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βHS). We take the trace over the system part and we can write
exp(−βHS). We take the trace over the system part and we can write

![[script L]](https://www.rsc.org/images/entities/char_e144.gif) − = −i[HSB, •] and
− = −i[HSB, •] and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) + = [HSB, •]+ − 2χ.
+ = [HSB, •]+ − 2χ. ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the time-ordering operator153 and
is the time-ordering operator153 and 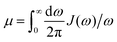 .
.


 and
and 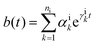 with ni = 2n, nr = 2n + n′ (n′ is the number of Matsubara frequencies). We then define a new set of auxiliary density matrices
with ni = 2n, nr = 2n + n′ (n′ is the number of Matsubara frequencies). We then define a new set of auxiliary density matrices

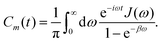
 . The bath correlation function Cm(t) in eqn (77) can be written as a sum of exponentially decaying functions, which shows the form
. The bath correlation function Cm(t) in eqn (77) can be written as a sum of exponentially decaying functions, which shows the form

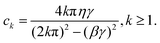
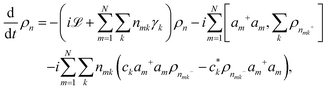
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ρ = [HS,ρ] and HS is the system Hamiltonian with electronic DoFs. The subscript n denotes the set of indices n = {n1, n2, …, nN} = {{n10, n11, …}, …, {nN0, nN1, …}}. The index of nmk± differs from n only by changing the specified nmk to nmk ± 1. The ρ0 with 0 = {{0, 0, …}, …,{0, 0, …}} is the real system reduced density operator and the other ρn are the auxiliary density operators (ADOs). The ADOs shows in the hierarchy levels of coupled differential equations and contain the information of collective bath modes and also their interaction with the system part. The schematic diagram of reduced and auxiliary density operators is shown in Fig. 6.
ρ = [HS,ρ] and HS is the system Hamiltonian with electronic DoFs. The subscript n denotes the set of indices n = {n1, n2, …, nN} = {{n10, n11, …}, …, {nN0, nN1, …}}. The index of nmk± differs from n only by changing the specified nmk to nmk ± 1. The ρ0 with 0 = {{0, 0, …}, …,{0, 0, …}} is the real system reduced density operator and the other ρn are the auxiliary density operators (ADOs). The ADOs shows in the hierarchy levels of coupled differential equations and contain the information of collective bath modes and also their interaction with the system part. The schematic diagram of reduced and auxiliary density operators is shown in Fig. 6.


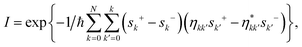
 are
are