Alpha oxygen – a unique oxidation active site from a quantum chemical viewpoint

Abstract

The alpha oxygen (also α-O, Fe(IV)=O, and Fe(III)–O⁻˙) stabilized in zeolite matrices exhibits a unique reactivity. It is, for example, able to oxidize methane to methanol at room temperature. Such a high oxidation activity makes the alpha oxygen an extremely attractive species from the point of view of oxidation catalysis. The alpha oxygen can be prepared by splitting either N₂O or O₂ also at low temperatures over different transition metal cations stabilized in extra-framework cationic sites of zeolites in the form of either isolated cations or two cooperating cations forming distant binuclear cationic sites. The alpha oxygen was primarily defined by its reactivity, and up to now, experimental data concerning its structure are rather scarce. Quantum chemical calculations are used to interpret experimental data and thus yield significantly deeper insights into the preparation, structure, and reactivity of this otherwise omitted active species with enormous potential for applications. This review represents the first collection and systematic interpretation of experimental data and quantum chemical calculations to provide a complex description of the alpha oxygen and its structure, reactivity, and properties.

---

Stepan Sklenak

Stepan Sklenak is a Research Professor at the J. Heyrovsky Institute. After obtaining his PhD, he spent almost a decade at the Technion; Yale University; University of California; and Michigan State University before beginning his career as an independent researcher at the J. Heyrovsky Institute. His current research focuses on DFT calculations of zeolites to model their structure, reactivity, catalytic activity, and properties. He identified the distant binuclear cationic sites in zeolites. Moreover, Stepan computationally predicted splitting dioxygen over zeolites with the distant binuclear cationic sites. Subsequently, his theoretical predictions were confirmed experimentally by Dr Dedecek and collaborators.

Jiri Dedecek

Jiri Dedecek, currently a Research Professor at the J. Heyrovsky Institute of Physical Chemistry, the Czech Academy of Sciences, Prague, Czech Republic, received his PhD degree from the same institution. After a postdoctoral fellowship at Lehigh University, Bethlehem, PA, he became a scientist at the J. Heyrovsky Institute of Physical Chemistry, where he is currently leading the Department of Structure and Dynamics in Catalysis. His current research focuses on acid–base and redox heterogeneous catalysis, syntheses of aluminosilicate molecular sieves, and applications of spectroscopic methods (MAS NMR, UV/vis absorption/emission, and FTIR) in the characterization of catalysts at the atomic level.

---

1. Introduction

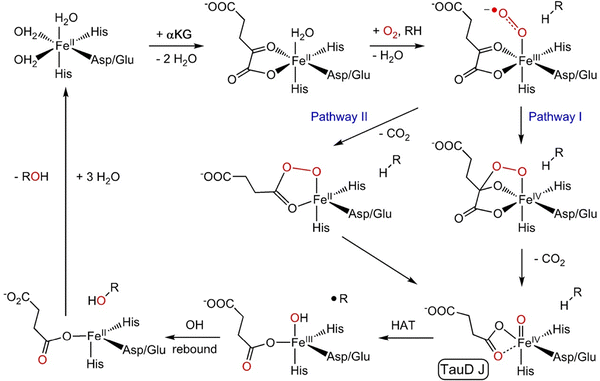
The alpha oxygen (also α-O, Fe(IV)=O, and Fe(III)–O⁻˙) has been a very unusual, unique, and interesting species since its discovery.^1–23 This oxygen species exhibits a high reactivity in oxidation reactions, as evidenced by its capability to activate strong bonds such as C–H bonds in methane at very low temperatures, reflected in the oxidation of methane at room temperature. The alpha oxygen has been prepared from N₂O^1–17 and O₂^18–23 on Fe(II) cations stabilized in extra-framework cationic positions of microporous crystalline aluminosilicate molecular sieves (i.e., zeolites). The alpha oxygen (illustrated in Fig. 1 and Fig. S1 of the SI (species 5)) can be considered as a fully inorganic analogue of some oxidized forms of non-heme monoatomic iron enzymes.²⁴ Similarly, bare Fe(II) cations in zeolite frameworks resemble Fe(II) cations of the reduced form of such enzyme species. However, the process of the formation of the alpha oxygen significantly differs. The alpha oxygen can be created in zeolites in three different ways – by splitting (i) N₂O over isolated Fe(II) cations, (ii) N₂O and (iii) O₂ over a pair of distant cooperating Fe(II) cations. Enzymes form the alpha oxygen from molecular oxygen (Scheme 1).

Fig. 1 Optimized structures of the alpha oxygen formed on the Fe(II) cations accommodated in the α, β1, and β2 sites of ferrierite. (A) Top and (B) side views of the α center. (C) Top and (D) side views of the β1 site. (E) Top and (F) side views of the β2 site. The Fe–O distances are in Å. Silicon atoms are in gray, oxygen atoms in red, aluminum atoms in yellow, and iron atoms in violet.

Scheme 1 Consensus mechanism of Fe(II)–2OG enzyme catalyzed hydroxylation. Reproduced from ref. 25 licensed under a Creative Commons Attribution License 4.0 (CC BY-NC). https://creativecommons.org/licenses/by/4.0/.

One O atom of O₂ becomes the alpha oxygen while the other O atom is abstracted by a cofactor. Conversely, both the O atoms of O₂ turn into the alpha oxygen in zeolite frameworks. This is possible because the cooperating Fe(II) cation plays the role of the acceptor of the second oxygen atom. Therefore, the second alpha oxygen atom is formed on the cooperating Fe(II) cation. It should be noted that the systems yielding the alpha oxygen, which are based on two distantly cooperating transition metal cations, differ significantly in both the structure and function from enzyme binuclear centers for the activation of oxygen or their recently developed analogues in (mainly Cu) zeolites.²⁶ Metal cations in these centers are significantly closer and the activation of dioxygen proceeds via the formation of an oxygen bridge. These structures are out of the scope of this paper. It is worth mentioning that in the case of two distant cooperating cations, a significant expansion of the field occurred since transition metal cations other than Fe(II) (e.g. Co(II), Mn(II), and Ni(II)) have been reported to be able to split N₂O^17,27 and O₂¹⁹ and take part in the formation of the alpha oxygen, which therefore has to be generalized as M(IV)=O species.

When Panov and collaborators discovered the alpha oxygen at the end of the eighties,¹ this species attracted significant attention because of both its exceptional activity and uniqueness. The alpha oxygen featured an exclusive oxidation activity, and, moreover, potential for applications (e.g., oxidation of (i) methane to methanol and (ii) benzene to phenol), but its structure was unknown. Moreover, the preparation process of the alpha oxygen – a high temperature treatment of a zeolite with iron in the framework was rather unusual and represented a significant obstacle in the elucidation of its structure. Therefore, the investigation of the alpha oxygen was focused rather on its unique reactivity in the nineties.^{2–4,28–32} The structure of the alpha oxygen was suggested^{11,12,33–40} in the first decade of the new millennium. The decomposition of N₂O over Fe-zeolites which represents the first step in the abatement of N₂O attracted significantly more attention.^{11,12,28–32,41–49} This reflects the fact that the high price of N₂O as an oxidant handicaps potential industrial applications of oxidation of methane or benzene by the alpha oxygen from N₂O. Conversely, the elimination of N₂O as a strong greenhouse gas represented from the start of the new millennium an important political, economic, and environmental issue. Moreover, in addition to the high cost of N₂O, another major limitation associated with the use of the alpha oxygen from N₂O was that the products of the oxidation of methane by the alpha oxygen were formed as strongly bound methoxy species. Consequently, an extraction using water or water–organic media (e.g., acetonitrile or dimethyl ether) was required to release these methoxy groups and obtain methanol.^2–4

A dramatic change in the knowledge regarding alpha oxygen research occurred through a combination of several events. Göltl et al.⁵⁰ theoretically and later Dedecek and collaborators¹⁷ experimentally showed that methanol was formed from the alpha oxygen active sites and subsequently released to the gas phase without the need for any effluent. Snyder et al.¹⁵ experimentally confirmed the structure (and the mechanism of the formation from N₂O as well) of the alpha oxygen. Finally, Sklenak and collaborators¹⁸ showed that the alpha oxygen can be prepared by a cleavage of molecular oxygen. This resulted, on the one hand, in extensive research of the alpha oxygen prepared by splitting N₂O^51–60 since it represents a unique counterpart of non-heme iron enzymes, and, on the other hand, in the investigation of the alpha oxygen prepared from molecular oxygen^{19,20,22,23,61} as a possible catalyst for the selective oxidation of methane to methanol. The alpha oxygen as the active site for the selective oxidation of methane possesses some advantages with respect to the active species in Cu-zeolite catalysts, which are most likely oxygen bridges. The alpha oxygen is highly active in the oxidation of methane at low temperatures and, above all, the assistance of an effluent (water vapor) for methanol release is not required. This makes the oxidation of methane to methanol a simpler and robust process. Moreover, the alpha oxygen with its unique oxidation activity prepared from molecular oxygen has significant potential in other areas of oxidation catalysis.

The aim of this review is to present the current knowledge on this specific area of zeolite science focusing on the formation and performance of the alpha oxygen species created and stabilized in zeolite matrices, also including the promising fields for possible applications.

2. Experimental methods for evidence and analysis of the alpha oxygen

2.1. Reaction tests evidencing the alpha oxygen

The alpha oxygen was first evidenced by its unique reactivity with no knowledge of its structural and spectroscopic properties.¹ It was defined as an Fe-oxygen species capable of oxidizing methane,^1,4 hydrogen, carbon monoxide,¹ and benzene at room temperature.^5,7 The reason why only its unique reactivity¹ was used to define the alpha oxygen was the rather low concentration of the alpha oxygen prepared in the beginning by a high temperature release of isomorphously substituted Fe atoms from the ZSM-5 zeolite framework. Even at the present time, the reactivity of the alpha oxygen represents the only unambiguous and universal way to evidence its formation. However, with some specifications:

(a) The reaction of the alpha oxygen with larger reactants such as benzene can be in some zeolite matrices such as ferrierite and mordenite limited by the opening of the channels/cavities containing the alpha oxygen. Moreover, the creation of a pair of the alpha oxygen atoms in the distance of ca. 3–4 Å depending on the zeolite by splitting dioxygen can be accompanied by the steric hindrances even for small molecules such as CO. Thus, the oxidation of methane^1,4 or dihydrogen⁶² at room temperature can serve as unambiguous proof of the formation of the alpha oxygen in various zeolite matrices from both N₂O and O₂.

(b) When the alpha oxygen was discovered, it was associated only with strongly bound (methoxy group) and strongly adsorbed (methanol and dimethyl ether) products of the oxidation of methane. In this case, the oxidation of methane can be evidenced by FTIR spectroscopy of the products adsorbed onto the zeolite surface. It should be noted that due to the low extinction coefficients of methanol or methoxy groups, these species can often only be recognized in the differential mode of the FTIR spectra. Conversely, an extraction of the products from the zeolite with subsequent analysis of the liquid phase by various methods represents a significantly more reliable approach.^{1–10,13–15}

(c) Recently, volatile products of the oxidation of methane by the alpha oxygen were reported.^{17–19,22,23,63} In this case, analysis of the output gas stream is essential. Application of gas chromatography is strictly limited by the fact that in contrast to the steady state reaction conditions, the oxidation products in the quasi-catalytic regime (oxidation of metallo-zeolites followed by the reaction with methane) are present in the gas stream only for a short time and continuous analysis of the gas stream by MS or FTIR spectroscopy is necessary. Adsorption of the oxidation products on some adsorbent followed by their extraction and analysis represents another possibility. It should be noted that depending on the reaction conditions, CO₂ can be a product of the oxidation of methane by the alpha oxygen.

In conclusion, the oxidation of methane at room temperature followed by the detection of the products of the oxidation of methane is the most suitable and unambiguous proof of the formation of the alpha oxygen in zeolites and other materials. Analysis of the products adsorbed on the zeolite surface and in the gas stream is essential for unambiguous information in the absence/presence of the alpha oxygen in the zeolite.

2.2. Mössbauer spectroscopy

Mössbauer spectroscopy⁶⁴ was historically the first spectroscopic method employed to investigate the alpha oxygen. It has to be pointed out that Mössbauer spectroscopy can be employed only to investigate the alpha oxygen created on Fe(II) cations and not, as recently reported, on other transition metal cations (Mn(II), Co(II), and Ni(II)). Moreover, Mössbauer spectroscopy does not evidence the alpha oxygen directly, but “only” the changes in the oxidation state of the Fe cations in the activated zeolite upon the reaction with N₂O or O₂, and subsequently, with methane. Nevertheless, Mössbauer spectroscopy provided the first experimental indications of the alpha oxygen structure because of a significant similarity of the Mössbauer parameters of Fe cations bearing the alpha oxygen and Fe cations in oxidized forms of some Fe enzymes.

However, there is one significant disadvantage of Mössbauer spectroscopy for the investigation of the formation and reactivity of the alpha oxygen which is the acquisition time (hours) of Mössbauer spectra. Thus, this spectroscopy can be employed only for the study of stable Fe structures in zeolites and cannot be employed to study the kinetics of processes of the creation of the alpha oxygen and the oxidation of methane to methanol.

2.3. X-ray absorption spectroscopy (XAS)

X-ray absorption was employed for the study of the alpha oxygen only in a few cases.^27,65 Nevertheless, it has significant potential. In contrast to Mössbauer spectroscopy, X-ray absorption can also be employed to study the alpha oxygen formed on transition metal cations other than Fe, e.g., Mn, Co, and Ni. Moreover, the collection of X-ray absorption spectra is quick, and experiments can be performed under in situ or operando conditions. Thus, the application of XAS bears significant potential far beyond the simple evidence of the oxidation state of transition metal cations in zeolites.

2.4. FTIR spectroscopy of anti-symmetric T–O–T vibrations of the zeolite framework

The ligation of divalent cations to framework oxygens of zeolite extra-framework cationic sites results in the perturbation of the anti-symmetric zeolite T–O–T vibrations which in turn causes the shift of the perturbed T–O–T vibrations to the spectral region in which they can be detected.⁶⁶ Thus, analysis of transition metal cations accommodated in extra-framework cationic sites is possible including quantitative analysis of the cation siting. A change in the oxidation state of the cation as well as the presence of some ligands on the cation results in a change in the perturbation of the T–O–T vibrations and is reflected in the FTIR spectrum of the zeolite.^18,19 These experiments can be performed even under operando conditions and can be employed for the study of the kinetics of the formation of the alpha oxygen or its reactivity. Furthermore, this method can be employed to study divalent cations in general. However, there is a significant disadvantage of this method. The perturbation of the T–O–T vibrations is not specific and can also reflect other processes resulting in the change of the FTIR spectra in the T–O–T regions other than the change in the oxidation state of the cation and the creation of the alpha oxygen. Therefore, confirmation of the oxidation state of transition metal cations and the formation of the alpha oxygen by other methods is essential.

2.5. UV-vis spectroscopy

The change in the oxidation state of transition metal cations due to the formation of the alpha oxygen can be reflected by the presence of a new band in the diffuse reflectance spectrum of the metallo-zeolites which corresponds to the charge transfer from the oxygen (the alpha oxygen) to the transition metal cation. Such charge transfer has been reported for Fe and Mn zeolites with the alpha oxygen prepared from N₂O decomposition over isolated Fe(II) cations.^15,16 Surprisingly, this charge transfer band was not reported for the alpha oxygen prepared over binuclear cationic sites.¹⁸ It should also be noted that this spectroscopic feature is not unambiguous, and the formation of the alpha oxygen requires further confirmation.

2.6. Magnetic circular dichroism

It has to be pointed out that electronic transitions can provide significantly more detailed information than the change of the oxidation state when a more sophisticated methodology than UV-vis spectroscopy is employed. Variable-temperature variable-field magnetic circular dichroism spectroscopy was successfully employed to analyze in detail the electronic structure of the Fe cation. Comparison of the experimental data with the prediction of spectroscopic properties using quantum chemical calculations for various structural models allowed elucidation of the structure of the alpha oxygen. It should be noted that this approach is up to now the only one providing experimental information on the structure of the alpha oxygen.¹⁵ This method is illustrated in Fig. 2.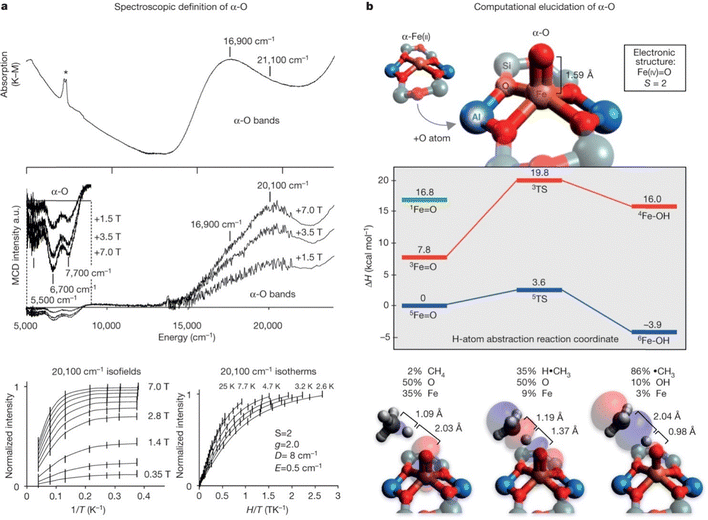

Fig. 2 Spectroscopic and computational elucidation of the alpha oxygen. (a) Top, room-temperature DR-UV-vis data (* = OH overtone), and middle, 3 K MCD data from N₂O-activated BEA. Bottom, VTVH-MCD saturation magnetization data from the 20 100 cm⁻¹ band of the alpha oxygen, including ± 1σ error bars and fit (black curves) to a positive ZFS S = 2 model, with parameters given in the inset. (b) Top, DFT-optimized structure of α-⁵Fe(IV)=O in the S = 2 ground state. Middle, energetics of the CH₄ HAA reaction. Bottom, evolution of the lowest unoccupied molecular orbital along the reaction coordinate (reactant, left; transition state, middle; and product, right). Reproduced with permission from ref. 15. Copyright 2016 Springer Nature.

In conclusion, there is still a significant lack of information on the alpha oxygen and its structure. To date, this uniquely reactive type of oxygen has been evidenced only by its reactivity or indirectly by its effect on the cation hosting this oxygen species. Up until now, the application of methods of structural analysis (e.g., diffraction) has not been reported. The best insight regarding the structural analysis of the alpha oxygen species thus represents the combination of rather demanding circular dichroism spectroscopy approaches combined with quantum chemical calculations.

3. Computational methods

Atomistic simulations of catalytic reactions over solid catalysts are a challenge to modern computational chemistry. To model a catalytic process, the computational method used should correctly evaluate: (a) the interactions between the reactants, transition states, intermediates, products on the one hand and the catalyst on the other hand; (b) the thermodynamics and kinetics of the catalytic reaction steps to provide reasonable values for reaction energies and barriers; (c) the method should also be able to correctly describe the structural complexity of the catalyst.

A twofold approach is needed to computationally model a catalyst. On the one hand, the theoretical model used must include all the important features (e.g., the alpha oxygen species) as well as the structural complexity of the zeolite. On the other hand, the theoretical method employed has to be able to correctly describe all the important interactions. Since the computer time and resource demand grow polynomially with the size of the model, there is always a tradeoff between the size and complexity of the catalyst model on the one hand, and the theoretical method used on the other hand.

In order to realistically model the structure, reactivity, and properties of Alpha oxygen species accommodated in various cationic sites of zeolites as well as to computationally investigate their catalytic activity, a computational model of these structurally complex systems has to be built based on experimental structural data. The best structures are those obtained by X-ray crystallography and neutron diffraction crystallography at good resolution. Realistic computational models of the structure and especially the reactivity of Alpha oxygen species accommodated in zeolites require the inclusion of one^12,67 or more^{12,17,18,20,21,62,67} unit cells of zeolites.

3.1. Periodic DFT approaches

Since zeolites are crystalline matrices, periodic DFT methods are well suited for their theoretical study. A development of these methods and advances in computer technology in the 2000s have allowed simulations based on the full crystalline lattice of zeolites employing pure DFT functionals.^68–70 Periodic DFT methods were extensively employed to study the alpha oxygen accommodated in zeolites.^{12,17,18,20,21,62,67,71} The major advantage of the periodic DFT approach is that there is no need for artificial division of the studied system between the different layers (e.g. inner layer, outer layer) as is necessary when embedded cluster methods are used. Zeolites are crystalline solids. Their constituents (i.e., atoms of Si, Al, and O) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. Therefore, periodic calculations describe crystalline matrices significantly better than finite cluster models.

Since zeolites have large unit cells with a lot of constituent atoms ranging from ca. one hundred (e.g., CHA, FER) to several hundred (e.g., ZSM-5, TNU-9, FAU), and moreover, frequently more unit cells must be included in the computational models, only DFT methods employing mainly pure functionals (currently primarily PBE^{17,18,20,21,50,62,72–74}) are routinely applicable at the present time to investigate Alpha oxygen species accommodated in various cationic sites of zeolites. The advantage of the PBE⁷⁵ functional for studying solids is that it is not parametrized on molecules. Periodic DFT calculations of zeolites using hybrid functionals are by more than an order of magnitude more time consuming.^76–78

Transition metal-exchanged forms of zeolites have been extensively computationally studied, however, the main drawback of the majority of the calculations in the past was the use of single determinant quantum chemistry methods (mainly DFT) which might fail in the case that the studied system is of multireference character (e.g., when the d-orbitals of the transition metal are partly occupied).⁷⁹ Single reference methods are appropriate mainly for transition metals which have their d-orbitals either empty or fully occupied (e.g., Sc and Cu, respectively). Conversely, periodic DFT studies employing spin-polarized calculations with plane-wave basis sets and pseudopotentials as implemented, for example, in the VASP program,^80–83 yield reasonable results for systems containing transition metals with partly occupied d orbitals.^{12,17,18,20,21,50,62,67,69,72–74,84–89} Such systems are well known to be difficult cases for single determinant quantum chemistry methods.⁷⁹

Molecular dynamics (MD) based on periodic DFT emerged as a valuable means to simulate crystalline solid catalysts, allowing more complete sampling of the configuration space than only localizing minima on the potential energy surface. Studies showed that using MD simulations, or other similar global optimization techniques which allowed the structural rearrangement of the cationic sites upon binding divalent cations, were needed to obtain reliable structures of Alpha oxygen species accommodated in various cationic sites of zeolites.^{12,17,18,20,21,62,88}

3.2. Periodic wavefunction based approaches

These methods are not yet routinely applicable since their usage would be prohibitively computationally demanding for realistic computational models of Alpha oxygen species accommodated in zeolites.

3.3. Cluster DFT approaches

These approaches were used to study Alpha oxygen species^33–40 mainly in the past. At the present time, a finite cluster approach is only rarely used to investigate the reactivity⁹⁰ of the alpha oxygen while embedded cluster methods are still used to study the reactivity of transition-metal exchanged zeolites.⁹¹ The latter approach offers additional choice regarding the usage of various functionals, basis functions, and eventually implemented methods to calculate various properties (e.g., spectroscopic) in comparison with the otherwise superior periodic DFT approach. Catlow and collaborators⁹¹ used the hybrid PBE0 and B97-2 functionals besides employing the pure PBE functional to study Fe-BEA. Employing periodic DFT calculations with the hybrid PBE0 and B97-2 functionals instead of the embedded cluster method would be significantly more computationally demanding.

3.4. Cluster wavefunction based approaches

Wavefunction method studies using smaller finite cluster models can be employed to investigate spectroscopic properties⁹² of Alpha oxygen species accommodated in zeolites. The clusters are too small to properly study the reactivity, but they are large enough to calculate spectroscopic properties of Alpha oxygen species which can be compared with experiments. The limited size of the clusters allows the employment of multireference CASSCF^93–95 and CASPT2⁹⁶ methods. The CASSCF method is appropriate for dealing with the static electron correlation – arising from nearly-degenerate configurations – but it does not capture the dynamic correlation – mostly due to short-range electron-electron repulsion. The CASPT2 method incorporates the effect of dynamic correlation employing the adequate reference wave function obtained by CASSCF. Solomon and collaborators employed CASSCF/CASPT2 to spectroscopically identify Fe(IV)=O in Fe-BEA¹⁵ and Fe-CHA.¹⁶

Table 1 summarizes the advantages and disadvantages of the periodic and cluster approaches.

Table 1 Advantages and disadvantages of the periodic and cluster approaches

Approach	Advantages	Disadvantages
Periodic	More realistic model	Computationally expensive
	Inclusion of long-range effects	Limited choice of computational methods (both DFT functionals and post-Hartree–Fock methods)
	Good for studying bulk properties (e.g., adsorption energies in zeolite pores and channels)	Limited choice of basis sets
Cluster	Less computationally intensive	Artificial boundaries (terminations may introduce artifacts)
	Allows the use of high-level quantum chemical methods	Cannot capture long-range effects
	Good for studying properties of local sites (e.g., spectroscopic)	Choice of the cluster size and termination introduces the model dependency

---

3.5. Dispersion corrections

DFT methods improperly account for the important long-range London dispersion effects (van der Waals forces). Therefore, various dispersion correction schemes have to be used in DFT studies of zeolites.⁹⁷ The periodic DFT studies^{17,18,20,21,62} of Alpha oxygen species accommodated in various cationic sites of zeolites employed the density-dependent energy correction (dDsC) dispersion correction^98,99 for optimizations and the DFT-D2 method¹⁰⁰ for molecular dynamics calculations.

3.6. Models of dehydrated zeolites

Computational models of Alpha oxygen species accommodated in various cationic sites of zeolites employ dehydrated zeolites which are composed of framework atoms and extra-framework cations.^{12,17,18,20,21,62,67,71} The tetrahedral framework Al atoms are fully charge balanced. The starting structures are generated from available structures determined by diffraction methods.

4. Structure of alpha oxygen atoms and their formations

The formation of the alpha oxygen from N₂O or O₂ over Fe(II) cations accommodated in zeolites requires accessibility to the Fe(II) cations and their open coordination sphere. Therefore, the Fe(II) cations must be located in extra-framework cationic sites and not in framework tetrahedral ones. While Panov et al. prepared the first Alpha oxygen using (Fe)ZSM-5 zeolites with iron isomorphously substituted in (Fe)ZSM-5 framework tetrahedral sites, the (Fe)ZSM-5 zeolite samples had previously undergone a high temperature treatment which had caused a release of the iron from the zeolite framework to the extra-framework cationic sites.¹ Moreover, Fe(II) cations accommodated in extra-framework sites were later experimentally confirmed as the active sites.^11,12,15,16

Since all alpha oxygen is the same species regardless of whether it is prepared (i) from N₂O or O₂ and (ii) on isolated Fe(II) cationic sites or the distant binuclear Fe(II) cationic sites, their structures and formation are discussed together in Section 4.

4.1. Cationic sites for bare divalent cations

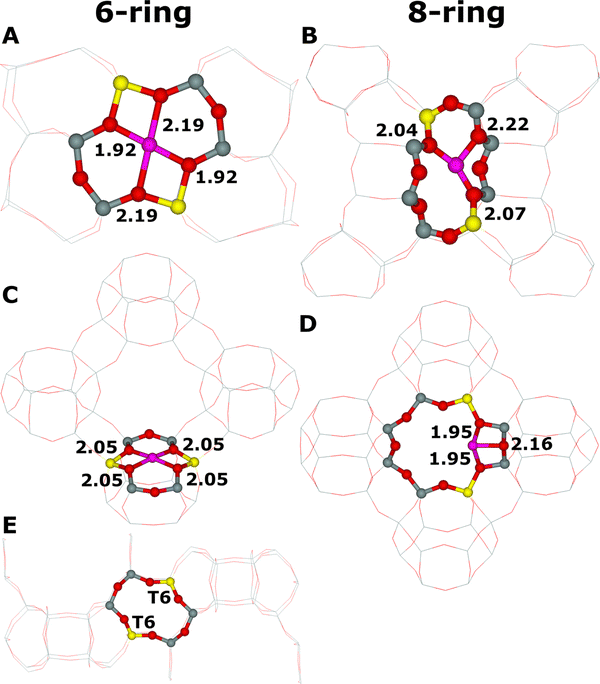
Cationic sites for bare divalent cations are formed mainly by 6-rings⁶⁶ (e.g., ZSM-5,¹⁰¹ FER,^12,86 TNU-9,⁸⁷ and BEA¹⁰²) and for some zeolite structures (e.g., MOR²¹ and CHA⁸⁸) by 8-rings (Fig. 3).

Fig. 3 Cationic sites accommodating Fe(II) in various zeolites of different topologies. (A) FER, (B) MOR, (C) and (D) CHA, and (E) *BEA (both Al atoms in T6). The Fe–O distances are in Å. Silicon atoms are in gray, oxygen atoms in red, aluminum atoms in yellow, and iron atoms in violet.

These 6-rings and 8-rings must contain two Al atoms^84,85 (each having a formal negative charge of −1) to charge balance the positive charge of +2 of the bare divalent cation. The two Al atoms in the ring forming the cationic site are separated by at least one Si atom (Loewenstein rule¹⁰³), but for zeolites with a Si/Al ratio larger than ca. 7, the two Al atoms are isolated by at least two Si atoms.^104,105

Due to the complexity of various topologies of zeolite frameworks, two Al atoms can be located in diverse 6-rings and 8-rings differing in their detailed arrangements. For pentasil-ring zeolites such as ZSM-5, beta zeolite, mordenite, ferrierite, MCM-22, and TNU-9, two centers for bare divalent cations with an open coordination sphere were suggested – the α and β sites.⁶⁶ They were determined using X-ray diffraction (XRD) for mordenite^106,107 and ferrierite.^108–110 The α site in both ferrierite (Fig. 4D) and mordenite corresponds to an elongated 6-ring formed of two connected 5-rings with the bare divalent cation located on the top of a pyramid with the base of four framework oxygen atoms, while the β site relates to a single elongated 6-ring (ferrierite, Fig. 3A) or twisted 8-ring (mordenite, Fig. 3B) with approximately planar cation coordination to four framework oxygen atoms.

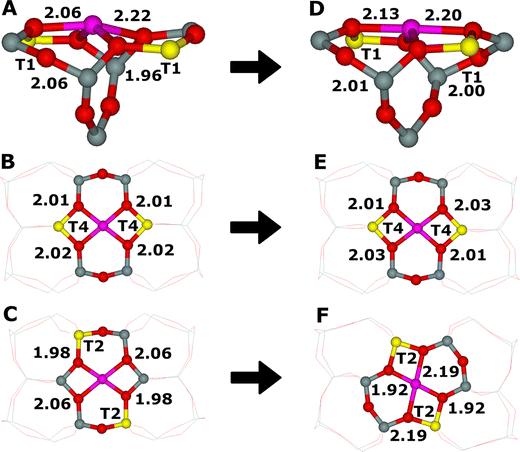Fig. 4 Optimized structures before the DFT molecular dynamics simulations based on the starting structures of the cationic sites generated from the experimental orthorhombic structure¹¹¹ of ferrierite accommodating Fe(II).¹² (A) The α cationic site (both Al atoms in T1), (B) the β1 cationic site (both Al atoms in T4), and (C) the β2 cationic site (both Al atoms in T2). Optimized structures after the DFT molecular dynamics simulations of the cationic sites accommodating Fe(II) in ferrierite. (D) The α cationic site (both Al atoms in T1), (E) the β1 cationic site (both Al atoms in T4), and (F) the β2 cationic site (both Al atoms in T2). The Fe–O distances are in Å. Silicon atoms are in gray, oxygen atoms in red, aluminum atoms in yellow, and iron atoms in violet. Adapted with permission from ref. 12. Copyright 2010 Elsevier.

For zeolites with the chabazite topology, i.e., the chabazite and SSZ-13 zeolites, which are not pentasil-ring zeolites, the two centers for bare divalent cations with open coordination sphere of divalent cations represent regular 6-ring of the hexagonal prism (the σ site, Fig. 3C) with three-fold symmetry of the cation coordination and a planar 8-ring (the τ site, Fig. 3D).⁸⁸ It should be noted that there is no equivalence between the α cationic site and α-Fe(II) of Snyder et al.¹⁵ The former means a cationic site formed by a 6-ring with two Al atoms able to accommodate a bare divalent cation (Fig. 4D), while the latter means such Fe(II) cations which can serve as a precursor of the alpha oxygen atom, in other words, such Fe(II) which can be oxidized by N₂O to yield the alpha oxygen atom. There is an open question if all Fe(II) cations accommodated in the α cationic site in various zeolites are also α-Fe(II),¹⁵ i.e., can be oxidized by N₂O to form Fe(IV)=O species featuring the alpha oxygen.

There can be more different Al sitings⁸⁸ of the two Al atoms in the ring creating the cationic site,^12,86,112 and therefore, the corresponding cationic sites with different Al sitings may vary in their structure and reactivity. While the α site in the ferrierite zeolite (Fig. 4D) can have only one possible Al siting of the two Al atoms in the 6-ring forming the α site, there are two possible Al sitings of the two Al atoms creating the β site. The corresponding sites are β1 (Fig. 4E) and β2 sites (Fig. 4F). Sklenak et al.¹² showed using periodic DFT calculations a somewhat different reactivity regarding the N₂O decomposition for β1 and β2 sites accommodating Fe(II).

Sklenak et al.^12,86 employed the VASP program^80–83 to perform spin-polarized periodic DFT calculations including extensive molecular dynamics (MD) simulations to investigate the accommodation of bare divalent cations (Fe(II), Co(II), Cu(II)) in the α and β sites of ferrierite. The Kohn–Sham equations were solved variationally in a plane-wave basis set using the projector-augmented wave (PAW) method of Blöchl,¹¹³ as adapted by Kresse and Joubert.¹¹⁴ The exchange–correlation energy was described by the PW91 generalized gradient approximation (GGA) functional.^115,116 Brillouin zone sampling was restricted to the Γ-point. The plane-wave cutoff of 400 eV was utilized for geometry optimizations, while a smaller cutoff of 300 eV was used for the molecular dynamics simulations. The high-spin electron configurations Fe d⁵↑d¹↓,¹² Co d⁵↑d²↓,⁸⁶ and Cu d⁵↑d⁴↓⁸⁶ were employed for the corresponding cations accommodated in the zeolite. The neutron diffraction determined orthorhombic structure¹¹¹ of ferrierite was employed to generate the starting structures (Fig. 4A–C). The neutron diffraction structure¹¹¹ was used in the studies^12,86 to be compatible with the older periodic DFT studies of Hafner and collaborators^84,85 of the iron exchanged ferrierite zeolite which used this structure. Divalent metal cations accommodated in cationic centers adopt the coordination to oxygen atoms of AlO₄⁻ tetrahedra rather than SiO₄ tetrahedra, since the cations charge balance the negative charge of AlO₄⁻. However, the starting structures featured this appropriate coordination of M(II) (M(II) = Fe(II), Co(II), and Cu(II)) to four oxygen atoms of two AlO₄⁻ tetrahedra only for the β1 cationic sites (Fig. 4B). Conversely, the M(II) cation is ligated to only three and two oxygen atoms of two AlO₄⁻ tetrahedra for the α (Fig. 4A) and β2 (Fig. 4C), respectively, cationic sites. Therefore, the structure of the α and β2 cationic sites accommodating M(II) significantly rearranged during the MD calculations (Fig. 4D and F, respectively) while that of the β1 cationic site (Fig. 4E) did not. The M(II) cation correctly coordinates to four oxygen atoms of two AlO₄⁻ tetrahedra in the resulting structures for all three cationic sites (Fig. 4D–F). The rearrangement was confirmed by FTIR spectroscopy.⁸⁶

4.2. Formation of the alpha oxygen from N₂O and O₂

When Panov and collaborators discovered¹ the alpha oxygen, they only defined it by its catalytic properties while the structure remained unknown. First propositions^33–40 of a possible structure of the alpha oxygen were based on simple computational cluster models. These simple models were grounded in a usual coordination of bare transition metal cations in pentasil-ring zeolites (i.e., ZSM-5, ferrierite, mordenite, the beta zeolite, …). The proposed coordination of Fe is approximately planar and square resulting in the pentacoordinated pyramidal oxygen coordination.

Experimental and theoretical studies revealed that there were three possibilities of the formation of the alpha oxygen atom on Fe(II) cations accommodated in extra-framework cationic sites of zeolites. The first one is the creation of the alpha oxygen from N₂O over isolated Fe(II) cations (Scheme 2 and Fig. S1A of the SI).¹

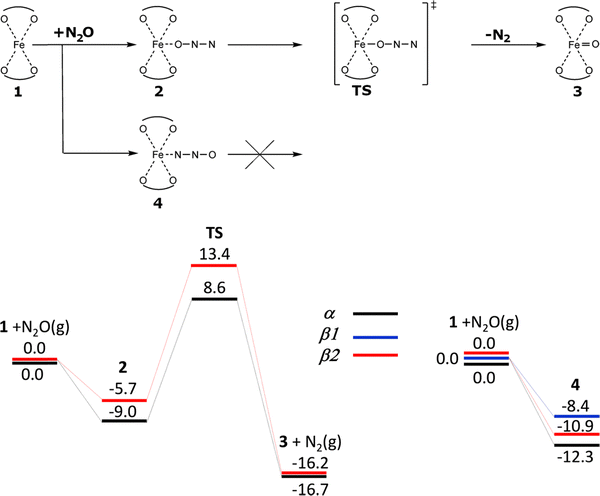Scheme 2 Mechanism and the schematic energy¹² (in kcal mol⁻¹) profiles (spin state S = 4/2) of the formation of the alpha oxygen atoms from N₂O over isolated Fe(II) cations. Adapted with permission from ref. 12. Copyright 2010 Elsevier.

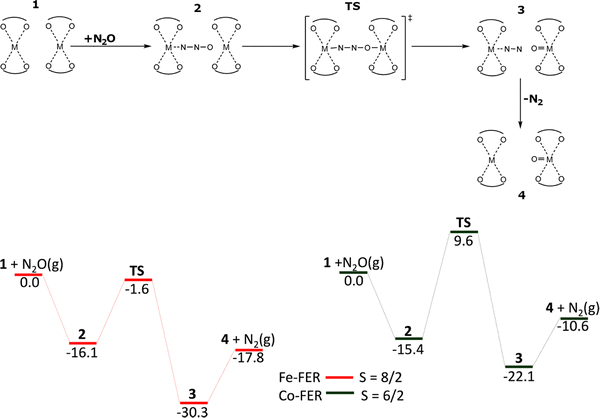
This way prevails as most studies in the literature belong to this category. The second one also employs N₂O but the active sites are pairs of cooperating Fe(II) cations called the distant binuclear cationic sites (Scheme 3 and Fig. S1B of the SI).^12,17

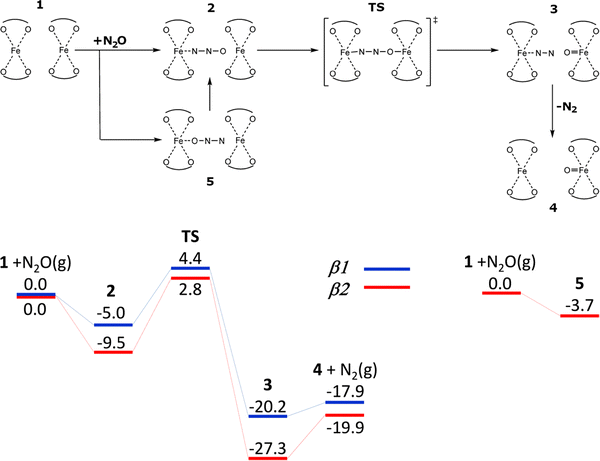Scheme 3 Mechanism and the schematic energy¹² (in kcal mol⁻¹) profiles (spin state S = 8/2) of the formation of the alpha oxygen atoms from N₂O over the distant binuclear Fe(II) cationic sites. Adapted with permission from ref. 12. Copyright 2010 Elsevier.

The third one uses O₂ instead N₂O over the distant binuclear cationic sites (Scheme 4 and Fig. S1C of the SI).^18,20,21

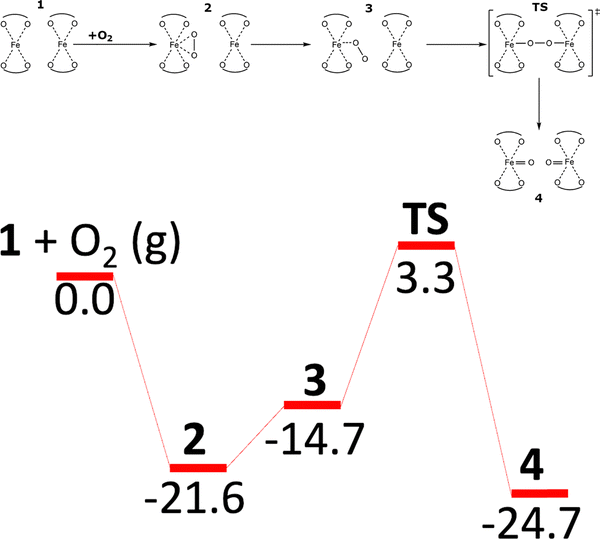Scheme 4 Mechanism and the schematic energy¹⁸ (in kcal mol⁻¹) profiles (spin state S = 8/2) of the formation of the alpha oxygen atoms from O₂ over the distant binuclear Fe(II) cationic sites. Adapted from ref. 18 licensed under a Creative Commons Attribution License 4.0 (CC BY). https://creativecommons.org/licenses/by/4.0/.

It should be noted that the alpha oxygen cannot be prepared from O₂ on isolated Fe(II) cationic sites.

Sklenak et al. used periodic DFT calculations¹² (for technical details see Section 4.1.) employing two unit cells of ferrierite with one (Scheme 2 and Fig. S1A of the SI) and two (Scheme 3 and Fig. S1B of the SI) Fe(II) cations in the high-spin configuration as the computational model to investigate the mechanism of N₂O decomposition over the iron exchanged ferrierite (Fe-ferrierite). In the study,¹² Sklenak et al. also suggested a plausible structure and mechanism of the creation of the alpha oxygen atom in the Fe-ferrierite structure since the first chemical step of the N₂O decomposition on Fe(II) is the concurrent cleavage of the N–O bond and the creation of the Fe(IV)=O bond (Schemes 2 and 3 plus Figs. S1A and B, respectively, of the SI).

4.3. Calculated structures of the alpha oxygen

All three distinct possibilities to create the alpha oxygen led to identical oxygen species which is the Fe(IV)=O group featuring the alpha oxygen atom and Fe(IV) in the high-spin configuration (Fig. S1 of the SI, structures 5). Fe(IV) is further charge balanced by the two Al atoms in the 6-ring forming the Fe(II) cationic sites. The calculated Fe=O bond length is ca. 1.62 Å. 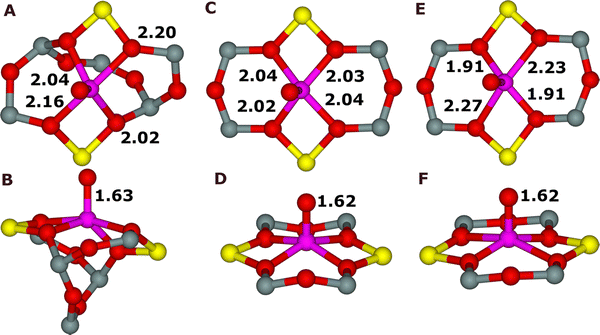The Fe atom of the Fe=O group is placed slightly more above the plane than the bare Fe(II) cation before the oxidation by N₂O indicating that the alpha oxygen atom pulls out (i.e., the four Fe–O bonds are elongated) the Fe moiety from the plane similarly as strong ligands, as for example NO, can pull out divalent cations accommodated in cationic sites.⁸⁶ The plane is formed by the four O atoms of two AlO₄⁻ tetrahedra to which the Fe atom is coordinated. The Fe=O bond is approximately perpendicular to the plane. The local structures (Fig. 1 and Fig. S1 of the SI (species 5)) of the active site featuring the alpha oxygen atom only slightly varies depending on the type of the cationic site (i.e., α, β1, and β2¹²).

Although the main feature, i.e. Fe(IV)=O, is similar both to the alpha oxygen in zeolites and enzymes, there are differences in the coordination of Fe. Dehydrated bare Fe(II) cations before the oxidation are pentacoordinated in pyramidal geometry in enzymes while Fe(II) is tetracoordinated and approximately square planar or located on the top of a low pyramid with almost a square base in zeolites. After the oxidation of Fe(II) to Fe(IV)=O, Fe(IV) is hexacoordinated in a bipyramidal geometry in enzymes, while Fe(IV) is pentacoordinated and pyramidal in zeolites.

While the structures of the alpha oxygen in zeolites and enzymes exhibit similarities, the mechanisms of their formation somewhat differ. The alpha oxygen in zeolites originates from splitting nitrous oxide and dioxygen over the active sites to yield the isolated Alpha oxygen atom and a pair of the alpha oxygen atoms, respectively. Conversely, Scheme 1 shows that O₂ adsorbs on Fe(II) of the enzyme (TauD²⁵) to give a monodentate complex. The O terminal atom attacks the C2 atom of the cofactor (α-ketoglutarate²⁵) to either (Pathway I) form a bicyclic complex and subsequently the O–O bond of dioxygen is cleaved together with decarboxylation, or (Pathway II) firstly decarboxylation occurs followed by splitting the O–O bond in the intermediate. In both cases, the structure with a Fe(IV)=O group featuring the alpha oxygen is created.²⁵

4.4. Mechanism of the creation of alpha oxygen from N₂O

The study¹² of Sklenak et al. (for technical details see Section 4.1.) on N₂O decomposition over Fe(II) exchanged ferrierite employed five computational models to investigate five distinct possible arrangements of the Fe(II) active sites in ferrierite. Three models (α, β1, and β2) represented three distinct isolated cationic sites (i.e., the α, β1, and β2 sites, Scheme 2 and Fig. S1A of the SI), while the other two models (β1 + β1 and β2 + β2) featured two cooperating adjacent β cationic sites (Scheme 3 and Fig. S1B of the SI), i.e. the distant binuclear cationic sites, permitting interactions of N₂O with both the Fe(II) cations. The results¹² revealed (i) the calculated structures of the Alpha oxygen atom for all five models were essentially identical and also (ii) the mechanism of the formation of Alpha oxygen for both types (i.e., isolated sites and the distant binuclear cationic sites) of the active sites. N₂O preferentially adsorbs by the N terminal atom (Scheme 2) with the adsorption energies: −12.3, −8.4, and −10.9 kcal mol⁻¹ for the α, β1, and β2 isolated sites, respectively, while the adsorption by the O atoms is weaker by 3.3 (i.e., −9.0) kcal mol⁻¹ for the α site and 5.2 (i.e., −5.7) kcal mol⁻¹ for the β2 site.¹² Surprisingly, N₂O does not adsorb by the O atom on Fe(II) accommodated in the β1 site.¹² The adsorption of N₂O by the N terminal atom on an isolated Fe(II) site leads to its blockage (Scheme 2), while the weaker adsorption by the O atom enables the first chemical step of the N₂O decomposition which is the formation of the Alpha oxygen atom on the isolated Fe(II) cation. The calculated barriers to oxidize Fe(II) in the isolated α and β2 (Scheme 2 and Fig. S1A of the SI) sites to yield Fe(IV)=O are 17.6 and 19.1 kcal mol⁻¹, respectively. The corresponding reaction energies are −7.7 and −10.5 kcal mol⁻¹, respectively.¹² It is not possible to oxidize isolated Fe(II) cations accommodated in the β1 site because N₂O does not adsorb via the O atom on such Fe(II). A subsequent ²⁷Al NMR investigation¹¹² of the ferrierite sample used in the study¹² revealed that only the α and β2 sites are present in the sample. Therefore, all Fe(II) exchanged into the isolated cationic sites of the ferrierite zeolite¹² (i.e., the α and β2 sites) can be oxidized by N₂O.

Conversely, when N₂O can interact with two Fe(II) cations accommodated in two adjacent β sites (i.e., the distant binuclear cationic sites, Scheme 3 and Fig. S1B of the SI), the adsorption of N₂O by the N terminal atom on one Fe(II) yields the [Fe⋯NNO Fe] complex. The corresponding adsorption energies are −5.0 and −9.5 kcal mol⁻¹ for the β1 + β1 and β2 + β2 centers, respectively. N₂O does not adsorb via the O atom on Fe(II) at the β1 site of the β1 + β1 center, while it slightly adsorbs by −3.7 kcal mol⁻¹, on Fe(II) at the β2 site of the β2 + β2 center to yield [Fe NNO⋯Fe] which, however, rearranges into more stable [Fe⋯NNO Fe] in which N₂O is adsorbed by the N terminal atom. The O atom of the adsorbed N₂O in [Fe⋯NNO Fe] is well positioned for the concurrent cleavage of the N–O bond and the creation of the Fe=O bond, because the distance between the O atom of the adsorbed N₂O and the other Fe(II) cation is ca. 3 Å and all five atoms (Fe, N, N, O, and Fe) lie almost in a line. This rare arrangement induces the concurrent cleavage of the N–O bond and the facile creation of the Fe=O bond. The calculated barriers are only 9.4 and 12.3 kcal mol⁻¹ for the β1 + β1 and β2 + β2 centers, respectively. The corresponding reaction energies to give [Fe⋯NN O=Fe] (N₂ is adsorbed on one Fe(II) while the other Fe(II) is oxidized to Fe(IV)=O)) are −15.2 and −17.8 kcal mol⁻¹, respectively. It should be noted that the distance between the two Fe(II) cations forming the distant binuclear cationic sites is ca. 7.4 Å, too far to form Fe–O–O–Fe bridges.

The lower barrier of 12.3 kcal mol⁻¹ for the rate determining step of the formation of the Alpha oxygen calculated for the distant binuclear cationic sites (i.e., the β2 + β2 centers present in the studied Fe-ferrierite sample^12,112) in comparison with the corresponding barriers for the isolated Fe(II) in the α and β2 cationic sites of Fe-ferrierite, both of which are also present in the studied sample,^12,112 i.e., 17.6 and 19.1 kcal mol⁻¹, respectively, explains the superior activity of Fe-ferrierite in the N₂O decomposition in the low temperature region with respect to the Fe-BEA and Fe-ZSM-5 zeolites containing only isolated Fe(II) cationic sites.

4.5. Mechanism of the formation of Alpha oxygen from O₂

Employing the VASP program^80–83 to perform spin-polarized periodic DFT calculations, Sklenak and collaborators predicted that the distant binuclear Fe(II) cationic sites were able to split dioxygen to yield pairs of Alpha oxygen atoms (Scheme 4 and Fig. S1C of the SI).¹⁸ This theoretical forecast was subsequently confirmed by Mössbauer and FTIR spectroscopy experiments and a titration by methane monitored by mass spectrometry measurements.¹⁸

The Kohn–Sham equations were solved variationally in a plane-wave basis set using the projector-augmented wave (PAW) method of Blöchl,¹¹³ as adapted by Kresse and Joubert.¹¹⁴ The exchange–correlation energy was described by the Perdew–Burke–Ernzerhof (PBE⁷⁵) generalized gradient approximation functional. Brillouin zone sampling was restricted to the Γ-point. A plane-wave cutoff of 600 eV and density-dependent energy correction (dDsC) dispersion correction^98,99 were used for geometry optimizations, and a smaller cutoff of 400 eV and the DFT-D2 method¹⁰⁰ were used for the molecular dynamics (MD) simulations. The high-spin electron configuration Fe d⁵↑d¹↓ was employed for the Fe cations accommodated in the zeolite.

The DFT results for the β2 + β2 centers present in the studied ferrierite zeolite showed¹⁸ that O₂ adsorbs on one Fe(II) cation of a pair of Fe(II) cations to yield the less stable monodentate complex (adsorption energy of −14.7 kcal mol⁻¹) and the more stable bidentate complex (adsorption energy of −21.6 kcal mol⁻¹). The adsorbed O₂ moiety in the monodentate complex is optimally positioned to interact with the neighboring Fe(II) center located at the adjacent β2 site. This facilitates the cleavage of dioxygen via a concerted [Fe–O–O–Fe] transition state, leading to the formation of a [Fe=O O=Fe] species. In this product complex, both the Fe centers are oxidized, generating a pair of the distant Alpha oxygen atoms. The reaction energy of the reaction from 1 + O₂(g) to yield [Fe=O O=Fe] is −24.7 kcal mol⁻¹. The calculated barrier of splitting molecular oxygen is 24.9 kcal mol⁻¹, revealing that the oxidation should be fast but slower than the oxidation of the same Fe(II)-ferrierite by N₂O¹⁷ [i.e., the barrier of 14.5 kcal mol⁻¹].¹⁸

The iron exchanged ferrierite featuring the distant binuclear Fe(II) cationic site is the first zeolite-based catalyst able to split dioxygen to yield pairs of the Alpha oxygen atoms able to oxidize methane to methanol even at room temperature.¹⁸ The delicately engineered distant binuclear Fe(II) site has achieved a major breakthrough by converting methane to methanol at room temperature using O₂ as the oxidant, marking significant progress in methane oxidation catalysis.¹¹⁷

4.6. Structure of the alpha oxygen determined by a combination of DFT and ab initio calculations and multi-spectroscopic experiments

Solomon and collaborators proposed the structure of Alpha oxygen in the Fe-BEA zeolite using an indirect site-selective spectroscopic method regularly used in bioinorganic chemistry.¹⁵ While the study did not directly determine the structure since diffraction methods were not employed, Snyder and collaborators suggested the structure mainly based on their magnetic circular dichroism (VTVH-MCD) measurements.¹⁵ Their results (Fig. 2) reveal that α-Fe(II) is a mononuclear, high-spin, square planar Fe(II) site, while the reactive intermediate, the Alpha oxygen, is a mononuclear, high-spin Fe(IV)=O species, whose exceptional reactivity derives from a constrained coordination geometry enforced by the zeolite lattice.¹⁵ The scientists¹⁵ carried out DFT and subsequently CASPT2 cluster calculations using larger and smaller clusters, respectively. Spin-unrestricted DFT cluster calculations were performed with Gaussian 09.¹¹⁸ The B3LYP functional,^119,120 the 6-311G* basis set¹¹⁸ for Fe, for atoms directly coordinated to Fe, and the 6-31G* basis set¹¹⁸ for all other atoms were employed. For geometry optimizations, the six T sites of the 6-rings were allowed to relax, and all other atoms were frozen (O and Si atoms at their crystallographic positions).¹⁵ It should be noted that the B3LYP functional and 6-31G* and 6-311G* basis sets employed in the study¹⁵ were rather obsolete while more modern DFT functionals and especially basis sets were available.¹²¹ Moreover, if the structure of the Fe-BEA zeolite was optimized by periodic DFT,²¹ the calculated structure would have been significantly more reliable.

Moreover, the scientists¹⁵ carried out DFT cluster calculations of the isomer shifts with the ORCA computational package¹²² using the B3LYP functional to interpret their Mössbauer spectroscopy measurements. The CP(PPP)¹²³ basis set was used on Fe, with 6-311G* on coordinating O atoms and 6-31G* on all others.

The scientists¹⁵ also performed CASSCF/CASPT2 calculations using the DFT-optimized geometries employing the MOLCAS-8.1 program.¹²⁴ In the multiconfigurational approach used, relativistic effects were treated in two steps, both based on the Douglas–Kroll Hamiltonian.⁹⁶ Scalar terms were included in the basis-set generation and used to determine spin-free wave functions and energies through the use of the CASSCF method. Electron correlation effects were included employing CASPT2. The spin–orbit coupling was treated in the mean field (AMFI)⁹⁶ by means of the restricted active space state interaction (RASSI) method,¹²⁵ which uses the optimized CASSCF/CASPT2 wave functions as the basis states.

The CASPT2 results allowed the assignment of the 15 900 cm⁻¹ ligand−field band of α-Fe(II) to the 3d_z² → 3d_x²–y² transition of a square planar site. The high energy of this transition reflects the equatorial anisotropy of the α-Fe(II) ligand field, as well as the unique stability of 3d_z² in square planar geometry brought about by 4s mixing in the absence of axial ligands. The small Mössbauer quadrupole splitting of 0.55 mm s⁻¹ has similar origins: the combination of an equatorial ligand field with a doubly occupied 3d_z² orbital (that is, axial distribution of d electron density) leads to near-cancellation of large, oppositely signed lattice and valence contributions to the quadrupole splitting.

The scientists¹⁵ also claimed that these calculations permitted the determination of the Al siting of the two Al atoms in the 6-ring¹⁰² forming cationic sites for Fe(II), i.e., α-Fe(II). The β cationic site is the only one type of cationic sites in the beta zeolite accommodating bare divalent cations with an open coordination sphere.⁶⁶ The site is created by a 6-ring forming a double 6-ring (i.e., hexagonal prism, Fig. 3E). Several possible Al sitings were employed to predict parameters of their circular dichroism. The best agreement was obtained for the two Al atoms occupying the two T6 sites (Fig. 3E).¹⁵ Their calculations further yielded the local geometry of the Alpha oxygen for the β cationic site formed by two Al(T6). However, it should be noted that considering the limited reliability of the optimized structure of the Fe-BEA zeolite (see above) and the restricted accuracy of (i) the quantum chemistry approaches and (ii) the experimental methods used, we conclude that the Al siting of the two Al atoms in the 6-ring of Fe-BEA remains rather uncertain.

The calculated structure¹⁵ is essentially identical with that calculated previously for Fe-ferrierite.¹² The Fe(IV)=O group presents the Alpha oxygen atom and Fe(IV) in the high-spin configuration. Fe(IV) is further charge balanced by the two Al(T6) atoms. The calculated Fe=O bond length is 1.59 Å. The Fe(IV) atom of the Fe(IV)=O group is placed above the plane formed by the four O atoms of two AlO₄⁻ tetrahedra to which the Fe(IV) atom is coordinated. The Fe(IV)=O bond is approximately perpendicular to the plane.

A subsequent study by the same scientists provided the structure of the Fe(IV)=O group accommodated in the 6-ring of the Fe-SSZ-13 zeolite of the chabazite topology based on DFT and CASPT2 cluster calculations and Mössbauer and DR-UV-vis-NIR spectroscopies.¹⁶ Open-shell DFT cluster calculations¹⁶ were performed with the Turbomole software¹²⁶ using the B3LYP^119,120 functional, the def2-QZVPP¹²⁷ basis set on Fe, and def2-TZVP¹²⁸ basis sets on all other atoms to optimize the structure of the cluster models of the double 6-ring or the 8-ring cationic sites of Fe-SSZ-13. The terminal O atoms were end-capped with H and frozen during the geometry optimization, whereas H was allowed to optimize its O–H bond distance, but the direction of the bond was fixed. Then, Fe (or Fe=O) was placed in the ring and a new structure optimization was performed on the quintet surface (i.e., four unpaired electrons with their spins aligned), keeping the terminal O and H atoms fixed in position. While the def2-QZVPP and def2-TZVP basis sets are of superior quality relative to the 6-31G* and 6-311G* basis sets used to optimize the structure of the Alpha oxygen of the Fe-BEA zeolite,¹⁵ if the structure of the Fe-SSZ-13 zeolite was optimized by periodic DFT,⁸⁸ the calculated structure would have been more reliable. Using the optimized structures of the Fe-SSZ-13 zeolite, the authors carried out CASSCF/CASPT2 calculations, and furthermore, DFT cluster calculations of the isomer shifts to interpret their Mössbauer spectroscopy experimental results, both in a very similar manner as in their prior study of the Fe-BEA zeolite.¹⁵ To conclude, the obtained optimized structure of the Fe(IV)=O group in Fe-SSZ-13¹⁶ is very close to that of the Fe-BEA zeolite.¹⁵

4.7. Formation of Alpha oxygen from N₂O on Fe(II) cations in Fe-zeolites

Panov et al. employed a high temperature treatment (600 °C) of the (Fe)ZSM-5 zeolite to release framework Fe to prepare extra-framework Fe(II) cations able to be oxidized by N₂O to give Alpha oxygen.¹ Later an even higher temperature (900 °C) was used by the same group to activate the iron containing zeolites to prepare Alpha oxygen.^6,8 Snyder et al. introduced Fe into the beta zeolite by diffusion impregnation of Fe(acetylacetonate)₃ in toluene solution but still subjected the beta zeolite samples to high-temperature treatment at 900 °C.¹⁵ There is a question of why a high-temperature treatment is needed especially when Fe as Fe(acetylacetonate)₃ is introduced into the zeolite extra-framework sites so there is no need to release Fe from the zeolite framework.¹⁵ Bare Fe(II) cations located in cationic sites are formed at maximally 450 °C.¹¹ However, the same study showed that the high-temperature treatment of Fe-ferrierite at 700 °C resulted in an increase in the catalytic activity.¹¹

Periodic DFT calculations (for technical details regarding ref. 12 and 17 see Sections 4.1 and 4.5, respectively) employing realistic computational models based on the available XRD data of ferrierite^108–110 revealed that Fe(II) cations accommodated in a majority of the types of cationic sites should have been capable of being oxidized by N₂O to yield Fe(IV)=O featuring the Alpha oxygen,^12,17 in other words, should have been α-Fe(II).¹⁵ However, the calculation may provide a clue since they showed that N₂O did not adsorb by the O atom on Fe(II) accommodated in the β1 site and so such isolated Fe(II) in β1 cannot be oxidized to give Fe(IV)=O by N₂O.¹² We can only speculate that inactive Fe(II) cations may be activated by a defect (e.g., framework Al Lewis sites^{102,129–133}) created in their vicinity by the high-temperature treatment. One possibility is that this kind of defect causes an inactive cationic center, such as the Fe(II) β1 site, to change its local structure and become active. Another opportunity is that N₂O adsorbs on the defect by the N terminal atom and by chance the O atom is well positioned to oxidize the Fe(II) in an otherwise inactive cationic center. The reaction mechanism would be similar to that of the distant binuclear cationic sites.

5. Formation of alpha oxygen on systems other than Fe(II)-ferrierite

5.1. Formation of alpha oxygen from N₂O on M(II) cations other than Fe(II) in Me-zeolites

The first study revealing the formation of Alpha oxygen on a different cation than Fe(II) was reported by Radu et al. for Mn-ZSM-5.²⁷ Mn(IV)=O evidenced by X-ray absorption spectroscopy was created by a reaction of N₂O with the Mn(II) cations exchanged in ZSM-5. However, the oxidation properties of the Mn(IV)=O species were not tested by their reaction with methane at room temperature.

The periodic DFT study of Co(II)-ferrierite prevised the capability of the Co(II) cations to abstract the oxygen atom from N₂O to yield the Co(IV)=O species¹⁷ (for technical details see Section 4.5.). The high-spin electron configuration Co d⁵↑d²↓ was employed for the Co cations accommodated in the zeolite. The formation of the Alpha oxygen atoms on Co(II) and Ni(II) were afterward supported by experiments including the ability of Co(IV)=O and Ni(IV)=O to directly oxidize methane to methanol (at room temperature) which can be desorbed.¹⁷ The study¹⁷ employed two computational models for the Co(II) cation (β2 + β2 (Scheme 5) corresponding to the distant binuclear Co(II) cationic sites and β2 (no scheme as there is no reaction) related to isolated Co(II) cationic sites) and one model for the Fe(II) cation for comparison (β2 + β2 (Scheme 5) corresponding to the distant binuclear Fe(II) cationic sites).

Scheme 5 Mechanism and the schematic energy¹⁷ (in kcal mol⁻¹) profiles of the formation of Alpha oxygen atoms from N₂O over the distant binuclear M(II) (M(II) = Fe(II) and Co(II)) cationic sites. Adapted from ref.¹⁷ licensed under a Creative Commons Attribution License 4.0 (CC BY). https://creativecommons.org/licenses/by/4.0/.

The calculations using the β2 model revealed that N₂O did not adsorb on Co(II) via the oxygen atom showing that the Alpha oxygen cannot be formed on isolated Co(II) cations located in the β2 sites of ferrierite. Conversely, the computations employing the β2 + β2 model yielded the mechanism of the formation of Co(IV)=O which is essentially identical with that of the creation of Fe(IV)=O. Firstly, a [Co⋯NNO Co] complex is created by the adsorption of N₂O by the terminal N atom. In this complex, the O atom of N₂O is optimally located to attack the bare Co(II) cation in the adjacent β2 site. The DFT calculations revealed the adsorption energy of −15.4 kcal mol⁻¹ (−16.1 kcal mol⁻¹ for Fe(II)-ferrierite). In the next step, a cleavage of the N–O bond occurs via the [Co–NNO–Co] transition state and the bare Co(II) cation in the adjacent β2 site is oxidized to give a [Co⋯NN O=Co] intermediate. A barrier of 25.0 kcal mol⁻¹ is calculated implying that the oxidation of Co(II) to yield the Alpha oxygen should be fast but slower than the same reaction step on Fe(II)-ferrierite (i.e., the barrier of 14.5 kcal mol⁻¹). The calculated energy for this reaction step is −6.7 kcal mol⁻¹ (−14.2 kcal mol⁻¹ for Fe(II)-ferrierite). Afterward, N₂ desorbs costing 11.5 kcal mol⁻¹ (12.5 kcal mol⁻¹ for Fe(II)-ferrierite) and the [Co O=Co] product with the Alpha oxygen is created.

5.2. Splitting dioxygen over Fe(II)-zeolites other than ferrierite

Periodic DFT calculations including extensive molecular dynamics simulations²¹ (for technical details see Section 4.5.) were employed to investigate the influences of the local arrangement of the distant binuclear Fe(II) centers and framework topology on the ability to cleave the O–O bond of dioxygen to create pairs of the Alpha oxygen atoms. The aim of the periodic DFT calculations was to gain knowledge regarding the origin of the low barriers of the cleavage of dioxygen, whether it resulted from the unique topology of the ferrierite zeolite and the Al organization (especially the Al siting in the rings forming the cationic sites) in the ferrierite used or if the activity regarding splitting dioxygen represents a general property of the distant binuclear Fe(II) centers stabilized in the aluminosilicate matrix. If the latter is the case, it could serve as a highly promising foundation for developing highly active systems with more concentrated active sites for the direct oxidation of methane. Breaking the O–O bond of O₂ across the distant binuclear Fe(II) centers located at the opposite sides of the wall of larger channels may enable the Alpha oxygen to directly oxidize larger molecules that otherwise have limited access through the ferrierite side channels (i.e., through the 8-rings). The synthesis of zeolites with various topologies and the controlled Al organization is a complex and challenging process that requires extensive, long-term research. This clearly shows that periodic DFT calculations are the only way to gain the required knowledge concerning the source of the low barriers of splitting dioxygen. The study²¹ investigated the effect of (i) the Al siting in the rings forming the cationic sites, (ii) the distance, and (iii) the mutual geometrical position of the rings accommodating Fe(II) on the activity of the distant binuclear Fe(II) sites in splitting dioxygen. The ferrierite, mordenite, beta, and A zeolites were employed for this purpose. The molecular dynamics simulations revealed²¹ significant rearrangements of some cationic sites, especially for mordenite with 8-rings forming β sites with various Al sitings (Fig. 5).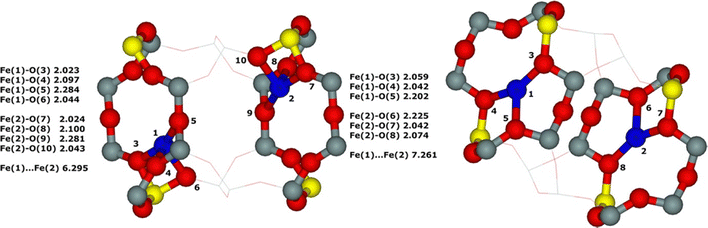

Fig. 5 Optimized structures of 2 Fe(II) in mordenite before (left) and after (right) the DFT molecular dynamics simulations for two adjacent βT1 (MORβT1βT1 model) sites. The distances are in Å. Silicon atoms are in gray, aluminum atoms are in yellow, iron atoms are in blue, and oxygen atoms are in red. Reproduced with permission from ref. 21 Copyright 2021 American Chemical Society.

Marked rearrangements of cationic sites formed by 6-rings can arise, but the mutual geometrical position of the cationic sites (i.e., facing or not facing each other, parallel or nonparallel, and if parallel, whether axial or nonaxial) linked with the structure of the “empty” zeolite remains.²¹ Conversely, the rearrangement of 8-rings (i.e., the β sites in mordenite) can cause a significant change in the local structure of a zeolite, altering the mutual geometrical positions of the cationic sites compared to the original, “empty” zeolite.²¹ This structural change is difficult to predict based solely on the structure of the “empty” zeolite.²¹ To summarize the main results of the study:²¹ the distant binuclear Fe(II) sites with appropriate specifications located in different zeolites could cleave the O–O bond of dioxygen and create a pair of the Alpha oxygen atoms able to oxidize methane to methanol. The ability to split the O–O bond of dioxygen is a common feature of the binuclear Fe(II) centers stabilized in aluminosilicate matrices. This suggests that Fe-zeolite-based systems could be developed for dioxygen activation in direct oxidation reactions using different zeolite matrices. The study²¹ revealed the appropriate specifications of the two cationic sites forming the distant binuclear Fe(II) centers as follows: (i) facing each other, (ii) parallel, and (iii) axial. (iv) The Fe⋯Fe distance has to lie in a narrow range from ca. 7 to ca. 8 Å (ca. 7–ca. 10 Å for the distance between the two rings (forming the corresponding cationic sites) in empty zeolites since this distance is equal or larger than the Fe⋯Fe distances). The Fe⋯Fe distance cannot be directly determined from diffraction measurements. However, it can be inferred through periodic DFT calculations, including MD simulations or other global optimization methods, which allow for potential rearrangements of the cationic sites. The Al siting in the rings creating the cationic centers only indirectly affects breaking the O–O bond of O₂ through the change in the local structure of the active centers and their mutual geometrical positions (i.e., the β sites in mordenite). The DFT calculations²¹ also showed that the adsorption energies of O₂ on Fe(II) depended on the zeolite topology as the values ranged from −11 kcal mol⁻¹ for the βT1βT1 site in mordenite to −27 kcal mol⁻¹ for the βT7βT8 site in the beta zeolite.

5.3. Splitting dioxygen over M(II)−zeolites

The periodic DFT investigation of M(II)-ferrierite zeolites²⁰ (M(II) = Co(II) and Mn(II)) predicted their ability to split dioxygen to give pairs of the Alpha oxygen atoms (Scheme 6).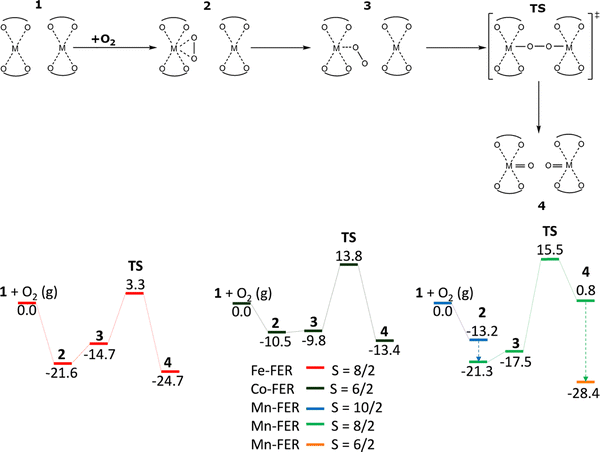

Scheme 6 Mechanism and the schematic energy²⁰ (in kcal mol⁻¹) profiles of the formation of Alpha oxygen atoms from O₂ over the distant binuclear M(II) (M(II) = Fe(II), Co(II), and Mn(II)) cationic sites. Adapted with permission from ref. 20 Copyright 2021 Wiley.

The technical details are revealed in Section 4.5. The high-spin electron configuration Mn d⁵↑d⁰↓ was employed for the Mn cations accommodated in the zeolite. These predictions were subsequently confirmed experimentally for M(II) = Co(II), Mn(II), and Ni(II) including the ability of M(IV)=O to directly oxidize at room temperature methane to methanol which can be desorbed.¹⁹ The DFT calculations revealed that the ability of dioxygen splitting represented a general property of the distant binuclear M(II) centers capable of the M(II) → M(IV) redox cycle with the M⋯M distance of ca. 7.4 Å stabilized in M-ferrierite. The calculated adsorption energies of O₂ on M(II) are the weakest for Co-ferrierite (−10.5 kcal mol⁻¹) and the strongest for both Fe(II)-ferrierite and Mn(II)-ferrierite (−21.6 and −21.3 kcal mol⁻¹, respectively). The calculated barriers for splitting dioxygen are 24.3, 24.9, and 36.8 kcal mol⁻¹ for Co-ferrierite, Fe(II)-ferrierite, and Mn(II)-ferrierite, respectively, indicating a more facile reaction for Co-ferrierite and Fe(II)-ferrierite than for Mn(II)-ferrierite. Combining the findings of the studies of M(II)-ferrierite^18–20 with those obtained for Fe(II)-zeolite²¹ (zeolite = ferrierite, mordenite, beta, and A zeolites), it could be concluded that the distant binuclear M(II) centers capable of the M(II) to M(IV) redox cycle and with the appropriate specifications²¹ are able to split dioxygen to create a pair of Alpha oxygen atoms which can directly oxidize methane to methanol. This proposes creating tunable systems using M(II)-zeolites, where various transition metal cations are incorporated into different zeolite matrices, to activate dioxygen for direct oxidation reactions.

6. Reactivity of alpha oxygen

6.1. Mechanism of the direct oxidation of methane to methanol by the alpha oxygen in Fe-zeolites

Two possible pathways were suggested for the conversion of methane to methanol by the Alpha oxygen created in a zeolite, namely, the rebound mechanism^134,135 and a concerted mechanism.¹³⁶ However, the rebound mechanism has been accepted as the actual mechanism in Fe-zeolites.^50,137 Göltl et al. employed the VASP program^80–83 to perform spin-polarized periodic DFT calculations with the DFT-D2 method¹⁰⁰ using the PBE functional⁷⁵ and ACFDT-RPA method¹³⁸ to investigate the rebound mechanism in the iron exchanged SSZ-13 zeolite of the chabazite structure.⁵⁰ The Kohn–Sham equations were solved variationally in a plane-wave basis set using the projector-augmented wave (PAW) method of Blöchl,¹¹³ as adapted by Kresse and Joubert.¹¹⁴ The exchange–correlation energy was described by the Perdew–Burke–Ernzerhof (PBE⁷⁵) generalized gradient approximation functional and the ACFDT-RPA method in the implementation discussed by Harl and Kresse.¹³⁸ Brillouin zone sampling was restricted to the Γ-point. A plane-wave cutoff of 600 eV and the DFT-D2 method¹⁰⁰ were used for geometry optimizations. The high-spin electron configuration Fe d⁵↑d¹↓ was employed for the Fe cations accommodated in the zeolite. The authors also used the cluster approach to compare it with the periodic approach. The cluster model contained only six T sites and the respective OH terminations and was constructed by keeping the positions of all atoms fixed in the positions of the periodic calculations and only allowing the terminating H atoms to be optimized. The same PBE-D2 and ACFDT-RPA methods were used for the cluster calculations.

The calculations revealed (Scheme 7) that methane adsorbs close to the Alpha oxygen atom and subsequently one hydrogen is abstracted to form an intermediate.

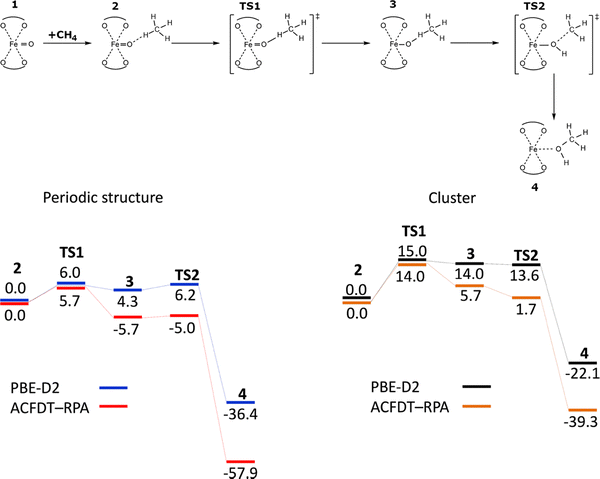Scheme 7 The rebound mechanism and the schematic energy⁵⁰ (in kcal mol⁻¹) profiles (spin state S = 4/2) of the oxidation of methane to yield methanol. Adapted with permission from ref. 50 Copyright 2016 American Chemical Society.

Afterward, the OH group rotates away in the rebound step to form the C–O bond to yield adsorbed methanol. Both the periodic DFT and ACFDT-RPA methods found the abstraction of hydrogen to be the rate determining step with the barrier of ca. 6 kcal mol⁻¹. This computational prediction is in excellent agreement with experiments showing a fast oxidation reaction even at room temperature. The calculated barrier for the rebound step is tiny, up to 2 kcal mol⁻¹ depending on the computational method. The total reaction is highly exothermic, with an energy gain of more than 36 and 58 kcal mol⁻¹, calculated using periodic DFT and ACFDT-RPA methods, respectively, for the adsorbed methanol, compared to the initially adsorbed methane molecule.⁵⁰

A very small cluster with only six T sites was employed to elucidate the impact of the confinement. The cluster calculations yielded the energies for both the methods which differed significantly compared to the calculations for the periodic structure. For the cluster, the barrier for the abstraction of hydrogen increases to ca. 14 kcal mol⁻¹ for both the methods and the intermediate is stabilized significantly more strongly for ACFDT-RPA than for PBE-D2. However, compared to fully periodic calculations, they are more than 10 kcal mol⁻¹ higher in energy, which is a trend that is also seen for the rebound transition state. Interactions between the molecule and the zeolite wall appear to stabilize the intermediate structure significantly more than the transition state for the rebound step that leads to a lower energy for this TS in the cluster calculations. Again, the reaction is highly exothermic, but energies are 14–19 kcal mol⁻¹ higher than for the periodic structures. The substantial energy differences undoubtedly reveal that confinement effects stabilize the reaction intermediates and products in zeolites by 10–19 kcal mol⁻¹ and lower the observed effective reaction barriers by more than 50% for the given structures.

There are marked energy dissimilarities between the ACFDT-RPA and PBE-D2 methods for the cluster calculations which are not due to the confinement. Therefore, the differences must be connected with the changes regarding the description of the chemical interactions between the molecule and the active site. Sauer and collaborators made an analogous opinion when they compared the PBE−D2 and MP2 reaction pathways for the deprotonation of tert-butyl to isobutane and its conversion to surface alkoxides. They concluded that it was not possible to capture the full complexity of interactions using an approach as simple as PBE−D2, since it does not include the self-interaction correction.¹³⁹

Panov and collaborators showed that the selective oxidation of methane by N₂O proceeded by hydrogen abstraction mechanism yielding methoxy and hydroxy groups bound to the α sites.^2,3,13,14 Afterward, a water or water-organic medium (e.g., acetonitrile, dimethyl ether) extraction of methoxy groups strongly bound is needed to obtain methanol.^2,3,13,14 Also, other studies of the selective oxidation of methane by N₂O over Fe-zeolites employed product extraction using a solvent or steam at 25–200 °C as the subsequent step following the methane oxidation step.^140,141 These results are in clear disagreement with the rebound mechanism which leads to adsorbed methanol on Fe(II) cations. Conversely, there are studies in which the Alpha oxygen oxidized methane to methanol which could have been desorbed, and no extraction was needed.^17,18,22,23

In an attempt to reconcile the need to extract methoxy groups strongly bound to the zeolite catalyst on the one hand and the mechanism of the rebound mechanism yielding adsorbed methanol on the other hand, Snyder et al.⁶³ compared two iron exchanged zeolites, one with a small pore aperture (the Fe-SSZ-13 zeolite of the chabazite topology) and one with a large pore aperture (the Fe-BEA zeolite of the *BEA topology). While the size of the chabazite cage is similar to that of the *BEA pore, reactants have to traverse through a constricted 8-ring aperture to get into the cage of the Fe-SSZ-13 zeolite. Snyder et al.⁶³ oxidized Fe(II) in both the zeolites by N₂O to form the Alpha oxygen atoms. Methane is oxidized by the Alpha oxygen and Mössbauer spectroscopy, Resonance Raman spectroscopy, and UV-vis spectroscopy are used to track the state of the iron active sites. The interpretation of the experiments is partly based on DFT calculations of the (i) rebound and (ii) methyl radical escape mechanisms. While the cage escape pathways for the Fe-BEA zeolite and Fe-SSZ-13 differ, their radical rebound mechanisms are similar. The study⁶³ concludes that for the Fe–BEA zeolite (and other zeolites with large pore apertures), the release of CH₃ from Fe(III)–OH⋯CH₃ is most likely a diffusive process that gives catalytically inactivated Fe(III) products featuring Fe(III)–OCH₃ and Fe(III)–OH groups. Steaming has to be applied to gain methanol via hydrolysis of the Fe(III)–OCH₃ groups and the corresponding Fe(III) sites are then autoreduced back to Fe(II) cations⁹ at high temperatures. Conversely, the constricted pore apertures of Fe–SSZ-13 restrict CH₃, supporting its recombination with Fe(III)–OH groups to form methanol adsorbed on Fe(II) cations and returning the active site to its reduced Fe(II) state to permit further turnover after the desorption of methanol. However, the explanation of Snyder et al.⁶³ was ruled out by an afterward study of Kornas et al. on the Fe–BEA zeolite containing the distant binuclear Fe(II) cationic sites.²² Dioxygen was split over the Fe–BEA zeolite to form pairs of the Alpha oxygen atoms which were used to oxidize methane to methanol, however, adsorbed methanol was formed. These results²² refute the explanation of Snyder et al.⁶³ regarding the size of the ring as the decisive factor determining whether adsorbed methanol or Fe(III)–OCH₃ and Fe(III)–OH groups are formed.

Moreover, Scott¹⁴² pointed out that when the distant binuclear Fe(II) cationic sites are used to prepare pairs of the Alpha oxygen atoms, the proximity of two Fe(II) cations (ca. 7.4 Ź⁸) should enhance the undesired ferryl trapping of methyl radicals that leads to Fe(III)–OCH₃ and Fe(III)–OH sites.¹⁴² While this assumption appears to be logical, the experimental results are not in agreement with it as adsorbed methanol is formed when the distant binuclear cationic sites oxidized by either N₂O¹⁷ or O₂^18,19,22,23 are employed.

The Reactive Mode Composition Factor method was developed¹⁴³ to evaluate the kinetic energy distribution within the reactive mode of a transition state. This method was subsequently used¹⁴⁴ to predict the selectivity toward either the rebound mechanism or the dissociation mechanism (i.e., analogical to the methyl radical escape mechanism) following H-atom abstraction from a substrate C–H bond by high-valent iron-oxo oxidants present in various enzymes. The results showed that the mechanism depended on the structure and chemical composition of the substrate.¹⁴⁴ However, this method most likely cannot be used to explain the mechanisms of the direct oxidation of methane to methanol using the Alpha oxygen prepared in various Fe-zeolites since both the structure and chemical composition of the reactant, i.e., methane, are the same. Similarly, the structures of the Fe(IV)=O groups in various zeolites are close and the chemical compositions in various zeolites are identical.

We can only speculate that adsorbed methanol is formed in most or eventually all experiments concerning the direct oxidation of methane to methanol by the Alpha oxygen, but when methanol is desorbed, it can interact with various defect (e.g., framework Al Lewis sites^{102,129–133}) or other reactive sites eventually present in the zeolite to form methoxy groups. It is clear that this issue requires further investigations.

The rebound mechanism is responsible for the direct oxidation of methane leading to methanol. Conversely, dimethyl ether could be formed via the methyl radical escape mechanism. Methyl radicals react further with methoxy groups to yield dimethyl ether. However, methanol when it desorbs can react with more Alpha oxygen atoms to give formaldehyde, formic acid, and finally carbon dioxide. The reaction barriers for the subsequent oxidations of methanol to formaldehyde, formaldehyde to formic acid, and formic acid to carbon dioxide are assumed to be even lower than the already low barrier for the first step, i.e., methane to methanol (ca. 6 kcal mol⁻¹)⁵⁰ since methane is the least reactive. Since the product of the direct oxidation of methane over the distant binuclear cationic sites is adsorbed methanol,^{17–19,22,23} the selectivity of the entire reaction is limited due to subsequent oxidations to formaldehyde, formic acid, and finally carbon dioxide. Therefore, the desorption of methanol can play a substantial role in the control of the product selectivity. Contrarily, when extraction of methoxy groups strongly bound is needed to obtain methanol,^2,3,13,14 the chance of the oxidation to carbon dioxide is low.

6.2. Mechanism of the oxidation of dihydrogen to water by the alpha oxygen in Fe-ferrierite

The oxidation of dihydrogen by the Alpha oxygen to give water is the simplest model reaction which allows comparison of the reactivity of isolated Alpha oxygen atoms with that of pairs of the Alpha oxygen atoms. Sklenak et al.⁶² employed periodic DFT using a computational model of Fe-ferrierite featuring two adjacent β2 sites. The technical details are revealed in Section 4.5. The study⁶² revealed that (i) the two Fe(IV)=O sites of pairs of the distant Alpha oxygen atoms are not reduced in a concerted manner, (ii) dihydrogen firstly reacts with one Fe(IV)=O site of a pair of the distant Alpha oxygen atoms and reduces it to give adsorbed water on Fe(II) and at the same time the other Fe(IV)=O center does not react, and afterward, one of the H atoms of the adsorbed H₂O is abstracted by the other Alpha oxygen atom to form two Fe(III)–OH groups, which are subsequently reduced by another H₂ to yield two H₂O each adsorbed on one Fe(II) cation, (iii) the reduction of an isolated Fe(IV)=O center occurs by the same mechanism as one Fe(IV)=O site of a pair of the distant Alpha oxygen atoms, and (iv) the Fe(IV)=O sites of pairs of the distant Alpha oxygen atoms exhibit lower reducibility with respect to the isolated Fe(IV)=O sites.

The abstraction of one of the hydrogen atoms of the adsorbed water by the other Alpha oxygen atom to yield two Fe(III)–OH groups indicates that when one molecule of methane is oxidized by one Alpha oxygen atom of a pair of the Alpha atoms to yield adsorbed methanol, the other Alpha oxygen can abstract hydrogen from the adsorbed methanol to create Fe(III)–OCH₃ and Fe(III)–OH groups in agreement with the assumption of Scott.¹⁴² However, since the experimental results^{17–19,22,23} are not in agreement with the assumption, the mechanism of the direct oxidation of methane to methanol must be more complex. This problem demands further investigations.

The results⁶² from the oxidation of H₂ highlight that the presence of an adjacent Fe(IV)=O center within the confined reaction space of a zeolite cavity significantly alters the behavior of both the cooperating Alpha oxygen atoms and the reaction mechanism. This effect likely extends to other molecules beyond dihydrogen. The reaction mechanism over Fe(IV)=O sites of a pair of the distant Alpha oxygen atoms can vary from that observed with isolated Fe(IV)=O sites.

7. Perspectives

Due to the significant potential of the utilization of the Alpha oxygen in chemical technology, the perspective of research in this field splits into two segments – (i) the scientific perspective and (ii) the prospect regarding the application field. Nevertheless, a detail understanding of both (i) the structure of the active sites and (ii) their catalytic performance has not only scientific relevance but also represents a necessary base for the application of Alpha oxygen for the benefit of society as a whole. The latter also includes the reaction mechanisms of both the formation of the Alpha oxygen and its subsequent reactions with various molecules.

7.1. Scientific challenges

Surprisingly, although the formation of a pair of Alpha oxygen atoms by the cleavage of molecular oxygen has been investigated for a significantly shorter time than the formation of the Alpha oxygen from N₂O,^1–10,13,14 the studies reveal that the Alpha oxygen produced from N₂O is the same as that created from O₂.^18–23 Moreover, the Alpha oxygen is the same regardless of the slightly different active sites in different zeolite topologies on which it is formed.

Conversely, when Alpha oxygen is prepared from N₂O, the substantial role of the high temperature treatment (temperatures of 600 °C¹ and higher up to 900 °C^6,8,15,16 are essential to create highly active samples) of the zeolite still represents a mystery. The local structure of the active Fe(II) sites resulting from the interpretation of experimental data and DFT calculations is the same as that typically obtained by dehydration of metallo-zeolites at significantly lower temperatures (ca. 450 °C).^11,12 Detailed studies of the complex local structure, not only of the active sites but also of a significantly larger portion of the zeolite including possible defects, are necessary to solve this mystery. However, the elucidation of the reaction mechanism of the oxidation of methane by the Alpha oxygen represents without any doubt the biggest scientific challenge. Namely, why in most cases are the products of the oxidation of methane over isolated Alpha oxygen atoms a hydroxy group on one Fe cation (i.e., Fe–OH) and a methoxy group on the other Fe (i.e., Fe–OCH₃), while in at least one case (i.e., Fe–SSZ-13⁶³) only methanol is formed and no methoxy and hydroxy groups are created. One explanation of the creation of Fe–OH and Fe–OCH₃ groups is that the oxidation of methane proceeds via the dissociation mechanism. Another possibility is that the oxidation of methane occurs always via the rebound mechanism yielding methanol, however, when CH₃OH is desorbed in some zeolite systems (i.e., those which underwent a high temperature treatment (600–900 °C) which created defects and other reactive sites), methanol reacts with either defects or other reactive sites to give methoxy and hydroxy groups which do not have to be bound to Fe. The selective oxidation of methane over one beta zeolite sample gave methanol²² while a different beta zeolite sample yielded Fe–OH and Fe–OCH₃ groups.⁶³ The Reactive Mode Composition Factor method¹⁴³ able to predict the selectivity toward either the rebound mechanism or the dissociation mechanism most likely cannot be used either since very minor differences in the local structure of the Fe(II) active sites in various zeolites cannot result in the change of the reaction mechanism of the oxidation of methane (e.g., the case of the oxidation methane by isolated Alpha oxygen atoms vs. pairs of the Alpha oxygen in the beta zeolite).¹⁴⁴ It should be noted that a significantly more pronounced variability of the arrangement and electronic properties of the distant binuclear cationic sites formed using either different transition metal cations^18,19 or different zeolite topologies^18,22,23,63 does not affect the reaction pathway.

Another interesting issue that deserves attention is the electronic structure of the Alpha oxygen (i.e., Fe(IV)=O or Fe(III)–O⁻˙) and its relevance to the reactivity. The former structure corresponds to the majority opinion.^15,21 DFT calculations revealed that the Fe=O species with four unpaired electrons represented the ground state.²¹ The iterative Hirshfeld charges were calculated to be +1.75 for the Fe cation and −0.39 for the Alpha oxygen atom, revealing that the species corresponds mainly to the [Fe(IV)=O]²⁺ structure balanced by two Al atoms of the zeolite framework.²¹

A specific issue of the reaction pathway is the oxidation of methane over a pair of the Alpha oxygen atoms formed by cleavage of dioxygen. While the two Alpha oxygen atoms facing each other across the zeolite channel with a distance of ca. 3.4 Å represent the optimum structure for the formation of a hydroxy group on one Fe cation (i.e., Fe–OH) and a methoxy group on the other Fe (i.e., Fe–OCH₃), only methanol is formed and no methoxy and hydroxy groups are created.¹⁸ This result is without any doubt a puzzle. However, this counterintuitive result is of extreme importance as it constitutes the basis for possible industrial applications of the distant binuclear sites in selective oxidations, namely the conversion of methane to methanol.

Another extremely interesting question, waiting to be solved, is the role of water in (i) the process of the formation of Alpha oxygen atoms and (ii) subsequent oxidation reactions of Alpha oxygen with methane or other molecules. Water molecules are present in small concentrations in a number of experiments and the water presence can dramatically affect the active site performance, as is well known and studied in the detail for processes utilizing activation of molecular oxygen via oxygen bridges. The elucidation of the role of water is important for the interpretation of experiments. Moreover, the presence of water can primarily represent a key issue in the field of the application of the Alpha oxygen in industrial processes.

7.2. Challenges in the application field

Without any doubt, the potential of applications of the Alpha oxygen in the field of chemical technology including fuel industry is enormous. Alpha oxygen prepared from molecular oxygen, which corresponds to a cheap, easily available, benign, and environmentally friendly oxidant, can participate in solving some crucial issues facing contemporary society.

7.2.1. Methane to methanol. Methane as the main natural gas component is greenhouse gas with a significantly higher global warming potential compared to carbon dioxide. The selective oxidation of methane using the Alpha oxygen prepared from molecular oxygen can serve as a solution regarding the methane emissions by several ways: (i) highly efficient transformation of methane/natural gas to liquid. (ii) Transformation of methane to methanol as a step in the synthesis of e-fuels when methane is prepared from CO₂ and hydrogen using low CO₂ emitting energy sources and methanol is finally converted to gasoline. Beside the two above mentioned ultimate goals – chemical gas to liquid transformation of natural gas or synthesis of “solar” fuels via the methanol pathway, the selective oxidation of methane to methanol can solve (iii) the utilization of methane in flare gases of the oil production and (iv) the facilitation of the transport and storage of biogas in areas without a simple connection to pipeline networks.

It can be concluded that although it seems that one reaction, the selective oxidation of methane to methanol by molecular oxygen, is a promising possible solution for a number of tasks, in reality it relates to a number of different processes matching with significantly different requirements and working at different conditions (e.g., composition of the feedstock, absence/presence of water sources at the locality of the process application). It is necessary to develop new materials exhibiting high yields per hour of this quasi-catalytic (cyclic) reaction to reach the applicability of the conversion of methane to methanol in some of the above-mentioned processes using the Alpha oxygen. A high number of the active sites capable of splitting molecular oxygen is one of the key assumptions for reaching this task. Thus, both the increase in (i) the framework Al content and (ii) the fraction of Al atoms in pairs cannot raise the number of possible binuclear sites. Therefore, new topologies with adjacent/opposite rings at the appropriate distance and with the Al organization guaranteeing the presence of Al pairs in these rings have to be developed to increase the concentration of binuclear sites in the zeolite. Synthesis of Al-rich beta zeolites with a high number of Al pairs shows that this way is possible.²²

In addition, the development of active sites with a high adsorption energy for dioxygen, low barrier for splitting dioxygen, and thermodynamically more stable pairs of the Alpha oxygen atoms than O₂ molecules creating the reverse reaction (i.e., [Fe(II) Fe(II)] + O₂ ← [Fe(IV)=O O=Fe(IV)]) is extremely demanding. DFT calculations show that the nature of the cation forming the distant binuclear sites in combination with the geometry of the site given by the zeolite topology results in significant variations of all these parameters.²⁰ However, a major part of possible sites has not been exanimated yet. Only Fe(II), Co(II), Mn(II), and Ni(II) cations embedded in the ferrierite matrix were investigated for this purpose.^18,19

7.2.2. Other oxidation reactions. The capability of the Alpha oxygen to selectively oxidize other molecules than methane has been known from the time of its discovery. The main attention was focused on the oxidation of benzene to phenol, although also the dehydrogenation (ODH) reaction over the Alpha oxygen was suggested. However, the high price of N₂O as an oxidant represents a significant obstacle for applications of the Alpha oxygen in these reactions. Splitting molecular oxygen to yield a pair of the Alpha oxygen atoms can be regarded as a game changer from an economical point of view for the selective oxidation/ODH of small molecules, but the restriction of the accessibility of the distant binuclear cationic sites and thus of the Alpha oxygen in ferrierite by 8-rings still represents a significant limitation from the reaction point of view. Conversely, the formation of easily accessible isolated Alpha oxygen atoms from N₂O or pairs of the Alpha oxygen atoms in the 12-ring channel system of the beta zeolites opens up the possibility of selective oxidations of larger molecules with dioxygen and might open new perspectives in the field of selective oxidation catalysis science and technology.

7.3. So far unexamined or low examined materials

7.3.1. Mesoporous molecular sieves. The territory of other materials close to zeolite – mesoporous molecular sieves – is completely uncharted. Mesoporous aluminosilicates can be regarded as mesoporous analogues to zeolites. Although these materials lack long-range ordering, their inner channel surface is composed of rings, some of them containing two framework Al atoms and exhibiting analogous behavior as zeolite rings with two framework Al atoms. They are also able to accommodate bare divalent transition metal cations with an open coordination sphere accessible for reactants as is typical for cationic sites in zeolites. While the formation of two adjacent/opposite cooperation cations of the distant binuclear cationic sites is improbable, an accommodation of isolated Fe(II) bare cations analogous to Fe-zeolites in, for example, (Al)MCM-41, is expected in analogy with the Co(II) siting in Co-(Al)MCM-41.¹⁴⁵ This opens up the possibility of the formation of Alpha oxygen atoms by the decomposition of N₂O on a wall of a mesoporous channel. Such isolated Fe(IV)=O sites would be accessible for large molecules. The high price of N₂O as the oxidant required to create the Alpha oxygen over isolated Fe(II) cations represents a limiting factor for possible applications in the case of zeolites allowing transformations of only small molecules. Conversely, this economic limitation may not play a role in the matter of the selective oxidation of some bulky molecules. Therefore, the combination of unique properties of the Alpha oxygen with their stabilization in mesoporous molecular sieves could potentially bring both very interesting insights into the reactivity of bulky molecules and possible application in selective oxidation processes. No attempt to prepare the Alpha oxygen in metallo-mesoporous aluminosilicates molecular sieves has been reported.

7.3.2. MOFs. Metal organic frameworks are another type of porous materials with a number of properties typical for zeolites – i.e., crystallinity, high porosity, and regularity of active sites. In opposition to mesoporous molecular sieves, some attempts have been made to investigate the possibility of the formation of Alpha oxygen atoms in these materials and their employment for selective oxidation of methane. Vitillo et al.¹⁴⁶ used quantum chemical characterization of Fe(II) cations present as structural moieties in several metal–organic frameworks. The calculations showed that these materials are potentially promising catalysts for C–H bond activation, with energetic barriers as low as ca. 10 kcal mol⁻¹ for ethane and ca. 15 kcal mol⁻¹ for methane following the oxidative activation of iron. The activation of N₂O was computed to be the rate-determining step with a barrier of ca. 35 kcal mol⁻¹. Adamji et al.¹⁴⁷ theoretically investigated the potential of MOFs to form the Alpha oxygen and subsequently selectively oxidize methane. It was shown that MOF materials with transition metal cation sites with an open coordination sphere exist and that Mn cations in these positions are able to interact with N₂O, split N₂O with a rather low barrier of some 10 kcal mol⁻¹ to yield Alpha oxygen which is then able to react with methane via the rebound mechanism and form methanol with an energy barrier of ca. 10 kcal mol⁻¹. However, N₂O represents the source of the creation of the Alpha oxygen. This fact makes the study highly scientifically important, but rather unpromising for possible applications. Tofoni et al.¹⁴⁸ even spectroscopically proved a redox cycle connected with the formation of the Alpha oxygen on Fe from O₂ and its subsequent reduction via interaction with methane. Moreover, the suggested mechanism of the Alpha oxygen formation is very close to that in enzymes – assistance of some oxygen acceptors is required (another molecule of methane in their calculations without any significant experimental support), as well as its structure (Fe(II) cation is five coordinated and the Fe(IV) cation of Fe(IV)=O exhibits bipyramidal coordination). It should be noted that other organic molecules or fragments can be present in the MOF which can serve as oxygen atom acceptors. Thus, it can be concluded that the Alpha oxygen can be formed in MOF materials, but rather only by splitting N₂O.^146–149 However, the real challenge is the formation of a pair of Alpha oxygen atoms by splitting dioxygen on something other than zeolite catalysts.

7.4. Discovery of additional zeolite topologies able to form Alpha oxygen from O₂

On the one hand, only a small subset of existing zeolites (i.e., only those which are important matrices heavily used in industrial catalysis) have been studied by periodic DFT calculations²¹ whether they can form the distant binuclear cationic structures able to split dioxygen to yield pairs of the Alpha oxygen atoms. On the other hand, there have been zeolites synthesized with more than 200 different topologies. It was shown²¹ that using only the distance between the 6-rings and 8-rings could not predict the ability to split O₂. Periodic DFT calculations with extensive conformational sampling of transition metal cations²¹ accommodated in various 6-rings and 8-rings of zeolites are the fastest and cheapest way to find zeolite candidates which can be subsequently experimentally examined. It is conceivable that machine learning could be employed in such an endeavor to expedite the search for zeolite topologies. The extensive conformational sampling of the transition metal cations located in different 6-rings and 8-rings of zeolite frameworks is very time consuming, and therefore, after the machine learning method is trained on several zeolite topologies, it can automatically interpolate between known training systems that were previously calculated ab initio to significantly speed up the calculations. Afterward, the selected zeolite candidates can be recalculated fully ab initio to increase the reliability of the computational predictions.

8. Conclusions

The discovery of a possible preparation route for pairs of Alpha oxygen atoms via cleavage of molecular oxygen over the distant binuclear cationic sites in zeolites together with a possible formation of Alpha oxygen accessible to large molecules despite the oxygen atom source (i.e., from both N₂O and O₂) exhibits enormous potential. The main challenge is in the conversion of methane to valuable liquid products. It should be noted that selective oxidation using Alpha oxygen is not a guaranteed route of reaching this goal, but the potential impact of any success is of global importance. Moreover, applications of Alpha oxygen in the field of selective oxidations of other molecules is also an important field, that is relatively unexplored from both scientific and application points of view.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data sharing is not applicable to this article because this is a review article and no datasets were generated.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5cs00496a.

Acknowledgements

The authors gratefully acknowledge the financial support from the project “The Energy Conversion and Storage” funded as project CZ.02.01.01/00/22_008/0004617 by the Programme Johannes Amos Commenius, call Excellent Research. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90254).

References

1. G. I. Panov, V. I. Sobolev and A. S. Kharitonov, J. Mol. Catal., 1990, 61, 85–97.
2. V. I. Sobolev, K. A. Dubkov, O. V. Panna and G. I. Panov, Catal. Today, 1995, 24, 251–252.
3. K. A. Dubkov, V. I. Sobolev, E. P. Talsi, M. A. Rodkin, N. H. Watkins, A. A. Shteinman and G. I. Panov, J. Mol. Catal. A:Chem., 1997, 123, 155–161.
4. K. A. Dubkov, V. I. Sobolev and G. I. Panov, Kinet. Catal., 1998, 39, 72–79.
5. K. A. Dubkov, E. A. Paukshtis and G. I. Panov, Kinet. Catal., 2001, 42, 205–211.
6. K. A. Dubkov, N. S. Ovanesyan, A. A. Shteinman, E. V. Starokon and G. I. Panov, J. Catal., 2002, 207, 341–352.
7. D. P. Ivanov, V. I. Sobolev and G. I. Panov, Appl. Catal., A, 2003, 241, 113–121.
8. E. V. Starokon, K. A. Dubkov, L. V. Pirutko and G. I. Panov, Top. Catal., 2003, 23, 137–143.
9. G. I. Panov, E. V. Starokon, L. V. Pirutko, E. A. Paukshtis and V. N. Parmon, J. Catal., 2008, 254, 110–120.
10. L. V. Pirutko, V. S. Chernyavsky, E. V. Starokon, A. A. Ivanov, A. S. Kharitonov and G. I. Panov, Appl. Catal., B, 2009, 91, 174–179.
11. K. Jisa, J. Novakova, M. Schwarze, A. Vondrova, S. Sklenak and Z. Sobalik, J. Catal., 2009, 262, 27–34.
12. S. Sklenak, P. C. Andrikopoulos, B. Boekfa, B. Jansang, J. Novakova, L. Benco, T. Bucko, J. Hafner, J. Dedecek and Z. Sobalik, J. Catal., 2010, 272, 262–274.
13. E. V. Starokon, M. V. Parfenov, L. V. Pirutko, S. I. Abornev and G. I. Panov, J. Phys. Chem. C, 2011, 115, 2155–2161.
14. E. V. Starokon, M. V. Parfenov, S. S. Arzumanov, L. V. Pirutko, A. G. Stepanov and G. I. Panov, J. Catal., 2013, 300, 47–54.
15. B. E. R. Snyder, P. Vanelderen, M. L. Bols, S. D. Hallaert, L. H. Bottger, L. Ungur, K. Pierloot, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Nature, 2016, 536, 317–321.
16. M. L. Bols, S. D. Hallaert, B. E. R. Snyder, J. Devos, D. Plessers, H. M. Rhoda, M. Dusselier, R. A. Schoonheydt, K. Pierloot, E. I. Solomon and B. F. Sels, J. Am. Chem. Soc., 2018, 140, 12021–12032.
17. E. Tabor, M. Lemishka, Z. Sobalik, K. Mlekodaj, P. C. Andrikopoulos, J. Dedecek and S. Sklenak, Commun. Chem., 2019, 2, 71.
18. E. Tabor, J. Dedecek, K. Mlekodaj, Z. Sobalik, P. C. Andrikopoulos and S. Sklenak, Sci. Adv., 2020, 6, eaaz9776.
19. K. Mlekodaj, M. Lemishka, S. Sklenak, J. Dedecek and E. Tabor, Chem. Commun., 2021, 57, 3472–3475.
20. J. Dedecek, E. Tabor, P. C. Andrikopoulos and S. Sklenak, Int. J. Quantum Chem., 2021, 121, e26611.
21. E. Tabor, M. Lemishka, J. E. Olszowka, K. Mlekodaj, J. Dedecek, P. C. Andrikopoulos and S. Sklenak, ACS Catal., 2021, 11, 2340–2355.
22. A. Kornas, E. Tabor, D. K. Wierzbicki, J. E. Olszowka, R. Pilar, J. Dedecek, M. Sliwa, H. Jirglova, S. Sklenak, D. Rutkowska-Zbik and K. Mlekodaj, Appl. Catal., B, 2023, 336, 122915.
23. K. Tarach, J. Sobalska, A. Held, J. Dedecek, E. Tabor and K. Góra-Marek, J. Phys. Chem. C, 2024, 128, 3759–3769.
24. B. E. R. Snyder, M. L. Bols, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Chem. Rev., 2018, 118, 2718–2768.
25. J. C. Paris, Y. H. Cheung, T. Zhang, W. C. Chang, P. H. Liu and Y. S. Guo, ChemBioChem, 2024, 25, e202400307.
26. H. Li, C. Paolucci, I. Khurana, L. Wilcox, F. Göltl, J. D. Albarracin-Caballero, A. J. Shih, F. H. Ribeiro, R. Gounder and W. F. Schneider, Chem. Sci., 2019, 10, 2373–2384.
27. D. Radu, P. Glatzel, A. Gloter, O. Stephan, B. M. Weckhuysen and F. M. F. de Groot, J. Phys. Chem. C, 2008, 112, 12409–12416.
28. V. I. Sobolev, G. I. Panov, A. S. Kharitonov, V. N. Romannikov, A. M. Volodin and K. G. Ione, J. Catal., 1993, 139, 435–443.
29. V. I. Sobolev, G. I. Panov, A. S. Kharitonov, V. N. Romannikov and A. M. Volodin, Kinet. Catal., 1993, 34, 797–802.
30. Y. F. Chang, J. G. McCarty and Y. L. Zhang, Catal. Lett., 1995, 34, 163–177.
31. F. Kapteijn, G. Marban, J. RodriguezMirasol and J. A. Moulijn, J. Catal., 1997, 167, 256–265.
32. M. Rauscher, K. Kesore, R. Mönnig, W. Schwieger, A. Tissler and T. Turek, Appl. Catal., A, 1999, 184, 249–256.
33. K. Yoshizawa, Y. Shiota, T. Yumura and T. Yamabe, J. Phys. Chem. B, 2000, 104, 734–740.
34. K. Yoshizawa, T. Yumura, Y. Shiota and T. Yamabe, Bull. Chem. Soc. Jpn., 2000, 73, 29–36.
35. N. A. Kachurovskaya, G. M. Zhidomirov, E. J. M. Hensen and R. A. van Santen, Catal. Lett., 2003, 86, 25–31.
36. C. R. F. Lund, J. Catal., 2006, 243, 438–441.
37. M. F. Fellah and I. Onal, Catal. Today, 2008, 137, 410–417.
38. M. F. Fellah and I. Önal, Turk. J. Chem., 2009, 33, 333–345.
39. M. F. Fellah, R. A. van Santen and I. Onal, J. Phys. Chem. C, 2009, 113, 15307–15313.
40. M. F. Fellah and I. Onal, J. Phys. Chem. C, 2010, 114, 3042–3051.
41. B. R. Wood, J. A. Reimer and A. G. Bell, J. Catal., 2002, 209, 151–158.
42. G. D. Pirngruber, J. Catal., 2003, 219, 456–463.
43. B. R. Wood, J. A. Reimer, A. T. Bell, M. T. Janicke and K. C. Ott, J. Catal., 2004, 224, 148–155.
44. A. Waclaw, K. Nowinska, W. Schwieger and A. Zielinska, Catal. Today, 2004, 90, 21–25.
45. G. D. Pirngruber and P. K. Roy, Catal. Lett., 2004, 93, 75–80.
46. J. A. Z. Pieterse, S. Booneveld and R. W. van den Brink, Appl. Catal., B, 2004, 51, 215–228.
47. G. Mul, M. W. Zandbergen, F. Kapteijn, J. A. Moulijn and J. Pérez-Ramírez, Catal. Lett., 2004, 93, 113–120.
48. D. A. Bulushev, L. Kiwi-Minsker and A. Renken, J. Catal., 2004, 222, 389–396.
49. J. Nováková, M. Schwarze and Z. Sobalík, Catal. Lett., 2005, 104, 157–162.
50. F. Göltl, C. Michel, P. C. Andrikopoulos, A. M. Love, J. Hafner, I. Hermans and P. Sautet, ACS Catal., 2016, 6, 8404–8409.
51. B. E. R. Snyder, M. L. Bols, H. M. Rhoda, P. Vanelderen, L. H. Böttger, A. Braun, J. J. Yan, R. G. Hadt, J. T. Babicz, M. Y. Hu, J. Y. Zhao, E. E. Alp, B. Hedman, K. O. Hodgson, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12124–12129.
52. J. B. Lim, S. H. Cha and S. B. Hong, Appl. Catal., B, 2019, 243, 750–759.
53. E. Tabor, G. Sádovská, M. Bernauer, P. Sazama, J. Nováková, V. Fíla, T. Kmjec, J. Kohout, K. Záveta and Z. Sobalík, Appl. Catal., B, 2019, 240, 358–366.
54. G. Y. Zhao, E. Benhelal, A. Adesina, E. Kennedy and M. Stockenhuber, J. Phys. Chem. C, 2019, 123, 27436–27447.
55. T. Zhang, Y. Qiu, G. H. Liu, J. J. Chen, Y. Peng, B. Liu and J. H. Li, J. Catal., 2020, 392, 322–335.
56. G. Y. Zhao, K. Chodyko, E. Benhelal, A. Adesina, E. Kennedy and M. Stockenhuber, J. Catal., 2021, 400, 10–19.
57. M. L. Bols, B. E. R. Snyder, H. M. Rhoda, P. Cnudde, G. Fayad, R. A. Schoonheydt, V. Van Speybroeck, E. I. Solomon and B. F. Sels, Nat. Catal., 2021, 4, 332–340.
58. M. L. Bols, J. Devos, H. M. Rhoda, D. Plessers, E. Solomon, R. A. Schoonheydt, B. F. Sels and M. Dusselier, J. Am. Chem. Soc., 2021, 143, 16243–16255.
59. C. Ouyang, J. W. Li, Y. Q. Qu, S. Hong and S. B. He, Green Energy Environ., 2023, 8, 1161–1173.
60. S. Wang, C. C. Li, C. Liu and W. Zhuang, ChemCatChem, 2025, 17, e202401416.
61. K. Mlekodaj, M. Lemishka, A. Kornas, D. K. Wierzbicki, J. E. Olszowka, H. Jirglová, J. Dedecek and E. Tabor, ACS Catal., 2023, 13, 3345–3355.
62. S. Sklenak, T. Groizard, H. Jirglova, P. Sazama and J. Dedecek, J. Phys. Chem. C, 2022, 126, 4854–4861.
63. B. E. R. Snyder, M. L. Bols, H. M. Rhoda, D. Plessers, R. A. Schoonheydt, B. F. Sels and E. Solomon, Science, 2021, 373, 327–331.
64. A. Kornas, K. Mlekodaj and E. Tabor, ChemPlusChem, 2024, 89, e202300543.
65. J. van Bokhoven and C. Lamberti, Coord. Chem. Rev., 2014, 277, 275–290.
66. J. Dedecek, E. Tabor and S. Sklenak, ChemSusChem, 2019, 12, 556–576.
67. P. Andrikopoulos, Z. Sobalik, J. Novakova, P. Sazama and S. Sklenak, ChemPhysChem, 2013, 14, 520–531.
68. T. Demuth, X. Rozanska, L. Benco, J. Hafner, R. van Santen and H. Toulhoat, J. Catal., 2003, 214, 68–77.
69. L. Benco, T. Bucko, J. Hafner and H. Toulhoat, J. Phys. Chem. B, 2004, 108, 13656–13666.
70. T. Bucko, L. Benco and J. Hafner, Stud. Surf. Sci. Catal., 2005, 158, 601–608.
71. V. Avdeev and A. Bedilo, Chem. Phys. Lett., 2018, 695, 222–227.
72. G. Li, E. Pidko, R. van Santen, Z. Feng, C. Li and E. Hensen, J. Catal., 2011, 284, 194–206.
73. G. Li, E. Pidko, R. van Santen, C. Li and E. Hensen, J. Phys. Chem. C, 2013, 117, 413–426.
74. G. Li, E. Pidko, I. Filot, R. van Santen, C. Li and E. Hensen, J. Catal., 2013, 308, 386–397.
75. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
76. F. Göltl and J. Hafner, J. Chem. Phys., 2012, 136, 064501.
77. F. Göltl and J. Hafner, J. Chem. Phys., 2012, 136, 064502.
78. F. Göltl and J. Hafner, J. Chem. Phys., 2012, 136, 064503.
79. N. Balabanov and K. Peterson, J. Chem. Phys., 2006, 125, 074110.
80. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
81. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
82. G. Kresse and J. Furthmuller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
83. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
84. L. Benco, T. Bucko, R. Grybos, J. Hafner, Z. Sobalik, J. Dedecek and J. Hrusak, J. Phys. Chem. C, 2007, 111, 586–595.
85. L. Benco, T. Bucko, R. Grybos, J. Hafner, Z. Sobalik, J. Dedecek, S. Sklenak and J. Hrusak, J. Phys. Chem. C, 2007, 111, 9393–9402.
86. S. Sklenak, P. C. Andrikopoulos, S. R. Whittleton, H. Jirglova, P. Sazama, L. Benco, T. Bucko, J. Hafner and Z. Sobalik, J. Phys. Chem. C, 2013, 117, 3958–3968.
87. R. Karcz, J. Dedecek, B. Supronowicz, H. M. Thomas, P. Klein, E. Tabor, P. Sazama, V. Pashkova and S. Sklenak, Chem. – Eur. J., 2017, 23, 8857–8870.
88. K. Mlekodaj, J. Dedecek, V. Pashkova, E. Tabor, P. Klein, M. Urbanova, R. Karcz, P. Sazama, S. R. Whittleton, H. M. Thomas, A. V. Fishchuk and S. Sklenak, J. Phys. Chem. C, 2019, 123, 7968–7987.
89. P. Sazama, J. Moravkova, S. Sklenak, A. Vondrov, E. Tabor, G. Sadovska and R. Pilar, ACS Catal., 2020, 10, 3984–4002.
90. E. Starokon, S. Malykhin, M. Parfenov, G. Zhidomirov and A. Kharitonov, Mol. Catal., 2017, 443, 43–51.
91. J. Nasir, J. Guan, T. Keal, Y. Lu, A. Sokol and C. Catlow, J. Catal., 2024, 438, 115696.
92. S. Hallaert, M. Bols, P. Vanelderen, R. Schoonheydt, B. Sels and K. Pierloot, Inorg. Chem., 2017, 56, 10681–10690.
93. B. Roos, P. Taylor and P. Siegbahn, Chem. Phys., 1980, 48, 157–173.
94. B. Roos, Int. J. Quantum Chem., 1980, 17, 175–189.
95. P. Siegbahn, J. Almlof, A. Heiberg and B. Roos, J. Chem. Phys., 1981, 74, 2384–2396.
96. K. Andersson, P. Malmqvist and B. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
97. J. Hermann, M. Stöhr, S. Góger, S. Chaudhuri, B. Aradi, R. Maurer and A. Tkatchenko, J. Chem. Phys., 2023, 159, 174802.
98. S. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117.
99. S. Steinmann and C. Corminboeuf, J. Chem. Theory Comput., 2011, 7, 3567–3577.
100. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
101. P. Rzepka, T. Huthwelker, J. Dedecek, E. Tabor, M. Bernauer, S. Sklenak, K. Mlekodaj and J. van Bokhoven, Science, 2025, 388, 423–428.
102. P. Sazama, E. Tabor, P. Klein, B. Wichterlova, S. Sklenak, L. Mokrzycki, V. Pashkkova, M. Ogura and J. Dedecek, J. Catal., 2016, 333, 102–114.
103. W. Loewenstein, Am. Mineral., 1954, 39, 92–96.
104. T. Takaishi, M. Kato and K. Itabashi, J. Phys. Chem., 1994, 98, 5742–5743.
105. T. Takaishi, M. Kato and K. Itabashi, Zeolites, 1995, 15, 21–32.
106. W. J. Mortier, J. Phys. Chem., 1977, 81, 1334–1338.
107. J. L. Schlenker, J. J. Pluth and J. V. Smith, Mater. Res. Bull., 1978, 13, 169–174.
108. M. C. Dalconi, G. Cruciani, A. Alberti, P. Ciambelli and M. T. Rapacciuolo, Microporous Mesoporous Mater., 2000, 39, 423–430.
109. M. C. Dalconi, A. Alberti and G. Cruciani, J. Phys. Chem. B, 2003, 107, 12973–12980.
110. M. C. Dalconi, A. Alberti, G. Cruciani, P. Ciambelli and E. Fonda, Microporous Mesoporous Mater., 2003, 62, 191–200.
111. I. J. Pickering, P. J. Maddox, J. M. Thomas and A. K. Cheetham, J. Catal., 1989, 119, 261–265.
112. J. Dedecek, M. J. Lucero, C. Li, F. Gao, P. Klein, M. Urbanova, Z. Tvaruzkova, P. Sazama and S. Sklenak, J. Phys. Chem. C, 2011, 115, 11056–11064.
113. P. E. Blochl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
114. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
115. J. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
116. J. Perdew and Y. Wang, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
117. S. Yuan, Y. Li, J. Peng, Y. M. Questell-Santiago, K. Akkiraju, L. Giordano, D. J. Zheng, S. Bagi, Y. Roman-Leshkov and Y. Shao-Horn, Adv. Energy Mater., 2020, 10, 2002154.
118. M. J. Frisch, et al., Gaussian 09, Revision E.01, Gaussian, Wallingford, 2009.
119. A. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
120. C. Lee, W. Yang and R. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789.
121. M. Bursch, J. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735.
122. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
123. F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192.
124. F. Aquilante, J. Autschbach, R. Carlson, L. Chibotaru, M. Delcey, L. De Vico, I. Galván, N. Ferré, L. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
125. P. Malmqvist, B. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
126. R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169.
127. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
128. A. Schafer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
129. J. Brus, L. Kobera, W. Schoefberger, M. Urbanová, P. Klein, P. Sazama, E. Tabor, S. Sklenak, A. V. Fishchuk and J. Dedecek, Angew. Chem., Int. Ed., 2015, 54, 541–545.
130. P. Sazama, L. Mokrzycki, B. Wichterlova, A. Vondrova, R. Pilar, J. Dedecek, S. Sklenak and E. Tabor, J. Catal., 2015, 332, 201–211.
131. P. Sazama, D. Kaucky, J. Moravkova, R. Pilar, P. Klein, J. Pastvova, E. Tabor, S. Sklenak, I. Jakubec and L. Mokrzycki, Appl. Catal., A, 2017, 533, 28–37.
132. J. Pastvova, R. Pilar, J. Moravkova, D. Kaucky, J. Rathousky, S. Sklenak and P. Sazama, Appl. Catal., A, 2018, 562, 159–172.
133. L. Kobera, J. Dedecek, P. Klein, E. Tabor, J. Brus, A. V. Fishchuk and S. Sklenak, J. Chem. Phys., 2022, 156, 104702.
134. S. Shaik, S. Cohen, S. P. de Visser, P. K. Sharma, D. Kumar, S. Kozuch, F. Ogliaro and D. Danovich, Eur. J. Inorg. Chem., 2004, 207–226.
135. S. F. Ye, C. Y. Geng, S. Shaik and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 8017–8030.
136. K. Yoshizawa, Y. Shiota and T. Yamabe, Organometallics, 1998, 17, 2825–2831.
137. A. Rosa, G. Ricciardi and E. J. Baerends, Inorg. Chem., 2010, 49, 3866–3880.
138. J. Harl and G. Kresse, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 045136.
139. C. Tuma, T. Kerber and J. Sauer, Angew. Chem., Int. Ed., 2010, 49, 4678–4680.
140. M. H. Mahyuddin, Y. Shiota and K. Yoshizawa, Catal. Sci. Technol., 2019, 9, 1744–1768.
141. N. F. Dummer, D. J. Willock, Q. He, M. J. Howard, R. J. Lewis, G. D. Qi, S. H. Taylor, J. Xu, D. Bethell, C. J. Kiely and G. J. Hutchings, Chem. Rev., 2023, 123, 6359–6411.
142. S. L. Scott, Science, 2021, 373, 277–278.
143. M. Maldonado-Domínguez, D. Bím, R. Fucík, R. Curík and M. Srnec, Phys. Chem. Chem. Phys., 2019, 21, 24912–24918.
144. M. Maldonado-Domínguez and M. Srnec, J. Am. Chem. Soc., 2020, 142, 3947–3958.
145. J. Dedecek, N. Zilková and J. Cejka, Microporous Mesoporous Mater., 2001, 44, 259–266.
146. J. G. Vitillo, A. Bhan, C. J. Cramer, C. C. Lu and L. Gagliardi, ACS Catal., 2019, 9, 2870–2879.
147. H. Adamji, A. Nandy, I. Kevlishvili, Y. Román-Leshkov and H. J. Kulik, J. Am. Chem. Soc., 2023, 145, 14365–14378.
148. A. Tofoni, F. Tavani, M. Vandone, L. Braglia, E. Borfecchia, P. Ghigna, D. C. Stoian, T. Grell, S. Stolfi, V. Colombo and P. D'Angelo, J. Am. Chem. Soc., 2023, 145, 21040–21052.
149. M. C. Simons, S. D. Prinslow, M. Babucci, A. S. Hoffman, J. Y. Hong, J. G. Vitillo, S. R. Bare, B. C. Gates, C. C. Lu, L. Gagliardi and A. Bhan, J. Am. Chem. Soc., 2021, 143, 12165–12174.

---