Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing physically separated bimetallic catalysts through cooperative redox enhancement (CORE)
Bohyeon Kim†
 a,
Isaac T. Daniel†
a,
Isaac T. Daniel† b,
Mark Douthwaiteb,
Samuel Pattisson
b,
Richard J. Lewis
b,
Mark Douthwaiteb,
Samuel Pattisson
b,
Richard J. Lewis
 b,
Ouardia Akdim
b,
Steven McIntosh
b,
Ouardia Akdim
b,
Steven McIntosh
 *a and
Graham J. Hutchings
*a and
Graham J. Hutchings
 *b
*b
aDepartment of Chemical and Biomolecular Engineering, Lehigh University, Bethlehem, PA, USA. E-mail: mcintosh@lehigh.edu
bMax Planck-Cardiff Centre on the Fundamentals of Heterogeneous Catalysis FUNCAT, Cardiff Catalysis Institute, School of Chemistry, Cardiff University, Translational Research Hub, Cardiff, CF24 4HQ, UK. E-mail: hutch@cardiff.ac.uk
First published on 2nd January 2026
Abstract
Liquid-phase heterogeneous catalysis underpins numerous chemical manufacturing processes, ranging from essential products to renewable energy sources, such as hydrogen. Despite the differences in reactor setups and the driving forces between thermos- and electro-catalysis, it is commonly overlooked that the two disciplines are fundamentally governed by the same underlying fundamentals. In this tutorial review, we explore the similarities between electro- and thermocatalysis and introduce how electrochemical methodologies can be applied to characterize thermocatalysis to gain both fundamental and experimental insights. Here, we discuss the recent discovery of Cooperative Redox Enhancement (CORE), a phenomenon whereby selectivity differences for two electrochemical half reactions on two physically separated but electrochemically connected dissimilar metal catalyst particles lead to acceleration of the overall catalytic rate. This approach suggests a new paradigm for the design of heterogeneous catalysis.
 Bohyeon Kim | Bohyeon Kim is a PhD candidate at Lehigh University studying interfacial phenomena on catalytic surfaces using electrochemical methods. |
Key learning pointsCorrelation between thermo- and electro-catalysis.Surface interaction and open circuit potential of a catalyst. Electrochemical tools to predict thermocatalytic system (linear sweep voltammetry and Tafel analysis). |
1. Introduction
Traditionally, we consider that thermocatalytic reactions occur without a significant role of electrochemical driving forces or mechanistic steps. In considering heterogeneously catalyzed reactions, we frequently draw a conceptual line between traditional thermochemical reactors, where the oxidation and reduction reaction steps occur on the same or neighboring catalytic sites, and electrochemical reactors, where oxidation and reduction steps are explicitly separated to occur separately at the macroscale anode and cathode. However, this view has recently been questioned by a number of studies,1–11 which demonstrates that some apparently thermocatalytic reactions occur through electrocatalytic steps, prompting the suggestion that we may conceptually consider these reactions to be occurring via a nanoscale short-circuited electrochemical circuit. This reframes our approach to understanding such catalytic reactions, further prompting research that seeks to utilize these inherent electrochemical driving forces to enhance the performance of the ‘thermocatalytic’ system, through a process we have named Cooperative Redox Enhancement (CORE).1,2,4–6Designing a catalytic system that is operated by the mechanism of CORE is a fundamentally different approach to understanding bimetallic catalytic systems. Bimetallic catalysts are traditionally designed and studied with a focus on how their physical and atomic architecture influences catalytic turnover and selectivity; CORE adds the additional consideration of electrochemical interaction. Foundational concepts in this area include bimetallic alloys, characterized by a solid solution of two metals; intermetallic compounds, which possess highly ordered stoichiometric structures; core–shell nanoparticles, featuring a distinct core of one metal encapsulated by another; and bimetallic clusters, which describe discrete, ultra-small ensembles of atoms.12–14 Unlike the traditional bimetallic catalysts, focused on the physical and chemical property modifications, CORE provides a mechanistic framework to understand how two disparate active sites synergistically interact to enhance redox processes during catalysis. This perspective moves beyond the traditional view of bimetallic catalysis and offers new catalyst design principles and requires the development and application of electrochemical techniques to probe and describe their function.
In this tutorial paper, we describe several electrochemical methodologies that have been developed to reveal the underlying electrochemical nature of these thermocatalytic processes and to leverage CORE to design enhanced catalytic systems. Specifically, this tutorial review aims to explain (1) the fundamental links between thermo- and electro-catalysis, (2) the appropriate experimental methodologies and their backgrounds, and (3) the design of bimetallic heterogeneous catalysts that leverage the CORE phenomenon.
2. Reconsideration of thermocatalysts to short-circuit electrochemical cells
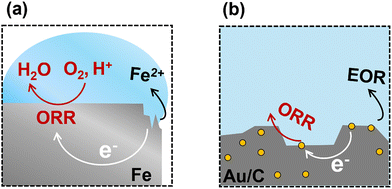
Spontaneous electrochemical and thermochemical reactions are thermodynamically indistinguishable when no external potential is applied. The reactions proceed according to the Gibbs free energy difference between reactants and products, regardless of whether the transformation involves electron transfer through an external circuit or internally through a conductive substrate. In the absence of an applied voltage, spontaneous redox reactions involving electron and ion flow can be considered thermodynamically equivalent to traditional thermocatalytic reactions.Iron corrosion is perhaps the most studied example of this spontaneous redox coupling without an external bias, Fig. 1(a). The corrosion of iron in water occurs via a range of anodic iron oxidation steps. As an example, one possible oxidation half-reaction is the oxidation of metallic Fe to Fe2+:
| Fe(s) → Fe2+(aq) + 2e−, E°ox = 0.44 V vs. SHE | (1) |
The released electrons travel through the bulk metal and participate in a reduction half-reaction at another surface site, typically involving water in the presence of oxygen. An example of the reduction half-reaction is the four-electron oxygen reduction reaction (ORR):
| O2(g) + 4H+(aq) + 4e− → 2H2O(aq), E°red = +1.23 V vs. SHE | (2) |
We consider a metal surface where both half-reactions can occur, but at different reaction sites. A driving force will be established between the reaction sites equal to an electrochemical potential difference of 1.67 V. This cell potential is a direct measurement of the Gibbs free energy driving force for the overall reaction, i.e., the sum of the two half reactions. The Gibbs free energy and potential are related through the Nernst equation ΔG = −nFEcell, where n is the number of electrons for a reaction, and F is Faraday's constant. In practice, the two reaction sites are connected by the conductive metal, placing both sites at the same electrical potential, consuming this driving force to overcome the kinetic barriers for the reactions. Corrosion thus commences spontaneously, as indicated by the positive cell potential and negative Gibbs free energy or reaction. The rate of corrosion is dictated by the magnitude of the kinetic barriers, primarily species diffusion and reaction, that dictate the relationship between potential and resulting current for both half reactions, see Section 3.3.
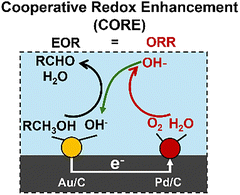
We expand this concept away from the dissolution of metals to now consider coupling two chemical reactions occurring on separated catalytic surfaces, Fig. 1(b). For example, oxidative dehydrogenation (ODH) of ethanol can be separated into the ORR and ethanol oxidation reaction (EOR).
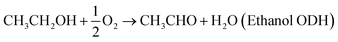 | (3) |
| CH3CH2OH + 2OH− → CH3CHO + 2e− + 2H2O (EOR) | (4) |
| O2 + 2H2O + 4e− → 4OH− (four-electron ORR) | (5) |
The overall Gibbs free energy change of reaction (3) is negative, again indicating that it is a spontaneous reaction. From a macroscopic view, this reaction is typically considered a thermocatalytic reaction. However, at the nanoscale, we propose that thermocatalysts may behave more like nanoscale electrochemical reactors, but without the explicit separation of the half-reactions. If this hypothesis is true, we can treat the system as we would the corrosion of iron by replacing the iron oxidation step with the oxidation of a molecule, in this example, the ethanol oxidation half-reaction.
We have recently demonstrated that this hypothesis does hold for a range of ODH reactions when performed on nanoscale catalysts consisting of two different metal nanoparticles that are physically separated but electrically connected through a conductive support material. We have named this phenomenon cooperative redox enhancement (CORE).1,2,4–6 CORE yields a significant enhancement in observed overall catalytic activity by separating the half reactions between two electrochemically connected catalytic nanoparticles of differing metals.1,2,4–6
Continuing with the example of the ethanol ODH, we have, for example, demonstrated that CORE occurs between connected Au/C and Pd/C catalysts, Fig. 2. When the two catalysts are electrochemically connected (but physically separated), the ORR half reaction is kinetically more facile on, and thus primarily occurs on, Pd nanoparticles, with the EOR more facile on Au nanoparticles. These two particles then spontaneously polarize to rest at an EM and provide a jM that corresponds to a higher rate than observed for either Au/C or Pd/C alone or the sum of the two disconnected rates. In this CORE system, the two particles are electrically connected through the underlying graphitic support and ionically connected through the alkaline aqueous electrolyte reaction media. As the EOR occurs on the Au particle, electrons are released and transported through the support to the Pd site, where they are consumed in the ORR (white arrow from Fig. 2). The generated OH− anion is transported back to the Au particle, where it is consumed in the EOR to complete the cycle (green arrow from Fig. 2). This electrochemical circuit is driven by the Gibbs free energy driving force for the reaction in an analogous manner to a corrosion reaction couple or a short-circuited electrochemical cell.
2.1 A growing body of evidence
The application of electrochemical concepts to understand heterogeneous catalysts is growing with active and impactful work from a number of research groups. We encourage the reader to explore this growing body of literature beyond this tutorial review.The mixed-potential-driven catalysis concept, introduced by the Takayasu and Nakamura Group, proposed that certain thermocatalytic systems operate via corrosion-like mechanisms: a spontaneous, short-circuited electrochemical process similar to the CORE framework.8,15–17 They experimentally demonstrated this by showing a short-circuit current flow between physically separated Au/C and Pt/C particles during ODH of glucose, strongly implying spontaneous redox coupling of the half-reactions and their spontaneous separation to occur on separated electrodes.8 Further work on CO oxidation using gold catalysts coupled with nitrogen-doped reduced graphene oxide (NrGO) showed that the conductive support can play a more active role than just facilitating electron transport, acting as a direct partner in the redox coupling.16
The Surendranath and Román–Leshkov Groups have studied a range of thermocatalytic reactions to uncover electrochemical mechanisms.7,9,18–24 As an example, by examining the nitrate hydrogenation reaction on a partially alloyed PdCu/C catalyst, they postulated that the hydrogen oxidation reaction (HOR) half-reaction can be decoupled from the substrate reduction half-reaction. They supported this postulate by demonstrating that the HOR primarily occurs on the Pd sites and that the substrate reduction half-reaction primarily occurs on the electrochemically connected Cu sites. This mechanism implies that electron transport occurs between sites of partially alloyed particles, expanding the scope of the redox coupling mechanism. They are also developing experimental approaches to overcome the inherent limitations in traditional electrochemical potential measurements by utilizing redox-sensing probe molecules.22,25 This wireless potentiometry can measure the operating potential of the catalyst suspended in solution, avoiding the need to support the catalyst on an electrode and the challenges and changes to operation that this can present.
The Flaherty and López Groups were among the first to systematically investigate how electrochemical potential influences thermocatalytic reactions, using the hydrogen peroxide production reaction as a key model system.10,26–28 They have been active in applying high-throughput electrochemical experimentation and in situ/operando spectroscopy to provide detailed mechanistic insights into these complex, electrochemically-influenced thermocatalytic processes.
The rapid growth and high-impact nature of this research are further evidenced by significant contributions from other groups, including the Yan29 and the Zheng groups,30 indicating a promising and active future for the electrochemical interpretation of thermocatalysis.31
Based on fundamental electrochemistry, the concept of CORE has been demonstrated as a new approach to designing thermocatalytic systems by our group and others. In Section 3, we will discuss how CORE can be demonstrated experimentally and the key techniques necessary to characterize the phenomenon and translate the electrochemical results to thermal catalyst design (Tables 1 and 2).
| Experiments | How it works | Can measure/predict | Specific considerations |
|---|---|---|---|
| Open circuit potential (OCP) | It measures the potential of an electrode (catalyst) without external bias. More details in Section 3.2. | EM | Mass transfer limitation can happen for some reactions with high activity. |
| ECORE | |||
| Linear sweep voltammetry (LSV) | It sweeps the potential of an electrode into a specific direction to understand the activity of a half-reaction. You can get the response as a current. More details in Section 3.3. | EM | Minimizing capacitance current from support by using a lower scan rate or subtracting the background curve. |
| JM | |||
| Tafel | It sweeps the potential of an electrode, same as the LSV but with the presence of both reactants. More details in Section 3.4. | EM | Avoiding to broad potential range to minimize mass transfer limitation, which can create inaccurate results for the Tafel fitting. |
| JM | |||
| Galvanic coupling (also known as galvanic corrosion) | It short-circuits two electrodes and measures the current and the potential over time. Typically conducted in thermocatalytically active conditions. More details in Section 3.5. | Short-circuit current | The cell volume has to be small to produce enough products for quantification. You can consider running the experiment without a reference electrode. |
| Short-circuit potential |
| Term | Explanations |
|---|---|
| Mixed potential (EM, EMTafel) | The potential at which both anodic and cathodic reactions are balanced for a specific catalyst under specific conditions. EM is observed through open-circuit potential (OCP) measurement. EMTafel is an estimated mixed potential that is determined by the Tafel slope of a catalyst. |
| CORE potential (ECORE) | CORE potential specifically describes a potential that is measured as a result of the polarisation of two mixed potentials from bimetallic catalysts. It can be measured by using the OCP measurement of bimetallic catalysts. |
| Short-circuit potential | The potential measured when the two catalysts are short-circuited, with no external voltage applied. |
| Mixed current density (JMTafel) | The current density derived from the mixed potential in Tafel analysis. |
3. Electrochemical methodologies for the prediction of thermocatalytic systems and CORE
General considerations on electrochemical measurements, such as cell types, selection of electrodes, and normalization, are described in the SI.3.1 Mixed potential theory (MPT)
Mixed potential theory (MPT) in electrochemistry is utilized to determine an average potential at an electrode when more than one reaction couple occurs simultaneously on the electrode surface. Each reaction will have a different thermodynamic potential. The mixed potential (EM) is measured as an open circuit potential (OCP) under this condition and represents an average of the two thermodynamic potentials. The contributions of each reaction to the measured EM are determined by the relative catalytic activity of the electrode surface towards each half-reaction. For example, low activity towards the oxidation half-reaction will yield an EM close to the thermodynamic potential of the reduction reaction. Indeed, the activity, or lack thereof, of an electrode towards each half reaction is an important consideration in the selection of electrode materials.The concept of a mixed potential is frequently utilized in corrosion science and electroless deposition, where both the metal oxidation and ORR occur on the same electrode (see Fig. 1).33–35 There is no net current flowing to or from the electrode; however, a net reaction does occur at a rate determined by the slowest of the oxidation or reduction reaction steps. The net rate at the EM is termed the mixed current density (jM) and is a measure of the catalytic activity. For example, a low jM can occur when the activity of the ORR is low on the metal surface, limiting the overall rate of corrosion. Note that jM cannot be directly measured electrochemically, as there is no net current flow between electrodes to measure. As discussed in Section 2, this MPT can be applied to thermocatalytic redox reactions. Thus, we can determine a mixed potential (EM) for our catalysts as the observed OCP measurement with both reactants present at the electrode surface and correlate the mixed current density (JM) to the reaction rate observed from a thermal catalytic reaction. Both will depend on the type of catalysts and the reaction conditions.
3.2 Open circuit potential (OCP) measurements to determine EM
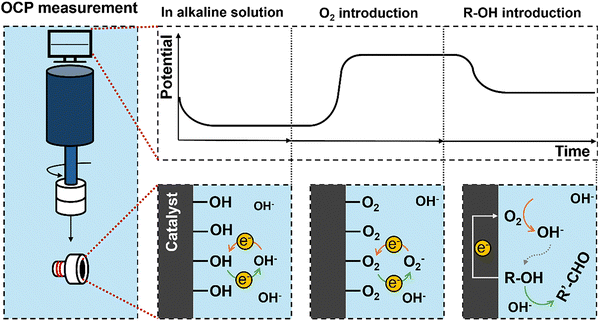
The open circuit potential (OCP) is the potential of the electrode at rest measured relative to a known reference electrode potential.36 There is no detectable current through the electrochemical workstation. The OCP is purely established by the surface interaction between the catalyst and the electrolyte ions. It can take considerable time to establish a stable measurement due to slow equilibration, and it is essential to maintain stable conditions. We can walk through an example of using this approach to determine EM for the reaction couple of R-OH oxidation reactions (R-OH OR) and the ORR measured against a standard hydrogen electrode (SHE) reference electrode.A catalyst-coated electrode is first placed in a basic electrolyte and purged with inert gas, Fig. 3. The dominant surface interaction is then the adsorption and desorption of hydroxyl ions on the catalytic surface, setting a low OCP vs SHE. When oxygen is introduced into the solution, dissolved oxygen species (O2(aq), O2−, O22−) strongly interact with the catalyst, replacing the hydroxyl ions, Fig. 3. This change in surface interaction establishes a new balance between the adsorbed and desorbed oxygen species, leading to an increase in the measured OCP. In theory, we will measure the OCP set by the Nernst equation, Eqn (6), for the specific reaction conditions.
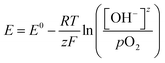 | (6) |
We then introduce R-OH as a substrate such that both the R-OH OR and ORR half reactions can occur on the catalyst surface with no net current flow, Fig. 3. The resulting measured OCP is established based on the relative rates and electrochemical potentials of both the ORR and R-OH OR; the resulting measured value is the mixed potential EM under these conditions. The EM is not affected by the order of adding reactants.
Importantly, the net reaction is occurring at EM in the same way as it occurs on what we would consider a thermal catalytic surface (i.e., R-OH ODH); we are merely measuring the electrochemical potential at which this occurs. We can disconnect the electrochemical workstation, and the reaction will continue in exactly the same manner. Care must be taken not to significantly deplete either reactant during this measurement period, as this will lead to a drift in EM as the conditions change. The final value of EM is influenced by the relative activity of the surface towards each half reaction, indicating that the stirring speed should be maintained.35 Because of the surface sensitivity of the measurement, it can be a valuable tool to support how and why some catalysts are active for the thermocatalytic reactions.
Fig. 4 shows the OCP dependence of Au/C toward the ORR and ethanol oxidation reaction (EOR). First considering the black line, we first observe a stable OCP of 0.94 V vs. RHE set by the interaction between the Au surface and the dissolved oxygen in the O2 saturated electrolyte. Upon injection of ethanol, the OCP shifts to a more negative value as ethanol molecules interact with the surface, and both the ORR and EOR actively occur on the surface. The potential stabilizes at an EM of 0.86 V vs. RHE (orange dotted line). Switching the additional sequence, the red line shows an initial OCP of 0.66 V vs. RHE when ethanol is present in an oxygen-purged electrolyte, rising to the same final EM after the introduction of bubbling O2. As noted, the EM is not path dependent, as we would expect for a thermodynamic measurement, even if reflecting different equilibrium kinetics on the surface. We emphasize that the EM under the same conditions depends on the catalyst utilized due to the influence of relative ratios of the oxidation and reduction reactions on that surface; this is discussed further in Section 3.4.
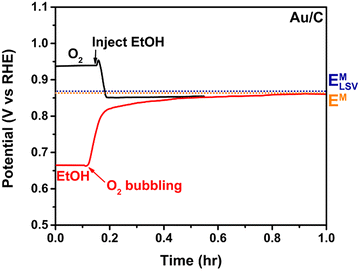 | ||
| Fig. 4 OCP measurement on Au/C while changing reactants. The conditions of the black and red lines are the same after injecting ethanol or bubbling O2, respectively. Reproduced from ref. 3 with permission American Chemical Society, copyright 2024. | ||
From the comparison between EM and initial potential of each reactant, we can see how the ethanol ODH on Au/C is driven by the chemical potential of the half reactions. The potentials of 0.18 V and 0.20 V were polarized to the EM only when O2 or ethanol was present in the solution, respectively, Fig. 4. The polarization to the mixed potential is the point where the rates of the half reactions are maximized at the same rate (see Fig. 1 for more detail).
The EM is dependent on the reactants in the solution, meaning that the measurement conditions, including solution concentration, purging gas, and temperature, must closely match the conditions of the targeted thermocatalytic reaction. Both a two-electrode setup, a WE (catalyst-coated electrode), and an RE, and the standard three-electrode setup can be used for EM measurements as the current is not flowing from an external circuit, Fig. 5(a). It is also recommended to use a sufficiently large volume of electrolytes and reactants to minimize any concentration changes over time.
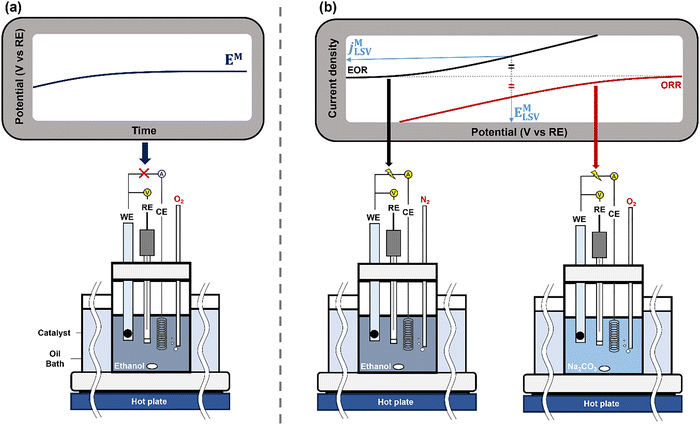 | ||
| Fig. 5 Schematics illustrating setup for OCP measurement and LSV measurements. For OCP measurement, two reactants for ethanol ODH, ethanol and O2, are both used to mimic the chemical reaction. For LSV measurements, two independent measurements containing only one reactant are conducted. WE: working electrode, CE: counter electrode, RE: reference electrode. Reproduced from ref. 3 with permission American Chemical Society, copyright 2024. | ||
3.3 Linear sweep voltammetry (LSV)
While the OCP measurement holds its benefits, it is not useful to quantify the kinetics of individual half reactions, as no measurable net current flows, and the overall rate reflects only the slowest reaction step of either half reaction mechanism. As an attempt to estimate the thermocatalytic rate, linear sweep voltammetry (LSV) can be applied. During LSV, the potential of the working electrode to be studied is linearly increased or decreased as a function of time vs the reference electrode potential. Upon reaching a potential where a reaction occurs, the current flows between the working and counter electrodes at a rate determined by the working electrode response. The experimental design considerations are discussed in detail in the literature,37 with an important consideration being sufficient activity at the counter electrode, such that it does not limit the rate. Combining this concept with controlling the working electrode potential vs. reference enables the isolation of the half reaction occurring on the catalyst at the working electrode.The isolated half-reaction characteristics determined by LSV provide an alternative approach to measure an EM simultaneously with a value for jM of a catalyst. Analyzing the two independent LSV curves for the half reactions together provides insights into how the overall chemical reaction behaves on the catalyst surface, Fig. 5(b). Continuing with the ethanol oxidation example, the EOR activity can be measured from the solution containing only ethanol as a reactant (black arrow) and the ORR activity evaluated from an oxygen-saturated solution free of ethanol (red arrow). We can derive a value for a mixed potential EM by finding a potential at which the rate of EOR and ORR are balanced. This also provides an estimate for the mixed current density jM, proportional to the catalytic activity of the surface, as the current density measured at the estimated EM.
This approach is effective considering that the half-reaction activity in focus will have the same activity whether the operating potential for the half-reaction is set by interaction with the other half-reaction or by an external electrical potential; the reacting species only feel a potential without ‘knowledge’ of the source Therefore, we can predict the corresponding chemical reaction activity by finding the estimated EM and jM from the LSV measurements. Critically, this estimation is based on measurements of each half reaction in the absence of the other. As such, it inherently assumes an ideal scenario where the two half reactions do not interact on the catalyst surface and are perfectly separated on independent active sites when both reactants are present. For more complex and non-ideal situations, we suggest the Tafel analysis, which will be discussed in Section 3.4.
The comparison of these two LSV measurements reveals three general possible outcomes, Fig. 6. First, if the mixed potential is located within a kinetically controlled regime, the mixed current density will align with catalytic activity, making it a useful tool for evaluating the overall reaction. However, he measured current can be controlled by diffusion, particularly if there is limited solubility of gases in the chosen electrolyte. In this case, estimating the mixed potential and mixed current density can be inaccurate and may not reflect the performance of a nanoscale catalyst; the length scale of a reactant concentration profile on dispersed power catalysts can be much shorter than that of a catalyst coated on an electrode. Lastly, if the onset potential of both half reactions does not overlap, no spontaneous redox reaction can occur under these conditions. In such instances, adjustments to reaction conditions (e.g., temperature, pressure, concentration) or changes in catalysts may be necessary.
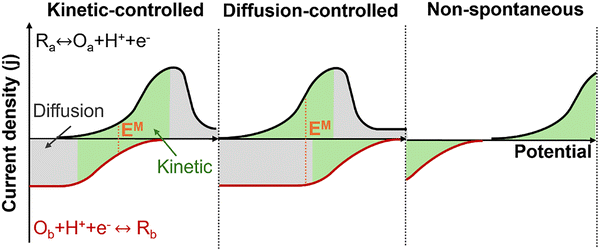 | ||
| Fig. 6 The schematic illustrates three scenarios of LSV measurements for determining the estimated EM. | ||
It is important to recognize that the jM from LSV measurements is not equivalent to catalytic activity due to the influence of capacitive current, which arises from potential sweeps rather than the actual target reaction. Since capacitive current is scan rate-dependent, reducing the scan rate can help minimize its effect. Additionally, performing blank runs without reactants can provide a baseline to account for capacitance effects in the system, ensuring a more accurate prediction of the chemical system. There are additional significant challenges with exactly matching electrochemical and thermochemical rates, including accurately determining the number of active electrocatalytic sites.
3.4 Tafel analysis
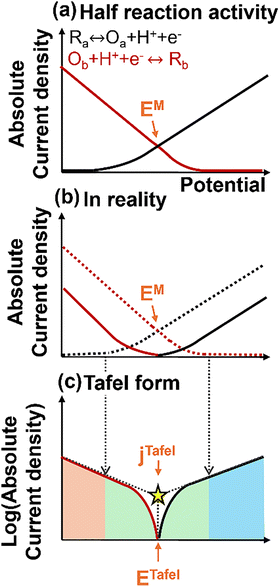
The primary limitation of the LSV approach is that each reaction is measured in the absence of the other reactants, thus assuming no interaction between sites and no competitive adsorption of active species. LSV measurements often fail to provide accurate predictions when applied to real reaction systems. Tafel analysis is suggested as a more reliable alternative, as it is conducted under actual reaction conditions with all reactants present.4 As an example, one of our recent studies on ethanol ODH revealed that oxygen adsorption on Pd/C is significantly stronger than that of ethanol, preventing ethanol from adsorbing onto the Pd surface.4 This creates a large discrepancy between the LSV prediction, which suggested high activity for Pd/C, and the experimental reality, almost zero catalytic activity for Pd/C. This highlights the limitations of LSV in capturing competitive adsorption effects, while Tafel analysis provides a more realistic evaluation of catalytic behavior under operating conditions.Tafel analysis and LSV are similar in methodology; in both cases, we scan a potential range over time and measure the corresponding current density response. In Tafel analysis, we perform the measurement with both reactants present and scan the potential over a range that includes both reducing and oxidizing potential. We can then estimate the mixed current density via extrapolation from the resulting potential–current density curves. To illustrate, we can consider a chemical reaction consisting of two half-reactions, Fig. 7. The absolute current density of each half-reaction can be represented as shown in Fig. 7(a). Under real reaction conditions, where both half reactions occur at the same time, the actual current curve will appear after the subtraction between oxidation and reduction currents at the same potential, Fig. 7(b), and the logarithmic form of this curve is known as the Tafel curve, Fig. 7(c).
In a Tafel plot, three distinct potential regions emerge, Fig. 7(c). The red region represents the potential range where only the reduction reaction occurs, while the blue region corresponds to the oxidation reaction. The green region, or mixed area, is the potential range where both reactions can take place simultaneously. The linear extrapolation of the potential vs current density plots from the red and blue areas infers the amount of current density of individual half reactions that occur before being subtracted by the other half reaction. The Tafel potential (ETafel) can be calculated from the crosspoint where we can see the minimum current density. The ETafel is analogous to the mixed potential EM, as this is the potential at which the rates of the two half reactions are balanced. The Tafel current density (jTafel) can be obtained from the crosspoint of the extrapolation lines (yellow star), the predicted mixed current density based on the activities of the two half reaction activities determined under real conditions.
The correct potential range of the Tafel analysis is important for accurate measurements. For instance, if the catalyst is sufficiently stabilized, which can be monitored by OCP testing, ETafel can be positioned close to the center of the potential range. Too wide a range of the potential may cause the measurement to start from the diffusion control regime, which can be an issue when conducting the extrapolations.38
3.5 Approaches to identify CORE in bimetallic catalysis
From earlier sections, we have explained how and why the mixed potential of a catalyst is established by a chemical reaction. In Section 3.5, we explain how we can leverage these properties to enhance the catalytic system by exploiting an electrochemically originated driving force, known as cooperative redox enhancement (CORE).1,2,4–6As individual catalysts possess different catalytic properties, the EM of each catalyst varies even during the same chemical reaction. In Fig. 8(a), Au/C shows an estimated EM (black dotted line) that is lower than that of Pd/C (red dotted line) for the hydroxymethylfurfural (HMF) ODH reaction. This variation is due to the differing activities of the catalysts for the two half-reactions and the preferential adsorption of the reactants on the catalyst surface, as discussed in Sections 3.3 and 3.4.
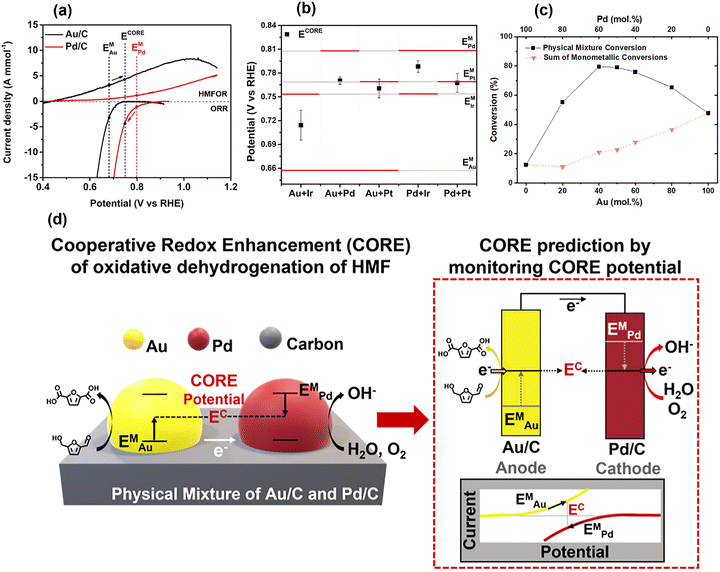 | ||
| Fig. 8 (a) LSV curves of Au/C and Pd/C for HMF oxidation reaction and ORR, (b) Mixed potential of monometallic catalysts and corresponding CORE potential of the mixed catalysts, (c) thermocatalytic HMF conversion of Au/C, Pd/C, and their mixture with molar ratios. (d) A schematic to elucidate the CORE mechanism. Reproduced from ref. 2 with permission American Chemical Society, copyright 2023. | ||
Now, we consider placing the Au and Pd catalysts as isolated particles on a conductive support. When they are electrochemically connected via conductive support and the alkaline electrolyte solution, the established EM of the two catalysts must be balanced, similar to the example in Section 2 (see Fig. 1 and 2). This polarization results in a higher EM for Au (black arrow in Fig. 8(a)) and a lower EM for Pd/C (red arrow), establishing a new operating potential that lies between these two EM that we term the CORE potential (ECORE). This process can significantly increase catalytic activity, as the HMFOR activity on Au and the ORR activity on Pd become much higher at ECORE than they were previously. The schematic in Fig. 8(d) explains the CORE in more detail. When two catalysts are electronically connected under reaction conditions, the electrons produced from HMFOR on Au transfer to Pd through conductive support. The ions produced from ORR on Pd return to the Au site, completing the cycle, much like the cathodic protection of two metals.
The CORE potential, a result of polarization between two catalysts, can be measured by the OCP measurement using the catalyst mixture. Fig. 8(b) shows the mixed potential of the catalysts (red bars) and the corresponding CORE potentials (black squares) by the OCP measurement. The ECORE of the Au/C and Pd/C mixture is well-positioned between the two EM, indicating the spontaneous polarization, which will lead to catalytic enhancement. As expected, Fig. 8(c) exhibits a substantial increase in HMF conversion rate for the Au/C and Pd/C mixture as well as catalytic activity compared to the sum of monometallic counterparts. At the best molar ratio, the enhancement by CORE exceeds more than 3-fold, and this excellent synergistic effect was observed from multiple reaction systems, including the hydrogenation reaction.1,2,4–7
Direct monitoring of short-circuit current between two catalysts is an alternative approach to determine the magnitude of CORE. This approach was first conducted in an H-Cell, where reactants are separated by an ion-conducting membrane.1 Two different catalysts are applied to each cell, and electron transfer was monitored by short-circuiting the two electrodes, Fig. 9. For both sides, an HMF-containing solution was used, but oxygen was only used on the Pd side, where the ORR predominantly occurs under the CORE mechanism. Continuous current flow was observed between the catalysts, indicating that the reaction coupling between two catalysts is possible without any potential applied.
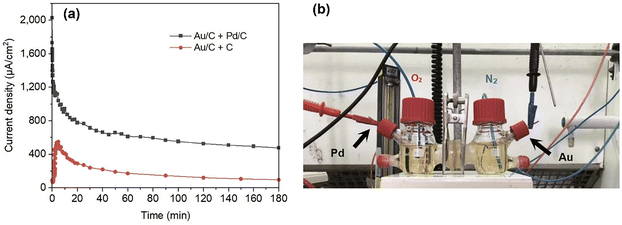 | ||
| Fig. 9 (a) Short-circuit current of the H-Cell test while bubbling O2 on Pd or C side and N2 on Au side in HMF-containing alkaline solution, (b) corresponding H-Cell setup. Reproduced from ref. 1 with permission Nature Springer, copyright 2021. | ||
More directly comparable to the thermocatalytic environment, we can measure the short-circuit current between the two catalysts when placed in the same solution containing both oxygen and the hydrocarbon.8,16,32 In this scenario, the current flowing between the two electrodes is directly measured as the result of the differing selectivity for oxidation and reduction reactions of the two catalysts and the resulting CORE coupling between them. The electrocatalytic fraction of the total catalytic turnover can then be calculated by measuring the short-circuit current over a specified time and performing product analysis of the reaction solution after this period. The fraction of the turnover occurring via CORE is then calculated by using Faraday's law to convert the total electrical charge passed and comparing it to the total turnover calculated from product analysis. Our latest publication utilized this approach to demonstrate that 43.3 ± 10.3% of total reactions were driven by the redox coupling from the CORE mechanism between Au and Pd for the ODH of HMF, exemplifying the importance of CORE in these catalytic systems.
This single-chamber cell experiment can include a reference electrode to directly measure ECORE between the catalysts, which, if the electrodes are carefully prepared, will match the ECORE determined by OCP and Tafel analysis. Such experiments can also be used to rapidly screen catalysts for the CORE phenomenon and map the optimal molar ratio of the two catalysts for catalyst design. The single-chamber cell allows working with low volume (<10 ml) with a heated and pressured setup, matching the setup as close to the thermocatalytic setup. The challenges of using any type of electrochemical cell to characterize the thermal catalysts are described in Section 4.1.
3.6 Consideration when designing bimetallic catalysts using the CORE mechanism
In addition to typical heterogeneous catalyst design considerations, there are additional parameters to consider when designing a bimetallic catalyst to leverage CORE. First, the shared support must be an electronic conductor to minimize electron transport resistance between the two physically separated catalytic sites. While we have utilized catalyst particles on carbon support and shown that the conductivity of the support is critical,1 engineering the distance between particles may enhance activity. For example, Janus-type bimetallic catalysts, where the two components are in direct, intimate contact, may exhibit higher activity for CORE.1 Similarly, developing approaches to control the placement and local ratio of catalytic particles may provide routes to minimizing losses and matching the local rates of the half reactions to optimize catalyst utilization and turnover. For example, increasing the number of lower activity particles for the oxidation steps closer to a higher activity particle for the reduction steps can match unbalanced half-reaction kinetics, resulting in better catalytic activity.It is worth noting that not every bimetallic combination can enhance overall catalytic activity by the CORE mechanism and significant differences in half-reaction selectivity. As shown by LSV or Tafel analysis, one must choose a bimetallic combination where the redox coupling results in a combined catalytic turnover rate that is superior to the simple sum of the individual metals performing their reactions independently. In our experience, screening of catalytic materials for redox coupling is most rapidly achieved through the direct measurement of current flow in Tafel analysis or a single chamber cell; the latter being slightly more straightforward in experimental setup.
The catalyst components must also be stable under the operating conditions for CORE, including potentially high or low pH to enable ionic transport. Our previous study has shown that one metal, for example, Pt, can sometimes migrate to and deposit on the surface of the other metal component.2 This migration leads to alloying or encapsulation and disrupts the intended CORE geometry, reducing the overall catalytic turnover rather than enhancing it. Careful selection of stable catalyst systems that maintain their structure in the given conditions is therefore imperative.
4. Challenges
4.1 Difficulties from differences between electro- and thermo-catalytic setup
Inherent differences between electro- and thermo-catalytic setups can create a gap between understanding the thermocatalytic reactions and what is measured during electrochemical testing. One major challenge is the difference in catalyst loading. In electrochemical testing, the amount of catalyst applied is generally much smaller compared to thermocatalytic reactions, as the catalyst needs to be loaded onto an electrode. This disparity can create issues in analyzing products and observing kinetic changes over longer testing periods. Product analysis is not usually problematic in general electrocatalysis, where sufficient current can be generated through applied potential; however, applying mixed potential to mimic the thermochemical system does not create enough current during long-term tests, requiring substantial additional time to produce product quantities sufficient for accurate analysis. Potential solutions to address these differences include increasing the electrode size, increasing the catalyst loading, or decreasing the volume of the electrolyte.The catalyst distribution on a prepared electrode is also likely quite different from that in solution due to the necessary deposition and drying steps, potential use of binder materials, and the pore structure of a conductive electrode support, for example, carbon paper. This makes direct quantitative comparison of thermocatalytic and electrocatalytic turnover highly prone to error and not useful to pursue. However, qualitative analysis is highly predictive and productive with the trends in electrocatalytic current very closely matching the trends in the CORE enhancement.32 The Surendranath group is developing redox-active molecules as a route to measure the potential of the active catalyst in solution and avoid the need to create catalyst-coated electrodes.22,25 This is promising as a route to determine potential, but techniques to directly measure the relative contribution of thermocatalytic and electrocatalytic turnover still rely on electrode preparation.
Electrocatalytic testing typically involves a higher molar ratio of reactants to catalysts, which minimizes concentration changes over time. This contrasts with thermocatalytic reactions, where the concentration of chemicals can vary significantly during the reaction, possibly leading to inaccurate analysis over a longer period. To ensure consistency in measurements, the reaction conditions and molar ratios should match closely between electro- and thermo-catalytic setups. Additionally, the need for electrodes to be wired poses challenges for cell design, especially when studying thermocatalytic reactions under high-temperature and high-pressure conditions. Although air-tight electrochemical cells capable of operating under such conditions are now available, their high cost and complexity can make this method less approachable.
4.2 Solution conductivity
Solution conductivity can be a challenge when analyzing chemical reaction rates based on electrochemical data. Low ionic conductivity in the electrolyte can be a significant resistance in macroscale electrode measurements and may limit the measured current. This could be mistakenly interpreted as slow reaction kinetics and a lack of CORE in the system. Similarly, low conductivity in the thermocatalytic system may limit CORE, although the length scales of ionic current flow are likely substantially shorter. While this is unlikely to be an issue in high or low pH environments, to minimize this risk, the ionic conductivity of the solution can be measured via electrochemical impedance spectroscopy (EIS).4.3 Operando/in situ spectroscopy
The development of applicable operando and in situ measurement techniques, including XPS, Raman, and X-ray adsorption, offers a route to further understanding of CORE.The primary challenge in developing these is the design of the requisite test cells to probe both the thermocatalytic and electrocatalytic systems at high temperature with a controlled reaction atmosphere. While beyond most individual laboratories and hard to source from suppliers, such custom sample environments are often available and national user facilities.
Further challenges are introduced by the low concentration of active metal typically employed in these thermocatalytic reactions, usually ranging from only 1 to 5 wt% of the total catalyst mass. This inherently low concentration of the active species often results in insufficient signal intensity for benchtop analysis techniques. Moreover, the active catalytic components are often dispersed as extremely small nanoparticles, sometimes existing as clusters or even single atoms, and typically measuring less than 5 nm in diameter. This particle size provides an additional physical barrier to obtaining high-quality, actionable spectroscopic data.
5. Future outlook
5.1 Expanding the scope of the CORE mechanism
Although catalytic systems to verify the CORE and related mechanisms have primarily focused on precious metals, expanding to include lower-cost transition metals is conceptually feasible if they possess sufficient activity and stability under reaction studies.While we have discussed the need for electronically conductive support, other interactions between the support and the catalyst, or the use of a catalytically active support, could prove a promising direction for research. Although our previous studies focused on using the support as solely an electron conductor, it is possible to use the supporting materials as a coupled conductor and catalytic component of the redox couple.16
Furthermore, more traditional approaches to tailor catalytic activity, such as particle size, defects, and grain boundaries, contribute to the effectiveness of CORE. For example, the Surendranath group23 recently utilized scanning electrochemical cell microscopy (SECCM) to sense the catalytic rate via the Tafel analysis and the LSV measurements using polycrystalline Pt. The EM and the kinetics of half reactions vary depending on their grains, creating a local potential gradient and making a galvanic redox couple within the same electrode.
5.2 Electrochemical steps in CORE
From an electrochemical view, investigating the possible impact of, for example, double-layer capacitance and the electrochemical mechanistic steps, including ion and electron transfer, on CORE is likely a fruitful area for future exploration of the CORE mechanism. The formation of a dissimilar mixed potential between the two distinct catalysts inherently generates a localized electric field. This field, in turn, can significantly influence the local concentration profile of reactants and intermediates at the electrode surface, thereby impacting reaction kinetics and selectivity. Experimentally measuring this effect in a dispersed catalyst solution is nearly impossible due to the complexity of the dynamic system. This challenge necessitates the use of experimental systems such as specially designed dual-electrode systems to accurately isolate and measure the interfacial phenomena. Alternatively, this type of subtle electronic effect is highly amenable to investigation through computational calculations, which can provide molecular-level insights into the charge distribution and potential gradients at the interface.Conflicts of interest
There are no conflicts to declare.Data availability
All data is available in the manuscript and the supplementary information (SI). The supplementary file includes information on considerations for the selection of electrodes and the normalization of the active surface. See DOI: https://doi.org/10.1039/d4cs00479e.Acknowledgements
BK and SM would like to thank Lehigh University for its financial support. ITD, MD, SP, RJL, OA and GJH would like to thank the Max Planck Centre on the Fundamentals of Heterogeneous Catalysis (FUNCAT) for funding.References
- X. Huang, O. Akdim, M. Douthwaite, K. Wang, L. Zhao, R. J. Lewis, S. Pattisson, I. T. Daniel, P. J. Miedziak, G. Shaw, D. J. Morgan, S. M. Althahban, T. E. Davies, Q. He, F. Wang, J. Fu, D. Bethell, S. McIntosh, C. J. Kiely and G. J. Hutchings, Nature, 2022, 603, 271–275 CrossRef CAS.
- I. T. Daniel, B. Kim, M. Douthwaite, S. Pattisson, R. J. Lewis, J. Cline, D. J. Morgan, D. Bethell, C. J. Kiely, S. McIntosh and G. J. Hutchings, ACS Catal., 2023, 13, 14189–14198 CrossRef CAS PubMed.
- B. N. Zope, D. D. Hibbitts, M. Neurock and R. J. Davis, Science, 2010, 330(6000), 74–78 CrossRef CAS.
- B. Kim, I. Daniel, M. Douthwaite, S. Pattisson, G. J. Hutchings and S. McIntosh, ACS Catal., 2024, 14, 8488–8493 CrossRef CAS.
- I. T. Daniel, L. Zhao, D. Bethell, M. Douthwaite, S. Pattisson, R. J. Lewis, O. Akdim, D. J. Morgan, S. McIntosh and G. J. Hutchings, Catal. Sci. Technol., 2023, 13, 47–55 RSC.
- L. Zhao, O. Akdim, X. Huang, K. Wang, M. Douthwaite, S. Pattisson, R. J. Lewis, R. Lin, B. Yao, D. J. Morgan, G. Shaw, Q. He, D. Bethell, S. McIntosh, C. J. Kiely and G. J. Hutchings, ACS Catal., 2023, 13, 2892–2903 CrossRef CAS.
- K. M. Lodaya, B. Y. Tang, R. P. Bisbey, S. Weng, K. S. Westendorff, W. L. Toh, J. Ryu, Y. Román-Leshkov and Y. Surendranath, Nat. Catal., 2024, 7, 262–272 CrossRef CAS.
- M. Yan, R. Arsyad, N. A. Putri Namari, H. Suzuki and K. Takeyasu, ChemCatChem, 2024, 16, e202400322 CrossRef CAS.
- J. Ryu, D. T. Bregante, W. C. Howland, R. P. Bisbey, C. J. Kaminsky and Y. Surendranath, Nat. Catal., 2021, 4, 742–752 CrossRef CAS.
- J. S. Adams, M. L. Kromer, J. Rodríguez-López and D. W. Flaherty, J. Am. Chem. Soc., 2021, 143, 7940–7957 CrossRef CAS.
- G. V. Fortunato, E. Pizzutilo, I. Katsounaros, D. Göhl, R. J. Lewis, K. J. J. Mayrhofer, G. J. Hutchings, S. J. Freakley and M. Ledendecker, Nat. Commun., 2022, 13, 1–7 Search PubMed.
- K. D. Gilroy, A. Ruditskiy, H. Peng, D. Qin and Y. Xia, Chem. Rev., 2016, 116, 10414–10472 CrossRef CAS.
- L. Liu and A. Corma, Chem. Rev., 2023, 123, 4855–4933 CrossRef CAS.
- J. H. Sinfelt, Acc. Chem. Res., 1977, 10, 15–20 CrossRef CAS.
- M. Yan, N. A. P. Namari, J. Nakamura and K. Takeyasu, Commun. Chem., 2024, 7, 1–7 CrossRef.
- M. Yan, M. Asif, R. Singh, K. Takeyasu and J. Nakamura, Adv. Sci., 2025, e05994, 1–9 Search PubMed.
- M. Yan, Chem. – Asian J., 2025, e00862, 1–5 Search PubMed.
- W. C. Howland, J. B. Gerken, S. S. Stahl and Y. Surendranath, J. Am. Chem. Soc., 2022, 144, 11253–11262 CrossRef CAS PubMed.
- T. S. Wesley, Y. Román-Leshkov and Y. Surendranath, ACS Cent. Sci., 2021, 7, 1045–1055 CrossRef CAS PubMed.
- T. S. Wesley, Y. Román-leshkov and Y. Surendranath, ChemRxiv, 2025, 1–9 Search PubMed.
- K. S. Westendorff, M. J. Hülsey, T. S. Wesley, Y. Román-Leshkov and Y. Surendranath, Science, 2024, 383(6684), 757–763 CrossRef CAS PubMed.
- N. K. Razdan, K. S. Westendorff and Y. Surendranath, Nat. Catal., 2025, 8, 315–327 CrossRef CAS.
- X. Xu, W. C. Howland, D. Martín-yerga, C. Cadaram, M. Deiaa, G. D. West, P. R. Unwin and Y. Surendranath, ChemRxiv, 2025, 1–19 Search PubMed.
- H. Wang and Y. Surendranath, Nat. Chem., 2025, 1–8 Search PubMed.
- S. McIntosh, Nat. Catal., 2025, 8, 287–288 CrossRef.
- Y. Zhao, J. S. Adams, A. Baby, M. L. Kromer and D. W. Flaherty, ACS Sustainable Chem. Eng., 2022, 10, 17207–17220 CrossRef CAS.
- M. Chung, K. O. Albrecht, J. M. Terrian, W. T. Broomhead and D. W. Flaherty, ACS Catal., 2025, 15, 13015–13029 CrossRef CAS.
- R. Ghosh, G. M. Hopping, J. W. Lu, D. W. Hollyfield and D. W. Flaherty, J. Am. Chem. Soc., 2025, 147, 1482–1496 CrossRef CAS PubMed.
- H. An, G. Sun, M. J. Hülsey, P. Sautet and N. Yan, ACS Catal., 2022, 12, 15021–15027 CrossRef CAS.
- M. Qiao, Q. Wu, Y. Wang, S. Gao, R. Qin, S. Liu, K. Ding, D. Zhao and N. Zheng, Chem, 2024, 10, 3385–3395 CAS.
- X. Qin, J. Li, T. Jiang, X. Ma, K. Jiang, B. Yang, S. Chen and W. Cai, Nat. Commun., 2024, 15, 7509 CrossRef CAS PubMed.
- B. Kim, J. Spragg, I. Daniel, S. Miller, S. Pattisson, R. J. Lewis, G. J. Hutchings and S. Mcintosh, ACS Catal., 2025, 15, 18063–18068 CrossRef CAS.
- G. P. Power, W. P. Staunton and I. M. Ritchie, Electrochim. Acta, 1982, 27, 165–169 CrossRef CAS.
- R. W. Revie and H. H. Uhlig, Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering: Fourth Edition, 2008 Search PubMed.
- P. Bindra and J. Roldan, J. Appl. Electrochem., 1987, 17, 1254–1266 CrossRef CAS.
- T. J. Smith and K. J. Stevenson, Reference Electrodes, Elsevier, 2007 Search PubMed.
- V. S. Bagotsky, Fundamentals of Electrochemistry, 2005 Search PubMed.
- D. Li, C. Lin, C. Batchelor-McAuley, L. Chen and R. G. Compton, J. Electroanal. Chem., 2018, 826, 117–124 CrossRef CAS.
Footnote |
| † Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2026 |