Dipole-bound states in the meta form of the green fluorescent protein chromophore observed by cryogenic action spectroscopy
Anne P.
Rasmussen
 *ab,
Nikolaj
Klinkby
*ab,
Nikolaj
Klinkby
 a and
Lars H.
Andersen
a and
Lars H.
Andersen
 a
a
aDepartment of Physics and Astronomy, Aarhus University, Aarhus 8000, Denmark. E-mail: apr@phys.au.dk, lha@phys.au.dk
bUniversité Paris-Saclay, CNRS, Institut des Sciences Moléculaires d'Orsay, 91405 Orsay, France
First published on 15th January 2026
Abstract
We report the observation of states arising from the interaction of an excess electron with the dipole moment of a biochromophore, the meta form of the green fluorescent protein (GFP) model chromophore p-hydroxybenzylidene-2,3-dimethylimidazolinone (mHBDI), using cryogenic ion action spectroscopy. Distinct spectral features appear in the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–20
400–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 region near the electron detachment threshold of mHBDI. Dipole-bound (DBS) and dipole-resonance (DRS) states are identified below and above the detachment energy, respectively. The vertical detachment energy is determined to be 19
100 cm−1 region near the electron detachment threshold of mHBDI. Dipole-bound (DBS) and dipole-resonance (DRS) states are identified below and above the detachment energy, respectively. The vertical detachment energy is determined to be 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 cm−1. The DBS-band origin is at 19
620 cm−1. The DBS-band origin is at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 cm−1 with a binding energy of 176 cm−1. Complementary DFT (ωB97X-D/aug-cc-pVTZ) calculations provide insight into the structure and vibrational resonances of the excess electron in this biologically relevant chromophore. The results extend the understanding of dipole-bound and resonance states in complex molecular systems. We find that one low-energy mode of the neutral radical is particularly Franck–Condon active. The same mode has previously been found to dominate absorption spectra of other GFP-chromophore derivatives. It is suggested that the DRSs are potential doorway states for capture of low energy electrons.
444 cm−1 with a binding energy of 176 cm−1. Complementary DFT (ωB97X-D/aug-cc-pVTZ) calculations provide insight into the structure and vibrational resonances of the excess electron in this biologically relevant chromophore. The results extend the understanding of dipole-bound and resonance states in complex molecular systems. We find that one low-energy mode of the neutral radical is particularly Franck–Condon active. The same mode has previously been found to dominate absorption spectra of other GFP-chromophore derivatives. It is suggested that the DRSs are potential doorway states for capture of low energy electrons.
1. Introduction
Non-valence-bound states (NBSs) are anionic states in which an excess electron is weakly bound to a neutral molecule through interactions that extend well beyond the range of valence orbitals.1–4 NBSs have been found in molecular anions relevant in a range of different fields, from atmospheric chemistry5,6 or astrophysics7–10 to biology.11–14The most common type of NBS is the dipole-bound state (DBS), which can form when a neutral molecule possesses a sufficiently large dipole moment to support an electron bound below the detachment threshold.2,3,15,16 A theoretical lower limit for the dipole moment required to support a DBS is approximately 1.6 D,2,17 while, in practice, dipole-bound states are typically observed only for molecules with dipole moments greater than about 2.5 D.2,16 DBSs were first identified as resonances in the photodetachment spectrum of enolate anions,18–20 and have since been reported for a wide variety of molecular anions.
While the dipole potential typically gives the strongest electron binding, higher-order contributions can also provide binding, as for quadrupole-bound states4,21 and correlation-bound states.22–24 These interactions all act over distances much larger than typical valence-bond lengths, although decaying more rapidly with distance than the Coulomb potential. The binding energy of the excess electron in these nonvalence-bound states is therefore generally small, resulting in highly diffuse electronic wavefunctions.
Dipole-bound states typically occur within a narrow energy window just below the electron-detachment threshold. When nuclear vibrational energy is present in the molecular core—for example, at finite temperature—the total energy can exceed the energy for electron-detachment, and the states manifest as autodetaching dipole-resonance states (DRSs) in the continuum.14 Dipole-resonance states are thus analogous to dipole-bound states, except that they possess sufficient nuclear energy to eject a loosely dipole-bound electron through non–Born–Oppenheimer coupling between electronic and nuclear motions i.e. through vibrational autodetachment.
DBSs are relevant in the field of photoactive proteins and biomolecules, as they have been suggested to be a 'doorway' for the formation of valence-bound anions.25–27 In particular, DBSs and DRSs were detected in two anionic model chromophores of the Photoactive Yellow Protein (PYP).13,14 PYP is a bacterial photoreceptor involved in the negative phototaxis response of Halorhodospira halophila28,29 and two model-chromophores have received recent attention in connection with DBS, the deprotonated para-coumaric acid with a methyl ester group, pCE−, and its ketone derivative, pCK−.14 Another important photoactive protein is the Green Fluorescent Protein (GFP), which is widely used as a biomarker within biological and life sciences due to its characteristic green bioluminescence.30–33 The most commonly used model-chromophore of GFP is the deprotonated p-hydroxybenzylidene-2,3-dimethylimidazolinone (pHBDI−).34 Studying the photophysics of these chromophores in isolation (i.e. gas phase) is important to understand the influence of the protein environment and to benchmark theory.
The photo-physical properties of pHBDI− have been extensively studied in the gas phase,35–40 yet so far no DBSs have been detected for pHBDI, even though the dipole moment of the neutral radical core has been calculated to be about 7 D,41 well above the |µ| > 2.5 D limit to support DBSs. The pHBDI− has a bright S0→ S1 absorption that extends over the detachment-energy threshold. Since the weakly bound DBSs and DRSs only exist in a narrow energy range close to the detachment threshold they are difficult to identify spectroscopically when many strong valence transitions exist in the same energy region. Moving the oxygen atom on the phenolate ring from the para to the meta position leads to pronounced spectroscopic changes.42 In meta-HBDI− (mHBDI−), the S0 → S1 transition is red-shifted to about 700 nm, well under the detachment threshold, and it becomes optically dark due to its charge-transfer character.42 This makes it an excellent system for studying dipole-type resonances near the detachment threshold without interference from valence-bound states.
Detecting subtle dipole-bound/resonance states in molecular anions has been challenging due to experimental limitations. We overcome these challenges using a novel action–absorption approach combining a cryogenic ion trap with an ion-storage ring,43 revealing DBSs previously inaccessible.44 Here, we report the gas-phase action–absorption spectrum of mHBDI−, with DBSs and DRSs near the electron-detachment threshold. Quantum chemical calculations at the ωB97X-D/aug-cc-pVTZ45,46 level of theory support the observations, demonstrating the power of cryogenic trapping and ion-storage-ring spectroscopy to uncover new electronic states in bio-chromophores.
2. Methods
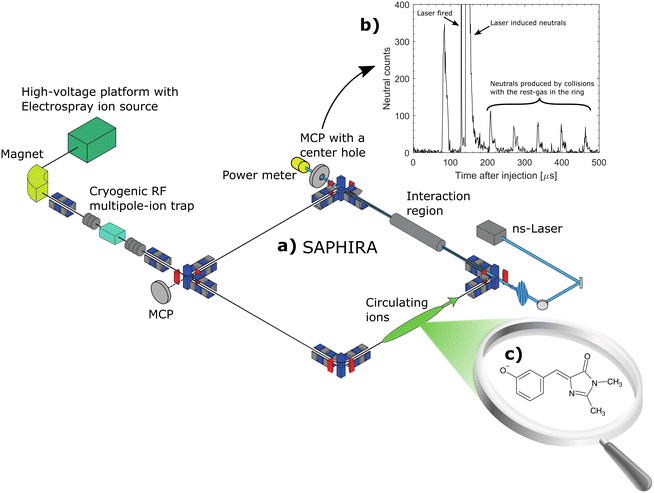
The setup, which has previously been described,38,43,47,48 is illustrated in Fig. 1. Briefly, chromophore ions are continuously produced in an electrospray-ionization source and accumulated in a 16-pole radio frequency (RF) ion trap. After accumulating for 200 ms, the ions are released as a bunch and accelerated to 4 keV. A magnet is used to mass-to-charge select the relevant ions. The ions are then slowed down and trapped in another 16-pole RF trap. This trap is cooled to 6 K by a liquid helium cryo-cooler system, and cooled He-buffer gas is introduced to cool the ions. The ions are cooled for 150 ms, again accelerated to 4 keV and finally injected into the ring. Ions are accumulated in the first trap while the previous bunch of ions is simultaneously cooled in the cold trap, resulting in a duty cycle of 5 Hz. The ring is held at room temperature at a pressure of ∼10−9 mbar.A nano-second laser is used to excite the ions in the interaction region (see Fig. 1b) during their second revolution in the ring, before the ions have time to heat up either by collisions with the residual gas or through black-body radiation.38,43 When addressing bound excited states, resonant two-photon excitation results in prompt electron emission rendering a detectable neutral product.44 Above the detachment limit, neutrals are in addition produced from non-adiabatic vibrational auto-detachment.38 Neutral detection is achieved using a microchannel plate (MCP) detector positioned behind the interaction region. The detector features a central hole that allows laser-light monitoring with a downstream power meter. A second MCP, placed at the end of the last straight section of the ring, records neutrals produced after the ions have passed the corner, which for mHBDI occurs approximately 10 µs after photo excitation. At the end of the measurement cycle, the remaining ions are dumped on the second MCP to measure the total ion count. The action–absorption spectrum is generated by counting the number of neutrals created as a function of wavelength (λ) and normalizing to the number of ions and photons as
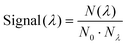 | (1) |
3. Results
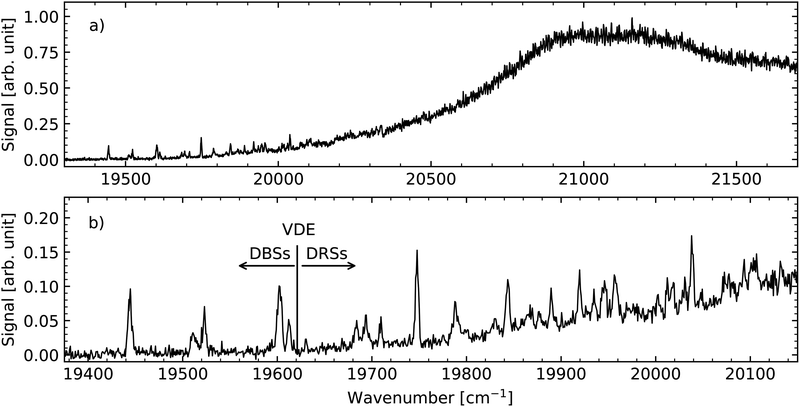
The measured action–absorption spectrum of mHBDI− is shown in Fig. 2. Panel (a) presents the full spectrum, while panel (b) highlights a narrow region exhibiting distinct spectral features near the electron-detachment limit. Previous photoelectron spectroscopy studies have placed the vertical detachment energy (VDE) in the range of (2.4–2.54) ± 0.1 eV (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360–20
360–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 cm−1), with the spread attributed to inhomogeneous broadening caused by internal rotation along single C–C bonds in the ground state.42 The action signal shown in Fig. 2a rises significantly in this threshold region, and we assign the VDE to 19
490 cm−1), with the spread attributed to inhomogeneous broadening caused by internal rotation along single C–C bonds in the ground state.42 The action signal shown in Fig. 2a rises significantly in this threshold region, and we assign the VDE to 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 ± 20 cm−1, corresponding to the onset of the non-resonant background (see Fig. 2b and the SI for details).
620 ± 20 cm−1, corresponding to the onset of the non-resonant background (see Fig. 2b and the SI for details).
The mHBDI− is predicted to possess a dark S1 charge-transfer state at around 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1 with a very low oscillator strength.42 Consequently, the S1 state does not contribute to the action signal observed in the 19
250 cm−1 with a very low oscillator strength.42 Consequently, the S1 state does not contribute to the action signal observed in the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–20
400–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 region. Moreover, the S2 state, located near 25
100 cm−1 region. Moreover, the S2 state, located near 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, lies well above the energy range considered here. The neutral mHBDI radical has a dipole moment that exceeds the ∼2.5 D threshold required to support dipole-bound states. Given that only a single isomer is present in the experiment, the spectral features observed below the VDE are assigned to DBSs, while the features just above the VDE, extending up to 20
000 cm−1, lies well above the energy range considered here. The neutral mHBDI radical has a dipole moment that exceeds the ∼2.5 D threshold required to support dipole-bound states. Given that only a single isomer is present in the experiment, the spectral features observed below the VDE are assigned to DBSs, while the features just above the VDE, extending up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1, are assigned to DRSs (more discussion below). The distinct resonance structures are hence related to the vibrations of the neutral radical core molecule. With a band origin of 19
100 cm−1, are assigned to DRSs (more discussion below). The distinct resonance structures are hence related to the vibrations of the neutral radical core molecule. With a band origin of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 cm−1 and VDE of 19
444 cm−1 and VDE of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 cm−1 the binding energy of the lowest DBS is 176 cm−1. This binding energy is within the usual range found for DBSs (40–200 cm−1).14,49–51
620 cm−1 the binding energy of the lowest DBS is 176 cm−1. This binding energy is within the usual range found for DBSs (40–200 cm−1).14,49–51
No delayed action was observed on the second MCP detector, so all action occurred faster than the approximately 10 µs it takes the ions to pass the corner of the ring and enter into the subsequent straight sections. The same observation was also made for phenoxide, although some resonances (DRSs) were observed to decay on a microsecond time scale for this particular system.44 Vibrational autodetachment on a picosecond time scale52 has also been reported.
Table 1 lists the relative energies (Erel) of the four stable isomers of mHBDI− (see Fig. S2), as well as the calculated adiabatic and vertical detachment energies (ADE, VDE), and the dipole moments of the radical neutral. The ADEs were calculated as the energy differences between the anion and radical neutral at their respective optimized geometries, including zero-point energy (ZPE) corrections, while the VDEs were obtained as the energy difference between the anion and the radical neutral, both at the anion's optimized geometry. Details for the calculations and the vibronic spectra of each of the four isomers are shown in the SI (Fig. S3). The ADEs and VDEs are almost isomer-independent (identical within a few hundred wavenumbers), but the energy of the two E-isomers is significantly higher than for the two Z-isomers. From the relative energies, we expect a ratio of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 for Z1
23 for Z1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z2, assuming a 300 K Boltzmann distribution followed by rapid cooling and kinetic trapping.
Z2, assuming a 300 K Boltzmann distribution followed by rapid cooling and kinetic trapping.
| E rel [cm−1] | ADE [cm−1] | VDE [cm−1] | |μ| [D] | |
|---|---|---|---|---|
| Z1 | 0 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 932 932 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 903 903 |
7.70 |
| Z2 | 311 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 806 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 682 |
3.54 |
| E1 | 1203 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 866 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 881 |
6.81 |
| E2 | 2007 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422 422 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 337 337 |
5.62 |
The vibronic spectrum was calculated using the Franck–Condon method as implemented in the Gaussian 16 program package.53 The ground state of the anion (S0) was taken as the initial state, and the neutral ground state (D0) as the final state, since DBSs do not significantly influence the structure of the neutral core. Geometry optimizations and vibrational frequency calculations were performed at the ωB97X-D/aug-cc-pVTZ level of theory.45,46 The simulated spectrum was generated at 6 K. The calculated frequencies of the stick spectrum were scaled by 0.956654 and convoluted with a Gaussian line shape having a full width at half maximum (FWHM) of 4 cm−1.
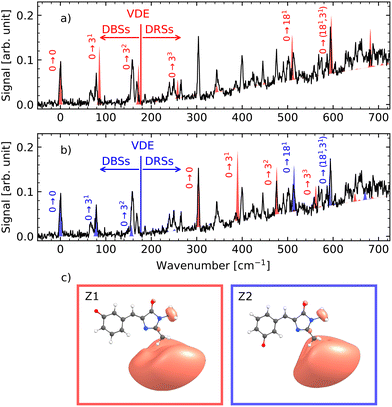
Fig. 3a compares the measured and calculated spectra. The theoretical spectrum was shifted by 512 cm−1 so that the calculated band origin coincides with the lowest observed peak. While the DFT calculations reproduce several prominent features of the experimental spectrum, numerous bands remain unassigned. This discrepancy may arise from the limitations of the theoretical model or from the presence of multiple isomers. The DBSs are very diffuse states, which can be a challenge for DFT, even when using a basis set with diffuse functions. For other smaller systems, couple cluster (CCSD) and equation-of-motion-CCSD (EOM-CCSD) have been used to describe the DBSs.44,55,56 However, this is not feasible with a molecule of this size and is not done in the present study. Different isomers can form during the room-temperature electrospray process and become kinetically trapped upon cryogenic cooling. Similar behavior has been reported for other biomolecular anions produced via electrospray ionization and subsequently cooled to cryogenic temperatures.57–59
Fig. 3b shows the experimental spectrum together with calculated vibronic spectra of the two lowest isomers; Z1 and Z2. Based on the order of the calculated VDEs we here assign the first resonances at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 cm−1 to be the band origin of the Z2 isomers, and the 19
444 cm−1 to be the band origin of the Z2 isomers, and the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748 cm−1 peak to be that of the Z1 isomer (see Fig. 2b). A shift of 816 cm−1 and 638 cm−1 is given to the calculated spectrum of Z1 and Z2, respectively to fit the experimental spectrum. Each spectrum is scaled so that the height of its band origin fits the experimental spectrum, and a linear background starting from the VDE is given to the calculated spectrum to account for the direct detachment signal. Only the lowest lying threshold (VDE) belonging to the Z2 isomer is visible in the spectrum. Even with the inclusion of the vibronic spectra of two isomers, many peaks remain unexplained. This may be due to the level of theory used, and further studies with a higher level of theory will be needed to disentangle the spectrum fully.
748 cm−1 peak to be that of the Z1 isomer (see Fig. 2b). A shift of 816 cm−1 and 638 cm−1 is given to the calculated spectrum of Z1 and Z2, respectively to fit the experimental spectrum. Each spectrum is scaled so that the height of its band origin fits the experimental spectrum, and a linear background starting from the VDE is given to the calculated spectrum to account for the direct detachment signal. Only the lowest lying threshold (VDE) belonging to the Z2 isomer is visible in the spectrum. Even with the inclusion of the vibronic spectra of two isomers, many peaks remain unexplained. This may be due to the level of theory used, and further studies with a higher level of theory will be needed to disentangle the spectrum fully.
The Z1 and Z2 isomers of the neutral radical each exhibit an active bending vibration of the central bridge moiety (Fig. S6), which dominates their spectra. This mode appears at 90 cm−1 and 82 cm−1 for Z1 and Z2, respectively (see SI). An equivalent mode is also active in pHBDI− at 80 cm−1 (ref. 38) and in ortho-HBDI− at 98 cm−1.59 In pHBDI−, the active mode persists over about 1500 cm−1, making it one of the most prominent features of its spectrum.38 In contrast, the lowest-energy modes of mHBDI− (near 30 and 60 cm−1) are not observed in the present spectrum, although it is noteworthy that their harmonics coincide closely with the ∼90 cm−1 feature.
In low-energy electron–molecule scattering, a molecule can transiently capture an incoming electron into a dipole-resonance state (DRS) when the electron's kinetic energy is used to excite low-energy vibrational modes and the neutral molecule has a sufficiently large dipole moment. The resonance state will ordinarily autodetach unless it is stabilized. Stabilization can occur through internal conversion (IC), where the excess electronic energy is transferred non-radiatively into molecular vibrations and subsequently redistributed via intramolecular vibrational redistribution (IVR), or through radiative decay. These processes can channel population from the dipole-bound electronic resonance state into vibrationally hot levels of the anion, effectively trapping the electron and suppressing autoionization. The scattering outcome is governed by the competition of rates: autodetachment versus stabilization (IC/IVR/radiative/collisional). In this work, we have shown that there exist relevant dipole-bound–type resonance states in mHBDI− just above the continuum limit, associated with low-energy vibrations of the radical core. These states were probed here via photoexcitation, but they could equally be populated in a scattering event with a free electron interacting with a dipolar molecule, acting as a doorway for electron capture.
4. Conclusions
This work presents the observation of non-valence bound states (NBSs) in a meta-derivative of the GFP model chromophore (mHBDI−), using cryogenic action spectroscopy. These NBSs appear in the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400–20
400–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 region around the detachment threshold and are attributed to dipole-bound states (DBSs) below the detachment energy and dipole-resonance states (DRSs) above it. The band origin is found at 19
100 cm−1 region around the detachment threshold and are attributed to dipole-bound states (DBSs) below the detachment energy and dipole-resonance states (DRSs) above it. The band origin is found at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 cm−1, and the detachment energy is determined to be 19
444 cm−1, and the detachment energy is determined to be 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 cm−1, yielding a binding energy of 176 cm−1 for the lowest DBS of mHBDI−. Importantly, our work reveals the presence of unbound dipolar resonance states that may act as doorway states for electron capture in scattering processes involving dipolar (bio)molecules.
620 cm−1, yielding a binding energy of 176 cm−1 for the lowest DBS of mHBDI−. Importantly, our work reveals the presence of unbound dipolar resonance states that may act as doorway states for electron capture in scattering processes involving dipolar (bio)molecules.
The experimental spectra were complemented by quantum-chemical calculations at the DFT ωB97X-D/aug-cc-pVTZ45,46 level of theory. While the calculations reproduce several prominent features—particularly those associated with the ν3 vibration- a precise assignment of all observed peaks requires a higher level of theory. This underscores the need for more advanced theoretical treatments to fully characterize the role of NBSs in biologically relevant chromophores.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04796j.Acknowledgements
This work was supported by a research grant (VIL71404) from VILLUM FONDEN.References
- E. Fermi and E. Teller, Phys. Rev., 1947, 72, 399–408 CrossRef CAS
.
- K. D. Jordan and F. Wang, Annu. Rev. Phys. Chem., 2003, 54, 367–396 CrossRef CAS PubMed
.
- J. Simons, J. Chem. Phys. A, 2008, 112, 6401–6511 CrossRef CAS PubMed
.
- D. H. Kang and S. K. Kim, Chem. Phys. Rev., 2024, 5, 041301 CrossRef CAS
.
- Y. Albeck, K. G. Lunny, Y. Benitez, A. J. Shin, D. Strasser and R. E. Continetti, Angew. Chem., 2019, 131, 5366–5369 CrossRef
.
- Y.-R. Zhang, D.-F. Yuan and L.-S. Wang, J. Chem. Phys. Lett., 2022, 13, 11481–11488 CrossRef CAS PubMed
.
- F. Güthe, M. Tulej, M. V. Pachkov and J. P. Maier, Astrophys. J., 2001, 555, 466 CrossRef
.
- T. J. Millar, C. Walsh and T. A. Field, Chem. Rev., 2017, 117, 1765–1795 CrossRef CAS PubMed
.
- B. A. Laws, Z. D. Levey, T. W. Schmidt and S. T. Gibson, J. Am. Chem. Soc., 2021, 143, 18684–18692 CrossRef CAS PubMed
.
- J. N. Bull, C. S. Anstoter, M. H. Stockett, C. J. Clarke, J. A. Gibbard, E. J. Bieske and J. R. Verlet, J. Chem. Phys. Lett., 2021, 12, 11811–11816 CrossRef CAS PubMed
.
- J. N. Bull, C. W. West and J. R. Verlet, Chem. Sci., 2016, 7, 5352–5361 RSC
.
- E. Matthews and C. E. Dessent, J. Chem. Phys. Lett., 2018, 9, 6124–6130 CrossRef CAS PubMed
.
- J. N. Bull, C. S. Anstöter and J. R. Verlet, Nat. Commun., 2019, 10, 5820 CrossRef CAS PubMed
.
- L. H. Andersen, A. P. Rasmussen, H. B. Pedersen and N. Klinkby, Phys. Rev. A, 2025, 112, 022821 CrossRef CAS
.
- C. Desfrançois, H. Abdoul-Carime, N. Khelifa and J. Schermann, Phys. Rev. Lett., 1994, 73, 2436 CrossRef PubMed
.
- C.-H. Qian, G.-Z. Zhu and L.-S. Wang, J. Chem. Phys. Lett., 2019, 10, 6472–6477 CrossRef CAS PubMed
.
- J.-M. Lévy-Leblond, Phys. Rev., 1967, 153, 1–4 CrossRef
.
- A. H. Zimmerman and J. I. Brauman, J. Chem. Phys., 1977, 66, 5823–5825 CrossRef CAS
.
- K. R. Lykke, R. D. Mead and W. Lineberger, Phys. Rev. Lett., 1984, 52, 2221 CrossRef CAS
.
- R. D. Mead, K. R. Lykke, W. Lineberger, J. Marks and J. I. Brauman, J. Chem. Phys., 1984, 81, 4883–4892 CrossRef CAS
.
- M. Gutowski, P. Skurski, X. Li and L.-S. Wang, Phys. Rev. Lett., 2000, 85, 3145 CrossRef CAS PubMed
.
- S. Klaiman, E. V. Gromov and L. S. Cederbaum, J. Chem. Phys. Lett., 2013, 4, 3319–3324 CrossRef CAS
.
- V. K. Voora and K. D. Jordan, Nano Lett., 2014, 14, 4602–4606 CrossRef CAS PubMed
.
- J. N. Bull and J. R. Verlet, Sci. Adv., 2017, 3, e1603106 CrossRef PubMed
.
- A. Kunin and D. M. Neumark, Phys. Chem. Chem. Phys., 2019, 21, 7239–7255 RSC
.
- J. Narayanan SJ, D. Tripathi and A. K. Dutta, J. Chem. Phys. Lett., 2021, 12, 10380–10387 Search PubMed
.
- D. H. Kang, J. Kim, H. J. Eun and S. K. Kim, J. Am. Chem. Soc., 2022, 144, 16077–16085 CrossRef CAS PubMed
.
- M. Baca, G. E. Borgstahl, M. Boissinot, P. M. Burke, D. R. Williams, K. A. Slater and E. D. Getzoff, Biochemistry, 1994, 33, 14369–14377 CrossRef CAS PubMed
.
- U. K. Genick, S. M. Soltis, P. Kuhn, I. L. Canestrelli and E. D. Getzoff, Nat., 1998, 392, 206–209 CrossRef CAS PubMed
.
- R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544 CrossRef CAS PubMed
.
- M. Zimmer, Chem. Rev., 2002, 102, 759–782 Search PubMed
.
- R. N. Day and M. W. Davidson, Chem. Soc. Rev., 2009, 38, 2887–2921 RSC
.
- D. M. Chudakov, M. V. Matz, S. Lukyanov and K. A. Lukyanov, Physiol. Rev., 2010, 90, 1103–1163 Search PubMed
.
- V. Helms, C. Winstead and P. Langhoff, J. Mol. Struct., 2000, 506, 179–189 Search PubMed
.
- S. B. Nielsen, A. Lapierre, J. U. Andersen, U. Pedersen, S. Tomita and L. Andersen, Phys. Rev. Lett., 2001, 87, 228102 CrossRef CAS PubMed
.
- A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771 CrossRef CAS PubMed
.
- W. Zagorec-Marks, M. M. Foreman, J. R. Verlet and J. M. Weber, J. Chem. Phys. Lett., 2019, 10, 7817–7822 CrossRef CAS PubMed
.
- L. H. Andersen, A. P. Rasmussen, H. B. Pedersen, O. B. Beletsan and A. V. Bochenkova, J. Chem. Phys. Lett., 2023, 14, 6395–6401 CrossRef CAS PubMed
.
- A. P. Rasmusssen, H. B. Pedersen and L. H. Andersen, Phys. Chem. Chem. Phys., 2023, 25, 32868–32874 RSC
.
- T. T. Lindkvist, I. Djavani-Tabrizi, L. H. Andersen and S. B. Nielsen, Phys. Rev. Lett., 2025, 134, 093001 CrossRef CAS PubMed
.
- Y. Toker, D. B. Rahbek, B. Klærke, A. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2012, 109, 128101 CrossRef CAS PubMed
.
- A. V. Bochenkova, B. Klærke, D. B. Rahbek, J. Rajput, Y. Toker and L. H. Andersen, Angew. Chem., Int. Ed., 2014, 53, 9797–9801 Search PubMed
.
- H. B. Pedersen, H. Juul, F. K. Mikkelsen, A. P. Rasmussen and L. H. Andersen, Phys. Rev. A, 2022, 106, 053111 Search PubMed
.
- L. H. Andersen, A. P. Rasmussen, H. B. Pedersen and N. Klinkby, Phys. Rev. Lett., 2025, 134, 193002 Search PubMed
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef
.
- H. B. Pedersen, A. Svendsen, L. S. Harbo, H. V. Kiefer, H. Kjeldsen, L. Lammich, Y. Toker and L. H. Andersen, Rev. Sci. Instrum., 2015, 86, 063107 CrossRef CAS PubMed
.
- H. V. Kiefer, E. Gruber, J. Langeland, P. A. Kusochek, A. V. Bochenkova and L. H. Andersen, Nat. Commun., 2019, 10, 1210 Search PubMed
.
- H.-T. Liu, C.-G. Ning, D.-L. Huang, P. D. Dau and L.-S. Wang, Angew. Chem., Int. Ed., 2013, 52, 8976–8979 CrossRef CAS PubMed
.
- G.-Z. Zhu, C.-H. Qian and L.-S. Wang, J. Chem. Phys., 2018, 149, 164301 Search PubMed
.
- D.-F. Yuan, Y. Liu, C.-H. Qian, Y.-R. Zhang, B. M. Rubenstein and L.-S. Wang, Phys. Rev. Lett., 2020, 125, 073003 CrossRef CAS PubMed
.
- D. H. Kang, S. An and S. K. Kim, Phys. Rev. Lett., 2020, 125, 093001 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed
.
- CCCBDB listing of precalculated vibrational scaling factors, https://cccbdb.nist.gov/vibscalejustx.asp, [Accessed 25-Aug-2025].
- W. Skomorowski, S. Gulania and A. I. Krylov, Phys. Chem. Chem. Phys., 2018, 20, 4805–4817 Search PubMed
.
- T. J. Santaloci and R. C. Fortenberry, Chemistry, 2021, 3, 296–313 Search PubMed
.
- A. G. S. Lauridsen, A. P. Rasmussen, N. Klinkby and L. H. Andersen, Phys. Chem. Chem. Phys., 2025, 27, 17686–17691 Search PubMed
.
- J. Dezalay, E. K. Ashworth, J. E. Fulker, M. H. Stockett, J. A. Noble and J. N. Bull, Phys. Chem. Chem. Phys., 2025, 27, 16738–16743 Search PubMed
.
- T. T. Lindkvist, A. P. Rasmussen, N. Klinkby, L. H. Andersen and S. B. Nielsen, J. Chem. Phys. Lett., 2025, 16, 13277–13283 CrossRef CAS PubMed
.
| This journal is © the Owner Societies 2026 |