Open Access Article
Open Access ArticleInvestigating the structure–stability relationship in bridging isomers of bistetrazoles
Sarika Venugopala,
Bhargav Kolekar b,
Rahul V. Pinjari
b,
Rahul V. Pinjari *b and
Anuj A. Vargeese
*b and
Anuj A. Vargeese *a
*a
aLaboratory for Energetic and Energy Materials Research, Department of Chemistry, National Institute of Technology Calicut (NITC), NIT Campus P. O., Calicut, Kerala 673601, India. E-mail: aav@nitc.ac.in
bDepartment of Chemistry, Institute of Chemical Technology Mumbai, Maharashtra, 400019, India. E-mail: rv.pinjari@ictmumbai.edu.in
First published on 4th December 2025
Abstract
Subtle modifications in the molecular structure of materials can have a profound impact on their properties because of the nature of bonding, strength of inter and intramolecular interactions, and the spatial arrangement of atoms. 5,5′-Bis-1H-tetrazole and 5-(tetrazol-1-yl)-2H-tetrazole are two structural isomers, with C–C and C–N linkages between the two tetrazole rings. These structural isomers exhibit distinct thermal behaviors and significant differences in their decomposition temperatures. To understand the differences in thermal stability, a combined experimental and computational study was performed using thermal analysis, Hirshfeld surface analysis, and 2D fingerprint plot analysis. The activation energy for the decomposition of these compounds was computed using isoconversional kinetic analysis to obtain insights into the stability of these compounds at elevated temperatures. A plausible fragmentation pattern was elucidated using high-resolution mass spectrometry (HRMS) and tandem mass spectrometry (MS/MS) data. Density functional theory (DFT) calculations of both the neutral and anionic forms were performed to understand the transition pathways for the decomposition of these compounds and to validate the fragmentation patterns obtained from mass spectrometry.
Introduction
High-nitrogen containing heterocycles, especially the tetrazole derivatives, have been considered as good high energy density materials (HEDMs), owing to their high nitrogen content, high density, thermal stability, and tendency towards lower sensitivity.1 Moreover, their decomposition yields environmentally benign by-products, making them more appealing as eco-friendly HEDMs.2 Introduction of explosophoric groups such as –NO2, –NHNO2, –N3, –C(NO2)3, etc. to an azole ring or a bridged azole molecule enhances the detonation performance of the derived azole derivatives.3 The sensitivity of such HEDMs is greatly influenced by the kind of explosophoric group introduced in the tetrazole, the layered structure,4,5 and face-to-face π–π stacking.6 Our recent investigation on the influence of various explosophoric groups on the stability and decomposition pathways of 1,2,4-triazole derivatives suggests that replacing the amino group with a nitramino group alters the decomposition behaviour of the compound.7 However, the direct incorporation of explosophoric groups into tetrazole or any other azole ring may lead to high sensitivity towards various stimuli (impact, friction, and electrostatic discharge), which hinders their practical utility (Fig. 1(a) and Table 1).8–10 To overcome these drawbacks, coupling one azole ring with another to enhance molecular conjugation has become a widely adopted strategy. This strategy enhances the tunability of both sensitivity and energetic parameters.11 In addition to extended conjugation, strong hydrogen bonding and a well-defined planar structure contribute to the stability and performance of these compounds.12 Recently, the C-nitro group in a fully nitrated triazole (IV) was replaced with a C-tetrazole ring, resulting in the formation of a more stable 1-(trinitromethyl)-5-nitroimino-3-tetrazole-1,2,4-triazole (V) (Fig. 1(b)) with better performance.13 | ||
| Fig. 1 (a) Sensitive molecules with explosophoric groups linked to tetrazole rings (I,8 II,9 III10) and (b) C-triazole derivatives.13 | ||
| Properties | 5-Azido-1H-tetrazole (I) | 5-Nitrotetrazole (II) | 4,5-Dihydro-5-(nitrimino)-1H-tetrazole (III) |
|---|---|---|---|
| Impact sensitivity (J) | <1 | <1 | 1.5 |
| Friction sensitivity (N) | <5 | <5 | 8 |
| Electrostatic discharge (mJ) | <2.2 | — | — |
In the literature, the thermal decomposition of two structural isomers of energetic azoles, pyrazole and imidazole, was studied theoretically at low and high densities, and nitrogen formation was observed in the initial and final stages of pyrazole and imidazole decomposition, respectively. Hydrogen cyanide generation has been proposed as the main decomposition channel for imidazole at normal density, whereas at high density its relevance has decreased. The thermal decomposition of their nitro-derivatives was also investigated and the results showed that ammonia formation is promoted at high density for both nitrocompounds.14 A computational study of 5,5′-bis(1H-tetrazolyl)amine molecular conformations based on density functional theory (DFT) revealed that a non-minimum energy conformation of the 5,5′-bis(1H-tetrazolyl)amine molecule was more favorable for dense packing, with hydrogen bonding contributing to the stabilization of the entire system.15 A comparative investigation on the decomposition of 5,5′-bis-1H-tetrazole, 1,5′-bistetrazole, and 5-(5-azido-(1 or 4)H-1,2,4-triazol-3-yl)tetrazole following electronic state excitation revealed that the decomposition of these molecules yielded nitrogen as the primary decomposition product. Nitrogen formation in 5,5′-bistetrazole and 1,5′-bistetrazole occurs through the opening of the tetrazole ring; however, in 5-(5-azido-(1 or 4)H-1,2,4-triazol-3-yl)tetrazole, it occurs by the cleavage of the N–N bond of the azide group.16
5,5′-Bis-1H-tetrazole (1) and 5-(tetrazol-1-yl)-2H-tetrazole (2) are N-rich heterocyclic structural isomers, with the only difference being the established bridge (Fig. 2). However, they exhibit a significant difference in their decomposition temperatures and, consequently, in their thermal stability. This observation motivated us to explore the reasons for the differences in stability. The thermal stability of compounds 1 and 2 was examined using different thermal analysis techniques, and kinetic analysis was performed by employing Vyazovkin's non-linear integral isoconversional method.17 Tandem mass spectrometry (MS/MS) was used to propose the fragmentation pathways of the ions, where the parent ion was further fragmented through collisions with the inert gas argon. This approach facilitated the determination of specific fragmentation pathways for both the parent and daughter ions. In our previous investigation, mass spectrometric fragmentation patterns confirmed that the incorporation of an alkylidene bridge between two tetrazole moieties significantly enhances the thermal stability of the resulting bistetrazole compounds.18
Trigger or weak bonds prone to dissociation can be identified using computational tools. A computational analysis was performed using DFT calculations to validate the fragmentation patterns deduced from high-resolution mass spectrometry (HRMS). Additionally, Hirshfeld surface graphs and 2D fingerprint plots of these molecules were generated to understand the structure–property relationships. The significant difference in the decomposition temperatures of these isomers was explained on the basis of the extent of hydrogen bonding and crystal packing.
Experimental
Materials and methods
5,5′-Bis-1H-tetrazole (1) was synthesized from manganese 5,5′-bis-1H-tetrazolate using water as the solvent.19 5-(Tetrazol-1-yl)-2H-tetrazole (2) was synthesized from 5-aminotetrazole, sodium azide, and triethyl orthoformate using acetic acid as the solvent.20 The detailed synthetic procedures, thermal analysis results, and computational approaches for the kinetic evaluation are provided in the SI.Thermal analysis
Thermogravimetric (TG) analysis was performed using a PerkinElmer Simultaneous Thermal Analyzer (STA 6000). For all experiments, approximately 0.35–0.5 mg of the sample was loaded in an open 100 µL alumina sample pan and heated under nitrogen flow maintained at 20 mL min−1. Non-isothermal TG runs were performed at heating rates (β) of 2.5, 4, and 5.5 °C min−1 and the thermal data were collected from 50 to 350 °C at different heating rates. DSC analysis was carried out using a TA Instruments Q20 differential scanning calorimeter. Nitrogen was used as the purge gas at a flow rate of 50 mL min−1. About 0.6–0.7 mg of the sample was loaded into an aluminium pan, sealed and the DSC runs were conducted at 5 °C min−1.Kinetic computations
The kinetic parameters can be computed by either model-fitting methods or model-free (isoconversional) methods.21 The model-free method is advantageous over the model-fitting method as it does not follow any assumptions for the reaction mechanism and thus minimizes the possibility of homogeneous and heterogeneous kinetic data errors.22 Also, this method allows the determination of activation energy as a function of temperature or the extent of conversion.23 In the present study, Vyazovkin's non-linear integral isoconversional method was employed for the computations of kinetic parameters and further kinetic analysis. In Vyazovkin's method, numerical integration is used, and hence it provides more precise apparent activation energy values.17 The mass loss data obtained from the non-isothermal TG runs were converted to the extent of conversion (α) using the standard eqn (1),
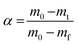 | (1) |
HRMS analysis
Both the compounds were analysed using a Waters Synapt XS high resolution mass spectrometer. LC-MS-grade acetonitrile solvent was used to dissolve the sample in Waters certified 2 mL glass vials to obtain a concentration on the order of 100 ppb. Electrospray ionization (ESI) was performed for data acquisition in negative mode. The data range was 50–600 Da, and leucine enkephalin (200 pg μL−1) was used as the lock mass (m/z 554.2615) for mass correction. The source temperature applied was 120 °C, and the desolvation gas flow was at 896 L h−1 with a desolvation temperature of 400 °C. The capillary voltage was 2.8 kV, and the cone voltage was 35 V. All the tandem mass spectra (MS/MS) were recorded using argon as the collision gas with a collision energy of 20 V. The obtained mass fragments were fitted to the possible molecular formulas using the i-Fit software available with the instrument.Computational studies
All calculations were performed with the molecules in the gas phase using the Gaussian 16W program suite.24 Geometry optimizations of all the structures were achieved using the uB3LYP25,26 functional with the 6-311++G(d,p)27,28 basis set. Optimized geometries were verified with no imaginary frequencies. The first-order saddle points (transition states) were confirmed by the presence of a single negative frequency. Intrinsic reaction coordinate (IRC) calculations were also performed for selected cases to affirm the transition states obtained. The crystal structures of compounds 1 and 2 were generated using Vesta 3 software. Hirshfeld surfaces and 2D finger plots of the compounds were generated using the CrystalExplorer software.Results and discussion
To confirm the formation of compounds 1 and 2, they were characterized using multi-nuclear NMR, HRMS, and Fourier transform infrared (FTIR) spectroscopies (Fig. S1–S10). In the 13C NMR spectrum, compound 1 showed a peak at 148.12 ppm corresponding to the bridge carbon atoms connecting the tetrazole rings (C1) (Fig. S2). However for compound 2, the bridge carbon atom resonated at 155.40 ppm (C2) and the ring carbon atom resonated at 144.21 ppm (C1) (Fig. S7). In the 15N NMR spectrum of 1, two peaks were observed at 360.69 (N2/N3/N6/N7) and 288.43 (N1/N4/N5/N8) (Fig. S3). Similarly, for compound 2, six different types of nitrogens were observed at 390.008 (N7), 357.94 (N6), 341.78 (N2/N3), 325.63 (N8), 291.54 (N1/N4), and 223.25 (N5) (Fig. S8).Thermal analysis
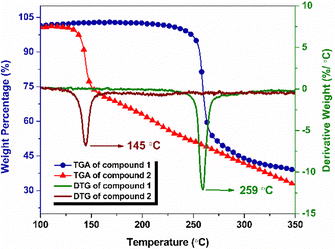
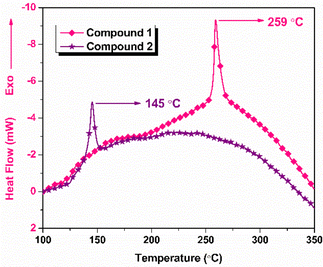
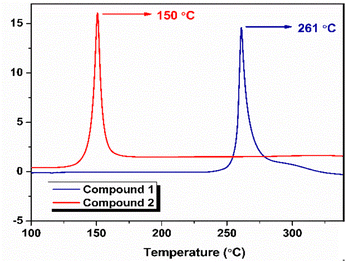
The thermogravimetric-differential thermal analysis (TG-DTA) data of the compounds obtained at a heating rate of 2.5 °C are shown in Fig. 3 and Fig. 4, respectively. From the DTG curve (Fig. 3), compound 1 exhibited an onset decomposition temperature of 233 °C and a peak temperature of 259 °C. Similarly, for compound 2, the onset decomposition and peak of decomposition were observed at 120 and 145 °C, respectively. In TGA, compound 1 exhibited weight loss up to 279 °C, resulting in a total weight loss of 51%, whereas compound 2 exhibited a weight loss of 29% and was continued up to a temperature of 160 °C with a slow weight loss observed after major decomposition. The slow weight loss indicates the possible oxidation of the carbonaceous decomposition products formed after the major decomposition event. As shown in the DTA curves (Fig. 4), compound 1 decomposed at 259 °C and compound 2 decomposed at 145 °C.DSC plots for both compounds were recorded at 5 °C min−1 (Fig. 5). The onset and peak temperatures of decomposition of compound 1 were found to be 238 and 261 °C, respectively, and the decomposition process was completed at 292 °C. Similarly, the onset of decomposition of compound 2 occurred at 135 °C, and the decomposition peak was observed at 150 °C, and the process was completed at 167 °C. Table S1 summarizes the results of thermal analysis. The significant difference in the peak decomposition temperature indicated that compound 1 was more thermally stable than compound 2.
Kinetic analysis
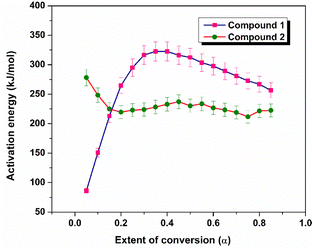
The thermogravimetric data recorded at heating rates of 2.5, 4, and 5.5 °C min−1 were used to compute the extent of conversion (α) values and the kinetic parameters were computed within the temperature range of 230–265 °C for compound 1 and 130–160 °C for compound 2. Fig. S11 and S12 show the α–T curves of compounds 1 and 2. The activation energy (Eα) values were calculated using Vyazovkin's method and plotted as a function of α (Fig. 6). For compound 1, the activation energy increases within the conversion range of 0.05–0.42, and the region is defined by an average activation energy of 203 kJ mol−1. Subsequently, a decrease in Eα was observed within the 0.43 to 0.85 region of α, with an average activation energy of 284 kJ mol−1. For compound 2, the activation energy is independent of the extent of conversion and the average activation energy was found to be 224 kJ mol−1 in the 0.15–0.85 region of α. The independence of the activation energy with α suggests two possibilities, a single-step process defined by a single activation energy, or the convergence of a multi-step process to a unified activation energy value.Tandem mass spectrometry analysis
ESI-HRMS spectra were recorded for the compounds in negative mode, and the results are tabulated in Table 2. Mass fragmentation analysis and the possible pattern of compound 1 were reported in our earlier studies.18 Fig. S4 shows the ESI-HRMS spectrum of compound 1, and the compound exhibits a base peak at 137.0325, which represents the (M–H)− ion. Fig. S9 shows the ESI-HRMS spectrum of compound 2. A base peak was observed at m/z 137.0335 (2A), corresponding to the (M–H)− ion. Furthermore, the results showed peaks at m/z 297.0565 and 457.0786, corresponding to the possible adducts [(2M–H) + Na]− and [(3M–2H) + 2Na]−, respectively.| Compound | Molecular weight | Possible Species | Elemental composition | Observed mass (m/z) | Calculated mass (Da) | Error (ppm) |
|---|---|---|---|---|---|---|
| Compound 1 | 138.0909 | (M–H)− | C2HN8− | 137.0325 | 137.033 | 3.6 |
| Compound 2 | 138.0909 | (M–H)− | C2HN8− | 137.0335 | 137.033 | 3.6 |
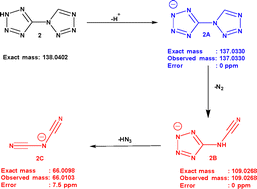
Subsequently, MS/MS analysis of the (M–H)− ion detected at m/z 137.04 for both compounds 1 and 2 was carried out to investigate the fragmentation pathways of the compounds. Fig. S13 and S14 represent the MS/MS spectra of compounds 1 and 2, respectively. The results of MS/MS analysis are listed in Table 3. The MS/MS of compound 1 showed major daughter ions at m/z 109.0273 and 94.0208 (Fig. S13 and Table 3).18 The fragmentation pattern for compound 1 suggests the possible formation of (C2HN6)− and (C2N5)− via nitrogen extrusion and HN3 elimination reactions of the (M–H)− ion.18 For compound 2, the spectrum showed significant peaks at m/z 109.0268 and 66.0103 (Fig. S14 and Table 3). Accordingly, a probable fragmentation pathway for compound 2 was proposed and is shown in Scheme 1. From the parent ion peak at m/z 137.033 ((C2HN8)−, 2A), the nitrogen extrusion reaction produced 2B [(C2HN6)−] at m/z 109.0268, and 2B eliminated HN3 to form 2C [(C2N3)−] at m/z 66.0103. Hence, both compounds eliminated molecular nitrogen and hydrazoic acid during fragmentation. The only difference is that, in compound 1, both eliminations occur from the same parent ion, whereas for compound 2, the elimination occurs in a sequence starting from the parent ion.
| Compound | Peak selected for MS/MS analysis | Observed mass (m/z) (daughter ions) | Molecular formula | Exact mass (Da) |
|---|---|---|---|---|
| Compound 1 | 137.04 (C2HN8)− | 109.0273 | (C2HN6)− | 109.0268 |
| 94.0208 | (C2N5)− | 94.0159 | ||
| Compound 2 | 137.04 (C2HN8)− | 109.0268 | (C2HN6)− | 109.0268 |
| 66.0103 | (C2N3)− | 66.0098 |
Computational studies
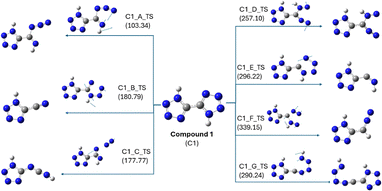
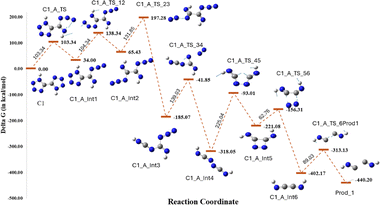
To identify the decomposition pathways of both compounds, the individual bonds were systematically cleaved to yield simpler molecules such as N2, HCN, HNC, and HN3. The central theme of this approach is determining the relative strength of the bonds within each compound by calculating their bond dissociation energies with respect to the parent compound. This approach led to the identification of transition states (TS) produced from the parent compound. The optimized structures of all the TS were obtained upon completion of the calculations. Subsequently, the decomposition pathway was determined by identifying the most stable species based on their total energy. Minima calculations for the TS with higher energies were not performed to save computational time and effort.For compound 1, all possible scan jobs were performed by breaking individual bonds in the system to obtain simpler molecules such as N2, HCN, HNC, and HN3, which resulted in the formation of seven transition states, as shown in Fig. 7. C1_A_TS showed the lowest energy (103.34 kJ mol−1), indicating that it is the most energetically favourable TS. The other transition states, C1_B_TS to C1_G_TS, have barriers from 177.77 kJ mol−1 to 339.15 kJ mol−1. The TS energy trend was found to be: C1_A_TS < C1_C_TS < C1_B_TS < C1_D_TS < C1_G_TS < C1_E_TS < C1_F_TS. Thus, further decomposition of compound 1 was considered to occur from the intermediate C1_A_Int1 formed from C1_A_TS only (Fig. 8). Initially, transition state C1_A_TS was formed by breaking the bond between N1 and N2 or between N5 and N6. The rate-determining step in the degradation pathway of compound 1 is the formation of the intermediate C1_A_Int5, following the sequential elimination of two dinitrogen molecules, one each from the tetrazole ring. This step proceeds via transition state C1_A_TS_45, with an associated activation energy barrier of 225.04 kJ mol−1. After a series of successive bond cleavages, two molecules of HNC were obtained as the decomposition products. The results show that the two isomers undergo distinct multistep decomposition pathways, with compound 2 displaying lower activation barriers and fewer steps, consistent with its experimentally lower thermal stability.
To investigate the influence of the functional and basis set on the computed energies, the energies (Table S2) of the transition state (TS) for compound 1 (Fig. 7) were computed using Grimme's D3 dispersion-corrected DFT29 with the uB3LYP and uM06-2X functionals, employing the 6-311++G(d,p) and 6-311++G(2d,2p) basis sets. Among all combinations of the functionals and basis sets, the C1_A_TS exhibited the lowest energy. The transition state energies show a small variation with the change in basis set from 6-311G++(d,p) to 6-311G++(2d,2p), with a maximum difference of 3.8 kJ mol−1 observed for C1_D_TS. Similarly, with the change in functional from uB3LYP to uM06-2X, despite the increase in transition state energy barriers (by about 25 kJ mol−1), the overall trend in TS energy remained unchanged. Thus, the calculations henceforth were performed using the uB3LYP-D3/6-311++G(d,p) level of theory to save computational cost.
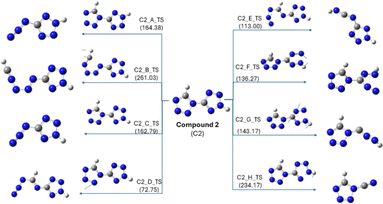
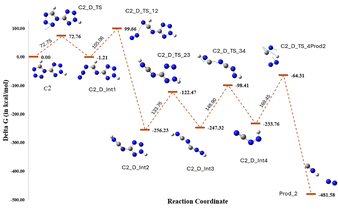
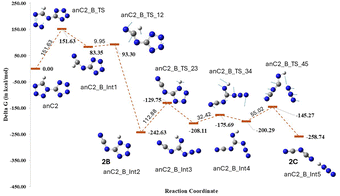
For compound 2, eight transition states were obtained, in which C2_D_TS formed by breaking the N5–N6 bond showed the lowest energy barrier (72.75 kJ mol−1) (Fig. 9). The rate-determining step for compound 2 had an energy barrier of 169.45 kJ mol−1 (Fig. 10), which was ∼55 kJ mol−1 lower than that of compound 1. Furthermore, the overall lower energy barrier for compound 2 compared with that of compound 1 is consistent with the experimentally observed lower onset of decomposition for compound 2. Unlike compound 1, compound 2 produces N2 and HNC as decomposition products, with relatively fewer bond cleavage steps. The kinetic data suggest the possibility of a single-step process defined by a single activation energy or the convergence of a multi-step process to a unified activation energy value. However, the decomposition pathway obtained from DFT calculations ruled out the possibility of a single-step decomposition and hence concluded that compound 2 exhibited multi-step decomposition.
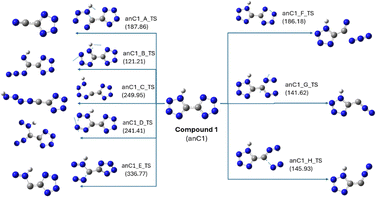
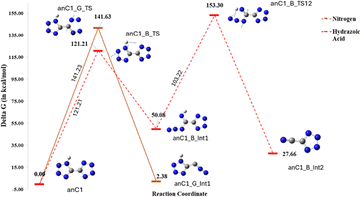
DFT calculations were performed for the anionic forms of both compounds to validate the mass fragmentation patterns obtained from the MS/MS data. Similar to neutral compounds, the individual bonds in the anionic species of compound 1 were systematically cleaved, resulting in the formation of transition states as shown in Fig. 11; several transition states led to the same minima product and were therefore combined in the figure. The transition states, anC1_B_TS and anC1_G_TS, with energies of 121.21 and 141.62 kJ mol−1, respectively, were identified as the lowest energy transition states and were considered for further DFT calculations (Fig. 12). The decomposition pathway for anC1_B_TS yielded hydrazoic acid, while anC1_G_TS yielded molecular nitrogen as the decomposition product, which is consistent with the proposed mass fragmentation pattern from the MS/MS data.18
The transition states for the anionic form of compound 2 were obtained by the cleavage of the individual bonds, as shown in Fig. 13. Transition state anC2_A_TS was identified as the lowest TS with the supply of an energy of 112.38 kJ mol−1; however, further calculations revealed that the subsequent steps exhibited a high energy barrier of 170.62 kJ mol−1 and produced the same minima obtained directly from anC2_B_TS, which involved a relatively low-energy barrier of 151.62 kJ mol−1. Hence, anC2_B_TS was selected for further calculations, and its decomposition pathway is illustrated in Fig. 14. After a series of successive bond cleavages, C2N3 was formed as a decomposition product, which supports the mass fragmentation pattern obtained. Overall, the computational analysis of the anionic species corroborates the MS/MS fragmentation patterns for both compounds, reinforcing the proposed decomposition mechanisms.
Crystal structure, Hirshfeld surface and 2D fingerprint plot analysis
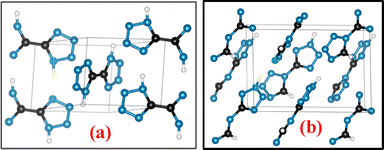
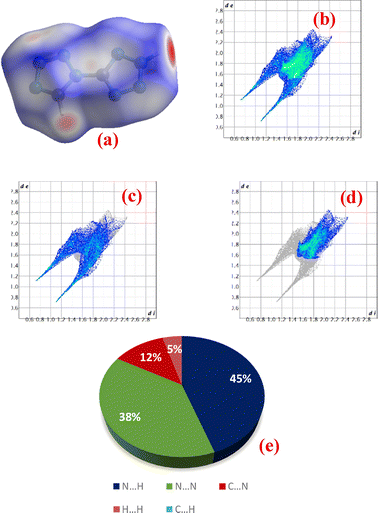
The crystal structures of compounds 1 and 2 were generated using Vesta 3 software and are shown in Fig. 15(a) and (b).30 Compound 1 (CCDC number: 2336252) belongs to the monoclinic P21/n space group and contains two molecules per unit cell. It features a well-defined planar structure and is packed in chains with strong hydrogen bonding, resulting in a layered three-dimensional framework.32 Compound 2 (CCDC number: 709126) belongs to the chiral monoclinic space group Pn with four molecules per unit cell. In compound 2, the proton is located on the N2 nitrogen atom, whereas compound 1 exists as a 1H, 1′H-tautomer.20 The packing arrangement of compound 1 is shown in Fig. S15,30 and Fig. S16 shows a view of the unit cell of compound 2 along the inverse a-axis.20To gain a better understanding of the correlation between intermolecular interactions and physicochemical properties, as well as to explain the molecular stability and sensitivity of the compounds, Hirshfeld surfaces and 2D fingerprint plots were generated from the crystal structures, and the percentage contributions of close contacts were computed using CrystalExplorer software (Fig. 16 and 17). The molecular stability and crystal packing of energetic materials are largely governed by hydrogen bonding, which is stronger than van der Waals bonding.32 Red and blue dots on the Hirshfeld surface represent distances that are shorter and longer than the van der Waals radii, respectively, and white dots indicate distances equal to the sum of van der Waals radii, respectively. The red region denotes the hydrogen-bond acceptor sites, responsible for the molecular stability and packing of the crystals, and the blue region denotes the hydrogen-bond donor sites.33,34 The significant spikes at the bottom of the 2D fingerprint plots indicate strong intermolecular hydrogen bonds.32
As shown in Fig. 16(a), compound 1 shows a red region appearing on the nitrogen atoms, which denotes the electronegative character and possible protonation and hydrogen bonding sites.33 For both compounds, N⋯H contacts were responsible for the molecular stability and crystal packing (Fig. 16 and 17(c, e)). For compound 1, the N⋯H and H⋯H close contacts contributed 44% and 3%, respectively, which slightly increased to 45% and 5%, respectively, for compound 2.
Additionally, the significant spikes at the bottom of the 2D fingerprint plot indicate that both compounds exhibit stronger intermolecular hydrogen bonding. The contribution from the N⋯N atomic contacts is responsible for destabilization, which results in an increase in the sensitivity of energetic materials.35 In compounds 1 and 2, the N⋯N atomic contacts contributed 40% and 38% of the total weak interactions, respectively. Hence, both compounds showed relatively similar contributions from different atomic close contacts, suggesting comparable stability. The lattice energies for both compounds were computed using CrystalExplorer software and were found to be −143.3 and −103.35 kJ mol−1 for compounds 1 and 2, respectively. A more negative lattice energy indicates better stability. Hence compound 1 is more stable than compound 2.
The D–H⋯A (dihedral) angles for compounds 1 and 2 were 168° and 152°, where D, H, and A represent the donor atom, the hydrogen atom attached to the donor atom, and acceptor atoms, respectively (Fig. S17 and S18).30 The closer the dihedral angle is to 180°, the stronger the hydrogen bonding. Hence, compound 1 is more stable, which could result in a higher decomposition temperature. In addition, DFT analysis showed that the total electronic energy of compound 2 exceeded that of compound 1 by 26.27 kJ mol−1 (Fig. S19). The dimerization energy was also calculated (Fig. S20) using ΔΔGDimerization = ΔGDimer − 2 × ΔGMonomer to compare the stability of these compounds. Compound 1 forms a dimer with a similar hydrogen bonding pattern to the crystal structure, stabilized by −32.76 kJ mol−1 through N–H⋯N intermolecular hydrogen bonds, with an N–H⋯N bond angle of 173.8°. Compound 2 formed five dimers with ΔΔGDimerization values of −6.81, −6.02, −4.72, 4.47, and 17.57 kJ mol−1. Dimers 1, 2, and 3 were stabilized with negative dimerization energies, while dimers 4 and 5 were destabilized. Among the stable dimers of compound 2, Dimer-1, with N–H⋯N and C–H⋯N intramolecular hydrogen bonding, showed the lowest energy compared to Dimer-2 with N–H⋯N hydrogen bonding. Furthermore, the more directional hydrogen bonding in Dimer-1, with an N–H⋯N bond angle of 143.9°, contributed to its improved stability compared to Dimer-2 with an N–H⋯N bond angle of 124.5°. Compound-2-Dimer-1 and Dimer-3 have similar hydrogen bonding but differ in C–H bond orientation, matching the zig-zag arrangement of the crystal structure. In addition, the dimer of compound 1 was five times more stable than the most stable dimer of compound 2, indicating its higher stability of compound 1.
Conclusions
The thermal stability of two structural isomers, 5,5′-bis-1H-tetrazole (1, with a C–C bridge) and 5-(tetrazol-1-yl)-2H-tetrazole (2, with a C–N bridge), was investigated using a combination of experimental and computational methods. Kinetic analysis revealed that compound 1 underwent a multi-step decomposition, whereas compound 2 exhibited a linear Eα–α relationship. However, the computational findings indicated a more complex decomposition pathway for compound 2, ruling out a simple single-step mechanism. MS/MS analysis showed that both compounds generated molecular nitrogen (N2) and hydrazoic acid (HN3) as major degradation fragments, which is consistent with computational fragmentation simulations. Despite similar intermolecular interaction patterns observed in the Hirshfeld surface analysis and 2D fingerprint plots, compound 2 decomposed at a lower temperature. This difference is attributed to the stronger hydrogen bonding and more rigid crystal packing in compound 1, which also exhibited a planar structure, higher dihedral angle, and more negative dimerization energy. In contrast, compound 2 exhibited lower planarity and weaker hydrogen-bonding interactions. These findings confirm the crucial role of intermolecular interactions, molecular geometry, and crystal packing in governing the thermal behavior of the structural isomers. This study provides insights into the influence of bridging entities and crystal structures on the thermal stability and decomposition behavior of structurally-related bistetrazole-based energetic materials.Author contributions
The manuscript was written through the contributions of all authors.Conflicts of interest
There are no conflicts of interest to declare.Data availability
Most of the data supporting the findings of this study are included in the supplementary information (SI). The synthesis details of the compounds, characterization data, details of the kinetic analysis, HRMS data, thermal analysis data, and additional computational data are provided in the supplementary information. See DOI: https://doi.org/10.1039/d5cp04469c.Additional data are available from the corresponding author upon reasonable request.
Acknowledgements
S. V. acknowledges the Department of Science and Technology (DST) for the INSPIRE Fellowship [IF190991]. The authors thank DST-FIST for the HRMS facility at NIT Calicut and Center for Materials Characterization (CMC)-NIT Calicut for the NMR facility.Notes and references
- T. Wang, H. Gao and J. M. Shreeve, Functionalized Tetrazole Energetics: A Route to Enhanced Performance, Z. Anorg. Allg. Chem., 2021, 647, 157–191 CrossRef CAS.
- B. Chen, H. Lu, J. Chen, Z. Chen, S. F. Yin, L. Peng and R. Qiu, Recent Progress on Nitrogen-Rich Energetic Materials Based on Tetrazole Skeleton, Springer Science and Business Media Deutschland GmbH, 2023, preprint DOI:10.1007/s41061-023-00435-8.
- K. Mohammad, V. Thaltiri, N. Kommu and A. A. Vargeese, Octanitropyrazolopyrazole: A gem-trinitromethyl based green high-density energetic oxidizer, Chem. Commun., 2020, 56, 12945–12948 RSC.
- Y. Feng, M. Deng, S. Song, S. Chen, Q. Zhang and J. M. Shreeve, Construction of an Unusual Two-Dimensional Layered Structure for Fused-Ring Energetic Materials with High Energy and Good Stability, Engineering, 2020, 6, 1006–1012 CrossRef CAS.
- Y. Feng, J. Wang and Z. Li, Construction of Layered High-Energy Materials via Directional Hydrogen Bonding, Cryst. Growth Des., 2021, 21, 4725–4731 CrossRef CAS.
- Z.-H. Xue, H. Zhang, Z. Wang, R. Xu, Y. Zhang and Q.-L. Yan, Layered assembling of energetic molecules with improved thermostability templated by in-situ generated 2D crosslinked macromolecules, Chem. Eng. J., 2024, 489, 151429 CrossRef CAS.
- S. Venugopal, S. Saha, N. Kumbhakarna and A. A. Vargeese, Insights into triazole-based energetic material design from decomposition pathways of triazole derivatives, Phys. Chem. Chem. Phys., 2025, 27, 4269–4277 Search PubMed.
- J. Stierstorfer, T. M. Klapötke, A. Hammerl and R. D. Chapman, 5-Azido-1 H -tetrazole – Improved Synthesis, Crystal Structure and Sensitivity Data, Z. Anorg. Allg. Chem., 2008, 634, 1051–1057 CrossRef CAS.
- T. M. Klapötke, C. M. Sabaté and J. Stierstorfer, Neutral 5-nitrotetrazoles: easy initiation with low pollution, New J. Chem., 2009, 33, 136–147 Search PubMed.
- T. M. Klapötke and J. Stierstorfer, Nitration Products of 5-Amino-1 H -tetrazole and Methyl-5-amino-1 H -tetrazoles – Structures and Properties of Promising Energetic Materials, Helv. Chim. Acta, 2007, 90, 2132–2150 CrossRef.
- H. Zhang, Y. Zou, X. Hao, Y. Liu, G. Zhang, Z. Dong and Z. Ye, Boosting Intermolecular Interactions of Tetrazole and 1,2,4-Oxadiazole Enables Achieving High-Energy Insensitive Materials, Cryst. Growth Des., 2024, 24, 6204–6210 CrossRef CAS.
- G. Zhang, X. Hao, Y. Zou, S. Liu, J. Wei, Z. Dong and Z. Ye, Towards advanced N-rich energetic explosives: based on tetrazole and triazole groups with large conjugated systems and extensive hydrogen bonds, J. Mater. Chem. A, 2024, 12, 33249–33256 RSC.
- Y. Zou, H. Zhang, X. Hao, G. Zhang, Z. Dong and Z. Ye, Replacing C-Nitro with C-Tetrazole: A Promising Strategy to Enhance the Detonation Performance and Stability of Explosives, Cryst. Growth Des., 2025, 25, 2439–2445 Search PubMed.
- S. Zhu, W. Yang, Q. Gan, N. Cheng and C. Feng, Comparative study on the thermal decomposition of structural isomers: Pyrazole and imidazole energetic materials, Mater. Chem. Phys., 2022, 278, 125607 CrossRef CAS.
- D. Laniel, E. Sebastiao, C. Cook, M. Murugesu, A. Hu, F. Zhang and S. Desgreniers, Dense nitrogen-rich energetic materials: A study of 5,5′-bis(1 H -tetrazolyl)amine, J. Chem. Phys., 2014, 140, 184701 CrossRef PubMed.
- B. Yuan, Z. Yu and E. R. Bernstein, Initial mechanisms for the decomposition of electronically excited energetic materials: 1,5′-BT, 5,5′-BT, and AzTT, J. Chem. Phys., 2015, 142, 124315 CrossRef PubMed.
- S. Vyazovkin, Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature, J. Comput. Chem., 1997, 18, 393–402 CrossRef CAS.
- S. Venugopal and A. A. Vargeese, Decomposition Mechanism of Alkylidene Bridged Tetrazoles With Different Carbon Chain Lengths, ChemPhysChem, 2025, 26, e202400943 CrossRef CAS PubMed.
- Z. Noorpoor and S. Tavangar, Preparation and characterization of Cu based on 5,5’-bistetrazole as a recyclable metal-organic framework and application in synthesis of diaryl ether by the Ullmann coupling reaction, J. Coord. Chem., 2021, 74, 1651–1662 Search PubMed.
- N. Fischer, D. Izsák, T. M. Klapötke and J. Stierstorfer, The chemistry of 5-(tetrazol-1-yl)-2H-tetrazole: An extensive study of structural and energetic properties, Chem. - Eur. J., 2013, 19, 8948–8957 CrossRef CAS PubMed.
- J. E. White, W. J. Catallo and B. L. Legendre, Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies, J. Anal. Appl. Pyrolysis, 2011, 91, 1–33 CrossRef CAS.
- M. Azam, A. Ashraf, S. S. Jahromy, W. Raza, H. Khalid, N. Raza and F. Winter, Isoconversional nonisothermal kinetic analysis of municipal solid waste, refuse-derived fuel, and coal, Energy Sci. Eng., 2020, 8, 3728–3739 CrossRef CAS.
- S. Vyazovkin and C. A. Wight, Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data, Thermochim. Acta, 1999, 340–341, 53–68 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. McLean and G. S. Chandler, Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- P. J. Steel, Heterocyclic tautomerism. XI. Structures of 5,5′-bitetrazole and 1-methyl-5-(2′-pyridyl)tetrazole at 130 K, J. Chem. Crystallogr., 1996, 26, 399–402 CrossRef CAS.
- X. Yu, J. Tang, C. Lei, C. Xue, H. Yang, C. Xiao and G. Cheng, A novel synthesis method for nitrogen-rich energetic frameworks containing bistetrazoles: assembling an advanced high-energy density material with high nitrogen content and good oxygen balance, J. Mater. Chem. A, 2024, 12, 29638–29644 RSC.
- R. S. Mathpati, A. K. Yadav, V. D. Ghule and S. Dharavath, Potential energetic salts of 5,5′-methylenedi(4H-1,2,4-triazole-3,4-diamine) cation: Synthesis, characterization and detonation performance, Energy Mater. Front., 2022, 3, 90–96 CrossRef CAS.
- A. K. Yadav, V. D. Ghule and S. Dharavath, Thermally Stable and Insensitive Energetic Cocrystals Comprising Nitrobarbituric Acid Coformers, Cryst. Growth Des., 2023, 23, 2826–2836 CrossRef CAS.
- A. K. Yadav, S. Kukreja and S. Dharavath, Highly Promising Primary Explosive: A Metal-Free, Fluoro-Substituted Azo-Triazole with Unmatched Safety and Performance, JACS Au, 2025, 5(2), 1031–1038 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |