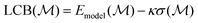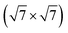Active Δ-learning with universal potentials for global structure optimization
Joe
Pitfield
 ,
Mads-Peter Verner
Christiansen
,
Mads-Peter Verner
Christiansen
 and
Bjørk
Hammer
and
Bjørk
Hammer

Center for Interstellar Catalysis, Department of Physics and Astronomy, Aarhus University, DK-8000 Aarhus C, Denmark. E-mail: joepitfield@gmail.com; hammer@phys.au.dk
First published on 1st December 2025
Abstract
Universal machine learning interatomic potentials (uMLIPs) have recently been formulated and shown to generalize well. When applied out-of-sample, further data collection for improvement of the uMLIPs may, however, be required. In this work we demonstrate that, whenever the envisaged use of the MLIPs is global optimization, the data acquisition can follow an active learning scheme in which a gradually updated uMLIP directs the finding of new structures, which are subsequently evaluated at the density functional theory (DFT) level. In the scheme, we augment foundation models using a Δ-model based on this new data using local SOAP-descriptors, Gaussian kernels, and a sparse Gaussian process regression model. We compare the efficacy of the approach with different global optimization algorithms, random structure search, basin hopping, a Bayesian approach with competitive candidates (GOFEE), and a replica exchange formulation (REX). We further compare several foundation models, CHGNet, MACE-MP0, and MACE-MPA. The test systems are silver–sulfur clusters and sulfur-induced surface reconstructions on Ag(111) and Ag(100). Judged by the fidelity of identifying global minima, active learning with GPR-based Δ-models appears to be a robust approach. Judged by the total CPU time spent, the REX approach stands out as being the most efficient.
I. Introduction
Over the past two decades, the fields of molecular, colloid, and materials science have supported the development of highly flexible machine learning interatomic potentials (MLIPs).1–4 Formulated using frameworks such as feed-forward deep neural networks5 or Gaussian process regression models,6 such MLIPs have proven highly efficient for atomistic simulations allowing larger and more complex systems7 and longer time-scales compared to simulations performed fully with density functional theory (DFT).8–11 The data used to train such models is collected according to various protocols,12 including random sampling,13,14 global optimization searches,15,16 normal mode analysis,17 molecular dynamics,18,19 and saddle point searching.20 Active learning schemes have been invoked, in which the models are retrained upon assembly of data, often using uncertainty to guide data selection.21–31Recently, equivariant graph-neural network models have been introduced for MLIPs.32,33 These models encode the vectorial properties of the local environment and embed information about farther environments via message passing. Such models are generally more data efficient34 and have supported the introduction of foundation models,35–37 where general purpose, “universal” MLIPs (uMLIPs) are trained on huge preassembled databases spanning the entire periodic table and including compounds bonded covalently, ionically, dispersively, and metallically. A swathe of recent advancements in the field of foundation models have shown rapid improvement in benchmarking, evidencing their suitability for direct application.38,39
A common procedure for making such advancements and improving uMLIPs and MLIPs in general, focuses on adding more diverse training data.40 An example of this is the emergence of the successive models MACE-MP0 and MACE-MPA.37 The training datasets are for both models that of the materials project database (MPtrj),36 and in the case of MACE-MPA a portion of the Alexandria database.41 The larger training dataset for MACE-MPA causes the model to perform more accurately in predictions across the matbench discovery benchmark.42 An alternative approach for improving foundation MLIPs is via loss function engineering and change of design philosophy. The FAIR META eSEN-30M-OAM model43 shows iterative improvement by acknowledging the relevance of quality metrics, such as KSRME (symmetric relative mean error in the phonon contribution to the thermal conductivity, which correlates with the smoothness of the energy landscape) in describing when a potential is truly performative.
Whilst it does not fall within the scope of most materials scientists to perform such bespoke model training from scratch (more so than ever with models such as the 1.6 billion parameter UMA model44), other methods of either changing or adding to existing models to fit a given application, do. When changing an existing model is limited in scope to adding more data (and potentially changing the loss function), the approach is commonly referred to as “fine-tuning”.
Fine-tuning has shown to be effective in improving the accuracy of models, so much so that the training methodology for some of the best performing models (eSEN) actually included fine-tuning explicitly. It has been found that such fine-tuning is effective at remedying systematic problems such as softening of the potential energy landscape (PES).40 Other systematic examples, such as surface energies,45 alloy mixing,46 thermal conductivity,47 phonons48 and sublimation enthalpies,49 have shown similar improvement under fine-tuning with 10–1000 s of supplementary datapoints, depending on the property.
Crucially, the current metrics for fine-tuning or training large models in general do not place any emphasis on the energetic ordering of low energy structures. Often, the global minimum energy configuration for a system exists outside of the intuitive, thanks to effects which one can describe as phenomenological rather than systematic. uMLIPs, without proportional incentive to understand such phenomena, can become deficient in the discovery regime. Studying silicate clusters and ultra-thin surface-oxides on Ag(111), we have previously demonstrated that fine-tuning a uMLIP is reliably able to correct structural inconsistencies and yield correct ordering of low-energy configurations.50 Notably, this required a dataset obtained through active learning enhanced exploration of the PES. This procedure would have been difficult and expensive to carry out with iterative fine-tuning. Furthermore, if less data is provided to the network than during initial training, the possibility exists that during the fine-tuning procedure, some of the insight obtained through the initial training step is lost or distorted: known as “catastrophic forgetting”. An alternative means to correct a uMLIP is that of an additive Gaussian process regression (GPR) Δ-model,50 which does not involve altering the weights of the uMLIP. Utilizing a GPR ensures that corrections are local to the new training data, and that the predictions of the model return to that of the uMLIP outside of this region.50 Such a model is agnostic to several elements of the original uMLIP, including (i) the choice of loss function, (ii) the network architecture, and (iii) the data used in the original training. This correction is often able to encode phenomenological effects, which are not well described by the uMLIP. A further benefit of a scheme with a Δ-model is, that the training is computationally cheap and can be applied often, not requiring the collection of large batches of new data before updating the potential.
In the current work, we investigate the viability of establishing a reliable Δ-model corrected uMLIP via an active-learning scheme. The use-case envisaged for the resulting corrected uMLIP is global structure optimization, and hence the data-collection is guided by structures realized during such optimizations. Different algorithms are considered: random structure search, basin hopping, and some more elaborate ones introduced below. With these methods, the global minimum DFT energy structures (GMs) of a range of [Ag2S]X clusters and sulfur-induced reconstructions of silver surfaces can be found via active-learning of a Δ-model added to a uMLIP. Comparing the rate of identifying the GMs for different choices of uMLIP – CHGNet, MACE-MP0, and MACE-MPA – we find negligible effects for the clusters and only minor effects for the surface reconstructions. However, the more accurate uMLIP, MACE-MPA, generally boasts the highest rates. Overall, we demonstrate, that for the problems considered, simultaneous global optimization and improvement of uMLIPs via active learning is a viable approach.
The paper is outlined as follows: in the Methodology section we introduce the three elements of the active learning: (i) the different uMLIPs used, (ii) the Gaussian process regression-based Δ-model, and (iii) and the four different global optimization algorithms. The Results section starts with a discussion of prior understanding of the uMLIPs without any correction. It proceeds by presenting how the active learning performs for [Ag2S]X clusters when varying the optimization method. Then the use of different uMLIPs in the context of active learning is considered, first for the clusters and next for the sulfur induced surface reconstructions. As the final topic in the Results section, the use of prior collected data for pre-correction of the uMLIPs is considered. The paper ends with a discussion and details on data and code availability.
II. Methodology
A. Universal MLIPs and training datasets
MPTrj consists primarily of bulk structural information, namely 1.58 million unique structures and relaxation trajectories, computed at the PBE51 level of DFT. The Alexandria dataset is more diverse, containing 1D and 2D periodic systems alongside 3D bulk structures, providing more chemical insight into finite size effects particularly relevant to those investigated in this work. Overall, the dataset contains 30+ million structures, although this dataset is often sub-sampled to avoid structures being overrepresented (the sub-sampled dataset is only 10 million structures). These structures are computed with the PBEsol52 and SCAN53 XC functionals.In this work, we will examine three different uMLIPs namely CHGNet,36 MACE-MP0-large (henceforth referred to simply as MACE-MP0), and MACE-MPA-0 (MACE-MPA).37 CHGNet is a graph neural network potential, in which site based magnetic moments have been incorporated into the training data. The architecture of CHGNet involves both an atom graph where nodes are atoms carrying atomic embeddings and an auxiliary bond graph where the nodes are bonds and edges carry angular information. Using interactions between these elements CHGNet incorporates angular information into the atomic embeddings. Ultimately, the atomic embeddings are used to predict total energies and magnetic moments in addition to forces and stresses through the use of automatic differentiation of the total energy.
MACE is also a graph neural network, but unlike CHGNet it is equivariant with higher bond-order information gathered through tensor products involving directional information decomposed through spherical harmonics – making it capable of directly encoding angular information, dihedrals and beyond. These architectural differences have proven to increase performance across various benchmarks, as evidenced by MatBench discovery.42 We use two variants of MACE, namely MACE-MP0 trained solely on the MPTrj dataset that CHGNet is also trained on, and MACE-MPA which is trained on MPTrj and a subset of the Alexandria dataset. The larger training set used for the MACE-MPA uMLIP improves its performance on the aforementioned benchmarks compared to MACE-MP0. We employ the ‘large’ version of MACE-MP0, with ∼16 million parameters and the medium version of MACE-MPA, with ∼9 million parameters. Both models use the same building blocks and we attribute the majority of the differences in their behaviour that we observe to the difference in training set while acknowledging that we cannot prove this to be the case. In particular we later investigate the energetic ordering of clusters and observe significant inconsistencies in the ordering between MACE-MP0 and MACE-MPA, which we attribute to the differing training sets, but could also be partially caused by the architectural differences or even the random initialization of the network parameters.
B. Δ-Model
A GPR-based MLIP is usually formulated as follows: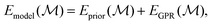 | (1) |
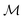 specifies a structure (super cell, atomic identities, and positions), and where
specifies a structure (super cell, atomic identities, and positions), and where 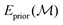 represents the prediction for the energy obtained from some simple prior function. In previous work25 the form of this prior was that of a simple repulsive potential which ensured that atoms did not collapse into themselves.
represents the prediction for the energy obtained from some simple prior function. In previous work25 the form of this prior was that of a simple repulsive potential which ensured that atoms did not collapse into themselves. 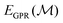 , the remainder, is left to account for all interactions between atoms, and is thus doing the majority of the actual modelling.
, the remainder, is left to account for all interactions between atoms, and is thus doing the majority of the actual modelling.
However, there is no reason that the prior function must be chosen to be trivial. Previously, Δ-models have been used in bridging the gap between levels of theory,54–57 including excited states58 and prediction of correlation energies.59 Their potential application in translating between levels of prediction has been demonstrated to be effective.60
Here, we apply that same translation between uMLIP predictions and DFT predictions using a Δ-model.50,61,62 The corrected energy prediction for a structure 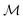 , is now given by:
, is now given by:
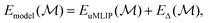 | (2) |
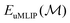 is the unmodified uMLIP, and where
is the unmodified uMLIP, and where 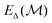 is the correction fitted to the residuals between the data and the incorrect uMLIP predictions. Whilst the form of this equation is identical to that in eqn (1), the role of the terms fundamentally shifts as the contribution from the prior becomes significant in encoding the interactions between atoms. As a result,
is the correction fitted to the residuals between the data and the incorrect uMLIP predictions. Whilst the form of this equation is identical to that in eqn (1), the role of the terms fundamentally shifts as the contribution from the prior becomes significant in encoding the interactions between atoms. As a result, 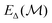 contributes a smaller, more precise correction in comparison.
contributes a smaller, more precise correction in comparison.
In this work we evaluate 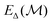 as a sparse Gaussian process regression based on a Gaussian kernel evaluating the similarities between the local atomic SOAP63 descriptors of the query structure and the training structures for the Δ-model. See ref. 15 and 64 for details on the GPR model.
as a sparse Gaussian process regression based on a Gaussian kernel evaluating the similarities between the local atomic SOAP63 descriptors of the query structure and the training structures for the Δ-model. See ref. 15 and 64 for details on the GPR model.
The training structures are comprised of the structures emerging from the global optimization algorithms detailed in the next subsection. In cases where data is available prior to the searches, some pretraining data will be included in the pool of training data for the sparse-GPR model, while being excluded from the pool of structures undergoing iterative improvement according to the global optimization scheme, where relevant.
The SOAP descriptor is implemented in DScribe.65,66 We use (n, l) = 3, 2 and rcut = 7 Å. The sparse-GPR15 is implemented in AGOX.67 We use 1000 inducing points and train only on energies to keep the size of the kernel matrix manageable. This formalism extends trivially to training on forces, with the caveat that the large dataset size can quickly become impractical computationally. Force predictions continue to improve with energy data only, see Fig. S1.
C. Global optimization methods
Many choices exist for which global optimization method to employ for the actively learned data collection of the Δ-model introduced above. We have chosen a collection of methods ranging from the almost completely unbiased random structure search, to a Monte Carlo based basin hopping method, alongside two more elaborate Bayesian- and parallel tempering-inspired methods. This allows for an assessment of the dependence of the active learning scheme on the optimization method. All methods introduced will use the Δ-corrected uMLIP model for surrogate relaxation and perform the model update whenever new DFT data becomes available. Relaxations are performed for up to a certain number of steps, or until a force convergence threshold is reached. For RSS and basing hopping, up to 500 relaxation steps are performed. For the Bayesian method and for the parallel tempering-inspired method, we allow for up to 100 relaxation steps. When using the latter method for surfaces, however, using 30 steps was sufficient. The force convergence threshold is 0.05 eV Å−1, with the exception of the Ag(100)- , for which a more stringent 0.025 eV Å−1 is used. Relaxations are conducted with the BFGS68 local optimization technique implemented in ASE.69Fig. 1 presents a graphical overview of the global optimization methods used. All of the optimization methods we employ are implemented in the modular framework of the AGOX global optimization package.67
, for which a more stringent 0.025 eV Å−1 is used. Relaxations are conducted with the BFGS68 local optimization technique implemented in ASE.69Fig. 1 presents a graphical overview of the global optimization methods used. All of the optimization methods we employ are implemented in the modular framework of the AGOX global optimization package.67
 | ||
| Fig. 1 Schematic outlining the data collection and progression schemes of RSS, basin hopping, GOFEE, and REX. The key highlights the processes represented in the schematic. The conditioned acceptances, eqn (3) and (5), of rattled and surrogate relaxed structures in basin hopping and REX are left out for clarity. The swapping events of REX are shown as walkers interchanging temperatures. In AGOX, this is coded as walkers swapping structures. | ||
Common to all methods is that atoms are bounded by confinement cells both when they are introduced and during relaxation. For each of the [Ag2S]X structures, a 20 × 20 × 20 Å unit cell houses a 15 × 15 × 15 Å confinement cell. The sulfur-induced surface reconstruction searches are done over 4 layer slabs of static Ag atoms in either Ag(111)-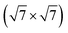 or Ag(100)-
or Ag(100)-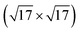 cells using (6 × 6) and (2 × 2) k-point grids for sampling of the corresponding 2D Brillouin zones. The reconstructions are built from 3 × Ag+3 × S and 12 × Ag+8 × S atoms introduced in confinement cells with the same dimensionality as the lattices in the xy directions and having a z component of 4 Å. All DFT calculations are performed with plane wave GPAW70 (500 eV cutoff) and employing the PBE XC-functional.51
cells using (6 × 6) and (2 × 2) k-point grids for sampling of the corresponding 2D Brillouin zones. The reconstructions are built from 3 × Ag+3 × S and 12 × Ag+8 × S atoms introduced in confinement cells with the same dimensionality as the lattices in the xy directions and having a z component of 4 Å. All DFT calculations are performed with plane wave GPAW70 (500 eV cutoff) and employing the PBE XC-functional.51
This structure, after surrogate relaxation, is then evaluated with first principles methods. As seen in Fig. 1, each instance of RSS is entirely independent from others, with the exception that the surrogate potential landscape is built from predecessor structures, introducing slight correlation between structures over time.
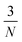 , where N is the number of atoms, according to a uniform random distribution within a sphere around their original position (whilst still accounting for reasonable bond lengths). The radius of the sphere is determined by the displacement magnitude, which for basin hopping is set to a static 3 Å. Structures are subsequently relaxed in the Δ-corrected uMLIP. The new candidate,
, where N is the number of atoms, according to a uniform random distribution within a sphere around their original position (whilst still accounting for reasonable bond lengths). The radius of the sphere is determined by the displacement magnitude, which for basin hopping is set to a static 3 Å. Structures are subsequently relaxed in the Δ-corrected uMLIP. The new candidate,  is accepted according to the Metropolis Monte Carlo criterion probability, given by:
is accepted according to the Metropolis Monte Carlo criterion probability, given by: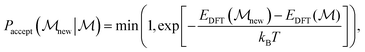 | (3) |
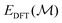 is the energy of the current structure,
is the energy of the current structure, 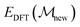 is the energy of the proposed state, and kBT is the product of the Boltzmann constant and the temperature, which is 0.15 eV. Basin hopping introduces explicit correlation in the time domain between structures considered – i.e. structures depend on their structural predecessors, and are commonly referred to as walkers to promote this notion. These are illustrated by arrows on the basin hopping diagram shown in Fig. 1. As the acceptance criterion is based solely on DFT energies, eqn (3), a new structure is evaluated with DFT and added to the training set during each iteration.
is the energy of the proposed state, and kBT is the product of the Boltzmann constant and the temperature, which is 0.15 eV. Basin hopping introduces explicit correlation in the time domain between structures considered – i.e. structures depend on their structural predecessors, and are commonly referred to as walkers to promote this notion. These are illustrated by arrows on the basin hopping diagram shown in Fig. 1. As the acceptance criterion is based solely on DFT energies, eqn (3), a new structure is evaluated with DFT and added to the training set during each iteration.
where
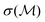 is the predicted uncertainty on
is the predicted uncertainty on 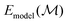 . κ is a constant, typically 2, which we maintain in this work. The structure with the lowest value in the lower confidence bound is then evaluated with DFT. This structure is finally added to the pool of evaluated structures, and a single DFT relaxation step is performed. The process is then iteratively repeated. More details can be found in ref. 73. The uncertainty is evaluated employing an ensemble of GPR models trained on data with artificial noise (σp = 0.001 eV per atom, σl = 0.025 eV per atom) added as proposed in ref. 64.
. κ is a constant, typically 2, which we maintain in this work. The structure with the lowest value in the lower confidence bound is then evaluated with DFT. This structure is finally added to the pool of evaluated structures, and a single DFT relaxation step is performed. The process is then iteratively repeated. More details can be found in ref. 73. The uncertainty is evaluated employing an ensemble of GPR models trained on data with artificial noise (σp = 0.001 eV per atom, σl = 0.025 eV per atom) added as proposed in ref. 64.
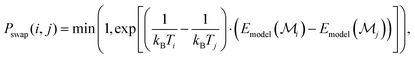 | (4) |
In our implementation, we leverage the main features of RE, but use basin hopping walkers, i.e. walkers that are relaxed in the surrogate energy landscape of the Δ-corrected uMLIP before being subjected to the Metropolis Monte Carlo acceptance test, which is further based on the surrogate energies,
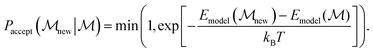 | (5) |
As walkers retain relaxed structures (as opposed to as-rattled structures), detailed balance will be violated, and hence rigorous thermal samples are not obtained by our RE implementation. However, the method still benefits fully from the exploratory behavior of coupled walkers.
We dub our method replica exchange X (REX), where the X denotes the departure from previous methods, and the presence of other additions to the aforementioned algorithms, such as the uMLIP-based surrogate potential.
For each REX search, 10 walkers are instantiated with pseudo-random structures, exactly as with RSS. Each walker is assigned a value for kBT according to a geometric series between 0.1 and 1. Similarly, each walker is assigned a different initial value for displacement magnitude, linearly between 0.1 and 5 Å. This determines the magnitude of attempted displacements, which are exactly as in basin hopping other than that every atom is displaced. The highest temperature walker always generates a pseudo-random structure. The displacement magnitude dynamically alters over the course of the calculation to target a 50% Metropolis acceptance rate for new structures. 10 iterations of independent basin hopping events are performed between swapping attempts. In GOFEE, we use an uncertainty obtained through Bayesian statistics to dictate structure selection for DFT, which drives exploration. In REX, we have an ensemble of structures to provide this, and do not rely on an explicit uncertainty. Rather, we have a set criterion for how often we sample from these walkers for DFT. The criterion in expressed as a number of iterations between DFT evaluations. For [Ag2S]X nanoclusters, we use 30, 40, 40, 50, 50 iterations for X ∈ {4, 6, 8, 10, 12}, respectively, and for surface reconstructions we use 40 iterations. When DFT is to be performed, 5 structures are randomly selected from the 9 lowest temperature walkers, thereby avoiding the pseudo-random structure. This process is repeated until the alloted time budget has expired.
D. Comparison metrics
Below we present results by way of success curves.25,67 Each vertical increment of a success curve indicates that one independent search has identified the solution at the given x-coordinate (usually CPU time or number of search episodes). Many searches together then provide a statistical ensemble of success (with each individual search termed a repeat), which is more indifferent towards flukes. This can also be viewed as the integral of the histogram of success. For the nanoclusters, we construct an adjacency matrix for a given structure, and the eigenvalues of this adjacency matrix are then computed, sorted and condensed in a hashable form. Structures with spectra identical to the solution are considered to be successes. The solution is defined to be the lowest energy structure ever observed. This measure is primarily concerned with conformation, as small changes to bondlength do not alter the graph. More details about the exact formulation of this spectral adjacency decomposition can be found in ref. 67. In the case of surface reconstructions, we define success as having an energy within a threshold of the solution. In order to obtain a comparable value for the CPU time, we ensure each search is performed on identical architecture and resources, namely 10 cores from 48 of 2 Intel Xeon Gold 6248R CPUs, such that the CPU time is equivalent to ten times the elapsed time. DFT calculations are run in parallel on all 10 CPUs. Surrogate calculations run on 1 CPU, and multiple will run in parallel across the 10 CPUs if allowed by the algorithm.III. Results
The results of the above methods when applied to a variety of systems are discussed in this section, which is organized as follows: we first discuss how well the three uMLIPs describe the low-energy conformers of [Ag2S]X clusters for five values of X. In more than half of the combinations of uMLIP and cluster size, it is found that the global minimum uMLIP energy structure (uMLIP-GM) deviates significantly from the global minimum DFT energy structure (DFT-GM). The section proceeds to demonstrate that for a given uMLIP the DFT-GM can be found using the proposed active learning Δ-model. From this analysis, it is further established that as the cluster size and hence the complexity of the optimization problem increases, more advanced search algorithms must be used. The section moves on to consider the importance of the quality of the uMLIP. For the [Ag2S]X clusters, the discrepancies between uMLIP-GMs and DFT-GMs do not appear to delay the finding of the DFT-GMs in our active learning scheme. This suggests that the problem of probing the proper configuration dominates the problem of correcting the uMLIP. For sulfur-induced surface reconstructions, the situation is reversed for the most complex problem, and MACE-MPA, which needs less correction to describe the DFT-GM, also facilitates its faster finding. The section ends with a discussion of the usefulness of pre-correcting a uMLIP using data from prior searches.A. [Ag2S]X with uncorrected uMLIPs
Fig. 2 shows the uMLIP-GM predictions of the three universal potentials together with the DFT-GMs for [Ag2S]X clusters having X ∈ {4, 6, 8, 10, 12}. The uMLIP-GMs were found by conducting exhaustive REX searches, without the active Δ-learning, while the DFT-GMs were compiled from the results of the active learning searches presented below in Sections III B and C. The cluster illustrations are annotated with the total DFT energies and the maximum magnitude of the atomic forces. A green tick or red cross indicate whether or not a DFT-based relaxation causes the structure to assume the DFT-GM configuration, respectively.For the smaller clusters, X ∈ {4, 6}, the uMLIP-GMs and DFT-GMs agree except for the combination of CHGNet with [Ag2S]4. Interestingly, this wrong prediction involves a cluster of higher symmetry than the DFT-GM. In contrast, a view at the DFT-GM for [Ag2S]6 reveals that it is a highly symmetric structure. This coincides with all three uMLIPs predicting the correct structure for this cluster size, and hints that the network architectures and training datasets of the uMLIPs might favor high symmetry.
For the larger clusters, X ∈ {8, 10, 12}, only the MACE-MPA predictions for [Ag2S]10 and [Ag2S]12 are correct, while all other predictions are wrong. We associate the higher fail rate for the larger clusters with their configuration spaces being considerably larger, putting the uMLIPs to a more stringent test. Particularly, the incorrect prediction for [Ag2S]10 by CHGNet can be attributed to the misplaced energetic bias towards sulfur coordinated sulfur atoms in the structure.
Focusing on the DFT-based forces evaluated for the uMLIP-GMs, there is a clear tendency of decreasing force magnitudes going from CHGNet, to MACE-MP0 and then MACE-MPA. Comparing CHGNet and MACE-MP0, the difference must originate from the network architecture, as they have been trained on the same materials project dataset. Comparing MACE-MP0 and MACE-MPA, that are based on more similar network architectures, the difference more likely lies in the datasets, and it is seen that adding the Alexandria dataset has the desired effect of leading to a more accurate uMLIP. Regardless, none of the structures could be considered fully relaxed in the DFT landscape, revealing that these potentials have incorrect bondlengths in these structures.
The DFT-GMs presented in Fig. 2 pertain to a DFT setting using the PBE-XC functional. The uMLIPs are also trained on PBE-based data, rendering the above comparison meaningful. In the literature, GM structures for other XC functionals have been reported. Using e.g. PBE0, a GM structure has been reported82 which is similar to the MACE-MPA prediction for the [Ag2S]8 cluster shown in Fig. 2. Relaxing our MACE-MPA and DFT GM structures with PBE0 we confirm this result, but we also find that by including the D383 van der Waals dispersion term and performing PBE0-D3 DFT calculations, the PBE DFT-GM again becomes the preferred structure. We stress, however, that since the currently used uMLIPs were trained on primarily PBE data, the fair comparison is to other PBE based results. Hence, the green ticks in Fig. 2 indicate the uMLIP predicting the correct PBE DFT-GM structure.
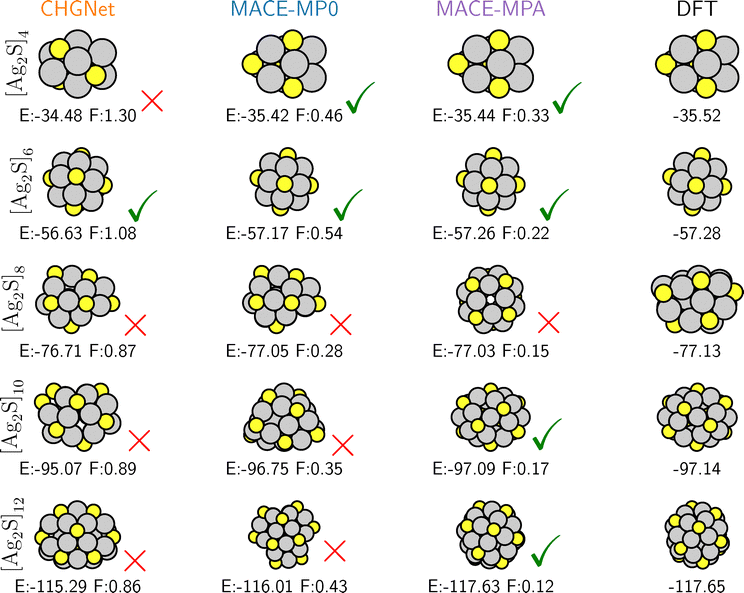
In order to provide a more comprehensive picture of the quality of the uncorrected uMLIPs, Fig. 3 presents the relative stability of a set of different low-energy conformers of the [Ag2S]8 cluster. The structures are the uMLIP-GMs (one of which is shared between CHGNet and MACE-MP0), the DFT-GM, three other structurally distinct nanoclusters (red, pink, cyan) and a distribution of further structures (grey).
The structures in Fig. 3 were obtained from a set of REX searches either with active learning of a Δ-model corrected MACE-MP0 model to obtain local DFT minima, or without active learning in three sets of REX searches to identify local minima in each of the three uMLIPs considered. From each set of searches, a sample of 25 structures is drawn at even intervals of energetic ordering from all structures produced, to avoid oversampling structures which occur with high frequency. These structures are then combined into one dataset, with the resulting 100 structures thus representative for both DFT and the individual potentials. The structures are finally relaxed separately in the uMLIPs or in DFT. The resulting structures show the relative ordering of minima as they appear in each potential. This procedure was also repeated for each other cluster size, seen in Fig. S2.
Comparing the stability order of the various conformers within each uMLIP to that in DFT, it is seen that the relative order is highly sensitive to the model, as we postulate from Fig. 2. Firstly, the CHGNet and MACE-MP0 structures are configurationally alike, residing in the same basin and differing only through finer structural parameters, and thus share a structural model and blue/orange coloring. The small differences between the MACE-MP0 and CHGNet structures are nonetheless significant enough to contribute to a large difference between the respective energy predictions. As seen in Fig. 2, the CHGNet minimum structure has both larger DFT forces and a higher energy than the similar structure suggested by MACE-MP0. Moreover, MACE-MPA undervalues it this structure compared to its own suggested GM (purple) on the order 0.2 eV. When relaxed and evaluated at the DFT level, this highly symmetric and well coordinated MACE-MPA-GM structure is slightly less stable than both the DFT-GM and the CHGNet/MACE-MP0-GM structures. On the contrary, when described at the CHGNet and MACE-MP0 level, its stability is strongly underestimated compared to the same GM structures. Furthermore, MACE-MPA evaluates the DFT-GM, CHGNet/MACE-MP0-GM, and red structures as being almost energetically degenerate, a behaviour absent from the other potentials and DFT. The MACE-MPA prediction for the cyan structure is similarly worse than MACE-MP0, with that for the pink structure varying by almost 0.3 eV, yielding no net improvement.
It seems as though the inclusion of the Alexandria dataset codes for the stability of such structures as the MACE-MPA-GM prediction, and highlights the importance of more diverse datasets in capturing the behavior of such phases. However, it is clear that adding more data (even data which one might conclude is more relevant to the system in hand) is not guaranteed to improve or even maintain performance, with MACE-MPA having become more inconsistent on a majority of relative energy predictions than MPtrj-only models.
However, the impact of this larger dataset is the opposite when considering [Ag2S]10, for which MACE-MPA alone is able to reproduce the correct DFT-GM structure, cf.Fig. 2. There is demonstrable improvement in mean max forces and the difference in energy between the potential minima and the DFT minima as the dataset size increases, but also evidence that adding more data can change the performance in unexpected ways for systems which were previously consistent. Thus, it is a reasonable assumption to make that when applying such potentials to a problem, particularly one for which the ordering of low energy structures is relevant, one should employ corrective measures as an assurance.
As a final note, we return to the largest cluster considered in Fig. 2, the [Ag2S]12. For this system MACE-MP0 and CHGNet produce structures which clearly obey some rationale of chemical understanding, but still deviate to the order of at least 1 eV from the DFT-GM, which is a highly symmetric combination of motifs observed in the smaller clusters. MACE-MPA continues to succeed at identifying these motifs and predicts the DFT GM correctly.
B. Finding DFT-GMs from active learning of Δ-model corrected uMLIP
In this section, we investigate the ease with which the DFT-GM can be found, while performing active learning to correct a uMLIP alongside the global optimization. To showcase this correction, we select MACE-MP0 as the uMLIP for this experiment as a compromise: forces and energies are closer to their DFT values than CHGNet, and conformationally there is more to correct than for MACE-MPA. The five sizes of [Ag2S]X clusters present in Fig. 2 are considered, and for each of them, the different search algorithms presented in Section II C are employed. For the smaller clusters, MACE-MP0 already codes for the correct DFT-GM and requires no Δ-model correction, which allows us to consider the effectiveness of the search algorithm in isolation. In order to compromise between the complexity of the configurational problem, which is reducible via symmetry, and the computational cost, our algorithm neglects explicit symmetries throughout. Justification for this choice can be seen in Fig. S3, for which the highly symmetric [Ag2S]12 structure is solved with and without exploiting symmetry. Had we enforced symmetry,84 contrasting between methods would have been difficult, requiring larger systems and a largely increased DFT budget.Fig. 4 compares the four different structure search methodologies previously outlined, when applied to the five [Ag2S]X cluster sizes. Firstly, [Ag2S]4 is a very simple problem to solve configurationally, which can be understood intuitively from the relatively small number of atoms present. Furthermore, MACE-MP0 encodes sufficient information to solve the problem correctly (see Fig. 2), so the impact of active learning on the outcome is likely minimal. Fig. 4 evidences this, with all but RSS solving the problem almost immediately. Even in this very simple regime, RSS is far from matching the other methods, succeeding in only 80% of cases after a substantial investment of resources.
The struggle of RSS continues for [Ag2S]6, where once again MACE-MP0 is able to predict the solution correctly itself (cf.Fig. 2). Here, RSS has a ∼15% chance of finding the solution given 48 hours of calculation time (480 CPU hours), compared to the near 100% chance in a fraction of the time for the other methods. For this cluster size, it further becomes apparent that the proposed REX methodology outperforms both GOFEE and basin hopping.
[Ag2S]8 is the point where the configurational complexity and the incomplete map of the PES provided by the uMLIP begin to differentiate the approaches. RSS fails to uncover the true structure even once across all repeats, indicating that attempting relaxation of almost purely random structures as a strategy for identifying the minimum of the PES whilst simultaneously correcting a surrogate potential becomes an unreliable strategy quite rapidly. This highlights the importance of the search strategy, and demonstrates that configurational complexity correlates with the system size, when comparing [Ag2S]X with X ∈ {4, 6, 8}. RSS is omitted from further examples with X > 8 on these grounds. REX, however, demonstrates over 80% success in about one quarter of the 48 hours provided, thereby outperforming GOFEE and basin hopping, which reach ∼75% and ∼65% in the full duration, respectively.
Similarly for [Ag2S]10, the performance of GOFEE and basin hopping drop with respect to REX, which while slower than for the smaller stoichiometry still achieves a success of 80% in the allotted time.
The same trend is echoed once again for [Ag2S]12, with diminishing success for GOFEE and basin hopping, and >80% for REX. Now, only one in 25 basin hopping or GOFEE repeats are able to obtain success at this size. The single early success suggests a coincidental occurrence of the solution, indicating that the exploration becomes stunted as time progresses. Meanwhile, REX continues to perform without the same abrupt decrease in success. This demonstrates that REX is a powerful explorative tool, effective at increasing systems sizes and regardless of the understanding of the underlying universal potential. REX effectively couples augmentative active learning to configurational exploration.
Notably, in the regime where ab initio evaluation dominates the computational resource budget (many atoms, for periodic systems many k-points, expensive XC functionals, and wavefunction methods), REX is at a further advantage when compared to the other methods. Both basin hopping and GOFEE devote a larger fraction of their compute budget to performing DFT, and thus perform more DFT calculations per unit time than REX. This can be seen in Fig. S4, which depicts the same data as Fig. 4, repostulated in terms of the number of first-principles calculations performed. This alternative metric more heavily favours REX, as the number of DFT calculations is agnostic to the extent of the repeated replica exchange cycle, and is indicative that REX would also perform excellently in the limit that the computational cost of first principles evaluation is the dominant factor. Finally, serialized versions of each algorithm which only utilize one CPU core, to eliminate yet more advantages from newer methods, does not demonstrate significant deviation from the results presented above, see Fig. S5.
C. Comparing the success of different uMLIPs
The previous section demonstrated for MACE-MP0 that the DFT-GMs can reliably be determined in an active learning Δ-model approach. In this section, we widen the investigation to the two other uMLIPs introduced. Since we have already seen the limitations of the optimization algorithms we limit the study to a few combinations of algorithms and cluster sizes.Fig. 5 presents the results. Starting with the RSS algorithm, the smallest cluster, [Ag2S]4, is considered. All three uMLIPs support the finding of the DFT-GM very well with this method. CHGNet in particular, which has the wrong GM encoded, cf.Fig. 2, appears efficient, which we attribute to the fast inference times of that uMLIP.
That speed is more important than precise insight becomes apparent when omitting the uMLIP and instead using a simple repulsive prior,73 as in eqn (1), that only acts to avoid the collapse of atoms onto the same positions. The success curve of RSS with a repulsive prior is included in green in Fig. 5 and is seen to reach success in e.g. half of the repeats in a matter of 1–2 hours (10–20 CPU hours), for which the uMLIP assisted methods require 5–10 hours (50–100 CPU hours). That a simple potential is useful for solving such problems is consistent with findings of other investigations.14
Another testimony to the importance of speed of the underlying relaxation calculations comes from the black curve in RSS Fig. 5. The curve shows the success obtained from a purely DFT-based RSS search for the [Ag2S]4 cluster. This search has no uMLIP and does not construct a surrogate potential to enable cheap structural relaxations, rather every relaxation step is done at the full DFT level. This example represents a historical benchmark moreso than a viable modern strategy.
The basin hopping algorithm is applied to the [Ag2S]6 nanocluster. The rate at which each tested potential reaches 70% success is indistinguishable, with small deviations occurring past this point. Interestingly, the simple repulsive potential is the only one to reach 100% during the allocated time, which as for [Ag2S]4 highlights the importance of the inference time of the surrogate potential for such problems.
The next optimization algorithm considered in Fig. 5 is GOFEE, which is tested on [Ag2S]8. The rate at which the DFT-GM is identified starts out very similar for the three uMLIPs. After about 10 hours (100 CPU hours) one in three repeats have indeed found the DFT-GM, irrespective of which uMLIP is used. From there on, the performance of the uMLIPs remains more or less consistent, with MACE-MPA performing the best, reaching over 80% success in the allotted time.
Like for RSS and basin hopping, GOFEE can be run without a uMLIP, using instead a repulsive prior in the surrogate potential as originally conceived.25 This results in the green curve for [Ag2S]8 in Fig. 5, but unlike for RSS and basin hopping, this is now far less efficient than when a uMLIP is available, and requires the full 48 hours (480 CPU hours) to reach the 33% success rate. That the use of the uMLIP is more efficient, we attribute to the increased complexity of the energy landscape for the [Ag2S]8 compared to those for the smaller clusters solved with RSS and basin hopping, and we conjecture that despite its faster inference time, the repulsive prior-based potential suffers from requiring more datapoints to form a reliable description of the energy landscape.
Fig. 5 finally presents the results of search for the DFT-GM with the REX method for the [Ag2S]12 cluster. As the REX method relies heavily on many rattle-relaxation cycles of walkers, it benefits from the use of the faster CHGNet method just as much as it does from the more accurate MACE potentials. This is evidenced by observing that, even at this size, REX obtains a high success rate of >80% regardless of whether the chosen uMLIP knew the solution (MACE-MPA), or not (CHGNet, MACE-MP0).
We note that it is not possible to use the REX method just based on a repulsive prior, as the extensive searches done by the REX method before any Δ-model can be established would find that atoms should separate as far as possible. This could be circumvented by using a prior with some atomic attraction or by applying pretraining based on precalculated data.
Summarizing this section, we find surprisingly little variance in the efficacy of the three different uMLIPs considered. Despite their differences in initial accuracy, they all support the usage as initial surrogate models and lend themselves to being corrected via our active learning Δ-model protocol.
D. AgS surface reconstructions
We now move to consider sulfur-induced surface reconstructions. Based on the experimental information available,85,86 the two systems, Ag(111)-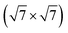 -Ag3S3 and Ag(100)-
-Ag3S3 and Ag(100)-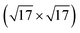 -Ag12S8, were chosen. With their different sizes and hence complexity of the involved GMs, these two systems allow for an assessment of the efficiency of the presented methods for active learning and global optimization. The GM structures for the two systems are shown in Fig. 6 and 7, respectively. For the smaller system, all three uMLIPs and the full DFT description agree on a GM in which a triangular Ag3S3 motif forms atop the Ag(111). This motif is reminiscent of some of the facets found on the [Ag2S]X clusters. The structure shown as the DFT GM in Fig. 6 agrees fully with that proposed in ref. 85. Rotating the Ag3S3 motif by 60 degrees brings the Ag atoms from fcc to hcp sites, and is associated with a small ∼0.01 eV energy penalty. In our statistical analysis below, we consider both conformations to be solutions to the problem.
-Ag12S8, were chosen. With their different sizes and hence complexity of the involved GMs, these two systems allow for an assessment of the efficiency of the presented methods for active learning and global optimization. The GM structures for the two systems are shown in Fig. 6 and 7, respectively. For the smaller system, all three uMLIPs and the full DFT description agree on a GM in which a triangular Ag3S3 motif forms atop the Ag(111). This motif is reminiscent of some of the facets found on the [Ag2S]X clusters. The structure shown as the DFT GM in Fig. 6 agrees fully with that proposed in ref. 85. Rotating the Ag3S3 motif by 60 degrees brings the Ag atoms from fcc to hcp sites, and is associated with a small ∼0.01 eV energy penalty. In our statistical analysis below, we consider both conformations to be solutions to the problem.
 | ||
Fig. 6 Depicted is the DFT GM structure for the 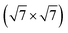 surface reconstruction of Ag(111) under sulfurization. Silver atoms which do not reorganize have their color lightened to highlight the reconstruction. surface reconstruction of Ag(111) under sulfurization. Silver atoms which do not reorganize have their color lightened to highlight the reconstruction. | ||
For the larger system, none of the uMLIPs predict the correct GM as given by DFT. This is detailed in Fig. 7 from which it appears that CHGNet and MACE-MP0 energetically overvalue the formation of the Ag3S3 motif indicated by the blue triangle (the presence of this motif is unsurprising, given its prevalence in examples thus far). This overvaluing draws the required silver atom away from the slanted Ag4S4 motif indicated by the black rhombus. MACE-MPA appears aware that forming the triangles is not as much of an energetic priority, but as seen in the black rhombus, still fails to correctly establish the Ag4S4 motif. This failure is reflected by the slight clockwise rotation of the structure with respect to the surface present in the DFT solution i.e. silver atoms in the reconstruction do not fill exact sites of the lattice (hollow), but rather shifted sites. Comparing the DFT-GM of Fig. 7 to that suggested in ref. 86 leads us to believe that the present search has revealed a new, more stable PBE DFT-GM than hitherto proposed, which further testifies to the efficiency of the REX method in combination with active learning on top of a uMLIP.
Clearly each of the tested uMLIPs has remarkable understanding of the general chemistry involved, and the nature of the required correction, whilst variable between potentials, is small.
Fig. 8 presents the results when we search for the GMs for the surface reconstructions with active learning using the different uMLIPs. The first panel of Fig. 8 shows the case of the small, Ag(111)- -Ag3S3 problem, where the uMLIPs all code for the right GM. Owing to the small size of the problem, we employ the simple RSS optimization method, as REX solves this stoichiometry too quickly to provide valuable insight into the performance of the potentials. The success curves show that the GM may be found with 33% success, i.e. in every 3rd repeat, after about 14 hours (140 CPU hours) in the two MACE potentials, with a considerably slower timeframe for CHGNet. Contrasting to this success, both a set of 75 full DFT random structure searches, and 25 repulsive prior GPR enhanced RSS searches, obtained the solution to the problem only once each in the provided time. We attribute this substantial decrease in performance to the increase in cost of DFT for surface problems when compared to nanoclusters. Clearly the uMLIP Δ-model enhanced RSS enabled this search to succeed where more traditionally it would have been very expensive.
-Ag3S3 problem, where the uMLIPs all code for the right GM. Owing to the small size of the problem, we employ the simple RSS optimization method, as REX solves this stoichiometry too quickly to provide valuable insight into the performance of the potentials. The success curves show that the GM may be found with 33% success, i.e. in every 3rd repeat, after about 14 hours (140 CPU hours) in the two MACE potentials, with a considerably slower timeframe for CHGNet. Contrasting to this success, both a set of 75 full DFT random structure searches, and 25 repulsive prior GPR enhanced RSS searches, obtained the solution to the problem only once each in the provided time. We attribute this substantial decrease in performance to the increase in cost of DFT for surface problems when compared to nanoclusters. Clearly the uMLIP Δ-model enhanced RSS enabled this search to succeed where more traditionally it would have been very expensive.
The active learning results for the larger system of Ag(100)- -Ag12S8 are shown in the second panel of Fig. 8. Due to the increased complexity of the problem, the REX optimization method is used. Despite the uMLIPs being confused about the exact GM (cf.Fig. 7), the correct DFT GM is eventually found reliably with all three uMLIPs using the Δ-model approach.
-Ag12S8 are shown in the second panel of Fig. 8. Due to the increased complexity of the problem, the REX optimization method is used. Despite the uMLIPs being confused about the exact GM (cf.Fig. 7), the correct DFT GM is eventually found reliably with all three uMLIPs using the Δ-model approach.
For this system reasonable differences in the efficacy of using the various uMLIPs are found. CHGNet reaches 65% success in 172 hours (1720 CPU hours), whereas the two MACE models reach around 90% in the same timeframe.
MACE-MPA is found to be considerably faster than the other two uMLIPS at obtaining the solution in general, requiring just over 90 hours to reach the same success as CHGNet did in the full 172. That MACE-MPA is the one to perform the best can be rationalized in terms of its GM deviating less from the DFT-GM than the other two uMLIPs, as discussed in connection with Fig. 7. The Δ-model thus requires less data to be gathered by the active learning in order to correct the uMLIP.
Unlike the nanocluster example, none of the uMLIPs fully encode the solution. This is not particularly surprising, given that the difference between the DFT solution and the uMLIP solutions boils down to a small rotation of the reconstruction with respect to the underlying surface layer, a highly specific surface phenomenon.
To create an example where one might be able to compare between a uMLIP which is aware of the solution and one which is not, we construct a MACE-MPA Δ-model from the structures gathered by a REX search for Ag(100)-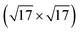 -Ag12S8. We select the search which contained the lowest energy structure, and train the Δ-model on all 200 structures identified by that search. This model has thus been informed of the relevant surface phenomena, and serves as a point of comparison to the uncorrected uMLIP. Using this Δ-model as the starting point for new REX repeats we obtain the purple curve in the right panel of Fig. 8. This success curve turns out to be a substantial improvement to that of MACE-MPA without pretraining (cf. purple curve in middle panel of Fig. 8), reducing the average time to reach the solution by up to a full day, with the first repeat to find the solution requiring under 6 hours, compared the 18 hours of the base uMLIP. Regardless, the induction time present before the majority the repeats identify the correct solution suggests that the solution is configurationally difficult to come by, requiring a reasonable amount of REX relaxations and swaps to manifest. The most important conclusion to draw is, however, that the magnitude of the improvement achieved with this small amount of extra, highly relevant data, is significant. It then seems likely that the data gathered by the combination of REX and an active learned uMLIP Δ-model is particularly descriptive.
-Ag12S8. We select the search which contained the lowest energy structure, and train the Δ-model on all 200 structures identified by that search. This model has thus been informed of the relevant surface phenomena, and serves as a point of comparison to the uncorrected uMLIP. Using this Δ-model as the starting point for new REX repeats we obtain the purple curve in the right panel of Fig. 8. This success curve turns out to be a substantial improvement to that of MACE-MPA without pretraining (cf. purple curve in middle panel of Fig. 8), reducing the average time to reach the solution by up to a full day, with the first repeat to find the solution requiring under 6 hours, compared the 18 hours of the base uMLIP. Regardless, the induction time present before the majority the repeats identify the correct solution suggests that the solution is configurationally difficult to come by, requiring a reasonable amount of REX relaxations and swaps to manifest. The most important conclusion to draw is, however, that the magnitude of the improvement achieved with this small amount of extra, highly relevant data, is significant. It then seems likely that the data gathered by the combination of REX and an active learned uMLIP Δ-model is particularly descriptive.
To confirm that the data provided to the MACE-MPA Δ-model was indeed efficient at describing the relevant regions of the PES, we repeated the search, using eqn (1), with a GPR pretrained on the same dataset, but with the simple repulsive prior instead of the uMLIP. The green curve in the last panel of Fig. 8 shows the success curve of this model, which having seen both the solution and a significant amount of relevant data, performs as well as the corrected MACE-MPA from the previous analysis. This is not altogether surprising. It stands to reason that a naive model without extensive extrapolation can produce highly accurate results within the interpolation domain of its training data. This is compelling evidence that the data collected by this method of active learning captures the relevant PES almost completely. With this we underscore that REX results in both robust ab initio quality global optimization and comprehensive sampling of the PES.
IV. Conclusion
In this article, we have presented universal potential enhanced structure searching, comparing and contrasting several methods across a variety of silver sulfide nanocluster sizes and surface reconstructions.Active learning appears a stable method for gathering data for improving the behaviour of uMLIPs. From the four search algorithms considered as vehicles for active learning, REX is the clear standout. We demonstrate significant advantages in efficiency and speed that can be achieved when searching with the REX methodology, combining universal potential Δ-models with replica exchange structure search. Regardless of the underlying knowledge (or lack thereof) of a particular potential, the REX Δ-model approach is quickly and efficiently able to correct inconsistencies and converge to the DFT solution in comparable timeframes. These results encourage that for any universal potential, such an explorative strategy provides a robust and reliable method to (a) safely apply and (b) improve and discover, with such potentials. Our findings heavily encourage the adoption of such potentials into structure search methodologies, under the provision that they can be corrected incrementally with active learning. Universal potential Δ-models resulting from such searches prove to become more effective as search landscapes than the unaugmented potentials, confirming that iterative adaptations effectively alter the form of the PES.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04302f.The datasets supporting the findings in this paper are available on Zenodo at https://doi.org/10.5281/zenodo.16368472 along with Python scripts to reproduce our findings. The optimization methods employed are available in version 3.10.2 of the AGOX package available to install from PyPI and the source code is openly available on Gitlab https://gitlab.com/agox/agox.
Acknowledgements
We would like to thank Chris J. Pickard for discussions regarding symmetry. We acknowledge support from VILLUM FONDEN through Investigator grant, project no. 16562, and by the Danish National Research Foundation through the Center of Excellence “InterCat” (grant agreement no: DNRF150).References
- K. Butler, D. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547 CrossRef CAS PubMed.
- O. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 4895 CrossRef CAS PubMed.
- N. Fedik, R. Zubatyuk, M. Kulichenko, N. Lubbers, J. S. Smith, B. Nebgen, R. A. Messerly, Y. W. Li, A. Boldyrev, K. Barros, O. Isayev and S. Tretiak, Nat. Rev. Chem., 2022, 6, 653 CrossRef CAS PubMed.
- J. Xia, Y. Zhang and B. Jiang, Chem. Soc. Rev., 2025, 54, 4790 RSC.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- L. Hörmann, W. G. Stark and R. J. Maurer, npj Comput. Mater., 2025, 11, 196 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192 RSC.
- Y. Mishin, Acta Mater., 2021, 214, 116980 CrossRef CAS.
- A. P. Bartók, J. Kermode, N. Bernstein and G. Csányi, Phys. Rev. X, 2018, 8, 041048 Search PubMed.
- V. Kapil, C. Schran, A. Zen, J. Chen, C. J. Pickard and A. Michaelides, Nature, 2022, 609, 512 CrossRef CAS PubMed.
- T. Maxson, A. Soyemi, B. W. J. Chen and T. Szilvási, J. Phys. Chem. C, 2024, 128, 6524–6537 CrossRef CAS.
- V. L. Deringer, C. J. Pickard and G. Csányi, Phys. Rev. Lett., 2018, 120, 156001 CrossRef CAS PubMed.
- C. J. Pickard, Phys. Rev. B, 2022, 106, 014102 CrossRef CAS.
- N. Rønne, M.-P. V. Christiansen, A. M. Slavensky, Z. Tang, F. Brix, M. E. Pedersen, M. K. Bisbo and B. Hammer, J. Chem. Phys., 2022, 157, 174115 CrossRef PubMed.
- C. Larsen, S. Kaappa, A. Vishart, T. Bligaard and K. W. Jacobsen, npj Comput. Mater., 2025, 11, 222 CrossRef CAS.
- Z. Tang, S. T. Bromley and B. Hammer, J. Chem. Phys., 2023, 158, 224108 CrossRef CAS PubMed.
- A. Khorshidi and A. A. Peterson, Comput. Phys. Commun., 2016, 207, 310 CrossRef CAS.
- J. Timmermann, F. Kraushofer, N. Resch, P. Li, Y. Wang, Z. Mao, M. Riva, Y. Lee, C. Staacke, M. Schmid, C. Scheurer, G. S. Parkinson, U. Diebold and K. Reuter, Phys. Rev. Lett., 2020, 125, 206101 CrossRef CAS PubMed.
- M. J. Waters and J. M. Rondinelli, J. Phys.: Condens. Matter, 2022, 34, 385901 CrossRef CAS PubMed.
- S. Ma, C. Shang and Z.-P. Liu, J. Chem. Phys., 2019, 151, 050901 CrossRef.
- L. Zhang, D.-Y. Lin, H. Wang, R. Car and W. E, Phys. Rev. Mater., 2019, 3, 023804 CrossRef CAS.
- N. Bernstein, G. Csányi and V. Deringer, npj Comput. Mater., 2019, 5, 99 CrossRef.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- M. K. Bisbo and B. Hammer, Phys. Rev. Lett., 2020, 124, 086102 CrossRef CAS PubMed.
- M. L. Paleico and J. Behler, J. Chem. Phys., 2020, 153, 054704 CrossRef CAS PubMed.
- J. Wang, H. Gao, Y. Han, C. Ding, S. Pan, Y. Wang, Q. Jia, H.-T. Wang, D. Xing and J. Sun, Nat. Sci. Rev., 2023, 10, nwad128 CrossRef CAS PubMed.
- M. Kulichenko, B. Nebgen, N. Lubbers, J. S. Smith, K. Barros, A. E. A. Allen, A. Habib, E. Shinkle, N. Fedik, Y. W. Li, R. A. Messerly and S. Tretiak, Chem. Rev., 2024, 124, 13681 CrossRef CAS PubMed.
- R. Wanzenböck, E. Heid, M. Riva, G. Franceschi, A. M. Imre, J. Carrete, U. Diebold and G. K. H. Madsen, Digital Discovery, 2024, 3, 2137 RSC.
- Y. Lee, X. Chen, S. M. Gericke, M. Li, D. N. Zakharov, A. R. Head, J. C. Yang and A. N. Alexandrova, Angew. Chem., Int. Ed., 2025, 64, e202501017 CrossRef CAS PubMed.
- F. Grasselli, S. Chong, V. Kapil, S. Bonfanti and K. Rossi, Digital Discovery, 2025, 4, 2654 RSC.
- V. G. Satorras, E. Hoogeboom and M. Welling, Proceedings of the 38th International Conference on Machine Learning, Proceedings of Machine Learning Research, ed. M. Meila and T. Zhang, PMLR, 2021, vol. 139, pp. 9323–9332.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- N. Leimeroth, L. C. Erhard, K. Albe and J. Rohrer, Model. Simul. Mater. Sci. Eng., 2025, 33, 065012 CrossRef.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718 CrossRef PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031 CrossRef.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwin, F. Berger, N. Bernstein, A. Bhowmik, S. M. Blau, V. Cărare, J. P. Darby, S. De, F. D. Pia, V. L. Deringer, R. Elijošius, Z. El-Machachi, F. Falcioni, E. Fako, A. C. Ferrari, A. Genreith-Schriever, J. George, R. E. A. Goodall, C. P. Grey, P. Grigorev, S. Han, W. Handley, H. H. Heenen, K. Hermansson, C. Holm, J. Jaafar, S. Hofmann, K. S. Jakob, H. Jung, V. Kapil, A. D. Kaplan, N. Karimitari, J. R. Kermode, N. Kroupa, J. Kullgren, M. C. Kuner, D. Kuryla, G. Liepuoniute, J. T. Margraf, I.-B. Magdău, A. Michaelides, J. H. Moore, A. A. Naik, S. P. Niblett, S. W. Norwood, N. O'Neill, C. Ortner, K. A. Persson, K. Reuter, A. S. Rosen, L. L. Schaaf, C. Schran, B. X. Shi, E. Sivonxay, T. K. Stenczel, V. Svahn, C. Sutton, T. D. Swinburne, J. Tilly, C. van der Oord, E. Varga-Umbrich, T. Vegge, M. Vondrák, Y. Wang, W. C. Witt, F. Zills and G. Csányi, J. Chem. Phys., 2025, 163, 184110 CrossRef CAS PubMed.
- N. T. Taylor, J. Pitfield, F. H. Davies and S. P. Hepplestone, npj Comput. Mater., 2025, 11, 258 CrossRef.
- K. S. Jakob, K. Reuter and J. T. Margraf, Adv. Intell. Discovery, 2025, 202500031 CrossRef.
- B. Deng, Y. Choi, P. Zhong, J. Riebesell, S. Anand, Z. Li, K. Jun, K. A. Persson and G. Ceder, npj Comput. Mater., 2025, 11, 9 CrossRef CAS.
- M. M. Ghahremanpour, P. J. Van Maaren and D. Van Der Spoel, Sci. Data, 2018, 5, 180062 CrossRef CAS PubMed.
- J. Riebesell, R. E. Goodall, P. Benner, Y. Chiang, B. Deng, G. Ceder, M. Asta, A. A. Lee, A. Jain and K. A. Persson, Nat. Mach. Intell., 2025, 7, 836 CrossRef.
- X. Fu, B. M. Wood, L. Barroso-Luque, D. S. Levine, M. Gao, M. Dzamba and C. L. Zitnick, arXiv, 2025, preprint, arXiv:2502.12147 DOI:10.48550/arXiv.2502.12147.
- B. M. Wood, M. Dzamba, X. Fu, M. Gao, M. Shuaibi, L. Barroso-Luque, K. Abdelmaqsoud, V. Gharakhanyan, J. R. Kitchin, D. S. Levine, et al., arXiv, 2025, preprint, arXiv:2506.23971 DOI:10.48550/arXiv.2506.23971.
- B. Focassio, L. P. M. Freitas and G. R. Schleder, ACS Appl. Mater. Interfaces, 2024, 17, 13111 CrossRef PubMed.
- D. Marchand, MRS Bull., 2025, 50, 805 CrossRef.
- B. Póta, P. Ahlawat, G. Csányi and M. Simoncelli, arXiv, 2024, preprint, arXiv:2408.00755 DOI:10.48550/arXiv.2408.00755.
- H. Lee, V. I. Hegde, C. Wolverton and Y. Xia, Mater. Today Phys., 2025, 53, 101688 CrossRef.
- H. Kaur, F. Della Pia, I. Batatia, X. R. Advincula, B. X. Shi, J. Lan, G. Csányi, A. Michaelides and V. Kapil, Faraday Discuss., 2025, 256, 120 RSC.
- J. Pitfield, F. Brix, Z. Tang, A. M. Slavensky, N. Rønne, M.-P. V. Christiansen and B. Hammer, Phys. Rev. Lett., 2025, 134, 056201 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. V. Terentjev, L. A. Constantin and J. M. Pitarke, Phys. Rev. B, 2018, 98, 214108 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- A. Nandi, C. Qu, P. L. Houston, R. Conte and J. M. Bowman, J. Chem. Phys., 2021, 154, 051102 CrossRef CAS PubMed.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2020, 11, 5223 CrossRef CAS PubMed.
- B. Huang and O. A. Von Lilienfeld, Chem. Rev., 2021, 121, 10001 CrossRef CAS PubMed.
- M. Ruth, D. Gerbig and P. R. Schreiner, J. Chem. Theory Comput., 2022, 18, 4846 CrossRef CAS PubMed.
- W. Yang and P. W. Ayers, arXiv, 2024, preprint, arXiv:2403.04604 DOI:10.48550/arXiv.2403.04604.
- P. Bandyopadhyay, B. K. Isamura and P. L. Popelier, J. Chem. Phys., 2025, 162, 074102 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087 CrossRef CAS PubMed.
- P. Lyngby, C. Larsen and K. W. Jacobsen, Phys. Rev. Mater., 2024, 8, 123802 CrossRef CAS.
- M.-P. V. Christiansen and B. Hammer, J. Chem. Phys., 2025, 162, 184701 CrossRef CAS PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- M.-P. V. Christiansen, N. Rønne and B. Hammer, Mach. Learn.: Sci. Technol., 2024, 5, 045029 Search PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, J. Chem. Phys., 2023, 158, 234802 CrossRef CAS PubMed.
- M.-P. V. Christiansen, N. Rønne and B. Hammer, J. Chem. Phys., 2022, 157, 054701 CrossRef CAS PubMed.
- R. Fletcher, Practical methods of optimization, John Wiley & Sons, 2000 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. Schäfer and E. Ö. Jónsson, et al. , J. Chem. Phys., 2024, 160, 092503 CrossRef CAS PubMed.
- C. J. Pickard and R. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- N. Metropolis and S. Ulam, J. Am. Stat. Assoc., 1949, 44, 335 CrossRef CAS PubMed.
- M. K. Bisbo and B. Hammer, Phys. Rev. B, 2022, 105, 245404 CrossRef CAS.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141 CrossRef CAS.
- R. Zhou and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12777 CrossRef CAS PubMed.
- A. E. Garca and J. N. Onuchic, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13898 CrossRef PubMed.
- R. Yamamoto and W. Kob, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5473 CrossRef CAS PubMed.
- R. H. Swendsen and J.-S. Wang, Phys. Rev. Lett., 1986, 57, 2607 CrossRef PubMed.
- N. Unglert, L. B. Pártay and G. K. Madsen, J. Chem. Theory Comput., 2025, 21, 7304 CrossRef CAS PubMed.
- U. H. Hansmann, Chem. Phys. Lett., 1997, 281, 140 CrossRef CAS.
- P. A. Frantsuzov and V. A. Mandelshtam, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 72, 037102 CrossRef PubMed.
- C. Song and Z. Tian, J. Mol. Model., 2019, 25, 310 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Brix, M.-P. Verner Christiansen and B. Hammer, J. Chem. Phys., 2024, 160, 174107 CrossRef CAS PubMed.
- M. Shen, D.-J. Liu, C. J. Jenks and P. A. Thiel, J. Phys. Chem. C, 2008, 112, 4281 CrossRef CAS.
- S. M. Russell, M. Shen, D.-J. Liu and P. A. Thiel, Surf. Sci., 2011, 605, 520 CrossRef CAS.
| This journal is © the Owner Societies 2026 |