Unraveling unusual torquoselectivity in ring-opening electrocyclic reactions: a DFT perspective

Abstract

Torquoselectivity in the electrocyclic ring-opening of perfluoro-3,4-dimethylcyclobutene is investigated through electron density-based approaches, including DFT, QTAIM, and stress tensor analysis. The study examines electronic redistribution and bonding patterns along the reaction pathway to elucidate and predict atypical stereochemical outcomes, such as the formation of the Z,Z isomer, with the aim of enhancing stereocontrol beyond the scope of traditional orbital-based models. A previously developed model based on Sanderson's electronegativity equalization principle is employed to compute the local reactivity indices. To identify the local contributions most relevant to the global properties, multiple regression analysis is applied. This approach allowed us to establish meaningful correlations between global and local descriptors, offering a deeper insight into the reactivity patterns observed in the studied reactions. Alongside, information-theoretic descriptors are employed to uncover the electronic structure basis of reaction pathway selectivity and molecular stability.

---

1. Introduction

Electrocyclic ring-opening reactions are fundamental in organic synthesis, offering precise control over regioselectivity and stereoselectivity in the formation of unsaturated compounds. A central concept in this area is torquoselectivity, which refers to a reaction's preference for a particular stereochemical outcome around a rotatable single bond.^1–3 It governs the orientation of substituents during bond rotation, influencing the formation of different stereoisomers or conformational isomers. Torquoselectivity has been widely studied in the thermal electrocyclic ring-opening of substituted cyclobutenes,^4–11 where factors such as steric effects, electronic influences, and reaction conditions play a critical role. Mastery of torquoselectivity is essential for synthesizing stereochemically defined compounds, crucial in fields like natural product and pharmaceutical synthesis, where different stereoisomers may exhibit distinct biological or chemical properties.

Torquoselectivity, the tendency of a system to favor outward or inward conrotatory transition states (TSOC or TSIC) during electrocyclic ring-opening reactions, has been extensively explored with a focus on the influence of substituent electronic properties.^4,12–14 For example, cyclobutene undergoes thermally allowed conrotatory ring-opening to form either Z- or E-dienes depending on the direction of twisting. However, analyzing these reactions solely through transition state activation energy (ΔTS) has limitations, particularly at high temperatures, due to the constraints of transition state theory. Alternative methods beyond pure energy-based models are needed to better assess reaction pathways. Orbital symmetry considerations, first proposed by Rondan and Houk,^4,15 and the Woodward–Hoffmann rules based on orbital symmetry conservation, have been widely used to explain torquoselectivity.¹¹ Nonetheless, these models sometimes fall short, especially for reactions with lower symmetry, as molecular orbitals are not directly observable and predictions may not always match experimental outcomes.

Although the orbital model is commonly used to predict torquoselectivity, its limitations have encouraged the development of alternative approaches that avoid orbital-based descriptions. Density functional theory (DFT) has offered a new perspective on the Woodward–Hoffmann rules for various pericyclic reactions,^16–18 allowing the molecular mechanism of ring-opening processes to be interpreted systematically through electron density ρ(r), which is experimentally observable via X-ray crystallography. From a perturbative perspective, chemical reactivity can be studied through global and local responses to changes in electron density, with second-order descriptors like chemical hardness and the dual descriptor providing valuable insights.^19–34 Building on this foundation, the present work focuses on developing models based on electronic redistribution descriptors to analyze reactivity along the reaction coordinate using both global and local indices.

Torquoselectivity, a pathway-dependent form of stereoselectivity, can theoretically be analyzed using directional parameters. However, the electron localization function (ELF) derived from DFT lacks such parameters, prompting the development of approaches based on ρ(r) combined with vector-based methods like quantum theory of atoms in molecules (QTAIM), stress tensor analysis, and Ehrenfest force partitioning. These tools enable the prediction of torquoselectivity by considering directional influences and have successfully described bond formation and charge transfer in ring-opening reactions. In this study, we examined the thermal ring-opening of cis- and trans-perfluoro-3,4-dimethylcyclobutene (Scheme 1), where the experimental results showed an unusual preference for the Z,Z isomer over E,E, despite steric and electronic expectations. Activation barriers differ notably, with Z,Z at 30.5 kcal mol⁻¹ and E,E at 49.7 kcal mol⁻¹. Since FMO theory fails to explain this behavior, we applied QTAIM and stress tensor methodologies to investigate the bonding and structural rearrangements, providing a deeper mechanistic insight into torquoselectivity beyond conventional orbital-based interpretations.

Scheme 1 Schematic representation of thermal ring-opening reaction of cis- and trans-perfluoro-3,4-dimethylcyclobutene systems. The numbering corresponding to the studied reactions has been included.

Our objective is to validate the applicability of the proposed theoretical framework and demonstrate its ability to accurately predict torquoselectivity in the ring-opening electrocyclic reactions of the compounds shown in Scheme 1, thereby providing synthetic chemists with tools to enhance stereochemical control and anticipate favorable reaction pathways in this and related systems. In this study, we applied QTAIM and stress tensor methodologies to analyze total local energy density H(r_b), ellipticity (ε), metallicity ξ(r_b), and stress tensor polarizability (P_σ) at the C2–C3 bond critical points (BCPs) during ring opening. Moreover, we employed Sanderson's electronegativity equalization principle with multiple regression analysis to correlate global and local reactivity descriptors, and further used information-theoretic indices to gain insights into electronic structure, reaction pathway selectivity, and molecular stability. Following an overview of the key theoretical principles and computational details in Section 2, we will discuss the results in Section 3, followed by a summary of our main findings in Section 4.

2. Methodology and computations

2.1. QTAIM and stress tensor BCP descriptors

QTAIM offers a systematic framework for analyzing electron density ρ(r) and characterizing atomic bonding environments through the topology dominated by nuclear forces. By examining the gradient ∇ρ(r) and the Hessian matrix eigenvalues (λ₁ < λ₂ < λ₃), critical points are classified as nuclear, bond, ring, or cage critical points. Key descriptors such as ellipticity (ε, ε = |λ₁|/|λ₂| − 1) and metallicity (ξ) provide insights into bond nature and behavior during reactions. When ε > 0, the eigenvalues λ₁ and λ₂ of the Hessian matrix of ρ(r) correspond to the smallest and largest axes of the elliptical distribution of ρ(r_b), respectively. Ellipticity measures electron density distribution at bond critical points (BCPs), while metallicity, ξ(r_b) = ρ(r_b)/∇²ρ(r_b), captures bond-path changes during ring-opening. The terms ρ(r_b) and ∇²ρ(r_b) are the total electronic charge density and the corresponding Laplacian density, respectively. During ring-opening, the BCP typically shows shared-shell characteristics prior to bond elongation, transitioning to closed-shell characteristics as the bond path elongates. During this stretching process, the rate at which ρ(r_b) decreases relative to ∇²ρ(r_b) varies, leading to a region indicative of metallic characteristics. Stress tensor analysis, through stiffness (S_σ) and stress tensor polarizability (P_σ, P_σ = |λ_3σ|/|λ_1σ|), further assesses a bond's resistance to distortion. Here, QTAIM and stress tensor methods are jointly employed to track bond-path dynamics and predict preferred transition states (TSIC or TSOC) in ring-opening reactions.

2.2. Global and local reactivity descriptors

The electronic chemical potential (μ) and global hardness (η) are fundamental descriptors of chemical reactivity, estimated using the finite difference approach as μ = (∂E/∂N)_v ≈ −(IP + EA)/2 and η = (∂²E/∂N²)_v ≈ −(IP − EA), where IP and EA are the ionization potential and electron affinity, respectively. On the other hand, E, N and ν are the total energy, number of electrons and external potential of the system, respectively. When an electrophilic species accepts charge, the maximum charge transfer is given by ΔN_max = −μ/η, with an associated energy stabilization ΔE_min = −μ²/2η. Parr²² introduced the electrophilicity index (ω), defined as ω = μ²/2η, to quantify this stabilization. Sánchez-Márquez³⁵ proposed a model for energy variation of the form ΔE ≈ μΔN + 1/2ηΔN², extended by including a cubic term for atomic energy variations of orbital “i”, ΔE_i ≈ μΔN_i + 1/2η_iΔN_i² + 1/6γ_iΔN_i³, leading to a modified electronic chemical potential μ′ ≈ μ + η_iΔN_i + 1/2γ_iΔN_i², where γ_i is the local hyper softness for the “i” orbital. Following the electronegativity equalization principle (EEP) based on Sanderson's principle,³⁵ atomic chemical potentials equalize at equilibrium and local parameters can be derived. From this, the maximum electron transfer at the atomic level is given by and the corresponding local electrophilicity index is defined as ω_i = −ΔE(ΔN^max_i), providing an enhanced framework to describe charge redistribution among atoms within a molecule.

2.3. Information-theoretic analysis

Information-theoretic (IT) descriptors, based on electron density ρ(r), are valuable tools for predicting molecular properties and chemical reactivity within density functional reactivity theory (DFRT).^36–45 At the microscopic level, reaction rates are linked to the probabilistic evolution of reactants, analogous to information flow. Shannon entropy⁴⁶ (S_S,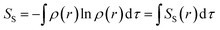 ) quantifies electron density delocalization and system uncertainty, paralleling the stochastic nature of chemical reactions. The term S_S(r) represents the local Shannon entropy density. Ghosh–Berkowitz–Parr (GBP) entropy⁴⁷ (, where t(r;ρ) is kinetic energy density, t_TF(r;ρ) is Thomas–Fermi kinetic energy density, and c and k are constants), incorporating kinetic energy densities, offers insights into chemical bonding and binding energies. Together, these IT descriptors provide a framework for understanding reactivity from an information perspective.

2.4. Computational details

All transition states (TS) were optimized and confirmed by a single imaginary frequency in the Hessian matrix. Intrinsic reaction coordinate (IRC) calculations in both directions ensured correct TS connectivity. Reaction paths used mass-weighted coordinates with consistent step size (0.1 amu^1/2 Bohr). Final IRC geometries were re-optimized to confirm convergence to minima. Single-point energy calculations were performed using Gaussian's iop(5/33 = 1) keyword. Energy differences (ΔE) between reactants and TS were calculated from these values. All structures were optimized using B3LYP/6-311+G(d,p) in the Gaussian 16 program package.⁴⁸ QTAIM and stress tensor analysis were performed using Multiwfn 3.8.⁴⁹ Energy decomposition followed DFT-based models, avoiding arbitrary fragment partitioning. Information-theoretic descriptors were computed using Multiwfn software.

Electronic densities of neutral, cationic, and anionic species were also obtained. TS structures were further validated by harmonic frequency analysis. A custom script was used to compute reactivity descriptors along the reaction path. Statistical analysis (multiple linear regression) was carried out with STATGRAPHICS Centurion 19 (version 19.3.03),⁵⁰ focusing particularly on the coefficient of determination and the degree of similarity between the plots of global descriptors and their respective regression models.

3. Results and discussion

3.1. Structure and energetics of thermal ring opening electrocyclic reactions

This work aims to develop a comprehensive approach to interpreting chemical bonding, electronic rearrangement, and stereochemical behavior, guided by experimental observations. Although FMO theory predicts the E,E isomer as favored due to steric and electronic considerations, the Z,Z isomer is unexpectedly preferred. Fig. 1 illustrates the reaction energy profiles for cis- and trans-perfluoro-3,4-dimethylcyclobutene systems. Thermal conrotation typically allows the cis reactant to form Z,E or E,Z isomers (Scheme 1), while the trans isomer yields Z,Z and E,E products depending on inward or outward rotation per Woodward–Hoffmann rules. However, twisting can lead to the unusual formation of E,E and Z,Z isomers from the cis-reactant (Scheme 1). The inward (TSIC) and outward (TSOC) pathways from cis-perfluoro-3,4-dimethylcyclobutene have energy barriers of 33.78 and 33.77 kcal mol⁻¹, respectively, whereas the unusual Z,Z and E,E isomers have much higher barriers of 74.42 and 76.60 kcal mol⁻¹. For the trans isomer, the Z,Z and E,E products form with barriers of 27.82 and 44.31 kcal mol⁻¹, respectively. Dolbier et al.¹¹ showed that the E,E/Z,Z to E,Z isomer leakage rates were difficult to measure precisely, but the estimated activation energies (∼42 kcal mol⁻¹) matched the mechanism of double-bond isomerization. Our theoretical results indicate that an extra 40.6–42.8 kcal mol⁻¹ is needed for the atypical bond rotation of the cis-reactant. Overall, the cis compound is predicted to form a mixture of E,Z and Z,E isomers, since energy barriers on the order of 74–77 kcal mol⁻¹ would not produce a significant amount of the product even at relatively high temperatures.

Fig. 1 Reaction energy profiles of the ring-opening cis- and trans-perfluoro-3,4-dimethylcyclobutene systems. (TSIC/TSOC denotes transition state inward/outward conrotatory, R = reactant, P = product).

Table S1 presents the total energy partitioning values in DFT for the studied reactions. The noninteracting kinetic energy term (ΔT_s) and Fermionic quantum term (ΔE_q) both contribute negatively to the barrier height. Notably, ΔE_x should not be considered alone, only the exchange–correlation energy (ΔE_xc) has physical significance. For the cis isomer, TSIC and TSOC contribute similarly to the barrier height. In the unusual torquoselectivity of the cis conformer, the positive values of electrostatic energy (ΔE_e) and steric energy (ΔE_s) indicate their role in increasing the barrier. The Z,Z isomer shows a slightly higher steric contribution than the E,E isomer due to increased hindrance, whereas its ΔE_e contribution is slightly lower. Although ΔE_xc contributes less than other energy components, when combined with ΔE_e, it plays a significant role in outweighing the repulsive term, thereby supporting the inherent molecular stability. For trans-perfluoro-3,4-dimethylcyclobutene systems, the higher electrostatic and exchange–correlation energy contributions and lower steric energy contribution for the TSIC path compared to the TSOC path, make the Z,Z isomer more favorable than the E,E isomer.

Fig. S1 illustrates relative energy (ΔE) variations along the reaction pathways, showing that in trans-perfluoro-3,4-dimethylcyclobutene, the TSIC path is favored, leading to Z,Z formation. Likewise, the cis isomer also unusually favors the Z,Z product.

3.2. QTAIM and stress tensor analysis

A new criterion is proposed to classify reactions as competitive or non-competitive, based on the degeneracy of chemical topological properties rather than relying on arbitrary activation energy thresholds such as |ΔTS| < 1.0 kcal mol⁻¹. Molecular graph snapshots (Fig. S2) illustrate the TSIC and TSOC pathways for both the cis- and trans-perfluoro-3,4-dimethylcyclobutene systems, where the bond critical points (BCPs) associated with the ring-opening of the C2–C3 bond are clearly visible. The evolution of metallicity (ξ(r_b)) along the intrinsic reaction coordinate (IRC) highlights key differences between the pathways (Fig. 2).

Fig. 2 The variation in metallicity (ξ(r_b)) along the IRC for the C2–C3 BCPs during the ring-opening of (a) trans- and (b) cis- perfluoro-3,4-dimethylcyclobutene systems. (C) and (T) stands for cis- and trans-perfluoro-3,4-dimethylcyclobutene systems.

Variations in metallicity (ξ(r_b)) along the IRC reveal distinct, non-competitive behavior in the trans ring-opening reaction. This highlights metallicity as a key factor in identifying the electronic reorganization of the ring-opening BCPs along the reaction pathways. The transition from a shared-shell C2–C3 BCP to a ring-opening closed-shell C2—C3 BCP is reflected by a change in the sign of the Laplacian, ∇²ρ(r_b) (∇²ρ(r_b) < 0 to ∇²ρ(r_b) > 0), accompanied by the total local energy density (H(r_b)) variation, depicted in Fig. S3 and S4. This transformation is often referred to as bond breaking and is determined using the reaction electronic flux (REF). Additionally, the shift from a shared-shell to a closed-shell C2–C3 BCP is associated with a reduction in the double-bond character into two shared-shell BCPs: C3–C4 and C1–C2. In the context of QTAIM, this is reflected in increasing ellipticity (ε) values, as illustrated in Fig. S5 and S6. Along the IRC, the reverse-to-forward reaction pathway for the cis- and trans-perfluoro-3,4-dimethylcyclobutene isomers shows a decrease in the ellipticity (ε) value for C1–C4 BCP, while the value increases for the C1–C2 and C3–C4 BCPs along the same pathway. The variation of ellipticity (Δε) between the TSIC and TSOC paths is more significant in the reverse direction compared to the forward direction for the trans conformer.

For cis-perfluoro-3,4-dimethylcyclobutene, TSIC and TSOC are competitive (|ΔTS| < 1 kcal mol⁻¹), while the unusual torquoselective path forming Z,Z and E,E is non-competitive. In trans systems, the large energy difference between TSIC and TSOC indicates non-competitive behavior. Metallicity analysis shows degenerate pathways for the regular cis ring-opening path (C2–C3/C2—C3) but non-degenerate for the unusual cis and trans pathways. For the cis reactant, the ellipticity (ε) and H(r_b) plots of the TSIC and TSOC paths coincide for all the selective BCPs. However, a significant difference is observed for the unusual torquoselective pathway. The difference is also observed for the trans conformer. Stress tensor polarizability (P_σ) further distinguishes between degenerate (cis) and non-degenerate (trans) systems, as shown in Fig. 3. It shows that, for trans torquoselectivity, the energetically preferred TSIC path has a less polarizable C2–C3 BCP compared to the TSOC path. On the other hand, for the unusual torquoselectivity of the cis conformer, the polarizability is marginally lower forming the Z,Z isomer compared to the E,E isomer. Overall, metallicity and P_σ confirm that typical cis ring-opening is competitive, while unusual cis torquoselectivity and trans reactions are non-competitive. This noticeable difference highlights trans torquoselectivity as TSIC and unusual cis torquoselectivity forming the Z,Z isomer.

Fig. 3 The variation of the stress tensor polarizability (P_σ) along the IRC for the (a) trans- and (b) cis- perfluoro-3,4-dimethylcyclobutene systems along C2–C3/C2—C3 BCPs.

3.3. Reactivity descriptors analysis

This study analyzed the correlation between global and local electrophilicity (ω) along the reaction path from the reactants to the transition state (range 1) for the six reactions that are shown in Scheme 1 and are listed in Table 1 (in Fig. S7, the transition states corresponding to these six reactions can be seen). It also examined the correlation from the transition state to the products (range 2). In the multiple regression analysis presented in Table 1, the local electrophilicities of atoms C2 and C3 were selected as variables. These atoms were chosen because they form the σ-bond that is cleaved during the opening of the four-membered ring. As shown in the table, the correlation between global electrophilicity and local electrophilicities is generally very high, in most cases exceeding 0.98. This suggests that the global electrophilicity value is strongly influenced by the rupture of this bond along the reaction pathway. The coefficients of the multiple linear regression were calculated, as shown in Table S2. The variables ω(2) and ω(3) represent the local electrophilicities of the carbon atoms C2 and C3, respectively. We extended the analysis to all the carbon atoms of the four-membered ring. Table S3 reports the regression equations for the linear correlation between global electrophilicity and local electrophilicity for the studied reactions. In this case, four variables, ω(1) to ω(4), corresponding to the local electrophilicities of carbons C1–C4, were included. This set of carbons was chosen because, in the products, two π bonds are formed (C1–C2 and C3–C4), which represent the most significant structural change along the reaction path segment between the transition state and the products. As shown in Table 2, the determination coefficients are closer to unity than those in Table 1; however, the improvement is only moderate since the R² values in Table 1 were already very close to unity. In addition, the errors associated with the regression coefficients were estimated, as presented in Tables S4 and S5. In general, the errors are not negligible: although most estimates fall below 5%, in many other cases the errors are remarkably high. We attribute these large errors to autocorrelations between the local variables corresponding to C2 and C3, as observed in Tables S6 and S7. This correlation is likely due to the similar chemical environments of C2 and C3 and their strong mutual influence along the reaction pathway. Furthermore, Fig. S8 and S9 clearly show that global electrophilicity and multiple regression exhibit very similar trends. The errors in the linear combination coefficients are also generally high, as observed in Table S5, and in some particular cases they reach values on the order of 100%. We believe that these large errors are due to the strong autocorrelation among the local variables (as was also the case in the previous analysis), as evidenced in Tables S6 and S7.

Table 1 Coefficient of determination (R²) for the multiple linear regression of global electrophilicity vs. local electrophilicity for the reactions under study. Range 1 corresponds to the reaction path from reactants to the transition state, while range 2 corresponds to the path from the transition state to the products. Two independent variables were considered: the local electrophilicities of atoms C2 and C3

	Reaction 1	Reaction 2	Reaction 3	Reaction 4	Reaction 5	Reaction 6
Range 1	0.9870	0.9918	0.9908	0.9872	0.9844	0.9876
Range 2	0.9583	0.9917	0.9956	0.9974	0.9621	0.9876

---

Table 2 Coefficient of determination (R²) for the multiple linear regression of global electrophilicity vs. local electrophilicity for the reactions of the study. Range 1 and range 2 indicate the reaction path between the reactants and the transition state and the transition state to the products. Four independent variables were considered: the local electrophilicities of atoms C1–C4

	Reaction 1	Reaction 2	Reaction 3	Reaction 4	Reaction 5	Reaction 6
Range 1	0.9993	0.9979	0.9980	0.9982	0.9996	0.9941
Range 2	0.9997	0.9997	0.9998	0.9993	0.9999	0.9941

---

In this work, we also analyzed the global softness (η⁻¹) along the reaction path from the reactants to the transition state (range 1) for the six studied reactions, and additionally from the transition state to the products (range 2). For reactions 1–6, multiple regression analysis revealed a strong correlation (high R² values in Table 3) between global softness (η⁻¹) and the local softness of atoms C2 and C3 (η⁻¹(2) and η⁻¹(3)), as illustrated in Fig. S10 and S11 (see also Table S8). These two atoms are the main contributors to the global softness, particularly during the C2–C3 bond formation in the four-membered ring. The results suggest that C2 and C3 follow the same trends as electrophilicity in this reaction phase, closely mirroring the behavior of global softness. However, Table S9 shows that the errors in the coefficients of the multiple linear regression are not negligible. We attribute these large errors to the strong correlation between the independent variables η⁻¹(2) and η⁻¹(3) (Tables S10 and S11), a phenomenon already observed in the case of electrophilicity.

Table 3 Coefficient of determination (R²) for the multiple linear regression of global softness vs. local softness for the studied reactions. Two independent variables: C2 and C3

	Reaction 1	Reaction 2	Reaction 3	Reaction 4	Reaction 5	Reaction 6
Range 1	0.186	0.9593	0.9531	0.6053	0.9620	0.9127
Range 2	0.9782	0.9937	0.9944	0.9920	0.8643	0.8971

---

We extended the analysis to all four carbons of the ring. Table S12 presents the regression equations for the linear regression of global softness versus local softness for the studied reactions. In this case, four variables, η⁻¹(1) to η⁻¹(4), corresponding to the local softness values of carbons C1–C4, were included. For reactions 1–6, Table 4 shows a slightly stronger correlation when using these four independent variables, which are directly involved in the formation of the product π-bonds (Fig. S10 and S11). The formation of π-bonds involving these carbons appears to play a key role in determining molecular softness during this phase of the reaction across all studied systems, in line with the electrophilicity trends. For this case, we also computed the errors of the multiple linear regression coefficients, reported in Table S13. As can be seen, they follow the same trend observed for electrophilicity, including the high autocorrelations among independent variables, as shown in Tables S10 and S11.

Table 4 Coefficient of determination (R²) for the multiple linear regression of global softness vs. local softness (regressions) for the reactions of the study. Four independent variables (C1–C4)

	Reaction 1	Reaction 2	Reaction 3	Reaction 4	Reaction 5	Reaction 6
Range 1	0.9917	0.9902	0.9896	0.9924	0.9969	0.9331
Range 2	0.9847	0.9943	0.9950	0.9988	0.8888	0.9021

---

The global maximum charge variation was intentionally omitted from the analysis due to its strong correlation with global electrophilicity, avoiding redundancy. This high linear correlation (R²) between the two parameters was observed across all studied reactions, as can be seen in Table 5, the table is divided into two segments of the reaction coordinate (ranges 1 and 2). A visual comparison of these parameters for each reaction is available in Fig. S12 and S13.

Table 5 Coefficient of determination (R²) for the multiple linear regression of global electrophilicity vs. global maximum charge variation for the reactions of the study

	Reaction 1	Reaction 2	Reaction 3	Reaction 4	Reaction 5	Reaction 6
Range 1	0.997	0.999	0.999	0.995	0.997	0.997
Range 2	0.998	0.995	0.994	0.999	0.995	0.997

---

3.4. Information-theoretic descriptors

The analogy between Shannon entropy (S_S) and chemical kinetics connects uncertainty and system dynamics. Although arising from different contexts, both concepts relate to disorder: chemical reactions progress stochastically from ordered states toward equilibrium, much like Shannon entropy⁴⁵ quantifies uncertainty in information systems. In kinetics, entropy change (ΔS) influences spontaneity per the second law of thermodynamics, and the reaction rates at the microscopic level depend on probabilistic molecular states, analogous to decision-making processes. Molecules “choose” reaction paths based on probability, reflecting Shannon-type uncertainty. Shannon entropy thus models the uncertainty and dynamic evolution of chemical reactions in terms of information. In our study, the TSIC (T) trajectory shows lower uncertainty (lower entropy values) compared to the TSOC (T) path (Fig. 4). For cis systems, the Z,Z isomer shows lower randomness, and thus a lower Shannon entropy, matching experimental observations (Fig. 4). The GBP entropy (S_GBP)⁴⁶ quantifies the degree of non-uniformity in the electron density distribution. The TSIC (T) path shows lower GBP entropy along the IRC, suggesting a more directed and less random electronic reorganization. On the other hand, for the cis conformer, the Z,Z isomer, having lower GBP entropy, reflects a more structured and less delocalized electron density, consistent with greater stability and experimental preference.

Fig. 4 Information-theoretic descriptors calculated for cis- and trans-perfluoro-3,4-dimethylcyclobutene systems along the IRC.

4. Conclusion

In conclusion, the unusual torquoselectivity observed in the electrocyclic ring-opening of perfluoro-3,4-dimethylcyclobutene was investigated, revealing an unexpected preference for the Z,Z isomer. Traditional orbital models fail to adequately explain this selectivity. The study employed electron density-based methods—c-DFT, QTAIM, and stress tensor analysis—to uncover the underlying factors. It was found that the inward conrotatory pathway (TSIC), which leads to the Z,Z product, is energetically favored for the trans isomer and, unexpectedly, also for the cis isomer, contradicting conventional expectations. Electron density descriptors such as metallicity and stress tensor polarizability effectively distinguish between competitive and non-competitive pathways. Global vs. local electrophilicity and softness analyses identify atoms C2 and C3 (and C1–C4 in the products) as key reactive sites. Additionally, Shannon entropy indicates lower uncertainty for the kinetically favored Z,Z isomer. This work contributes to establishing a predictive framework for stereochemical control in similar systems.

Conflicts of interest

The authors declare that they have no conflicts of interest regarding the publication of this article, financial, and/or otherwise.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. The data supporting this article (SI) contains the plot of variation of relative energy (∆E) along the IRC, Molecular graph snapshots, The plot of variation of total local energy density (H(r_b)) along the IRC for cis- and trans- perfluoro-3,4-dimethylcyclobutene systems, The plot of variation of ellipticity (ε) along the IRC, the transition states for all the reactions, the multiple regression analysis plots, Total energy difference and its component analysis, cartesian coordinates for all transition states. See DOI: https://doi.org/10.1039/d5cp04207k.

Acknowledgements

PKC would like to thank DST, New Delhi for the J. C. Bose National Fellowship, grant number SR/S2/JCB-09/2009. AP thanks IIT Kharagpur for her fellowships. The authors gratefully acknowledge the high-performance supercomputing system of IIT Kharagpur, the “PARAM Shakti and the Supercomputational area of University of Cadiz (Research Support Cluster) and CICA (Centro Informático Científico de Andalucía) for the computations.

References

1. S. Niwayama, E. A. Kallel, D. C. Spellmeyer, C. Sheu and K. N. Houk, J. Org. Chem., 1996, 61, 2813–2825.
2. H. D. Banks, J. Org. Chem., 2010, 75, 2510–2517.
3. T. D. R. Morgan, L. M. Leblanc, G. H. Ardagh, R. J. Boyd and D. J. Burnell, J. Org. Chem., 2015, 80, 1042–1051.
4. W. Kirmse, N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1984, 106, 7989–7991.
5. M. Yasui, Y. Naruse and S. Inagaki, J. Org. Chem., 2004, 69, 7246–7249.
6. R. Momen, A. Azizi, A. Morales-Bayuelo, M. Pazhoohesh and X. Ji, Int. J. Quantum Chem., 2022, 122, e26826.
7. J. E. Barquera-Lozada, J. Phys. Chem. A, 2016, 120, 8450–8460.
8. A. Azizi, R. Momen, A. Morales-Bayuelo, T. Xu, S. R. Kirk and S. Jenkins, Int. J. Quantum Chem., 2018, 118, e25707.
9. A. Morales-Bayuelo, Int. J. Quantum Chem., 2013, 113, 1534–1543.
10. J. Sánchez-Márquez and A. Morales-Bayuelo, Int. J. Quantum Chem., 2024, 124, e27494.
11. W. R. Dolbier Jr, H. Koroniak, D. J. Burton, A. R. Bailey, G. S. Shaw and S. W. Hansen, J. Am. Chem. Soc., 1984, 106, 1871–1872.
12. W. R. Dolbier, H. Koroniak, K. N. Houk and C. Sheu, Acc. Chem. Res., 1996, 29, 471–477.
13. M. J. Walker, B. N. Hietbrink, B. E. Thomas, K. Nakamura, E. A. Kallel and K. N. Houk, J. Org. Chem., 2001, 66, 6669–6672.
14. X. N. Wang, E. H. Krenske, R. C. Johnston, K. N. Houk and R. P. Hsung, J. Am. Chem. Soc., 2014, 136, 9802.
15. N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1985, 107, 2099–2111.
16. P. W. Ayers, C. Morell, F. De Proft and P. Geerlings, Chem. – Eur. J., 2007, 13, 8240–8247.
17. P. Geerlings, P. W. Ayers, A. Toro-Labbé, P. K. Chattaraj and F. De Proft, Acc. Chem. Res., 2012, 45, 683–695.
18. P. Jaque, J. V. Correa, F. De Proft, A. Toro-Labbé and P. Geerlings, Can. J. Chem., 2010, 88, 858–865.
19. P. K. Chattaraj and R. G. Parr, in Chemical Hardness, Structure and Bonding, ed. K. D. Sen, Springer, Berlin, 1993, pp. 11.
20. R. G. Pearson, Chemical Hardness: Applications from Molecules to Solids, WileyVCH, Weinheim, 1997.
21. W. T. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726.
22. R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
23. P. K. Chattaraj and D. R. Roy, Chem. Rev., 2007, 107, PR46–PR74.
24. R. G. Parr and P. K. Chattaraj, J. Am. Chem. Soc., 1991, 113, 1854.
25. E. Chamorro, P. K. Chattaraj and P. Fuentealba, J. Phys. Chem. A, 2003, 107, 7068–7072.
26. F. De Proft, P. K. Chattaraj, P. W. Ayers, M. Torrent-Sucarrat, M. Elango, V. Subramanian, S. Giri and P. Geerlings, J. Chem. Theory Comput., 2008, 4, 595–602.
27. P. W. Ayers, C. Morell, F. De Proft and P. Geerlings, Chem. – Eur. J., 2007, 13, 8240–8247.
28. C. Morell, V. Labet, A. Grand, P. W. Ayers, F. De Proft, P. Geerlings and H. Chermette, J. Chem. Theory Comput., 2009, 5, 2274–2283.
29. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873.
30. S. B. Liu, Acta Phys.-Chim. Sin., 2009, 25, 590–600.
31. P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Theor. Chem. Acc., 2020, 139, 36.
32. S. B. Liu, Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, Wiley-VCH, Weinheim, 2022.
33. B. Wang, P. Geerlings, S. Liu and F. De Proft, J. Chem. Theory Comput., 2024, 20, 1169–1184.
34. N. Flores-Holguín, J. Frau and D. Glossman-Mitnik, Front. Chem., 2022, 10, 1003106.
35. J. Sánchez-Márquez, V. García, D. Zorrilla and M. Fernández, Int. J. Quantum Chem., 2019, 119, 1–13.
36. S. B. Liu, Acta Phys.-Chim. Sin., 2016, 32, 98–118.
37. J. Fu, M. Li, C. Rong, D. Zhao and S. Liu, J. Mol. Model., 2024, 30, 341.
38. A. Poddar, A. Chordia and P. K. Chattaraj, J. Chem. Sci., 2024, 136, 23.
39. A. Poddar, R. Pal, C. Rong and P. K. Chattaraj, J. Math. Chem., 2023, 61, 1143–1164.
40. A. Poddar and P. K. Chattaraj, J. Chem. Sci., 2025, 137, 77.
41. A. Poddar and P. K. Chattaraj, Materials Informatics I: Methods, Springer Nature, Switzerland, 2025, pp. 139–166.
42. A. Poddar, R. Pal, S. G. Patra and P. K. Chattaraj, in Mathematical Descriptors of Molecules and Biomolecules: Applications in Chemistry, Drug Design, Chemical Toxicology, and Computational Biology, ed. S. C. Basak, Springer, Switzerland, 2024, pp. 91–111.
43. R. Pal, A. Poddar and P. K. Chattaraj, J. Phys. Chem. A, 2022, 126, 6801–6813.
44. S. G. Patra, A. Poddar, R. Jha, S. S. Kadam, C. Paul and P. K. Chattaraj, ChemPhysChem, 2025, 2500019.
45. C. Rong, D. Yu and S. Liu, Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, John Wiley & Sons, 2022, 1, 281–299.
46. C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 379–423.
47. S. K. Ghosh, M. Berkowitz and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 8028–8031.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
49. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
50. Statgraphics Centurion, version 19, Statgraphics Technologies, Inc., The Plains, VA, USA, 2020.

---

Footnote

† These authors contributed equally.

---