 Open Access Article
Open Access ArticleTwist, grind, translocate: pepper-mill dynamics of MSPA protein pore during ssDNA transport
Priya
Dey
,
Brandon
Meza-González
 ,
Ganesh N.
Pandian
and
Daniel M.
Packwood
*
,
Ganesh N.
Pandian
and
Daniel M.
Packwood
*
Institute for Integrated Cell-Material Sciences (iCeMS), Kyoto University, Kyoto 606-8501, Japan. E-mail: dpackwood@icems.kyoto-u.ac.jp
First published on 28th January 2026
Abstract
DNA translocation through membrane-bound protein nanopores lies at the heart of both fundamental biological processes and next-generation sequencing technologies. Among these nanopores, Mycobacterium smegmatis porin A (MSPA) has emerged as a robust β-barrel protein with a narrow constriction suitable for single-molecule sensing. However, the atomic-scale mechanism by which DNA interacts and couples with the dynamic motions of the pore remains poorly understood. In this work, we combine atomistic molecular dynamics (MD) simulations with dimensionality reduction and cross-correlation analyses to elucidate the mechanism of single-stranded DNA (ssDNA) translocation through MSPA. Our results reveal a previously unrecognized “pepper-mill”-like motion of MSPA during the translocation of ssDNA. This collective domain motion plays a crucial role in modulating analyte-pore interactions and influencing the dynamics of DNA passage. Furthermore, our scheme provides a generalizable and data-driven strategy for extracting mechanistic insights from large-scale biomolecular simulations. Together, these findings highlight the potential of data-driven computational strategies to guide nanopore engineering and accelerate the development of next-generation sequencing and biosensing technologies.
1 Introduction
Membrane-bound nanopores provide a cost-effective, label-free method for analyzing biopolymers at the single-molecule scale.1–3 They are widely used for applications in single-molecule biosensing,4–7 protein identification, and DNA sequencing.8–10 Over the past twenty years, the growing diversity of nanopore-based applications has prompted the quest to discover new nanopores and nanopore mutants which obtain high spatial resolution and molecular specificity.11–13 Naturally-occurring protein nanopores originate from pore-forming proteins found in membranes. It is generally accepted that different protein nanopores have distinct structural properties, such as shape, size, or surface charge distribution, which qualify it for a particular class of sensing applications. In order to discover new nanopores for specific applications, it is essential that the atomic-scale mechanism of the pore's sensing mechanism be clarified. To the best of our knowledge, however, this mechanism is still not understood comprehensively.The Mycobacterium smegmatis porin A (MSPA) is a homooctameric β-barrel membrane protein that forms a stable and highly conductive channel in the outer membrane of Mycobacterium smegmatis, a non-pathogenic mycobacterial species.14,15 Structurally, MSPA resembles a goblet-shaped pore with a narrow constriction zone, ∼1 nm in diameter, formed by a ring of aspartate residues. This unique geometry enables MSPA to act as a selective filter for hydrophilic molecules and ions, playing a critical role in nutrient uptake and maintaining homeostasis in mycobacterial cells. Due to its high thermal and chemical stability, MSPA has emerged as a promising candidate for bioengineering applications. In the field of nanopore technology, MSPA is particularly significant as a biological nanopore for DNA sequencing and molecular sensing.14,16–19 Unlike α-hemolysin and other traditional nanopores,20,21 MSPA's narrow and short constriction enhances nucleotide discrimination, making it especially well-suited for single-stranded DNA sequencing when combined with DNA-processing enzymes. Engineered variants of MSPA have been used in nanopore sequencing platforms to achieve high sensitivity and base resolution, pushing the frontier of real-time, label-free genetic analysis. Its biological robustness and modifiable architecture also make it a valuable tool in biosensing, antibiotic screening, and membrane protein studies.
 | ||
| Fig. 1 Schematic representation of the engineered MSPA nanopore embedded (a) top, bottom and front view, (b) simulation setup of MSPA pore in a lipid bilayer with translocating ssDNA. | ||
In recent years, computational approaches have played a pivotal role in understanding the structural dynamics and transport properties of the MSPA nanopore. Molecular dynamics (MD) simulations have been used to probe ion and DNA translocation through the channel, investigate the impact of mutations on pore conductivity, and explore the electrostatics and hydration behavior within the constriction zone.22–25 These studies have revealed critical atomic-level interactions governing the selectivity and sensing ability of MSPA, complementing experimental findings. However, challenges remain in capturing the complex interplay between structural flexibility, local environments, and functionally relevant transitions that occur over microsecond timescales or longer. Although long-term MD simulations of large molecular systems can be carried out on modern supercomputers, it remains difficult to obtain conclusive insights from the massive amounts of simulation output.
In this paper, we characterize the dynamics of MSPA during ssDNA translocation in detail using a combination of atomistic molecular dynamics simulations, dimensionality reduction techniques, and cross-correlation analysis. We show for the first time that the domains in the bottom part of the MSPA nanopore exhibits concerted, alternating motions, resulting in a twisting dynamics that drives the translocation of single-stranded DNA (ssDNA). We refer to this motion as ‘pepper-mill’ dynamics. The dynamic cross-correlation analysis further elucidates the coupling between different regions of the nanopore and the translocating strand. This overcomes the limitations of traditional analysis methods by providing a more comprehensive view of the structural dynamics at play.
2 Material and methods
The atomic coordinates of wild-type MSPA were obtained from the RCSB Protein Data Bank (PDB ID:1UUN)15 (see Section S1 of SI for structural information of MSPA). To generate an engineered version of MSPA optimized for nucleotide sensing, site-specific mutations were introduced at residues 90, 91, and 93 using Pymol.16,26 These residues lie near the constriction zone of the pore and are known to influence ionic selectivity and nucleotide discrimination. The engineered MSPA variant offers enhanced sensitivity and resolution for nanopore-based molecular detection, particularly in sequencing applications.27Single-stranded DNA (ssDNA) homopolymers, each consisting of 40 nucleotides of a single base type (polyA, polyG, polyC, or polyT), were constructed using the Nucleic Acid Builder (NAB)28 module of the AMBER29 software suite. Each ssDNA strand was initially positioned approximately 35 Å away from the entrance of the engineered MSPA nanopore along the pore's central (z) axis, representing the pre-translocation state.18 The MSPA nanopore was embedded in a palmitoyloleoylphosphatidylcholine (POPC)30 lipid bilayer to model a realistic membrane environment. The complete system was solvated in a rectangular TIP3P31 water box containing 1 M KCl to reproduce physiological ionic strength. The final simulation box dimensions were approximately 130 × 130 × 440 Å3, comprising roughly 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms (Fig. 1). System assembly and initial preparation were performed using the CHARMM-GUI32 membrane builder where the topology and coordinate files are generated, force-field parameters are assigned and an initial energy minimization protocol is performed to remove steric clashes and stabilize the system. All molecular dynamics simulations were carried out using NAMD (version 2.14)33 with the CHARMM36m force field34 applied consistently to proteins, lipids, and nucleic acids. Long-range electrostatic interactions were treated using the particle mesh Ewald (PME)35 method, and periodic boundary conditions were applied in all directions. A time step of 2 fs was used, and the system temperature was maintained at 300 K using a Langevin thermostat.36 For more details see Sections S2 and S3 of SI.
000 atoms (Fig. 1). System assembly and initial preparation were performed using the CHARMM-GUI32 membrane builder where the topology and coordinate files are generated, force-field parameters are assigned and an initial energy minimization protocol is performed to remove steric clashes and stabilize the system. All molecular dynamics simulations were carried out using NAMD (version 2.14)33 with the CHARMM36m force field34 applied consistently to proteins, lipids, and nucleic acids. Long-range electrostatic interactions were treated using the particle mesh Ewald (PME)35 method, and periodic boundary conditions were applied in all directions. A time step of 2 fs was used, and the system temperature was maintained at 300 K using a Langevin thermostat.36 For more details see Sections S2 and S3 of SI.
To investigate ssDNA translocation through the MSPA nanopore, steered molecular dynamics (SMD)33,37 simulations were performed. A constant-velocity pulling force was applied along the negative z-axis, aligned with the pore axis. The 3′-terminal nucleotide of the ssDNA was chosen as the pulling group, while a reference atom on the opposite side of the membrane was fixed to define the pulling direction. A pulling velocity of 0.0005 nm ps−1 and a harmonic spring constant of 7 kcal mol−1 Å−2 were used. These parameters were selected based on prior literature and physical considerations to balance computational efficiency with near-equilibrium translocation behavior.23 ssDNA is therefore initially constructed in a canonical B-DNA-like helical, however it adopts a flexible, non-helical conformation during translocation.
To address the challenge of extracting meaningful insights from the complex, high-dimensional data generated by MD simulations, we employed principal component analysis (PCA) to reduce the dimensionality of atomic trajectories and uncover collective motions. Principal component analysis has been extensively applied to biomolecular dynamics, reducing the dimensionality of molecular dynamics trajectories to reveal collective motions, such as domain rearrangements, thereby enhancing the interpretability of complex conformational changes in biological systems.38–40 By projecting the trajectories onto a reduced set of principal components (PCs) that capture the dominant variances, PCA simplifies the analysis of large-scale motions while preserving key dynamic features.41,42 Principal component analysis can be applied to molecular dynamics trajectories or other structural ensembles to identify dominant modes of motion. The procedure typically involves three main steps. First, the configurations in the ensemble are superimposed to remove the overall rotational and translational motion, isolating internal fluctuations. This alignment is commonly performed by a least-squares fit of each configuration to a reference structure. Second, the aligned trajectory is used to construct a variance–covariance matrix of atomic positional fluctuations, where diagonal elements represent variances and off-diagonal elements represent covariances between atomic displacements. Diagonalization of this symmetric matrix yields eigenvectors (collective modes) and eigenvalues, which are typically ordered by decreasing eigenvalue magnitude. The eigenvalues quantify the variance associated with each mode, and in most cases, a small subset of modes captures the majority of the total fluctuation. Finally, the trajectory is projected onto selected principal components to facilitate visualization and interpretation. Two- or three-dimensional projections along the dominant components provide a reduced representation of the sampled configurational space and enable comparison between ensembles. These projections can also be back-transformed into cartesian coordinates to generate ensembles or animations illustrating motion along specific principal modes.
To investigate the correlated dynamics between the MSPA nanopore and translocating DNA during the sequencing process, we utilized dynamic cross-correlation (DCC)43 analysis enhanced by principal component analysis (PCA). Conventional DCC measures pairwise correlations in atomic displacements from molecular dynamics trajectories,44 given by
 | (1) |
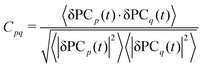 | (2) |
This PCA-augmented DCC approach allows us to elucidate how MSPA pore collective motions couple with DNA translocation modes, offering insights into the behavior of MSPA pore. The cross-correlation matrices, based on Pearson's correlation coefficients (CCpq), were employed to quantify correlated and anticorrelated motions along the molecular dynamics trajectory. The values of CCpq range from −1 (entirely anticorrelated motion) to +1 (fully correlated motion), with 0 indicating no correlation.
3 Results and discussion
On ultrashort (femtosecond) timescales, molecular dynamics are dominated by high-frequency bond vibrations, as atoms oscillate around their individual equilibrium positions. At longer (picosecond) timescales, the diffusion of atomic groups from their initial positions makes the molecule behave more dynamically. On the nanosecond timescales, molecules exhibit large-scale, global oscillatory motions. Molecular dynamics simulations can be difficult to evaluate due to the complexity of biomolecular systems, making it challenging to understand the motions of interest or to identify functional mechanisms. Often, principal component analysis (PCA), resolves this issue. It aims to statistically extract these collective motions from simulation trajectories. By focusing on the subspace in which the majority of atomic motion occurs, often called the essential subspace, PCA provides a reduced yet informative description of the molecule's dynamic behavior.38,403.1 First principal component (PC1)
In PCA, the original data are projected onto a new coordinate system defined by orthogonal axes (principal components), each ordered by the proportion of variance it explains. The cumulative explained variance (CEV) is defined as the variance captured within the subspace spanned by the first i eigenvectors, where i denotes the number of retained components. In practice, the CEV is typically visualized as a monotonically increasing curve, with the initial components accounting for the majority of variance and subsequent components contributing progressively less. We have calculated cumulative explained variance for the the different parts of MSPA pores: top barrel, upper barrel, lower barrel and pore exit and the ssDNA for all the four systems polyT, polyA, polyC and polyG. For the parts of MSPA pore, it is observed that top barrel and upper barrel of the pore exhibits a cumulative explained variance of approximately 0.7 after the first 20 principal components, whereas lower barrel and pore exit reaches a CEV greater than 0.9 within the same number of component. This is a typical behavior for large, flexible, or multi-domain systems.38,46 A higher CEV within a smaller number of components indicates that the dominant structural fluctuations are captured by a smaller subspace, reflecting more collective motions. Conversely, a lower CEV implies that the variance is distributed across many modes, suggesting more heterogeneous and less collective dynamics. The magnitude of CEV therefore provides physical insight into the degree of conformational organization and the complexity of the underlying dynamical processes. For ssDNA, the first principal component alone accounts for nearly the entire cumulative explained variance (∼1). This behavior arises because the ssDNA is subjected to a constant velocity along the negative z-direction, resulting in a highly collective and coherent motion. Consequently, almost all of the variation in the dataset is captured by a single dominant mode indicating that the imposed translational motion overrides internal dynamical fluctuations and leaves little contribution from higher principal components. The corresponding plots are provided in Fig. S4 of SI.To capture only the internal dynamics of the complex, each frame of the trajectory is root-mean-square (RMS) fitted to a reference structure obtained as the average structure from each MD run thereby removing overall rotational and translational motions. The cross-correlation matrices (normalized covariance matrices) were then computed from these covariance matrices. The first principal component (PC) represents the direction in the data space along which the variance is maximized, capturing the most significant pattern of variation in the dataset. In the context of molecular dynamics simulations, the first PC often corresponds to the most dominant collective motion of the system, such as large-scale conformational changes or global oscillations.
The first principal component is evaluated for distinct structural regions of the MSPA pore. To characterize the dominant rotational dynamics of the MSPA pore, we computed the angular momentum along the z-axis (Lz) projected onto the XY plane for the first principal component of each domain in Fig. 2(a). The results reveal distinct motions across the pore regions: the top, upper, and lower domains exhibit clockwise rotation, whereas the exit curl rotates counterclockwise. The strongest rotational contributions arise from the lower barrel and pore exit, with mean Lz values of −6.59 and 10.30, respectively, indicating significant motion in opposing directions. When these region-specific motions are considered collectively, the pore exhibits a striking “pepper-mill-like” dynamics, in which alternating clockwise and anticlockwise modes propagate along the pore axis as shown in Fig. 2(b). Such rotational behavior might facilitate the progressive translocation of ssDNA through the nanopore, acting as a mechanical aid to its movement. Also, the first principal component (PC1) of the translocating ssDNA displays a dominant motion along the negative z-direction, consistent with the directed pulling force applied during the simulation represented in Fig. 2(c).
3.2 Other principal components
To gain a deeper understanding of the internal dynamics of different pore regions, we calculated the second (PC2) and third (PC3) principal components for each structural segment of the pore. Interestingly, while the global principal components (derived from the entire pore) remain largely orthogonal representing well-separated collective modes of motion, the local principal components from individual subregions exhibit partial angular deviations from orthogonality. This deviation reflects the coupling of local fluctuations, where PC2 and PC3 collectively capture twisting or shearing motions within the β-barrel architecture rather than purely translational displacements. These rotational distortions can modulate the effective pore diameter and mechanical compliance of the translocation channel, suggesting that while the global modes describe overall pore stability, the local non-orthogonal motions from PC2–PC3 coupling represent intrinsic twisting and bending responses that enable dynamic adaptation to the translocating nucleic acid. This interplay between global rigidity and local twist flexibility highlights the mechanical sophistication essential for maintaining structural integrity while facilitating functional motion during the translocation process.3.3 Dynamic cross-correlation (DCC) analysis
Coupling between this collective motion in the pore and the translocating ssDNA can be examined in a more quantitative manner through the calculation of dynamic cross-correlations between different structural regions of the MSPA pore with the first principal components (PC1s) of the translocating ssDNA. In this analysis, the cross-correlation matrix provides a systematic measure of the relationship between the dominant motions of individual pore segments as well as their coupling with the translocating single-stranded DNA (ssDNA). In particular, the sign of the leading matrix element reflects whether the motions of two regions (or a region and the ssDNA) are aligned or opposed, thereby serving as an indicator of the directionality of their primary displacement modes. Fig. 2(d) presents the dynamic cross-correlation values between the first principal components (PC1s) of the translocating ssDNA and the PC1–PC3 components of the MSPA pore domains. The DNA strand first enters through the open barrel and subsequently interacts with the upper and lower barrels before finally exiting through the pore exit domain. At the start of translocation, the top and upper barrels exhibit synchronized motions with the DNA, showing correlation values of −0.90 and +0.95, respectively, with lower values observed for the PC2 and PC3 correlations. This means that as the ssDNA passes through the pore, the top barrel tends to move oppositely to the motion shown in Fig. 2a. Conversely, the upper barrel tends to move in the same direction as the motion shown in Fig. 2a. Following this, the lower barrel shows a strong anticorrelation (−0.81) with the strand, showing that the lower barrel tends to twist in an anticlockwise manner, opposite to the clockwise twist shown in Fig. 2a. Following this, a pronounced positive correlation of +0.70 between the DNA and the pore exit indicates that this domain twists in the anticlockwise direction shown in Fig. 2a as the translocating passes through. Interestingly, for these last two domains, the correlations of PC2 and PC3 are also significant, as shown in Fig. 2(d). This behavior suggests that both the lower barrel and the pore exit respond strongly to ssDNA translocation, as supported by the structural data discussed in Section 3.5.3.4 Pepper-mill dynamics in MSPA
The dynamic cross-correlation analysis reveals a sequence of structural responses during ssDNA translocation. The DNA first enters through the top barrel and then interacts with the upper and lower barrels, but the strongest contact emerges at the pore exit. This region shows a pronounced positive correlation with the DNA PC1, indicating that it adapts its collective motion to the advancing strand. Following this, the lower barrel (connected to the pore exit) exhibits a strong anticorrelation with the strand, suggesting a compensatory twisting motion in response to the rotation of the pore exit region. The upper and top barrels show synchronized but anticorrelated motions with each other. This counter-rotating behavior supports a pepper-mill-like dynamics, in which the four structural domains of the MSPA protein operate in concert in response to ssDNA passage. We propose that this coordinated motion originates at the pore exit and propagates upward through the protein structure, ensuring an efficient and mechanically coupled translocation process. Moreover, this coordinated pepper-mill motion does not occur in the absence of translocating DNA (see Section S5 of the SI).Fig. 3 presents the resulting cross-correlation matrices among the pore regions. Significant positive correlations are observed between the top barrel and lower barrel regions, indicating that these segments tend to move in a coordinated manner. In contrast, the upper barrel exhibits strong negative correlations with both the top and lower barrels, suggesting that its motion is anticorrelated with these regions. The pore exit also shows negative correlations with the lower barrel and top barrel regions, while displaying a positive correlation with the upper barrel. This intricate pattern of correlations further highlighting the complex interplay of motions within the pore architecture. Overall, the cross-correlation analysis reveals a sophisticated pattern of coordinated and anticorrelated dynamics among the different pore segments, which likely plays a crucial role in facilitating the translocation of ssDNA through the nanopore. These results highlight how local torsional dynamics is coordinated across the pore architecture and reveal the degree to which pore motions may assist the passage of ssDNA. The combined dynamic cross-correlation and principal component analyses offer a detailed depiction of how various regions of the MspA nanopore move relative to one another, revealing the intricate interplay of internal motions that culminate in the characteristic pepper-mill dynamics of the pore. The cross-correlation of PC2 and PC3 between pore regions is complex because local twisting and bending motions are coupled but not uniform. Some domains move in concert, while others exhibit opposing deformations, reflecting differences in flexibility, steric constraints, and interactions with the translocating ssDNA. This interplay of reinforcing and counteracting motions produces intricate correlation patterns that enable dynamic adaptation of the pore while preserving overall structural integrity. The reported rotational behavior reflects internal collective fluctuations captured by principal component analysis, rather than sustained rigid-body rotation, and therefore does not indicate the presence of a net torque.
3.5 Structural analysis
The root-mean-square deviation (RMSD) analysis is performed for the entire MSPA pore protein to monitor its structural stability throughout the simulation in Fig. 4(a). The overall RMSD profile indicates that the protein maintains a stable conformation, particularly within the lower, upper and top barrel regions. However, the pore exit region exhibited comparatively higher RMSD values, suggesting enhanced flexibility or local structural rearrangements at this site. This increased mobility can be attributed to the interaction between the pore exit residues and the translocating single-stranded DNA. As the DNA passes through the channel, it induces local structural adjustments and transient contacts with the pore-lining residues, leading to higher RMSD values in this region. Such enhanced dynamics at the pore exit likely facilitate the accommodation and release of the translocating strand, reflecting the functional flexibility required for efficient transport.To complement the RMSD analysis, the number of contacts between different regions of the MSPA pore and the translocating ssDNA was quantified throughout the simulation in Fig. 4(b). The results revealed that the pore exit formed a markedly higher number of contacts with the ssDNA compared to the lower, upper and top barrel regions, consistent with its greater structural flexibility. The contact map displayed a distinct oscillatory pattern, characterized by periodic increases and decreases in contact numbers over time. This fluctuation likely reflects the stepwise translocation of ssDNA, during which the strand transiently interacts with and subsequently disengages from the pore-lining residues as it advances through the channel. We suggest that between steps the lower barrel and pore exit show the opposing clockwise-anticlockwise twisting motions shown in Fig. 2a. Conversely, when ssDNA undergoes a downward step, the lower barrel adopts an anticlockwise twising motion, aligning with the pore exit, as suggested by the opposing correlations in Fig. 2d. Such dynamic binding-release behavior highlights the coupled motion between the ssDNA and the pore exit, emphasizing the functional importance of local flexibility in facilitating smooth and efficient strand translocation.
The pore radius profiles were calculated for each region of the MSPA pore to assess local structural flexibility during ssDNA translocation, as shown in Fig. 4(c). The analysis revealed that the pore exit region exhibited the most pronounced fluctuations in radius over time, indicating enhanced flexibility compared to the lower, upper, and top barrel regions. This increased variability in pore radius at the exit likely reflects local conformational adjustments that accommodate the translocating ssDNA strand. As the DNA passes through the channel, the pore exit residues may undergo transient expansions and contractions to facilitate strand passage. In contrast, the lower, upper, and top barrel regions displayed relatively stable radius profiles, suggesting a more rigid structural framework. The differential flexibility observed across the pore architecture highlights the functional specialization of the pore exit in enabling efficient ssDNA translocation through dynamic structural adaptations. Here, we present only polyA as a representative case, and the selection of this system is independent of the observed dynamics. The results for other polynucleotides and more detailed analysis are provided in the Section S6–S13 of the SI.
In Fig. 4(d), we further investigated the dwell time associated with the translocation of homonucleotide single-stranded DNA (ssDNA) through the nanopore. The measured dwell times for the four nucleotides exhibited a clear and consistent trend, following the order guanine > adenine > cytosine > thymine. This trend aligns with expectations based on the intrinsic physicochemical properties of the nucleotides, such as base stacking interactions, hydrogen bonding potential, and hydrophobicity, which influence their interactions with the nanopore and consequently their translocation kinetics.47,48 Guanine, with the largest aromatic surface area and strongest stacking interactions, exhibited the longest dwell time, indicating a greater interaction with the nanopore environment. Adenine and cytosine displayed intermediate dwell times, reflecting moderate interactions, while thymine, with the weakest base-stacking and hydrophobic interactions, translocated the fastest. These observations highlight the important role of nucleotide-specific interactions in modulating ssDNA dynamics during nanopore translocation.
4 Conclusions
In summary, molecular dynamics simulations combined with principal component analysis (PCA) and dynamic cross-correlation (DCC) analysis were employed to elucidate the atomic-scale mechanistic details of the ssDNA translocation process through the MSPA nanopore. The collective motions derived from PCA and the correlated residue dynamics captured in the DCC matrix reveal that MSPA operates through a “pepper-mill”-like rotational mechanism that couples with the passing ssDNA strand. Investigation of the pore exit region further highlights its critical contribution to modulating translocation dynamics and selectivity. Dwell time analyses corroborate the pore's distinct responsiveness toward different polynucleotide types, underscoring its intrinsic ability to discriminate between molecular species. Together, these findings provide new mechanistic insights into the dynamic behaviour of the MSPA pore and establish a procedure for understanding and engineering nanopores with enhanced selectivity and functional control.Author contributions
P. Dey: conceptualization, methodology, formal analysis, investigation, writing – original draft, visualization. B. Meza-González: conceptualization, formal analysis, investigation, writing – original draft, visualization. D. Packwood: conceptualization, resources, supervision, writing – review & editing. G. N. Pandian: resources, supervision.Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study, including molecular dynamics trajectories, analysis scripts, and processed datasets, are available from the corresponding author upon reasonable request.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5cp04174k.
Supplementary data has been deposited with Protein Data Bank.49
Acknowledgements
This work was supported by the JST K Program (grant number JPMJKP23H4) and the Kyoto University OnSite Lab Program.References
- M. Kukwikila and S. Howorka, Anal. Chem., 2015, 87, 9149–9154 Search PubMed
.
- X. Chen, G. M. Roozbahani, Z. Ye, Y. Zhang, R. Ma, J. Xiang and X. Guan, ACS Appl. Mater. Interfaces, 2018, 10, 11519–11528 CrossRef CAS PubMed
.
- S. Rauf, L. Zhang, A. Ali, Y. Liu and J. Li, ACS Sens., 2017, 2, 227–234 Search PubMed
.
- M. Wanunu, T. Dadosh, V. Ray, J. Jin, L. McReynolds and M. Drndić, Nat. Nanotechnol., 2010, 5, 807–814 Search PubMed
.
- A. H. Laszlo, I. M. Derrington, B. C. Ross, H. Brinkerhoff, A. Adey, I. C. Nova, J. M. Craig, K. W. Langford, J. M. Samson and R. Daza,
et al.
, Nat. Biotechnol., 2014, 32, 829–833 CrossRef CAS PubMed
.
- C. J. W. H.-C. Jayasinghe, Nat. Nanotechnol., 2009, 4, 265–270 CrossRef PubMed
.
- J. A. Cracknell, D. Japrung and H. Bayley, Nano Lett., 2013, 13, 2500–2505 CrossRef CAS PubMed
.
- P. R. Singh, I. Barcena-Uribarri, N. Modi, U. Kleinekathofer, R. Benz, M. Winterhalter and K. R. Mahendran, ACS Nano, 2012, 6, 10699–10707 Search PubMed
.
- Q. Zhao, R. S. S. de Zoysa, D. Wang, D. A. Jayawardhana and X. Guan, J. Am. Chem. Soc., 2009, 131, 6324–6325 CrossRef CAS PubMed
.
- B. Cressiot, L. Bacri and J. Pelta, Small Methods, 2020, 4, 2000090 Search PubMed
.
- S. Howorka, S. Cheley and H. Bayley, Nat. Biotechnol., 2001, 19, 636–639 CrossRef CAS PubMed
.
- S. Wen, T. Zeng, L. Liu, K. Zhao, Y. Zhao, X. Liu and H.-C. Wu, J. Am. Chem. Soc., 2011, 133, 18312–18317 CrossRef CAS PubMed
.
- R. F. Purnell and J. J. Schmidt, ACS Nano, 2009, 3, 2533–2538 CrossRef CAS PubMed
.
- T. Z. Butler, M. Pavlenok, I. M. Derrington, M. Niederweis and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20647–20652 CrossRef CAS PubMed
.
- M. Faller, M. Niederweis and G. E. Schulz, Science, 2004, 303, 1189–1192 CrossRef CAS PubMed
.
- I. M. Derrington, T. Z. Butler, M. D. Collins, E. Manrao, M. Pavlenok, M. Niederweis and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16060–16065 CrossRef PubMed
.
- A. H. Laszlo, I. M. Derrington, H. Brinkerhoff, K. W. Langford, I. C. Nova, J. M. Samson, J. J. Bartlett, M. Pavlenok and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18904–18909 CrossRef CAS PubMed
.
- E. A. Manrao, I. M. Derrington, A. H. Laszlo, K. W. Langford, M. K. Hopper, N. Gillgren, M. Pavlenok, M. Niederweis and J. H. Gundlach, Nat. Biotechnol., 2012, 30, 349–353 CrossRef CAS PubMed
.
- E. A. Manrao, I. M. Derrington, M. Pavlenok, M. Niederweis and J. H. Gundlach, PLoS One, 2011, 6, e25723 Search PubMed
.
- M. Akeson, D. Branton, J. J. Kasianowicz, E. Brandin and D. W. Deamer, Biophys. J., 1999, 77, 3227–3233 Search PubMed
.
- A. F. Sauer-Budge, J. A. Nyamwanda, D. K. Lubensky and D. Branton, Phys. Rev. Lett., 2003, 90, 238101 CrossRef PubMed
.
- J. Comer and A. Aksimentiev, J. Phys. Chem. C, 2012, 116, 3376–3393 CrossRef CAS PubMed
.
- T. Diederichs, K. Ahmad, J. R. Burns, Q. H. Nguyen, Z. S. Siwy, M. Tornow, P. V. Coveney, R. Tampé and S. Howorka, ACS Nano, 2021, 15, 16194–16206 Search PubMed
.
- A. Gubbiotti, M. Baldelli, G. Di Muccio, P. Malgaretti, S. Marbach and M. Chinappi, Adv. Phys.: X, 2022, 7, 2036638 Search PubMed
.
- A. Sauciuc, B. Morozzo della Rocca, M. J. Tadema, M. Chinappi and G. Maglia, Nat. Biotechnol., 2024, 42, 1275–1281 CrossRef CAS PubMed
.
- S. Bhattacharya, I. M. Derrington, M. Pavlenok, M. Niederweis, J. H. Gundlach and A. Aksimentiev, ACS Nano, 2012, 6, 6960–6968 CrossRef CAS PubMed
.
- M. Pavlenok, I. M. Derrington, J. H. Gundlach and M. Niederweis, PLoS One, 2012, 7, e38726 Search PubMed
.
- A. Alenaizan, J. L. Barnett, N. V. Hud, C. D. Sherrill and A. S. Petrov, Nucleic Acids Res., 2021, 49, 79–89 Search PubMed
.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 Search PubMed
.
- K. Murzyn, T. Róg and M. Pasenkiewicz-Gierula, Biophys. J., 2005, 88, 1091–1103 CrossRef CAS PubMed
.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 Search PubMed
.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed
.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed
.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha,
et al.
, J. Phys. Chem. B, 1998, 102, 3586–3616 Search PubMed
.
- T. Darden, D. York and L. Pedersen,
et al.
, J. Chem. Phys., 1993, 98, 10089 Search PubMed
.
-
P. H. Hünenberger, Advanced computer simulation: Approaches for soft matter sciences I, 2005, pp. 105–149 Search PubMed
.
- S. Park, F. Khalili-Araghi, E. Tajkhorshid and K. Schulten, J. Chem. Phys., 2003, 119, 3559–3566 Search PubMed
.
- S. Moradi, A. Nowroozi, M. Aryaei Nezhad, P. Jalali, R. Khosravi and M. Shahlaei, Comput. Biol. Med., 2024, 183, 109245 CrossRef CAS PubMed
.
- J. P. B. Arango, D. Y. M. Rodriguez, S. L. Cruz and G. T. Ocampo, Comput. Biol. Chem., 2026, 120, 108626 CrossRef CAS PubMed
.
- T. Yasuda, Y. Shigeta and R. Harada, J. Chem. Inf. Model., 2020, 60, 4021–4029 CrossRef CAS PubMed
.
-
S. Bowerman and J. Wereszczynski, Detecting Allosteric Networks Using Molecular Dynamics Simulation, Elsevier, 2016, pp. 429–447 Search PubMed
.
- D. M. Packwood and P. Pattanasattayavong, J. Phys.: Condens. Matter, 2020, 32, 275701 CrossRef CAS PubMed
.
- K. Kasahara, I. Fukuda and H. Nakamura, PLoS One, 2014, 9, e112419 Search PubMed
.
- P. Hünenberger, A. Mark and W. van Gunsteren, J. Mol. Biol., 1995, 252, 492–503 Search PubMed
.
- D. K. Brown, D. L. Penkler, O. Sheik Amamuddy, C. Ross, A. R. Atilgan, C. Atilgan and O. Tastan Bishop, Bioinformatics, 2017, 33, 2768–2771 Search PubMed
.
-
S. A. M. Stein, A. E. Loccisano, S. M. Firestine and J. D. Evanseck, Principal Components Analysis: A Review of its Application on Molecular Dynamics Data, Elsevier, 2006, ch. 13, pp. 233–261 Search PubMed
.
- H. S. Martin, S. Jha and P. V. Coveney, J. Comput. Chem., 2014, 35, 692–702 CrossRef CAS PubMed
.
- J. Li, Y. Zhang, J. Yang, K. Bi, Z. Ni, D. Li and Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062707 CrossRef PubMed
.
- M. Faller, M. Niederweis and G. E. Schulz, Science, 2004, 303, 1189–1192 Search PubMed
.
| This journal is © the Owner Societies 2026 |



