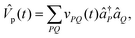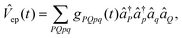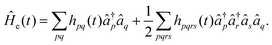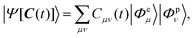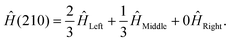Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Approximate quantum circuit compilation for proton-transfer kinetics on quantum processors
Arseny Kovyrshin *ab,
Dilhan Manawadu
*ab,
Dilhan Manawadu c,
Edoardo Altamuracd,
George Penningtonc,
Benjamin Jaderberge,
Sebastian Brandhoferf,
Anton Nykäneng,
Aaron Millergh,
Walter Talaricogi,
Stefan Knecht
c,
Edoardo Altamuracd,
George Penningtonc,
Benjamin Jaderberge,
Sebastian Brandhoferf,
Anton Nykäneng,
Aaron Millergh,
Walter Talaricogi,
Stefan Knecht g,
Fabijan Pavošević
g,
Fabijan Pavošević g,
Alberto Baiardij,
Francesco Tacchino
g,
Alberto Baiardij,
Francesco Tacchino j,
Ivano Tavernelli
j,
Ivano Tavernelli j,
Stefano Mensac,
Jason Crainkl,
Lars Tornberg
j,
Stefano Mensac,
Jason Crainkl,
Lars Tornberg a and
Anders Broo
a and
Anders Broo a
a
aPredictive Science, Digital and Automation, Pharmaceutical Sciences, R&D, AstraZeneca Gothenburg, Pepparedsleden 1, Molndal SE-431 83, Sweden. E-mail: arseny.kovyrshin@astrazeneca.com
bDepartment of Microtechnology and Nanoscience, Chalmers University of Technology, Gothenburg SE-412 96, Sweden
cThe Hartree Centre, STFC, Sci-Tech Daresbury, Warrington WA4 4AD, UK
dYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
eIBM Quantum, IBM Research Europe, Hursley, Winchester SO21 2JN, UK
fIBM Quantum, IBM Germany Research & Development, Böblingen, Germany
gAlgorithmiq Ltd., Kanavakatu 3C, FI-00160 Helsinki, Finland
hSchool of Physics, Trinity College Dublin, College Green, Dublin 2, Ireland
iQTF Centre of Excellence, Department of Physics, University of Helsinki, P.O. Box 43, FI-00014 Helsinki, Finland
jIBM Quantum, IBM Research Zürich, 8803 Rüschlikon, Switzerland
kIBM Research Europe, The Hartree Centre, STFC, Sci-Tech Daresbury, Warrington WA4 4AD, UK
lClarendon Laboratory, University of Oxford, Oxford OX1 3PU, UK
First published on 14th January 2026
Abstract
Proton transfer reactions are central to chemical and biological systems, where quantum effects—such as tunneling, delocalization, and zero-point motion—critically influence reaction kinetics. Classical methods that capture these phenomena scale poorly with system size, limiting their applicability. Here, we extend and benchmark a quantum computing framework based on the Nuclear–Electronic Orbital formalism, treating the transferring proton quantum mechanically, to assess the feasibility of computing accurate energy barriers on current quantum devices. Using malonaldehyde as a prototypical system, we construct deep initial circuits via ADAPT-VQE combined with the frozen natural orbital approximation and apply adaptive approximate quantum compiling to balance circuit depth and fidelity. Transpiling these circuits for the ibm_pittsburgh device and simulating with realistic noise models, we compute barrier heights and delocalized proton densities along the reaction pathway. Circuit refinement and compression yield compact representations that preserve essential quantum features of the transfer process. Notably, our shallowest circuits (AQC-low) reproduce key qualitative features, such as proton density localization, and are near the frontier of feasibility for current hardware. In contrast, deeper circuits (AQC-high) retain higher fidelity to reference barrier height, reducing the error to 1.6 mHa (13%) while still yielding a 98% underestimation of the rate constant at 120 K.
I. Introduction
Proton transfer plays a crucial role in many physical and biochemical processes. For example, several enzymes, particularly those involved in metabolic pathways, use proton transfer as part of the catalytic cycle.1 Kinases,2 oxidoreductases,3 and dehydrogenases4 rely on the transfer of protons between the residues of the active site to catalyze reactions. Coupled proton and electron transfers are known to be important for drugs targeting mitochondrial function or redox-based mechanisms,5 and their rates can influence the overall reactivity and efficiency of drug candidates targeting redox enzymes. Similarly, proton transfer can be the rate-determining step in enantioselective reactions involving chiral substrates.6Typically, the reaction rates k(T) of these proton transfer processes at a temperature T are related to the barrier height Eb by an Arrhenius law k(T) ∝ e−Eb/RT, which assumes that the mobile nuclei behave classically.7 Given such exponential sensitivities, accurate prediction of the proton transfer energy barriers involved is critical for rate control and in the design of reactions that favor one pathway over another. However, a significant complexity arises because proton transfer often involves light nuclei, for which the classical approximation fails, leading to deviations from the classical Arrhenius behavior due to quantum mechanical phenomena such as zero-point energy, nuclear delocalization and tunneling. Consequently, reactions proceed at rates inconsistent with classical transition state theory. In these circumstances, treating the labile protons quantum mechanically is necessary to recover physically realistic models.
Several theoretical approaches have been developed over the past decades that can accurately describe proton transfer;8,9 however, they are mainly based on trajectories (quantum or classical) or on the quantization of vibrational modes. The nuclear–electronic orbital (NEO) approach,10,11 on the other hand, has emerged as a computationally efficient alternative for capturing nuclear quantum effects using localized basis functions. In the NEO method, both electrons and selected transferring protons are treated quantum mechanically with a molecular orbital theory approach. Therefore, the NEO framework offers an ideal computational platform for the simulation of proton transfer processes12–16 on a quantum computer. These simulations typically rely on multicomponent density functional theory (DFT) mean-field method17–19 either in the context of real-time NEO time-dependent density functional theory (RT–NEO–TDDFT)12 and RT–NEO–TDDFT Ehrenfest dynamics13 or multi-state NEO density functional theory (NEO–MSDFT).20 Due to the well-known limitations of currently available electron–electron21 and electron–proton functionals,18,19 these methods do not provide adequate accuracy to meet practical experimental demands22 (below 1 kcal mol−1), providing the impetus for the development of NEO methods of much higher accuracy.
On classical computers, the resources required for exact solutions of NEO-based models grow exponentially with system size.11 By contrast, advances in quantum computing technology and algorithm developments have opened a path for solving this problem nearly exactly on quantum devices in a more efficient way.23–28 As fault-tolerant quantum computing (FTQC) remains a prospect, algorithms tailored to address the challenges posed by noisy intermediate-scale quantum (NISQ)29 hardware are currently being developed.
In this work, we extend the recently developed NEO framework for modelling proton transfer reactions.27 First, we enhance the physical realism of the model by employing larger basis sets, the frozen natural orbitals (FNO) approach, and by accounting for scaffold relaxation effects. Second, we use the adaptive derivative-assembled pseudo-Trotter ansatz variational quantum eigensolver (ADAPT-VQE) algorithm for efficient wavefunction parametrization,30 followed by circuit compression using approximate quantum compiling (AQC),31–33 enabling applications on noisy intermediate-scale quantum (NISQ) hardware. Third, the resulting circuits, at varying levels of compression, are then used to simulate adiabatic proton transfer in the malonaldehyde molecule,27 with a focus on computing the transfer barrier in the presence of quantum nuclei.
II. Theory
We investigate the quantum dynamics of proton transfer in malonaldehyde using a time-dependent quantum simulation framework. Rather than a static description, this approach captures the evolution of both electronic and nuclear degrees of freedom, guided along a well-defined, chemically relevant proton transfer pathway. The core of our approach is to solve the time-dependent Schrödinger equation (TDSE) for the coupled proton–electron system, leveraging the NEO framework. In Section II A we describe the TDSE without going into details regarding the actual molecular setup, which will be covered in Section II B.A. Coupled electron–proton dynamics
The dynamics of the system is governed by the TDSE
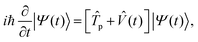 | (1) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) p is the kinetic energy operator for the proton, and
p is the kinetic energy operator for the proton, and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) is a time-dependent potential incorporating both the proton's interaction with its environment and the coupling between protonic and electronic components. The explicit time dependence in
(t) is a time-dependent potential incorporating both the proton's interaction with its environment and the coupling between protonic and electronic components. The explicit time dependence in ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) arises from our protocol for steering the system Hamiltonian along the reaction pathway, as described in Section II B. The total time-dependent potential is given by
(t) arises from our protocol for steering the system Hamiltonian along the reaction pathway, as described in Section II B. The total time-dependent potential is given by![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) = (t) = ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) p(t) + p(t) + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ep(t) + Ĥe(t) ep(t) + Ĥe(t) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) p(t) describes the time-dependent interaction of the proton with the classical nuclear scaffold,
p(t) describes the time-dependent interaction of the proton with the classical nuclear scaffold, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ep(t) is the proton–electron interaction, and Ĥe(t) defines the electronic Hamiltonian contribution. Specifically, the proton–classical–nuclear interaction is represented in second quantization as
ep(t) is the proton–electron interaction, and Ĥe(t) defines the electronic Hamiltonian contribution. Specifically, the proton–classical–nuclear interaction is represented in second quantization asThe coupling between protonic and electronic degrees of freedom is written as
and the purely electronic part is given by
In this work, the lower case p, q, r, s indices denote general electronic spin orbitals, whereas the upper case indices denote protonic spin orbitals. The operators â†p and âp are creation and annihilation operators which satisfy the normal Fermionic anticommutation relations. The explicit time dependence of integrals vPQ(t), gPQpq(t), hpq(t), and hpqrs(t) arises from the fact that the underlying electronic molecular orbitals are defined with reference to a representative proton transfer pathway (see Section II B for more details). This prescribed evolution of the electronic orbitals steers the quantum dynamics of both the electronic and protonic degrees of freedom.
For the time-dependent wave function with protonic (nuclear) and electronic components |Φpν〉 and |Φeμ〉 respectively, we write
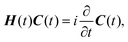 | (2) |
Hκλ,μν(t) = 〈Φeκ| 〈Φpλ|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) p + p + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t)|Φeμ〉 |Φpν〉. (t)|Φeμ〉 |Φpν〉.
| (3) |
The rate of change of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (t) determines whether the system is in the adiabatic or non-adiabatic regime. Previously, Kovyrshin et al. (2023)27 explored dynamics through Suzuki decomposition in both cases. While highly accurate, this approach requires quantum circuits of substantial depth for time evolution—a limitation for near-term quantum hardware.
(t) determines whether the system is in the adiabatic or non-adiabatic regime. Previously, Kovyrshin et al. (2023)27 explored dynamics through Suzuki decomposition in both cases. While highly accurate, this approach requires quantum circuits of substantial depth for time evolution—a limitation for near-term quantum hardware.
To address these computational challenges, we adapt our protocol for compatibility with variational quantum algorithms, specifically the variational quantum eigensolver (VQE),34 thus extending the application of VQE to simulation of dynamics in the adiabatic regime. Rather than simulating explicit real-time evolution according to eqn (2), we approximate the time-dependent energy and wavefunction variationally at each point along the reaction pathway; that is, at each time, the energy and ground state of the instantaneous proton–electron Hamiltonian are obtained by minimizing
 | (4) |
Hence eqn (2) is introduced for context, but the quantum dynamics are simulated by variational minimization rather than explicit numerical integration. Although limited to the adiabatic regime—i.e., evolution under a slowly varying time-dependent Hamiltonian—this strategy allows for quantum simulation of proton transfer using compact variational ansätze of nearly constant size. This makes the problem tractable on near-term devices while still incorporating electron–proton coupling and capturing key quantum effects such as zero-point energy and proton delocalization.
B. Malonaldehyde setup
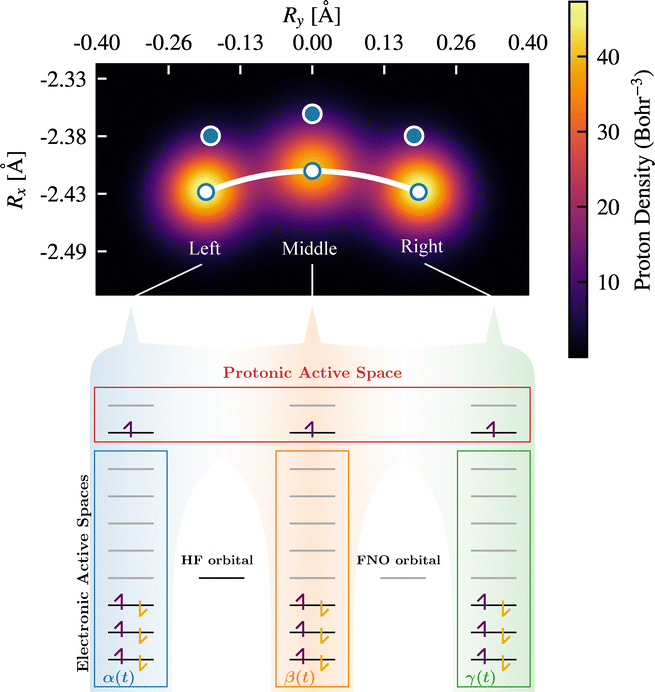
The process of proton-coupled electron transfer (PCET) in malonaldehyde,35 a prototypical model for enantioselective isomerization, has been previously studied by Kovyrshin et al.27 in adiabatic and nonadiabatic limits. That study served as a proof-of-concept demonstration, which was limited to near-minimal electronic and nuclear basis sets. In this work, we focus on enhancing the physical realism of the model to obtain quantitatively accurate results comparable to experimental measurements. This is done by employing a larger basis set for electronic and protonic orbitals (see Appendix A), allowing scaffold relaxation,35 and leveraging the FNO technique.30 Next, we describe the procedures for generating the set of molecular orbitals needed to represent the system and for modelling the proton transfer through the adiabatic steering of the system Hamiltonian.Similarly to, ref. 27, we describe the dynamics of proton transfer by first generating the structure of the molecule at three stationary points along a predefined reaction path. These describe the initial (Left), transition (Middle) and final (Right) states respectively. These structures and their corresponding molecular orbitals, which are needed to model the system, are obtained in three steps.
First, the three possible positions for the H atom and the corresponding scaffolds are modelled within the Born–Oppenheimer approximation, treating all nuclei as classical point particles. This is done using second-order Møller–Plesset (MP2) theory, which yields the fully optimised structure under the Cs point-group symmetry (see Appendix A for basis set specifications). The corresponding geometries are provided in Table 4 in Appendix B. Thus, in contrast to ref. 27, our setup includes scaffold relaxation upon proton transfer. The resulting proton positions (see blue points in Fig. 1 and Table 5 in Appendix B) serve as a good initial guess for the subsequent step where we go beyond the Born–Oppenheimer approximation by treating the transferring proton quantum mechanically. Second, we perform one nuclear–electronic orbital Hartree–Fock (NEO-HF) calculation per scaffold, keeping the protonic orbitals centered at these positions. This step yields the occupied protonic and electronic molecular orbitals for the system. Third, to obtain more accurate virtual orbital space (i.e., unoccupied orbitals), a higher accuracy method—NEO–MP2—is used to generate the corresponding NEO–FNO orbitals (see Section III B for more details).
The construction of the orbitals for the Right, Middle and Left configurations enables us to define a Hamiltonian which represents a changing external potential in which the proton under study evolves. In order to describe this situation, we construct the three Hamiltonian operators in second quantization based on the sets of protonic and electronic orbitals derived above. The protonic active space (AS) was chosen to contain two orbitals from Left, Middle, and Right setups, and is shared among the three Hamiltonians. Specifically, one occupied NEO-HF and one FNO orbital from each setup result in 6 protonic orbitals. As these orbitals originate from separate calculations, they are not orthogonal, and a Löwdin orthogonalization procedure36 was performed before inclusion of these to protonic (AS). While the same protonic AS was used for all Hamiltonians, the three different electronic AS were comprised of 3 NEO-HF and 5 FNO orbitals from Left, Middle, and Right configurations (the 16 lowest occupied orbitals were considered frozen). Thus, the protonic and electronic active spaces were doubled in size compared to ref. 27, and six electrons were considered in the active space instead of four. A schematic representation of the active spaces is shown in the lower part of Fig. 1.
First, we benchmark the combined effect of these methodological improvements by comparing active space configuration interaction (CASCI) energies computed for the Left and Middle Hamiltonians using our current approach, FNO–NEO–CASCI, with the results from Ref. 27, referred to as NEO–CASCI. In Table 1 we list the calculated energy barrier, ΔE = EM − EL/R, for the two methods along with the experimental and semi-empirical values for comparison. We find that FNO–NEO–CASCI doubles the proton transfer barrier compared to ref. 27, yielding a value of 11.9 mHa. This value falls between the experimentally inferred estimate of approximately 13.5 mHa37 and the semi-empirical model-derived value of approximately 11.2 mHa.38 The former is based on a broad IR absorption near 2960 cm−1 tentatively attributed to motion along the proton transfer coordinate. Notably, the Born–Oppenheimer approximation systematically overestimates the barrier,27,39 yielding 16.4 mHa when applied in CASCI with the current basis set and structures (see Table 1).† In addition, we observe an effect on proton–electron entanglement within the system. The entanglement entropy is calculated from the single-proton reduced density matrix, obtained by tracing out the electronic degrees of freedom, for the Left, Middle, and Right ground states. As shown in Table 1, a considerable increase in entanglement is observed for the Middle state, while Left and Right states show only minor improvements. This indicates that the new framework, FNO–NEO–CASCI, is better suited to capturing proton–electron entanglement compared to NEO–CASCI.27
To assess the spatial delocalization arising from the quantum treatment of the proton, we analyze the protonic density and deviation from the classical reference position. Specifically, we evaluate the protonic densities and the expectation values of the proton position operator from a protonic one-particle density matrix constructed for Left, Middle, and Right FNO–NEO–CASCI states (see Fig. 1). The corresponding proton densities reveal a strongly delocalised character across all three setups, emphasizing the inadequacy of a purely classical treatment. The expectation values for the proton position (white points in Fig. 1 and Table 5) exhibit substantial displacement from the original centres of protonic basis functions—i.e., the classical reference positions. These findings highlight the importance of quantum nuclear effects where proton motion plays a central role.
With the Left, Middle, and Right Hamiltonians prepared (see Appendix A for more details), we now define the time-dependent Hamiltonian for the system
| H(t) = α(t)HLeft + β(t)HMiddle + γ(t)HRight. | (5) |
C. Transition rate constant
To highlight the importance of accurately estimating the reaction barrier, it is useful to demonstrate its effect on reaction kinetics. The temperature-dependent rate constant for proton transfer, incorporating quantum nuclear effects via the NEO method, can be computed using a transition state theory (TST) expression7
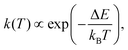 | (6) |
III. Methods
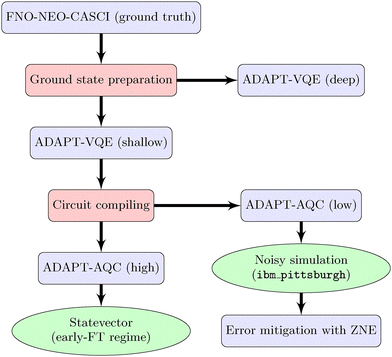
The methods presented in this section detail the computational pipeline used to simulate quantum proton transfer dynamics in malonaldehyde. We begin with a schematic overview of our multi-stage workflow, which integrates accurate ab initio reference calculations, variational quantum algorithms, circuit compression, and error mitigation techniques. Subsequent subsections provide in-depth descriptions of the ADAPT-VQE method for quantum wavefunction preparation, the frozen natural orbital concept, the adaptive approximate quantum compiling (ADAPT-AQC) approach for circuit depth reduction, and the implementation of zero-noise extrapolation (ZNE) to address the effects of hardware noise in realistic quantum simulations.A. Pipeline overview
The computational workflow for simulating quantum proton transfer dynamics in malonaldehyde is illustrated in Fig. 2. Our pipeline integrates high-level ab initio electronic structure theory with state-of-the-art quantum algorithms, ensuring both accuracy and practical feasibility for near-term quantum hardware. The steps are as follows.First, we compute ground-state energies using the FNO–NEO–CASCI approach described in Section II B, which we refer to as CASCI in the following. This provides a reliable theoretical reference for benchmarking proton transfer barriers and quantum simulation outcomes.
Next, the ADAPT-VQE (see Section III B for details) is used to prepare quantum circuits representing the ground-state wavefunction for the time-dependent Hamiltonian at different times. This procedure is carried out at two distinct accuracy thresholds: an energy error of 10−3 Ha and a less conservative value of 10−2 Ha, relative to the CASCI reference energy. The selected convergence threshold affects the required circuit depth, balancing computational accuracy and quantum hardware feasibility. The resulting deep circuit, VQE-deep, will be used as a benchmark to represent the early fault-tolerant regime, whereas the shallow circuits, VQE-shallow, will be further compressed as described below. To ensure compatibility with near-term quantum devices, where circuit depth and gate error rates are critical constraints, we further compress the ADAPT-VQE circuits utilizing ADAPT-AQC.41 This procedure significantly reduces circuit depth at the cost of a further accuracy trade-off. The method provides control over the level of compression tailored to different hardware capabilities. In our specific case, we produce both high- and low-fidelity compiled circuits, denoted AQC-high and AQC-low.
The compiled circuits are subsequently simulated in two regimes: (1) the high-fidelity circuit is used in an ideal, noiseless statevector simulator (representative of the early fault-tolerant quantum era), and (2) the low-fidelity circuit is used under realistic noise models based on the ibm_pittsburgh Heron processor, which includes comprehensive device imperfections (see Appendix C for details). For the latter, we apply ZNE, an error mitigation protocol, to recover expectation values closer to the noise-free limit.
The following sections provide further details for the ADAPT-VQE, FNO, ADAPT-AQC, and ZNE techniques.
B. ADAPT-VQE with NEO–FNO pool
At the core of our quantum simulation protocol is the ADAPT-VQE algorithm,30 applied to a pool of the NEO excitation operators spanning the space defined by the FNO approach. It is used to approximate the ground state wavefunction |Ψ[C(t)]〉 for each time-dependent Hamiltonian along the adiabatic trajectory. This method, detailed in ref. 30, delivers a wave function with a compact circuit and high accuracy; we briefly review it below. As an extension of its electronic counterpart,42 it bears similar features: the wavefunction ansatz is built iteratively by adding operators from a pool comprising single and double electronic, protonic, and mixed Fermionic excitations:| τμ ∈ {aai − aia, aAI − aIA, aabij − aijab, aABIJ − aIJAB, aaAiI − aiIaA}, |
| |Ψ(n)ADAPT-VQE〉 = eθnτn…eθ2τ2eθ1τ1|0e0p〉 | (7) |
| γba = 〈ΨNEO|aba|ΨNEO〉 |
| γBA = 〈ΨNEO|aBA|ΨNEO〉 |
C. Circuit compression with approximate quantum compiling
The quantum circuits constructed via ADAPT-VQE, while compact relative to traditional approaches, may still exceed the limitation of current quantum hardware, particularly in two-qubit gate depth. To further reduce circuit depth, we apply ADAPT-AQC.41,49 In this variational approach, a parameterised circuit![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (θ)|0〉 is optimised to approximate the target ADAPT-VQE state by minimizing the fidelity-based cost function
(θ)|0〉 is optimised to approximate the target ADAPT-VQE state by minimizing the fidelity-based cost function
C = 1 − |〈ΨADAPT-VQE|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (θ)|0〉⊗n|2. (θ)|0〉⊗n|2.
| (8) |
It should be noted that the fidelity cost function (eqn (8)) is evaluated classically using the matrix product state (MPS) representation: ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) †(θ)|ΨADAPT-VQE〉. Therefore, the target state for compilation, in this case |ΨADAPT-VQE〉, must be efficiently represented as an MPS. AQC is a classical method designed to construct shallow circuits which approximate MPSs to a desired level of accuracy. AQC may be applied to a classically-intractable state, |ψ〉, provided that a circuit which prepares the state is already known: |ψ〉 = Û|0〉. The circuit Û can always be factored into two parts: Û = Û1Û0, such that the initial part Û0 produces a state |ψ0〉 = Û0|0〉 which can be efficiently represented as an MPS. By using AQC to find a shallow approximation of |ψ0〉, denoted
†(θ)|ΨADAPT-VQE〉. Therefore, the target state for compilation, in this case |ΨADAPT-VQE〉, must be efficiently represented as an MPS. AQC is a classical method designed to construct shallow circuits which approximate MPSs to a desired level of accuracy. AQC may be applied to a classically-intractable state, |ψ〉, provided that a circuit which prepares the state is already known: |ψ〉 = Û|0〉. The circuit Û can always be factored into two parts: Û = Û1Û0, such that the initial part Û0 produces a state |ψ0〉 = Û0|0〉 which can be efficiently represented as an MPS. By using AQC to find a shallow approximation of |ψ0〉, denoted 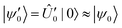 , a shallower approximation of the original state |ψ〉 may be obtained by
, a shallower approximation of the original state |ψ〉 may be obtained by 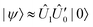 .
.
D. Error mitigation using zero-noise extrapolation
The quantum computing NEO framework has been shown to produce accurate energy estimates in idealised, noise-free simulations.27,30 In this work, we aim to study the effects of hardware noise and assess the ability to recover the expectation values through error mitigation. This involves performing simulations that take into account sampling (shot) noise and a realistic device noise model derived from noise characterization protocols on the ibm_pittsburgh system.‡ In this work, we apply the ZNE technique,51,52 which involves deliberately amplifying the noise in a quantum circuit—typically by repeating certain gates—and measuring the resulting expectation values at different noise levels. By fitting these noisy results to an analytical curve and extrapolating back to the zero-noise limit, ZNE provides an improved estimate of the expectation value that would be obtained on an ideal, noise-free device.For noisy simulations, we use the device characterization data (see Appendix C), including qubit-specific T1, T2 coherence times, single- and two-qubit gate error rates, and readout errors, as determined from randomised benchmarking and echo protocols.53,54 The noise model selected corresponds to an error per layered gate (EPLG) of 0.001471 across 18 qubits, representative of device behavior during the study. The employed noise model includes (i) depolarizing channels derived by the 1- and 2-qubit gate error rates, followed by a thermal relaxation channel derived from the T1, T2 times and the corresponding gate lengths;55 (ii) bit-flip errors on the measurement outcomes derived from the readout error rates (see Appendix C).
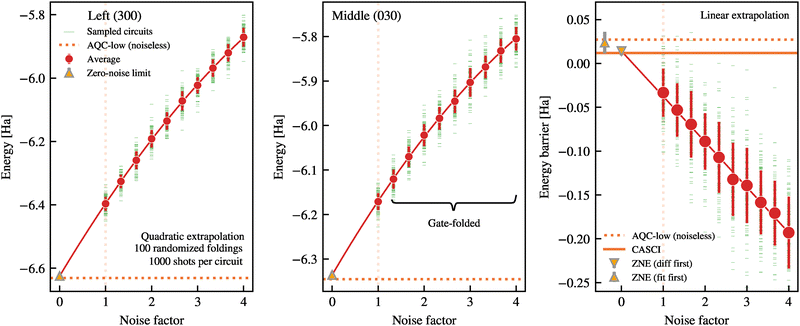
Following the ZNE description in ref. 51, we first run the original circuit to obtain the unmitigated expectation value. Subsequently, copies of the circuit with folded gates to amplify the noise56 are run, where the gate-folding steps are performed locally on randomly selected gates, using the Mitiq noise-mitigation software package.57 The noise-amplified circuits, alongside the original circuit, are executed using the Qiskit Aer simulation library58 to compute noise-free and noisy expectation values. The resulting noisy expectation values are fit to a linear or quadratic function of the noise scaling factor λ ∈ [1, 4], and extrapolated back to λ → 0 to estimate the noise-free energies and barrier heights, as demonstrated in Fig. 5 and 6.
In this work, we adopted ZNE with 2-qubit gate unfolding as a standard and widely implemented benchmark approach for error mitigation. While other techniques—such as probabilistic error amplification (PEA)59 and probabilistic error cancellation (PEC)60—can offer improved accuracy when combined with noise suppression methods, they introduce significantly higher computational overhead (for both quantum and classical resources), particularly for Hamiltonians with thousands of terms requiring high-precision measurements. These advanced methods remain promising and will be the subject of future investigations, but were beyond the practical scope of the present study.
IV. Results and discussion
A. Barrier height evaluation
The computational pipeline introduced in Section III approximates the ground state wavefunction, with the aim of progressively reducing quantum circuit depth and thereby enabling execution on near-term devices. In Table 2 and Fig. 3 (left panel), we report the computed energies and barrier heights, ΔE, for proton transfer in malonaldehyde using various quantum and classical approaches, while the comparison of temperature dependence for the rate constants is shown in the right panel of Fig. 3. The CASCI result serves as a high-level quantum chemistry benchmark, while various quantum circuit-based methods demonstrate different trade-offs between circuit depth and fidelity. All quantum circuits presented in this work are transpiled to the ibm_pittsburgh device with Heron r3 architecture,61 and quantum resource requirements for their implementation are shown in Table 2.| Method | Label | State | 2Q-count | 2Q-depth | Fidelity | E [mHa] | ΔE [mHa] |
|---|---|---|---|---|---|---|---|
| FNO–NEO–CASCI | CASCI | Left | — | — | — | −600.666 | |
| Middle | — | — | — | −588.809 | 11.857 | ||
| HF-product | HF-product | Left | 0 | 0 | 0.888 | −552.090 | |
| Middle | 0 | 0 | 0.936 | −549.241 | 2.850 | ||
| ADAPT-VQE (deep) | VQE-deep | Left | 1844 | 1362 | 0.998 | −599.268 | |
| Middle | 940 | 662 | 0.999 | −587.497 | 11.771 | ||
| ADAPT-VQE (shallow) | VQE-shallow | Left | 551 | 411 | 0.971 | −591.237 | |
| Middle | 271 | 211 | 0.976 | −579.609 | 11.628 | ||
| ADAPT-AQC (high) | AQC-high | Left | 81 | 51 | 0.961 | −578.785 | |
| Middle | 405 | 90 | 0.967 | −565.358 | 13.427 | ||
| ADAPT-AQC (low) | AQC-low | Left | 81 | 51 | 0.961 | −578.785 | |
| Middle | 85 | 12 | 0.953 | −551.645 | 27.140 | ||
| ADAPT-AQC (low + ZNE) | ZNE (fit first) | Left | — | — | — | −572 ± 7 | |
| Middle | — | — | — | −542 ± 7 | 30 ± 10 | ||
| ZNE (diff first) | Left, Middle | — | — | — | — | 14 ± 5 |
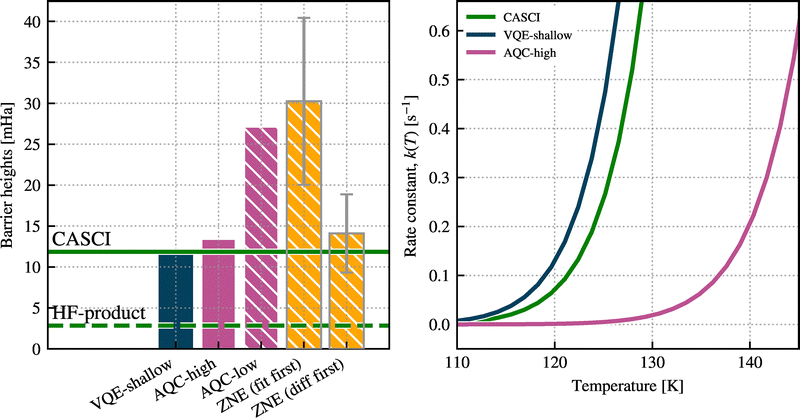 | ||
| Fig. 3 Left: Energy difference of the potential barrier (in mHa) for the VQE-shallow circuits, AQC-high and -low (noiseless, pink hatched), and the noisy AQC-low circuits with ZNE using two extrapolation methods (‘fit first’ and ‘diff first’, yellow hatched). The horizontal solid line indicates the CASCI result, and the dashed line the HF-product result (without correlations) for the energy barrier, as a guideline. The ZNE-based bars indicate the median value sampled from 100 randomised gate-folded circuits. The AQC-based methods overestimate the barrier height in the noiseless regime and, on average, in the presence of noise. Right: Proton transfer rate constants, k(T), as a function of temperature, T, computed using different methods based on a quantum-corrected TST expression of eqn (6). The green, blue, and pink lines indicate the CASCI, VQE-shallow, and AQC-high results, respectively. Energies estimated from AQC-low circuits would yield k(T) ≈ 0 in the temperature range shown and are omitted for clarity. | ||
The Hartree–Fock state significantly underestimates ΔE compared to CASCI reference. This highlights the critical role of correlation for accurate barrier evaluation and the need for quantum circuits balancing entanglement depth with hardware feasibility. For this, we apply two layers of approximations as discussed in Section III. First, employing ADAPT-VQE in a noiseless statevector simulation regime, we construct circuits labelled VQE-deep and VQE-shallow, yielding energies within 10−3 Ha and 10−2 Ha of the CASCI ground state, respectively (see Table 2). The resource requirements of VQE-deep circuits are too large for execution on currently available quantum processors, while they deliver outstanding accuracy for energy barrier and absolute energies. Although VQE-shallow produces circuits with relatively less overhead and delivers outstanding accuracy with respect to CASCI, their practical deployment remains unrealistic in the near term. Specifically, the two-qubit gate depth is the most important factor for reducing noise on current superconducting quantum computers, where decoherence over time is more significant than errors from imperfect execution of gates.
We further optimise the VQE-shallow circuits using ADAPT-AQC running with two settings. The first, ADAPT-AQC (high), is set to retain high fidelity relative to the target circuit at the cost of a deeper solution. The second, ADAPT-AQC (low), is set to prioritise reducing the entangling gate depth, at the cost of lower fidelity. Running the algorithm under both of these settings produces two sets of circuits we label AQC-high and AQC-low, as shown in Table 2.
The AQC-high circuits are able to reduce the two-qubit gate depth of the VQE-shallow circuits by 88% and 57% for the Left and Middle systems, respectively, while still maintaining fidelity 99% relative to the VQE-shallow target. Furthermore, evaluating the states produced by the AQC-high circuits yields a barrier height within approximately 13% (1.6 mHa) of the CASCI reference, but leads to a 98% underestimate in the rate constant at 120 K (Fig. 3, right panel). This discrepancy arises due to the exponential dependence of rate constants on barrier height. To quantify the sensitivity of the rate constant to barrier height errors, we note that an error δE in the barrier leads to a fractional error in the rate constant δk/k approximately given by δk/k ≈ −δE/kBT. At 120 K, this implies that the barrier must be accurate to within ≈0.08 mHa (≈2 meV) in order to keep the error in the corresponding rate constant below 20%. This sets a stringent requirement on quantum energy estimation algorithms to yield reliable kinetics in this temperature regime. Reaching this level of precision remains a key challenge—and benchmark—for emerging quantum algorithms applied to chemical reaction dynamics.
The AQC-low circuits have a minimum fidelity of 97% with respect to the VQE-shallow target. Whilst no improvement over the AQC-high could be achieved for the Left system, a solution for the Middle circuit is found with only 12 two-qubit gate depth. Thus, the AQC-low circuits have small enough resource requirements to be realised on currently available quantum hardware. However, the cost of the significant depth reduction of the ADAPT-AQC (low) protocol means the evaluated circuits overestimate the barrier by approximately 130%, resulting in an overwhelming suppression of the computed rate constant across the entire temperature range. This result underscores the importance of high-precision energy estimation when using quantum algorithms for chemical kinetics. Nevertheless, we accept these inaccuracies as a trade-off in order to evaluate the feasibility of using the NISQ devices, which remain limited by the depth of circuits they can reliably execute.
Our results show that noiseless simulations can recover the proton transfer energy barrier accurately with significant compression from ADAPT-AQC. Circuits produced by AQC-high significantly reduce the depth of entangling gates compared to VQE-shallow while maintaining good accuracy; however, they are still too deep to be executed reliably on noisy devices. Further compromising fidelity in favor of lower depth, the circuits produced by AQC-low offer a more realistic scenario for noisy quantum hardware, though they severely overestimate the barrier. Nonetheless, this may represent the only currently feasible option for application on a real device.
B. Proton transfer dynamics
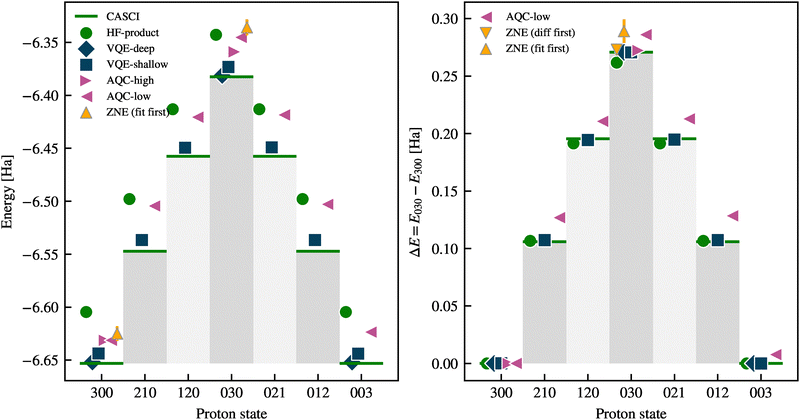
To simulate the proton transfer processes, we construct 7 Hamiltonians defined along the adiabatic trajectory by interpolating between Left, Middle, and Right as defined in eqn (5). We use the nomenclature LMR to label the resulting time-dependent Hamiltonians and corresponding states, where each digit reflects the weight of the respective Left, Middle, and Right setups. For example, the label 210 corresponds to the following Hamiltonian:We then repeat the application of our pipeline in Fig. 2 on each of these Hamiltonians to produce a ground state for each intermediate point that can be run on current quantum hardware. Specifically, we use ADAPT-VQE (shallow), followed by ADAPT-AQC (low) to produce 7 circuits that approximate the ground state wavefunctions along the adiabatic proton transfer process for the time dependent Hamiltonian in eqn (5). Fig. 6 illustrates the full adiabatic proton-transfer pathway from the left to the right states. The plotted energies correspond to expectation values of the NEO Hamiltonian without the addition of the scalar constant arising from classical nuclear and frozen-core electron interactions. The hardware requirements for these circuits, along with the corresponding errors, are summarised in Table 3. One can observe shifts in energy across all states, which are not always systematic. In addition, asymmetries in the two-qubit gate depth of circuits are evident. Both effects originate from asymmetries in the ADAPT-VQE procedure, which initially uses the Hartree–Fock state of the Left setup (see Fig. 1) as a starting point for all steps along the adiabatic trajectory. These initial imbalances are inherited and further amplified by ADAPT-AQC compression.
| State | Error (Ha) | 2Q-depth | 2Q-count |
|---|---|---|---|
| 300 (Left) | 0.022 | 51 | 81 |
| 210 | 0.043 | 12 | 87 |
| 120 | 0.037 | 12 | 86 |
| 030 (Middle) | 0.037 | 12 | 85 |
| 021 | 0.039 | 12 | 87 |
| 012 | 0.044 | 20 | 67 |
| 003 (Right) | 0.030 | 16 | 130 |
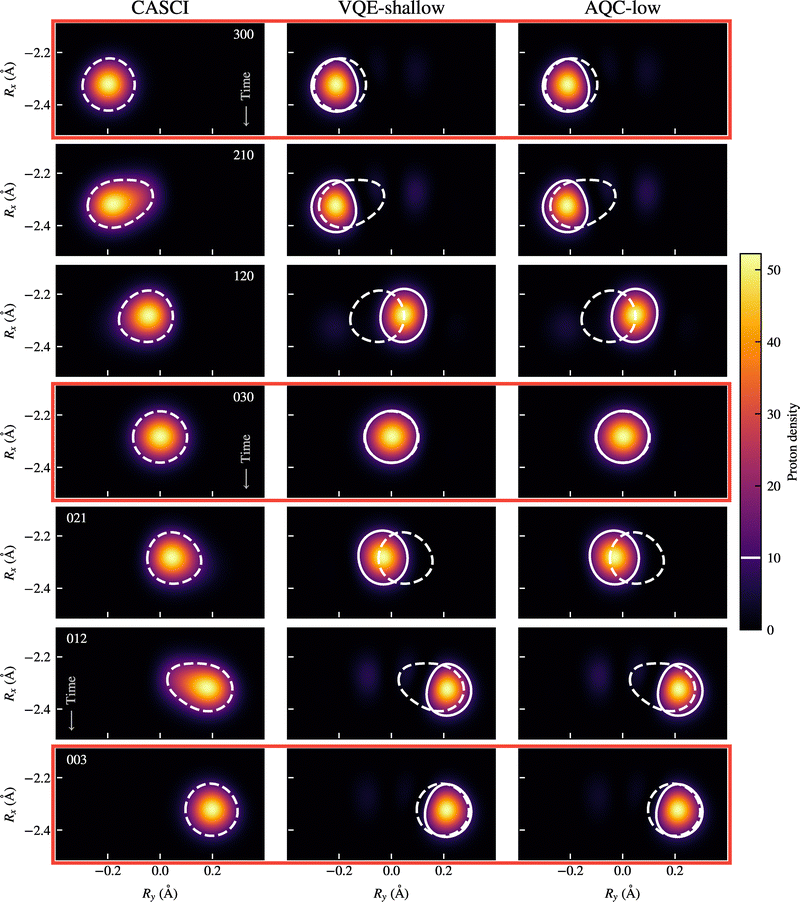
For illustration purposes, we plot the proton densities along the proton transfer process in malonaldehyde. Fig. 4 compares these proton densities as computed using the increasing approximations of our pipeline: a high-accuracy CASCI reference (left), the VQE-shallow solution (middle), and the AQC-low solution (right).
The CASCI calculations show the exact nuclear delocalization at each geometry along the adiabatic transfer trajectory. The VQE-shallow solution qualitatively reproduces the key features of the nuclear density, particularly capturing the delocalization and correct spread of the proton wave packet at the Left, Middle, and Right states. However, at intermediate points along the reaction path, the VQE-shallow wave packets appear somewhat more localised than in the CASCI reference, suggesting that the variationally constructed ansatz, though compact, does not fully capture all the correlations needed for accurate delocalization at these states.
This limitation stems from the core approximations in ADAPT-VQE. The ansatz is constructed iteratively from a predefined operator pool, targeting ground-state energy minimization at each step. While this approach ensures efficiency and adaptivity, it can under-represent entanglement or spatial correlation effects that are not sufficiently prioritised by the energy gradient criterion used in operator selection, and these inaccuracies persist even in VQE-deep.
The right panel in Fig. 4 demonstrates how, despite its reduced depth, AQC-low solution almost exactly reproduces the key features of the VQE-shallow (middle panel) densities across the entire transfer pathway, including the subtle asymmetries and spatial localization patterns. This highlights the utility of AQC not only as a tool for circuit compression but also as a robust method for preserving chemically and physically meaningful wavefunction features, given an appropriate initial state.
C. Hardware noise simulations
In the following, we present results from the noisy simulations of the Left and Middle circuits, transpiled for the ibm_pittsburgh backend and executed with ZNE error mitigation. The ground-state energies for the Left (300) and Middle (030) configurations obtained with the AQC-low circuits under the ibm_pittsburgh noise model (see Table 6) are evaluated for noise amplification factor λ ∈ [1, 4]. For each value of λ, we constructed 100 distinct circuits with randomised folding of the 2-qubit gates. Each noise-scaled circuit is sampled 1000 times, and the noisy expectation values are then fitted to a quadratic function (see Appendix D for a discussion about model selection). The difference between the estimated intercepts for the Left and Middle configurations is used as an estimate for the ZNE energy. We refer to this as the ‘fit first’ method. The error bars in the ZNE energy estimates are given by standard error of the corresponding intercepts, which are added in quadrature to yield the 1σ uncertainty of the ‘fit first’ barrier energy. In Fig. 5 we plot the measured energies for the H030 and H300 along with the fitted lines that are used to estimate the ZNE energy of the barrier. Notably, the ZNE correction applied to the noisy simulations recovers the absolute energies for Left and Middle states within 6 mHa and 9 mHa respectively. While the absolute energy for Middle is slightly above HF results, we note that the noise simulations of the Left are able to capture some of the correlation energy (see Table 2 and Fig. 6). However, the barrier computed from these zero-noise limit (‘fit first’, yellow upward triangles in Fig. 5) closely approaches the ideal, noiseless circuit energies (dotted lines in the left panel of Fig. 5), i.e., within 3 mHa on average. While this agreement may be partly coincidental—given that ZNE performs comparatively poorly for absolute energies—it suggests that the noise-scaling fit may better capture energy differences than absolute values.Motivated by the above observation, we explore an alternative approach in which the energy difference between Middle and Left is first computed at each λ, and then the difference is extrapolated to λ = 0. We refer to this method as ‘difference first’. In the right panel of Fig. 5 we plot this energy difference along with a fitted, linear function (see Appendix D for a discussion about model selection). The ‘difference first’ method yields a barrier height of 14 ± 5 mHa (yellow, downward triangles in Fig. 6), which is lower than the ‘fit first’ result (30 ± 10 mHa). The uncertainty is also smaller (which is confirmed using non-parametric bootstrap estimation, see Appendix D for details), placing the noiseless AQC-low results 13 mHa away from the so-obtained zero-noise limit. Further investigation is needed to determine whether this effect is systematic or accidental.
These results suggest that, despite aggressive circuit compression the proposed framework remains too resource-intensive for near-term devices and will likely only become practical in the FTQC regime. Preliminary hardware experiments were also carried out on the ibm_pittsburgh device under conditions that differed from the simulated setups. Due to limited computational resources and the approximate nature of the noise model, these runs should be interpreted with caution. The results are therefore included in Section E of the Appendix for completeness rather than for quantitative comparison.
V. Conclusions
This work establishes a practical framework for simulating proton transfer with quantum resources that are compatible with both near-term and future quantum computing architectures. By combining nuclear–electronic orbital methods with adaptive quantum circuit construction (ADAPT-VQE and ADAPT-AQC), we demonstrate that it is possible to approximate the proton transfer barrier in malonaldehyde with high accuracy while significantly reducing quantum circuit depth. Notably, our shallowest circuits, AQC-low, reproduce key qualitative features of the proton-transfer process, such as proton density localization, thereby positioning them near the frontier of feasibility for current hardware. By contrast, the deeper circuits, AQC-high, retain higher fidelity to the reference transfer barrier, with an error of 1.6 mHa, and point the way toward early fault-tolerant implementations. While the proposed approach reaches the frontier of what is currently achievable on NISQ hardware, reliable results remain premature even with noise mitigation and classically pre-optimized circuits. Nevertheless, the methodology offers a route toward constructing compact circuit initial states for proton-transfer kinetics within trotterized quantum time evolution27 on early fault-tolerant quantum devices.Beyond malonaldehyde, this methodology offers a modular pipeline for tackling a broader class of proton-coupled electron transfer problems, where the interplay of light nuclei and electronic structure challenges classical methods. As quantum hardware continues to improve, the techniques presented here offer a path toward achieving chemical accuracy in simulating proton dynamics, representing a promising early application for the first generation of fault-tolerant quantum computers.
Author contributions
Author contributions are listed according the CRediT (contributor roles taxonomy) classification; funding acquisition: S. M., J. C., A. B.; conceptualization: A. K., L. T., A. B.; methodology: A. K., L. T., E. A., A. B., S. B., D. M., A. N., F. P.; software: A. K., L. T., E. A., S. B., D. M., A. N., A. M.; investigation: A. K., L. T., D. M., E. A., A. N., A. M.; writing – original draft: A. K., L. T., S. B., D. M., E. A., F. P.; writing – review & editing: all authors.Conflicts of interest
The authors declare no conflict of interest.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. The Supplementary Information contains a video illustrating adiabatic proton-transfer dynamics and associated diagnostics within the NEO framework. See DOI: https://doi.org/10.1039/d5cp04097c.Data and code associated with this article is available as a public repository at https://github.com/stfc/quantum-neo-dynamics with DOI: https://doi.org/10.5281/zenodo.15924624. The repository contains (1) Hamiltonians and circuits used in this work, (2) demonstrative scripts to perform the simulations, and (3) the data generated from the simulations. Details on the basis sets, molecular coordinates, quantum device characteristics, and statistical analyses supporting this work are provided in the appendices of the article.
Appendices
Appendix A: basis set setups and Hamiltonian constructions
The protonic orbitals are constructed using the PB-type 4s3p2d2f (PB4-F2)69 basis set, which is significantly larger than the split-valence double-ζ nuclear basis set composed of 2 uncontracted Cartesian S functions (DZSNB)70 used in ref. 27. For the electronic orbitals centered at positions of proton transfer, we use the ghost basis functions from the correlation-consistent polarised valence five-ζ (cc-pV5Z)71 basis set instead of split-valence double-ζ Gaussian basis set in 6-31 contraction scheme (6-31G). The single-ζ (minimal) basis set contracted from 6 Gaussian primitives (STO-6G),72 6-31G,73 and correlation-consistent polarised valence double-ζ (cc-pVDZ)71 basis sets are used for the peripheral hydrogen, carbon, and oxygen atoms, respectively. This choice of basis sets improved the physical accuracy of the orbitals involved in PCET, leading to a more realistic representation of the underlying physics, while maintaining the total number of orbitals tractable.The molecular integrals were generated using the GAMESS-US package, employing the Cs point-group symmetry. The frozen natural orbitals (FNOs) were constructed following the procedures described in ref. 47. The resulting one- and two-electron integrals were then mapped to a qubit Hamiltonian using the Jordan–Wigner transformation, yielding a 22-qubit representation. All present Z2 symmetries of the system were identified by applying the procedure introduced by Bravyi et al.74 to the Hamiltonian. This approach applies a Clifford transformation to the qubit Hamiltonian, allowing certain qubits to be treated classically and subsequently tapered off, thereby reducing the system to an 18-qubit Hamiltonian used in the simulations.
Appendix B: Cartesian coordinates and proton positions for malonaldehyde setups
Table 4 reports the full set of Cartesian coordinates (in Å) for the nine-atom malonaldehyde system in three representative proton-transfer configurations: the Left, Middle, and Right setups. Each configuration involves two oxygen atoms, three carbon atoms, and four hydrogen atoms (one of which participates directly in the intramolecular hydrogen bond). The molecular origin is placed at the central carbon atom, and all atomic positions are given relative to this point. The Left and Right geometries correspond to the proton localised on each oxygen, whereas the Middle geometry represents the proton symmetrically shared between the two oxygens. The structures corresponding to the Left and Middle setups are shown in Fig. 7.| x | y | z | |
|---|---|---|---|
| Left setup | |||
| O | −2.01516150 | 1.25951633 | 0.00000000 |
| O | −2.05554525 | −1.16937003 | 0.00000000 |
| C | −0.74721061 | 1.23462704 | 0.00000000 |
| C | −0.72001126 | −1.17773733 | 0.00000000 |
| C | 0.00000000 | 0.00000000 | 0.00000000 |
| H | 1.08331158 | 0.00000000 | 0.00000000 |
| H | −0.20901142 | 2.19223326 | 0.00000000 |
| H | −0.26674493 | −2.16891499 | 0.00000000 |
| H | −2.22176148 | −0.18711600 | 0.00000000 |
| Middle setup | |||
| O | −2.04864177 | 1.15865439 | 0.00000000 |
| O | −2.04864177 | −1.15865439 | 0.00000000 |
| C | −0.74990078 | 1.19199519 | 0.00000000 |
| C | −0.74990078 | −1.19199519 | 0.00000000 |
| C | 0.00000000 | 0.00000000 | 0.00000000 |
| H | 1.08244928 | 0.00000000 | 0.00000000 |
| H | −0.27965698 | 2.17995088 | 0.00000000 |
| H | −0.27965698 | −2.17995088 | 0.00000000 |
| H | −2.18129112 | 0.00000000 | 0.00000000 |
| Right setup | |||
| O | −2.05554525 | 1.16937003 | 0.00000000 |
| O | −2.01516150 | −1.25951633 | 0.00000000 |
| C | −0.72001126 | 1.17773733 | 0.00000000 |
| C | −0.74721061 | −1.23462704 | 0.00000000 |
| C | 0.00000000 | 0.00000000 | 0.00000000 |
| H | 1.08331158 | 0.00000000 | 0.00000000 |
| H | −0.26674493 | 2.16891499 | 0.00000000 |
| H | −0.20901142 | −2.19223326 | 0.00000000 |
| H | −2.22176148 | 0.18711600 | 0.00000000 |
| Method | x | y | z |
|---|---|---|---|
| Left setup—300 | |||
| Orb. center | −2.22176148 | −0.18711600 | 0.00000000 |
| CASCI | −2.32501550 | −0.19558330 | 0.00000000 |
| ADAPT | −2.32567623 | −0.19555274 | 0.00000000 |
| AQC | −2.32567623 | −0.19555274 | 0.00000000 |
| Middle setup—030 | |||
| Orb. center | −2.18129112 | 0.00000000 | 0.00000000 |
| CASCI | −2.28629872 | 0.00000000 | 0.00000000 |
| ADAPT | −2.28548356 | 0.00007774 | 0.00000000 |
| AQC | −2.28548356 | 0.00007774 | 0.00000000 |
Appendix C: characteristics of IBM quantum devices
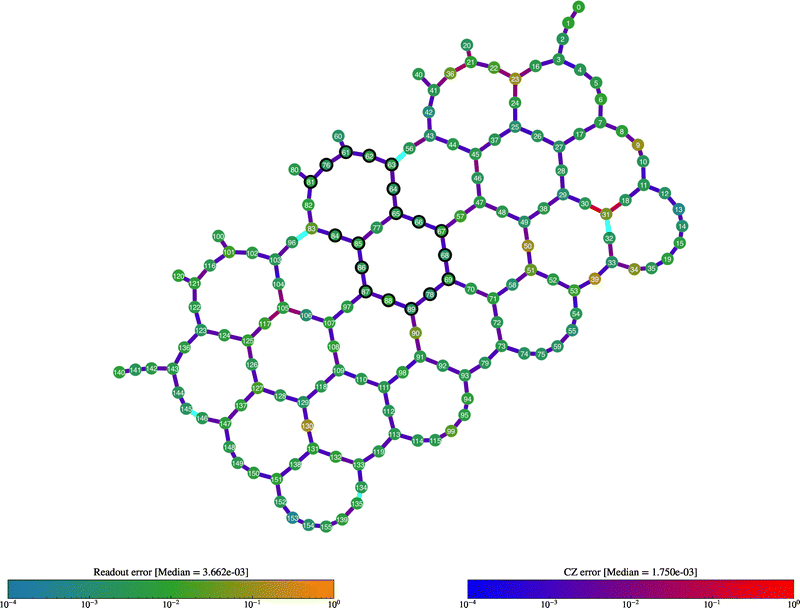
The ibm_pittsburgh device is a superconducting quantum processor built on IBM's third-generation Heron architecture, implementing 156 fixed-frequency transmon qubits arranged in a heavy-hexagonal lattice topology. This design minimises qubit crosstalk and enables efficient connectivity through tunable coupler technology.54,75 Each qubit is characterised by individual relaxation (T1), dephasing (T2), single- and two-qubit gate fidelities, and readout error rates, which are determined via standard quantum benchmarking protocols, including randomised benchmarking and Hahn echo sequences.54,76 Device performance is monitored using the error per layered gate (EPLG) metric,77 which quantifies the cumulative noise contribution across layers of a quantum circuit. A summary of noise models sampled is shown in Table 6. For this work, we selected a representative noise model based on calibration data recorded on August, 10th 2025 at 18:59:40 UTC, which yielded the lowest 18-qubit EPLG of 0.001471 across the sampled noise models. The corresponding analytic noise model incorporates depolarizing gate errors, thermal relaxation channels, and qubit-specific readout errors as captured by IBM's Qiskit Aer simulator. The qubit error map of the chosen noise model is shown in Fig. 8. While these characteristics represent the current state-of-the-art in superconducting quantum hardware, they continue to limit the accuracy of quantum simulations requiring high energy resolution, such as those involved in proton transfer dynamics.| Timestamp (UTC) | EPLG 18 qubit error |
|---|---|
| 2025-06-27 22:26:13 + 00:00 | 0.001620 |
| 2025-06-28 11:11:03 + 00:00 | 0.001779 |
| 2025-06-29 14:13:59 + 00:00 | 0.001653 |
| 2025-06-30 15:42:31 + 00:00 | 0.001675 |
| 2025-07-01 17:20:35 + 00:00 | 0.001671 |
| 2025-07-04 01:49:06 + 00:00 | 0.001664 |
| 2025-07-05 03:12:27 + 00:00 | 0.001545 |
| 2025-07-10 12:10:28 + 00:00 | 0.001640 |
| 2025-07-12 15:06:02 + 00:00 | 0.001679 |
| 2025-07-13 16:02:19 + 00:00 | 0.001669 |
| 2025-07-14 20:01:47 + 00:00 | 0.001776 |
| 2025-07-17 04:37:45 + 00:00 | 0.001510 |
| 2025-07-20 10:58:33 + 00:00 | 0.001689 |
| 2025-08-05 12:50:53 + 00:00 | 0.001654 |
| 2025-08-10 18:59:40 + 00:00 | 0.001471 |
| 2025-08-12 13:59:19 + 00:00 | 0.001778 |
| 2025-08-17 03:00:45 + 00:00 | 0.001726 |
| 2025-08-24 06:54:56 + 00:00 | 0.001724 |
| 2025-09-02 07:58:00 + 00:00 | 0.001786 |
| 2025-09-05 15:31:25 + 00:00 | 0.001691 |
Appendix D: zero-noise extrapolation with bootstrap resampling
To identify the most appropriate model describing the relationship between the noise factor and the measured energy output from the quantum device, polynomial regression models of varying degrees were evaluated. Model performance was quantified using the root mean squared error (RMSE), calculated separately for a hold out test set where the optimal polynomial degree was determined as the one minimizing this quantity, thereby achieving a balance between model complexity and generalizability while avoiding bias towards the intercept at λ = 0. In Fig. 9, the RMSE is shown as a function of polynomial degree for the measured energies of the Left system (H300). As illustrated, the lowest RMSE is attained for a polynomial degree of 2. In Fig. 10, the same procedure is applied to the difference in energies between the Middle and Left systems ΔE = E030 − E300 which is used to compute the ‘difference first’ barrier height shown in Table 2. In this case, the optimal polynomial degree is found to be 1. In both figures, model fits corresponding to the selected optimal polynomial degrees are presented alongside the observed data to enable qualitative assessment of model performance.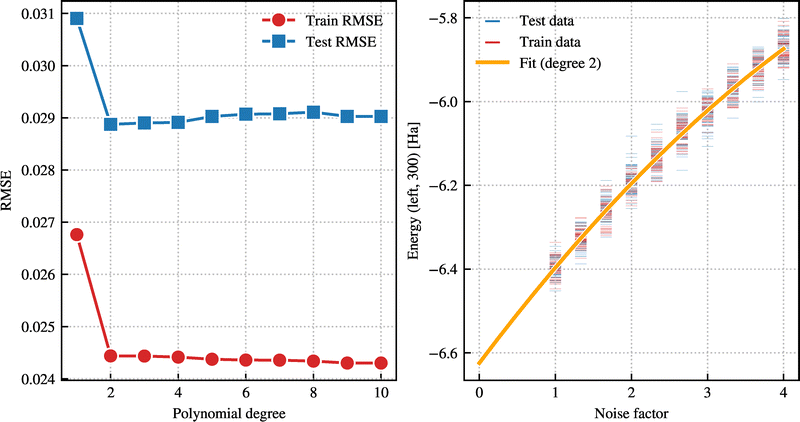 | ||
| Fig. 9 RMSE as a function of polynomial degree (left panel) and optimal fit to data (right panel) for the energies of the Left system H300. | ||
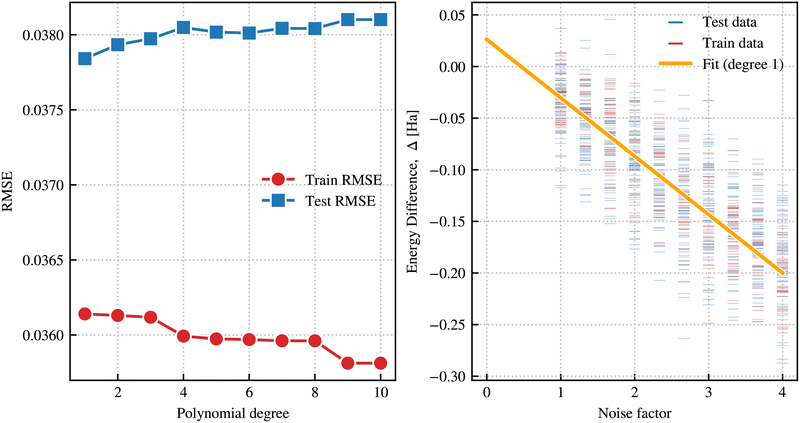 | ||
| Fig. 10 RMSE as a function of polynomial degree (left panel) and optimal fit to data (right panel) for the difference in energies between the Middle and Left systems Δ = E030 − E300. | ||
Given the optimal polynomial degree, bootstrap resampling was employed to estimate the variability and confidence intervals for the intercept parameter of the regression model corresponding to the error-mitigated estimate of the barrier height. To maintain the experimental structure, each bootstrap iteration consisted of resampling, with replacement, the observed data for each unique value of λ, thereby ensuring that the number of replicates per noise setting was preserved. For every resampled dataset, the polynomial regression model, using the previously determined optimal degree, was refitted, and the intercept coefficient was recorded. In Fig. 11, the empirical distributions for the ‘fit first’ and ‘diff first’ methods are presented. The ‘fit first’ distribution is derived by generating bootstrap samples of the intercepts for the Left and Middle systems, respectively, and taking their difference, whereas the ‘diff first’ distribution is derived by generating bootstrap samples of ΔE directly. The empirical distribution of the intercept values across all bootstrap replicates was subsequently used to quantify the uncertainty in this parameter. To capture the interval corresponding to ±1σ, the 15th and 85th percentiles of this distribution were used, while the median value served as a robust point estimate for the intercept. These results are summarized in Table 7 for both extrapolation methods. Excellent agreement is observed when comparing these bootstrap-based values with those obtained from estimation of the standard error of the intercept, as described in Section III D and presented in Table 2.
| Extrapolation method | Median | 15th percentile | 85th percentile |
|---|---|---|---|
| Fit first | 24 | 15 | 32 |
| Diff first | 17 | 14 | 21 |
Appendix E: hardware experiments
To evaluate the performance of our circuits on quantum hardware, we performed ZNE on Left and Middle circuits of the AQC-low system on ibm_pittsburgh device.78 Hamiltonian of the Left state contains 5229 Pauli terms which can be grouped to 910 groups that preserve pairwise commutativity. As such, we performed ZNE for five noise amplification factors λ ∈ {1.0, 1.33, 1.66, 2.0, 2.33}. Each noise factor was sampled 2000 times to keep inline with the job execution limits.79 We utilised measurement error mitigation and Pauli twirling. For twirling, 2-qubit Clifford gate twirling was enabled and the number of randomisations and shots per randomisation were determined automatically as 32 and 64 respectively.80 Hamiltonian of the Middle state contains 567 commutative groups, which afforded us reach larger noise amplification factors λ ∈ {1.0, 1.75, 2.5, 3.25, 4.0} as well as increase the shot budget to 3500 per noise factor. Here too, we utilised measurement mitigation and twirling, and the number of randomisations was set to 300. Pauli twirling can improve the result quality of a hardware experiment as it turns coherent errors that accumulate quadratically into incoherent, statistical Pauli noise that accumulates linearly.Results of the hardware experiments are shown in Fig. 12. As can be seen in Fig. 12, there appears to be an offset between the hardware results and the results from simulations subject to noise. While the Left state exhibits a large (>0.5 Ha) offset of energy for the unfolded expectation value, we note that this offset grows with the noise amplification factor as expected from gate-folding ZNE. The Middle state has a smaller offset around 0.2 Ha for the gate-unfolded case, however it shows a spurious constant offset across all noise factors. The offset between these two results may come from the simplified noise model used in simulations or from drift in the device noise profile since the time of calibration, at which the noise model was generated.
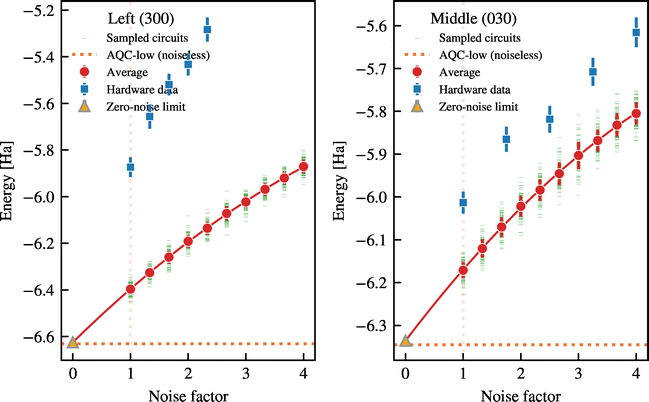 | ||
| Fig. 12 ZNE results of hardware experiments for the Left and Middle states of the AQC-low method, performed on ibm_pittsburgh device. The blue markers denote the hardware results, and noisy simulation results of Fig. 5 are included for reference. | ||
Appendix F: details of classical circuit compression
All ADAPT-VQE simulations were performed using a noise-free statevector simulator based on the full matrix representation of the quantum circuits, which eliminates the need for measurement-based sampling. The optimization of variational parameters was carried out using the L-BFGS-B algorithm similar to ref. 30. The ADAPT-AQC settings used for classical circuit compression are as follows:| Setting | Value |
|---|---|
| Optimiser | Rotosolve and rotoselect |
| Rotosolve frequency | 1 |
| Rotoselect tolerance | 1 × 10−5 |
| Rotosolve tolerance | 1 × 10−3 |
| Coupling map | Nearest-neighbour |
| Layer ansatz | U4 |
Further details about what these settings mean and the algorithm itself can be found in ref. 41. Rotosolve and rotoselect were developed in ref. 81. The U4 ansatz is based on a general two-qubit unitary as decomposed in ref. 82 such that each of the 15 single-qubit unitaries are parameterized.
Acknowledgements
We thank the anonymous reviewers for their comments and suggestions, which improved the quality of this work. This research was supported by funding from the Wallenberg Center for Quantum Technology (WACQT), and the NCCR MARVEL, a National Centre of Competence in Research, funded by the Swiss National Science Foundation (grant number 205602). This work was supported by the Hartree National Centre for Digital Innovation, a UK Government-funded collaboration between STFC and IBM. We acknowledge the use of IBM Quantum services for this work. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission. IBM, the IBM logo, and https://www.ibm.com are trademarks of International Business Machines Corp., registered in many jurisdictions worldwide. Other product and service names might be trademarks of IBM or other companies. The current list of IBM trademarks is available at https://www.ibm.com/legal/copytrade. The research in this paper made use of the following software packages and libraries: Python,62 Numpy,63 Scipy,64 Matplotlib,65,66 Unyt,67 Qiskit.68References
- Z. Liu, C. Calvó-Tusell, A. Z. Zhou, K. Chen, M. Garcia-Borràs and F. H. Arnold, Dual-function enzyme catalysis for enantioselective carbon–nitrogen bond formation, Nat. Chem., 2021, 13(12), 1166–1172 CrossRef CAS PubMed.
- R. Liu, S. Zhan, Y. Che and J. Shen, Reactivities of the front pocket N-terminal cap cysteines in human kinases, J. Med. Chem., 2021, 65(2), 1525–1535 CrossRef PubMed.
- P. J. Silva and Q. Cheng, An alternative proposal for the reaction mechanism of light-dependent protochlorophyllide oxidoreductase, ACS Catal., 2022, 12(4), 2589–2605 CrossRef CAS PubMed.
- S. T. Stripp, B. R. Duffus, V. Fourmond, C. Léger, S. Leimkühler and S. Hirota, et al., Second and outer coordination sphere effects in nitrogenase, hydrogenase, formate dehydrogenase, and CO dehydrogenase, Chem. Rev., 2022, 122(14), 11900–11973 Search PubMed.
- D. H. Murgida and P. Hildebrandt, Proton-coupled electron transfer of cytochrome c, J. Am. Chem. Soc., 2001, 123(17), 4062–4068 Search PubMed.
- J. Cao and S. F. Zhu, Catalytic enantioselective proton transfer reactions, Bull. Chem. Soc. Jpn., 2021, 94(3), 767–789 CrossRef CAS.
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, Oxford, UK, 9th edn, 2010 Search PubMed.
- M. H. Beck, A. Jäckle, G. A. Worth and H. D. Meyer, The Multiconfiguration Time-Dependent Hartree (MCTDH) Method: A Highly Efficient Algorithm for Propagating Wavepackets, Phys. Rep., 2000, 324(1), 1–105 CrossRef CAS.
- S. Habershon, D. E. Manolopoulos, T. E. Markland and T. F. Miller III, Ring-Polymer Molecular Dynamics: Quantum Effects in Chemical Dynamics from Classical Trajectories in an Extended Phase Space, Annu. Rev. Phys. Chem., 2013, 64(1), 387–413 CrossRef CAS PubMed.
- S. P. Webb, T. Iordanov and S. Hammes-Schiffer, Multiconfigurational Nuclear-Electronic Orbital Approach: Incorporation of Nuclear Quantum Effects in Electronic Structure Calculations, J. Chem. Phys., 2002, 117(9), 4106–4118 CrossRef CAS.
- F. Pavoševic, T. Culpitt and S. Hammes-Schiffer, Multicomponent Quantum Chemistry: Integrating Electronic and Nuclear Quantum Effects via the Nuclear–Electronic Orbital Method, Chem. Rev., 2020, 120(9), 4222–4253 CrossRef PubMed.
- L. Zhao, Z. Tao, F. Pavoševic, A. Wildman, S. Hammes-Schiffer and X. Li, Real-time Time-dependent Nuclear-Electronic Orbital Approach: Dynamics Beyond The Born–Oppenheimer Approximation, J. Phys. Chem. Lett., 2020, 11(10), 4052–4058 CrossRef CAS PubMed.
- L. Zhao, A. Wildman, F. Pavosevic, J. C. Tully, S. Hammes-Schiffer and X. Li, Excited State Intramolecular Proton Transfer with Nuclear-Electronic Orbital Ehrenfest Eynamics, J. Phys. Chem. Lett., 2021, 12(14), 3497–3502 CrossRef CAS PubMed.
- Z. Tao, Q. Yu, S. Roy and S. Hammes-Schiffer, Direct Dynamics With Nuclear–Electronic Orbital Density Functional Theory, Acc. Chem. Res., 2021, 54(22), 4131–4141 CrossRef CAS PubMed.
- J. A. Dickinson, Q. Yu and S. Hammes-Schiffer, Generalized Nuclear-Electronic Orbital Multistate Density Functional Theory for Multiple Proton Transfer Processes, J. Phys. Chem. Lett., 2023, 14(26), 6170–6178 CrossRef CAS PubMed.
- J. A. Dickinson and S. Hammes-Schiffer, Nonadiabatic Hydrogen Tunneling Dynamics for Multiple Proton Transfer Processes with Generalized Nuclear-Electronic Orbital Multistate Density Functional Theory, J. Chem. Theory Comput., 2024, 20(18), 7716–7727 CAS.
- M. V. Pak, A. Chakraborty and S. Hammes-Schiffer, Density Functional Theory Treatment of Electron Correlation in the Nuclear-Electronic Orbital Approach, J. Phys. Chem. A, 2007, 111(20), 4522–4526 CrossRef CAS PubMed.
- Y. Yang, K. R. Brorsen, T. Culpitt, M. V. Pak and S. Hammes-Schiffer, Development of a Practical Multicomponent Density Functional for Electron-Proton Correlation to Produce Accurate Proton Densities, J. Chem. Phys., 2017, 147(11), 114113 CrossRef PubMed.
- K. R. Brorsen, Y. Yang and S. Hammes-Schiffer, Multicomponent Density Functional Theory: Impact of Nuclear Quantum Effects on Proton Affinities and Geometries, J. Phys. Chem. Lett., 2017, 8(15), 3488–3493 CrossRef CAS PubMed.
- Q. Yu and S. Hammes-Schiffer, Nuclear-Electronic Orbital Multistate Density Functional Theory, J. Phys. Chem. Lett., 2020, 11(23), 10106–10113 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for Density Functional Theory, Chem. Rev., 2012, 112(1), 289–320 CrossRef CAS PubMed.
- K. R. Brorsen, P. E. Schneider and S. Hammes-Schiffer, Alternative forms and transferability of electron-proton correlation functionals in nuclear-electronic orbital density functional theory, J. Chem. Phys., 2018, 149(4), 044110 CrossRef PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated Quantum Computation of Molecular Energies, Science, 2005, 309(5741), 1704–1707 CrossRef CAS PubMed.
- L. Veis, J. Viš
![[s with combining breve]](https://www.rsc.org/images/entities/char_0073_0306.gif) ák, H. Nishizawa, H. Nakai and J. Pittner, Quantum Chemistry Beyond Born–Oppenheimer Approximation on a Quantum Computer: A Simulated Phase Estimation Study, Int. J. Quantum Chem., 2016, 116(18), 1328–1336 CrossRef CAS.
ák, H. Nishizawa, H. Nakai and J. Pittner, Quantum Chemistry Beyond Born–Oppenheimer Approximation on a Quantum Computer: A Simulated Phase Estimation Study, Int. J. Quantum Chem., 2016, 116(18), 1328–1336 CrossRef CAS. - Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson and M. Kieferová, et al., Quantum Chemistry in The Age of Quantum Computing, Chem. Rev., 2019, 119(19), 10856–10915 CrossRef CAS PubMed.
- B. Bauer, S. Bravyi, M. Motta and G. Kin-Lic Chan, Quantum Algorithms for Quantum Chemistry and Quantum Materials Science, Chem. Rev., 2020, 120(22), 12685–12717 CrossRef CAS PubMed.
- A. Kovyrshin, M. Skogh, L. Tornberg, A. Broo, S. Mensa and E. Sahin, et al., Nonadiabatic Nuclear–Electron Dynamics: A Quantum Computing Approach, J. Phys. Chem. Lett., 2023, 14(31), 7065–7072 CrossRef CAS PubMed.
- T. Culpitt, Z. Chen, F. Pavoševic and Y. Yang, Constrained Nuclear-Electronic Orbital Theory for Quantum Computation, J. Chem. Theory Comput., 2025, 21(16), 7845–7854 CrossRef CAS PubMed.
- J. Preskill, Quantum Computing in The NISQ Era and Beyond, Quantum, 2018, 2, 79 CrossRef.
- A. Nykänen, A. Miller, W. Talarico, S. Knecht, A. Kovyrshin and M. Skogh, et al., Toward Accurate Post- Born–Oppenheimer Molecular Simulations on Quantum Computers: An Adaptive Variational Eigensolver with Nuclear-Electronic Frozen Natural Orbitals, J. Chem. Theory Comput., 2023, 19(24), 9269–9277 CrossRef PubMed.
- S. Khatri, R. LaRose, A. Poremba, L. Cincio, A. T. Sornborger and P. J. Coles, Quantum-assisted quantum compiling, Quantum, 2019, 3, 140 CrossRef.
- K. Sharma, S. Khatri, M. Cerezo and P. J. Coles, Noise resilience of variational quantum compiling, New J. Phys., 2020, 22(4), 043006 CrossRef.
- B. Jaderberg, Solving optimisation problems on near-term quantum computers, PhD thesis, University of Oxford, Oxford, UK, 2022 Search PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M. H. Yung, X. Q. Zhou and P. J. Love, et al., A Variational Eigenvalue Solver on a Photonic Quantum Processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- Q. Yu, S. Roy and S. Hammes-Schiffer, Nonadiabatic Dynamics of Hydrogen Tunneling with Nuclear-Electronic Orbital Multistate Density Functional Theory, J. Chem. Theory Comput., 2022, 18(12), 7132–7141 CrossRef CAS PubMed.
- P. O. Löwdin, On The Non-Orthogonality Problem Connected with The Use of Atomic Wave Functions in The Theory of Molecules and Solids, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- Z. Smith, E. B. Wilson and R. W. Duerst, The infrared spectrum of gaseous malonaldehyde (3-hydroxy-2-propenal), Spectrochim. Acta, Part A, 1983, 39(12), 1117–1129 CrossRef.
- F. Fillaux and B. Nicolaï, Proton transfer in malonaldehyde: From reaction path to Schrödinger's Cat, Chem. Phys. Lett., 2005, 415(4), 357–361 CrossRef CAS.
- A. Kovyrshin, M. Skogh, A. Broo, S. Mensa, E. Sahin and J. Crain, et al., A Quantum Computing Implementation of Nuclear-Electronic Orbital (NEO) Theory: Toward an Exact Pre-Born–Oppenheimer Formulation of Molecular Quantum Systems, J. Chem. Phys., 2023, 158(21), 214119 CrossRef CAS PubMed.
- P. O. Löwdin, Twenty-five years of Sanibel symposia: A brief historic and scientific survey, Int. J. Quantum Chem., 1985, 28(S19), 19–37 CrossRef.
- B. Jaderberg, G. Pennington, K. V. Marshall, L. W. Anderson, A. Agarwal, L. P. Lindoy, I. Rungger, S. Mensa and J. Crain, Variational preparation of normal matrix product states on quantum computers, arXiv, 2025, preprint, arXiv:2503.09683 DOI:10.48550/arXiv.2503.09683.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, An Adaptive Variational Algorithm for Exact Molecular Simulations on a Quantum Computer, Nat. Commun., 2019, 10(1), 1–9 CrossRef CAS PubMed.
- P. Jordan, J. V. Neumann and E. P. Wigner, On an Algebraic Generalization of the Quantum Mechanical Formalism, The Collected Works of Eugene Paul Wigner, Springer, 1993, pp. 298–333 Search PubMed.
- S. B. Bravyi and A. Y. Kitaev, Fermionic Quantum Computation, Ann. Phys., 2002, 298(1), 210–226 CAS.
- A. Miller, Z. Zimborás, S. Knecht, S. Maniscalco and G. García-Pérez, Bonsai Algorithm: Grow Your Own Fermionto- Qubit Mappings, PRX Quantum, 2023, 4(3), 030314 CrossRef.
- C. Sosa, J. Geertsen, G. W. Trucks, R. J. Bartlett and J. A. Franz, Selection of the Reduced Virtual Space for Correlated Calculations. An Application to the Energy and Dipole Moment of H2O, Chem. Phys. Lett., 1989, 159(2–3), 148–154 CrossRef CAS.
- F. Pavoševic, B. J. Rousseau and S. Hammes-Schiffer, Multicomponent Orbital-Optimized Perturbation Theory Methods: Approaching Coupled Cluster Accuracy at Lower Cost, J. Phys. Chem. Lett., 2020, 11(4), 1578–1583 CrossRef PubMed.
- J. H. Fetherolf, F. Pavoševic, Z. Tao and S. Hammes-Schiffer, Multicomponent Orbital-Optimized Perturbation Theory with Density Fitting: Anharmonic Zero-Point Energies in Protonated Water Clusters, J. Phys. Chem. Lett., 2022, 13(24), 5563–5570 CrossRef CAS PubMed.
- Adaptive approximate quantum compiling (ADAPTAQC), 2025, https://github.com/qiskit-community/adapt-aqc/.
- N. F. Robertson, A. Akhriev, J. Vala and S. Zhuk, Approximate quantum compiling for quantum simulation: A tensor network based approach, arXiv, 2023, preprint, arXiv:2301.08609 DOI:10.48550/arXiv.2301.08609.
- K. Temme, S. Bravyi and J. M. Gambetta, Error mitigation for short-depth quantum circuits, Phys. Rev. Lett., 2017, 119(18), 180509 CrossRef PubMed.
- Y. Li and S. C. Benjamin, Efficient variational quantum simulator incorporating active error minimization, Phys. Rev. X, 2017, 7(2), 021050 Search PubMed.
- E. Magesan, J. M. Gambetta and J. Emerson, Characterizing quantum gates via randomized benchmarking, Phys. Rev. A:At., Mol., Opt. Phys., 2012, 85(4), 042311 CrossRef.
- P. Krantz, M. Kjaergaard, F. Yan, T. P. Orlando, S. Gustavsson and W. D. Oliver, A quantum engineer’s guide to superconducting qubits, Appl. Phys. Rev., 2019, 6(2), 021318 Search PubMed.
- Generating a simulator that mimics a device; 2025. Accessed: 2025-05-30. https://qiskit.github.io/qiskit-aer/tutorials/2_device_noise_simulation.html#Generating-a-simulator-that-mimics-a-device.
- R. Majumdar, P. Rivero, F. Metz, A. Hasan and D. S. Wang, Best practices for quantum error mitigation with digital zeronoise extrapolation, 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), IEEE, 2023, vol. 1, pp. 881–887.
- R. LaRose, A. Mari, S. Kaiser, P. J. Karalekas, A. A. Alves and P. Czarnik, et al., Mitiq: A software package for error mitigation on noisy quantum computers, Quantum, 2022, 6, 774 CrossRef.
- J. Doi, H. Horii and C. Wood, Efficient techniques to gpu accelerations of multi-shot quantum computing simulations, arXiv, 2023, preprint, arXiv:2308.03399 DOI:10.48550/arXiv.2308.03399.
- A. Mari, N. Shammah and W. J. Zeng, Extending quantum probabilistic error cancellation by noise scaling, Phys. Rev. A:At., Mol., Opt. Phys., 2021, 104(5), 052607 CrossRef CAS.
- E. van den Berg, Z. K. Minev, A. Kandala and K. Temme, Probabilistic error cancellation with sparse Pauli-Lindblad models on noisy quantum processors, Nat. Phys., 2023, 19(8), 1116–1121 Search PubMed.
- IBM Quantum Heron QPU; 2025, Accessed: 2025-05-30. https://docs.quantum.ibm.com/guides/processor-types.
- G. Van Rossum and F. L. Drake Jr, Python tutorial, Centrum voor Wiskunde en Informatica Amsterdam, The Netherlands, 1995, vol. 620 Search PubMed.
- C. R. Harris, K. J. Millman, S. J. Van Der Walt, R. Gommers, P. Virtanen and D. Cournapeau, et al., Array programming with NumPy, Nature, 2020, 585(7825), 357–362 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy and D. Cournapeau, et al., SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17(3), 261–272 CrossRef CAS PubMed.
- J. D. Hunter, Matplotlib: A 2D graphics environment, Comput. Sci. Eng., 2007, 9(03), 90–95 Search PubMed.
- T. A. Caswell, M. Droettboom, A. Lee, J. Hunter, E. Firing, E. Sales De Andrade, et al., matplotlib/matplotlib: REL: v3. 3.1, Zenodo, 2020 Search PubMed.
- N. J. Goldbaum, J. A. ZuHone, M. J. Turk, K. Kowalik and A. L. Rosen, unyt: Handle, manipulate, and convert data with units in Python, arXiv, 2018, preprint, arXiv:1806.02417 DOI:10.48550/arXiv.1806.02417.
- A. Javadi-Abhari, M. Treinish, K. Krsulich, C. J. Wood, J. Lishman, J. Gacon, S. Martiel, P. D. Nation, L. S. Bishop, A. W. Cross, B. R. Johnson and J. M. Gambetta, Quantum computing with Qiskit, arXiv, 2024, preprint, arXiv:2405.08810 DOI:10.48550/arXiv.2405.08810.
- Q. Yu, F. Pavoševic and S. Hammes-Schiffer, Development of Nuclear Basis Sets for Multicomponent Quantum Chemistry Methods, J. Chem. Phys., 2020, 152(24), 244123 CrossRef PubMed.
- S. P. Webb, T. Iordanov and S. Hammes-Schiffer, Multiconfigurational nuclear-electronic orbital approach: Incorporation of nuclear quantum effects in electronic structure calculations, J. Chem. Phys., 2002, 117, 4106–4118 CrossRef CAS.
- T. H. Dunning Jr, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- W. J. Hehre, R. Ditchfield, R. F. Stewart and J. A. Pople, Self- Consistent Molecular Orbital Methods. IV. Use of Gaussian Expansions of Slater-Type Orbitals. Extension to Second-Row Molecules, J. Chem. Phys., 1970, 52(5), 2769–2773, DOI:10.1063/1.1673374.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54(2), 724–728, DOI:10.1063/1.1674902.
- S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, Tapering Off Qubits to Simulate Fermionic Hamiltonians, arXiv, 2017, preprint, arXiv:1701.08213 DOI:10.48550/arXiv.1701.08213.
- I. Quantum IBM Quantum Heron QPU, 2025. Accessed: 2025-05-30. https://docs.quantum.ibm.com/guides/processor-types Search PubMed.
- E. Magesan, J. M. Gambetta and J. Emerson, Characterizing quantum gates via randomized benchmarking, Phys. Rev. A:At., Mol., Opt. Phys., 2012, 85(4), 042311 CrossRef.
- D. C. McKay, I. Hincks, E. J. Pritchett, M. Carroll, L. C. Govia and S. T. Merkel, Benchmarking quantum processor performance at scale, arXiv, 2023, preprint, arXiv:2311.05933 DOI:10.48550/arXiv.2311.05933.
- IBM Quantum; 2025. Accessed: 2025-10-15. https://quantum.cloud.ibm.com.
- IBM Quantum Job Limits Job Limits; 2025. Accessed: 2025-10-15. https://quantum.cloud.ibm.com/docs/en/guides/job-limits.
- IBM Quantum Twirling Options; 2025. Accessed: 2025-10-15. https://quantum.cloud.ibm.com/docs/en/api/qiskit-ibm-runtime/options-twirling-options.
- M. Ostaszewski, E. Grant and M. Benedetti, Structure optimization for parameterized quantum circuits, Quantum, 2021, 5, 391, DOI:10.22331/q-2021-01-28-391.
- F. Vatan and C. Williams, Optimal quantum circuits for general two-qubit gates, Phys. Rev. A:At., Mol., Opt. Phys., 2004, 69, 032315, DOI:10.1103/PhysRevA.69.032315.
Footnotes |
| † Even though the Born–Oppenheimer CASCI barrier reported in ref. 39 lies close to the experimental value, this agreement reflects fortuitous error cancellation arising from basis-set incompleteness and insufficient correlation—a classic “Pauling point” in the sense of Löwdin.40 |
| ‡ The ibm_pittsburgh quantum device contains 156 superconducting qubits on a Heron (3rd-generation) architecture. These qubits are connected via tunable-coupler technology in a heavy-hexagonal pattern. |
| This journal is © the Owner Societies 2026 |