Balancing accuracy and efficiency in density functional theory studies of SiO₂ polymorphs

Abstract

The ability of dispersion-corrected density functional theory (DFT) calculations to reproduce framework densities and relative stabilities of silica polymorphs has been the subject of a number of prior investigations. Most of these studies either considered only a limited number of DFT approaches or included relatively few structures in the validation against experimental data. Using the Gaussian and plane wave DFT code CP2K, this work aims at a more comprehensive assessment, comparing 27 semilocal approaches that include dispersion interactions either by means of a pairwise correction (“Grimme-type” D3) or in the framework of a nonlocal density functional. The set of silica polymorphs encompasses three minerals and 16 all-silica zeolites. For those approaches that perform well with a moderately sized (triple-zeta) basis set, the effect of adding additional basis functions is evaluated. This (slightly) improves the performance in the majority of cases, especially for relative energies. All in all, those functionals that deliver best agreement with experiment achieve overall errors (as expressed by the mean unsigned error) on the order of 0.2 T atoms per 1000 ų for framework densities and of 1.0 kJ mol⁻¹ (per SiO₂ formula unit) for relative energies. Due to the favourable scaling behaviour of CP2K, structure optimisations of complex zeolites structures are routinely feasible. This is demonstrated through additional calculations for three recently reported all-silica zeolites with extra-large pores.

---

1 Introduction

While α-quartz is the thermodynamically stable form of SiO₂ at ambient conditions, a number of other silica polymorphs like β-quartz, cristobalite, tridymite, coesite, and stishovite occur in nature.¹ Starting with the successful preparation of silicalite-1,² numerous all-silica zeolites, synthetic silica polymorphs exhibiting an intrinsic porosity, have been reported, with a recent article listing nearly 70 topologically distinct zeolite frameworks that can be prepared in purely siliceous form.³ In recent years, the synthesis of all-silica zeolites with extra-large pores (i.e., zeolites having pore apertures formed by more than 12 SiO₄ tetrahedra) has been a particularly active field of research.⁴

Knowledge of the thermochemistry of SiO₂ polymorphs can help to rationalise observations made in nature or in the lab, as well as allowing conclusions on the potential “feasibility” of hitherto unknown structures, for example, new all-silica zeolites.⁵ Experimentally measured enthalpies of transition with respect to α-quartz, usually reported for T = 298 K and designated as ΔH_trans throughout this work, have been reported for about 20 silica polymorphs, including some minerals (e.g., cristobalite, tridymite) and a larger number of synthetic all-silica zeolites.^6–8 It has been observed that the enthalpy of transition increases with decreasing density of the silica framework (or, equivalently, increasing molar volume).

The calorimetric determination of ΔH_trans requires a sophisticated experimental setup. It is therefore not surprising that computational modelling methods have gained considerable popularity as a more widely accessible method to predict stability trends among SiO₂ polymorphs, not least because they can also cover structures that are difficult or impossible to synthesise in (essentially) defect-free all-silica form. Both force field (FF) methods and electronic structure calculations, most prominently density functional theory (DFT), have been employed in this context. In the field of FF calculations, fairly comprehensive comparisons of interatomic potential parameters have been presented.^9,10 For DFT calculations, it has been established that the choice of exchange–correlation (XC) functional and dispersion correction has a significant impact on calculated structural parameters and relative stabilities, as will be discussed in more depth in the following paragraphs. A typical approximation that is made in this context is the neglect of thermal contributions to the free energy.¹¹ In this way, ΔE_DFT, the difference of the DFT total energies of the SiO₂ polymorph of interest and α-quartz (after optimisation of both structures and normalisation to one formula unit of SiO₂), can be directly compared to the experimentally measured enthalpy of transition ΔH_trans. Although more wide-ranging studies appear to be lacking, results reported for some SiO₂ polymorphs indicate that the error introduced by this approximation is below 1.0 kJ mol⁻¹ per formula unit.^12,13 In the present article, ΔE_DFT is referred to as “relative energy”, in keeping with prior work.¹³

DFT investigations of silica polymorphs published prior to ∼2010 typically did not include any dispersion correction.^12,14–16 Although reasonable agreement of ΔE_DFT with experimental ΔH_trans values could sometimes be achieved for individual systems, systematic tendencies to under- or overestimate the relative stabilities were more commonly found. This is not entirely surprising, as DFT calculations employing semilocal XC functionals, such as the popular and computationally inexpensive generalised gradient approximation (GGA), fail to capture long-range dispersion interactions.¹⁷ Indeed, two independent investigations published in 2015 highlighted the important influence of dispersion contributions on the relative energies of silica polymorphs: first, in a study comprising 14 all-silica zeolites, Román-Román and Zicovich-Wilson showed that the inclusion of a pairwise (“Grimme-type”) D2 dispersion correction¹⁸ in calculations with hybrid XC functionals, which incorporate a fraction of exact exchange, resulted in a significantly improved prediction of relative energies.¹¹ Even for the best-performing approach, PBE0-D2,^18,19 the mean unsigned error (MUE) in relative energies amounted to 3.8 kJ mol⁻¹, a rather significant magnitude when considering that the ΔH_trans values fall between 5 and 15 kJ mol⁻¹. Moreover, molar volumes were overestimated by about 10%, indicating some systematic problems with the description of the crystal structures. Second, Hay et al. investigated only a smaller number of silica polymorphs, but compared different dispersion corrections, considering, on the one hand, combinations of the GGA-type PBE functional²⁰ with the pairwise D2¹⁸ and Tkatchenko–Scheffler (TS)²¹ corrections, and, on the other hand, nonlocal vdW-DF (van der Waals density functional²²) and rVV10 (= revised Vydrov–Van Voorhis 2010 functional²³) approaches.²⁴ Overall, the inclusion of dispersion interactions improved the prediction of relative energies and structural parameters compared to PBE without dispersion correction, with the pairwise correction schemes performing somewhat better than nonlocal approaches. However, some systematic error cancellations were also pointed out, with an overestimation of Si–O bond distances being compensated by an underestimation of Si–O–Si angles.

After the importance of including dispersion corrections in DFT-based predictions of structures and energetics of silica polymorphs had been demonstrated in these two papers, a number of benchmarking studies evaluating the performance of different approaches for all-silica zeolites (and, in some instances, AlPO₄ zeotypes) appeared. Two investigations employing the CASTEP plane wave (PW) DFT code²⁵ identified the PBE-TS^20,21 and PBEsol-TS^21,26 functionals as giving particularly good agreement with experimental structural parameters, whereas PBE-D2^18,20 and PBEsol-D2^18,26 performed better for relative energies.^13,27 Notably, a MUE in relative energies of 1.1 kJ mol⁻¹ was achieved with the PBEsol-D2 functional, which is almost on par with the typical experimental uncertainty of ΔH_trans of ∼1 kJ mol⁻¹. As pointed out in a subsequent investigation, however, usage of PBEsol-D2 results in unexpectedly low cell volumes (high framework densities) for zeolites with certain structural features, indicating that caution must be exercised when using it for predictive purposes.²⁸

A study using the VASP PWDFT code^29,30 compared pairwise dispersion schemes and nonlocal vdW-DF methods.³¹ Here, combinations of the PBE functional with a pairwise dispersion correction (PBE-D2/-D3/-MBD³²) showed a robust performance for different quantities, with MUEs in framework densities on the order of 0.3 to 0.5 T atoms per 1000 ų and MUEs in relative energies approaching 1.0 kJ mol⁻¹. While all these studies exclusively considered GGA-type functionals, Albavera-Mata et al. compared GGA and hybrid functionals.³³ Using the CRYSTAL code, which uses Gaussian-type basis functions,³⁴ they found that the lsRPBE-D2 functional (GGA)³⁵ outperformed all hybrid functionals considered. Although the MUEs reported in that work were somewhat higher than those reported in the aforementioned studies, their findings corroborated that dispersion-corrected GGA functionals are capable of calculating framework densities and relative energies with good accuracy.

The motivation to add, with the present article, yet another DFT benchmarking investigation centered on silica polymorphs to the existing body of literature is twofold: first, most previous investigations were either focused on thermochemistry, but considered only a few different DFT approaches,^11,13,28 or they compared a larger variety of approaches, but included only a limited number of zeolite structures for which thermochemical data are available.^24,27,31 Second, none of the previously mentioned benchmarking investigations used the CP2K code, where the Gaussian and plane wave (GPW) approach is implemented in the Quickstep module.³⁶ The orbital transformation method that can be used in CP2K exhibits a cubic scaling behaviour with system size, even when using large basis sets.³⁷ The code is hence particularly well suited for highly accurate calculations on periodic structures with 1000s of atoms in the unit cell, which are not uncommon in zeolites and related materials (zeotypes). The structure database of the International Zeolite Association (IZA) lists 19 frameworks whose unit cell volumes exceed 10 000 ų, with the current “record holder” being MWF (ZSM-25, cell volume ∼90 000 ų, 4320 framework atoms).³⁸ CP2K has been used in many DFT studies of zeolites where good scaling behaviour is key, for example, in DFT-based ab initio molecular dynamics (AIMD) simulations of water in aluminosilicate and all-silica zeolites,^39,40 of CO₂ and CH₄ in zeolite RHO,⁴¹ and of pharmaceuticals in FAU-type zeolites having different Si/Al ratios.^42–44 A recent AIMD study of AFI-type AlPO₄-5 used a 3 × 3 × 6 supercell to enable the prediction of diffuse scattering intensities.⁴⁵ The supercell contained 3888 atoms and had a volume of ∼74 000 ų. Even though such simulations are only feasible with high-performance computing facilities, the computational demand is not massive by present-day standards, with approximately 100 000 core hours required for a trajectory covering 5 picoseconds in that particular case.

In addition to its good performance for large systems, the CP2K code also allows to choose from a wide range of dispersion-corrected DFT approaches by virtue of the inclusion of the libxc library.⁴⁶ It therefore seems warranted to exploit the capabilities of this code to determine reliable, computationally efficient DFT approaches that simultaneously predict relative stabilities and framework densities of silica polymorphs with satisfactory accuracy. Expanding upon previous benchmarking investigations, the present study compares the performance of 27 approaches, using experimental data as reference. The range of DFT approaches comprises GGA and meta-GGA functionals as well as pairwise and nonlocal dispersion correction schemes. When using a pairwise D3 correction, the influence of using different damping schemes and of including a three-body term is also evaluated for some/all XC functionals considered. The set of structures encompasses three non-porous SiO₂ polymorphs (α-quartz and the high-temperature forms α-cristobalite and monoclinic tridymite⁴⁷) as well as 16 all-silica zeolites. From the list of crystalline silica materials for which thermochemical data were reported by Navrotsky and co-workers (Table 1 in ref. 8), only coesite, a high-pressure SiO₂ polymorph having a higher framework density than α-quartz, the hydrous mineral moganite, and zeolite EMT, which has a non-negligible amount of framework aluminium, are excluded.

2 Computational details

2.1 Starting structures

The following structures were included in the benchmarking: α-quartz, α-cristobalite, tridymite and all-silica zeolites with the AFI, AST, BEA, CFI, CHA, FAU, FER, IFR, ISV, ITE, MEI, MEL, MFI, MTW, MWW, and STT framework types. For the zeolites, visualisations of the framework structures are provided in the SI, Fig. S1.³⁸ For all systems except tridymite, the input structures for the DFT optimisations were taken from previous work,¹³ where the structures had been fully optimised with the CASTEP PWDFT code²⁵ using the PBEsol-TS functional.^21,26 For tridymite, which had not been included in the previous study, the structure of the monoclinic form was taken from the experimental study by Hirose et al.⁴⁷

After having assessed the performance of various DFT approaches, additional calculations were carried out for three recently reported zeolites with extra-large pores for which no experimental ΔH_trans values are available, namely, the JZT and HZF frameworks and the ZMQ-1 zeolite. Here, the starting structures were taken from experimental data.^48–50

All calculations used the Γ point approximation in the GPW framework. Therefore, unit cells were, where necessary, multiplied so that each cell axis was at least about 10 Å long. These cell multiplications are listed in the SI Microsoft EXCEL file. The PDB files of DFT-optimised structures that are also supplied as SI (ZIP archive) always correspond to these supercells, i.e., the structures were not transformed back to the conventional unit cells.

2.2 Setup of DFT calculations

DFT calculations were carried out within the GPW framework that is implemented in the Quickstep electronic structure module of the CP2K code.^36,51 CP2K version 2024.1 was used on the cpu-clx partition of the “Lise” high-performance computer, NHR@ZIB, Berlin (Germany). All calculations employed a PW energy cutoff of 900 Ry for the finest level of the multigrid, using a total of four levels (CP2K keyword: NGRIDS) and a relative cutoff of 40 Ry (CP2K keyword: REL_CUTOFF). Goedeker–Teter–Hutter (GTH) pseudopotentials developed by Krack were used to represent the core electrons.⁵² Since customised pseudopotentials are not available for the large majority of approaches considered, pseudopotentials developed for use with the PBE functional were employed in most calculations, in analogy to earlier work.⁴⁰ Only BLYP-D3 calculations used different GTH pseudopotentials that were derived specifically for use with this functional. As described in more detail in the Results and discussion section, a total of four “molecularly optimised” basis sets of different size that were devised by VandeVondele and Hutter⁵³ were compared in preliminary calculations. This comparison included m-DZVP-SR (CP2K input: DZVP-MOLOPT-SR-GTH), m-TZVP (TZVP-MOLOPT-GTH), m-TZV2P (TZV2P-MOLOPT-GTH) and m-TZV2PX (TZV2PX-MOLOPT-GTH) basis sets. Among them, m-TZVP and m-TZV2PX basis sets were used in the remaining calculations. All atomic coordinates and cell parameters were fully relaxed, using a BFGS optimiser and restricting the optimisation of the cell parameters to obey the symmetry of the respective crystal system. Optimisations were considered converged when the following criteria had been simultaneously met: maximal gradient of 1.0 × 10⁻⁵ Ha a₀⁻¹, maximal displacement of 2.5 × 10⁻⁵a₀ (a₀ = 0.529177 Å), pressure tolerance of 10 bar.

2.3 Dispersion-corrected DFT approaches

A total of 27 dispersion-corrected DFT approaches were considered in this work, which are listed in Table 1. The approaches belong to the following “families”:

Table 1 Overview of dispersion-corrected DFT approaches. Numbers/letters in brackets correspond to the labels used in Fig. 5 and 6

Group	Functional	Ref.
GGA+D3	PBE-D3 (1)	20 and 54
	PBEsol-D3 (2)	26, 54 and 58
	revPBE-D3 (3)	54 and 59
	RPBE-D3 (4)	54, 60 and 61
	SSB-D3 (5)	54, 58 and 62
	revSSB-D3 (6)	54, 58 and 63
	BLYP-D3 (7)	54, 64 and 65
	mPWLYP-D3 (8)	54, 58, 65 and 66
	B97-D3 (9)	18, 54 and 67
	HCTH120-D3 (10)	54 and 68
	HCTH407-D3 (11)	54, 61 and 69
meta-GGA+D3	τ-HCTH-D3 (i)	54, 61 and 70
	TPSS-D3 (ii)	54 and 71
	revTPSS-D3 (iii)	54 and 72
vdW-DF1 (DRSLL)	vdW-DF (a)	22, 59 and 73
	vdW-DF-C09 (b)	22, 73 and 74
	vdW-DF-cx (c)	22, 73 and 75
	optB88-vdW (d)	22, 73 and 76
	PBEκ = 1-vdW (e)	22, 73 and 76
	optPBE-vdW (f)	22, 73 and 76
	optB86b-vdW (g)	22, 73 and 77
vdW-DF2 (LMKLL)	vdW-DF2 (A)	55, 73 and 78
	rev-vdW-DF2 (B)	55, 73 and 79
	BEEF-vdW (C)	20, 55, 56 and 73
rVV10	rVV10 (X)	23, 73 and 78
	PBE-rVV10 (Y)	20, 23 and 80
	PBE-rVV10L (Z)	20, 23 and 57

---

• Eleven GGA functionals with a pairwise D3 dispersion correction: GGA+D3.⁵⁴

• Three meta-GGA functionals, which also make use of the kinetic energy density, with a D3 correction: meta-GGA+D3.

• Seven (GGA-based) vdW-DF approaches using the nonlocal dispersion scheme proposed by Dion et al.: vdW-DF1.²² They differ in the choice of exchange functional.

• Three approaches including the revised version of the vdW-DF approach proposed by Lee et al.: vdW-DF2.⁵⁵ Among these, vdW-DF2 and rev-vdW-DF2 differ in the exchange functional, whereas BEEF-vdW uses an XC model developed using a Bayesian error estimation.⁵⁶

• Three approaches using the rVV10 dispersion correction scheme.²³ Here, the original rVV10 uses rPW86 exchange, whereas the other two implementations use PBE exchange and differ only in the choice of one parameter determining the magnitude of the dispersion correction.⁵⁷

The reader is referred to the original papers (Table 1) and to a comprehensive review article⁸¹ for a more technical description of the different XC functionals and dispersion correction schemes. Their respective performance for different (non-zeolite) systems can be inferred from those sources and from the plethora of benchmarking papers that focused either on molecules or solids.^{58,61,82–85}

In initial calculations, several other meta-GGA functionals with and without dispersion correction were included, notably functionals from the SCAN family^86–89 as well as Minnesota functionals.^90–93 It was observed that structure optimisations using these functionals typically converged slowly, and the results pointed to a general tendency to overestimate framework densities and (for dispersion-corrected variants) relative energies. Due to these issues, they were not considered in the analysis presented here. For future reference, selected results are compiled in Table S1 (SI), and further, more comprehensive work to assess their performance for silica polymorphs is explicitly encouraged.

2.4 Assessment of errors

For a given silica polymorph, the errors in framework density and relative energy per SiO₂ formula unit were defined as follows, with experimental reference data (FD_exp, ΔH_trans) from Table 1 of ref. 8:

err(FD) = FD_DFT − FD_exp (1)

err(ΔE_DFT) = ΔE_DFT − ΔH_trans (2)

For each DFT approach considered, the mean signed error (MSE) and the mean unsigned error (MUE, also termed mean absolute error) were then calculated over all error values (19 values for FD, 18 values for ΔE_DFT because the value of α-quartz is zero by definition), as described in prior work.¹³

When analysing the errors of the DFT calculations, error bars of the experimental values have to be taken into account. For enthalpies of transition, uncertainties quoted in ref. 8 vary from ±0.4 kJ mol⁻¹ to ±1.5 kJ mol⁻¹. The precision is much higher for experimental framework densities, which are typically calculated using unit cell volumes obtained at room temperature (RT). However, it is clear that a certain systematic deviation between DFT and experiment will arise from the neglect of temperature effects and, consequently, thermal expansion (positive or negative) in the calculations. To estimate the impact of this difference, it is useful to compare FD values obtained at low temperatures to RT values. For silica polymorphs where such data have been reported, framework densities calculated for the lowest measurement temperature (mostly between 10 and 30 K) and for RT are compiled in Table S2 (SI). When heating from cryogenic temperatures to RT, the largest changes in FD of −0.16/−0.26 T atoms per 1000 ų occur for α-quartz and α-cristobalite,^94,95 whereas changes for all-silica FAU, FER, and IFR are well below ±0.1 T atoms per 1000 ų.^96–98

In the view of these sources of uncertainty, it is clear that it would be unreasonable to expect “perfect” agreement with experiment for any DFT approach. In the first place, the individual DFT approaches are therefore grouped according to their performance in three broad categories, as described in the Results and discussion section. While the definition of these categories is arbitrary and made purely for convenience, it should be noted that the boundaries of category 1, the “best” category, in terms of relative energies are already relatively close to typical experimental uncertainties.

3 Results and discussion

3.1 Preliminary considerations

3.1.1 Comparison of basis sets. To begin with, separate optimisations were performed using the PBE-D3 functional with zero-damping (see below for details on damping schemes) using four types of basis sets from the set of “molecularly optimised” (m-) Gaussian basis sets proposed by VandeVondele and Hutter.⁵³ As smallest basis, shorter-range double-zeta (m-DZVP-SR: 2s2p1d/2s1p) basis sets were considered. Although these efficient basis sets have been widely used in studies of zeolite structures and properties using the CP2K code,^99–101 they are known to overestimate relative energies of all-silica zeolites.¹⁰¹ Moreover, double-zeta basis sets deliver too negative adsorption energies, where triple-zeta basis sets give almost converged results when compared to basis-set-extrapolated values.^40,102,103 Among the triple-zeta basis sets, variants with one or two sets of polarisation functions (m-TZVP: 3s3p1d/3s1p; m-TZV2P: 3s3p2d/3s2p) and with two sets of polarisation functions as well as f orbitals (m-TZV2PX: 3s3p2d1f/3s2p1d) were considered.

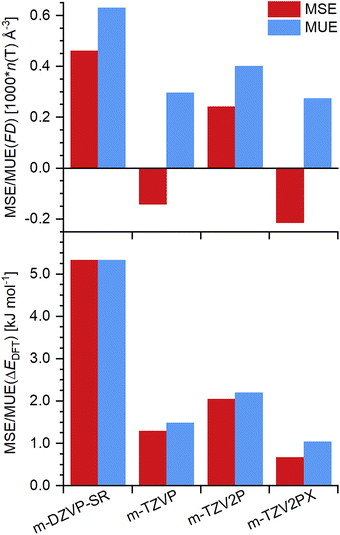
The MSEs and MUEs in framework density and relative energy obtained with the four different basis sets are visualised in Fig. 1. It is apparent that use of the m-DZVP-SR basis sets results in significantly larger framework densities and relative energies in comparison to triple-zeta basis sets. Among these, inclusion of a second set of polarisation functions increases the errors in both quantities, whereas the addition of two polarisation functions and f orbitals delivers the smallest overall MUEs. Altogether, however, the variations among the three triple-zeta basis sets are relatively intricate. It is inferred that m-TZVP basis sets are sufficiently large to allow for solid conclusions regarding the suitability of individual approaches. Therefore, the comparison of all DFT approaches presented below made use of these basis sets, and calculations using larger m-TZV2PX basis sets were carried out only for the more promising cases.

Fig. 1 MSE and MUE in framework densities (top) and relative energies (bottom) obtained with the PBE-D3 functional and different basis set sizes.

3.1.2 The D3 dispersion correction: comparison of damping schemes. In the original publication proposing the pairwise D3 dispersion correction, Grimme and co-workers employed a damping scheme in which the dispersion energy vanishes when the distance R_AB between a pair of atoms A and B approaches zero (“zero-damping”).⁵⁴ A damping scheme in which the dispersion energy assumes a finite value at vanishing distances R_AB, termed Becke–Johnson (BJ) damping, was discussed as an alternative soon after the introduction of the D3 correction.¹⁰⁴ It has become more popular than the original zero-damping in calculations for molecular complexes due to a better description of dispersion interactions at short- and medium-range distances.⁶¹ On the other hand, it was shown recently that zero-damping outperforms BJ-damping in reproducing the structure, density, and dynamic properties of liquid water when using the PBE-D3 or PBE-TS functionals.¹⁰⁵ In previous work addressing neutral-framework zeotypes, PBE-D3 with BJ-damping performed somewhat better than its counterpart with zero-damping for framework densities and bulk moduli, but worse for relative energies.³¹

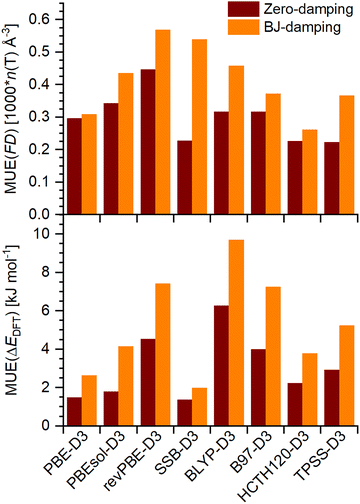
In order to test the impact of the damping scheme for a broader range of functionals, comparative calculations were carried out for eight DFT-D3 approaches (PBE-D3, PBEsol-D3, revPBE-D3, SSB-D3, BLYP-D3, B97-D3, HCTH120-D3, TPSS-D3). The resulting MUE values are summarised in Fig. 2. It is evident that the use of zero-damping delivers smaller MUEs for framework densities and relative energies across the board, although the individual differences between zero- and BJ-damping vary rather markedly, from almost negligible (e.g., MUE(FD) obtained with PBE-D3) to very pronounced (e.g., MUE(ΔE_DFT) obtained with PBEsol-D3 or BLYP-D3). Altogether, it can be concluded that use of zero-damping usually results in better agreement with experiment. To treat all D3-corrected functionals in a consistent way, only zero-damping was considered in all calculations presented in the following.

Fig. 2 MUE in framework densities (top) and relative energies (bottom) obtained with selected DFT-D3 approaches, comparing zero-damping (dark red) and BJ-damping (orange). Calculations used m-TZVP basis sets.

3.1.3 The D3 dispersion correction: including a three-body term. Upon presenting the DFT-D3 approach, Grimme and co-workers also discussed the inclusion of a three-body (Axilrod–Teller–Muto) dispersion term.⁵⁴ This term, which depends on distances and angles for groups of three atoms, makes use of C₉ dispersion coefficients that can, in a first approximation, be computed from the C₆ dispersion coefficients supplied in the DFT-D3 framework. Grimme et al. highlighted that the three-body (C₉) term becomes repulsive for small interatomic angles and that it is “insignificant for small (<10 atoms) molecules and can be neglected but might be substantial for larger complexes.”⁵⁴ The impact of including the C₉ term has been investigated for molecular crystals and layered solids,^106,107 but – to the author's knowledge – its role has not been discussed explicitly for silica polymorphs. When using the D3 dispersion correction in CP2K, the C₉ term is not included by default, but it can be switched on using the CALCULATE_C9_TERM keyword. To speed up the calculation of this term, the coordination numbers can be kept fixed by using the REFERENCE_C9_TERM keyword, which appears as a reasonable approach in cases where no drastic changes in local environments are expected.

To gauge the influence of the three-body dispersion term on framework densities and relative energies, separate optimisations were performed for the entire set of reference structures using all DFT-D3 approaches listed in Table 1 both without and with the C₉ keywords mentioned above. The results are visualised in Fig. 3. When looking at the errors in framework densities, it is noteworthy that the MSEs are always shifted to somewhat lower (less positive/more negative) values, in other words, the inclusion of the C₉ term results in larger unit cell volumes (= lower densities). However, the changes in both MSE and MUE never exceed 0.1 T atoms per 1000 ų. More marked changes occur for the relative energies, where the MSEs are also shifted to lower values. The magnitude of the change is similar for all 14 functionals, falling between −1.1 and −1.3 kJ mol⁻¹. Since all D3-corrected functionals tend to overestimate ΔE_DFT in the absence of the three-body correction, the inclusion of this term improves agreement with experiment and reduces the MUEs. For some of the functionals (notably PBE-D3, SSB-D3, revSSB-D3, mPW91LYP-D3, and τ-HCTH-D3), the MSEs are very close to zero or even slightly negative, showing that the inclusion of the C₉ term removes their tendency to systematically overestimate relative energies. The observed trends of slightly smaller framework densities and significantly reduced relative energies can be explained with the aforementioned repulsive nature of the three-body term. Since the C₉ term appears to have a very consistent effect on the results, usually improving agreement with experiment (at least for the functionals considered here when used with m-TZVP basis sets), it seems altogether advisable to include this term.

Fig. 3 MSE and MUE in framework densities (left) and relative energies (right) obtained with DFT-D3 approaches (m-TZVP basis sets). Solid/open bars represent results obtained without/with inclusion of a three-body dispersion term.

3.2 Categorisation of DFT approaches: results obtained with m-TZVP basis sets

Fig. 4 presents the results for those approaches from Table 1 that include a nonlocal dispersion correction. Combining the information from this figure and Fig. 3, the 27 approaches can be categorised using, for convenience, the following three categories: category 1 encompasses all functionals for which MUE(FD) is below (or equal to) 0.3 T atoms per 1000 ų and MSE(FD) falls in an interval from −0.2 to 0.2 T atoms per 1000 ų, with MUE(ΔE_DFT) being smaller than 1.5 kJ mol⁻¹ and the corresponding MSE falling in an interval between −1.0 and 1.0 kJ mol⁻¹. Category 2 is constituted by those functionals outside category 1 whose MUEs do not exceed 0.45 T atoms per 1000 ų and 3.0 kJ mol⁻¹, respectively. Category 3 includes all remaining functionals. For each approach, the MUEs of both quantities are visualised in Fig. 5, where the short-hand labels introduced in Table 1 are given for each datapoint.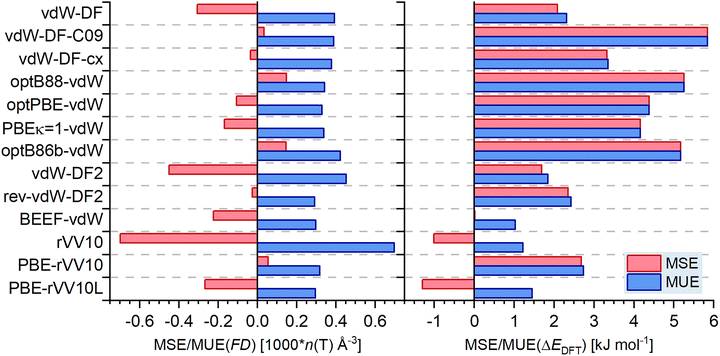

Fig. 4 MSE and MUE in framework densities (left) and relative energies (right) obtained with approaches including a nonlocal dispersion correction (m-TZVP basis sets).

Fig. 5 Plot of MUE(ΔE_DFT) against MUE(FD) for all 27 functionals (m-TZVP basis sets), with MUE ranges of categories 1 and 2 highlighted in green and yellow, respectively. Labels are assigned according to Table 1.

Four GGA+D3 and one meta-GGA+D3 functionals belong to category 1. Among them, τ-HCTH-D3 (i) gives the smallest MUEs for both framework densities and relative energies (as well as very small MSEs, see Fig. 3), with SSB-D3 (5) and revSSB-D3 (6) performing only minimally worse. RPBE-D3 (4) and HCTH120-D3 (10) form a second tier within this category, with slightly larger errors in relative energies in particular. The two remaining datapoints in the green-shaded area in Fig. 5 belong to the BEEF-vdW (C) and PBE-rVV10L (Z) functionals. For both of them, the MUE values fall into the range defined for category 1, but their MSEs are too large to be included in this category, with both functionals systematically underestimating framework densities and PBE-rVV10L also underestimating relative energies.

Category 2 can be sub-divided into several groups. PBE-D3 (1) and PBEsol-D3 (2) narrowly miss the MUE(FD) criterion, but apart from that perform well for both quantities simultaneously. TPSS-D3 (ii) gives very good agreement with framework densities, but systematically overestimates relative energies. The same is true, although with altogether larger errors, for B97-D3 (9) as well as rev-vdW-DF2 (B) and PBE-rVV10 (Z). In contrast, mPW91LYP-D3 (8) performs very well for relative energies, with a MUE below 1.0 kJ mol⁻¹, but very poorly for framework densities, which are drastically underestimated. The original implementation of the vdW-DF functional (a), which uses revPBE exchange, gives substantial errors in both quantities, but still performs better than the more recent variants using this dispersion correction, all of which fall in category 3. The vdW-DF2 functional (A) narrowly misses category 2 on account of its large underestimation of FD, despite giving better agreement with experiment in relative energies than rev-vdW-DF2.

The large majority of functionals clearly falling outside the boundaries of category 2 systematically overestimate the relative energies, with MUEs above 3.0 kJ mol⁻¹. This problem affects all vdW-DF approaches except the original version (b to g) as well as revPBE-D3 (3), BLYP-D3 (7), HCTH407-D3 (11), and revTPSS-D3 (iii). The only exception in this category is rVV10 (X), which – somewhat like mPW91LYP-D3 – does a satisfactory job for relative energies (despite a systematic tendency to underestimate them), but performs exceptionally poorly for framework densities.

In the view of the substantial variation in MUEs among the different approaches observed, it seems safe to conclude that the functionals listed in category 1 are well suited if a simultaneous prediction of framework density and relative energy is desired. Many of those in category 2 give rise to relatively modest systematic errors that may often be acceptable, for example, in cases where use of a particular functional is preferred due to its good performance for other quantities.

3.3 Extension to m-TZV2PX basis sets for selected approaches

In the preliminary calculations using PBE-D3, the use of m-TZV2PX instead of m-TZVP basis sets resulted in an overall improvement of the calculated framework densities and relative energies. To this end, it appears appropriate to evaluate how an increase of the basis set size affects the results for those functionals that fell into categories 1 and 2 according to the analysis presented above. A full comparison of the MSEs and MUEs in both quantities obtained with m-TZVP and m-TZV2PX basis sets for these 16 functionals is shown in Fig. S2 of the SI PDF. Fig. 6 condenses the results into a plot of MUE(ΔE_DFT) against MUE(FD), in analogy to Fig. 5. Generally, it can be observed that the replacement of m-TZVP by m-TZV2PX basis sets leads, on average, to a slight reduction in framework densities and a more pronounced decrease in relative energies. As a consequence, the performance of functionals that already underestimate those quantities with m-TZVP basis sets becomes worse and the MUEs increase. A prominent example is PBE-rVV10L (Z), which falls close to the border of category 1 with m-TZVP basis sets, but well outside this area with the larger basis. The opposite is true for those functionals that systematically overestimate FD and/or ΔE_DFT, for which the MUEs decrease. Examples are PBEsol-D3 (2), TPSS-D3 (ii), and rev-vdW-DF2 (B), which fall into category 1 or at least close to its boundary in Fig. 6. For some functionals that gave a MSE(ΔE_DFT) close to zero when using m-TZVP basis sets, this MSE becomes negative in the m-TZV2PX results. This is the case for the SSB-D3 (5), revSSB-D3 (6), τ-HCTH-D3 (i), and BEEF-vdW (C) functionals, with MSEs of revSSB-D3 and BEEF-vdW falling outside the MSE interval of −1.0 to 1.0 kJ mol⁻¹ that was used to define category 1. Nevertheless, all these four functionals remain among the best-performing approaches. MSE(ΔE_DFT) values close to zero, reflecting the absence of any systematic tendency to under- or overestimate relative energies, are observed for the PBEsol-D3 (2), RPBE-D3 (4), and HCTH120-D3 (10) functionals, which can be recommended for use with TZV2PX basis sets in particular.

Fig. 6 Plot of MUE(ΔE_DFT) against MUE(FD) for 16 selected functionals (m-TZV2PX basis sets), with MUE ranges of categories 1 and 2 highlighted in green and yellow, respectively. Labels are assigned according to Table 1.

3.4 Additional considerations

3.4.1 Tuning the b parameter of the PBE-rVV10 functional. Many of the dispersion-corrected DFT approaches considered in this work make use of one or several adjustable parameters that determine the magnitude of the dispersion correction. Notably, the pairwise DFT-D3 method with zero-damping uses three parameters, which correspond to the scaling of the 6th-order dispersion coefficients (s₆), of the cutoff radii (s_r,6), and of the 8th-order dispersion coefficients (s₈), respectively.⁵⁴ While the s₆ parameter is typically fixed to unity, the other two parameters have to be adjusted for each exchange–correlation functional, normally by a fit to reference data from high-level calculations. The exhaustive list of functional-dependent coefficients presented by Goerigk et al. shows that both parameters vary rather significantly, even if the underlying functionals are “related” (for example, PBE-D3 uses s_r,6 = 1.217 and s₈ = 0.722, whereas s_r,6 = 0.872 and s₈ = 0.514 are recommended for RPBE-D3).⁶¹ While the vdW-DF and vdW-DF2 approaches do not use any functional-dependent scaling parameter(s), the rVV10 dispersion correction employs an empirical parameter b that determines the short-range behaviour of the dispersion correction.^23,108 A second parameter C that influences the behaviour at large interatomic distances is also adjustable, however, it is commonly recommended to fix it to 0.0093 when using semilocal XC functionals.^{23,57,87,89,108} In the initial combination of the PBE XC functional with the rVV10 dispersion correction (PBE-rVV10), b = 6.2 was proposed on the basis of a fit to reference energies for weakly bonded molecular complexes from “gold-standard” coupled cluster (CCSD(T)) calculations.⁸⁰ Subsequently, Peng and Perdew refitted the b parameter to reproduce interlayer binding energies of layered materials, leading to the PBE-rVV10L approach with b = 10.⁵⁷ They also (slightly) adjusted the b parameter of the original PBE-rVV10 functional to b = 6.6, which is the value used in the present work.

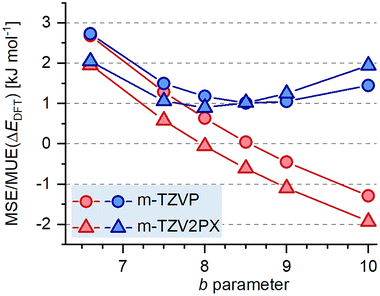
As Fig. 4 shows, the PBE-rVV10 functional overestimates relative energies rather drastically, at the same time giving a small MSE for framework densities. PBE-rVV10L, on the other hand, underestimates both quantities. Since an increase of b decreases the magnitude of the dispersion correction term, it appears that an intermediate value between 6.6 and 10 would be required to minimise the error in relative energies for silica polymorphs. To evaluate this, further calculations were performed in which the b parameter was varied systematically between 7.5 and 9.0. Fig. 7 visualises the MSE and MUE in relative energies from calculations employing m-TZVP and m-TZV2PX basis sets. Three things can be inferred from this figure: first, it is clear that the trends in error values are very systematic. Second, optimisation of the b parameter results in MUE(ΔE_DFT) values on the order of 1.0 kJ mol⁻¹, while the MSE is very small. These values are on par with the best-performing functionals discussed above. Third, the basis set size influences which value of b gives the smallest error, with the best results obtained with b values of 8.5/8.0 when using m-TZVP/m-TZV2PX basis sets. Looking beyond relative energies, it has to be noted that no choice of b delivers an agreement with experimental framework densities that matches that obtained with the best functionals identified above, with MUE(FD) values falling between 0.26 and 0.38 T atoms per 1000 ų. This highlights that the simple adjustment of the b parameter, while improving performance with respect to previous parameterisations of PBE-rVV10, is not sufficient to obtain an “optimised” functional that reproduces both quantities of interest equally well.

Fig. 7 MSE (red) and MUE (blue) in relative energies obtained with PBE-rVV10 using different b parameters. The datapoints at b = 6.6/10 correspond to the PBE-rVV10/PBE-rVV10L functionals as used in the preceding sections.

3.4.2 Application to extra-large-pore zeolites. In the last few years, a number of extra-large-pore high-silica/all-silica zeolites have been reported.⁴ Additional calculations for three of these zeolites were carried out, employing some of the best-performing approaches identified above in order to evaluate whether they deliver consistent results for zeolite frameworks that were not considered previously. The three structures selected for this purpose are the JZT framework (ZEO-3⁴⁸), the HZF framework (ZEO-5⁴⁹), and ZMQ-1.⁵⁰ In terms of functionals, RPBE-D3, SSB-D3, HCTH120-D3, τ-HCTH-D3, and BEEF-vdW were included due to their good performance, with PBE-D3 and rev-vdW-DF2 being added as popular and (perceivedly) robust options. The results obtained with these seven functionals and m-TZV2PX basis sets are shown in Fig. 8 (m-TZVP results are shown in Fig. S3). With regard to framework densities, all functionals give values that are reasonably close to the published experimental values. Among them, SSB-D3 and τ-HCTH-D3 stand out, as they give framework densities within ±0.2 T atoms per 1000 ų of the experimental data, with the remaining functionals underestimating the framework densities. While no experimental enthalpies of transition are available for these frameworks, the relative energies predicted by most functionals fall very close to each other, with HCTH120-D3 and rev-vdW-DF2 giving values that are systematically larger.

Fig. 8 Plot of ΔE_DFT against FD for three zeolites with extra-large pores. Dotted green lines correspond to experimental values of FD, and the grey line corresponds to the correlation between FD and ΔH_trans derived from experimental data.

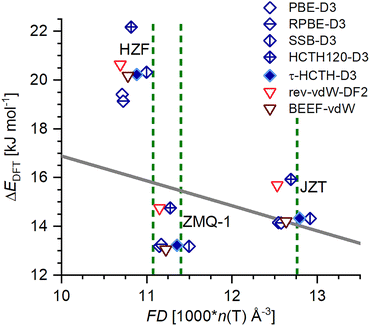
For the case of JZT, the calculated relative energies fall very close to the correlation between FD and ΔH_trans that was established on the basis of experimental data in prior work.^7,31 In other words, the DFT-calculated relative energy is in line with the stability that would be expected for this framework density according to the empirical relationship. Interestingly, the datapoints for ZMQ-1 fall about 3 kJ mol⁻¹ below the linear correlation, thus, this framework is unusually stable given its low FD. Although this appears surprising for a structure with very large pores, the largest of which are delineated by 28-membered rings of TO₄ tetrahedra, it has already been established that the linear relationship between molar volume (used instead of FD because it can also be determined for amorphous materials) and ΔH_trans breaks down for mesoporous silica materials (see, for example, the flattening off of the curve shown in Fig. 2 of ref. 8). As ZMQ-1 is a mesoporous zeolite, the observed departure from the trend derived for purely microporous all-silica zeolites may therefore not be completely unexpected. HZF exhibits the opposite behaviour, with the ΔE_DFT values lying 3 to 6 kJ mol⁻¹ above the value that would be inferred from the empirical correlation. Thus, HZF, which was synthesised through calcination of an interchain-expanded interrupted zeolite framework, constitutes an “unusually unstable” framework. This reduced stability can most probably be attributed to the presence of “triple four-ring” (t4r) building units in the HZF structure, which are not known in any other zeolite framework. It was already observed in the experimental crystal structure that the Si–O–Si angles in the central plane of these t4r units are unusually small, approaching 120 degrees.⁴⁹ The corresponding angles in the DFT-optimised structures have similar magnitudes. Since previous computational studies have shown that such low Si–O–Si angles incur a significant energetic penalty,^109,110 it appears straightforward to attribute the reduced stability of HZF to the presence of these strained building units.

Although comments on computational efficiency cannot be generalised, it is worth summarising the computational demand of the structure optimisations of ZMQ-1, which has 720 atoms in the unit cell. Using 2 nodes with 96 compute cores each, these optimisations typically took between 2.5 and 5 hours with m-TZVP basis sets and between 6 and 8 hours with m-TZV2PX basis sets. This underlines the feasibility of such calculations at a moderate computational cost, on the order of 500 to 1500 core hours.

4 Conclusions

In a comprehensive comparison of DFT-calculated relative stabilities and framework densities of silica polymorphs against experimental data, covering three dense, naturally occurring modifications of SiO₂ and 16 all-silica zeolites, a number of functionals were shown to reproduce experimental data very well. The best-performing approaches achieved overall errors in framework densities on the order of 0.2 T atoms per 1000 ų, and, simultaneously, errors in relative energies of about 1.0 kJ mol⁻¹, the latter value being on the same order as the experimental uncertainty. Encouragingly, an increase of the basis set size resulted in a reduction of the error values in the majority of cases. For the family of functionals including a pairwise D3 dispersion correction, it was found that usage of zero-damping and inclusion of a three-body (C₉) term tend to improve agreement with experiment, especially for relative energies. A particularly good performance was observed for the RPBE-D3, SSB-D3, and HCTH120-D3 GGA functionals and the τ-HCTH-D3 meta-GGA functional. While most approaches using a nonlocal dispersion correction showed an inferior performance, two functionals from the vdW-DF2 family, BEEF-vdW and rev-vdW-DF2, are only slightly worse than the best D3-corrected functionals.

The most accurate approaches identified in this work can thus be recommended for predictions of the relative stability of other silica polymorphs (such as new or hypothetical all-silica zeolites) and to obtain good equilibrium structures, which could be used in further modelling studies (for example, Monte Carlo simulations of adsorption), as starting points for structure refinements from powder data, or in the training of machine-learning interatomic potentials. They should also be suited for AIMD simulations of guest-free silica frameworks, which could be used to investigate thermal expansion behaviour or dynamic disorder, as done in the past for aluminophosphate zeotypes.^45,111 However, the focus on relative stabilities and framework densities in the present work means that further validation will be necessary when targeting other quantities, such as vibrational or NMR spectra, or when investigating host–guest interactions, where dedicated benchmarking studies have been reported for different types of guest molecules.^40,103,112

Given the approximations inherent to any (meta-)GGA-based, dispersion-corrected DFT approach, it is clear that error cancellation will play a certain role. Notably, Hay et al. pointed out that the good performance of some DFT approaches in reproducing experimental cell volumes was due to a concurrent overestimation of Si–O bond distances and underestimation of Si–O–Si angles.²⁴ Although bond distances and angles were not in the focus of the present work, a partial comparison was made for α-quartz and α-cristobalite, where high-quality low-temperature data from neutron diffraction experiments are available.^94,95 The overview provided in Tables S3 and S4 (SI PDF) does not provide clear evidence for a systematic tendency to overestimate bond distances and underestimate angles, at least for the majority of approaches. In fact, the opposite trend is observed for some of them, such as revSSB-D3 and τ-HCTH-D3. Increase of the basis set size from m-TZVP to m-TZV2PX results in shorter bond distances and larger angles, indicating that the systematic errors observed in prior works might be related to basis set incompleteness.

Finally, it has to be emphasised that findings of a poor performance of certain approaches in the context of the present study cannot necessarily be generalised. For example, it is possible that a different choice of pseudopotentials, basis sets, and possibly other computational settings will impact the calculated relative energies and/or framework densities and, consequently, the agreement with experimental values. In this regard, the present study aims to provide recommendations on approaches that deliver robust predictions within the given computational framework, but it is by no means suggested that functionals that performed poorly in the present work should be discarded entirely from further consideration.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: PDF contains additional figures (S1: visualisation of zeolite frameworks; S2: comparison of m-TZVP and m-TZV2PX basis sets; S3: extra-large pore zeolites: m-TZVP basis sets) and tables (S1: selected results obtained with r²SCAN and Minnesota meta-GGA functionals; S2: experimental framework densities at different temperatures; S3 and S4: Si–O distances and Si–O–Si angles in α-quartz and α-cristobalite). Microsoft EXCEL file contains individual results for all functionals. The ZIP archive contains all optimised structures (in PDB format). See DOI: https://doi.org/10.1039/d5cp04069h.

Acknowledgements

This research was funded by the Deutsche Forschungsgemeinschaft (German Research foundation, DFG) through a Heisenberg fellowship (project no. 455871835). The author gratefully acknowledges the computing time made available to him on the high-performance computer “Lise” at the NHR center NHR@ZIB. This center is jointly supported by the Federal Ministry of Education and Research and the state governments participating in the NHR (https://www.nhr-verein.de).

References

1. M. Okrusch and H. E. Frimmel, Mineralogy – An Introduction to Minerals, Rocks, and Mineral Deposits, Springer, Berlin, Germany, 2010.
2. E. M. Flanigen, J. M. Bennett, R. W. Grose, J. P. Cohen, R. L. Patton, R. M. Kirchner and J. V. Smith, Nature, 1978, 271, 512–516.
3. S. Leon and G. Sastre, J. Phys. Chem. C, 2022, 126, 2078–2087.
4. H. Yu, L. A. Villaescusa, Z. R. Gao and M. A. Camblor, Angew. Chem., Int. Ed., 2024, 63, e202412170.
5. M. D. Foster, A. Simperler, R. G. Bell, O. Delgado-Friedrichs, F. A. Almeida Paz and J. Klinowski, Nat. Mater., 2004, 3, 234–238.
6. I. Petrovic, A. Navrotsky, M. E. Davis and S. I. Zones, Chem. Mater., 1993, 5, 1805–1813.
7. P. M. Piccione, C. Laberty, S. Yang, M. A. Camblor, A. Navrotsky and M. E. Davis, J. Phys. Chem. B, 2000, 104, 10001–10011.
8. A. Navrotsky, O. Trofymluk and A. A. Levchenko, Chem. Rev., 2009, 109, 3885–3902.
9. K. de Boer, A. P. J. Jansen and R. A. van Santen, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 52, 12579–12590.
10. A. F. Combariza, D. A. Gomez and G. Sastre, Chem. Soc. Rev., 2013, 42, 114–127.
11. E. I. Román-Román and C. M. Zicovich-Wilson, Chem. Phys. Lett., 2015, 619, 109–114.
12. M. Catti, B. Civalleri and P. Ugliengo, J. Phys. Chem. B, 2000, 104, 7259–7265.
13. M. Fischer and R. J. Angel, J. Chem. Phys., 2017, 146, 174111.
14. B. Civalleri, C. M. Zicovich-Wilson, P. Ugliengo, V. R. Saunders and R. Dovesi, Chem. Phys. Lett., 1998, 292, 394–402.
15. R. Astala, S. M. Auerbach and P. A. Monson, J. Phys. Chem. B, 2004, 108, 9208–9215.
16. M. A. Zwijnenburg, F. Corá and R. G. Bell, J. Phys. Chem. B, 2007, 111, 6156–6160.
17. W. Kohn, Y. Meir and D. E. Makarov, Phys. Rev. Lett., 1998, 80, 4153–4156.
18. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
19. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
22. M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
23. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 041108.
24. H. Hay, G. Ferlat, M. Casula, A. P. Seitsonen and F. Mauri, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 144111.
25. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
26. J. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
27. M. Fischer, F. O. Evers, F. Formalik and A. Olejniczak, Theor. Chem. Acc., 2016, 135, 257.
28. M. Trachta, M. Rubeš and O. Bludský, J. Chem. Phys., 2022, 156, 094708.
29. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
30. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. M. Fischer, W. J. Kim, M. Badawi and S. Lebègue, J. Chem. Phys., 2019, 150, 094102.
32. A. Tkatchenko, R. A. Di Stasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
33. A. Albavera-Mata, C. M. Zicovich-Wilson, J. L. Gázquez, S. B. Trickey and A. Vela, Theor. Chem. Acc., 2018, 137, 26.
34. R. Dovesi, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. Bush, P. D'Arco, Y. Noël, M. Rérat, P. Carbonnière, M. Causà, S. Salustro, V. Lacivita, B. Kirtman, A. M. Ferrari, F. S. Gentile, J. Baima, M. Ferrero, R. Demichelis and M. De La Pierre, J. Chem. Phys., 2020, 152, 204111.
35. J. C. Pacheco-Kato, J. M. Del Campo, J. L. Gázquez, S. B. Trickey and A. Vela, Chem. Phys. Lett., 2016, 651, 268–273.
36. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöß, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
37. J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369.
38. C. Baerlocher, D. H. Brouwer, B. Marler and L. McCusker, Database of Zeolite Structures, 2025, https://www.iza-structure.org/databases/.
39. E. Grifoni, G. Piccini, J. A. Lercher, V.-A. Glezakou, R. Rousseau and M. Parrinello, Nat. Commun., 2021, 12, 2630.
40. K. Stanciakova, J. N. Louwen, B. M. Weckhuysen, R. E. Bulo and F. Göltl, J. Phys. Chem. C, 2021, 125, 20261–20274.
41. F.-X. Coudert and D. Kohen, Chem. Mater., 2017, 29, 2724–2730.
42. M. Fischer, ChemPhysChem, 2023, 24, e202300022.
43. M. Fischer, CrystEngComm, 2024, 26, 3795–3807.
44. A. Domke, M. Fischer, M. Jakubowski, A. Pacholak, M. Ratajczak, A. Voelkel and M. Sandomierski, J. Drug Delivery Sci. Technol., 2024, 99, 105997.
45. M. Fischer, D. A. Chaney, O. A. Uwumwonse, E. Neumann, I. Spieß, C. Wiggers and E. M. Schmidt, Microporous Mesoporous Mater., 2026, 401, 113912.
46. S. Lehtola, C. Steigemann, M. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5.
47. T. Hirose, K. Kihara, M. Okuno, S. Fujinami and K. Shinoda, J. Mineral. Petrol. Sci., 2005, 100, 55–69.
48. J. Li, Z. R. Gao, Q.-F. Lin, C. Liu, F. Gao, C. Lin, S. Zhang, H. Deng, A. Mayoral, W. Fan, S. Luo, X. Chen, H. He, M. A. Camblor, F.-J. Chen and J. Yu, Science, 2023, 379, 283–287.
49. Z. R. Gao, H. Yu, F.-J. Chen, A. Mayoral, Z. Niu, Z. Niu, X. Li, H. Deng, C. Márquez-Álvarez, H. He, S. Xu, Y. Zhou, J. Xu, H. Xu, W. Fan, S. R. G. Balestra, C. Ma, J. Hao, J. Li, P. Wu, J. Yu and M. A. Camblor, Nature, 2024, 628, 99–103.
50. P. Lu, J. Xu, Y. Sun, R. Guillet-Nicolas, T. Willhammar, M. Fahda, E. Dib, B. Wang, Z. Qin, H. Xu, J. Cho, Z. Liu, H. Yu, X. Yang, Q. Lang, S. Mintova, X. Zou and V. Valtchev, Nature, 2024, 636, 368–373.
51. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
52. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
53. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
54. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
55. K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 081101.
56. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 235149.
57. H. Peng and J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 2017, 95, 081105.
58. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
59. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
60. B. Hammer, L. Hansen and J. Nørskov, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
61. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
62. M. Swart, M. Solà and F. M. Bickelhaupt, J. Chem. Phys., 2009, 131, 094103.
63. M. Swart, M. Solà and F. M. Bickelhaupt, J. Comput. Chem., 2011, 32, 1117–1127.
64. A. D. Becke, Phys. Rev. A:At., Mol., Opt. Phys., 1988, 38, 3098–3100.
65. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785–789.
66. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
67. A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560.
68. A. D. Boese, N. L. Doltsinis, N. C. Handy and M. Sprik, J. Chem. Phys., 2000, 112, 1670–1678.
69. A. D. Boese and N. C. Handy, J. Chem. Phys., 2001, 114, 5497–5503.
70. A. D. Boese and N. C. Handy, J. Chem. Phys., 2002, 116, 9559–9569.
71. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
72. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403.
73. J. P. Perdew and Y. Wang, Phys. Rev. B:Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
74. V. R. Cooper, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 161104.
75. K. Berland and P. Hyldgaard, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 035412.
76. J. Klimeš, D. Bowler and A. Michaelides, J. Phys.:Condens. Matter, 2010, 22, 022201.
77. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 195131.
78. E. D. Murray, K. Lee and D. C. Langreth, J. Chem. Theory Comput., 2009, 5, 2754–2762.
79. I. Hamada, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 121103.
80. J. Aragó, E. Ortí and J. C. Sancho-García, J. Chem. Theory Comput., 2013, 9, 3437–3443.
81. S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154.
82. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
83. J. Claudot, W. J. Kim, A. Dixit, H. Kim, T. Gould, D. Rocca and S. Lebègue, J. Chem. Phys., 2018, 148, 064112.
84. F. Tran, J. Stelzl and P. Blaha, J. Chem. Phys., 2016, 144, 204120.
85. F. Tran, L. Kalantari, B. Traoré, X. Rocquefelte and P. Blaha, Phys. Rev. Mater., 2019, 3, 063602.
86. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
87. H. Peng, Z.-H. Yang, J. P. Perdew and J. Sun, Phys. Rev. X, 2016, 6, 041005.
88. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215.
89. J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Phys. Rev. B, 2022, 106, 075422.
90. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–67.
91. R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 117–124.
92. L. Goerigk, J. Phys. Chem. Lett., 2015, 6, 3891–3896.
93. H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293.
94. G. A. Lager, J. D. Jorgensen and F. J. Rotella, J. Appl. Phys., 1982, 53, 6751–6756.
95. J. J. Pluth, J. V. Smith and J. Faber, J. Appl. Phys., 1985, 57, 1045–1049.
96. M. P. Attfield and A. W. Sleight, Chem. Commun., 1998, 601–602.
97. I. Bull, P. Lightfoot, L. A. Villaescusa, L. M. Bull, R. K. B. Gover, J. S. O. Evans and R. E. Morris, J. Am. Chem. Soc., 2003, 125, 4342–4349.
98. L. A. Villaescusa, P. Lightfoot, S. J. Teat and R. E. Morris, J. Am. Chem. Soc., 2001, 123, 5453–5459.
99. S. E. Boulfelfel, P. I. Ravikovitch, L. Koziol and D. S. Sholl, J. Phys. Chem. C, 2016, 120, 14140–14148.
100. K. De Wispelaere, S. Bailleul and V. Van Speybroeck, Catal. Sci. Technol., 2016, 6, 2686–2705.
101. M. Fischer, J. Phys. Chem. C, 2019, 123, 1852–1865.
102. K. Alexopoulos, M.-S. Lee, Y. Liu, Y. Zhi, Y. Liu, M.-F. Reyniers, G. B. Marin, V.-A. Glezakou, R. Rousseau and J. A. Lercher, J. Phys. Chem. C, 2016, 120, 7172–7182.
103. M. Fischer and J. Brauer, ChemistryOpen, 2024, 13, e202300273.
104. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
105. K. N. Lausch, R. El Haouari, D. Trzewik and J. Behler, J. Chem. Phys., 2025, 163, 034101.
106. A. O. von Lilienfeld and A. Tkatchenko, J. Chem. Phys., 2010, 132, 234109.
107. J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621.
108. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
109. G. Sastre and A. Corma, J. Phys. Chem. C, 2010, 114, 1667–1673.
110. C. J. Dawson, R. Sanchez-Smith, P. Rez, M. O'Keeffe and M. M. J. Treacy, Chem. Mater., 2014, 26, 1523–1527.
111. M. Fischer, ChemPhysChem, 2021, 22, 2063–2077.
112. J. Klimeš and D. P. Tew, J. Chem. Phys., 2019, 151, 234108.

---