Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
NMR relaxometry probes solvent-polarity-dependent molecular interactions in stimuli-responsive lyogels
Muhammad Adrian *a,
Kathrin Marina Eckert
*a,
Kathrin Marina Eckert bh,
M. Raquel Serial
bh,
M. Raquel Serial ac,
Artyom Tsanda
ac,
Artyom Tsanda de,
Lukas Rennpferdt
de,
Lukas Rennpferdt g,
Stefan Benders
g,
Stefan Benders ah,
Hoc Khiem Trieu
ah,
Hoc Khiem Trieu g,
Tobias Knopp
g,
Tobias Knopp def,
Irina Smirnova
def,
Irina Smirnova bh and
Alexander Penn
bh and
Alexander Penn ah
ah
aInstitute of Process Imaging, Hamburg University of Technology, Hamburg, Germany. E-mail: muhammad.adrian@tuhh.de
bInstitute of Thermal Separation Processes, Hamburg University of Technology, Hamburg, Germany
cDepartment of Process and Energy, Delft University of Technology, Delft, The Netherlands
dInstitute for Biomedical Imaging, Hamburg University of Technology, Hamburg, Germany
eSection for Biomedical Imaging, University Medical Center Hamburg-Eppendorf, Hamburg, Germany
fFraunhofer Research Institution for Individualized and Cell-based Medical Engineering IMTE, Lübeck, Germany
gInstitute of Microsystems Technology, Hamburg University of Technology, Hamburg, Germany
hUnited Nations University Hub on Engineering to Face Climate Change at the Hamburg University of Technology, United Nations University Institute of Water, Environment and Health, Hamburg, Germany
First published on 11th December 2025
Abstract
Stimuli-responsive gels demonstrate macroscopic changes upon exposure to external stimuli, offering potential for the development of adaptive chemical reactors. Early investigations into hydrogels established that crosslinked polymer networks experience reversible volume phase transitions, with temperature, pH, and solvent composition governing swelling and shrinking dynamics. Although hydrogels behavior in aqueous environments has been extensively characterized, lyogels that incorporate organic solvents remain comparatively underexplored, despite their potential for enhanced chemical compatibility and functional versatility. Here, we investigate how solvent polarity and crosslinking density govern the swelling behavior, pore formation, and molecular-scale dynamics of poly(N-isopropylacrylamide)-based lyogels. Using a combination of swelling measurement, scanning electron microscopy, and multiscale NMR relaxometry and diffusometry, we demonstrate that solvent polarity fundamentally alters lyogel structure and dynamics. Lyogels swollen in a high-polarity solvent exhibits macroporous networks and slower solvent exchange rates, whereas a low-polarity solvent induces shrinkage, denser microstructures, faster solvent exchange rates, and stronger surface interactions. These results establish a mechanistic framework linking thermodynamic affinity, solvent dynamics, and microstructural confinement to macroscopic gel responsiveness. This framework provides guidance for tailoring lyogels in dynamic environments, with potential applications in adaptable and tunable chemical reactors.
1. Introduction
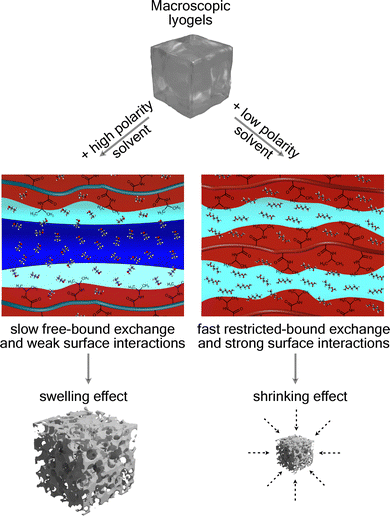
Stimuli-responsive gels have emerged as a versatile class of materials that exhibit macroscopic changes in response to external stimuli. Their adaptive behavior makes them highly attractive for applications in flow control systems,1 sensor applications,2 and functionally adaptable-tunable or SMART reactors.3,4 Earlier studies from Tanaka et al.5–8 demonstrated that polymer networks, such as hydrogels, can undergo volume phase transition in response to environmental changes. Since then, extensive studies have shown that external stimuli, such as temperature, pH, electric fields, and chemical species, can induce the swelling and shrinking of such networks.9,10 Hoare and Kohane11 later emphasized the importance of tuning solvent–polymer interactions to achieve precise control over material responses.Gels consist of a three-dimensional polymer network that can retain many times their own mass of solvents within the polymer matrix (Fig. 1). Based on the solvent absorbed in the matrix, a distinction can be made between hydrogels, which contain water, and lyogels, which contain organic solvents. The use of organic solvents not only broadens chemical compatibility but also enables the introduction of diverse functional groups, enhancing responsiveness and allowing property tuning for specific applications.12
 | ||
| Fig. 1 Schematic illustration of lyogels spanning from macroscopic to microscopic scale. Unlike hydrogels, lyogels incorporate organic solvents instead of water. | ||
In this study, we focus on lyogels synthesized from N-isopropylacrylamide (NIPAM), a thermoresponsive polymer with amphiphilic character arising from hydrophilic amide groups and hydrophobic isopropyl side chains.13–15 This dual affinity controls molecular-scale solvent–polymer interactions to macroscopic swelling behavior, making NIPAM-based lyogels an ideal platform for studying solvent effects across a range of polarities.
Understanding the fundamental physical and chemical principles that occur at the microstructural level during swelling and shrinking is crucial for optimizing lyogels for practical applications.16 Despite significant progress in understanding stimuli-responsive hydrogels, the mechanisms by which solvent–polymer interactions and microstructural dynamics control the macroscopic lyogel behavior remain incompletely understood. To address this gap, a multiscale characterization approach is required. Swelling measurements provide valuable data on macroscopic changes and kinetics.16,17 In comparison, advanced microscopic techniques such as (environmental) scanning electron microscopy (ESEM/SEM), transmission electron microscopy (TEM), or micro-computed tomography (µCT) offer insights into microstructural properties.18–20 Most of these microscopic techniques require dried samples or demand extensive methodological development to be adapted for use of gels in the solvated state.18,19 As a result, correlating the structures obtained using these methods with solvent-induced properties is often not straightforward. Moreover, small-angle X-ray scattering (SAXS) can complement these techniques by providing structural and morphological information on wet gels, but it is a highly resource-intensive method.21,22
Another useful technique is nuclear magnetic resonance (NMR) relaxometry and diffusometry, which enable non-invasive access into molecular structure dynamics. NMR relaxometry probes relaxation times that are sensitive to molecular motion, confinement, and structural heterogeneity.23,24 NMR diffusometry, on the other hand, probes molecular displacement and transport properties, providing insight into translational motion over micrometer length scales. The diffusion measurement is based on the pulsed-field gradient spin-echo (PGSE) technique introduced by Stejskal and Tanner,25 which was later complemented by Cotts through the development of the pulsed-field gradient stimulated echo (PGSTE) method,26 enabling quantification of diffusion in heterogeneous environments. Many studies have adapted NMR techniques to elucidate solvent dynamics and microstructural features such as binding interactions within polymer networks, while tailoring these methods to meet diverse experimental conditions and application-specific requirements.27–32 For example, D’Agostino et al.33,34 investigated swelling-induced structural changes in gelatin gels and molecular motion in emulsion gels using NMR relaxometry and diffusometry, while Knörgen et al.35 examined swelling and diffusion in hydrogels through 1H NMR imaging. Despite these advances, to the best of the author's knowledge, no similar investigations have been performed in lyogels.
To investigate polymer and solvent dynamics at the molecular level, 1H NMR relaxometry and diffusometry were complemented by other analytical techniques to develop a framework for understanding solvent–polymer interactions in NIPAM-based lyogels with varying solvent polarities. A multi-technique approach is essential for characterizing poly(N-isopropylacrylamide) (pNIPAM) lyogels in various solvents and capturing their structural complexity. Macroscopic swelling measurements provide initial insights into how solvent polarity and crosslinker concentration influence the lyogel's bulk behavior, while SEM allows for visualization of changes in the porous microstructure across solvents. At the molecular scale, NMR relaxometry and diffusometry enable mechanistic interpretation of solvent–polymer interactions and transport phenomena within the lyogel matrix.
2. Experimental
2.1. Lyogel synthesis and preparation
Lyogels were synthesized by dissolving 2.175 g of NIPAM with N,N′-methylenebisacrylamide (MBA) in 23 g of deionized water, followed by nitrogen degassing for 30 min. Sodium metabisulfite (SMBS, 2.5 mg) and ammonium persulfate (APS, 2.5 mg), were each dissolved in 1 mL of deionized water and subsequently added to the mixture. Lyogels with varying crosslinker concentrations (0.007–0.050 g crosslinker per g monomer) were prepared using MBA as the crosslinker. The resulting lyogel monoliths were cast in 10 mL syringes sealed with parafilm. After polymerization, the gels were cut into cylinders approximately 1.5 cm in height and thoroughly washed with deionized water for three days.Lyogel synthesis was performed via a two-step solvent exchange protocol designed to probe the influence of solvent polarity. Ethanol (EtOH) was selected as a representative high-polarity solvent, while butyl acetate (BuAc) was the low-polarity solvent. For EtOH-based lyogels, the samples underwent three successive solvent exchanges followed by equilibration for 48 h at 25 °C. In the case of BuAc-based lyogels, an additional solvent exchange step was introduced to transition from EtOH to BuAc. This transition induced shrinkage, which altered the final gel structure and properties.
2.2. Standard gel characterization
In addition to the NMR-based analysis, the macroscopic swelling was determined by calculating the degree of swelling (Dos):
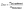 | (1) |
For this analysis, the equilibrated lyogel was weighed and subsequently dried at 40 °C (± 0.1 °C) for 48 h to obtain the mass of the dried polymer.
Furthermore, the porous structure of the lyogel was characterized using SEM. Prior to imaging, the samples were dried with supercritical CO2. The lyogels were sealed in bags of filter paper and dried in a custom-built autoclave with a volume of 250 mL. The drying was performed for 3 h at 60 °C and 125 bar to preserve their native pore architecture. The samples were then cut open and sputtered with a thin carbon layer of approximately 10 nm. The SEM analysis was conducted using a Zeiss Supra VP55 equipped with a cold field emission gun and in-lense detector for imaging. The measurements were performed using an acceleration voltage of 5.00 kV. Supercritical drying was employed to preserve the native structure.18 It must be emphasized that the SEM images only reflect the structure of the dried samples, which could often exhibit a certain shrinkage upon CO2 drying. Therefore, no absolute conclusions about the pore structure in the wet gels can be drawn from them. Only trends of the different structure in varying solvents can be inferred from this data. This structural imaging information from SEM analysis was used to correlate with NMR relaxometry and diffusometry, providing insights into the relationship between microstructure and solvent dynamics at the molecular level.
2.3. NMR measurement
Equilibrated lyogels with five distinct crosslinker concentrations, prepared in EtOH and BuAc, were left under ambient conditions for 3 min to facilitate bulk solvent evaporation. Subsequently, the samples were cut to a uniform mass of approximately 20 mg and placed into custom microfabricated glass holders, produced via selective laser-induced etching (SLE) (Fig. 2). This holder was inserted into a 5 mm NMR tube and was specifically designed to ensure consistent sample positioning and optimal signal quality.All NMR experiments were performed using a 60 MHz benchtop spectrometer equipped with a pulsed field gradient system and temperature control maintained at 26 °C (Spinsolve 60, Magritek, Germany). Three key parameters were quantified: (a) transverse relaxation time (T2) measured using the Carr–Purcell–Meiboom–Gill (CPMG) sequence with an echo time of 300 µs, (b) longitudinal–transverse relaxation correlation (T1–T2) measurements performed with an inversion recovery–CPMG (IR-CPMG) sequence using an echo time of 300 µs, and (c) self-diffusion coefficient (D) determined using the pulsed gradient stimulated echo (PGSTE) method with a diffusion time (Δ) of 80 ms (Tables 1 and 2). Parameters such as echo time and diffusion time were carefully optimized to account for the time sensitivity of the lyogels. As prior studies report no measurable dependence of PFG attenuation on diffusion times in hydrogel,33 the present measurements were treated as effectively diffusion-time independent. Dwell time and related acquisition parameters were further optimized to ensure reproducibility and adequate relaxation between scans.
| NMR relaxometry | CPMG | IR-CPMG |
|---|---|---|
| Echo time [µs] | 300 | 300 |
| Number of echoes | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Repetition time [s] | 15 | 21 |
| Number of points | 32 | 32 |
| Number of scans | 4 | 4 |
| NMR diffusometry | PGSTE |
|---|---|
| Diffusion time [ms] | 80 |
| Gradient pulse duration [ms] | 2 |
| Repetition time [s] | 15 |
| Max gradient strength [mT m−1] | 552 |
| Number of points | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
| Number of scans | 4 |
NMR data from three different batches of measurements were processed using custom Python scripts designed to analyze both one- and two-dimensional relaxation and diffusion datasets. Distribution functions of relaxation times from CPMG data were obtained using the inverse Laplace transform (ILT)36,37 with Tikhonov regularization (α = 0.1). The regularization parameter was selected using L-curve approach38 (see SI, Fig. S2) to balance between noise suppression and resolution, ensuring the identified peaks represent physically meaningful solvent populations. For methodological consistency, the same regularization parameter was applied to IR-CPMG data. Signal components with amplitudes exceeding 1% of the amplitude-normalized intensity were considered indicative of distinct populations. The diffusion data was processed using monoexponential fitting, assuming that the solvent molecules primarily exhibit free diffusion. To further quantify solvent–polymer interactions, binding dynamics were evaluated by calculating solvent exchange rates (kex) and standard Gibbs energy of binding (ΔBG°) at equilibrium state.39–41 Molecular exchange between two sites involves transitions between environments with different local relaxation properties. Under the slow exchange limit, free and bound solvent populations were resolved based on their characteristic T2 relaxation times, modeled as:
 | (2) |
| kex = kbinding + kdissociation | (3) |
and slow exchange conditions were defined by:
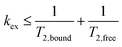 | (4) |
The binding constant (KB), describing the balance of bound and free solvent, was calculated as:
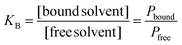 | (5) |
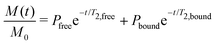 | (6) |
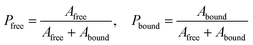 | (7) |
ΔBG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KB KB
| (8) |
3. Results and discussion
3.1. Standard characterization of lyogels
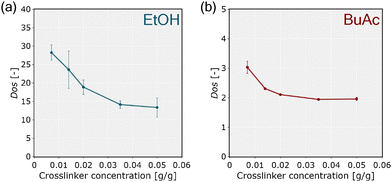
The macroscopic analysis of the Dos reveals solvent-induced shrinkage and the influence of crosslinker concentration on swelling behavior. While pNIPAM lyogels exhibited strong swelling in EtOH, significant shrinkage occured after solvent exchange to BuAc (Fig. 3). A study16 attributed this effect to the higher polarity of EtOH, which enhances solvent–polymer interactions, in contrast to those observed for BuAc. Furthermore, in the macroscopic analysis, decreasing swelling for increasing crosslinker concentrations could be observed in EtOH and BuAc. This effect was particularly pronounced at higher crosslinker concentrations, where the constrained polymer network restricted solvent absorption, leading to shrinkage. These observations align to previous studies highlighting how solvent polarity and crosslinker concentration affect hydrogel swelling.5,19,45A recent study by Eckert et al.16 utilized COSMO-RS (conductor-like screening model for real solvents)46 as thermodynamic model to provide a quantitative framework for predicting solvent–polymer interactions based on the molecular structure of the monomers. With this approach, quantitative predictions of activity coefficients, hydrogen bonding, and van der Waals interactions between NIPAM and the two solvents were provided. The model results confirmed that hydrogen bonding interactions prevail in EtOH, while in BuAc, weaker hydrogen bonding is formed (Table 3).
| Solvent | EtOH | BuAc |
|---|---|---|
| ln(γ∞i) | 0.026 | 0.813 |
| EHB [kJ mol−1] | −9.91 | −1.37 |
| EVdW [kJ mol−1] | −81.19 | −83.00 |
The theoretical calculations were consistent with the observed swelling equilibria. As expected, stronger interactions between the lyogel monomer and the solvent correlated with increased swelling behavior. The COSMO-RS calculations describe bulk properties, but do not account for structural effects, such as steric hindrance within the gel matrix. The calculations were performed under conditions of infinite dilution, representing a single monomer in a bulk solvent. Thus, the model is suitable for assessing component miscibility and predicting bulk thermodynamic properties. The model, however, does not capture surface interactions or structural constraints arising from the polymer network.
Furthermore, the significant differences in the macromolecular structure of lyogels prepared in EtOH compared to BuAc are consistently reflected by the SEM analysis (Fig. 4). While lyogels prepared in EtOH exhibit a macroporous structure, no distinct pore architecture could be identified in lyogels in BuAc based on the SEM analysis. The pore sizes in the BuAc-derived lyogels are significantly smaller and not resolvable by SEM, likely due to the pronounced shrinkage observed under these solvent conditions. Consequently, we conclude that a dense and collapsed polymer network is formed in the presence of BuAc.
3.2. NMR relaxometry and diffusometry
Based on solvent thermodynamic interactions with the polymer network and in accordance with previous studies on hydrogels and other porous media,32,47,48 NMR relaxometry further enables the differentiation of distinct solvent populations within the lyogel matrices. As illustrated schematically in Fig. 5, three distinct solvent populations could be identified within the lyogel: (i) bound solvent, which is strongly attached to polymer side chains, exhibiting severely restricted molecular motion and short T2 values; (ii) restricted solvent, weakly bound and confined between polymer chains, where partial hindrance of motion results in intermediate T2 values; and (iii) free solvent, unbound and freely mobile within the interconnected pore space of the polymer matrix, displaying high molecular mobility and long T2 relaxation times. This classification provides a useful framework for interpreting the relaxation populations obtained from NMR relaxometry and highlights the hierarchical nature of molecular dynamics in lyogels. | ||
| Fig. 5 Schematic illustration of pNIPAM interaction with solvents categorizing them into; bound solvent (where the first solvent interacts with the polymer side chain), restricted solvent (subsequent solvent molecules with limited mobility), and free solvent. Molecular structures used in figures were generated with Avogadro (version 1.2.0).49 | ||
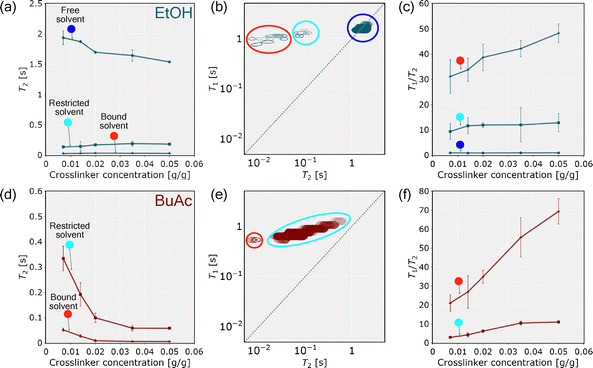
Analysis of CPMG relaxation data revealed three distinct T2 populations in lyogels swollen with EtOH, while only two were identified in lyogels swollen with BuAc (Fig. 6). This finding contrasts the typical observations in other porous media, where usually only two solvent populations, free and bound are detected. The presence of a third, intermediate population in lyogels highlights the complex solvent–polymer interaction mechanism unique to gels. The three T2 populations correspond to (i) free solvent (T2 ≈ 1 s), which is highly mobile and experience minimal interaction with the polymer network, detectable only in lyogels swollen with EtOH; (ii) restricted solvent (T2 ≈ 100 ms), which is partially confined within the polymer mesh; and (iii) bound solvent (T2 ≈ 10 ms), which is closely associated with or interact onto the polymer backbone, exhibiting significantly reduced mobility (Fig. 6).
These relaxation times reflect the degree of confinement and solvent–polymer interactions, with shorter T2 values corresponding to more restricted, decreased mobility environments (solid-like). Furthermore, an increase in the crosslinker concentration resulted in a systematic decrease in T2 values across identified populations, with the most pronounced reductions observed in the free solvent fraction of lyogels in EtOH and in the restricted solvent fraction of lyogels in BuAc (Fig. 7a and d). This trend indicates a denser, more compact polymer network, leading to increasingly reduced solvent mobility and enhanced shrinkage of the lyogels. These observations are consistent with earlier studies on crosslinking-dependent swelling and molecular dynamics in hydrogels, where increased crosslinking density reduces network porosity and solvent mobility.7,27,33
In addition to T2 relaxation times, T1–T2 correlation maps were examined, from which the T1/T2 ratios have been derived (Fig. 7b, c, e and f). The T1/T2 ratio serves as a probe for surface relaxation effects, owing to its sensitivity to molecular motion, and is commonly employed as an indicator of surface interaction strength.50 When molecules interact with a polymer surface, their rotational and translational motion are hindered, resulting in increased T1/T2 ratio.29,51 According to the Bloembergen–Purcell–Pound (BPP) theory,52 nuclear spin relaxation arises from local magnetic field fluctuations caused by molecular motion, characterized by the correlation time (τc). In low-viscosity fluids, where molecular motion is rapid (τc << 1/ω0, with ω0 being the Larmor frequency), both T1 and T2 are relatively long and of similar magnitude. In confined environments, for example near polymer surfaces, molecular motion becomes restricted, leading to enhanced surface relaxation for both T1 and T2, with T2 exhibiting higher sensitivity due to magnetic susceptibility induced internal field gradients.53 These gradients shorten T2 by inducing spin dephasing that further attenuates the signal and increases sensitivity to surface interactions. T1 is largely unaffected by such internal gradients,54 leading to increases in the T1/T2 ratio in liquids where stronger surface interactions are present. Consequently, a higher T1/T2 ratio reflects slower rotational and translational dynamics and stronger molecular interactions with the surrounding matrix.39 This effect is evident from the measurements, as the free solvent population in EtOH, which exhibits minimal interactions with the polymer surface, remains the least affected, despite a reduction in T2 relaxation times when crosslinker concentration increases (highlighted by the blue circle in Fig. 7a and c). As an initial step, T1–T2 correlation maps were evaluated, which provided further evidence for distinct solvent populations, in agreement with T2 relaxation profiles (in Fig. 7b and e, blue, cyan, and red circles mark distinct populations corresponding to free solvent, restricted solvent, and bound solvent, respectively). Notably, a free solvent population was observed exclusively in EtOH, as indicated by signal intensity in close proximity to the diagonal line (T1 = T2), which is characteristic of freely moving solvent with minimal motional restriction (Fig. 7b). The absence of a free solvent in BuAc is attributed to the shrinkage of the polymer network, which expels the free solvent during lyogel shrinkage, leaving only restricted or bound fractions (Fig. 7e). When examining the relaxation time distributions derived from the T1–T2 correlation maps, the T1 distributions are comparatively narrow, whereas the T2 distributions exhibit pronounced broadening, consistent with previous observations in hydrogels.55 This difference arises from the distinct sensitivity of the two relaxation mechanisms to molecular motion and structural heterogeneity within the lyogel network.52 The T1 relaxation primarily reflects molecular reorientation processes at Larmor frequencies and is therefore less affected by spatial restrictions. In contrast, T2 relaxation is strongly influenced by slow molecular motions and local magnetic field inhomogeneities caused by pore geometry and solvent–polymer interactions. Consequently, variations in pore size and connectivity within the heterogeneous lyogel matrix lead to a broad distribution of T2 values, while the T1 relaxation remains largely invariant across different regions of the lyogels. These observations further confirm the progressive confinement of pores and the enhanced surface interactions, as reflected by the increasing T1/T2 ratio with higher crosslinker concentration (Fig. 7c and f).
Comparing lyogels in EtOH and BuAc highlights pronounced differences in their relaxation behavior. Relative to EtOH, lyogels in BuAc exhibit lower T2 values and predominantly high T1/T2 ratios, consistent with more restricted molecular motion and enhanced surface interactions. This difference can be attributed to the smaller pore sizes in BuAc, which result in stronger surface interactions compared to the more macroporous network in EtOH. Referring to the thermodynamic modeling (Table 3), stronger solvent–polymer interactions were predicted in EtOH than in BuAc, which may appear to contradict the interpretation derived from the NMR relaxometry discussed above. Although both approaches consider solvent–polymer interactions, they capture fundamentally different aspects: thermodynamic modeling reflects the bulk properties of the system, whereas NMR relaxometry provides direct insight into the changing interactions at the polymer surface. Furthermore, since the COSMO-RS calculations were performed on monomers and oligomers,16 this technique can only capture a limited impact of the lyogels’ structural properties. In contrast, NMR relaxometry enables the analysis of both structural characteristics and solvent to polymer–surface interactions or surface interaction strength.
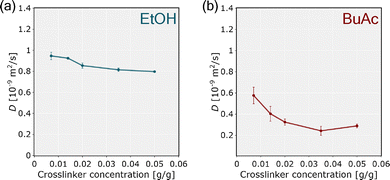
Since solvent-induced shrinkage influences not only the structural changes but also the diffusive properties of lyogels, the subsequent analysis focuses on the solvent self-diffusion coefficient as a quantitative measure for comparison. The self-diffusion coefficients of bulk EtOH and BuAc were determined by NMR diffusometry, yielding values of 1.11 × 10−9 m2 s−1 and 1.62 × 10−9 m2 s−1, respectively. The comparison of effective self-diffusion coefficient (D) showed that lyogels in BuAc exhibited higher restriction than those in EtOH (Fig. 8). The larger deviation between the bulk and effective (D) values further evidences that molecular transport within the lyogel matrix is more hindered in BuAc than in EtOH. The results align with the previously determined higher fraction of free solvent in EtOH-based lyogels compared to those in BuAc, as revealed by the ILT analysis (Fig. 6). The lower self-diffusion coefficient in BuAc lyogels is likely attributable to stronger surface interactions and increased microstructural complexity. These factors reduce the accessible bulk volume for diffusion, resulting in a smaller and more constrained porous network, supported by the SEM micrographs (Fig. 4). The observed trends are evident not only when comparing the effects of EtOH and BuAc on the porous structure, but also with increasing crosslinker concentration, indicating a more compact network in highly crosslinked lyogels. These findings are consistent with previous studies on diffusion in polymer networks, where solvent quality, network architecture, or polymer chain dynamics were shown to significantly influence diffusivity.31,33,56
3.3. Solvent exchange rate and standard Gibbs energy of binding
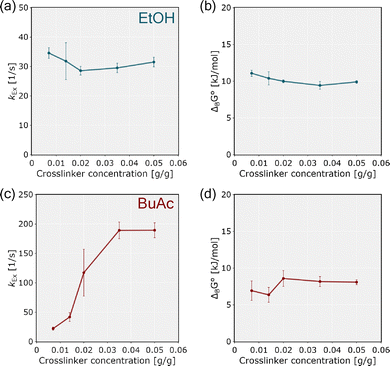
Binding dynamics within lyogels were characterized by quantifying solvent exchange rates (kex) between different populations and by determining the standard Gibbs energy of binding (ΔBG°) at equilibrium, following the principles outlined in Section 2.3. It is important to note that these analyses are intended for qualitative interpretation; for a more comprehensive understanding, they should be complemented with further methods such as molecular dynamics simulations.In the context of solvent exchange rate analysis, higher solvent exchange rates were observed mainly in BuAc compared to EtOH, indicating faster exchange between restricted and bound states, and lower kinetic barriers within the pNIPAM polymer network (Fig. 9a and c). This observation is consistent with the weaker solvent–polymer interactions predicted by COSMO-RS simulations. In contrast, EtOH exhibited lower solvent exchange rates, reflecting stronger binding affinities and increased kinetic limitations.
When examining the standard Gibbs energy of binding, the results provide only limited scope for a direct comparison between EtOH and BuAc. A lower ΔBG° was observed in BuAc, suggesting a stronger thermodynamic affinity for the polymer side chains, likely the hydrophobic isopropyl groups of pNIPAM, shaped by the polymer's steric environment (Fig. 9b and d). In contrast, the moderately higher ΔBG° in EtOH may result from limited access to the amide groups, which serve as primary binding sites and are located within hydrophobic domains.
These results reveal fundamental differences in solvent–polymer interactions. In BuAc, simulation model reveals weaker thermodynamic binding, while experimental measurements demonstrate faster solvent exchange between the two sites, together indicating rapid exchange between the different binding states of the solvent within network. The solvent molecules solvating the polymer chains are continuously replaced due to these accelerated exchange rates, leading to changes in the solvation states of the chains, ultimately resulting to structural collapse and gel shrinkage. In EtOH, on the other hand, stronger binding and slower exchange occur due to its higher hydrogen-bonding potential and the restricted access to binding sites imposed by the polymer's steric environment, thereby stabilizing the lyogels in a swollen state. As has been concluded in earlier works,11,28,57 our findings further emphasize the need to balance thermodynamic affinity and steric accessibility when designing lyogels with tailored transport properties and responsive behavior.
3.4. Proposed solvent–polymer interaction model
Based on these experimental findings, a mechanistic model of solvent–polymer interactions for pNIPAM in EtOH and BuAc is proposed (Fig. 10). In EtOH, strong hydrogen bonding with the amide groups facilitates solvent binding to the polymer side chains. In contrast, BuAc binds preferentially to the hydrophobic isopropyl groups and exhibits strong surface interactions with the polymer backbone. Structurally, pNIPAM in EtOH exhibits network swelling and the formation of macropores, while in BuAc a more compact structure with reduced porosity is observed. At equilibrium in EtOH, slow solvent exchange rates are indicative of strong solvent–polymer interactions, which support the formation of a stable solvation layer around the polymer backbone and side chains. This stabilizing effect contributes to preserve the gel's structural integrity. In contrast, BuAc exhibits fast exchange, which limit the formation of such a solvation layer. As a result, the polymer matrix experiences reduced solvation and increased structural contraction, ultimately leading to shrinkage of the lyogel network.NMR relaxometry and diffusometry provide molecular level evidence for these behaviors, revealing fundamental differences in solvent–polymer interactions between EtOH and BuAc, which represents solvents of differing polarity. While a high-polarity solvent promotes swelling through slower exchange kinetics and side-chain binding limitation, a low-polarity solvent induces shrinkage due to rapid exchange and enhancing surface interactions.
4. Conclusions
This study demonstrates the effectiveness of combining NMR relaxometry and diffusometry with complementary techniques such as macroscopic swelling analysis and SEM imaging to investigate the microstructural dynamics of pNIPAM lyogels in solvents of varying polarity. In these systems, solvent polarity critically influences solvent–polymer interactions, exchange kinetics, and network morphology. EtOH, a high-polarity solvent with strong hydrogen bond energy, binds primarily to the amide groups, inducing swelling and macropore formation through slower solvent exchange. In contrast, BuAc, a low-polarity solvent, binds to hydrophobic isopropyl groups and exhibits faster solvent exchange, leading to a denser network, stronger surface interactions, and greater confinement.These contrasting behaviors illustrate the importance of balancing thermodynamic affinity, kinetic accessibility, and steric factors when designing lyogels for targeted performance. This work not only deepens our understanding of solvent–polymer interactions but also provides insight into the structural and steric properties relative to bulk models, while highlighting NMR as a powerful tool for guiding the design of responsive soft materials for applications in dynamic chemical environments. These findings elucidate the interplay between molecular-scale dynamics, network structure, steric constraints, and thermodynamic binding, offering new insights into lyogel responsiveness and enabling rational design of materials for adaptive applications, including flow control and process intensification in functionally adaptable-tunable reactors. In future work, ultra-fast NMR measurement approaches can be implemented to overcome conventional timing limitations and enable the characterization of dynamic confinement behavior and rapidly evolving lyogel microstructures that remain inaccessible with standard acquisition methods.
Author contributions
Muhammad Adrian: conceptualization, data curation, formal analysis, investigation, visualization, writing – original draft, writing – review & editing. Kathrin Marina Eckert: conceptualization, data curation, formal analysis, investigation, writing – review & editing. M. Raquel Serial: conceptualization, formal analysis, supervision, writing – review & editing. Artyom Tsanda: conceptualization, writing – review & editing. Lukas Rennpferdt: resources. Stefan Benders: conceptualization, supervision, writing – review & editing. Hoc Khiem Trieu: funding acquisition. Tobias Knopp: funding acquisition, writing – review & editing. Irina Smirnova: funding acquisition, writing – review & editing. Alexander Penn: funding acquisition, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article, including Python scripts are available at https://doi.org/10.15480/882.16324.The data supporting this article are included in both the main text and the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04032a.
Acknowledgements
This project is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1615 – 503850735. The authors gratefully acknowledge valuable discussions with Johannes Gmeiner. This paper was copy-edited with the assistance of the AI technology ChatGPT (v5.0) in order to improve clarity and readability. The authors have thoroughly checked all the proposed edits and take full responsibility for the content of this manuscript.References
- A. Richter, D. Kuckling, S. Howitz, T. Gehring and K.-F. Arndt, J. Microelectromech. Syst., 2003, 12, 748–753 CrossRef.
- G. Gerlach, M. Guenther, J. Sorber, G. Suchaneck, K.-F. Arndt and A. Richter, Sens. Actuators, B, 2005, 111, 555–561 CrossRef.
- X. Hu, J. Karnetzke, M. Fassbender, S. Drücker, S. Bettermann, B. Schroeter, W. Pauer, H.-U. Moritz, B. Fiedler and G. Luinstra, et al., Chem. Eng. J., 2020, 387, 123413 CrossRef CAS.
- X. Hu, C. Spille, M. Schlüter and I. Smirnova, Ind. Eng. Chem. Res., 2020, 59, 19458–19464 CrossRef CAS.
- T. Tanaka, Phys. Rev. Lett., 1978, 40, 820 CrossRef CAS.
- Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365–1371 CrossRef CAS.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- T. Tanaka, L. O. Hocker and G. B. Benedek, J. Chem. Phys., 1973, 59, 5151–5159 CrossRef CAS.
- T. Tanaka, I. Nishio, S.-T. Sun and S. Ueno-Nishio, Science, 1982, 218, 467–469 CrossRef CAS PubMed.
- R. Yoshida, K. Uchida, Y. Kaneko, K. Sakai, A. Kikuchi, Y. Sakurai and T. Okano, Nature, 1995, 374, 240–242 CrossRef CAS.
- T. R. Hoare and D. S. Kohane, Polymer, 2008, 49, 1993–2007 CrossRef CAS.
- N. A. Guziewicz, A. Best, B. Perez-Ramirez and D. Kaplan, Biomaterials, 2011, 32(10), 2642–2650 CrossRef CAS PubMed.
- T. Tanaka, D. Fillmore, S.-T. Sun, I. Nishio, G. Swislow and A. Shah, Phys. Rev. Lett., 1980, 45, 1636 CrossRef CAS.
- S. Hirotsu, Y. Hirokawa and T. Tanaka, J. Chem. Phys., 1987, 87, 1392–1395 CrossRef CAS.
- H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249 CrossRef CAS.
- K. M. Eckert, S. Müller, G. A. Luinstra and I. Smirnova, Fluid Phase Equilib., 2024, 586, 114182 CrossRef CAS.
- K. Poschlad and S. Enders, J. Chem. Thermodyn., 2011, 43, 262–269 CrossRef CAS.
- A. Rege, Adv. Eng. Mater., 2023, 25, 2201097 CrossRef CAS.
- K. M. Eckert, J. Bonsen, A. Hajnal, J. Gmeiner, J. Hasse, M. Adrian, J. Karsten, P. A. Kißling, A. Penn and B. Fiedler, et al., Fluid Phase Equilib., 2025, 114462 CrossRef CAS.
- B. Fu, H. Luo, F. Wang, G. Churu, K. Chu, J. C. Hanan, C. Sotiriou-Leventis, N. Leventis and H. Lu, J. Non-Cryst. Solids, 2011, 357, 2063–2074 CrossRef CAS.
- P. Gupta, K. Vermani and S. Garg, Drug Discovery Today, 2002, 7, 569–579 CrossRef CAS PubMed.
- M. Jaspers, A. C. H. Pape, I. Voets, A. E. Rowan, G. Portale and P. Kouwer, Biomacromolecules, 2016, 17(8), 2642–2649 CrossRef CAS PubMed.
- A. Abragam, The principles of nuclear magnetism, Oxford university press, 1961 Search PubMed.
- P. T. Callaghan, Principles of nuclear magnetic resonance microscopy, Clarendon press, 1993 Search PubMed.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- R. Cotts, M. Hoch, T. Sun and J. Markert, J. Magn. Reson., 1989, 83, 252–266 CAS.
- K. Saalwächter, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 51, 1–35 CrossRef.
- J. M. Giussi, M. I. Velasco, G. S. Longo, R. H. Acosta and O. Azzaroni, Soft Matter, 2015, 11, 8879–8886 RSC.
- E. V. Silletta, M. I. Velasco, C. G. Gomez, M. C. Strumia, S. Stapf, C. Mattea, G. A. Monti and R. H. Acosta, Langmuir, 2016, 32, 7427–7434 CrossRef CAS PubMed.
- W. S. Price, Concepts Magn. Reson., 1997, 9, 299–336 CrossRef CAS.
- J. Kärger, M. Avramovska, D. Freude, J. Haase, S. Hwang and R. Valiullin, Adsorption, 2021, 27, 453–484 CrossRef.
- B. Maillet, R. Sidi-Boulenouar and P. Coussot, Langmuir, 2022, 38, 15009–15025 CrossRef CAS PubMed.
- C. D'Agostino, R. Liuzzi, L. F. Gladden and S. Guido, Soft Matter, 2017, 13, 2952–2961 RSC.
- C. D’Agostino, V. Preziosi, C. Schiavone, M. V. Maiorino, G. Caiazza and S. Guido, Soft Matter, 2025, 21, 3022–3029 RSC.
- M. Knörgen, K.-F. Arndt, S. Richter, D. Kuckling and H. Schneider, J. Mol. Struct., 2000, 554, 69–79 CrossRef.
- R. Serial and F. Jaureguialzo Zahnd, Spinsolveproc, 2025 DOI:10.5281/zenodo.17079446.
- P. D. Teal and C. Eccles, Inverse Probl., 2015, 31, 045010 CrossRef.
- C. R. Vogel, Inverse Probl., 1996, 12, 535 CrossRef.
- P. T. Callaghan, Translational dynamics and magnetic resonance: principles of pulsed gradient spin echo NMR, Oxford University Press, 2011 Search PubMed.
- X. Du, Y. Li, Y.-L. Xia, S.-M. Ai, J. Liang, P. Sang, X.-L. Ji and S.-Q. Liu, Int. J. Mol. Sci., 2016, 17, 144 CrossRef PubMed.
- J. S. Jiménez and M. J. Bentez, Biophysica, 2024, 4, 298–309 CrossRef.
- K.-J. Dunn, D. J. Bergman and G. A. LaTorraca, Nuclear magnetic resonance: Petrophysical and logging applications, Elsevier, 2002, vol. 32 Search PubMed.
- W. Jencks, Proc. Natl. Acad. Sci. U. S. A., 1981, 78(7), 4046–4050 CrossRef CAS PubMed.
- M. Popovic, Microb. Risk Anal., 2022, 22, 100231 CAS.
- T. Canal and N. A. Peppas, J. Biomed. Mater. Res., 1989, 23, 1183–1193 CrossRef CAS PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- V. M. Gun’ko, I. N. Savina and S. V. Mikhalovsky, Gels, 2017, 3, 37 CrossRef PubMed.
- H. Sugiyama, K.-i Katoh, N. Sekine, Y. Sekine, T. Watanabe and T. Ikeda-Fukazawa, Chem. Phys. Lett., 2024, 856, 141655 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- P. McDonald, J.-P. Korb, J. Mitchell and L. Monteilhet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011409 CrossRef CAS PubMed.
- C. D'Agostino, J. Mitchell, M. D. Mantle and L. F. Gladden, Chem. – Eur. J., 2014, 20, 13009–13015 CrossRef PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679 CrossRef CAS.
- D. Weber, J. Mitchell, J. McGregor and L. F. Gladden, J. Phys. Chem. C, 2009, 113, 6610–6615 CrossRef CAS.
- K. Washburn, C. Eccles and P. Callaghan, J. Magn. Reson., 2008, 194, 33–40 CrossRef CAS PubMed.
- J. C. Gore, M. S. Brown, J. Zhong, K. F. Mueller and W. Good, Magn. Reson. Med., 1989, 9, 325–332 CrossRef CAS PubMed.
- L. G. Linck, S. A. M. Ochoa, M. Ceolin, H. Corti, G. A. Monti, F. V. Chávez and R. H. Acosta, Microporous Mesoporous Mater., 2020, 305, 110351 CrossRef CAS.
- M. C. Koetting, J. T. Peters, S. D. Steichen and N. A. Peppas, Mater. Sci. Eng., R, 2015, 93, 1–49 CrossRef PubMed.
| This journal is © the Owner Societies 2026 |