Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrophobic hydration of analgesics and diltiazem complexes explored by electrochemical impedance spectroscopy and diffusion-ordered spectroscopy
Ryotaro
Koga†
a,
Takatoshi
Kinoshita†
a,
Masahiro
Ishiguro
a,
Momoko
Fujita
a,
Hitoshi
Chatani
a,
Hikaru
Kataoka
 a,
Hideshi
Yokoyama
a,
Hideshi
Yokoyama
 a,
Takehisa
Hanawa
a,
Takehisa
Hanawa
 a,
Isao
Shitanda
a,
Isao
Shitanda
 b and
Satoru
Goto
b and
Satoru
Goto
 *ac
*ac
aFaculty of Pharmaceutical Sciences, Tokyo University of Science, 6-3-1 Niijuku, Katsushika, Tokyo 125-8585, Japan. E-mail: 3b22537@alumni.tus.ac.jp; 3b19522@alumni.tus.ac.jp; 3a19003@ed.tus.ac.jp; 3b18578@alumni.tus.ac.jp; 3b17645@alumni.tus.ac.jp; hikaru276@gmail.com; yokoyama@rs.tus.ac.jp; t-hanawa@rs.tus.ac.jp
bFaculty of Science and Technology, Tokyo University of Science, 2641 Yamazaki, Noda, Chiba 278-8510, Japan. E-mail: shitanda@rs.tus.ac.jp
cResearch Institute for Science and Technology, Tokyo University of Science, 2641, Yamasaki, Noda, Chiba, Japan. E-mail: s.510@rs.tus.ac.jp
First published on 2nd January 2026
Abstract
In the context of drug–drug interactions, the combination of benzodiazepine (BDZ) or benzothiazepine (BTZ) antidepressant/hypnotics with commonly used analgesics, including over-the-counter nonsteroidal anti-inflammatory drugs (NSAIDs), has been reported to decrease the effectiveness of analgesics. This study aimed to analyze the diffusion behavior of analgesics and diltiazem (DTZ), which was used as a structural model of BDZ/BTZ, in solution using NMR diffusion-ordered spectroscopy (DOSY) and electrochemical impedance spectroscopy (EIS). Analgesics and DTZ were dispersed as free entities in deuterated dimethyl sulfoxide (an aprotic solvent), whereas oligomeric clathrates were observed in heavy water (a protic solvent). These findings suggest that the hydrophobic hydration of the complex formed by acidic and basic drugs may involve intermolecular electrostatic interactions embedded within the hydrogen-bonding network in water.
1. Introduction
The aging global population and the increasing prevalence of cancer and lifestyle-related diseases have led to greater reliance on the combined use of multiple drugs.1,2 This practice, known as polypharmacy, is generally defined as the concurrent use of five or more medications.3,4 It is common among patients with complex chronic diseases and cancer.5,6 Although polypharmacy aims to achieve therapeutic effects that surpass those of a single active pharmaceutical ingredient (API) by leveraging the benefits of multiple APIs and minimizing adverse effects, it presents significant challenges.7–9 Drug–drug interactions, which can either enhance or reduce API efficacy or cause adverse reactions, are often underexplored in randomized controlled trials (RCTs).10Pharmacokinetic and pharmacodynamic interactions, such as those mediated by drug-metabolizing enzymes (e.g., cytochromes) and drug-binding proteins (e.g., serum albumin), have been reported in studies assessing the side effects and changes in API efficacy.11–13 However, the physicochemical interactions that influence drug properties such as water solubility and API bioavailability remain unclear.14,15 Understanding these interactions is crucial, as they directly affect a drug's clinical performance and warrant further investigation.16–20 Knowledge sharing among contemporary research institutions and enterprises has optimized API development, with a focus on enhancing bioavailability and clinical efficacy. While improving administrative efficiency and drug delivery is valuable, it is also crucial to consider the deductive proposition and inevitability of reaching the site of action. Pharmaceutical companies often prioritize assessing the dissolved states of APIs as an effective strategy for delivering them to their intended therapeutic targets.
Regarding the solubility of acidic analgesics—classified as nonsteroidal anti-inflammatory drugs (NSAIDs, Scheme 1)—and the basic benzodiazepine derivative diltiazem (DTZ, Scheme 1), Kinoshita et al.15 reported that the presence of DTZ reduced the water solubility of these analgesics. Changes in 1H-NMR chemical shifts indicated that interactions between analgesics and DTZ varied depending on the solvent used: methanol-d4 (a protic solvent that can dissolve apolar associated complexes due to hydrophobic hydration, consuming the entropy) and dimethyl sulfoxide-d6 (DMSO-d6) (an aprotic polar solvent that separately disperses solutes, producing the entropy).18 This suggests that solvent effects have a clear, dominant impact on intermolecular interactions.14,20
 | ||
Scheme 1 Chemical structures and physicochemical properties of APIs. Strictly, aspirin is not classified as an NSAID. While the pKa and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P were referred to Avdeef's Gold Standard,25–29 those of LXP were from the Loxonin® interview form, Daiichi Sankyo Co., Ltd. P were referred to Avdeef's Gold Standard,25–29 those of LXP were from the Loxonin® interview form, Daiichi Sankyo Co., Ltd. | ||
The use of NSAIDs in patients with cardiac conditions is clinically discouraged because of their adverse effects on the cardiovascular system. To investigate the drug interaction between the daily and frequently (sometimes excessively) used acidic and basic drugs, i.e., analgesics and benzodiazepine or benzothiazepine drugs, respectively, their derivative DTZ (used as an antianginal and antihypertensive drug) is a more available reagent than psychotropic drugs under domestic legal regulations. The present authors considered that DTZ corresponds to a model derivative of such heptacyclic aza-aliphatic antidepressants/hypnotics,21,22 which impose a considerable environmental load owing to their psychotropic effects on humans (prescribed for children), and other animals.23 Clinical doses of these antidepressants cannot be within the essential minimum, and analgesics are commonly and frequently used (which could be used excessively and lead to drug abuse).24 Their drug interactions are a prominent issue for patients.
Intermolecular interactions between acidic and basic drugs suggested that enthalpy–entropy compensation, which governs solvation and dissolution, primarily affects the solubility of these mixtures.30 Although the prevailing opinion is that acid–base intermolecular interactions involve the formation of a single acid–base pair, at temperatures above room temperature, a basic anesthetic lidocaine (LDC) reduced the solubility of an acidic analgesic indomethacin (INM) without causing precipitation, suggesting that suspended flocculation may occur instead of the formation of poorly soluble acid–base pairs.18 Hydrophobic counterions can shield the charges of these solutes, thereby promoting direct contact between the solutes and counterions. Furthermore, concentration-dependent changes in the fluorescent spectra of analgesic molecules indicated monomeric, dimeric, and polymeric aggregations.20 These processes disrupt the hydration shell, increasing entropy. Consequently, the dissolution enthalpy and entropy are balanced, allowing for adjustments in the solubility of hydrophobic solutes. Subsequently, hydrophobic electrolytes can lead to liquid–liquid phase separation (LLPS).31–35
On the other hand, for solid or amorphous medicinal resources, the mechanism of solubility enhancement for certain drugs has been studied in ionic liquids (ILs) and deep eutectic solvents (DESs),36–39 which form supramolecular assemblies through supramolecular synthons (often involving hydrogen-bonding acceptors and donors).40–43 Drugs in the DES state were considered innovative for their ability to solubilize and regulate API crystal growth at room temperature, with the added potential to control polymorphism.44 A theoretical study on the dissolution of LDC in DES focused on the dissolution of heteroaromatic drugs in DES.45 The supramolecular synthons that equilibrate in cocrystals or the amorphous phase might not be preserved upon dissolution. Generally, well-dissolving solids create a supersaturation in solution, but their solubility should be temporary.46–48 Therefore, we should focus on maintaining suspension in solution or dispersion to maintain concentration rather than on the release of the API from the solid. The authors cannot believe that all intermolecular interactions between a drug and its solubilizing agent form a soluble complex.
In this study, we developed a method to measure the diffusion coefficient to investigate the dissolution behavior of hydrophobic drugs in aqueous solutions and to track their intermolecular interactions.46,47,49
2. Materials and methods
2.1. Materials
Aspirin (ASP, CAS RN 50-78-2), diclofenac (DCF) sodium salt (15307-79-6), INM (53-86-1), and naproxen (NPX, 22204-53-1) were purchased from Fujifilm Wako Pure Chemical Industries Ltd (Osaka, Japan). DCF acid (15307-86-5), DTZ (42399-41-7) hydrochloride (33286-22-5), ibuprofen (IBP, 15687-27-1), loxoprofen (LXP) acid (68767-14-6), and LXP sodium salt dihydrate (226721-96-6) were obtained from Tokyo Kasei Industry Co., Ltd (Tokyo, Japan). Simultaneously, (S)-(+)-ketoprofen (KTP, 22071-15-4) was sourced from Combi-Blocks Inc. (San Diego, CA, USA). Special-grade reagents were used in all cases. Distilled deionized water generated by the Milli-Q ultrapure water purification system (Millipore Billerica, MA, USA), with a resistivity exceeding 18 MΩ, was used.2.2. Electrochemical impedance spectroscopy (EIS)
To determine the single impedance of a drug, 1.0, 3.3, 6.7, and 10.0 mmol dm−3 aqueous solutions of ASP, DCF, IBP, KTP, LXP, NPX, and DTZ sodium salts were prepared by adding equivalent moles of 1 M aqueous sodium hydroxide as needed. Cyclic voltammetry (CV) and EIS measurements were performed by adding 5.0 mL of these solutions to a triode cell consisting of a glass cell (HX-111), with a glassy carbon working electrode (HX-W8), platinum counter electrode (HX-C13), and silver–silver chloride reference electrode (HX-R14) (Hokuto Denko Co., Ltd, Tokyo, Japan) at a measurement temperature of 295 K using the Vertex 1A (Ivium Technologies B. V., AJ Eindhoven, The Netherlands), as shown in Fig. S1. The AC frequency ranged from 500 kHz to 1.0 Hz, and the applied voltage was within 200 mV of the reference voltage. For the mixed solution of ASP and DTZ, a sample solution adjusted to 10 mmol dm−3 was prepared at constant volume and diluted to obtain uniformly measured 0.50, 1.7, 3.3, and 5.0 mmol dm−3 solutions. The cell constants were determined by calibration using a 10 mmol dm−3 KCl aqueous solution for each measurement. Fig. 1a shows the Bode plot analysis used to obtain the solution resistance, Rsol (Ω), which represents the flattening of the impedance on the high-frequency side. The molar electrical conductivity Λ (S m2 mol−1) is expressed by the following equation using the solution resistance Rsol obtained from the Bode plot: | (1) |
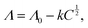 | (2) |
| Λ0 = λ+ + λ−. | (3) |
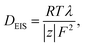 | (4) |
2.3. Differential scanning calorimetry (DSC)
Thermal analyses were conducted using a DSC 8230 instrument (Rigaku Co., Ltd, Tokyo, Japan) with the analgesics or DTZ (5.0 mg) in an aluminum pan. Alumina of equal weight as the sample served as the reference material for the heat flow. Once the pan was sealed, the temperature was scanned from 300 K under a nitrogen gas flow (30 mL min−1) at a rate of 5.0 K min−1 until an endothermic peak, indicating the melting of the crystals, was observed.152.4. Diffusion-ordered spectroscopy (DOSY)
NMR DOSY spectra were measured using a 400 MHz NMR spectrometer (JNM-ECZ 400 S, Japan Electronics Co., Ltd, Tokyo, Japan), which showed that bipolar pulse pairs stimulated the echo longitudinal eddy-current delay (BPPLED).52 A solution was prepared using heavy water (D2O) as the protic solvent and dimethyl sulfoxide-d6 (DMSO-d6) as the aprotic solvent, yielding a sample concentration of 1.5 w/v% or higher.52 The molecular forms of analgesics dissolved in D2O were dispersed in an equivalent molar amount of aqueous sodium hydroxide solution and in sufficient ethanol. The mixture was then dried under reduced pressure in a rotary evaporator and heated to dryness at a temperature below the melting point of the analgesic sodium salts. The formation of sodium salts was assessed by measuring their melting points using DSC.15When the DTZ hydrochloride salt was dissolved in DMSO-d6, a small amount of water was added, followed by a few drops of trimethylamine. The crystals were dried overnight in a desiccator at 298 K to adjust their molecular form.15 The DOSY measurements were conducted at 303 K, and the relaxation time was optimized to 7.0–14 s. The duration of the pulsed-field gradient and the diffusion time were adjusted to achieve a residual signal with a maximum field strength of 10%.53 The Stokes radius of the solute was calculated from the diffusion coefficient obtained using the Stokes–Einstein equation.
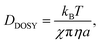 | (5) |
3. Results
3.1. Diffusion coefficients determined using EIS experiments
Electrochemical impedance spectroscopy (EIS) is a technique that measures the impedance of an object by applying a small alternating current (AC) voltage while controlling the oxidation–reduction reaction and AC frequency.56–60 EIS is commonly used to study ionic liquids and innovative battery materials in solution.51,61 However, its application in the pharmaceutical industry remains limited.62,63 As the drugs we studied are organic electrolytes, their diffusion coefficients and viscosities in an electric field can be determined using the Nernst–Einstein equation.44 This requires measuring the electrical resistance at a voltage range where redox reactions do not occur, thereby reflecting the mobility of the solute ions.52,64–66To investigate the electrochemical behaviors of the analgesics and DTZ, the impedance (|Z|) of the aqueous drug solutions was measured using the setup shown in Fig. S1. The acidic and analgesics analyzed included ASP, DCF, IBP, KTP, LXP, and NPX, whereas the basic drug used was DTZ. The drugs were dissolved in water as their sodium or hydrochloride salts. CV measurements were conducted to determine whether redox reactions occurred within the applied voltage range for each sample (Fig. S2). As shown in Fig. 1a, no redox peaks were observed, indicating that the pure solution resistance solely contributed to the impedance measurements.
Fig. 1b presents the molar electrical conductivity (Λ, S cm2 mol−1) plotted against the square root of LXP concentration (see Fig. S4 for references and other APIs). According to Kohlrausch's square root law, the data confirmed the electrochemical behavior of all drugs. The limiting molar conductivity (Λ0, S cm2 mol−1) was calculated, representing the sum of the transference numbers (λ) of analgesic anions, DTZ cations, and their respective counterions. The individual λ values for ionic species were derived from the net λ values and are displayed in Table 1.
| APIs | λ/S cm2 mol−1 | D EIS/10−9 m2 s−1 | D DOSY/10−9 m2 s−1 |
|---|---|---|---|
| a An EIS measurement for INM acid failed because of its poor solubility, which prevents obtaining linearity on the Λ − C1/2 diagram. | |||
| ASP | 81.840 | 2.156 | 0.713 |
| DCF | 28.926 | 0.762 | 0.586 |
| IBP | 61.862 | 1.629 | 0.577 |
| INM | n.d.a | n.d.a | 0.432 |
| KTP | 67.416 | 1.776 | 0.584 |
| LXP | 50.780 | 1.337 | 0.506 |
| NPX | 37.040 | 0.976 | 0.518 |
| DTZ | 12.586 | 0.332 | 0.322 |
| Mean (μ) | 56.644 ± 24.004 | 1.439 ± 0.632 | 0.527 ± 0.116 |
| s.d. (σ) | |||
The transference numbers of the sodium cations and chloride anions were determined in advance using EIS measurements of their respective inorganic salts. A deviation from linearity was observed only for hydrochloric acid, which was attributed to the proton jump mechanism,67 in which hydrogen ions rapidly transfer charge through the aqueous solvent. The calculated transference numbers for the inorganic salts are consistent with literature values.68–70 Using the Nernst–Einstein equation and the transference numbers, the diffusion coefficients of the drug ions (DEIS) were calculated and represented in units of m2 s−1.
3.2. Diffusion coefficients determined using NMR DOSY experiments
Pulsed-field gradient nuclear magnetic resonance (PFG-NMR) is another technique for determining diffusion coefficients. This was achieved by analyzing the attenuation of NMR signals arising from self-diffusion due to Brownian motion.53 Diffusion-ordered spectroscopy (DOSY), which utilizes PFG-NMR, separates 1H-NMR peaks based on their respective diffusion coefficients. Unlike EIS, DOSY is not limited to electrolytes, making it an ideal method for studying the solvent effects in both protic and aprotic solvents.18,54To evaluate the impact of the solvent environment on drug interactions, diffusion coefficients were measured using NMR DOSY in an aprotic solvent (DMSO-d6) and a protic solvent (D2O). The diffusion coefficients of the drugs in D2O (DDOSY, m2 s−1) are presented in Table 1.
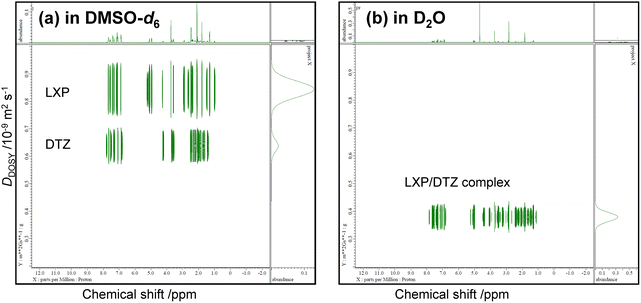
Fig. 2 shows the DOSY spectra for LXP/DTZ mixtures in DMSO-d6 and D2O, with signal assignments available in Fig. S6. Distinct diffusion peaks corresponding to the LXP-enriched and DTZ-enriched signal sets were observed in DMSO-d6, while only one diffusion peak was detected in D2O (excluding the solvent peak). Fig. S7–S11 present comparable results for mixtures of other analgesics. The diffusion constants of the DLZ-enriched signals in DMSO-d6 exhibited variations, indicating that the hydrodynamic radius of the DLZ-enriched particles changed depending on the coexistence of the acidic drugs.
Table 2 presents the hydrodynamic radii (a/nm) and hydrodynamic volumes (V/nm3) for each drug, calculated from DDOSY of neat APIS and analgesic/DTZ complexes using the Stokes–Einstein equation. Because D2O and DMSO-d6 have relatively high viscosities, it was assumed that convection in the sample tube could be neglected in the comparative study of the complex of acidic analgesics and basic DTZ, which exhibits a strong attractive interaction.
| D DOSY/10−9 m2 s−1 | Radiusa/nm | Volume/nm3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DMSO-d6 | D2O | DMSO-d6 | D2O | DMSO-d6 | D2O | Ratiob | |||
| Analgesic | DTZ | Complex | Analgesic | DTZ | Complex | ||||
| a Hydrodynamic radii a were calculated using eqn (5), with the solvent parameters χD2O = 4 and χDMSO = 6. b Particle volume ratios represent the hydrodynamic volumes of the complexes divided by those of neat analgesics in D2O. c Reposted from Table 1. | |||||||||
| DTZ | 0.190 | 0.322c | 0.595 | 0.595 | 0.210 | 0.539 | |||
| ASP | 0.233 | 0.713c | 0.470 | 0.368 | 0.104 | 0.050 | |||
| ASP/DTZ | 0.917 | 0.669 | 0.445 | 0.119 | 0.164 | 0.589 | 0.004 | 0.204 | 4.11 |
| DCF | 0.233 | 0.586c | 0.470 | 0.447 | 0.104 | 0.089 | |||
| DCF/DTZ | 0.722 | 0.559 | 0.395 | 0.152 | 0.196 | 0.663 | 0.007 | 0.292 | 3.27 |
| IBP | 1.010 | 0.557c | 0.108 | 0.470 | 0.001 | 0.104 | |||
| IBP/DTZ | 0.613 | 0.882 | 0.474 | 0.178 | 0.124 | 0.553 | 0.002 | 0.169 | 1.62 |
| INM | 0.349 | 0.432c | 0.313 | 0.607 | 0.031 | 0.223 | |||
| INM/DTZ | 0.738 | 0.611 | 0.437 | 0.148 | 0.179 | 0.600 | 0.006 | 0.126 | 0.97 |
| KTP | 0.604 | 0.584c | 0.181 | 0.449 | 0.006 | 0.090 | |||
| KTP/DTZ | 0.643 | 0.786 | 0.458 | 0.170 | 0.139 | 0.572 | 0.003 | 0.187 | 2.07 |
| LXP | 0.506c | 0.518 | 0.139 | ||||||
| LXP/DTZ | 0.849 | 0.638 | 0.372 | 0.129 | 0.171 | 0.704 | 0.005 | 0.350 | 2.52 |
| NPX | 0.261 | 0.518c | 0.419 | 0.506 | 0.074 | 0.129 | |||
| NPX/DTZ | 0.435 | 0.535 | 0.448 | 0.252 | 0.205 | 0.585 | 0.009 | 0.200 | 1.55 |
Fig. S5a shows the correlation between hydrodynamic volume and molecular weight for the analgesics. Fig. S5b shows the correlation between these and the Corey–Pauling–Koltun (CPK) volumes of the analgesics. These illustrate the partial linearity, [hydrodynamic volume] = 1.171 [CPK volume] − 0.1334 (r2 = 0.983, n = 5, except for KTP and DCF). The slope of this regression line suggests that the hydrophobic hydration shell compresses the analgesic molecules. The estimated hydrodynamic volumes, based on the Mw of KTP, DCF, and LXP, as well as on the CPK volumes of KPT and DCF, were insufficient. LXP has a considerable molecular weight, but a small CPK volume, suggesting that its particles in D2O can be condensed to a high density. The compressed conformation of LPX results in a small hydrodynamic volume. As the CPK volumes of KTP and DCF were not small, we speculated that intermolecular interactions caused the keto- or imine-linked aromatic rings to be packed in the dissolved particles, unlike those of ASP, IBP, NPX, and INM.
The hydrodynamic volumes of the complex in D2O were once four times larger than those of the neat analgesics, indicating the ability to form high- or low-density complexes between analgesics and DTZ in protic solvents. This unique intermolecular interaction between the analgesics and DTZ occurs in D2O, indicating that solute ionization and solvent effects are confined to the protic environment. These findings suggest the potential for liquid–liquid phase separation (LLPS) particles stabilized by the hydrophobic hydration shell of the water–molecule network.31–35
3.3. Diffusion coefficient analysis using regression models
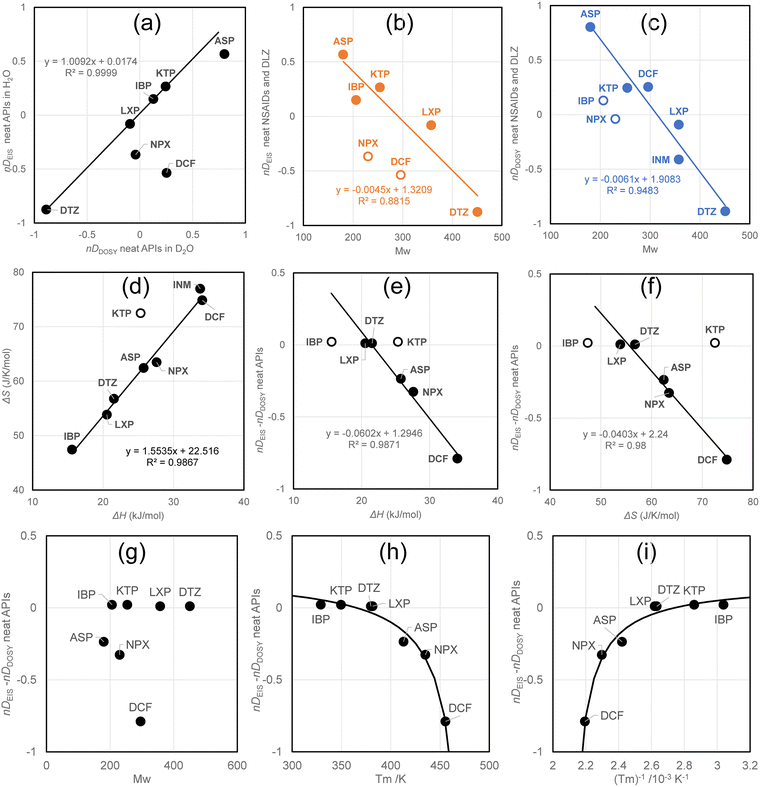
The EIS and DOSY experiments provided the diffusion coefficients of the analgesics and DTZ; however, they were not identical. In the AC electrochemical experiments, the analytes were exposed to an electric field that polarized them. In pulsed-field gradient DOSY experiments, the magnetic field is assumed to influence electrons rather than the molecular-size dipole moments. Consequently, the DEIS values (with a mean of 1.4391 ± 0.632) were overestimated more than the DDOSY (with a mean of 0.527 ± 0.116), as shown in Table 1. Although this systematic tendency would be rational, as mentioned above, we focused on the properties of the drugs based on their values determined in the same experiments. Therefore, the observed diffusion coefficients were normalized to nDEIS and nDDOSY using eqn (6), with the average value adjusted to zero.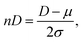 | (6) |
Fig. 3a illustrates the positive correlation between the normalized diffusion coefficients, nDEIS and nDDOSY, indicating that DCF and NPX are outliers. Subsequently, regression analyses for nDEIS and nDDOSY were conducted as a function of the molecular weight (Mw, g mol−1) of APIs, as shown in Fig. S5c and d. Except for NPZ and DCF, a strong correlation between nDEIS and molecular weight was demonstrated, whereas the relationship between nDDOSY and molecular weight posed challenges for IBP and NPX. These findings differ from those of previous regression analyses for the hydrodynamic volume, suggesting that a causal relationship between the diffusion coefficient or hydrodynamic volume and molecular weight may not be necessary, but rather a coincidental correlation. Next, we examined the differences between nDEIS and nDDOSY.
Previously, we reported the melting temperatures (Tm, K) and fusion enthalpies (ΔH, kJ mol−1) of analgesics.15 The fusion entropy (ΔS, J K−1 mol−1) can be approximated using the Clausius definition, ΔS = ΔH/Tm.71,72Fig. 3d illustrates the enthalpy–entropy compensation,73,74 indicating a linear correlation, except for KTP, which exhibited a high entropy of fusion. According to Walden's rule for the fusion entropy of organic compounds, the fusion entropies of analgesics would increase with their conformational flexibility in the liquid phase. In particular, KTP has tight packing in the crystalline state or high diversity in the liquid state.
Fig. 3e and f illustrate the difference in the diffusion coefficients as a function of the fusion enthalpy and fusion entropy. Their linear correlations were confirmed; however, KTP exhibited a high enthalpy of fusion and fusion entropy. Furthermore, IBP was found to have low fusion enthalpy and entropy. Moritake et al.20 reported flocculation of KTP, NPX, and IBP, as indicated by bathochromic shifts in the fluorescence excitation wavelengths with increasing concentration.71,72 The comparison of these analgesics suggests that they tend to flocculate at low concentrations, whereas KTP is less easily flocculated.
However, we recognize the differences between nDEIS and nDDOSY as invariants of IBP, KTP, LXP, and DTZ. Fig. 3g shows the molecular weights corresponding to the differences between nDEIS and nDDOSY, indicating that this approach is ineffective. Fig. 3h shows a melting temperature diagram comparing nDEIS and nDDOSY. APIs with high melting temperatures exhibited low diffusion coefficients, resulting in reduced mobility due to flocculation. In the EIS experiments, a single anion species moved within an alternating electric field. In DOSY experiments, APIs with strong intermolecular associations may form flocculants. Therefore, nDDOSY was positioned higher than the correlation line in Fig. 3a. This perspective appears to be rational. We attempted to analyze the relationship between the nDEIS − nDDOSY difference and reciprocal temperature using a saturation curve, specifically a hyperbolic function (eqn (7)),75 as shown in Fig. 3i.
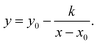 | (7) |
Fig. 4a presents a diagram of the plain DDOSY values for the analgesic/DTZ complex in D2O, along with the molecular weights of the neat analgesics, confirming the absence of discernible correlations. Screening was unable to identify any suitable structural descriptors (Hansch–Fujita parameters, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, CPK volume, polar surface area, pKa, and dipole moment). Fig. 4b shows the DDOSY values of the complexes and the pure analgesics in D2O. The diagram shows the two linear correlations. Although the quantitative gradients remain unclear (r2 = 0.6407), the difference between the regression lines indicates an intensity of approximately 20% (0.08 × 10−9 m2 s−1) on the ordinate. The upper group includes IBP, KTP, NPX, and INM (represented by triangles), whereas the lower group comprises ASP, DCF, and LXP (represented by rhombuses).
P, CPK volume, polar surface area, pKa, and dipole moment). Fig. 4b shows the DDOSY values of the complexes and the pure analgesics in D2O. The diagram shows the two linear correlations. Although the quantitative gradients remain unclear (r2 = 0.6407), the difference between the regression lines indicates an intensity of approximately 20% (0.08 × 10−9 m2 s−1) on the ordinate. The upper group includes IBP, KTP, NPX, and INM (represented by triangles), whereas the lower group comprises ASP, DCF, and LXP (represented by rhombuses).
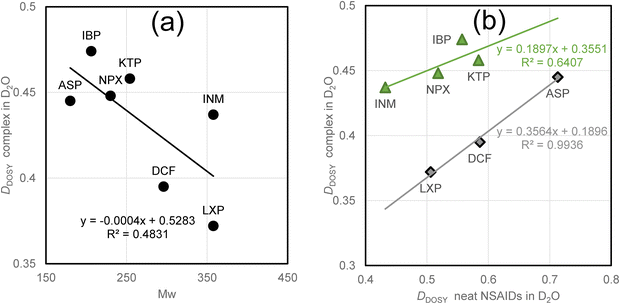 | ||
| Fig. 4 Single correlation of the diffusion coefficients observed for analgesics to molecular weights (a), and the diffusion coefficients for analgesics (b). | ||
DSC experiments yielded no evidence or relevant data to distinguish the analgesic/DTZ complex groups.15 In the empirical data, the individual hydrodynamic volume ratios of the complexes to the pure analgesics exceeded 2.5 in ASP, DCF, and LXP, resulting in notably low diffusion coefficients for the complexes. This suggests that these low coefficients were due to the affinities of ASP, DCF, and LXP for DTZ. In the previous section, it was noted that pure ASP, NPX, and DCF exhibited high flocculating abilities. In cases involving analgesics and DTZ, LXP was used instead of NPX. There are multiple hydrogen-bond acceptors and donors in ASP (acetyl group), DCF (imine and chloride), KTP (linking keto), and LXP (endocyclic keto), in addition to their COOH groups, which may facilitate intermolecular interactions among themselves and with DTZ. We propose that ASP, DCF, and LXP can form aggregate particles that contain DTZ and themselves within the hydrophobic hydration shells.
3.4. Hydrodynamic and electrochemical behavior of analgesic/DTZ mixtures
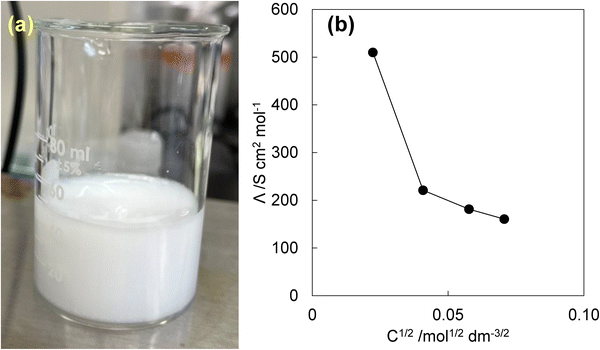
Diffusion coefficients were used to explore further interactions aimed at estimating solute ion radii and changes in particle size, reflecting intermolecular interactions in the analgesic/DTZ systems. Turbidity was observed when aqueous solutions of analgesics and DTZ were mixed, as illustrated in Fig. 5a with a 5.0 mmol dm−3 DCF/DTZ solution. The insoluble complex required extensive mixing and time to dissolve, consistent with earlier findings that analgesic solubility decreases in the presence of DTZ. EIS revealed that DTZ significantly altered the electrochemical behavior of analgesics (Fig. 5b).Fig. S3 shows the molar electrical conductivities of inorganic electrolytes. Although the Λ values of inorganic electrolytes correlate linearly with the square root of their concentration as stated in the Kohlrausch expression, the value for acetic acid (AcOH) demonstrates a downward convex curve concerning the square root of its concentration. This classic interpretation suggests that the Λ value depends on the activity of acetic acid. Acetic acid can be considered a weak electrolyte because carboxylic acids are only slightly dissociated at neutral pH. However, in a dilute solution, approximated as an ideal solution, acetic acid dissociates readily under an electric field.
Fig. S4 shows the Λ values for analgesics, illustrating a linear correlation with the square root of concentration over the examined range (excluding sufficiently diluted concentrations). By contrast, Fig. 5b shows that ASP in the DTZ solution did not exhibit the typical electrochemical behavior, indicating charge loss due to electrolyte aggregation at high concentrations. These findings support the idea that analgesics and DTZ form intermolecular complexes in water, influencing their hydrodynamic and electrochemical behaviors while reducing their solubility.
Although DOSY and EIS experiments with single APIs demonstrated the universality of diffusion, the EIS method cannot be used to determine the apparent diffusion coefficients of the analgesic/DTZ complexes. The effect of complexation on the drug dispersion was examined using DOSY.
4. Discussion
Our previous empirical study indicated that acidic and basic drugs interact in aqueous solutions through ionization of these electrolyte solutes and the solvent effects of water.14,16–19 In the Schröder–van Laar plot (van't Hoff plot) of the aqueous solubility of acidic analgesics and basic drugs (DTZ and LDC), a linear relationship was observed between the intercepts (representing melting entropy) and the slopes (indicating melting enthalpy).15 It was proposed that the analgesics and DTZ displayed sufficient hydrophobicity and were encapsulated within the hydrogen-bonding networks of the hydrophobic hydration shell. When the neutralization of acidic and basic drugs forms the analgesic/DTZ complex, the individual hydrated water networks in the surrounding area cannot be maintained and reorganize around the complex.30 The enthalpy of molecular interactions and the entropy of water network reorganization are balanced, leading to enthalpy–entropy compensation.73,74Moritake et al.20 found that propionic acid- and acetic acid-type NSAIDs form dimeric and polymeric clathrates at acidic pH, emitting fluorescence with bathochromically shifted excitation wavelengths that depend on concentration (which was not observed in oxicam-type NSAIDs without a COOH group). The intermolecular interactions of dimerization and oligomerization, along with the rearrangement of the surrounding hydrogen-bonding network, proceed via enthalpy–entropy compensation.
In general, it is well known that apolar gas molecules, such as oxygen and carbon dioxide, dissolve readily in water at low temperatures (as in pond water with fish or in carbonated beverages such as cold beer). As water molecules are perturbed by thermodynamic motion, which increases the dissolution entropy, the dissolution of gas molecules is exothermic. Frank and Evans55 stated that water adhered to hydrophobic solutes like microscopic icebergs. It is now still considered to correspond to a clathrate (e.g., methane hydrate).76 The gas molecules disperse as clathrates, which are wrapped in hydrophobic hydration shells (cages) consisting of hydrogen-bonding networks of the protic solvents.77 Based on these mechanisms, locally ordered protic solvents produce entropy when the clathrate is formed.
Theoretically, van der Waals’ interaction energy between two contacting methane molecules in free space is −2.5 × 1021 J, while it is −14 × 1021 J in water.78 The hydrophobic hydration shell of hydrophobic solutes plays a significant role in this process in water. No intermolecular interactions are involved in this primarily entropic phenomenon, which arises primarily from the rearrangement of hydrogen-bond configurations within the overlapping solvation zones as the two hydrophobic species combine. Three statistical thermodynamic approaches have been proposed for hydrophobic interactions. (i) The vapor bridge model is based on the attractive capillary force between the bridging nanoscopic bubbles. (ii) The water structure model suggests that an attractive hydration force is linked to changes in the density or ordering of water between two approaching hydrophobic surfaces. (iii) The electrostatic model is based on the attractive electrostatic forces between charges or dipoles at the surface.78
Based on our previous study mentioned above, we pondered that nanoscopic bubbles or ordered water shells (cages) around hydrophobic surfaces could not be maintained. They tend to reorganize into a new hydrogen-bonding network surrounding the solute complex. The fusion process resembles Ostwald ripening of bubbles but would reach thermodynamic equilibrium, balancing monomeric and oligomeric states for hydrophobic solutes. We emphasize that this equilibrium determines the apparent solubility of drugs and their acidic and basic drug complexes.
To verify this hypothesis, hydrodynamic experiments utilizing DOSY and EIS methods explored the relationship between the diffusion coefficients of individual drugs. Table 1 lists the observed DEIS and DDOSY values along with their means and standard deviations. The difference between the normalized DEIS and DDOSY values resulted in a hyperbolic curve plotted against the reciprocal of the melting temperature, suggesting that ASP, NPX, and DCF exhibit low diffusion coefficients in D2O. EIS was used to determine the mobility of the dissociated ions in an alternating electric field. By contrast, the DOSY measurements reflected the self-diffusion of the APIs, and the low diffusion coefficients of ASP, NPX, and DCF indicated flocculation, which corresponded to their high melting temperatures (probably reflecting their potent intermolecular interactions that can be maintained in the aqueous solution phase). These APIs are expected to form complexes comprising several molecules within the hydrophobic hydration shell of the protic solvent.
DOSY experiments were used to investigate analgesic/DLZ complexes, yielding self-diffusion coefficients in aprotic solvents (for isolated drugs) and in protic solvents (for complexed analgesics). In Table 2, the particle volume ratios of the complexes and the pure analgesics were determined from their self-diffusion coefficients. The ratios of the complexes with ASP, DCF, and LXP were large at 4.11, 3.27, and 2.52, respectively. In this work, we cannot provide rational evidence for why ASP, DCF, and LXP attenuate the diffusion coefficients of these complexes in the presence of DTZ. The chemical structures of ASP, DCF, and LXP contain rotatable bonds that can be altered through intermolecular hydrogen bonding with DTZ. Conversely, the bridge between the aromatic rings in KTP is a keto group conjugated with aryl groups, which may prevent the formation of rotamers via intermolecular hydrogen bonding with DTZ. In ASP, DCF, and LXP, the interaction could entangle the analgesics and DTZ molecules. We interpreted structural flexibility to lead to the formation of condensed particle aggregates, such as those observed in LLPS.79
Moritake et al.20 confirmed a bathochromic shift in emission and fluorescence wavelengths with increasing NSAID concentration, although DOSY spectroscopy and EIS experiments were unsuccessful. Fluorescence spectrometry is specific, highly accurate, and has a wide concentration range, provided the sample exhibits its own fluorescence, which is a strict requirement. Meanwhile, the EIS experiment's requirement that the sample be charged is not stringent: few drugs without acid dissociation or basification are generally found, except for nifedipine, carbamazepine, and other compounds. DOSY spectroscopy is available for the appropriate deuterated solvent. A limitation of these approaches is their narrow, detectable concentration range. The present study would be pioneering in the investigation of drug nano- and microscale aggregation in complementary ways.
5. Conclusion
EIS was used to study the electrochemical behavior of the analgesics and DTZ in aqueous solutions. The drugs show no redox activity in their salt form, with solution resistance being the only factor affecting impedance. Molar conductivity followed Kohlrausch's law, allowing the calculation of limiting molar conductivity (Λ0) and transference numbers (λ). The diffusion coefficients (DEIS) were determined using the Nernst–Einstein equation. NMR DOSY measurements in DMSO-d6 (aprotic) and D2O (protic) solvents showed separate diffusion peaks for analgesics and DTZ in DMSO-d6, but a single peak in D2O, indicating complex formation. Stokes radii and hydrodynamic volumes in D2O were larger, suggesting that analgesic/DTZ complexes form in water due to solute ionization and solvent effects, resulting in particles similar to ionic liquids or deep eutectic solvents stabilized by hydrophobic hydration. The normalized diffusion coefficients (nDEIS and nDDOSY) showed positive correlation with ASP, DCF, and NPX, although outliers weakened these correlations. Their high melting points enhance their ability to aggregate, increasing nDDOSY. DOSY experiments were performed to investigate analgesic/DTZ complexes, providing self-diffusion coefficients in both aprotic and protic solvents. The particle volume ratios of the complexes relative to pure ASP, DCF, and LXP were high at 4.11, 3.27, and 2.52, respectively. The chemical structures of ASP, DCF, and LXP contain rotatable bonds that can be modified via intermolecular hydrogen bonding with DTZ. Such interactions may entangle analgesic and DTZ molecules, promoting hydrophobic hydration.Author contributions
R. Koga and T. Kinoshita investigated, visualized, and wrote the original draft; M. Ishiguro assisted with the EIS examinations. M. Fujita provided the fundamental perspectives. H. Chatani, H. Kataoka, and H. Yokoyama edited and discussed; T. Hanawa financially supported for EIS systems; I. Shitanda provided experimental support and instructed procedures, and S. Goto supervised, conceptualized, and wrote.Conflicts of interest
The authors declare that they have no conflicts of interest.Abbreviations
| AC | Alternating current |
| AcOH | Acetic acid |
| API | Active pharmaceutical ingredient |
| ASP | aspirin |
| BPPLED | Bipolar pulse pairs stimulated echo longitudinal eddy current delay |
| CV | Cyclic voltammetry |
| DCF | Diclofenac |
| DMSO | Dimethyl sulfoxide |
| DOSY | Diffusion-ordered spectroscopy |
| DSC | Differential scanning calorimetry |
| DTZ | Diltiazem |
| EIS | Electrochemical impedance spectroscopy |
| IBP | Ibuprofen |
| INM | Indomethacin |
| KTP | (S)-(+)-Ketoprofen |
| LLPS | Liquid–liquid phase separation |
| LDC | Lidocaine |
| LXP | rac-Loxoprofen |
| NMR | Nuclear magnetic resonance |
| NPX | (S)-(+)-Naproxen |
| NPT | Constant particle number-isobaric-isothermal ensemble |
| NSAID | Non-steroidal anti-inflammatory drug |
| PFG | Pulsed-field gradient |
| QOL | Quality of life, and |
| RCT | Randomized controlled trial |
Data availability
The data supporting the findings of this study are available in the article and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03960f.Acknowledgements
This study was partially supported by JSPS KAKENHI (grant numbers 17K05366, 23540141, and 2054119; Kazushi Komatsu). The authors express their gratitude to Professor Kazushi Komatsu, Department of Mathematics, Kochi University, for his valuable discussions, and to Dr. Nariko Sawabe and Dr Motoo Iida, Faculty of Pharmaceutical Sciences, Tokyo University of Science, for their technical support with the PFG-NMR (DOSY) determination. We acknowledge Editage (https://www.editage.jp) for its English language editing services.References
- Scottish Government, “General Principles”, Polypharmacy Model of Care Group. Polypharmacy Guidance; Realistic Prescribing, Scottish Government, 3rd edn, 2018, pp. 8–22 Search PubMed.
- K. Barnett, S. W. Mercer, M. Norbury, G. Watt, S. Wyke and B. Guthrie, Epidemiology of multimorbidity and implications for health care, research, and medical education: a cross-sectional study, Lancet, 2018, 380, 37–43, DOI:10.1016/S0140-6736(12)60240-2.
- M. Khezrian, C. J. McNeil, A. D. Murray and P. K. Myint, An overview of prevalence, determinants and health outcomes of polypharmacy, Ther. Adv. Drug Saf., 2020, 11, 1–10, DOI:10.1177/2042098620933741.
- N. Masnoon, S. Shakib, L. K. Ellett1 and G.-E. Caughey, What is polypharmacy? A systematic review of definitions, BMC Geriatr., 2017, 17, 230–239, DOI:10.1186/s12877-017-0621-2.
- C. C. Murphy, H. M. Fullington, C. A. Alvarez, A. C. Betts, S. J. C. Lee, D. A. Haggstrom and E. A. Halm, Polypharmacy and patterns of prescription medication use among cancer survivors, Cancer, 2018, 124, 2850–2857, DOI:10.1017/cts.2018.297.
- A. Rieckert, U. S. Trampisch, R. Klaaβen-Mielke, E. Drewelow, A. Esmail, T. Johansson, S. Keller, I. Kunnamo, C. Löffler, J. Mäkinen, G. Piccoliori, A. Vögele and A. Sönnichsen, Polypharmacy in older patients with chronic diseases: a cross-sectional analysis of factors associated with excessive polypharmacy, BMC Fam. Pract., 2018, 19, 113–121, DOI:10.1186/s12875-018-0795-5.
- Y. Hashimoto, J. Uno, T. Miwa, M. Kurihara, H. Tanifuji and M. Tensho, Effects of antipsychotic polypharmacy on side-effects and concurrent use of medications in schizophrenic outpatients, Psychiatry. Clin. Neurosci., 2012, 66, 405–410, DOI:10.1111/j.1440-1819.2012.02376.x.
- E. E. Roughead, J. D. Barratt and A. L. Gilbert, Medication-related problems commonly occurring in an Australian community setting, Pharmacoepidemiol. Drug Saf., 2004, 13, 83–87, DOI:10.1002/pds.912.
- Y. Schenker, S. Y. Park, K. Jeong, J. Pruskowski, D. Kavalieratos1, J. Resic1, A. Abernethy and J. S. Kutner, Associations between polypharmacy, Symptom Burden, and quality of life in patients with advanced, Life-limiting illness, J. Gen. Intern. Med., 2018, 34, 559–566, DOI:10.1007/s11606-019-04837-7.
- M. R. Mohamed, E. Ramsdale, K. P. Loh, A. Aratsu, H. Xu, S. Obrecht, D. Castillo, M. Sharma, H. M. Holmes, G. Nightngale, K. M. Juba and S. G. Mohile, Associations of polypharmacy and inappropriate medications with adverse outcomes in older adults with cancer: a systematic review and meta-analysis, Oncologist, 2020, 25, 94–108, DOI:10.1634/theoncologist.2019-0406.
- L. Ferrucci, J. M. Guralnik, S. Studenski, L. P. Fried, G. B. Cutler Jr and J. D. Walston, Interventions on frailty working group, designing randomized, controlled trials aimed at preventing or delaying functional decline and disability in frail, older persons: a consensus report, J. Am. Geriatr. Soc., 2004, 52, 625–634, DOI:10.1111/j.1532-5415.2004.52174.x.
- N. Moore, C. Pollack and P. Butkerait, Adverse drug reactions and drug–drug interactions with over-the-counter NSAIDs, Ther. Clin. Risk Manage., 2015, 11, 1061–1075, DOI:10.2147/TCRM.S79135.
- J. P. van den Berg, H. E. M. Vereecke, J. H. Proost, D. J. Eleveld, J. K. G. Wietasch, A. R. Absalom and M. M. R. F. Struys, Pharmacokinetic and pharmacodynamic interactions in anaesthesia. A review of current knowledge and how it can be used to optimize anaesthetic drug administration, Br. J. Anaesth., 2017, 118, 44–57, DOI:10.1093/bja/aew312.
- T. Kasai, K. Shiono, Y. Otsuka, Y. Shimada, H. Terada, K. Komatsu and S. Goto, Molecular recognizable ion-paired complex formation between diclofenac/indomethacin and famotidine/cimetidine regulates their aqueous solubility, Int. J. Pharm., 2020, 590, 119840, DOI:10.1016/j.ijpharm.2020.119841.
- T. Kinoshita, C. Tsunoda, S. Goto, K. Hasegawa, H. Chatani, M. Fujita, H. Kataoka, Y. Katahara, Y. Shimada, Y. Otsuka, K. Komatsu and H. Terada, Enthalpy–entropy compensation in the structure-dependent effect of nonsteroidal anti-inflammatory drugs on the aqueous solubility of diltiazem, Chem. Pharm. Bull., 2020, 70, 120–129, DOI:10.1248/cpb.c21-00834.
- Y. Shimada, S. Goto, H. Uchiro, H. Hirabayashi, K. Yamaguchi, K. Hirota and H. Terada, Features of heat-induced amorphous complex between indomethacin and lidocaine, Colloids Surf., B, 2013, 102, 590–596, DOI:10.1016/j.colsurfb.2012.08.060.
- H. Kataoka, Y. Sakaki, K. Komatsu, Y. Shimada and S. Goto, Melting process of the peritectic mixture of lidocaine and ibuprofen interpreted by site percolation theory model, J. Pharm. Sci., 2017, 106, 3016–3021, DOI:10.1248/cpb.c21-00834.
- H. Chatani, S. Goto, H. Kataoka, M. Fujita, Y. Otsuka, Y. Shimada and H. Terada, Effects of phosphate on drug solubility behavior of mixture ibuprofen and lidocaine, Chem. Phys., 2019, 525, 110415, DOI:10.1016/j.chemphys.2019.110415.
- R. Koga, T. Tsuchida, C. Tsunoda, H. Kataoka, S. Suenaga and S. Goto, Physicochemical properties of diclofenac regulated by its intermolecular interactions with caffeine evaluated via vector space model, nuclear magnetic resonance, and Fourier-transform infrared analyses, Mater. Chem. Phys., 2024, 333, 130158, DOI:10.1016/j.matchemphys.2024.130158.
- K. Moritake, T. Tsuchida, R. Koga, K. Hasegawa, W. Kuwashima, H. Kataoka, S. Goto and H. Terada, Equilibrium of monomers, dimers, and polymeric aggregates in the α-aryl-propionic acid-type analgesics naproxen, ketoprofen, and ibuprofen: comparative study with oxicam-type meloxicam and piroxicam, Int. J. Pharm., 2025, 670, 125167, DOI:10.1016/j.ijpharm.2025.125167.
- S. Goto and K. Komatsu, The configuration space of a model for ringed hydrocarbon molecules, Hiroshima Math. J., 2022, 42(1), 115–126, DOI:10.32917/hmj/1333113009.
- S. Goto, K. Komatsu and H. Terada, Topology and the interconversion pathway networks of cycloheptane conformations and those of related n-membered rings, Bull. Chem. Soc. Jpn., 2013, 86(2), 230–242, DOI:10.1246/bcsj.20110252.
- A. Sidorchuk, K. Isomura, Y. Molero, C. Hellner, P. Lichtenstein, Z. Chang, J. Franck, L. F. de la Cruz and D. Mataix-Cols, Benzodiazepine prescribing for children, adolescents, and young adults from 2006 through 2013: a total population register-linkage study, PLoS Med., 2018, 15, e1002635, DOI:10.1371/journal.pmed.1002635.
- T. Brodin, J. Nordling, A. Lagesson, J. Klaminder, G. Hellström, B. Christensen and J. Fick, Environmentally relevant levels of a benzodiazepine (oxazepam) alters important behavioral traits in a common planktivorous fish, (Rutilus rutilus), J. Toxicol. Environ. Health, Part A, 2017, 80, 963–970, DOI:10.1080/15287394.2017.1352214.
- C. Hansch and A. Leo, Substituent Constants for Correlation Analysis in Chemistry and Biology, John Wiley & Sons, Inc., 1979 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, A survey of Hammet substituent constants and resonance and field parameters, Chem. Rev., 1991, 91, 165–195, DOI:10.1021/cr00002a004.
- C. Hansch, A. L. Leo and D. Hoekman, Exploring QSAR, Hydrophobic, Electronic, and Steric Constants, American Chemical Society, 1995 Search PubMed.
- J. Sangster, Octanol-Water Partition Coefficients: Fundamentals and Physical Chemistry, John Wiley & Sons, Inc., 1997 Search PubMed.
- A. Avdeef, Absorption and Drug Development, Solubility, Permeability, and Charge State, John Wiley & Sons, Inc., 2003 Search PubMed.
- S. Goto, Y. Kurosawa, C. Tsunoda, K. Hasegawa, T. Tsuchida, K. Komatsu and H. Terada, Solubility dynamics and hydrophobic interactions of acidic analgesics and basic anesthetics, in Colloids and Interfacial Dynamics: Basics to Application, ed. M. Hashizume and Y. Imura, 2025, 293, pp. 293–311 Search PubMed.
- G. A. Ilevbare and L. S. Taylor, Liquid–liquid phase separation in highly supersaturated aqueous solutions of poorly water-soluble drugs: implications for solubility-enhancing formulations, Cryst. Growth Des., 2013, 13, 1497–1509, DOI:10.1021/cg301679h.
- L. I. Mosquera-Giraldo and L. S. Taylor, Glass–liquid phase separation in highly supersaturated aqueous solutions of telaprevir, Mol. Pharm., 2015, 12, 496503, DOI:10.1021/mp500573z.
- L. S. Taylor and G. G. Z. Zhang, Physical chemistry of supersaturated solutions and implications for oral absorption, Adv. Drug Delivery Rev., 2016, 101, 122–142, DOI:10.1016/j.addr.2016.03.006.
- A. S. Indulkar, Y. Gao, S. A. Raina, G. G. Z. Zhang and L. S. Taylor, Exploiting the phenomenon of liquid–liquid phase separation for enhanced and sustained membrane transport of a poorly water-soluble drug, Mol. Pharm., 2016, 13, 2059–2069, DOI:10.1021/acs.molpharmaceut.6b00202.
- A. S. Indulkar, Y. Gao, S. A. Raina, G. G. Z. Zhang and L. S. Taylor, Crystallization from supersaturated solutions: role of lecithin and composite simulated intestinal fluid, Pharm. Res., 2018, 35, 158, DOI:10.1007/s11095-018-2441-2.
- C. Liu, B. Chen, W. Shi, W. Huang and H. Qian, Ionic liquids for enhanced drug delivery: recent progress and prevailing challenges, Mol. Pharm., 2022, 19, 1033–1046, DOI:10.1021/acs.molpharmaceut.1c00960.
- M. M. Abdelquader, S. Li, G. P. Andrews and D. S. Jones, Therapeutic deep eutectic solvents: a comprehensive review of their thermodynamics, microstructure and drug delivery applications, Eur. J. Pharm. Biopharm., 2023, 186, 85–104, DOI:10.1016/j.ejpb.2023.03.002.
- F. Oyoun, A. Toncheva, L. Castillo Henríquez, R. Grougnet, F. Laoutid, N. Mignet, K. Alhareth and Y. Corvis, Deep eutectic solvents: an eco-friendly design for drug engineering, ChemSusChem, 2023, 16, e202300669, DOI:10.1002/cssc.202300669.
- A. Sharma, Y. R. Park, A. Garg and B.-S. Lee, Deep eutectic solvents enhancing drug solubility and its delivery, J. Med. Chem., 2024, 67, 14807–14819, DOI:10.1021/acs.jmedchem.4c01550.
- Y. Otsuka, W. Kuwashima, Y. Tanaka, Y. Yamaki, Y. Shimada and S. Goto, Effects of heat treatment on indomethacin-cimetidinemixture; Investigation of drug–drug interaction using FT-IR spectroscopy with singular value decomposition and powder X-ray diffractometry, J. Pharm. Sci., 2020, 110(3), 1142–1147, DOI:10.1016/j.xphs.2020.09.049.
- B. Albertini, S. Bertoni, S. Sangiorgi, G. Nucci, N. Passerini and E. Mezzina, NaDES as a Green Technological Approach for the Solubility Improvement of BCS Class II APIs: An Insight into the Molecular Interactions, Int. J. Pharm., 2023, 634, 122696, DOI:10.1016/j.ijpharm.2023.122696.
- W. Kuwashima, K. Hasegawa, C. Tsunoda, T. Tsuchida and S. Goto, Amendment in Singular Value Decomposition Approach for FTIR Spectra of Heat-treated Indomethacin–Cimetidine Mixture: Study of Solid Intermolecular Interaction, ChemRXiv., 2025, preprint DOI:10.26434/chemrxiv-2025-k5zbp.
- W. Kuwashima, K. Hasegawa, C. Tsunoda, S. Sunada, T. Tsuchida and S. Goto, Supramolecular synthonic portions in heat-treated indomethacin-carbamazepine mixture: a singular value decomposition approach for Fourier-Transform infrared spectral analysis, Int. J. Pharm., 2025, 685, 126199, DOI:10.1016/j.ijpharm.2025.126199.
- N. Karimi, M. H. Dokoohayi, A. R. Zolghadr and A. Klein, Solvation and aggregation of heteroaromatic drugs in the reline deep eutectic solvent – a combined molecular dynamics simulation and DFT study, Phys. Chem. Chem. Phys., 2025, 27, 15527–15543, 10.1039/D5CP01312G.
- J. Potticary, C. Hall, V. Hamilton, J. F. McCabe and S. R. Hall, Crystallization from Volatile Deep Eutectic Solvents, Cryst. Growth Des., 2020, 20, 2877–2884, DOI:10.1021/acs.cgd.0c00399.
- M. Fujita, S. Goto, H. Chatani, Y. Otsuka, Y. Shimada, H. Terada and K. Inoo, The function of oxybuprocaine: a parachute effect that sustains the supersaturated state of anhydrous piroxicam crystals, RSC Adv., 2020, 10, 1572–1579, 10.1039/C9RA09952B.
- M. Fujita, T. Tsuchida, H. Kataoka, C. Tsunoda, K. Moritake and S. Goto, Model on the thermodynamics of irreversible processes, Int. J. Pharm., 2024, 667 A, 124886, DOI:10.1016/j.jphotochem.2024.116142.
- Y. Oshite, A. Wada-Hirai, R. Ichii, C. Kuroda, K. Hasegawa, R. Hiroshige, H. Yokoyama, T. Tsuchida and S. Goto, Comparative study on the effects of the inclusion complexes of non-steroidal anti-inflammatory drugs with 2-hydroxypropyl-β-cyclodextrins on dissociation rates and supersaturation, RSC Pharm., 2024, 1, 80–97, 10.1039/D3PM00039G.
- M. Ben-Eltriki, S. Deb and E. S. T. Guns, Calcitriol in combination therapy for prostate cancer: pharmacokinetic and pharmacodynamic interactions, J. Cancer, 2016, 7, 391–407, DOI:10.7150/jca.13470.
- A. C. Khazraji and S. Robert, Interaction effects between cellulose and water in nanocrystalline and amorphous regions: a novel approach using molecular modeling, J. Nanomater., 2013, 2013, 409676, DOI:10.1155/2013/409676.
- O. Nordness and J. F. Brennecke, Ion dissociation in ionic liquids and ionic liquid solutions, Chem. Rev., 2020, 120, 12873–12902, DOI:10.1021/acs.chemrev.0c00373.
- M. Forsyth, H. Yoon, F. Chen, H. Zhu, D. R. MacFarlane, M. Armand and P. C. Howlett, Novel Na+ ion diffusion mechanism in mixed organic–inorganic ionic liquid electrolyte leading to high Na+ transference number and stable; High rate electrochemical cycling of sodium cells, J. Phys. Chem. C, 2016, 120, 4276–4286, DOI:10.1021/acs.jpcc.5b11746.
- G. Pagès, V. Gilard, R. Martino and M. Malet-Martino, Pulsed-field gradient nuclear magnetic resonance measurements (PFG NMR) for diffusion ordered spectroscopy (DOSY) mapping, Analyst, 2017, 142, 3771–3796, 10.1039/C7AN01031A.
- Z. He and F. Mansfeld, Exploring the use of electrochemical impedance spectroscopy (EIS) in microbial fuel cell studies, Energy Environ. Sci., 2009, 2, 215–219, 10.1039/B814914C.
- H. S. Frank and M. W. Evans, Free volume and entropy in condensed systems III. Entropy in binary liquid mixtures; Partial molal entropy in dilute solutions; Structure and thermodynamics in aqueous electrolytes, J. Chem. Phys., 1945, 13, 507–532, DOI:10.1063/1.1723985.
- B.-Y. Chang and S.-M. Park, Electrochemical impedance spectroscopy, Annu. Rev. Anal. Chem., 2010, 3, 207–229, DOI:10.1146/annurev.anchem.012809.102211.
- D. D. Stupin, E. A. Kuzina, A. A. Abelit, A. K. Emelyanov, D. M. Nikolaev, M. N. Ryazantsev, S. V. Koniakhin and M. V. Dubina, Bioimpedance spectroscopy: basics and applications, ACS Biomater. Sci. Eng., 2021, 7, 1962–1986, DOI:10.1021/acsbiomaterials.0c01570.
- S. Wang, J. Zhang, O. Gharbi, V. Viver, M. Gao and M. E. Orazem, Electrochemical impedance spectroscopy, Nat. Rev. Methods Primers, 2021, 1, 41 CrossRef CAS Electrochemical impedance spectroscopy | Nature Reviews Methods Primers.
- N. Hallemans, D. Howey, A. Battistel, N. F. Saniee, F. Scarpioni, B. Wouters, F. La Mantia, A. Hubin, W. D. Widanage and J. Lataire, Electrochemical impedance spectroscopy beyond linearity and stationarity—A critical review, Electrochim. Acta, 2023, 466, 142939, DOI:10.1016/j.electacta.2023.142939.
- A. C. Lazanas and M. I. Prodromidis, Electrochemical impedance spectroscopy–A tutorial, ACS Meas. Sci. Au, 2023, 3, 162–193, DOI:10.1021/acsmeasuresciau.2c00070.
- T. F. Kellici, M. V. Chatziathanasiadou, D. Diamantis, A. V. Chatzikonstantinou, I. Andreadelis, E. Christodoulou, G. Valsami, T. Mavromoustakos and A. G. Tzakos, Mapping the interactions and bioactivity of quercetin-(2-hydroxypropyl)-β-cyclodextrin complex, Int. J. Pharm., 2016, 511, 303–311, DOI:10.1016/j.ijpharm.2016.07.008.
- V. J. Nagaraj, M. Jacobs, K. M. Vattipalli, V. P. Annam and S. Prasad, Nanochannel-based electrochemical sensor for the detection of pharmaceutical contaminants in water, Environ. Sci. Process. Impacts., 2014, 16, 135–140, 10.1039/C3EM00406F.
- G. Han, B. Maranzano, C. Welch, N. Lu and Y. Feng, Deep-learning-guided electrochemical impedance spectroscopy for calibration-free pharmaceutical moisture content monitoring, ACS Sens., 2024, 9, 4186–4195, DOI:10.1021/acssensors.4c01180.
- R. Vedalakshmi, R. R. Devi, B. Emmanuel and N. Palaniswamy, Determination of diffusion coefficient of chloride in concrete: an electrochemical impedance spectroscopic approach, Mater. Struct., 2008, 41, 1315–1326, DOI:10.1617/s11527-007-9330-1.
- R. Vedelakshmi, V. Sarawathy, H.-W. Song and N. Palaniswamy, Determination of diffusion coefficient of chloride in concrete using Warburg diffusion coefficient, Corros. Sci., 2009, 51, 1299–1307, DOI:10.1016/j.corsci.2009.03.017.
- J. Cui, T. Kobayashi, R. L. Sacci, R. A. Matsumoto, P. T. Cummings and M. Pruski, Diffusivity and structure of room temperature ionic liquid in various organic solvents, J. Phys. Chem. B, 2020, 124, 9931–9937, DOI:10.1021/acs.jpcb.0c07582.
- P. Colomban and A. Novak, Proton transfer and superionic conductivity in solids and gels, J. Mol. Struct., 1988, 177, 277–308, DOI:10.1016/0022-2860(88)80094-2.
- J. Bowers, C. P. Butts, P. J. Martin and M. C. Vergara-Gutierrez, Aggregation behavior of aqueous solutions of ionic liquids, Langmuir, 2004, 20, 2191–2198, DOI:10.1021/la035940m.
- H. Hanibah, N. Z. N. Hashim and I. J. Shamsudin, Molar conductivity behavior of ionic liquid compared to inorganic salt in electrolyte solution at ambient temperature, AIP Conf. Proc., 2017, 1877, 050003, DOI:10.1063/1.4999877.
- A. Panuszko, P. Bruździak, M. Śmiechowski, M. Stasiulewicz, J. Stefaniak and J. Stangret, DMSO hydration redefined: unraveling the hydrophobic hydration of solutes with a mixed hydrophilic–hydrophobic characteristic, J. Mol. Liq., 2019, 294, 111651, DOI:10.1016/j.molliq.2019.111661.
- K. Hasegawa, S. Goto, H. Kataoka, H. Chatani, T. Kinoshita, H. Yokoyama and T. Tsuchida, Quantification of crystallinity during indomethacin crystalline transformation from α- to γ-polymorphic forms and of the thermodynamic contribution to dissolution in aqueous buffer and solutions of solubilizer, RSC Adv., 2024, 14, 4129, 10.1039/d3ra08481g.
- K. Hasegawa, S. Ogawa, H. Chatani, H. Kataoka, T. Tsuchida and S. Goto, Thermodynamic and kinetic analysis of the melting process of S-ketoprofen and lidocaine mixtures, RSC Pharm., 2024, 1, 536–547, 10.1039/D4PM00039K.
- U. Ryde, A fundamental view of enthalpy–entropy compensation, Med. Chem. Commun., 2014, 5, 1324–1336, 10.1039/C4MD00057A.
- F. Peccati and G. Jiménez-Osés, Enthalpy–entropy compensation in biomolecular recognition: a computational perspective, ACS Omega, 2021, 6, 11122–11130, DOI:10.1021/acsomega.1c00485.
- M. Dixon and E. C. Webb, Enzymes, Longmans, Green and Co., London, 1958 Search PubMed.
- P. Mantré. L’eau dans la cellule, Une interface hérérogène et dynamique des macromolécules, (Japanese translated by S. Tsuji et al. 2006 Univ. Tokyo Press), Masson, Paris, 1996 Search PubMed.
- V. Conti Nibali, S. Pezzotti, F. Sebastiani, D. R. Galimberti, G. Schwaab, M. Heyden, M.-P. Gaigeot and M. Havenith, Wrapping Up Hydrophobic Hydration: Locality Matters, J. Phys. Chem. Lett., 2020, 11, 4809–4816, DOI:10.1021/acs.jpclett.0c00846.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, Inc., Amsterdam, 3rd edn, 2011ISBN 978-0-12-391927-4 Search PubMed.
- A. Takara, K. Kobayashi, S. Watanabe, K. Okuyama, Y. Shimada and S. Goto, Dibucaine inhibits ketoprofen photodegradation via a mechanism different from that of antioxidants, J. Photochem. Photobiol., A, 2017, 333, 208–212, DOI:10.1016/j.jphotochem.2016.10.026.
Footnote |
| † R. Koga and T. Kinoshita accomplished the EIS and DOSY approaches, respectively, and are considered to have contributed equally as co-first authors. |
| This journal is © the Owner Societies 2026 |