Acceleration of butane vapor nucleation by carbon dioxide gas
Received
9th October 2025
, Accepted 9th December 2025
First published on 15th December 2025
Abstract
Carbon dioxide (CO2) gas is known to strongly accelerate nucleation of other gas phase components, such as water and toluene. The acceleration was attributed to the formation of transient heteromolecular dimers and referred to as the chaperon mechanism. In this work, we investigate this phenomenon for butane–CO2 gas mixtures with mass spectrometry in the post-nozzle flow of a Laval expansion at a temperature of 51 K and a pressure of 40 Pa. At moderate CO2 and butane concentrations, we observed an acceleration of butane nucleation by the chaperon mechanism, albeit only by a factor of about two compared to unary butane nucleation. The fact that the chaperon mechanism is less important for butane than for water and toluene can be rationalized by the weaker intermolecular interactions between butane and CO2. At higher CO2 and butane concentrations, nucleation and cluster growth overlap in time, which leads to saturation of the measured total butane concentration. Using a kinetic model, we show that saturation is caused by the formation of heteromolecular butane–CO2 clusters of different sizes and compositions. Studies on nucleation at low temperatures in such systems are relevant for flue or natural gas separation.
1 Introduction
Supersonic expansions and cryogenic cooling have emerged as a promising method for flue and natural gas separation.1–6 In both processes, condensation of target components is induced by gas phase nucleation. Supersonic separation relies on the expansion of a gas mixture through a Laval nozzle where the gas is accelerated to supersonic speeds, resulting in a sudden pressure drop and rapid cooling. The successful implementation of such removal methods would benefit from a better molecular-level understanding of the complex nucleation dynamics of multi-component vapors and molecular nucleation models. Conventional nucleation modeling approaches are often based on the limited predictability of classical nucleation theory (CNT) to explain experimental findings.7–11 Recent advances also include atomistic approaches, with molecular dynamic simulations and quantum chemistry calculations, which yield more reliable results than CNT.8,12–20 Comparable conditions in experiments and models are often difficult to realize.
Laval supersonic expansion is a widely used tool to experimentally study gas-phase nucleation.21–29 The Laval setup at ETH Zurich25,30,31 has allowed the determination of nucleation rates directly from time-dependent, cluster-size resolved mass spectra recorded during nucleation. Nucleation is induced in the uniform post-nozzle flow of the Laval expansion, and the nucleating clusters are detected after soft photoionization by time-of-flight mass spectrometry. Previously, the nucleation of pure propane, pure CO2 and pure H2O gases – all key components of natural gas – have been studied.10,32,33 In this work, we report unary nucleation rates for butane at 51 K and 40 Pa at different monomer concentrations (we refer to nucleation in single-component gases as unary nucleation). The result shows a linear increase in the nucleation rate with the square of the concentration, as expected from a simple ‘monomer association’ model.34,35 However, the linear fit implies that a minimum monomer concentration is required for nucleation to occur.
Numerous studies have demonstrated that the introduction of a second gas component can accelerate sulfuric acid nucleation e.g. by acid–base chemistry.36–38 More recent research shows that CO2 can accelerate nucleation of species such as toluene, water, propanol, hexane, and butane in two-component mixtures without chemical modification.35,39 We refer to this as binary nucleation. These studies suggest that the observed rate enhancement arises from the catalytic effect of CO2, which is based on the formation of a transient heteromolecular dimer, called a chaperon complex.35,39 The binary nucleation rate, Jbi, can be expressed as
| | |
Jbi = Jun + βCnucCacc
| (1) |
where
Jun is the unary nucleation rate,
Cnuc and
Cacc are the concentrations of the nucleating (butane, toluene…) and accelerating (CO
2) species, respectively, and
β represents the effective rate constant associated with the formation of the chaperon complex. Here, we explore the binary nucleation of Bu and CO
2 under the same conditions as the unary butane nucleation. Our experiments show that CO
2 accelerates butane nucleation, but to a significantly lesser extent compared to that of water and toluene.
35,39 At higher CO
2 contents, we further observed that the total number concentration of the homomolecular butane clusters does no longer increase with increasing growth time but instead levels off,
i.e. that the growth of homomolecular butane clusters is hindered. Kinetic modeling along with the experimental results suggests that this is caused by an increasingly dominant contribution of heteromolecular clusters with varying CO
2 and butane content that grow at the expense of the homomolecular butane clusters. This observation might have implications for gas separation technologies, highlighting how sensitively separation can depend on changes in the concentration of a component.
2 Experiment and modeling
2.1 Experimental setup
The details of the experimental setup are given elsewhere,25,31,39–41 and only a brief description is provided here. A schematic of the experimental setup is shown in Fig. 1. We used gas mixtures of condensable gases (butane and CO2), carrier gases argon and nitrogen, and an internal standard methane. The specific mixing ratios of the gas were regulated using mass flow controllers (Bronkhorst EL-FLOW Prestige). The total flow rate was kept fixed at 950 SCCM (standard cubic centimeters per minute). The flow rates of the individual gas components as a fraction of this total flow are proportional to their partial pressure and thus their respective number concentrations (ideal gas law).
 |
| | Fig. 1 Schematic of the Laval setup. p0 and T0 are the pressure and temperature in the stagnation volume and pF and TF are the pressure and temperature in the flow region. Nucleation and growth take place in the post-nozzle flow of the Laval expansion. The formed clusters are detected in the time-of-flight (TOF) mass spectrometer after soft photoionization. A variation of the nozzle-to-skimmer distance (L) corresponds to a variation of the nucleation/growth time (t). | |
The gas mixture was pulsed into the stagnation volume of the Laval nozzle using solenoid valves (Parker). In the stagnation volume, gas pressures p0 were in the range of 1.7 bar and 2.1 bar at a temperature T0 of approximately 294 K. Supersonic expansion by the Laval nozzle resulted in post-nozzle flow temperatures and pressures of TF 51 K and pF 40 Pa, respectively. TF was controlled by adjusting the ratio of the carrier gases argon and nitrogen. This was especially important when using high concentrations of CO2, as higher CO2 concentrations would change TF without adjustment of the carrier gas composition.42 pF and TF in the post-nozzle flow were deduced from the measured impact pressure using an impact pressure transducer (Omega PX170) as described in ref. 25 and 30.
The isentropic core of the gas beam was sampled by a skimmer into the home-built time-of-flight (TOF) mass spectrometer, where the clusters were photo-ionized and detected. Cluster fragmentation was largely avoided by softly ionizing using photoionization with 13.8 eV.43 The ionized clusters were then accelerated with a six-plate stack of extraction plates44 with up to 20 kV and detected with a micro-channel plate detector (MCP; Photonics). The high monomer concentrations of the condensable gases would induce detector ringing, making cluster detection difficult. To prevent this, a short electric pulse was applied using a mass gate (DEI PVX-4140 Pulse Generator) to deflect the monomers and prevent them from hitting the detector.40
2.2 Determination of experimental nucleation rates
The experimental nucleation rate Jexp was determined from the temporal derivative of the measured total number concentration of butane clusters CBu,tot(t):10,31,39| |
 | (2) |
t is the nucleation time, which is determined from the velocity of the post-nozzle flow and the nozzle-to-skimmer distance L. CBu,tot(t) is| |
 | (3) |
CBu,i(t) is the concentration of pure butane clusters with i butane molecules. Note that we only observed pure butane clusters in the mass spectra for both unary and binary nucleation. CBu,i(t) was determined from the measured integrated ion signal Ii from:| |
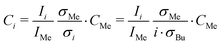 | (4) |
where CMe, IMe and σMe = 16.6 Mb45 are the known concentration, the measured ion signal, and the photoionization cross section of the internal standard methane, respectively. σi is the photoionization cross section of a butane cluster containing i butane monomers. It is approximated as i times the butane ionization cross section, σBu = 91.7 Mb.45 Under our conditions, we can neglect monomer depletion, cluster coagulation and cluster evaporation.10,32,40 Note that the monomer concentration (∼1020 m−3) is orders of magnitude higher than the cluster concentrations (∼1017 m−3).
2.3 Modeling of unary nucleation rates
We have shown in previous studies that the unary nucleation rate is governed by the dimerization rate:10,31,39| |
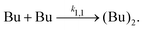 | (5) |
k1,1 is the rate constant for the formation of butane dimers. This results in a modeled unary nucleation rate,| | |
Jun = k1,1·(CBu)2 + ξ,
| (6) |
where C(Bu)1 is the concentration of the butane monomer. ξ is a constant negative shift that accounts for the fact that unary butane nucleation was only observed above a minimum butane monomer concentration (minimum concentration; see Section 3.1).
2.4 Modeling of binary nucleation rates
As in our previous binary nucleation studies,35,39 we assume also for binary CO2–butane nucleation that the dominant nucleation step (rate determining step) is the formation of the heteromolecular CO2–butane dimer, referred to as chaperon complex (eqn (7), rate constant β). Collision of this complex with a butane monomer results in fast butane dimer formation (eqn (8); rate constant γ) and in the subsequent growth to larger, homomolecular butane clusters, which are observed in the mass spectra.| |
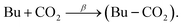 | (7) |
| |
 | (8) |
The above mechanism is a CO2 catalyzed butane dimerization. In this simple model, the binary nucleation rate Jbi is the sum of the unary nucleation rate Jun and an acceleration term due to the chaperon effect, as given in eqn (1). For Bu–CO2,| | |
Jbi = Jun + βCBuCCO2 = k1,1·(CBu)2 + ξ + βCBuCCO2.
| (9) |
CCO2 is the CO2 monomer concentration. In the following, we will also use this equation in the linearized form:| |
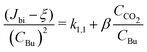 | (10) |
It is important to mention that all rate constants (e.g. k1,1, β) are effective rate constants that effectively include the cooling effect by the bath gas.
3 Result and discussion
3.1 Unary nucleation of butane
For the analysis of the acceleration of butane nucleation in the presence of CO2 gas (Section 3.2), we must know the unary butane nucleation rates k1,1 recorded under the same conditions (pressure of 40 Pa, temperature of 51 K). We extracted k1,1 (Table 1 for butane) from a fit of eqn (6) to a series of measurements of Jexp as a function of CBu (Fig. 2 and Table S1 in the SI). As expected from the simple model in eqn (5), Jexp increases linearly with CBu2 with k1,1 representing the slope (Table 1 for butane). However, the linear fit does not intersect the ordinate at zero, but instead at a negative value of ξ (eqn (6), Table 1). This implies that a minimum monomer concentration 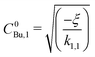 is required for unary nucleation to occur. Compared to the unary nucleation of other compounds we have previously studied (see, for example, the unary water nucleation in Table 1 and Fig. S1A in the SI), where the minimum concentration is negligible for the kinetics within uncertainties, it turns out that it is clearly not negligible in the case of unary butane nucleation.
is required for unary nucleation to occur. Compared to the unary nucleation of other compounds we have previously studied (see, for example, the unary water nucleation in Table 1 and Fig. S1A in the SI), where the minimum concentration is negligible for the kinetics within uncertainties, it turns out that it is clearly not negligible in the case of unary butane nucleation.
| |
T [K] |
k1,1 [10−20 m3 s−1] |
ξ [1021 m−3 s−1] |
β [10−20 m3 s−1] |
k1,1/β |
| Butane–CO2 |
51 |
160 ± 30 |
−19 ± 3 |
1.7 ± 0.5 |
94 ± 33 |
| Water–CO2 |
57 |
70 ± 20 |
−4 ± 2 |
11 ± 3 |
6.4 ± 2.5 |
 |
| | Fig. 2 Unary butane nucleation. Circles: experimental data points Jexp as a function of (CBu)2. Dashed line: linear fit using eqn (6) and Jexp = Jun. | |
We have not yet found a conclusive explanation for the minimum concentration. It could arise from the presence of cluster decay processes (not accounted for in eqn (5)), with ξ representing an effective decay rate. The intermolecular interactions between two butane molecules are weak, for example compared with those between two water molecules, which might explain why this phenomenon is particularly pronounced for butane. According to the simulations we performed in the SI (Fig. S2), experimental artifacts, such as cluster loss during ionization or limitations due to detection, can be ruled out as the reason since they would not result in a negative axis intercept.
3.2 Acceleration of butane nucleation by CO2
Fig. 3 shows the effect of CO2 on butane cluster formation in the mass spectra for three different nucleation times (labels on upper abscissa) for 0.19% butane and at T = 51 K. Note that all cluster peaks correspond to pure butane clusters. The upper row shows unary butane nucleation in the absence of CO2 (right ordinate). Almost no butane cluster peaks are observed under these conditions. This changes systematically with the addition of more and more CO2 (from top to bottom for each nucleation time in Fig. 3): the higher the CO2 content in the gas mixture the more butane clusters are observed. Obviously, butane nucleation is accelerated by the presence of CO2 gas – a phenomenon we had observed for other binary gas mixtures as well.35,39
 |
| | Fig. 3 Mass spectra recorded during butane nucleation in the absence (unary nucleation, top row) and in the presence of CO2 gas (binary nucleation, all other rows). All spectra were recorded at a butane monomer concentration of CBu = 0.19% and a temperature of T = 51 K. The CO2 to butane monomer ratio in the gas mixture increases from the top spectra to the bottom spectra (right ordinate) from 0 to 10, 20 and 30. The left, middle and right panel are recorded at three different nucleation times t (upper abscissa) corresponding to three different nozzle-to-skimmer distances L distances of 20, 30, and 40 mm. m/z is the mass-to-charge ratio. The vertical dashed gray lines denote the different pure butane clusters, starting at the dimer. | |
Using eqn (2), we extracted (CBu,tot(t)) from these spectra, which are shown as a function of the nucleation time t and for all measured CO2 to butane monomer ratios (CCO2/CBu) in Fig. 4A. For each CCO2/CBu ratio, we extracted Jexp from these data from eqn (2) (reported in Table S2 in the SI). Only t up to 60 s were used for these fits as the data quality decreases for longer times, where fluctuations and deviations from linear behavior were observed (Fig. 4A). The acceleration rate constant β (Table 1) was then extracted from a linear fit to eqn (10) (see Fig. 4B), assuming Jexp = Jbi and using the rate constants k1,1 and ξ as determined from the unary butane nucleation (Section 3.1, Table 1). There is an acceleration due to the chaperon mechanism (eqn (7) and (8)) of butane nucleation when CO2 is present. However, it is less pronounced than for the binary mixtures we studied before.35,39 At the higher CO2 concentration, the additional chaperon term in eqn (9) results in about a doubling of the reaction rate compared with unary butane reaction (see eqn (9) and Tables S1, S2 in the SI).
 |
| | Fig. 4 (A) Binary butane–CO2 nucleation. Symbols: experimentally measured total number concentrations of pure butane clusters, (CBu,tot), as a function of the nucleation time t for binary nucleation for thirteen different CCO2/CBu ratios. All spectra were recorded at a butane monomer concentration of CBu = 0.19% and a temperature of T = 51 K. Full lines: linear fits of CBu,tot(t) for t up to 60 µs. (B) Linear fit to determine β from the experimental data in panel A using eqn (10) and Jexp = Jbi. The red data point denotes kξ1,1. The values of kξ1,1 and ξ were taken from the unary measurements as shown in Table 1. | |
Table 1 compares the rate constants retrieved for binary butane–CO2 nucleation with binary water–CO2 nucleation (see also butane–CO2). Fig. S1B in the SI shows a graph for the binary water–CO2 system which is equivalent to the one for butane–CO2 in Fig. 4B. The comparison of the two graphs reveals that the fit is better constrained for the water–CO2 case, as a consequence of the more pronounced acceleration in this case. The fact that the acceleration effect of CO2 is stronger for water–CO2 than butane–CO2 can directly be seen from the ratio of k1,1/β, which is much higher (about 15 times) in the latter case (Table 1 and eqn (9)). This clearly suggests that the chaperon mechanism is less effective in the butane–CO2 case. A likely explanation is the comparatively weak intermolecular interactions (dispersion and induction interactions) between butane and CO2 compared to the stronger intermolecular interactions (additional dipole-induced dipole interactions) between H2O and CO2. This increases the collision cross section (e.g. long range capture cross section) for the formation of the chaperon complex in the water case compared with the butane case, and therefore the effectiveness of the chaperon mechanism (eqn (7) and (8)).
3.3 Behavior at high CO2 concentrations
At higher butane concentrations and longer nucleation times t, CBu,tot(t) starts to deviate from the expected (Fig. 4A) linear increase with t. This is shown in Fig. 5 for a butane monomer concentration of 0.21%. For CCO2/CBu ratios of 0 and 5, the increase is still more or less linear, following the behavior expected for unary nucleation (eqn (6)) and binary nucleation with a chaperon mechanism (eqn (9)). However, at higher CCO2/CBu ratios of 20 and 30, a linear increase is only observed for short t, which then saturates at longer t. For the highest CCO2/CBu ratio of 60 saturation is reached almost from the beginning on and CBu,tot(t) becomes even somewhat smaller at longer t. The deviation from the expected linear behavior clearly hints at early cluster growth, reducing the number of pure butane clusters and thus the amount of CBu,tot(t), due to the formation of heteromolecular butane–CO2 clusters. Under these conditions, nucleation and growth can no longer be separated in time.
 |
| | Fig. 5 Binary butane–CO2 nucleation at a higher butane concentration (0.21%) than in Fig. 4A for CCO2/CBu ratios up to 60 (see legend). Symbols: experimental data. Lines: linear interpolations to guide the eye. | |
This hypothesis is confirmed by the cluster peaks we observe in the mass spectra. Fig. 6 shows the baseline-corrected mass spectra for the case CCO2/CBu ratio of 60 (= 12.70% CO2/0.21% butane, middle panels) together with the corresponding unary butane (0.21% butane; top panels) and unary CO2 (12.70% CO2; bottom panels) case for two different t of 77 µs and 173 µs. Both binary spectra in panels C and D show heteromolecular butane–CO2 clusters (see also Table S3 in the SI for peak assignment for panel C). Interestingly, the abundance of the heteromolecular butane–CO2 and pure butane clusters (vertical dashed gray lines) are weaker in panel D than in panel C. This is even more surprising when looking at the unary butane cases in the top traces. More butane clusters are formed by unary nucleation at t = 173 µs compared to t = 77 µs, but less of those pure butane clusters survive as pure butane clusters when CO2 is added (panels D and C, respectively). Furthermore, the bottom spectra for CO2 only show that under these conditions unary CO2 nucleation takes place and forms pure CO2 clusters (vertical dashed-dotted gray lines). The fact that heteromolecular butane–CO2 clusters are observed (panels C and D) and that the number of pure butane clusters is reduced in the binary case (panel D) compared to the unary case (panel B) clearly hints that under these conditions growth phenomena dominate the mass spectra.
 |
| | Fig. 6 Top rows (A, B): mass spectra for unary butane nucleation for CBu = 0.21%. Middle rows (C, D): mass spectra recorded during binary butane–CO2 nucleation for CBu = 0.21% and CCO2 = 12.70% (corresponding to CCO2/CBu ratio of 60) for two different t of 77 µs and 173 µs (see Fig. 5). Bottom rows (E, F): mass spectra for unary butane nucleation for CCO2 = 12.70%. The vertical dashed gray lines indicate the mass-to-charge rations (m/z) of pure butane clusters. The vertical dashed-dotted gray lines indicate the mass-to-charge rations of pure CO2 clusters. The vertical dotted gray lines indicate the mass-to-charge rations of heteromolecular butane–CO2 clusters. | |
To support this more quantitatively, we constructed a detailed sequential kinetic model which simulates unary nucleation of butane and CO2, binary nucleation of butane–CO2 and early cluster growth. Details of the model will be published in a forthcoming article where growth processes in the present and other systems will be the focus. Here, the model only serves to support the above hypothesis. For nucleation, we used the experimentally determined rate constants according to eqn (6) (without ξ) and eqn (9). Growth was modeled to be due to monomer association of butane and CO2 monomers. The corresponding growth rate constants were derived from the time-dependent information in the experimental cluster spectra for the unary butane and CO2 measurements and a suitable interpolation for the formation rates of the mixed clusters. Cluster coagulation, evaporation, and fragmentation were not considered in the simulation.
Fig. 7 shows the result of the simulations for CCO2/CBu ratios of 0, 5 and 50, respectively. Panel a shows the total cluster concentration of the pure butane clusters CBu,tot(t) as extracted from the simulations. This can be directly compared with the experiment in Fig. 5, which shows the concentration of the pure butane clusters extracted from the experimental mass spectra. The simulations capture the experimental results at least semi-quantitatively. A more or less linear increase with t is observed for the CCO2/CBu ratios of 0 and 5 (Fig. 5 and 7A), while for a CCO2/CBu ratio of 50, saturation is observed with increasing time. This confirms that saturation of CBu,tot(t) originates from cluster growth. The simulation also allows us to confirm that the saturation is due to the growth to heteromolecular clusters which depletes the number of pure butane clusters. This can be seen by the comparison of Fig. 7A and B. In contrast to panel A, panel B shows the sum of the total cluster concentrations of pure butane and mixed butane–CO2 clusters, i.e. CBu,tot(t) + Cmixed,tot. If the contribution of the mixed clusters is considered, saturation effects disappear and the expected linear behavior is retrieved again for the total cluster concentration. It should be noted here that because of the detection limit in the experimental mass spectra it is not possible to extract from the experimental spectra data that correspond to the ones in Fig. 7B. There are many different heteromolecular clusters with different masses, so that the abundance of individual mixed clusters lies below the experimental detection limit. This experimental limitation can also be seen by the weak signals of the heteromolecular clusters in the extreme case when the ratio of CCO2/CBu is 60 (Fig. 6, see also Fig. S3 in the SI).
 |
| | Fig. 7 Simulations of the total cluster number concentration during nucleation and growth as a function of the nucleation time t from a kinetic model that considers nucleation and monomer association. (A) Concentration of only pure butane clusters CBu,tot(t) as predicted by the model. The saturation at longer t is caused by the formation of hetermomolecular butane–CO2, the abundance of which lies often below the experimental detection limit. (B) Sum of the concentration of pure butane clusters (CBu,tot(t)) and all different hetermomolecular butane–CO2 (CBu,tot(t) +Cmixed,tot) clusters as predicted by the model. | |
4 Conclusion
We have investigated butane nucleation in unary butane and binary butane–CO2 gas mixtures at a temperature of 51 K and a pressure of 40 Pa in the post-nozzle flow of a Laval expansion using mass spectrometric detection. This provides time-dependent molecular-level information on the chemical composition and abundance of nucleating clusters, thus enabling the determination of kinetic mechanisms based on molecularly resolved information.
For unary butane nucleation, we observed butane nucleation only above a minimum butane monomer concentration, which could be caused by cluster decay processes which are not considered in our simple model. For the binary butane–CO2 gas mixtures, butane nucleation rates lie in the range (2–10) × 1021 m−3 s−1, which is only about a factor of two higher than the rate observed for the unary butane system. Compared with the binary mixtures water–CO2 and toluene–CO2 we had previously studied,35,39 acceleration of nucleation by CO2 gas is much less important in the case of butane; i.e. the previously proposed chaperon mechanism35 is less effective. The weaker intermolecular interactions between butane and CO2 molecules compared to the interactions between water or toluene and CO2 provide a plausible explanation. This might also be the reason why we observe substantial cluster growth and temporal overlap of growth with nucleation already at only slightly higher butane and CO2 concentrations. In the mass spectra, growth results in saturation effects of pure butane clusters, caused by the formation of many different heteromolecular butane–CO2 clusters with abundances below the experimental detection limit. We confirmed this hypothesis by simulations using a kinetic nucleation-growth model. The reported results are relevant for flue or natural gas separation. They demonstrated how sensitively the effectiveness of separation by e.g. low-temperature separation methods depends on the actual gas composition and temperature.
Author contributions
Conceptualization & supervision: R. S.; methodology: R. S., C. L.; investigation: A. C., F. G., S. F., J. Kr., J. Kh., F. T. H.; data curation: A. C., F. G., S. F.; software: F. G., S. F., J. Kr.; formal analysis & validation: A. C., F. G.; writing – original draft: A. C., F. G.; writing – review & editing: A. C., F. G., R. S.; funding acquisition & resources: R. S.
Conflicts of interest
The authors have no conflicts of interest to disclose.
Data availability
The data that support the findings of this study are openly available in the ETH Research Collection at https://doi.org/10.3929/ethz-c-000788721.
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03900b.
Acknowledgements
The authors thank Philipp Albrecht, Markus Steger and Bruce Yoder for their technical support. The financial support was provided by the Swiss National Science Foundation (SNSF, grant no. 200021-236446).
References
- R. L. Garrett, W. K. Oehlschlager and J. F. Tomich, Vapor-Liquid Separation at Supersonic Velocities, J. Eng. Ind., 1968, 90(4), 609–612, DOI:10.1115/1.3604696.
- A. Hart and N. Gnanendran, Cryogenic CO2 capture in natural gas, Energy Procedia, 2009, 1(1), 697–706, DOI:10.1016/j.egypro.2009.01.092.
- P. B. Machado, J. G. M. Monteiro, J. L. Medeiros, H. D. Epsom and O. Q. F. Araujo, Supersonic separation in onshore natural gas dew point plant, J. Nat. Gas Sci. Eng., 2012, 6, 43–49, DOI:10.1016/j.jngse.2012.03.001.
- M. Haghighi, K. A. Hawboldt and M. A. Abdi, Supersonic gas separators: Review of latest developments, J. Nat. Gas Sci. Eng., 2015, 27, 109–121, DOI:10.1016/j.jngse.2015.08.049.
- X. Cao and J. Bian, Supersonic separation technology for natural gas processing: A review, Chem. Eng. Process., 2019, 136, 138–151, DOI:10.1016/j.cep.2019.01.007.
- J. Bian, X. Cao, W. Yang, X. Song, C. Xiang and S. Gao, Condensation characteristics of natural gas in the supersonic liquefaction process, Energy, 2019, 168, 99–110, DOI:10.1016/j.energy.2018.11.102.
- K. Iland, J. Wölk, R. Strey and D. Kashchiev, Argon nucleation in a cryogenic nucleation pulse chamber, J. Chem. Phys., 2007, 127(15), 20, DOI:10.1063/1.2764486.
- V. I. Kalikmanov, J. Wölk and T. Kraska, Argon nucleation: Bringing together theory, simulations, and experiment, J. Chem. Phys., 2008, 128(12), 32, DOI:10.1063/1.2888995.
- D. James, S. Beairsto, C. Hartt, O. Zavalov, I. Saika-Voivod, R. K. Bowles and P. H. Poole, Phase transitions in fluctuations and their role in two-step nucleation, J. Chem. Phys., 2019, 150(7), 74501, DOI:10.1063/1.5057429.
- J. Krohn, M. Lippe, C. Li and R. Signorell, Carbon dioxide and propane nucleation: the emergence of a nucleation barrier, Phys. Chem. Chem. Phys., 2020, 22(28), 15986–15998, 10.1039/D0CP01771J.
- C. Li and R. Signorell, Understanding vapor nucleation on the molecular level: A review, J. Aerosol Sci., 2021, 153, 105676, DOI:10.1016/j.jaerosci.2020.105676.
- D. Reguera and H. Reiss, Fusion of the Extended Modified Liquid Drop Model for Nucleation and Dynamical Nucleation Theory, Phys. Rev. Lett., 2004, 93(16), 165701, DOI:10.1103/PhysRevLett.93.165701.
- K. K. Tanaka, H. Tanaka, T. Yamamoto and K. Kawamura, Molecular dynamics simulations of nucleation from vapor to solid composed of Lennard-Jones molecules, J. Chem. Phys., 2011, 134(20), 204313, DOI:10.1063/1.3593459.
- S. Ayuba, D. Suh, K. Nomura, T. Ebisuzaki and K. Yasuoka, Kinetic analysis of homogeneous droplet nucleation using large-scale molecular dynamics simulations, J. Chem. Phys., 2018, 149(4), 44504, DOI:10.1063/1.5037647.
- J. Diemand, R. Angélil, K. K. Tanaka and H. Tanaka, Large scale molecular dynamics simulations of homogeneous nucleation, J. Chem. Phys., 2013, 139(7), 74309, DOI:10.1063/1.4818639.
- L. Inci and R. K. Bowles, Vapor condensation onto a non-volatile liquid drop, J. Chem. Phys., 2013, 139(21), 214703, DOI:10.1063/1.4834676.
- K. K. Tanaka, A. Kawano and H. Tanaka, Molecular dynamics simulations of the nucleation of water: Determining the sticking probability and formation energy of a cluster, J. Chem. Phys., 2014, 140(11), 114302, DOI:10.1063/1.4867909.
- R. Angélil, J. Diemand, K. K. Tanaka and H. Tanaka, Homogeneous SPC/E water nucleation in large molecular dynamics simulations, J. Chem. Phys., 2015, 143(6), 64507, DOI:10.1063/1.4928055.
- A. Aasen, Ø. Wilhelmsen, M. Hammer and D. Reguera, Free energy of critical droplets—from the binodal to the spinodal, J. Chem. Phys., 2023, 158(11), 114108, DOI:10.1063/5.0142533.
- R. Halonen, Atomistic insights into argon clusters and nucleation dynamics, J. Aerosol Sci., 2024, 181, DOI:10.1016/j.jaerosci.2024.106406.
- S. Lee, R. J. Hoobler and S. R. Leone, A pulsed Laval nozzle apparatus with laser ionization mass spectroscopy for direct measurements of rate coefficients at low temperatures with condensable gases, Rev. Sci. Instrum., 2000, 71(4), 1816–1823, DOI:10.1063/1.1150542.
- A. Bonnamy, R. Georges, A. Benidar, J. Boissoles, A. Canosa and B. R. Rowe, Infrared spectroscopy of (CO2)N nanoparticles (30 < N < 14500) flowing in a uniform supersonic expansion, J. Chem. Phys., 2003, 118(8), 3612–3621, DOI:10.1063/1.1539036.
- J. Bourgalais, V. Roussel, M. Capron, A. Benidar, A. W. Jasper, S. J. Klippenstein, L. Biennier and S. D. Le Picard, Low Temperature Kinetics of the First Steps of Water Cluster Formation, Phys. Rev. Lett., 2016, 116(11), 113401, DOI:10.1103/PhysRevLett.116.113401.
- D. Ghosh, D. Bergmann, R. Schwering, J. Wölk, R. Strey, S. Tanimura and B. E. Wyslouzil, Homogeneous nucleation of a homologous series of n-alkanes (CiH2i + 2,i = 7–10) in a supersonic nozzle, J. Chem. Phys., 2010, 132(2), 24307, DOI:10.1063/1.3274629.
- B. Schläppi, J. H. Litman, J. J. Ferreiro, D. Stapfer and R. Signorell, A pulsed uniform Laval expansion coupled with single photon ionization and mass spectrometric detection for the study of large molecular aggregates, Phys. Chem. Chem. Phys., 2015, 17, 25761, 10.1039/C5CP00061K.
- C. Li, N. Singh, A. Andrews, B. A. Olson, T. E. Schwartzentruber and C. J. Hogan, Mass, momentum, and energy transfer in supersonic aerosol deposition processes, Int. J. Heat Mass Transfer, 2019, 129, 1161–1171, DOI:10.1016/j.ijheatmasstransfer.2018.10.028.
- K. K. Dingilian, R. Halonen, V. Tikkanen, B. Reischl, H. Vehkamäki and B. E. Wyslouzil, Homogeneous nucleation of carbon dioxide in supersonic nozzles I: experiments and classical theories, Phys. Chem. Chem. Phys., 2020, 22(34), 19282–19298, 10.1039/D0CP02279A.
- B. Wyslouzil and R. Signorell. Nucleation Studies in Supersonic Flow. Uniform Supersonic Flows in Chemical Physics: Chemistry Close to Absolute Zero Studied Using the CRESU Method, 2022, pp. 351–392 DOI:10.1142/9781800610996_0006.
- L. H. Desmond Li, K. M. Douglas, F. Hall, A. Kirker, L. Driver, G. N. de Boer, N. Kapur, J. H. Lehman, M. A. Blitz and D. E. Heard, Experimental and Theoretical Study of the Kinetics of Dimerization of Ammonia at Low Temperatures, J. Phys. Chem. A, 2025, 129, 6305, DOI:10.1021/acs.jpca.5c03008.
- J. J. Ferreiro, T. E. Gartmann, B. Schläppi and R. Signorell, Can we Observe Gas Phase Nucleation at the Molecular Level?, Z. Phys. Chem., 2015, 229(10–12), 1765–1780, DOI:10.1515/zpch-2015-0603.
- S. Chakrabarty, J. J. Ferreiro, M. Lippe and R. Signorell, Toluene Cluster Formation in Laval Expansions: Nucleation and Growth, J. Phys. Chem. A, 2017, 121(20), 3991–4001, DOI:10.1021/acs.jpca.7b03162.
- M. Lippe, S. Chakrabarty, J. J. Ferreiro, K. K. Tanaka and R. Signorell, Water nucleation at extreme supersaturation, J. Chem. Phys., 2018, 149(24), 244303, DOI:10.1063/1.5052482.
- M. Lippe, U. Szczepaniak, G.-L. Hou, S. Chakrabarty, J. J. Ferreiro, E. Chasovskikh and R. Signorell, Infrared spectroscopy and mass spectrometry of co2 clusters during nucleation and growth, J. Phys. Chem. A, 2019, 123(12), 2426–2437, DOI:10.1021/acs.jpca.9b01030 . PMID: 30835464 .
- G. K. Schenter, S. M. Kathmann and B. C. Garrett, Dynamical Nucleation Theory: A New Molecular Approach to Vapor-Liquid Nucleation, Phys. Rev. Lett., 1999, 82(17), 3484, DOI:10.1103/PhysRevLett.82.3484.
- C. Li, J. Krohn, M. Lippe and R. Signorell, How volatile components catalyze vapor nucleation, Sci. Adv., 2021, 7(3), eabd9954, DOI:10.1126/sciadv.abd9954.
- R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Atmospheric new particle formation enhanced by organic acids, Science, 2004, 304(5676), 1487–1490, DOI:10.1126/science.1095139.
- C. N. Jen, P. H. McMurry and D. R. Hanson, Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res., 2014, 119(12), 7502–7514, DOI:10.1002/2014JD021592.
- S. Schobesberger, H. Junninen, F. Bianchi, G. Lönn, M. Ehn, K. Lehtipalo, J. Dommen, S. Ehrhart, I. K. Ortega, A. Franchin, T. Nieminen, F. Riccobono, M. Hutterli, J. Duplissy, J. Almeida, A. Amorim, M. Breitenlechner, A. J. Downard, E. M. Dunne, R. C. Flagan, M. Kajos, H. Keskinen, J. Kirkby, A. Kupc, A. Kürten, T. Kurtén, A. Laaksonen, S. Mathot, A. Onnela, A. P. Praplan, L. Rondo, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Sipilä, A. Tomé, G. Tsagkogeorgas, H. Vehkamäki, D. Wimmer, U. Baltensperger, K. S. Carslaw, J. Curtius, A. Hansel, T. Petäjä, M. Kulmala, N. M. Donahue and D. R. Worsnop, Molecular understanding of atmospheric particle formation from sulfuric acid and large oxidized organic molecules, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(43), 17223–17228, DOI:10.1073/pnas.1306973110.
- S. Feusi, F. Graber, J. Khatri, C. Li and R. Signorell, How CO2 gas accelerates water nucleation at low temperature, J. Chem. Phys., 2024, 161(18), 184304, DOI:10.1063/5.0233794.
- C. Li, M. Lippe, J. Krohn and R. Signorell, Extraction of monomer-cluster association rate constants from water nucleation data measured at extreme supersaturations, J. Chem. Phys., 2019, 151(9), 094305, DOI:10.1063/1.5118350.
- S. Feusi, J. Krohn, C. Li and R. Signorell, Mutual independence of water and n -nonane nucleation at low temperatures, J. Chem. Phys., 2023, 158(7), 74301, DOI:10.1063/5.0138628.
- S. Feusi. How Different Vapor Components Influence Nucleation Kinetics, PhD thesis, ETH Zurich, 2025 DOI:10.3929/ethz-c-000783079.
- F. Dong, S. Heinbuch, J. J. Rocca and E. R. Bernstein, Dynamics and fragmentation of van der Waals clusters: (H2O)n, (CH3OH)n, and (NH3)n upon ionization by a 26.5ev soft x-ray laser, J. Chem. Phys., 2006, 124(22), 2243119, DOI:10.1063/1.2202314.
- W. C. Wiley and I. H. McLaren, Time-of-flight mass spectrometer with improved resolution, Rev. Sci. Instrum., 2004, 26(12), 1150–1157, DOI:10.1063/1.1715212.
- K. Kameta, N. Kouchi, M. Ukai and Y. Hatano, Photoabsorption, photoionization, and neutral-dissociation cross sections of simple hydrocarbons in the vacuum ultraviolet range, J. Electron Spectrosc. Relat. Phenom., 2002, 123(2–3), 225–238, DOI:10.1016/S0368-2048(02)00022-1.
Footnote |
| † These authors contributed equally. |
|
| This journal is © the Owner Societies 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Felix Graber†
a,
Felix Graber† a,
Stefan Feusia,
Jan Krohna,
Jai Khatria,
Fernando Torres Hernandez
a,
Stefan Feusia,
Jan Krohna,
Jai Khatria,
Fernando Torres Hernandez a,
Chenxi Li
a,
Chenxi Li b and
Ruth Signorell
b and
Ruth Signorell *a
*a


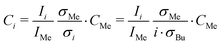
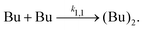
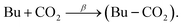

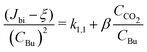
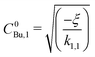 is required for unary nucleation to occur. Compared to the unary nucleation of other compounds we have previously studied (see, for example, the unary water nucleation in Table 1 and Fig. S1A in the SI), where the minimum concentration is negligible for the kinetics within uncertainties, it turns out that it is clearly not negligible in the case of unary butane nucleation.
is required for unary nucleation to occur. Compared to the unary nucleation of other compounds we have previously studied (see, for example, the unary water nucleation in Table 1 and Fig. S1A in the SI), where the minimum concentration is negligible for the kinetics within uncertainties, it turns out that it is clearly not negligible in the case of unary butane nucleation.







