 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interactions between calcium ion and functional groups of organic scale inhibitors in aqueous solutions: an ab initio study
Yue Li ,
Jiarui Zhang
,
Jiarui Zhang ,
Hongbo Zeng
,
Hongbo Zeng and
Hao Zhang
and
Hao Zhang *
*
Department of Chemical and Materials Engineering, University of Alberta, Edmonton, Alberta T6G 1H9, Canada. E-mail: hao.zhang@ualberta.ca; Tel: +1-780-492-8340
First published on 7th January 2026
Abstract
The anti-scaling performance of organic inhibitors is closely related to the Ca-trapping capacity of functional groups in polymer frameworks. In this study, we performed static density functional theory calculations and ab initio metadynamics simulations to systematically investigate the association behaviors of Ca2+ with carbonate species (CO32− and HCO3−) and representative functional groups of organic inhibitors (carboxylate, phosphonate, and sulfonate) in aqueous solutions. By calculating the binding free energies and activation barriers for separating contact ion pairs, we propose a new strategy for predicting the Ca-trapping capacity of organic additives. Simulation results revealed that carboxylate and phosphonate groups possess potential calcium sequestration abilities, while the formation of the calcium–sulfonate pair is almost impossible in aqueous solutions. For the carboxylate group, which possesses a planar structure akin to that of the carbonate species, its presence has less impact on the solvation structure of Ca2+. The monodentate and bidentate configurations have similar stabilities for the contact ion pair. However, for the phosphonate and sulfonate groups that possess a trigonal pyramid structure, their association with Ca2+ disrupts the symmetry of the coordination structure to a greater extent. The monodentate state is clearly favored over the more tightly coordinated bidentate state. Moreover, since CO32− exhibits the strongest affinity for Ca2+, a rising CO32− concentration at a high pH diminishes the anti-scaling efficiency of all inhibitors. Overall, we offer new insights into the inhibiting effects of organic additives on the initial stage of CaCO3 formation by analyzing calcium-organic compound interactions. These findings provide theoretical support for the development of more effective scale inhibitors in the industry.
1. Introduction
Calcium carbonate (CaCO3) scale deposition has been recognized as one of the major issues in industrial production.1 The development of scale layers in circulating cooling water systems blocks pipes and boilers and lowers the efficiency of heat exchangers, thus resulting in severe machine damage.2 In the oil and gas industries, water-flooding operations are commonly required to enhance secondary recovery from mature fields.3 However, excessive precipitation of scale impedes fluid flow in the wellbore, reservoir, tubing, casing, and even the oil-producing formation matrix, reducing well productivity and ultimately leading to considerable treatment costs and deterioration of the oil extraction process.4 Additionally, membrane distillation has emerged as one of the most promising technologies in desalination for water separation and purification.5 Nevertheless, undesired scale deposits progressively clog the pores and increase the wettability of the membrane, resulting in a decline in both the permeate flux and separation efficiency.6,7 Therefore, in recent years, increasing attention has been directed toward exploring the nucleation and growth mechanisms of CaCO3 and how to regulate such crystallization events in a particular context.8–10A typical method for hindering CaCO3 precipitation is the use of environmentally friendly chemicals, which act as anti-scaling reagents, that is, inhibitors.11 The commonly used organic inhibitors include, but are not limited to, carboxylic acids (e.g., polyacrylic acid (PAA),12 polyepoxysuccinic acid (PESA),13 and polyaspartic acid (PASP)14), phosphonic acids (e.g., amino trimethylene phosphonic acid (ATMP),15 2-phosphonobutane-1,2,4-tricarboxylic acid (PBTCA),16 and diethylenetriamine pentamethylene phosphonic acid (DTPMP)17), and sulfonates (e.g., polystyrene sulfonate (PSS)18).
As discussed in detail in our previous review article,19 inhibitors can restrain scale deposition by influencing one or multiple stages of CaCO3 crystallization, ranging from the aggregation of prenucleation clusters (PNCs), formation of amorphous CaCO3 (ACC) particles, and crystallization of ACC to the growth of crystals. Notably, the anti-scaling performance of an inhibitor is largely determined by the type, concentration, and arrangement of the functional groups within the polymer structure.20 In titration experiments conducted by Verch et al.,21 carboxylate groups were found to possess a stronger affinity toward Ca2+ than sulfonate groups in aqueous solutions, so the carboxylate-containing additive PASP can reduce the concentration of free Ca2+ ions involved in CaCO3 crystallization to a greater extent and therefore manifests a stronger inhibiting effect on scale deposition than the sulfonate-containing additive PSS. Li et al.8 employed scanning electron microscopy (SEM) to observe the crystal structure of scale deposits in both the presence and absence of inhibitors. They discovered that the carboxylate-containing additive PAA exhibits a rather insignificant effect on the surface structure of CaCO3 crystals, while the phosphonate-containing additives PBTCA and DTPMP fully open the crystal layers and effectively retard the growth of CaCO3 in a three-dimensional direction. Cui et al.22 synthesized a terpolymer scale inhibitor incorporating carboxylate, sulfonate, and amide groups and proposed that the synergistic effects of multiple functional groups in the polymer structure are beneficial in improving inhibition efficiency.
Although exceptional progress has been made in experimental techniques for evaluating the anti-scaling performance of inhibitors, the cardinal fact that one has to acknowledge is that the discovery of new inhibitors still relies on the labor-intensive “trial-and-error” paradigm, which consumes too much time and resources. In the past two decades, with the rapid development of computing facilities, there have been major advances in computer simulation, which plays a momentous role in providing atomic-level insights to uncover the physical mechanisms underlying the convoluted phenomena and thus exhibits remarkable potential to offer suggestions for the continuous development of more effective scale inhibitors in the industry.
To the best of our knowledge, the earliest attempt that employed atomistic simulations to investigate the inhibiting effects of organic additives on CaCO3 formation was the classical molecular dynamics (MD) studies conducted by de Leeuw and Cooper.23–25 They used a combination of three empirical potential models to describe the interatomic interactions in the system: the model by Pavese et al.26 for CaCO3 crystals, the consistent valence force field (CVFF)27 for organic molecules, and the water potential model by de Leeuw and Parker.28 Based on an analysis of the adsorption properties of a selection of organic molecules on calcite surfaces, they suggested that carboxylic acids can block the active growth sites of CaCO3 crystals, reduce the direct contact between surfaces and solutions, and thus retard crystal growth. Duchstein et al.29 utilized the assisted model building and energy refinement (AMBER) force field30 for the organic part and performed MD simulations to examine the dynamic interaction modes of carboxylate- and phosphonate-containing additives with PNCs. Their findings revealed the significance of scale inhibitors as “surfactants” in the initial stage of CaCO3 formation, reducing interactions among PNCs, restraining their aggregation, and delaying the formation of ACC. Recently, Schuitemaker et al.31 developed and characterized a new polarizable model for both calcium carbonate and organic functional groups (carboxylate and ammonium) in water based on sophisticated electrostatic treatment within the atomic multipole optimized energetics for biomolecular application (AMOEBA) force field.32 Compared with conventional rigid-ion (RI) models, not only the thermodynamics but also the solvation structures around the species are improved. Although numerous force fields have been proposed in MD studies to evaluate the effects of organic inhibitors on CaCO3 precipitation, the applicability of these models is severely restricted to chemical environments intended for parametrization. With the ever-growing complexity of the investigated problems, some degree of compromise between accuracy and transferability is inevitable.33
Compared with classical MD, quantum-mechanics-based density functional theory (DFT) describes interatomic interactions by directly solving the time-independent Schrödinger equation, thereby providing accurate and consistent predictions for chemical systems without relying on empirical data. Saharay et al.34 examined the interactions of Ca2+ and CO32− with representative amino acid functional groups, including guanidinium, acetate, acetic acid, and ethanol, in the gas phase. Delgado et al.35 and Dooley et al.36 incorporated implicit solvation models into their DFT studies and successfully reproduced the solvation structures of Ca2+ and CO32−. Lopez-Berganza et al.37 and Di Tommaso et al.38 explored the structural and energetic properties of CaCO3(H2O)n and CaHCO3(H2O)n+ clusters, respectively, advancing the understanding of ion association behaviors in the initial stage of CaCO3 nucleation. Unfortunately, no DFT study has evaluated the interaction strength between Ca2+ and anionic groups in aqueous environments. Despite the broad application of DFT, it is worth noting that this method is fundamentally static because it computes the energies and forces for fixed configurations and cannot capture the real-time evolution of microstructures under specific conditions.
Recently, the ab initio molecular dynamics (AIMD) method has emerged as an appealing alternative for overcoming the intrinsic limitations of both classical MD and static DFT calculations.39 On the one hand, interatomic interactions are determined using DFT, which goes beyond the feasibility of empirical models. On the other hand, atomic trajectories are generated by integrating Newton's laws of motion, which enables the analysis of dynamical properties. In particular, in recent studies,40 AIMD simulations were combined with some enhanced sampling methods, e.g., umbrella sampling (US)41 and metadynamics (MetaD),42 to study the thermodynamics and kinetics of chemical reactions and material processes. Henzler et al.43 employed US in their AIMD simulations to construct potentials of mean force between Ca2+ and carbonate species (CO32− and HCO3−). Li et al.44 utilized a two-dimensional set of collective variables characterized by the coordination number in their ab initio MetaD simulations to monitor the association processes of calcium silicate aqua complexes. In studies conducted by Gale and co-workers,45,46 ab initio MetaD simulations were carried out to calculate the ion-pairing free energy profiles between Ca2+ and either carbonate species (CO32− and HCO3−) or SO42−. Notably, there are also some issues associated with AIMD, including the charge delocalization error induced by exchange–correlation functionals46 and the limited time and length scales due to high computational costs. However, integrating the AIMD results with those from MD, DFT, and experimental studies can facilitate a more comprehensive understanding of the interactions between Ca2+ ions and organic-scale inhibitors in aqueous solutions.
In this study, we first carried out static DFT calculations to examine the pairwise interactions between Ca2+ and organic scale inhibitors in implicit solvents. Given that the majority of inhibitors, including carboxylic acids,47 phosphonic acids,48 and sulfonates,49 exist in deprotonated forms in slightly alkaline environments, where the formation efficiency of CaCO3 reaches its maximum,50 we opted to use acetate (CH3CO2−, ACE−), mesylate (CH3SO3−, MES−), and two methylphosphonates (CH3PO32−, MP2− and CH3PO3H−, MP−) as the basic units representing the functional groups within the polymer frameworks of organic inhibitors. Hereafter, using AIMD simulations and the MetaD method, we obtained the Helmholtz free energy surfaces for ion pairing, calculated the activation barriers for separating the contact ion pairs, and analyzed the dynamic structures of the ion complexes in real aqueous environments. The discussion of the association behaviors of calcium–organic ion pairs has provided new insights into the functional mechanisms of organic inhibitors on CaCO3 formation.
2. Computational methods
Pairwise interactions were investigated using the quantum chemistry package Gaussian 16.51 All structures were fully optimized at the level of B3LYP/def2-TZVP52,53 with the DFT-D3 dispersion correlation.54 Vibration frequency analyses were performed to ensure that the obtained stable minima had no imaginary frequencies. Based on the optimized geometries, single-point energies were calculated within the framework of the expensive ωB97X-D functional55 and the def2-QZVPP basis set53,56 of the quadruple zeta quality. At such a high level of theory, the influence of the basis set superposition error (BSSE) can be neglected, as recommended in previous studies.56–58 In addition, the implicit solvation model based on solute electron density (SMD)59 with the water parameter (ε = 78.4) was used to depict the solvation status. As utilized in the parametrization of SMD, the solvation free energies of all species were calculated at the level of M05-2X/6-31G(d).60,61 The binding free energies between Ca2+ and various anions were calculated following Scheme S1 and eqn (S1)–(S6). Please refer to Section S1 of the SI for more details.Hereafter, the optimized stable complexes, i.e., aqueous Ca2+–CO32−, Ca2+–HCO3−, Ca2+–ACE−, Ca2+–MP2−, Ca2+–MP−, and Ca2+–MES− ion pairs, were selected as candidates for the explicit solvation model in further AIMD simulations to explore their association behaviors in real aqueous environments. All the AIMD simulations reported in this work were carried out using the CP2K/quickstep package62,63 with a mixed Gaussian and plane wave (GPW) approach.64 The generalized gradient approximation (GGA) proposed by Perdew, Burke, and Ernzerhof (PBE)65 was applied to describe the exchange–correlation energy functional. Grimme's DFT-D354 dispersion correlation was used to depict the van der Waals interactions. Core electrons were described using Goedecker–Teter–Hutter (GTH) pseudopotentials.66–68 For valence electrons, a DZVP–MOLOPT–SR–GTH basis set64 was chosen for real space representation, and plane waves up to a cutoff energy of 500 Ry were employed to expand the electron density in reciprocal space. Brillouin zone sampling was performed only at the Γ-point.
In CP2K, periodic boundary conditions (PBCs) are employed to approximate an infinite system using a finite unit cell. However, if the investigated system carries a net charge, the long-range Coulomb interactions between the cell and its periodic replicas become divergent.69 To address this issue, a uniform background charge, often referred to as a “jellium” background, was introduced to neutralize the net charge,70 enabling charged systems, such as the aqueous Ca2+–HCO3−, Ca2+–ACE−, Ca2+–MP−, and Ca2+–MES− pairs in this work, to be studied within the periodic framework. In contrast, Gaussian 16 treats the system as an isolated finite molecule without applying PBCs, thereby avoiding divergence of the electrostatic energy. The change in the total charge is implemented by adjusting the number of electrons in the system and constructing the corresponding spin state. In Section S2, we discuss the influence of the system charge on the calculated results.
In AIMD simulations, the initial structures of bulk aqueous systems were constructed by randomly solvating an optimized ion pair in a 14.41 × 14.41 × 14.41 Å3 periodic cubic box with 100 water molecules (for a density of 1 g cm−3) using the PACKMOL code.71 Energy minimization was first performed to optimize the initial structures. Hereafter, the AIMD simulations were carried out within the isothermal–isochoric (NVT) ensemble at 330 K for 270 ps, where the last 240 ps run was used for the statistical analysis. As suggested by previous studies,72–74 elevating the temperature by ∼30 K is an economical and effective approach that mitigates the over-structured description of liquid water by GGA functionals and mimics the real properties of aqueous solutions at room temperature. During AIMD, the time step for the integration of the equations of motion was set to 0.5 fs. A three-chain Nosé–Hoover thermostat75–77 was used to regulate the temperature with a coupling constant of 100 fs.
The well-tempered MetaD method78 was combined with AIMD simulations to accelerate the sampling of the configuration space. In MetaD, a chemical reaction or material process can be represented by a set of carefully selected geometric parameters, typically referred to as collective variables (CVs). During the simulation, the bias potential is constructed by periodically depositing Gaussian hills along the CVs, which forces the system away from the traps and drives it toward unexplored regions of the energy landscape. Once the CV space is sufficiently sampled, the accumulated bias potential with its sign inverted provides an estimate of the free energy surface (FES). In this study, we used the distance d between the Ca2+ ion and the central atom of the anionic group (C for CO32−, HCO3−, and ACE−; P for MP2− and MP−; and S for MES−) as the CV to investigate the thermodynamics of ion pairing. As suggested in previous studies,43,79–81 the interionic distance d provides a physically unambiguous descriptor for distinguishing the bidentate, monodentate, solvent-shared, and dissociated states of an ion pair. In the resulting FES, as a function of d, the depths of the local minima quantify the stability of each state, while the swells between neighboring minima indicate the reaction barriers along the corresponding pathways. The Gaussian hills were deposited every 60 time steps (30 fs) with an initial height of 2.5 kJ mol−1, a width of 0.1 Å, and a bias factor of 6. A quadratic upper wall with a force constant of 500 kJ mol−1 nm−2 was introduced at d = 6.2 Å in all systems to prevent the exploration of distances beyond half the box length. The time evolutions of CV during the whole simulation time and the convergence tests for FESs are shown in Section S3 of the SI.
In addition, we utilized a two-dimensional set of CVs characterized by the coordination number (CN) to monitor the ion association processes. Notably, the CVs defined here were used only for analysis and not for constructing the bias potential. CN(Ca–Oa) is the coordination number of the Ca2+ ion with O atoms from anionic groups, while CN(Ca–Ow) is the coordination number of the Ca2+ ion with O atoms from water molecules. As defined in the PLUMED plugin,82 CN has the following expression:
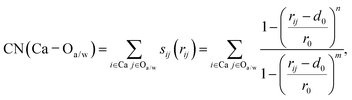 | (1) |
3. Results and discussion
3.1. Pairwise interactions
We first investigated the pairwise interactions between the Ca2+ ion and either the carbonate species (CO32− and HCO3−) or the functional groups of organic scale inhibitors (ACE−, MP2−, MP−, and MES−) in implicit solvents. The structures and energetics of the ion complexes were explored by initiating simulations with a number of starting geometries in which the anionic groups were placed around Ca2+ via a monodentate or bidentate binding mode. Hereafter, twelve explicit water molecules were introduced into the systems using the PACKMOL code71 to generate solvation shells around ion pairs. As reported in previous studies,84–86 such a mixed explicit/implicit solvation method captures both local and bulk solvent effects and thus enhances the accuracy of thermodynamic properties. In Section S4, we discussed the influence of the number of explicit water molecules on the binding free energy. The most stable configurations of all aqueous calcium–anion complexes after optimization are illustrated in Fig. 1(a)–(f), while the corresponding atomic coordinates are included in Table S1. The structural and energetic information of several representative, less stable calcium–anion complexes is displayed in Table S2. | ||
| Fig. 1 The most stable configurations of aqueous (a) Ca2+–CO32−, (b) Ca2+–HCO3−, (c) Ca2+–ACE−, (d) Ca2+–MP2−, (e) Ca2+–MP−, and (f) Ca2+–MES− ion pairs. | ||
Table 1 summarizes the binding free energies of the contact ion pairs. The calculated results agree well with the existing experimental and theoretical data from previous studies (see Table 1), indicating the accuracy achieved in our calculations. Generally, a more negative binding free energy is associated with a stronger interaction. Hence, among four organic functional groups, Ca2+ ion prefers to bind MP2− with the lowest binding free energy of −14.0 kJ mol−1, followed by ACE−, MP−, and MES− ions of −6.2, −5.3, and +4.4 kJ mol−1, respectively. For the Ca2+–ACE− pair, Ca2+ is coplanar with the COO− group and coordinates with the carboxylate O in a bidentate mode. For MP2−, MP−, and MES− ions that contain a trigonal pyramid –XO3(H) (X = P, S) structure, even if the phosphonate or sulfonate group is placed in a bidentate coordination with Ca2+ in the initial setup, one O atom from anions is detached from Ca2+ during the energy minimization, forming the monodentate binding mode in the end.
| Ion pair | This work | Exp. | Theor. |
|---|---|---|---|
| a Ref. 87.b Ref. 88.c Ref. 89.d Ref. 46.e Ref. 81.f Ref. 90.g Ref. 91.h Ref. 80.i Ref. 92.j Ref. 31. | |||
| Ca2+–CO32− | −17.0 | −19.0a, −18.0b | −20.3c, −17.3d, −12.5e |
| Ca2+–HCO3− | −8.1 | −6.2a, −7.5f | −11.3c, −8.0d |
| Ca2+–ACE− | −6.2 | −4.4 to −7.1g, −3.2h | −9.5i, −8.0j |
| Ca2+–MP2− | −14.0 | ||
| Ca2+–MP− | −5.3 | ||
| Ca2+–MES− | +4.4 | ||
To ascertain the competition among carbonate species and organic inhibitors for interactions with Ca2+, we examined the binding of CO32− and HCO3− ions to Ca2+, as shown in Fig. 1(a) and (b), respectively. Relative to the HCO3− ion, three organic functional groups, including MP2−, ACE−, and MP−, exhibit a stronger or comparable affinity to Ca2+, indicating the potential capacity of these groups as Ca-trapping agents in near-neutral environments where HCO3− dominates the carbonate species.93 With the binding of Ca2+ to organic inhibitors, fewer ions are involved in PNC formation, and the crystallization process is therefore retarded. In contrast, the positive binding free energy for the Ca2+–MES− pair demonstrates that the association of the sulfonate group with Ca2+ is energetically unfavorable in aqueous solutions. This is one of the reasons that the sulfonate-containing additive PSS cannot practically reduce the concentration of free Ca2+ ions in carbonate buffer, as observed in the titration experiments by Verch et al.21
With increasing solution pH, CO32− ion gradually dominates the carbonate species.93 In this case, the binding energy of the Ca2+–CO32− pair reaches −17.0 kJ mol−1, and all interactions between Ca2+ and inhibitors lose their advantages. This finding can explain the diminishment in the anti-scaling performance of organic inhibitors in alkaline environments.94 However, since a substantial portion of the phosphonic acids exist as the fully deprotonated form (–PO32−) at high pH48 and Ca2+ displays a stronger affinity toward MP2− than MP− with a lower binding free energy, the Ca-trapping capacity of the phosphonate-containing inhibitors can be maintained to a greater extent. As evidenced by the experiments by Yao et al.,95 the inhibition rate of the carboxylate-containing additive PAA decreases by 21%, while the phosphonate-containing additive PBTCA merely decreases by 6% in the pH ranging from 5 to 10.
Moreover, in Section S6, we performed an analysis of the charge density difference to estimate the bonding strength between Ca2+ and the anionic groups. Combining the values of binding free energy in Table 1 with the results of the charge density difference in Fig. S4–S6, one can notice that stronger calcium–anion interactions typically result in enhanced stability. The only exception is the Ca2+–MP− pair, which exhibits a stronger Ca–O bonding strength but less negative binding free energy in comparison with the Ca2+–HCO3− pair. We attributed this phenomenon to differences in the geometries of the functional groups. Compared to the planar (bi)carbonate or carboxylate, the attachment of the trigonal pyramidal phosphonate group with Ca2+ squeezes the living space of water molecules in the first solvation shell of Ca2+ and thus weakens the stability of the contact ion pair. The bulky structure of the phosphonate group also restricts its coordination with Ca2+. For the Ca2+–MP2− pair that exhibits stability second only to Ca2+–CO32−, the monodentate state is favored over the more tightly coordinated bidentate state.
3.2. Free energy profiles
After analyzing the pairwise interactions from the static DFT calculations, we performed ab initio MetaD simulations with explicit water molecules to investigate the thermodynamics of ion pairing in real aqueous solutions. Fig. 2 shows the free energy profiles as a function of ion separation for all systems. The free energy minima, or shoulders, at calcium–anion distances of approximately 3 and 3.5 Å correspond to the bidentate and monodentate binding modes of ion complexes, respectively. The activation barriers for the decomposition of the contact ion pairs are shown in Table 2.| Ion pair | This work | AIMD | Force field | ||
|---|---|---|---|---|---|
| RI | AMOEBA | ML | |||
| a Ref. 43.b Ref. 46.c Ref. 81.d Ref. 97.e Ref. 98.f Results for the Ca2+–HCOO− ion pair from ref. 79.g Ref. 31. | |||||
| Ca2+–CO32− | 20.9 | 16.3a, 10–16b, 16c | 18d | 25b | 20c |
| Ca2+–HCO3− | 12.9 | 13.4a | 16d | 10b | |
| Ca2+–ACE− | 16.8 | 14e, 19f | 15g | 21g | |
| Ca2+–MP2− | 17.2 | ||||
| Ca2+–MP− | 11.5 | ||||
| Ca2+–MES− | 5.7 | ||||
For the Ca2+–CO32− system, the bidentate configuration is 4.5 kJ mol−1, which is preferred over the monodentate counterpart. For the Ca2+–HCO3− system, the Ca2+ ion favors coordinating with only one O atom from HCO3−, which is consistent with the findings displayed in our static DFT calculations. According to the simulation results presented in Table 2, the total activation barrier for separating the contact Ca2+–CO32− pair reaches 20.9 kJ mol−1, which is 8.0 kJ mol−1 higher than that of the Ca2+–HCO3− pair. Therefore, we can predict that CO32− exhibits a stronger affinity to Ca2+ compared with HCO3−, leading to the formation of a more stable precursor phase in the prenucleation stage, which benefits subsequent CaCO3 nucleation. This finding is consistent with the experiment of Andritsos and Karabelas,96 who reported that an increased CO32− concentration in the pH range of 8.8–10 promotes CaCO3 scale deposition from 2 to 12 mg cm−2 after a 2 h run.
However, when comparing the results between the present work and previous AIMD studies, one notices that there are some clear differences, even though all calculations were performed using a similar-sized box. Henzler et al.43 proposed that both the CO32− and HCO3− ions favor coordinating with Ca2+ in a bidentate manner. This viewpoint is not completely consistent with our findings because the monodentate state of the Ca2+–HCO3− pair is effectively a point of inflection in our calculations. Although the lowest-energy configuration is debated, their study also reported a higher activation barrier for separating the Ca2+–CO32− pair than for the Ca2+–HCO3− pair (16.3 kJ mol−1 vs. 13.4 kJ mol−1). This suggests that we are consistent with each other on the most essential conclusion; for example, CO32− ion exhibits a stronger affinity to Ca2+ compared with HCO3−. Scrutinizing the computational methodology, it is evident that the primary difference lies in the system temperature. Henzler et al.43 used a temperature of 300 K, while in this study, we elevated the temperature to 330 K to mitigate the over-structured description of liquid water by GGA functionals. Here, the “over-structured” behavior indicates that the hydrogen-bond network described within the GGA framework is more persistent and less flexible than in real liquid water. Therefore, if Henzler et al. initialized the Ca2+–HCO3− pair in a bidentate configuration, the overly strong hydrogen-bond network may restrict the structural evolution of the contact ion pair and result in an underestimation of the free energy at this state. Compared with implementing expensive meta-GGA or hybrid functionals, elevating the temperature by ∼30 K is an economical and effective approach that mimics the real properties of aqueous solutions at room temperature.
Notably, system temperature is merely one of the factors that can potentially affect AIMD results. In the ab initio MetaD simulations conducted by Raiteri et al.,46 the free energy landscape at 330 K suggests that the monodentate state of the Ca2+–CO32− pair is ∼1 kJ mol−1 more stable than the bidentate state, which is different from both our results and those of Henzler et al.43 This discrepancy is partly due to the selection of CVs. Raiteri et al.46 employed a two-dimensional set of CVs characterized by the calcium–anion distance and the coordination number of calcium by water to monitor ion pairing. Although this setup considers various solvation structures of ion pairs at the same distance, offering deeper insights into the ion association processes in theory, it poses additional challenges for the convergence of MetaD calculations. Notably, uneven sampling of different solvation structures within the same binding mode may influence the determination of the lowest-energy configuration. In the present study, we utilized the calcium–anion distance as the sole CV to provide an overall assessment of the stability of the monodentate and bidentate states. In a more recent study, Piaggi et al.81 utilized the same one-dimensional CV and obtained similar results to ours; that is, the bidentate configuration is the most stable state for the contact Ca2+–CO32− pair. Apart from the parameter set in MetaD, some intrinsic weaknesses of the DFT method, such as the charge delocalization error induced by GGA functionals, have also been reported to affect ion association behaviors.46
Given the systematic errors associated with AIMD simulations, it is reasonable for researchers to question whether the classical MD method, which utilizes a carefully parametrized force field, is a better choice for investigating the association behaviors of ion pairs. The MD method exhibits a striking advantage in computational speed, allowing the configuration space to be fully sampled within a sufficient simulation time. In addition, AIMD simulations can be performed only in small periodic cells. Even at the farthest calcium–anion distance considered in our simulations (∼6 Å), the ion pairs are not completely dissociated but exist in a solvent-shared state. Hence, AIMD simulations are incapable of mimicking the entire ion association process, as is carried out in MD simulations. However, it is worth noting that the quality of MD simulations is largely determined by the accuracy of the applied force field. In the case of the Ca2+–CO32− pair, the polarizable AMOEBA force field46 suggests that bidentate coordination is more stable than its monodentate counterpart. In the conventional RI force field,97 the opposite order of stability is offered with a weaker minimum for the bidentate binding arrangement. Overall, our findings are more consistent with those obtained from the AMOEBA force field although the activation barrier for separating the contact Ca2+–CO32− pair provided by this model is ∼4 kJ mol−1 higher than our result. In 2025, Piaggi et al.81 developed a new force field based on advanced machine learning (ML) technology. In this model, the activation barrier for separating the Ca2+–CO32− pair was corrected to 20 kJ mol−1, closely aligning with our result of 20.9 kJ mol−1.
Based on the aforementioned discussion, it can be concluded that there is no perfect approach for studying ion-pairing thermodynamics in aqueous solutions. The selection of the simulation method largely depends on the problem being investigated. In this study, we aim to devise a simple strategy for screening organic functional groups with excellent Ca-trapping capacity to offer suggestions for the development of effective scale inhibitors in the industry. Therefore, constructing a reliable and transferable force field that encompasses all organic functional groups in CaCO3 solutions is unrealistic and uneconomical for us. In this case, we must use some general-purpose force fields to describe the calcium–organic interactions in MD simulations. A study by Kahlen et al.98 has certified that the general-purpose force fields are far from accurate in describing the ion-pairing thermodynamics, resulting in a deviation of ∼30 kJ mol−1 on binding free energy for the Ca2+–ACE− pair. In view of this, the AIMD method is a more practical choice for us. Integrating the ab initio results with available MD and experimental studies can facilitate a more comprehensive understanding of the calcium–anion interactions. Actually, the main concerns regarding the ab initio MetaD simulations mainly focus on areas with calcium–anion distances above 5 Å,46 where the rapidly expanding configuration space cannot be fully sampled within the limited time scale of AIMD simulations. However, as shown in Fig. 2, both the lowest energy states of the contact ion pairs and the transition states during the ion separation process are located in the area with calcium–anion distances below 4.5 Å. Therefore, the derived activation barriers should be reliable. Notably, the small peaks or minima observed at larger calcium–anion distances on free energy profiles should be considered numerical artifacts arising from insufficient sampling rather than specific configuration states. In Section S7 of the SI, we conducted three independent ab initio MetaD simulations for the Ca2+–CO32− system, each starting from distinct initial structures, to confirm the consistency of our calculations within the given methodological framework.
Next, we studied the ion-pairing thermodynamics of Ca2+ with organic functional groups in aqueous solutions. For the Ca2+–ACE− system, the bidentate configuration is found to be 1.5 kJ mol−1 preferred over the monodentate counterpart. The nearly equal stability between bidentate and monodentate configurations aligns well with the findings presented in the AIMD study of Mendes de Oliveira80 although they reported that the monodentate configuration is ∼1 kJ mol−1 favored. Moreover, the activation barrier for separating the Ca2+–ACE− pair is predicted to be 16.8 kJ mol−1, which falls within the range of results obtained from previous studies (14–21 kJ mol−1).31,79,98 Notably, this value is 3.9 kJ mol−1 higher than that of the Ca2+–HCO3− pair, indicating that the carboxylate group exhibits a potential calcium sequestration ability in near-neutral environments. However, as the CO32− ion exhibits a stronger affinity to Ca2+ than ACE−, with a higher separation barrier of 20.9 kJ mol−1, an increase in the concentration of CO32− at alkaline pH diminishes the inhibition efficiency of carboxylate-containing additives.
Additionally, for phosphonate and sulfonate groups that contain a trigonal pyramid structure, their association with Ca2+ favors the monodentate binding mode. The bidentate state in Ca2+–MP2− and Ca2+–MP− pairs are still local free energy minima, which are separated by small activation barriers of 3.6 and 0.5 kJ mol−1, respectively. However, for the Ca2+–MES− system, the bidentate state essentially becomes a point of inflection rather than a distinct minimum. Regarding the decomposition processes, the activation barrier for separating the contact Ca2+–MP− pair is only 11.5 kJ mol−1, which is 1.4 kJ mol−1 lower than that in the Ca2+–HCO3− system. Combining the less negative binding free energy between Ca2+ and MP− shown in Section 3.1, we can confirm that the phosphonate group is actually a substandard Ca-trapping agent at near-neutral pH, whose affinity to Ca2+ has no obvious advantage compared with HCO3−. This finding provides crucial evidence in support of the viewpoint of Duchstein et al.,29 where they proposed that the inhibiting effect of the phosphonate-containing additives is mainly achieved by stabilizing the prenucleation phases in the initial stage of CaCO3 formation, which is independent of a strong calcium sequestration ability. Although the strong interaction between Ca2+ and MP2− enhances the decomposition barrier to 17.2 kJ mol−1, it is still 3.7 kJ mol−1 lower than that of the Ca2+–CO32− pair.
For the Ca2+–MES− system, the free energy profile illustrates that the Ca2+ ion favors keeping a distance from MES−. Any contact ion pairs, whether following the monodentate or bidentate binding mode, are energetically unfavorable in aqueous solutions. Although ab initio MetaD simulations exhibit limited accuracy in calculating the free energy of states where the calcium–anion distances exceed 5 Å, such a special phenomenon is sufficient to demonstrate the lability of the contact Ca2+–MES− pair. Even if minor amounts of ion pairs can be formed occasionally, it is effortless to separate them with a decomposition barrier of 5.7 kJ mol−1. As shown in Table 2, this value is the lowest among all ion pairs considered, indicating that the Ca2+–MES− pair is almost impossible to form in the presence of carbonate species in aqueous solutions. This finding is supported by the crystallization experiments by Verch et al.,21 who estimated the amount of free and bound Ca2+ ions in solutions by means of a Ca2+-ion selective electrode and discovered that only 0.04 Ca2+ ions are bound per sulfonate group in the presence of a carbonate buffer. In contrast, one carboxylate group can adsorb 0.21 Ca2+ ions in the same environment, demonstrating a stronger calcium sequestration ability.
3.3. Structural analysis
During ab initio MetaD simulations, we utilized a two-dimensional set of CVs characterized by CN(Ca–Oa) and CN(Ca–Ow) to monitor the solvation structures of all ion pairs in real aqueous environments. The probability distributions of CNs and the configurations of the representative states on the heat maps are illustrated in Fig. 3. The coordinates of each state are presented in the form of (CN(Ca–Oa), CN(Ca–OW)). As depicted in Fig. S8, the spatial distributions of Ca2+ around the anionic groups illustrate the effect of the anion type on the binding mode of the ion pair.At CN(Ca–Oa) equals 0, the Ca2+ ion tends to be surrounded by several water molecules to form the hydrated Ca(H2O)n2+ (n = 5–7) clusters, wherein the six-coordinated (0, 6) states with a nearly octahedral symmetry are commonly regarded as the starting points for the association processes of all ion pairs. For carbonate species and the carboxylate group that possess a planar structure, as shown in Fig. 3(a)–(c), their association with Ca2+ is initiated by introducing one O atom from anions into the first solvation shell of Ca2+. After going through the seven-coordinated (1, 6) states, the systems reach (1, 5) with one water molecule detached from Ca2+, and the total coordination number returns to six. Moreover, since the occurrence probability of (1, 5) is higher than that of (1, 6), the seven-coordinated (1, 6) states with distorted pentagonal bipyramidal structures serve as intermediates of the association processes. Therefore, the formation of the contact Ca2+–CO32−, Ca2+–HCO3−, and Ca2+–ACE− pairs with the CN(Ca–Oa) value increasing from 0 to 1 can be simplified as a water–anion exchange process, which follows an associative ligand substitution mechanism. The derived formation process of the Ca2+–CO32− pair agrees well with the findings presented in the AIMD study carried out by Raiteri et al.46 Hereafter, the Ca2+ ion can connect with the second O atom from the anionic groups to form the bidentate binding arrangement at CN(Ca–Oa) equals 2. In particular, for Ca2+–CO32− and Ca2+–ACE− systems, the bidentate configurations are actually ion complexes that encompass 4–5 water molecules. Notably, for contact ion pairs, the total coordination number of Ca2+ generally falls in the range of 6–7. This result is consistent with previous AIMD simulations of Ca2+ in water,38 demonstrating that the presence of carbonate species and the carboxylate group does not change the coordination preference of Ca2+ in its first solvation shell.
However, for the phosphonate and sulfonate groups, their association with Ca2+ is much more complicated. As shown in Fig. 3(d)–(f), the intermediate states (1, 6) almost disappear. Instead, a large number of transition states emerge in the area where CN(Ca–Oa) and CN(Ca–Ow) vary from 0.5 to 1 and from 5.5 to 6, respectively. Based on the analysis of the dynamic structures of the calcium–organic ion complexes, we primarily ascribed this difference to the varying geometries of functional groups. Compared to the planar (bi)carbonate/carboxylate, the attachment of the trigonal pyramidal phosphonate or sulfonate group with Ca2+ undoubtedly disrupts the symmetry of the coordination structure to a greater extent. To accommodate the bulky phosphonate or sulfonate, the Ca2+ ion at (0, 6) has to simultaneously liberate one water ligand to prepare ample room for ion association. More interestingly, the formation of the contact ion pairs can potentially follow the dissociative ligand substitution mechanism. In other words, the Ca2+ ion discards one water ligand at first and coordinates one anion O afterward to keep the total coordination number no more than six. Actually, it has been reported that the release of water ligands from the metal ion's solvation shell can increase the translational and rotational degrees of freedom of water molecules and, therefore, enhance the entropy of the system.88,99 As proposed by Byrne et al.,45 such entropic terms drive the association of ions.
Structural analysis of ion complexes can also be used to explain why the phosphonate group fails to serve as a qualified calcium sequestration agent. In real aqueous environments, as the MP2− or MP− ion approaches Ca2+ and connects with it via bridging oxygen, the remaining –O or –OH moiety of the phosphonate group strongly squeezes the living space of water molecules in the first solvation shell of Ca2+ and even compels the Ca2+ ion to release more water ligands to balance the structure. As shown in Fig. 3(d) and (e), the probability of the monodentate configurations encompassing 4–5 water molecules increases significantly in comparison with the Ca2+–CO32−, Ca2+–HCO3−, and Ca2+–ACE− systems, indicating a decrease in the total coordination number of Ca2+. In this case, the Ca2+ ion has a tendency to restore coordination symmetry, and the stability of the Ca2+–MP2− and Ca2+–MP− pairs is, therefore, degraded. For the Ca2+–MES− system, considering the weak interaction between Ca2+ and MES− and the bulky structure of the sulfonate group, it is not surprising that the probability of contact ion pairs is lower than in the other systems.
4. Conclusions
In the current study, we performed static DFT calculations and ab initio MetaD simulations to systematically explore the association behaviors of Ca2+ ions with either carbonate species or organic inhibitors in aqueous solutions. Here, we employed acetate (ACE−), mesylate (MES−), and two methylphosphonates (MP− and MP2−) as the basic units representing carboxylate, sulfonate, and phosphonate groups, respectively, within the polymer frameworks of organic inhibitors.By analyzing the thermodynamic and structural properties of the calcium–anion ion pairs, we discovered that the Ca-trapping capacity of an inhibitor is determined by two factors. The first one depends on the strength of the interaction. Apparently, a strong interionic interaction is a crucial prerequisite for the stable existence of an ion complex. The second one is derived from the geometry of the functional group. For the carboxylate group, which possesses a planar structure akin to the carbonate species, its presence has less impact on the solvation structure of Ca2+. The monodentate and bidentate binding modes have similar stability for the contact ion pair. However, for phosphonate and sulfonate groups that contain a trigonal pyramid structure, their association with Ca2+ disrupts the symmetry of the coordination structure and decreases the capacity of Ca2+ for accommodating O. The monodentate binding arrangement is preferred for contact ion pairs.
By considering the synergistic effects of these two factors on ion pairing, we confirmed that carboxylate and phosphonate groups possess potential calcium sequestration ability, while the formation of the calcium–sulfonate pair is almost impossible in near-neutral environments, where HCO3− dominates the carbonate species. Moreover, since CO32− exhibits the strongest affinity to Ca2+, an increase in the concentration of CO32− from near-neutral to alkaline pH diminishes the Ca-trapping capacity of all organic functional groups. Because a substantial portion of the phosphonic acids exist as the fully deprotonated form (–PO32−) at high pH and Ca2+ displays a stronger affinity toward MP2− than MP− with a more negative binding free energy and a higher separation barrier, the calcium sequestration ability of the phosphonate group can be maintained to a greater extent compared with the carboxylate in alkaline environments. Notably, we discovered that all functional groups of organic inhibitors considered in this study have no obvious advantage for interactions with Ca2+ compared to carbonate species, indicating that Ca-trapping capacity is perhaps not the dominant factor that directly determines anti-scaling efficiency. A more comprehensive strategy is needed to evaluate the overall effects of organic inhibitors on CaCO3 crystallization.
Overall, we provided new insights into the understanding of the inhibiting effects of organic additives on the initial stage of CaCO3 formation by analyzing the calcium–organic interactions in aqueous environments. However, we must acknowledge the limitations of this ab initio study. First, we neglected the possible multibody interactions between the dissolved species in solutions, e.g., the synergistic effects of multiple functional groups and the interactions between organic inhibitors and larger molecular clusters (PNCs or ACC particles). Second, due to the limitations of AIMD studies on time and length scales, the impact of some macroscopic factors on anti-scaling efficiency (e.g., the concentrations of organic inhibitors) was not considered. MD simulations based on force field methods are more adequate for solving these complex problems. Our calculation results can be utilized as reference data in future research to accelerate the construction of more accurate force fields for describing the role of organic additives in CaCO3 crystallization.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: pairwise interaction calculation, influence of the system charge on the calculated results, MetaD convergence tests, influence of the number of explicit water molecules on the calculated results, optimized structures and atomic coordinates of ion complexes, analysis of charge density difference, effects of initial structures on simulation results and spatial distributions of Ca2+ around the anionic groups. See DOI: https://doi.org/10.1039/d5cp03876f.Acknowledgements
Y. L., H. Z., and H. B. Z. gratefully acknowledge the support of the Natural Sciences and Engineering Research Council of Canada under the Alliance program (ALLRP 557113 - 20).References
- C. Li, C. Liu and W. Xu, et al., Formation mechanisms and supervisory prediction of scaling in water supply pipelines: A review, Water Res., 2022, 222, 118922 CrossRef PubMed.
- Y. Guo, Z. Xu and S. Guo, et al., Selection of anode materials and optimization of operating parameters for electrochemical water descaling, Sep. Purif. Technol., 2021, 261, 118304 CrossRef.
- S. Qazvini, A. Golkari and A. Azdarpour, et al., Experimental and modelling approach to investigate the mechanisms of formation damage due to calcium carbonate precipitation in carbonate reservoirs, J. Pet. Sci. Eng., 2021, 205, 108801 CrossRef.
- A. A. Olajire, A review of oilfield scale management technology for oil and gas production, J. Pet. Sci. Eng., 2015, 135, 723–737 CrossRef.
- L. D. Tijing, Y. C. Woo and J.-S. Choi, et al., Fouling and its control in membrane distillation—A review, J. Membr. Sci., 2015, 475, 215–244 CrossRef.
- M. Gryta, The influence of magnetic water treatment on CaCO3 scale formation in membrane distillation process, Sep. Purif. Technol., 2011, 80, 293–299 CrossRef.
- K. Ali and M. I. Hassan Ali, A numerical study of CaCO3 deposition on the membrane surface of direct contact membrane distillation, Desalination, 2024, 576, 117364 CrossRef.
- A. Li, H. Zhang and Q. Liu, et al., Effects of chemical inhibitors on the scaling behaviors of calcite and the associated surface interaction mechanisms, J. Colloid Interface Sci., 2022, 618, 507–517 CrossRef PubMed.
- Y. Li, H. Zeng and H. Zhang, Influence of impurity metal doping on calcite growth: A first-principles study, Appl. Surf. Sci., 2023, 637, 157927 CrossRef.
- Y. Li, J. Zhang and H. Zeng, et al., Ion association behaviors in the initial stage of calcium carbonate formation: An ab initio study, J. Chem. Phys., 2024, 161, 014503 CrossRef PubMed.
- M. Chaussemier, E. Pourmohtasham and D. Gelus, et al., State of art of natural inhibitors of calcium carbonate scaling. A review article, Desalination, 2015, 356, 47–55 CrossRef.
- A. L. Kavitha, T. Vasudevan and H. G. Prabu, Evaluation of synthesized antiscalants for cooling water system application, Desalination, 2011, 268, 38–45 CrossRef.
- D. Liu, W. Dong and F. Li, et al., Comparative performance of polyepoxysuccinic acid and polyaspartic acid on scaling inhibition by static and rapid controlled precipitation methods, Desalination, 2012, 304, 1–10 CrossRef.
- J. Yang, Z. Hu and Z. Wang, et al., Preparation and scale inhibition performance of modified polyaspartic acid (M-PASP), J. Mol. Liq., 2024, 401, 124712 CrossRef.
- Y. Ji, Y. Chen and J. Le, et al., Highly effective scale inhibition performance of amino trimethylenephosphonic acid on calcium carbonate, Desalination, 2017, 422, 165–173 CrossRef.
- M. F. Mady, S. Abdel-Azeim and M. A. Kelland, Antiscaling evaluation and quantum chemical studies of nitrogen-free organophosphorus compounds for oilfield scale management, Ind. Eng. Chem. Res., 2021, 60, 12175–12188 CrossRef.
- Z. Kiaei and A. Haghtalab, Experimental study of using Ca-DTPMP nanoparticles in inhibition of CaCO3 scaling in a bulk water process, Desalination, 2014, 338, 84–92 CrossRef.
- X.-R. Xu, A.-H. Cai and R. Liu, et al., The roles of water and polyelectrolytes in the phase transformation of amorphous calcium carbonate, J. Cryst. Growth, 2008, 310, 3779–3787 CrossRef CAS.
- Y. Li, H. Zeng and H. Zhang, Atomistic simulations of nucleation and growth of CaCO3 with the influence of inhibitors: A review, Mater. Genome Eng. Adv., 2023, 1, e4 CrossRef.
- H. Du and E. Amstad, Water: How Does It Influence the CaCO3 Formation?, Angew. Chem., Int. Ed., 2020, 59, 1798–1816 CrossRef CAS PubMed.
- A. Verch, D. Gebauer and M. Antonietti, et al., How to control the scaling of CaCO3: a “fingerprinting technique” to classify additives, Phys. Chem. Chem. Phys., 2011, 13, 16811–16820 RSC.
- K. Cui, C. Li and B. Yao, et al., Synthesis and evaluation of an environment-friendly terpolymer CaCO3 scale inhibitor for oilfield produced water with better salt and temperature resistance, J. Appl. Polym. Sci., 2020, 137, 48460 CrossRef.
- N. H. de Leeuw, S. C. Parker and K. H. Rao, Modeling the competitive adsorption of water and methanoic acid on calcite and fluorite surfaces, Langmuir, 1998, 14, 5900–5906 CrossRef.
- T. G. Cooper and N. H. de Leeuw, Adsorption of methanoic acid onto the low-index surfaces of calcite and aragonite, Mol. Simul., 2002, 28, 539–556 CrossRef.
- N. H. de Leeuw and T. G. Cooper, A computer modeling study of the inhibiting effect of organic adsorbates on calcite crystal growth, Cryst. Growth Des., 2004, 4, 123–133 CrossRef.
- A. Pavese, M. Catti and S. C. Parker, et al., Modelling of the thermal dependence of structural and elastic properties of calcite, CaCO3, Phys. Chem. Miner., 1996, 23, 89–93 CrossRef.
- P. Dauber-Osguthorpe, V. A. Roberts and D. J. Osguthorpe, et al., Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system, Proteins: Struct., Funct., Bioinf., 1988, 4, 31–47 CrossRef PubMed.
- N. H. de Leeuw and S. C. Parker, Molecular-dynamics simulation of MgO surfaces in liquid water using a shell-model potential for water, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 13901–13908 CrossRef.
- P. Duchstein, P. I. Schodder and S. Leupold, et al., Small-molecular-weight additives modulate calcification by interacting with prenucleation clusters on the molecular level, Angew. Chem., Int. Ed., 2022, 61, e202208475 CrossRef PubMed.
- W. D. Cornell, P. Cieplak and C. I. Bayly, et al., A second generation force field for the simulation of proteins, nucleic acids, and organic molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef.
- A. Schuitemaker, J. Aufort and K. B. Koziara, et al., Simulating the binding of key organic functional groups to aqueous calcium carbonate species, Phys. Chem. Chem. Phys., 2021, 23, 27253–27265 RSC.
- J. W. Ponder, C. Wu and P. Ren, et al., Current status of the AMOEBA polarizable force field, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef PubMed.
- N. Yao, X. Chen and Z.-H. Fu, et al., Applying classical, ab initio, and machine-learning molecular dynamics simulations to the liquid electrolyte for rechargeable batteries, Chem. Rev., 2022, 122, 10970–11021 CrossRef PubMed.
- M. Saharay and R. J. Kirkpatrick, Ab initio and metadynamics studies on the role of essential functional groups in biomineralization of calcium carbonate and environmental situations, Phys. Chem. Chem. Phys., 2014, 16, 26843–26854 RSC.
- A. A. A. Delgado, D. Sethio and I. Munar, et al., Local vibrational mode analysis of ion–solvent and solvent–solvent interactions for hydrated Ca2+ clusters, J. Chem. Phys., 2020, 153, 224303 CrossRef PubMed.
- M. R. Dooley and S. Vyas, Role of explicit solvation and level of theory in predicting the aqueous reduction potential of carbonate radical anion by DFT, Phys. Chem. Chem. Phys., 2025, 27, 6867–6874 RSC.
- J. A. Lopez-Berganza, Y. Diao and S. Pamidighantam, et al., Ab initio studies of calcium carbonate hydration, J. Phys. Chem. A, 2015, 119, 11591–11600 CrossRef PubMed.
- D. D. Tommaso and N. H. de Leeuw, The onset of calcium carbonate nucleation: A density functional theory molecular dynamics and hybrid microsolvation/continuum study, J. Phys. Chem. B, 2008, 112, 6965–6975 CrossRef PubMed.
- A. A. Hassanali, J. Cuny and V. Verdolino, et al., Aqueous solutions: State of the art in ab initio molecular dynamics, Philos. Trans. R. Soc., A, 2014, 372, 20120482 CrossRef PubMed.
- D. Ray and M. Parrinello, Kinetics from metadynamics: principles, applications, and outlook, J. Chem. Theory Comput., 2023, 19, 5649–5670 CrossRef PubMed.
- G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef PubMed.
- K. Henzler, E. O. Fetisov and M. Galib, et al., Supersaturated calcium carbonate solutions are classical, Sci. Adv., 2018, 4, eaao6283 CrossRef PubMed.
- Y. Li, H. Pan and Z. Li, Ab initio metadynamics simulations on the formation of calcium silicate aqua complexes prior to the nuleation of calcium silicate hydrate, Cem. Concr. Res., 2022, 156, 106767 CrossRef.
- E. H. Byrne, P. Raiteri and J. D. Gale, Computational insight into calcium–sulfate ion pair formation, J. Phys. Chem. C, 2017, 121, 25956–25966 CrossRef.
- P. Raiteri, A. Schuitemaker and J. D. Gale, Ion pairing and multiple ion binding in calcium carbonate solutions based on a polarizable AMOEBA force field and ab initio molecular dynamics, J. Phys. Chem. B, 2020, 124, 3568–3582 CrossRef PubMed.
- M. Müller, L. Wirth and B. Urban, Determination of the carboxyl dissociation degree and pKa value of mono and polyacid solutions by FTIR titration, Macromol. Chem. Phys., 2021, 222, 2000334 CrossRef.
- N. Aliouane, S. Chafaa and T. Douadi, et al., Novel polydentate phosphonic acids: Protonation and stability constants of complexes with Fe(III) and Cu(II) in aqueous medium, Heteroat. Chem., 2010, 21, 51–62 CrossRef.
- K. C. Kwong, M. M. Chim and E. H. Hoffmann, et al., Chemical transformation of methanesulfonic acid and sodium methanesulfonate through heterogeneous OH oxidation, ACS Earth Space Chem., 2018, 2, 895–903 CrossRef.
- M. D. G. de Luna, A. S. Sioson and A. E. S. Choi, et al., Operating pH influences homogeneous calcium carbonate granulation in the frame of CO2 capture, J. Cleaner Prod., 2020, 272, 122325 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony and S. Ehrlich, et al., A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef.
- R. Knochenmuss, R. K. Sinha and A. Poblotzki, et al., Intermolecular dissociation energies of hydrogen-bonded 1-naphthol complexes, J. Chem. Phys., 2018, 149, 204311 CrossRef PubMed.
- S. P. Veccham and M. Head-Gordon, Density functionals for hydrogen storage: Defining the H2Bind275 test set with ab initio benchmarks and assessment of 55 functionals, J. Chem. Theory Comput., 2020, 16, 4963–4982 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef PubMed.
- M. M. Francl, W. J. Pietro and W. J. Hehre, et al., Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- J. VandeVondele, M. Krack and F. Mohamed, et al., Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef.
- T. D. Kühne, M. Iannuzzi and M. Del Ben, et al., CP2K: An electronic structure and molecular dynamics software package – Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Relativistic separable dual-space Gaussian pseudopotentials from H to Rn, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef.
- M. Krack, Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- P. A. Schultz, Local electrostatic moments and periodic boundary conditions, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 60, 1551–1554 CrossRef.
- G. Makov and M. C. Payne, Periodic boundary conditions in ab initio calculations, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef PubMed.
- L. Martínez, R. Andrade and E. G. Birgin, et al., PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- R. A. DiStasio, Jr., B. Santra and Z. Li, et al., The individual and collective effects of exact exchange and dispersion interactions on the ab initio structure of liquid water, J. Chem. Phys., 2014, 141, 084502 CrossRef PubMed.
- Y.-L. S. Tse, C. Knight and G. A. Voth, An analysis of hydrated proton diffusion in ab initio molecular dynamics, J. Chem. Phys., 2015, 142, 014104 CrossRef PubMed.
- L. Ruiz Pestana, O. Marsalek and T. E. Markland, et al., The quest for accurate liquid water properties from first principles, J. Phys. Chem. Lett., 2018, 9, 5009–5016 CrossRef PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A:At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: A smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- T. Martinek, E. Duboué-Dijon and Š. Timr, et al., Calcium ions in aqueous solutions: Accurate force field description aided by ab initio molecular dynamics and neutron scattering, J. Chem. Phys., 2018, 148, 222813 CrossRef PubMed.
- D. Mendes de Oliveira, S. R. Zukowski and V. Palivec, et al., Binding of divalent cations to acetate: Molecular simulations guided by Raman spectroscopy, Phys. Chem. Chem. Phys., 2020, 22, 24014–24027 RSC.
- P. M. Piaggi, J. D. Gale and P. Raiteri, Ab initio machine-learning simulation of calcium carbonate from aqueous solutions to the solid state, Proc. Natl. Acad. Sci. U. S. A., 2025, 122, e2415663122 CrossRef PubMed.
- G. A. Tribello, M. Bonomi and D. Branduardi, et al., PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef.
- Z. Liu, T. He and X. Zhi, et al., Critical role of alkali-metal ions in a β-dicalcium silicate hydration reaction: Well-tempered metadynamics, J. Phys. Chem. C, 2024, 128, 8206–8218 CrossRef.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, SM6:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A density functional theory continuum solvation model for calculating aqueous solvation free energies of neutrals, ions, and solute–water clusters, J. Chem. Theory Comput., 2005, 1, 1133–1152 CrossRef PubMed.
A density functional theory continuum solvation model for calculating aqueous solvation free energies of neutrals, ions, and solute–water clusters, J. Chem. Theory Comput., 2005, 1, 1133–1152 CrossRef PubMed. - C. P. Kelly, C. J. Cramer and D. G. Truhlar, Adding explicit solvent molecules to continuum solvent calculations for the calculation of aqueous acid dissociation constants, J. Phys. Chem. A, 2006, 110, 2493–2499 CrossRef PubMed.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard Iii, Calculation of solvation free energies of charged solutes using mixed cluster/continuum models, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef PubMed.
- L. N. Plummer and E. Busenberg, The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90 °C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O, Geochim. Cosmochim. Acta, 1982, 46, 1011–1040 CrossRef.
- M. Kellermeier, P. Raiteri and J. K. Berg, et al., Entropy drives calcium carbonate ion association, ChemPhysChem, 2016, 17, 3535–3541 CrossRef PubMed.
- R. Demichelis, P. Raiteri and J. D. Gale, et al., Stable prenucleation mineral clusters are liquid-like ionic polymers, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- O. I. Martynova, L. G. Vasina and S. A. Pozdniakova, Dissociation constants of certain scale forming salts, Desalination, 1974, 15, 259–265 CrossRef.
- E. L. Shock and C. M. Koretsky, Metal-organic complexes in geochemical processes: Estimation of standard partial molal thermodynamic properties of aqueous complexes between metal cations and monovalent organic acid ligands at high pressures and temperatures, Geochim. Cosmochim. Acta, 1995, 59, 1497–1532 CrossRef.
- P. Raiteri, R. Demichelis and J. D. Gale, et al., Exploring the influence of organic species on pre- and post-nucleation calcium carbonate, Faraday Discuss., 2012, 159, 61–85 Search PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Stable prenucleation calcium carbonate clusters, Science, 2008, 322, 1819–1822 Search PubMed.
- A. Li, J. Chang and T. Shui, et al., Probing interaction forces associated with calcite scaling in aqueous solutions by atomic force microscopy, J. Colloid Interface Sci., 2023, 633, 764–774 CrossRef PubMed.
- Q. Yao, R. Zhan and H. Ren, et al., Carboxyl or phosphate functionalization polyamidoamine dendrimer efficient scale inhibitor: Preparation and properties, J. Mol. Struct., 2022, 1252, 132130 CrossRef.
- N. Andritsos and A. J. Karabelas, The influence of particulates on CaCO3 scale formation, J. Heat Transfer, 1999, 121, 225–227 CrossRef.
- P. Raiteri, R. Demichelis and J. D. Gale, Thermodynamically consistent force field for molecular dynamics simulations of alkaline-earth carbonates and their aqueous speciation, J. Phys. Chem. C, 2015, 119, 24447–24458 CrossRef.
- J. Kahlen, L. Salimi and M. Sulpizi, et al., Interaction of charged amino-acid side chains with ions: An optimization strategy for classical force fields, J. Phys. Chem. B, 2014, 118, 3960–3972 Search PubMed.
- X. Yang, M. Ji and C. Zhang, et al., Physical insight into the entropy-driven ion association, J. Comput. Chem., 2022, 43, 1621–1632 CrossRef PubMed.
| This journal is © the Owner Societies 2026 |


