Vacancy-induced phonon localization and lattice softening for reduced thermal conductivity in Mg3Sb2
Sheng
Zhang
a,
Jinbao
Zhang
a,
Liqi
Ren
a,
Yijing
Shao
a,
Wanyue
Yan
a,
Meng
Tian
 b,
Kunling
Peng
*b,
Ping
Lin
b,
Kunling
Peng
*b,
Ping
Lin
 *c and
Yunzhen
Du
*de
*c and
Yunzhen
Du
*de
aSchool of Intelligence Science and Technology, Nanjing University of Science and Technology, Jiangyin 214443, China
bSchool of New Energy, Nanjing University of Science and Technology, Jiangyin 214443, China. E-mail: klpeng@njust.edu.cn
cSchool of Mechanical and Electrical Engineering, Weifang University of Science and Technology, Weifang, 262700, China. E-mail: linping@wfust.edu.cn
dComputer Network Information Center, Chinese Academy of Sciences, Beijing, 100083, China. E-mail: duyz2024@163.com
eInstitute of Modern Physics, Chinese Academy of Science, Lanzhou, 730000, China
First published on 4th December 2025
Abstract
With the natural abundance, low cost, and compatibility with sustainable technologies, Mg3Sb2 has emerged as a promising mid-temperature thermoelectric material. Intrinsic point defects, particularly vacancies, are common in Mg3Sb2 and play a crucial role in shaping its thermoelectric properties, guiding experimental design and performance optimization. However, their impact on lattice thermal conductivity (κL) remains insufficiently understood. This work investigates the effects of Mg and Sb vacancies on the κL of Mg3Sb2 using a neural network potential (NNP). Our results show that both types of vacancies significantly reduce κL, primarily due to enhanced phonon-defect scattering. Comprehensive analyses of phonon dispersion, group velocities, mean square displacement (MSD), the phonon participation ratio (PPR), and elastic properties demonstrate that vacancies trigger pronounced phonon softening, slow down phonon transport, and promote strong localization, while simultaneously amplifying atomic vibrations and weakening interatomic bonding. This work clarifies the microscopic mechanisms by which point defects affect phonon transport and identifies defect engineering as an effective strategy for controlling thermal properties in thermoelectric materials.
1. Introduction
Thermoelectric (TE) materials enable the direct conversion between thermal and electrical energy, making them attractive for solid-state cooling and waste-heat recovery applications.1–3 Their performance is commonly evaluated by the dimensionless figure of merit ZT,4 defined as, ZT = S2σT/(κL + κe), where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ = κL + κe is the total thermal conductivity, with κe and κL representing the electronic and phonon contributions, respectively. Because S, σ, and κe are all governed by charge-carrier transport, they are intrinsically interdependent, which complicates their independent optimization. By contrast, strategies that intensify phonon scattering offer a more decoupled route to suppressing lattice thermal conductivity (κL).Over the past few decades, substantial progress has been achieved in high-performance TE materials—including Bi2Te3,5,6 PbTe,7 SiGe,8 and SnSe9—through a variety of approaches that improve energy-conversion efficiency. However, the reliance on toxic or scarce elements (e.g., Te, Pb, and Se), along with the associated raw-material costs, has hindered large-scale deployment. In response, there has been growing interest in developing environmentally benign and cost-effective alternatives. Among them, Mg3Sb2 has emerged as a promising mid-temperature (300–900 K) TE material owing to its low cost, environmental compatibility, and excellent thermoelectric performance.10 In Wu et al.'s work, a Mg3Sb2 based thermoelectric generation device was successfully designed and developed.11,12 Experiment13 has revealed the presence of intrinsic point defects, including vacancies, in Mg3Sb2, which strongly influence its performance in practical applications. These vacancies may originate from the evaporation of Mg during the sintering process, a phenomenon that can be mitigated by adding excess Mg or introducing Ag doping.14 According to density functional theory (DFT) simulations by Chong et al.,15 vacancies in p-type Mg3Sb2 contribute to high hole carrier concentrations, which are also sensitive to thermal effects.
Although such defects play a critical role in guiding experimental design and performance optimization,16–18 their influence on lattice thermal conductivity remains insufficiently understood. The lattice thermal conductivity calculations primarily rely on two approaches: the Boltzmann transport equation (BTE)19 for phonons and molecular dynamics (MD) simulations.20–22 First-principles-based BTE calculations provide high theoretical accuracy, but their application to defective systems is severely constrained by the high computational cost associated with the large and complex supercells required to capture intrinsic defects.23 In contrast, MD simulations are better suited for handling such structural complexity. Nevertheless, empirical interatomic potentials for Mg3Sb2 have not yet been reported, and their development is challenging due to the material's intricate crystal structure. Neural-network potentials (NNPs) bridge this gap by combining near first-principles accuracy with MD-level efficiency,24,25 thereby enabling large-scale simulations of anharmonic phonon transport and defect scattering.
Here, we develop a NNP for the Mg3Sb2 system from a first-principles training set that covers both pristine and vacancy-containing configurations. The NNP reproduces the lattice thermal conductivity of defect-free Mg3Sb2 in excellent agreement with DFT benchmarks. Leveraging this validated NNP, we systematically quantify how intrinsic vacancy defects suppress heat transport and elucidate the underlying defect–phonon coupling mechanisms. Our results provide actionable guidance for defect engineering aimed at optimizing the thermoelectric performance of Mg3Sb2.
2. Methodology
The overall methodological workflow was introduced in our previous work.26,27 The structural configurations were initially optimized using DFT calculations performed with the Vienna Ab-initio Simulation Package (VASP).28 These optimized structures were then used in ab initio molecular dynamics (AIMD) simulations to generate configurations. The selected configurations were subsequently employed in DFT calculations to generate the training dataset, which was then used to train a NNP using the DeePMD-kit.29 Once the NNP was obtained, the κL was calculated using the BTE method and EMD simulations.2.1. NNP construction
In constructing an accurate NNP, two steps are usually performed: (1) dataset generation and (2) NNP training.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, as depicted in Fig. 1. The lattice constants were reported30 as a = b = 4.573 Å and c = 7.229 Å. Mg3Sb2 exhibits two distinct magnesium coordination environments: Mg1, which behaves as a divalent cation Mg2+, and Mg2, which engages in covalent interactions with antimony atoms to form discrete [Mg2Sb2]2− anionic entities. These anionic groups are further linked to surrounding Mg2+ ions via ionic bonds, giving rise to a three-dimensional, charge-balanced framework.
m1, as depicted in Fig. 1. The lattice constants were reported30 as a = b = 4.573 Å and c = 7.229 Å. Mg3Sb2 exhibits two distinct magnesium coordination environments: Mg1, which behaves as a divalent cation Mg2+, and Mg2, which engages in covalent interactions with antimony atoms to form discrete [Mg2Sb2]2− anionic entities. These anionic groups are further linked to surrounding Mg2+ ions via ionic bonds, giving rise to a three-dimensional, charge-balanced framework.
To construct the training datasets for Mg3Sb2, we first performed full structural optimization of a Mg3Sb2 single crystal using the VASP28 to obtain the optimized structure (a = b = 4.60 Å and c = 7.27 Å). All DFT calculations employed the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).31 A plane-wave kinetic energy cutoff of 700 eV was adopted. For geometry optimization, a Monkhorst–Pack K-point mesh32 of 9 × 9 × 5 was employed.
After fully relaxing the crystal structure of Mg3Sb2, a 3 × 3 × 2 supercell was constructed, as depicted in Fig. 2(a), containing 54 Mg and 36 Sb atoms. To model vacancy defects, single atoms were selectively removed from the 3 × 3 × 2 supercell, resulting in two distinct Mg-vacancy configurations (VMg1 and VMg2) and one Sb-vacancy configuration (VSb), as depicted in Fig. 2(b)–(d), respectively. AIMD simulations were then performed for both the pristine and vacancy-containing supercells under the canonical (NVT) ensemble. A 1 × 1 × 1 Monkhorst–Pack K-point mesh was selected. The simulation temperature ranged from 50 K to 1000 K, with a time step of 2 fs and a total simulation length of 40 ps for each configuration.
To enhance the structural diversity of the training dataset, configurations were systematically sampled from the AIMD trajectories using an interval-based strategy. Specifically, for each trajectory spanning 50–1000 K, configurations were sampled uniformly in time to achieve comprehensive phase-space exploration. By focusing high-precision DFT calculations (using a 3 × 3 × 2 Monkhorst–Pack K-point mesh) only on selected snapshots, this approach achieves a substantial reduction in computational burden without compromising the fidelity of the training dataset. The composition of the training set is listed in Table 1.
| Structures | The number of structures |
|---|---|
| Defect-free Mg3Sb2 | 774 |
| Mg1-vacancy (VMg1) | 757 |
| Mg2-vacancy (VMg2) | 686 |
| Sb-vacancy (VSb) | 730 |
The neural network architecture consists of an embedding layer with 25, 50, and 100 neurons, followed by a fitting block composed of three 240-neuron layers. The total loss is constructed from contributions of atomic energy, forces, and virial, as given in eqn (1).
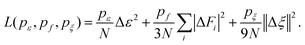 | (1) |
Here, N represents the atom count, and pe, pf and pξ are tunable weighting factors that balance the contributions of energy, force, and virial, in the loss function. The terms ΔE, ΔFi and Δξ represent the root mean square (RMS) errors associated with energy, force, and virial, respectively. The symbols |…| and ||…|| represent the norm of the force vector and the norm of the virial tensor. We employed an adaptive weighting scheme: pe, pf and pξ began at 0.02, 1000, and 0.8 and converged to 8, 1, and 1 as training progressed. A total of 2 million optimization steps were performed to ensure convergence.
2.2. Lattice thermal conductivity calculations
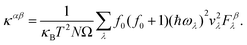 | (2) |
The variables κB, Ω, vλ, and ωλ refer to the Boltzmann constant, unit cell volume, phonon group velocity, and angular frequency, respectively. α and β represent the components of the phonon polarization. Fβλ is the scattering matrix element. f0 represents the equilibrium phonon distribution.
The core of the BTE-based thermal conductivity calculation lies in the accurate determination of the interatomic force constants (IFCs), which describe the key interactions between atoms in the material. In this study, the second-order force constants, which describe the harmonic interactions between atoms, were computed through NNP combined with the PHONOPY program.33,34
To account for anharmonic interactions, the third-order force constants were calculated using the thirdorder_vasp.py.19 In this study, the lattice thermal conductivity was calculated using an iterative solution of the BTE. We selected the 4 × 4 × 2 supercell and 13th nearest neighbor (cutoff radius of 8 Å) for the calculation of the third-order force constants, ensuring that the interaction range captured the significant anharmonic effects in the system. Convergence with respect to the neighbor-shell cutoff is shown in Fig. S1 of the SI. Once the force constants were obtained, lattice thermal conductivity was calculated using the ShengBTE package.19
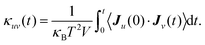 | (3) |
Here Ju and Jv are the heat fluxes in the u and v directions, and V is the volume. The heat flux J is given by:
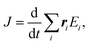 | (4) |
In this study, EMD simulations were performed using the LAMMPS package.36 The simulation systems were first equilibrated in the NVT for 800 ps to reach thermal equilibrium at the target temperature, followed by a 10 ns production run in the microcanonical (NVE) ensemble. The final lattice thermal conductivity was obtained by averaging the results over 25 independent simulations.
2.3. Defect formation energy
Point vacancies are among the most common intrinsic defects in materials and significantly influence both structural integrity and thermal transport behavior. The defect formation energy reflects the cost of removing an atom from its lattice site and placing it in a reservoir, and its magnitude directly correlates with the likelihood of defect generation during synthesis or operation. The defect formation energy23 is computed using the formula defined as follows: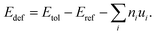 | (5) |
Here, Etol denotes the total energy of the supercell containing the vacancy defect, while Eref corresponds to the total energy of the perfect supercell. ni represents the atom count of species i that are either removed (ni < 0) or added (ni > 0) to create the defect. ui denotes the chemical potential.
3. Results and discussion
3.1. Evaluation of the NNP
The performance of the NNP was assessed through a comprehensive comparison with DFT calculations, covering atomic energy, force, and virial stress predictions, as depicted in Fig. 3(a–c). The RMS errors are 0.04 eV for energy, 0.03 eV Å−1 for forces, and 0.4 eV for virial stresses, demonstrating excellent agreement with DFT. Moreover, Fig. 3(d) presents a comparison of the phonon dispersion spectra generated using both approaches. The near-perfect overlap of the phonon branches from NNP and DFT confirms the NNP's effectiveness in capturing vibrational dynamics. Importantly, no imaginary frequencies are observed in either the DFT or NNP calculations, confirming the dynamic stability of the Mg3Sb2 system. | ||
| Fig. 3 Comparison of (a) total energy, (b) atomic forces, (c) virial stress, and (d) phonon dispersion relations for Mg3Sb2, calculated by the NNP and DFT. | ||
The vacancy formation energies were evaluated as described in Section 2.3. In this study, the chemical potentials of Mg and Sb were determined via DFT calculations, yielding values of −1.50 eV and −4.13 eV, respectively. The chemical potential of Mg was evaluated using a 5 × 5 × 3 supercell (150 atoms), while that of Sb was obtained from a 5 × 5 × 1 supercell (150 atoms). The detailed parameters (including plane-wave energy cutoff and k-point sampling) are provided in Table 2.
| Parameters | Value | |
|---|---|---|
| Mg | Sb | |
| Cutoff energy (eV) | 700 | 600 |
| K-point mesh | 2 × 2 × 2 | 2 × 2 × 3 |
As summarized in Table 3, the vacancy formation energies calculated by the NNP are 1.58 eV and 1.62 eV for the Mg1 and Mg2 vacancies, respectively, and 2.18 eV for the Sb vacancies. Furthermore, the vacancy formation energies predicted by the NNP exhibit strong consistency with DFT results, with maximum deviations below 0.09 eV, demonstrating the NNP's capability to accurately reproduce defect energetics.
| Vacancy | Vacancy formation energy (eV) | |
|---|---|---|
| DFT | NNP | |
| VMg1 | 1.50 | 1.58 |
| VMg2 | 1.53 | 1.62 |
| VSb | 2.18 | 2.18 |
To assess the accuracy of the NNP in capturing the mechanical behavior of Mg3Sb2, we calculated the bulk modulus, shear modulus, Young's modulus, and Poisson's ratio using the NNP, and compared the predictions with DFT calculations and experimental data,38 as summarized in Table 4. The NNP-predicted bulk modulus is 43.3 GPa, closely matching the DFT value of 42.0 GPa and the experimental result of 45.9 GPa. Similarly, the shear modulus and Young's modulus predicted by the NNP (14.3 GPa and 38.6 GPa, respectively) are consistent with the DFT (16.9 GPa and 44.7 GPa) and experimental results (16.0 GPa and 43.0 GPa). The predicted Poisson's ratio of 0.35 also closely matches the experimental value of 0.34. These results demonstrate that the NNP can reliably reproduce the key elastic constants of Mg3Sb2, thereby validating its applicability for further thermal transport and defect property predictions.
3.2. Lattice thermal conductivity
The lattice thermal conductivities were evaluated for both DFT and NNP, combined with the BTE method, in the x- and z-directions. Details of the BTE method are given in Section 2.2.1. As depicted in Fig. 4, the NNP-predicted κL is 1.14 W m−1 K−1 along the x-direction and 1.35 W m−1 K−1 along the z-direction at 300 K, which are close to the DFT results calculated by Ning et al.,39 and also consistent with the experimental value40 of 1.39 W m−1 K−1. This agreement further validates the effectiveness of the NNP approach for predicting lattice thermal conductivity. | ||
| Fig. 4 Temperature dependence of κL calculated using DFT and NNP computed via the BTE method. The DFT-calculated κL values were obtained from the study reported by Ning et al.,39 and the experimental values were derived from the study reported by Song et al.40 | ||
Researchers commonly observe that κL in crystalline materials decreases with temperature according to κL ∼ 1/Tα, where α values range from 0.85 to 1.05.41 The κL of Mg3Sb2 over the temperature range of 300–800 K is illustrated in Fig. 4, revealing a characteristic κL ∼ 1/T dependence. At room temperature, the lattice thermal conductivities along the x- and z-directions are approximately 1.14 W m−1 K−1 and 1.35 W m−1 K−1, respectively. As the temperature increases, κL decreases gradually, dropping to approximately 0.43 W m−1 K−1 in the x-direction and 0.50 W m−1 K−1 in the z-direction at 800 K. This substantial reduction in κLat elevated temperatures is primarily driven by increased phonon–phonon scattering rates.
To clarify the origin of the temperature-induced reduction in lattice thermal conductivity, we analyzed the evolution of two key quantities with increasing temperature: the phonon scattering rate as a function of phonon frequency and the normalized cumulative lattice thermal conductivity as a function of phonon mean free path (MFP).42 As shown in Fig. 5(a), at 300 K, the phonon scattering rate is relatively low, indicating fewer scattering events. As the temperature increases to 800 K, the scattering rate increases significantly—particularly at higher frequencies—reflecting stronger anharmonic phonon–phonon interactions. In the phonon-gas model, 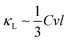 , where C, v, and l are the modal heat capacity, group velocity, and MFP, respectively. As shown in Fig. 5(b), the curve at 800 K shifts markedly toward shorter MFPs relative to 300 K in both the x and z directions; correspondingly, the MFP value required to reach 50% of the cumulative κL is reduced. This indicates that increasing the temperature lowers the κL by shortening phonon mean free paths and increasing phonon scattering rates.
, where C, v, and l are the modal heat capacity, group velocity, and MFP, respectively. As shown in Fig. 5(b), the curve at 800 K shifts markedly toward shorter MFPs relative to 300 K in both the x and z directions; correspondingly, the MFP value required to reach 50% of the cumulative κL is reduced. This indicates that increasing the temperature lowers the κL by shortening phonon mean free paths and increasing phonon scattering rates.
3.3. Impact of vacancies on lattice thermal conductivity
We calculated the lattice thermal conductivity of Mg3Sb2 with and without point defects (Mg and Sb vacancies) using the EMD approach. The simulation details, including the EMD framework and key computational settings, are outlined in Section 2.2.2. Table 5 lists the atom count for each EMD simulation.| System | Number of atoms | Vacancy ratio (%) |
|---|---|---|
| Mg3Sb2 | 5760 | 0 |
| VMg, Vsb | 5754 | 0.1 |
| VMg, Vsb | 5743 | 0.3 |
| VMg, Vsb | 5731 | 0.5 |
| VMg, Vsb | 5720 | 0.7 |
| VMg, Vsb | 5708 | 0.9 |
| VMg, Vsb | 5702 | 1.0 |
For the Mg3Sb2 system with 0.1% Mg vacancies, a correlation time of 100 ps is sufficient to achieve convergence of the thermal conductivity, as demonstrated by the heat current autocorrelation function (HCACF) at 300 K along the in-plane and out-of-plane directions (Fig. 6a and b, respectively). The final lattice thermal conductivities at 300 K, obtained by averaging over 25 independent EMD simulations, are 1.25 W m−1 K−1 along the in-plane direction (Fig. 6c) and 1.11 W m−1 K−1 along the out-of-plane direction (Fig. 6d). For the pristine crystal, EMD simulations yield an in-plane κL of 1.37 W m−1 K−1 and an out-of-plane value of 1.20 W m−1 K−1.
To elucidate the effect of vacancy defects on the κL of Mg3Sb2 we calculated the κL at 300 K for both Mg and Sb vacancies with concentrations ranging from 0.1% to 1.0%. The results are summarized in Fig. 7. At a Mg vacancy concentration of 0.1%, the in-plane and out-of-plane thermal conductivities are 1.25 W m−1 K−1and 1.11 W m−1 K−1, respectively. When the concentration increases to 1.0%, thermal conductivities decrease significantly to 0.88 W m−1 K−1 (in-plane) and 0.55 W m−1 K−1 (out-of-plane). Similarly, for Sb vacancies, the in-plane and out-of-plane thermal conductivities at 0.1% concentration are 1.24 W m−1 K−1 and 1.15 W m−1 K−1, respectively, decreasing to 0.79 W m−1 K−1 and 0.63 W m−1 K−1 at 1.0% vacancy concentration. This consistent decreasing trend in thermal conductivity with increasing vacancy concentration for both Mg and Sb sites indicates enhanced phonon-defect scattering, in agreement with previous findings in other alloys.23,43 Therefore, defect engineering emerges as a promising strategy for tuning phonon transport.
 | ||
| Fig. 7 κ L of Mg3Sb2 as a function of Mg and Sb vacancy concentration, calculated using the EMD method at 300 K. (a) In-plane; (b) out-of-plane. | ||
To elucidate the mechanism by which vacancy defects reduce the lattice thermal conductivity of Mg3Sb2, we calculated the phonon dispersion curves for both the pristine and defective structures. For the defective cases, we employed a 3 × 3 × 2 supercell consisting of 89 atoms, in which either one Mg atom or one Sb atom was removed, corresponding to a vacancy concentration of approximately 1.1% in each case. The calculation results are shown in Fig. 8(a–c). The acoustic branches (lower frequency regions) and optical branches (higher frequency regions) of all structures exhibit no imaginary frequencies throughout the entire Brillouin zone, confirming the dynamical stability of these structures. Furthermore, compared to the pristine Mg3Sb2 system, both vacancy-containing structures (VMg and Vsb) exhibit pronounced phonon softening, particularly in the optical branches, indicating reduced vibrational stiffness. This softening is accompanied by a marked decrease in phonon group velocity,42 as presented in Fig. 8(d). The reduction in group velocity is a key contributor to the diminished heat-carrying capacity of phonons.
To gain further insight, we analyzed the phonon participation ratio (PPR), Pλ, which quantifies the fraction of atoms effectively involved in the vibrational mode λ and thereby reflects the degree of phonon localization.44,45Pλ ranges from 0 to 1:45Pλ = 1 denotes a fully extended (propagating) mode, whereas Pλ → 0 indicates a highly localized mode. According to prior study,46 modes with Pλ < 0.4 are considered localized. When phonons become localized, the wave-like nature of the vibrations is disrupted, and only a subset of atoms contribute to the vibrational mode. The stronger the localization, the smaller the PPR. This localization effect significantly impacts the thermal conductivity by limiting phonon transport within the material, making it a key mechanism for understanding how vacancies affect κL. As shown in Fig. 9, for pristine Mg3Sb2, the PPR is relatively high, indicating that most atoms participate in lattice vibrations. However, with the introduction of vacancies, the PPR decreases in all vacancy-containing structures. These results indicate that vacancies localize vibrational modes, reduce atomic participation, enhance phonon scattering, and thus lower the κL. Furthermore, the phonon dispersion relations of the vacancy-containing structures exhibit pronounced phonon softening. These flat optical branches correspond to vibrational modes with extremely low phonon group velocities, indicating that the vibrations are confined to a limited number of atoms—another manifestation of phonon localization.
To understand the mechanism by which vacancies affect atomic vibrations and lattice stability, we calculated the mean square displacement (MSD) for different vacancy structures. A larger MSD indicates greater atomic deviation from the equilibrium position, which typically reflects weaker atomic bonding. This reduction in bonding strength leads to a decrease in the constraint forces, allowing atoms to vibrate with larger amplitudes. The results presented in Fig. 10 demonstrate the atomic vibrational behavior caused by vacancies. In the structure containing Mg vacancies, the MSD of Mg atoms reaches approximately 0.13 Å2, which is larger than that of the defect-free Mg3Sb2. The absence of Mg atoms significantly weakens the binding force on neighboring Mg atoms, leading to lattice distortion. Besides, compared to the defect-free Mg3Sb2, the MSD of Sb atoms also increases in the structure with Sb vacancies. The enhanced MSD reflects local bond softening, which elevates lattice anharmonicity,42 ultimately suppressing the lattice thermal conductivity. Moreover, at a 0.3% vacancy concentration, VMg induces a substantially larger MSD than VSb, implying stronger local bond softening and weaker restoring forces around VMg. This bond softening—evidenced by the larger MSD—enhances anharmonic phonon scattering,42 leading to a greater reduction of κL for VMg than for VSb at 0.3%.
 | ||
| Fig. 10 MSD at 300 K for (a) pristine Mg3Sb2, (b) Mg3Sb2 with 0.3% Mg vacancies (VMg), and (c) Mg3Sb2 with 0.3% Sb vacancies (VSb). | ||
Young's modulus E quantifies stiffness – the stress/strain ratio in the elastic regime – and at the atomic scale reflects bond strength and crystal stability. Microscopically, it reflects the bond strength between atoms and the structural stability of the crystal. Previous studies47 have demonstrated a strong correlation between Young's modulus and κL, as described by the relation:
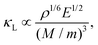 | (6) |
| Properties | VMg | VSb |
|---|---|---|
| Bulk modulus (GPa) | 40.0 | 42.3 |
| Shear modulus (GPa) | 12.7 | 13.7 |
| Young's modulus (GPa) | 34.5 | 37.2 |
| Poisson's ratio | 0.34 | 0.33 |
Conclusions
In this study, we systematically investigated the impact of vacancy defects on the κL of Mg3Sb2 by combining NNP, BTE, and MD. The NNP accurately reproduces the DFT-calculated phonon spectra, elastic properties, vacancy formation energies, and lattice thermal conductivity, validating its reliability for large-scale phonon transport simulations. The results demonstrate that both Mg and Sb vacancies induce a reduction in κL, primarily due to enhanced phonon-defect scattering. To elucidate the underlying mechanisms, we analyzed phonon dispersion relations, phonon group velocities, MSD, PPR, and elastic properties. The phonon spectra of defect-containing structures exhibit clear phonon softening, particularly in the optical branches, indicating increased lattice anharmonicity. Correspondingly, the calculated phonon group velocities are markedly reduced in the vacancy-containing systems, which directly limits the heat-carrying capability of phonons. MSD analysis reveals that vacancy-induced lattice distortions weaken local bonding and increase atomic vibrational amplitudes. Furthermore, PPR calculations show a reduced number of atoms participating in vibrational modes in defective structures, reflecting stronger phonon localization. In addition, the reduction in elastic properties further confirms the weakening of interatomic bonding, providing a microscopic basis for the observed suppression of the phonon group velocity. Overall, our findings not only offer fundamental insights into the phonon scattering mechanisms induced by point defects but also provide guidance for tuning the thermal transport properties of thermoelectric materials through defect engineering.Author contributions
Design of the research project: Sheng Zhang, Ping Lin, Kunling Peng, and Meng Tian. Conceptualization: Sheng Zhang and Kunling Peng. Methodology: Sheng Zhang, Ping Lin, Kunling Peng, Meng Tian, and Yunzhen Du. Software: Jinbao Zhang, Liqi Ren, Yijing Shao, and Wanyue Yan. Data calculation: Jinbao Zhang, Liqi Ren, Yijing Shao, Wanyue Yan, and Yunzhen Du. Data analysis: Sheng Zhang, Ping Lin, and Meng Tian. Visualization: Yunzhen Du and Sheng Zhang. Writing – review and editing: Sheng Zhang, Ping Lin, Kunling Peng, Meng Tian, and Yunzhen Du.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting the findings of this study, including the trained neural network potential and the associated training dataset, will be made available upon reasonable request.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5cp03757c.
Acknowledgements
The authors thank Dongjiang Yuan Intelligent Computing Center for computational support. This paper was financially supported by the National Natural Science Foundation of China (Grant No. 12304084) and the Fundamental Research Funds for the Central Universities (No. 30925010418).References
- A. Bahrami, G. Schierning and K. Nielsch, Adv. Energy Mater., 2020, 10, 1904159 CrossRef CAS
.
- J. Mao, G. Chen and Z. Ren, Nat. Mater., 2021, 20, 454–461 CrossRef CAS PubMed
.
- X. Li, B. Yang, H. Xie, H. Zhong, S. Feng, Y. Zhang, Y. Ma, J. Zhang and H. Su, Mater. Res. Bull., 2023, 159, 112106 CrossRef CAS
.
- Z. Z. Zhou, K. L. Peng, S. J. Xiao, Y. Wei, Q. Dai, X. Lu, G. Wang and X. Zhou, J. Phys. Chem. Lett., 2022, 13, 2291–2298 CrossRef PubMed
.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto and D. Vashaee, Science, 2008, 320, 634–638 CrossRef CAS PubMed
.
- H. Wang, G. Luo, C. Tan, C. Xiong, Z. Guo, Y. Yin, B. Yu, Y. Xiao, H. Hu and G. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 31612–31618 CrossRef CAS PubMed
.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557 CrossRef CAS PubMed
.
- A. Kallel, G. Roux and C. Martin, Mater. Sci. Eng., A, 2013, 564, 65–70 CrossRef CAS
.
- W. Shi, M. Gao, J. Wei, J. Gao, C. Fan, E. Ashalley, H. Li and Z. Wang, Adv. Sci., 2018, 5, 1700602 CrossRef PubMed
.
- S. Song, J. Mao, J. Shuai, H. Zhu, Z. Ren, U. Saparamadu, Z. Tang, B. Wang and Z. Ren, Appl. Phys. Lett., 2018, 112, 092103 CrossRef
.
- X. Wu, Z. Han, Y. Zhu, B. Deng, K. Zhu, C. Liu, F. Jiang and W. Liu, Acta Mater., 2022, 226, 117616 CrossRef CAS
.
- X. Wu, Y. Lin, Z. Han, H. Li, C. Liu, Y. Wang, P. Zhang, K. Zhu, F. Jiang, J. Huang, H. Fan, F. Cheng, B. Ge and W. Liu, Adv. Energy Mater., 2022, 12, 2203039 CrossRef CAS
.
- S. Priyadharshini, V. Vijay, S. Kamalakannan, J. Archana and M. Navaneethan, Surf. Interfaces, 2025, 63, 106204 CrossRef CAS
.
- J. Li, R. Chetty, Z. Liu, W. Gao and T. Mori, Small, 2025, 21, 2408059 CrossRef CAS PubMed
.
- X. Chong, P.-W. Guan, Y. Wang, S.-L. Shang, J. Paz Soldan Palma, F. Drymiotis, V. A. Ravi, K. E. Star, J.-P. Fleurial and Z.-K. Liu, ACS Appl. Energy Mater., 2018, 1, 6600–6608 CrossRef CAS
.
- R. Stern, T. Wang, J. Carrete, N. Mingo and G. K. Madsen, Phys. Rev. B, 2018, 97, 195201 CrossRef CAS
.
- M. Ghim, Y.-J. Choi and S.-H. Jhi, Phys. Rev. B, 2023, 107, 184301 CrossRef CAS
.
- P. Zhang, D. Jin, M. Qin, Z. Zhang, Y. Liu, Z. Wang, Z. Lu, R. Xiong and J. Shi, Phys. Rev. Appl., 2024, 21, 024043 CrossRef CAS
.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS
.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 144306 CrossRef
.
- D. P. Sellan, E. S. Landry, J. Turney, A. J. McGaughey and C. H. Amon, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 214305 CrossRef
.
- J. Yue, S. Tian, Y. Liu, D. Ma and S. Hu, Appl. Phys. Lett., 2025, 127, 052202 CrossRef CAS
.
- Y. Du, Y. Yao, K. Peng, J. Duan, C. Hao, Y. Tian, W. Duan, L. Yang, P. Lin and S. Zhang, Phys. Chem. Chem. Phys., 2024, 26, 24342–24351 RSC
.
- P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761 CrossRef CAS PubMed
.
- J. Yue, R. Chen, D. Ma and S. Hu, Chin. Phys. Lett., 2025, 42, 036301 CrossRef CAS
.
- Y. Du, Z. Meng, Q. Yan, C. Wang, Y. Tian, W. Duan, S. Zhang and P. Lin, Phys. Chem. Chem. Phys., 2022, 24, 18361–18369 RSC
.
- Y. Du, K. Peng, J. Duan, M. Qi, Y. Chen, C. Hao, W. Duan, L. Yang, S. Zhang and P. Lin, Int. Commun. Heat Mass Transfer, 2024, 159, 108361 CrossRef CAS
.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed
.
- H. Wang, L. Zhang and J. Han, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS
.
- J.-i Tani, M. Takahashi and H. Kido, Phys. B, 2010, 405, 4219–4225 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef
.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001 CrossRef CAS PubMed
.
- A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef
.
- M. S. Green, J. Chem. Phys., 1954, 22, 398–413 CrossRef CAS
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- J. Cheng, C. Duan, Y. Du, J. Duan, M. Qi, Y. Chen, L. Yang, W. Duan, S. Zhang and P. Lin, J. Mater. Sci., 2025, 1–14 Search PubMed
.
- M. T. Agne, K. Imasato, S. Anand, K. Lee, S. K. Bux, A. Zevalkink, A. J. Rettie, D. Y. Chung, M. G. Kanatzidis and G. J. Snyder, Mater. Today Phys., 2018, 6, 83–88 CrossRef
.
- S. Ning, S. Huang, Z. Zhang, N. Qi, M. Jiang, Z. Chen and X. Tang, J. Materiomics, 2022, 8, 1086–1094 CrossRef
.
- L. Song, J. Zhang and B. B. Iversen, J. Mater. Chem. A, 2017, 5, 4932–4939 RSC
.
- G. Qin, Z. Qin, H. Wang and M. Hu, Phys. Rev. B, 2017, 95, 195416 CrossRef
.
- L. Yu, A. Chen, X. Wang, H. Wang, Z. Qin and G. Qin, Phys. Rev. B, 2022, 106, 125410 CrossRef CAS
.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 RSC
.
- H. Bao, J. Chen, X. K. Gu and B. Y. Cao, ES Energy Environ., 2018, 1, 16–55 Search PubMed
.
- J. Yue, S. Hu, B. Xu, R. Chen, L. Xiong, R. Guo, Y. Li, L.-L. Nian, J. Shiomi and B. Zheng, Phys. Rev. B, 2024, 109, 115302 CrossRef CAS
.
- P. Bi, Y. Wan, Y. Yi and S. Bi, Phys. Rev. B, 2025, 112, 155404 CrossRef CAS
.
- Y. Xiao, C. Chang, Y. L. Pei, D. Wu, K. Peng, X. Zhou, S. Gong, J. He, Y. Zhang and Z. Zeng, Phys. Rev. B, 2016, 94, 125203 CrossRef
.
| This journal is © the Owner Societies 2026 |






