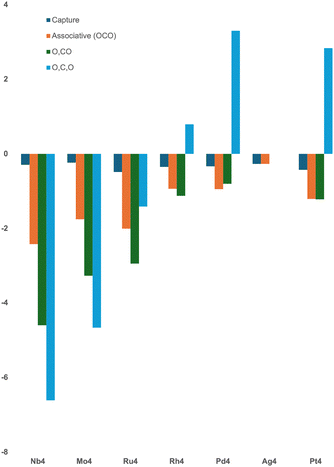Associative vs. dissociative binding of CO₂ on M₄ transition metal clusters

Abstract

Density functional theory calculations were performed to determine reaction paths for the reaction of CO₂ with M₄ transition metal clusters (M = Nb, Mo, Ru, Rh, Pd, Ag, Pt). Geometries incorporating associatively bound (CO₂), partly dissociated (O + CO) and fully dissociated (O + C + O) carbon dioxide were identified for all clusters except Ag₄. Nb₄ and Mo₄ are likely to dissociate CO₂ fully. For Ru₄, both partly and fully dissociative geometries were competitive, while Rh₄, Pd₄ and Pt₄ activate CO₂ without breaking either CO bond. Ag₄ was found to interact only minimally with CO₂. The change in ν_bend, the energy of the CO₂ π_u orbital in the physisorbed M₄CO₂ capture species and the charge transfer to the CO₂ molecule, q(CO₂), in the first transition state were found to correlate with the eventual fate of the CO₂ molecule.

---

1 Introduction

Carbon dioxide CO₂, is one of the key pollutant gasses contributing to global warming and ocean acidification.¹ In recognition of the urgency of this problem, in recent years there have been increasing efforts to develop and deploy carbon capture and storage systems. To go one step further, rather than storing carbon captured from the atmosphere (as CO₂), valorizing it as a C₁ feedstock. Captured CO₂ could be used to produce common feedstock chemicals and fuels such as formaldehyde, methanol and formic acid.^2,3 Reduction of CO₂ via the reverse Water Gas Shift (rWGS) reaction produces carbon monoxide, CO, that can be employed in a variety of industrially relevant reactions.^4,5

Somewhat frustrating the aim of employing captured CO₂ as a reactant in various chemical processes, is its exceptional thermodynamic and kinetic stability: the Gibbs free energy of formation, Δ_fG at 298 K is −394.36 kJ mol⁻¹.⁶ Therefore, activating the CO₂ molecule, by partly or fully breaking one of the two C=O bonds requires one or more of; a careful choice of reactants that can donate to the CO₂ molecule, a similarly careful choice of product, shifting the equilibrium – e.g. by removing product, and a large energy input.⁷

Considering the mechanism of how a catalytic system can activate CO₂, upon CO₂ adsorption or coordination to the system, often at the site of a metal centre, electron density is introduced into the antibonding π* orbitals of CO₂. The C=O bonds are thereby weakened and the molecule subsequently adopts a bent geometry (θ_OCO ≈ 120–140°), creating a dipole and increasing the reactivity of CO₂.^7–11

A variety of novel catalysts for the activation of CO₂ have been proposed, including MOFs,^12–14 ceria^15,16 and a variety of metal (oxide) surfaces including Fe¹⁷, Ti¹⁸, Cu¹⁹ and Pd/Mo.²⁰ A key feature of all of these proposed catalysts is that they involve one or more metal atoms at the active site as the source of the electron density donated to the CO₂ molecule.

Transition metal clusters have been studied both experimentally and computationally for many years for their capacity to adsorb and activate various small molecules including CO₂.^21,22 Transition metal clusters were initially studied as models of bulk surfaces.²³ However, it was rapidly identified that the properties of these clusters is both size-²⁴ and geometry-dependent,^25,26 and therefore, that by modifying the size and composition of the (nano)clusters, that the properties, especially the reactivity, of the clusters could be tuned.^23,27,28 Most recently, transition metal clusters have been confined within the pockets of porous framework materials, with the goal of protecting the active metal clusters from sintering, whilst the porous framework still allows mass transfer.^29,30

Computational studies, normally employing density functional theory (DFT), are key in determining the geometric structures and reaction mechanisms in both gas-phase^31–33 and surface studies,³⁴ especially identifying where barriers may prevent thermodynamic products from being observed.³⁵ A recent DFT-based mechanistic study from Mondal et al. showed that beyond simply the static cluster geometry, the fluxionality of the cluster was important in determining the reduction of CO₂ on supported copper tetramers.³⁶ Da Silva and coworkers studied a the reverse water gas shift reaction on series of M₁₃ clusters, M = Fe–Cu and observed that increasing the d-state occupation favoured COOH formation.⁵ Recently, Mohanta and Jena attempted to address the poor selectivity of the Cu₁₃ cluster by investigating a series of XCu₁₂ clusters, where X was a variety of first and second row transition metal atoms.

With a similar aim of understanding cluster behaviour across the periodic table, in this work, we present DFT calculated reaction paths for CO₂ addition to second row M₄ transition metal clusters from Nb₄ to Ag₄, we exclude technetium, due to its radioactivity, but we include the third-row Pt₄ cluster due to the popularity of platinum as a catalyst.

2 Computational method

Structures of M₄ clusters, for M = Nb–Ag (excluding Tc) and Pt were generated using the Kick stochastic structure search procedure with four individual M atoms supplied.^37,38 Full searches were undertaken on the lowest possible multiplicity (singlet for all M₄ clusters) and all minima identified were re-optimized at higher multiplicities. For all species, the lowest four multiplicities were calculated, but for rhodium, palladium and platinum, the search was extended up to the nonet. Ruthenium is known to have low lying minima with high numbers of unpaired electrons and so the search was further extended up to the 15-tet. No symmetry was imposed at any point in the search, nevertheless, several clusters adopted clear point group symmetry, as evidenced by geometric parameters and frequencies. Where point group symmetry was observed in either bare M₄ or M₄CO₂ clusters, we refer to this apparent symmetry, but we did not confirm the symmetry by further constrained calculation, as the addition of CO₂, or further steps on the reaction path would immediately break symmetry.

The lowest energy structure of each M₄ cluster was then adopted as a fragment in a further stochastic search process. Kick runs were undertaken searching for with the following configurations: M₄ + CO₂ (i.e. intact CO₂); M₄ + CO + O; M₄ + C + O + O. As activation of the CO₂ molecule is expected to proceed via electron donation into the CO₂ π_u orbitals, thus bending the CO₂ molecule,¹⁰ two Kick runs were also undertaken explicitly searching for minima and transition states, employing the M₄ cluster and a bent CO₂ molecule as fragments. Additional starting geometries were generated by hand (e.g. CO₂ bound to different symmetry-distinct metal atoms, end-on/side-on, linear/bent, μ¹/μ²/μ³-bound). From these calculations, the physisorbed “capture” species and the M₄CO₂ global minimum were identified, and the reaction pathway was then filled in and confirmed by a series of Quasi-Synchronous Transit (QST) and Intrinsic Reaction Coordinate (IRC) calculations. Where the global minimum was not a dissociated structure (i.e. M₄ + O + C + O), the lowest energy dissociated structure was also identified and a pathway to that structure was calculated using QST and IRC calculations as above.

The zero energy for each M₄ + CO₂ system is defined as the sum of the energies of the M₄ metal cluster in the singlet multiplicity and the CO₂ molecule. Thus structures with a negative relative energy (below zero energy) are more stable than the separated reactants; structures with a positive relative energy (energy higher than zero energy) are unstable with respect to the infinitely separated reactants. As in a previous study, basis set superposition error (BSSE) was disregarded, as were zero-point energies and entropic contributions.³⁹ All structure searches (Kick runs) were undertaken with the B3P86 density functional⁴⁰ and Stuttgart Relativistic Small Core (SRSC) basis set,^41–43 as previous studies^39,44 have shown this to be an accurate and computationally efficient combination. The final pathways were re-optimized at all relevant multiplicities using the TPSS functional⁴⁵ with the Def2TZVP basis set^46,47 and employing the D3-BJ empirical dispersion term.⁴⁸ This latter combination, while more expensive, has also been shown to reproduce energetic ordering and vibrational data for reactions of small molecules on gas phase transition metal clusters including Rh_n⁴⁹ and Pt_n.⁵⁰ Gaussian 16 was used for all calculations.⁵¹ Absolute and relative energies for all structures calculated with both functionals are presented in the SI (xlsx), structures are included in xyz format (zipfile).

3 Results and discussion

All M₄ tetramers are even-electron species, and thus we calculate the singlet – septet surfaces by default.

3.1 Nb₄

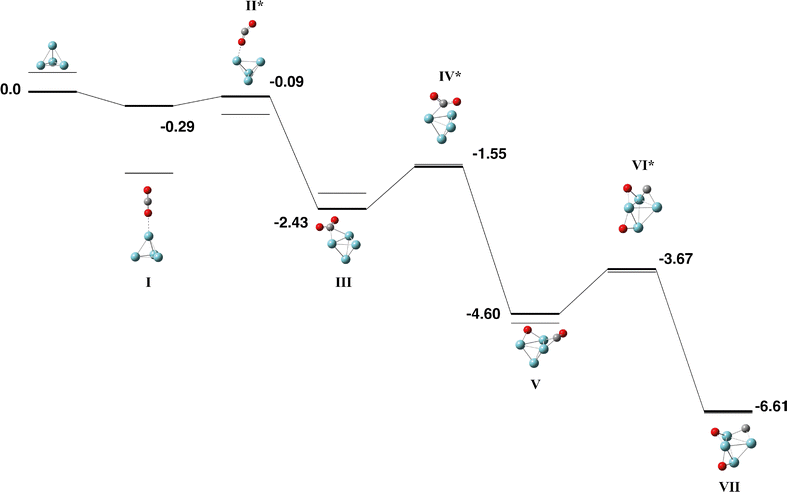
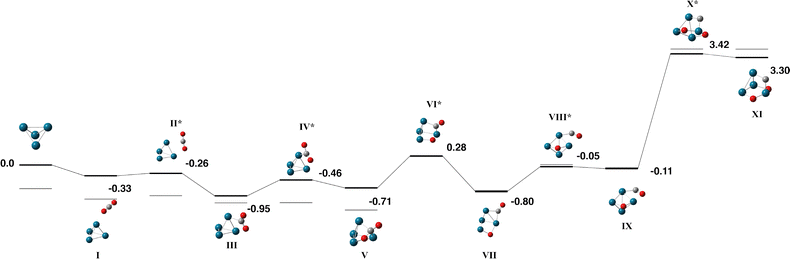
For the Nb₄ cluster we find a tetrahedral structure of singlet multiplicity to be the lowest in energy, in line with previous calculations using several DFT methods,^52–55 and confirmed by coupled cluster⁵⁶ and multireference singles and doubles configuration interaction (MRSDCI).⁵⁷ This cluster was used for the CO₂ pathway without constraint.

The Nb₄ + CO₂ pathway is shown in Fig. 1 and the corresponding geometric data is tabulated in Table S1. Only the singlet and triplet surfaces are shown as the quintet and septet were high in energy. The capture species (Fig. 1-I) is bound by −0.29 eV and consists of the CO₂ molecule approaching one vertex of the Nb₄ tetrahedron. The CO₂ molecule bends in the first transition state and the central carbon atom is μ² bound to a Nb–Nb edge, rotation of the CO₂ molecule over a Nb₃ face allows the first oxygen atom to dissociate (Fig. 1-V) and the remaining CO molecule dissociates the same way over the adjacent face resulting in a fully dissociated global minimum with a relative energy −6.61 eV below zero energy.

Fig. 1 Stationary points on the Nb₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet multiplicity is shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.2 Mo₄

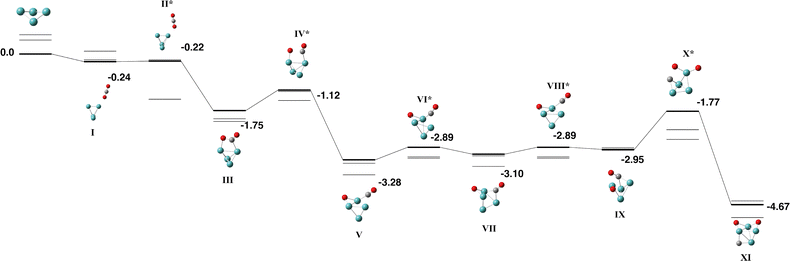
Several groups have undertaken calculations on the Mo₄ cluster: a recent DFT study by Kantorovich and coworkers predicted seven isomers within 1 eV of the global minimum, and two of those structures were separated by only 0.034 eV per atom – both structures were “tetrahedron-like” and possessed D_2d symmetry, but differed in the hinge angle.⁵⁸ Liebing et al. predict a stretched tetrahedral structure,⁵⁹ while Yin et al. predict a tetrahedral global minimum with an open “butterfly” structure 0.34 eV higher in energy.⁶⁰ Sumer and Jellinek reverse this order, predicting an open butterfly structure with μ_B = 4 being 0.01 eV per atom lower in energy than a tetrahedral structure with μ_B = 2.⁶¹ Pis Diez undertook a detailed study of the symmetry of the Mo₄ structure and identified four distorted tetrahedra of D_2d symmetry, a D₂ structure and a C_3v triangular pyramid.⁶² Our structure search on the singlet surface identified the open butterfly (ϕ = 130°), stretched tetrahedron (ϕ = 50°) and tetrahedral structures and the open butterfly was employed as a fragment in the reaction path with CO₂. It is to be noted, that despite starting from the open butterfly structure, upon interaction with CO₂, the Mo₄ cluster became more compact, resembling either the tetrahedron or stretched tetrahedral structures.

The reaction path for Mo₄ + CO₂ is very similar to that of Nb₄ and is shown in Fig. 2 with the corresponding geometric data in Table S2. The singlet–quintet surfaces are shown as the septet surface is high in energy. The CO₂ molecule initially approaches a single Mo atom in the capture species before binding in a η² fashion across a Mo–Mo bond (Fig. 2-III). The first O–CO bond breaks to yield a μ²-bound oxygen atom and a μ¹-bound CO molecule (Fig. 2-V), which rotates to become μ²-bound (Fig. 2-VII) before dissociating. The lowest energy structure has CO₂ fully dissociated and is −4.67 eV below the energy of the separated Mo₄ (singlet) and CO₂. The equivalent triplet structure is −5.07 eV below zero energy.

Fig. 2 Stationary points on the Mo₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet–quintet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.3 Ru₄

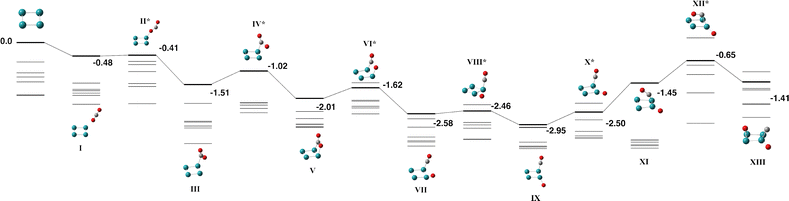
As ruthenium is known to have low-lying states with a high number of unpaired electrons, multipliticities up to 15-tet are investigated for the Ru₄ + CO₂ reaction. The lowest energy Ru₄ structure was determined to be a singlet rectangle with side lengths of 2.21 and 2.24 Å which is in approximate agreement with previous calculations on the Ru₄ cluster that predict a D_4h singlet square structure.^63–65

Fig. 3 and Table S3 show the reaction path for Ru₄ + CO₂. Multiplicities up to the 13-tet are shown, the 15-tet was approximately 1 eV higher in energy throughout the entire pathway. The CO₂ molecule interacts first with a single ruthenium atom in the capture species (Fig. 3-I), before bending and rotating to form a Ru–C covalent bond (Fig. 3-III). On the singlet surface this step requires surmounting a barrier at +0.57 eV, but for all other multiplicities, this transition state is below zero energy. The CO₂ molecule rotates to locate one oxygen atom over the adjacent Ru atom, forming a μ²η² structure. The lowest energy structure is Fig. 3-IX, where the CO₂ molecule has partly dissociated to a μ¹-bound oxygen atom in the Ru₄ plane and a μ¹-bound CO molecule approximately perpendicular to the plane. The remaining CO molecule can then fall across the Ru₄ face and dissociate (Fig. 3-XIII), however, the dissociation of the second CO bond, while still below zero energy, is less favoured than the partly dissociated CO₂ structure (Fig. 3-VII).

Fig. 3 Stationary points on the Ru₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet-13-tet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.4 Rh₄

As with ruthenium, we consider additional multiplicities for the Rh₄ cluster reaction, from singlet–nonet. The lowest energy Rh₄ cluster was identified to be a singlet tetrahedron of T_d symmetry and a side length of 2.45 Å. This result is consistent with that of many authors^66–70 and we employ this structure, without constraint, as a fragment for reaction with CO₂.

Fig. 4 shows the reaction path for Rh₄ + CO₂, the corresponding geometric data is tabulated in Table S4. From the η¹-O bound capture species, the CO₂ molecule falls across a Rh–Rh bond, binding in a μ²η² fashion, with a O–C–O angle, θ_OCO = 140°, but only marginally lengthening the CO bond (r_CO = 1.26 and 1.27 Å). The transition state stretching the coordinated CO bond (ν_imag = 464 cm⁻¹) is +0.52 eV higher than zero energy. After the first CO bond breaks, both the intact CO molecule and the dissociated oxygen atom rotate around the cluster, shifting from μ¹ to μ² binding in the lowest energy Rh₄CO₂ cluster (Fig. 4-VII). To reach the lowest energy fully dissociated structure, Fig. 4-IX, +0.79 eV above zero energy, the second CO bond needs to be stretched over an adjacent Rh₃ face, surmounting a transition state of +1.42 eV. Given that all transition states involving stretching of a CO bond have energy above that of the separated reactants, it is likely that CO₂ would remain intact on the Rh₄ cluster.

Fig. 4 Stationary points on the Rh₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet–nonet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.5 Pd₄

Pd₄ has also been extensively calculated. Futschek et al. calculated square, rhombus and tetrahedral structures with different multiplicities and point group symmetries, concluding that the triplet tetrahedron was the global minimum.⁶⁷ This assignment is in agreement with Kawazoe and coworkers⁷¹ Moc et al. also employ a tetrahedral triplet (³A″) Pd₄ structure in their reaction with H₂ molecules. Our structure search also identified a triplet global minimum, with a tetrahedral structure, though with a slightly expanded dihedral angle of 74° (viz. 80° in the singlet and 70.5° in T_d symmetry). We use this fragment going forward.

In addition to calculations determining the structure of the Pd₄ cluster, there have been many DFT studies on reactions of Pd₄. Borbolla et al. in their B3LYP/6-31G(d,p) study, determined that the adsorption of formic acid on Pd₄ would favourably produce CO₂.⁷² Lian and coworkers showed that Pd₄⁻ had a lower barrier to dissociating N₂O than the neutral or cationic tetramers⁷³ and Dutta et al. compared the bare and ZSM-5-supported Pd₄ cluster for the same reaction.⁷⁴ Kalita and Deka calculated reaction profiles for CO oxidation on bare and oxidized Pd₄ clusters.⁷⁵

The reaction path calculated for Pd₄ + CO₂ is shown in Fig. 5 with geometric data in Table S5. The lowest energy species for Pd₄CO₂ is Fig. 5-III, just after the capture species (Fig. 5-I). In structure Fig. 5-III, the CO₂ molecule is bent over a Pd–Pd bond, with θ_OCO = 136° and r_CO = 1.24 and 1.30 Å. From this lowest energy structure, the CO₂ molecule can rotate over the Pd₃ face to form a μ³η² geometry, which possesses approximate C_s symmetry, and a highly activated CO bond, r_CO = 1.36 Å. In transition state Fig. 5-VI, the activated CO bond breaks (ν_imag = 261 cm⁻¹), but this barrier lies above zero energy at +0.28 eV. Structure Fig. 5-VII is very similar to the μ²-O and μ²-CO structure calculated by Kalita and Deka for the coadsorption of O₂ and CO on Pd₄.⁷⁵ Continuing the reaction path in order to dissociate the CO molecule is highly disfavoured, crossing a barrier of +3.42 eV in order to reach a minimum +3.30 eV higher in energy than the separated Pd₄ + CO₂ reactants.

Fig. 5 Stationary points on the Pd₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet multiplicity is shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.6 Pt₄

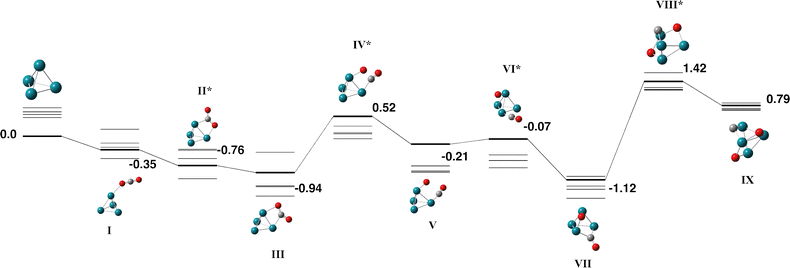
Our structure search identified a singlet open butterfly structure (ϕ = 135°) as the global minimum structure. In contrast, Sebetci predicted a distorted tetrahedron ground state, followed by a butterfly structure, though these differed by only 0.1 eV per atom in binding energy.⁷⁶ Grönbeck and Andreoni reversed this prediction for the neutral Pd₄ cluster, and additionally predicted a Y-shape cluster as being low in energy, further noting that the singlet and triplet states were quasi-degenerate.⁷⁷ The butterfly structure was also predicted by Singh et al.⁷⁸ and by Kawazoe and coworkers.⁷⁹ We employ our singlet butterfly as a fragment with CO₂.

Platinum is of long-standing interest and use as a catalyst. Of particular note, Mafuné and coworkers used DFT to show that small Pt_n (n = 4–12) clusters could undergo oxygen transfer reactions with N₂O the but did not catalyse the oxidation of CO, instead co-adsorbing O + CO.⁸⁰ Mass spectra generated in the same joint experimental – computational study were unable to identify CO₂ desorption from the Pt_n clusters. In a later work, Green et al. predicted a dissociative (O + CO) global minimum for the reaction of the anionic Pt₄⁻ cluster, but infrared multiphoton dissociation (IR-MPD) showed that the CO₂ molecule remained intact.³⁵

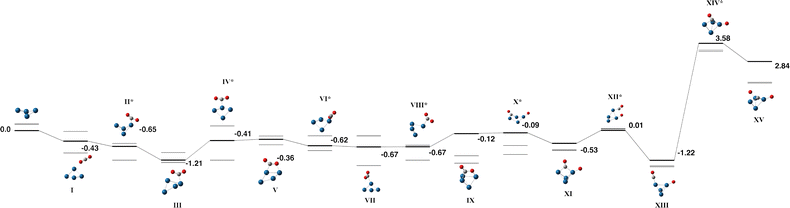
The calculated reaction path for neutral Pt₄ + CO₂ is shown in Fig. 6 with the corresponding data in Table S6. Green et al. noted that the anionic Pt₄⁻ cluster is a fluxional species,³⁵ and similar fluxionality is observed here for the neutral Pt₄ cluster, which contracts from an open butterfly structure, ϕ = 135° for Pt₄ to a tetrahedral structure, ϕ = 76° for the lowest energy structure Fig. 6-XIII. The key features on the reaction path are similar to those identified for the anionic cluster; after the capture species (Fig. 6-I), which is bound by −0.43 eV, a C-bound η¹ structure is formed (Fig. 6-III). The CO₂ molecule may be η¹-bound in this way to either an apex (Fig. 6-III) or spinal atom (Fig. 6-VII) of the Pt₄ butterfly, converting via an η² CO binding across the Pt–Pt bond (Fig. 6-V). From Fig. 6-IX, the CO₂ molecule could dissociate via either a opening/closing of the Pt₄ cluster (Fig. 6-X) or via stretching of the OC bond (Fig. 6-XII). The lowest energy Pt₄CO₂ structure has a μ¹-bound CO molecule with the dissociated oxygen atom μ¹ bound to an adjacent Pt atom. Searching for a pathway to dissociate the intact CO molecule identified a transition state +3.58 eV above zero energy and a minimum +2.84 eV above zero energy, indicating that full dissociation of the CO₂ molecule to O + C + O is not thermodynamically feasible on the Pt₄ cluster.

Fig. 6 Stationary points on the Pt₄ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet–quintet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.7 Ag₄

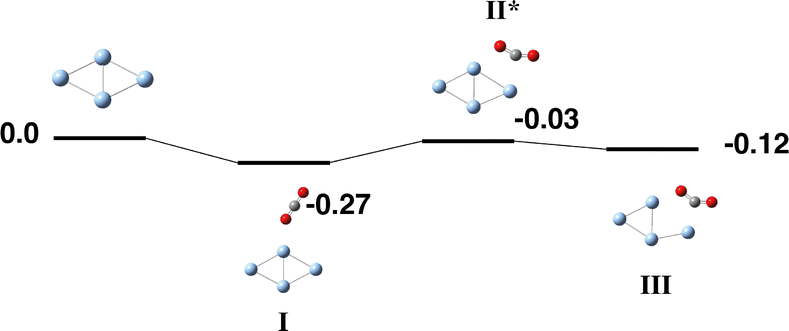
Silver has an electronic configuration of 4d¹⁰5s¹, and we study the singlet–septet multiplicities. The global minimum Ag₄ structure is predicted to be a planar singlet rhombus structure of D_2h symmetry, in agreement with several previous calculations.^81–84 Attempts to converge a tetrahedral structure, similar to the Ag₄²⁺ structure calculated by Shimizu and coworkers, resulted in a stretched tetrahedron 0.95 eV higher in energy.⁸⁵ A recent study indicated that the diamond/rhombus structure of Ag₄ contributed strongly to the activation of O₂.⁸⁶

The global minimum planar rhombus Ag₄ structure was used as the basis for the reaction path finding and the resulting Ag₄ +CO₂ reaction path is shown in Fig. 7 and Table S7. Only the singlet surface is shown as all other multiplicities were significantly above zero energy. CO₂ interacts only weakly with the Ag₄ cluster, the capture species (Fig. 7-I) has CO₂ μ¹-bound to a spinal Ag atom. The CO₂ molecule could then rotate in the Ag₄ plane and bend to form a μ²η² structure, but at the expense of the Ag–Ag bond, which is broken (3.79 Å vs. 2.76 Å). In Fig. 7-III, r(Ag–C) and r(Ag–O) are 2.23 and 2.24 Å respectively. No structures with CO₂ either partly (O + CO) or fully (O + C + O) dissociated were obtained.

Fig. 7 Stationary points on the Ag₄ + CO₂ potential energy surface. The singlet multiplicity is shown with bold lines. Other multiplicities are high in energy and are not shown. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.8 Periodic trends

For each M₄ + CO₂ reaction path, several key species are identified, these are: (1) the capture species, which is always the first structure shown on each reaction path and represents the first (physisorption) interaction between CO₂ with the M₄ cluster, the CO₂ molecule is therefore still linear in the capture species. (2) The lowest energy species with associatively-bound CO₂, the CO₂ molecule is, by definition, intact, but may not be linear. This species represents an activated CO₂ molecule. If a stable activated CO₂ molecule could be thermodynamically or kinetically prevented from further activation → dissociation (to O + CO), the activated CO₂ might thus be available for reaction with e.g. H₂ to form formaldehyde. (3) The lowest energy structure with one CO bond broken, i.e. M₄O·CO. (4) The lowest energy structure with the CO₂ fully dissociated to atoms. In the context of CO₂ activation, this would represent a catalyst poisoning process. The relative energies of these four geometric motifs are shown in Fig. 8.

Fig. 8 Plot of the relative energies of capture, lowest energy associative (OCO), lowest energy partly dissociated (O,CO) and fully dissociative (O,C,O) structures of M₄ metal clusters in the singlet multiplicity.

The energy of the capture species is consistent across the periodic table, ranging from −0.23 eV (Mo₄) up to −0.48 eV for the square planar Ru₄ cluster. The consistency of this interaction is expected, given the definition of the capture species as the minimally interacting species and has been observed previously.³⁹ The relative energies of the associative (OCO), partly dissociated (O + CO) and fully dissociated (O + C + O) structures steadily increasing as one moves left to right across the periodic table, from Nb₄ to Ag₄. Note that no stuctures with dissociatively bound CO₂ were identified for Ag₄. The apparent ‘slope’ of energy increase, is mild for associative structures, moderate in the case of partly dissociated structures (O + CO) and strong for the fully dissociated structures. Fully dissociated structures are disfavoured (higher than zero energy) for Rh₄, Pd₄ and Pt₄. The energies for the third row Pt₄ cluster are similar, but slightly lower than the equivalent Pd₄CO₂ structures, suggesting that small clusters to the right of (and including) rhodium, would not fully dissociate CO₂.

The initial adsorption step is considered key to the activation of CO₂,⁸⁷ it is the first step where charge transfer from the cluster to the CO₂ molecule, typically via the electrophilic carbon atom occurs, weakening the C=O bonds, bending θ_OCO and thereby leading to a variety of stable intermediate structures.⁸⁷ We therefore consider the properties of the M₄CO₂ capture species for each reaction pathway: Table 1 shows the calculated vibrational frequencies of CO₂ in the capture species for each M₄ cluster. The two bending frequencies, now non-degenerate, are strongly red-shifted on interaction with the M₄ cluster, by ≈60 cm⁻¹, consistent with the CO₂ π_u antibonding orbitals receiving electron density from the cluster. Considering the first of the two formerly degenerate frequencies (the one with the larger redshift), there is an apparent, though approximate, correlation between the degree of redshift and the energy of the fully dissociative species, with clusters that possess a fully dissociated CO₂ below zero energy, regardless of whether this structure is the global minimum or not, show a redshift >60 cm⁻¹ (viz. Nb₄, Mo₄ and Ru₄). Clusters to the right of and including Rh₄ yield a smaller redshift.

Table 1 CO₂ vibrational frequencies (ν_CO2), key orbital energies and adsorption and interaction energies for M₄CO₂ capture species. Absolute energy of the CO₂ π_u orbital is −0.893 eV (−0.03280 a.u)

System	Bend 1	Bend 2	Symm stretch	Asym stretch	E(M4,HOMO)	E(M4,LUMO)	E(πu)	ΔE(πu)	Eads	Eint
	(cm^−1)				(eV)
CO2	622	622	1283	2319			−0.893	0.0
Nb4	546	547	1256	2317	−4.237	−2.304	−2.304	−1.411	−0.291	−0.292
Mo4	471	540	1251	2333	−3.920	−2.399	−2.399	−1.507	−0.237	−0.516
Ru4	527	579	1268	2324	−4.905	−3.470	−2.140	−1.248	−0.481	0.514
Rh4	572	587	1275	2322	−5.416	−3.000	−1.393	−0.501	−0.349	−0.351
Pd4	581	585	1277	2322	−5.495	−4.245	−1.498	−0.605	−0.333	−0.341
Ag4	599	606	1292	2331	−5.232	−3.130	−1.822	−0.930	−0.269	−0.269
Pt4	567	588	1280	2330	−6.060	−4.227	−1.797	−0.904	−0.430	−0.433

---

Table 1 also shows the energy of the CO₂ π_u orbital and the ΔE, with respect to the calculated value for free CO₂ (−0.03280 a.u.). Clusters that thermodynamically dissociate CO₂ lower the energy of the π_u orbital by ≈1.2–1.5 eV, while clusters without a fully dissociated CO₂ below zero energy, lower the orbital energy by only ≈0.5–0.9 eV. Both of these correlations are indicative only, and provide no information on the relative stability of intermediate species (e.g. M₄O·CO) but do act as a barometer for the thermodynamic stability (below zero energy) of the fully dissociative structure.

Table 1 shows the properties of the capture species for each reaction pathway, defined previously as the initial contact of CO₂ with the metal cluster. As this species possesses CO₂ physisorbed to the M₄ cluster, the interaction of the two species is minimal, and it is perhaps unsurprising that consideration of this species alone is insufficient to predict the eventual fate of CO₂. Table 2 shows the Hirshfeld charges on CO₂ molecule in the capture species and the first transition state for each of the reaction pathways. q(CO₂) for the capture species is consistent and positive (≈0.1) for all M₄ clusters, and clearly represents the initial donation of charge from the CO₂ molecule to the cluster. The charge transfer observed in the first transition state (i.e. the back-donation from the M₄ cluster to the CO₂ molecule upon chemisorption) is diagnostic, with the three species where full CO₂ dissociation is thermodynamically possible (viz. Nb₄, Mo₄ and Ru₄) having q(CO₂) < −0.35e⁻. Clusters that do not dissociate either CO₂ bond, (Pd₄ and Ag₄) have low back-donation to CO₂, < 0.2e⁻ and clusters that are likely to activate CO₂ without fully dissociating it, Rh₄, Pt₄, having intermediate q(CO₂) values.

Table 2 Hirshfeld charge on CO₂ in capture species and first transition state for M₄CO₂ reaction pathways

System	Capture species	TS 1
	q(CO2)	q(CO2)
Nb4	0.098	−0.577
Mo4	0.097	−0.488
Ru4	0.125	−0.354
Rh4	0.097	−0.299
Pd4	0.080	−0.006
Ag4	0.087	−0.151
Pt4	0.114	−0.250

---

Fig. 9 shows the barrier heights (transition state energies) for the key transition states in each pathway. The chosen barriers correspond to each CO bond breaking. Accordingly, no barriers are plotted for Ag₄. Two trends can be clearly observed. Firstly, there is a clear left-right divide with all Nb₄–Ru₄ barriers being below zero energy, whereas Rh₄–Pd₄ barriers are above zero energy. The barrier to breaking the first CO bond on Pt₄ is slightly below zero energy at −0.12 eV, reflecting the softer surface presented by the 5d metal compared to its 4d counterpart. Secondly, the barriers to the first CO bond breaking are relatively consistent either side of the left-right divide defined by Ru/Rh, whereas the barrier to the second CO bond breaking rises when moving from left to right (Nb₄–Ag₄), suggesting that activated CO₂ or O + CO are likely outcomes of reaction on the Rh₄ and Pd₄ clusters.

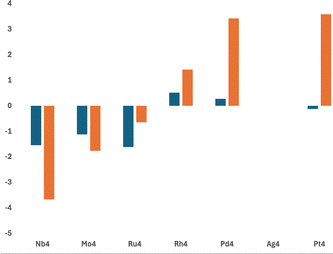Fig. 9 Plot of the relative energies of barriers to dissociation of the first (blue) and second (orange) C⋯O bonds for M₄CO₂ reaction pathways on the singlet surface.

The general trends in adsorption energies shown in Fig. 8 are consistent with other materials proposed for CO₂ adsorption. Peng and coworkers studied the adsorption of molecular CO₂ on M₂N MXenes, and found that end-on CO₂ binding had a consistent binding energy, of ≈−0.25 eV, corresponding to a physisorbed geometry, but the adsorption energy of side-on CO₂ rose from −2.5 eV for Y₂N to −1.5 eV for Mo₂N, and MXenes to the right of Ru₂N bound CO₂ only weakly, ≈−0.42 eV. Jurado et al. also studied a range of M₂X MXenes, finding similar binding energies and trends with CO₂ adsorption energies of −2.83, −1.73 and −1.34 eV for M = Zr, Nb and Mo respectively. In addition, they also noted the non-negligible role of the X atom, with carbides having lower adsorption energies than equivalent nitrides, and M₃N₂ MXenes having adsorption energies ≈1 eV greater than the equivalent M₂N species. A study on single-atom doped Ti₂CO₂ showed that CO₂ remains intact on these species, which is consistent with the CO₂ adsorption energy on Y-doped Ti₂CO₂ of −0.808 eV,⁸⁸ compared to ≈2 eV for the M₄ species that dissociate CO₂ in this work.

4 Conclusions

We have calculated reaction pathways for the reaction of CO₂ on a series of neutral M₄ transition metal clusters. Moving from left to right across the periodic table, the energies of the capture species remained relatively constant. The energies of the lowest energy M₄CO₂ species with CO₂ fully intact (associatively bound CO₂), lowest energy M₄O·CO species and M₄O·C·O (fully dissociated CO₂) species all rose moving from Nb₄ to Ag₄, with the rate of increase M₄O·C·O > M₄O·CO > M₄CO₂. Therefore it is predicted that Nb₄ and Mo₄ will fully dissociate CO₂. Ru₄ may also fully dissociate CO₂, but would be more likely to only break the first CO bond, resulting in a Ru₄O·CO product. Rh₄, Pd₄ and Pt₄ are good candidates to observe an activated CO₂ molecule. The Ag₄ cluster interacts only weakly with CO₂. The energy of the CO₂ π_u orbital in the M₄CO₂ capture species and the related ν_bend was found to indicate those structures that dissociate CO₂ fully (Nb₄, Mo₄ and Ru₄) from those that do not, but did not distinguish between partly dissociated (O + CO) and fully intact CO₂, however the degree of charge transfer in the first transition state was found to indicate all three possible fates of CO₂.

Author contributions

SS, BAV, NA, MS: investigation, writing – original draft MAA: conceptualization of this study, methodology, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: geometric parameters (pdf), structures (xyz) and energies, vibrational data (xlsx) for all pathways. See DOI: https://doi.org/10.1039/d5cp03419a.

Acknowledgements

MAA is grateful for HPC time via the UK Materials and Molecular Modelling Hub via grant no. (EP/T022213).

Notes and references

1. G. A. Olah, G. K. S. Prakash and A. Goeppert, J. Am. Chem. Soc., 2011, 133, 12881–12898.
2. E. V. Kondratenko, G. Mul, J. Baltrusaitis, G. O. Larrazábal and J. Pérez-Ramírez, Energy Environ. Sci., 2013, 6, 3112–3135.
3. R. W. Dorner, D. R. Hardy, F. W. Williams and H. D. Willauer, Energy Environ. Sci., 2010, 3, 884–890.
4. A. G. Saputro, A. L. Maulana, F. D. Aprilyanti and H. K. Dipojono, J. Eng. Technol. Sci., 2021, 53, 210402.
5. V. K. Ocampo-Restrepo, L. G. Verga and J. L. F. Da Silva, J. Phys. Chem. C, 2021, 125, 26296–26306.
6. X. Li, J. Yu, M. Jaroniec and X. Chen, Chem. Rev., 2019, 119, 3962–4179.
7. T. Sakakura, J.-C. Choi and H. Yasuda, Chem. Rev., 2007, 107, 2365–2387.
8. V. K. Ocampo-Restrepo, L. G. Verga and J. L. F. Da Silva, J. Phys. Chem. C, 2021, 125, 26296–26306.
9. V. K. Ocampo-Restrepo, L. Zibordi-Besse and J. L. F. Da Silva, J. Chem. Phys., 2019, 151, 214301.
10. J. M. Weber, Int. Rev. Phys. Chem., 2014, 33, 489–519.
11. M. C. Thompson, J. Ramsay and J. M. Weber, J. Phys. Chem. A, 2017, 121, 7534–7542.
12. C. Wu, M. Luo, Y. Zhao, S. Wang, A. Zavabeti, P. Xiao and G. K. Li, Chem. Eng. J., 2023, 475, 146411.
13. Q. Sun, S. Huang, Z. Li, D. Su and J. Sun, J. Environ. Chem. Eng., 2023, 11, 109065.
14. M. Zhang, D. Zhang, X. Jing, B. Xu and C. Duan, Angew. Chem., Int. Ed., 2024, 63, e202402755.
15. P. Du, G. Deng, Z. Li, J. Sun, L. Wang, Y. Yang, J. Wang, Y. Li, X. Xu, Y. Zhang, W. Liu, G. Liu, Z. Zou and Z. Li, J. Mater. Sci. Technol., 2024, 189, 203–210.
16. Y. Wang, Y. S. Chan, R. Zhang and B. Yan, Chem. Eng. J., 2024, 481, 148360.
17. O. Hurtado-Aular, R. M. Ferullo and P. G. Belelli, Comput. Mater. Sci., 2024, 233, 112741.
18. Y. Shao, S. Zhang, X. Ou, F. Zeng, R. Cai, X. Fan and H. Chen, Chem. Eng. J., 2025, 518, 164589.
19. D. Y. Shin, J. H. Jo, J.-Y. Lee and D.-H. Lim, Comput. Theor. Chem., 2016, 1083, 31–37.
20. H. Sugiyama, M. Miyazaki, M. Sasase, M. Kitano and H. Hosono, J. Am. Chem. Soc., 2023, 145, 9410–9416.
21. V. Muman, A. Tennyson-Davies, O. Allegret and M. A. Addicoat, Phys. Chem. Chem. Phys., 2024, 26, 2218–2227.
22. M. A. Addicoat, K. F. Lim and G. F. Metha, J. Chem. Phys., 2012, 137, 034301.
23. A. Fielicke, Chem. Soc. Rev., 2023, 52, 3778–3841.
24. A. Yamada, K. Miyajima and F. Mafune, Phys. Chem. Chem. Phys., 2012, 14, 4188–4195.
25. D. Harding, M. S. Ford, T. R. Walsh and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2007, 9, 2130–2136.
26. S. Nayak, B. Rao, S. Khanna and P. Jena, Chem. Phys. Lett., 1996, 259, 588–592.
27. G. Kwon, G. A. Ferguson, C. J. Heard, E. C. Tyo, C. Yin, J. DeBartolo, S. Seifert, R. E. Winans, A. J. Kropf, J. Greeley, R. L. Johnston, L. A. Curtiss, M. J. Pellin and S. Vajda, ACS Nano, 2013, 7, 5808–5817.
28. R. K. Raju, P. Rodriguez and E. N. Brothers, Phys. Chem. Chem. Phys., 2023, 25, 11630–11652.
29. K. Mori, J. Matsuo, Y. Kondo, H. Hata and H. Yamashita, ACS Appl. Energy Mater., 2021, 4, 11634–11642.
30. S. H. Pulumati, D. K. Sannes, C. R. Jabbour, L. D. B. Mandemaker, B. M. Weckhuysen, U. Olsbye, A. Nova and E. Skulason, ACS Catal., 2023, 14, 382–394.
31. M. N. Collacique, V. K. Ocampo-Restrepo and J. L. F. Da Silva, J. Chem. Phys., 2022, 156, 124106.
32. D. Guo, J. Liu, X. Zhao, X. Yang and X. Chen, Sep. Purif. Technol., 2023, 313, 123462.
33. J. Li, P. Gonzalez-Navarrete, M. Schlangen and H. Schwarz, Chem. – Eur. J., 2015, 21, 7780–7789.
34. M. A. Nolen, S. A. Tacey, S. Kwon and C. A. Farberow, Appl. Surf. Sci., 2023, 637, 157873.
35. A. E. Green, J. Justen, W. Schöllkopf, A. S. Gentleman, A. Fielicke and S. R. Mackenzie, Angew. Chem., Int. Ed., 2018, 57, 14822–14826.
36. U. Mondal and P. Ghosh, Catal. Today, 2021, 370, 93–103.
37. M. A. Addicoat and G. F. Metha, J. Comput. Chem., 2009, 30, 57–64.
38. M. A. Addicoat, S. Fukuoka, A. J. Page and S. Irle, J. Comput. Chem., 2013, 34, 2591–2600.
39. M. A. Addicoat, M. A. Buntine, B. Yates and G. F. Metha, J. Comput. Chem., 2008, 29, 1497–1506.
40. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
41. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
42. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
43. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
44. M. A. Addicoat, K. F. Lim and G. F. Metha, J. Chem. Phys., 2012, 137, 034301.
45. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
47. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
48. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
49. E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2019, 21, 13959–13967.
50. G. Meizyte, A. E. Green, A. S. Gentleman, S. Schaller, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2020, 22, 18606–18613.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision B.01, Gaussian Inc., Wallingford CT, 2016.
52. X. X. Jin, J. G. Du, G. Jiang, X. Luo and X. W. Wang, Eur. Phys. J. D, 2011, 64, 323–329.
53. P. V. Nhat, V. T. Ngan and M. T. Nguyen, J. Phys. Chem. C, 2010, 114, 13210–13218.
54. P. Calaminici and R. Mejia-Olvera, J. Phys. Chem. C, 2011, 115, 11891–11897.
55. X. Wang, M. Lin and Q. Zhang, Acta Chim. Sin., 2004, 62, 1689–1694.
56. C. V. S. Costa, L. d S. Barbosa, R. Gargano and D. L. Azevedo, J. Mol. Mod., 2024, 30, 406.
57. D. Majumdar and K. Balasubramanian, J. Chem. Phys., 2004, 121, 4014–4032.
58. Y. Wei, V. Veryazov and L. Kantorovich, APL Mater., 2024, 12, 031127.
59. S. Liebing, C. Martin, K. Trepte and J. Kortus, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155421.
60. Y.-H. Yin and J. Chen, Comput. Theor. Chem., 2022, 1212, 113720.
61. A. Sumer and J. Jellinek, J. Chem. Phys., 2022, 157, 034301.
62. R. Pis Diez, Int. J. Quantum Chem., 2000, 76, 105–112.
63. G.-X. Ge, H.-X. Yan, Q. Jing and Y.-H. Luo, J. Cluster Sci., 2011, 22, 473–489.
64. Y.-C. Bae, H. Osanai, V. Kumar and Y. Kawazoe, Mater. Trans., 2005, 46, 159–162.
65. F. Aguilera-Granja, L. C. Balbás and A. Vega, J. Phys. Chem. A, 2009, 113, 13483–13491.
66. B. V. Reddy, S. K. Nayak, S. N. Khanna, B. K. Rao and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5214–5222.
67. T. Futschek, M. Marsman and J. Hafner, J. Phys.: Condens. Matter, 2005, 17, 5927.
68. C.-H. Chien, E. Blaisten-Barojas and M. R. Pederson, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 2196–2202.
69. S. K. Nayak, S. E. Weber, P. Jena, K. Wildberger, R. Zeller, P. H. Dederichs, V. S. Stepanyuk and W. Hergert, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8849–8854.
70. Y. Jinlong, F. Toigo and W. Kelin, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7915–7924.
71. V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 144413.
72. R. L. Camacho-Mendoza and J. Cruz-Borbolla, Chem. Phys. Lett., 2020, 755, 137794.
73. X. Tang, W. Zeng, H. Duan, S. Chen and X. Lian, React. Kinet., Mech. Catal., 2023, 136, 1933–1943.
74. P. Dutta, N. Biswakarma, D. Dowerah, S. Neog, A. Phonglo, P. J. Sarma, N. K. Gour and R. C. Deka, J. Phys. Chem. C, 2024, 128, 21263–21279.
75. B. Kalita and R. C. Deka, J. Am. Chem. Soc., 2009, 131, 13252–13254.
76. A. Sebetci, J. Chem. Phys., 2006, 331, 9–18.
77. H. Grönbeck and W. Andreoni, Chem. Phys., 2000, 262, 1–14.
78. N. B. Singh and U. Sarkar, J. Mol. Mod., 2014, 20, 2537.
79. V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 205418.
80. H. Yamamoto, K. Miyajima, T. Yasuike and F. Mafuné, J. Phys. Chem. A, 2013, 117, 12175–12183.
81. N. Hartmann, R. Mitric, B. Stanca and V. Bonacic-Koutecky, Eur. Phys. J. D, 2001, 16, 151–155.
82. V. Bonačić-Koutecky, L. Češpiva, P. Fantucci and J. Koutecky, J. Chem. Phys., 1993, 98, 7981–7994.
83. Y. Wang and X. G. Gong, Eur. Phys. J. D, 2005, 34, 19–22.
84. R. Fournier, J. Chem. Phys., 2001, 115, 2165–2177.
85. S. Yasumura, T. Kato, T. Toyao, Z. Maeno and K.-I. Shimizu, Phys. Chem. Chem. Phys., 2023, 25, 8524–8531.
86. W. Wang, X. Liu and J. Pérez-Ros, J. Phys. Chem. A, 2021, 125, 5670–5680.
87. M. N. Collacique, V. K. Ocampo-Restrepo and J. L. F. Da Silva, J. Chem. Phys., 2022, 156, 124106.
88. Y.-X. Yu, J. Colloid Interface Sci., 2025, 695, 137799.

---