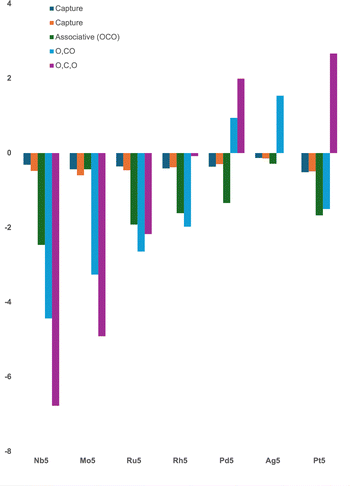Associative vs. dissociative binding of CO₂ on M₅ transition metal clusters

Abstract

Reaction paths were calculated using density functional theory for the reaction of carbon dioxide with a series of transition metal pentamers, M₅ + CO₂, (M = Nb, Mo, Ru, Rh, Pd, Ag, Pt). A stochastic search algorithm was used to identify geometries with intact CO₂, as well as geometries where the CO₂ molecule was partly (O + CO) and fully dissociated (O + C + O). Nb₅ and Mo₅ clusters were found to thermodynamically dissociate CO₂. Pd₅ and Ag₅ were found to leave the CO₂ molecule intact, Ru₅ could partly dissociate CO₂, while for Rh₅ and Pt₅, the fate of the adsorbed CO₂ was dependent on the cluster geometry. The change in the CO₂ π_u orbital energy in the capture species on initial reaction with the M₅ cluster was found to distinguish clusters where CO₂ fully dissociated, but could not distinguish clusters where CO₂ was found to partly dissociate. The charge transfer to the CO₂ molecule at the first transition state, did however, distinguish clusters that fully dissociate CO₂, those that partly dissociate CO₂ to O + CO, and those that leave CO₂ fully intact.

---

1. Introduction

In recent years, there has been increasing interest in the activation of CO₂. Especially in the context of the environment, the ability to activate captured CO₂ towards further reaction, turns a problem of needing to store the captured CO₂¹ into a solution – a cheap C1 feedstock.^2,3 CO₂ is unfortunately well-known for its thermodynamic and kinetic stability, and it is unreactive in the gas phase,⁴ thus requiring activation via some catalyst species in order to weaken and/or break the CO bonds. Activation of CO₂ typically proceeds via introducing electron density into the antibonding π* orbitals of CO₂, weakening the C=O bonds and allowing the CO₂ the molecule to bend away from linear, simultaneously creating a dipole and increasing the reactivity of CO₂.^5–7

Several manufactured materials including foams,⁸ CaCO₃ microspheres,⁹ and novel cements¹⁰ have been proposed and used to capture and store CO₂. More recently, novel materials including, Metal- and Covalent Organic Frameworks,^11–13 carbon nanotubes,¹⁴ MXenes,^15–20 and nanofilms²¹ have been proposed to not only capture, but to valorize CO₂ for further use. CO₂ is activated by electron donation into the antibonding π* orbitals of CO₂, weakening the C=O bonds allowing the CO₂ molecule to bend.^5–7,22,23 In the majority of these materials above, the active site of the catalyst is a metal atom²⁴ and thus there is considerable interest in the mechanism of CO₂ activation by various metals²⁵ and there has been a great volume of spectroscopic and theoretical work over decades^26–29 investigating the interaction of CO₂ with single transition metal atoms/ions, M^+/0/−. A range of CO₂ binding motifs have thus been identified, including η¹ coordination (via the C atom), bidentate η² binding (via C, O), and dissociative addition where binding produces CO and O species. Where multiple CO₂ molecules adsorb, oxalate formation has also been identified.^7,30

In between single atoms and bulk surfaces, transition metal clusters have long been an avenue for the investigation of gas phase reactions, with a variety of substrates including CO,^22,31 N₂O³² and notably CO₂.^32,34,35 Size effects are well-known in the cluster regime, with several experimental³⁶ and computational studies³⁷ noting properties varying over several orders of magnitude upon single atom addition.

One study from Mackenzie group illustrated these size effects with respect to CO₂ activation, employing small Pt₄⁻ and Pt₅⁻ anionic clusters. They showed that while Pt₄⁻ + CO₂ has a dissociative global minimum (i.e. Pt₄⁻(CO)O), the spectroscopically observed species possessed intact CO₂ (Pt₄⁻OCO), whereas for the one atom larger cluster anion, Pt₅⁻, infrared multiphoton dissociation (IR-MPD) spectroscopy showed the computationally predicted global minimum, dissociatively bound Pt₅⁻(CO)O exists and in contrast to Pt₄⁻, no evidence of molecularly bound CO₂ was seen, despite such a species being predicted within the energy of their cluster source.³⁸

Inspired by this work of Mackenzie et al.,³⁸ and following on from our work on M₄ clusters,³⁹ we report a “horizontal” study, investigating the reaction of CO₂ with M₅ neutral transition metal clusters from niobium through silver and additionally including platinum.

2. Computational method

The computational method employed here is the same as in our previous work, and recapped here.³⁹ Structures of M₅ clusters, for M = Nb–Ag (excluding Tc) and Pt were generated using the Kick stochastic structure search procedure with five individual M atoms supplied.^40,41 Full searches were undertaken on the lowest possible multiplicity (singlet or doublet) and all minima identified were re-optimized at higher multiplicities. For all metal species, the lowest four multiplicities were calculated, but for ruthenium and rhodium, the search was extended up to the 15-tet and the 12-tet, respectively. No symmetry was imposed at any point in the search, nevertheless, several clusters adopted clear point group symmetry, as evidenced by geometric parameters and frequencies. We chose not to confirm the symmetry by further calculation, as the addition of CO₂ would immediately break symmetry.

The lowest energy structure of each M₅ cluster was then adopted as a fragment in a further stochastic search process. Kick runs were undertaken with the following configurations: M₅ + CO₂(linear); M₅ + CO₂(bent); M₅ + CO + O; M₅ + C + O + O. In order to easily identify the transition state where the CO₂ molecule first began to dissociate, a Kick run was also undertaken explicitly searching for transition states, employing the M₅ cluster and the bent CO₂ molecule as fragments. Additional starting geometries were generated by hand (e.g. CO₂ bound to different symmetry-distinct metal atoms, end-on/side-on, linear/bent, µ¹/µ²/µ³-bound). From these calculations, the physisorbed “capture” species and the M₅CO₂ global minimum were identified, and the reaction pathway was then filled in and confirmed by a series of Quasi-Synchronous Transit (QST) and Intrinsic Reaction Coordinate (IRC) calculations.

The zero energy for each M₅ + CO₂ system is defined as the sum of the energies of the M₅ metal cluster in the lowest possible multiplicity and the CO₂ molecule. Thus structures with a negative relative energy (below the zero energy) are more stable than the separated reactants; structures with a positive relative energy (energy higher than the zero energy) are unstable with respect to the infinitely separated reactants. basis set superposition error (BSSE) was disregarded, as were zero-point energies and entropic contributions, as previous work that the effect of BSSE and ZPE on relative energies is minimal and that adding entropic effects was found to consistently raise relative energies by ≈0.5 eV at 298 K.³¹ All structure searches were undertaken with the B3P86 density functional⁴² and Stuttgart Relativistic Small Core (SRSC) basis set,^43–45 as previous studies^31,46 have shown this to be an accurate and computationally efficient combination. The final pathways were re-optimized at all relevant multiplicities using the TPSS functional⁴⁷ with the Def2TZVP basis set^48,49 and employing the D3-BJ empirical dispersion term.⁵⁰ This latter combination, while more expensive, has also been shown to reproduce energetic ordering and vibrational data for reactions of small molecules on gas phase transition metal clusters including Rh_n⁵¹ and Pt_n.⁵² All calculations were undertaken using the Gaussian 16 software.⁵³ All structures presented are included in the SI (xyz, zip) and absolute and relative energies for each structure at all multiplicities studied are presented in the SI (xlsx).

3. Results and discussion

3.1. Nb₅

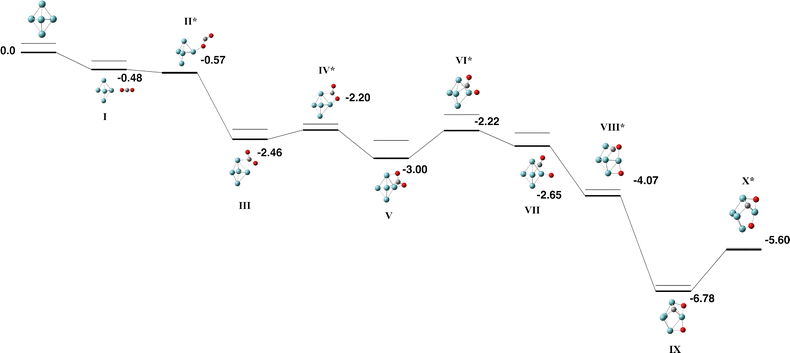
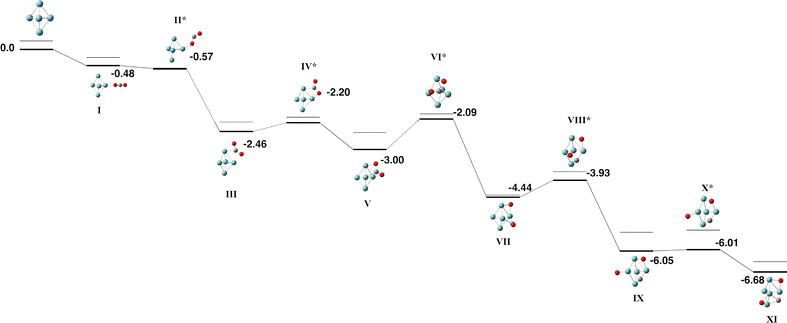
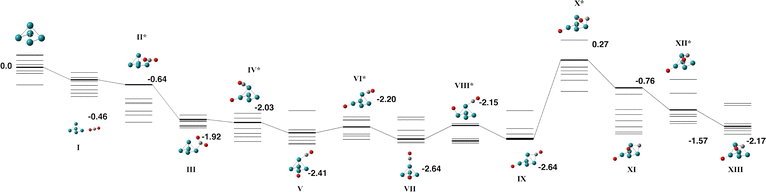
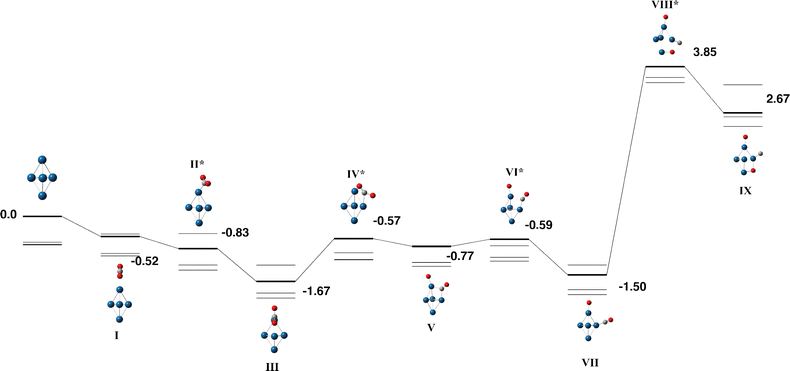
The Nb₅ cluster is an odd-electron species and therefore may be a doublet, quartet,…. The doublet multiplicity was found to be the lowest in energy, in line with previous calculations.⁵⁴ In slight contrast to the early calculations of Salahub et al. on neutral Nb₅, we identified the minimum energy structure to be of C_2v symmetry with equatorial–equatorial bond lengths of 2.63 (2) and 2.87 Å and axial–equatorial bond lengths of 2.49 (2) and 2.61 Å. This cluster was used for the CO₂ pathway without constraint.

Two pathways were identified for the reaction of Nb₅ + CO₂, shown in Fig. 1 and 2. Corresponding geometric data is shown in Table S1. Both pathways begin with the CO₂ molecule approaching the equatorial niobium atoms, and the CO₂ molecule bending over one of the triangular faces of the Nb₅ cluster. Structures I–V of both pathways are therefore the same. The two pathways diverge with a choice of which CO bond breaks first. In the pathway shown in Fig. 1, the CO bond that is closest to the equatorial plane of the Nb₅ cluster breaks first resulting in a CO molecule bound to an axial niobium atom and the lone oxygen atom attached to an equatorial niobium atom. The second pathway, shown in Fig. 2 breaks the other CO bond, resulting in the CO molecule bound to equatorial niobium atoms and the dissociated oxygen atom bound to an axial niobium atom. Both pathways result in very similar global minima, with the CO₂ molecule completely dissociated, at relative energies of −6.76 and −6.68 eV respectively. These two structures, Fig. 1-IX and 2-XI, may interconvert, via a transition state shown on the first pathway, Fig. 1-X.

Fig. 1 Stationary points on the Nb₅ + CO₂ potential energy surface. The doublet multiplicity is shown in bold and the quartet multiplicity is shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

Fig. 2 Second reaction pathway on the Nb₅ + CO₂ potential energy surface. The doublet multiplicity is shown in bold and the quartet and sextet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.2. Mo₅

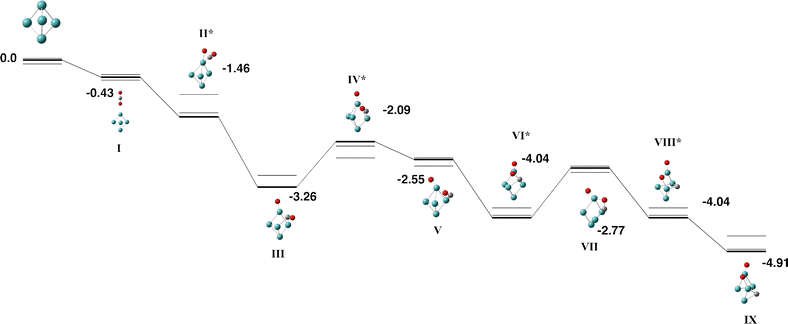
The molybdenum atom is and even-electron species and therefore the Mo₅ cluster is also an even-electron species and we investigate the singlet, triplet,… surfaces. Several authors have calculated the structure and properties of the Mo₅ cluster using a variety of density functional methods, basis sets and structure search approaches. Plá and Diez identified a singlet global minimum of a capped out-of-plane rhombus, but with singlet and triplet trigonal bipyramid structures both only 0.03 eV per atom higher in energy.⁵⁵ Vega and coworkers predicted a triplet bipyramid with C_2v symmetry,⁵⁶ while Yin and Chen identified a singlet trigonal bipyramid with C₁ symmetry.⁵⁷ Kantorovich and coworkers used the AIRSS approach⁵⁸ to identify 9 Mo₅ structures within 1 eV of the global minimum, which they predict to be a C_2v singlet trigonal bipyramid.⁵⁹ Sumer and Jellinek identified a similar set of low energy structures, but their global minimum had only C₂ symmetry.⁶⁰ Lei predicted a singlet trigonal bipyramid structure.⁶¹ In general agreement with these studies, we identified the global minimum to be a singlet trigonal bipyramid with approximately D_3h symmetry and bond lengths of 2.34 Å (axial–equatorial) and 2.83 Å (equatorial–equatorial) and we employed this structure, without symmetry constraint, in our reaction with CO₂.

A single pathway was identified for the reaction of Mo₅ + CO₂, it is shown in Fig. 3 and Table S2. The pathway begins with the CO₂ molecule approaching the axial molybdenum atoms, and the CO₂ molecule breaks over the axial atom of the Mo₅ cluster in the first transition state (structure Fig. 3-II). The remaining CO molecule binds in a µ³ fashion to a triangular face of the Mo₅ cluster, before twisting, rotating parallel to the face and then dissociating. The Mo₅CO₂ global minimum therefore has the CO₂ molecule fully dissociated with the carbon atom µ³-bound, and the oxygen atoms µ² and µ¹-bound, with a relative binding energy of −4.91 eV with respect to the singlet Mo₅ + CO₂.

Fig. 3 Reaction pathway of Mo₅ + CO₂. The singlet potential energy surface is shown in bold and the triplet and quintet multiplicities are shown with thin lines. Relative energies for the singlet surface are given in eV, energies of higher multiplicities are included in SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.3. Ru₅

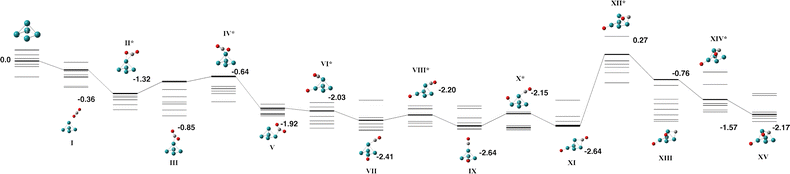
Ruthenium also has an even number of electrons and therefore we consider the singlet, triplet, quintet and septet multiplicities for the Ru₅ cluster. The Ru₅ cluster has been calculated previously by different authors and DFT methods,^62–65 but there is good agreement amongst researchers that the ground state structure of Ru₅ is a square pyramid structure with singlet multiplicity. We similarly identify a square pyramidal singlet structure with bond distances of 2.28 and 2.49 Å for the base–base and base–apex bonds respectively.

Two pathways were identified for the Ru₅ + CO₂ reaction, they are shown in Fig. 4 and 5. Corresponding geometric data is shown in Table S3. The singlet to nonet multiplicities were quite close in energy and so the pathway calculations were extended up to the 15-tet. The CO₂ molecule may approach either the apex ruthenium atom (Fig. 4) or one of the base ruthenium atoms (Fig. 5). In both cases, the first CO bond breaks with a barrier below the zero energy defined by E[Ru₅(singlet)] + E[CO₂], and leaving the CO molecule bound to the apex ruthenium atom. Two candidates for the global minimum Ru₅CO₂ structure are identified: The first structure has the CO molecule bound in a µ¹ geometry to the apex Ru atom and the dissociated oxygen atom µ¹-bound to a base Ru atom and in the Ru₄ plane. The second geometry has the CO molecule µ²-bound to the Ru(apex)–Ru(base) bond opposite the µ¹-bound oxygen atom. These two geometries are interconvertible by a transition state at −2.15 eV (i.e. a 0.49 eV barrier) with an imaginary frequency of 134i cm⁻¹. The barrier to dissociating the second CO bond is 0.27 eV above zero energy for the singlet pathway, but below zero energy for the triplet to the 13-tet multiplicities. The lowest energy structure identified with CO₂ completely dissociated has a µ¹ and a µ² oxygen atom and a µ²-bound carbon atom. This structure has an energy of −2.17 eV, 0.47 eV higher in energy than the Ru₅OCO global minima.

Fig. 4 Stationary points on the Ru₅ + CO₂ reaction pathway. The singlet potential energy surface is bolded and the triplet - 15-tet multiplicities are shown with thin lines. Relative energies are given in eV for the singlet multiplicity and included in the SI (xlsx) for all multiplicities. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

Fig. 5 Alternate reaction path on the Ru₅ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet - 15-tet multiplicities are shown with thin lines. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.4. Rh₅

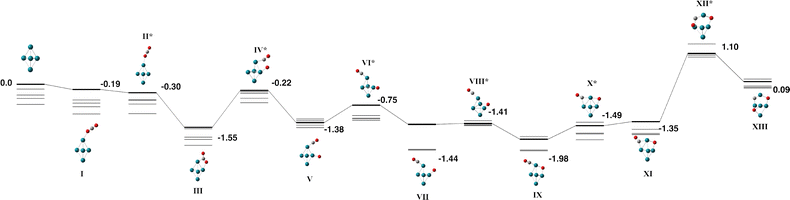
The Rh₅ cluster is an odd-electron species and therefore we consider the doublet – 12-tet multiplicities. Rhodium is of intense interest as a catalyst and many researchers have calculated the Rh₅ cluster. In an early study, Kelin and co-workers chose to model a trigonal bipyramid Rh₅, but did not investigate other geometries due to computational expense.⁶⁶ Rubio-Arroyo and coworkers predicted a twisted bowtie structure and two trigonal bipyramidal strucutres.⁶⁷ Aguilera-Granja et al. predict a square pyramidal Rh₅ cluster.⁶² Futschek et al. predict three Rh₅ isomers, a C_4v square pyramid and both a “tall” and a “flat” trigonal bipyramid structure, both of D_3h symmetry.⁶⁸ Similarly, Pederson and coworkers present a sextet square pyramid as the ground state, with a trigonal bipyramid being higher in energy at all spin multplicities.⁶⁹ Nguyen and Pham⁷⁰ and Poulain and coworkers,³² both employ a square pyramidal Rh₅ structure in their reactivity studies with N₂O.

Our initial search on the doublet surface, yielded a square pyramid ground state, but had a trigonal bipyramid structure only 0.12 eV higher in energy. Re-optimizing these structures at higher multiplicities (up to the 12-tet) showed that the sextet square pyramid was the lowest energy Rh₅ structure and that it is isoenergetic with the sextet and octet trigonal bipyramid structures. Therefore both square pyramid and trigonal bipyramid structures were considered for reaction with CO₂. In the reaction pathways below, pathways for the doublet – decet surfaces are presented as the 12-tet was higher in energy.

3.4.1. Square pyramidal Rh₅. Two pathways are shown for the square pyramid Rh₅ in Fig. 6 and 7 with geometric data in Table S4, it is possible to interconvert between them. The two pathways illustrate two “choices”: Firstly, the capture species, when the CO₂ molecule first binds to the Rh₅ cluster, may employ either a base rhodium atom (Fig. 7) or an apex atom (Fig. 6). Either of these capture species leads to a bent CO₂ molecule bound to a Rh(apex)–Rh(base) bond, which is the lowest energy structure (Fig. 7-III and 6-III) at −1.61 eV. From this structure, the CO₂ molecule may break resulting in the CO molecule bound to the base rhodium atom (Fig. 7) with an energy of −1.06 eV, or leave the CO molecule bound to the apex rhodium atom (Fig. 6), where the barrier energy is −0.26 eV. This pathway leads to a structure (Fig. 6-VII), with CO µ²-bound to an Rh(apex)–Rh(base) bond and the dissociated oxygen atom µ¹-bound to an adjacent Rh(base) atom, this structure is effectively isoenergetic with the bent CO₂ structure, Fig. 6-III. On either pathway, further dissociating the remaining CO molecule faces a high barrier, 1.20 or 1.92 eV above zero energy, indicating that CO₂ dissociation into three separate atoms is unlikely to occur on this cluster.

Fig. 6 Stationary points on the Rh₅ + CO₂ potential energy surface for the square pyramidal Rh₅ isomer. Doublet multiplicity is shown in bold and the quartet – decet multiplicities are shown with thin lines. Relative energies of doublet geometries are given in eV and included for all multiplicities in the SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

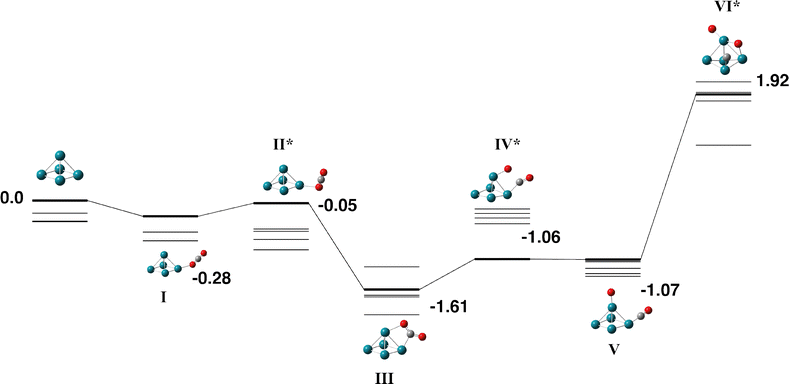Fig. 7 Alternate pathway on the Rh₅ + CO₂ potential energy surface for the square pyramidal Rh₅ isomer. In this pathway, the first CO bond breaking in transition state VI leaves the CO molecule attached to the base Rh atom. The doublet multiplicity is shown in bold and the quartet – decet multiplicities are shown with thin lines. The final transition state leads to the same final structure as Fig. 6 as the CO breaks across the triangular Rh₃ face. Relative energies are given in eV. Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.4.2. Trigonal bipyramidal Rh₅. A single pathway is presented for the reaction of trigonal bipyramid Rh₅ + CO₂ in Fig. 8 and Table S5. The features of the pathway are broadly similar to that of the square pyramidal pathways shown in Fig. 6 and 7. The CO₂ molecule approaches an apex rhodium atom, a bent CO₂ molecule lies across a Rh(apex)–Rh(equatorial) bond (Fig. 8-III), the first CO bond breaks leaving the CO molecule bound to an apex rhodium atom, leading to the lowest energy structure, Fig. 8-IX at −1.98 eV, where the oxygen atom is µ²-bound to a Rh(apex)–Rh(equatorial) bond and the CO molecule is µ¹-bound to an apex rhodium atom. Breaking the second CO bond requires 1.10 eV above zero energy.

Fig. 8 Reaction pathway for trigonal bipyramidal Rh₅ + CO₂. The doublet multiplicity is shown in bold and the quartet – decet multiplicities are shown with thin lines. Relative energies shown are for the doublet surface and are given in eV, relative energies for all multiplicities are included in the SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.5. Pd₅

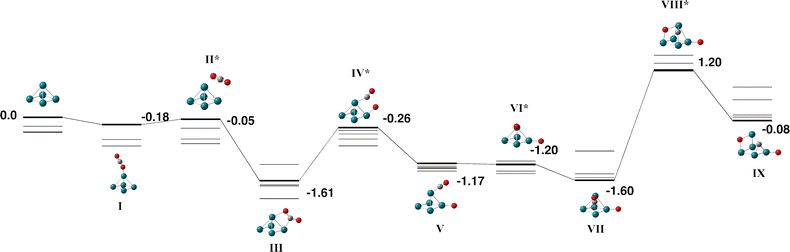
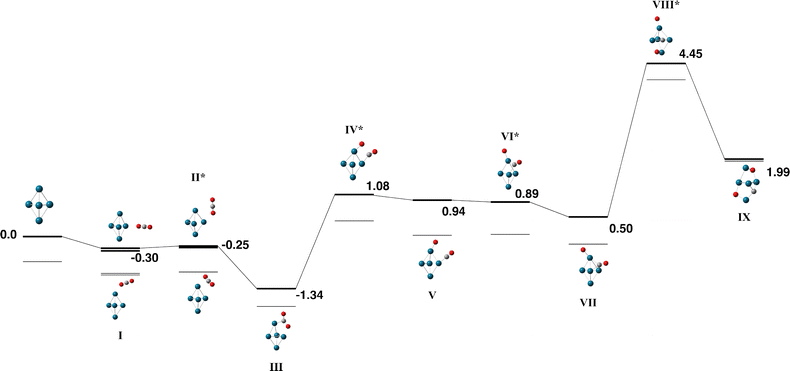
The Pd₅ cluster is an even-electron species and therefore we consider the singlet – septet multiplicities. Small Pd clusters have also been calculated by a variety of different methods over many years: Morokuma and coworkers predicted a Pd₅ ground state of a triplet trigonal bipyramid Pd₅ structure with D_3h symmetry but noted a C_2v trigonal bipyramid only 0.4 kcal mol⁻¹ higher in energy, and also a triplet C_4v square pyramid only 2.3 kcal mol⁻¹ higher in energy.⁷¹ Several other authors predict a triplet trigonal bipyramid structure.^72–76 Our search also identified a triplet trigonal bipyramid as the global minimum, and while we did not constrain symmetry, the structure has C_2v symmetry. We did also identify the square pyramidal structure, the triplet was the lowest energy multiplicity for this structure and was 0.11 eV higher than the triplet trigonal bipyramid. While these two structures are sufficiently close in energy such that they are likely to coexist, we choose only the trigonal bipyramid to react with CO₂.

The Pd₅ + CO₂ reaction pathway is shown in Fig. 9 and Table S6, the quintet and septet pathways were high in energy and so only the singlet and triplet are shown. The capture species and adjacent transition state (structures Fig. 9-I and II) are shown for both an apex atom approach and an equatorial atom approach. Both approaches result in a bent CO₂ molecule weakly bound to the central Pd(apex)–Pd(equatorial) bond with a binding energy of −1.34 eV relative to the zero energy. This is the global minimum structure for the pathway, breaking the first of the two CO bonds requires +1.08 eV and the barrier to breaking the second CO bond is +4.45 eV.

Fig. 9 Stationary points on the Pd₅ + CO₂ potential energy surface. The singlet multiplicity is shown in bold and the triplet multiplicity is shown with thin lines. Relative energies corresponding to singlet geometries are given in eV, all relative energies are included in SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.6. Pt₅

The 5d transition metal, platinum was also studied due to its intense interest and frequent use as a catalyst. The Pt₅ cluster is studied at the singlet – septet multiplicities. A variety of structures have been obtained for the Pt₅ cluster with significant differences in predicted energetics and several authors debating whether the cluster is planar or three-dimensional.⁷⁷ Sumer and Jellinek identified several Pt₅ low-energy isomers, including a planar edge-capped square, trigonal bipyramid, edge-capped tetrahedron, square pyramid, planar trapezoidal and planar bowtie. On inclusion of spin–orbit effects, only the first three structures remained.⁶⁰ Kleinman and coworkers also studied the effect of spin–orbit coupling identifying the planar edge-capped square, followed by square pyramid, trigonal bipyramid, trapezoidal and bowtie structures.⁷⁸ Wang et al. identified a quintet trigonal bipyramid as their gas-phase global minimum.⁷⁹ Sebetci predicts a edge-capped tetrahedron global minimum, followed by a distorted rhombus, a trigonal bipyramid, a bowtie and trapezoidal structures.⁸⁰ Grönbeck and Andreoni noted that the class of density functional had a strong effect on the predicted isomer, with a planar edge-capped square favoured by BLYP whereas a distorted square pyramid was predicted by LSDA.⁸¹ Singh et al. and Kumar and Kawazoe both predict the planar edge-capped square as the global minimum,^82,83 but Cao identified a square pyramidal structure as the basis of their reactivity study.⁸⁴ MRSDCI calculations of Majumdar et al. identified a distorted tetragonal pyramid.⁸⁵

3.6.1. Trigonal bipyramidal Pt₅. In our search on the singlet surface, we identified bent trapezoidal, twisted bowtie, trigonal bipyramid and square pyramid structures all within 0.05 eV. The trigonal bipyramid and square pyramid structures were chosen to react with CO₂ and are shown in Fig. 10 and 11 respectively. Geometric data for both pathways is tabulated in Tables S7 and S8. Somewhat analogously to the Pd₅ + CO₂ reaction, the lowest energy Pt₅CO₂ structure at −1.67 eV has a bent CO₂ molecule bound to a Pt(apex)–Pt(equatorial) bond. This minimum could convert via a structure with µ²-bound CO and a µ¹-bound oxygen atom (structure Fig. 10-V) (−0.77 eV) to a low-energy (−1.50 eV) structure (Fig. 10-VII) with the CO molecule µ¹-bound to an equatorial platinum atom and the dissociated oxygen atom µ¹-bound to an apex platinum atom. From that structure, dissociating the CO molecule has a barrier of +3.85 eV, and the product is also higher than zero energy by +2.67 eV. This is consistent with the IR-MPD + DFT study of Green et al., who did not observe CO₂ frequencies in their [Pt₅CO₂]⁻, but did observe a band at 1980 cm⁻¹, which they assigned to η¹-bound CO.⁵²

Fig. 10 Stationary points on the Pt₅ + CO₂ potential energy surface beginning with the trigonal bipyramidal Pt₅ isomer. The singlet multiplicity is shown in bold and the triplet – septet multiplicities are shown with thin lines. Relative energies for the singlet surface are given in eV, relative energies for all multiplicities are included in SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

Fig. 11 Stationary points on the Pt₅ + CO₂ potential energy surface for the square pyramidal Pt₅ isomer. The singlet multiplicity is shown in bold and the triplet – septet multiplicities are shown with thin lines. Singlet relative energies are given in eV, other multiplicities are included in SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.6.2. Square pyramidal Pt₅. The pathway for the reaction of CO₂ to the square pyramidal isomer of Pt₅ is shown in Fig. 11 and Table S8. The CO₂ molecule approaches the apex platinum atom before twisting over a triangular face of the cluster (structure Fig. 11-III, −0.84 eV). Breaking the first CO bond requires +0.25 and +0.14 eV on the singlet and triplet surfaces, but is exothermic by −0.09 and −0.53 eV for the triplet and septet surfaces respectively. The lowest energy structure, Fig. 11-V, at −0.88 eV, has the CO molecule µ²-bound across a Pt(apex)–Pt(base) bond and the dissociated oxygen atom µ¹-bound to a platinum atom on the base of the cluster. Attempting to continue the pathway search to break the second CO bond resulted in the Pt₅ cluster deforming to a trigonal bipyramid, applying constraints to the Pt₅ coordinates resulted in structures with multiple imaginary frequencies. The fluxional nature of small transition metal complexes is well known, and it is not unexpected that these two Pt₅ clusters may interconvert.

3.7. Ag₅

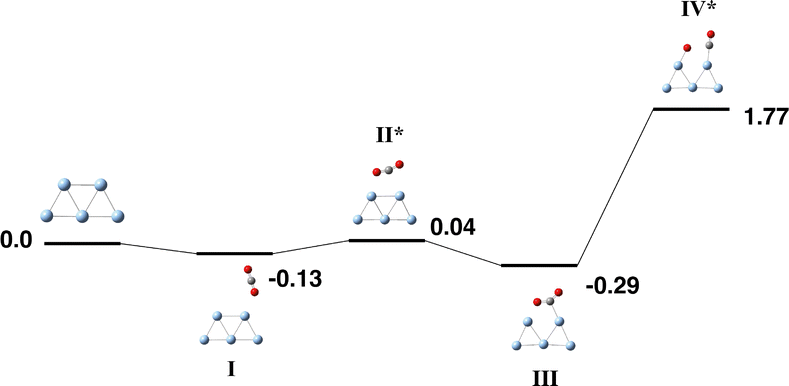
The Ag₅ cluster is an odd-electron species and we consider the doublet – octet multiplicities. Atolabi et al. conducted one of several studies into the gas-phase Ag₅ structure and predicted that the doublet planar trapezoidal structure was 0.49 eV lower in energy than the doublet trigonal bipyramid structure.⁸⁶ The B3PW91 calculations of Hisayoshi and coworkers predicted a similar energy difference of 0.53 eV.⁸⁷ Fournier,⁸⁸ Wang and coworkers,⁸⁹ and Koutecký and coworkers all predict a C_2v doublet trapezoidal structure.⁹⁰ Fazli and coworkers also employed a trapezoidal Ag₅ cluster in their DFT study. Recent synthetic advances have produced a ligand-free trigonal bipyramid Ag₅ cluster,⁹¹ which has been tested as an anti-tumour agent.⁹² The same cluster was employed by Atolaibi et al. in their DFT-study with CO₂, CH₄, and H₂O molecules. While these authors considered the trapezoidal Ag₅ isomer for reaction with CH₄ and indicated that the trapezoidal isomer was more stable, they only calculated the trigonal bipyramid for their calculations with CO₂, showing weak interaction of the CO₂ molecule with both the apex and equatorial silver atoms.⁹³

The trapezoidal Ag₅ structure was chosen as the basis for the reaction path search, and the resulting pathway for the reaction of Ag₅ + CO₂ is shown in Fig. 12 with geometric data tabulated in Table S9. The doublet surface only is presented as all higher multiplicities were more than 1 eV higher in energy. CO₂ interacts only very weakly with the Ag₅ cluster, the capture species has the CO₂ molecule interacting with one of the atoms on the short edge of the trapezoid and is only −0.13 eV below zero energy. Only one other structure, Fig. 12-III was below zero energy, with an energy of −0.29 eV. Attempting to break the first CO₂ bond requires +1.77 eV. Searches were made for structures with the CO₂ molecule dissociated (e.g. CO + O, C + 2(O)), and an IRC was started from the transition state Fig. 12-IV, but in all these calculations the Ag₅ cluster did not remain intact and therefore we did not continue the reaction path.

Fig. 12 Reaction pathway for the Ag₅ + CO₂ doublet potential energy surface. Other multiplicities are high in energy and are not shown. Relative energies are given in eV, and are included for higher multiplicities in the SI (xlsx). Metal atoms are shown in blue/green, oxygen atoms are shown in red and the carbon atom is shown in grey.

3.8. Periodic trends

A previous computational study on the reaction of carbon monoxide, CO, with second-row transition metal timers showed that capture species were very similar in energy across the periodic table, with the exception of silver clusters, which bound CO only weakly.³¹ This was observed similarly here for the M₅ clusters with CO₂, and is shown in Fig. 13. The consistent energy of the capture species can be rationalized in both cases that the capture species is defined as the first interaction of the two species and represents physisorption, where the chemical/electronic structure of the two species is barely perturbed. This is also consistent with the axial and equatorial, or apex and base capture species having similar interaction energies, where both were identified for the one M₅ cluster.

Fig. 13 Plot of the relative energies of capture, lowest energy associative (OCO), lowest energy partly dissociated (O,CO) and fully dissociative (O,C,O) structures of M₅ metal clusters in the lowest possible multiplicity.

In the previous study of the interaction of M₃ + CO, there were only two other species of interest, the associative and dissociatively bound species.³¹ In the case of CO₂ as a reactant, there are now three species of interest: the lowest energy bound OCO, the lowest energy O + CO and the lowest energy fully dissociated 2(O) + C structure. The energies of the associatively bound OCO species are relatively similar across the periodic table, ranging from −2.463 eV (Nb₅) to −1.340 eV (Pd₅), the two exceptions were Ag₅, which binds weakly, with a Ag₅⋯OCO binding energy of only −0.289 eV, and Mo₅, where CO₂ molecule dissociates via interaction with the axial atom of the cluster only. In structure Fig. 3-II, the C⋯O distance is 1.80 Å and the θ_OCO angle is 122°. The lowest energy associative structure for Mo₅CO₂ is therefore the capture species.

Similar trends are observed for the energies of the partly dissociative (O + CO) and fully dissociative (2(O) + C) structures. Both energies rise moving left to right across the second row of transition metals (Nb–Ag). The M₅O + CO energies become disfavourable (positive) for Pd₅, while the fully dissociated structures are disfavoured to the right of Rh₅ inclusive. The lone third row pentamer in this study, Pt₅, favourably dissociates CO₂ to CO + O, but the fully dissociative structure is disfavoured with respect to the zero energy, Pt₅ + CO₂.

Table 1 shows the calculated vibrational frequencies of CO₂ in the capture species for each M₅ cluster. The two bending frequencies, now non-degenerate, are red-shifted by ≈60 cm⁻¹, but no trend was observed for this reduction. The frequencies of the symmetric and asymmetric CO₂ stretches do not change significantly on interaction with the M₅ cluster. To attempt a diagnostic for the fate of CO₂, the energy of the CO₂ π_u orbital and the ΔE, with respect to the calculated value for free CO₂ (−0.03280 a.u.) is also shown in Table 1. For Nb₅ and Mo₅, a strong reduction in the orbital energy of ≈0.05 a.u. is observed. Both of these clusters dissociate CO₂ fully. All other M₅ clusters lowered the CO₂ π_u orbital energy by ≈0.02 a.u. and no distinction between clusters that possess a fully intact CO₂ in their minimum energy structure vs. clusters that partly dissociate CO₂ to O + CO was observed. Nevertheless, the orbital energy does indicate those clusters that fully dissociate CO₂ into atoms.

Table 1 CO₂ vibrational frequencies (ν_CO2), key orbital energies and adsorption and interaction energies for M₅CO₂ capture species. Absolute energy of the CO₂ π_u orbital is −0.893 eV (−0.03280 a.u)

System	Bend 1	Bend 2	Symm stretch	Asym stretch	E(M5,HOMO)	E(M5,LUMO)	E(πu)	ΔE(πu)	Eads	Eint
	(cm^−1)				(eV)
CO2	622	622	1283	2319			−0.893	0.0
Nb5	554	577	1277	2341	−4.332	−2.730	−2.351	−1.458	−0.483	−0.484
Mo5	560	560	1279	2340	−4.388	−2.406	−2.383	−1.491	−0.438	−0.439
Ru5 apex	521	557	1259	2323	−5.655	−2.817	−1.394	−0.502	−0.361	−0.370
Ru5 base	462	585	1254	2326	−4.637	−2.808	−1.476	−0.583	−0.462	−0.466
Rh5 sq. py.	546	571	1268	2325	−4.970	−3.471	−1.455	−0.563	−0.282	−0.452
Rh5 tri. bipy.	528	571	1266	2328	−5.028	−3.226	−1.446	−0.554	−0.188	−0.499
Pd5 a	583	587	1281	2326	−5.304	−4.239	−1.512	−0.620	−0.301	−0.346
Pd5 b	581	587	1278	2325	−5.373	−4.252	−1.609	−0.716	−0.368	−0.369
Ag5	593	605	1281	2314	−5.074	−2.813	−1.379	−0.487	−0.133	−0.133
Pt5 tri. bipy.	552	564	1277	2336	−5.606	−4.416	−1.742	−0.849	−0.516	−0.547
Pt5 sq. py.	551	570	1261	2310	−5.466	−4.272	−1.536	−0.643	−0.360	−0.377

---

Table 2 shows the Hirshfeld charges on CO₂ molecule in the capture species and the first transition state for each of the reaction pathways. The q(CO₂) for the physisorbed capture species, as in the previously presented M₄ clusters,³⁹ is consistent and positive (≈0.1) for all M₅ clusters, except Ru₅ with CO₂ bound to the apex atom, suggesting that this species is actually a chemisorbed species. Considering the charge transfer observed in the first transition state, the same diagnostic holds for M₅ clusters also as the M₄ clusters; For the left-most three clusters, full CO₂ dissociation is thermodynamically possible, though for Ru₅, this would require surmounting a +0.27 eV barrier on the singlet surface, but a below zero energy barrier on higher multiplicity surfaces (see SI spreadsheet for details) having q(CO₂) < −0.35 e⁻. Right-most clusters, Pd₅ and Ag₅, do not dissociate either CO₂ bond and have low back-donation to CO₂, < 0.2e⁻, and clusters that likely activate CO₂ without fully dissociating it, Rh₄, Pt₄, have intermediate q(CO₂) values.

Table 2 Hirshfeld charge on CO₂ in capture species and first transition state for M₅CO₂ reaction pathways

System	Capture species q(CO2)	TS 1 q(CO2)
Nb5	0.142	−0.418
Mo5	0.118	−0.494
Ru5 apex	−0.381	−0.3747
Ru5 base	0.098	−0.434
Rh5 sq. py.	0.094	−0.336
Rh5 tri. bipy.	0.106	−0.314
Pd5 a	0.086	0.037
Pd5 b	0.088	0.008
Ag5	0.043	−0.112
Pt5 tri. bipy.	0.121	−0.247
Pt5 sq. py.	0.095	−0.332

---

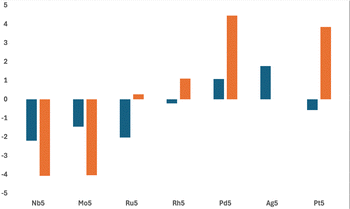
Fig. 14 shows the barrier heights (transition state energies) for two key transition states in each pathway, corresponding to the breaking of the first and second CO bond. The trends seen are broadly similar to the equivalent M₄ clusters.³⁹ The left-right divide previously seen for both barriers between Ru/Rh, is slightly less clear for the M₅ clusters, with both Ru₅ and Rh₅ being likely to break the first CO bond, but not the second. The softer barriers for Pt₅ compared to Pd₅ also suggest that the first CO bond would break on this cluster, leading to O + CO products on the cluster surface in this case also. Han and coworkers studied a range of mono and bimetallic metal surfaces and made similar conclusions, that activation energies for CO₂ dissociation increase left to right across the periodic table, with Au, Ag, and Pd based alloys having CO₂ dissociation barriers >1.50 eV.¹⁸

Fig. 14 Plot of the relative energies of barriers to dissociation of the first (blue) and second (orange) C⋯O bonds for M₅CO₂ reaction pathways on the lowest multiplicity (singlet or doublet) surface.

3.9. M₄ vs. M₅ clusters

Each reaction path presented here and for the equivalent M₄ clusters³⁹ may be distilled into a profile containing six species; the capture species, lowest energy M_nCO₂, TS_O⋯CO, lowest energy M_nO·CO, TS_C⋯O and lowest energy M_nO·C·O. These abbreviated reaction profiles are shown in Fig. S1–S7. Reactions on M₅ surfaces are typically more exothermic than the equivalent M₄ clusters. Excluding palladium, increasing the cluster size lowers the energy of the first barrier by ≈0.5 eV. This is consistent with the B3LYP results for Zr₄ and Zr₅ clusters computed by Ghanty and coworkers.³³ The height of the second barrier on adding the fifth metal atom is less consistent, lowering for Nb, Mo and Rh, but rising for the other metals. This is consistent with the left hand metals (Nb, Mo) dissociating CO₂ fully, right side metals (Pd, Ag, Pt) keeping CO₂ intact, and central metals (Ru, Rh) showing intermediate behaviour, which is therefore the most tunable by alteration of the cluster size.

4. Conclusions

We have explored the chemistry of CO₂ reaction on a series of M₅ transition metal clusters, by deriving reaction pathways using Density Functional Theory. Rh₅ and Pt₅ clusters had multiple competitive ground state geometries, and reaction paths were derived for each, noting that the trigonal bipyramid and square pyramidal geometries may interconvert.

Moving from left to right across the M₅ series, the energies of the capture species remained relatively constant as expected for the minimally interacting, physisorbed species. The energies of the lowest energy associatively-bound species with CO₂ fully intact also fell within a narrow range of −2.463 to −1.340 eV, generally rising from Nb₅ to Ag₅. The energetics of the partly (O + CO), and fully (O + C + O) dissociated species define the outcome of the reaction, with both rising strongly as one moves to the right of the periodic table. The partly dissociated species was found to be disfavoured with respect to the separated M₅ +CO₂ reactants for Pd₅, Ag₅ and Pt₅, while the fully dissociated species was disfavoured from Rh₅ and could not be located for Ag₅.

The energy of the CO₂ π_u orbital was found to distinguish those structures that dissociate CO₂ fully (Nb₅ and Mo₅) from those that do not, but could not resolve clusters that partly dissociate CO₂ from those that leave CO₂ fully intact. The magnitude of charge transfer to the CO₂ fragment was found to be diagnostic with strong (>0.35e), weak (<0.2e) and intermediate values indicating full CO₂ dissociation, no dissociation, and activation respectively.

Author contributions

NTTY, AN, YR, MR, IN: investigation, writing – original draft MAA: conceptualization of this study, methodology, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: geometric parameters (pdf), structures (xyz) and energies, vibrational data (xlsx) for all pathways. See DOI: https://doi.org/10.1039/d5cp03418c.

Acknowledgements

MAA is grateful for HPC time via the UK Materials and Molecular Modelling Hub via grant no. (EP/T022213).

References

1. Y. Peng, J. Gao, Y. Zhang, J. Zhang, Q. Sun, Q. Du, Z. Tang and T. Zhang, J. Energy Storage, 2023, 58, 106286.
2. X. Zhang, G. Liu, K.-H. Meiwes-Broer, G. Ganteför and K. Bowen, Angew. Chem., Int. Ed., 2016, 55, 9644–9647.
3. Z. Yang, C. Yue, W. Pang, H. Wang, X. Cong, S. Huang, J. Qi, J. Lv, M.-Y. Wang and X. Ma, Chem. Eng. Sci., 2025, 317, 122104.
4. M. Aresta, A. Dibenedetto and E. Quaranta, Reaction Mechanisms in Carbon Dioxide Conversion, Springer Berlin, Heidelberg, 2015, pp. 1–409.
5. T. Sakakura, J.-C. Choi and H. Yasuda, Chem. Rev., 2007, 107, 2365–2387.
6. J. M. Weber, Int. Rev. Phys. Chem., 2014, 33, 489–519.
7. M. C. Thompson, J. Ramsay and J. M. Weber, J. Phys. Chem. A, 2017, 121, 7534–7542.
8. T. Foyen, Z. P. Alcorn, M. A. Ferno, A. Barrabino and T. Holt, J. Pet. Sci. Eng., 2021, 196, 107651.
9. X. Meng, L. Zhao, H. Guo, F. Sha, H. Shi, Z. Wu and J. Zhang, Crystals, 2019, 9, 433.
10. R. Shahbaz and F. Bahadori, Sustain. Chem. Pharm., 2025, 46, 102099.
11. S. Kumari, M. Gusain, B. Y. Lamba and S. Kumar, J. Mater. Chem. A, 2025, 13, 21352–21388.
12. J. Jang, E. P. Delmo, W. Chen, Z. Sun, D. H. C. Wan, Y. Liu, S. Zhu, Y. Wang, T. Li, H. Huang, J. Ge and M. Shao, Carbon Energy, 2025, e70019.
13. Y. Ren, H. Liu, F. Duan, S. Lu, X. Chen and M. Du, J. Mater. Chem. A, 2025, 13, 24988.
14. B. Liu, J. A. Wang and D. Niu, Carbon, 2025, 243, 120562.
15. Y.-X. Yu, J. Colloid Interface Sci., 2025, 695, 137799.
16. Á. Morales-Garca, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385.
17. I. Persson, J. Halim, H. Lind, T. W. Hansen, J. B. Wagner, L.-Å. Näslund, V. Darakchieva, J. Palisaitis, J. Rosen and P. O. Å. Persson, Adv. Mater., 2019, 31, 1805472.
18. J. Ko, B.-K. Kim and J. W. Han, J. Phys. Chem. C, 2016, 120, 3438–3447.
19. J. Yang, L. Sun, Z. He, W. Xu and J. Peng, J. Mater. Sci., 2025, 60, 4669–4686.
20. A. Jurado, K. Ibarra, Á. Morales-Garca, F. Viñes and F. Illas, ChemPhysChem, 2021, 22, 2456–2463.
21. J. Li, J. Jia, X. Wang, X. Wang, J. Wang, C. Zhang, Y. Bai and X. Zhang, Appl. Surf. Sci., 2025, 710, 163887.
22. V. K. Ocampo-Restrepo, L. Zibordi-Besse and J. L. F. Da Silva, J. Chem. Phys, 2019, 151, 214301.
23. J. M. Weber, Int. Rev. Phys. Chem., 2014, 33, 489–519.
24. H. Liu, L. An, P. Wang, C. Yu, J. Zhang, H. Shin, B. Peng, J. Li, M. Li, H. An, J. Yu, Y. Chen, P. Wang, K.-S. Lee, K. Lalit, Z. Liu, O. K. Farha, W. Huang, J. Z. Liu, L. Qi, K. Xie and E. H. Sargent, Nat. Commun., 2025, 16, 6185.
25. H. Schwarz, Coord. Chem. Rev., 2017, 334, 112–123.
26. M. Sievers and P. Armentrout, Int. J. Mass Spec., 1998, 179–180, 103–115.
27. A. M. Ricks, A. D. Brathwaite and M. A. Duncan, J. Phys. Chem. A, 2013, 117, 11490–11498.
28. Z. Zhao, X. Kong, D. Yang, Q. Yuan, H. Xie, H. Fan, J. Zhao and L. Jiang, J. Phys. Chem. A, 2017, 121, 3220–3226.
29. A. Iskra, A. S. Gentleman, A. Kartouzian, M. J. Kent, A. P. Sharp and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 133–140.
30. M. C. Thompson, L. G. Dodson and J. M. Weber, J. Phys. Chem. A, 2017, 121, 4132–4138.
31. M. A. Addicoat, M. A. Buntine, B. Yates and G. F. Metha, J. Comput. Chem., 2008, 29, 1497–1506.
32. O. Olvera-Neria, R. Avilés, H. Francisco-Rodrguez, V. Bertin, R. Garca-Cruz, J. C. González-Torres and E. Poulain, J. Mol. Mod., 2015, 21, 80.
33. Megha, K. Mondal, A. Banerjee and T. K. Ghanty, Phys. Chem. Chem. Phys., 2020, 22, 16877–16886.
34. M. N. Collacique, V. K. Ocampo-Restrepo and J. L. F. Da Silva, J. Chem. Phys, 2022, 156, 124106.
35. V. K. Ocampo-Restrepo, L. G. Verga and J. L. F. Da Silva, J. Phys. Chem. C, 2021, 125, 26296–26306.
36. A. Yamada, K. Miyajima and F. Mafune, Phys. Chem. Chem. Phys., 2012, 14, 4188–4195.
37. P. C. D. Mendes, V. K. Ocampo-Restrepo and J. L. F. Da Silva, Phys. Chem. Chem. Phys., 2020, 22, 8998–9008.
38. A. E. Green, J. Justen, W. Schöllkopf, A. S. Gentleman, A. Fielicke and S. R. Mackenzie, Angew. Chem., Int. Ed., 2018, 57, 14822–14826.
39. S. Sherif, B. A. Velmurugan, N. Abbas, M. Shaikh and M. A. Addicoat, Phys. Chem. Chem. Phys., 2025, 27, 1.
40. M. A. Addicoat and G. F. Metha, J. Comput. Chem., 2009, 30, 57–64.
41. M. A. Addicoat, S. Fukuoka, A. J. Page and S. Irle, J. Comput. Chem., 2013, 34, 2591–2600.
42. A. D. Becke, J. Chem. Phys, 1993, 98, 5648–5652.
43. P. J. Hay and W. R. Wadt, J. Chem. Phys, 1985, 82, 270–283.
44. W. R. Wadt and P. J. Hay, J. Chem. Phys, 1985, 82, 284–298.
45. P. J. Hay and W. R. Wadt, J. Chem. Phys, 1985, 82, 299–310.
46. M. A. Addicoat, K. F. Lim and G. F. Metha, J. Chem. Phys, 2012, 137, 034301.
47. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
48. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
49. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
50. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
51. E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2019, 21, 13959–13967.
52. G. Meizyte, A. E. Green, A. S. Gentleman, S. Schaller, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2020, 22, 18606–18613.
53. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian-16 Revision B.01, 2016, Gaussian Inc., Wallingford CT.
54. L. Goodwin and D. R. Salahub, Phys. Rev. A, 1993, 47, R774–R777.
55. J. Del Pla and R. Pis Diez, J. Phys. Chem. C, 2016, 120, 22750–22755.
56. M. Ziane, F. Amitouche, S. Bouarab and A. Vega, J. Nano. Res., 2017, 19, 380.
57. Y.-H. Yin and J. Chen, Comput. Theor. Chem., 2022, 1212, 113720.
58. C. J. Pickard and R. J. Needs, J. Phys. Cond. Mat., 2011, 23, 053201.
59. Y. Wei, V. Veryazov and L. Kantorovich, APL Mater., 2024, 12, 031127.
60. A. Sumer and J. Jellinek, J. Chem. Phys, 2022, 157, 034301.
61. L. Xue-Ling, Chin. Phys. B, 2010, 19, 107103.
62. F. Aguilera-Granja, L. C. Balbás and A. Vega, J. Phys. Chem. A, 2009, 113, 13483–13491.
63. Y.-C. Bae, H. Osanai, V. Kumar and Y. Kawazoe, Mater. Trans., 2005, 46, 159–162.
64. W. Zhang, H. Zhao and L. Wang, J. Phys. Chem. B, 2004, 108, 2140–2147.
65. G.-X. Ge, H.-X. Yan, Q. Jing and Y.-H. Luo, J. Cluster Sci., 2011, 22, 473–489.
66. Y. Jinlong, F. Toigo and W. Kelin, Phys. Rev. B, 1994, 50, 7915–7924.
67. M. A. Mora, M. A. Mora-Ramírez and M. F. Rubio-Arroyo, Int. J. Quant. Chem., 2010, 110, 2541–2547.
68. T. Futschek, M. Marsman and J. Hafner, J. Phys. Condens. Matter, 2005, 17, 5927.
69. C.-H. Chien, E. Blaisten-Barojas and M. R. Pederson, Phys. Rev. A, 1998, 58, 2196–2202.
70. H. M. T. Nguyen and N. T. T. Pham, J. Phys. Chem. C, 2014, 118, 28562–28571.
71. J. Moc, D. G. Musaev and K. Morokuma, J. Phys. Chem. A, 2003, 107, 4929–4939.
72. X. Xing, A. Hermann, X. Kuang, M. Ju, C. Lu, Y. Jin, X. Xia and G. Maroulis, Sci. Rep., 2016, 6, 19656.
73. V. Kumar and Y. Kawazoe, Phys. Rev. B, 2002, 66, 144413.
74. M. Moseler, H. Häkkinen, R. N. Barnett and U. Landman, Phys. Rev. Lett., 2001, 86, 2545–2548.
75. B. Kalita and R. C. Deka, J. Chem. Phys, 2007, 127, 244306.
76. Y. Mu, Y. Han, J. Wang, J.-G. Wan and G. Wang, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 053201.
77. L. Xiao and L. Wang, J. Phys. Chem. A, 2004, 108, 8605–8614.
78. M. N. Huda, M. K. Niranjan, B. R. Sahu and L. Kleinman, Phys. Rev. A, 2006, 73, 053201.
79. Y. Wang, B. Xiang, H.-Q. Yang and C.-W. Hu, ACS Omega, 2017, 2, 3250–3259.
80. A. Sebetci, Chem. Phys., 2006, 331, 9–18.
81. H. Grönbeck and W. Andreoni, Chem. Phys., 2000, 262, 1–14.
82. N. B. Singh and U. Sarkar, J. Mol. Mod., 2014, 20, 2537.
83. V. Kumar and Y. Kawazoe, Phys. Rev. B, 2008, 77, 205418.
84. P. Cao and H. Wang, J. Phys. Conf. Ser., 2021, 1992, 032151.
85. D. Majumdar, D. Dai and K. Balasubramanian, J. Chem. Phys., 2000, 113, 7928–7938.
86. M. Alotaibi, Q. Wu and C. Lambert, Appl. Surf. Sci., 2023, 613, 156054.
87. T. Yumura, M. Kumondai, Y. Kuroda, T. Wakasugi and H. Kobayashi, RSC Adv., 2017, 7, 4950–4959.
88. R. Fournier, J. Chem. Phys., 2001, 115, 2165–2177.
89. Y. Wang and X. G. Gong, Eur Phys. J. D, 2005, 34, 19–22.
90. V. Bonačič-Koutecký, L. Češpiva, P. Fantucci and J. Koutecký, J. Chem. Phys., 1993, 98, 7981–7994.
91. I. R. Arias, D. Buceta, G. Barone, M. C. Giménez-López, H. Lozano, M. Lazzari and M. Arturo López-Quintela, J. Colloid Interface Sci., 2022, 628, 437–447.
92. V. Porto, D. Buceta, B. Domínguez, C. Carneiro, E. Borrajo, M. Fraile, N. Davila-Ferreira, I. R. Arias, J. M. Blanco, M. C. Blanco, J. M. Devida, L. J. Giovanetti, F. G. Requejo, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, G. Barone, A. M. James, T. García-Caballero, D. M. González-Castaño, M. Treder, W. Huber, A. Vidal, M. P. Murphy, M. A. López-Quintela and F. Domínguez, Adv. Func. Mater., 2022, 32, 2113028.
93. M. Alotaibi, T. Alotaibi, M. Alshammari and A. K. Ismael, Crystals, 2023, 13, 1691.

---