Covalent bonding and extreme shielding in xenon–icosagen fluoride cations

Abstract

Although icosagen cations are known to interact significantly with noble gases, well-defined examples exhibiting strong binding energies indicative of covalent character, particularly for the heavier icosagens, remain scarce. In this work, we explore the stability and bonding of a series of XeMF₂⁺ and Xe₂MF₂⁺ (M = B–Tl) cations, focusing on global-minimum structures featuring Xe–M bonds. Ab initio calculations indicate that these species are thermodynamically viable at 298 and 398 K, with all considered dissociation pathways being endergonic. Bonding analyses reveal strong covalent Xe–icosagen interactions for B, Al, and Ga, while In and Tl exhibit weaker bonding character that suggests more ionic interactions, as supported by the selected complementary analyses. Fluoride ion affinities and relativistic ¹²⁹Xe NMR chemical shifts further support the strong electron-withdrawing nature of the MF₂⁺ cations. Overall, the results suggest that, beyond the previously reported XeBF₂⁺, Xe–icosagen compounds such as XeAlF₂⁺ and XeGaF₂⁺ may also be experimentally accessible.

---

Introduction

The synthesis, characterization, and theoretical prediction of noble-gas (Ng) compounds have long posed a scientific challenge. The long-held assumption of Ng chemical inertness was overturned in 1962,^1–3 and since then, Ng chemistry has evolved into a dynamic field of experimental and theoretical research.^4–8 While compounds of heavier Ngs such as Kr, Xe, and Rn can be stabilized under relatively mild conditions (despite the high radioactivity of Rn), those of He, Ne, and Ar require extreme conditions, such as cryogenic temperatures or very high pressures.^9,10 Most known Ng compounds involve halogen or oxygen, but a broader range of elements, including the icosagens (Group-13), can also form neutral or cationic species incorporating Ngs. This reactivity is often driven by a combination of suitable electronegativity and electron-donation capabilities.

In recent years, there has been growing interest in compounds featuring covalent Ng–B bonds.^11–24 Several boron-containing cations, such as NgBF₂⁺,²⁵ NgBH₄⁺,²¹ NgBH₂⁺, and Ng₂BH₂⁺ (Ng = Ar–Rn),²⁶ have been reported as both thermodynamically and kinetically viable. In contrast, much less attention has been paid to species involving heavier icosagens. Only a few studies have examined E⁺–Ng (E = Al–In) cations,^27,28 or the insertion of Ng atoms into B- and Al-containing fluorides²⁹ or hydroxides.³⁰ Donor–acceptor complexes, such as F₃Al–Ng–NH₃, have also been investigated,³¹ revealing bonding scenarios that include covalent Ng–AlF₃ and electrostatic Ng–NH₃ contacts. Additionally, metastable Xe compounds of the type XXe–EX₂ (X = F–I; E = B–Ga) have been reported,³² where the Xe–E bond retains a covalent character regardless of the halogen involved. These findings collectively highlight the potential of heavier icosagens to engage in bonding with noble gases, yet comprehensive studies in this area remain limited.

The ability of icosagens to form strong interactions with Ngs offers a promising route for designing novel, stable compounds with distinctive electronic and structural properties. Among these, Xe–icosagen compounds are particularly intriguing due to the unique electronic, magnetic, and structural features of Xe.³³ Xenon's large, polarizable electron cloud makes it highly sensitive to its chemical environment, a property that underlies its exceptional performance in nuclear magnetic resonance (NMR) spectroscopy. ¹²⁹Xe NMR chemical shifts span an unusually broad range of approximately 7500 ppm,³⁴ enabling it to serve as a powerful probe for detecting weak interactions.^35,36 Consequently, there is considerable interest in modeling and interpreting ¹²⁹Xe NMR chemical shifts, especially in systems where Xe engages in covalent or electrostatic bonding with other elements.^37–42

In this study, we examine the nature and strength of Xe–icosagen bonding in the cationic species XeEF₂⁺ and Xe₂EF₂⁺ (E = B–Tl). To evaluate their stability, we performed ab initio calculations of dissociation energies (D_e), enthalpies (ΔH), and Gibbs free energies (ΔG). We also employed various bonding descriptors to characterize the Xe–E interactions. Furthermore, we calculated fluoride ion affinities (FIA) and predicted ¹²⁹Xe NMR chemical shifts to gain deeper insight into the electronic environment in these complexes and to guide future experimental studies. Finally, we analyzed the impact of relativistic effects on the NMR shifts using both two-component ZORA and fully four-component DKS approaches.

Computational details

The potential energy surfaces of the XeEF₂⁺ and Xe₂EF₂⁺ (E = B–Tl) compounds were systematically explored using a modified genetic algorithm implemented in the Global Optimization of Molecular Systems (GLOMOS) program⁴³ at the PBE0/def2-TZVP^44,45 level. The lowest-energy structures were then reoptimized at the MP2 level using either the def2-TZVP or aug-cc-pVTZ basis sets. For Xe, In and Tl atoms, quasi-relativistic pseudopotentials were employed to account for core electrons.^46–48 Final single-point energies were computed at the CCSD(T)/def2-TZVP level, with zero-point energy corrections obtained from MP2/def2-TZVP frequencies. All quantum chemical calculations were performed using Gaussian 16.⁴⁹

To probe the nature of the Xe–icosagen bonding, several complementary approaches were applied. Energy decomposition analysis (EDA)^50–52 was conducted at the BP86-D3(BJ)/TZ2P//MP2/def2-TZVP level,^53–56 using the zeroth-order regular approximation (ZORA) Hamiltonian to account for scalar relativistic effects,^57–61 as implemented in ADF.⁶² Additional bonding analyses included adaptive natural density partitioning (AdNDP),^63,64 natural population analysis (NPA), and Wiberg bond indexes (WBI), all computed at the MP2/def2-TZVP level. To further probe bonding characteristics, we also evaluated non-covalent interactions (NCI),^65,66 the electron localization function (ELF),^67,68 and the localized-orbital locator (LOL).^69–72 These analyses were carried out using Multiwfn.⁷³ Full methodological details for EDA, AdNDP, ELF, and LOL are provided in the SI.

Fluoride ion affinities (FIA) were evaluated to further investigate the Lewis acidity of the EF₂⁺ fragments in the XeEF₂⁺ and Xe₂EF₂⁺ cations. FIA values correspond to the negative enthalpy change (−ΔH) of the following reaction:

Enthalpies were obtained from geometry optimizations at the CCSD(T)/def2-TZVPP level. For the larger B(C₆F₅)₂⁺ species, the ωB97X-D/def2-TZVPP level was employed instead, due to computational cost constraints.

Relativistic ¹²⁹Xe NMR chemical shifts were computed in the gas phase using the fully four-component Dirac–Kohn–Sham (4c-DKS) method with the Dirac–Coulomb Hamiltonian,^74,75 as implemented in the ReSpect program.⁷⁶ The hybrid PBE0 functional was combined with the uncontracted Dyall's VQZ^77–79 basis set. To evaluate the impact of relativistic effects, additional calculations were carried out using the scalar relativistic ZORA (SR-ZORA) and the two-component spin–orbit ZORA (SO-ZORA) approximations, both available in ADF. In these cases, the PBE0 functional was also used, together with the all-electron Slater-type QZ4P⁸⁰ basis set. All ¹²⁹Xe NMR chemical shifts are reported relative to XeOF₄. Gauge-origin dependence was handled using the gauge-including atomic orbitals (GIAO) approach.^75,81

All computational data are available in the ioChem-BD repository⁸² and can be accessed viahttps://doi.org/10.19061/iochem-bd-6-567.

Results and discussion

Structure and stability

The global and local minimum structures of the XeEF₂⁺ and Xe₂EF₂⁺ (E = B–Tl) compounds are summarized in Tables S1 and S2. We first focus on the XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a) systems with E = B–In; the Tl analogues are discussed separately, as they exhibit a distinct potential-energy surface topology. The global minima identified for the former species correspond to singlet states with C_2v symmetry, formed by the interaction of one or two Xe atoms with the EF₂⁺ cation (Fig. 1). The 1a species represent deep energy minima, with the next lowest isomers lying more than 50 kcal mol⁻¹ higher in energy (Table S1). In contrast, 2a species have a competitive C_2v planar form (2b) that is only slightly less stable by 2.0 (B), 16.1 (Al), 15.0 (Ga), and 13.4 (In) kcal mol⁻¹. Interestingly, 2b arises from the insertion of a second Xe atom into the XeEF₂⁺ (1a) fragment (Table S2).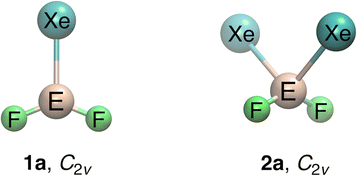

Fig. 1 Minimum-energy structures of the XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a) species (E = B–Tl) at the MP2/def2-TZVP level.

Geometrical parameters for the 1a and 2a species are listed in Tables S4 and S5, respectively. At the MP2/def2-TZVP level, the Xe–B and B–F bond lengths in XeBF₂⁺ are 2.274 and 1.272 Å, respectively, in excellent agreement with previously reported values of 2.278 and 1.273 Å at the MP2/aug-cc-pVTZ/SDD level.²⁵ Moreover, the Xe–E bond lengths in both 1a and 2a species closely match the sum of the covalent radii and are substantially shorter than those found in Xe–E⁺ (E = Al–In) systems,^27,28 indicating a strong interaction between Xe and the EF₂⁺ core. Comparison of the geometries of 1a and 2a reveals minor elongation in the Xe–E and E–F bonds in 2a, suggesting that the addition of a second Xe atom does not significantly alter the electronic structure of 1a.

The stability of XeTlF₂⁺ and Xe₂TlF₂⁺ differs slightly from that of the lighter congeners (Tables S1 and S2). After refinement of the relative energies at the CCSD(T)/def2-TZVP level, 1a remains the global minimum for both species. However, additional low-lying isomers are identified. For XeTlF₂⁺, a nearly isoenergetic linear C_∞v isomer (1c) lies only 0.3 kcal mol⁻¹ above the global minimum (Table S1). Likewise, five local minima within 15.0 kcal mol⁻¹ of the global minimum are found for Xe₂TlF₂⁺ (Tables S2 and S3). These results indicate that Xe–Tl bonding is weaker than in the lighter analogues. High-spin structures were also considered but proved significantly less stable. The lowest-energy triplet structure lies 55.4 and 45.0 kcal mol⁻¹ above 1a and 2a, respectively.

To evaluate the thermodynamic and kinetic stability of 1a and 2a, we calculated dissociation energies (D_e), enthalpies (ΔH), and Gibbs free energies (ΔG) at room temperature using the MP2/def2-TZVP level. Three dissociation channels were considered (where n = 1, 2):

Xe_nEF₂⁺ → nXe + EF₂⁺ (1)

Xe_nEF₂⁺ → Xe_nE⁺ + F₂ (2)

Xe_nEF₂⁺ → nXe + E⁺ + F₂ (3)

Among these three dissociation pathways, the one described in eqn (1) is the most favorable for both 1a and 2a (Table 1). This process is endothermic and endergonic, with dissociation being more endothermic for 2a than for 1a. In contrast, the other two channels, loss of F₂ (eqn (2)) and full fragmentation into Xe, E⁺, and F₂ (eqn (3)), require significantly more energy. The relative stability of 1a against Xe loss follows the trend Al > B ≅ Ga > In > Tl, with the Al-containing complex being more stable than even its boron analogue. This trend is supported by D_e calculated at the CCSD(T)/def2-TZVP level (values in parentheses in Table 1) and by ΔG values computed at higher temperatures (298 and 373 K; Table S6). Moreover, the estimated D_e for XeBF₂⁺ (25.7 kcal mol⁻¹) agrees with the previously reported value of 27.7 kcal mol⁻¹ at the CCSD(T) level.²⁵

Table 1 Dissociation energies (D_e), enthalpies (ΔH), and Gibbs free energies (ΔG) for XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a) species computed at the MP2/def2-TZVP level. All values are expressed in kcal mol⁻¹

M	XeEF2^+ (1a)			Xe2EF2^+ (2a)
	D e	ΔH	ΔG^b	D e	ΔH	ΔG^b
a Dissociation energies calculated at the CCSD(T)/def2-TZVP level are shown in parentheses. b Computed at 273.15 K.
(1)	XenEF2^+ → nXe + EF2^+
B	24.9 (25.7)	25.0	19.1	30.6 (30.2)	30.8	18.6
Al	28.2 (29.0)	28.2	22.6	46.4 (47.0)	46.1	33.5
Ga	24.5 (25.1)	24.6	19.2	41.8 (42.1)	41.6	29.7
In	19.0 (18.5)	19.0	14.4	34.7 (33.4)	34.5	23.3
Tl	13.9 (12.8)	14.0	9.1	26.5 (24.1)	26.3	15.6
(2)	XenEF2^+ → XenE^+ + F2
B	270.0 (252.7)	266.8	257.5	265.4 (248.3)	262.3	251.9
Al	201.9 (189.5)	200.5	192.0	214.5 (202.4)	212.8	201.9
Ga	134.9 (123.3)	133.9	125.1	146.1 (134.9)	144.9	134.1
In	88.8 (83.0)	88.1	80.1	99.0 (93.3)	98.0	88.0
Tl	30.7 (30.3)	30.0	21.6	37.2 (36.8)	36.2	26.5
(3)	XenEF2^+ → nXe + E^+ + F2
B	288.8 (271.3)	285.8	272.1	294.5 (275.8)	291.6	271.6
Al	208.2 (195.6)	207.1	194.7	226.4 (213.6)	225.0	205.6
Ga	141.7 (129.7)	141.0	128.3	159.0 (146.7)	158.0	138.7
In	94.6 (87.9)	94.1	82.3	110.3 (102.8)	109.6	91.3
Tl	36.9 (35.3)	36.5	24.3	49.5 (46.5)	48.8	30.8

---

Nature of bonding

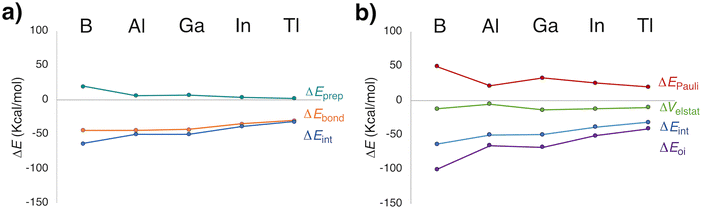
Given the predicted energetic viability of several species, we analyzed the nature of Xe–icosagen bonding using various theoretical approaches. First, an energy decomposition analysis (EDA), a method widely used to explore bonding in Ngs compounds,^83,84 was conducted. The MF₂⁺ cation and the Xe atom(s) were selected as fragments, consistent with the most favorable dissociation channels. For 1a (Fig. 2a), the overall bond energy (ΔE_bond) indicates stronger Xe–EF₂⁺ interactions when E = B, Al, or Ga. The interaction energy (ΔE_int) decreases from B to Tl, with the orbital interaction term (ΔE_oi) being the dominant component (Table S7). Notably, the percentage contribution of ΔE_oi reveals the highest covalent character for the Xe–Al bond (92%), followed by Xe–B (89%) and Xe–Ga bonds (83%). Although the Pauli repulsion (ΔE_Pauli) is larger for the boron compound, it is compensated by the high ΔE_oi magnitude (Fig. 2b). Overall, EDA suggests that the bonding stability in 1a follows the trend: B ≅ Al ≅ Ga > In > Tl. A similar pattern is found for the 2a species. However, ΔE_bond reveals stronger Xe₂–E interactions for Al and Ga (Table S8 and Fig. S1), resulting in a revised stability trend: Al ≅ Ga > B ≅ In > Tl.

Fig. 2 (a) Decomposition of the bonding energy upon formation of XeEF₂⁺ (1a) from the EF₂⁺ and Xe fragments. (b) Energy decomposition analysis (EDA) of the interaction between EF₂⁺ and Xe in the C_2v geometry adopted in 1a.

Natural population analysis (NPA) indicates a net electron transfer from Xe to the EF₂⁺ fragment (Table 2). In both 1a and 2a, Xe and E atoms carry partial positive charges, while the F atoms are negatively charged. The Xe atomic charge decreases from B to Tl, suggesting reduced charge transfer in the heavier analogues. Consistently, WBI values for the Xe–E bond range from 0.74–0.44 (B, Al, and Ga) to 0.34–0.24 (In and Tl). In particular, the relatively high WBI in XeBF₂⁺ supports a strong covalent Xe–B interaction, in agreement with previous findings of Lv et al.²⁵ These results confirm that the Xe–E bond strength decreases along the series from B to Tl.

Table 2 Wiberg bond indices for Xe–E and E–F bonds, and NPA charges (q, in |e|), calculated at the MP2/def2-TZVP level

	XeEF2^+ (1a)					Xe2EF2^+ (1b)
	WBIXe–E	WBIE–F	q Xe	q E	q F	WBIXe–E	WBIE–F	q Xe	q E	q F
B	0.735	0.874	0.503	1.449	−0.476	0.514	0.797	0.339	1.358	−0.518
Al	0.455	0.422	0.264	2.279	−0.771	0.422	0.405	0.246	2.062	−0.777
Ga	0.442	0.472	0.262	2.201	−0.732	0.424	0.429	0.253	2.001	−0.754
In	0.337	0.425	0.194	2.317	−0.756	0.352	0.400	0.204	2.131	−0.770
Tl	0.244	0.524	0.141	2.182	−0.661	0.263	0.503	0.153	2.053	−0.679

---

The AdNDP analysis further corroborates these findings. For the B, Al, and Ga species, a localized two-center, two-electron (2c-2e) Xe–E σ-bond is found, with an ideal occupation number (ON) of 2.00|e| (Fig. 3a). In contrast, no such bonding is present in the In and Tl species; instead, a 1c-2e lone pair is localized on the Xe atom, with ON values ranging from 1.82 to 1.87|e| (Fig. 3b). These results confirm that 2c-2e σ-bonding occurs only for the lighter elements, emphasizing a clear bonding distinction between B, Al, Ga, and their heavier congeners. A complete set of AdNDP analyses is provided in Fig. S2–S5.

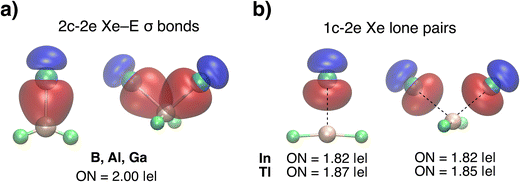Fig. 3 AdNDP orbitals and occupation numbers (ON) for XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a): (a) localized 2c-2e Xe–E σ-bonds (E = B, Al, Ga); (b) 1c-2e lone pairs on Xe for In and Tl.

To further investigate the electronic structure, we employed the localized orbital locator (LOL) and electron localization function (ELF), both derived from kinetic energy density. In these scalar fields, high values of η(r) or ν(r) typically indicate covalent bonds, lone pairs, or core electron regions.^67–72 The 2D LOL and ELF plots for 1a and 2a show an increasing polarization of the Xe–E bond toward Xe from B to Tl (Fig. S6). This trend is especially apparent when comparing the bonding regions of the B and Tl species. As shown in Fig. 4, the Xe–B bond exhibits the most localized bonding region, consistent with its higher covalent character. These observations align well with the conclusions drawn from both AdNDP analysis and EDA.

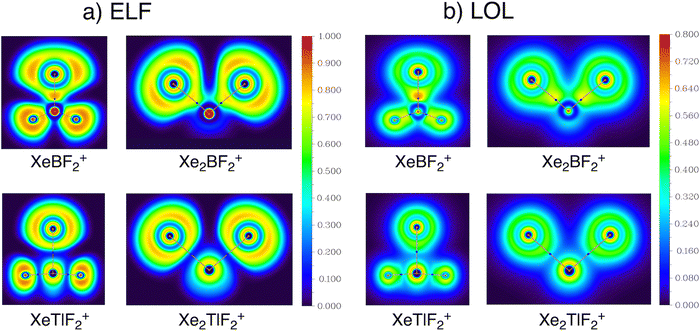Fig. 4 Bonding analysis for XeEF₂⁺ and Xe₂EF₂⁺ (E = B and Tl) based on (a) electron localized function (ELF) and (b) localized orbital locator (LOL) maps.

NCI analysis^65,66 was performed to identify potential weak interactions. In the B-containing species, the isosurface maps display a blue region between Xe and B, while Xe₂BF₂⁺ exhibits a small green region between the Xe atoms (Fig. S7 and S8). However, the absence of (λ₂)ρ peaks in the −0.05 to 0.05 a.u. range confirms a lack of significant non-covalent interactions in these systems. In contrast, the Al and Ga species show blue isosurfaces and corresponding negative (λ₂)ρ peaks, indicative of attractive non-covalent interactions. These features are even more pronounced in the In and Tl species, as shown in Fig. 5, with deeper blue regions and more negative (λ₂)ρ values.

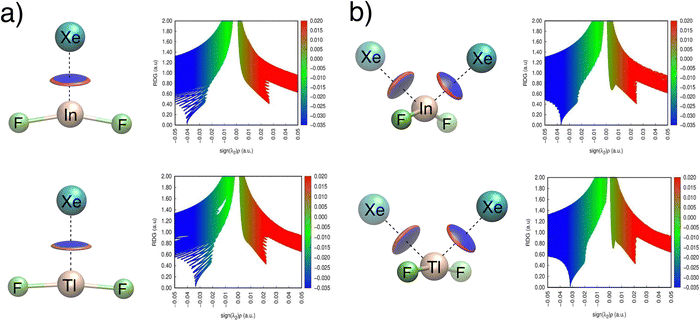Fig. 5 Non-covalent interaction (NCI) isosurfaces and (λ₂)ρ plots for (a) XeEF₂⁺ and (b) Xe₂EF₂⁺ species with E = In and Tl.

Overall, these findings are consistent with the bonding patterns established by EDA, NPA, WBI, and AdNDP: while a covalent Xe–B interaction dominates in the lighter species, non-covalent interactions increasingly contribute to the bonding in the heavier In and Tl compounds.

Lewis acidity

Given the preceding findings, a key question arises: what makes the Xe–icosagen interactions strong enough to stabilize these compounds and render them viable for experimental detection? A plausible explanation lies in the pronounced Lewis acidity of the EF₂⁺ cations (E = B–Tl). A reliable metric of Lewis acidity is the fluoride ion affinity (FIA), defined as the negative enthalpy of the gas-phase reaction between a fluoride ion and a Lewis acid.⁸⁵ The computed FIA values for the EF₂⁺ cations are summarized in Table 3. Higher FIA values indicate stronger Lewis acidity. For comparison, typical p-block Lewis acids exhibit FIA values in the range of 119.5–148.9 kcal mol⁻¹.⁸⁶ Notably, all EF₂⁺ cations analyzed here exceed this range, with BF₂⁺ and AlF₂⁺ displaying even greater Lewis acidity than several well-known strong acids such as B(C₆F₅)₂⁺ and BH₂⁺.

Table 3 Fluoride ion affinity (FIA, in kcal mol⁻¹) and A–F bond lengths (in Å) for A⁺ species, computed at the CCSD(T)/def2-TZVPP level

A^+	FIA	A–F
B(C6F5)2^+	250.2	1.3224
BH2^+	297.3	1.3226
BF2^+	349.9	1.3145
AlF2^+	310.0	1.6325
GaF2^+	293.7	1.7239
InF2^+	266.3	1.9173
TlF2^+	248.1	1.9924

---

The acidity trend follows the order: BF₂⁺ > AlF₂⁺ > GaF₂⁺ > InF₂⁺ > TlF₂⁺. This strong electron-withdrawing character facilitates interaction with Xe, thereby stabilizing the Xe–icosagen bond. Consequently, beyond the previously reported XeBF₂⁺ species, other Xe–icosagen compounds such as XeAlF₂⁺ and XeGaF₂⁺, which also show significant thermodynamic and kinetic stability, emerge as promising candidates for experimental detection.

¹²⁹Xe NMR chemical shift calculations

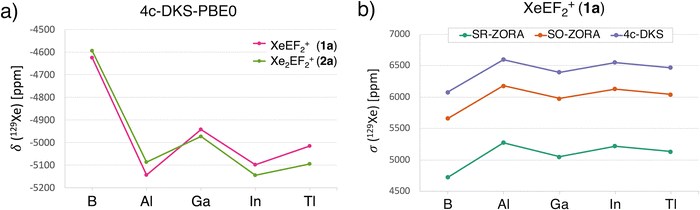
Given the high sensitivity of ¹²⁹Xe NMR to its chemical environment, the prediction of chemical shifts provides an additional probe for the Xe-icosagen interactions. To this end, we performed relativistic ¹²⁹Xe NMR chemical shift calculations in the gas phase (see the Computational methods for details). The predicted ¹²⁹Xe NMR chemical shifts (δ) for the 1a and 2a species range from −5145 to −4600 ppm (Fig. 6a), significantly more shielded than those reported for the most upfield-shifted cationic Xe environments observed experimentally, such as in XeL⁺ cations: C₆F₅Xe⁺ (−3967.5 ppm),⁸⁷ F₅TeN(H)Xe⁺ (ca. −2900 ppm),⁸⁸ F₅SN(H)Xe⁺ (−2886 ppm),⁸⁹ and F₄S = NXe⁺ (−2672 ppm).⁹⁰ In these species, polarization and relativistic effects distort the electron cloud, enhancing shielding and leading to strongly upfield shifts.

Fig. 6 (a) Predicted ¹²⁹Xe NMR chemical shifts (δ) for XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a) using the 4c-DKS-PBE0 method. (b) ¹²⁹Xe NMR shielding constants (σ) for 1a computed with SR-ZORA, SO-ZORA, and 4c-DKS methods at the PBE0 level.

The more negative ¹²⁹Xe NMR chemical shifts predicted for 1a and 2a suggest that the EF₂⁺ fragments induce greater polarization in Xe, promoting stronger covalent interactions. Among the series, XeBF₂⁺ and Xe₂BF₂⁺ are ∼300 ppm less shielded than their heavier analogues (Fig. 6a). This trend suggests that Xe–E bonding in the Al–Tl species possesses greater covalent character. Notably, the 1a species with AlF₂⁺ exhibits the most negative δ value (–5144 ppm), indicating the highest shielding. In the 2a series, however, AlF₂⁺ is slightly less shielded, allowing InF₂⁺ to exhibit the most upfield shift.

To further assess the influence of relativistic effects, especially important for heavier atoms, we compared three computational approaches: the scalar relativistic (SR) ZORA approximation, the two-component spin–orbit (SO) ZORA, and the fully four-component Dirac–Kohn–Sham (4c-DKS) method based on the Dirac–Coulomb Hamiltonian. The calculated ¹²⁹Xe NMR shielding constants (σ) for 1a and 2a are shown in Fig. 6b and Fig. S9, respectively. At the SR-ZORA level, σ(¹²⁹Xe) values for 1a range from 4724 to 5276 ppm (green line, Fig. 6b). Inclusion of SO effects via the 2c-ZORA method increases shielding by ∼900 ppm, while the 4c-DKS approach yields an additional ∼400 ppm increase. Although the 4c-DKS method does not alter the trend from B to Tl, it significantly enhances overall shielding values. These results underscore the critical role of relativistic effects, particularly spin–orbit coupling, in accurately modeling ¹²⁹Xe NMR chemical shifts in Xe–icosagen species.

Conclusions

This study presents the first comprehensive analysis of Xe–icosagen interactions by examining the global minima of the XeEF₂⁺ (1a) and Xe₂EF₂⁺ (2a) cations (E = B–Tl), explicitly including the heavier icosagens In and Tl. Our computational results show that these species are both thermodynamically and kinetically stable in the gas phase, making them viable candidates for experimental detection. The most favorable dissociation pathway involves Xe loss and is consistently endothermic and endergonic across the series, highlighting the robustness of Xe–EF₂⁺ bonding.

Energy Decomposition Analysis (EDA) indicates that the Xe–E bond stability in 1a follows the trend B ≅ Al ≅ Ga > In > Tl, with comparable bonding strength among B, Al, and Ga. For the 2a series, the trend shifts to Al ≅ Ga > B > In > Tl, where Al and Ga species exhibit even greater stability than their boron analogues. In both 1a and 2a, orbital interactions (ΔE_oi) dominate the bonding, with the highest covalent character observed for the Xe–Al bond.

AdNDP analysis confirms the presence of a 2c-2e σ-bond between Xe and E for the lighter elements (B, Al, and Ga), while only lone-pair character was found for In and Tl. This covalent-to-noncovalent transition is further supported by LOL and ELF descriptors, which reveal increasing polarization of the Xe–E bond and a gradual decline in covalent character down the group.

The EF₂⁺ cations exhibit exceptionally high Lewis acidity, with FIA values surpassing those of well-known p-block Lewis acids. This strong electron-withdrawing capacity promotes Xe coordination and significantly contributes to complex stabilization.

Relativistic ¹²⁹Xe NMR chemical shift calculations reveal highly negative σ values, indicative of strong shielding and consistent with covalent Xe–E interactions. The inclusion of relativistic effects, particularly spin–orbit coupling, is crucial for accurately reproducing these NMR parameters.

In summary, Xe can form energetically stable and potentially covalent bonds with a broad range of icosagens, including heavier elements such as Al and Ga. The combination of high Lewis acidity, favorable thermodynamics, and distinctive ¹²⁹Xe NMR signatures identifies compounds like XeAlF₂⁺ and XeGaF₂⁺, alongside XeBF₂⁺, as promising targets for experimental observation.

Conflicts of interest

There are no conflicts to declare.

Data availability

All computational data are available in the ioChem-BD repository and can be accessed viahttps://doi.org/10.19061/iochem-bd-6-567. Researchers and interested parties can access the dataset to facilitate further research and validation of the findings presented in this study.

Additional tables, figures and plots have been included as part of the supplementary information (SI). See DOI: https://doi.org/10.1039/d5cp03397g.

Acknowledgements

E. C. acknowledges the support provided by the Kukulcan Computing Center of Cinvestav Mérida. J. A. G.-C. and A. C. C. acknowledge the support from the Norwegian Research Council (grant no. 325231 and Centre of Excellence grant no. 262695) and the Norwegian Metacenter for Computational Science (NOTUR) through a grant of computer time (nn4654k). J. O. C. J.-H. acknowledges the Supercomputer Centre of the University of Guanajuato.

References

1. N. Bartlett, Xenon hexafluoroplatinate(V), Xe [PtF₆], Proc. Chem. Soc., 1962, 218.
2. R. Hoppe, W. Dähne, H. Mattauch and K. Rödder, Fluorination of Xenon, Angew. Chem., Int. Ed. Engl., 1962, 1(11), 599.
3. H. H. Claassen, H. Selig and J. G. Malm, Xenon Tetrafluoride, J. Am. Chem. Soc., 1962, 84(18), 3593.
4. W. Grochala, Atypical compounds of gases, which have been called 'noble', Chem. Soc. Rev., 2007, 36(10), 1632–1655.
5. F. Grandinetti, Gas-phase ion chemistry of the noble gases: recent advances and future perspectives, Eur. J. Mass Spectrom., 2011, 17(5), 423–463.
6. F. Grandinetti, Noble Gas Chemistry: Structure, Bonding, and Gas-Phase Chemistry, John Wiley & Sons, 2018.
7. R. Saha, G. Jana, S. Pan, G. Merino and P. K. Chattaraj, How Far Can One Push the Noble Gases Towards Bonding?: A Personal Account, Molecules, 2019, 24, 2933.
8. S. Pan, G. Merino and P. K. Chattaraj, Editorial: “Changing the Perspective of the Noble Gas Reactivity”, Front. Chem., 2021, 9, 658318.
9. L. Khriachtchev, M. Pettersson, N. Runeberg, J. Lundell and M. Rasanen, A stable argon compound, Nature, 2000, 406(6798), 874–876.
10. X. Dong, A. R. Oganov, A. F. Goncharov, E. Stavrou, S. Lobanov, G. Saleh, G.-R. Qian, Q. Zhu, C. Gatti and V. L. Deringer, A stable compound of helium and sodium at high pressure, Nat. Chem., 2017, 9(5), 440–445.
11. A. Sirohiwal, D. Manna, A. Ghosh, T. Jayasekharan and T. K. Ghanty, Theoretical Prediction of Rare Gas Containing Hydride Cations: HRgBF(+) (Rg = He, Ar, Kr, and Xe), J. Phys. Chem. A, 2013, 117(41), 10772–10782.
12. A. Ghosh, S. Dey, D. Manna and T. K. Ghanty, Noble-Gas-Inserted Fluoro(sulphido)boron (FNgBS, Ng = Ar, Kr, and Xe): A Theoretical Prediction, J. Phys. Chem. A, 2015, 119(22), 5732–5741.
13. Y. H. Huang, Z. Z. Li and A. Y. Li, Hexagonal boron-noble gas compounds B(6)Ng(n)(4 +): Structures and bonding, Chem. Phys. Lett., 2017, 689, 82–91.
14. J. Y. Jin, W. Li, Y. H. Liu, G. J. Wang and M. F. Zhou, Preparation and characterization of chemically bonded argon-boroxol ring cation complexes, Chem. Sci., 2017, 8(9), 6594–6600.
15. M. Rohdenburg, M. Mayer, M. Grellmann, C. Jenne, T. Borrmann, F. Kleemiss, V. A. Azov, K. R. Asmis, S. Grabowsky and J. Warneke, Superelectrophilic Behavior of an Anion Demonstrated by the Spontaneous Binding of Noble Gases to B₁₂Cl₁₁(-), Angew. Chem., Int. Ed., 2017, 56(27), 7980–7985.
16. Z. Tan and A. Y. Li, Noble gas supported boron-pentagonal clusters B₅Ng_n³⁺: exploring the structures and bonding, J. Mol. Model., 2018, 24(4), 1–12.
17. Z. Z. Li, M. Wen and A. Y. Li, Rg(n)Be(3)B(3)(+): theoretical investigation of Be₃B₃⁺ and its rare gas capability, J. Mol. Model., 2019, 25(12), 12.
18. Z. Huang, Y. Guo and Y. Li, The bonds and aromaticities of [NgB_xO_y]⁺(Ng = Ar, Kr and Xe; x = 3–5, y = 5–7), Comput. Theor. Chem., 2020, 112798.
19. M. Mayer, M. Rohdenburg, V. van Lessen, M. C. Nierstenhöfer, E. Aprà, S. Grabowsky, K. R. Asmis, C. Jenne and J. Warneke, First steps towards a stable neon compound: Observation and bonding analysis of [B₁₂(CN)₁₁Ne]⁻, Chem. Commun., 2020, 56(33), 4591–4594.
20. S. P. Kuntar, A. Ghosh and T. K. Ghanty, Superstrong Chemical Bonding of Noble Gases with Oxidoboron (BO⁺) and Sulfidoboron (BS⁺), J. Phys. Chem. A, 2022, 126(43), 7888–7900.
21. R. P. Rios, A. Vásquez-Espinal, S. Pan, E. Cerpa, W. Tiznado and G. Merino, BH₄Ng⁺ (Ar–Rn): Viable Compounds with a B-Ng Covalent Bond, ChemPhysChem, 2022, e202200601.
22. D. H. Tan, S. Y. Xian and A. Y. Li, Substituent Effects of Structures and Bonds of Noble Gas Compounds F–Rg–BR₂ (Rg= Ar, Kr, Xe, and Rn; R= F, OH, CN, and CCH), Russian J. Phys. Chem. A, 2022, 96(3), 611–623.
23. S. P. Kuntar, A. Ghosh and T. K. Ghanty, Theoretical prediction of donor–acceptor type novel complexes with strong noble gas–boron covalent bond, Phys. Chem. Chem. Phys., 2024, 26(6), 4975–4988.
24. G. Wang, Q. Ma, B. Wang, Y. Yang, L. Zhao, M. Zhou and G. Frenking, Spectroscopy and Bonding Analysis of ArnBO+ (n = 1–3) Cations That Possess Argon–Boron Multiple Bonds, J. Am. Chem. Soc., 2025, 147(3), 2491–2501.
25. Z. Lv, G. H. Chen, D. Li, D. Wu, X. C. Huang, Z. R. Li and W. G. Liu, RgBF(2)(+) complexes (Rg = Ar, Kr, and Xe): The cations with large stabilities, J. Chem. Phys., 2011, 134(15), 154302.
26. L. Arrué and R. Pino-Rios, Boron–noble gas covalent bonds in borenium and boronium compounds, Phys. Chem. Chem. Phys., 2021, 23(11), 6896–6902.
27. A. M. Gardner, K. A. Gutsmiedl, T. G. Wright, W. Breckenridge, C. Y. Chapman and L. A. Viehland, Theoretical study of Al⁺–RG (RG= He–Rn), J. Chem. Phys., 2010, 133(16), 164302.
28. A. M. Gardner, K. A. Gutsmiedl, T. G. Wright, E. P. F. Lee, W. H. Breckenridge, S. Rajbhandari, C. Y. N. Chapman and L. A. Viehland, Theoretical Study of M⁺−RG Complexes (M = Ga, In; RG = He−Rn), J. Phys. Chem. A, 2011, 115(25), 6979–6985.
29. T. Jayasekharan and T. K. Ghanty, Insertion of rare gas atoms into BF₃ and AlF₃ molecules: An ab initio investigation, J. Chem. Phys., 2006, 125(23), 234106.
30. A. Ghosh, A. Mallick and T. K. Ghanty, Anomaly in the stability of the hydroxides of icosagens (B and Al) and their noble gas (Xe and Rn) derivatives: a comparative study, Phys. Chem. Chem. Phys., 2020, 22(25), 14109–14124.
31. L. A. Mück, A. Y. Timoshkin, M. V. Hopffgarten and G. Frenking, Donor acceptor complexes of noble gases, J. Am. Chem. Soc., 2009, 131(11), 3942–3949.
32. E. Makarewicz, A. J. Gordon and S. Berski, The electronic structure of the xenon insertion compounds XXe–MX₂ (X = F, Cl, Br, I; M = B, Al, Ga), Polyhedron, 2016, 117, 97–109.
33. J. Haner and G. J. Schrobilgen, The Chemistry of Xenon(IV), Chem. Rev., 2015, 115(2), 1255–1295.
34. D. Raftery, Xenon NMR Spectroscopy, in Annual Reports on NMR Spectroscopy, ed. Webb, G. A., Academic Press, vol. 57, 2006, pp. 205–270.
35. A. Bagno and G. Saielli, DFT Study of the NMR Properties of Xenon in Covalent Compounds and van der Waals Complexes—Implications for the Use of ¹²⁹Xe as a Molecular Probe, Chem. – Eur. J., 2003, 9(7), 1486–1495.
36. M. Gerken and G. J. Schrobilgen, The impact of multi-NMR spectroscopy on the development of noble-gas chemistry, Coord. Chem. Rev., 2000, 197(1), 335–395.
37. P. Lantto and J. Vaara, Xe¹²⁹ chemical shift by the perturbational relativistic method: Xenon fluorides, J. Chem. Phys., 2007, 127(8), 084312.
38. M. Straka, P. Lantto and J. Vaara, Toward Calculations of the ¹²⁹Xe Chemical Shift in Xe@C₆₀ at Experimental Conditions:  Relativity, Correlation, and Dynamics, J. Phys. Chem. A, 2008, 112(12), 2658–2668.
39. S. Standara, P. Kulhánek, R. Marek, J. Horníček, P. Bouř and M. Straka, Simulations of ¹²⁹Xe NMR chemical shift of atomic xenon dissolved in liquid benzene, Theor. Chem. Acc., 2011, 129(3), 677–684.
40. P. Lantto, S. Kangasvieri and J. Vaara, Rovibrational effects on NMR shieldings in a heavy-element system: XeF₂, J. Chem. Phys., 2012, 137(21), 214309.
41. P. Lantto, S. Standara, S. Riedel, J. Vaara and M. Straka, Exploring new ¹²⁹Xe chemical shift ranges in HXeY compounds: hydrogen more relativistic than xenon, Phys. Chem. Chem. Phys., 2012, 14(31), 10944–10952.
42. M. A. Gonçalves, G. A. Andolpho, E. F. F. da Cunha and T. C. Ramalho, Exploring ¹²⁹Xe NMR parameters for structural investigation of biomolecules: relativistic, solvent, and thermal effects, J. Mol. Model., 2022, 28(11), 372.
43. J. L. Cabellos, F. Ortiz-Chi, A. Ramirez and G. Merino, GLOMOS 1.0, Cinvestav Merida, Yuc. Mexico, 2013.
44. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170.
45. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
46. B. Metz, M. Schweizer, H. Stoll, M. Dolg and W. Liu, A small-core multiconfiguration Dirac–Hartree–Fock-adjusted pseudopotential for Tl–application to Tl X (X= F, Cl, Br, I), Theor. Chem. Acc., 2000, 104(1), 22–28.
47. B. Metz, H. Stoll and M. Dolg, Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO, J. Chem. Phys., 2000, 113(7), 2563–2569.
48. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements, J. Chem. Phys., 2003, 119(21), 11113–11123.
49. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016.
50. K. Morokuma, Why do molecules interact? The origin of electron donor-acceptor complexes, hydrogen bonding and proton affinity, Acc. Chem. Res., 1977, 10(8), 294–300.
51. T. Ziegler and A. Rauk, On the Calculation of Bonding Energies by the Hartree Fock Slater Method, Theor. Chim. Acta, 1977, 46, 1–10.
52. F. M. Bickelhaupt and E. J. Baerends, Kohn-Sham density functional theory: predicting and understanding chemistry, Rev. Comput. Chem., 2000, 15, 1–86.
53. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822–8824.
54. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100.
55. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
56. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465.
57. E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular 2-component hamiltonians, J. Chem. Phys., 1993, 99(6), 4597–4610.
58. E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total-energy using regular approximations, J. Chem. Phys., 1994, 101(11), 9783–9792.
59. E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, Int. J. Quantum Chem., 1996, 57(3), 281–293.
60. E. van Lenthe, J. G. Snijders and E. J. Baerends, The zero-order regular approximation for relativistic effects: The effect of spin-orbit coupling in closed shell molecules, J. Chem. Phys., 1996, 105(15), 6505–6516.
61. E. van Lenthe, A. Ehlers and E. J. Baerends, Geometry optimizations in the zero order regular approximation for relativistic effects, J. Chem. Phys., 1999, 110(18), 8943–8953.
62. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967.
63. D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217.
64. D. Y. Zubarev and A. I. Boldyrev, Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning, J. Org. Chem., 2008, 73(23), 9251–9258.
65. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132(18), 6498–6506.
66. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: A Program for Plotting Noncovalent Interaction Regions, J. Chem. Theory Comput., 2011, 7(3), 625–632.
67. A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular-systems, J. Chem. Phys., 1990, 92(9), 5397–5403.
68. Y. Grin, A. Savin and B. Silvi, The ELF Perspective of chemical bonding, in Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH, 2014, pp. 345–382.
69. H. Jacobsen, Localized-orbital locator (LOL) profiles of chemical bonding, Can. J. Chem., 2008, 86(7), 695–702.
70. H. Jacobsen, Chemical Bonding in View of Electron Charge Density and Kinetic Energy Density Descriptors, J. Comput. Chem., 2009, 30(7), 1093–1102.
71. H. Jacobsen, Localized-orbital locator (LOL) profiles of transition-metal hydride and dihydrogen complexes(1,2), Can. J. Chem., 2009, 87(7), 965–973.
72. H. Jacobsen, Topology maps of bond descriptors based on the kinetic energy density and the essence of chemical bonding, Phys. Chem. Chem. Phys., 2013, 15(14), 5057–5066.
73. T. Lu and F. W. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592.
74. S. Komorovský, M. Repiský, O. L. Malkina, V. G. Malkin, I. Malkin Ondík and M. Kaupp, A fully relativistic method for calculation of nuclear magnetic shielding tensors with a restricted magnetically balanced basis in the framework of the matrix Dirac–Kohn–Sham equation, J. Chem. Phys., 2008, 128(10), 104101.
75. S. Komorovský, M. Repiský, O. L. Malkina and V. G. Malkin, Fully relativistic calculations of NMR shielding tensors using restricted magnetically balanced basis and gauge including atomic orbitals, J. Chem. Phys., 2010, 132(15), 154101.
76. M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, ReSpect: Relativistic spectroscopy DFT program package, J. Chem. Phys., 2020, 152(18), 184101.
77. K. G. Dyall, Relativistic double-zeta, triple-zeta, and quadruple-zeta basis sets for the 5d elements Hf–Hg, Theor. Chem. Acc., 2004, 112(5), 403–409.
78. Basis sets are available from the Dirac web site, https://dirac.chem.sdu.dk.
79. K. G. Dyall, Core correlating basis functions for elements 31–118, Theor. Chem. Acc., 2012, 131(5), 1217.
80. E. van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24(9), 1142–1156.
81. R. Ditchfield, Self-consistent perturbation theory of diamagnetism, Mol. Phys., 1974, 27(4), 789–807.
82. M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, Managing the Computational Chemistry Big Data Problem: The ioChem-BD Platform, J. Chem. Inf. Model., 2015, 55(1), 95–103.
83. D. Chakraborty and P. K. Chattaraj, In quest of a superhalogen supported covalent bond involving a noble gas atom, J. Phys. Chem. A, 2015, 119(12), 3064–3074.
84. S. Pan, A. Gupta, S. Mandal, D. Moreno, G. Merino and P. K. Chattaraj, Metastable behavior of noble gas inserted tin and lead fluorides, Phys. Chem. Chem. Phys., 2015, 17(2), 972–982.
85. K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, On a quantitative scale for Lewis acidity and recent progress in polynitrogen chemistry, J. Fluor. Chem., 2000, 101(2), 151–153.
86. P. Erdmann, J. Leitner, J. Schwarz and L. Greb, An Extensive Set of Accurate Fluoride Ion Affinities for p-Block Element Lewis Acids and Basic Design Principles for Strong Fluoride Ion Acceptors, ChemPhysChem, 2020, 21(10), 987–994.
87. H.-J. Frohn, A. Klose, T. Schroer, G. Henkel, V. Buss, D. Opitz and R. Vahrenhorst, Structural, Chemical, and Theoretical Evidence for the Electrophilicity of the [C₆F₅Xe]⁺ Cation in [C₆F₅Xe][AsF₆], Inorg. Chem., 1998, 37(19), 4884–4890.
88. B. Fir, J. M. Whalen, H. P. A. Mercier, D. A. Dixon and G. J. Schrobilgen, Syntheses of [F₅TeNH₃][AsF₆], [F₅TeN(H)Xe][AsF₆], and F₅TeNF₂ and Characterization by Multi-NMR and Raman Spectroscopy and by Electronic Structure Calculations:  The X-ray Crystal Structures of α- and β-F₅TeNH₂, [F₅TeNH₃][AsF₆], and [F₅TeN(H)Xe][AsF₆], Inorg. Chem., 2006, 45(5), 1978–1996.
89. G. L. Smith, H. P. A. Mercier and G. J. Schrobilgen, F₅SN(H)Xe⁺; a Rare Example of Xenon Bonded to sp3-Hybridized Nitrogen; Synthesis and Structural Characterization of [F₅SN(H)Xe][AsF₆], Inorg. Chem., 2008, 47(10), 4173–4184.
90. G. L. Smith, H. P. A. Mercier and G. J. Schrobilgen, Solid-State and Solution Rearrangements of F₃S ≡ NXeF⁺ Leading to the F₄S=NXe⁺ Cation; Syntheses, HF Solvolyses, and Structural Characterizations of [F₄S=NXe][AsF₆] and [F₄S=NH₂][AsF₆], J. Am. Chem. Soc., 2009, 131(21), 7272–7286.

---