Computational investigation of coordinating electrolytes with vanadium ions in redox flow batteries
Christopher S.
Mills
 ab and
Anna L.
Garden
ab and
Anna L.
Garden
 *ab
*ab
aDepartment of Chemistry, University of Otago, P.O. Box 56, Dunedin 9054, New Zealand. E-mail: anna.garden@otago.ac.nz; Tel: +64 3 479 7928
bThe MacDiarmid Institute for Advanced Materials and Nanotechnology, Victoria University of Wellington, P.O. Box 600, Wellington 6140, New Zealand
First published on 20th November 2025
Abstract
The solvation environments of the vanadium ions central to vanadium redox flow battery (VRFB) operation (V2+, V3+, VO2+, and VO2+) in the presence of common supporting electrolytes: sulfate, bisulfate, chloride, dihydrogen phosphate, and methanesulfonate were investigated via a combined classical molecular dynamics (MD) and density functional theory (DFT) thermodynamic framework. Classical MD simulations, validated by ab initio MD, showed that vanadium–electrolyte coordination increases with supporting electrolyte concentration and varies with vanadium species, with V3+ exhibiting the highest coordination and VO2+ the lowest. Chloride and dihydrogen phosphate coordinated readily with all vanadium ions even at low concentrations, while methanesulfonate exhibited minimal coordination even at 6 mol kg−1. DFT energetic analysis aligned with these trends, indicating favourable complexation for sulfate, chloride, and dihydrogen phosphate, but unfavourable complexation for bisulfate and methanesulfonate. Additionally, peripheral (non-coordinated) electrolyte molecules were found to shift half-cell reduction potentials negatively—more significantly in the negative half-cell—resulting in an overall increase in cell voltage. This was found to occur even if the electrolyte molecule was not directly coordinated with the vanadium centre. Together, these results clarify the atomistic coordination behaviour of supporting electrolytes with vanadium ions and their implications for VRFB performance.
1 Introduction
Transitioning away from a fossil fuel energy economy to one that prioritises renewable energy sources requires large scale energy storage solutions, due to the intermittancy of many renewable energy sources.1,2 Vanadium redox flow batteries (VRFBs) are one such storage solution utilising an electrolyte containing V2+/V3+ and VO2+/VO2+ redox pairs, in an acidic solution.3–5 By employing vanadium in both half-cells, the risk of contamination is minimised and the aqueous phase redox couples lead to long life cycles and high chemical stability.6,7Within VRFB design, the choice of supporting electrolytes is critical to both the electrochemical performance and the operational lifespan of the battery.8,9 These electrolytes must support the redox-active vanadium ion pairs, V2+/V3+ (V(II)/V(III)) and VO2+/VO2+ (V(IV)/V(V)), by enhancing their thermal stability and solubility in aqueous media.9 Thermal stability governs the ability of the battery to withstand heat generated during charge–discharge cycles, with current systems often requiring substantial cooling infrastructure to prevent vanadium precipitation.10 Meanwhile, energy density depends on the maximum concentration of solvated vanadium ions. Since VRFBs typically offer lower energy densities than other energy storage technologies,11 improving vanadium solubility remains a key research priority.
A key early breakthrough in VRFB technology was in the synthesis of the V(V) electrolyte. The solubility of V(V) compounds is generally very low, which thus hampers the overall VRFB energy density. However, Skyllas-Kazacos et al. found a feasible synthetic route to V(V) by electrochemical oxidation of VOSO4 in a 2 mol L−1 H2SO4 solution, yielding a 2 mol L−1 V(V) solution.7
Later efforts to increase VRFB energy density by raising vanadium concentrations revealed limitations in sulfate-based electrolytes, particularly due to vanadium precipitation.11,12 At low temperatures, the solubility of V2+, V3+, and VO2+ is poor, whereas at higher temperatures, the solubility of VO2+ is hampered. In sulfate electrolytes, this gives a practical operational thermal range of between 10–40 °C.12,13 This, therefore, restricts vanadium concentrations to between 1.4–2.0 mol L−1, although typically closer to 1.7 mol L−1, in 3.0–5.0 mol L−1 H2SO4.13–15
The above limitations spurred the development of VRFBs beyond the standard sulfate-supported systems by using alternative supporting electrolytes in pure solutions, mixed-acid solutions (MASs), or in small amounts as additives to increase vanadium solubility and expand the operating temperature range. Common alternative supporting electrolytes include: chloride, methanesulfonic acid and phosphates.
Pure chloride-supported VRFBs using 10 mol L−1 Cl− have been demonstrated to be able to extend the thermal operating range to 0–50 °C and achieve vanadium concentrations of up to 2.3 mol L−1, resulting in modest gains in energy density.10 However, while chloride improves the stability of V2+, VO2+, and VO2+, it has been found to destabilise V3+ at higher vanadium concentrations.16 To address this, MASs combining sulfate and chloride electrolytes have been developed to capitalise on the complementary benefits of each. These MAS–VRFBs offer improved thermal stability across a broader range (−20–50 °C) and support vanadium concentrations up to 2.5 mol L−1, offering further improvement in energy density.16–18
Methanesulfonic acid has been investigated both as a component of MASs—comprising methanesulfonic and sulfuric acid—and as a sole supporting electrolyte in the positive half-cell of VRFBs. In these MAS systems, multiple studies report that VRFBs can stably accommodate high vanadium concentrations (up to 2 mol L−1) with delayed onset of precipitation, provided the methanesulfonic acid concentration remains below 0.5 mol L−1.19,20 In addition to enabling greater energy density through increased vanadium loading, methanesulfonic acid-containing systems often exhibit faster reaction kinetics and lower mass transport resistance.20,21 However, this kinetic improvement is generally confined to low methanesulfonic acid concentrations; higher concentrations (e.g., 1 mol L−1 and above) lead to diminished electrochemical performance.19
Since the upper thermal limit in VRFBs, primarily attributed to VO2+ precipitation, is often the most critical concern, recent research has focused on the use of low-concentration electrolyte additives to stabilise these vanadium ions in sulfate-supported systems.22 In particular, studies of isolated cells have shown that phosphate-based additives, even at very low concentrations (<0.15 mol L−1), can effectively support VO2+ at elevated vanadium concentrations up to 4 mol L−1 and temperatures as high as 50 °C.11,23,24 However, in full-cell VRFBs containing all vanadium oxidation states, the maximum achievable vanadium concentration remains limited to 3.5 mol L−1 with 6 mol L−1 total sulfate, within a narrower thermal operating range of 5–40 °C to avoid precipitation risks.11 While the thermal window offered by phosphate additives does not greatly exceed that of pure sulfate systems, the increased vanadium solubility yields a substantial enhancement in energy density up to 70% higher than sulfate-only VRFBs operating at 2 mol L−1 V.
From the above examples, it is clear that the choice of electrolytes can have a significant impact on the stabilisation of the various vanadium species. Therefore it is of great interest to understand the interactions between the electrolytes and the various vanadium ions. To this end, nuclear magnetic resonance (NMR) spectroscopy is commonly employed. However, the insights gained are often ambiguous or difficult to interpret. For instance, the use of 35Cl NMR identified two Cl environments: one corresponding to low chloride concentrations, where chloride ions are presumed to remain uncoordinated, and another associated with [VO2Cl(H2O)2]+ formation at higher concentrations.18 On the other hand, interpretation of a broad signal observed in 51V NMR proposed a mix of monomeric [VO2Cl(H2O)2]+ and dinuclear [V2O3Cl(H2O)]3+ complexes.10
Similarly contrasting results are obtained regarding the role of methanesulfonate—the conjugate base of methanesulfonic acid—in VRFBs. One investigation using 51V NMR spectroscopy found no evidence of complexation between vanadium species and methanesulfonate at a concentration of 1 mol L−1 of methanesulfonic acid.20 However, in another study utilising higher methanesulfonic acid concentrations (up to 3 mol L−1), VRFBs were reported to exhibit slower kinetics and increased resistance at these elevated concentrations, which was proposed to stem from methanesulfonate–vanadium complexation.19 For phosphate additives, again an ambiguous picture of complexation emerges, with observed peak broadening in 51V, 17O, and 1H NMR spectra being attributed to either inner-sphere complexation or outer-sphere interactions between vanadium ions and phosphate species.11,25 Without conclusive experimental data, atomistic modelling may offer a valuable means to clarify these vanadium–electrolyte interaction.
Several computational studies have aimed to clarify the speciation of vanadium ions in the presence of electrolytes by determining the degree to which electrolyte molecules coordinate to the various V species.26–28 Molecular dynamics (MD) calculations are particularly well-suited to this task, as they can simulate the vanadium ions, the electrolyes and the bulk (aqueous) phase, as a function of time and temperature.
Gupta et al. investigated the solvation behaviours of vanadium ions in the presence of individual supporting electrolytes (HSO4−, SO42−, Cl−, and H2PO4−) using classical MD.26 Their results suggested that sulfate-derived species preferentially remained in the bulk phase, whereas chloride and dihydrogen phosphate exhibited a greater tendency to coordinate directly with vanadium ions. However, it is important to note that these conclusions were based solely on classical force-field descriptions, which lack the accuracy of higher-level methods such as DFT.
An ab initio molecular dynamics (AIMD) study of sulfate–chloride MAS systems relevant to VRFBs, where systems contained both sulfate and chloride electrolytes, was performed by Bon et al.27 The findings are largely in accordance with the classical MD results; coordination with chloride ions (sometimes multiple ions) was more thermodynamically stable than water molecules alone, favouring direct coordination to vanadium. Sulfate, on the other hand, predominantly remained in the bulk phase, although in some cases cooperative binding involving both chloride and sulfate led to the most stable complexes.27 While this study provided valuable insight and improved accuracy into the solvation dynamics of MAS systems, it did not consider bisulfate (HSO4−), which is expected to dominate under the highly acidic conditions.
While unable to capture dynamic effects and large scale solvent behaviour, static DFT is a useful tool to investigate different solvation geometries and quantify energetic preferences for coordination. Oldenburg et al. used static DFT to investigate the coordination structures of isolated vanadium complexes containing sulfate/bisulfate and phosphoric acid/dihydrogen phosphate ligands by computing their relative thermodynamic stabilities across both conjugate acid–base pairs.28 The results indicated that, for V2+, neither supporting electrolyte exhibited a strong preference for coordination, whereas the other vanadium ions generally showed some affinity for coordination with these species, though no dominant preference was observed.
As discussed above, while computational modelling has previously been employed to explore the solvation environments and coordination interactions of vanadium ions with various supporting electrolyte species—such as sulfates, chlorides, and phosphates—no known studies have systematically compared a broad range of electrolytes using both MD and static approaches to obtain comprehensive, atomistic insight into vanadium–electrolyte solvation behaviour. Moreover, there is a complete lack of atomic-scale modelling concerning the interactions between methanesulfonate anions and the vanadium ions present in VRFB systems. The present study addresses these gaps by employing classical MD simulations, validated against ab initio MD, and static DFT thermodynamic analyses to characterise vanadium solvation in multiple electrolytes, as well as quantify the effect of electrolytes on the redox potentials of the vanadium ion pairs. In doing so, it aims to clarify the interactions underpinning the stability of vanadium complexes within the context of electrolyte coordination in VRFBs, as well as offer a first estimation of how the redox reactions themselves are affected by electrolytes.
2 Methodology
The workflow of this study comprises several key stages, summarised as follows. First, the classical force field was validated for modelling solvated vanadium ions through qualitative comparison with parallel ab initio molecular dynamics (MD) simulations. Second, long-timescale classical MD simulations were performed to qualitatively assess the behaviour of vanadium ions in the presence of common supporting electrolytes. Third, quantitative density functional theory (DFT) free energy calculations were conducted to compare the relative stability of isolated vanadium complexes with various supporting electrolytes, both coordinated and uncoordinated. Finally, the influence of supporting electrolytes and their coordination on vanadium redox flow battery (VRFB) reduction potentials was predicted based on the preceding DFT results. A schematic summary of this workflow is presented in Fig. 1.2.1 Validation of classical molecular dynamics simulations
Classical MD simulations of each of the solvated vanadium ions, V2+ (V(II)), V3+ (V(III)), VO2+ (V(IV)), and VO2+ (V(V)), were modelled in the presence of the following electrolytes: sulfate (SO42−) and its conjugate base bisulfate (HSO4−), methanesulfonate (CH3SO3−), dihydrogen phosphate (H2PO4−), and chloride (Cl−) in aqueous solutions. The extended SPC (SPC/E) force field was used to describe the interactions of water molecules,29,30 and the DREIDING-UT force field for all other molecules and ionic species.31 However, the DREIDING-UT force field does not contain Lennard-Jones (LJ) parameters for vanadium, these were adopted from the work of Hinkle et al.,32 who compiled values from several earlier studies.33–35For electrostatic interactions in DREIDING-UT, charges for molecular species were derived from restrained electrostatic potentials (RESP)36 calculated from geometry optimisations at the MP2/cc-pVQZ level with an RI approximation in conjunction with the corresponding Coulomb-fitting auxiliary basis set (cc-pVQZ/C) and SMD water solvent model within the ORCA software.37–43 Here, the MultiWFN software was implemented to extract the RESP charges from the MP2 calculated wavefunction.44,45 For all LJ parameters and partial charges see the SI. Classical MD simulations were performed within the large-scale atomic/molecular massively parallel simulator (LAMMPS).46
To compare and validate the classical MD force field, parallel ab initio MD simulations with the four vanadium ions and same electrolytes were performed within the Vienna ab initio Software Package (VASP),47–50 using the PBE-D3 functional.51,52 Valence electrons were described via a periodic plane-wave basis-set with a kinetic energy cut-off of 500 eV and a projector augmented wave (PAW) method was used for core electrons.53 A 2 × 2 × 2 Monkhorst–Pack k-point scheme was invoked to sample reciprocal space.54
Equilibrated systems were then assessed across a 20 ps canonical (NVT) ensemble with a Nosé–Hoover thermostat for both computational methods,56,57 where T = 298 K, V was derived from the NPT ensemble, with a 1 fs timestep.
2.2 Long-timescale classical molecular dynamic simulations
Classical MD simulations of the four vanadium ions in aqueous solutions were individually modelled with the following electrolytes: SO42−, HSO4−, CH3SO3−, H2PO4−, and chloride Cl−. For each vanadium ion and electrolyte combination, simulations were initiated in 20 × 20 × 20 Å periodic cells that contained a single vanadium ion with 56 water molecules positioned randomly corresponding to a battery loading of 1 mol kg−1 of vanadium ions per kilogram of water. Various concentrations of the electrolytes were investigated and required individual separate simulations with randomised initial molecular positions for both electrolytes, vanadium ions, and water molecules per simulation. Electrolyte loadings were tested across all integer values in the ranges presented in the SI. Protons were also added to neutralise the charge of the cells. For all species simulated, the LJ parameters and partial charges remained consistent with the classical descriptions provided in Section 2.1.Following the initial geometry and cell setup, the system was minimised such that the energy was converged to 1.0 × 10−4 kcal mol−1 and forces acting on all atoms were less than 1.0 × 10−6 kcal mol−1 Å−1. An MD simulation was then performed starting with a Nosé–Hoover isothermal–isobaric (NPT) ensemble for 0.5 ns at 1 atm, at 450 K and then at 298 K for 0.5 ns. To conclude the MD simulation, a canonical (NVT) ensemble with a Nosé–Hoover thermostat was utilised for 1.0 ns at 298 K, giving rise to an overall simulation period of 2.0 ns modelled with a 1.0 fs time-step.
To account for the influence of initial conditions on MD outcomes, ten replicates were performed for each vanadium–electrolyte–concentration combination, with randomised starting coordinates.
2.3 Static DFT calculations of vanadium–electrolyte complexes
Initial geometry optimisations and frequency calculations were performed with the ORCA (Version 5.0)42,43 software at the BP86-D3(BJ)/def2-SVP level with def2/J auxiliary basis sets and the RI approximation, in the presence of a water SMD implicit continuum solvation model.39–41,60–63 Tight SCF convergence criteria and the “TightOpt” keyword were employed to ensure reliable optimised structures.Frequency calculations were carried out numerically, using a step size of 0.005 Bohr. Thermodynamic corrections to the Gibbs free energy were computed at 298 K and 1 atm, as implemented in ORCA. No imaginary frequencies were found, confirming that all optimised structures correspond to local minima.
To improve the accuracy of the electronic energies used in the free energy evaluations, single-point calculations were performed at the ωB97X-D3(BJ)/def2-TZVPP level of theory on the BP86-D3(BJ)/def2-SVP-optimised geometries. These calculations employed the def2/J auxiliary basis set, the RIJCOSX approximation, and the same SMD water solvation model.40,41,62–66 The resulting higher-level electronic energies were combined with the previously computed thermodynamic corrections to yield final Gibbs energies.
Each solvation model contained one of each of the vanadium ions, V2+, V3+, VO2+, and VO2+, in the presence of six water molecules for V2+ and V3+, and five and four water molecules for VO2+ and VO2+, respectively. Furthermore either one electrolyte ion (SO42−, HSO4−, CH3SO3−, H2PO4−) or up to a maximum three Cl− ions were included.
Electrolyte preference in the first solvation sphere was assessed by comparing Gibbs energies of vanadium ion complexes coordinated with water and/or electrolytes. For each ion, structures with mono-, bi-, and tridentate electrolyte coordination were evaluated against fully hydrated analogues with peripheral electrolytes. A range of coordination geometries were considered corresponding to those commonly identified in literature:27,67 octahedral for V2+ and V3+, and tetrahedral, trigonal-bipyramidal, square-planar, and octahedral for VO2+ and VO2+, corresponding to four-, five-, and six-coordinate configurations.
2.4 Calculation of standard reduction potentials
Standard reduction potentials (E°) for the V3+/V2+ and VO2+/VO2+ redox pairs were determined following the approach of Tussupbayev and Kudaibergenova,68 using a Born–Haber thermochemical cycle. This method relates thermodynamic contributions for redox processes in both the gas and solution phases to obtain the standard Gibbs energy change in solution,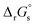 , for each vanadium redox pair in aqueous solution (with implicit solvation) as follows:
, for each vanadium redox pair in aqueous solution (with implicit solvation) as follows: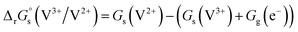 | (1) |
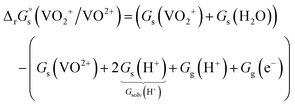 | (2) |
The absolute standard reduction potential is calculated from 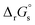 using the Nernst equation:
using the Nernst equation:
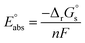 | (3) |
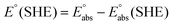 | (4) |
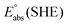 represents the absolute potential of the SHE, taken to be 4.44 V.71
represents the absolute potential of the SHE, taken to be 4.44 V.71
Gibbs energies used to calculate the standard reduction potentials of the V3+/V2+ and VO2+/VO2+ redox pairs—both in the presence of and coordinated to various electrolytes—were obtained from calculations detailed in Section 2.3, and therefore share identical computational parameters. To enable comparison with purely water-solvated vanadium ions, additional calculations were performed for V2+, V3+, VO2+, and VO2+ species complexed with six, six, five, and four water molecules, respectively, thereby achieving a maximal octahedral coordination environment. For VO2+ and VO2+, several hydration geometries were examined, and the lowest-energy configuration was used to determine the standard reduction and overall cell potentials for the water-only reference systems.
3 Results and discussion
3.1 Validation of classical molecular dynamic simulations
Given that the DREIDING-UT force field used in this work is a general-purpose model not specifically parametrised for VRFB chemistry,72 its ability to accurately capture the solvation and coordination properties of vanadium ions in aqueous environments is unknown. Therefore, prior to large-scale classical force-field modelling of the solvation dynamics of common vanadium ions in VRFBs, smaller classical models with shorter total simulation times were investigated and compared in parallel with the same systems using ab initio methods.To facilitate a direct comparison between the methods, variation arising from the initial starting configuration was minimised by ensuring that the parallel classical and ab initio systems shared identical atomic positions at the outset. Consequently, any subtle differences in solvation dynamics could be attributed to inherent differences originating from the derivation of energies and forces between the methods.
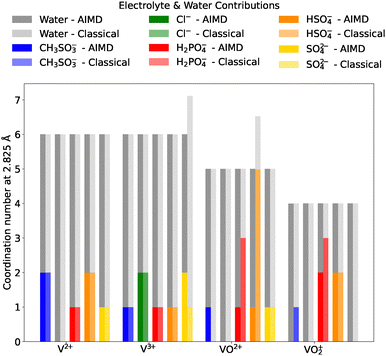
The coordination number of donor atoms bound to vanadium ions was chosen as an important validation parameter for the MD simulations. This was determined through the integration of radial distribution functions (RDFs) of donor-atom–vanadium distances (see SI). A cutoff distance of 2.825 Å was selected, corresponding to the first minimum in the RDF, to ensure that only atoms within the first solvation shell, directly coordinated to the vanadium ions, were included in the coordination number calculations. The coordination numbers for each vanadium–electrolyte system were then compared between the classical MD and AIMD simulations, as shown in Fig. 2. Note that these results are obtained from a single, small-scale MD simulation, therefore focus is on comparison between the two methods, rather than detailed elucidation of coordination behaviour, which can be found in Section 3.2.
Inspecting the overall bar height in Fig. 2. It can be seen that the total coordination numbers (including water and electrolytes) are in very good agreement between the two methods. Both V2+ and V3+ predominantly adopt a six-coordinate octahedral geometry, while VO2+ and VO2+ coordinate with five and four donor atoms, respectively, maintaining an overall octahedral geometry when accounting for the oxygen atoms directly bound to vanadium. However, some deviations between the methods related to coordination geometry were observed. For V3+ with sulfate and VO2+ with bisulfate the classical model overestimates the total coordination number, compared with the AIMD method. Upon further investigation, it was found that the seven-coordinate geometry of V3+ with sulfate is likely an artefact of the initial structural guess, as subsequent removal of an excess water molecule did not return to a seven-coordinate geometry. However, for the VO2+ and bisulfate system, the seven-coordinate geometry was found to persistently reform. This surprising geometry is likely because the classical description inherently lacks any form of directionality related to electronic structure, leading to less rigid structural motifs. Despite these variations, the overall first shell structures between the two methods remained largely in agreement, with only 5 of the 20 systems considered showing variation between the classical and ab initio descriptions.
Examining the finer details specific to the number of coordinating electrolyte molecules only, again, a general agreement between the two methods is observed. The most significant electrolyte coordination number discrepancy arises with methanesulfonate: in AIMD, it is found to coordinate with VO2+ but not VO2+, whereas in the classical model, the opposite is true. Differences in electrolyte coordination numbers are also observed, particularly for VO2+ with dihydrogen phosphate and bisulfate, where a higher number of O-donor atoms coordinate in the classical MD simulation, compared to AIMD. In other cases, coordination numbers differ slightly, typically by a single additional donor atom.
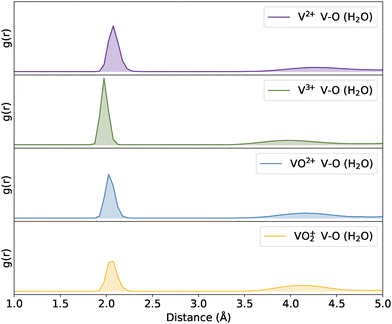
Some of the discrepancies in coordination numbers between the classical and AIMD methods can be rationalised by examining their respective RDFs. For instance, the bisulfate RDFs in Fig. 3 show bimodal distributions within the 1.8–2.8 Å range for classical VO2+ and AIMD VO2+, whereas the corresponding model counterparts do not. Note, that the RDFs in this section only depict the interactions between the vanadium ion centre and the donor atoms of the supporting electrolytes; oxygen atoms in water molecules and the vanadium ions are thus neglected.
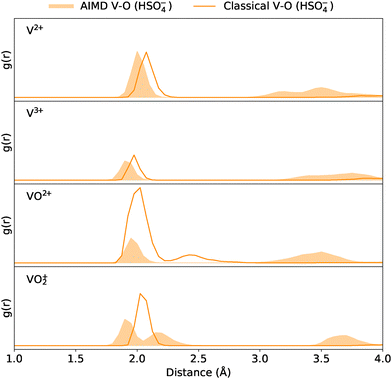 | ||
| Fig. 3 Comparison of classical and AIMD RDFs between the vanadium centre and the O-donor atom of HSO4−, across the vanadium ions. | ||
Focusing first on the classical RDF for the VO2+-bisulfate system, integration up to 2.825 Å yields an unexpectedly high coordination number of approximately 6.5, compared to the expected value of 5 observed in other VO2+ models (Fig. 2). This discrepancy may partly stem from a smaller peak at 2.4 Å, which complicates the definition of a strict coordination cutoff. The broad peak likely reflects the multidentate nature of bisulfate binding and the dynamic (labile) behaviour of its oxygen atoms in the classical model. In this model, bisulfate oxygen atoms are frequently found within the coordination sphere, while additional oxygen atoms occasionally remain just beyond it—unable to fit within the close-packed geometry of the immediate coordination shell—as suggested by the non-zero g(r) value in the RDF trough between the two peaks.
While the second peak partly explains the higher coordination number, a clear discrepancy remains: the dominant classical peak at ∼2.0 Å is significantly larger than the corresponding AIMD peak, indicating an overestimation of O-donor coordination by the classical method. Nonetheless, the classical model correctly captures the qualitative presence of HSO4− coordination with VO2+.
The second bimodal distribution is observed in the AIMD VO2+-bisulfate system, as shown in Fig. 3. In this case, distinct peaks at approximately 1.9 Å and 2.2 Å correspond to the axial and equatorial coordination of bisulfate oxygens around the VO2+ ion; similar observations have been described with hydrated VO2+ in prior studies.67,73–75 The ability to resolve these coordination environments reflects the ability of AIMD to capture such subtleties in bonding differences. In contrast, the classical force field lacks the resolution to differentiate between axial and equatorial interactions and does not reproduce this bimodal feature.
Another distinction between the methods can be observed in Fig. 3 and the RDFs of other electrolytes (see SI). AIMD generally predicts closer coordination of O-donor atoms compared to the classical model and, due to its higher-order treatment of interactions, captures variations in bond lengths depending on coordination sites.
Despite the above-mentioned exceptions and subtleties, the overall agreement between classical and AIMD results provides confidence in the chosen force fields and parameters for larger-scale simulations. This confidence is appropriate given that the focus of this study is on the presence of electrolyte species within the first solvation shell, rather than on precise bond lengths or the frequency of individual donor atoms—features which, as previously shown in the case of HSO4−, can be overestimated in classical models.
3.2 Long-timescale molecular dynamics simulations
Having validated the chosen force fields, classical MD simulations were extended to longer timescales and larger system sizes to more accurately sample the bulk aqueous environment representative of VRFBs.We first investigate the solvation behaviour of the four vanadium species in the absence of electrolytes, that is solvation by water only. RDFs between the V atoms and H2O molecules are shown in Fig. 4. It can be seen that a distinct peak is observed within the first coordination sphere for all V species, indicating direct coordination of H2O to the V. However, the intensity of this peak is lower for the oxo-vanadium species, likely due to the fewer available coordination sites for these species, in agreement with previous calculations.76 There is a also smaller peak at the second nearest neighbour distances, suggesting some structure of the solvent beyond the first solvation sphere, but this is rather broad suggesting that this structure is minimal.
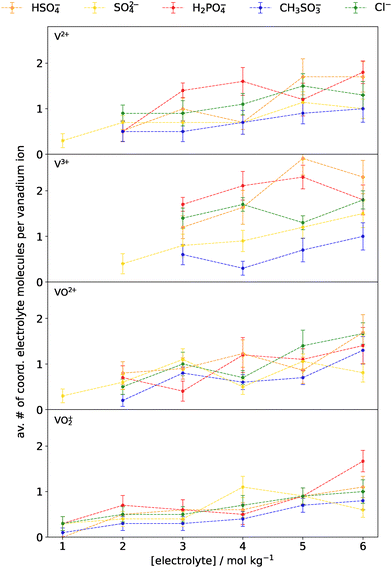
We next turn our attention to the solvation dynamics of vanadium–electrolyte systems, as a function of electrolyte concentration. RDFs of all vanadium–electrolyte systems can be found in the SI, from which the total number of coordinating electrolyte molecules were obtained by integration of the first peak in the RDF; the results are shown in Fig. 5. Across all vanadium ion-electrolyte combinations there is a positive association between electrolyte concentration and the average number of electrolyte molecules coordinated to each respective vanadium ion. However, the extent of coordination for each vanadium species appears to be influenced by both ionic charge, which affects ion–ion interaction strength, and the number of accessible coordination sites, particularly for oxo-vanadium ions, as observed in the case of water-only coordination.
To begin the discussion on the coordination behaviour of the individual electrolyte species, we focus first on sulfate, which, although exhibiting relatively low coordination numbers compared to some other electrolytes, shows notable variation depending on the oxidation state of the vanadium ion. Sulfate shows greater coordination tendencies with the monoatomic vanadium ions, particularly V3+, which surpasses an average coordination number of 1.0 electrolyte molecule per vanadium at concentrations above 5 mol kg−1. In contrast, V2+ requires a higher sulfate concentration (6 mol kg−1) to reach comparable coordination levels. The oxo-vanadium species (VO2+ and VO2+) rarely exceed an average coordination number of 1.0 electrolyte molecule per vanadium, even at the highest modelled sulfate concentrations. Interestingly, at lower sulfate concentrations, the VO2+ ion occasionally displays modest coordination numbers (i.e. 3 mol kg−1), outperforming the monoatomic vanadium ions in this regime and also coordinating more than alternative electrolytes.
Bisulfate, despite being geometrically and chemically similar to sulfate, exhibits markedly different coordination characteristics – most notably, significantly higher coordination numbers at elevated concentrations. This trend holds across all vanadium ions. At 6 mol kg−1, bisulfate demonstrates an average coordination number between approximately 1.1 electrolyte molecules per VO2+ ion and 2.3 electrolyte molecules per V3+ ion. This observation is particularly surprising given that the RESP charges assigned to the O-donor atoms in sulfate are more negative than those in bisulfate, and the generic DREIDING-UT force field applies the same LJ parameters to both. Based on this, one would expect the stronger electrostatic interactions from the more negatively charged oxygen atoms within sulfate to drive greater complexation; however, the opposite trend is observed. These results suggest that other factors such as solvent-mediated effects, hydrogen bonding capacity, or increased flexibility in the bisulfate structure may play a critical role in enhancing coordination propensity. The outcome of this higher affinity towards coordination leads to an average of at least one bisulfate molecule coordinated to VO2+ and VO2+, nearly an average of two bisulfate molecules coordinated to V2+, and between two and three bisulfate molecules coordinated to V3+ at 6 mol kg−1.
For the monoatomic V2+ and V3+ ions, and the VO2+ ion, chloride ion coordination is generally favourable across all concentrations. Trends indicate coordination numbers of 0.9, 1.4, and 1.0 electrolyte molecules per vanadium at 3 mol kg−1 of chloride, respectively, highlighting a strong driving force for complex formation even at low chloride loadings. In contrast, the VO2+ ion exhibits much lower coordination numbers under the same conditions, with 0.5 electrolyte molecules per vanadium at 3 mol kg−1 of chloride. At the highest modelled chloride concentration (12 mol kg−1), all vanadium ions converge to form bis-chloro complexes on average (see SI for broader chloride concentration range). This indicates that at the extreme chloride loadings employed in some high-performance VRFB systems (e.g., 10 mol L−1, as used by Kim et al.10), coordination of chloride ions is highly likely.
In the average coordination trends for dihydrogen phosphate, clear differences emerge amongst the vanadium ions, although dihydrogen phosphate tends towards coordination with all species, particularly at higher concentrations. For the oxo-vanadium ions, at lower dihydrogen phosphate concentrations, coordination with the oxo-vanadium ions is generally less favoured, with coordination numbers of 0.7 molecules per vanadium at 2 mol kg−1 for each of the oxo-vanadium species. However, at higher concentrations (6 mol kg−1), coordination becomes more favourable, with average coordination numbers of approximately 1.4 for VO2+ and 1.5 electrolyte molecules for VO2+. A similar pattern of coordination is observed for V2+.
In the case of V3+, consistently high average coordination values are observed across the entire concentration range suggesting that V3+ readily coordinates with multiple dihydrogen phosphate molecules, even at low concentrations, leading to early saturation and possibly steric bulk or electrostatic repulsion preventing further binding.
Several studies have highlighted the role of phosphates and their derivatives in thermally stabilising vanadium ions, particularly by mitigating the aggregation of VO2+ species.11,22,23,25 Our results support this view, indicating that dihydrogen phosphate may function as a coordinating electrolyte species, even at relatively low concentrations. This coordination could play a role in limiting the formation of vanadium-containing precipitates by interacting not only with individual vanadium ions but also by bridging between pairs of ions,77 inhibiting the vanadium dimerisation and eventual precipitation. Further computational work is needed to explore the extent to which such interactions might inhibit vanadium dimerisation and the subsequent aggregation pathways that compromise electrolyte stability.
Finally, methanesulfonate consistently exhibits the lowest coordination frequencies with all vanadium ions across the concentration range studied. This is evident from the blue data points in Fig. 5, which generally fail to exceed an average coordination number of 1.0 molecule per vanadium ion – even at higher concentrations. At lower concentrations, the average number of coordinated methanesulfonate molecules remains below or well below 0.5 methanesulfonate molecules per vanadium ion. These observations suggest that methanesulfonate coordination to vanadium ions in VRFB electrolytes is generally unfavourable unless present at sufficiently high loadings (e.g., ≥4 mol kg−1).
When using methanesulfonic acid as a mixed acid additive to typical sulfuric acid based VRFBs, most studies report increased solubility, stability, and reaction kinetics of vanadium redox couple pairs provided that methanesulfonic acid concentrations are limited to below 2 mol L−1 (∼2 mol kg−1).8,19–22 Our findings suggest that, within these concentration regimes, coordination of methanesulfonate to vanadium ions is minimal, implying that any performance benefits are unlikely to arise from the formation of vanadium–methanesulfonate complexes. Instead, enhancements in electrolyte properties – such as solubility, thermal stability, or redox kinetics – are likely driven by indirect effects of the electrolyte. When using methanesulfonate as the sole electrolyte (substituting sulfate), a study by Tang and Zhou55 demonstrated that a 4 mol L−1 methanesulfonic acid solution could be used as a direct substitute to sulfuric acid as the supporting electrolyte in the VO2+/VO2+ half-cell, even at vanadium concentrations up to 3 mol L−1. In such high-concentration regimes, our coordination trends would suggest that some degree of vanadium–methanesulfonate complexation is likely.
3.3 DFT calculated stabilities of vanadium–electrolyte complexes
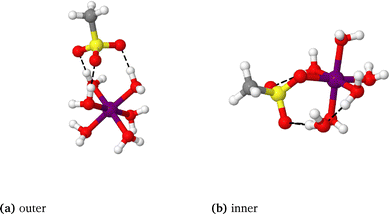
To rationalise the coordination outcomes observed in the large-scale classical MD simulations in the previous section, static DFT calculations of isolated complexes were conducted on a range of structural configurations for each vanadium–electrolyte pairing. These calculations aimed to quantify the relative stability of complexes in which the electrolyte is directly coordinated to the vanadium ion within the first solvation sphere, compared with those where the electrolyte resides more peripherally in the second solvation sphere. A range of different coordination geometries for the oxo-vanadium species were considered including octahedral, tetrahedral, square-based pyramidal (for VO2+), and trigonal bipyramidal (for VO2+) configurations. For Cl−, the possibility of multiple coordinating electrolyte molecules were considered.The relative stability of each coordinated complex was determined by comparing the Gibbs energy of the most stable directly coordinated, or inner-sphere geometry (labelled “inner”) to that of the most stable geometry in which the electrolyte was positioned beyond the first solvation sphere, or outer-sphere geometry (labelled “outer”); an example of these configurations is given Fig. 6, for all other vanadium–electrolyte structures see the SI. The relative stability was quantified using the descriptor ΔGinner–outer, defined as:
| ΔGinner–outer = Ginner − Gouter | (5) |
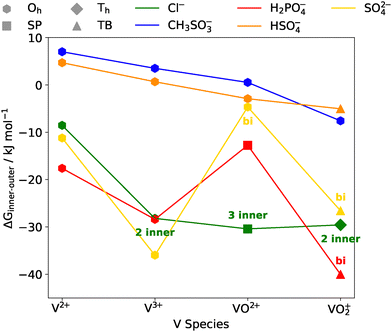
Values of ΔGinner–outer for all four vanadium species, and all electrolytes considered earlier in this work are presented in Fig. 7, as well as the nature of the most stable coordination geometry. Considering first the coordination geometry, for V2+ and V3+, octahedral, monodentate binding is preferred for most electrolyte species. For Cl−, the most favourable arrangement has two Cl atoms directly coordinated to V3+. More variation in the preferred geometry is observed for VO2+ and VO2+, where octahedral, square planar, trigonal bipyramidal and tetrahedral geometries are all observed. Previous work identified that the octahedral and trigonal bipyramidal geometries are preferred for the hydrated VO2+ and VO2+ complexes, respectively, in the absence of supporting electrolytes.67,78 However, this is not the case for certain electrolytes whereby coordination facilitates alternate geometries, such as square-based pyramidal for VO2+. The most variation in coordination geometry is observed for VO2+, where octahedral, trigonal bipyramidal and tetrahedral coordination geometries were all observed to be the most stable geometry for at least one electrolyte. Furthermore, bidentate coordination is favoured for sulfate with VO2+ and VO2+, and dihydrogen phosphate with VO2+.
In terms of the relative stability of inner- and outer-sphere coordination, most evident within this data are the relative instabilities of vanadium complexes with direct coordination of methanesulfonate and bisulfate. These electrolytes exhibit unfavourable coordination for the most reduced vanadium species (i.e. V2+), with coordination becoming only marginally more favourable as the oxidation state of the vanadium ion increases. While the unfavourable coordination of methanesulfonate aligns with the MD simulations, where it consistently showed the lowest coordination numbers compared to other electrolytes, this contrasts with bisulfate, which demonstrated generally favourable coordination behaviour in the MD results. However, this apparent contradiction may be attributed to the limitations of the static study, which considered only a single electrolyte molecule per complex whereas the MD simulations considered up to 6 electrolyte molecules (up to 12 for chloride), over a range of concentrations. Closer inspection of the MD results show that, at low concentrations of electrolyte, bisulfate shows similar coordination behaviour to many of the other electrolytes. However, as the concentration increases, for V2+ and V3+, bisulfate frequently coordinated in pairs or even triplets. Therefore, it is perhaps unsurprising that a single bisulfate coordination is thermodynamically less favourable than a fully water-solvated complex. Another possible reason for the discrepancy could be the inclusion of only the first solvation shell in the static DFT calculations, where the electrolyte molecule is placed either within, or outside this first solvation shell. Therefore, any effects from the wider solvation environment are not taken into account, such as disruption to the water network, or (de)stabilisation of free electrolytes.
For the remaining electrolytes—sulfate, chloride, and dihydrogen phosphate—direct coordination is consistently favourable, although the degree of stabilisation varies with the oxidation state of the vanadium ion. In general, the more oxidised vanadium species in each half-cell (V3+ and VO2+) are more strongly stabilised upon coordination with these electrolytes. A notable exception is VO2+ with chloride, which is marginally more stabilised than VO2+ (−30.42 kJ mol−1) due to the presence of a third chloride ion, compared to the next most stable configuration with two chloride ions (−18.91 kJ mol−1; see SI). This trend may be influenced by the structural limitations of VO2+ in its most stable coordinated geometry—tetrahedral—which likely prevents accommodation of a third chloride ion, thereby contributing to its relatively lower stabilisation.
A previous study by Bon et al.,27 which investigated mixed sulfate–chloride electrolytes using ab initio metadynamics, yielded similar results to the present work for the V2+, V3+, and VO2+ ions in terms of the relative stability and favourable coordination of chloro-complexes over their hydrated counterparts. An exception exists for VO2+, as Bon et al. reported chloride coordination to be marginally less favourable than water molecules for this ion regardless of coordination number or geometry. However, their study did not identify the most stable tris-chloro square-planar VO2+ complex found in the present work, which may account for the discrepancy between the two results. Overall, both our static DFT calculations and our MD investigation of chloride–vanadium ion systems, indicate that, in VRFBs utilising chloride as a stabilising electrolyte, chloride is likely to coordinate with each of the vanadium ions.
As mentioned previously, this static investigation indicates that vanadium ions are favourably complexed by sulfate ions, though the magnitude of stabilisation varies depending on the oxidation state. In the literature, the preferential direct coordination of sulfate at low concentrations with vanadium ions remains inconclusive—particularly for the VO2+ ion. Some studies report that the formation of aqueous VOSO4 is thermodynamically favoured over the hydrated form, as indicated by positive equilibrium constants,79,80 while others argue that sulfate resides in the second solvation sphere, without direct coordination with VO2+.81 These seemingly contradictory claims may be reconciled by our findings, which show only a slight thermodynamic preference for a coordinated octahedral bidentate complex of VO2+ over the most stable uncoordinated form—by just −4.66 kJ mol−1—in which sulfate remains in the second solvation sphere while water fully occupies the first. Interestingly, literature reports of higher equilibrium constants for bis-sulfate complexes compared to mono complexes may suggest that coordination involving a second sulfate anion further stabilises VO2+, perhaps leading to the known precipitation of vanadium sulfate salts; however, this falls beyond the scope of the present study and warrants future investigation.
Dihydrogen phosphate is also found to favourably coordinate with vanadium ions, with the more oxidised species of each VRFB half-cell being most favourably stabilised via complexation with dihydrogen phosphate. Similar to the behaviour of sulfate, VO2+ is stabilised the least with dihydrogen phosphate. Notably, among all vanadium–electrolyte combinations examined, VO2+ complexed with dihydrogen phosphate exhibits the greatest thermodynamic stabilisation—yielding a ΔGinner–outer value of −40.04 kJ mol−1 compared to its fully hydrated form. These thermodynamic results align closely with our MD findings, which revealed frequent coordination events for dihydrogen phosphate, supporting its strong tendency to bind within the first solvation sphere of vanadium ions in VRFB-relevant environments.
3.4 Effects of electrolytes on reduction and cell potentials
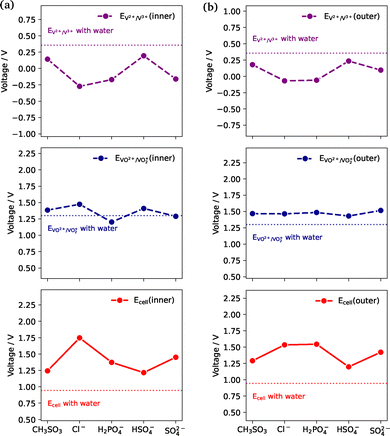
Using the most stable complex geometries found in the previous section, we now investigate how the presence of electrolytes affects the standard reduction potentials of the V3+/V2+ and VO2+/VO2+ redox couples, as well as the overall cell potential. Standard reduction potentials are calculated as described in Section 2.4.Deriving accurate reduction potentials from DFT calculations presents a significant challenge due to limitations in accurately describing the solvation of transition metal ions and in the choice of functional and basis set pairing. For example, it has been noted that, for 3d transition metals, better accuracy is obtained by explicitly modelling both the first and second solvation spheres.82 Furthermore the choice of functional has been found to significantly impact the reduction potentials of standard reduction potentials of vanadium complexes, with the V3+/V2+ reduction potential consistently overestimated by all functionals tested.68 Consequently, deviations from experimental reduction potentials are expected in the present study—particularly for the V3+/V2+ pair—given that our systems only explicitly model the first solvation sphere, with the remaining solvation environment treated implicitly. The calculated standard reduction potentials for the purely water-solvated V3+/V2+ (EV3+/V2+) and VO2+/VO2+ (EVO2+/VO2+) couples are 0.357 V and 1.300 V, respectively. The deviation from the experimentally determined potentials of −0.255 V and 1.001 V,83 is consistent with benchmarking of the functional and basis set used in this study.68 Consequently, we emphasise that the absolute reduction potentials reported here are likely overestimated relative to experiment, particularly for the V3+/V2+ redox pair. However, the relative changes in reduction and cell potentials induced by different electrolytes are still expected to offer reliable insights into how electrolyte composition may influence VRFB performance.
Calculated reduction potentials and cell potentials are shown in Fig. 8, where both inner-sphere (direct) complexation and outer-sphere (peripheral) interaction of the electrolytes are considered. Considering first the case where electrolytes are directly coordinated to the vanadium ions (Fig. 8a), it can be seen that the reduction potentials of both half-cells are perturbed upon electrolyte coordination. The V3+/V2+ redox pair is particularly affected, with coordination of chloride, dihydrogen phosphate and sulfate shifting the reduction potential by up to −0.5 V, relative to the water-only values. The VO2+/VO2+ redox pair exhibits a smaller degree of variation with electrolyte coordination, but the direction of the shift compared to water-only values differs; methanesulfonate, chloride and bisulfate all shift the reduction potential to more positive values, while the remaining electrolytes cause a negative shift in the reduction potentials. Due to the more significant effect of electrolyte on the V3+/V2+ redox pair, the overall cell potential largely reflects changes in the reduction potential of this redox pair.
Interestingly, when considering the case of electrolyte molecules peripheral to the first coordination sphere (Fig. 8b), variation is also observed in the individual reduction potentials and overall cell potential. Again, the V3+/V2+ redox pair is most affected, with shifts of up to ∼0.25 V. For the VO2+/VO2+ redox pair, the presence of any electrolyte shifts the reduction potential relative to water, but minimal variation between the electrolytes is observed. Consequently, shifts in the cell potential reflect those in the V3+/V2+ redox pair.
Regardless of whether electrolyte coordination is direct or peripheral, the mere inclusion of electrolytes more significantly shifts the reduction potential of the negative half-cell (EV3+/V2+) compared to the positive half-cell (EVO2+/VO2+). This asymmetric influence on the two half-cells results in an overall increase in the cell potential relative to the purely water-solvated case, thus enhancing the cell voltage.
From a design perspective, this suggests that careful selection of supporting electrolytes in VRFBs can be used not only to stabilise vanadium species but also to optimise cell potential, potentially improving energy density and overall battery performance.
4 Conclusions
In this investigation of the solvation environments of vanadium ions in VRFBs, a combination of dynamic, bulk aqueous simulations and static, isolated complex calculations were employed to predict the coordination behaviour of water and electrolyte molecules with the four relevant vanadium species: V2+, V3+, VO2+, and VO2+.Using validated classical MD models of vanadium ions in the presence of common VRFB electrolyte additives, a positive correlation was identified between electrolyte concentration and the coordination number of electrolyte molecules. However, the extent of electrolyte uptake into the first coordination sphere varied depending on the vanadium species and the electrolyte. On average, the electrolyte coordination number followed the trend V3+ > V2+ > VO2+ > VO2+. This trend can be attributed to the reduced number of accessible coordination sites in oxo-vanadium species—especially VO2+, where two sites are occupied by oxygen atoms—and the greater electrostatic attraction between more highly charged ions (e.g. V3+) and electrolyte anions.
Electrolyte-specific trends also emerged. Cl− and H2PO4− showed consistent coordination with vanadium ions even at low concentrations. This was confirmed by static thermodynamic calculations, which indicated that coordination of these anions was energetically favourable relative to their positioning outside the first coordination sphere. These findings implicate that direct coordination of Cl− and H2PO4− to vanadium ions may be a contributing factor in either the enhanced performance or stability of VRFBs as reported in experimental literature.
In contrast, methanesulfonate was predicted by MD simulations to coordinate poorly across all vanadium species. This aligns with the results of static calculations, which showed methanesulfonate coordination to be generally endergonic or only weakly exergonic (in the case of VO2+). Consequently, any experimentally observed benefits from methanesulfonate additives are likely to arise from mechanisms other than direct coordination to vanadium ions. Indeed, it has been suggested in the literature that the stability afforded from the inclusion of methansulfonate is derived from the initial dissociation of protons from the conjugate acid derivative, methanesulfonic acid.20
The coordination behaviour of sulfate and bisulfate was more ambiguous. Static calculations suggested that sulfate, but not bisulfate, should coordinate to vanadium ions. However, MD simulations showed high bisulfate coordination across all species and concentrations, while sulfate coordination was only significant at high loadings. A possible explanation for this discrepancy is the limitation of static calculations in the absence of modelling multi-molecule coordination scenarios for molecules with multiple donor atoms, which were indicated by MD results, particularly in the case of bisulfate.
Lastly, the modulation of vanadium ion redox potentials by electrolyte inclusion was explored. This effect was most evident in the negative half-cell (V3+/V2+), where the reduction potential shifted more significantly—towards more negative values—than in the corresponding positive half-cell. Notably, this shift occurred even in the absence of direct coordination and was attributed to a preferential stabilisation of V3+ relative to V2+, resulting in a greater reduction in its free energy. Consequently, the overall VRFB cell voltage was predicted to increase upon electrolyte inclusion.
These findings contribute to the growing understanding of the burgeoning field of VRFBs by providing insights into the coordination behaviour and solvation dynamics of vanadium ions in aqueous electrolyte environments. This work highlights the potential interplay in electrolyte selection, whereby the targeted design of VRFB systems could exploit the complementary benefits of additives that directly coordinate to vanadium ions alongside those that confer advantages more peripherally, beyond the first coordination sphere.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03216d.Acknowledgements
The authors gratefully acknowledge the New Zealand Ministry of Business, Innovation & Employment (MBIE) (Smart Ideas, Endeavour Fund, grant number UOCX2111) for financial support, including the provision of a doctoral scholarship for C. S. M. The University of Otago is also thanked for financial support. The authors wish to acknowledge the use of New Zealand eScience Infrastructure (NeSI) high-performance computing facilities as part of this research. New Zealand's national facilities are provided by NeSI and funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation & Employment's Research Infrastructure programme. URL: https://www.nesi.org.nz.References
- C. Liu, F. Li, L.-P. Ma and H.-M. Cheng, Adv. Mater., 2010, 22, E28–E62 CAS.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55 CrossRef CAS.
- E. Sum and M. Skyllas-Kazacos, J. Power Sources, 1985, 15, 179–190 CrossRef CAS.
- E. Sum, M. Rychcik and M. Skyllas-Kazacos, J. Power Sources, 1985, 16, 85–95 CrossRef CAS.
- M. Skyllas-Kazacos, M. Rychcik, R. G. Robins, A. G. Fane and M. A. Green, J. Electrochem. Soc., 1986, 133, 1057 CrossRef CAS.
- M. Skyllas-Kazacos, US4786567A, 1988.
- X. Wu, J. Liu, X. Xiang, J. Zhang, J. Hu and Y. Wu, Pure Appl. Chem., 2014, 86, 661–669 CAS.
- R. Joy, T. George, A. Das, M. J. Jabeen Fatima, A. Pullanchiyodan and P. Raghavan, Advanced Technologies for Rechargeable Batteries, CRC Press, 1st edn, 2024 Search PubMed.
- S. Kim, M. Vijayakumar, W. Wang, J. Zhang, B. Chen, Z. Nie, F. Chen, J. Hu, L. Li and Z. Yang, Phys. Chem. Chem. Phys., 2011, 13, 18186–18193 RSC.
- F. Rahman and M. Skyllas-Kazacos, J. Power Sources, 2017, 340, 139–149 CrossRef CAS.
- F. Rahman, Stability and Properties of Supersaturated Vanadium Electrolytes for High Energy Density Vanadium Redox Battery, PhD thesis, University of New South Wales, Sydney, Australia, 1998.
- M. Cheng, Electrolyte Optimization and Studies for the Vanadium Redox Flow Battery, PhD thesis, University of New South Wales, Sydney, Australia, 1991.
- Y. Wen, Y. Xu, J. Cheng, G. Cao and Y. Yang, Electrochim. Acta, 2013, 96, 268–273 CrossRef CAS.
- W. Xue-Wen, L. Su-Qin and H. Kelong, J. Inorg. Mater., 2010, 25, 641–646 CrossRef.
- Y. Yang, Y. Zhang, T. Liu and J. Huang, J. Power Sources, 2019, 415, 62–68 CrossRef CAS.
- Y. Yang, Y. Zhang, L. Tang, T. Liu, J. Huang, S. Peng and X. Yang, J. Power Sources, 2019, 434, 226719 CrossRef CAS.
- L. Li, S. Kim, W. Wang, M. Vijayakumar, Z. Nie, B. Chen, J. Zhang, G. Xia, J. Hu, G. Graff, J. Liu and Z. Yang, Adv. Energy Mater., 2011, 1, 394–400 CAS.
- Y. Chu, C. Liu, H. Ren, Y. Zhang and C. Ma, Int. J. Electrochem. Sci., 2016, 11, 1987–1996 CrossRef CAS.
- G. Kim, Y. Kim, T. Yim and K. Kwon, J. Ind. Eng. Chem., 2021, 99, 326–333 CrossRef CAS.
- S. Peng, N.-F. Wang, X.-J. Wu, S.-Q. Liu, D. Fang, K.-L. Huang and Y.-N. Liu, Int. J. Electrochem. Sci., 2012, 7, 643–649 CrossRef CAS.
- J. Zhang, L. Li, Z. Nie, B. Chen, M. Vijayakumar, S. Kim, W. Wang, B. Schwenzer, J. Liu and Z. Yang, J. Appl. Electrochem., 2011, 41, 1215–1221 CrossRef CAS.
- S. Roe, C. Menictas and M. Skyllas-Kazacos, J. Electrochem. Soc., 2015, 163, A5023 CrossRef.
- N. Kausar, A. Mousa and M. Skyllas-Kazacos, ChemElectroChem, 2016, 3, 276–282 CrossRef CAS.
- N. V. Roznyatovskaya, V. A. Roznyatovsky, C.-C. Höhne, M. Fühl, T. Gerber, M. Küttinger, J. Noack, P. Fischer, K. Pinkwart and J. Tübke, J. Power Sources, 2017, 363, 234–243 CrossRef CAS.
- S. Gupta, T. M. Lim and S. H. Mushrif, Electrochim. Acta, 2018, 270, 471–479 CrossRef CAS.
- M. Bon, T. Laino, A. Curioni and M. Parrinello, J. Phys. Chem. C, 2016, 120, 10791–10798 CrossRef CAS.
- F. J. Oldenburg, M. Bon, D. Perego, D. Polino, T. Laino, L. Gubler and T. J. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 23664–23673 RSC.
- H. Berendsen, J. Postma, W. van Gunsteren and J. Hermans, Intermol. Forces, 1981, 331–342 CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- K. Sasaki and T. Yamashita, J. Chem. Inf. Model., 2021, 61, 1172–1179 CAS.
- K. R. Hinkle, C. J. Jameson and S. Murad, J. Phys. Chem. C, 2014, 118, 23803–23810 CrossRef CAS.
- P. Li, B. P. Roberts, D. K. Chakravorty and K. M. J. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748 CrossRef CAS PubMed.
- J. C. Evans, Inorg. Chem., 1963, 2, 372–375 Search PubMed.
- I. Persson, Pure Appl. Chem., 2010, 82, 1901–1917 Search PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2002, 4, 4185–4191 RSC.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 Search PubMed.
- T. Lu, J. Chem. Phys., 2024, 161, 082503 CrossRef CAS PubMed.
- S. J. Plimpton, A. Kohlmeyer, A. P. Thompson, S. G. Moore and R. Berger, LAMMPS: Large-scale Atomic/Molecular Massively Parallel Simulator, 2023 DOI:10.5281/zenodo.10806852.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- C. Tang and D. Zhou, Electrochim. Acta, 2012, 65, 179–184 CrossRef CAS.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A:At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- P. Langevin, C. R. Acad. Sci., 1908, 146, 530–533 CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- A. D. Becke, Phys. Rev. A:At., Mol., Opt. Phys., 1988, 38, 3098–3100 CAS.
- J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822–8824 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Sepehr and S. J. Paddison, Chem. Phys. Lett., 2013, 585, 53–58 CrossRef CAS.
- S. N. Tussupbayev and G. M. Kudaibergenova, Russ. J. Phys. Chem. A, 2020, 94, 1616–1622 CrossRef CAS.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422 CrossRef CAS PubMed.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- M. Bühl and M. Parrinello, Chem. – Eur. J., 2001, 7, 4487–4494 CrossRef.
- J. Krakowiak, D. Lundberg and I. Persson, Inorg. Chem., 2012, 51, 9598–9609 CrossRef CAS PubMed.
- C. Choi, S. Kim, R. Kim, Y. Choi, S. Kim, H.-Y. Jung, J. H. Yang and H.-T. Kim, Renewable Sustainable Energy Rev., 2017, 69, 263–274 CrossRef CAS.
- C. Choi, H. Noh, S. Kim, R. Kim, J. Lee, J. Heo and H.-T. Kim, J. Energy Storage, 2019, 21, 321–327 CrossRef.
- Y. Zhang, R. C. Haushalter and J. Zubieta, Inorg. Chim. Acta, 1997, 260, 105–110 CrossRef CAS.
- Z. Jiang, K. Klyukin and V. Alexandrov, J. Chem. Phys., 2016, 145, 114303 CrossRef.
- A. A. Ivakin and E. M. Voronova, Russ. J. Inorg. Chem., 1973, 18, 956–959 Search PubMed.
- V. H. Strehlow and H. Wendt, Inorg. Chem., 1963, 2, 6–10 CrossRef.
- M. Vijayakumar, S. D. Burton, C. Huang, L. Li, Z. Yang, G. L. Graff, J. Liu, J. Hu and M. Skyllas-Kazacos, J. Power Sources, 2010, 195, 7709–7717 CrossRef CAS.
- M. Uudsemaa and T. Tamm, J. Phys. Chem. A, 2003, 107, 9997–10003 CrossRef CAS.
- S. G. Bratsch, J. Phys. Chem. Ref. Data, 1989, 18, 1–21 CrossRef CAS.
| This journal is © the Owner Societies 2026 |