Paratropic ring currents discovered in six-membered rings of conical nanographenes: carboncones

Abstract

The magnetically induced current density in carboncone[1,3] and [1,5] has been determined and visualized, qualitatively in terms of maps of current, and quantitatively in terms of bond current strengths. The divergence of the isotropically averaged Lorentz force density has also been calculated. All these theoretical tools provide a coherent picture of the magnetic response of carboncones, which reveals unusual robust paratropic current loops located in many of the six-membered rings.

---

1 Introduction

Conical allotropes of carbon have been known for a long time.^1–5 However, only recently the rational synthesis of a carboncone containing 70 carbon atoms, with one pentagon on the cone cap, has been independently reported by two groups.^6–8

The presence of a pentagonal face deeply affects the magnetic response as it hosts a paratropic (antiaromatic) ring current. Actually, this type of circulation also characterizes the 5-membered rings of corannulene⁹ as well as those of fullerenes¹⁰ and carbon nanotubes (CNT).¹¹ It is therefore expected that a paratropic ring current will also occur in the 5-membered rings of carboncones, leaving open the question of what type of current will flow in the rest of the molecule.

Fascinated by the beautiful structure of these conical nanographenes and intrigued to know the shape and intensity of their ring currents, if any, we initiated a study of the magnetically induced current density in carboncones. We were especially interested in using the magnetic criterion to evaluate the local aromaticity of the various types of rings that form the cone wall, which were shown to vary greatly on the basis of NICS values reported in ref. 7. Furthermore, we wanted to learn more about the current density induced in the π electron cloud, in particular to see how it compares with that induced in planar polycyclic aromatic hydrocarbons of similar size, see for example ref. 12.

According to the proposed nomenclature⁷ of carboncone[n,m], where n refers to the number of pentagons on the cone cap, and m refers to the number of intact circles of fused hexagonal rings between the cone tip and the cone rim, we have considered carboncone[1,3] (C₈₀H₂₀), as well as carboncone[1,5] (C₁₈₀H₃₀), to study the effect of increasing the height of carboncones, see Fig. 1. We have also expanded our studies to include the truncated carboncone[1,3], C₇₀H₂₀, which is the first carboncone ever obtained by rational synthesis,^6,7 but, as we will see shortly, its magnetic response is quite similar to that of carboncone[1,3] (see details in the SI). Results concerning the truncated carboncone[1,5] C₁₇₀H₃₀ are also reported in the SI.

Fig. 1 Intact carboncones in different colors: carboncone[1,1] (light blue, corannulene, C₂₀H₁₀), carboncone[1,3] (dark blue, C₈₀H₂₀), and carboncone[1,5] (orange, C₁₈₀H₃₀). Intermediate carboncone[1,2] and [1,4] have odd numbers of carbon atoms and are not considered in the present work.

2 Computational details and methods

A brief description of the methods employed in this work are given here in the following. Molecular geometries were optimized within the Born–Oppenheimer approximation¹³ for the (closed-shell) singlet electronic state at the B3LYP/6-31G(d,p) level of theory, assuming the C_5v symmetry point group for all molecules, using the Gaussian-16 system of programs.¹⁴ The stability of each found state was verified by means of the standard technique provided by the Gaussian package. The absence of imaginary vibrational frequencies was also verified. Optimal Cartesian coordinates are collected within the SI.

The local aromaticity indices HOMA, and NAO-MCBO (see below) have been computed with Multiwfn.¹⁵

2.1 Current density calculation

When an external, uniform, static magnetic field (B_ext) acts on a molecule, the linear approach has been found to provide sufficiently accurate predictions of the response properties. Therefore, for our purposes, we rely on the Rayleigh–Schrödinger perturbation theory to obtain the first-order correction to the magnetically induced current density (MICD) J^B = [scr J, script letter J]B_ext, where [scr J, script letter J] is the second-rank current density tensor. Furthermore, to ensure origin independence of the calculated MICD, we use the CSGT approach developed by Keith and Bader,¹⁶ also known as continuous transformation of the origin of the current density (CTOCD),¹⁷ adopting the DZ2 variant which enhances the quality of the current in the vicinity of the nuclei.^18,19 Overall, the DZ2 method provides current density maps that are equivalent to those obtained adopting the so called ipsocentric approach.^20,21 In agreement with the latest implementation of the method, the required perturbed orbitals are obtained using the Gaussian program²² by means of the “NMR(CSGT)” keyword, together with the “output(wfx,csgt)” option at the B3LYP/6-311+G(2d,1p) level of theory. The SYSMOIC package²³ can then be used to calculate, for any direction of the perturbing magnetic field, induced current density maps (CDM), bond current strengths (BCS) and many other quantities connected with the current density.²⁴

2.2 Orbital selection

In carboncones σ/π orbital separation is not strictly possible due to the absence of a molecular plane. However, descendants of p orbitals can be easily detected by using a combination of symmetry arguments and analysis of the contributions to the electron density given by each individual orbital. Details on the procedure we adopted for the π orbital detection are given within the SI. Thanks to the almost smooth surfaces of the carbon cones only few π-orbital candidates were not considered for the too large σ contamination. In summary 31, 40, 83, and 87 π-orbitals were detected and used in the following for C₇₀H₂₀, C₈₀H₂₀, C₁₇₀H₃₀, and C₁₈₀H₃₀, respectively.

2.3 Bond current strengths

Integration of the current density, induced by a unitary magnetic field, crossing perpendicularly a plane bisecting the line connecting a pair of bonded atoms, provides the so-called bond current strength (BCS), or current susceptibility.²⁵ According to our implementation,^26,27 integration domains are enclosed within contour levels of the current cross section over the bisecting plane. In this way calculated BCS do not depend on the shape and size of the intersection plane, depending only on the chosen value of the contour level. Assuming a fixed absolute value of 0.001 a.u. for the contour value that delimits the integration domain, a good balance of current flowing in both directions across the plane, as well as the ability to compare BCSs within the molecule and even with those of other molecules, is obtained. This last aspect has been used below to report BCS values in percentage with respect to the benzene ring current strength (BRCS) of 12 nA T⁻¹ taken as the yardstick. In the case of paratropic ring currents, one might argue that a different reference would be more appropriate, such as, for example, cyclobutadiene. However, this is not strictly necessary. In fact, considering that the cyclobutadiene ring current strength (CRCS) has been evaluated to be 20 nA T⁻¹, same method used to evaluate the BRCS,²⁸ then it is sufficient to scale down any BCS in percentage of the BRCS by a factor of 1.67 to obtain the same BCS in percentage of the CRCS.

A notable feature of BCS is the ability to reveal current delocalization that is characteristic of conjugated systems, especially aromatic/antiaromatic ones. In an ideal case, a current density localized within a bond region makes no contribution to the BCS due to equal amounts of current flow through the intersection plane in both directions. In contrast, a non-zero BCS reveals that a portion of the current flows out from one bond side and then returns on the other side for continuity. In cyclic and polycyclic aromatic hydrocarbons bond current strengths are given almost entirely by the π-electrons thanks to their mobility over the molecule.²⁷ This makes BCSs excellent quantitative indicators of aromaticity that do not depend explicitly on geometrical parameters.

2.4 π-DIAL method

In general, for both CDM and BCS the choice of the direction of the perturbing field is not as straightforward as in the case of planar polycyclic aromatic hydrocarbons (PAH). Fortunately, for carbon cones the situation is not particularly difficult, and considering the magnetic field perpendicular to the pentagonal face of the cone cap seems the most appropriate choice. However, it should be noted that various methods that are independent of the direction of the magnetic field are available. These are related to the current density tensor (CDT) and are known by acronyms such as the very well known ACID,^29,30 the AACID,³¹ or the CDT trace.³² Another recently introduced quantity, which is independent of the orientation of the magnetic field, is the isotropically averaged Lorentz force density (IALFD).³³ IALFD is a vector field which accounts for the energy change of a randomly tumbling closed shell molecule placed in an uniform magnetic field. In contrast with field-independent quantities previously defined, IALFD has a direct physical interpretation. The negative or positive value of its divergence, which we have termed DIAL, gives the amount of local diamagnetism or paramagnetism, respectively, allowing the distinction of aromatic, antiaromatic, and non-aromatic molecules on the basis of a magnetic criterion.³³ Visualization of the π contribution to the divergence of the isotropically averaged Lorentz force density, i.e., π-DIAL, has been found useful to differentiate the aromaticity amount of the different rings in non planar PAH.³⁴

3 Results and discussion

3.1 Carboncone[1,3]

The calculated current density map of carboncone[1,3], induced in the π-electrons by a magnetic field parallel to the main symmetry axis of the molecule, is shown on the left of Fig. 2. All-electrons BCS are reported on the right of Fig. 2. Separate contributions to BCSs from π-electrons and all but π-electrons can be found within the SI. As discussed above, the contribution to BCS from all but π-electrons is negligible. Therefore, the two maps in Fig. 2 provide complementary information on a qualitative and quantitative basis, respectively.

Fig. 2 Left: Current density map induced in the π-electrons of carboncone[1,3] (C₈₀H₂₀) by a uniform magnetic field parallel to the C₅ symmetry axis. Current lower than 0.033 a.u. is not shown. Right: All-electrons bond current strengths. Numbers attached to each arrow give the current strength in percentage of the benzene ring current strength (BRCS) of 12.0 nA T⁻¹ taken as the yardstick.²⁷ Diatropic/paratropic circulations are clockwise/anticlockwise.

The most striking observations is the appearance of six paratropic ring current loops enclosed within a strong diatropic global current flowing along the rim of the molecule. The current strength on the rim is estimated to exceed 20 nA T⁻¹ (∼70% greater than the BRCS). The expected paratropic ring current on the pentagonal face of the cone cap is nearly 20% greater than the BRCS. The remaining five paratropic ring current loops, having a strength ranging from 56% to 65% of the BRCS, represent something unusual rarely seen before with such clarity. For convenience of the discussion, in the following we will refer to these paratropic 6-membered rings as P6R. At first glance, comparison with probability current density maps calculated for ideal Clar systems reported in ref. 12 seems to indicate some similarity. Nothing could be more misleading. As said, the induced current in these five rings of carboncone[1,3] is paratropic instead of being diatropic as in ideal Clar systems; second, placing a Clar sextet in each of the P6R would result in an unpaired electron inside the pentagonal ring of the cone cap. In a sense, the five P6Rs around the corannulene fragment are the result of many adjacent circulations, which add together to provide the enhanced paratropic loops, see later for a discussion.

The π-DIAL map shown in Fig. 3 clearly emphasizes the antiaromatic character of these rings. Since this kind of map considers all possible orientations of the inducting magnetic field, it is quite evident that the current flow generated when the field is parallel to the symmetry axis strongly prevails compared to all other directions. The isosurface value, adopted to produce Fig. 3, was calibrated to provide a closed surface for the central pentagonal ring. Consequently, all other rings have a perforated surface; the size of the hole varies depending on the current strength.^24,34 Although the calculated NICS^36,37 for the antiaromatic rings are in qualitative agreement with what has just been described, a quantitative agreement is lacking. Reported NICS values are 12.79 and 2.65 for the central pentagonal ring and the surrounding rings, respectively,⁷ which corresponds to a ratio of ∼4.8, whilst the current strength ratio is ∼2. Evidently, there is an overestimation/underestimation of the NICS of the central/outer paratropic loops. In fact, the use of the NICS as a magnetic indicator of aromaticity has often been criticized,^38–44 mostly because the tensor character of the magnetic response is neglected and also because it contains a supplementary paratropic contribution due to very localized currents around bonds and nuclei of σ and inner-shell electrons. Our current strengths are free from any geometrical factor, such as loop area or some inverse power of the loop radius;⁴⁵ therefore they provide a reliable estimation of the ring antiaromaticity.

Fig. 3 π-DIAL map of carboncone[1,3]. Red/blue isosurface values are +0.003 and −0.003 a.u., respectively. The ChimeraX program³⁵ was used to make the plot.

Now, let us return to the point raised above concerning the possibility of discussing the five paratropic currents in benzenoid rings in terms of superposition of current circulations. Later on we will discuss the decomposition of the overall pattern in terms of circulations running on individual rings. For the time being, we start considering the sum of orbital contributions to the current density. According to the few-electron model, only a small subset of the high-lying π electrons dominate the more complex patterns of current in polycyclic π systems.²¹ Moreover, orbital contributions to the current density obey a symmetry-based selection rule.²⁰ In this regards, it is interesting to observe that the symmetries of the HOMO and HOMO−1 are E₁ and E₂, respectively. Also their energies are very close, differing only at the forth decimal place (the HOMO−2 is much below). The symmetry of the LUMO is E₁. Therefore a pure paratropic contribution is predicted for the HOMO → LUMO virtual transition; a pure diatropic contribution is predicted for the HOMO−1 → LUMO virtual transition; and these two should prevail over all other contributions. This is very satisfactorily confirmed by the calculated HOMO and HOMO−1 contributions to the MICD shown in Fig. 4. The plots have been made calculating the individual orbital contributions over surfaces of points having the shape of the cone at a distance of 1 a.u. outside (left) and inside (right) from the molecular rings, where the maximum of π-electron density is expected to occur. As can be observed, the HOMO (top) provides three concentric homotropic anticlockwise (paratropic) circulations, one over/below (left/right) the pentagonal cone cap, an external over/below the rim, and another between the rim and the corannulene fragment. An interesting feature of the latter is that it bifurcates as it passes through the corner hexagons of the smaller carboncone^1,2 fragment. Inside the cone the current strength is higher due to the major overlap of the carbon p atomic orbitals. Conversely, the HOMO−1 contribution, shown in the center of Fig. 4, display only two concentric clockwise (diatropic) current circulations, one internal along the corannulene fragment border, and a second over/below the external rim. The latter bifurcates as it passes through the corner hexagonal rings. The sum of the HOMO and HOMO−1 contributions to the MICD is shown in the bottom of Fig. 4 and, as it can be appreciated, it already corresponds very satisfactorily to the total π-electron MICD shown in Fig. 2. Including the contributions of others low energy orbitals results in only small changes to the final result.

Fig. 4 Frontier orbital contributions to the MICD of carboncone[1,3]. Top HOMO; center HOMO−1; bottom the sum of the two. Left: At 1 a.u. outside the cone; right: at 1 a.u. inside the cone. Current lower than 0.033 a.u. is not shown.

The orbital decomposition provides one way to understand the forming of the five paratropic loops. The currents generated by the HOMO and HOMO−1 between the rim and the cone cap, flow on two circuits that only partially overlap. Along the shared portions of the circuits there is a cancellation of current. The non-shared portions provide the paratropic loops in those rings that cannot be classified as a Clar's sextet to form a Clar system, namely, a resonance structure with the largest number of disjoint aromatic π-sextets, i.e., benzene-like moieties.⁴⁶

This last consideration opens an interesting question that leads to an equally interesting conclusion, i.e., since carboncone[1,3] is not “fully benzenoid”, how many Clar structures can we devise and how many of them present a Clar's sextet in the P6R? Starting from the corannulene fragment, two separated sextets can be placed at once which can migrate to the adjacent rings in 5 different ways. For each of them, it is possible to position at most 7 additional Clar setxtets in 3 different ways, resulting in a total of 5 × 5 = 25 Clar structures with 9 sextets each, see Fig. 5 for a scheme of one of them.

Fig. 5 One of the 15 Clar structures of carboncone[1,3].

Now, one can count how many times a sextet is found in the P6R. Such a counting turns out to be zero, a result which is not easy to guess a priori. With the exception of the rings on the corners, for which the number of sextets is also 0, all other rings do have Clar sextets for some of the 25 Clar structures (Fig. 6). This means that P6Rs (e.g. ring D in Fig. 6) experience diatropic currents induced in the rings around them. In other words, one can think of a migrating diatropic ring current around each P6R, which manifests itself through the fixed paratropic loops.

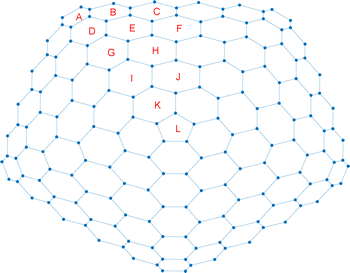
Fig. 6 Unique rings of carboncone[1,3] and number of times a Clar sextet is found in them when one considers the 25 Clar structures.

Another interesting fact, which explains the difference of ∼1 ppm between the ¹H NMR chemical shifts of the two types of perimeter protons, is the bifurcation of the perimeter current into two branches of different strengths at the corner rings, i.e., 76% of the BRCS of the outer branch and 103% of the BRCS of the inner branch, see left of Fig. 2. This can be fully rationalized by considering the sum of the HOMO and HOMO−1 contributions shown in Fig. 4. The HOMO current does not bifurcate and remains only on the outer edge thus reducing the HOMO−1 contribution. The proton attached to the corner rings (rings A in Fig. 6) resonates at higher field.

3.2 Carboncone[1,5]

To study the effect of the cone elongation on the MICD, we have considered carboncone[1,5], C₁₈₀H₃₀. Calculated current density map induced in the π-electrons by a magnetic field parallel to the main symmetry axis of the molecule, is shown on the left of Fig. 7. All-electrons BCS are shown on the right.

Fig. 7 Magnetically induced current density in carboncone[1,5] (C₁₈₀H₃₀). See caption of Fig. 2 for details. Due to some calculation inaccuracies, BCS values deviate slightly from the C_5v symmetry point group.

A huge diatropic current flowing on the external rim of the molecule can be seen, which bifurcates as it passes through the rings annexed to both sides at each corner. Before first bifurcation the strength is nearly 220% of BRCS, after the first bifurcation the strength of the outer branch is ∼133% of BRCS, and after the second bifurcation the strength of the outer branch goes down to ∼48% of BRCS. As a consequence, the three symmetry non-equivalent protons are predicted to give rise to three distinct NMR signals, the one at lowest field for protons nearest to the highest current, and the one at highest field for protons attached to the corner rings. Relative to the chemical shift of the protons on the corner ring, the signals for the more strongly deshielded protons are calculated to lie 1.4 and 1.7 ppm further downfield.

Sixteen paratropic current loops, ten more than in carboncone[1,3], are enclosed by the external diamagnetic current, proving that P6Rs are not rare events. In this regard, we underline that some P6Rs have been previously reported, as in the case of the central ring of coronene[9] and in one hexabenzocoronene isomer (see 3 in ref. 47). The latter, in particular, is interesting as the central hexagon is surrounded by six, radially disposed, naphthalene units, which support the P6R as a consequence of the merging of as many migrating sextets, as well as the huge diatropic perimeter current. P6Rs are also found in fullerene-240 of I_h symmetry, where each of the 12 pentagonal faces is surrounded by three intact circles of fused hexagonal rings, i.e., exactly as in carboncone[1,3]. A substantially similar current density map induced in the π-electron cloud of this large fullerene is reported in the SI. The calculated magnetizability of the I_h fullerene-240 is 8.5 times higher than that of fullerene-60,⁴⁸ indicating that the presence of P6Rs does not cause any increase in molecular paramagnetism.

The strength of the paratropic loop on the pentagonal face of the cone cap of carboncone[1,5] is considerably larger than in carboncone[1,3], reaching nearly 170% of the BRCS, slightly larger than the bond current strength in cyclobutadiene. The remaining fifteen P6Rs can be divided into two circles, one with five P6Rs, similar to the one in carboncone[1,3], the second with ten P6R having a smaller strength. Unlike carboncone[1,3], the P6Rs in each circle can be seen to be interconnected by a current that is anything but negligible, i.e., 34% of BRCS in the first circle flowing counterclockwise (paratropic), and 25% of BRCS in the larger circle flowing clockwise (diatropic). Interestingly, the currents along the circles are disconnected from each other, as well as to the current in the cone cap and to the current along the perimeter, i.e., the current strengths for radial bonds are all vanishingly small.

Fig. 8 π-DIAL map of carboncone[1,5]. See Fig. 3 caption for other details.

The π-DIAL map of carboncone[1,5] nicely summarize the results described above. All the paratropic regions are well represented. The size of the hole inside the perforated surfaces increases as the P6R current strength decreases. In particular, the red surfaces in the second circle are indeed open.

In carboncone[1,5] the symmetries of the HOMO and HOMO−1 are reversed with respect to those in carboncone[1,3], being E₂ and E₁ respectively. The symmetry of the LUMO is E₁. Therefore a pure diatropic contribution is predicted for the HOMO → LUMO virtual transition; a pure paratropic contribution is predicted for the HOMO−1 → LUMO virtual transition; and these two should prevail over all other contributions. This is nicely confirmed by the calculated contributions shown in Fig. 9. Three/four concentric diatropic/paratropic currents can be easily identified for the HOMO/HOMO−1 contributions. As before, these contributions flow on circuits that only partially overlap. Along the shared portion of the circuits, a substantial, though not complete, cancellation of currents occurs. The sum of the two shown in the bottom of Fig. 9 prove also in this case the P6R formation.

Fig. 9 Frontier orbital contributions to the MICD of carboncone[1,5]. Top HOMO; center HOMO−1; bottom the sum of the two. Left: At 1 a.u. outside the cone; right: at 1 a.u. inside the cone. Current lower than 0.033 a.u. is not shown.

Results for the truncated carboncones containing just 70 and 170 carbon atoms, respectively, are collected in the SI. Apart from the absence of corner rings, no substantial differences are noted compared to the intact carbon cones. Paratropic currents localized on the six-membered rings, which cannot accommodate a Clar sextet, persist in all the cases considered here.

3.3 Local aromaticity and Clar structures

Although aromaticity has been first introduced as a molecular property, the presence of many rings in a polycyclic system has naturally led to the quest for definitions of local aromaticity. The concept of local aromaticity arises naturally in Clar's theory, as in polycyclics different rings host Clar's sextets in different numbers out of the possible Kekulé structures,⁴⁹ but the quantification of local aromaticity has been and still is a matter of concern.

For the carboncones, we have computed 4 indices, that are considered useful for the quantification of local aromaticity: the Polansky–Derflinger (PD) index ρ_L, the Harmonic Oscillator Model of Aromaticity (HOMA) index, the natural atomic orbital based normalized multi-center bond order (NAO-MCBO),⁵⁰ and the ring current strength (RCS). Before presenting the results, we breifly summarize some basic features of these indices, which have significantly different backgrounds.

The Polansky–Derflinger (PD) index⁵¹ is one of the oldest wavefunction-based indices; its discussion appears particularly appropriate here, as it was introduced to check whether, in the framework of molecular orbital calculations, it was possible to identify as more aromatic the same rings which were identified according to Clar. The PD index, called ρ_L in the original paper, is a measure of the similarity of a given six-membered ring L within a polycyclic compound to benzene itself; it requires a computation in the framework of Hückel theory, where Coulson bond order is an indicator of bonding. In practice, the index requires the computation of the sum of the squares of all Coulson bond orders of the ring, upon substitution of one of the two factors of each product appearing in the sum of squares with the corresponding term coming from a calculation of an isolated benzene. Further details can be found in the SI. In the original paper the PD index was tested for several alternant polycyclics, and it was shown to be effectively higher for those rings endowed with a Clar sextet in a larger fraction of Kekulé structures.

In a study on benzenoid hydrocarbons,⁵² the PD index has been shown to correlate well (logarithmically, not linearly) with six-center indices,^52,53 which are generalizations of Mayer two-center bond order⁵⁴ and have been also called Multi-Center Bond Orders (MCBO).⁵⁰ These six-centers bond orders are known to strongly depend on the basis set^50,52 and the dimension of the ring. The basis-set dependence is reduced using a Natural Atomic Orbital (NAO) basis,⁵⁰ and the ring-size dependence is effectively accounted for using the n-th root for a cycle of size n.⁵⁵ As opposed to the PD index, the normalized NAO-MCBO is not limited to the Hückel method, and can thus be computed with modern DFT and large basis sets.

The widely used HOMA index is based on comparison of bond lengths of the ring with ideal reference values; the differences of lengths are squared, pre-multiplied by a parameter, and subtracted from 1.^56,57 This index has been recently restated as a good tool to identify similarity between fragments and target cyclic molecules, even saturated.⁵⁸

Finally, the ring current strength (RCS) has had a dominat role in the field of aromaticity as it was used in early works on magnetic aromaticity, studied at the Hückel level.^59–61 Its definition relies on the continuity equation: for a delocalized continuous current, it is always possible to write bond current strengths as a summation of currents flowing over individual rings, which is the essence of Kirchhoff's law.⁶² This approach will give a decomposition of the total current, that is alternative to that performed in terms of orbital contributions within the ipsocentric approach, as discussed commenting Fig. 4. Inasmuch as the basis set is large enough and the bond current strengths are accurately obtained by integration, RCS can be retrieved from BCS obtained at DFT level.⁶³ In the presence of small errors of integration, optimal RCSs can be obtained as follows: starting from an Ansatz of all homotropic rings, each BCS comes out from the difference of the RCSs of the two abutting rings, e.g. BCS_i = +RCS_i1 − RCS_i2, with positive sign if the bond current flows in the direction of the Ansatz ring current. Considering that there are more bonds than rings, equations like the one exemplified define an overdetermined set, that can be solved by linear least squares. As we have determined RCS from BCS that have been normalized by the BCS of benzene, the RCS are also normalized by the benzene value: an RCS of 100 means a ring current strength of the same tropicity and value of that of benzene.

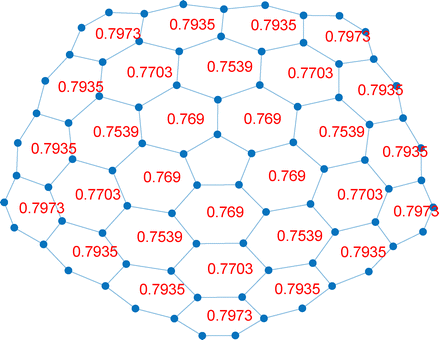
The values obtained are collected in Table 1, where the unique rings are labeled by letters (see Fig. 6–10). The PD indices are shown in a redundant manner (also for non-unique rings) in Fig. 11 and 12.

Table 1 Aromaticity indices (all adimensional) of the rings of two carboncones. Lettering of the rings as in Fig. 6 and 10

Carbon cone	Ring	PD	NAO MCBO	HOMA	RCS	#Clar sextets
[1,3]	A	0.7973	0.5182	0.3919	76	0
	B	0.7935	0.5451	0.6461	171	12
	C	0.7703	0.5369	0.6753	179	11
	D	0.7539	0.5087	0.5610	113	0
	E	0.7690	0.5311	0.7116	171	10
	F	—	0.4854	0.6918	52
[1,5]	A	0.7937	0.5099	0.3393	49
	B	0.7820	0.5247	0.5423	133
	C	0.7804	0.5376	0.6410	218
	D	0.7689	0.5345	0.6943	246
	E	0.7641	0.5279	0.6732	234
	F	0.7609	0.5183	0.6242	186
	G	0.7603	0.5189	0.6434	198
	H	0.7644	0.5274	0.6627	259
	I	0.7651	0.5316	0.6598	260
	J	0.7559	0.5104	0.5637	174
	K	0.7648	0.5283	0.6870	255
	L	—	0.4867	0.6930	56

---

Fig. 10 Unique rings of carboncone[1,5].

Fig. 11 Polansky indices (PD) of carboncone[1,3].

Fig. 12 Polansky indices (PD) of carboncone[1,5].

The PD results show that all rings are endowed with a local aromatic character. However the local aromaticity of the rings where a paratropic current has been observed in the DFT current density map, is smaller than the local aromaticity of all abutting rings. As an example, starting from the PD index, ring D in carboncone[1,3] has a PD of 0.7539, which is smaller than the PD of all abutting rings, which are of kind B (0.7935), C (0.7703) and E (0.7690). The same is true for rings J and F in carboncone[1,5]. Notably, the same result is obtained with the other three indices. It is also interesting to consider whether the indices are somehow correlated with the numbers of Clar sextets counted over the 25 Clar structures (Fig. 6 and Table 1). For carboncone[1,3], it turns out that both NAO-MCBO and RCS have a good correlation coefficient with the numbers of Clar sextets (0.945 and 0.948, respectively), while the correlation is poorer for the HOMA (0.837) and definitely poorer for PD (0.115). In particular, the PD has a high value for ring A, which is devoid of Clar sextets. Likely, the non-alternant nature of carboncones causes this bad performance of the PD index.

3.4 Predicted magnetizabilities and chemical shifts

The linear magnetic response properties of a molecule, in terms of magnetizability (ξ) and nuclear magnetic shielding (σ^I) tensors, are fully determined by the second-rank current density tensor via: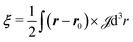where r₀ is an arbitrary origin and R_I is the position of a magnetic nucleus I.⁶⁴ Considering the isotropic value of the shielding tensor σ_I = 1/3Tr(σ^I), the chemical shift relative to TMS of a magnetic nucleus I can be calculated as⁶⁵

δ_I = σ_ref − σ_I + δ_ref (3)

where “ref” stands for a proper reference compound, for example, benzene.

Now, before presenting the predicted magnetizability and nuclear magnetic shielding constants of the carboncones examined in this paper, we believe it is essential to provide some credibility support to the quality of MICDs described above using available experimental data. This can be done by comparing the experimental ¹H and ¹³C NMR chemical shifts of the penta-mesityl carboncone[1,2] derivative of C₇₀H₂₀, reported in ref. 7, with the results obtained using the same method of computation, i.e. B3LYP/6-311+G(2d,1p)//B3LYP/6-31G(d,p). As detailed in the SI, the agreement between experimental and computed values is excellent: a standard deviation of 1.21 ppm for the 20 unique aromatic C atoms and of 0.13 ppm for the 3 unique aromatic H atoms (mean absolute errors are 0.99 and 0.06 ppm, respectively). Focusing on the ¹H NMR chemical shifts, the large downfield shift of the aromatic protons (measured at 9.90, 9.83, and 8.72, and computed at 10.06, 10.00 and 8.78 ppm) ougth to come out from a very intense global diatropic current flowing on the carboncone rim, which in the pristine nanocone is indeed computed to be 27–53% larger than that of benzene (see Fig. S5). Owing to the orientation of mesityl groups, which are almost perpendicular to the carboncone surface,⁷ protons close to the substituent undergo an additional shielding effect by the ring current in mesityl-moieties, which is larger for the protons 82 (see Fig. S7 in the SI) facing the benzene ring centre (appearing as a doublet at 8.72 ppm). The excellent agreement obtained leave us confident of the quality of computation performed on the pristine nanocones, devoid of the mesityl substituents, which will now be discussed.

The calculated magnetizabilities of carboncones[1,3] and [1,5] are collected in the Table 2. Within the same table the magnetizability of benzene, calculated at the same level of theory, is also reported to emphasize again the good quality of the calculation. In both carboncones the parallel component of the magnetizability tensor is much larger than the perpendicular one, which leads to a large value of the anisotropy defined as Δξ = ξ_‖ − ξ_⊥.

Table 2 Calculated magnetizabilities at B3LYP/6311+G(2d,1p) level of theory (in cgs ppm) obtained via eqn (1)

Carboncone	ξ⊥	ξ‖	ξAv	Δξ
[1,3]	−491.2	−2009.2	−997.2	−1518.0
[1,5]	−1312.9	−6038.5	−2888.1	−4725.6
C6H6 Theo	−33.5	−99.1	−55.4	−65.7
C6H6 Expt^66	−34.9	−94.6	−54.8	−59.7

---

The ratio of the calculated values of the parallel components of the two cones, which is very close to 3, can be related to the different molecular sizes and different induced current intensities. From the optimized geometries of the two carboncones, we obtain an average radius of the circles running over the terminal carbons equal to 10.08 and 6.67 Å; then, assuming that ξ_‖ ≈ IA, where A in the circle area, we write 3 ≈ I_[1,5]/I_[1,3](10.08/6.67)² from which we get I_[1,5]/I_[1,3] ≈ 1.31, a value that is very close to the BCS ratio 220/170 = 1.29 discussed above. Therefore, it is the global diatropic current delocalized at the edge of the cone that determines the magnetizability of the molecules, with likely little contribution from other types of circulations.

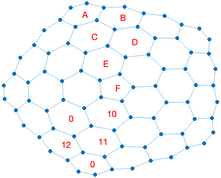
Calculated chemical shifts have been obtained integrating the current density by means of the Becke's method,⁶⁷ adopting a Lebedev's quadrature of order 35 and a Gauss–Chebyshev radial integration with 35 radial points. Results are reported from largest to smallest in Table 3 for both [1,5] and [1,3] carboncones and both magnetic nuclei. Enumeration for the assignment is given in the schemes collected in Fig. 13.

Table 3 Calculated chemical shift at B3LYP/6311+G(2d,1p) level of theory with respect to TMS in ppm obtained via eqn (2) and (3)

^13C	[1,5]	[1,3]	^1H	[1,5]	[1,3]
C1	139.79	138.44	H1	13.15	10.34
C2	135.87	131.87	H2	11.72	9.24
C3	134.28	131.50	H3	10.00
C4	132.28	129.90
C5	131.69	129.67
C6	128.45	124.07
C7	127.26	123.65
C8	125.51	121.43
C9	125.32	121.36
C10	122.21	118.02
C11	121.93
C12	120.81
C13	120.19
C14	118.86
C15	118.69
C16	117.91
C17	117.78
C18	117.59
C19	117.54
C20	116.11
C21	115.04

---

Fig. 13 Enumeration schemes for [1,3] and [1,5] carboncones from largest to smallest chemical shift.

According to C_5v symmetry point group, we observe that: (i) carboncone[1,5] displays 21 different ¹³C signals within the aromatic range 139.79–115.04 ppm, with carbons C1, C3, C6, C12, C16, and C21 5-fold degenerate, while the other 15 are 10-fold degenerate; (ii) instead, 10 are the ¹³C signals in carboncone[1,3] within the aromatic range 138.44–118.02 ppm, with carbons C1, C3, C4, and C10 5-fold degenerate while the other 6 are 10-fold degenerate; (iii) 3 and 2 are the unique protons in [1,5] and [1,3] respectively, all of them 10-fold degenerate.

A similar trend of ¹³C chemical shifts can be seen in both shorter and longer carboncones. In particular, the carbons forming the pentagonal cap are the most de-shielded, followed by the carbons on the outermost perimeter. Carbons at higher field are spread between the cone cap and border ring.

As it concerns proton chemical shifts, the calculated separation of signals, which amounts to 1.1 ppm in carboncone[1,3] and 1.43 and 1.72 ppm in carboncone[1,5], follows perfectly the shape and strength of the induced current along the border ring, see Fig. 2 and 7. In absolute terms, the exceptionally very low-field ¹H chemical shift of 13.15 ppm calculated for carboncone[1,5] is determined by a current whose strength is almost 220% of the BRCS, i.e., quite a big one.

We hope that the provided predictions of magnetizability and chemical shifts will prove useful in the near future for the characterization of the carboncones after their synthesis.

4 Conclusions

The magnetic response of carboncones[1,m], in terms of magnetically induced current density, reveals something unusual for neutral closed-shell polycyclic aromatic hydrocarbons, namely: robust paratropic current loops located in six-membered rings.

We have provided arguments in favor of the fact that these paratropic loops are actually the result of many migrating diatropic loops all around rings that cannot host Clar's sextets. Can we say that those rings are antiaromatic when it is the aromaticity of the surrounding rings that produces the paratropic loops? We cannot. In fact, the four indices of local aromaticity that we have computed here, the PD index, the HOMA, the normalized NAO-MCBO and the DFT-derived RCS, all agree in assigning a local aromaticity to all six-membered rings. However they all agree in assigning a larger local aromaticity to all of the rings abutting those rings endowed with a paratropic current in the current density map.

Thus, the carboncones offer a clear example that local aromaticity should not be inferred at first sight from current density maps.

Author contributions

All authors contributed equally to this work.

Conflicts of interest

There are no conflicts to declare.

Data availability

The code for calculating the magnetically induced current density, as well as bond current strengths and isotropically averaged Lorentz force densities, can be found at https://sysmoic.chem.unisa.it/DISTRIB/. Part of the data supporting this article have been included as part of the supplementary information (SI). Supplementary information: a PDF file is provided with Cartesian coordinates, energies, frontier orbitals schemes, and current density maps for C₇₀H₂₀, C₁₇₀H₃₀. See DOI: https://doi.org/10.1039/d5cp03021h.

Acknowledgements

Financial support from FARB 2022 and FARB 2023 is gratefully acknowledged.

References

1. J. Gillot, W. Bollmann and B. Lux, Carbon, 1968, 6, 381–387.
2. S. Iijima, Nature, 1991, 354, 56–58.
3. M. Ge and K. Sattler, Chem. Phys. Lett., 1994, 220, 192–196.
4. K. Sattler, Carbon, 1995, 33, 915–920.
5. J. A. Jaszczak, G. W. Robinson, S. Dimovski and Y. Gogotsi, Carbon, 2003, 41, 2085–2092.
6. K. Shoyama and F. Würthner, J. Am. Chem. Soc., 2019, 141, 13008–13012.
7. Z.-Z. Zhu, Z.-C. Chen, Y.-R. Yao, C.-H. Cui, S.-H. Li, X.-J. Zhao, Q. Zhang, H.-R. Tian, P.-Y. Xu, F.-F. Xie, X.-M. Xie, Y.-Z. Tan, S.-L. Deng, J. M. Quimby, L. T. Scott, S.-Y. Xie, R.-B. Huang and L.-S. Zheng, Sci. Adv., 2019, 5, eaaw0982.
8. Q. Zhang, X. Xie, S. Wei, Z. Zhu, L. Zheng and S. Xie, Small Methods, 2021, 5, 2001086.
9. E. Steiner, P. W. Fowler and L. W. Jenneskens, Angew. Chem., Int. Ed., 2001, 40, 362–366.
10. R. Zanasi and P. Fowler, Chem. Phys. Lett., 1995, 238, 270–280.
11. G. Monaco, E. L. T. Scott and R. Zanasi, ChemistryOpen, 2020, 9, 616–622.
12. E. Steiner, P. W. Fowler, A. Soncini and L. W. Jenneskens, Faraday Discuss., 2007, 135, 309–323.
13. M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
15. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
16. T. A. Keith and R. F. Bader, Chem. Phys. Lett., 1993, 210, 223–231.
17. P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304.
18. R. Zanasi, J. Chem. Phys., 1996, 105, 1460.
19. P. Fowler, R. Zanasi, B. Cadioli and E. Steiner, Chem. Phys. Lett., 1996, 251, 132–140.
20. E. Steiner and P. W. Fowler, Chem. Commun., 2001, 2220–2221.
21. E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562.
22. J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497–5509.
23. G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2020, 61, 270–283.
24. G. Monaco, F. F. Summa and R. Zanasi, SYSMOIC Version 3.3, 2022, on-line manual: https://SYSMOIC.chem.unisa.it/MANUAL/.
25. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952.
26. G. Monaco, R. Zanasi, G. Maroulis and T. E. Simos, AIP Conference Proceedings, 2009, pp. 425–428.
27. G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 3343–3351.
28. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500.
29. R. Herges and D. Geuenich, J. Phys. Chem. A, 2001, 105, 3214–3220.
30. D. Geuenich, K. Hess, F. Köhler and R. Herges, Chem. Rev., 2005, 105, 3758–3772.
31. G. Monaco and R. Zanasi, J. Phys. Chem. A, 2018, 122, 4681–4686.
32. P. Lazzeretti, J. Chem. Phys., 2018, 148, 134109.
33. G. Monaco and R. Zanasi, J. Chem. Phys., 2020, 153, 104114.
34. G. Monaco, F. F. Summa, R. Zanasi and P. Lazzeretti, Chem. – Eur. J., 2024.
35. T. D. Goddard, C. C. Huang, E. C. Meng, E. F. Pettersen, G. S. Couch, J. H. Morris and T. E. Ferrin, Protein Sci., 2017, 27, 14–25.
36. P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. V. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
37. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888.
38. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
39. E. Steiner and P. W. Fowler, Phys. Chem. Chem. Phys., 2004, 6, 261–272.
40. P. Bultinck, S. Fias and R. Ponec, Chem. – Eur. J., 2006, 12, 8813–8818.
41. P. Seal and S. Chakrabarti, J. Phys. Chem. A, 2007, 111, 9988–9994.
42. R. Carion, B. Champagne, G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 2002–2018.
43. S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666.
44. G. Monaco and R. Zanasi, J. Phys. Chem. Lett., 2017, 8, 4673–4678.
45. S. Pelloni, G. Monaco, R. Zanasi and P. Lazzeretti, AIP Conf. Proc., 2012, 114–118.
46. M. Solà, Front. Chem., 2013, 1.
47. A. Soncini, E. Steiner, P. W. Fowler, R. W. A. Havenith and L. W. Jenneskens, Chem. – Eur. J., 2003, 9, 2974–2981.
48. Unpublished result obtained at B3LYP/6-311+G(2D) level and CTOCD-DZ2 method. The calculated magnetizability of fullerene-240 of Ih symmetry is −2350 cgs ppm, which turns out to be 8.5 times larger in magnitude than that calculated for fullerene-60, i.e., −274 cgs ppm in nice agreement with the experimental value of (−260 ± 20 cgs ppm reported in ref. 68).
49. M. Solà, A. I. Boldyrev, M. K. Cyrański, T. M. Krygowski and G. Merino, Aromaticity and Antiaromaticity: Concepts and Applications, John Wiley & Sons, Inc, Hoboken, NJ, 2023.
50. T. Lu, Multiwfn Manual (Version 3.8 dev), 2025, Available at: https://sobereva.com/multiwfn/download.htm.
51. O. E. Polansky and G. Derflinger, Int. J. Quantum Chem., 1967, 1, 379–401.
52. P. Bultinck, R. Ponec and S. Van Damme, J. Phys. Org. Chem., 2005, 18, 706–718.
53. M. Giambiagi, M. Segre De Giambiagi, C. D. Dos Santos Silva and A. Paiva De Figueiredo, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392.
54. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
55. J. Cioslowski, E. Matito and M. Solà, J. Phys. Chem. A, 2007, 111, 6521–6525.
56. J. Kruszewski and T. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842.
57. T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78.
58. J. C. Dobrowolski and S. Ostrowski, J. Chem. Inf. Model., 2023, 63, 7744–7754.
59. J. A. Pople, Mol. Phys., 1958, 1, 175–180.
60. R. McWeeny, Mol. Phys., 1958, 1, 311–321.
61. T. K. Dickens and R. B. Mallion, MATCH, 2016, 76, 297–356.
62. T. K. Dickens and R. B. Mallion, Chem. Commun., 2015, 51, 1819–1822.
63. A. Landi, F. F. Summa, R. Zanasi and G. Monaco, ChemPhysChem, 2022, 23, e202200411.
64. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
65. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
66. J. Hoarau, N. Lumbroso and A. Pacault, C. R. Acad. Sci., 1956, 242, 1702.
67. A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553.
68. R. C. Haddon, L. F. Schneemeyer, J. V. Waszczak, S. H. Glarum, R. Tycko, G. Dabbagh, A. R. Kortan, A. J. Muller, A. M. Mujsce, M. J. Rosseinsky, S. M. Zahurak, A. V. Makhija, F. A. Thiel, K. Raghavachari, E. Cockayne and V. Elser, Nature, 1991, 350, 46–47.

---