Thermal runaway mechanism of LiFePO4 battery electrolytes: a molecular dynamics and density functional theory simulation study
Jun
Xie
 *a,
Ping
Huang
*a,
Ping
Huang
 a,
Guowei
Xia
a,
Yixiao
Zhang
a,
Yutong
Zhang
a,
Kun
Tian
a and
Qing
Xie
a,
Guowei
Xia
a,
Yixiao
Zhang
a,
Yutong
Zhang
a,
Kun
Tian
a and
Qing
Xie
 b
b
aHebei Provincial Key Laboratory of Power Transmission Equipment Security Defense, North China Electric Power University, Baoding 071003, China. E-mail: junxie@ncepu.edu.cn
bState Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China
First published on 5th December 2025
Abstract
LiFePO4 (LFP) batteries are widely used in power and energy storage applications due to their high safety, but their large-scale applications are still constrained by the thermal runaway problem, and the mechanism of electrolyte thermal stability has yet to be elucidated. To deeply understand the behavior of LFP battery electrolytes during thermal runaway, this study uses a commercial mixed-solvent electrolyte system as the research object and adopts the method of combining molecular dynamics (MD) and density functional theory (DFT) to systematically analyse ionic migration, solvation structures, and degradation pathways. Calculation results show that in the undegraded stage of the electrolyte, temperature increase has a dual effect on the migration behavior of ions, where the molecular thermal motion and the dynamics of the solvation shell synergistically enhance the diffusion rate of ions. In the thermal degradation stage, the degradation rate of solvent molecules generally shows a three-stage characteristic of “rise-fall-rise”, in which EC is the first to decompose and dominates the initial degradation due to the concentration of electrostatic potential and the high ring strain. In addition, the thermal degradation behavior of each solvent is significantly different due to the molecular structure, the catalytic effect of PF5, and the coupling of bond dissociation energies.
1. Introduction
In recent years, the global energy structure transition has accelerated, and it is crucial to develop energy storage systems with high safety and reliability.1 Lithium-ion batteries (LIBs), as efficient and environmentally friendly energy storage media, have significantly propelled the advancement of electrochemical energy storage technologies. Among them, lithium iron phosphate (LFP) batteries have gained widespread adoption in electric vehicles and grid-scale storage systems due to their excellent thermal stability and cost-effectiveness.2 However, the increasing deployment scale and battery capacity have amplified safety concerns,3 with thermal runaway emerging as a critical bottleneck to large-scale applications.4 Once initiated, thermal runaway leads to rapid heat accumulation and the release of flammable gases, triggering chain reactions and potentially causing catastrophic events such as fires or explosions.1,5,6The key thermal events involved in the thermal runaway of LFP batteries typically include the decomposition of the solid electrolyte interphase (SEI), electrolyte degradation, and parasitic reactions at the electrode–electrolyte interface,7,8 where electrolytes serve as active participants throughout. Notably, the combustion of electrolytes can release two to three times more energy than that stored electrochemically, making them the primary source of safety hazards.9 To improve thermal stability, researchers have actively explored new electrolyte systems. Fluorination has been demonstrated to enhance the oxidation resistance and flame retardancy of solvents.10,11 Consequently, fluorinated electrolytes—such as fluorinated sulfones,12 fluoronitriles,13 and perfluorinated solvents14 have attracted increasing attention. For example, Fan et al. designed a fluorinated electrolyte composed of methyl (2,2,2-trifluoroethyl) carbonate (FEMC), ethylene fluorocarbonate (FEC), tetrafluoro-1-(2,2,2-trifluoroethoxy)ethane (D2), and LiFSI, exhibiting excellent thermal adaptability.15 However, the practical application of fluorinated solvents remains limited by their high cost and environmental concerns from decomposition byproducts. Additionally, interfacial compatibility issues with electrodes require further investigation.16 Solid electrolytes, owing to their intrinsic structural and interfacial stability, also exhibit significant potential for enhancing battery safety.17–19 Their relatively high Young's modulus can suppress the formation of lithium dendrites. Nevertheless, challenges such as low ionic conductivity and poor solid–solid interfacial contact hinder their performance. Additionally, electrolyte additives, often referred to as “molecular switches” for tuning the physicochemical properties of electrolytes, have emerged as an effective strategy to balance electrochemical performance and safety.20–22 Yet, their concentration must be carefully optimized, as excessive use may impede ion mobility.
Despite substantial experimental advances in electrolyte modification, many critical degradation mechanisms remain difficult to observe directly. Molecular simulations offer an atomistic perspective for investigating electrolyte behavior, providing reliable predictions of solvent structures, free energies, and activation barriers23,24 quantities that are often inaccessible under complex battery operating conditions.25 Previous studies have employed classical molecular dynamics (CMD), ab initio molecular dynamics (AIMD), reactive molecular dynamics (RMD), and quantum mechanical methods based on the density functional theory (DFT) to explore the evolutionary mechanisms of lithium salt hydrolysis26 and solvent reduction decomposition27–29 forming SEI components, as well as the temperature-dependent thermal decomposition of solvents,30 providing fundamental insights into the electrochemical stability of battery electrolytes.31 However, these studies often focus on single components, involve limited system sizes, and are primarily based on ideal conditions, thus falling short of capturing the dynamic evolution of complex electrolyte systems under thermal abuse scenarios.
In this work, the electrolyte of a commercially used LiFePO4 battery was selected as the research subject. By combining molecular dynamics (MD) simulations with density functional theory (DFT) calculations, we systematically investigated the structural evolution and detailed molecular degradation mechanisms of the electrolyte in the LFP system under thermal runaway conditions. The study examined the effects of temperature on ion diffusion, Li+ solvation shell structures, and ion-pair formation mechanisms. Additionally, the chemical bond dissociation energies were calculated based on the types of degradation products from solvent molecules, and the differences in degradation rates of various solvent molecules during PF5 catalysis were analyzed. These findings contribute to a deeper understanding of solvent-dependent thermal stability and provide theoretical guidance for the rational selection of low-reactivity solvents and additives. In addition, the early-stage decomposition patterns extracted from simulations offer a foundation for developing predictive models for thermal runaway risk, which can aid the future design of safer electrolytes and the development of battery safety monitoring strategies.
2. Modeling and simulation
In this study, molecular dynamics (MD) simulations32 and density functional theory (DFT) calculations33 were performed using Materials Studio. The electrolyte system of a commercial 280-Ah LiFePO4 battery provided by a certain company was selected as the model system. In the simulation, 1 mol LiPF6 was dissolved in a mixed solvent with a volume ratio of EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC
DEC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC
DMC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC = 4
EMC = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The molecular model was constructed based on the actual electrolyte composition. A total of 40 LiPF6 salt molecules, along with 126 EC, 70 DEC, 174 DMC, and 82 EMC molecules, were randomly distributed in a simulation box with periodic boundary conditions, and the initial density of the simulation was set to 1.088 g cm−3. Fig. 1 shows the basic structure of the LFP batteries and the modeling of the electrolyte composition, while Table 1 summarizes the structural information of each solvent molecule. To obtain a stable configuration consistent with realistic material behavior, the system was subjected to geometry optimization, annealing, and molecular dynamics simulations. Geometry optimization was performed using 30
4. The molecular model was constructed based on the actual electrolyte composition. A total of 40 LiPF6 salt molecules, along with 126 EC, 70 DEC, 174 DMC, and 82 EMC molecules, were randomly distributed in a simulation box with periodic boundary conditions, and the initial density of the simulation was set to 1.088 g cm−3. Fig. 1 shows the basic structure of the LFP batteries and the modeling of the electrolyte composition, while Table 1 summarizes the structural information of each solvent molecule. To obtain a stable configuration consistent with realistic material behavior, the system was subjected to geometry optimization, annealing, and molecular dynamics simulations. Geometry optimization was performed using 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of the Smart algorithm implemented in the Forcite module, with the COMPASS III force field34–36 applied to calculate atomic interactions. The COMPASS III force field employs parameterized empirical potential functions that include bond stretching, angle bending, torsional rotation, and van der Waals interaction terms. It is capable of accurately describing both gas-phase properties (such as molecular structure, conformation, and vibrational frequencies) and condensed-phase properties (such as equation of state and cohesive energy) of molecules and polymers.34 After geometry optimization, periodic annealing was applied to the system to eliminate local structural distortions. The annealing was performed over a temperature range from 300 K to 600 K, with five heating and cooling cycles. Each temperature increment was 50 K, and 1000 MD steps were conducted at each temperature, resulting in a total annealing duration of 60 ps and an effective heating/cooling rate of 50 K ps−1. MD simulations were subsequently carried out in two stages. First, an equilibrium simulation of 500 ps was performed under the NPT ensemble at a pressure of 1 × 10−4 GPa, allowing the system density to fully relax to a stable state. Subsequently, the simulation was switched to NVT conditions at this density, and a 1000-ps production simulation was conducted. Finally, ion migration dynamics characteristics were extracted through trajectory analysis. A time step of 1 fs was used throughout the simulation. van der Waals interactions were calculated using the atom-based method, and long-range electrostatic interactions were treated using the Ewald technique with a cutoff radius of 15.5 Å and an Ewald accuracy of 1 × 10−4 kcal mol−1. Temperature and pressure control were achieved using the Nose–Hoover thermostat and the Berendsen barostat, respectively.
000 steps of the Smart algorithm implemented in the Forcite module, with the COMPASS III force field34–36 applied to calculate atomic interactions. The COMPASS III force field employs parameterized empirical potential functions that include bond stretching, angle bending, torsional rotation, and van der Waals interaction terms. It is capable of accurately describing both gas-phase properties (such as molecular structure, conformation, and vibrational frequencies) and condensed-phase properties (such as equation of state and cohesive energy) of molecules and polymers.34 After geometry optimization, periodic annealing was applied to the system to eliminate local structural distortions. The annealing was performed over a temperature range from 300 K to 600 K, with five heating and cooling cycles. Each temperature increment was 50 K, and 1000 MD steps were conducted at each temperature, resulting in a total annealing duration of 60 ps and an effective heating/cooling rate of 50 K ps−1. MD simulations were subsequently carried out in two stages. First, an equilibrium simulation of 500 ps was performed under the NPT ensemble at a pressure of 1 × 10−4 GPa, allowing the system density to fully relax to a stable state. Subsequently, the simulation was switched to NVT conditions at this density, and a 1000-ps production simulation was conducted. Finally, ion migration dynamics characteristics were extracted through trajectory analysis. A time step of 1 fs was used throughout the simulation. van der Waals interactions were calculated using the atom-based method, and long-range electrostatic interactions were treated using the Ewald technique with a cutoff radius of 15.5 Å and an Ewald accuracy of 1 × 10−4 kcal mol−1. Temperature and pressure control were achieved using the Nose–Hoover thermostat and the Berendsen barostat, respectively.
 | ||
| Fig. 1 Basic structure of LFP batteries and the modeling of electrolyte composition. (a) Schematic of the battery structure; (b) electrolyte model; and (c) molecular structure diagrams. | ||
| EC | DEC | DMC | EMC | |
|---|---|---|---|---|
| Molecular formula | C3H4O3 | C5H10O3 | C3H6O3 | C4H8O3 |
| Molecular weight (g mol−1) | 88.06 | 118.13 | 90.08 | 104.10 |
| Density (g cm−3) | 1.321 | 0.975 | 1.064 | 1.006 |
In order to investigate the structural evolution and reaction kinetic properties of the electrolyte during thermal runaway, ReaxFF-Li, a reactive force field parameterized for lithium-containing systems,37–39 was employed in the GULP module. The simulations were performed under the NVT ensemble with a gradual temperature increase, where each reaction cycle comprised 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps to simulate the evolutionary behavior of the electrolyte system. Considering that the simulation timescale is much shorter than that of actual chemical reactions, elevated temperatures are often required to trigger reactions within the accessible computational time. Therefore, following previous studies,40–42 an appropriate temperature ramping strategy was adopted to accelerate the reaction processes. The initial temperature range of the system was 380–580 K. In the simulation, the overall temperature was raised to 760–1160 K, and six isothermal simulation temperature points were set at 80 K intervals, i.e., 760 K, 840 K, 920 K, 1000 K, 1080 K, and 1160 K. Each temperature point was simulated with 50-ps isothermal kinetics. Isothermal kinetic simulations were carried out for 50 ps at each temperature point with a time step of 0.1 fs, and a Nose–Hoover thermostat was used to control the temperature to ensure the smoothness of the thermodynamic behavior of the system.
000 time steps to simulate the evolutionary behavior of the electrolyte system. Considering that the simulation timescale is much shorter than that of actual chemical reactions, elevated temperatures are often required to trigger reactions within the accessible computational time. Therefore, following previous studies,40–42 an appropriate temperature ramping strategy was adopted to accelerate the reaction processes. The initial temperature range of the system was 380–580 K. In the simulation, the overall temperature was raised to 760–1160 K, and six isothermal simulation temperature points were set at 80 K intervals, i.e., 760 K, 840 K, 920 K, 1000 K, 1080 K, and 1160 K. Each temperature point was simulated with 50-ps isothermal kinetics. Isothermal kinetic simulations were carried out for 50 ps at each temperature point with a time step of 0.1 fs, and a Nose–Hoover thermostat was used to control the temperature to ensure the smoothness of the thermodynamic behavior of the system.
In addition, to further elucidate the degradation mechanisms of solvent molecules during the thermal runaway process, the Perdew–Burke–Ernzerhof (PBE) functional based on the generalized gradient approximation (GGA)43 was employed. The TS dispersion correction44 was applied to accurately describe non-bonded interactions. The electrostatic interaction strength between PF5 and solvent molecules was quantitatively assessed through electrostatic potential (ESP) mapping. By calculating the dissociation energy of typical chemical bonds in the key degradation paths, the reaction energy barrier of solvent molecules in the thermal runaway process was calculated systematically, which provided support for the degradation differences in different paths. The energy convergence threshold was set to 1 × 10−5 eV atom−1. To improve calculation accuracy, the triple numerical polarization (TNP) basis set45 was used, whose extended orbitals effectively characterize the charge transfer behavior between PF5 and solvent molecules.
3. Results and discussion
3.1. Ion diffusion characteristics of undegraded systems
The diffusion characteristics of lithium ions in the electrolyte play a critical role in determining the overall performance and safety of the battery. This is particularly important under high-temperature conditions, where ion diffusion directly influences the system's conductivity, interfacial stability, and the rates of possible side reactions.46 Investigating the diffusion behavior in the undegraded electrolyte system helps establish a reference state for comparison, which is essential for analyzing changes in diffusion characteristics following electrolyte degradation. The ionic diffusion coefficient can be calculated using the following equation: | (1) |
 denotes the mean square displacement (MSD), whose slope with respect to time can be obtained from long-time simulations to calculate the diffusion coefficient.
denotes the mean square displacement (MSD), whose slope with respect to time can be obtained from long-time simulations to calculate the diffusion coefficient.
In this study, three temperatures, 300 K, 320 K, and 340 K, were selected to represent the typical temperature range of LiFePO4 batteries under actual operating conditions. Based on the MD simulations described in Section 2, the MSDs of Li+ and PF6− in the electrolyte system at each temperature were calculated separately, and the results are plotted in Fig. 2(a). It can be observed that the MSD curves of Li+ and PF6− increase approximately linearly with time, indicating that the diffusion behavior of the two ions in the electrolyte follows the classical diffusion law. To further quantify the diffusion rate, the study used linear regression to fit a straight line for each MSD curve and calculate the diffusion coefficients at each temperature using the slope of the fitted straight line in combination with formula (1). The results are shown in Fig. 2(b).
The calculations show that the diffusion coefficient increases with increasing temperature, which follows the expectation of Arrhenius' law that higher temperatures enhance the thermal motion of ions, thereby promoting faster diffusion. In addition, the diffusion coefficient of PF6− is found to be, on average, approximately 5.84% higher than that of Li+ at the same temperature, indicating that PF6− migrates faster in the electrolyte. This observation is consistent with previous simulation results obtained for single-solvent systems.47 However, from the physical properties, PF6−, as an anion, has a molecular weight and volume significantly larger than those of Li+. It would be expected to exhibit a lower diffusion rate. To investigate this anomaly, the solvation effect and inter-ionic interactions were further analyzed in this study to reveal the potential mechanism affecting ion diffusion.
3.2. Ionic solvation structure and interaction
To reveal the solvation characteristics of the ions in the electrolyte, the radial distribution functions (RDFs) of Li+–Os, PF6−–Os, and Li+–PF6− were calculated, and the solvation coordination numbers (CNs) around Li+ and PF6− were calculated using eqn (2), where Os represents the carbonyl oxygen atom in the solvent molecule. Additionally, to quantify the interactions between ions and solvent molecules, the potential of mean force (PMF) and binding free energy ΔGbind were calculated using eqn (3) and (4), respectively.48–50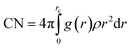 | (2) |
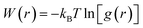 | (3) |
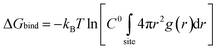 | (4) |
As shown in Fig. 3, the first solvation shell peak of Li+–Os appears at 1.97 Å at 300 K, which is closer than that of PF6−–Os, and the coordination number of Li+–Os is 3.26, while the coordination number of PF6−–Os is less than 1, indicating the presence of a stable first solvation shell around Li+. In contrast, the solvation extent of PF6− is weaker than that of Li+, consistent with its larger molecular volume and lower solvation ability. As the temperature increases, the RDF peak of Li+–Os decreases, and the coordination number gradually decreases to 2.89, while the changes in PF6−–Os are relatively small. Further calculations of the PMF and binding free energy ΔGbind are shown in Fig. 4 and Table 2, respectively. The PMF curve of Li+–Os exhibits a stable and deep potential well, with the binding free energy value ΔGbind-LO being approximately twice that of ΔGbind-PO. This indicates that the binding between Li+ and the solvent is stronger, the solvation is more stable, and desolvation is more difficult. Therefore, during migration, Li+ carries solvent molecules, leading to an increase in its effective mass and spatial steric hindrance. In contrast, PF6− has a larger mass, stronger inertia, and weaker solvation; therefore, its movement is not severely hindered, resulting in a higher diffusion rate than Li+.
 | ||
| Fig. 3 Radial distribution functions and coordination numbers of ions at three temperatures. (a) g(r) and (b) CN. | ||
| 300 K | 320 K | 340 K | |
|---|---|---|---|
| Li+–Os | −1.48915 | −1.48253 | −1.44313 |
| PF6−–Os | −0.69994 | −0.71550 | −0.73947 |
To further investigate the binding modes between Li+ and PF6− at different temperatures, the solvation structures of the electrolyte system were classified, including solvent-separated ion pairs (SSIPs), contact ion pairs (CIPs), and aggregates (AGGs). Representative structures of each category are shown in Fig. 5. The data in Table 3 show that AGGs are the predominant form (>50%) at all three temperatures, indicating that Li+ and PF6− exist mainly in the form of clusters. However, the proportion of AGGs gradually decreases with increasing temperature, and the proportion of CIPs increases from 32.74% at 300 K to 44.64% at 340 K. Meanwhile, the proportion of SSIPs decreases from 5.95% to 0.95%. This trend suggests that some AGGs gradually dissociate into smaller contact ion pairs and that some Li+ gradually complete pairing with anions due to the loosening of the solvation shell. Although the formation of CIPs enhances the direct electrostatic interactions between Li+ and PF6−, the dissociation of small aggregates effectively reduces the effective mass of the lithium-containing clusters in the system. In addition, the intensified thermal motion at higher temperatures further weakens inter-ionic binding. The two effects synergize to enhance the overall diffusion rate of lithium ions.
| SSIPs (%) | CIPs (%) | AGGs (%) | |
|---|---|---|---|
| 300 K | 5.95 | 32.74 | 61.31 |
| 320 K | 3.45 | 39.88 | 56.67 |
| 340 K | 0.95 | 44.64 | 54.40 |
Based on the above analysis, it can be concluded that the temperature increase has a dual effect on the migration behavior of lithium ions: on the one hand, the dynamic exchange rate of the Li+ solvation shell is increased, which enhances its migration ability. On the other hand, although the number of Li+ and PF6− pairing increases and the binding effect of ion pairing is enhanced, the diffusion enhancement driven by thermal motion is more dominant. Thus, the overall diffusion coefficient increases with the temperature.
3.3. Degradation rate
Fig. 6 shows snapshots of the structural evolution of the electrolyte system during the gradient temperature rise obtained using the Materials Studio “Original” display mode. Although some molecules are located outside the box, this is only for visual representation purposes; in reality, they are still constrained by periodic boundary conditions. It can be observed that the decomposition of solvent molecules and lithium salts progressively intensifies as the temperature increases. To further quantify this change, the number of decomposed solvent and salt molecules at different temperatures within the same simulation time was counted, as shown in Fig. 7. The results show that the amount of degraded solvent molecules and PF6− anions increases monotonically with increasing temperature, but their kinetic characteristics are significantly different. For the solvent system, the degradation process presents three-stage characteristics in the temperature range of 380–580 K. The initial stage (380–460 K) shows a high degradation rate of 13.18%/40 K, which is due to the preferential ring-opening decomposition and ester bond cleavage in the low-temperature region, leading to chain decomposition. The degradation rate in the intermediate stage (500–540 K) plummets to 7.44%/40 K. This is attributed to the precipitation of gas-phase products, such as CO2, formed in the preliminary reaction from the electrolyte, which significantly reduces the concentration of reactive solvent molecules and suppresses subsequent decomposition. When the temperature increases to 580 K, the accumulation of thermal energy overcomes the activation barrier for C–C bond cleavage, producing gas-phase products such as ethylene and methane. The accumulation of these gases raises the system pressure and increases the molecular collision frequency, resulting in a renewed increase in the degradation rate to 16.62% per 40 K. In contrast, the degradation rate of PF6− is relatively homogeneous throughout the process of temperature increase and does not show a significant abrupt change.It is noteworthy that the PF6− anion decomposes at the fastest rate during the initial stage of thermal degradation of the electrolyte (380 K), followed by the cyclic molecule EC, and finally the linear carbonate solvents. This difference in degradation rates can be rationalized by the molecular stability and ESP distribution. LiPF6 starts to decompose at lower temperatures (60–80 °C) to produce PF5 and LiF. PF5, as a strong Lewis acid, can preferentially attack the solvent molecules, thereby accelerating the degradation process of the electrolyte and catalyzing solvent decomposition to a certain extent.40 The electrostatic potentials of the optimized multi-solvent molecule system and the “PF5− multi-solvent molecule” system were calculated, and the ESP mapping diagram shown in Fig. 8 was obtained by splitting. It can be seen that the addition of PF5 increases the negative potentials on the solvent molecules to different degrees. Among them, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O region of EC has the strongest negative potential, which is easily attacked. This promotes ring-opening reactions and thus accelerates EC degradation. In addition, EC is more prone to bond cleavage at high temperatures due to its inherent ring strain, whereas DMC, DEC, and EMC have higher thermal stability due to their linear structures, uniform electron density distributions, lower electrostatic potentials, and weaker interactions with PF5. As a result, the significant degradation of these linear solvents requires higher temperatures or stronger external catalytic effects.
O region of EC has the strongest negative potential, which is easily attacked. This promotes ring-opening reactions and thus accelerates EC degradation. In addition, EC is more prone to bond cleavage at high temperatures due to its inherent ring strain, whereas DMC, DEC, and EMC have higher thermal stability due to their linear structures, uniform electron density distributions, lower electrostatic potentials, and weaker interactions with PF5. As a result, the significant degradation of these linear solvents requires higher temperatures or stronger external catalytic effects.
 | ||
| Fig. 8 ESP mapping diagrams. (a) EC and PF5-EC; (b) DEC and PF5-DEC; (c) DMC and PF5-DMC; and (d) EMC and PF5-EMC. | ||
3.4. Degradation pathway and mechanism
To further explore the principle of solvent thermal degradation, the degradation pathways and quantities of reactions were organized and classified in the study, and the results are shown in Fig. 9 and Fig. 10, respectively. | ||
| Fig. 10 Decomposition quantity of solvent molecules in different paths. (a) EC; (b) DMC; (c) DEC; and (d) EMC. | ||
There are three main effective pathways for the reaction of EC molecules during the heating degradation process. The results show that 68.89% of the EC molecules undergo ring-opening dissociation through the main reaction path (Path I), generating ethylene molecules and CO3 molecules, with the latter further decomposing into CO2 and oxygen radicals. The proportion of EC molecules decomposed via Path I gradually increases with the temperature, and it can reach 76.92% under high-temperature conditions. In contrast, 26.67% of EC molecules decompose into C2H4O radicals and CO2, while 4.44% undergo dehydrogenation. DFT calculations (Table 4) show that the bond dissociation energies of Path II and Path III are 316.38 kJ mol−1 and 415.21 kJ mol−1, respectively, suggesting that Path II is more thermodynamically favorable due to its lower energy barrier. It is worth noting that Path I, although having higher bond energies, still maintains a high degradation rate due to the catalytic effect of the previously mentioned PF5 on EC ring opening. The degradation behavior of the DMC molecules also follows three paths. Initially, 52.78% of the DMC molecules undergo ester bond cleavage, yielding CH3CO2 and CH3O groups, and then, the former is further cleaved to methyl radicals and CO2. 44.44% of the DMC molecules follow a C–O bond cleavage route, producing CH3 and CH3CO3 groups that subsequently release CO2. The remaining 2.78% of the DMC molecules undergo dehydrogenation to produce unsaturated derivatives. Because the bond dissociation energy of DMC pyrolysis Path II is significantly lower than that of the other paths, its contribution gradually dominates with increasing temperature. For DEC and EMC, which have more complex structures, the degradation paths are even more complicated. Similar to DMC, the distribution of DEC molecules in different pathways is also affected by the bond energies of the key degradation pathways. It is noteworthy that EMC pyrolysis Path V does not appear at the beginning of the degradation because its corresponding bond has a high dissociation energy and cannot cross the energy barrier at low temperatures. It is also observed that Path I exhibits a higher reaction proportion throughout the pyrolysis process despite its relatively high bond energy. Different from EC, the pyrolysis behavior of EMC under the catalytic action of PF5 is not only controlled by the reaction energy barriers, but also significantly influenced by the structural features of the molecule itself. Due to its asymmetry, the intramolecular strain in EMC is unevenly distributed under thermodynamic conditions, promoting ester bond cleavage and making it a preferentially activated degradation route. It is worth noting that although high temperatures may enhance the contribution of high-energy-barrier pathways and thus potentially affect the quantitative distribution of reaction products, the qualitative characteristics of the reaction pathways are primarily governed by the potential energy surface according to the transition state theory, including the location of initial bond cleavage and the formation of key intermediates. Therefore, the major pyrolysis mechanisms revealed in this study remain representative and informative.
| Path I | Path II | Path III | Path IV | Path V | |
|---|---|---|---|---|---|
| EC | 436.95 | 316.38 | 415.21 | — | — |
| DMC | 419.92 | 351.02 | 453.50 | — | — |
| DEC | 446.64 | 348.05 | 418.27 | 414.17 | — |
| EMC | 417.28 | 349.92 | 349.61 | 417.34 | 446.71 |
4. Conclusions
This paper focuses on the micro-scale evolution behavior of the electrolyte system of LiFePO4 batteries under thermal runaway conditions. By combining MD simulations and DFT calculations, the structural evolution and reaction kinetic mechanism of the multi-component electrolyte system under heating conditions are systematically analyzed, focusing on ionic migration behavior, solvation structural remodeling, degradation pathway selection, and thermal degradation mechanism. The main conclusions are as follows:(1) Elevated temperatures exert a significant dual effect on the diffusion behavior of ions. On the one hand, the temperature increase enhances the thermal motion of the particles, and on the other hand, although the ion pairs of CIPs and AGGs are relatively large, the solvation shell of Li+ tends to become loose, and the dynamic change in the coordination structure and thermal motion cooperate to improve the overall diffusion coefficient.
(2) In the thermal degradation stage, the degradation rate of solvent molecules generally shows a three-stage characteristic of “rise-fall-rise”, and it is found by DFT calculations that EC in solvent molecules is most likely to be thermally decomposed and dominates the initial degradation process owing to the concentration of the electrostatic potential and significant ring strain.
(3) For the four solvents EC, DMC, DEC, and EMC, the thermal decomposition paths and degradation quantities of each solvent are systematically counted, and combined with the ESP electrostatic potential distribution and bond dissociation energy calculations, the coupling mechanism of molecular structure, PF5 catalysis and bond stability on solvent degradation behavior is quantitatively revealed.
This study provides theoretical support for identifying key reaction pathways during the thermal runaway process of LFP batteries and points out directions for optimizing the electrolyte system. From the perspective of molecular design, reducing the carbonyl group density, introducing steric hindrance structures, and increasing the local electron cloud density help enhance the thermal stability of solvents. Based on these insights, molecular screening criteria can be established in the future to guide the optimized selection of solvents and additives. Meanwhile, the early decomposition behavior features extracted from simulations can offer prior information for thermal runaway risk identification. Additionally, the formation characteristics of intermediates such as ethylene and CO2 hold potential as precursor signals. By combining their typical kinetic parameters (e.g., rate changes and inflection points) with sensor data, a digital twin-based risk modeling framework can be developed to improve the early detection and warning capabilities for battery thermal runaway. In this study, BDE- and ESP-based analyses are effective for exploring thermal degradation trends and pathways. However, they are insufficient for building a quantitative kinetic model and are limited in handling multi-step reactions and environmental influences. In future work, transition state searches or constrained DFT calculations will be introduced to enhance the mechanistic depth of the study. In addition, the effects of battery conditions such as SOC, aging, and mechanical strain have been simplified in this work. Future studies may reflect SOC variations indirectly by adjusting Li+ concentrations or introducing phase-segregated lithium species. Defective interfacial models can also be constructed by introducing damaged SEI layers or aging products, enabling a more comprehensive evaluation of the correlation between battery conditions and thermal runaway behavior. Meanwhile, experimental validation remains essential. Techniques such as FTIR and high-temperature in situ X-ray diffraction (XRD) may be employed in the future to further validate the simulation results.
Author contributions
Jun Xie: writing – review and editing, conceptualization, methodology, supervision, funding acquisition, project administration. Ping Huang: writing – original draft, software, methodology, investigation, formal analysis, data curation, conceptualization. Guowei Xia: writing – review and editing, software, investigation. Yixiao Zhang: writing – review and editing, methodology. Yutong Zhang: writing – review and editing, methodology. Kun Tian: writing – review and editing. Qing Xie: writing – review and editing, supervision, resources, funding acquisition, conceptualization.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The datasets generated and analyzed during the current study are not publicly available due to confidentiality agreements and the ongoing nature of the research project. The project has not yet been completed, and data sharing is restricted until formal closure. Limited data may be available from the corresponding author upon reasonable request and subject to institutional and contractual approval.Acknowledgements
The authors acknowledge the financial support from the National Key Research and Development Program of China (2023YFB2408203).Notes and references
- D. He, J. Wang, Y. Peng, B. Li, C. Feng, L. Shen and S. Ma, Sustainable Mater. Technol., 2024, 41, e01017 CrossRef CAS.
- H. Zhang, H. Zhao, M. A. Khan, W. Zou, J. Xu, L. Zhang and J. Zhang, J. Mater. Chem. A, 2018, 6, 20564–20620 RSC.
- L. Kong, Y. Li and W. Feng, Electrochem. Energy Rev., 2021, 4, 633–679 CrossRef CAS.
- D. Hu, S. Huang, Z. Wen, X. Gu and J. Lu, Renewable Sustainable Energy Rev., 2024, 206, 114882 CrossRef CAS.
- G. Wei, R. Huang, G. Zhang, B. Jiang, J. Zhu, Y. Guo, G. Han, X. Wei and H. Dai, Appl. Energy, 2023, 349, 121651 CrossRef CAS.
- X. Feng, M. Ouyang, X. Liu, L. Lu, Y. Xia and X. He, Energy Storage Mater., 2018, 10, 246–267 CrossRef.
- X. Feng, S. Zheng, D. Ren, X. He, L. Wang, H. Cui, X. Liu, C. Jin, F. Zhang and C. Xu, Appl. Energy, 2019, 246, 53–64 CrossRef CAS.
- B. Xu, J. Lee, D. Kwon, L. Kong and M. Pecht, Renewable Sustainable Energy Rev., 2021, 150, 111437 CrossRef CAS.
- G. G. Eshetu, S. Grugeon, S. Laruelle, S. Boyanov, A. Lecocq, J.-P. Bertrand and G. Marlair, Phys. Chem. Chem. Phys., 2013, 15, 9145–9155 RSC.
- X. Fan and C. Wang, Chem. Soc. Rev., 2021, 50, 10486–10566 RSC.
- G. Yan, X. Li, Z. Wang, H. Guo, W. Peng, Q. Hu and J. Wang, J. Solid State Electrochem., 2017, 21, 1589–1597 CrossRef CAS.
- C.-C. Su, M. He, J. Shi, R. Amine, Z. Yu, L. Cheng, J. Guo and K. Amine, Energy Environ. Sci., 2021, 14, 3029–3034 RSC.
- X. Zhou, D. Peng, K. Deng, H. Chen, H. Zhou and J. Wang, J. Power Sources, 2023, 557, 232557 CrossRef CAS.
- D. Ouyang, J. Guan, X. Wan, B. Liu, C. Miao and Z. Wang, ACS Appl. Mater. Interfaces, 2024, 16, 42894–42904 CrossRef CAS PubMed.
- X. Fan, X. Ji, L. Chen, J. Chen, T. Deng, F. Han, J. Yue, N. Piao, R. Wang and X. Zhou, Nat. Energy, 2019, 4, 882–890 CrossRef CAS.
- B. Vinay, Y. Nikodimos, T. Agnihotri, S. A. Ahmed, T. M. Hagos, R. Hasan, E. B. Tamilarasan, W.-N. Su and B. J. Hwang, Energy Environ. Sci., 2025, 18, 7326–7372 RSC.
- W. Xiao, J. Wang, L. Fan, J. Zhang and X. Li, Energy Storage Mater., 2019, 19, 379–400 CrossRef.
- D. Zhou, D. Shanmukaraj, A. Tkacheva, M. Armand and G. Wang, Chem, 2019, 5, 2326–2352 CAS.
- L. Han, C. Liao, X. Mu, N. Wu, Z. Xu, J. Wang, L. Song, Y. Kan and Y. Hu, Nano Lett., 2021, 21, 4447–4453 CrossRef CAS PubMed.
- J. Liu, X. Song, L. Zhou, S. Wang, W. Song, W. Liu, H. Long, L. Zhou, H. Wu and C. Feng, Nano Energy, 2018, 46, 404–414 CrossRef CAS.
- G. Xu, C. Pang, B. Chen, J. Ma, X. Wang, J. Chai, Q. Wang, W. An, X. Zhou and G. Cui, Adv. Energy Mater., 2018, 8, 1701398 CrossRef.
- Z. Gao, S. Rao, Z. Zhang, Y. Wang, Y. Xiao, Q. Yuan and W. Li, J. Electrochem. Energy Conv. Storage, 2025, 1–13 Search PubMed.
- M. D. Bhatt, M. Cho and K. Cho, J. Solid State Electrochem., 2012, 16, 435–441 CrossRef CAS.
- X. Cao, P. Gao, X. Ren, L. Zou, M. H. Engelhard, B. E. Matthews, J. Hu, C. Niu, D. Liu and B. W. Arey, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020357118 CrossRef CAS PubMed.
- M. D. Bhatt and C. O'Dwyer, Phys. Chem. Chem. Phys., 2015, 17, 4799–4844 RSC.
- S. Di Muzio, A. Paolone and S. Brutti, J. Electrochem. Soc., 2021, 168, 100514 CrossRef.
- J. Gao, R. He and K. H. Luo, Phys. Chem. Chem. Phys., 2024, 26, 22189–22207 RSC.
- D. Kuai and P. B. Balbuena, ACS Appl. Mater. Interfaces, 2022, 14, 2817–2824 CrossRef CAS PubMed.
- Y. Wang, Y. Liu, Y. Tu and Q. Wang, J. Phys. Chem. C, 2020, 124, 9099–9108 CrossRef CAS.
- G. Guo, Z. Wang, S. Wu and H. Ju, Int. J. Hydrogen Energy, 2024, 82, 979–985 CrossRef CAS.
- Y. Mabrouk, N. Safaei, F. Hanke, J. Carlsson, D. Diddens and A. Heuer, Sci. Rep., 2024, 14, 10281 CrossRef CAS PubMed.
- X. Tan, M. Chen, J. Zhang, S. Li, H. Zhang, L. Yang, T. Sun, X. Qian and G. Feng, Adv. Energy Mater., 2024, 14 CAS.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 1–13 Search PubMed.
- R. L. Akkermans, N. A. Spenley and S. H. Robertson, Mol. Simul., 2021, 47, 540–551 CrossRef CAS.
- C. M. Efaw, Q. Wu, N. Gao, Y. Zhang, H. Zhu, K. Gering, M. F. Hurley, H. Xiong, E. Hu and X. Cao, Nat. Mater., 2023, 22, 1531–1539 CrossRef CAS PubMed.
- Q. Wu, M. T. McDowell and Y. Qi, J. Am. Chem. Soc., 2023, 145, 2473–2484 CrossRef CAS PubMed.
- M. M. Islam, A. Ostadhossein, O. Borodin, A. T. Yeates, W. W. Tipton, R. G. Hennig, N. Kumar and A. C. Van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3383–3393 RSC.
- M. M. Islam, V. S. Bryantsev and A. C. Van Duin, J. Electrochem. Soc., 2014, 161, E3009 CrossRef CAS.
- D. Bedrov, G. D. Smith and A. C. van Duin, J. Phys. Chem. A, 2012, 116, 2978–2985 CrossRef CAS PubMed.
- X. Lu, X. Wang, Q. Li, X. Huang, S. Han and G. Wang, Polym. Degrad. Stab., 2015, 114, 72–80 CrossRef CAS.
- Y. Wang, S. Gong, H. Wang, L. Li and G. Liu, J. Anal. Appl. Pyrolysis, 2021, 155 CAS.
- D. Hong, T. Si and X. Guo, Proc. Combust. Inst., 2021, 38, 4023–4032 CrossRef CAS.
- Z. Wang, Y. Sun, Y. Mao, F. Zhang, L. Zheng, D. Fu, Y. Shen, J. Hu, H. Dong and J. Xu, Energy Storage Mater., 2020, 30, 228–237 CrossRef.
- B. Kim, S. Kim, D. G. Lee, D. Lee, J. Son, H. Seong, B. J. Kim, T. K. Lee and N. S. Choi, Small Methods, 2025, 2401957 CrossRef CAS PubMed.
- B. Delley, J. Phys. Chem. A, 2006, 110, 13632–13639 CrossRef CAS PubMed.
- Z.-H. Fu, X. Chen, N. Yao, X. Shen, X.-X. Ma, S. Feng, S. Wang, R. Zhang, L. Zhang and Q. Zhang, J. Energy Chem., 2022, 70, 59–66 CrossRef CAS.
- T. Gao and W. Lu, Electrochim. Acta, 2019, 323 Search PubMed.
- E. S. Boek, D. S. Yakovlev and T. F. Headen, Energy Fuels, 2009, 23, 1209–1219 CrossRef CAS.
- Y. Deng and B. Roux, J. Phys. Chem. B, 2009, 113, 2234–2246 CrossRef CAS PubMed.
- S. Doudou, N. A. Burton and R. H. Henchman, J. Chem. Theory Comput., 2009, 5, 909–918 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |






