A theoretical study of CH₃SH pyrolysis kinetics

Abstract

The decomposition mechanism of methanethiol (CH₃SH) under pyrolysis conditions has been investigated using electronic structure calculations at the CCSD(T)-F12/cc-pVTQ∞ Z-F12//CCSD(T)-F12/cc-pVDZ-F12 level of theory for several potential energy surfaces such as CH₃SH + SH, CH₃SH + CH₃, CH₂S + SH, CH₂S + CH₃ and CS + SH. Pressure dependent reaction rates for the associated reactions have been deduced from energies, frequencies and geometries calculations by solving the master equation for each surface. Complex behavior is observed for these systems with very low to submerged energy barriers for the CH₂S + SH addition on the S atom, mainly due to multireference effects and van der Waals complex formation. The former has been explored in detail with CASPT2-F12/cc-pVTZ-F12 calculations up to an active space size of 13 electrons in 15 orbitals, and the latter was accounted for with phase space theory. Comparison with available experimental data shows that the resulting mechanism robustly predicts the abundance of the main species over the full temperature range.

---

1. Introduction

High temperature kinetics of sulfur-bearing compounds in the gas phase are relevant to a wide span of applications, ranging from practical industrial applications of combustion, up to theoretical research on photochemistry and atmospheric chemistry.^1–3 In combustion applications, the Claus process is the standard method to purify natural gas and extract sulfur from gases containing hydrogen sulfide, such as sour shale gas, to produce elemental sulfur for the chemical industry.⁴ This process involves the oxidation of hydrogen sulfide (H₂S), which is the main sulfur-bearing species in natural gas, but other contaminants such as methanethiol CH₃SH can also be present in concentrations sufficient to impair sulfur yields.⁵ The highly exothermic nature of this oxidation leads to high temperatures in the reactor and to the thermal decomposition of these sulfur-bearing compounds. Research for optimizing this process has also been increasing in popularity due to the recent interest in biogas production as a renewable energy source. This type of gas also contains high amounts of sulfur compounds in the form of H₂S and CH₃SH that need to be removed for its use in gas turbines.^6,7

The kinetics of CH₃SH have also been previously explored by atmospheric chemists, because of its crucial role in the sulfur cycle on Earth. It involves sulfur emissions from organic sulfur compounds of living organisms in the oceans, released in the form of gases such as CH₃SH and CH₃SCH₃ (dimethylsulfide or DMS), the latter constituting its main form in the atmosphere.^8,9 These molecules have a very short residence time in the atmosphere (about 1 day) because they are quite rapidly oxidized by atmospheric molecular oxygen, which promptly reacts with the CH₃S and CH₃SCH₂ radicals produced by the reaction of CH₃SH and DMS with other radicals produced by photochemistry such as the hydroxyl radical (OH).^10–13

These reactions happen on Earth at relatively low temperatures, but the need for high temperature data has been increasing these past few years in the field of astrophysics, in particular in exoplanet atmospheric studies, due to the recent observational evidence of high-temperature photochemistry. Since the launch of the James Webb Space Telescope in December 2021, the exoplanet atmospheric chemistry community has reported multiple detections of sulfur, notably in the warm atmospheres of planets such as WASP-39 b and WASP-107 b.^14,15 The observations of these 2 planets constitute the very first detections of sulfur element in exoplanet atmospheres. Surprisingly, sulfur dioxide (SO₂), the highly oxidized state of sulfur, has been detected, whereas its presence was not expected according to chemical equilibrium predictions. The presence of SO₂ has been explained through a pathway initiated by photochemistry.^14,15 Multiple sulfur kinetic networks have been used to try to model the atmosphere of these planets and reproduce the observational data,^14,16–19 but these networks only include sulfur chemistry as an S/O/H system, although in hydrogen dominated atmospheres such as the ones expected for WASP-39 b and WASP-107 b, carbon and nitrogen are also present in higher concentrations than sulfur, in the form of CH₄ and NH₃. Photochemistry of these two species could couple to photochemistry of sulfur compounds through C/H/S species, of which CH₃SH is the simplest representative. To our knowledge, this coupling remains to this day an unexplored area of sulfur chemistry in exoplanets and has not been included in any chemical network used to model these atmospheres. Hence, this possibility should at least be explored and appropriately modeled to improve our confidence in the predictions of these networks.

This work aims to develop and validate a detailed kinetic model for the pyrolysis of CH₃SH, using high-level ab initio calculations, such as CCSD(T)-F12 and CASPT2-F12, to calculate the rate constants of key reactions of the mechanism. First, we discuss in Section 2 how we identify the most sensitive reactions for the validation of the kinetic model against pyrolysis speciation data. Then, we present in Section 3.3 the results of our calculations and simulate experimental pyrolysis data from the literature with this kinetic model in Section 3.4. The final section concludes with a discussion of the implications of this work.

2. Methodology

Detailed kinetic models for the pyrolysis of CH₃SH are scarce in the literature. Recently, Colom-Diaz et al. (2021)²⁰ proposed a mechanism validated against their experimental data measured in a jet stirred reactor. This model is based on a previous work from the group²¹ that models CH₃SH oxidation and validates it against species abundance profiles obtained in a plug flow reactor. Other works on C/S species such as CS₂ exist, for example in Glarborg et al. (2014),²² but usually without including C/H/S species. For C/H/S species, Alzueta et al. (2019)²¹ and Colom-Diaz et al. (2021)²⁰ proposed a mechanism used to simulate their experiments from CH₃SH combustion and pyrolysis in flow and jet-stirred reactors. If their model is able to capture the oxidation behavior of CH₃SH, the pyrolysis mechanism still needs to be improved. However, given the lack of available data on the rate constants of reactions involving C/H/S species, the accurate modeling of CH₃SH pyrolysis and especially its decomposition products over wide ranges of temperatures is a very complex and delicate task.

In consequence, we chose to build the C/H/S mechanism from scratch, using exhaustive analogies with equivalent oxygenated species to build a strong core for the mechanism. This is applied to CH₃SH and its primary pyrolysis products such as CH₂S, CS₂ and their corresponding radicals. Enthalpy differences were considered in the activation energies of these reactions when the original or new reaction was implemented in the endothermic direction. For example when implementing the CH₃SH + HS₂ → CH₂SH + H₂S₂ reaction, because the analog reaction CH₃OH + HO₂ → CH₂OH + H₂O₂ was already implemented in the endothermic direction in our C/H/O/N core, we subtracted its enthalpy difference at 1000 K (about 9.9 kcal mol⁻¹) from its activation energy (18.8 kcal mol⁻¹) and added the enthalpy difference of the analogous sulfur reaction (26.4 kcal mol⁻¹) to yield its activation energy (35.3 kcal mol⁻¹). This was done systematically to avoid bias in the activation energy when the reaction enthalpy differs too much from those of the analog reaction available. In contrast to CH₃SH chemistry, H₂S and C₀–C₂ chemistry were included based on extensive validations done against literature data. This was done starting from a full C/H/O/N mechanism from a previous work,²³ in which we integrated an S/H/O sub-mechanism from Stagni et al. (2022)²⁴ without replacing our H/O submechanism. The references for the C/H/O reactions used for the C/H/S analogies are directly taken from the C/H/O core mechanism of Veillet et al. (2024),²³ and is based on the work of Burke et al. (2016).²⁵ This resulted in over 120 analogies, which can be found in the text file of the mechanism in the SI. For thermodynamic data, we used NASA polynomials from Glarborg et al. (2014)²² for C/S and O/C/S species, from Colom-Diaz et al. (2021)²⁰ and Sirjean et al. (2017)²⁶ for C/H/S species and Stagni et al. (2022)²⁴ for S/H and S/H/O species. Available experimental data on CH₃SH pyrolysis were then simulated with the resulting kinetic model and compared with its predictions. Formation pathway and sensitivity analyses were performed to target key reactions and further improve the model by computing their corresponding rates with state of the art ab initio methods.

3. Results

3.1. Target experimental data

After building the core of the C/H/S kinetic mechanism on these analogies, we simulated experimental data from the literature using the open source kinetic solver Cantera.²⁷ The simulated conditions were taken from the pyrolysis experiments of Alzueta et al. (2019),²¹ listed as Set 1 in their work, and performed at atmospheric pressure between 800 K and 1400 K in a turbulent flow reactor with a temperature-dependent residence time of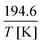 seconds. The input gas mixture was composed of 983 ppm of CH₃SH and 42 ppm of O₂, resulting in an effective oxidizer-to-fuel equivalence ratio of 0.014. The remaining bath gas used for dilution was N₂. At the exit of the flow reactor, the abundance of CH₃SH, CH₄, CO, CS₂, H₂, H₂S and SO₂ was measured. These data have been used to validate our mechanism performances and suggest improvements with ab initio calculations by looking at the discrepancies between experimental data and our modeling. More specifically, we performed sensitivity and formation pathway analyses using Cantera to identify key reactions involved in the formation of major species. Simulations were performed with an ideal plug flow reactor and fixed temperature, as the high dilution and temperature control should prevent deviations from the target temperature.

3.2. Decomposition mechanism

Results from sensitivity and formation pathway analyses under the conditions around 1400 K suggested the decomposition mechanism shown in Fig. 1. In the first step of the decomposition, CH₃SH gets thermally dissociated into CH₃ and SH radicals. In our mechanism, this reaction has been approximated by analogy with the pressure dependent CH₃OH → CH₃ + OH reaction from Jasper et al. (2007).²⁸ As detailed in Section 2, this means that the pre-exponential and temperature exponent parameters of the Arrhenius expression were assumed identical with CH₃OH → CH₃ + OH but the activation energy was modified by adding the reaction enthalpy difference to CH₃SH → CH₃ + SH, which was computed from each species NASA polynomials in the thermochemical data. This assumes that the enthalpy and entropy difference of the loose transition state to the reactant, the geometry of the corresponding dividing surface, its rotational and vibrational partition functions and their temperature dependence are all identical between these reactions, with the exception of the translational mode in the reaction coordinate which is assumed to be the only varying parameter resulting in the previously described modification of the activation energy. The parameters for the pressure dependence of the reaction rate are also assumed to be identical to CH₃OH → CH₃ + OH with this approach, resulting in the same Troe parameters (A = −0.4748, T₃ = 35 580 K, T₁ = 1116 K, and T₂ = 9023 K) and Arrhenius coefficients for high pressure (A = 2.084 × 10¹⁸ s⁻¹, n = −0.615, and E = 74 000 cal mol⁻¹) and low pressure (1.500 × 10⁴³ cm³ mol⁻¹ s⁻¹, n = −6.995, and E = 79 000 cal mol⁻¹). These assumptions are strong but seem reasonable due to the very similar geometry between CH₃OH and CH₃SH, and their validity was later confirmed by their good agreement with available experimental data and subsequent theoretical calculations (VRC-TST and ILT) that were beyond the scope of this work and will be the focus of a future publication. Briefly, these results showed that VRC-TST and our analogy usually agreed at least qualitatively, staying within the same order of magnitude in the whole P–T range studied (1000–10⁻⁶ bar, 200–5000 K), with up to a factor of 7 in the fall-off region, and significantly better agreement for low temperatures (below 1000 K). For high temperatures, ILT showed similar agreement but disagrees with our analogy and VRC-TST for low temperatures, predicting a rate constant up to 5 orders of magnitude lower at 300 K and an unphysical reverse rate for the recombination reaction CH₃ + SH → CH₃SH (10¹⁶ cm³ mol⁻¹ s⁻¹) in the high pressure limit, which hints towards numerical issues in the procedure. The approximate nature of this analogy should therefore be kept in mind when using the present rate constant far from the experimental conditions for which its accuracy has been confirmed.

Fig. 1 Thermal decomposition mechanism for CH₃SH.

Following the CH₃SH dissociation, the CH₃ and SH radicals produced then react with CH₃SH through H-abstraction reactions, mainly CH₃SH + CH₃ → CH₃S + CH₄ and CH₃SH + SH → CH₃S + H₂S, as CH₃S has a lower energy than its CH₂SH isomer, contrary to their CH₃ O and CH₂OH analogs. Addition on the S lone pair has been investigated, but no stable structure was found. The resulting radicals CH₃S and CH₂SH can then undergo a β-scission through CH₃S → CH₂S + H and CH₂SH → CH₂S + H or react with CH₃ and SH radicals through the disproportionation reactions CH₃S + CH₃ → CH₂S + CH₄, CH₂SH + CH₃ → CH₂S + CH₄, CH₃S + SH → CH₂S + H₂S and CH₂SH + SH → CH₂S + H₂S. The latter reactions are highly favored by reaction enthalpies at 1000 K (calculated based on thermodynamic data from our mechanism) of −56.4, −68.1, −42.0, and −53.6 kcal mol⁻¹, respectively. For CH₂SH + CH₃ and CH₃S + CH₃, the C₂H₄ + H₂S exit channel was also considered, but requires multiple isomerization and is not favorable in terms of entropy (respectively −13.4 and −4.0 cal mol⁻¹ K⁻¹ for the C₂H₄ + H₂S exit channel in comparison to −16.3 and −6.9 cal mol⁻¹ K⁻¹ for the CH₂S + CH₄ exit channel at 1000 K), while being about the same in enthalpy (1.4 kcal mol⁻¹ lower for C₂H₄ + H₂S). For the CH₃S + SH and CH₂SH + SH pathways, the other possible exit channel is CH₄ + S₂, which has an enthalpy lower by 10.1 kcal mol⁻¹, but no transition state was found for this reaction on the triplet surface.

These reactions all create the intermediate species CH₂S, that can then undergo either an H-abstraction through CH₂S + CH₃ → CHS + CH₄, CH₂S + SH → CHS + H₂S or an addition on each side of the C–S double bond with the CH₃ and SH radicals. Formation and consumption of CH₂S is found to be a major kinetic bottleneck that controls both the relative and absolute proportions of the major pyrolysis end products. The description of its reactions with CH₃ and SH is thus crucial, as the pressure dependence of the branching ratios between the different exit channels heavily depends on the enthalpy difference for each channel. This effect cannot be easily corrected for due to the vastly different behavior of SH radicals in comparison to OH radicals in regard to double bond addition, as shown by Degirmenci et al. (2016).²⁹ Radicals with an unpaired electron localized on the sulfur atom also are subject to way lower barriers and higher enthalpy differences when the double bond also involves an S atom. As a result, OH and CH₃ additions on CH₂O are usually minor reaction pathways in comparison to the H-abstraction and are supposed to approach the high pressure limit for its rate constant. However, this may not be true on the potential energy surface of the S analog, especially at the high temperatures imposed during pyrolysis which favors the dissociation of the adduct. This is especially crucial because if the H-abstraction dominates, the formation of CHS will lead to end products such as CS₂, which is formed almost exclusively from CHS through the CS intermediate species by the reactions CHS + CH₃ → CS + CH₄, CHS + SH → CS + H₂S and then by the ipso-addition CS + SH → CS₂ + H. Otherwise, if the addition dominates, other exit channels such as CH₂S + SH → CH₃ + S₂ or CH₂S + CH₃ → C₂H₄ + SH leads to products with a broken C–S bond and may prevent the formation of CS₂.

3.3. Ab initio calculations

To improve the core C/H/S mechanism that was built using analogies, we identified five crucial potential energy surfaces from key reactions mentioned in the previous section: CH₃SH + SH, CH₃SH + CH₃, CH₂S + SH, CH₂S + CH₃, and CS + SH. For each of them, all the geometries and vibrational frequencies were computed at the CCSD(T)-F12/cc-pVDZ-F12 level of theory using the Molpro software.^30–32 Energies were extrapolated to the CCSD(T)-F12 complete basis set limit from cc-pVTZ-F12 and cc-pVQZ-F12 energy calculations. Pressure-dependent phenomenological rate constants were then deduced using the Master Equation solver MESS.³³ Internal rotors were corrected from the partition function using the 1D hindered rotor model with scans at the B2PLYPD3/cc-pVDZ level of theory with the Gaussian 16 software. Thermodynamical data in the NASA 7 polynomial format were computed using the atomization method with the Thermrot³⁴ software and energies/frequencies/geometries as previously mentioned. For reactions involving H-atom transfer, tunneling corrections were applied using an asymmetric Eckart potential. Computed geometries, vibrational frequencies, torsional potentials, and the parameters used to solve the master equation are available in the SI in the form of MESS and Thermrot inputs. We detail hereafter the calculations for each reaction.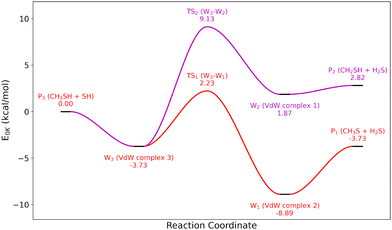

3.3.1. CH₃SH + SH and CH₃SH + CH₃. Because of the importance and sensitivity of the first H-abstractions with CH₃SH, we decided to compute the full potential energy surface for CH₃SH + SH and CH₃SH + CH₃. Two different exit channels were identified for each surface: CH₃S + H₂S, CH₂SH + H₂S for CH₃SH + SH, and CH₃S + CH₄, CH₂SH + CH₄ for CH₃SH + CH₃, each corresponding to a different H-abstraction site. The corresponding potential energy surfaces are shown in Fig. 2 and 3.

Fig. 2 Potential energy surface of the CH₃SH + SH reaction at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory.

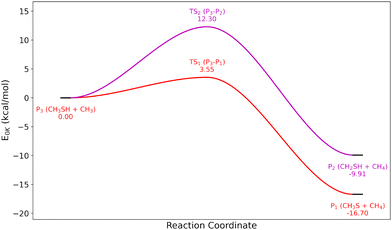Fig. 3 Potential energy surface of the CH₃SH + CH₃ reaction at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory.

For CH₃SH + SH, the formation of two van der Waals complexes was found to have a significant impact on the kinetics at low temperatures. Indeed, this van der Waals interaction results in an almost submerged barrier for CH₃SH + SH → CH₃S + H₂S, which features a barrier height lower than the depth of the pre-reactive complex that crucially affects the perceived barrier height when including the effect of tunneling. To account for the formation of this pre-reactive complex, phase space theory, implemented in the MESS code³³ was used for the barrierless formation of the entrance channel complex, based on a 1-dimensional potential between the centers of mass of the two reactants calculated at the B2PLYPD3/aug-CC-pVTZ level of theory. The resulting rate constants for these reactions are shown in Fig. 4, compared to the previously obtained values from the analog reaction CH₃OH + OH. The effect of bond dissociation energy differences between CH₃S–H (−86.8 kcal mol⁻¹) and CH₃ O–H (−105.2 kcal mol⁻¹) are clearly seen for the reaction CH₃SH + SH → CH₃S + H₂S. The exit channel CH₃S + H₂S is highly favored over CH₂SH + H₂S at low temperatures, although at high temperatures (1000–2000 K) both reactions contribute significantly to the total abstraction rate constant. This behavior is clearly in contrast with their oxygenated analog, where CH₂OH + OH is always the preferred exit channel for all the plotted temperature range. Differences in the slope of the curves also show variations in the activation energy between the two systems, particularly for the reaction yielding CH₂SH. For the similar CH₃SH + CH₃ H-abstraction reactions, the entrance channel complex had a negligible energy in comparison to the activation energy (0.5 kcal mol⁻¹ at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory). Thus, for these reactions the rate constant were computed using Thermrot,³⁴ and only considering the reactants, the transition states and the products. The resulting rate constants for this potential energy surface are shown in Fig. 5, as well as the rate constants determined by analogy with the CH₃OH + CH₃ equivalents. We observe the same behavior as previously stated with CH₃SH + SH, with the exit channel CH₃S + CH₄ dominating at low temperatures while CH₂SH + CH₄ only significantly contributes at very high temperatures. However, its amplitude is different, as the ratio between each corresponding rate at 500 K is around one order of magnitude for the CH₃SH + SH surface, and around three orders of magnitude for the CH₃SH + CH₃ surface. Comparison with the oxygen analog also shows the inverse behavior between CH₃SH and CH₃OH, the latter favoring the CH₂OH exit channel. This has a huge impact on the accuracy of the analogy for the CH₃SH + CH₃ → CH₃S + CH₄ reaction, but surprisingly has little impact on the rate constant of CH₃SH + CH₃ → CH₂SH + CH₄.

Fig. 4 Computed rate coefficients for the CH₃SH + SH abstractions. Analogies with the CH₃OH + OH equivalents from Xu et al. (2007)³⁵ are shown in dashed lines.

Fig. 5 Computed rates coefficients for the CH₃SH + CH₃ H-abstractions. Analogies with the CH₃OH + CH₃ equivalents from Alecu et al. (2011)³⁶ are shown in dashed lines.

3.3.2. CH₂S + SH and CH₂S + CH₃. As explained in Section 2, the reactions of CH₂S with SH and CH₃ and the competition between addition and H-abstraction play a crucial role in controlling the products. In consequence, we decided to compute the full potential energy surface for both cases.

For CH₂S + SH, we considered the H-abstraction to CHS + H₂S and the additions on the double bond, both on the sulfur atom, forming CH₂S₂H and on the carbon atom, forming HSCH₂S. We also considered isomerizations both by H and SH transfers, adding the respective pathways CH₂S₂H → CH₃S₂ and HSCH₂S → CH₂S₂H. For the exit channels, we considered the β-scissions CH₃S₂ → CH₃ + S₂ and HSCH₂S → SCHSH + H. Due to the barrierless behavior of the CH₃ + S₂ exit channel, its inclusion required using multireference methods. This was done using Phase Space Theory together with a C–S bond scan at the CASPT2(11e,8o)/cc-pVDZ//CASSCF(11e,8o)/cc-pVDZ level of theory. The contributing determinants to the wavefunction during this relaxed scan are shown in Fig. S1 (SI). The resulting full potential energy surface is shown in Fig. 6.

Fig. 6 Potential energy surface of the CH₂S + SH reaction at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory.

The first issue was the transition state TS₂ of the addition on the sulfur atom, which has an energy lower than the entry channel by 4.2 kcal mol⁻¹. When doing the intrinsic reaction coordinate scan to search for the geometry of the van der Waals complex W₁ at the B2PLYPD3/cc-pVDZ level of theory, we noticed the formation of two van der Waals complexes with peculiar geometry, as shown in Fig. 7. The first one (VdW 1) is found to have a very close geometry to the transition state, with a S–S distance of 2.92 Å in comparison to 2.67 Å for the transition state. The S–H bond of the SH radical is not in the same plane as the CH₂S molecule, and this structure seems almost covalently bound given the orientation of the SH fragment. The second one (VdW2, W₁ in Fig. 6) is more in line with the expected geometry for such a system, with SH and CH₂S in the same plane, and the H atom oriented towards the S atom of CH₂S and a more distant position of the SH fragment. The first one was found to have a lower energy in our preliminary B2PLYPD3/cc-pVDZ calculations. We also tried comparing the energies of the two geometries with the CCSD/cc-pVDZ level of theory to confirm this relationship, but we obtained the opposite result, with no van der Waals complex with similar geometry to the first one and the second one behind the configuration minimizing the energy of the system. To try to understand the discrepancies between these results, we also tried to optimize the geometries with Gaussian counterpoise correction of the basis set superposition error, but we did not find significant contribution to justify these changes. To account for the van der Waals complex formation, we therefore decided to use phase space theory with the second geometry complex based on a 1-dimensional potential between the centers of mass of the two reactants calculated at the B2PLYPD3/aug-CC-pVDZ level of theory. Moreover, the subsequent calculations we performed at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory exhibited convergence issues for both the transition state of the addition on the sulfur atom and the van der Waals complex (TS₂ and W₁ in Fig. 6 respectively), which forced us to investigate on the matter. For these calculations, the T₁ diagnostic³⁷ was found to be above 0.05, which induced important oscillations in the CCSD iterative solver of Molpro, that were not solvable with a level shift nor incrementing the number of maximum steps. Therefore, given this extreme contribution of the triplets to the total energy, we used CASPT2 calculations. To determine the relevant active space size, we first performed a single point energy calculation in CASSCF with all the valence electrons included and 3 unoccupied valence orbitals, which resulted in 19 electrons in 13 orbitals, and looked at the occupation of the lower energy orbitals. From there, it was found that the LUMO was occupied at around 10%, and when looking at the Slater determinants composition of the wavefunction, this occupation was mainly caused by an excited electron pair occupying this level, which contributed with a negative amplitude of around −0.15. Other determinants formed by the unpairing of electrons were also found to contribute to the LUMO occupation, but also for the next orbital (LUMO+1), which was occupied at around 3%. As the involved electron pairs were the two doubly occupied orbitals with the highest energy, we decided to include these orbitals in the active space, as well as the singly occupied orbital and the next two unoccupied orbitals, which resulted in an active space of 5 electrons in 5 orbitals.

Fig. 7 B2PLYPD3/cc-pVDZ geometries of the two van der Waals complexes found for the addition reaction CH₂S + SH → CH₂S₂H. The first one is the minimum at this level of theory, while at the CCSD/cc-pVDZ level, the second one is the minimum. CCSD(T)-F12/cc-pVDZ-F12 calculations on this second geometry indicated a T₁ diagnostic above 0.05 that prevented convergence of the wavefunction.

We performed a relaxed scan of the S–S bond length from 2 to 11 Å in CASPT2(5e,5o)/cc-pVDZ to capture the full van der Waals interaction. We also recomputed the same scan from 2 to 3.6 Å with both CASPT2(5e,5o)-F12/cc-pVTZ-F12//CASPT2(5e,5o)/cc-pVDZ and CCSD(T)-F12/cc-pVDZ-F12 level of theories to focus on the transition state position. The results of this comparison are shown in Fig. 8 and 9. The position of the two minima on the potential energy surface is clearly visible on the full scan with CASPT2(5e,5o)/cc-pVDZ, but contrary to B2PLYPD3/cc-pVDZ, CCSD(T)-F12/cc-pVDZ-F12 and also CASPT2(5e,5o)-F12/cc-pVTZ-F12//CASPT2(5e,5o)/cc-pVDZ calculations, the second geometry with both fragments in the same plane (VdW 2) is of lower energy. However, this seems to be caused by an insufficient basis set size, as the energy calculations with CASPT2(5e,5o)-F12/cc-pVTZ-F12 using geometries from CASPT2(5e,5o)/cc-pVDZ calculations results in this geometry (VdW 2) being higher in energy than the out-of-plane geometry (VdW 1). Also, with the CASPT2(5e,5o)-F12/cc-pVTZ-F12 level of theory, the transition state seems to be of higher energy than the CH₂S + SH asymptote, which is not true anymore with all the other levels of theory previously mentioned. This can be seen on the second, finer close-range scan that was performed in Fig. 9, together with the transition state position that is very sensitive to the level of theory used. Another notable difference between CASPT2(5e,5o)/cc-pVDZ and CCSD(T)-F12/cc-pVDZ-F12 geometry optimization is that the former has available analytical gradients in Molpro, while the second uses the analytical gradient from the Alaska program.³⁸ Different options for computing the numerical gradients were tested (finer step size, tighter convergence criteria, different coordinate system…) and the energy and position of the transition state seem to be quite dependent on these parameters, indicating that the flat geometry of the potential energy surface might result in a loose transition state and convergence to geometries far from its real one. However, for the default parameters, the relatively good agreement with geometries from the CASPT2(5e,5o)/cc-pVDZ analytical gradient seems to indicate that the precision of the results from numerical gradients might be sufficient for the purposes of this kinetic study.

Fig. 8 Relaxed scan of the S–S bond length in the CH₂S + SH potential energy surface with the CASPT2(5e,5o)/cc-pVDZ level of theory.

Fig. 9 Relaxed scan of the S–S bond length in the CH₂S + SH potential energy surface with two levels of theory: CCSD(T)-F12/cc-pVDZ-F12 (yellow) and CASPT2(5e,5o)-F12/cc-pVTZ-F12//CASPT2(5e,5o)/cc-pVDZ (blue). Starting from 3 Å, oscillations in the coupled cluster iterative solver prevents the wavefunction from converging.

For the reaction rate calculations, we therefore used the CCSD(T)-F12/cc-pVDZ-F12 geometries and energies, while using the coplanar van der Waals complex geometry obtained (VdW 2) for its Phase Space Theory treatment. The resulting branching ratio for each exit channel and the rates at 1 bar are shown in Fig. 10 and 11 respectively.

Fig. 10 Computed branching ratio for the CH₂S + SH potential energy surface in Fig. 6.

Fig. 11 Computed rate coefficients at 1 bar for the CH₂S + SH potential energy surface. H-abstraction is shown in black, additions in red, and β-scission in blue.

For the full pressure and temperature range (10⁻⁶–100 bar, 300–2500 K), we see that mainly two exit channels are relevant: the H-abstraction CHS + H₂S and the addition on the sulfur atom yielding CH₂S₂H. At high pressures and low temperatures, stabilization of the HSCH₂S radical also contributes significantly to the total reaction rate. At 1 bar, which corresponds to the pressure in the experiments of Colom-Diaz et al. (2021),²⁰ we see that the H-abstraction dominates above 1000 K, while under this value, the addition on the sulfur atom dominates, stabilizing on the CH₂S₂H radical, but also to a lesser extent on the HSCH₂S radical, which contributes increasingly at higher temperatures. The addition on the sulfur atom followed by the isomerization and stabilization to CH₃S₂, however, is negligible. β-scission exit channels such as CH₃ + S₂ are never the favored reaction, but can possibly occur in multiple steps after the addition at low temperatures (<1000 K). For the SCHSH + H exit channels, its high energy transition state prevents it from any significant contribution, and thus is assumed to be negligible.

For the CH₂S + CH₃ potential energy surface, we considered the H-abstraction yielding to CHS + CH₄ (TS₃, P₂) and both the addition on the carbon atom to CH₃CH₂S (TS₁, W₁) and the addition on the sulfur atom to CH₂SCH₃ (TS₂, W₂). We also considered the isomerizations by H atom transfer CH₃CH₂S → CH₂CH₂SH (TS₅) and CH₃ fragment transfer CH₂SCH₃ → CH₃CH₂S (TS₄). The β-scission exit channel to C₂H₂ + SH (TS₆, P₃) was also considered. The resulting potential energy surface is shown in Fig. 12. Branching ratios and reaction rates are shown in Fig. 13 and 14 respectively. For the full pressure–temperature range computed, we can see that mainly three exit channels dominate: either the β-scission C₂H₄ + SH at low temperatures and low pressures, the H-abstraction to CHS + CH₄ at high temperatures and low pressures, or the addition on the sulfur atom to CH₂SCH₃ at high pressures and low temperatures. At 1 bar, we see that the H-abstraction to CHS + CH₄ only becomes dominant above 1600 K, while under 1200 K the addition on the sulfur atom to CH₂SCH₃ dominates. Between these temperatures, the exit channel to the β-scission C₂H₄ + SH is the major process that happens directly from the CH₂S + SH input channel. In comparison to the CH₂S + SH reaction rates, we can also see that the reactivity is a bit lower as the reaction rates only exceed 10¹² cm³ mol⁻¹ s⁻¹ for the H-abstraction above 1700 K, but the reaction enthalpy is also greater, which should result in slower reversed reactions.

Fig. 12 Potential energy surface of the CH₂S + CH₃ reaction at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory.

Fig. 13 Computed branching ratio for the CH₂S + CH₃ potential energy surface in Fig. 12.

Fig. 14 Computed rate coefficients at 1 bar for the CH₂S + CH₃ potential energy surface. H-abstraction is shown in black, additions in red, and β-scission in blue.

3.3.3. CS + SH. Due to the formation of CHS radicals and their abstraction to CS, the next crucial reaction towards the formation of CS₂ is CS + SH. This reaction has been investigated with the same methodology described in Section 3.3, and the full resulting potential energy surface is shown in Fig. 15. We identified one addition site on the carbon atom to form the SCSH radical (W₁ through TS₃), which can then undergo a β-scission to the CS₂ + H products (P₂ through TS₂) to form the ipso-addition CS + SH → CS₂ + H. This radical can also undergo an isomerization to the more stable SCHS radical (W₂ through TS₄) due to a resonance between the S atoms bearing the unpaired electron. This radical can also undergo a β-scission to the products CS₂ + H (P₂ through TS₁). The evaluation of the energy of the addition transition state revealed a very low barrier, under the energy of the CS + SH products. The formation of a van der Waals complex with a linear geometry was identified (W₁) and treated with Phase Space Theory. The electronic energy of this complex was found to be about 0.5 kcal mol⁻¹ under the transition state energy, but when adding the zero point energy of both structures their energy difference becomes lower than the computation accuracy (computed difference of 0.02 kcal mol⁻¹). The corresponding branching ratios and reaction rates for this potential energy surface are shown in Fig. 16 and 17 from the CS + SH perspective and in Fig. 18 and 19 from the CS₂ + H perspective, respectively. For the CS + SH entry point, there is only one relevant pathway, which is the ipso-addition CS + SH → CS₂ + H that has a branching ratio of one over the whole range of pressures and temperatures used for the calculation. This results from its reaction rate being over 6 orders of magnitude higher than the two other reactions that stabilizes the radicals SCSH and SCHS, and is itself due to a combination of two factors. First, the rate for this reaction is effectively restricted by the collision limit, as the limiting step is the formation of the van der Waals complex due to the energy barrier of the transition state for the addition being lower than the CS + SH energy. The energy difference between this barrier and the complex is so low that it cannot be stabilized even at low temperatures and high pressures, given that it is lower than thermal energy even at 200 K. Second, the β-scission transition state is lower than the CS + SH energy by around 19 kcal mol⁻¹ and the low well depth of about 18 kcal mol⁻¹ under this transition state prevents the resulting radical from being stabilized at any pressure explored here. Conversely, if we look at CS₂ + H as the entrance channel, the SCSH → CS + SH β-scission has to overcome the reverse reaction enthalpy, which creates a region at low temperatures (<1000 K at atmospheric pressure) where the addition product SCSH is stabilized, while the ipso-addition CS₂ + H → CS + SH only dominates at high temperatures. The other addition to SCHS, while favorable in enthalpy in comparison to SCSH, is never dominant because of the higher energy of transition state for this pathway.

Fig. 15 Potential energy surface of the CS + SH reaction at the CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory.

Fig. 16 Computed branching ratio for the CS + SH potential energy surface in Fig. 15.

Fig. 17 Computed rate coefficients at 1 bar for the CS + SH potential energy surface. Addition is shown in red and ipso-addition in blue. The dashed line also requires an isomerization.

Fig. 18 Computed branching ratio for the CS + SH potential energy surface in Fig. 15 from the perspective of the CS₂ + H entrance channel.

Fig. 19 Computed rate coefficients at 1 bar for the CS₂ + H potential energy surface. Addition is shown in red and ipso-addition in blue. The dashed line also requires an isomerization.

3.4. Comparison with experimental data

From the calculations in Section 3.3, we included in the mechanism every rate constant shown in Fig. 4, 5, 11, 14 and 17 in addition to each dominant pathway from other entrance channels that didn't correspond to a reverse reaction of these. The performance of the mechanism developed is tested against the experimental data on CH₃SH pyrolysis of Alzueta et al. (2019)²¹ in Fig. 20, and the corresponding sensitivity and rate of production analysis for T = 1400 K are given in Fig. S2 and S3 (SI) respectively. For CH₃SH consumption, the mechanism perfectly reproduces the experimental data mainly thanks to the analogy used for the CH₃SH thermal decomposition CH₃SH → CH₃ + SH, which used the differences in reaction enthalpies to compute the activation energy. This major initiation reaction is, as expected, the most sensitive reaction for every species. The production of CH₄ is in good agreement with the experimental data, as the mechanism correctly reproduces the shape of the temperature dependence, but underestimates its abundance by about 100 ppm over 1000 K. Fig. S3 (SI) shows that CH₄ is mainly produced by the reaction CH₃ + H₂S → CH₄ + SH, although it is not a sensitive reaction. The most sensitive reaction excluding the initiation is CH₃ + CH₃SH → CH₃S + CH₄, which has been computed in Section 3.3. The reevaluation of this rate constant is the main cause of the improvement of the simulations over the Colom-Diaz et al. (2021)²⁰ mechanism. As we already extensively investigated both the abstractions and the additions on CH₂S, we know it is not the cause of the underestimated abundance of CH₄. Fig. S4 (SI) gives an idea of the species to which the remaining carbon is distributed. Among the species CH₂S CS₂, C₂H₆, C₂H₄ and C₂H₂ that all bear carbon atoms, CH₂S and C₂H₆ are intermediate species that do not contribute to the final carbon balance. The overabundance of the CS₂ is also too small to fully explain the difference, and does not correspond to the same temperature range as the under-abundance of CH₄, which it cannot explain between 1000 and 1200 K. Therefore, the issue probably lies in C₂H₄ and C₂H₂, which have significant abundances of 80 and 60 ppm respectively at the end of the simulation. As these species contain 2 carbon atoms, together they represent a potential of 280 ppm of CH₄ if hydrogen is supplied from another source. As previously seen in Section 3.3 and observed by Degirmenci et al. (2016),²⁹ the addition of SH radicals on double bonds is highly favored in comparison to OH, and could potentially be the cause of C₂H₄ and C₂H₂ decomposition to CH₄ above 1000 K. Further study of the full potential energy surface of C₂H₄ + SH and C₂H₂ + SH with both H-abstraction and addition considered would be needed, but is out of the scope of this work. The production of CS₂ matches also quite well the experimental data, despite overestimating its abundance by around 50 ppm over 1250 K. Its main production pathway is the reaction CS + SH → CS₂ + H and to a lesser extent the reaction CS + S₂ → CS₂ + S. The most sensitive reactions besides the initiation are the H-abstraction CH₂S + SH → CHS + H₂S and the ipso-addition CS + SH → CS₂ + H, which we computed in Section 3.3, and believe to be the cause of improvement over the mechanism of Colom-Diaz et al. (2021).²⁰ Improvement in the CS₂ abundance above 1200 K could probably be achieved by considering other reactions of CS, which is very reactive in contrast to CO, despite being a closed-shell molecule. This could include the study of the full CS + CH₃ potential energy surface, or reactions with other abundant closed-shell species such as CH₃SH, H₂, H₂S and CH₄. The abundance of H₂S is also well reproduced with a slight underestimation similar to CH₄, although its magnitude is closer to 50 ppm. At 1400 K, H₂S seems to approach thermochemical equilibrium, with production mainly coming from H-abstractions on CH₂S and CH₃SH through the reactions CH₂S + SH → CHS + H₂S and CH₃SH + SH → CH₃S + H₂S. On the opposite side, destruction reactions are mainly H-abstractions on H₂S by the H and CH₃ radicals through the reactions H₂S + H → H₂ + SH and H₂S + CH₃ → CH₄ + SH. Sensitive reactions are mainly H-abstraction on CH₃SH by SH radicals for both channels CH₃SH + SH → CH₃S + H₂S and CH₃SH + SH → CH₂SH + H₂S, and to a lesser extent the non-thermal addition/isomerisation/beta-scission reaction CH₂S + SH → CH₃ + S₂ that were all computed in Section 3.3. The massive improvement over the Colom-Diaz et al. (2021)²⁰ mechanism is therefore believed to be mainly due to the accurate computation of the H-abstraction reactions on CH₃SH by SH radicals with the treatment of the van der Waals complex in Section 3.3. The abundance of H₂ is almost perfectly reproduced. In comparison, the Colom-Diaz et al. (2021)²⁰ mechanism overestimates H₂ by a factor of 2, and underestimates H₂S and CH₄ by more than a factor of 3. Its formation mainly involves H-abstraction on H₂S, CH₂S and CH₃SH by the H atom through the reactions H₂S + H → H₂ + SH, CH₂S + H → CHS + H₂ and CH₃SH + H → CH₃S + H₂. When looking at the most sensitive reactions, the H-abstraction on CH₃SH is the most significant, along with the thermal decomposition of the CH₃S radical through the beta-scission CH₃S → CH₂S + H. This reaction has seen its activation energy adjusted by preliminary B2PLYPD3/cc-pVDZ calculations, which are believed to be a source of improvement over the Colom-Diaz et al. (2021)²⁰ mechanism. As some residual oxygen was left in the experimental conditions, CO was also measured in the original data set, and although the temperature dependence doesn't match the experimental data perfectly, the order of magnitude is well reproduced with the present mechanism. This species is produced exclusively through the thermal decomposition of HCO through the reaction HCO → CO + H, which seems to be produced by the oxidation mechanism through the addition of O₂ and its non-thermal decomposition to CH₂O through the reaction CH₂S + O₂ → CH₂O + SO and the H-abstraction of CH₂O through the reaction CH₂O + SH → HCO + H₂S. These reactions were also analogies with activation energies approximated thanks to B2PLYPD3/cc-pVDZ calculations. Further work would be needed on the oxidation mechanism, but this kind of study is outside the scope of this work.

Fig. 20 Comparison between the present work (yellow) and Colom-Diaz et al. (2021)²⁰ (blue) mechanisms on experimental CH₃SH pyrolysis data from Alzueta et al. (2019).²¹

4. Conclusions

We have presented here an extensive theoretical study of the kinetics of CH₃SH pyrolysis. A reaction mechanism was built upon available reaction sub-mechanisms from the literature for H/O/S and C/S kinetics, and using analogies with oxygenated molecules for the basic C/H/S coupling. Sensitivity and rates of production analysis were then obtained to determine key reactions of CH₃SH + SH, CH₃SH + CH₃, CH₂S + SH, CH₂S + CH₃, and CS + SH for which theoretical reactions rates were calculated. Pressure dependence and pre-reactive complex formation were treated using master equation and phase space theory methods together with a CCSD(T)-F12/CBS//CCSD(T)-F12/cc-pVDZ-F12 level of theory. Multireference effects were also investigated using CASPT2 calculations. Additions on CH₂S are found to have a significant contribution in contrast to the case of CH₂O, due to the very low energy of the transition states. This often causes transition states with negative energies relative to the enthalpy asymptotes and creates cases where pre-reactive complex treatment is necessary. Available experimental data have been compared to kinetics simulations, and the developed mechanism exhibits robust behavior that correctly reproduces the experimental data.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: all theoretical data as inputs of MESS and THEMROT codes, the kinetic mechanism in CHEMKIN and CANTERA formats, and supplementary Fig. S1–S4. See DOI: https://doi.org/10.1039/d4cp04873c.

Acknowledgements

This project is funded by the ANR project “EXACT” (ANR-21-CE49-0008-01). In addition, O.V. acknowledges funding from the Centre National d’Études Spatiales (CNES). High performance computing resources were provided by IDRIS under the allocation AD010812434R3 made by GENCI and also by the EXPLOR center hosted by the University of Lorraine. This work was partly supported by a Science and Technology Facilities Council Small Award [ST/Y00261X/1].

References

1. J. S. Eow, Environ. Prog., 2002, 21, 143–162.
2. H. Bian, B. Xu, H. Zhang, Q. Wang, H. Zhang, S. Zhang and D. Xia, Int. J. Quantum Chem., 2019, 119, e25822.
3. D. J. Kieber, J. Jiao, R. P. Kiene and T. S. Bates, J. Geophys. Res.: Oceans, 1996, 101, 3715–3722.
4. N. J. Nabikandi and S. Fatemi, J. Ind. Eng. Chem., 2015, 30, 50–63.
5. R. K. Rahman, A. G. Raj and S. Ibrahim, Abu Dhabi International Petroleum Exhibition and Conference, 2017, p. D021S052R004.
6. W. Burgers, P. Northrop, H. Kheshgi and J. Valencia, Energy Procedia, 2011, 4, 2178–2184.
7. E. Dumont, Int. J. Energy Environ., 2015, 6, 479–498.
8. B. Nguyen, B. Bonsang and A. Gaudry, J. Geophys. Res.: Oceans, 1983, 88, 10903–10914.
9. T. Bates, B. Lamb, A. Guenther, J. Dignon and R. Stoiber, J. Atmos. Chem., 1992, 14, 315–337.
10. M. Chin, D. J. Jacob, G. M. Gardner, M. S. Foreman-Fowler, P. A. Spiro and D. L. Savoie, J. Geophys. Res.: Atmos., 1996, 101, 18667–18690.
11. D. Davis, G. Chen, P. Kasibhatla, A. Jefferson, D. Tanner, F. Eisele, D. Lenschow, W. Neff and H. Berresheim, J. Geophys. Res.: Atmos., 1998, 103, 1657–1678.
12. G. S. Tyndall and A. Ravishankara, Int. J. Chem. Kinet., 1991, 23, 483–527.
13. J. Chen, T. Berndt, K. H. Møller, J. R. Lane and H. G. Kjaergaard, J. Phys. Chem. A, 2021, 125, 8933–8941.
14. S.-M. Tsai, E. K. Lee, D. Powell, P. Gao, X. Zhang, J. Moses, E. Hébrard, O. Venot, V. Parmentier and S. Jordan, et al., Nature, 2023, 617, 483–487.
15. A. Dyrek, M. Min, L. Decin, J. Bouwman, N. Crouzet, P. Mollière, P.-O. Lagage, T. Konings, P. Tremblin and M. Güdel, et al., Nature, 2024, 625, 51–54.
16. S.-M. Tsai, M. Malik, D. Kitzmann, J. R. Lyons, A. Fateev, E. Lee and K. Heng, Astrophys. J., 2021, 923, 264.
17. J. I. Moses, C. Visscher, J. J. Fortney, A. P. Showman, N. K. Lewis, C. A. Griffith, S. J. Klippenstein, M. Shabram, A. J. Friedson and M. S. Marley, et al., Astrophys. J., 2011, 737, 15.
18. P. B. Rimmer and S. Rugheimer, Icarus, 2019, 329, 124–131.
19. B. Drummond, P. Tremblin, I. Baraffe, D. S. Amundsen, N. J. Mayne, O. Venot and J. Goyal, Astron. Astrophys., 2016, 594, A69.
20. J. Colom-Daz, M. Alzueta, Z. Zeng, M. Altarawneh and B. Dlugogorski, Fuel, 2021, 283, 119258.
21. M. U. Alzueta, R. Pernía, M. Abián, Á. Millera and R. Bilbao, Combust. Flame, 2019, 203, 23–30.
22. P. Glarborg, B. Halaburt, P. Marshall, A. Guillory, J. Troe, M. Thellefsen and K. Christensen, J. Phys. Chem. A, 2014, 118, 6798–6809.
23. R. Veillet, O. Venot, B. Sirjean, R. Bounaceur, P.-A. Glaude, A. Al-Refaie and E. Hébrard, Astron. Astrophys., 2024, 682, A52.
24. A. Stagni, S. Arunthanayothin, L. Pratali Maffei, O. Herbinet, F. Battin-Leclerc and T. Faravelli, Chem. Eng. J., 2022, 446, 136723.
25. U. Burke, W. K. Metcalfe, S. M. Burke, K. A. Heufer, P. Dagaut and H. J. Curran, Combust. Flame, 2016, 165, 125–136.
26. B. Sirjean, J.-C. Lizardo-Huerta, L. Verdier, R. Fournet and P.-A. Glaude, Proc. Combust. Inst., 2017, 36, 499–506.
27. D. G. Goodwin, H. K. Moffat, I. Schoegl, R. L. Speth and B. W. Weber, Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes, Version 3.0.0, 2023. https://www.cantera.org.
28. A. W. Jasper, S. J. Klippenstein, L. B. Harding and B. Ruscic, J. Phys. Chem. A, 2007, 111, 3932–3950.
29. I. Degirmenci and M. L. Coote, J. Phys. Chem. A, 2016, 120, 1750–1755.
30. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
31. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al., J. Chem. Phys., 2020, 152, 144107.
32. H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2022.1, a package of ab initio programs, see https://www.molpro.net.
33. Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154.
34. J. Lizardo-Huerta, B. Sirjean, R. Bounaceur and R. Fournet, Phys. Chem. Chem. Phys., 2016, 18, 12231–12251.
35. S. Xu and M.-C. Lin, Proc. Combust. Inst., 2007, 31, 159–166.
36. I. Alecu and D. G. Truhlar, J. Phys. Chem. A, 2011, 115, 14599–14611.
37. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
38. R. Lindh, Theor. Chim. Acta, 1993, 85, 423–440.

---