Kinetics of radiation-induced Cr(II) and Cr(III) redox chemistry in molten LiCl–KCl eutectic

Abstract

Chromium (Cr) is a frequent constituent of the metal alloys proposed for molten salt nuclear reactor (MSR) applications, and is typically the least noble metal ion present. Consequently, chromium is preferentially corroded into molten salt solutions. The redox poise and redox cycling of chromium ions in the salt can greatly influence its corrosivity towards structural alloys, ultimately impacting the longevity of MSR systems. Radiation-induced chemistry is expected to play a significant role in determining the chromium oxidation state distribution during MSR operations. In the present research, electron pulse radiolysis techniques were employed to characterize the reactivity of Cr(II) and Cr(III) ions with primary radiolysis products in molten lithium chloride–potassium chloride (LiCl–KCl) eutectic over a temperature range of 400–600 °C. Both chromium oxidation states were found to rapidly react with the primary products of molten chloride salt radiolysis, i.e., the solvated electron (e_S⁻) and the dichlorine radical anion (Cl₂˙⁻). For reactions with the e_S⁻, second-order rate coefficients (k) of k = (4.1 ± 0.2) and (6.1 ± 0.3) × 10¹⁰ M⁻¹ s⁻¹ at 400 °C for Cr(II) and Cr(III), respectively, were determined. Temperature-dependent measurements allowed for the derivation of activation parameters for electron capture by Cr(II) and Cr(III). Both chromium ions also react with Cl₂˙⁻, k = (7.2 ± 0.3) and (1.4 ± 0.1) × 10⁹ M⁻¹ s⁻¹ at 400 °C for Cr(II) and Cr(III), respectively.

---

Introduction

Halide molten salts (MS) have two significant applications within a nuclear fuel cycle: as an electrolyte for the pyroprocessing of used nuclear fuel,^1,2 and as a coolant and/or fuel matrix for next-generation molten salt reactors (MSRs).^3–5 Both applications entail extreme environments, due to the high temperatures (>350 °C) and intense, multicomponent (alpha, beta, gamma, neutron, and recoiling daughter nuclei), ionizing radiation fields.⁶ Consequently, extensive investigation has been devoted to developing and testing different metal alloys in regard to compatibility with MS under such types of extreme conditions.⁷ Of the various alloys evaluated, chromium is a frequent constituent, e.g., in Inconel 600 (Ni–15Cr–7Fe) and Hastelloy N (Ni–16Mo–7Cr–4.5Fe), and because it is typically the least noble element in these alloys, it is preferentially corroded and dissolved in MS by contaminants such as moisture and oxygen.^7–10 This leads to chromium depletion that eventually compromises the integrity and performance of the metal alloy.^8,11 Furthermore, the dissolution of chromium into the MS changes the redox potential of the solution and ultimately its ability to propagate corrosion. For example, Cr(III) ions have been shown to accelerate the dissolution of chromium and iron metals in molten alkali metal fluorides.¹² Similar effects have been observed when Eu(III) ions are present.¹³

An important question is whether a radiation field of the kind that would exist in a MSR would have an accelerating or decelerating effect on reactor alloy corrosion. A study by Zhou et al. reported radiation-induced deceleration of chromium corrosion in Ni–20Cr alloy.¹⁴ Under their solution conditions (FLiNaK plus 5 wt% EuF₃ as a corrosion promoter), proton irradiation afforded less extensive corrosion than in the absence of an ionizing radiation field. Notably, a subsequent study¹⁵ by the same group applying the same methodology to three different alloys reported accelerated corrosion for 316L stainless steel and Incoloy 800 H under proton irradiation, and no radiation effect for Inconel 600. In all cases, the observed irradiation effects were attributed to the radiation-induced migration of chromium and nickel ions towards alloy grain boundaries that were actively depleted of chromium via MS corrosion processes. The effect of this migration is deemed to be protective at low concentrations of corrosion-susceptible elements (Cr and Fe) in the alloy, but corrosion-promoting at high concentrations of Cr and Fe. A separate study from Oak Ridge National Laboratory using neutron irradiation in molten NaCl–MgCl₂ eutectic in the presence or absence of moisture showed radioprotection of 316L stainless steel but no effect on alloy N corrosion.¹⁶

Note that the mechanisms proposed above only rely on radiation-induced changes in alloy microstructure. There is no consideration of the effect of radiolysis on the MS itself, i.e., the influence of MS irradiation on the speciation of the chromium or europium species that contribute to corrosion mechanisms, nor the effect of irradiation on the redox poise of the salt mixture, in the bulk or locally near the interface.

Irradiation of molten alkali metal halides (M⁺X⁻) induces the formation of solvated electrons (e_S⁻) and halide atoms (X˙), eqn (1), the latter of which rapidly combine with neighbouring halide anions (X⁻) to yield dihalogen radical anions (X₂˙⁻) eqn (2):^17–24

M⁺X⁻ [long arrow, wavy then straight] M⁺ + e_S⁻ + X˙, (1)

X˙ + X⁻ → X₂˙⁻. (2)

These primary molten salt radiolytic species (e_S⁻ and X₂˙⁻) are redox active and thus capable of altering metal ion oxidation state distributions. For example, in earlier work we showed that Zn(II) ions in LiCl–KCl eutectic at 400 °C rapidly react with the e_S⁻ (eqn (3)), but not with the dichlorine radical anion (Cl₂˙⁻), whereas the Zn(I) ions generated through eqn (3) do:²⁴

Zn²⁺ + e_S⁻ → Zn⁺ k₃ = (4.2 ± 0.1) × 10¹⁰ M⁻¹ s⁻¹, (3)

Zn⁺ + Cl₂˙⁻ → Zn²⁺ + 2Cl⁻ k₄ = (2.0 ± 0.2) × 10¹⁰ M⁻¹ s⁻¹. (4)

Under our experimental conditions, eqn (3) is first-order with respect to the e_S⁻, whereas eqn (4) is second-order. Thus, in the presence of a constant ionizing radiation field and a reasonable concentration of metal ion electron acceptors, a steady-state concentration of reduced metal ions—Zn(I) in this example—will be produced, representing a shift in redox poise and metal ion speciation that may alter mechanisms of corrosion or lead to metal nanoparticle formation.²⁵

Considering the significance of chromium ions as corrosion product solutes in irradiated molten salt systems, and as potential redox catalysts for corrosion, it is important to characterize the reactivity of Cr(II) and Cr(III) ions with the primary products of molten chloride salt radiolysis (i.e., the e_S⁻ and Cl₂˙⁻). To this end, we undertook an electron pulse radiolysis study to characterize the kinetics of these reactions in molten LiCl–KCl eutectic salt mixtures over a range of temperatures (400–600 °C) and examine the speciation and reactivity of subsequent products.

Experimental

Chemicals

All salt samples were procured in sealed ampoules and were opened and stored inside an argon atmosphere glovebox. Acetone (99.9% reagent grade), chromium dichloride (CrCl₂, anhydrous, 99.99% trace metal basis), chromium trichloride (CrCl₃, anhydrous, 99.99% trace metal basis), ethanol (absolute, anhydrous), isopropanol (99.9% reagent grade), lithium chloride–potassium chloride eutectic (LiCl–KCl, anhydrous beads, 99.99% trace metal basis), and potassium thiocyanate (KSCN, ≥99.0% ACS Reagent Grade) were procured from MilliporeSigma (Burlington, MA, USA). Argon (>99.998%) and nitrous oxide (UHP) gases were supplied by Airgas (Radnor, PA, USA).

Sample preparation

Salt mixtures were prepared inside an argon atmosphere glovebox (VTI, VTISS1-1809-0100) at Idaho National Laboratory (INL). Stock salt solutions of CrCl₂ (0.064 wt%) and CrCl₃ (0.079 wt%) in LiCl–KCl eutectic were prepared by mixing the constituent solid chlorides in a glassy carbon crucible (GAT6, 64-mL Sigradur tapered crucible, HTW Germany). The crucible was cleaned with ethanol prior to use, vacuum dried at 100 °C for 4 hours, then baked under argon at 700 °C for 12 hours to remove any residual moisture. The stock solutions were prepared by loading LiCl–KCl eutectic and CrCl₂ or CrCl₃ in the required proportions into a pre-baked glassy carbon crucible. Masses were recorded to 0.1 mg precision using a Mettler Toledo balance (model no. TLE204E). The solid contents were heated to 500 °C for melting and maintained at this temperature for 6 hours with occasional stirring to ensure homogeneity. This process was carried out using a ThermoScientific Thermolyne box furnace (model no. FB1315M) inside the glovebox.

The salt mixtures were allowed to solidify and cool prior to removal from the crucible, then were ground to a powder using an agate mortar and pestle. Neat LiCl–KCl eutectic and the chromium-containing salt mixtures were shipped in sealed vials to Brookhaven National Laboratory (BNL). Salt samples for electron pulse radiolysis experiments were then prepared at BNL by diluting the chromium-containing stocks with neat LiCl–KCl eutectic inside an argon atmosphere glovebox (MBRAUN, UNIlab, Garching, Germany) to achieve the desired concentrations of CrCl₂ or CrCl₃. The samples were then flame-sealed under vacuum (<100 mTorr) in 5 × 5 mm Spectrosil® quartz fluorescence cuvettes (Starna Cells, Atascadero, CA, USA).

Time-resolved electron pulse radiolysis

Kinetics for the reactions of Cr(II) and Cr(III) with the e_S⁻ and Cl₂˙⁻ in LiCl–KCl eutectic salt were measured using the BNL Laser Electron Accelerator Facility (LEAF)²⁶ and 2 MeV Van de Graaff (VdG) electron accelerator. Salt mixture samples were heated until molten using bespoke heated sample holders,²⁷ then pulse-irradiated with doses per pulse in the range of 15–30 Gy (J kg⁻¹) for LEAF, and 21.5 Gy for the VdG accelerator, except as noted below. The dosimetry for both electron accelerators was determined by using the N₂O-saturated aqueous 10 mM KSCN dosimeter,²⁸ and corrected for the electron density ratio between the aqueous dosimeter at room temperature and the molten salt at a given temperature. Electron density value corrections are summarized in Table S1 of the ESI.‡ The calibration curve of dose per pulse as a function of electron beam current was obtained by changing the beam's intensity and measuring with an integrating current transformer located just before the beam port. The average electron beam current for each measurement was recorded and the total absorbed dose per sample was determined using this calibration curve, considering the electron beam current within one set of measurements.

For LEAF experiments, time-resolved changes in absorption intensity were measured using silicon photodiode detectors (FND-100QH [EG&G Optoelectronics, Boston, MA, USA] or S5973-01 [Hamamatsu Photonics, Shizuoka, Japan]) over the 300–1050 nm range, or a GEP-600 germanium PIN photodiode (GPD Optoelectronics Corp, Salem, NH, USA) between 800–1700 nm, and subsequently digitized using Teledyne LeCroy (Chestnut Ridge, NY, USA) WaveRunner oscilloscopes (model HRO 66Zi: 600 MHz, 12 bit; or model 640Zi: 4 GHz, 8 bit). The choices of detector and oscilloscope were driven by the timescale of the kinetics to be observed. Interference filters (passband ∼10 nm below 800 nm, and ∼25 nm above and including 800 nm) were used for wavelength selection of the analysing light. For the VdG experiments, a monochromator (Gemini 180, Horiba, Kyoto, Japan) with a set of long-pass filters were used for wavelength selection, and optical signals were recorded using a photomultiplier tube (9659QB, EMI Electronics Ltd, London, United Kingdom) and LeCroy HDO 4034 oscilloscope (350 MHz, 12 bit).

Transient absorption spectra were assembled from select time slices of kinetic traces measured at discrete wavelengths. The measured absorbance changes were converted into Gε values by using the absorbed dose and optical path length, where G is the radiolytic yield or G-value (species/100 eV) and ε is the molar extinction coefficient for a given species (M⁻¹ cm⁻¹). Reaction kinetics—rate coefficients and activation parameters—were then determined by fitting kinetic traces at wavelengths at or near the absorbance maxima of the species of interest, depending on the background absorbance: e_S⁻ (660 or 700 nm) and Cl₂˙⁻ (340 or 400 nm). Observed pseudo-first-order rate coefficients (k′) were calculated from these initial fits over a range of temperatures (400, 450, 500, 550, and 600 °C), then used to derive the corresponding second-order rate coefficients (k) from concentration-dependent plots. The associated activation parameters—Arrhenius (activation energy, E_a, and pre-exponential factor, A) and Eyring (enthalpy of activation, ΔH^‡, and entropy of activation, ΔS^‡)—were obtained from the temperature-dependent k values.

Spectro-kinetic analysis

In situations where overlapping absorbances obscured the reaction kinetics of individual species, spectro-kinetic analysis (SK-Ana) software²⁹ was used to resolve the 3-D absorbance-wavelength-time data for individual species. SK-Ana employs singular value decomposition and alternating least squares to deconvolute multiple superimposed species’ spectra in the observed wavelength range and resolve the kinetics and spectral shapes of these components in order to achieve a best fit. Accurate fits were guided by importing previously isolated absorption spectra for e_S⁻ and Cl₂˙⁻.²⁴

Spectroelectrochemical measurements

A Gamry 1010E potentiostat–galvanostat (Warminster, PA, USA) was used for the electrochemical measurements. All electrochemical cell components were prepared and assembled in an argon-filled glovebox (<0.1 ppm O₂, <0.1 ppm H₂O) to minimize exposure of the hygroscopic chloride salts to atmospheric moisture. Graphite working and counter electrodes (99.99%, 1.65 mm diameter, McMaster-Carr, Elmhurst, IL, USA) were polished up to 800 grit and inserted into an alumina tube with two 2-mm holes (McMaster-Carr). The reference electrode was fabricated by weighing ∼2 g of pre-melted LiCl–KCl eutectic containing 1 wt% AgCl (MilliporeSigma) into a 0.25 mm OD thick mullite tube (McDanel Ceramics, Beaver Falls, PA, USA) with Ag wire (99.9%, Alfa Aesar, Ward Hill, MA, USA) as the electrical lead. The bottom of the mullite tube was sanded to obtain a better connection between the reference electrode and the salt.

4 and 15 mM solutions of CrCl₂ in LiCl–KCl eutectic were prepared by weighing the requisite amounts of LiCl–KCl and CrCl₂. The electrolyte mixture (∼9 g) was poured into a 20 × 10 mm quartz cuvette and placed inside a previously-described spectroscopy furnace²⁷ within an Ar-filled glovebox. The optical path passed through the 10 mm axis of the cuvette. Spectroelectrochemistry measurements were performed at a temperature of 510 °C, which was monitored using a K-type thermocouple. The reference electrode was submerged and left overnight in the eutectic mixture for conditioning. The counter electrode and working electrode were introduced into the cell 20 minutes prior to measurement, while the open circuit potential (OCP) of the working electrode was measured. Cyclic voltammograms were obtained at various scan rates (between 50–300 mV s⁻¹) to determine the optimal conditions for Cr(II) oxidation, which was monitored by chronoamperometry studies performed on a fresh sample of 4 mM CrCl₂ in LiCl–KCl eutectic at a potential of 500 mV vs. Ag/AgCl for 16 hours.

UV-Vis spectroscopy was performed in situ at intervals during the electrolysis to detect the formation of Cr(III), using a QEPro Ocean Optics (Orlando, FL, USA) extended range spectrometer (190– 980 nm) and a DH-2000-Bal (Deuterium–Tungsten/halogen) light source, both coupled to the high-temperature furnace.

Results and discussion

Transient absorption spectra

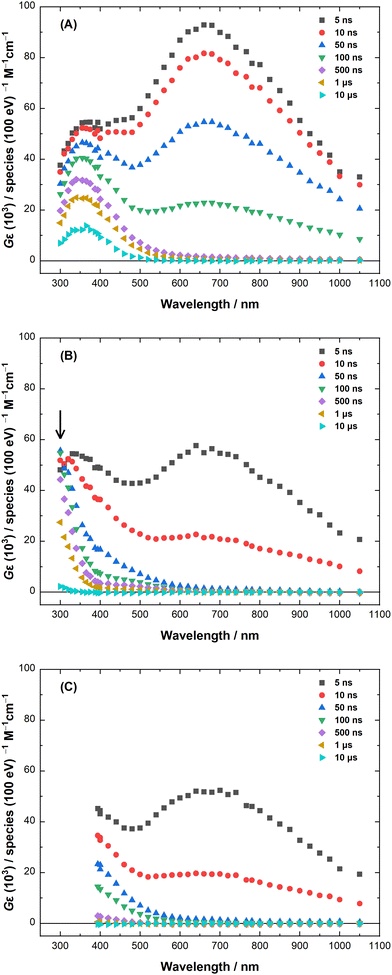
Fig. 1 shows absorption spectra observed at different delays after the electron pulse for neat LiCl–KCl eutectic, as well as for 2.01 mM CrCl₂ and 2.02 mM CrCl₃ in LiCl–KCl eutectic salt solutions at 400 °C. As previously reported,²⁴ the transient spectra in neat LiCl–KCl eutectic (Fig. 1(A)) show two distinct absorption features. The first rapidly decays (<500 ns) with a λ_max at ∼660 nm and is attributed to the e_S⁻. The second exhibits a much slower decay (>1 μs) in the UV region with a λ_max of ∼355 nm, as is consistent with the Cl₂˙⁻ spectrum reported in water.³⁰ These two species are also observed in the presence of Cr(II) and Cr(III) ions (Fig. 1(B) and (C), respectively), albeit the decay rates of both species increase with increasing Cr(II) or Cr(III) ion concentration. Spectra obtained at other chromium ion concentrations in LiCl–KCl eutectic are shown in Fig. S1 and S2 (ESI‡). In the case of Cr(III), Fig. 1(C), 400 nm is the shortest wavelength at which the samples transmitted sufficient light for measurement. Interestingly, evidence of a third absorption component (indicated by an arrow in Fig. 1(B)) was observed in the UV region (<400 nm) in the presence of Cr(II) ions. The origin and nature of the species responsible for this feature will be discussed later. But first, we will focus on the reactions of the e_S⁻ and Cl₂˙⁻ with the Cr(II) and Cr(III) ions.

Fig. 1 Transient absorption spectra in molten LiCl–KCl eutectic (A), 2.01 mM CrCl₂ in LiCl–KCl eutectic (B), and 2.02 mM CrCl₃ in LiCl–KCl eutectic (C) at selected times: 5 ns (■), 10 ns (), 50 ns (), 100 ns (), 500 ns (), 1 μs (), and 10 μs () at 400 °C. In (B), the arrow indicates a third transient species discussed in the text. In the case of (C), high background absorption precluded measurements below 395 nm.

Solvated electron reactions

The decay kinetics of the e_S⁻ at 700 nm in molten LiCl–KCl eutectic in the presence of various concentrations of Cr(II) and Cr(III) ions are presented in Fig. 2(A) and 3(A), respectively. In the absence of added chromium ions, the e_S⁻ primarily decays by reacting with trace contaminants in the salt,²⁴ affording an average decay rate of (1.0 ± 0.4) × 10⁷ s⁻¹ at 400 °C for the particular batch of LiCl–KCl eutectic used in this study (the black traces in Fig. 2(A) and 3(A)). Chromium ion concentrations in the millimolar range were selected here so that the observed pseudo-first-order decays of the e_S⁻ would be significantly faster than the intrinsic e_S⁻ lifetime in the base LiCl–KCl eutectic salt samples.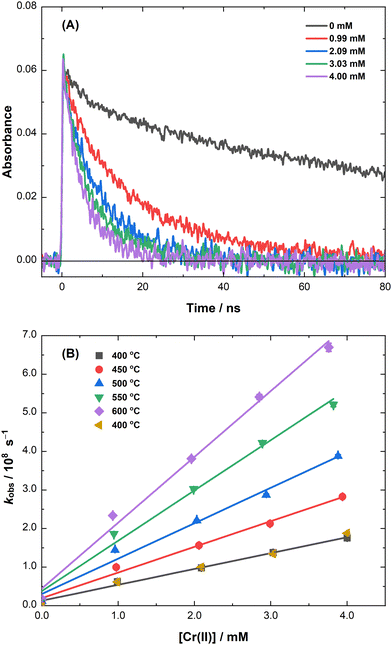

Fig. 2 (A) Transient absorption kinetics at 700 nm as a function of Cr(II) concentration in molten LiCl–KCl eutectic at 400 °C. (B) Average observed pseudo-first-order rate coefficients for eqn (5) measured at 700 nm as a function of Cr(II) concentration and temperature: 400 (■), 450 (), 500 (), 550 (), 600 (), and 400 °C repeated at the end of measurement series (). Cr(II) concentrations are corrected for changes in density with temperature. Error bars are one standard deviation using four repeated measurements at each experimental condition. (They are smaller than the symbols).

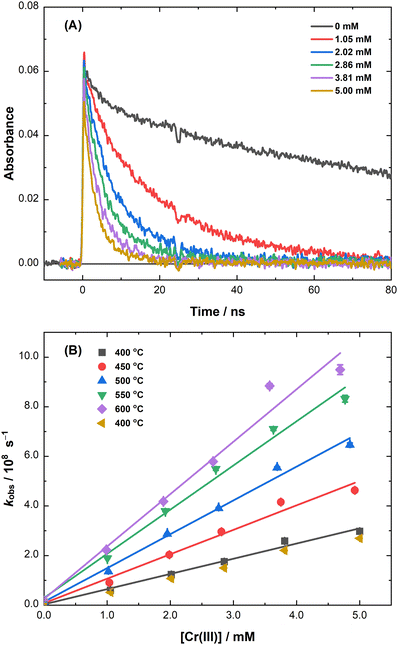Fig. 3 (A) Transient absorption kinetics at 700 nm as a function of Cr(III) concentration in molten LiCl–KCl eutectic at 400 °C. (B) Average observed pseudo-first-order rate coefficients for eqn (6) measured at 700 nm as a function of Cr(III) concentration and temperature: 400 (■), 450 (), 500 (), 550 (), 600 (), and repeated 400 °C at the end of measurement series (). Cr(III) concentrations are corrected for changes in density with temperature. Error bars are one standard deviation using four repeated measurements at each experimental condition. (They are smaller than the symbols).

The kinetics for the reaction of the e_S⁻ with Cr(II) ions are shown in Fig. 2(A). The decay rate of the e_S⁻ increased as the Cr(II) concentration increased, per eqn (5):

Cr²⁺ + e_S⁻ → Cr⁺, (5)

for which a second-order rate coefficient of k₅ = (4.1 ± 0.2) × 10¹⁰ M⁻¹ s⁻¹ at 400 °C was derived from the plot of observed pseudo-first-order rate coefficients vs. concentration in Fig. 2(B). This value is very close to that obtained for the reaction of the e_S⁻ with Zn(II) at 400 °C (eqn (3)),²⁴ which is also divalent and tetrahedrally coordinated like Cr(II).³¹ The Cr(II) ion concentrations at each temperature were scaled using the reported³² densities of LiCl–KCl eutectic at those temperatures (Table S1, ESI‡) to correct for the thermal expansion of the salt solution. As shown in Fig. 2(B), rate coefficients were also determined at 450, 500, 550, and 600 °C, and then repeated at 400 °C to determine the extent to which the observed kinetics were affected by cumulative dose and heating effects. The pseudo-first-order rate coefficient for the repeat measurement at 400 °C was faster than the original by only 1.4 standard deviations, which is not significant for calculating the activation parameters. The observed pseudo-first-order and calculated second-order rate coefficients for each temperature are reported in Table S2 (ESI‡). From these values, the corresponding activation parameters were calculated for eqn (5) (Fig. S3, ESI‡): A = (2.0 ± 0.5) × 10¹³ M⁻¹ s⁻¹, E_a = 31.8 ± 0.5 kJ mol⁻¹, ΔH^‡ = 32.0 ± 1.3 kJ mol⁻¹, and ΔS^‡ = −1.9 ± 1.7 J mol⁻¹ deg⁻¹. For comparison, the activation parameters derived for eqn (3) (Zn(II)) are: A = (2.4 ± 0.5) × 10¹³ M⁻¹ s⁻¹, E_a = 35.6 ± 1.2 kJ mol⁻¹, ΔH^‡ = 29.3 ± 1.3 kJ mol⁻¹, and ΔS^‡ = −4.9 ± 1.7 J mol⁻¹ deg⁻¹. Note that the E_a above differs from that reported in ref. 24 because the change of solute concentration with temperature, which is due to the thermal expansion of the salt, was not accounted for in that work. We re-calculated the A, E_a, ΔH^‡, and ΔS^‡ values above from the original data to take expansion into account.

It is also worth noting that neither transient absorption spectroscopy nor SK-Ana analysis of the above-described Cr(II) systems show any sign of a product from eqn (5), i.e., Cr(I). The contribution of Cr(I) to the observed transient absorption kinetics is expected to be negligible, as it is isoelectronic with Mn(II), and therefore, expected to be a high-spin d⁵ complex with a ⁶A_1g ground state. Consequently, there would be no spin-allowed ligand-field transitions, leaving only very weak spin-forbidden transitions in the ligand-field region of the spectrum. Though ligand-to-metal charge transfer transitions are possible for Cr(I) in molten LiCl–KCl eutectic, by the nature of the transition they are likely to be at higher energy than those for Cr(II), and therefore, above the Cr(II) sample absorption cutoff at the concentrations used.

The decay kinetics for the reaction of the e_S⁻ with Cr(III) ion in molten LiCl–KCl eutectic are shown in Fig. 3(A). As with Cr(II), the presence of Cr(III) ions decreased the lifetime of the e_S⁻ by electron capture (eqn (6)):

Cr³⁺ + e_S⁻ → Cr²⁺. (6)

Using the data plotted in Fig. 3(B), a second-order rate coefficient of k₆ = (6.1 ± 0.3) × 10¹⁰ M⁻¹ s⁻¹ was obtained for eqn (6) at 400 °C. This reaction is about 1.5× faster than the rate coefficient obtained for the e_S⁻ reaction with Cr(II) (eqn (5)), which is consistent with their corresponding reactions with the hydrated electron (e_aq⁻) in water: k_Cr(II) = 2.0–4.0 × 10¹⁰ M⁻¹ s⁻¹ and k_Cr(III) = 3.0–6.0 × 10¹⁰ M⁻¹ s⁻¹ at 25 °C.^33–36 Second-order rate coefficients were also determined for eqn (6) between 400 and 600 °C, and again, repeated at 400 °C to determine the extent to which the observed kinetics were affected by cumulative dose and heating effects. The pseudo-first-order rate coefficient for the repeat measurement was only 1.2 standard deviations slower than the original result, which is again not significant for calculating the activation parameters. The resulting rate coefficients for the e_S⁻ with Cr(II) and Cr(III) are reported in Table S2 (ESI‡), from which the corresponding activation parameters were calculated for eqn (6) (Fig. S3, ESI‡): A = (1.7 ± 0.2) × 10¹³ M⁻¹ s⁻¹, E_a = 33.5 ± 0.6 kJ mol⁻¹, ΔH^‡ = 27.2 ± 1.6 kJ mol⁻¹, and ΔS^‡ = −4.6 ± 2.1 J mol⁻¹ deg⁻¹.

The activation parameters for eqn (3), (5), and (6) are all reasonably similar. Since these are among the first points of data available for electron capture reactions by transition metals in high-temperature molten salts, it is difficult—even perilous—to infer much mechanistic insight from this limited set of parameters. For instance, many ions in molten salts, including several transition metals and f-block elements, are known to exist in a distribution of coordination states (e.g., coordination numbers) that changes with temperature and the composition of the bulk salt, and also with the redox state of the ion.^31,37–42 This means that in many cases the temperature-dependent speciation of the reactant metal ion and that of the reduced product of electron capture may not yet be well defined, thus confounding measured activation parameters with other effects that need to be more thoroughly understood to describe the whole mechanism.

With that in mind, it is still interesting to note that the activation entropies are negative in all three cases, though small in magnitude. While the reduction of a metal ion would normally be considered to have positive entropic effects via reduction of electrostriction, bond lengthening, force constant reduction, and possible reduction in coordination number, the solvated cavity electron in water (for example) is considered a structure-breaking ion⁴³ with a positive entropy of formation ().⁴⁴ Given that excess electrons in molten LiCl–KCl eutectic are believed to exist as cavity electrons, effectively filling anion vacancies, they are also likely to be structure breakers with positive formation entropies that make a negative contribution to the activation entropy as they attach to a metal ion.

We hope that by accumulating more kinetics and activation parameter data on reactions of electrons with different metal ions in LiCl–KCl eutectic and in salts with different compositions, we will be able to build a clearer picture of the nature of the e_S⁻ in molten salts and the mechanisms of metal ion redox reactions that are key to the radiation-driven chemistry inside MSRs.

Reactions with dichlorine radical anions

In neat LiCl–KCl eutectic salt, the relatively slow decay (>10 μs) of Cl₂˙⁻ is attributed²⁴ to both its disproportionation, eqn (7):²⁴

Cl₂˙⁻ + Cl₂˙⁻ → Cl⁻ + Cl₃⁻ k₇ = (2.2 ± 2.0) × 10⁹ M⁻¹ s⁻¹, (7)

and to contributions from reactions (eqn (8)) involving reduced species (M⁽ⁿ⁻¹⁾⁺_imp or H˙) in the base salt formed from the reaction of the e_S⁻ with trace impurity metal ions or protons from residual moisture:²⁴

Cl₂˙⁻ + (M⁽ⁿ⁻¹⁾⁺_imp or H˙) → 2Cl⁻ + (Mⁿ⁺_imp or H⁺). (8)

In our previous work,²⁴ we observed that under normal experimental conditions (radiolytic doses producing micromolar concentrations of e_S⁻ and Cl₂˙⁻), eqn (8) dominates eqn (7). In this work, an effective average second-order rate coefficient of k = (1.87 ± 0.01) × 10¹⁰ M⁻¹ s⁻¹ at 400 °C was obtained for the combined effects of eqn (7) and (8) at the dose per pulse used for these measurements (assuming ε(Cl₂˙⁻) = 8000 M⁻¹ cm⁻¹, as in ref. 24). This rate coefficient is comparable to that of eqn (4) for the reaction with Zn(I) (as an example of M⁽ⁿ⁻¹⁾⁺_imp), and is consistent with our previous work.²⁴

However, the decay of Cl₂˙⁻ becomes pseudo-first-order in the presence of millimolar concentrations of Cr(II) or Cr(III) ions, as shown at 400 nm in Fig. 4(A) and 5(A). In the case of Cr(II), Fig. 4(A), the rate of Cl₂˙⁻ decay increased with increasing Cr(II) concentration, as according to eqn (9):

Cr²⁺ + Cl₂˙⁻ → Cr³⁺ + 2Cl⁻. (9)

Fig. 4 (A) Transient absorption kinetics at 400 nm as a function of CrCl₂ concentration in molten LiCl–KCl eutectic at 400 °C. (B) Average observed pseudo-first-order rate coefficients for eqn (9) measured at 400 nm as a function of Cr(II) concentration at 400 °C. The weighted linear fit corresponds to k(Cr²⁺ + Cl₂˙⁻) = (7.2 ± 0.3) × 10⁹ M⁻¹ s⁻¹ (intercept = (3.3 ± 1.0) × 10⁶ s⁻¹). Error bars are one standard deviation using four repeated measurements at each experimental condition.

Fig. 5 (A) Transient absorption kinetics at 400 nm as a function of CrCl₃ concentration in molten LiCl–KCl eutectic at 400 °C. (B) Average observed pseudo-first-order rate coefficients for eqn (10) measured at 400 nm as a function of Cr(III) concentration at 400 °C. The weighted linear fit corresponds to k(Cr³⁺ + Cl₂˙⁻) = (1.4 ± 0.1) × 10⁹ M⁻¹ s⁻¹ (intercept = (1.9 ± 0.3) × 10⁶ s⁻¹). Error bars are one standard deviation using four repeated measurements at each experimental condition. (They are smaller than the symbols).

At 400 nm, the major contributions to the transient absorbance are due to Cl₂˙⁻, and (at short timescales below 15 ns) the tail of the e_S⁻ absorption. Therefore, a double exponential function was used for fitting the 400 nm transient absorption data to obtain the Cl₂˙⁻ decay kinetics. Note that the absorbance does not return to baseline when the Cl₂˙⁻ has completely decayed. This observation indicates the presence of a third transient species (vide infra), the contribution of which decays to the baseline on the time scale of ∼10 μs. The observed decay rate of the e_S⁻ at 700 nm for the same Cr(II) ion concentration was fixed as the rate coefficient of one of the exponential terms to account for the contribution from the decaying e_S⁻ absorbance at short time. The other exponential term was allowed to float to obtain the pseudo-first-order rate coefficient for eqn (9) at that Cr(II) ion concentration. The resulting rate coefficients are reported in Table S3 (ESI‡). Using this approach, a second-order rate coefficient for eqn (9) of k₉ = (7.2 ± 0.3) × 10⁹ M⁻¹ s⁻¹ at 400 °C was obtained (Fig. 4(B)). As mentioned just above, a value of k₄ = (2.0 ± 0.2) × 10¹⁰ M⁻¹ s⁻¹ was estimated for the reaction of Cl₂˙⁻ with Zn(I) (eqn (4)).²⁴ Note, no change in kinetics with cumulative dose was observed for the reaction of Cr(II) with Cl₂˙⁻ (Fig. S4A, ESI‡).

In the presence of Cr(III) ions, Fig. 5(A) clearly shows biexponential decay of the absorbance signals at 400 nm, with both parts becoming faster with increasing Cr(III) concentration. The behaviour of the faster component is consistent with the kinetics of the e_S⁻ decay measured at 700 nm for each Cr(III) ion concentration. The slower component corresponds to the reaction of Cl₂˙⁻ with Cr(III), eqn (10):

Cr³⁺ + Cl₂˙⁻ → Cr⁴⁺ + 2Cl⁻ or Cr²⁺ + Cl₂. (10)

The same fitting method was used to derive the rate coefficients for the reaction of Cr(III) with Cl₂˙⁻, affording a second-order rate coefficient of k₁₀ = (1.4 ± 0.1) × 10⁹ M⁻¹ s⁻¹ at 400 °C, significantly slower than for Zn(I) and Cr(II). The resulting rate coefficients are reported in Table S4 (ESI‡). By analogy with eqn (9), one would expect the consumption of Cl₂˙⁻viaeqn (10) to proceed via oxidation to produce Cr(IV). However, evidence exists for eqn (10) to proceed by reduction to produce Cr(II). Although the Cr(II) ion product from eqn (6) may also contribute to the decay of Cl₂˙⁻ in the Cr(III)-ion-containing salt mixtures, its expected concentration is on the order of micromolar per electron pulse, and thus, it is readily out-competed by the millimolar amounts of Cr(III) ions at low cumulative doses (≤600 Gy). However, when these measurements were repeated on the same sample after accumulating a dose of ∼3000 Gy, the resulting first-order fits were ∼8% slower for the e_S⁻ (Table S2, ESI‡) and ∼60% faster for Cl₂˙⁻ (Fig. S4 and S5, ESI‡). These changes are a consequence of the progressive radiation-induced consumption of Cr(III) ions—as evident from the presence of a background bleach at 400, 550, and 660 nm (Fig. S6, ESI‡)—and the subsequent accumulation of the initial and subsequent products from eqn (6) and (10), which ultimately impact the aforementioned competition kinetics. Although the current kinetic data are insufficient to deconvolute the spectra in order to give more information on eqn (10), deterministic kinetic modelling calculations are underway to investigate the feasibility of each pathway.

The third transient species in the case of Cr(II)

As mentioned above, Fig. 1(B) contains an additional transient absorption band (indicated by an arrow) that peaks below 400 nm on the 500 ns time scale, which is after the e_S⁻ and Cl₂˙⁻ have both been completely consumed. SK-Ana was used to deconvolute these kinetics traces, for which a solution comprised of three principal components was found to be the most statistically consistent (Fig. S7, ESI‡), affording the normalized spectra shown in Fig. 6(A). Two of the deconvoluted spectra and their Cr(II)-dependent decay kinetics align closely to those of the e_S⁻ and Cl₂˙⁻ (Fig. S8, ESI‡). The third species (S3) has a large absorption band below 400 nm, and a small absorption peak at around 500 nm. The temporal evolution of S3 (Fig. 6(B)) is dependent on the concentration of Cr(II) and correlates with the decay of Cl₂˙⁻. This observation suggests that S3 is a product of eqn (9), i.e., Cr(III). Comparison of the derived spectrum of S3 (Fig. 6(A)) with those reported in the literature for Cr(III) in LiCl–KCl eutectic at 400–600 °C^31,45,46 is difficult because those reports understandably focus on the two moderately-strong and temperature-dependent ligand field bands located around 550 and 815 nm (ε = 39.9 and 33.2 L mol⁻¹ cm⁻¹, respectively, at 500 °C)⁴⁶ instead of the intense ligand-to-metal charge transfer (LMCT) band in the UV. However, the absorption from the ligand field bands at the micromolar concentrations of transients that are generated in the pulse radiolysis experiments is very weak. Assignment of S3 therefore, must be made via the much more intense Cr(III) LMCT band, which required the determination of the peak absorption wavelength for S3 at shorter wavelengths than the LEAF detection system can reach.

Fig. 6 (A) Normalized spectral components from SK-Ana analysis of the measured absorbance vs. time and wavelength transient data matrix for 2.01 mM CrCl₂ in LiCl–KCl eutectic at 400 °C. Components S1 and S2 are assigned as Cl₂˙⁻ and e_S⁻, respectively. (B) Kinetics traces derived by SK-Ana for species S3 at 300 nm at different CrCl₂ concentrations.

To obtain more information on the spectrum and reactivity of S3, experiments were performed on the BNL 2 MeV VdG to extend the optical detection range down to 250 nm (limited by sample absorption) and the radiolytic dose range to much higher levels. The transient absorption spectra of 8.72 mM Cr(II) in LiCl–KCl eutectic at 400 °C at intervals after 500 ns are shown in Fig. 7(A). The spectra for all the Cr(II) concentrations (0.99, 3.10, 4.99, and 8.72 mM) are shown in Fig. S9 (ESI‡). The spectra collected on the VdG system indicate that the peak maximum of the S3 UV absorption band is around 270–280 nm.

Fig. 7 (A) Transient absorption spectra at selected time intervals in 8.72 mM CrCl₂ in LiCl–KCl at 400 °C. (B) Transient absorption kinetics at 300 nm with different doses per pulse in 8.72 mM CrCl₂ in LiCl–KCl eutectic at 400 °C. The rising part of the signal curves as the dose increases due to reactivity occurring within the width of the pulse. Pathlength 0.5 cm.

Having better characterized the UV absorption of S3, we needed to measure the position and shape of the lowest-energy Cr(III) LMCT band in LiCl–KCl eutectic. Attempts to directly prepare a very dilute solution by adding CrCl₃ to molten LiCl–KCl eutectic led to inconsistent results and saturation of the dynamic range of the spectrometer. Much better results were obtained spectroelectrochemically by chronoamperometric oxidation of a 4 mM solution of CrCl₂ in LiCl–KCl eutectic at 510 °C and a fixed potential of +0.500 V vs. Ag/AgCl. These conditions were selected for the efficient oxidation of Cr(II) based on cyclic voltammograms (Fig. S11, ESI‡). Fig. S12A (ESI‡) shows the successive growth of the absorbance traces in the UV region with increasing time (10-minute intervals) as Cr(II) is oxidized to Cr(III) in a controlled fashion. Fig. S12B (ESI‡) shows the cumulative difference spectra obtained by subtracting the first trace in Fig. S12A (ESI‡) from each of the subsequent traces. The difference spectra show clearly that an absorption band peaking around 270 nm grows in as the concentration of Cr(III) increases, and the shape of that band is consistent with the spectra in Fig. S9 (ESI‡) obtained by pulse radiolysis. We therefore conclude that species S3 is Cr(III).

As observed in Fig. 1(B), the absorption due to Cr(III) decays on a timescale of microseconds. To characterize the mechanism of that decay, a sample of 8.72 mM Cr(II) in LiCl–KCl eutectic was pulse-irradiated at the VdG over a wide dose range (39–333 Gy per pulse, 100–1000 ns pulse widths) to obtain the 300 nm absorbance traces shown in Fig. 7(B). The decay kinetics exhibit a classical second-order dependence on dose. This behaviour indicates that the process by which the transient Cr(III) decays involves the reaction between two species produced by radiolysis in roughly equal amounts. This is evidenced in Fig. S10A (ESI‡) by the linearity of the reciprocal absorbance plots of the same data, which have roughly identical slope values (average (2.4 ± 0.1) × 10⁶ s⁻¹) for all doses per pulse (Fig. S10B, ESI‡). As Cr(I) is produced viaeqn (5) in similar yield to the production of Cr(III) viaeqn (9), two reactions could potentially be responsible for the clearly second-order behaviour observed in Fig. 7(B) and Fig. S10A (ESI‡):

Cr³⁺ + Cr³⁺ → Product(s), (11)

Cr³⁺ + Cr⁺ → 2Cr²⁺. (12)

Since we have no direct means of detecting Cr(I) via transient absorption spectroscopy in this system due to its expected weak absorbance, our direct observations cannot resolve between the two mechanisms. However, in combination with our observed reaction kinetics, eqn (11) implies that millimolar solutions of Cr(III) in molten LiCl–KCl eutectic would not be stable on the timescale of microseconds, which is clearly not the case since such solutions of Cr(III) were prepared and used for this and many other studies. Therefore, the observed decay of radiolytically-produced Cr(III) must proceed viaeqn (12). It is then reasonable to infer that unobservable Cr(I) is indeed being produced viaeqn (5), and it is not undergoing side reactions before reacting viaeqn (12), at least in fresh solutions. This also signifies that the rate coefficient for dimerization or disproportionation of Cr(I) (eqn (13)) must be substantially slower than that of eqn (12):

Cr⁺ + Cr⁺ → Cr₂²⁺ or Cr⁰ + Cr²⁺. (13)

It is possible to obtain an estimate of the second-order rate coefficient of eqn (12) at 400 °C by combining the average slope of k/el = 2.4 × 10⁶ s⁻¹ obtained for the inverse absorbance traces measured at 300 nm in Fig. S10A (ESI‡) with an estimate of the extinction coefficient of Cr(III) at 300 nm extracted from the SK-Ana analysis. Based on the intercept of the linear fit in Fig. 4(B) (3.3 × 10⁶ s⁻¹) and the observed pseudo-first-order rate coefficient for the highest concentration of Cr(II) in Table S2 (ESI‡) (4.99 mM, k_obs = 3.99 × 10⁷ s⁻¹), we calculate that under those conditions, 92% of the Cl₂˙⁻ that was formed reacts to produce Cr(III). We then compared the maximum absorbance value at 300 nm for Cr(III) formation in Fig. 6(B) at 4.99 mM Cr(II) (0.037 OD) with the maximum absorbance of Cl₂˙⁻ at its peak wavelength of 340 nm for the same Cr(II) concentration (0.023 OD) in Fig. S8A (ESI‡). In ref. 24 we used a value of 8000 M⁻¹ cm⁻¹ for ε(Cl₂˙⁻) at 340 nm in molten LiCl–KCl eutectic. From the assembled values we estimate that the extinction coefficient of Cr(III) at 300 nm is 14 000 M⁻¹ cm⁻¹ (eqn (14)):

ε(Cr³⁺)₃₀₀ = 0.037/0.023/0.92 × 8000 M⁻¹ cm⁻¹ = 14 000 M⁻¹ cm⁻¹. (14)

Consequently, we obtain an estimated second-order rate coefficient for eqn (12) of k = 1.7 × 10¹⁰ M⁻¹ s⁻¹viaeqn (15):

k₁₂ = 2.4 × 10⁶ s⁻¹ × 14 000 M⁻¹ cm⁻¹ × 0.5 cm = 1.7 × 10¹⁰ M⁻¹ s⁻¹. (15)

The rate coefficient obtained for the Cr(I)–Cr(III) comproportionation reaction (eqn (12)) is very similar to the one previously reported for the reaction of Zn(I) with Cl₂˙⁻ (eqn (4), (k₄) = 2.0 × 10¹⁰ M⁻¹ s⁻¹).²⁴ Note that both numerical results rest on the same extinction coefficient assumption, therefore they would remain similar no matter what ε is used. These reactions represent the ultimate recombination of the excess electron and hole species that were initially produced by radiolysis, which would result in no cumulative radiation damage to the sample apart from losses to side reactions. Therein lies the rub—we have observed that measurements on the Cr(I)–Cr(III) reaction involving cumulative radiolytic doses not far above the one accrued in making Fig. 7(B) (but well in excess of the cumulative doses used to study eqn (5), (6), (9), and (10)) begin to show deviations from second-order behaviour, indicating the eventual accumulation of side products that react in competition with eqn (5), (9), and/or (12). It takes a higher accumulation of side products to interfere with the fast reactions of the initial radiolysis products (eqn (5) and (9)) than with the slower processes involving the subsequent products such as eqn (12). Identifying those side products and determining their mechanistic roles in the accumulation of long-lived degradation products such as fugitive Cl₂ gas or reduced metal nanoparticles is the subject of ongoing investigations beyond the scope of this report.

Conclusions

The anticipated corrosion-induced presence of chromium ions in MSR coolants and fuel matrices can play a significant role in mediating the effects of molten salt radiolysis. Here, we quantified the reactions of the stable oxidation states of chromium in molten salts, Cr(II) and Cr(III), with the primary transient radical species from molten salt radiolysis (e_S⁻ and Cl₂˙⁻). The net effect of these reactions is to favour the reduction of Cr(III) to Cr(II). The resulting shift in the oxidation state distribution of chromium ions will affect the redox poise of other metal ions and the corrosion mechanisms of MSR components.

These findings afford an alternative perspective on the proposed radioprotection mechanism presented by Zhou et al. for the deceleration of Ni–20Cr corrosion in molten salts.¹⁴ In their system, europium ions were added (5 wt% EuF₃) to the salt mixture (Ni–20Cr in FLiNaK) to accelerate corrosion. However, based on our findings, we believe it is worth considering whether radiolysis may push the Eu(III/II) redox poise towards Eu(II) in analogy to the chromium case, inhibiting the catalysis of corrosion by Eu(III). Follow-on work will investigate the role of europium and other potentially catalytic ions in the radiolysis of molten salts.

Data availability

The digital data for all figures, tables, charts, and any other media contained in this publication and its associated ESI‡ files will be made accessible in the MSEE Community of the Zenodo repository, under Digital Object Identifier (DOI): 10.5281/zenodo.14919799.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Molten Salts in Extreme Environments Energy Frontier Research Center, funded by the U.S. Department of Energy Office of Science, Basic Energy Sciences, at BNL under contract no. DE-SC0012704, at INL under contract no. DE-AC07-05ID14517, and at Notre Dame under subcontract to BNL. The LEAF and the 2 MeV VdG of the BNL Accelerator Center for Energy Research are supported by the US-DOE Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences under contract DE-SC0012704.

References

1. K. Nagarajan, B. Prabhakara Reddy, S. Ghosh, G. Ravisankar, K. S. Mohandas, U. Kamachi Mudali, K. V. G. Kutty, K. V. Kasi Viswanathan, C. Anand Babu, P. Kalyanasundaram, P. R. Vasudeva Rao and B. Raj, Energy Procedia, 2011, 7, 431.
2. E.-Y. Choi and S. M. Jeong, Prog. Nat. Sci.: Mater. Int., 2015, 25(6), 572.
3. W. R. Grimes, Chemical research and development for molten-salt breeder reactors, ORNL-TM-1853 1967.
4. P. N. Haubenreich and J. R. Engel, Nucl. Appl. Technol., 1970, 8(2), 118.
5. H. G. MacPherson, Nucl. Sci. Eng., 1985, 90, 374.
6. H. Yu, G. Zhu, Y. Zou, R. Yan, Y. Liu, X. Kang and Y. Dai, J. Nucl. Eng., 2023, 4, 213.
7. S. Guo, J. Zhang, W. Wu and W. Zhou, Prog. Mater. Sci., 2018, 97, 448.
8. J. Zhang, C. W. Forsberg, M. F. Simpson, S. Guo, S. T. Lam, R. O. Scarlat, F. Carotti, K. J. Chan, P. M. Singh, W. Doniger, K. Sridharan and J. R. Keiser, Corros. Sci., 2018, 144, 44.
9. L. C. Olson, J. W. Ambrosek, K. Sridharan, M. H. Anderson and T. R. Allen, J. Fluorine Chem., 2009, 130, 67.
10. S. S. Raiman and S. Lee, J. Nucl. Mater., 2018, 511, 523.
11. F. Y. Ouyang, C. H. Chang, B. C. You, T. K. Yeh and J. J. Kai, J. Nucl. Mater., 2013, 437, 201.
12. Y. L. Wang, Q. Wang, H. J. Liu and C. L. Zeng, Corrosion Sci., 2016, 103, 268.
13. S. Guo, W. Zhuo, Y. Wang and J. Zhang, Corrosion Sci., 2020, 163, 108279.
14. W. Zhou, Y. Yang, G. Zheng, K. B. Woller, P. W. Stahle, A. M. Minor and M. P. Short, Nat. Commun., 2020, 11, 3430.
15. N. AlMousa, W. Zhou, K. B. Woller and M. P. Short, Corrosion Sci., 2023, 217, 111154.
16. N. D. B. Ezell, S. S. Raiman, J. M. Kurley and J. McDuffee, Nucl. Eng. Technol., 2021, 53, 920–926,  DOI:10.1016/j.net.2020.07.042.
17. I. E. Makarov, T. N. Zhukova and A. K. Pikaev, Radiat. Effects, 1974, 22, 71.
18. I. E. Makarov, T. N. Zhukova and A. K. Pikaev, Dokl. Akad. Nauk SSSR, 1975, 225(5), 1103.
19. I. E. Makarov, T. N. Zhukova, A. K. Pikaev and V. I. Spistyn, Inst. Phys. Chem. Acad. Sci. USSR, 1982, 4, 750.
20. A. K. Pikaev, I. E. Makarov and T. N. Zhukova, Radiat. Phys. Chem., 1982, 19, 377.
21. H. Hagiwara, S. Sawamura, T. Sumiyoshi and M. Katayama, Radiat. Phys. Chem., 1987, 30, 141.
22. S. Sawamura, J. L. Gebicki, J. Mayer and J. Kroh, Radiat. Phys. Chem., 1990, 36, 133.
23. R. Akiyama, M. Kitaichi, T. Fujiwara and S. Sawamura, J. Nucl. Sci. Technol., 1994, 31, 250.
24. K. Iwamatsu, G. P. Horne, R. Gakhar, W. C. Phillips, P. Halstenberg, B. Layne, A. Ramos-Ballesteros, J. A. LaVerne, S. M. Pimblott and J. F. Wishart, Phys. Chem. Chem. Phys., 2022, 24, 25088.
25. E. T. Dias, S. K. Gill, Y. Liu, P. Halstenberg, S. Dai, J. Huang, J. Mausz, R. Gakhar, W. C. Phillips, S. Mahurin, S. M. Pimblott, J. F. Wishart and A. I. Frenkel, J. Phys. Chem. Lett., 2021, 12, 157.
26. J. F. Wishart, A. R. Cook and J. R. Miller, Rev. Sci. Instrum., 2004, 75(11), 4359.
27. W. C. Phillips, R. Gakhar, G. P. Horne, B. Layne, K. Iwamatsu, A. Ramos-Ballesteros, M. R. Shaltry, J. A. LaVerne, S. M. Pimblott and J. F. Wishart, Rev. Sci. Instrum., 2020, 91(8), 083105.
28. G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 92, 279.
29. P. Pernot, SK-Ana: Analysis of Spectro-Kinetic Data (Version v3.4.7b), 2023 DOI:10.5281/zenodo.1064370, last accessed on 02/24/2025.
30. G. L. Hug, Optical Spectra of Nonmetallic Inorganic Transient Species in Aqueous Solution. U.S. Department of Commerce/National Bureau of Standards, NSRDS-NBS 69, 1981.
31. D. M. Gruen and R. L. McBeth, Pure Appl. Chem., 1963, 6, 23.
32. G. J. Janz, F. W. Dampier, G. R. Lakshminarayanan, P. K. Lorenz and R. P. T. Tomkins, Molten Salts: Volume 1, Electrical Conductance, Density, and Viscosity Data, U.S. Department of Commerce/National Bureau of Standards, NSRDS-NBS61, Part II, 1979.
33. M. Anbar and E. J. Hart, J. Phys. Chem., 1965, 69(3), 973.
34. H. Cohen and D. Meyerstein, J. Chem. Soc., Dalton Trans., 1974, 2559.
35. J. H. Baxendale, E. M. Fielden and J. P. Keene, Proc. R. Soc. London, Ser. A, 1965, A286320.
36. J. K. Conrad, A. Lisouskaya, S. P. Mezyk and D. M. Bartels, ChemPhysChem, 2023, 24, e202300465.
37. C. A. Angell and D. Gruen, J. Phys. Chem., 1966, 70, 1601.
38. S. K. Gill, J. H. Huang, J. Mausz, R. Gakhar, S. Roy, F. Vila, M. Topsakal, W. C. Phillips, B. Layne, S. Mahurin, P. Halstenberg, S. Dai, J. F. Wishart, V. S. Bryantsev and A. I. Frenkel, J. Phys. Chem. B, 2020, 124, 1253.
39. S. Roy, M. Brehm, S. Sharma, F. Wu, D. S. Maltsev, P. Halstenberg, L. C. Gallington, S. M. Mahurin, S. Dai, A. S. Ivanov, C. J. Margulis and V. S. Bryantsev, J. Phys. Chem. B, 2021, 125, 5971.
40. S. Roy, S. Sharma, W. V. Karunaratne, F. Wu, R. Gakhar, D. S. Maltsev, P. Halstenberg, M. Abeykoon, S. K. Gill, Y. Zhang, S. M. Mahurin, S. Dai, V. S. Bryantsev, C. J. Margulis and A. S. Ivanov, Chem. Sci., 2021, 12, 8026.
41. S. Roy, Y. Liu, M. Topsakal, E. Dias, R. Gakhar, W. C. Phillips, J. F. Wishart, D. Leshchev, P. Halstenberg, S. Dai, S. K. Gill, A. I. Frenkel and V. S. Bryantsev, J. Am. Chem. Soc., 2021, 143, 15298.
42. M. S. Emerson, S. Sharma, S. Roy, V. S. Bryantsev, A. S. Ivanov, R. Gakhar, M. E. Woods, L. C. Gallington, S. Dai, D. S. Maltsev and C. J. Margulis, J. Am. Chem. Soc., 2022, 144, 21751.
43. P. Han and D. M. Bartels, J. Phys. Chem., 1991, 95, 5367.
44. H. A. Schwarz, J. Phys. Chem., 1991, 95, 6697.
45. J. Fuller, W. Phillips, Q. An and R. Gakhar, Materials, 2022, 15, 1478.
46. S. Yoon and S. Choi, Electrochem. Soc., 2021, 168, 013504.

---

Footnotes

† Dedicated to Professor Rudi van Eldik on the occasion of his 80th birthday.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04190a

§ Current Address: Hunter College, City University of New York, New York, NY 10065, USA.

---