Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring non-covalent interactions in binary aromatic complexes†
Joseph C.
Bear
 a,
Jeremy K.
Cockcroft
a,
Jeremy K.
Cockcroft
 *b,
Alexander
Rosu-Finsen
b and
Jeffrey H.
Williams‡
*b,
Alexander
Rosu-Finsen
b and
Jeffrey H.
Williams‡
aSchool of Life Sciences, Pharmacy and Chemistry, Kingston University, Penrhyn Road, Kingston upon Thames KT1 2EE, UK
bDepartment of Chemistry, Christopher Ingold Laboratories, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: j.k.cockcroft@ucl.ac.uk
First published on 26th November 2025
Abstract
Crystal structure prediction for systems governed by weak non-covalent interactions remain a significant challenge due to the complex energy landscapes involved. Herein, we have experimentally investigated the impact of systematic halogen substitution in fluorinated aromatic co-formers on the formation, structure, and phase behaviour of donor–acceptor adducts and co-crystals with p-xylene (p-C6H4Me2). Using a combined approach of differential scanning calorimetry (DSC), variable-temperature powder X-ray diffraction (VT-PXRD), and single-crystal X-ray diffraction (SXD), we have characterized a series of co-crystals formed by p-C6H4Me2 with C6F5X (X = Cl, Br, I) and p-C6F4X2 derivatives. Our results revealed a clear evolution from columnar π-stacked adducts in the Cl-substituted systems to halogen-bonded structures with the heavier halogens (Br, I). The columnar 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts exhibit complex solid-state phase behaviour linked to molecular dipole and steric effects, whereas co-crystals involving Br and I show simpler behaviour, with discrete η2 and η6 halogen–π interactions both being observed. In one instance, a 1
1 adducts exhibit complex solid-state phase behaviour linked to molecular dipole and steric effects, whereas co-crystals involving Br and I show simpler behaviour, with discrete η2 and η6 halogen–π interactions both being observed. In one instance, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 co-crystal was formed with antiferroelectric ordering requiring halogen bonding to p-C6H4Me2 from two C6F5I molecules. The results underscore the tunability of solid-state architectures through targeted halogen substitution to probe subtle non-covalent interactions. In summary, this work advances our understanding of weak intermolecular forces in crystalline materials and provides data for the predictive design of functional co-crystals.
2 co-crystal was formed with antiferroelectric ordering requiring halogen bonding to p-C6H4Me2 from two C6F5I molecules. The results underscore the tunability of solid-state architectures through targeted halogen substitution to probe subtle non-covalent interactions. In summary, this work advances our understanding of weak intermolecular forces in crystalline materials and provides data for the predictive design of functional co-crystals.
Introduction
Since the famous quotation by John Maddox1 in the late 80′s, namely “one of the continuing scandals in the physical sciences is that it remains in general impossible to predict the structure of even the simplest crystalline solids from a knowledge of their chemical composition”, crystal structure prediction has advanced enormously, as demonstrated for example by the success rate in the series of blind tests2 organised by the Cambridge Crystallographic Data Centre. The targets used in these blind tests invariably feature molecules with both acceptor and donor groups that can interact strongly. However, when only weak non-covalent interactions are involved, a limitation in structure prediction is the sheer number of similar low-energy solutions in the energy landscape3 and it is evident that a far greater understanding of weak intermolecular forces in crystalline materials is required. In addition, interest in non-covalent interactions has been driven by rapid developments in materials science, where weak non-covalent interactions provide a greater, more intricate role in: molecular machines,4 pharmaceutical drug delivery,5 battery technologies,6 and fluorescent/phosphorescent optical materials.7Weak non-covalent (and non-ionic) intermolecular interactions encompass a wide range of intermolecular forces from van der Waals, which are non-directional, to hydrogen-bonding. Other weakly directing forces include: molecular dipoles and higher order electrostatic terms, bond dipoles, and the recently IUPAC-defined halogen bond.8 Of particular interest for crystal structure prediction are the stacking interactions between aromatic rings, as they are exacting to predict. Originally dubbed “π–π stacking”,9 it is perhaps more intuitive to think of crystal formation in these systems as being directed by the attraction of positive and negative molecular quadrupoles between co-formers, as in the highest temperature rhombohedral phase I of the prototypical system C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6.10,11 This special case of face-to-face stacking of aromatic units has also been termed a stacking interaction12 or an “aromatic donor–acceptor” interaction.13 However, when C6H6
C6F6.10,11 This special case of face-to-face stacking of aromatic units has also been termed a stacking interaction12 or an “aromatic donor–acceptor” interaction.13 However, when C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 is cooled to lower temperatures, an increase in the intercolumnar interactions leads to tilting of the rings.14,15 This tilting of the rings, often referred to as a so-called “slipped-stacked” arrangement, has been rationalized in terms of competition between London dispersion and Pauli repulsion forces, with electrostatics as an ambivalent spectator.16 The exchange repulsion energy contribution has a crucial influence on the structure of non-covalently bonded systems.17
C6F6 is cooled to lower temperatures, an increase in the intercolumnar interactions leads to tilting of the rings.14,15 This tilting of the rings, often referred to as a so-called “slipped-stacked” arrangement, has been rationalized in terms of competition between London dispersion and Pauli repulsion forces, with electrostatics as an ambivalent spectator.16 The exchange repulsion energy contribution has a crucial influence on the structure of non-covalently bonded systems.17
Derivatives of the parent adduct C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 have been studied extensively both experimentally18–20 and computationally.21–24 Supplementary experimental studies have attempted to answer the question: how does changing substituents on the benzene ring affect the non-covalent interaction between molecules and, ultimately, the structures formed? To that end, our experimental studies on adducts of C6F6 with methyl-substituted benzenes, namely: toluene, xylenes, and mesitylene all showed face-to-face stacking of the aromatic units.19,20 We refer to this arrangement of face-to-face stacking in a 1
C6F6 have been studied extensively both experimentally18–20 and computationally.21–24 Supplementary experimental studies have attempted to answer the question: how does changing substituents on the benzene ring affect the non-covalent interaction between molecules and, ultimately, the structures formed? To that end, our experimental studies on adducts of C6F6 with methyl-substituted benzenes, namely: toluene, xylenes, and mesitylene all showed face-to-face stacking of the aromatic units.19,20 We refer to this arrangement of face-to-face stacking in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal specifically as an adduct to distinguish it from other 1
1 co-crystal specifically as an adduct to distinguish it from other 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystals. Others have studied these derivative systems computationally.25,26
1 co-crystals. Others have studied these derivative systems computationally.25,26
However, to date, no in-depth studies involving modifying the C6F6 co-former have been made other than two studies from our group.27,28 We anticipated that substituting one or more of the fluorine atoms with a different halide (X = Cl, Br or I) will have several consequences. Firstly, the quadrupole moment of the co-former can be expected to be reduced as X will less electron withdrawing. Secondly, mono substitution introduces a permanent dipole into the system analogous to that produced by the methyl group in toluene. Thirdly, the substitution of F by a larger halide will reduce the “flatness” of the molecule, especially for Br and I. In a pilot study to this work,27 simple substitution of a single F for Cl in C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 produced an adduct that exhibited similar phases as a function of temperature (and at ambient pressure) to that of both the parent compound and the toluene adduct C6H5Me
C6F6 produced an adduct that exhibited similar phases as a function of temperature (and at ambient pressure) to that of both the parent compound and the toluene adduct C6H5Me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6. In a second pilot study, we changed a single F in the C6F6 molecule for H and used p-xylene (p-C6H4Me2) for the co-former.28
C6F6. In a second pilot study, we changed a single F in the C6F6 molecule for H and used p-xylene (p-C6H4Me2) for the co-former.28
In this paper, we have investigated the consequences of halide substitution but, in contrast to our first pilot study, we have used p-C6H4Me2 as one of the co-formers. The latter is easier to handle and less volatile than benzene, and it has no molecular dipole moment like benzene (in contrast to e.g. toluene). In this study, we posed the question: what is the effect of substituting one Cl for F in C6F6 on the formation of adducts/co-crystals with p-C6H4Me2? Subsequently, on discovering that the structure of the p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl adduct exhibits orientational disorder of the C6F5Cl moiety, we posed a second question: can C6F5Cl be replaced isostructurally in p-C6H4Me2
C6F5Cl adduct exhibits orientational disorder of the C6F5Cl moiety, we posed a second question: can C6F5Cl be replaced isostructurally in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl with p-C6F4Cl2? Finally, we posed a further question: what is the effect of increasing the polarizability (and size) of the X substituent by investigating whether monobromo- and monoiodo-substituted hexafluoro-benzenes formed similar co-crystals?
C6F5Cl with p-C6F4Cl2? Finally, we posed a further question: what is the effect of increasing the polarizability (and size) of the X substituent by investigating whether monobromo- and monoiodo-substituted hexafluoro-benzenes formed similar co-crystals?
Experimental
The chemicals: p-C6H4Me2 (Sigma-Aldrich, GC grade ≥ 99%), C6F5Cl (Sigma-Aldrich, purity 99%), C6F5Br (Fluorochem, 99.0%), C6F5I (Fluorochem, 99.0%), p-C6F4Cl2 (Manchester Organics, 95%) p-C6F4Br2 (Alfa Aesar, 99%), and p-C6F4I2 (Fluorochem, 99.0%) were used as received with the exception of p-C6F4Cl2. Adducts were prepared as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio mixtures of the individual components unless described otherwise. Adducts/co-crystals components were analysed by differential scanning calorimetry (DSC), variable-temperature powder X-ray diffraction (VT-PXRD), and single-crystal X-ray diffraction (SXD) with samples freezing below room temperature using our previously published method.28 Detailed information on the materials, experimental methods, and instrumentation are provided in the supplementary information (SI).
1 molar ratio mixtures of the individual components unless described otherwise. Adducts/co-crystals components were analysed by differential scanning calorimetry (DSC), variable-temperature powder X-ray diffraction (VT-PXRD), and single-crystal X-ray diffraction (SXD) with samples freezing below room temperature using our previously published method.28 Detailed information on the materials, experimental methods, and instrumentation are provided in the supplementary information (SI).
Results
Co-crystals of p-C6H4Me2 with C6F5X and p-C6F4X2 (X = Cl, Br, and I)
The prototypical adduct formed by benzene and hexafluorobenzene is noted for the formation of a solid at room temperature when the liquid components are added together in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio.10 However, at room temperature many of the adducts and co-crystals reported here are liquid despite the fact that some of the co-formers are solid at room temperature (see Table 1). Thus, on mixing the components, there is often no visible evidence to suggest adduct or co-crystal formation in the solid phase in contrast to the mixing of benzene and hexafluorobenzene. While the formation of a binary adducts by visual observation of the formation of a solid from liquid components is a useful undergraduate demonstration,11 the absence of solid formation should not be used to infer that no adduct has formed.
1 molar ratio.10 However, at room temperature many of the adducts and co-crystals reported here are liquid despite the fact that some of the co-formers are solid at room temperature (see Table 1). Thus, on mixing the components, there is often no visible evidence to suggest adduct or co-crystal formation in the solid phase in contrast to the mixing of benzene and hexafluorobenzene. While the formation of a binary adducts by visual observation of the formation of a solid from liquid components is a useful undergraduate demonstration,11 the absence of solid formation should not be used to infer that no adduct has formed.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 type adduct
C6F6 type adduct
| Substance | M.W./g mol−1 | m.p./K | Liq. at RT? | Adduct? |
|---|---|---|---|---|
| p-C6H4Me2 | 106.2 | 286 | Y | n/a |
| C6F6 | 186.1 | 278 | Y | n/a |
| C6F5Cl | 202.5 | 258 | Y | n/a |
| C6F5Br | 247.0 | 242 | Y | n/a |
| C6F5I | 294.0 | 244 | Y | n/a |
| C6F4Cl2 | 219.0 | 327 | N | n/a |
| C6F4Br2 | 307.9 | 354 | N | n/a |
| C6F4I2 | 401.9 | 383 | N | n/a |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 C6F6 |
292.3 | 301 | Y | Y |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl C6F5Cl |
308.7 | 273 | Y | Y |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br C6F5Br |
353.2 | 265 | Y | N |
(p-C6H4Me2)0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5I C6F5I |
347.1 | 275 | Y | N |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 p-C6F4Cl2 |
325.2 | 283 | Y | Y |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 p-C6F4Br2 |
414.1 | 352 | N | N |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2 p-C6F4I2 |
508.1 | 337 | n/a | N |
Initial evidence for the formation of a binary adduct or a co-crystal comes from DSC and VT-PXRD measurements. As seen in both DSC and VT-PXRD, all of the adducts/co-crystals in Table 1 exhibit melting points different to that of their constituent components. Furthermore, the observation of different indicative of adduct/co-crystal formation. The ultimate proof of adduct versus co-crystal formation was obtained by structure determination by SXD.
Adduct of p-C6H4Me2 with C6F5Cl
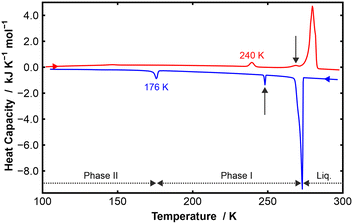
The DSC data for p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl shows two solid-state phases on both cooling and heating (Fig. 1). On cooling, a freezing transition was observed at 273 K and a solid–solid transition was observed at 176 K (ΔH = −1.6 kJ mol−1); on heating, a solid–solid transition was observed at 242 K (ΔH = +1.2 kJ mol−1) with a transition to the melt at 280 K. This solid-state transition shows considerable hysteresis with the I–II transition temperature varying from one run to another. Extra peaks observed at 251 K on cooling, and 268 K on heating, are attributed to a slight excess of C6F5Cl as confirmed in a DSC cycling experiment (Fig. S1). We note that there is a hint of an endothermic peak on heating at 147 K (with an equivalent one on cooling) that is probably due to non-structural changes relating to rotation of the methyl groups in p-C6H4Me2. Similar transitions in this temperature range have been observed previously.19
C6F5Cl shows two solid-state phases on both cooling and heating (Fig. 1). On cooling, a freezing transition was observed at 273 K and a solid–solid transition was observed at 176 K (ΔH = −1.6 kJ mol−1); on heating, a solid–solid transition was observed at 242 K (ΔH = +1.2 kJ mol−1) with a transition to the melt at 280 K. This solid-state transition shows considerable hysteresis with the I–II transition temperature varying from one run to another. Extra peaks observed at 251 K on cooling, and 268 K on heating, are attributed to a slight excess of C6F5Cl as confirmed in a DSC cycling experiment (Fig. S1). We note that there is a hint of an endothermic peak on heating at 147 K (with an equivalent one on cooling) that is probably due to non-structural changes relating to rotation of the methyl groups in p-C6H4Me2. Similar transitions in this temperature range have been observed previously.19
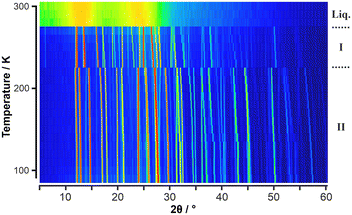
These two solid-state phases were also observed by VT-PXRD using 10 K steps in temperature (Fig. 2 and S2). In addition, VT-PXRD measurements were undertaken in 1 K temperature steps between 250 K and the melt (Fig. S3).
From the PXRD data, lattice parameters and molecular volume were obtained as a function of temperature (see Table S12, Fig. S4a–c and S5). At the I–II phase boundary, there is an abrupt change in volume.
As the I–II phase transition shows considerable hysteresis, care needs to be taken with regard to structure determination by SXD since, as we discovered, it is possible to measure both phases I and II at the same temperature (see SI). SXD measurements were made on phase II at 120 K, and on both phases I and II at 200 K.
Adduct of p-C6H4Me2 with p-C6F4Cl2
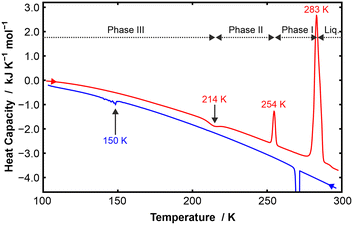
The DSC data on p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 shows three distinct solid phases on heating (Fig. 3). Solid–solid transitions were observed at 214 K (III → II) and 254 K (II → I) and a transition to the melt at about 283 K. On heating, the III → II transition is exothermic, which is unusual (for this class of materials). However, equivalent transitions are not evident on cooling, but a “sticky” transition is seen starting below around 170 K and extending over about a 40 K range. This sticky transition exhibited similar unusual behaviour to that seen for the protracted phase III to IV transition in C6H6
p-C6F4Cl2 shows three distinct solid phases on heating (Fig. 3). Solid–solid transitions were observed at 214 K (III → II) and 254 K (II → I) and a transition to the melt at about 283 K. On heating, the III → II transition is exothermic, which is unusual (for this class of materials). However, equivalent transitions are not evident on cooling, but a “sticky” transition is seen starting below around 170 K and extending over about a 40 K range. This sticky transition exhibited similar unusual behaviour to that seen for the protracted phase III to IV transition in C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6.15
C6F6.15
VT-PXRD on a quench-cooled sample of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 showed three solid-state phases on heating (Fig. 4 and S7) consistent with the DSC heating curve. The PXRD pattern for phase II has fewer peaks than those observed in the data for phases I and III, and is missing the low angle peak at about 5.9° seen in these phases. Phase II could be indexed in terms of a monoclinic cell; there is an excellent LeBail fit to the data despite the presence of residual p-C6F4Cl2 (Fig. S8). Furthermore, the effect of the sticky transition observed in the DSC was seen in a cooling VT-PXRD experiment in which the sample failed to transform from phase II to III despite being held at 120 K for about 6 hours (Fig. S9).
p-C6F4Cl2 showed three solid-state phases on heating (Fig. 4 and S7) consistent with the DSC heating curve. The PXRD pattern for phase II has fewer peaks than those observed in the data for phases I and III, and is missing the low angle peak at about 5.9° seen in these phases. Phase II could be indexed in terms of a monoclinic cell; there is an excellent LeBail fit to the data despite the presence of residual p-C6F4Cl2 (Fig. S8). Furthermore, the effect of the sticky transition observed in the DSC was seen in a cooling VT-PXRD experiment in which the sample failed to transform from phase II to III despite being held at 120 K for about 6 hours (Fig. S9).
From the VT-PXRD data, lattice parameters and molecular volume were obtained for phases I and II as a function of temperature (see Table S13, Fig. S10 and S11). Although the volume of phase II of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 is slightly smaller than that of phase I, the unusual change of symmetry from triclinic to higher symmetry monoclinic with decreasing temperature is indicative of a significant change of structure as seen in the phase III to IV transition of C6H6
p-C6F4Cl2 is slightly smaller than that of phase I, the unusual change of symmetry from triclinic to higher symmetry monoclinic with decreasing temperature is indicative of a significant change of structure as seen in the phase III to IV transition of C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6.15,16 This may explain why we were able to determine the structure of phase I from in situ crystal growth, but we struggled to obtain SXD data even to solve the structure of phase II.
C6F6.15,16 This may explain why we were able to determine the structure of phase I from in situ crystal growth, but we struggled to obtain SXD data even to solve the structure of phase II.
SXD measurements were made on phase I at 240 K, on phase II at 220 K, and on a new phase, labelled phase IV, at 130 K (see SI). We note that the SXD measurement temperature for phase I is below the II–I transition temperature (254 K) seen on heating in DSC, but this is possible due to the stability of phase I at this temperature as a result of hysteresis. The calculated PXRD pattern of phase IV (Fig. S12) surprisingly was not a match to the observed PXRD data of phase III, which could not be indexed. However, we were unable to obtain analysable SXD data on phase III despite repeated attempts. With regard to the measurement temperatures, the authors note that the DSC data was not very informative in this instance as the SXD measurements were made on cooling.
Co-crystal of p-C6H4Me2 with C6F5X (X = Br or I)
DSC data on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of p-C6H4Me2 with C6F5Br showed no solid-state phase transitions (Fig. S13). The structure of p-C6H4Me2
1 molar mixture of p-C6H4Me2 with C6F5Br showed no solid-state phase transitions (Fig. S13). The structure of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br at 120 K was determined by SXD as a 1
C6F5Br at 120 K was determined by SXD as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct. VT-PXRD data on this co-crystal showed no evidence for solid-state phase transitions (Fig. S14), and was consistent with the SXD data. From the PXRD data, lattice parameters and molecular volume were obtained as a function of temperature (Table S14, Fig. S15 and S16). However, cooling a 1
1 adduct. VT-PXRD data on this co-crystal showed no evidence for solid-state phase transitions (Fig. S14), and was consistent with the SXD data. From the PXRD data, lattice parameters and molecular volume were obtained as a function of temperature (Table S14, Fig. S15 and S16). However, cooling a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of p-C6H4Me2 and C6F5I to 120 K led to the growth of a crystal in which the molar ratio of p-C6H4Me2 and C6F5I components was shown to be 1
1 molar mixture of p-C6H4Me2 and C6F5I to 120 K led to the growth of a crystal in which the molar ratio of p-C6H4Me2 and C6F5I components was shown to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by SXD. This was consistent with DSC results using a sample prepared unwittingly in a 1
2 by SXD. This was consistent with DSC results using a sample prepared unwittingly in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (Fig. S17), which exhibited complex melting behaviour due to the sample being a 1
1 molar ratio (Fig. S17), which exhibited complex melting behaviour due to the sample being a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of C6H4Me2
1 molar mixture of C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 and excess C6H4Me2. Subsequent VT-PXRD measurements were made on a mixture of p-C6H4Me2 and C6F5I in a 1
(C6F5I)2 and excess C6H4Me2. Subsequent VT-PXRD measurements were made on a mixture of p-C6H4Me2 and C6F5I in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio. As for p-C6H4Me2
2 molar ratio. As for p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br, no solid-state phase transitions for p-C6H4Me2
C6F5Br, no solid-state phase transitions for p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 were observed (Fig. S18). Lattice parameters obtained from PXRD data on the sample at 120 K (Table S15) matched those from the SXD measurement.
(C6F5I)2 were observed (Fig. S18). Lattice parameters obtained from PXRD data on the sample at 120 K (Table S15) matched those from the SXD measurement.
Co-crystal of p-C6H4Me2 with p-C6F4X2 (X = Br or I)
Low-temperature DSC data on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixtures of p-C6H4Me2 with p-C6F4Br2 and p-C6F4I2 showed no evidence for solid-state phase transitions (Fig. S19 and S20). The solid-state structures of p-C6H4Me2
1 molar mixtures of p-C6H4Me2 with p-C6F4Br2 and p-C6F4I2 showed no evidence for solid-state phase transitions (Fig. S19 and S20). The solid-state structures of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 and p-C6H4Me2
p-C6F4Br2 and p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2 were determined from SXD. The unit cells determined by SXD matched those determined from the room temperature PXRD data (Fig. S21). As they were not columnar adducts, and as they exhibited no phase transitions, these co-crystals were not investigated further by VT-PXRD.
p-C6F4I2 were determined from SXD. The unit cells determined by SXD matched those determined from the room temperature PXRD data (Fig. S21). As they were not columnar adducts, and as they exhibited no phase transitions, these co-crystals were not investigated further by VT-PXRD.
A summary of all SXD results reported in this paper are given in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 measured in our previous studies21 but with a different choice of unit cell in order to aid comparison with new structures in this work
C6F6 measured in our previous studies21 but with a different choice of unit cell in order to aid comparison with new structures in this work
| Sample | Phase | T/K | S.G. | Z | a/Å | b/Å | c/Å | α/° | β/° | γ/° | V/Z/Å3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6‡ C6F6‡ |
II | 240 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.4824(5) | 7.2938(6) | 7.5328(5) | 105.295(7) | 101.979(6) | 96.465(7) | 330.74(5) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6‡ C6F6‡ |
III | 150 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.1308(4) | 7.2896(5) | 7.7362(4) | 107.632(5) | 101.940(5) | 95.058(5) | 318.12(4) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl C6F5Cl |
I | 200 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
2 | 6.5505(4) | 7.3190(4) | 14.6880(8) | 89.116(4) | 102.483(5) | 94.488(5) | 342.72(4) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl C6F5Cl |
II | 200 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.2099(4) | 7.4687(4) | 7.9874(4) | 109.801(5) | 99.549(5) | 95.567(5) | 339.00(3) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl C6F5Cl |
II | 120 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.1383(5) | 7.4411(7) | 7.9224(6) | 111.378(8) | 99.662(7) | 95.159(7) | 327.65(5) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 p-C6F4Cl2 |
I | 240 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
2 | 6.4620(4) | 7.4574(4) | 15.1315(7) | 90.380(4) | 100.429(5) | 94.132(5) | 357.57(4) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 p-C6F4Cl2 |
II | 220 | P21/n11 | 2 | 5.98846(7) | 7.90133(9) | 14.83490(17) | 96.4603(10) | 90 | 90 | 348.742(7) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 p-C6F4Cl2 |
IV | 130 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.3455(3) | 7.5012(3) | 7.7599(3) | 109.370(4) | 98.590(4) | 90.299(3) | 343.95(3) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br C6F5Br |
* | 120 | P121/n1 | 4 | 9.0813(3) | 15.2000(5) | 9.8653(2) | 90 | 99.229(2) | 90 | 336.11(2) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 p-C6F4Br2 |
* | 150 | C12/m1 | 2 | 8.4576(3) | 8.3594(3) | 9.8748(3) | 90 | 92.357(3) | 90 | 348.78(2) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 (C6F5I)2 |
* | 120 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1 | 6.04191(17) | 8.9855(2) | 9.9891(3) | 74.629(2) | 89.584(2) | 89.675(2) | 522.89(2) |
p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2 p-C6F4I2 |
* | 150 | C12/m1 | 2 | 8.5140(7) | 8.5541(8) | 10.2442(8) | 90 | 93.450(7) | 90 | 372.37(6) |
Discussion
Previously, our investigations focussed on perturbing the non-covalent interactions in the prototypical adduct C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 by either substitution of –H by –CH3 in the benzene ring or by substitution of –F by –Cl or –H in hexafluorobenzene.21,27,28 There are a number of advantages in expanding our studies with the use of p-xylene (p-C6H4Me2) with substituted hexafluorobenzenes. Like C6H6, p-C6H4Me2 has no dipole moment. Secondly, it is easier to handle due to its lower volatility. Thirdly, it was noticed that p-C6H4Me2 formed more solid adducts than C6H6 with different co-formers at room temperature. Solid adducts are easier to analyse via SXD as the crystallographer can select and mount a single crystal manually. However, recent work by our group on multi-grain crystallographic methods allows for the analysis of multiple single crystals in the beam grown in situ from the melt whilst mounted on the diffractometer.28 Thus, we were able to largely overcome this limitation and analyse mixtures, which are liquid at room temperature. The combination of low temperature DSC and VT-PXRD allows for the rapid identification of phase transitions, and thus suggest temperatures at which SXD experiments should be undertaken. In this way, we stood the best possible chance that the crystals would not undergo any phase transitions during SXD data acquisition.
C6F6 by either substitution of –H by –CH3 in the benzene ring or by substitution of –F by –Cl or –H in hexafluorobenzene.21,27,28 There are a number of advantages in expanding our studies with the use of p-xylene (p-C6H4Me2) with substituted hexafluorobenzenes. Like C6H6, p-C6H4Me2 has no dipole moment. Secondly, it is easier to handle due to its lower volatility. Thirdly, it was noticed that p-C6H4Me2 formed more solid adducts than C6H6 with different co-formers at room temperature. Solid adducts are easier to analyse via SXD as the crystallographer can select and mount a single crystal manually. However, recent work by our group on multi-grain crystallographic methods allows for the analysis of multiple single crystals in the beam grown in situ from the melt whilst mounted on the diffractometer.28 Thus, we were able to largely overcome this limitation and analyse mixtures, which are liquid at room temperature. The combination of low temperature DSC and VT-PXRD allows for the rapid identification of phase transitions, and thus suggest temperatures at which SXD experiments should be undertaken. In this way, we stood the best possible chance that the crystals would not undergo any phase transitions during SXD data acquisition.
The following discussion section follows the same sequence as the results section, allowing the reader to match the results from one system with the corresponding discussion.
The pure components
The solid-state structure of p-xylene has previously been well characterised.30 By contrast, until recently, the chlorine- and bromo-substituted fluorobenzenes used in this study had not been thoroughly characterised in solid form. As this essential data was missing, our group investigated the solid-state behaviour of C6F5Cl and C6F5Br, as well as p-C6F4Cl2 as a forerunner to our current work.31,32The structures of phases II and III of C6F5Cl were solved from SXD data obtained in situ from the sample at 200 K and 150 K, respectively. An additional transient phase was observed just below the melt, labelled as phase I but we were unable to determine its structure. Additionally, the crystal structure of p-C6F4Cl2 was determined by SXD at 150 K.31
The complex phase behaviour of C6F5Br has been reported by us recently32 whilst the structure of the p-C6F4Br2 has previously been determined.33–35 Likewise, the crystal structures of C6F5I and p-C6F4I2 have previously been determined by others.35–39
Adduct of p-C6H4Me2 with C6F6
In our previous work, we showed that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
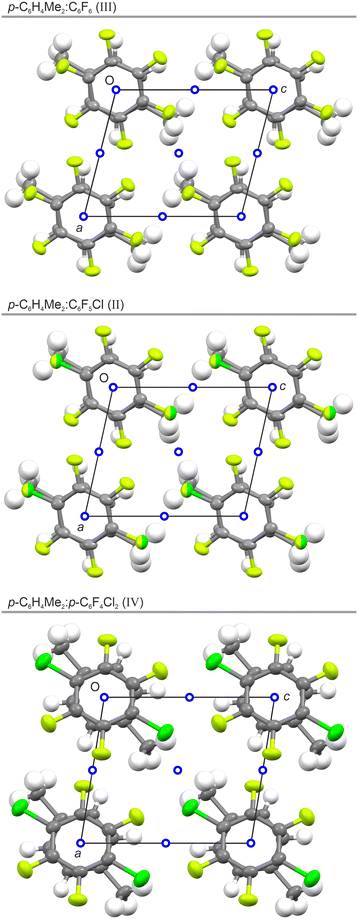
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of p-C6H4Me2 and C6F6 forms a columnar adduct with three solid-state phases.21 In the lowest temperature phase III, the molecules align such that the C–CH3 bonds in p-xylene are co-linear with the C–F bonds in C6F6 resulting in an eclipsed conformation (Fig. 5). On increasing the temperature, the bond dipole interaction between the C–CH3 and C–F bonds weakens leading to the formation of phase II in which the molecules now exhibit a staggered conformation (Fig. 6). Above 246 K, increased librational motion of the p-xylene molecules leads to the formation of monoclinic phase I in which the molecules exhibit mirror and twofold symmetry. On cooling back to the triclinic phase II, the molecules are in a position of unstable equilibrium with respect to mirror and twofold symmetry and these symmetry elements are therefore lost.
1 molar mixture of p-C6H4Me2 and C6F6 forms a columnar adduct with three solid-state phases.21 In the lowest temperature phase III, the molecules align such that the C–CH3 bonds in p-xylene are co-linear with the C–F bonds in C6F6 resulting in an eclipsed conformation (Fig. 5). On increasing the temperature, the bond dipole interaction between the C–CH3 and C–F bonds weakens leading to the formation of phase II in which the molecules now exhibit a staggered conformation (Fig. 6). Above 246 K, increased librational motion of the p-xylene molecules leads to the formation of monoclinic phase I in which the molecules exhibit mirror and twofold symmetry. On cooling back to the triclinic phase II, the molecules are in a position of unstable equilibrium with respect to mirror and twofold symmetry and these symmetry elements are therefore lost.
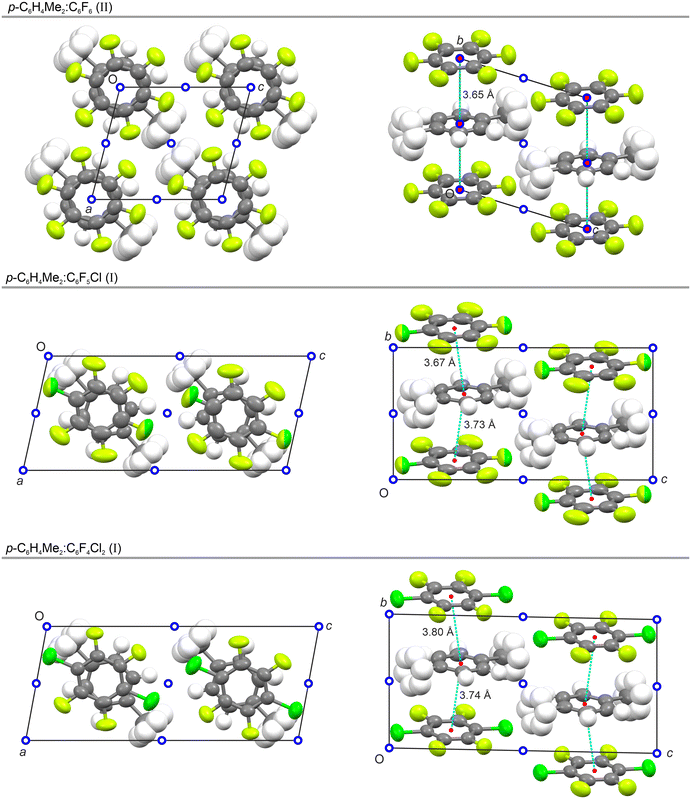
Adduct of p-C6H4Me2 with C6F5Cl
In this work, we investigated the effect of substitution of a single fluorine atom in C6F6 by a chlorine atom with respect to adduct formation and its properties as a function of temperature. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of p-C6H4Me2 and C6F5Cl forms a columnar adduct but this adduct only exhibits two solid-state phases as seen by DSC and VT-PXRD (Fig. 1 and 2). In the lowest temperature phase II, the molecules align such that the C–CH3 bonds in p-xylene are co-linear with the C–Cl bond in C6F5Cl resulting in an eclipsed conformation (Fig. 5), similar to the behaviour observed for phase III of p-C6H4Me2
1 molar mixture of p-C6H4Me2 and C6F5Cl forms a columnar adduct but this adduct only exhibits two solid-state phases as seen by DSC and VT-PXRD (Fig. 1 and 2). In the lowest temperature phase II, the molecules align such that the C–CH3 bonds in p-xylene are co-linear with the C–Cl bond in C6F5Cl resulting in an eclipsed conformation (Fig. 5), similar to the behaviour observed for phase III of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6. In both p-C6H4Me2
C6F6. In both p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 and p-C6H4Me2
C6F6 and p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl, the molecules are centred on the inversion points with space group P
C6F5Cl, the molecules are centred on the inversion points with space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , necessitating disorder of the C6F5Cl molecule over two opposite orientations in equal measure, i.e. 50
, necessitating disorder of the C6F5Cl molecule over two opposite orientations in equal measure, i.e. 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 percentage site occupation of Cl (for a F atom) across the two symmetry-related positions.
50 percentage site occupation of Cl (for a F atom) across the two symmetry-related positions.
In its higher temperature phase, C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl (I) exhibits a staggered conformation in the triclinic space group P
C6F5Cl (I) exhibits a staggered conformation in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . However, in contrast to phase II, the molecules are no longer centred on symmetry inversion points. Consequently, the disorder is no longer constrained to be 50
. However, in contrast to phase II, the molecules are no longer centred on symmetry inversion points. Consequently, the disorder is no longer constrained to be 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 percentage by symmetry, and the refined orientational disorder for the two positions is 38
50 percentage by symmetry, and the refined orientational disorder for the two positions is 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 percentage site occupation. The lack of molecular inversion symmetry results in twice the number of molecules per unit cell as evidenced by the cell doubling seen in the VT-PXRD experiment (Fig. 2). A transition leading to the doubling of the unit cell but with no change in space-group symmetry on heating is unusual.
62 percentage site occupation. The lack of molecular inversion symmetry results in twice the number of molecules per unit cell as evidenced by the cell doubling seen in the VT-PXRD experiment (Fig. 2). A transition leading to the doubling of the unit cell but with no change in space-group symmetry on heating is unusual.
The phase II to phase I transition appears to be driven by the combination of molecules moving from eclipsed to staggered plus a lateral movement of the molecules leading to a slipped-disc columnar structure. As seen in Fig. 6, the formation of a slipped-disc structure with staggered conformation of the molecules for phase I of C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl is in contrast to the behaviour seen in phases II and III of p-C6H4Me2
C6F5Cl is in contrast to the behaviour seen in phases II and III of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6, in which the molecules are staggered but remain aligned along the column axis.
C6F6, in which the molecules are staggered but remain aligned along the column axis.
This major structural change in going between phases I and II of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl is reflected in the DSC measurement where significant hysteresis is observed (Fig. 1). This large hysteresis enabled us to measure both phase I and phase II at the same temperature (200 K) in an SXD experiment! The observation of a monoclinic phase in p-C6H4Me2
C6F5Cl is reflected in the DSC measurement where significant hysteresis is observed (Fig. 1). This large hysteresis enabled us to measure both phase I and phase II at the same temperature (200 K) in an SXD experiment! The observation of a monoclinic phase in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 raised the question of the existence of a third solid-state phase existing just below the melt in p-C6H4Me2
C6F6 raised the question of the existence of a third solid-state phase existing just below the melt in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl. VT-PXRD in very fine (1 K) steps (Fig. S3) showed no evidence for an additional phase in contrast to the observation of a monoclinic phase just below the melt in p-C6H4Me2
C6F5Cl. VT-PXRD in very fine (1 K) steps (Fig. S3) showed no evidence for an additional phase in contrast to the observation of a monoclinic phase just below the melt in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6.21
C6F6.21
Adduct of p-C6H4Me2 with p-C6F4Cl2
The observation of a structure with either roughly 50% (phase I) or exactly 50% (phase II) orientational disorder of the C6F5Cl molecules in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl raised the question of whether an isomorphous structure would be formed when C6F5Cl is substituted with p-C6F4Cl2. Hence, we subsequently investigated the effect of substitution of C6F5Cl with p-C6F4Cl2 with regard to adduct formation and the properties of any adduct as a function of temperature. Our experiments showed that a 1
C6F5Cl raised the question of whether an isomorphous structure would be formed when C6F5Cl is substituted with p-C6F4Cl2. Hence, we subsequently investigated the effect of substitution of C6F5Cl with p-C6F4Cl2 with regard to adduct formation and the properties of any adduct as a function of temperature. Our experiments showed that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar mixture of p-C6H4Me2 and p-C6F4Cl2 forms a columnar adduct, but that this adduct exhibits at least three solid-state phases (Fig. 4 and 5). The crystal structures of phases I, II, and IV are illustrated in Fig. 6, 7, and 5, respectively; however, we were unable to determine the structure of phase III observed in the PXRD measurements.
1 molar mixture of p-C6H4Me2 and p-C6F4Cl2 forms a columnar adduct, but that this adduct exhibits at least three solid-state phases (Fig. 4 and 5). The crystal structures of phases I, II, and IV are illustrated in Fig. 6, 7, and 5, respectively; however, we were unable to determine the structure of phase III observed in the PXRD measurements.
The highest-temperature phase I of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 exhibits a staggered conformation in the triclinic space-group P
p-C6F4Cl2 exhibits a staggered conformation in the triclinic space-group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , the structure being isomorphous to that of C6H4Me2
, the structure being isomorphous to that of C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl (I) demonstrating that C6F5Cl can be replaced by p-C6F4Cl2. As with C6H4Me2
C6F5Cl (I) demonstrating that C6F5Cl can be replaced by p-C6F4Cl2. As with C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl (I), p-C6H4Me2
C6F5Cl (I), p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 (I) exhibits a slipped-disc column arrangement with two different centroid-to-centroid distances. The lattice parameters for both adducts are broadly similar (Table 2) and differ mainly due to the different measurement temperatures employed (200 K vs. 240 K), the latter chosen in light of the phase transitions observed in these two adducts.
p-C6F4Cl2 (I) exhibits a slipped-disc column arrangement with two different centroid-to-centroid distances. The lattice parameters for both adducts are broadly similar (Table 2) and differ mainly due to the different measurement temperatures employed (200 K vs. 240 K), the latter chosen in light of the phase transitions observed in these two adducts.
Although the monoclinic cell parameters of phase II of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 in space-group P21/n11 are broadly similar to those of phase I, the structures are quite different. Firstly, the columns of molecules in phase II are approximately close-packed leading to a significant reduction in volume per molecule (Table 2). Secondly, the molecules within a column do not exhibit a slipped-disc column arrangement as in phase I, but are instead eclipsed where the methyl groups of p-C6H4Me2 are superimposed upon the chlorine atoms of the p-C6F4Cl2. Finally, the molecules in one column are tilted at an opposite angle to those in a neighbouring column (Fig. 7). The tilting of the rings avoids direct face-to-face stacking of the electron dense π-clouds of the aromatic rings, which is a repulsive interaction. Given the observed tilts, this is evidently stronger than the competing quadrupole attraction between molecules, which by itself would favour face-to-face stacking.
p-C6F4Cl2 in space-group P21/n11 are broadly similar to those of phase I, the structures are quite different. Firstly, the columns of molecules in phase II are approximately close-packed leading to a significant reduction in volume per molecule (Table 2). Secondly, the molecules within a column do not exhibit a slipped-disc column arrangement as in phase I, but are instead eclipsed where the methyl groups of p-C6H4Me2 are superimposed upon the chlorine atoms of the p-C6F4Cl2. Finally, the molecules in one column are tilted at an opposite angle to those in a neighbouring column (Fig. 7). The tilting of the rings avoids direct face-to-face stacking of the electron dense π-clouds of the aromatic rings, which is a repulsive interaction. Given the observed tilts, this is evidently stronger than the competing quadrupole attraction between molecules, which by itself would favour face-to-face stacking.
The powder diffraction patterns of “phase III” of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 could not be indexed. Repeat measurements suggested that the solid produced by quenching might be a mixture of two phases. Attempts to produce phase III by slow cooling of the sample resulted solely in the observation of phase II (down to 120 K). In the absence of a crystal structure solution, one might speculate that the structure of phase III might have similar packing to phase II but with either a staggered arrangement of the rings (as seen in related materials at low temperature) or with a change to the relative tilts of the molecules within a column. However, in the SXD experiments, cooling the sample of p-C6H4Me2
p-C6F4Cl2 could not be indexed. Repeat measurements suggested that the solid produced by quenching might be a mixture of two phases. Attempts to produce phase III by slow cooling of the sample resulted solely in the observation of phase II (down to 120 K). In the absence of a crystal structure solution, one might speculate that the structure of phase III might have similar packing to phase II but with either a staggered arrangement of the rings (as seen in related materials at low temperature) or with a change to the relative tilts of the molecules within a column. However, in the SXD experiments, cooling the sample of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 in phase II resulted in at least one large crystal of “phase IV” being formed, whose calculated PXRD pattern differed to that of phase III (see Fig. S12). Phase IV has a larger volume than super-cooled phase II (Fig. S11), suggesting it to be a metastable phase.
p-C6F4Cl2 in phase II resulted in at least one large crystal of “phase IV” being formed, whose calculated PXRD pattern differed to that of phase III (see Fig. S12). Phase IV has a larger volume than super-cooled phase II (Fig. S11), suggesting it to be a metastable phase.
As shown in Fig. 5, the structure of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 (IV) exhibits a semi-eclipsed conformation similar to that seen in p-C6H4Me2
p-C6F4Cl2 (IV) exhibits a semi-eclipsed conformation similar to that seen in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 (III) and p-C6H4Me2
C6F6 (III) and p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl (II). As for the other two adducts at low temperature, we speculate that p-C6H4Me2
C6F5Cl (II). As for the other two adducts at low temperature, we speculate that p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 (IV) is the most thermodynamically stable phase. As for phase II, but in contrast to phase I, there is an equal distance between the centroids of the p-C6H4Me2 and p-C6F4Cl2 rings along the column axis.
p-C6F4Cl2 (IV) is the most thermodynamically stable phase. As for phase II, but in contrast to phase I, there is an equal distance between the centroids of the p-C6H4Me2 and p-C6F4Cl2 rings along the column axis.
It is interesting to note in each of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6, p-C6H4Me2
C6F6, p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl, and p-C6H4Me2
C6F5Cl, and p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 that staggered conformations between co-formers are seen at the higher temperatures. On lowering the temperature, an eclipsed conformation is preferred, though for p-C6H4Me2
p-C6F4Cl2 that staggered conformations between co-formers are seen at the higher temperatures. On lowering the temperature, an eclipsed conformation is preferred, though for p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 a perfectly eclipsed conformation is not achieved. There is competition between the alignment of C–Me with C–Cl bond dipoles and C–H with C–F bond dipoles and steric repulsion due to the presence of larger halides on the substituted C6F6 ring, leading to this imperfectly eclipsed conformation.
p-C6F4Cl2 a perfectly eclipsed conformation is not achieved. There is competition between the alignment of C–Me with C–Cl bond dipoles and C–H with C–F bond dipoles and steric repulsion due to the presence of larger halides on the substituted C6F6 ring, leading to this imperfectly eclipsed conformation.
Co-crystals of p-C6H4Me2 with C6F5X (X = Br or I)
The mono-halogen-substituted C6F5X co-formers, namely C6F5Cl, C6F5Br, and C6F5I have a molecular dipole that increases in going from Cl through to I. The effect of this is seen in the co-crystals formed. The single phase observed for p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br has a slipped-disc columnar adduct similar to phase I of p-C6H4Me2
C6F5Br has a slipped-disc columnar adduct similar to phase I of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl, but with antiferroelectric ordering of the molecular dipole (Fig. 8 and S22). The discs are slipped to a larger extent in the bromo co-crystal presumably to accommodate the larger size of the Br atom. In addition, the steric effect of the Br atoms leads to only partial alignment of the C–Me and C–Br bond dipoles and an imperfectly eclipsed conformation.
C6F5Cl, but with antiferroelectric ordering of the molecular dipole (Fig. 8 and S22). The discs are slipped to a larger extent in the bromo co-crystal presumably to accommodate the larger size of the Br atom. In addition, the steric effect of the Br atoms leads to only partial alignment of the C–Me and C–Br bond dipoles and an imperfectly eclipsed conformation.
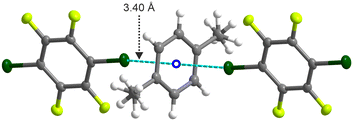
By contrast, the interaction of p-C6H4Me2 and C6F5I does not cause the formation of a columnar adduct as the non-covalent interactions are driven by halogen bonding tending towards an “η2” type halogen bond interaction (based on closest C–X distances) with the aromatic ring of p-C6H4Me2 (Fig. 9 and S23). As shown by Wong et al.39via a CCDC database study combined with DFT calculations, “η1” interactions (where the halogen points towards a single carbon atom) and “η2” (where the halogen points towards the C–C aromatic bond) dominate CCDC database entries of π-type halogen bonds and this is what we observe here. The increase in the molecular dipole moment in C6F5X in going from F to I favours antiferroelectric ordering of the C6F5X molecules. In addition, the larger size of I strongly discourages columnar adduct formation on steric grounds. The stronger antiferroelectric interactions in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 (and also in p-C6H4Me2
(C6F5I)2 (and also in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br) probably results in the absence of phase transitions to disordered phases on heating (as shown by DSC or VT-PXRD) in contrast to the behaviour shown, for example, by p-C6H4Me2
C6F5Br) probably results in the absence of phase transitions to disordered phases on heating (as shown by DSC or VT-PXRD) in contrast to the behaviour shown, for example, by p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl, or indeed by the parent co-crystal p-C6H4Me2
C6F5Cl, or indeed by the parent co-crystal p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6.
C6F6.
The co-crystal of p-C6H4Me2 and C6F5I is formed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio as found in previous work on C6H6
2 ratio as found in previous work on C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2.36 This enables halogen bonding to form on both sides of the aromatic ring of p-C6H4Me2 (Fig. S23). By contrast, we note that the co-crystal C6H6
(C6F5I)2.36 This enables halogen bonding to form on both sides of the aromatic ring of p-C6H4Me2 (Fig. S23). By contrast, we note that the co-crystal C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 has both high- and low-temperature phases, but in each form, the iodine atoms are found in layers with the C6H6 molecules sandwiched between two C6F5I molecules. Thus, despite the same compositional ratios, the crystal structures of p-C6H4Me2
(C6F5I)2 has both high- and low-temperature phases, but in each form, the iodine atoms are found in layers with the C6H6 molecules sandwiched between two C6F5I molecules. Thus, despite the same compositional ratios, the crystal structures of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 and C6H6
(C6F5I)2 and C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2 (in either phase) are not related demonstrating the effects of different competing non-covalent interactions.
(C6F5I)2 (in either phase) are not related demonstrating the effects of different competing non-covalent interactions.
Co-crystals of p-C6H4Me2 with p-C6F4X2 (X = Br or I)
The co-formers C6F6, p-C6F4Cl2, p-C6F4Br2, and p-C6F4I2 have no molecular dipole. In addition, the quadrupole moment of the molecules is expected to decrease in going from C6F6 through to p-C6F4I2. A consequence of this is that columnar adduct formation is expected to become less favourable, but halogen bond formation is expected to become more favourable for crystal growth.Initially, we posed the question as to whether a columnar adduct could be formed between p-C6H4Me2 and p-C6F4Br2, given that one forms between p-C6H4Me2 and C6F5Br. In contrast to the crystal structures formed by p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2, SXD showed that the structure formed by p-C6H4Me2
p-C6F4Cl2, SXD showed that the structure formed by p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 is not a columnar adduct, but a 1
p-C6F4Br2 is not a columnar adduct, but a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
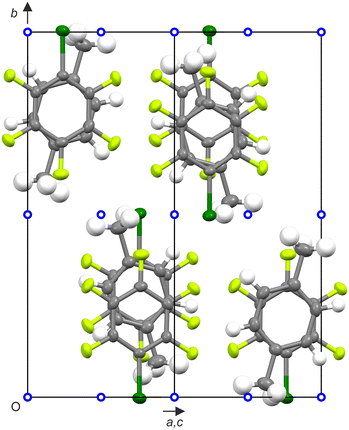
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal structure dominated by the less common η6 halogen bonding (Fig. 10), where the halogen atom is roughly equidistant from the six carbons of the aromatic ring, which is usually less favoured as the lone pair of the halogen experiences strong repulsion from the π-cloud.39 The molecules are arranged in a herringbone motif (Fig. S24).
1 co-crystal structure dominated by the less common η6 halogen bonding (Fig. 10), where the halogen atom is roughly equidistant from the six carbons of the aromatic ring, which is usually less favoured as the lone pair of the halogen experiences strong repulsion from the π-cloud.39 The molecules are arranged in a herringbone motif (Fig. S24).
Likewise, the crystal structure formed by p-C6F4I2 dissolved in an excess of p-C6H4Me2 also leads to the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal, which is isostructural to p-C6H4Me2
1 co-crystal, which is isostructural to p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 (Fig. S25). The halogen bond in p-C6H4Me2
p-C6F4Br2 (Fig. S25). The halogen bond in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2 still tends towards η6 but is less symmetric, leaning towards η1 type behaviour (with C⋯I varying from 3.64 Å to 3.76 Å), with the distance to the centroid of the p-C6H4Me2 ring being 3.43 Å.
p-C6F4I2 still tends towards η6 but is less symmetric, leaning towards η1 type behaviour (with C⋯I varying from 3.64 Å to 3.76 Å), with the distance to the centroid of the p-C6H4Me2 ring being 3.43 Å.
As an aside, we note that a co-crystal structure of C6H6 and p-C6F4I2 has been reported with triclinic symmetry.40 However, our measurements on C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2 showed that its crystal structure has the same monoclinic space-group symmetry (C2/m) as exhibited by p-C6H4Me2
p-C6F4I2 showed that its crystal structure has the same monoclinic space-group symmetry (C2/m) as exhibited by p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4X2 for X = Br and I, but it is not isostructural (Fig. S26). In the crystal structure of C6H6
p-C6F4X2 for X = Br and I, but it is not isostructural (Fig. S26). In the crystal structure of C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2, halogen bonding is via the more common η2 type interaction.
p-C6F4I2, halogen bonding is via the more common η2 type interaction.
It is interesting to contrast the structures formed by p-C6F4Br2 with p-C6H4Me2 and those stacked structures formed by p-C6F4Br2 with larger aromatics. A search of the Cambridge Structural Database reveals the following columnar adducts with aromatic hydrocarbons: phenanthrene (REVQAM),41 fluoranthene (NEHDOW),42 triphenylene (RINPEM),33 and pyrene (GUQRAN);7 all of which exhibit columnar structures. These structures indicate that there is seemingly a fine balance between the various structure-directing non-covalent interactions, namely quadrupole and bond-dipole moments versus halogen-bonds. This suggests that the different structural type formed by p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2 is a result of differences in the magnitude of these forces. It is noteworthy that a similar search of the Cambridge Structural Database revealed fewer columnar adducts between p-C6F4I2 and aromatic hydrocarbons. Thus a columnar adduct is formed with triphenylene (RINPOW)33 and pyrene (FARNOD);43 but not with fluoranthene (NEHCIP)42 or phenanthrene (NICSUP).44 This may be due to the greater tendency of iodinated aromatics to form halogen bonds in co-crystals with aromatic hydrocarbons.45
p-C6F4Br2 is a result of differences in the magnitude of these forces. It is noteworthy that a similar search of the Cambridge Structural Database revealed fewer columnar adducts between p-C6F4I2 and aromatic hydrocarbons. Thus a columnar adduct is formed with triphenylene (RINPOW)33 and pyrene (FARNOD);43 but not with fluoranthene (NEHCIP)42 or phenanthrene (NICSUP).44 This may be due to the greater tendency of iodinated aromatics to form halogen bonds in co-crystals with aromatic hydrocarbons.45
Conclusions
In this paper, we have investigated the consequences of mono- and p-di-halide substitution in C6F6 on the formation of adducts/co-crystals with p-C6H4Me2. The resulting stable adducts/co-crystals and their phase behaviour as a function of temperature have been characterised by a combination of DSC, VT-PXRD, and SXD. With p-C6H4Me2, C6F5Cl, p-C6F4Cl2, and C6F5Br formed columnar adducts whereas p-C6F4Br2, C6F5I, and p-C6F4I2 formed co-crystals with halogen bonding. The columnar adducts exhibited complex phase behaviour, often with several phase transitions up to the melt, whereas simple co-crystals exhibited a single solid phase down to 100 K.The difference between the two groups can be attributed to the change in the relative strengths of the different types of non-covalent interaction in these materials. When substituting F (in C6F6) with Cl, Br, and then I, the propensity for halogen bonding can be expected to increase; conversely, the quadrupole moment, which is thought to direct alignment of the molecules in columns (from the liquid phase), is expected to decrease. Although p-di-substituted C6F6 derivatives have no molecular dipole, the mono-substituted forms possess a molecular dipole whose strength is expected to increase in going from F down to I.
The structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystals formed by p-C6H4Me2 with p-C6F4Br2 and p-C6F4I2 are isomorphous. The solid-state structure are dominated by halogen bonding, with the I derivative forming the more common η2 bonding while for the Br derivative the less common η6 bonding is observed. Likewise, the co-crystal formed by C6F5I exhibits η2 bonding but with only one iodine atom available in C6F5I, two molecules are required to enable halogen bonding to both sides of the aromatic ring of p-C6H4Me2 leading to a 1
1 co-crystals formed by p-C6H4Me2 with p-C6F4Br2 and p-C6F4I2 are isomorphous. The solid-state structure are dominated by halogen bonding, with the I derivative forming the more common η2 bonding while for the Br derivative the less common η6 bonding is observed. Likewise, the co-crystal formed by C6F5I exhibits η2 bonding but with only one iodine atom available in C6F5I, two molecules are required to enable halogen bonding to both sides of the aromatic ring of p-C6H4Me2 leading to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 co-crystal. For C6F5I, the relatively large molecular dipole leads to a single solid-state phase with antiferroelectric ordering. However, for p-C6H4Me2:C6F5Br, the balance of non-covalent interactions still leads to antiferroelectric ordering but with the molecules now arranged in columns.
2 co-crystal. For C6F5I, the relatively large molecular dipole leads to a single solid-state phase with antiferroelectric ordering. However, for p-C6H4Me2:C6F5Br, the balance of non-covalent interactions still leads to antiferroelectric ordering but with the molecules now arranged in columns.
For the columnar adducts, the non-covalent interactions can lead to either “staggered” or “eclipsed” arrangements with respect to the alignment of the C–X and C–Me bonds (with eclipsed forms favoured at lower temperatures); hence the variable phase behaviour seen in these derivatives. The weaker molecular dipole in C6F5Cl is insufficient to cause antiferroelectric ordering in p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl, with disorder of the orientation of the C6F5Cl molecule being observed. A similar crystal structure was observed for one of the phases of p-C6H4Me2
C6F5Cl, with disorder of the orientation of the C6F5Cl molecule being observed. A similar crystal structure was observed for one of the phases of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 showing that one can indeed replace C6F5Cl with p-C6F4Cl2 isostructurally. In contrast to the parent p-C6H4Me2
p-C6F4Cl2 showing that one can indeed replace C6F5Cl with p-C6F4Cl2 isostructurally. In contrast to the parent p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F6 adduct, C6F5Cl, p-C6F4Cl2, and C6F5Br adducts all exhibited phases with a slipped-disc arrangement for the columns of molecules, which is especially pronounced in the Br derivative due to steric effects.
C6F6 adduct, C6F5Cl, p-C6F4Cl2, and C6F5Br adducts all exhibited phases with a slipped-disc arrangement for the columns of molecules, which is especially pronounced in the Br derivative due to steric effects.
In summary, this study provides valuable experimental data which will aid the development of crystal structure prediction (CSP) models and machine learning approaches. However, indexing of the powder diffraction pattern of “phase III” of p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 proved intractable, which throws open a challenge to our crystal-structure prediction colleagues.
p-C6F4Cl2 proved intractable, which throws open a challenge to our crystal-structure prediction colleagues.
Author contributions
The manuscript was written through contributions of all authors. All living authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
Additional experimental details, crystallographic tables, additional supporting figures, and CIF files including the unindexed PXRD patterns are supplied in the supplementary information (SI).Supplementary information is available. See DOI: https://doi.org/10.1039/d5ce00989h.
CCDC 2483307–2483317 (p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Cl (in phases I and II), p-C6H4Me2
C6F5Cl (in phases I and II), p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Cl2 (in phases I, II, and IV), p-C6H4Me2
p-C6F4Cl2 (in phases I, II, and IV), p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C6F5Br, p-C6H4Me2
C6F5Br, p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4Br2, p-C6H4Me2
p-C6F4Br2, p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (C6F5I)2, and p-C6H4Me2
(C6F5I)2, and p-C6H4Me2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2, plus C6H6
p-C6F4I2, plus C6H6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p-C6F4I2) contains the supplementary crystallographic data for this paper.46a–k
p-C6F4I2) contains the supplementary crystallographic data for this paper.46a–k
Acknowledgements
We acknowledge financial support from the EPSRC for funding the single-crystal X-ray diffractometer (grant reference EP/K03930X/1) and financial support from the Dean of Mathematical and Physical Sciences, Prof. Ivan P. Parkin, for its detector upgrade. A.R-F acknowledges funding from the European Research Council (ERC) under the European Union′s Horizon 2020 research and innovation programme (grant agreement no. 725271). We thank Prof. Christoph G. Salzmann for access to his low-temperature DSC calorimeter and Dr Dejan-Krešimir Bučar for freely providing the p-C6F4I2. We thank Martin Vickers for his help in maintaining the Stoe diffractometers in first-class condition and Dr Ronen E. Ghosh for VT-PXRD software support.References
- J. Maddox, Nature, 1988, 335, 201 CrossRef.
- (a) J. P. M. Lommerse, W. D. S. Motherwell, H. L. Ammon, J. D. Dunitz, A. Gavezzotti, D. W. M. Hofmann, F. J. J. Leusen, W. T. M. Mooij, S. L. Price and B. Schweizer, et al. , Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 697–714 CrossRef CAS PubMed; (b) A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell and R. Car, et al. , Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed; (c) L. Hunnisett, J. Cole and G. Sadiq, Acta Crystallogr., Sect. A: Found. Adv., 2022, 78, a136 Search PubMed; (d) L. Hunnisett, J. Nyman, N. Francia, G. Sadiq, I. Sugden, S. Reutzel-Edens and J. Cole, Acta Crystallogr., Sect. A: Found. Adv., 2023, 79, C160 Search PubMed.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- M. J. Webber and R. Langer, Chem. Soc. Rev., 2017, 46, 6600–6620 RSC.
- K. Nakao, Y. Kamakura, M. Fujiwara, T. Shimizu, Y. Yoshida, H. Kitagawa, H. Yoshikawa, Y. Kitagawa and D. Tanaka, Cryst. Growth Des., 2022, 22, 26–31 CrossRef CAS.
- X. Pang, H. Wang, W. Wang and W. J. Jin, Cryst. Growth Des., 2015, 15, 4938–4945 CrossRef CAS.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- C. R. Patrick and G. S. Prosser, Nature, 1960, 187, 1021 CrossRef CAS.
- B. J. J. Timmer and T. J. Mooibroek, J. Chem. Educ., 2021, 98, 540–545 CrossRef CAS PubMed.
- J. H. Williams, Acc. Chem. Res., 1993, 26, 593–598 CrossRef CAS.
- T. Dahl, Acta Chem. Scand., 1994, 48, 95–106 CrossRef CAS.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- J. H. Williams, J. K. Cockcroft and A. N. Fitch, Angew. Chem., Int. Ed. Engl., 1992, 31, 1655–1657 CrossRef.
- J. K. Cockcroft, A. Rosu-Finsen, A. N. Fitch and J. H. Williams, CrystEngComm, 2018, 20, 6677–6682 RSC.
- K. Carter-Fenk and J. M. Herbert, Chem. Sci., 2020, 11, 6758–6765 RSC.
- J. Henrichsmeyer, M. Thelen, M. Bröckel, M. Fadel, S. Behnle, M. Sekkal-Rahal and R. F. Fink, ChemPhysChem, 2023, 24, e202300097 CrossRef CAS PubMed.
- T. Dahl, Acta Chem. Scand., Ser. A, 1988, 42, 1–7 CrossRef.
- J. K. Cockcroft, R. E. Ghosh, J. J. Shephard, A. Singh and J. H. Williams, CrystEngComm, 2017, 19, 1019–1023 RSC.
- J. K. Cockcroft, J. G. Y. Li and J. H. Williams, CrystEngComm, 2019, 21, 5578–5585 RSC.
- S. Tsuzuki, T. Uchimaru and M. Mikami, J. Phys. Chem. A, 2006, 110, 2027–2033 CrossRef CAS PubMed.
- A. P. West, Jr., S. Mecozzi and D. A. Dougherty, J. Phys. Org. Chem., 1997, 10, 347–350 CrossRef.
- A. F. Tillack and B. H. Robinson, J. Phys. Chem. B, 2017, 121, 6184–6188 CrossRef CAS PubMed.
- J. Řezáč, K. E. Riley and Pavel Hobza, J. Chem. Theory Comput., 2012, 8, 4285–4292 CrossRef PubMed.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- J. C. Bear, R. E. Ghosh and J. K. Cockcroft, Cryst. Growth Des., 2024, 24, 3021–3029 CrossRef CAS.
- J. C. Bear, N. Terzoudis and J. K. Cockcroft, IUCrJ, 2023, 10, 720–728 CrossRef CAS PubMed.
- Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, London, 85th edn, 2004-5, ch. 3–74 Search PubMed.
- S. Konar, C. L. Hobday, C. L. Bull, N. P. Funnell, Q. F. Chan, A. Fong, N. Atceken and C. R. Pulham, Cryst. Growth Des., 2022, 22, 3862–3869 CrossRef CAS.
- J. C. Bear, A. Rosu-Finsen and J. K. Cockcroft, CrystEngComm, 2025, 27, 1386–1391 RSC.
- J. C. Bear and J. K. Cockcroft, Chem. – Eur. J., 2024, 30, e202402867 CrossRef CAS PubMed.
- S. d'Agostino, F. Spinelli, P. Taddei, B. Ventura and F. Grepioni, Cryst. Growth Des., 2019, 19, 336–346 CrossRef.
- S. J. Kruse, L. R. MacGillivray and T. Z. Forbes, Cryst. Growth Des., 2023, 23, 3357–3366 CrossRef CAS PubMed.
- H. J. Frohn, S. Görg, G. Henkel and M. Läge, Z. Anorg. Allg. Chem., 1995, 621, 1251–1256 CrossRef CAS.
- M. Bujak, H.-G. Stammler and N. W. Mitzel, Cryst. Growth Des., 2020, 20, 3217–3223 CrossRef CAS.
- S. L. Chaplot, G. J. McIntyre, A. Mierzejewski and G. S. Pawley, Acta Crystallogr., Sect. B, 1981, 37, 2210–2214 CrossRef.
- S. Y. Oh, C. W. Nickels, F. Garcia, W. Jones and T. Friščić, CrystEngComm, 2012, 14, 6110–6114 RSC.
- S. J. Ang, A. M. Mak, M. B. Sullivan and M. W. Wong, Phys. Chem. Chem. Phys., 2018, 20, 8685–8694 RSC.
- J. Vainauskas, et al. , Chem. Sci., 2023, 14, 13031–13041 RSC.
- X. Pang, H. Wang, X. R. Zhao and W. J. Jin, CrystEngComm, 2013, 15, 2722–2730 RSC.
- L. Li, H. Wang, W. Wang and W. J. Jin, CrystEngComm, 2017, 19, 5058–5067 RSC.
- Q. J. Shen, H. Q. Wei, W. S. Zhou, H. L. Sun and W. J. Jin, CrystEngComm, 2012, 14, 1010–1015 RSC.
- Q. J. Shen, X. Pang, X. R. Zhao, H. Y. Gao, H. L. Sun and W. J. Jin, CrystEngComm, 2012, 14, 5027–5034 RSC.
- M. K. Corpinot and D.-K. Bučar, Cryst. Growth Des., 2019, 19, 1426–1453 CrossRef CAS.
- (a) CCDC 2483307: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2pv; (b) CCDC 2483308: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2qw; (c) CCDC 2483309: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2rx; (d) CCDC 2483310: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2sy; (e) CCDC 2483311: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2tz; (f) CCDC 2483312: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2v0; (g) CCDC 2483313: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2w1; (h) CCDC 2483314: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2x2; (i) CCDC 2483315: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2y3; (j) CCDC 2483316: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc2z4; (k) CCDC 2483317: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2pc306.
Footnotes |
| † This paper is dedicated to Prof. Judith A. K. Howard CBE FRS on the occasion of her 80th Birthday. |
| ‡ Deceased. |
| This journal is © The Royal Society of Chemistry 2026 |