 Open Access Article
Open Access ArticleDynamic regulation of nucleic acid replication beyond the Watson–Crick base-pairing rule
Shuntaro
Takahashi
 *ab,
Lutan
Liu
a and
Naoki
Sugimoto
*ab,
Lutan
Liu
a and
Naoki
Sugimoto
 *a
*a
aFIBER (Frontier Institute for Biomolecular Engineering Research), Konan University, 7-1-20 Minatojima-Minamimachi, Chuo-ku, Kobe 650-0047, Japan, shtakaha@konan-u.ac.jp
bFIRST (Graduate School of Frontiers of Innovative Research in Science and Technology), Konan University, 7-1-20 Minatojima-Minamimachi, Chuo-ku, Kobe 650-0047, Japan
First published on 23rd December 2025
Abstract
Nucleic acids form various helical structures through base-pair formation. The most fundamental base pairing is Watson–Crick, which establishes a complementary rule in nucleic acids. According to this rule, living systems can replicate their genes to propagate them correctly to their daughter organisms. The complementary rule can be interpreted in chemistry, as the Watson–Crick base pairing is the most stable. On the other hand, non-Watson–Crick base pairings, termed mismatch base pairings, are also frequently found. Mismatched base pairings formed during gene replication lead to mutations, which can cause evolution of life or diseases such as cancer. Such metastable non-Watson–Crick base pairings are considered to be randomly occurring events, and their underlying chemistry has been neglected. However, the stability of Watson–Crick base pairs can be modulated by the environments, and sometimes non-Watson–Crick base pairs indicate higher stability than Watson–Crick base pairs. Moreover, the formation of non-Watson–Crick base pairs in the template strand creates non-duplex structures that can cause replication errors. Therefore, a quantitative study of non-Watson–Crick base pairing by changing the environments of the solutions can provide novel insights into genetic mutations regulated by chemistry-validated “non-Watson–Crick rules”. In this review, we summarise the basic and recent studies on the chemistry regulating replication by non-Watson–Crick base pairs and state how genetic mutations are chemically controllable. Furthermore, we discuss potential databases for predicting gene mutations under various solution conditions and their integration for future applications.
1. Introduction
All living systems utilise genes composed of nucleic acids. Nucleic acids are macromolecules comprising four nucleotides (A; adenine, G; guanine, C; cytosine, and T; thymine for DNA or U; uracil for RNA) arranged in linear chains, the sequence of which defines the genetic information. The phosphate–sugar moiety of the nucleic acid backbone contributes to the water solubility of nucleic acids, whereas the base moieties interact with each other to change the conformation of the nucleic acids. Nucleobases comprise purines (A and G) and pyrimidines (C and T (U)). These aromatic ring structures contain functional groups that act as hydrogen bond donors and acceptors, and the dispersive forces of π-electrons between the aromatic rings allow nucleobases to interact with one another. The steric structure and structural stability of nucleic acids are determined by structural factors such as hydrogen bonding, stacking interactions between base pairs, and the conformational entropy of the backbone, as well as environmental factors such as cations, hydration, and molecular crowding (Fig. 1(a)).1 Based on these interactions, the representative structure of nucleic acids is primarily the duplex structure. | ||
| Fig. 1 Chemical factors for determining the stability of nucleic acids in (a) the formed duplex and (b) the construction of duplexes. | ||
Watson–Crick base pairings determine the complementarity of the duplex of nucleic acids.2 This is chemically defined as the complementarity and orthogonality of donor and acceptor hydrogen bonds between A and T (U) or G and C bases, forming A·T and G·C base pairs which are considered to be more stable than others. In cells, genes are correctly replicated by the polymerisation of nucleic acid monomers (NTPs and dNTPs) along the template nucleic acid according to Watson–Crick base pairings (Fig. 1(b)).2 The complementarity of the base pairs of the four nucleic acid bases, which is uniquely determined, results in a duplex. Nucleobase sequences can be treated as digital information in living systems because of their duplex. Living systems digitalise and store genetic information by sequencing four types of nucleotides. Consequently, genetic information is stored and replicated with extreme accuracy. Genes must have digital information because genetic information is preserved.
Base-pair mismatches or mutations occur when an incorrect nucleic acid monomer is incorporated during replication. It is indisputable that genetic mutations are the main cause of threats to human health, such as the global pandemic of viral infections as exemplified by the new coronavirus,3 as well as cancer which is one of the leading causes of death worldwide.4 Therefore, elucidating the mechanisms of genetic mutations and developing technologies to predict and control them are important issues with high social demand. Genetic mutations have long been regarded as non-digital (i.e. analogue, containing complex elements, vulnerable to noise, and unsuitable for the maintenance and transmission of information) and occur randomly in the genome. The sites of mutagenesis associated with DNA damage and repair due to radiation and other factors are considered random.5,6 However, recent studies in genome biology have begun to show that the sequence pattern of gene mutations is biased by the intracellular environments influenced by chemicals.7,8 These studies suggest that a chemically metastable state in which genetic mutations are likely to occur may arise depending on both the sequence and surrounding chemical environments. Hoogsteen base pairings, a type of non-Watson–Crick base pairing, are observed in base-pair formations comprising A and U monomers.9,10 This indicates that Hoogsteen base pairings are more stable than Watson–Crick base pairings under monomer-to-monomer conditions. Hoogsteen-type base pairs have been shown to form transiently not only at the monomeric level but also in the duplex structure.11 Furthermore, Hoogsteen base pairings have been shown to cause formation of non-duplex nucleic acid structures, such as triplexes, guanine quadruplexes (G4), or i-motif structures (iM), which regulate gene replication and gene expression.12 Thus, owing to the structural dynamics of their backbone, the digital information in nucleic acids may also encode gene mutations and higher-order gene regulation by behaving in an analogue manner. Therefore, it is desirable to elucidate the influence of chemical factors that form metastable non-Watson–Crick base pairs, rather than genomic mutations that occur randomly during gene replication (Fig. 1).
Based on this background, it is important to analyse quantitatively and understand the effects of non-Watson–Crick-type base-pair formation on gene replication at the energetic level. The structural stability of nucleic acids is influenced by the solution environments, such as crowded intracellular environments. These solution environments affect the hydrogen bonding and stacking interactions of the base pairs and change the energy levels of base-pair formation. In this article, we present quantitative analyses of the solution environment effects on nucleic acid replication reactions. We also outline the new scientific perspectives and medical engineering technologies that can be expected from these studies.
2. Chemistry of the replication reaction
2.1 Polymerase-dependent fidelity of replication
The replication of DNA and RNA involves stepwise interactions between the template, substrate, and enzyme. As shown in Fig. 2(A), there are several intermediate steps during DNA replication, including polymerase binding to DNA (step 1), dNTP incorporation (step 2), formation of the catalytic transient complex before elongation of DNA (step 3), formation of the transient complex after elongation (step 4), formation of an intermediate state of the complex of the polymerase and elongated DNA with pyrophosphate (PPi) (step 5).13 Finally, the release of PPi complete the single turnover of DNA replication. To regulate the replication reactions, the thermodynamic stability of the formation of complexes at each step and the kinetics between each step are targeted (Fig. 2(B) and (C)). One such reaction is the selection of dNTPs for the template sequence. For proper replication, dNTP should be incorporated correctly according to the Watson–Crick rule. Polymerases usually have a higher energy barrier for forming a complex with an incorrect dNTP than with the correct dNTP (step 3 in Fig. 2(B)). However, even when an incorrect dNTP is incorporated, the energetic barrier to the catalytic reaction is still much higher (step 4 in Fig. 2(b)). The difference in the energetic and kinetic barriers of correct and incorrect dNTP incorporation leads to the definition of fidelity (quantified from the error frequency) of the polymerase. Moreover, the other regulatory reaction is dominated by the structure of the template strand, affecting the energetic barrier for the processivity of the polymerases (Fig. 2(C)), which is discussed in Section 4.As shown in the energy diagram, the fidelity of replication depends not only on the dNTPs but also on the enzyme structure. Replicative enzymes include proteinaceous polymerases, such as DNA polymerase (DNAP), RNA polymerase (RNAP; its catalysis is mainly for transcription), and RNA-dependent RNA polymerase (RdRp). Furthermore, RNA polymerases based on RNA enzymes (ribozymes) have been developed.14 The error frequency per nucleotide of one of the original ribozymes, R18, was 4.3 × 10−2 at 17 °C,15 and some improved ribozymes, tC19 and tC19Z, showed 2.7 × 10−2 and 8.8 × 10−3 at 17 °C, respectively.16 For the proteinaceous polymerases, the reported error frequencies vary depending on the polymerase family. Polymerases that play a role in the replication of genomic DNAs include family A (e.g. T7 DNAP), and family B (e.g. T4 DNAP, human Polδ, and Polε) and family C (e.g. E. coli Pol III) without consideration of these proofreading activities show low-error frequencies ranging from 10−4 to 10−6 (e.g. 3.4 × 10−5 for T7 DNAP at 37 °C). Following these classes, DNAPs related to DNA repair reactions showed relatively lower error frequencies (for example, 1.3 × 10−4 for Klenow fragment at 37 °C and 2.1 × 10−4 for Taq polymerases at 70 °C).17 The proteinaceous DNAP show lower error frequencies than ribozymes, which suggests that the evolved proteins have relatively higher enzymatic performance than ribozymes that existed in the prebiotic RNA world. However, some DNAP, such as translesion synthesis (TLS) polymerases (e.g. E. coli Pol IV and V and human Polη, Polκ and so on) that enable bypass of DNA lesions during DNA replication showed the highest error frequencies (10−1–10−3) at 37 °C. Interestingly, SARS-CoV2 RdRp (Nsp12/7/8) has similar high error frequencies (10−1–10−3) at 37 °C,18 which could generate various mutants of the viruses in a short period.
In solutions, the efficiency of incorporation varies depending on the identity of the mismatch.19,20 Besides canonical Watson–Crick base pairs, there are eight single mismatches which occur in DNA with varying frequencies and stabilities, namely A·A, A·C (or C·A), A·G (or G·A), C·C, C·T (or T·C), G·G, G·T (or T·G), and T·T.21 The crystal structure of the complex of DNAP and substrate DNA with mismatch dNTP were solved and found that A·G, C·T, G·G, G·T, T·G and T·T (the former letter in the pair means a base at the primer end and the latter comes from the template) are placed at the post-insertion site and are well ordered.22 These structural data suggest that certain mismatched base pairs can adopt thermodynamically stable conformations. From the perspective of thermodynamics, the differences in free energy between mismatched and matched base pairs in aqueous solutions (ΔΔG° = ΔG°(mismatch) − ΔG°(match)) can be quantitatively understood as the contribution of hydrogen bonding between mismatched base pairs. The calculation approach using the nearest-neighbour (NN) parameters explains that the 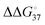 ranges less than approximately 3 kcal mol−1 at 37 °C.23 For example, the GC-rich base pairs shows relatively large deviation (
ranges less than approximately 3 kcal mol−1 at 37 °C.23 For example, the GC-rich base pairs shows relatively large deviation (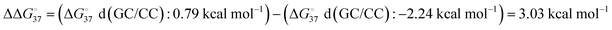 ), whereas the G·T wobble shows relatively small difference (
), whereas the G·T wobble shows relatively small difference (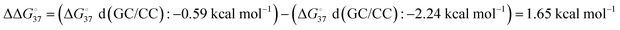 ).23 The measurements of the
).23 The measurements of the 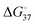 of the primer–template DNA strand reproducing the DNA structure during replication was also reported, in which
of the primer–template DNA strand reproducing the DNA structure during replication was also reported, in which 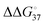 between strands containing a terminal mismatch and a matched terminus (ΔG°(mismatch) − ΔG°(match)) was less than 0.4 kcal mol−1 in the cases of the DNAs containing either correct (A·T) or incorrect (G·T, C·T or T·T) base pairs at the primer 3′ terminus.24 The
between strands containing a terminal mismatch and a matched terminus (ΔG°(mismatch) − ΔG°(match)) was less than 0.4 kcal mol−1 in the cases of the DNAs containing either correct (A·T) or incorrect (G·T, C·T or T·T) base pairs at the primer 3′ terminus.24 The 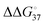 of less than 3 kcal mol−1 can account for one incorrect insertion for about 10 to a few hundred correct insertions, according to the assumption of the error frequency (f = e−ΔΔG°/RT; where f is the error frequency, T is temperature and R is the universal gas constant. The f value is 7.7 × 10−3 when
of less than 3 kcal mol−1 can account for one incorrect insertion for about 10 to a few hundred correct insertions, according to the assumption of the error frequency (f = e−ΔΔG°/RT; where f is the error frequency, T is temperature and R is the universal gas constant. The f value is 7.7 × 10−3 when 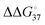 equals 3.).25 This error frequency corresponds well to polymerases with high error frequencies of 10−1–10−3. Thus, polymerases with high error frequencies, such as TLS polymerases and SARS-CoV2 RdRp, depend on the stability of matched or mismatched base pairs during replication. However, polymerases of the low-error frequency type should have additional and different mechanisms to incorporate (d)NTPs correctly, because the error frequency is within the range of 10−3–10−6 corresponding to 4–8 kcal mol−1 of ΔΔG° value.26 The
equals 3.).25 This error frequency corresponds well to polymerases with high error frequencies of 10−1–10−3. Thus, polymerases with high error frequencies, such as TLS polymerases and SARS-CoV2 RdRp, depend on the stability of matched or mismatched base pairs during replication. However, polymerases of the low-error frequency type should have additional and different mechanisms to incorporate (d)NTPs correctly, because the error frequency is within the range of 10−3–10−6 corresponding to 4–8 kcal mol−1 of ΔΔG° value.26 The 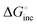 calculated from the equilibrium constant (Ka) of matched dNTP incorporation that form the state of Pol*·DNA+1·PPi in step 4 (Fig. 2(B)) at 37 °C shows a large negative value compared to those of mismatched dNTP incorporation (
calculated from the equilibrium constant (Ka) of matched dNTP incorporation that form the state of Pol*·DNA+1·PPi in step 4 (Fig. 2(B)) at 37 °C shows a large negative value compared to those of mismatched dNTP incorporation (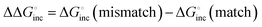 ranged 5.5–7 kcal mol−1).26 Thus, besides the ΔΔG° value predicted and measured from the ΔG° between matched and mismatched base pairing, the environment in the polymerase active site should be considered as an additional source of ΔΔG° value for the low-error polymerisation.
ranged 5.5–7 kcal mol−1).26 Thus, besides the ΔΔG° value predicted and measured from the ΔG° between matched and mismatched base pairing, the environment in the polymerase active site should be considered as an additional source of ΔΔG° value for the low-error polymerisation.
As shown in Fig. 1, the stability of base pairings is affected by the environmental factors. One potential explanation for the energetic source of low-error polymerases is the importance of water exclusion from the active site and geometric selection of the (d)NTPs caused by better fitting of the incorporated (d)NTPs and primer base and/or enzyme residue.27–29 Given that the stabilising hydrogen bonds formed with the solvent are included in the calculations, the interactions from hydrogen bonding and base stacking in DNA or RNA can generate enough ΔΔG° to explain the low-error rate of the polymerase reaction. One report indicated that the non-linear analysis of the enthalpy–entropy compensation for NN parameters of DNA duplexes provides information about the solvent effect on the thermodynamic parameters.30 As shown in Fig. 3(a), the relationship between the enthalpy and entropy changes of the NN base pairs (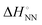 and
and 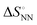 ), including matched and mismatched ones, was non-linear and hyperbolic. This phenomenon implies the inclusion of solvent organisation, as observed in a report on the influence of water as a solvent in protein interactions.31 Thus,
), including matched and mismatched ones, was non-linear and hyperbolic. This phenomenon implies the inclusion of solvent organisation, as observed in a report on the influence of water as a solvent in protein interactions.31 Thus, 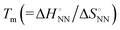 does not change simply with the ΔH° value. To account for the effect of solvent surrounding the base pair on the thermodynamic parameters, the relationship between
does not change simply with the ΔH° value. To account for the effect of solvent surrounding the base pair on the thermodynamic parameters, the relationship between 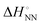 and
and 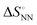 was analysed based on a hyperbolic function by introducing the solvation-dependent constant T0 as a component of Tm,
was analysed based on a hyperbolic function by introducing the solvation-dependent constant T0 as a component of Tm, 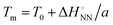 , where a is an entropy constant. According to this relationship,
, where a is an entropy constant. According to this relationship, 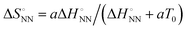 was obtained, which reproduced a better trend between
was obtained, which reproduced a better trend between 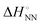 and
and 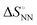 than that obtained by the linear progression (Fig. 3(a)). Using the database of matched NN parameters obtained in 1 M NaCl solution, the values of constants a = 80 kcal mol−1 K−1 and T0 = 273 K−1 were obtained.30 From these treatments, the parameters including solvent environments (noted as NN + e) around the base pair
than that obtained by the linear progression (Fig. 3(a)). Using the database of matched NN parameters obtained in 1 M NaCl solution, the values of constants a = 80 kcal mol−1 K−1 and T0 = 273 K−1 were obtained.30 From these treatments, the parameters including solvent environments (noted as NN + e) around the base pair 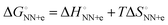 can be calculated from the relationship
can be calculated from the relationship 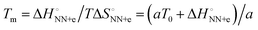 . For example,
. For example, 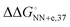 of
of 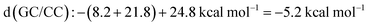 corresponds well to ΔGinc at 37 °C.28 Furthermore,
corresponds well to ΔGinc at 37 °C.28 Furthermore, 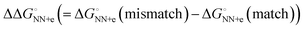 can be calculated to be equal to
can be calculated to be equal to 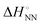 . The average
. The average 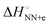 (match) was −8.33 kcal mol−1, whereas
(match) was −8.33 kcal mol−1, whereas 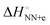 (mismatch) was −0.31 kcal mol−1. Although the parameters were estimated using the data of 1 M NaCl solution, which is far from the physiological solution condition, the magnitude of
(mismatch) was −0.31 kcal mol−1. Although the parameters were estimated using the data of 1 M NaCl solution, which is far from the physiological solution condition, the magnitude of 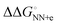 can account for the high fidelity of low-error polymerases. The relevance of the ΔΔG° values (obtained from NN-based thermodynamics added with solvent factor) to the
can account for the high fidelity of low-error polymerases. The relevance of the ΔΔG° values (obtained from NN-based thermodynamics added with solvent factor) to the 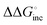 values (derived from polymerase kinetics) originates from the retention of hydrogen bonding and stacking primer–template interactions within the DNAP active site. Through induced-fit mechanisms, the active site enforces geometric selection by properly orienting the cognate (d)NTP and minimizing the entropic penalties arising from conformational and chemical transitions. In this way, the enzymes take full advantage of the different ΔH° values associated with the installation of matches and mismatches. Therefore, the fidelity of polymerases can be rationalised in terms of the thermodynamics of base-pair formation, wherein the polymerase active site modulates the energetics of hydrogen bonding, base stacking, and conformational entropy through finely tuned (de)hydration, preferentially stabilising the correctly paired bases according to the ΔG° of duplex formation (Fig. 3(b)).
values (derived from polymerase kinetics) originates from the retention of hydrogen bonding and stacking primer–template interactions within the DNAP active site. Through induced-fit mechanisms, the active site enforces geometric selection by properly orienting the cognate (d)NTP and minimizing the entropic penalties arising from conformational and chemical transitions. In this way, the enzymes take full advantage of the different ΔH° values associated with the installation of matches and mismatches. Therefore, the fidelity of polymerases can be rationalised in terms of the thermodynamics of base-pair formation, wherein the polymerase active site modulates the energetics of hydrogen bonding, base stacking, and conformational entropy through finely tuned (de)hydration, preferentially stabilising the correctly paired bases according to the ΔG° of duplex formation (Fig. 3(b)).
 | ||
Fig. 3 Energetic contribution of base pairing in the polymerase active site to the fidelity of the polymerase reaction. (a) Relationship between 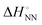 and and 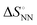 . The blue dotted line indicates the linear regression from the matched parameters.23 The pink line shows the fitting curve for the matched parameters by . The blue dotted line indicates the linear regression from the matched parameters.23 The pink line shows the fitting curve for the matched parameters by 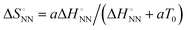 .30 (b) Schematic illustration of base pairing in the enzyme active centre. .30 (b) Schematic illustration of base pairing in the enzyme active centre. | ||
2.2 Accessibility of various substrates depending on the fidelity control
Because mismatched (d)NTPs can be incorporated during replication, various chemically modified (d)NTPs can be used as replication substrates. The modified (d)NTPs have different structures and chemical properties from the four natural nucleotides, which can perturb base pairing during replication and result in a high error efficiency. For example, the naturally modified substrates such as oxidised dGTP (8-oxo dGTP) and dATP (2-OH dATP) can exist in cells.32 These oxidised substrates cause genetic mutations that leads to cancerisation and apoptosis of the cells.33 8-oxo-dG and 2-OH-dA can form Watson–Crick base pairing with dC and dT, respectively, adopting anti-conformation of the deoxyribose.34–36 However, these oxidised nucleotides also adopt syn-conformation and form non-Watson–Crick base pairings with dA and dC.34–37 DNAPs sometimes incorporate the non-Watson–Crick base pairings in syn-conformation, resulting in replication errors (Fig. 4(a)).From the perspective of synthetic biology, the genetic alphabet has been expanded to develop orthogonal unnatural base pairs (UBPs) (Fig. 4(b)). One scheme to design UBPs is making de novo hydrogen bonding like Watson–Crick base pairings, reported firstly with iso-G·iso-C called S·B base pair.38,39 The other approach for UBPs is to utilise a hydrophobic interface without using hydrogen bonding-based base pairs.40–43 The first generation of UBPs based on this concept was Z·F (Z, 4-methylbenzimidazole; F, difluorotoluene), Q·F (Q, 9-methylimidazo[(4,5)-b]pyridine), 7AI·7AI (7-azaindole nucleosides) and Q·Pa (Pa, pyrrole-2-carbaldehyde). All (d)NTPs of the UBPs were efficiently incorporated into DNA and RNA polymerases, similar to the natural substrates. However, early reports revealed several limitations in the first-generation designs, including low nucleotide incorporation efficiency, poor extension kinetics and mispairing with natural bases.40,42,43 To address these issues, the second generation of UBPs such as Z·P (Z, 6-amino-3-(1′-β-D-2′-deoxy ribofuranosyl)-5-nitro-(1H)-pyridin-2-one; P, 2-amino-8-(1′-β-D-2′-deoxyribofuranosyl)-imidazo-[1,2a]-1,3,5-triazin-(8H)-4-one),44 TPT3·NaM,45 5SICS·NaM46 and Ds·Px47 have been developed to enhance catalytic efficiency and fidelity. Z·P base pairs are more thermodynamically stable than G·C base pairs, which enhances the selectivity of these base pairs.44,48 This technique has now been expanded to eight letters (Hachimoji) with S·B and Z·P base pairs.48 Other second-generation UBPs, such as TPT3·NAM and Ds·Px, achieved high selectivity using natural DNAPs (99.98% selectivity per doubling by polymerase chain reaction (PCR) using OneTaq DNAP and 99.97% selectivity per doubling by PCR using Deep Vent DNA polymerase, respectively).49,50 Similar structures have also been observed for four hydrogen bonding UBPs51,52 and other hydrophobic base pairs.53–55 Furthermore, 5-substituted pyrimidine or 7-substituted 7-deazapurine dNTPs are good substrates for DNAPs and can be used for enzymatic synthesis of base-modified DNA.56 DNA and RNA polymerases usually allow large and bulky structures to be modified on (d)NTPs for incorporation. Recent advances have enabled the incorporation of all four (d)NTPs modified with a fluorescent moiety to produce site-specific or fully modified DNA and RNA strands.57,58 Interestingly, these modified substrates are incorporated with higher fidelity than natural substrates. These studies indicate that the catalysis and fidelity of the polymerase can be regulated by the geometry of base pairing and the structure of the (d)NTPs.
Modification of the backbone of (d)NTPs is also a fascinating approach for developing novel nucleic acid systems, termed xeno-nucleic acids (XNAs), to create new nucleic acid drug modalities (Fig. 4(c)). Native DNAP and RNAP can catalyse reactions with modified substrates. For example, commercially available Therminator DNA polymerase can polymerise TNA synthesis on DNA template.59,60 However, numerous cases face difficulties because of low affinity or steric hindrance with the enzymes. Various polymerase mutants have been developed by directed evolution to incorporate efficiently XNA substrates for replication and transcription. Engineering polymerases by rational mutation on specificity determining residues improved the efficacy of TNA synthesis.61 Engineered Tgo polymerases can incorporate RNA,62 FANA,63 HNA63 and TNA.64 More recently, LNA synthesis and 2′-OMe RNA synthesis were demonstrated.65 Although the incorporation of XNA has succeeded, the error frequency of replication is on the order of 10−2–10−3,66 which is higher than that for native substrates. These findings indicate that replication fidelity does not require significant hydrogen bonding but is dominated by other factors. Crystallographic analysis suggests an imperfection in the geometry of the active site of XNA polymerase with its substrate.67 Therefore, the polymerase can accept relatively broad substrates. However, the efficiency of the polymerase reaction can affect the fidelity in the opposite direction because of the regulation of structural factors of nucleic acid stability (Fig. 1(a)). Moreover, environmental factors also affect significantly replication fidelity, as described in Section 3.
3. Environmental effects on replication fidelity
3.1 Induction of replication error by the environment of a polymerase active centre
Chemical perturbation of (d)NTP incorporation during replication can induce mismatch polymerisation. As a tool for the error-prone PCR, the addition of Mn2+ affects effectively the fidelity of the replication.68 There is a significant increase in the frequency with which the polymerase incorporates incorrect nucleotide, whereas the rate of incorporation of the correct nucleotide shows little change.69 Therefore, it has been suggested that the Mn2+ stabilises the transition state (in step 3 in Fig. 2(b)) and promotes incorrect incorporation of substrate.70 Moreover, the addition of chemicals such as urea and alcohol affects the protein structure, resulting in the decrease of fidelity differently from the addition of Mn2+.71A growing body of evidence indicates that Mn2+ can positively influence some DNAPs by conferring translesion synthesis activity or altering substrate specificity. For example, Polβ, which acts as a repair enzyme of abasic sites through the base excision repair (BER) process,72 has efficient polymerase activity in both Mg2+ and Mn2+ as cofactors.73 For the cisplatin-lesioned template DNA, Mn2+ promoted an eightfold enhancement in the correct lesion bypass activity of Polβ, which is achieved through a fourfold decrease in the Michaelis–Menten constant (Km), reflecting greater substrate affinity, and a twofold increase in the catalytic rate constant (kcat).74 Similar correct lesion bypasses have been observed in the cases of the template DNA containing oxidised lesions such as methylated guanine and thymine glycol.75,76 Despite the modest enhancement observed in most cases, its effect can be significant, as lesion bypass catalysed by Polβ is intrinsically inefficient in the presence of Mg2+. These findings suggest a close relationship between efficiency and fidelity, which can be regulated by the chemistry of the DNAP's active site. Another type of chemical that affects the polymerase reaction is a denaturant of DNA structures, such as dimethyl sulfoxide (DMSO) and urea. These chemicals are widely used for efficient PCR yields from GC-rich sequences.77 Although there is no direct evidence, the attenuation of the polymerase progression caused by the secondary structure may affect indirectly the fidelity; thus, these denaturants can control the replication fidelity of highly structured templates (for example, see Section 4 about the effect of quadruplex structures on replication).
The geometric perturbation of the relationship between the primer–template structure and the active site of the polymerase affects fidelity directly. The mutation of the Klenow fragment DNAP (KF) was investigated, and various mutations around the exposed surface of the polymerase cleft near the polymerase active site, which are highly conserved residues, increased drastically the error frequency.78 The engineering of the template has also been studied by introducing variably sized atoms (H, F, Cl, Br, and I) to replace the oxygen molecules of thymine.79 Interestingly, the maximum fidelity and efficiency were found at a base pair size significantly larger than the natural size, both in vitro and in cells. Thus, a tight steric fit between the substrate and polymerase active site is favourable for high fidelity. Similar engineering of the RNA polymerase reaction was studied using hydrogen bond-deficient nucleoside analogues in the template DNA.80 This study showed that the replication fidelity depended strongly on the discrimination of an incorrect pattern of hydrogen bonds, although the efficiency did not depend on hydrogen bonding. Remarkably, the deficiency in U–T wobble hydrogen bonding increased the error frequency by ∼1000-fold. Thus, hydrogen bonding, stacking, and steric compatibility maintain fidelity highly delicately.
Although chemical perturbations can be effective, they are rarely observed in biological systems. Therefore, the biological significance of cellular metabolism remains unclear. However, if replication fidelity–related perturbations are induced by an endogenous cellular component, they may be closely associated with mismatched replication events in cells. One potential trigger is molecular crowding, an environmental factor that alters the physicochemical properties of the intracellular environments and indirectly affects the stability of biomolecules, particularly nucleic acids.
3.2 Stability change of base pairings by molecular crowding
Unlike test tube conditions, intracellular conditions are heterogeneous and highly crowded because of the presence of various (macro)molecules, including 50–400 g L−1 biopolymers and biomolecules.81 This condition, known as molecular crowding, drastically affects the conformation and stability of biomolecules, including nucleic acids.82 To analyse quantitatively the stability of nucleic acid structures under crowding conditions, large amounts of co-solutes, such as poly(ethylene glycol)s (PEGs), have been used to mimic intracellular conditions.82 The biophysical effects of molecular crowding are mostly based on the excluded volume effect, which also lowers water activity and the dielectric constant. Therefore, the behaviour of nucleic acid structures depending on these biophysical factors should be influenced under molecular crowding conditions.83,84 Nucleic acids are inert to small-size PEGs and only slightly interact with large-size PEGs, indicating that PEGs do not impact directly the stability of nucleic acids.85 Interestingly, duplexes comprising Watson–Crick base pairs are destabilised, whereas triplexes and quadruplexes comprising Hoogsteen base pairs are stabilised under crowding conditions with PEGs.86,87 These stability changes are induced effectively by low-molecular-weight PEGs, such as PEG200, under solution conditions where highly concentrated co-solutes alter the physicochemical properties of the environments dynamically. DNA and RNA duplexes have been reported to be destabilised under intracellular conditions.88,89 Moreover, the thermodynamic stability of macromolecules and enzymatic processes are influenced by their molecular environments.70 The physicochemical changes caused by molecular crowding affect the folding and enzymatic activity of RNA, DNA, and proteins.90–96 Thus, the effect of molecular crowding on replication fidelity and activity is of interest.3.3 Fidelity control of replication by molecular crowding
Several model systems have been employed to study the effects of molecular crowding on replication. We used three types of polymerases: a ribozyme called tC9Y,97 which catalyses RNA polymerisation; a proteinaceous T7 RNA polymerase (T7 RNAP), which also catalyses RNA polymerisation; and a proteinaceous DNAP (KF), which catalyses DNA polymerisation. These three polymerases catalyse nucleotide polymerisation through similar Mg2+-mediated mechanisms. In the first step of polymerisation, each enzyme binds a nucleotide to an oligonucleotide primer paired with an RNA template.97–99Thus, tC9Y, which can polymerise NTP and dNTP, was activated by PEG200 during both NTP and dNTP polymerisation (Fig. 5(a)).100 However, T7 RNAP lost its NTP polymerisation activity with increasing PEG200 and simultaneously polymerised dNTPs (Fig. 5(b)). For KF, PEG200 only promoted dNTP polymerisation (Fig. 5(c)). The effect of PEGs on the fidelity of each polymerase was investigated using single-primer extension. In the presence of 20 wt% PEG200, tC9Y was more efficient at adding both matched and mismatched NTPs and certain dNTPs to RNA primer G than in the absence of PEG200 (Fig. 5(d)). Enhanced electrostatic interactions between the 2′-OH and the substrate-binding site in the presence of 20 wt% PEG200 resulted in the polymerisation of mismatched NTPs. The polymerisation of dGTP likely occurred because of the thermodynamic stability of the G·A mismatch.101 For T7 RNAP, the polymerisation of template-complementary UTP was observed at higher levels in the absence of 20 wt% PEG200 than in its presence, and mismatched NTPs were also polymerised at higher levels in 20 wt% PEG200 (Fig. 5(e)). Polymerisation of template-complementary dTTP was facilitated by 20 wt% PEG200, whereas polymerisation of mismatched dNTPs did not change significantly. Therefore, molecular crowding enhanced the accuracy of T7 RNAP DNA polymerisation. With KF, the presence of 20 wt% PEG200 increased the percentage of extended primers; however, incorrect dATP, dGTP, and UTP were also polymerised, indicating lower fidelity (Fig. 5(f)). When mismatched NTPs are incorporated, primer extension by T7 RNAP along the RNA template accelerates further misincorporation.102 These results indicate that molecular crowding can affect the hydrogen bonding and stacking of dNTPs and NTPs with the template and primers, resulting in increased activity and decreased fidelity.
 | ||
| Fig. 5 RNA and DNA polymerisation in 0–20 wt% PEG200 by different polymerases. (a)–(c) Percentage of primers extended by (a) tC9Y, (b) T7 RNAP and (c) KF using denaturing PAGE. (f) Percentage of primers extended by KF. In the graphs, the percentage of primers extended in reactions with NTPs is indicated in green, and the percentage extension in reactions with dNTPs is indicated in blue. (d)–(f) Efficiency of polymerisation of a single nucleotide by (d) tC9Y, (e) T7 RNAP and (f) KF without PEG (white) or with 20 wt% PEG200 (black) for 12 h. The original data has been published previously.100 Reproduced from ref. 100 with permission from American Chemical Society, copyright (2019). | ||
3.4 Quantitative analysis of the activity and fidelity of polymerases upon molecular crowding
Quantitative analysis based on physicochemical approaches is useful for understanding the effect of molecular crowding on polymerase activity and its fidelity. Thus, we further tested primer extension along a DNA template by T7 RNAP.103 Regardless of the matching of the 3′ terminus of the primer with the template DNA, primer extension by NTP incorporation occurred. The fidelity of polymerisation using mismatched primers was higher than that using matched primers. Furthermore, under crowding conditions with PEG2000, ATP and GTP were favoured as substrates, lowering the fidelity of polymerisation. These results suggest that crowding conditions induce substrate selection via stacking interactions over Watson–Crick base pairings owing to a decrease in the dielectric constant of the solutions. This study indicates that the balance between hydrogen bonding and stacking interactions in the nascent base pair is crucial for the fidelity of replication, which can be regulated by chemical perturbations, such as molecular crowding.Based on these findings, a quantitative analysis of the incorporation of dNTP along non-natural DNA templates was performed using a template containing different unnatural bases (inosine: Ino, 5-methyl-isocytosine: isoCMe, and isoguanine: isoG) and different sugars (deoxyribonucleic acids: DNA, hexitol nucleic acids: HNA, and arabinose nucleic acids: ANA) (Fig. 6(a)).104 Although dNTPs were non-cognate substrates against the unnatural nucleobases on the template, KF preferred to polymerise a certain dNTP. The efficiency of replication and fidelity were negatively correlated, which differed in the presence of PEG200 (Fig. 6(b)). The polymerisation trend indicated the high efficiency of the incorporation of preferred pyrimidine dNTPs with low fidelity (high error) but the low efficiency of the incorporation of preferred purine dNTPs with high fidelity (low error). However, in the presence of 20 wt% PEG 200, the efficiency of incorporation of the preferred pyrimidine dNTPs decreased, whereas that of the preferred purine dNTPs increased, resulting in similar efficiencies despite the chemical structure of the templates. These findings indicate that the preferred pyrimidine dNTPs depend on hydrogen bond formation, which is destabilised by molecular crowding due to decreased water activity. However, molecular crowding facilitates the incorporation of preferred purine dNTPs through base-stacking interactions. More importantly, molecular crowding can affect hydrogen bonding and base-stacking interactions in the base pairs of the incorporated natural dNTPs and the nucleobase of the unnatural template, which occurs in the active centre of the reacting DNAPs. These studies indicate that the fidelity of polymerase reactions, which is maintained by the chemistry of base pairing in the active site of the polymerase (Fig. 4), can be regulated by the environments of the solution. The solution environments can influence dynamically the global structures of DNA and RNA, affecting the processivity of polymerases and the fidelity and efficiency of polymerisation. Therefore, in the next section, we discuss the effect of the template strand on polymerase reactions.
 | ||
| Fig. 6 Effect of molecular crowding on efficiency and preference of replication along XNA templates.104 (a) Setup of the structures of XNA template for the primer extension assay. (b) Plots of the efficiency versus preference of the primer extension by KF in the absence (blue plots) and presence (red plots) of PEG 200. | ||
4. Control of the replication along the template DNA strand stability and conformation
Polymerases recognise the template strands and form complexes. The processive reaction alters dynamically the conformation of the complex depending on the sequence and structure of the template. Therefore, the stability of the polymerase complex and template strand, depending on the conformation, can affect indirectly the incorporation of the substrate (d)NTPs, which decreases the efficiency of polymerisation and can affect fidelity. The stability of the complexes depends on the environments of the solution. Molecular crowding is one factor that affect the conformation of biomolecules, including polymerases and nucleic acids.82,105,106 For nucleic acids (see Fig. 1 and Section 3.2), molecular crowding affects the stability of the template strands. The magnitude of stabilisation differs between the secondary and tertiary structures of nucleic acids, which can affect the binding and processivity of the polymerase on the template strand, as well as the complex formation of the polymerase-template structure. In this section, we focus on the formation of polymerase–DNA complexes affected by the solution environments through the stability and conformation of DNA structures. Here, we summarise a quantitative study using a primer extension assay with DNAP. From a chemical viewpoint, we also discuss the potential of chemically regulating polymerase reactions using small compounds to regulate environment-controlled replication.4.1 Replication control by regulating the stability of the polymerase–DNA complex
As shown in Fig. 2(c), the processivity of the polymerase can be affected by regulating the energetic state at each step (Fig. 2(a)) of the reaction. Therefore, solution environments that affect the interaction between the polymerase and template strand tune the polymerase reaction at each step. For example, electrostatic interactions drive the binding of polymerases to negatively charged nucleic acid templates. Thus, a high concentration of cations destabilises the complex formation of polymerases on the template DNA and reduces the yield of polymerised products.107 Under physiological conditions, the K+ concentration is over 140 mM, with coexistence of other cations including Na+ and Mg2+. Molecular crowding promotes the incorporation of dNTP by DNAPs even in the presence of such high concentrations of cations.108 Thus, molecular crowding can assist polymerases in binding and proceeding of the reaction in cells and accelerate the catalytic activity. Interestingly, larger PEGs or large dextran co-solutes promoted dNTP incorporation at high salt concentrations.108 Small-angle X-ray scattering also revealed that molecular crowding with relatively large PEGs made the replication machinery compact.109 A similar finding was reported that transcription by RNA polymerase was accelerated in a specific phase of the transcription step, such as the late initiation and promoter clearance, indicating the conformational change toward smaller volume during the reaction of the DNA–polymerase complex.110 Therefore, such co-solutes promoted DNAP binding to the DNA template due to the excluded volume effect, thus enhancing the opportunity to incorporate dNTPs.4.2 Replication control by the DNA template structure
As shown in Sections 2.2 and 3.4, DNAPs can replicate DNA templates containing chemically modified nucleobases, such as methylation and oxidation. The fidelity and efficiency of the reaction also depend on the combination of dNTP and the modified template base. In contrast, the secondary structure of the DNA template controls significantly the processivity of the polymerase and regulates the reaction (Fig. 7). The most well-studied case of this regulation process is triplet repeat expansion and deletion.111 Triplet repeats, such as (CAG/CTG)n and (CGG/CCG)n, can form an intramolecular hairpin-like structure within a single strand (Fig. 7(a)). The transition of the hairpin structure during replication on the nascent chain shifts the position of DNA priming, resulting in an increase in the length of the primer strand, whereas the formation of the hairpin structure on the template DNA causes a decrease in the length of the nascent chain. Finally, the expanded repeat is transcribed and translated into the abnormal extension of peptide sequences, which causes neurodegenerative diseases, including Fragile X syndrome and myotonic dystrophy.112More recently, the G-quadruplex (G4) and i-motif (iM) have been identified as regulators of gene replication and expression.113 G4 is a tetraplex structure composed of a repeat of guanines assembled via Hoogsteen base pairs, whereas iM is formed by two intercalated parallel hairpin structures from the hemi-protonated C–C base pair. The potential forming sequences of these structures are briefly denoted as (GnXm)4 or (CnXm)4 (X: any base, n ≥ 2, and m ≥ 1). As these sequences are frequently found in the genome and are relatively rich in the promoter region of genes, their roles in cells may be more general than those of triplet repeats. The most interesting aspect of G4 and iM is the stabilisation mechanism of these structures. G4s have specific sites between the G-quartets for the binding of Na+ and K+ to stabilise the structure.114 iMs require the protonation of cytosine and thus prefer acidic conditions to form.115 Moreover, molecular crowding facilitates the formation of G4s and iMs due to the water exclusion and compaction effect of the cosolute.82,83 Hence, these structures are highly environment-dependent in solution (see our previous reviews82,83). Therefore, G4s and iMs form depending on the cellular environments and regulate dynamically gene manipulation in cells via environmental factors affecting nucleic acid stability (Fig. 1(a)).
Regarding the effects of G4 and iM on replication, these structures on the template strand prevented DNAPs from undergoing a smooth processive reaction (Fig. 7(b)). This replication stall can cause double-strand breaks (DSB) during replication (Fig. 7(c)). DSBs formed at stalled forks are typically repaired by homologous recombination (HR) or, occasionally, break-induced replication (BIR). However, failure of the repair process causes mutations and/or lesions in genomic information and results in genomic instability.116 Replication stall is directly related to the frequency of formation and resolution of the G4/iM structure. Therefore, thermodynamic stability (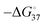 ) should be one of the dominant parameters for the fidelity of replication along the G4/iM forming template.117 The stability of these structures can be tuned using ligands that specifically bind to G4/iMs. To stabilise G4 structures in human cells, various G4 binders have been tested. As expected, G4 stabilising ligand further inhibits the processivity of the polymerase, which promotes genomic instability.118 Therefore, the efficiency of genomic instability can be described by the
) should be one of the dominant parameters for the fidelity of replication along the G4/iM forming template.117 The stability of these structures can be tuned using ligands that specifically bind to G4/iMs. To stabilise G4 structures in human cells, various G4 binders have been tested. As expected, G4 stabilising ligand further inhibits the processivity of the polymerase, which promotes genomic instability.118 Therefore, the efficiency of genomic instability can be described by the 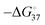 of the G4/iM. However, some relatively unstable G4s containing only two G-quartets on the leading strand also caused genomic instability, suggesting that there is another factor that determines genomic instability by G4, independent of its thermal stability.118 To investigate the mechanism of replication stall by G4/iM, a quantitative analysis of the replication stall is required.
of the G4/iM. However, some relatively unstable G4s containing only two G-quartets on the leading strand also caused genomic instability, suggesting that there is another factor that determines genomic instability by G4, independent of its thermal stability.118 To investigate the mechanism of replication stall by G4/iM, a quantitative analysis of the replication stall is required.
4.3 Quantitative study for the regulation of replication by template DNA structures
One method to investigate quantitatively the effect of the stability of G4/iM on biological reactions is the polymerase stop assay.119,120 In this assay, the template DNA contains a target G4/iM sequence. DNAP (e.g. Taq and KF) extends the primer strand and stalls when the polymerase meets the G4/iM. After resolving the structure, the polymerase proceeds with the reaction, replicating the full-template DNA. The stalling of the polymerase can be easily monitored by electrophoresis as a measure of the band intensity. As replication stalls depend highly on the stability of G4/iM, the trend of replication stall can be a measurable index of the biological role of G4/iM. The most common application of this polymerase stop assay is to study the stabilising effects of ligands on G4/iM formation. As the G4/iM stabilised by a ligand stalls the polymerase more efficiently than that without ligands, the degree of polymerase stalling can be evaluated as a property of the ligand in cells. For example, a series of modifications of G4 ligands was investigated using the polymerase stop assay, and the stalling strength was ranked based on the band intensity, which corresponded to the dissociation constant of the ligand from the target DNA.121 The polymerase stop assay using G4 ligands was also applied for genome-wide identification of G4 DNA.122 This technique uses the addition of the G4-binding ligands pyridostatin or K+ to stabilise the structure of G4 and stop the polymerase progression at the G4 DNA position during sequencing using next-generation sequencing (NGS). A polymerase stop assay identified approximately 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 G4 DNA sites in human B lymphocytes. Further analyses were subsequently conducted in several species, and the formation of G4 DNA was confirmed in all 12 species analysed.123 This approach is powerful for identifying G4 formation in the genome with a stability dependency of the structures. Conventional PCR has also been used to evaluate the frequency of G4 formation from the delay in DNA amplification by G4 formation.124 Recently, a high-throughput primer extension assay was developed to quantitatively measure how DNAPs stall at over 20
000 G4 DNA sites in human B lymphocytes. Further analyses were subsequently conducted in several species, and the formation of G4 DNA was confirmed in all 12 species analysed.123 This approach is powerful for identifying G4 formation in the genome with a stability dependency of the structures. Conventional PCR has also been used to evaluate the frequency of G4 formation from the delay in DNA amplification by G4 formation.124 Recently, a high-throughput primer extension assay was developed to quantitatively measure how DNAPs stall at over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 short tandem repeat (STR) sequences.125 In this study, without relying on prior secondary structure predictions, structured DNA motifs, such as G4s and hairpins, caused distinct replication-stalling patterns. Persistent stalling correlates with reduced STR expansion, suggesting that polymerase stalling in structured DNA serves as a natural constraint on repeat expansion, which is related to genomic stability and repeat expansion diseases. As shown in these studies, the polymerase stop assay is a useful technique for evaluating the formation of G4 and is related to the biological response from a thermodynamic point of view.
000 short tandem repeat (STR) sequences.125 In this study, without relying on prior secondary structure predictions, structured DNA motifs, such as G4s and hairpins, caused distinct replication-stalling patterns. Persistent stalling correlates with reduced STR expansion, suggesting that polymerase stalling in structured DNA serves as a natural constraint on repeat expansion, which is related to genomic stability and repeat expansion diseases. As shown in these studies, the polymerase stop assay is a useful technique for evaluating the formation of G4 and is related to the biological response from a thermodynamic point of view.
A more quantitative study using the polymerase stop assay could elucidate the mechanism of gene regulation by G4/iM formation using physicochemical approaches. To study replication stalls, we quantitatively investigated how G4/iMs affect the replication efficiency of DNA strands with different sequences showing topological differences, including anti-parallel G4, hybrid G4, parallel G4, iM, and hairpin.126 The iM derived from the Hif1a gene, a cancer-related gene, is stably formed with a stability (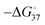 ) of 3.1 kcal mol−1 at pH 6.0. The replication rate constant required to overcome the stall and complete the reaction (ks) was 0.39 min−1 at 37 °C. In contrast, the G4 from human telomeres showed similar stability (
) of 3.1 kcal mol−1 at pH 6.0. The replication rate constant required to overcome the stall and complete the reaction (ks) was 0.39 min−1 at 37 °C. In contrast, the G4 from human telomeres showed similar stability ( ) but a larger ks of 2.6 min−1. Moreover, the hairpin structure with a relatively higher stability (
) but a larger ks of 2.6 min−1. Moreover, the hairpin structure with a relatively higher stability ( ) showed a much larger ks of 3.7 min−1. To analyse quantitatively the effects of the stability and topology of the DNA structure on replication efficiency, we developed a method called “quantitative study of topology-dependent replication (QSTR)” to determine a phase diagram of the replication rate vs. G4 stability and to reveal replication properties depending on the template DNA topology (Fig. 8(a)).126 When QSTR plots were generated from the results of various structures with different stabilities and topologies, including G4s, different linearity plots were obtained depending on the topology (Fig. 8(b)). Because the activation free energy ΔG‡ of the reaction is expressed by –RT
) showed a much larger ks of 3.7 min−1. To analyse quantitatively the effects of the stability and topology of the DNA structure on replication efficiency, we developed a method called “quantitative study of topology-dependent replication (QSTR)” to determine a phase diagram of the replication rate vs. G4 stability and to reveal replication properties depending on the template DNA topology (Fig. 8(a)).126 When QSTR plots were generated from the results of various structures with different stabilities and topologies, including G4s, different linearity plots were obtained depending on the topology (Fig. 8(b)). Because the activation free energy ΔG‡ of the reaction is expressed by –RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ks, the linearity of the plots indicates that the ratio of ΔG‡ and
ks, the linearity of the plots indicates that the ratio of ΔG‡ and  is the same for replication when DNAs with the same topology is replicated via the same unfolding mechanism of non-duplexes. The slope of the QSTR plot indicates that iM and the anti-parallel and parallel G4s had the greatest effect on replication stalling among the tested structures. However, this trend in topology-dependent replication changes dramatically under crowded conditions (Fig. 8(c)). The human telomere G4, transformed from a hybrid to a parallel topology under crowding conditions, effectively repressed replication, as observed for iMs in the absence of crowders.
is the same for replication when DNAs with the same topology is replicated via the same unfolding mechanism of non-duplexes. The slope of the QSTR plot indicates that iM and the anti-parallel and parallel G4s had the greatest effect on replication stalling among the tested structures. However, this trend in topology-dependent replication changes dramatically under crowded conditions (Fig. 8(c)). The human telomere G4, transformed from a hybrid to a parallel topology under crowding conditions, effectively repressed replication, as observed for iMs in the absence of crowders.
 | ||
| Fig. 8 Quantitative study of topology-dependent replication (QSTR) and its applications. (a) Parameters of the QSTR plot targeting the stability of the non-duplex (−ΔG°) and the activation energy required for polymerases to overcome the structure (ΔG‡). (b), (c) Plots of QSTR showing the relationship between the stability of the non-double helix structure and replication efficiency in the absence (b) or presence (c) of crowders at pH 6.0.126,127 The topology and dynamics dependency of replication inhibition is indicated by the difference in the slope of the QSTR plots. All the replication reactions were performed at 37 °C. | ||
Molecular crowding also affects dynamics of G4 and iM, regulating replication stalls. In the presence of 20 wt% PEG1000, the replication of iMs was effectively repressed (Fig. 8(c)). To study the effect of iM dynamics on the different responses to PEGs, MD simulations and NMR were conducted to investigate the structural changes in iM.127 As a result, MD simulations elucidated that the twisting of the iM strand was affected by the PEG size. This indicates that the twisting reaction, estimated to occur on the order of microseconds or less from the NMR and MD simulation data, affects the polymerase reaction, which should be slower than the twisting motion of iM. This may be because dynamic changes in DNA cause changes in the mobility and direction of motion, which perturb DNA recognition by the protein.128 These results suggest that the twisting dynamics triggered by molecular crowding increase or decrease the energy barrier for polymerase-mediated iM recognition, regulating the subsequent iM unfolding process. Therefore, each crowding condition differentially regulates the processivity of DNAP along a template DNA based on the activation free energy for unwinding by altering the stability and topology of the DNA structure. These energetic treatments provide an index for quantitatively interpreting the effect of the environments on gene replication and expression, depending on the stability and topology of the template DNA.
4.4 Chemical control of gene replication using G4/iM binders
Changes in Watson–Crick and Hoogsteen base-pair formation according to the chemical environments suggest the possibility of controlling gene replication and expression using chemical compounds. The polymerase stop assay can also be used to study quantitatively the effects of G4/iM binders on replication stalls. A pioneering report used to bind 2,6-diamidoanthraquinone BSU-1051 to the telomere G4 sequence on template DNA to determine the dose-dependent stall of telomerase by the compound.129 Using this assay, the properties of G4/iM ligands can be analysed quantitatively based on their stability effect on the replication stall. For example, a G4 ligand conjugated with a guide DNA was investigated using the polymerase stop assay to check the stability and selectivity of the target G4 quantitatively, giving the development of the G4 ligand a small off-target property.130 Topology-dependent G4 binders were also tested for the stability and specificity of the different G4s on the template DNA.131 Nucleolin is also known as an iM binder, and the polymerase stop assay is used to provide clues for understanding the functional roles of nucleolin upon iM binding.132 Therefore, it was revealed that nucleolin does not completely unwind the iM structure upon binding; instead, it relaxes the higher-order conformation and/or converts the iM into an alternative form that DNA polymerase can more readily process during elongation. The combination of qPCR provides the stabilisation score of G4 by the G4 binder to measure quantitatively the amplification of the PCR product.133 Small compounds and protein binders fit this assay because the melting assay can rarely be applied to proteins because of heat denaturation. Recently, this assay was used to identify essential domains and residues of nucleolin that bind strongly to G4 DNA, particularly cMyc G4.134For ligand-based assays, the QSTR method provides unique information about G4/iM binders. We found that the plant flavonol fisetin bound specifically to the iM derived from the promoter region of the human VEGF gene.135 This binding affected dramatically the photoinduction of the excited-state intramolecular proton transfer reaction, which significantly enhanced the intensity of the tautomer band of fisetin fluorescence.136 This unique response was due to the coincidence of the structural change from the iM to the hairpin structure by putative Watson–Crick base-pair formation between some guanines within the loop region of the iM and cytosines. The QSTR plot indicated that the replication property of iMs (Hoogsteen-type) shifted to that of hairpins (Watson–Crick-type) by fisetin. The VEGF iM did not block replication in the presence of fisetin, indicating that fisetin inhibits VEGF gene expression by altering the secondary structure of DNA from Hoogsteen to the Watson–Crick type.
The QSTR technique has also been used to design G4 binders rationally. Various compounds were analysed by systematically changing their functional groups. The QSTR plots suggested a relationship between the functional group on the G4 binder and its effect on both replication stall and G4 stabilisation. The systematic QSTR data could provide the design of specific binding to the human telomere G4, in which the naphthalene diamide compound binds simultaneously to the G-quartet surface and loop region.137 The newly designed compound had drastic stability and replication stall effects compared to the original compound.137
In another study, we investigated the chemical recovery of G4 formation using oxidised human VEGF. Guanine bases in G4 are sensitive to oxidation, which results in their transformation to 8-oxo-7,8-dihydroguanine (8-oxoG). Because G4 formation regulates the expression of some cancer genes, 8-oxoG in a G4 sequence may affect epigenetic modifications of the genome and cancer progression.138 We found that 8-oxoG-containing G4 derived from the promoter region of the human VEGF gene had a different topology from the unoxidised G4 structure and did not block replication, as shown in the QSTR plots.139 To recover the G4 function, we developed an oligonucleotide comprising a pyrene-modified guanine tract (5′-pyrene-UGGGT-3′) to replace the oxidised guanine tract and form stable intermolecular G4s with other intact guanine-tracts.139 The QSTR plots indicate that the function of G4 to stall replication was recovered by the modified oligonucleotide. As shown here, the unique point of QSTR is the discovery of the effect of G4/iM on replication, depending not only on the stability (–ΔG°) but also on other factors, such as the structural dynamics of the polymerase-G4/iM complex. Therefore, these quantitative outputs can be used to understand the dynamic regulation of replication by G4/iM and to develop novel materials that control the dynamics of G4/iM for specific biological behaviours of gene expression.
5. Conclusion
Here, we summarise how replication by polymerases is dynamically regulated by the solution environments. As the efficiency and fidelity of replication depend on the chemistry of nascent base-pair formation during replication, the regulation of the replication reaction is not always limited to Watson–Crick base pairings. Replication is a robust system that uses Watson–Crick base pairs but a flexible system that uses non-Watson–Crick base pairs (Fig. 9). Replication is fundamental to life. Such duality proves vital for living things' development. The solution-dependent regulation of this dual nature may have been a strategy since the origin of life. Our living system can utilise this dual system to maintain or evolve its genomic sequence including cancers and viruses. This concept of tuning replication by solution environments can also impact the field of synthetic biology, which requires novel replication systems using unnatural XNA templates and monomers. A thermodynamic and kinetic database for various solution environments should be useful for predicting mutations in various living systems and creating novel genetic materials. Moreover, the choice of crowder molecules can further expand the potential for tuning replication. PEG is a neutral polymer and is inert toward biomolecules. In living cells, however, many crowders are interactive molecules such as charged proteins. We previously evaluated the behaviours of DNA in various solutions and found that the environments of the nucleus, nucleolus, and cytosol resemble solutions containing PEG 200, Ficoll 70, and BSA, respectively.140 Mitochondrial environments can be mimicked by solutions containing highly concentrated 1,3-propanediol.141 Furthermore, the internal architecture of cells also affects the stability of DNA.142 More complex crowding agents will be explored to obtain a closer approximation of the intracellular environment and to develop conditions suitable for novel nanotechnologies.This article highlights that genomic manipulation is dominated by the steric structure and structural stability of nucleic acids, which are determined by a combination of structural factors, such as hydrogen bonding, stacking interactions between base pairs, and the conformational entropy of the backbone, and environmental factors, such as cations, hydration, and molecular crowding. These stability factors have been individually investigated; however, a comprehensive understanding of the energetic contributions to replication efficiency and fidelity remains unclear, particularly the contribution of conformational entropy. Interestingly, the polymerase active site in the current era is not tightly packed with substrate DNAs, although the fidelity and efficiency depend on the packing.79 This implies that living systems maintain room for conformational entropy to differentiate the functions of biomolecules, including DNA, RNA, and proteins. Understanding the energetic contribution of each factor to the replication process will open up new avenues in the field of genomic mutagenesis and functional materials.
Conflicts of interest
The authors declare no competing interests.Data availability
This is a review article. It does not contain original scientific data that need to be released.Acknowledgements
This work was supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) and the Japan Society for the Promotion of Science (JSPS) (21K05283, 24K01631 and 25K21727), especially the Grant-in-Aid for Scientific Research (S) (22H04975), JSPS Core-to-Core Program (JPJSCCA20220005), Konan New Century Strategic Research Project, Asahi Glass Foundation, and Chubei Itoh Foundation.References
- D. M. Crothers, V. A. Bloomfield and I. Tinoco, Nucleic acids: structures, properties, and functions, University science books, 2000 Search PubMed.
- J. D. Watson and F. H. Crick, Nature, 1953, 171, 737–738 CrossRef PubMed.
- D. Pan, H. Nishimura and J. W. Tang, Clin. Microbiol. Infect., 2024, 30, 700–702 CrossRef PubMed.
- F. Bray, M. Laversanne, H. Sung, J. Ferlay, R. L. Siegel, I. Soerjomataram and A. Jemal, Ca-Cancer J. Clin., 2024, 74, 229–263 CrossRef PubMed.
- P. Hahnfeldt, R. K. Sachs and L. R. Hlatky, J. Math. Biol., 1992, 30, 493–511 CrossRef PubMed.
- A. B. Adewoye, S. J. Lindsay, Y. E. Dubrova and M. E. Hurles, Nat. Commun., 2015, 6, 6684 CrossRef PubMed.
- J. G. Monroe, T. Srikant, P. Carbonell-Bejerano, C. Becker, M. Lensink, M. Exposito-Alonso, M. Klein, J. Hildebrandt, M. Neumann, D. Kliebenstein, M.-L. Weng, E. Imbert, J. Ågren, M. T. Rutter, C. B. Fenster and D. Weigel, Nature, 2022, 602, 101–105 Search PubMed.
- V. Thatikonda, S. M. A. Islam, R. J. Autry, B. C. Jones, S. N. Gröbner, G. Warsow, B. Hutter, D. Huebschmann, S. Fröhling, M. Kool, M. Blattner-Johnson, D. T. W. Jones, L. B. Alexandrov, S. M. Pfister and N. Jäger, Nat. Cancer, 2023, 4, 276–289 CrossRef PubMed.
- K. Hoogsteen, Acta Crystallogr., 1959, 12, 822–823 CrossRef.
- K. Hoogsteen, Acta Crystallogr., 1963, 16, 907–916 CrossRef.
- E. N. Nikolova, E. Kim, A. A. Wise, P. J. O'Brien, I. Andricioaei and H. M. Al-Hashimi, Nature, 2011, 470, 498–502 CrossRef PubMed.
- D. Rhodes and H. J. Lipps, Nucleic Acids Res., 2015, 43, 8627–8637 CrossRef PubMed.
- C. M. Joyce and S. J. Benkovic, Biochemistry, 2004, 43, 14317–14324 CrossRef PubMed.
- W. K. Johnston, P. J. Unrau, M. S. Lawrence, M. E. Glasner and D. P. Bartel, Science, 2001, 292, 1319–1325 CrossRef PubMed.
- J. Attwater, A. Wochner, V. B. Pinheiro, A. Coulson and P. Holliger, Nat. Commun., 2010, 1, 76 CrossRef PubMed.
- A. Wochner, J. Attwater, A. Coulson and P. Holliger, Science, 2011, 332, 209–212 CrossRef CAS PubMed.
- P. Keohavong and W. G. Thilly, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 9253–9257 CrossRef CAS PubMed.
- X. Yin, H. Popa, A. Stapon, E. Bouda and M. Garcia-Diaz, J. Mol. Biol., 2023, 435, 167973 CrossRef PubMed.
- T. A. Kunkel and K. Bebenek, Annu. Rev. Biochem., 2000, 69, 497–529 CrossRef.
- T. A. Kunkel, J. Biol. Chem., 2004, 279, 16895–16898 CrossRef.
- K. A. Johnson, Annu. Rev. Biochem., 1993, 62, 685–713 CrossRef PubMed.
- S. J. Johnson and L. S. Beese, Cell, 2004, 116, 803–816 CrossRef.
- J. SantaLucia, Jr. and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef.
- J. Petruska, M. F. Goodman, M. S. Boosalis, L. C. Sowers, C. Cheong and I. Tinoco, Jr., Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 6252–6256 CrossRef PubMed.
- M. E. Arana, M. Seki, R. D. Wood, I. B. Rogozin and T. A. Kunkel, Nucleic Acids Res., 2008, 36, 3847–3856 CrossRef PubMed.
- H. Echols and M. F. Goodman, Annu. Rev. Biochem., 1991, 60, 477–511 CrossRef PubMed.
- J. Petruska, L. C. Sowers and M. F. Goodman, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 1559–1562 CrossRef PubMed.
- K. Oertell, E. M. Harcourt, M. G. Mohsen, J. Petruska, E. T. Kool and M. F. Goodman, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E2277–2285 Search PubMed.
- J. Petruska and M. F. Goodman, Nat. Rev. Chem., 2017, 1, 0074 CrossRef.
- J. Petruska and M. F. Goodman, J. Biol. Chem., 1995, 270, 746–750 Search PubMed.
- R. Lumry and S. Rajender, Biopolymers, 1970, 9, 1125–1227 CrossRef PubMed.
- H. Kamiya, Nucleic Acids Res., 2003, 31, 517–531 Search PubMed.
- S. Reuter, S. C. Gupta, M. M. Chaturvedi and B. B. Aggarwal, Free Radical Biol. Med., 2010, 49, 1603–1616 CrossRef.
- L. A. Lipscomb, M. E. Peek, M. L. Morningstar, S. M. Verghis, E. M. Miller, A. Rich, J. M. Essigmann and L. D. Williams, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 719–723 CrossRef.
- M. C. Koag, H. Jung and S. Lee, Nucleic Acids Res., 2020, 48, 5119–5134 CrossRef PubMed.
- H. Kamiya and H. Kasai, J. Biol. Chem., 1995, 270, 19446–19450 Search PubMed.
- J. Kawakami, H. Kamiya, K. Yasuda, H. Fujiki, H. Kasai and N. Sugimoto, Nucleic Acids Res., 2001, 29, 3289–3296 CrossRef.
- S. A. Benner, R. K. Allemann, A. D. Ellington, L. Ge, A. Glasfeld, G. F. Leanz, T. Krauch, L. J. MacPherson, S. Moroney and J. A. Piccirilli, et al. , Cold Spring Harbor Symp. Quant. Biol., 1987, 52, 53–63 CrossRef PubMed.
- J. A. Piccirilli, T. Krauch, S. E. Moroney and S. A. Benner, Nature, 1990, 343, 33–37 CrossRef.
- S. Moran, R. X. Ren, S. Rumney and E. T. Kool, J. Am. Chem. Soc., 1997, 119, 2056–2057 CrossRef PubMed.
- E. T. Kool, Annu. Rev. Biochem., 2002, 71, 191–219 CrossRef PubMed.
- E. L. Tae, Y. Wu, G. Xia, P. G. Schultz and F. E. Romesberg, J. Am. Chem. Soc., 2001, 123, 7439–7440 CrossRef.
- T. Mitsui, A. Kitamura, M. Kimoto, T. To, A. Sato, I. Hirao and S. Yokoyama, J. Am. Chem. Soc., 2003, 125, 5298–5307 CrossRef.
- Z. Yang, D. Hutter, P. Sheng, A. M. Sismour and S. A. Benner, Nucleic Acids Res., 2006, 34, 6095–6101 Search PubMed.
- K. Dhami, D. A. Malyshev, P. Ordoukhanian, T. Kubelka, M. Hocek and F. E. Romesberg, Nucleic Acids Res., 2014, 42, 10235–10244 Search PubMed.
- D. A. Malyshev, Y. J. Seo, P. Ordoukhanian and F. E. Romesberg, J. Am. Chem. Soc., 2009, 131, 14620–14621 CrossRef.
- M. Kimoto, R. Kawai, T. Mitsui, S. Yokoyama and I. Hirao, Nucleic Acids Res., 2008, 37, e14–e14 CrossRef.
- S. Hoshika, N. A. Leal, M. J. Kim, M. S. Kim, N. B. Karalkar, H. J. Kim, A. M. Bates, N. E. Watkins, Jr., H. A. SantaLucia, A. J. Meyer, S. DasGupta, J. A. Piccirilli, A. D. Ellington, J. SantaLucia, Jr., M. M. Georgiadis and S. A. Benner, Science, 2019, 363, 884–887 CrossRef PubMed.
- L. Li, M. Degardin, T. Lavergne, D. A. Malyshev, K. Dhami, P. Ordoukhanian and F. E. Romesberg, J. Am. Chem. Soc., 2014, 136, 826–829 CrossRef.
- I. Okamoto, Y. Miyatake, M. Kimoto and I. Hirao, ACS Synth. Biol., 2016, 5, 1220–1230 CrossRef PubMed.
- N. Minakawa, N. Kojima, S. Hikishima, T. Sasaki, A. Kiyosue, N. Atsumi, Y. Ueno and A. Matsuda, J. Am. Chem. Soc., 2003, 125, 9970–9982 CrossRef PubMed.
- N. Tarashima, Y. Komatsu, K. Furukawa and N. Minakawa, Chem. – Eur. J., 2015, 21, 10688–10695 CrossRef.
- C. Brotschi, A. Häberli and C. J. Leumann, Angew. Chem., Int. Ed., 2001, 40, 3012–3014 CrossRef PubMed.
- S. Matsuda, J. D. Fillo, A. A. Henry, P. Rai, S. J. Wilkens, T. J. Dwyer, B. H. Geierstanger, D. E. Wemmer, P. G. Schultz, G. Spraggon and F. E. Romesberg, J. Am. Chem. Soc., 2007, 129, 10466–10473 Search PubMed.
- F. Wojciechowski and C. J. Leumann, Chem. Soc. Rev., 2011, 40, 5669–5679 RSC.
- M. Hocek, Acc. Chem. Res., 2019, 52, 1730–1737 CrossRef.
- M. Brunderová, V. Havlíček, J. Matyašovský, R. Pohl, L. Poštová Slavětínská, M. Krömer and M. Hocek, Nat. Commun., 2024, 15, 3054 CrossRef.
- M. Ondruš, V. Sýkorová, L. Bednárová, R. Pohl and M. Hocek, Nucleic Acids Res., 2020, 48, 11982–11993 CrossRef PubMed.
- J. K. Ichida, A. Horhota, K. Zou, L. W. McLaughlin and J. W. Szostak, Nucleic Acids Res., 2005, 33, 5219–5225 CrossRef PubMed.
- J. C. Chaput, J. K. Ichida and J. W. Szostak, J. Am. Chem. Soc., 2003, 125, 856–857 CrossRef.
- M. R. Dunn, C. Otto, K. E. Fenton and J. C. Chaput, ACS Chem. Biol., 2016, 11, 1210–1219 Search PubMed.
- C. Cozens, V. B. Pinheiro, A. Vaisman, R. Woodgate and P. Holliger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8067–8072 CrossRef.
- V. B. Pinheiro, A. I. Taylor, C. Cozens, M. Abramov, M. Renders, S. Zhang, J. C. Chaput, J. Wengel, S.-Y. Peak-Chew, S. H. McLaughlin, P. Herdewijn and P. Holliger, Science, 2012, 336, 341–344 Search PubMed.
- Y. Wang, Y. Wang, D. Song, X. Sun, Z. Zhang, X. Li, Z. Li and H. Yu, J. Am. Chem. Soc., 2021, 143, 8154–8163 Search PubMed.
- H. Hoshino, Y. Kasahara, M. Kuwahara and S. Obika, J. Am. Chem. Soc., 2020, 142, 21530–21537 Search PubMed.
- E. L. Medina and J. C. Chaput, Nucleic Acids Res., 2025, 53, gkaf038 CrossRef.
- N. Chim, C. Shi, S. P. Sau, A. Nikoomanzar and J. C. Chaput, Nat. Commun., 2017, 8, 1810 CrossRef PubMed.
- C. Chang, C. Lee Luo and Y. Gao, Nat. Commun., 2022, 13, 2346 CrossRef PubMed.
- M. F. Goodman, S. Keener, S. Guidotti and E. W. Branscomb, J. Biol. Chem., 1983, 258, 3469–3475 CrossRef.
- A. K. Vashishtha, J. Wang and W. H. Konigsberg, J. Biol. Chem., 2016, 291, 20869–20875 Search PubMed.
- S. Claveau, M. Sasseville and M. Beauregard, DNA Cell Biol., 2004, 23, 789–795 CrossRef.
- W. A. Beard and S. H. Wilson, Biochemistry, 2014, 53, 2768–2780 CrossRef CAS PubMed.
- M.-C. Koag, K. Nam and S. Lee, Nucleic Acids Res., 2014, 42, 11233–11245 CrossRef CAS PubMed.
- M. C. Koag, L. Lai and S. Lee, J. Biol. Chem., 2014, 289, 31341–31348 CrossRef CAS PubMed.
- M. C. Koag and S. Lee, J. Am. Chem. Soc., 2014, 136, 5709–5721 CrossRef CAS PubMed.
- E. A. Belousova, G. Maga, Y. Fan, E. A. Kubareva, E. A. Romanova, N. A. Lebedeva, T. S. Oretskaya and O. I. Lavrik, Biochemistry, 2010, 49, 4695–4704 CrossRef CAS PubMed.
- B. Xie, J. Chen, Z. Wang, Q. Yin and Z. M. Dai, PLoS One, 2024, 19, e0311939 CrossRef CAS PubMed.
- D. T. Minnick, K. Bebenek, W. P. Osheroff, R. M. Turner, Jr., M. Astatke, L. Liu, T. A. Kunkel and C. M. Joyce, J. Biol. Chem., 1999, 274, 3067–3075 CrossRef CAS.
- T. W. Kim, J. C. Delaney, J. M. Essigmann and E. T. Kool, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 15803–15808 CrossRef CAS PubMed.
- M. W. Kellinger, S. Ulrich, J. Chong, E. T. Kool and D. Wang, J. Am. Chem. Soc., 2012, 134, 8231–8240 CrossRef CAS PubMed.
- R. J. Ellis, Curr. Opin. Struct. Biol., 2001, 11, 114–119 CrossRef CAS.
- S. Takahashi and N. Sugimoto, Chem. Soc. Rev., 2020, 49, 8439–8468 RSC.
- S. Nakano, D. Miyoshi and N. Sugimoto, Chem. Rev., 2014, 114, 2733–2758 CrossRef CAS.
- A. P. Minton, J. Biol. Chem., 2001, 276, 10577–10580 CrossRef CAS PubMed.
- M. Trajkovski, T. Endoh, H. Tateishi-Karimata, T. Ohyama, S. Tanaka, J. Plavec and N. Sugimoto, Nucleic Acids Res., 2018, 46, 4301–4315 CrossRef CAS PubMed.
- D. Miyoshi, K. Nakamura, H. Tateishi-Karimata, T. Ohmichi and N. Sugimoto, J. Am. Chem. Soc., 2009, 131, 3522–3531 CrossRef CAS.
- Y. Teng, H. Tateishi-Karimata, T. Ohyama and N. Sugimoto, Molecules, 2020, 25, 387 CrossRef CAS PubMed.
- M. Gao, D. Gnutt, A. Orban, B. Appel, F. Righetti, R. Winter, F. Narberhaus, S. Müller and S. Ebbinghaus, Angew. Chem., Int. Ed., 2016, 55, 3224–3228 Search PubMed.
- T. J. Nott, T. D. Craggs and A. J. Baldwin, Nat. Chem., 2016, 8, 569–575 CrossRef CAS PubMed.
- I. M. Kuznetsova, K. K. Turoverov and V. N. Uversky, Int. J. Mol. Sci., 2014, 15, 23090–23140 CrossRef.
- D. Lambert and D. E. Draper, J. Mol. Biol., 2007, 370, 993–1005 CrossRef CAS PubMed.
- H. X. Zhou, G. Rivas and A. P. Minton, Annu. Rev. Biophys., 2008, 37, 375 Search PubMed.
- R. Desai, D. Kilburn, H. T. Lee and S. A. Woodson, J. Biol. Chem., 2014, 289, 2972–2977 CrossRef CAS PubMed.
- D. Lambert, D. Leipply and D. E. Draper, J. Mol. Biol., 2010, 404, 138–157 CrossRef CAS PubMed.
- K. Semrad and R. Green, RNA, 2002, 8, 401–411 CrossRef CAS.
- A. P. Minton, J. Cell Sci., 2006, 119, 2863–2869 CrossRef CAS PubMed.
- J. Attwater, A. Wochner and P. Holliger, Nat. Chem., 2013, 5, 1011–1018 CrossRef CAS PubMed.
- M. Ricchetti and H. Buc, EMBO J., 1993, 12, 387–396 CrossRef CAS PubMed.
- C. Cazenave and O. C. Uhlenbeck, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 6972–6976 CrossRef CAS PubMed.
- S. Takahashi, H. Okura and N. Sugimoto, Biochemistry, 2019, 58, 1081–1093 CrossRef CAS PubMed.
- N. B. Leontis, J. Stombaugh and E. Westhof, Nucleic Acids Res., 2002, 30, 3497–3531 CrossRef CAS PubMed.
- S. Takahashi, S. Matsumoto, P. Chilka, S. Ghosh, H. Okura and N. Sugimoto, Sci. Rep., 2022, 12, 1149 CrossRef CAS PubMed.
- S. Takahashi, H. Okura, P. Chilka, S. Ghosh and N. Sugimoto, RSC Adv., 2020, 10, 33052–33058 RSC.
- S. Takahashi, P. Herdwijn and N. Sugimoto, Molecules, 2020, 25, 4120 CrossRef CAS PubMed.
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef CAS PubMed.
- G. Rivas and A. P. Minton, Biophys. Rev., 2018, 10, 241–253 CrossRef CAS PubMed.
- K. Datta and V. J. LiCata, J. Biol. Chem., 2003, 278, 5694–5701 CrossRef CAS PubMed.
- S. B. Zimmerman and B. Harrison, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 1871–1875 CrossRef CAS PubMed.
- B. Akabayov, S. R. Akabayov, S.-J. Lee, G. Wagner and C. C. Richardson, Nat. Commun., 2013, 4, 1615 Search PubMed.
- S. Chung, E. Lerner, Y. Jin, S. Kim, Y. Alhadid, L. W. Grimaud, I. X. Zhang, C. M. Knobler, W. M. Gelbart and S. Weiss, Nucleic Acids Res., 2018, 47, 1440–1450 Search PubMed.
- H. Moore, P. W. Greenwell, C.-P. Liu, N. Arnheim and T. D. Petes, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 1504–1509 Search PubMed.
- J. R. Gatchel and H. Y. Zoghbi, Nat. Rev. Genet., 2005, 6, 743–755 Search PubMed.
- D. Varshney, J. Spiegel, K. Zyner, D. Tannahill and S. Balasubramanian, Nat. Rev. Mol. Cell Biol., 2020, 21, 459–474 Search PubMed.
- N. V. Hud, F. W. Smith, F. A. Anet and J. Feigon, Biochemistry, 1996, 35, 15383–15390 CrossRef CAS PubMed.
- K. Gehring, J.-L. Leroy and M. Guéron, Nature, 1993, 363, 561–565 Search PubMed.
- B. Lemmens, R. van Schendel and M. Tijsterman, Nat. Commun., 2015, 6, 8909 CrossRef CAS PubMed.
- M. L. Bochman, K. Paeschke and V. A. Zakian, Nat. Rev. Genet., 2012, 13, 770–780 CrossRef CAS PubMed.
- J. Lopes, A. Piazza, R. Bermejo, B. Kriegsman, A. Colosio, M. P. Teulade-Fichou, M. Foiani and A. Nicolas, EMBO J., 2011, 30, 4033–4046 CrossRef CAS PubMed.
- M. N. Weitzmann, K. J. Woodford and K. Usdin, J. Biol. Chem., 1996, 271, 20958–20964 CrossRef CAS PubMed.
- H. Han, L. H. Hurley and M. Salazar, Nucleic Acids Res., 1999, 27, 537–542 CrossRef CAS PubMed.
- S. Mandal, Y. Kawamoto, Z. Yue, K. Hashiya, Y. Cui, T. Bando, S. Pandey, M. E. Hoque, M. A. Hossain, H. Sugiyama and H. Mao, Nucleic Acids Res., 2019, 47, 3295–3305 CrossRef CAS PubMed.
- V. S. Chambers, G. Marsico, J. M. Boutell, M. Di Antonio, G. P. Smith and S. Balasubramanian, Nat. Biotechnol., 2015, 33, 877–881 CrossRef CAS PubMed.
- G. Marsico, V. S. Chambers, A. B. Sahakyan, P. McCauley, J. M. Boutell, M. D. Antonio and S. Balasubramanian, Nucleic Acids Res., 2019, 47, 3862–3874 CrossRef CAS PubMed.
- A. J. Stevens and M. A. Kennedy, Biochemistry, 2017, 56, 3691–3698 CrossRef CAS PubMed.
- P. Murat, G. Guilbaud and J. E. Sale, Genome Biol., 2020, 21, 209 Search PubMed.
- S. Takahashi, J. A. Brazier and N. Sugimoto, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 9605–9610 Search PubMed.
- S. Takahashi, S. Ghosh, M. Trajkovski, T. Ohyama, J. Plavec and N. Sugimoto, Nucleic Acids Res., 2025, 53 Search PubMed.
- K. Pederson, G. A. Meints and G. P. Drobny, J. Phys. Chem. B, 2023, 127, 7266–7275 CrossRef CAS PubMed.
- H. Han, L. H. Hurley and M. Salazar, Nucleic Acids Res., 1999, 27, 537–542 CrossRef CAS PubMed.
- A. Berner, R. N. Das, N. Bhuma, J. Golebiewska, A. Abrahamsson, M. Andréasson, N. Chaudhari, M. Doimo, P. P. Bose, K. Chand, R. Strömberg, S. Wanrooij and E. Chorell, J. Am. Chem. Soc., 2024, 146, 6926–6935 CrossRef CAS PubMed.
- S. Kumar, S. P. P. Pany, S. Sudhakar, S. B. Singh, C. S. Todankar and P. I. Pradeepkumar, Biochemistry, 2022, 61, 2546–2559 CrossRef CAS PubMed.
- Y. Ban, Y. Ando, Y. Terai, R. Matsumura, K. Nakane, S. Iwai, S. Sato and J. Yamamoto, Nucleic Acids Res., 2024, 52, 13530–13543 CrossRef CAS PubMed.
- I. Obi, M. Rentoft, V. Singh, J. Jamroskovic, K. Chand, E. Chorell, F. Westerlund and N. Sabouri, Nucleic Acids Res., 2020, 48, 10998–11015 CrossRef CAS PubMed.
- L. Chen, J. Dickerhoff, K.-W. Zheng, S. Erramilli, H. Feng, G. Wu, B. Onel, Y. Chen, K.-B. Wang, M. Carver, C. Lin, S. Sakai, J. Wan, C. Vinson, L. Hurley, A. A. Kossiakoff, N. Deng, Y. Bai, N. Noinaj and D. Yang, Science, 2025, 388, eadr1752 Search PubMed.
- S. Takahashi, S. Bhattacharjee, S. Ghosh, N. Sugimoto and S. Bhowmik, Sci. Rep., 2020, 10, 2504 CrossRef CAS PubMed.
- S. Bhattacharjee, S. Chakraborty, P. K. Sengupta and S. Bhowmik, J. Phys. Chem. B, 2016, 120, 8942–8952 CrossRef CAS.
- S. Takahashi, A. Kotar, H. Tateishi-Karimata, S. Bhowmik, Z. F. Wang, T. C. Chang, S. Sato, S. Takenaka, J. Plavec and N. Sugimoto, J. Am. Chem. Soc., 2021, 143, 16458–16469 CrossRef CAS PubMed.
- A. M. Fleming and C. J. Burrows, Chem. Soc. Rev., 2020, 49, 6524–6528 Search PubMed.
- S. Takahashi, K. T. Kim, P. Podbevsek, J. Plavec, B. H. Kim and N. Sugimoto, J. Am. Chem. Soc., 2018, 140, 5774–5783 CrossRef CAS PubMed.
- S. Takahashi, J. Yamamoto, A. Kitamura, M. Kinjo and N. Sugimoto, Anal. Chem., 2019, 91, 2586–2590 Search PubMed.
- L. Liu, S. Takahashi, S. Ghosh, T. Endoh, N. Yoshinaga, K. Numata and N. Sugimoto, Commun. Chem., 2025, 8, 135 CrossRef CAS PubMed.
- H. Tateishi-Karimata, K. Kawauchi, S. Takahashi and N. Sugimoto, J. Am. Chem. Soc., 2024, 146, 8005–8015 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |







