Thermodynamic stability and reactivity of amorphised tricalcium silicate

Abstract

Using a model for C–S–H growth kinetics in combination with calorimetry measurements, we show that amorphised tricalcium silicate is more thermodynamically stable than its crystalline form. However, the onset of the hydration reaction occurs more quickly in amorphised tricalcium silicate compared to its crystalline form.

---

The hydration reaction of tricalcium silicate (often referred to as alite in its impure form) to form calcium silicate hydrate (C–S–H) gel and calcium hydroxide is critical for the strength development of concrete, the world's most widely used inorganic material. The rate of the tricalcium silicate hydration reaction is industrially important, as it strongly determines the strength of concrete at early ages (<7 d after mixing).² There is growing industrial interest in accelerating the hydration reaction of cement, and hence its strength development, through high-energy grinding.^3,4 Laboratory studies using high-energy grinding methods (e.g. planetary ball mill, SPEX mill) have produced amorphised tricalcium silicate, with distinct hydration kinetics.^5–9 However, there are several knowledge gaps around the structure–property–performance relationships of partially amorphised tricalcium silicate and the hydration reaction.

In this study, tricalcium silicate was synthesised and intensively ground, to investigate how the evolution in its structural and physical characteristics affected the hydration reaction. The T₁ polymorph (triclinic) was synthesised (details in SI Section S1), to avoid ionic substitution defects and make it simpler to investigate changes in reaction kinetics.¹⁰ High-energy grinding was carried out using a vibratory disk mill (details in SI Section S2.1). Grinding for longer durations led to progressively finer particle size and higher specific surface area (Fig. 1A), as determined via laser diffraction and N₂ sorption respectively (details in SI Section S3.2). After 3 s of grinding, the particle morphology was angular (Fig. 1D); after 240 s of grinding, the particle morphology appeared to still be angular, but more fine particles were observed (Fig. 1E). Longer grinding also led to broadening of X-ray diffraction peaks (Fig. 1B and C). The amorphous content was estimated using addition of rutile as an internal standard (details in SI Section S3.1). The amorphous content increased from a negligible amount (<5 wt%) at 3 s of grinding to >35 wt% after 240 s of grinding (Fig. 1F).

Fig. 1 (A) Changes in the d₅₀ and BET specific surface area with grinding duration (via disk mill). (B) and (C) Progressive broadening in the X-ray diffraction peaks of tricalcium silicate with longer grinding durations. Images showing the morphology of tricalcium silicate particles after (D) 3 s of grinding, (E) 240 s of grinding. (F) Increase in amorphous content and decrease in crystalline tricalcium silicate with longer grinding duration, as determined via Rietveld refinement using a rutile internal standard.

Heat flow curves associated with the hydration reaction of tricalcium silicate were measured using isothermal calorimetry (details in SI Section S4). The hydration peak showed a progressive increase in maximum heat flow with longer grinding durations, and also a general tendency for the peak to occur at earlier times (Fig. 2A). The period between the end of the initial dissolution peak and the onset of the main hydration peak is referred to as the ‘induction period’.¹¹ The heat flow value during this period is expected to follow a linear dependence with the specific surface area of tricalcium silicate.¹² However, for these samples milled using high-energy grinding apparatus, the trend with heat flow during the expected ‘induction period’ and specific surface area was non-linear (Fig. 3B). This non-linearity can be explained by the presence of an additional exothermic event between 1 and 2 h, which is clearly resolved from the main hydration peak for the sample ground for 240 s (Fig. 2A). An additional peak in this time period was observed in previous studies on high-energy milling of tricalcium silicate, and was attributed to the hydration of amorphised tricalcium silicate.^5,8,9 Intensive grinding significantly increased the cumulative heat release at both 24 h (a 41.7% increase for 240 s compared to 3 s) and at 168 h (a 34.6% increase for 240 s compared to 3 s) (Fig. 2C). The apparent activation energy of hydration for each sample was measured using data collected from isothermal calorimetry measurements at 20, 30 and 40 °C (details in SI Section S4). Grinding increases surface defect density,¹³ and the type of surface defect affects the activation energy of tricalcium silicate hydration.¹⁴ Therefore, it was expected that longer grinding durations would lead to lower activation energy of hydration. To our surprise, this trend was not observed, with an initial decrease in apparent activation energy followed by a subsequent increase at longer grinding times (Fig. 2D).

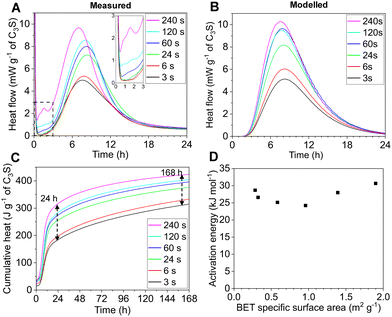Fig. 2 (A) Measured hydration curves via isothermal calorimetry; (B) modelled hydration curves, using the ‘needle growth’ model of Ouzia and Scrivener;¹ (C) cumulative heat hydration curves; (D) evolution of apparent activation energy of hydration.

Fig. 3 (A) Heat flow curves of tricalcium silicate ground to approximately the same specific surface area (∼2 m² g⁻¹) using high-energy milling apparatus (disk mill) and low-energy grinding apparatus (McCrone mill). (B) Heat flow at 1 h, for samples milled using high-energy milling apparatus (disk mill) and low-energy grinding apparatus (McCrone mill). (C) Heat flow curves for samples after annealing at 650 °C for 6 h. (D) Heat content measurements determined via drop calorimetry at 1400 °C.

To investigate the reasons governing the observed changes in hydration behaviour, modelled heat flow curves were generated using the ‘needle growth’ model of Ouzia and Scrivener¹ (Fig. 2B). The reduction in particle size distribution with longer grinding times were accounted for in the model, but all other parameters associated with C–S–H growth were kept constant (details in SI Section S5). The effect of increasing specific surface area on the maximum heat flow of the modelled hydration peak generally showed good agreement with the measured data (SI Fig. S4). Small deviations between the measured and modelled hydration peaks could be explained by differences between samples in the peak nucleation rate, characteristic growth rate and nucleation stopping time; the effect of these parameters are shown in a sensitivity analysis conducted by Ouzia and Scrivener (Fig. 10 in ref. 1). However, the model only considers the growth regime of C–S–H, and so does not capture the additional exothermic peak during the ‘induction’ period. This comparison indicates that the changes in the hydration behaviour of intensively ground tricalcium silicate cannot be fully explained by physical factors as treated in this model.

To isolate the effect of increased structural disorder from increased specific surface area, tricalcium silicate was milled using a low-energy grinding apparatus (i.e. a McCrone mill). The aim was to achieve the same specific surface area (∼2 m² g⁻¹) whilst introducing a lesser degree of structural disorder (details in SI Section S2.2). The low-energy milled sample exhibited a similar main hydration peak, but did not feature the additional exothermic peak at 1–2 h (Fig. 3A). A similar observation was made comparing between tricalcium silicate ground using other high-energy and low-energy milling devices (i.e. a planetary ball mill and a mortar mill).⁹ When the heat flow during the ‘induction period’ of the low-energy milled sample is plotted with the high-energy milled samples, it represents a continuation of a linear trend, as expected¹² (Fig. 3B). An additional investigation was made by thermally treating the samples at 650 °C for 6 h to anneal defects in the samples, as used by Costoya¹² (details in SI Section S2.3). For all samples, the annealing treatment shifted the hydration peak to later times as expected;^13,14 and, decreased the heat flow during the ‘induction period’ to very low levels (Fig. 3C). The two observations described above support the interpretation that the additional exothermic peak is the hydration of amorphous tricalcium silicate.

Heat content values determined by drop calorimetry are compared to the value for C₃S from the GTOX database¹⁵ in Fig. 3D. Assuming that the high temperature state at 1400 °C is the same for both the 3 s and 240 s ground samples, one can calculate the heat of amorphisation making a thermodynamic cycle. The reaction tricalcium silicate (crystalline) → (amorphous) has an enthalpy of reaction of −220 ± 116 J g⁻¹ (95% confidence interval). This value is in good agreement with the value of −162 ± 32 J g⁻¹ reported from Bergold et al.⁸ using hydration experiments. Contributions to measured enthalpy from defect annihilation and surface energy are negative. Hence, the true difference in intrinsic bulk values between the 3 s and 240 s samples is likely to be slightly larger than that measured here. However, the contribution of surface energy effects is considered negligible, estimated as ∼4 J g⁻¹ (calculation in SI Section S3.4). The result is counterintuitive as the heat of reaction is negative. Overgrinding tricalcium silicate samples leads to a higher thermodynamic stability from an enthalpy point of view, and therefore to a lower intrinsic thermodynamic reactivity.

Previous research on amorphisation of tricalcium silicate has used X-ray diffraction to measure the bulk amorphous content of a milled sample.⁸ However, bulk measurements do not give information about the spatial distribution of amorphised tricalcium silicate. In Raman spectroscopy, an increase in band breadth can indicate an increase in the structural disorder of the local bonding environment.¹⁶ Raman spectra have shown band broadening in intensively milled tricalcium silicate (albeit still as a bulk measurement),¹⁷ and also been used to distinguish amorphous regions in siliceous cement constituents.¹⁸ Here, we used Raman confocal microscopy to investigate the spatial variation in structural disorder of tricalcium silicate (details in SI Section S3.3).

For the 3 s ground sample, no significant difference in the profile of the v₁(SiO₄)⁴⁻ bands was observed between the centre and edge (i.e. outer 1 µm perimeter) regions of tricalcium silicate particles (Fig. 4A–C). This indicates that no meaningful amorphisation took place within 3 s of grinding, consistent with bulk measurements of amorphous content (Fig. 1F). For the 240 s ground sample, no significant differences in spectral profile were observed between centre and edge regions in some particles (Fig. 4D). However, larger particles (>20 µm diameter) with a distinct porous microstructure were also observed. The formation of large, agglomerated particles of amorphised tricalcium silicate occurs in parallel with ongoing comminution; very fine particles are present alongside the large agglomerates after 240 s grinding (Fig. S6 and S8). The parallel processes of comminution and agglomeration also explain the continuing increase of specific surface area at 240 s grinding duration (Fig. 1A). In several of these larger, porous particles, a degree of broadening of the main v₁(SiO₄)⁴⁻ bands was observed in multiple regions within each particle (Fig. 4E and F). These observations indicate that the distribution of amorphised tricalcium silicate is spatially heterogeneous.

Fig. 4 Optical microscope images and Raman spectra for individual particles of tricalcium silicate, for samples: (A)–(C) ground for 3 s, and (D)–(F) ground for 240 s. For (A)–(D), the “c” and “e” annotations represent the centre and edge regions, representing the spectra. For (E) and (F), the letters simply identify different regions within those particles. v₁ denotes the position of v₁(SiO₄)⁴⁻ bands.

This behaviour observed for tricalcium silicate (hardness of ∼9 GPa¹⁹) differs from the expected distribution of amorphous material for harder minerals such as quartz (hardness of ∼14.5 GPa²⁰). In quartz, the crystalline refinement and defect build-up is concentrated in a surface layer.²¹ A possible explanation for these spectral and microstructural changes is that the fine particles undergo amorphisation during repeated impacts, and simultaneously undergo a ‘cold-welding’ of successive fracture and welding events. This process eventually forms larger agglomerates made of fine individual crystallites (as is well-established in mechanical alloying).²¹ Types of defects known to exist in tricalcium silicate include vacancies,^22,23 twinning,²⁴ edge dislocations²³ and kink bands.²³ The formation and movement of dislocations could enable sufficient plasticity for cold-welding phenomena to take place, which are more commonly observed in metallic systems. However, the interpretation from this preliminary data needs further validation using complementary techniques, such as transmission electron microscopy.

In summary, the majority of the increase in hydration heat by 24 h was attributed to the higher bulk specific surface area of tricalcium silicate particles achieved via comminution during high-energy milling. In parallel, partial amorphisation of tricalcium silicate led to an earlier onset of hydration, but made a lower contribution to the heat of hydration.

Author contributions

A. T. M. M.: conceptualization, formal analysis, investigation, supervision, writing – original draft; T. R. S. N.: formal analysis, investigation; M. E.: investigation, software; A. P. formal analysis, investigation, supervision, writing – review & editing; K. L. S.: conceptualisation, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data used to plot the figures for this article are available at https://doi.org/10.5281/zenodo.17661470.

Additional information supporting this article (including methodological details and supporting data) have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cc05691h.

Acknowledgements

Dr Arnaud Magrez is thanked for assistance with Raman confocal spectroscopy.

References

1. A. Ouzia and K. Scrivener, Cem. Concr. Res., 2019, 115, 339–360.
2. H. F. W. Taylor, Cement chemistry, Thomas Telford Publishing, London, UK, 2nd edn, 1997.
3. M. Schneider, V. Hoenig, J. Ruppert and J. Rickert, Cem. Concr. Res., 2023, 173, 107290.
4. H. Zoz, D. Jaramillo V, Z. Tian, B. Trindade, H. Ren, O. Chimal-V and S. Torre, Busan, Korea, 2006.
5. J. N. Maycock, J. Skalny and R. Kalyoncu, Cem. Concr. Res., 1974, 4, 835–847.
6. I. Odler and J. Schüppstuhl, Cem. Concr. Res., 1981, 11, 765–774.
7. K. Mori, T. Fukunaga, Y. Shiraishi, K. Iwase, Q. Xu, K. Oishi, K. Yatsuyanagi, M. Yonemura, K. Itoh, M. Sugiyama, T. Ishigaki, T. Kamiyama and M. Kawai, Cem. Concr. Res., 2006, 36, 2033–2038.
8. S. T. Bergold, F. Goetz-Neunhoeffer and J. Neubauer, Cem. Concr. Res., 2015, 76, 202–211.
9. M. Reformat, F. Bellmann and H. M. Ludwig, Cem. Concr. Res., 2019, 120, 102–107.
10. L. Nicoleau, A. Nonat and D. Perrey, Cem. Concr. Res., 2013, 47, 14–30.
11. K. L. Scrivener, T. Matschei, F. Georget, P. Juilland and A. K. Mohamed, Cem. Concr. Res., 2023, 174, 107332.
12. M. M. Costoya Fernández, Effect of particle size on the hydration kinetics and microstructural development of tricalcium silicate, EPFL, 2008.
13. A. Bazzoni, M. Cantoni and K. L. Scrivener, J. Am. Ceram. Soc., 2014, 97, 584–591.
14. P. Juilland, E. Gallucci, R. Flatt and K. Scrivener, Cem. Concr. Res., 2010, 40, 831–844.
15. E. Yazhenskikh, T. Jantzen, K. Hack and M. Muller, Rasplavy, 2019, 116–124.
16. J. Toporski, T. Dieing and O. Hollricher, Confocal Raman Microscopy, Springer, Cham, 2018.
17. M. Conjeaud and H. Boyer, Cem. Concr. Res., 1980, 10, 61–70.
18. A. Witte and N. Garg, Cem. Concr. Res., 2024, 184, 107612.
19. K. Velez, S. Maximilien, D. Damidot, G. Fantozzi and F. Sorrentino, Cem. Concr. Res., 2001, 31, 555–561.
20. D. L. Whitney, M. Broz and R. F. Cook, Am. Mineral., 2007, 92, 281–288.
21. P. Baláž, in Mechanochemistry in Nanoscience and Minerals Engineering, ed. P. Baláž, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 1–102 DOI:10.1007/978-3-540-74855-7_1.
22. W. Sinclair and G. W. Groves, J. Am. Ceram. Soc., 1984, 67, 325–330.
23. Q. Zheng, C. Liang, J. Jiang, H. Mao, K. C. Bustillo, C. Song, J. A. Reimer, P. J. M. Monteiro, H. Zheng and S. Li, Cem. Concr. Res., 2024, 176, 107391.
24. K. E. Hudson and G. W. Groves, Cem. Concr. Res., 1982, 12, 61–68.

---