Open Access Article
Open Access ArticleAnalysis of thermochemical energy storage in metal carbonates: characterizing cycling-induced degradation
Michael J. Adams a,
Tae Kyu Kim
a,
Tae Kyu Kim a,
Samuel Pennell
a,
Samuel Pennell b,
Judith Vidal
b,
Judith Vidal b and
Akanksha K. Menon
b and
Akanksha K. Menon *ab
*ab
aGeorge W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA. E-mail: akanksha.menon@me.gatech.edu
bNational Renewable Energy Laboratory, Golden, CO 80401, USA
First published on 9th December 2025
Abstract
A solid–gas reaction rate modeling framework is applied to characterize degradation in thermochemical materials induced by thermal cycling. Time constants and a kinetic conversion ratio are established for a representative carbonation-calcination reaction, which provides insight into degradation mechanisms and reveals a mitigation strategy by tuning reaction duration.
The intrinsic intermittency of renewable energy sources poses challenges to the reliability and resilience of power grids.1 Energy storage based on lithium-ion batteries has shown promise over short durations, with typical discharge time ∼4 hours.1,2 However, there is a need for cost-effective storage with discharge times from 10 to 100 hours (long duration storage).3,4 Thermal energy storage (TES), particularly high-temperature TES (>500 °C) presents a low-cost solution to bolster grid reliability while also enabling industrial sustainability through efficient use of process heat.5,6
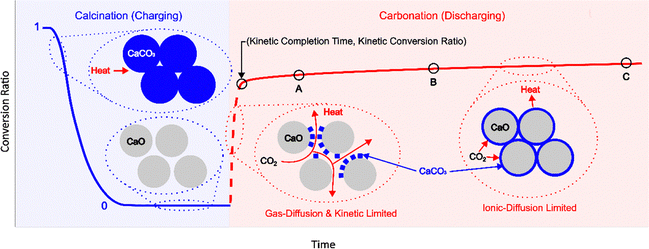
Among various types of storage media, thermochemical materials (TCMs) that undergo reversible solid–gas reactions offer notable advantages, such as high energy density, minimal self-discharge, and a wide range of reaction temperatures.7,8 A representative high-temperature TES is the calcium looping reaction due to its high enthalpy (178 kJ mol−1) at atmospheric pressure, as well as the use of low-cost and abundant materials (limestone).8,9 In the calcination reaction (endothermic charging step), CaCO3 is heated to 850 °C and spontaneously decomposes into CaO and CO2. This is followed by the carbonation reaction (exothermic discharging step) at 650 °C, in which CaO and CO2 recombine to form CaCO3.9 A challenge with this reaction is the reduction in CO2 carrying capacity as the solid material degrades with cycling.10 The capacity is reported in terms of a molar conversion ratio, with thermogravimetric analysis (TGA) being the primary analytical technique for characterizing multicyclic performance. Fig. 1 illustrates the conversion ratio over one cycle, which comprises the calcination reaction followed by the carbonation reaction. Below the decomposition temperature, CO2 off-gassing may occur which complicates analysis of the calcination reaction.11 However, calcination rapidly proceeds to completion in each cycle (horizontal blue curve), whereas carbonation is the limiting step with a two-stage process – an initial rapid reaction (dashed red curve) governed by gas diffusion and chemical kinetics, followed by a prolonged reaction (solid red plateau) limited by ionic diffusion.12,13 Degradation studies thus focus on the exponential decay in carbonation extent, which arises from the coupling between chemical reaction and transport (gas and ionic diffusion) that in turn is accompanied by microstructural changes (e.g., nascent sintering and pore blocking).14–16 While these are distinct mechanisms driven by high-temperature densification and product layer deposition, respectively, the main challenge arises in experimentally isolating their effect on reaction conversion.
Understanding the cycling-induced degradation in TCMs is hindered by the lack of standardized reaction completion criteria.17 The molar conversion ratio of CaO provides a quantitative measure of total carbonation extent, but it is time-dependent and increases with experimental duration. For example, in Fig. 1, a carbonation reaction that occurs until point C would have a higher conversion ratio compared to one that occurs until points A or B. Conversion ratio is also strongly dependent on reaction temperature – Criado et al. showed that carbonation at 650 °C results in minimal contribution of the ionic diffusion-limited region to total conversion compared to carbonation at a lower temperature of 450 °C, where the diffusion-limited region makes up a significant portion of the total conversion.18 Consequently, a comparative analysis of the same material cycled under different conditions or form factors (powders and pellets) is not possible.
In this work, we provide a framework (standardized experimental procedure and analysis method) to characterize TCMs. The application of this framework not only provides insight into degradation of storage materials by cycling, but it also highlights strategies to mitigate degradation. Specifically, the conversion extent increases after a sequence of short and long cycles, revealing a viable pretreatment that requires only the reaction duration to be varied. This provides a significant advantage over mitigation approaches in the literature, such as inert additives,19–21 reducing particle size,13 or modifying reaction conditions.22,23
Pellets were fabricated from calcium carbonate powder (99% purity, Thermo Fisher Scientific) using a cold sintering method described in the SI.24 A pellet with density of 2.16 ± 0.03 g cm−3 and 1.75 ± 0.02 mm thickness was diced into samples of ∼40 mg each; all samples in this work were from the same pellet to ensure consistency. Charge–discharge characterization was performed with thermogravimetric analysis (TGA) using a NETZSCH STA 449 F3 Jupiter system. Each cycle consists of a calcination segment (charging) at 850 °C under 100 mL min−1 argon, followed by a carbonation segment (discharging) at 650 °C under 100 mL min−1 CO2 at atmospheric pressure. Mass uptake is converted into a CaO molar conversion ratio, X using eqn (1), where m0 is the initial mass (at the onset of carbonation), m is the time-dependent mass uptake, and M is the molar mass.
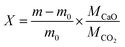 | (1) |
The carbonation reaction was analyzed by fitting a general rate model established for spherical particles in a solid–gas reaction.25 As shown in Fig. 1, the reaction rate comprises two stages – an initial fast reaction governed by chemical kinetics and gas diffusion, followed by a slow reaction limited by ionic diffusion through the solid product shell. The instantaneous reaction rate, dX/dt therefore comprises two terms proportional to the fraction of unreacted CaO reactant surface area (δ) and CaCO3 product layer surface area (1 − δ), as shown in eqn (2). The primary fitting parameters are the reaction rate constant ks, surface diffusion coefficient Ds, and a function β that contains the product layer diffusion coefficient.25 The remaining variables are geometric functions and physical constants, which are described in the SI.
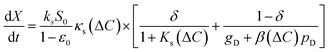 | (2) |
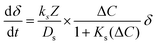 | (3) |
Ultimately, δ exhibits exponential decay with time, which can be characterized with a time constant. Again, 3τ corresponds to 95% completion, and we refer to this duration as the kinetic completion time. Fitting the general rate model to the carbonation reaction in the first cycle resulted in a kinetic completion time of 3 minutes – this is used as the optimal duration for a “short” carbonation reaction. The conversion ratio at this threshold is the kinetic conversion ratio, Xk, which is used herein to define the cycle conversion.
To relate the cycling-induced degradation to microstructural changes in the material, calcined pellets were sectioned with a razor blade and imaged using a Hitachi 4800 SEM with 5 kV accelerating voltage. Calcined pellets were imaged given their porous microstructure that evolves with cycling. Carbonated pellets revealed a dense material, as the product layer forms a solid shell, which is consistent with other studies.14,16 Over multiple cycles, degradation can be represented by a decay in the cycle conversion. This is because the calcination reaction proceeds to completion whereas carbonation is rate limited, as shown in Fig. 1. A quantitative definition of cycle conversion is necessary – we propose using δ(t) from the general rate model to calculate a standardized kinetic completion time and kinetic conversion ratio. The general rate model for solid–gas chemical reactions was chosen to represent the carbonation reaction as it provides a physical basis for its two-stage nature. This model has been validated with experimental data over a range of conditions, but applied herein for the first time to define the kinetic conversion ratio.25
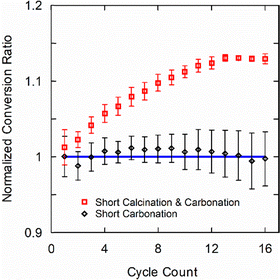
To quantify degradation under cycling, a baseline experiment was performed with “long” reaction times comprising 30-min calcination and 75-min carbonation segments (consistent with the initial characterization described in Methods). The kinetic conversion ratio under “long” cycling conditions, hereafter referred to as the baseline, provides a reference point for evaluating other cycling durations. Two scenarios are of interest that can influence degradation and boost long-term performance: (i) varying the duration of each reaction (calcination and carbonation), and (ii) varying the carbonation duration sequentially. Comparing the kinetic conversion ratio in these cases to the baseline provides insight into degradation mechanisms and mitigation strategies, which enables accelerated cycling and boosts long-term performance.
Nascent sintering of CaO formed by thermal decomposition of CaCO3 is known to degrade the conversion ratio by decreasing specific surface area of the reactant.26,27 As such, “short” calcination and carbonation durations are a potential mitigation strategy that can be implemented, and two such scenarios are studied. In one scenario, only the carbonation reaction was reduced to 3 min (equal to the kinetic completion time, see Methods), while maintaining the calcination duration of 30 min. In another experiment, the calcination duration was additionally reduced to 10 min (based on the time constant for calcination, see Methods). Despite the different timescales, the experiments can be directly compared using the standardized kinetic conversion ratio defined herein.
Fig. 2 shows that short carbonation alone has no effect on the conversion ratio, but short carbonation along with short calcination enhances conversion ratio by over 10% in 16 cycles. This reveals that degradation, primarily by sintering as we show later, occurs during the calcination step and it can be mitigated to some extent by shortening the reaction duration using the time constant. Interestingly, although short carbonation reactions alone do not enhance the conversion ratio normalized to the baseline value, it provides an opportunity to characterize materials rapidly. Specifically, the same degradation behavior can be measured over the same number of cycles in just one-third of the experimental time.
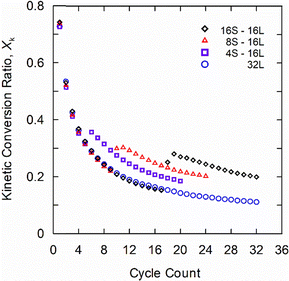
In a second scenario, the baseline experiment was extended to 32 “long” (L) cycles. The resulting kinetic conversion ratio shown in Fig. 3 exhibits a monotonic decay from 73% to 11%. This is analyzed with an empirical fit eqn (4) that captures exponential decay in the conversion ratio due to sintering, using a deactivation constant (k) and residual conversion (Xr) as fitting parameters.10 Residual conversion represents the plateau in storage capacity in carbonate TCMs from 50 to 500 cycles. Applying this to the 32L case with a constant cycle time yields a residual conversion of 5.2% and a deactivation constant of 0.51; these values are in agreement with previous reports.10 This reveals that there is a significant reduction in residual storage capacity with cycling, which can be predicted based on the conversion ratio for the first 32 cycles (N is cycle count).
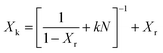 | (4) |
To decrease the extent of degradation, the carbonation time was varied sequentially as 4, 8, and 16 “short” (S) cycles of 3-min carbonation followed by 16 “long” (L) cycles of 75-min carbonation. A fixed calcination of 30 min was used to isolate the effects of carbonation duration. Fig. 3 shows that samples subjected to short carbonation cycles have the same performance as the baseline experiment, but subsequent long cycles increase the conversion ratio. For example, the case with 16S followed by 16L cycles (black diamonds) exhibits the same degradation as the baseline (blue circles) over the first 16 cycles. However, subjecting that sample to an additional 16L cycles results in 80% higher conversion than the baseline. The enhancement effect is amplified as the number of short cycles increases, suggesting that this can be used as a pretreatment strategy to boost the long-term performance of TCMs. This is consistent with prior findings for carbon capture applications.16
Since only the carbonation duration is being varied and sintering does not occur at these temperatures, we hypothesize that pretreatment based on alternating cycle times enhances performance by mitigating pore plugging. This is qualitatively confirmed with SEM images of pellet samples in the calcined state – Fig. 4 compares the microstructure of the 16S–16L and 32L cycled samples to that of pristine CaO. The pristine pellet shows a porous microstructure (comprising micron and submicron pores) throughout, whereas the cycled pellets have densified regions that are indicative of the loss of reactant surface area (by sintering of nascent CaO), resulting in the observed decay in conversion ratio with cycling. A reduction in connected porosity through the pellet slows down the kinetic-limited reaction; this is confirmed by comparing CO2 uptake in pellets and powder samples that exhibit the same kinetic conversion ratio but at different durations of 3 min and 16 s, respectively (see SI). With cycling, repeated formation and decomposition of the CaCO3 product layer causes CaO agglomeration, which restricts gas diffusion pathways to the unreacted surface. This pore blockage introduces significant transport resistance, which effectively lowers the available reactant surface area during the kinetic-limited reaction. The 16S–16L experiment thus retains more porous regions than the 32L experiment, enabling the gas to diffuse to the unreacted surface area during the kinetic reaction. Ultimately, the duration and number of initial cycles impact the final conversion ratio, thereby making thermal pretreatment (alternating S and L cycles) a viable strategy to mitigate degradation in TCMs.
 | ||
| Fig. 4 Electron micrographs showing representative microstructural comparison of pristine and cycled CaO pellets. | ||
Overall, this work advances the understanding of cycling-induced degradation in carbonates through: (i) a standardized kinetic conversion analysis framework enables direct comparison across different experimental conditions using a reaction time constant, (ii) degradation in the form of sintering is shown to occur during the high-temperature calcination reaction, which can be mitigated by ∼10% using short calcination cycles, and (iii) thermal pretreatment by alternating the carbonation duration is shown to enhance energy storage capacity by 80% by mitigating pore plugging. The outcome is that the experimental time for charge–discharge cycling is reduced by one-third, while also providing physical insight into different degradation mechanisms at play. Future work should apply this framework to other TCMs that exhibit a two-stage reaction (e.g., metal oxides and hydroxides), with modified rate models and experimental validation. New techniques for rapid and high-throughput characterization of TCMs over 1000 s of cycles are also needed for practical applications.
This work was supported by the U.S. Department of Energy, Office of Science Energy Earthshot Initiative as part of the Degradation Reactions in Electrothermal Energy Storage (DEGREES) project at the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. The views in the article do not necessarily represent the views of the DOE or the U.S. Government.
Conflicts of interest
The authors declare no competing interests.Data availability
The pellet fabrication methods, calcination time constant analysis, carbonation rate model analysis, total to kinetic conversion ratio comparison, and pellet to powder sample comparison data has been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cc04302f.References
- O. Smith, O. Cattell, E. Farcot, R. D. O’Dea and K. I. Hopcraft, Sci. Adv., 2022, 8, eabj6734 CrossRef.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS.
- P. Albertus, J. S. Manser and S. Litzelman, Joule, 2020, 4, 21–32 CrossRef CAS.
- J. A. Dowling, K. Z. Rinaldi, T. H. Ruggles, S. J. Davis, M. Yuan, F. Tong, N. S. Lewis and K. Caldeira, Joule, 2020, 4, 1907–1928 CrossRef.
- A. Henry, R. Prasher and A. Majumdar, Nat. Energy, 2020, 5, 635–637 CrossRef CAS.
- A. M. Pantaleo, S. Trevisan, F. Matteucci and L. F. Cabeza, J. Energy Storage, 2024, 103, 114261 CrossRef.
- A. Gil, M. Medrano, I. Martorell, A. Lázaro, P. Dolado, B. Zalba and L. F. Cabeza, Renewable Sustainable Energy Rev., 2010, 14, 31–55 CrossRef CAS.
- A. A. Khosa, T. Xu, B. Q. Xia, J. Yan and C. Y. Zhao, Sol. Energy, 2019, 193, 618–636 CrossRef CAS.
- C. Ortiz, J. M. Valverde, R. Chacartegui, L. A. Perez-Maqueda and P. Giménez, Renewable Sustainable Energy Rev., 2019, 113, 109252 CrossRef CAS.
- G. S. Grasa and J. C. Abanades, Ind. Eng. Chem. Res., 2006, 45, 8846–8851 CrossRef CAS.
- A. Scaltsoyiannes and A. Lemonidou, Chem. Eng. Sci.: X, 2020, 8, 100071 CAS.
- Z. Sun, S. Luo, P. Qi and L.-S. Fan, Chem. Eng. Sci., 2012, 81, 164–168 CrossRef CAS.
- D. Alvarez and J. C. Abanades, Ind. Eng. Chem. Res., 2005, 44, 5608–5615 CrossRef CAS.
- X. K. Tian, S. J. Guo, S. C. Lin, J. Yan, S. H. Ju and C. Y. Zhao, Sol. Energy Mater. Sol. Cells, 2023, 263, 112593 CrossRef CAS.
- Q. Hu, Y. Jiang and Z. Wang, J. Alloys Compd., 2025, 1010, 177960 CrossRef CAS.
- A. I. Lysikov, A. N. Salanov and A. G. Okunev, Ind. Eng. Chem. Res., 2007, 46, 4633–4638 CrossRef CAS.
- R. Bayón and E. Rojas, Int. J. Energy Res., 2019, 43, 6521–6541 CrossRef.
- Y. A. Criado, B. Arias and J. C. Abanades, Ind. Eng. Chem. Res., 2018, 57, 12595–12599 CrossRef CAS.
- H. Guo, J. Feng, Y. Zhao, S. Wang and X. Ma, J. CO2 Util., 2017, 19, 165–176 CrossRef CAS.
- W. Liu, B. Feng, Y. Wu, G. Wang, J. Barry and J. C. Diniz da Costa, Environ. Sci. Technol., 2010, 44, 3093–3097 CrossRef CAS PubMed.
- J. M. López, G. Grasa and R. Murillo, Chem. Eng. J., 2018, 350, 559–572 CrossRef.
- C. Luo, Y. Zheng, J. Guo and B. Feng, Fuel, 2014, 127, 124–130 CrossRef.
- B. V. Materic, C. Sheppard and S. I. Smedley, Environ. Sci. Technol., 2010, 44, 9496–9501 CrossRef PubMed.
- M. Cao, W. B. Hong, X. D. Yang, Y. Q. Jia, L. Li, S. Y. Wu, H. S. Yang and X. M. Chen, J. Am. Ceram. Soc., 2023, 106, 1668–1680 CrossRef CAS.
- Z. Li, Chem. Eng. Sci., 2020, 227, 115902 CrossRef CAS.
- R. H. Borgwardt, Chem. Eng. Sci., 1989, 44, 53–60 CrossRef CAS.
- J. C. Abanades and D. Alvarez, Energy Fuels, 2003, 17, 308–315 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |