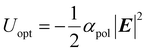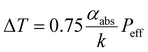Microanalysis of a single droplet produced by optical tweezers in an aqueous solution of bovine serum albumin

Abstract

The liquid–liquid phase separation of proteins is associated with the generation of membraneless organelles as well as of crystals and amyloid fibrils. The phase separation proceeds through spontaneous concentration fluctuations, and is therefore challenging to control. Here, we demonstrate a spatially and temporally controlled phase separation in an aqueous bovine serum albumin solution using optical tweezers. The protein solution contains trivalent ions and separates into two phases at elevated temperatures. Upon focusing a near-infrared (NIR) laser beam into the solution, a single microdroplet is produced at the laser focus site due to the photothermal effect and optical trapping. Taking advantage of this controllability, the droplets are individually characterized in terms of protein concentration, secondary structure, and growth modes. The droplets exhibit two distinct growth behaviors, depending on their size and secondary structure. This approach offers a platform for probing phase behavior at the single-droplet level with potential applications in crystallization and amyloidogenesis.

---

Introduction

Liquid–liquid phase separation (LLPS) involves separation into dilute and dense phases and typically results in the formation of microdroplets. The resultant metastable dense droplets have no membrane but high fluidity and thus can form and dissociate rapidly and reversibly in response to environmental changes. Owing to these properties, the LLPS of proteins plays an essential role in promoting or inhibiting local biochemical reactions in vivo.^1–3 Moreover, the droplet formation of proteins is occasionally associated with the formation of crystals and amyloid fibrils.^4–8 Thus, the ability to control LLPS in protein solutions is crucial for understanding their phase diagrams as well as for elucidating the pathways of protein association. Most systems exhibit upper-critical-solution-temperature (UCST) behavior, and their LLPS can be induced by increasing the protein concentration or decreasing the temperature. In contrast, lower-critical-solution-temperature (LCST) behavior is observed in some systems, where LLPS occurs at elevated temperatures. In both UCST and LCST systems, droplet formation is driven by stochastic liquid nucleation throughout the solution, and thus, establishing precise control over LLPS in protein solutions remains challenging.

Optical tweezing represents a promising technique for manipulating microparticles as well as for controlling phase separation.^9–12 A focused laser beam exerts an optical force on solute molecules, thereby generating an optical potential well, U_opt:

where α_pol denotes the polarizability of the solute and E represents the electric-field vector of the incident light. This optical potential plays a role in spatially confining the solute, leading to a local-concentration increase. Under these conditions, solid or liquid nucleation is initiated at the focal spot.^13,14 Indeed, a single liquid-like condensate has been successfully produced in HEWL and α-synuclein solutions, which are UCST systems.^15–17 These LLPS behaviors arise from the local-concentration increase due to optical trapping. Focused irradiation with a 1064 nm laser beam leads to the generation not only of U_opt, but also of a photothermal effect. In LCST systems, the photothermal effect initiates phase separation around the laser focus point. The resultant small droplets are then attracted toward U_opt, where they coalesce into a single droplet. Such laser-induced single-droplet-formation behavior has been demonstrated in various aqueous solutions containing polymers, alcohols, and ionic liquids.^18–21 However, protein solutions with LCST-type LLPS behavior have not yet been investigated using optical tweezers.

In this study, we successfully employed optical tweezers to induce the formation of a single protein-rich microdroplet in a protein solution comprising bovine serum albumin (BSA) and yttrium³⁺ chloride (YCl₃), which exhibits LCST-type LLPS. The high spatial control afforded by optical trapping enabled a subsequent in situ analysis of the droplet via both microscopic and microspectroscopic techniques. The progression of the LLPS was characterized at the single-droplet level in terms of protein concentration, secondary-structure changes, and growth modes. While protein droplets have been studied from these viewpoints separately,^17,22–24 we clearly demonstrate their correlation by preparing only one droplet in a spatially and temporally controlled manner. This approach, based on control of LLPS and multifaceted analysis, may provide a novel platform for investigating phase behavior in protein solutions and tuning pathways in protein crystallization and amyloidogenesis.

Experimental section

Sample preparation and characterization

BSA and YCl₃ were purchased from Sigma-Aldrich. Stock solutions of BSA (80 mg mL⁻¹) and YCl₃ (10 mM) were prepared by dissolving the respective compounds in deionized water. These stock solutions were then mixed to prepare sample solutions, and the final protein and salt concentrations were adjusted by dilution with deionized water. The size distribution and zeta potential of the sample solutions were characterized using a particle analyzer.

For optical-trapping experiments, sample solutions containing 40 mg mL⁻¹ of BSA were used. The concentration of YCl₃ was adjusted to either 4.0 or 4.2 mM in order to account for minor temperature fluctuations in the experimental environment (typically maintained at 24 °C). Prior to experiments, sample solutions were filtered through a membrane filter with a pore size of 0.45 µm. The phase-separation temperature of the prepared solutions was estimated to be 26 °C (for details, see SI section S1).

Optical setup

Details of the optical setup are described in detail elsewhere.²⁵ A continuous-wave (cw) 1064 nm laser was used as the optical tweezer. The near-infrared (NIR) laser beam was coupled with an inverted microscope and focused into the sample solution using an oil-immersion objective lens (numerical aperture: 1.45). Raman microspectroscopy was performed using a cw 488 nm laser as the excitation-light source. The scattered Raman signal was directed into a spectrograph and detected using a charge-coupled device detector. Fluorescence imaging was carried out under wide-field illumination using the 488 nm laser beam. Both optical transmission and fluorescence images were acquired using an imaging camera.

Results and discussion

Droplet formation

BSA is a globular protein with a 29.8 Å radius of gyration. Aqueous solutions containing BSA and trivalent cations exhibit LLPS above a critical temperature.^26–28 To investigate this behavior, we first confirmed that phase separation of the BSA/YCl₃ solutions was induced by homogeneous heating. A previous study suggested that the LLPS in such systems is driven by ion-mediated protein interactions, in which entropy changes in the hydration water play a critical role.²⁶ Both Y³⁺ ions and the carboxylic acid on the BSA surface are surrounded by stable hydration shells. In aqueous solution, Y³⁺ ions are typically coordinated by 8–10 water molecules, while the hydration shell on the protein surface consists of approximately 2 water molecules per hydrophilic residue. In the mixture, some of the hydration water is released upon cation binding, resulting in an increase in system entropy. Additionally, the charge distribution on the protein surface changes, and cations bridge protein molecules, releasing further hydration water. Thus, both direct cation binding and bridging contribute to increased entropy, which promotes the association of BSA molecules. This molecular association is further enhanced with increasing the temperature above the critical point, ultimately leading to phase separation.

We measured the zeta potential of solutions containing 1.0 mg mL⁻¹ BSA with varying concentrations of YCl₃. The zeta potential could not be measured in the absence of YCl₃, but has previously been reported to be approximately −9 mV.²⁹ With increasing YCl₃ concentration, the overall charge of the protein gradually became less negative and eventually became positive (SI S2), consistent with a previous report.²⁶ This charge inversion indicates the binding of cations to the protein surface, which promotes protein aggregation.

The occurrence of an aggregation process was supported by light-scattering measurements to estimate the size of BSA in the sample solutions. Fig. 1a shows the size distribution of the aqueous solutions of BSA with different YCl₃ concentrations and temperatures. In the absence of YCl₃, a light-scattering signal at ∼3 nm was observed, corresponding to isolated BSA molecules. Upon adding YCl₃, the signal shifted to 10–20 nm, indicating the formation of protein aggregates due to cation bridging. When the solution was heated to 33 °C, phase separation occurred, and micrometer-sized BSA-rich droplets were formed (Fig. 1b). The light-scattering signal shifted to several micrometers, corresponding to the formation of phase-separated droplets.

Fig. 1 (a) Size distribution in BSA aqueous solutions with and without YCl₃. The measurement temperature is indicated in each panel. (b) Optical-transmission image of the BSA/YCl₃ aqueous solution after heating to 33 °C ([YCl₃] = 4.2 mM).

An optical-tweezing technique enabled us to establish control over the phase separation (Fig. 2a). In contrast to the random nucleation of droplets observed under homogeneous heating, a single BSA-rich droplet was generated in a spatially and temporally controlled manner by focusing a NIR laser beam into the protein solution. Fig. 2b shows the time evolution of the optical-transmission micrographs near the focal point of the laser. The power of the laser (P_eff) was measured after the objective lens and tuned to 300 mW. No immediate visible changes were observed at the start of irradiation, and the solution remained homogeneous [Fig. 2b(i)]. After approximately 25 s of irradiation, a small droplet appeared at the focus point of the laser, indicating the onset of liquid nucleation. The droplet reached a diameter of 2.0 μm at 40 s [Fig. 2b(ii)] and continued to grow steadily while remaining stably trapped [Fig. 2b(iii)], eventually reaching a diameter of 10.0 μm after 130 s [Fig. 2b(iv)].

Fig. 2 (a) Schematic illustration of single-droplet formation using the optical-tweezing technique. (b) Optical-transmission micrographs under irradiation by a focused NIR laser beam (P_eff = 300 mW). The elapsed time from the start of irradiation is indicated in each panel. (c) Temporal evolution of the droplet diameter varying the laser power (P_eff = 300, 325, and 350 mW) ([YCl₃] = 4.2 mM).

Fig. 2c (black circles) shows the temporal evolution of the diameter of the droplet in Fig. 2b. Following liquid nucleation, the droplet continued to grow steadily under laser irradiation. When the laser power was reduced slightly, the growth ceased, and the droplet maintained a constant size. Similar single-droplet-formation behavior was also observed at higher laser powers (325 and 350 mW; Fig. 2c). The time required for liquid nucleation decreased with increasing P_eff. The dynamics of droplet growth under optical-trapping conditions will be discussed in a later section.

Raman spectroscopy

To estimate the BSA concentration within the individual droplets produced by the optical tweezers, we combined optical trapping with Raman microspectroscopy. First, a calibration curve was constructed using aqueous BSA solutions without YCl₃. For this, the Raman spectra of bulk BSA solutions with protein concentrations ranging from 0 to 600 mg mL⁻¹ were recorded under steady-state conditions. Two distinct Raman bands corresponding to BSA and water were observed in the C–H (2750–3080 cm⁻¹) and O–H (3080–3750 cm⁻¹) stretching regions, respectively (Fig. 3a). The signal intensity in the C–H stretching region increased with increasing BSA concentration. The ratio of the integrated band areas, [R_CH/R_CH + R_OH], was plotted as a function of the concentration of BSA to generate a calibration curve (Fig. 3b).

Fig. 3 (a) Raman spectra of bulk BSA solutions with varying protein concentrations. (b) Calibration curve showing the relationship between BSA concentration and the Raman band-area ratio [R_CH/R_CH + R_OH]. (c) Raman spectra of droplets with different diameters generated by the NIR laser optical-tweezing technique. (d) Relationship between droplet diameter and BSA concentration, using droplets generated via either optical tweezing or homogeneous heating. The spectra shown in (a) and (c) were normalized using the peak intensities in the O–H stretching region ([YCl₃] = 4.2 mM).

Single microdroplets of varying size were then produced under optical-trapping conditions in the aqueous protein solution, and their Raman spectra were measured. To maintain a constant droplet size during the measurements, P_eff was reduced slightly and carefully controlled once the droplet reached the desired size. Raman spectra were then recorded at the focal point of the NIR laser beam. As shown in Fig. 3c, the intensity of the signal in the C–H stretching region increased with increasing droplet size. From these Raman spectra, the band-area ratio [R_CH/R_CH + R_OH] was calculated and the BSA concentration was estimated on the basis of the calibration curve (Fig. 3b). The BSA concentration was found to increase with increasing droplet size (Fig. 3d), eventually reaching ∼600 mg mL⁻¹.

For comparison, we also estimated the BSA concentration in droplets formed via homogeneous heating. In that case, a 488 nm laser beam was used as both the excitation source for Raman spectroscopy and for optical trapping; no NIR laser irradiation was applied. From among the many droplets in the heated solution, a single droplet was selectively trapped, and its BSA concentration was estimated based on its Raman spectrum. In total, 12 droplets were analyzed; their diameter ranged from 2.0 to 6.0 µm and their BSA concentration from 200 to 300 mg mL⁻¹ (red circles in Fig. 3d). These results demonstrate that optical trapping enables the formation of BSA-rich single droplets with tunable size and concentration.

The BSA within the droplets was found to undergo structural changes during the growth process. The Raman amide I band (1500–1750 cm⁻¹) of proteins is highly sensitive to the secondary structure of the protein backbone and minimally affected by side chains, making it a valuable probe of changes in protein-backbone conformation.³⁰ To evaluate the evolution of the BSA conformation during the droplet-growth process, BSA droplets were produced under the NIR optical-trapping conditions and their Raman spectra in the amide I region were measured (Fig. 4a). The spectra were smoothed using the Savitzky–Golay algorithm and normalized with respect to the intensity of the peak at ∼1650 cm⁻¹. As the droplets condensed, the peak shifted slightly toward higher wavenumbers and changes in the band shape were observed. Specifically, the intensity decreased at the lower-wavenumber side of the peak, while it increased at the higher-wavenumber side. These spectral changes can be more clearly observed in the difference spectra in Fig. 4b, wherein the spectrum of the initial solution was subtracted from those of the droplets. With increasing droplet concentration, the signal in the 1550–1650 cm⁻¹ region weakened, whereas that in the 1650–1680 cm⁻¹ region intensified. Similar spectral changes have previously been reported for mixtures of BSA and guanidine hydrochloride, and are indicative of protein unfolding.³⁰

Fig. 4 (a) Evolution of the Raman spectra of the BSA-rich droplets with increasing protein concentration during the growth process. (b) Difference spectra of the droplets relative to the initial solution. (c) Second-derivative spectrum and deconvoluted Gaussian curves of the Raman spectrum of the initial solution (40 mg mL⁻¹). (d) Fractional areas of bands 2 and 3 ([YCl₃] = 4.0 mM).

The amide I band of the Raman spectra was deconvoluted using multiple Gaussian curves representing different secondary structures. Fig. 4c shows the analyzed data for the Raman spectrum of the initial solution. To set Gaussian functions for curve fitting, the second-derivative spectrum was calculated using the same algorithm. Blue curves represent the deconvoluted Gaussian components. The red line corresponds to the measured spectrum, while the black dotted line indicates the sum of all the fitted components. Four main peaks were identified within the 1600–1700 cm⁻¹ region, i.e., 1607 cm⁻¹ (band 1), 1648 cm⁻¹ (band 2), 1682 cm⁻¹ (band 3), and 1697 cm⁻¹ (band 4). Additionally, the deconvolution generated several bands in the 1500–1600 cm⁻¹ and 1700–1750 cm⁻¹ regions.

BSA is mostly helical (66% helices) with no β-sheets in its native conformation. The spectral range from 1648 to 1658 cm⁻¹ was assigned to α-helices; accordingly, the native-state BSA exhibits a broad and intense peak at 1650 cm⁻¹. The spectral bands at 1660–1670 cm⁻¹, 1670–1680 cm⁻¹, and 1680–1690 cm⁻¹ have been reported to correspond to β-sheets, β-turns, and random structures, respectively.³⁰ To obtain quantitative information regarding the change in the secondary structure of BSA during the growth process, we calculated the individual fractional area of bands 1–4 relative to the sum of their areas. The other bands were not included in the analysis due to their relatively small contribution to the structural change of the backbone. The fraction of band 2 should be correlated to the helix content. This fraction decreased slightly with increasing BSA concentration/droplet growth (Fig. 4d), implying a decrease in helix structures. On the other hand, the contribution of band 3 was strengthened with droplet growth. This result indicates that β-sheets, β-turns, and random structures accumulate with increasing BSA concentration during droplet growth under optical-trapping conditions.

We may have some effects of water in the spectral analysis above, because a weak band of the H₂O bending vibration is observed at 1550–1750 cm⁻¹ (SI S3). But the alterations in the protein secondary structure are also supported by the results on dissolution process. The concentration threshold for the structural change is likely 400 mg mL⁻¹, which corresponds to a droplet diameter of 4.5 µm (volume: 48 µm³). Indeed, once the droplet grew to a diameter of 6.0 µm, it did not dissolve completely after the NIR laser was switched off (SI S4), whereas a droplet of approximately 3.0 µm did completely dissolve.

Fluorescence imaging

To further investigate the structural changes of BSA within the droplet, we used the fluorescent probe dye Congo Red (CR) at a concentration of 500 μM to visualize BSA-rich droplets via fluorescence imaging. CR exhibits very weak fluorescence in solution but shows strong emission upon binding to amyloid fibrils, which are insoluble β-sheet-rich aggregates.³¹ Therefore, CR serves as a useful indicator for detecting β-sheet structures in BSA droplets.

Fig. 5 shows the time evolution of the fluorescence images near the focal spot of the NIR laser beam. These images were captured under wide-field illumination using a cw 488 nm laser. Prior to NIR laser irradiation, the solution exhibited negligibly small fluorescence due to the low quantum yield of CR in solution. This was attributed to the dominant non-radiative relaxation processes due to the efficient torsional motion of the dye. In contrast, the droplets exhibited red fluorescence, which may result from the binding of CR to β-sheet-rich structures and the consequent restriction of its torsional motion. These results suggest that the secondary structure of BSA undergoes changes during the droplet-growth process.

Fig. 5 Fluorescence micrographs under the focused irradiation of the NIR laser beam and wide-field illumination with a 488 nm laser beam ([YCl₃] = 4.2 mM).

Droplet-growth modes

The rate of change in the droplet volume during NIR-induced single-droplet growth provided crucial insight into the growth mechanism. In Fig. 6, the droplet volume is plotted as a function of time with logarithmic scales on both axes (for details, see Fig. S5 in the SI). The log–log plots exhibited different slopes in the early and late stages of droplet growth at all applied laser powers. At P_eff = 325 mW, the droplet volume increased proportionally to t^2.25 for volumes between 0 and 25 µm³. Beyond this size, the growth rate was approximately proportional to t^1.07. Similar trends were observed at the other examined laser powers; at P_eff = 300 mW, the volume grew proportional to t^2.18 up to 33 µm³ and to t^1.37 above that, while at P_eff = 350 mW, the growth was proportional to t^1.55 up to 40 µm³ and to t^1.23 above that. These results indicate that the droplet-growth mechanism changes depending on the droplet size.

Fig. 6 Log–log plot of the volume of the BSA-rich droplets as a function of time.

The observed growth rate is significantly higher than that reported for other systems, such as emulsion droplets in bulk solutions.^32,33 We attribute this discrepancy to the difference in the number of droplets present in the solution. In the present study, we focus on the time dependence of droplet volume and discuss the droplet growth mode. The growth rate of liquid droplets in LLPS is governed by mechanisms such as flocculation, coalescence, and Ostwald ripening. Flocculation and coalescence are considered to be diffusion-controlled aggregation processes in which dispersed phases collide and merge. In such cases, the droplet radius R_d follows the relationship R_d^1/0.57 ∝ t, where R_d is the droplet radius and t is the time. This implies a nonlinear increase in droplet volume with time, i.e., R_d³ ∝ t^1.71. In contrast, Ostwald ripening involves the growth of larger droplets at the expense of smaller ones, driven by the diffusion of dispersed molecules through the continuous phase. In this mechanism, the droplet volume increases linearly with time, i.e., R_d³ ∝ t, as reported in our previous study.³⁴

In the present study, the BSA-rich droplets exhibited a nonlinear volume increase with time during the early growth stage, suggesting that flocculation and coalescence dominate the initial growth process. In the later stage, the growth transitioned to an approximately linear regime, indicating that Ostwald ripening became the dominant mechanism. It is also noteworthy that the droplet-growth-mode changes at a volume of 25–40 µm³, which is close to the threshold of secondary-structure change.

Droplet formation and growth dynamics

Here, we consider the formation mechanism of a BSA-rich single droplet prepared under NIR laser irradiation. The BSA/YCl₃ mixture has a critical temperature above which phase separation occurs. The local temperature is an important factor in this mechanism. The initial solution partially absorbs the incident NIR laser beam due to overtones of the O–H vibrational mode of the solvent molecules (water). As a result, the solution temperature is elevated around the laser focus point. According to the literature,³⁵ the temperature elevation (ΔT) is expressed by the following equation:
where α_abs and k are the absorption coefficient and the thermal conductivity of the initial solution, respectively, while P_eff is the input laser power. We calculated ΔT using the parameters for a 40 mg mL⁻¹ aqueous solution of BSA, i.e., α_abs = 13.7 m⁻¹ (SI S5) and k = 0.59 W m⁻¹ K⁻¹.³⁶ The input laser power (P_eff) was 0.30 W. We estimated ΔT to be 5.2 K, which would give a local solution temperature of 29 °C around the laser focus spot (Fig. 7a). This value is very close to the experimentally estimated critical temperature.

Fig. 7 A schematic illustration showing the possible dynamics of BSA droplet formation together with the accompanying evolution of U_opt. The illustration presents (a) local heating, (b) droplet formation, (c) droplet growth, and (d) structural change.

This temperature rise triggers LLPS, generating small droplets around the laser focus site (Fig. 7b), which then aggregate and fuse to form a small single droplet (Fig. 7c). In this early stage, flocculation and coalescence are the dominant processes of droplet growth. Accordingly, the droplet volume increases nonlinearly with time. The polarizability of the droplet is increased with protein concentration. Once a small single droplet is formed at the laser focus site, the droplet becomes gradually condensed to deepen U_opt. BSA concentrated in the deep U_opt possibly exhibits structural change (Fig. 7d).

It should also be noted here that the local temperature rise is suppressed with droplet growth. Both α_abs and k decrease with the BSA concentration (SI S6), but the former has a steeper negative slope with BSA concentration.³⁶ Consequently, ΔT decreases with droplet growth. This implies that the driving force for droplet growth in the late stage is not laser heating. Therefore, we conclude that the growth is correlated to changes of the secondary structure of BSA. Partially denatured proteins may act as a kind of nuclei, thereby promoting subsequent droplet growth, similarly to the self-catalytic growth of amyloid fibrils.

Conclusions

We have demonstrated how optical tweezers can be used to establish spatial and temporal control of LLPS in a BSA/YCl₃ solution. A BSA-rich droplet was formed at the focal spot of an NIR laser, and the growth mechanism of the droplet changed as its size increased. The initial small droplets grow due to the photothermal effect, while the further growth of the resulting large, dense droplets is most likely associated with a change of the secondary structural of BSA. We plan to extend this work to other systems, such as more biologically relevant protein solutions or UCST-type protein solutions. The present approach provides a versatile platform for investigating the phase behavior of proteins at the single-droplet level, which could potentially be used to induce protein crystallization and amyloid-fibril formation via selective pathways in the phase diagram.

Author contributions

A. T.: investigation, formal analysis, visualization, validation, and data curation; Y. T.: supervision, resources, project administration, funding acquisition; K. Y.: writing – review & editing, supervision, resources, project administration, methodology, funding acquisition, and conceptualization. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

All relevant data are included within the manuscript and the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5an01045d.

Acknowledgements

This work was financially supported by JSPS KAKENHI grants JP20H02550, JP22H05138, JP23H04600, and JP25K08452. The authors are moreover grateful for financial support from the CANON Foundation.

References

1. J. A. Toretsky and P. E. Wright, J. Cell Biol., 2014, 206, 579–588.
2. S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298.
3. M. Dzuricky, B. A. Rogers, A. Shahid, P. S. Cremer and A. Chilkoti, Nat. Chem., 2020, 12, 814–825.
4. V. G. Taratuta, A. Holschbach, G. M. Thurston, D. Blankschtein and G. B. Benedek, J. Phys. Chem., 1990, 94, 2140–2144.
5. O. Galkin and P. G. Vekilov, J. Am. Chem. Soc., 2000, 122, 156–163.
6. T. Yamazaki, Y. Kimura, P. G. Vekilov, E. Furukawa, M. Shirai, H. Matsumoto, A. E. S. Van Driessche and K. Tsukamoto, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2154–2159.
7. S. Huang, X. Mo, J. Wang, X. Ye, H. Yu and Y. Liu, FEBS Lett., 2022, 596, 1388–1400.
8. M. D. Senft, G. Zocher, S. Retzbach, R. Maier, A. Hiremath, F. Zhang, T. Stehle and F. Schreiber, Cryst. Growth Des., 2025, 25, 2418–2429.
9. A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Opt. Lett., 1986, 11, 288–290.
10. Y. Harada and T. Asakura, Opt. Commun., 1996, 124, 529–541.
11. S. E. S. Spesyvtseva and K. Dholakia, ACS Photonics, 2016, 3, 719–736.
12. Z. Liao and K. Wynne, J. Am. Chem. Soc., 2022, 144, 6727–6733.
13. T. Sugiyama, K. Yuyama and H. Masuhara, Acc. Chem. Res., 2012, 45, 1946–1954.
14. O. Urquidi, J. Brazard, N. LeMessurier, L. Simine and T. B. M. Adachi, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122990119.
15. P.-W. Yi, W.-H. Chiu, T. Kudo, T. Sugiyama, R. Bresolí-Obach, J. Hofkens, E. Chatani, R. Yasukuni, Y. Hosokawa, S. Toyouchi and H. Masuhara, J. Phys. Chem. C, 2021, 125, 18988–18999.
16. P.-W. Yi, W.-H. Chiu, S. Toyouchi, R. Bresolí-Obach, J. Hofkens, E. Chatani, Y. Hosokawa, T. Sugiyama and H. Masuhara, Appl. Phys. Express, 2023, 16, 025501.
17. K. Yuzu, C.-Y. Lin, P.-W. Yi, C.-H. Huang, H. Masuhara and E. Chatani, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2402162121.
18. J. Hofkens, J. Hotta, K. Sasaki, H. Masuhara, T. Taniguchi and T. Miyashita, J. Am. Chem. Soc., 1997, 119, 2741–2742.
19. M. Tanaka, R. Kobayashi, Y. Tsuboi and K.-i. Yuyama, Phys. Chem. Chem. Phys., 2024, 26, 19083–19087.
20. N. Kitamura, K. Konno and S. Ishizaka, Bull. Chem. Soc. Jpn., 2017, 90, 404–410.
21. C. Zhai, C. Hu, S. Li, Y. Ma, Y. Zhang, T. Guo, H. Li and X. Hu, Nanoscale Adv., 2021, 3, 279–286.
22. S. Jonchhe, W. Pan, P. Pokhrel and H. Mao, Angew. Chem., Int. Ed., 2022, 13, e202113156.
23. K. Yokosawa, S. Kajimoto, D. Shibata, K. Kuroi, T. Konno and T. Nakabayashi, J. Phys. Chem. Lett., 2022, 13, 569.
24. C. K. Patel, A. Mallik, D. K. Rath, R. Kumar and T. K. Mukherjee, Langmuir, 2025, 41, 10562–10575.
25. R. Kobayashi, Y. Tsuboi and K.-i. Yuyama, ChemPhotoChem, 2025, 9, e202400394.
26. O. Matsarskaia, M. K. Braun, F. Roosen-Runge, M. Wolf, F. Zhang, R. Roth and F. Schreiber, J. Phys. Chem. B, 2016, 120, 7731–7736.
27. S. Da Vela, M. K. Braun, A. Dörr, A. Greco, J. Möller, Z. Fu, F. Zhang and F. Schreiber, Soft Matter, 2016, 12, 9334–9341.
28. R. Saha and R. K. Mitra, Phys. Chem. Chem. Phys., 2022, 24, 23661–23668.
29. F. Roosen-Runge, B. S. Heck, F. Zhang, O. Kohlbacher and F. Schreiber, J. Phys. Chem. B, 2013, 117, 5777–5787.
30. N. Kuhar and S. Umapathy, Anal. Chem., 2020, 92, 13509–13517.
31. C. Wu, J. Scott and J.-E. Shea, Biophys. J., 2012, 103, 550–557.
32. P. Taylor, J. Weiss, N. Herrmann and D. J. McClements, Adv. Colloid Interface Sci., 1999, 106, 261–285.
33. J. Weiss, N. Herrmann and D. J. McClements, Langmuir, 1999, 15, 6652–6657.
34. K. Ushiro, T. Shoji, M. Matsumoto, T.-A. Asoh, H. Horibe, Y. Katsumoto and Y. Tsuboi, J. Phys. Chem. B, 2020, 124, 8454–8463.
35. S. Ito, T. Sugiyama, N. Toitani, G. Katayama and H. Miyasaka, J. Phys. Chem. B, 2007, 111, 2365–2371.
36. B. K. Park, N. Yi, J. Park, T. Y. Choi, J. Y. Lee, A. Busnaina and D. Kim, Appl. Phys. Lett., 2011, 99, 163702.

---