Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel electrified sorption enhanced reforming process for blue hydrogen production†
Abdelrahman
Mostafa
 *a,
Alessandra
Beretta
*a,
Alessandra
Beretta
 a,
Gianpiero
Groppi
a,
Gianpiero
Groppi
 a,
Enrico
Tronconi
a,
Enrico
Tronconi
 a and
Matteo C.
Romano
a and
Matteo C.
Romano
 *b
*b
aLCCP – Laboratory of Catalysis and Catalytic Processes, Dipartimento di Energia, Politecnico di Milano, Via la Masa 34, 20156, Milano, Italy. E-mail: abdelrahmanmohamed.mostafa@polimi.it
bGECOS – Group of Energy Conversion Systems, Dipartimento di Energia, Politecnico di Milano, Via Lambruschini 4, 20156, Milano, Italy. E-mail: matteo.romano@polimi.it
First published on 11th March 2025
Abstract
Sorption enhanced reforming (SER) is emerging as a promising solution for the deployment of blue hydrogen and offers the flexibility to accommodate future green feedstocks. This study assesses the techno-economic feasibility of implementing electrified reactors for the endothermic sorbent regeneration step in SER-based hydrogen production plants, introducing the novel electrified sorption enhanced reforming (eSER) process. The analysis is conducted by integrating a 1-D dynamic heterogeneous model of an adiabatic fixed bed reactor into a process model of the complete plant. A natural gas-based hydrogen production plant with 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Nm3 h−1 capacity is considered, simulating five different cases, two of which are advanced plant configurations designed to capture more than 90% of the feed carbon. Evaluating a set of key performance indicators that covers technical, environmental, and economic aspects of the process, these simulated cases are benchmarked against existing studies utilizing conventional and state of the art steam methane reforming with carbon capture technology from the literature. The findings highlight the remarkable performance of eSER, achieving specific electric consumption of 12–14 kW h per kgH2 and natural gas to H2 conversion efficiency exceeding 100% calculated on a chemical energy basis. For the base case configuration, an overall energy efficiency of the eSER process of 74.3% and a CO2 capture rate of 86.3% are computed. For the advanced configurations, energy efficiency of 73.7% and 73.1%, CO2 capture rates of 90.3 and 96.6% and levelized cost of hydrogen of 2.50 and 2.52 € per kgH2 have been obtained.
000 Nm3 h−1 capacity is considered, simulating five different cases, two of which are advanced plant configurations designed to capture more than 90% of the feed carbon. Evaluating a set of key performance indicators that covers technical, environmental, and economic aspects of the process, these simulated cases are benchmarked against existing studies utilizing conventional and state of the art steam methane reforming with carbon capture technology from the literature. The findings highlight the remarkable performance of eSER, achieving specific electric consumption of 12–14 kW h per kgH2 and natural gas to H2 conversion efficiency exceeding 100% calculated on a chemical energy basis. For the base case configuration, an overall energy efficiency of the eSER process of 74.3% and a CO2 capture rate of 86.3% are computed. For the advanced configurations, energy efficiency of 73.7% and 73.1%, CO2 capture rates of 90.3 and 96.6% and levelized cost of hydrogen of 2.50 and 2.52 € per kgH2 have been obtained.
1. Introduction
Hydrogen can play a crucial role in reducing the carbon footprint of hard-to-decarbonize industries and for long duration energy storage. Additionally, it holds great importance as a chemical product, finding extensive use in refinery applications and serving as a fundamental platform in the production of key chemicals such as ammonia and methanol.1Currently, hydrogen production is largely dependent on the unabated use of fossil fuels, with natural gas contributing to 62% of global production, primarily through the steam methane reforming process (SMR).2 In conventional SMR plants, fossil fuel combustion generates heat to drive the strongly endothermic steam methane reforming reaction, leading to the emission of substantial amounts of CO2-containing flue gas; a typical fired SMR process using natural gas emits around 10 kg CO2 per kg H2.3 In such hydrogen production plants, two main sources of CO2 emissions exist: (i) CO2 resulting from the methane reforming reaction (syngas CO2), with a molar percent approaching 15% mol on dry basis, and (ii) CO2 resulting from combustion of fossil fuels to provide the necessary heat for the process, with a molar percentage of about 4% mol on a dry basis. While technology to separate CO2 from syngas has been available commercially for decades for ammonia production, the highly diluted CO2 in the combustion effluents makes the downstream carbon capture process more challenging.4
Given that the steam methane reforming process has been the dominating technology for hydrogen production, setting the reference hydrogen price in the market, several research activities have focused on improving the efficiency of the SMR process addressing different aspects of a typical H2 production plant.5 Among the technologies extensively studied, sorption enhanced reforming has re-emerged as a promising candidate for blue hydrogen production.6 Sorption enhanced reforming is a two-step process where initially, hydrocarbon reforming takes place in the presence of a reforming catalyst and CO2 sorbent. The presence of the CO2 acceptor in the catalytic reactor results in the removal of the CO2 from the reaction zone, shifting the thermodynamic equilibrium towards higher CH4 and CO conversion.7 An additional advantage is the substantial heat evolution resulting from the exothermic reaction between CO2 and the solid sorbent eliminating the need for external heat addition for reforming.8,9 Upon the saturation of the sorbent, a subsequent highly endothermic step of sorbent regeneration is required.
The nature of the SER process, alternating between the two steps of reforming and regeneration, makes it an ideal candidate to be conducted in interconnected fluidized bed reactors, where the bed fluidization ensures homogeneous sorbent properties and low temperature gradients in the reactors both in the reforming and regeneration steps.10 Several studies have been performed to evaluate the SER process of full-scale hydrogen production plants. The technology has been validated through experimental studies and is currently classified at Technology Readiness Level (TRL) 4.11 Recently, pilot plant experimental studies were initiated to advance the technology to the next TRL. Among these, the Gas Technology Institute (GTI) conducted a pilot-scale study, producing approximately 71 kWth of hydrogen with a purity exceeding 80%.12 In order to achieve a feasible CO2 abatement, the regeneration step must be conducted in a manner that results in concentrated streams of CO2. Thus, the conventional use of hot flue gases arising from fuel combustion in air as a direct medium for the sorbent regeneration is not possible for this application. A first option is to perform sorbent regeneration by oxyfuel combustion of natural gas and PSA off-gases. The integration of an oxyfuel SER process in a hydrogen production plant was assessed by Martínez et al.,13 who proposed plant designs achieving 74.2–76.6% equivalent hydrogen production efficiency and over 98% carbon capture ratio. More recently, as an alternative sorbent regeneration option, many studies addressed the integration of the SER process with the chemical looping technology, avoiding the need for an air separation unit. Zhu and Fan,14 Alam et al.,15 and Phuluanglue et al.16 have studied combining a Ni–NiO chemical cycle with the SER process to provide the heat required for sorbent regeneration. An additional air reactor is used to realize the exothermic Ni oxidation, resulting in heating up of the Ni based pellets that are then recycled to the fuel reactor where the reduction of NiO occurs with CH4. The heat released from the Ni–NiO cycle covers the heat demand for the sorbent regeneration in the calciner. Results presented in ref. 15 show that the process can achieve a hydrogen production efficiency of 70.7% while capturing 95.1% of the feed carbon. Yan et al.6 have evaluated the competitiveness of different SER configurations for blue H2 production. In their work, H2 production by SER-based processes equipped with: (i) calciners externally heated; (ii) chemical looping combustion (CLC); or (iii) H2 fired calciners were assessed. The authors showed that combining the SER with CLC could achieve a theoretical hydrogen production efficiency (cold gas efficiency) of 75.5% while capturing almost 100% of the carbon fed to the plant. The H2-fired calciner presents the worst theoretical performance, where an efficiency of around 51% and a carbon capture ratio of 94.2% were calculated. In comparison, the internally heated oxy-fired calciner results in a hydrogen production efficiency of 72.8% and a CO2 capture ratio approaching 100%.
A drawback of fluidized bed-based SER processes is related to the need to operate the interconnected fluidized bed system at low pressure difference between the reactors. Thus one of two solutions must be implemented for the calciner: (i) a process operating at high pressure (20–40 bar) but at calcination temperature far above 1000 °C, or (ii) a process operating at lower pressure and temperature which in turn requires challenging equipment to move the sorbent between the reformer and the calciner.17 On the other hand, fixed bed SER systems can be operated with pressure swing between the reforming stage, to be operated at high pressure, and the sorbent regeneration stage, to be operated at low pressure to avoid exceeding the catalyst and sorbent temperature limits. To overcome the technical challenges of high temperature heat transfer from hot combustion products in fixed bed SER reactors, novel approaches are required such as the integration of a Cu–CuO chemical looping cycle. The Ca–Cu process concept was originally proposed in ref. 18 and then underwent several experimental and modelling developments.19 Riva et al.20 studied the integration of the Ca–Cu process in a full-scale hydrogen plant, estimating a hydrogen production efficiency of 74.1% with a carbon capture ratio of 95.6% and a levelized cost of hydrogen of around 2.1 € per kgH2.
Even though sorption enhanced reforming is one of the very promising technologies for hydrogen production, the limitations that currently the process faces hinder its large scale implementation. Key challenges include the degradation and instability of sorbents during repeated cycles,21 high energy demands for sorbent regeneration, and CO2 slip.22 The integration of reforming and CO2 capture in a single reactor increases process complexity, making scale-up and control more challenging. These limitations underscore the need for advancements in sorbent materials, reactor design, and renewable energy integration to enhance the process's sustainability and scalability.
Recently, Tronconi et al.23 proposed the use of thermally conductive metallic and ceramic internals for mitigating the intrinsic heat transfer limitations of non-adiabatic processes. The study was extended later on presenting the packed foam reactor configuration where the empty porosity of open cell metallic foams was filled with active particles resulting in high reactor inventory of the active phase.24 These enabling features, that is the presence of conductive internals that can be packed with catalyst and sorbent particles, offer a solution to alleviate heat transfer limitations in fixed bed SER systems, avoiding high temperature heat transfer surfaces and preserving the properties of catalyst and sorbent.
Besides, given the substantial increase of the share of renewable energy sources transforming the electric energy production sector, the exploitation of electric energy as an unconventional method to provide heat for chemical reactions has been recently proposed.25 Works in the literature have confirmed the suitability of different heating approaches, including induction heating,26–28 microwave heating,29 and resistive ohmic heating,3,30–33 for overcoming the heat transfer limitation in heterogeneous catalytic systems. The inherent characteristic of the aforementioned heating systems of delivering the required heat locally has resulted in homogenous temperature profiles across the reactors, proving the technical possibility of uniform heat delivery. Compared to induction heating and microwave heating, resistive ohmic heating is expected to have a higher thermal efficiency as a result of the direct conversion of electric energy into thermal energy.32 Additionally, resistive ohmic heating is a commercially available technology; thus, rapid integration in novel processes is feasible.
In this context, this study proposes implementing electrified reactors with conductive internals for the endothermic sorbent regeneration step of a SER-based H2 production plant, giving rise to the novel process of electrified sorption enhanced reforming (eSER), herein proposed. The process leverages the use of resistive ohmic heating, in the presence of the thermally conductive internals, as a solution for the key technological hurdle of the process (i.e. the sorbent regeneration step) ensuring homogeneous heat delivery for sorbent regeneration. The analysis evaluates the techno-economic feasibility of the concept relying on a previously developed 1-D dynamic heterogeneous model of a fixed bed reactor to predict the reactor's behavior.34 The proposed process includes, besides the eSER reactor network, stages for H2 and CO2 separation and compression. The process is modeled using ASPEN plus software and the analysis compares key performance indicators (KPIs) calculated for the electrified SER plant (eSER) with conventional SMR fired tubular reformer (FTR) and electrified SMR plants including carbon capture units.
2. Process concept
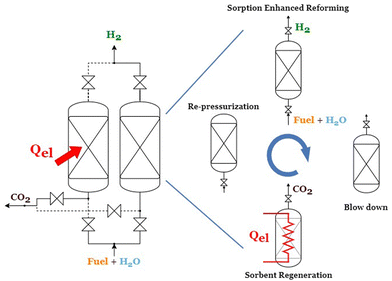
A typical industrial hydrogen production plant consists of a series of units, namely: a desulphurization section, a pre-reformer, the primary reformer, water gas shift (WGS) reactors, and H2 purification by pressure swing adsorption (PSA). In the case of CO2 capture, the plant is also equipped with a CO2 separation section, either from: (i) syngas, (ii) PSA off-gas, or (iii) SMR furnace flue gas. Due to the nature of the sorption enhanced reforming process, where reforming, WGS, and CO2 removal are combined in the same reactor, the proposed eSER process provides a simplified plant scheme. An ideal arrangement of the eSER process can approach a continuous steady production of hydrogen through alternating parallel reactors between the two steps of the process: the sorption enhanced reforming and the sorbent regeneration passing through the two intermediate steps of blow down and re-pressurization, as presented in Fig. 1. In the reforming step, the fuel and steam react in the presence of the active sorbent resulting in the production of a concentrated stream of hydrogen. Ideally the reforming step can be designed to work adiabatically, without the need for heat addition, where the demand of the endothermic SMR is provided by the CO2 sorption reaction and the bed thermal capacity. Subsequently to the reforming step, the reactor is depressurized, then it is switched to the regeneration step configuration where the solids are heated electrically, and the captured CO2 is released. Finally, the reactor is repressurized up to the reforming pressure and the cyclic process starts again.In order to obtain a stream of hydrogen with high purity, exceeding 99%, a conventional PSA unit is needed downstream from the eSER reactor network. The low-pressure PSA off-gas stream, characterized by its low carbon content, is combusted to generate steam and preheat the feed. The proposed process block diagram is presented in Fig. 2.
3. Methods
As presented in Fig. 1, a typical eSER reactor passes by four main steps: sorption enhanced reforming, blow down, sorbent regeneration, and re-pressurization. Given that the depressurization and re-pressurization steps are very short and have a negligible effect on the process, only the reforming and regeneration steps can be considered for modeling purposes. Regarding the full-scale process, where multiple reactors are operating in parallel with time mismatch to produce a steady flow of hydrogen, quasi steady state can be considered for the flow exiting the reactors. Thus, the eSER based hydrogen production plant is modeled to work under steady state conditions using AspenPlus® process simulation software. The adopted modeling approach has been used in many studies present in the literature based on high temperature packed bed systems both for sorption enhanced reforming and chemical looping processes.19,20,35–423.1. 1D SER reactor modeling
Starting with the reforming step of the process, being the most complex step where different reactions occur and where the reactor productivity is determined, the reactor behavior during the reforming step is modeled using a 1D reactor model. In a previous work,34 a heterogeneous one-dimensional dynamic model of methane sorption enhanced reforming in an adiabatic fixed bed reactor was developed. The model describes the dynamic evolution of concentration and temperature axial profiles across the SER reactor by solving the dynamic differential mass and energy balances and incorporating the kinetics and thermodynamics of all chemical processes. The model was further extended to include the presence of C2+ hydrocarbons in the feed43 making it suitable for a typical natural gas stream. The model is implemented in the gPROMS® software platform for dynamic simulation following the numerical scheme detailed in our previous work.34 Noteworthily, the electric components needed for heating the reactor during the regeneration step of the process are modeled as inert solids. The addition of this inert phase is important to consider the role of the thermal capacity of the reactor on the eSER process, both in the reforming and the regeneration steps.As explained by Riva et al.,20 dividing the required reactor volume into several sub-reactors sharing the same set of valves allows for a reduced vessel cost sustaining a proper length to diameter ratio. The same approach is used in this study, where six sub-reactors with a diameter of 2.25 m and a length of 5 m are assumed to collectively form the total reactor volume required for the production of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 N m3 h−1 of hydrogen. Each sub-reactor is modeled using the 1D reactor model and the time-average yields of all the species are computed by integrating the temporal flow profiles of the species entering and exiting the sub-reactor and ratioing them to the time on stream. Accordingly, for the full-scale process analysis, the collective eSER sub-reactors are modeled as a series of elementary units that reproduce the heat and mass balances of the reforming step of the process. The sub-reactor characteristics and the assumptions used in the 1D reactor model simulations are reported in Section A of the ESI.†
000 N m3 h−1 of hydrogen. Each sub-reactor is modeled using the 1D reactor model and the time-average yields of all the species are computed by integrating the temporal flow profiles of the species entering and exiting the sub-reactor and ratioing them to the time on stream. Accordingly, for the full-scale process analysis, the collective eSER sub-reactors are modeled as a series of elementary units that reproduce the heat and mass balances of the reforming step of the process. The sub-reactor characteristics and the assumptions used in the 1D reactor model simulations are reported in Section A of the ESI.†
3.2. Full-scale process modeling
As discussed in Section 2, the eSER hydrogen production plant would ideally contain two or more reactors, each operating in one of the steps of the process to guarantee the continuous production of hydrogen. As presented in Fig. 3, the simplified scheme of the modeled eSER H2 production plant can be divided into four main units: natural gas pretreatment unit, eSER reactors (operating both in SER and regeneration), hydrogen compression and purification unit, CO2 compression and liquification section. Additionally, the PSA-off gas leaving the H2 purification unit is combusted to provide the heat required to balance the plant, representing the source of emissions in the plant.In the core of the process, the SER reactors, modeled as a bundle of sub-reactors, an input-output model reproducing the time-average yields of all the species as calculated by the 1D reactor model is assumed. A set of reactors, mixers, separators, and heaters are used to reproduce the mass and energy balances of the process as computed by the 1D reactor model. The methodology used for modelling is detailed in Section A of the ESI.† This approach results in closing the material and enthalpy balances with a minor difference compared with the results of the 1D dynamic reactor model (<1% for the total mass and enthalpy balances). The differences in the balances are resulting from numerical errors in the 1D reactor model that led to higher errors in the overall mass and energy balance over a SER cycle. Typical values of the calculated variations in the material and enthalpy flows comparing the steady state ASPEN model and the 1D dynamic heterogeneous reactor model are reported in Table A2 in Section A of the ESI.†
Moving on to the regeneration step of the process, a simple modeling approach has been followed where pure CO2 release from the calcination reaction is assumed as a result of electric heating. Complete regeneration of the sorbent is assumed to take place in exactly the same duration of the reforming step indicating the need for two equivalent parallel reactor bundles to sustain the continuous H2 production. The duration of the regeneration step can be adjusted by tuning the electric power supplied to the reactor bed. The regeneration temperature is set at a value that thermodynamically guarantees the decomposition of the CaCO3 at the selected regeneration pressure as reported in ref. 44. A uniform temperature is assumed along the reactor during the regeneration step, a simplification that requires experimental validation and depends on the reactor's internal design. However, temperature variations in the outlet of the reactor during the regeneration step have a minor impact on the overall process, as heat recovered from the CO2 stream accounts for only 8.3% of the total heat recovered in the plant. Enthalpy balance across the reactor in this step is performed to calculate the energy required to heat up the solids from the final bed temperature up to the regeneration temperature in addition to the energy needed for the endothermic sorbent regeneration. Regarding the thermal behaviour of the reactor during the regeneration step, the uniform supply of heat along with the presence of the conductive internals in the reactor eliminates the presence of sharp thermal gradients during the regeneration step. Similar behaviour was shown experimentally by Balzarotti et al.45 and Zheng et al.46 for heat delivery to highly endothermic reactions.
It is worth mentioning that due to the dynamic nature of the process, the streams leaving the SER reactors, both in the reforming and regeneration steps, are expected to exhibit variable temperatures and flow rates. To limit thermal fatigue issues for the heat exchangers and instabilities of the reactor feed stream properties, indirect heat recovery is proposed, where the effluents of the reactors are used to generate saturated steam at different pressures that, while acting as a buffer, is later on used for preheating and evaporation of the main process steam. The main process assumptions are reported in Table 1.
| a Values depend on the modeled case. | ||
|---|---|---|
| Natural gas (NG) | ||
| Composition | CH4:89; C2H6:7; C3H8:1; CO2:2; N2:1 | vol% |
| LHV | 46.9 | MJ kg−1 |
| NG supply temperature | 25 | °C |
| NG pre-treatment | ||
| Operating temperature of the desulfurization unit | 365 | °C |
| Pressure loss in the desulfurization unit | 0.3 | bar |
| eSER process | ||
| Reforming step | ||
| Feed temperature | 550 | °C |
| Steam to carbon ratio | 4–6a | |
| Operating pressure | 10–30a | bar |
| Regeneration step | ||
| Regeneration temperature | 900–800a | °C |
| Regeneration pressure | 1–0.2a | bar |
| Heat recovery | ||
| ΔTmin gas–gas heat exchangers | 20 | °C |
| ΔTmin gas–evaporating water heat exchanger | 10 | °C |
| Evaporation pressure | 10–30 | bar |
| T in water | 15 | °C |
| T out cooling water | 25 | °C |
| Intercooled compressors | ||
| Isentropic efficiency | 72 | % |
| Electromechanical efficiency | 94 | % |
| Intercool water temperature | 35 | °C |
| Pumps | ||
| Hydraulic efficiency | 70 | % |
| Electromechanical efficiency | 94 | % |
| Hydrogen purification unit | ||
| PSA feed pressure | 30 | bar |
| Pressure loss in the PSA unit | 1 | bar |
| Hydrogen recovery efficiency | 90 | % |
| Combustors | ||
| Air composition | N2: 79; O2: 21 | vol% |
| T in air | 20 | °C |
| Hydrogen delivery pressure | 29 | bar |
| Liquified CO2 delivery pressure | 110 | bar |
The analysis is performed for a medium scale H2 production plant with a productivity of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 N m3 h−1. This study covers five cases, three of which are unconstrained by preset KPIs and are intended to examine the eSER performance under different configurations, while the remaining two aim for a carbon capture ratio (CCR) exceeding 90%. Maximizing the CCR is of the utmost importance to align with the current guidelines set by the European Union for low carbon hydrogen set since January 2021 at 3.38 kgCO2 per kgH2 by the renewable energy directive EU 2018/2001 (RED II). The unconstrained cases assess the impact of specific working conditions – namely, the reforming pressure and the regeneration pressure – on the technical and economic performance indices of the plant.
000 N m3 h−1. This study covers five cases, three of which are unconstrained by preset KPIs and are intended to examine the eSER performance under different configurations, while the remaining two aim for a carbon capture ratio (CCR) exceeding 90%. Maximizing the CCR is of the utmost importance to align with the current guidelines set by the European Union for low carbon hydrogen set since January 2021 at 3.38 kgCO2 per kgH2 by the renewable energy directive EU 2018/2001 (RED II). The unconstrained cases assess the impact of specific working conditions – namely, the reforming pressure and the regeneration pressure – on the technical and economic performance indices of the plant.
An increase in the reforming pressure of the plant is predicted to reduce the capital expenditure (CAPEX), as it eliminates the need for an expensive gas compressor to deliver the impure hydrogen to the PSA unit at the design pressure of 30 bar. However, a higher reforming pressure is projected to result in lower methane conversion, leading to reduced hydrogen production. Besides, lowering the regeneration pressure implies a reduced regeneration temperature, which in turn lowers the heating demand of the plant, predicting a decrease in the plant operating costs. It is important to note that delivering the CO2 at lower pressure necessitates higher compression power for delivering the liquified CO2 at the specified pressure of 110 bar.
As the sorption-enhanced reforming process integrates the functionalities of a steam reformer, shift reactor, and CO2 removal into a single reactor, a high steam-to-carbon ratio is needed to increase hydrocarbon conversion and carbon capture, as demonstrated in the literature.34,43,47 In the unconstrained simulated cases (base case, high-pressure reforming, and vacuum regeneration), the selected steam-to-carbon ratio is determined by the maximum amount of steam producible through heat recovery in the plant.
To increase the CO2 capture efficiency above 90%, two cases have been considered:
•low-pressure steam generation and steam compression (Fig. 4): this configuration allows to increase steam production by improved heat recovery, while the steam compressor raises the steam pressure to the reforming pressure of 10 bar.
•Three-stage eSER–eSMR–eSEWGS process (Fig. 5): in this configuration the eSER reactor is designed to work at high pressure, leading to moderate methane conversion. To increase CH4 conversion and CO2 capture, the effluent of the eSER reactor is first delivered to an electrified steam methane reformer (eSMR) operating at 950 °C that achieves high methane conversion. At the outlet of the eSMR reactor, an electrified sorption enhanced water gas shift (eSEWGS) step is added, converting CO while capturing CO2 on a CaO-based sorbent at high temperature. The adoption of the eSEWGS step is necessary to improve the carbon capture performance given that there are no downstream CO2 capture units in the typical eSER process scheme. Thus, this configuration improves carbon capture efficiency by decoupling the SMR from CO2 sorption reactions to capture the last portion of the carbon dioxide.
3.3. Key performance indicators
The technical performance of the different plant arrangements is evaluated based on a series of key performance indicators. Noteworthily, the same definitions of the performance indicators have been used to evaluate other similar processes allowing for the direct comparison of the novel eSER process with hydrogen production processes found in the literature.48As commonly used in the literature, the H2 production efficiency (ηH2) is defined as the ratio between the chemical energy flow rate of the produced hydrogen and the input chemical energy flow rate of the natural gas as defined in eqn (1).
 | (1) |
The total efficiency (ηtot) of the plant is calculated, as presented in eqn (2), to include the input electric power consumed within the plant battery limit.
 | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq.) is necessary to account for the indirect CO2 emission associated with electricity consumption. Equivalent CO2 emissions (ECO2
eq.) is necessary to account for the indirect CO2 emission associated with electricity consumption. Equivalent CO2 emissions (ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq.) as presented in eqn (4), consider both the process direct emissions, such as combustion flue gas, and indirect emissions arising from importing electricity from the grid, and from GHG emissions alongside the natural gas supply chain (methane leakage and emissions related to production and transportation of NG). ECO2
eq.) as presented in eqn (4), consider both the process direct emissions, such as combustion flue gas, and indirect emissions arising from importing electricity from the grid, and from GHG emissions alongside the natural gas supply chain (methane leakage and emissions related to production and transportation of NG). ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. is defined in eqn (4), where (ṁCO2
eq. is defined in eqn (4), where (ṁCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) emitted) is the direct emissions from the plant, CIgrid is the grid carbon intensity in the geographical location of the H2 production plant, LRCH4 is the equivalent methane leakage rate, which includes the GHG emissions rising from the NG supply chain, and GWPCH4 is the global warming potential of methane.
emitted) is the direct emissions from the plant, CIgrid is the grid carbon intensity in the geographical location of the H2 production plant, LRCH4 is the equivalent methane leakage rate, which includes the GHG emissions rising from the NG supply chain, and GWPCH4 is the global warming potential of methane. | (4) |
3.4. Economic modeling
The economic analysis is performed following a “bottom-up” approach where, initially, the capital costs of each installed equipment are estimated by means of cost functions as reported in ref. 49. Notably, all the calculated costs are referenced to the same year, 2022, using the Chemical Engineering Plant Cost Index (CEPCI), estimated at 709. The variables used for the equipment cost function parameters, along with the corresponding reference CEPCI, are tabulated in Section A of the ESI.†Regarding the novel eSER reactor cost estimation, the simplified reactor design presented in Fig. 6 is adopted to calculate the capital cost of the sub-reactors. The reactor length is selected to achieve a pressure drop of approximately 1 bar. The reactor is assumed to be constructed from high grade steel and provided with an inner insulation layer with a thickness of 470 mm that guarantees an outer wall temperature of around 60 °C. The steel shell thickness is calculated based on formulas from the ASME code Section VIII-Division I.50
The reactor is equipped with elements for providing the necessary heat electrically and thermally conductive structures to ensure homogeneous distribution of the temperature inside the reactor. The costs considered for the reactor structure and the aforementioned conductive elements are reported in Table 2. The overall reactor cost is then increased by 50% to account for labor and installation, 14% for indirect costs, and 15% for owner and contingency costs, as considered by Riva et al.20 A mixture of conventional reforming Ni-based catalyst and CaO based sorbent spherical pellets, with a sorbent to catalyst volumetric ratio of 5, are assumed to fill the reactor. As they are subject to cyclic degradation, the catalyst and the sorbent are considered to be replaced annually to sustain the performance of the process. The cost of the functional materials, catalyst and sorbent, are obtained from ref. 20.
| Material | Specific cost | |
|---|---|---|
| Steel vessel | 9.6 | € per kg |
| Insulation | 18 | € per kg |
| Electrical components | 50 | € per kWelectric |
| Conductive reactor internals | 0.1 | M€ per mreactor3 |
The different plant configurations are compared using the levelized cost of hydrogen (LCOH), evaluating the cost of production of hydrogen over the lifetime of a hydrogen production plant, as a widely used metric in the industry. The plant is assumed to have a capacity factor of 86% resulting in 7500 equivalent operating hours. The fixed annual operating costs include annual maintenance costs of 1.5% of the total plant cost (TPC), and direct labor cost of 2.16 M€ per year (for 12 employees for each shift). The plant is projected to have a lifetime of 25 years. Besides, the consumables, obtained from ref. 48 and the variable costs used in this analysis are included in Table 3. The sensitivity of LCOH to natural gas prices, electricity prices, and CO2 emission taxes is examined through a sensitivity analysis as reported in Section 4.2. Additionally, the sensitivity of the LCOH to the plant operating lifetime, labor cost, and capacity factor is reported in Section D of the ESI.†
| Variable costs | Specific cost | |
|---|---|---|
| Natural gas | 32.4 | € per MW hLHV |
| Electricity | 60 | € per MW h |
| Annual catalyst replacement | 50 | € per kg |
| Annual sorbent replacement | 5 | € per kg |
| CO2 transport and storage cost | 25 | € per tCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) captured captured |
| CO2 emission tax | 100 | € per tCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) emitted emitted |
4. Results and discussion
This section outlines the findings of the study, which are divided into two subsections. Firstly, the technical analysis results are presented, followed by the economic analysis results.4.1. Technical analysis results
Results of the simulations are summarized in Table 4. As a basis of comparison, the amount of feed NG is kept constant, calculated as the amount required for the production of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 N m3 h−1 of hydrogen in the base case. The temporal temperature and composition profiles downstream from the SER reactor during the reforming step, the stream properties tables and the TQ diagrams for heat recovery of the base case plant are reported in Section B of the ESI.† The simulated eSER hydrogen production plant arrangements are compared with two hydrogen production plants utilizing amine-based carbon capture units that are presented in the literature.48 The fired tubular reformer (FTR) plant represents the current commercial hydrogen production plants adopting conventional technologies. On the other hand, FTR Plus includes an advanced reforming plant, including an additional electrified reforming to improve methane conversion, a cooled low temperature water gas shift reactor to enhance the CO conversion, and increased CO2 separation and H2 recovery in the downstream syngas processing units. It is worth noting that the carbon capture units in both reference plants are located before the PSA units; thus, the carbon emitted from off gas combustion to balance the plant is released to the atmosphere.
000 N m3 h−1 of hydrogen in the base case. The temporal temperature and composition profiles downstream from the SER reactor during the reforming step, the stream properties tables and the TQ diagrams for heat recovery of the base case plant are reported in Section B of the ESI.† The simulated eSER hydrogen production plant arrangements are compared with two hydrogen production plants utilizing amine-based carbon capture units that are presented in the literature.48 The fired tubular reformer (FTR) plant represents the current commercial hydrogen production plants adopting conventional technologies. On the other hand, FTR Plus includes an advanced reforming plant, including an additional electrified reforming to improve methane conversion, a cooled low temperature water gas shift reactor to enhance the CO conversion, and increased CO2 separation and H2 recovery in the downstream syngas processing units. It is worth noting that the carbon capture units in both reference plants are located before the PSA units; thus, the carbon emitted from off gas combustion to balance the plant is released to the atmosphere.
| eSER plants | Ref. plants48 | |||||||
|---|---|---|---|---|---|---|---|---|
| Base case | High pressure | Vaccum regen. | High S/C | eSER–eSMR–eSEWGS | FTR | FTR plus | ||
| The process block diagrams for the simulated plant arrangements are presented in Fig. 2 for the base case, high pressure, vacuum regen.; Fig. 4 for high S/C; and Fig. 5 for eSER–eSMR–eSWGS. | ||||||||
| Reforming pressure | bar | 10 | 30 | 10 | 10 | 30 | 32.7 | 32.7 |
| Steam to carbon ratio | mol mol−1 | 4.8 | 5.1 | 4.4 | 6 | 4.6 | 3.4 | 3.4 |
| Regeneration pressure | bar | 1 | 1 | 0.2 | 1 | 1 | — | — |
| Regeneration temperature | °C | 900 | 900 | 800 | 900 | 900 | — | — |
| Natural gas thermal input | MW | 86.63 | 86.63 | 86.63 | 86.63 | 86.63 | ||
| Hydrogen thermal output | MW | 89.23 | 85.88 | 85.68 | 90.86 | 91.55 | ||
| Hydrogen output | N m3 h−1 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 875 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 806 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 548 548 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 780 |
||
| Hydrogen production KPIs | ||||||||
| Total efficiency | % | 74.33% | 72.87% | 73.51% | 73.75% | 73.12% | 76.24% | 73.71% |
| H2 production efficiency | MWH2 per MWNG | 103.0% | 99.1% | 98.9% | 104.9% | 105.7% | 74.6% | 71.3% |
| Specific electricity consumption | kW hel per kgH2 | 12.42 | 12.06 | 11.56 | 13.33 | 13.97 | −0.61 | −0.95 |
| Environmental KPIs | ||||||||
| Specific CO2 capture ratio | kgCO2 per kgH2 | 5.68 | 5.84 | 5.70 | 5.83 | 6.19 | 7.16 | 8.60 |
| Specific emission | kgCO2 per kgH2 | 0.90 | 0.99 | 1.15 | 0.63 | 0.22 | 1.94 | 0.91 |
| Specific emission | gCO2 per MJH2 | 7.49 | 8.27 | 9.60 | 5.24 | 1.83 | 16.16 | 7.58 |
| Electricity consumption | kW hel per kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cap. Cap. |
2.19 | 2.06 | 2.03 | 2.29 | 2.26 | −0.09 | −0.11 |
| Carbon capture ratio | % | 86.34% | 85.48% | 83.18% | 90.27% | 96.57% | 78.88% | 90.52% |
Starting with a comparison between the base case and the reference benchmark plants, given the higher feed steam to carbon ratio of the eSER plant compared to the reference plants, a higher hydrogen production efficiency is computed. An exceptional energetic efficiency of 103.0% is calculated for the eSER plant representing 86.61% of the theoretical maximum hydrogen production on a molar basis. On including the electric energy consumption, being a net electricity consumer, the eSER presents a total efficiency of 74.33%, which is 1.91 percentage points lower than the conventional FTR plant and 0.62 points higher than the FTR plus plant. It is worth mentioning that, on the contrary of the eSER plants, both the reference plants are net producers of electricity; thus, the calculated net efficiency includes the export of electric energy to the grid. Comparing the main environmental KPIs, the computed CCR of the base case eSER plant is 86.34%, which is 7.46 percentage points higher than the conventional FTR reference plant but 4.18 percentage points lower than the FTR plus plant arrangement. Noteworthily, due to the higher hydrogen production simulated for the eSER plant, the specific emissions evaluated for the eSER plant are 0.90 kgCO2 per kgH2, which is significantly lower than the 1.94 kgCO2 per kgH2 of the benchmark FTR plant and similar to 0.91 kgCO2 per kgH2 of the FTR plus plant.
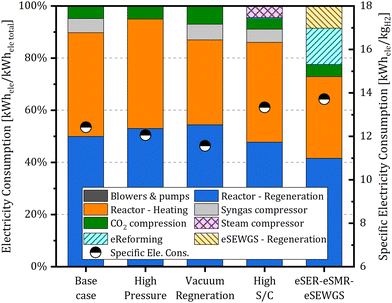
Focusing on the effect of the different operational configurations of the eSER plants, on increasing the sorption enhanced reformer pressure from 10 to 30 bar, a reduction of the hydrogen production efficiency from 103.0% to 99.1% and of the total efficiency by 1.46 percentage points, from 74.33% to 72.87% compared to the base case are computed. This results in a decrease of the plant's hydrogen production from 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 N m3 h−1 to 28
000 N m3 h−1 to 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 N m3 h−1 for the same natural gas feed flow rate. This behavior can be explained by a drop of the methane conversion, which is evident by examining Fig. 7, presenting the distribution of the uncaptured carbon leaving the process as off gas from the PSA unit. A significant increase in the uncaptured carbon is calculated, rising from 13.7% for the base case to 14.5% for the high-pressure case. The portion of the unconverted methane of the uncaptured carbon increased as well passing from 18% to 42% on operating the reformer at 30 bar. On the other hand, removing the need for a syngas compressor as the syngas is produced at the required pressure of the PSA unit leads to a reduction in the specific electricity consumption, which drops from 12.42 kW h per kgH2 to 12.06 kW h per kgH2 as reported in Table 4. The second configuration evaluates the performance of the eSER plant on operating the regeneration step of the process at sub atmospheric pressure, resulting in a reduction of the regeneration temperature. Compared to the base case, the vacuum regeneration case results in a drop in the hydrogen production efficiency from 103.0% to 98.9% and a reduction of the CCR from 86.3 to 83.2%. The lower regeneration temperature results in a lower initial bed temperature for the successive reforming step. Consequently, lower methane conversion is achieved leading to a drop in the hydrogen production and the CCR as explained in ref. 34. The significant reduction in the electricity consumption related to the reduced regeneration temperature helped in limiting the overall efficiency penalty of the vacuum regeneration case compared to the base case. Nevertheless, a reduction of the total efficiency by 0.79 percentage points is computed. As presented in Fig. 7, the uncaptured carbon for this case shows a more uniform division between CH4, CO, and CO2 distributed as 35.2%, 37.3%, and 27.5% of the total uncaptured carbon moles, respectively.
875 N m3 h−1 for the same natural gas feed flow rate. This behavior can be explained by a drop of the methane conversion, which is evident by examining Fig. 7, presenting the distribution of the uncaptured carbon leaving the process as off gas from the PSA unit. A significant increase in the uncaptured carbon is calculated, rising from 13.7% for the base case to 14.5% for the high-pressure case. The portion of the unconverted methane of the uncaptured carbon increased as well passing from 18% to 42% on operating the reformer at 30 bar. On the other hand, removing the need for a syngas compressor as the syngas is produced at the required pressure of the PSA unit leads to a reduction in the specific electricity consumption, which drops from 12.42 kW h per kgH2 to 12.06 kW h per kgH2 as reported in Table 4. The second configuration evaluates the performance of the eSER plant on operating the regeneration step of the process at sub atmospheric pressure, resulting in a reduction of the regeneration temperature. Compared to the base case, the vacuum regeneration case results in a drop in the hydrogen production efficiency from 103.0% to 98.9% and a reduction of the CCR from 86.3 to 83.2%. The lower regeneration temperature results in a lower initial bed temperature for the successive reforming step. Consequently, lower methane conversion is achieved leading to a drop in the hydrogen production and the CCR as explained in ref. 34. The significant reduction in the electricity consumption related to the reduced regeneration temperature helped in limiting the overall efficiency penalty of the vacuum regeneration case compared to the base case. Nevertheless, a reduction of the total efficiency by 0.79 percentage points is computed. As presented in Fig. 7, the uncaptured carbon for this case shows a more uniform division between CH4, CO, and CO2 distributed as 35.2%, 37.3%, and 27.5% of the total uncaptured carbon moles, respectively.
Finally, the two advanced plant configurations aimed at achieving a CCR exceeding 90% are compared with the base case eSER plant, following the same approach employed for the different eSER configurations. Starting with the high steam to carbon case, a higher steam to carbon ratio (6.0 vs. 4.8 of the base case) is achieved by utilizing low temperature heat recovery for evaporating the additional quantity of steam required. Subsequently, the low-pressure steam (2 bar) is pressurized to the selected reforming pressure of 10 bar using a steam compressor. Evaluating the key KPIs of this plant, it achieves a remarkable hydrogen production efficiency of 104.9%. However, compared to the base case, the electric demand of the steam compressor increases the specific electric consumption from 12.42 to 13.33 kW h per kgH2, resulting in a loss of 0.58 percentage points in the overall plant efficiency. The high steam to carbon ratio results in a higher extent of the SR and WGS reactions resulting in a higher concentration of the CO2 in the PSA off gas as shown in Fig. 7. The final simulated plant is designed to achieve high methane conversion at high pressure, facilitated by the addition of a subsequent eSMR reactor operating at 950 °C, followed by a high temperature eSEWGS to maximize hydrogen production and carbon capture. Comparing the KPIs of the eSER–eSMR–eSEWGS plant with the base case eSER plant, a significant increase in hydrogen production efficiency from 103.0% to 105.7% is observed representing the highest hydrogen production efficiency of all the simulated plants. Nevertheless, the overall efficiency dropped by 1.21 percentage points as a result of the increase in electricity consumption from 12.42 to 13.97 kW h per kgH2. Notably, the eSER–eSMR–eSEWGS arrangement shows a remarkably high carbon capture ratio reaching 96.57%.
Focusing on the electricity consumption, Fig. 8 illustrates the contribution of the different parts of the plant on the specific electricity consumption for the simulated eSER arrangements. The energy demand of the regeneration step of the process includes the sensible heat, to heat up the saturated sorbent to the regeneration temperature, and the enthalpy required for CaCO3 decomposition. As evident in the figure, more than 40% of the total consumed energy is attributed to CaCO3 decomposition for all the simulated plants. The next significant contribution is related to heating the reactor up to the necessary sorbent regeneration temperature. With the exception of the eSER–eSMR–eSEWGS plant, these two contributions collectively represent more than 85% of the specific electricity consumption for the simulated plants. Notably, the vacuum regeneration case, where the sorbent regeneration takes place under sub atmospheric conditions and hence at lower temperature, presents the lowest specific electricity consumption. In this case, compared to the base case, the increase in power consumption for CO2 compression is less than the reduction in the energy required to heat the reactor leading to a total drop of electricity consumption from 12.42 to 11.56 kW h per kgH2.
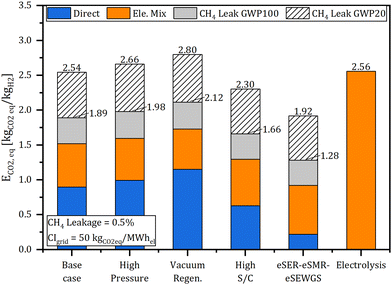
With eSER being a technology with a high electricity consumption, which is evaluated for fossil-based feeds, assessing the environmental performance of the eSER plants requires consideration of both direct emissions from the combustion of the PSA off gas and indirect emissions related to the carbon intensity of the consumed electricity and the methane leakage from the natural gas supply chain. As defined in eqn (4), equivalent CO2 emissions (ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq.) is used for such analysis. The analysis considers an impact of 82.5 kgCO2
eq.) is used for such analysis. The analysis considers an impact of 82.5 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgCH4 over a 20 year time-horizon (GWP20) and 29.8 kgCO2
eq. per kgCH4 over a 20 year time-horizon (GWP20) and 29.8 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgCH4 over 100 years (GWP100).4 Comparing the calculated ECO2
eq. per kgCH4 over 100 years (GWP100).4 Comparing the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of the different eSER arrangements, as presented in Fig. 9, the key role of the carbon intensity of the consumed electricity along with the methane leakage from the natural gas supply chain is evident. In fact, upon considering electricity mix with carbon intensity of 50 kgCO2 per MW hel, all the simulated plant arrangements resulted in ECO2
eq. of the different eSER arrangements, as presented in Fig. 9, the key role of the carbon intensity of the consumed electricity along with the methane leakage from the natural gas supply chain is evident. In fact, upon considering electricity mix with carbon intensity of 50 kgCO2 per MW hel, all the simulated plant arrangements resulted in ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. higher than 1 kgCO2
eq. higher than 1 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2, the threshold for ultralow-carbon hydrogen defined by the World Business Council for Sustainable Development. However, the calculated ECO2
eq. per kgH2, the threshold for ultralow-carbon hydrogen defined by the World Business Council for Sustainable Development. However, the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. for all the simulated plants remains below the threshold for the low-carbon hydrogen of 3 kgCO2
eq. for all the simulated plants remains below the threshold for the low-carbon hydrogen of 3 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 even when considering 0.5% CH4 leakage, representative of a low carbon intensity natural gas supply chain.51 Without methane leakage, the eSER–eSMR–eSEWGS presents the lowest ECO2
eq. per kgH2 even when considering 0.5% CH4 leakage, representative of a low carbon intensity natural gas supply chain.51 Without methane leakage, the eSER–eSMR–eSEWGS presents the lowest ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of 1.09 kgCO2
eq. of 1.09 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 rising up to 2.10 on considering 0.5% CH4 leakage. For the sake of comparison, the calculated ECO2
eq. per kgH2 rising up to 2.10 on considering 0.5% CH4 leakage. For the sake of comparison, the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of water electrolysis, with 65% efficiency (LHV-basis), using the same electricity mix, is 2.56 kgCO2
eq. of water electrolysis, with 65% efficiency (LHV-basis), using the same electricity mix, is 2.56 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2. Following the eSER–eSMR–eSEWGS case, the calculated ECO2
eq. per kgH2. Following the eSER–eSMR–eSEWGS case, the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of the high steam to carbon case is 1.30 kgCO2
eq. of the high steam to carbon case is 1.30 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 without CH4 leakage and 2.30 kgCO2
eq. per kgH2 without CH4 leakage and 2.30 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 with 0.5% CH4 leakage, representing an improvement compared to the base case of 0.22 and 0.24 kgCO2
eq. per kgH2 with 0.5% CH4 leakage, representing an improvement compared to the base case of 0.22 and 0.24 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq per kgH2, respectively. A breakdown of the contribution of direct and indirect emissions on the ECO2
eq per kgH2, respectively. A breakdown of the contribution of direct and indirect emissions on the ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. for the simulated eSER plants compared with the benchmark hydrogen production via electrolysis is presented in Fig. 9.
eq. for the simulated eSER plants compared with the benchmark hydrogen production via electrolysis is presented in Fig. 9.
A sensitivity analysis is performed to evaluate the impact of the methane leakage and the carbon intensity of the consumed electricity on the ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. Fig. 10 shows the effect of the carbon intensity of the electricity consumed (left) and the methane leakage (right) on the ECO2
eq. Fig. 10 shows the effect of the carbon intensity of the electricity consumed (left) and the methane leakage (right) on the ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. calculated for the base case (black lines), high steam to carbon case (red lines), and eSER–eSMR–eSEWGS case (green lines). The analysis examines the impact of the methane leakage over 20 years (GWP20), and 100 years (GWP100) represented by the solid and the dashed lines, respectively.
eq. calculated for the base case (black lines), high steam to carbon case (red lines), and eSER–eSMR–eSEWGS case (green lines). The analysis examines the impact of the methane leakage over 20 years (GWP20), and 100 years (GWP100) represented by the solid and the dashed lines, respectively.
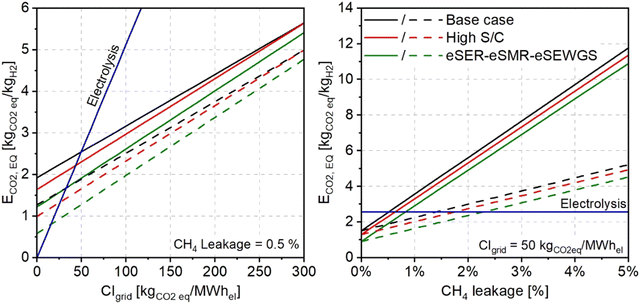 | ||
Fig. 10
E
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. for the base case, high steam to carbon, and eSER–eSMR–eSWEGS plants as a function of CIgrid (left) and CH4 leakage (right). Solid lines refer to GWP20 and dashed lines to GWP100. eq. for the base case, high steam to carbon, and eSER–eSMR–eSWEGS plants as a function of CIgrid (left) and CH4 leakage (right). Solid lines refer to GWP20 and dashed lines to GWP100. | ||
Starting with the effect of the electricity carbon intensity, assuming a constant value for the CH4 leakage of 0.5% and considering GWP20, the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. for the base case ranges from 1.92 kgCO2
eq. for the base case ranges from 1.92 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 when using completely carbon-free electricity to 5.65 kgCO2
eq. per kgH2 when using completely carbon-free electricity to 5.65 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 with a grid carbon intensity of 300 kgCO2 per MW hel. These values reduce to 1.27 and 4.99 kgCO2
eq. per kgH2 with a grid carbon intensity of 300 kgCO2 per MW hel. These values reduce to 1.27 and 4.99 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2, respectively, on considering GWP100. Relative to the water electrolysis technology, represented by the blue line in the figure, the computed ECO2
eq. per kgH2, respectively, on considering GWP100. Relative to the water electrolysis technology, represented by the blue line in the figure, the computed ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of water electrolysis is 0 kgCO2
eq. of water electrolysis is 0 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 for carbon free electricity and rises dramatically, due to the high consumption of electricity, with the grid carbon intensity exceeding 15.3 kgCO2
eq. per kgH2 for carbon free electricity and rises dramatically, due to the high consumption of electricity, with the grid carbon intensity exceeding 15.3 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 on considering a grid carbon intensity of 300 kgCO2 per MW hel. Noteworthily, the average carbon intensity of electricity generation in the EU is 244 kgCO2 per MW hel.52
eq. per kgH2 on considering a grid carbon intensity of 300 kgCO2 per MW hel. Noteworthily, the average carbon intensity of electricity generation in the EU is 244 kgCO2 per MW hel.52
Regarding the eSER cases with the highest CCR, considering GWP20, the calculated ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. high steam to carbon case is 1.64 kgCO2
eq. high steam to carbon case is 1.64 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 with carbon free electricity rising to 5.64 kgCO2
eq. per kgH2 with carbon free electricity rising to 5.64 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 considering a grid carbon intensity of 300 kgCO2 per MW hel. The eSER–eSMR–eSEWGS case shows the best performance of all the examined cases with an ECO2
eq. per kgH2 considering a grid carbon intensity of 300 kgCO2 per MW hel. The eSER–eSMR–eSEWGS case shows the best performance of all the examined cases with an ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of 1.22 and 5.41 considering the fully decarbonized grid and a typical grid with a carbon intensity of 300 kgCO2 per MW hel, respectively.
eq. of 1.22 and 5.41 considering the fully decarbonized grid and a typical grid with a carbon intensity of 300 kgCO2 per MW hel, respectively.
Looking at the effect of CH4 leakage on the environmental performance of the eSER plants, a significant impact is evident. With no methane leakage, considering grid carbon intensity of 50 kgCO2 per MW hel, the ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. of the base case, high steam to carbon case, and eSER–eSMR–eSEWGS case are 1.52, 1.30, and 0.92 kgCO2
eq. of the base case, high steam to carbon case, and eSER–eSMR–eSEWGS case are 1.52, 1.30, and 0.92 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 respectively. However, considering GWP20, a 1% increase in the methane leakage results in an important increase in the ECO2
eq. per kgH2 respectively. However, considering GWP20, a 1% increase in the methane leakage results in an important increase in the ECO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. reaching 3.57, 3.31, and 2.92 kgCO2
eq. reaching 3.57, 3.31, and 2.92 kgCO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eq. per kgH2 for the three examined plants, respectively. A comparison between the estimated Equivalent CO2 emissions for the different eSER configurations and the reference FTR plants is reported in Section C of the ESI† of this work.
eq. per kgH2 for the three examined plants, respectively. A comparison between the estimated Equivalent CO2 emissions for the different eSER configurations and the reference FTR plants is reported in Section C of the ESI† of this work.
4.2. Economic analysis results
Following the “bottom-up” method as explained in Section 3 of this work, the calculated capital expenditure (CAPEX) breakdown is reported in Table 5. The calculated total CAPEX of the base case is 82.81 M€ of which 43.3% are related to the cost of the eSER reactors, and 32.8% are associated to the steam generation and heat recovery section of the plant (Heat exchangers). The estimated cost of the syngas compressor and CO2 compressor are 6.39 M€, and 5.98 M€ representing 7.7%, and 7.2% of the total plant CAPEX. Designing the process for higher operating pressure of the reformer (high pressure case), results in eliminating the cost of the syngas compressor. However, the increase in the operating pressure of the reformer leads to a significant increase in the cost of the reactor vessels by 9.39 M€ resulting in a higher total CAPEX of the high-pressure case compared to the base case.| Base case | High pressure | Vacuum regeneration | High S/C | eSER–eSMR–eSEWGS | ||
|---|---|---|---|---|---|---|
| Blowers and pumps | M€ | 0.39 | 0.46 | 0.42 | 0.35 | 0.50 |
| Desulfurization unit | M€ | 0.35 | 0.34 | 0.38 | 0.31 | 0.39 |
| Heat exchangers | M€ | 27.17 | 25.64 | 24.40 | 27.44 | 23.35 |
| eSER reactors | M€ | 35.83 | 45.22 | 34.78 | 35.74 | 45.86 |
| Syngas compressor | M€ | 6.39 | — | 6.77 | 5.70 | — |
| CO2 compression | M€ | 5.98 | 5.77 | 7.77 | 5.46 | 7.01 |
| PSA | M€ | 6.69 | 6.16 | 7.26 | 5.65 | 7.79 |
| Steam compressor | M€ | — | — | — | 2.81 | — |
| eReformer | M€ | — | — | — | — | 2.15 |
| eSEWGS reactors | M€ | — | — | — | — | 6.97 |
| Total | M€ | 82.81 | 83.59 | 81.78 | 83.48 | 94.01 |
The calculated CAPEX breakdown for the vacuum regeneration case shows a significant reduction of the heat exchanger cost compared to the base case, given that lower regeneration temperature is used resulting in a lower need of heat recovery. Instead, as the regeneration step of the process operates in sub atmospheric pressures, the computed CO2 compressor CAPEX is higher. Overall, the estimated total CAPEX of the vacuum regeneration case is the lowest among all the examined plant arrangements.
The two plants with the added constraint of having a CCR higher than 90% show a higher CAPEX compared to the base case. The estimated total CAPEX of the high steam to carbon case and the eSER–eSMR–eSEWGS cases are 83.48, and 94.01 M€, respectively.
As presented in Fig. 11, the levelized cost of hydrogen is used to compare the different simulated configurations. The computed LCOH for the base case is 2.50 € per kgH2, which is comparable to the value of 2.27 € per kgH2 obtained for the FTR-plus plant from the literature.48 For all the simulated cases, the cost of natural gas represents the highest share of the cost of hydrogen followed by the cost of electricity. Operating the eSER process at high pressure or using the vacuum regeneration approach results in a higher LCOH as a result of the combined effect of the reduced hydrogen production efficiency and the carbon capture ratio, resulting in higher CO2 emission tax. A detailed breakdown of the estimated annual costs, used for the calculation of the LCOH, for all the simulated cases is provided in Table 6. It is worth noting that the CAPEX has a minor effect on the LCOH where even if the calculated CAPEX for the eSER–eSMR–eSEWGS case is 12.7% higher than the base case, the LCOH increases by less than 1% only.
| Annual cost | Base case | High pressure | Vacuum regeneration | High S/C | eSER–eSMR–eSEWGS | |
|---|---|---|---|---|---|---|
| Capital expenditure | M€ per year | 3.31 | 3.34 | 3.27 | 3.34 | 3.76 |
| Natural gas | M€ per year | 21.05 | 21.05 | 21.05 | 21.05 | 21.05 |
| Catalyst replacement | M€ per year | 1.95 | 1.97 | 1.97 | 1.82 | 1.97 |
| Sorbent replacement | M€ per year | 0.86 | 0.86 | 0.86 | 0.86 | 1.03 |
| Electricity | M€ per year | 14.95 | 13.98 | 13.37 | 16.36 | 17.27 |
| CO2 transport & storage | M€ per year | 2.85 | 2.82 | 2.75 | 2.98 | 2.90 |
| CO2 emission tax | M€ per year | 1.80 | 1.92 | 2.22 | 1.29 | 0.41 |
| Other OPEX | M€ per year | 3.40 | 3.41 | 3.39 | 3.41 | 3.57 |
| Levelized cost of H2 | € per kgH2 | 2.50 | 2.55 | 2.54 | 2.50 | 2.52 |
Fig. 12 presents a sensitivity analysis performed on the LCOH for three of the simulated cases: the base case, the high steam to carbon case, and the eSER–eSMR–eSEWGS case. The natural gas price (panel A) shows an almost equivalent effect on the three cases with a minor advantage for the high steam to carbon case as it has the highest H2 production efficiency. The electricity price (panel B) presents a strong effect as well, where, in the presence of cheap electricity, the high steam to carbon case becomes the most competitive case. The LCOH is evidently less sensitive to the CO2 tax, where a slight increase in the LCOH for all the evaluated cases is observed with the increase of a carbon tax. The favorable carbon capture performance of the high steam to carbon and eSER–eSMR–eSEWGS cases makes them more competitive plant arrangements in the presence of a high carbon tax. The base case presents the most competitive configuration in the absence of a carbon tax but is surpassed with a tax higher than 100 € per tonCO2 by the high steam to carbon case. When the carbon tax exceeds 150 € per tonCO2 the eSER–eSMR–eSEWGS case becomes the most economic option. Additionally, as reported in panel D of Fig. 12, the number of reactors is considered as a sensitivity parameter as well; where in all the aforementioned simulations, 12 sub-reactors are considered as explained in Section 3.1. However, a case where additional reactors may be needed to manage the depressurization/purge/re-pressurization stages, and hence the sensitivity of the LCOH to this parameter is evaluated. Evidently, the LCOH is less sensitive to the number of sub-reactors, as this number primarily impacts the CAPEX, which accounts for approximately 7% of the LCOH for all simulated cases.
5. Conclusions
This study assesses the technical and economic performance of the novel electrified sorption enhanced reforming (eSER) process. The process leverages the reactor electrification concept for covering the thermal demand of the endothermic sorbent regeneration step in sorption enhanced reforming. Electrified regeneration of the SER packed bed allows to overcome the limitations of conventional SER systems regenerated via heat transfer surfaces or additional chemical looping cycles (i.e. the Ca–Cu), significantly improving the technical feasibility of the process. In this work, natural gas-based hydrogen production plants with H2 production capacity of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 N m3 h−1 are considered. In the core of the process, electrified reactors are assumed as a bundle of sub-reactors that share the same set of valves where each of the sub-reactors is modeled using a 1-D dynamic heterogeneous model of an adiabatic fixed bed reactor. Five different cases are simulated with different operating conditions or plant arrangements. These simulated cases are compared with benchmark technology existing in the literature. The study shows that:
000 N m3 h−1 are considered. In the core of the process, electrified reactors are assumed as a bundle of sub-reactors that share the same set of valves where each of the sub-reactors is modeled using a 1-D dynamic heterogeneous model of an adiabatic fixed bed reactor. Five different cases are simulated with different operating conditions or plant arrangements. These simulated cases are compared with benchmark technology existing in the literature. The study shows that:
•eSER achieves natural gas to H2 efficiency on LHV basis exceeding 100% and specific electric consumption of 12–14 kW h per kgH2.
•Due to the competition between CH4 reforming (favored by high temperature and low pressure) and CO2 sorption by carbonation reaction (favored by low temperature and high pressure), it is challenging for SER processes to achieve a carbon capture ration (CCR) higher than 90%. In the base case (PSER 10 bar, PREG 1 bar), CCR of 86.3% was achieved. Increasing SER pressure and decreasing regeneration pressure and temperature led to the reduction of the CCR.
•To achieve >90% CCR, two options have been explored: (1) very high S/C (= 6), where steam is partly supplied by an LP evaporator and steam compressor, which led to CCR 90.3%; (2) a three-reactor process, where the eSER reactor is followed by an electrified steam methane reformer (eSMR) and an electrified CaO-based sorption-enhanced water gas shift reactor (eSEWGS), achieving CCR = 96.6% thanks to the decoupling between SMR and carbonation reactions after the primary eSER, where the bulk of the two reactions is carried out.
•With electricity carbon intensity of 50 kg per MW h and CH4 leakage rate from the natural gas supply chain of 0.5%, the total 100y carbon footprint of eSER systems was found to be between 1.9 kgCO2 per kgH2 (high CCR case) and 2.5 kgCO2 per kgH2 (base case), comparable to the carbon footprint of electrolytic hydrogen (2.6 kgCO2 per kgH2) with 65% electrolysis efficiency.
•With baseline assumptions (NG cost 9 € per GJ, electricity cost 60 € per MW h), the levelized cost of hydrogen between 2.5 and 2.6 € per kg has been estimated, and most of the cost is associated to the natural gas cost (42–44%) and to the electricity cost (28–32%).
Data availability
The cost function parameters and scaling function parameters used for the economic analysis, as well as the stream properties used for the technical analysis are reported in the ESI† of this work. Other data are available upon request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has received funding from M.U.R. Progetti di Ricerca di Rilevante Interesse Nazionale (PRIN) Bando 2020 under the project (2020N38E75-“PLUG-IN”).References
- G. Natrella, A. Borgogna, A. Salladini and G. Iaquaniello, Clean. Eng. Technol., 2021, 5, 100280 CrossRef.
- IEA, Global Hydrogen Review 2023, https://www.iea.org/reports/global-hydrogen-review-2023, (accessed 6 December 2023).
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, W. L. Eriksen, C. Frandsen, P. M. Mortensen and I. Chorkendorff, Chem. Eng. J., 2021, 425, 131509 CrossRef CAS.
- M. C. Romano, C. Antonini, A. Bardow, V. Bertsch, N. P. Brandon, J. Brouwer, S. Campanari, L. Crema, P. E. Dodds, S. Gardarsdottir, M. Gazzani, G. Jan Kramer, P. D. Lund, N. Mac Dowell, E. Martelli, L. Mastropasqua, R. C. McKenna, J. G. M. S. Monteiro, N. Paltrinieri, B. G. Pollet, J. G. Reed, T. J. Schmidt, J. Vente and D. Wiley, Energy Sci. Eng., 2022, 10, 1944–1954 CrossRef.
- A. M. Adris, B. B. Pruden, C. J. Lim and J. R. Grace, Can. J. Chem. Eng., 1996, 74, 177–186 CrossRef CAS.
- Y. Yan, D. Thanganadar, P. T. Clough, S. Mukherjee, K. Patchigolla, V. Manovic and E. J. Anthony, Energy Convers. Manage., 2020, 222, 113144 CrossRef CAS.
- A. R. Brun-Tsekhovoi, S. S. Kurdyumov, Y. R. Katsobashvili and N. V. Sidorova, Chem. Technol. Fuels Oils, 1976, 12, 97–101 CrossRef.
- B. Balasubramanian, A. L. Ortiz, S. Kaytakoglu and D. P. Harrison, Chem. Eng. Sci., 1999, 54, 3543–3552 CrossRef CAS.
- C. Han and D. P. Harrison, Chem. Eng. Sci., 1994, 49, 5875–5883 CrossRef CAS.
- K. Johnsen, J. R. Grace, S. S. E. H. Elnashaie, L. Kolbeinsen and D. Eriksen, Ind. Eng. Chem. Res., 2006, 45, 4133–4144 CrossRef CAS.
- S. Masoudi Soltani, A. Lahiri, H. Bahzad, P. Clough, M. Gorbounov and Y. Yan, Carbon Capture Sci. Technol., 2021, 1, 100003 CrossRef CAS.
- J. Mays, One Step Hydrogen Generation Through Sorption Enhanced Reforming, Golden, CO (United States), 2017.
- I. Martínez, M. C. Romano, P. Chiesa, G. Grasa and R. Murillo, Int. J. Hydrogen Energy, 2013, 38, 15180–15199 CrossRef.
- L. Zhu and J. Fan, Int. J. Energy Res., 2015, 39, 356–369 CrossRef CAS.
- S. Alam, J. P. Kumar, K. Y. Rani and C. Sumana, J. Cleaner Prod., 2017, 162, 687–701 CrossRef CAS.
- A. Phuluanglue, W. Khaodee and S. Assabumrungrat, Comput. Chem. Eng., 2017, 105, 237–245 CrossRef CAS.
- M. C. Romano, E. N. Cassotti, P. Chiesa, J. Meyer and J. Mastin, Energy Procedia, 2011, 4, 1125–1132 CrossRef CAS.
- J. C. Abanades García and R. Murillo Villuendas, Method for recovering CO2 by means of CaO and the exothermic reduction of a solid, US Pat., US8506915B2, 2009.
- I. Martínez, J. R. Fernández, M. Martini, F. Gallucci, M. van Sint Annaland, M. C. Romano and J. C. Abanades, Int. J. Greenhouse Gas Control, 2019, 85, 71–85 CrossRef.
- L. Riva, I. Martínez, M. Martini, F. Gallucci, M. van Sint Annaland and M. C. Romano, Int. J. Hydrogen Energy, 2018, 43, 15720–15738 CrossRef CAS.
- M. C. Iliuta, Advances in Chemical Engineering, Academic Press Inc, 2017, vol. 51, pp. 97–205 Search PubMed.
- A. N. Antzaras and A. A. Lemonidou, Renewable Sustainable Energy Rev., 2022, 155, 111917 CrossRef CAS.
- E. Tronconi, G. Groppi and C. G. Visconti, Curr. Opin. Chem. Eng., 2014, 5, 55–67 Search PubMed.
- C. G. Visconti, G. Groppi and E. Tronconi, Catal. Today, 2016, 273, 178–186 CAS.
- M. Ambrosetti, Chem. Eng. Process., 2022, 182, 109187 CAS.
- M. G. Vinum, M. R. Almind, J. S. Engbæk, S. B. Vendelbo, M. F. Hansen, C. Frandsen, J. Bendix and P. M. Mortensen, Angew. Chem., Int. Ed., 2018, 57, 10569–10573 CAS.
- M. R. Almind, S. B. Vendelbo, M. F. Hansen, M. G. Vinum, C. Frandsen, P. M. Mortensen and J. S. Engbæk, Catal. Today, 2020, 342, 13–20 CAS.
- V. Poletto Dotsenko, M. Bellusci, A. Masi, D. Pietrogiacomi and F. Varsano, Catal. Today, 2023, 418, 114049 CAS.
- E. Meloni, M. Martino, A. Ricca and V. Palma, Int. J. Hydrogen Energy, 2021, 46, 13729–13747 CAS.
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, F. B. Bendixen, W. L. Eriksen, K. Aasberg-Petersen, C. Frandsen, I. Chorkendorff and P. M. Mortensen, Science, 2019, 364, 756–759 CAS.
- L. Zheng, M. Ambrosetti, D. Marangoni, A. Beretta, G. Groppi and E. Tronconi, AIChE J., 2022, 69, e17620 Search PubMed.
- L. Zheng, M. Ambrosetti, F. Zaio, A. Beretta, G. Groppi and E. Tronconi, Int. J. Hydrogen Energy, 2023, 48, 14681–14696 CrossRef CAS.
- M. Ambrosetti, A. Beretta, G. Groppi, M. C. Romano and E. Tronconi, Reactor with electrically heated thermo-conductive structure for endothermic catalytic processes, WO2023062591A1, 2023 Search PubMed.
- A. Mostafa, I. Rapone, A. Bosetti, M. C. Romano, A. Beretta and G. Groppi, Int. J. Hydrogen Energy, 2023, 48, 26475–26491 CAS.
- V. Spallina, F. Gallucci, M. C. Romano and M. Van Sint Annaland, Chem. Eng. J., 2016, 294, 478–494 CrossRef CAS.
- I. Martínez, D. Armaroli, M. Gazzani and M. C. Romano, Ind. Eng. Chem. Res., 2017, 56, 2526–2539 CrossRef.
- V. Spallina, B. Marinello, F. Gallucci, M. C. Romano and M. Van Sint Annaland, Fuel Process. Technol., 2017, 156, 156–170 CrossRef CAS.
- H. P. Hamers, M. C. Romano, V. Spallina, P. Chiesa, F. Gallucci and M. Van Sint Annaland, Appl. Energy, 2015, 157, 422–432 CrossRef CAS.
- S. Cloete, A. Giuffrida, M. Romano, P. Chiesa, M. Pishahang and Y. Larring, Fuel, 2018, 220, 725–743 CrossRef CAS.
- S. Cloete, M. C. Romano, P. Chiesa, G. Lozza and S. Amini, Int. J. Greenhouse Gas Control, 2015, 42, 340–356 CrossRef CAS.
- J. R. Fernández, J. C. Abanades, R. Murillo and G. Grasa, Int. J. Greenhouse Gas Control, 2012, 6, 126–141 CrossRef.
- I. Martínez, R. Murillo, G. Grasa, J. R. Fernández and J. C. Abanades, AIChE J., 2013, 59, 2780–2794 CrossRef.
- A. Mostafa, I. Rapone, A. Bosetti, M. C. Romano, A. Beretta and G. Groppi, Ind. Eng. Chem. Res., 2023, 62, 15884–15896 CrossRef CAS.
- E. H. Baker, J. Chem. Soc., 1962, 464–470 RSC.
- R. Balzarotti, M. Ambrosetti, A. Beretta, G. Groppi and E. Tronconi, Chem. Eng. J., 2020, 391, 123494 CrossRef CAS.
- L. Zheng, M. Ambrosetti, A. Beretta, G. Groppi and E. Tronconi, Chem. Eng. J., 2023, 466, 143154 CrossRef CAS.
- X. Wang, N. Wang and L. Wang, Int. J. Hydrogen Energy, 2011, 36, 466–472 CrossRef CAS.
- A. de Cataldo, M. Astolfi, P. Chiesa, S. Campanari and M. C. Romano, Int. J. Hydrogen Energy, 2023, 49, 978–993 CrossRef.
- R. Turton, R. C. Bailie, W. B. Whiting, J. A. Shaeiwitz and D. Bhattacharyya, Analysis, Synthesis, and Design of Chemical Processes, 2001, vol. 40 Search PubMed.
- S. C. Roberts, Online Companion Guide to the ASME Boiler & Pressure Vessel Codes, ASME Press, 2020, p. 114 Search PubMed.
- J. Pettersen, R. Steeneveldt, D. Grainger, T. Scott, L. M. Holst and E. S. Hamborg, Energy Sci. Eng., 2022, 10, 3220–3236 CrossRef.
- M. Wiatros-Motyka, N. Fulghum, D. Jones, K. Altieri, R. Black, H. Broadbent, C. Bruce-Lockhart, M. Ewen, P. MacDonald, K. Rangelova, S. Brown, L. Copsey, R. Dizon, S. Hawkins, L. Heberer, S. Hong, R. Hutt, U. Lee, A. Lolla, J. Murdoch, J. Robinson, N. Rodrigues, C. Rosslowe and O. Zaimoglu, Global Electricity Review, 2024.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00540f |
| This journal is © The Royal Society of Chemistry 2025 |