Bandgap engineering in quasi-1D Zr_1−xTi_xS₃ (0 ≤ x ≤ 1) solid solutions

Abstract

TiS₃ and ZrS₃ are quasi-one-dimensional materials from the family of transition metal trichalcogenides with the general composition MX₃, where M is a transition metal and X is a chalcogen. Although isostructural, TiS₃ and ZrS₃ have very different bandgaps of approximately 1 eV and 2 eV, respectively. Consequently, Zr_1−xTi_xS₃ solid solutions are promising for achieving a composition-dependent bandgap that is tunable across a broad spectral range, from visible to infrared, for various electronic and optoelectronic applications. Previous studies demonstrated the synthesis of Zr_1−xTi_xS₃ solid solutions from elemental precursors at 800 °C, but only in a narrow compositional range of 0 ≤ x ≤ 0.33, while higher Ti content led to the formation of a secondary TiS₂ phase. In this work, we optimized the synthetic conditions and produced the entire range of Zr_1−xTi_xS₃ solid solutions (0 ≤ x ≤ 1) via a direct reaction between Zr–Ti alloys and sulfur vapor at a lower temperature of 600 °C. All Zr_1−xTi_xS₃ compositions crystallized as needle-like structures within the P2₁/m space group, with lattice parameters increasing with the Zr content, as confirmed by X-ray diffraction analysis. The optical bandgaps of the prepared crystals were within the 1 to 2 eV range and also increased with the Zr content, demonstrating that synthesis of Zr_1−xTi_xS₃ solid solutions is a viable route for bandgap engineering in transition metal trichalcogenides.

---

Introduction

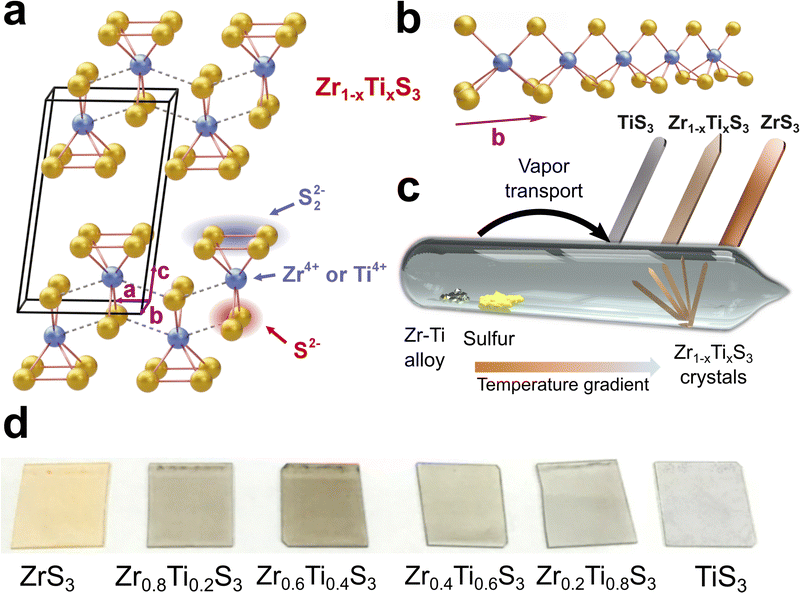
Transition metal trichalcogenides (TMTCs) are quasi-one-dimensional (quasi-1D) materials with the general composition MX₃, where M is a transition metal such as Ti, Zr, Hf, Ta, or Nb and X is S, Se, or Te.^1–5 Members of the TMTC family exhibit intriguing physical phenomena, including temperature-dependent metal–insulator transitions, charge density waves, and superconductivity,^3–8 possess remarkable properties, such as anisotropic electronic transport^9–12 and high breakdown current densities,^13,14 and show promise for numerous electronic and optoelectronic applications,^5,15 ranging from field-effect transistors,^11,16,17 polarization-sensitive photodetectors,^18–21 and printed electronics²² to thermoelectric converters,^23,24 gas sensors,^25–28 and charge transport materials in light-emitting devices.²⁹ Many of these applications benefit from the variable bandgaps of TMTCs that can be either metallic, such as TaS₃ and NbSe₃, have small bandgaps of about 1 eV or less, such as TiS₃, ZrSe₃, and HfSe₃, or have bandgaps around 2 eV or larger, such as ZrS₃ and HfS₃.⁵ Interestingly, despite the great diversity of TMTC materials, they do not cover the visible-to-near-infrared range from 1 to 2 eV, which is crucial for many optoelectronic and photonic technologies. Materials with bandgaps in this range are commonly used for efficient light absorption and charge carrier generation in photovoltaic devices.³⁰ They are also employed in light-emitting devices and photodetectors for telecommunications, integrated photonics, biomedical imaging, and many other applications. Therefore, the potential applications of TMTCs could be significantly expanded if these materials were engineered to exhibit tunable bandgaps within the 1–2 eV range.

In this work, for the bandgap engineering in TMTCs we considered solid solutions of TiS₃ and ZrS₃. These are isostructural compounds that have a monoclinic ZrSe₃-type crystal structure (space group P2₁/m) that is schematically shown in Fig. 1a and b. TiS₃ has a bandgap of about 1 eV,^31–33 while ZrS₃ has a larger bandgap of about 2 eV.^2,12,34,35 Therefore, Zr_1−xTi_xS₃ solid solutions (0 ≤ x ≤ 1) provide a promising material platform for realizing a composition-dependent bandgap that is tunable across a broad spectral range, from visible to infrared.

Fig. 1 (a) Scheme of crystal structure and unit cell of Zr_1−xTi_xS₃ solid solution. (b) Scheme of 1D chain of Zr_1−xTi_xS₃ solid solution along the b crystallographic direction. (c) Scheme of the chemical vapor transport method used to obtain Zr_1−xTi_xS₃ with crystal shape illustrations for TiS₃, ZrS₃ and Zr_1−xTi_xS₃ solid solutions. (d) Photographs of glass slides with slot-die printed layers of the full range of Zr_1−xTi_xS₃ solid solutions.

Several previous works focused on the synthesis and characterization of Zr_1−xTi_xS₃ solid solutions.^36–39 Gard and co-workers performed spectroscopic studies of Zr_1−xTi_xS₃ (0 ≤ x ≤ 1) crystals³⁷ although did not disclose their preparation and referenced a prior study.³⁶ However, that study by Sieber and co-workers, which investigated chemical vapor transport reaction between metallic Ti, Zr and sulfur vapor at 800 °C, reported the synthesis of Zr_1−xTi_xS₃ solid solutions only with 0 ≤ x ≤ 0.33.³⁶ We also studied the reaction between the metals and sulfur at 800 °C and reached a similar conclusion that under these conditions the Zr_1−xTi_xS₃ solid solutions can only be obtained in a narrow compositional range.³⁹ When a high titanium content is used in the precursor mixture, the resulting Zr_1−xTi_xS₃ crystals still have x < 0.33, while the Ti excess results in the formation of a secondary TiS₂ phase.³⁹ Therefore, while prior literature suggests that Zr_1−xTi_xS₃ solid solutions with x > 0.33 are realistic, the procedure for their synthesis remains missing in literature. In this study, we aimed to address this gap in knowledge and establish synthetic procedures for the entire series of solid solutions with 0 ≤ x ≤ 1, which is necessary to cover the whole 1–2 eV range of bandgaps with Zr_1−xTi_xS₃ compounds.

We optimized the synthetic conditions and produced the entire range of Zr_1−xTi_xS₃ solid solutions (0 ≤ x ≤ 1) via a direct reaction between Zr–Ti alloys and sulfur vapor at a lower temperature of 600 °C. We demonstrate that the resulting Zr_1−xTi_xS₃ compositions formed needle-like crystals, consistent with the quasi-1D structure of ZrSe₃-type compounds. The lattice parameters of Zr_1−xTi_xS₃ solid solutions systematically increased with the Zr content, as confirmed by X-ray diffraction analysis. The optical bandgaps of the prepared crystals were within the 1 to 2 eV range and linearly increased with the Zr content, demonstrating that Zr_1−xTi_xS₃ solid solutions are viable route for bandgap engineering in TMTC materials for electronic and optoelectronic applications.

Results and discussion

Previous reports on the synthesis of Zr_1−xTi_xS₃ crystals utilized pure powders of Ti and Zr as precursors and noted that even when employing high titanium-to-zirconium ratios, the resulting solid solutions were deficient in titanium.^36,38,39 This could be due to the difference in the vapor pressures of Ti and Zr under the chosen synthetic conditions. Our approach, involving precisely controlled Zr_1−xTi_x alloys instead of mixtures of elemental Zr and Ti (Fig. 1c), aimed to achieve a more even evaporation of the metallic precursors.³⁹ However, we also observed a reduced titanium concentration in the produced Zr_1−xTi_xS₃ solid solutions when the ampoules were annealed at 800 °C.³⁹ In this study, we attempted synthesis of Zr_1−xTi_xS₃ crystals at different temperatures and found that when the temperature is reduced from 800 °C to 600 °C, the resulting solid solutions have the same Ti/Zr ratio as in the precursor alloys. The reaction products were imaged by optical (Fig. 1d) and scanning electron microscopy (SEM), and their composition was confirmed by energy-dispersive X-ray spectroscopy (EDX), see Fig. S1–S4. In Fig. 2, we demonstrate SEM images of all Zr_1−xTi_xS₃ crystals as well as provide EDX mapping data for Zr_0.2Ti_0.8S₃, the solid solution with the highest titanium content, while EDX maps for other compositions are shown in Fig. S5. The maps show that for all Zr_1−xTi_xS₃ compositions the elements are evenly distributed throughout the crystals.

Fig. 2 SEM images (top and middle rows) of Zr_1−xTi_xS₃ crystals for the following x values: (a) 0.8, (b) 0.6, (c) 0.4, and (d) 0.2. The bottom row belongs to panel (a) and shows SEM image and EDX maps of Ti, Zr and S for Zr_0.2Ti_0.8S₃.

Most of the Zr_1−xTi_xS₃ crystals had similar shapes across different Ti/Zr ratios. The ends of the solid solution crystals were typically sharp, resembling a sword tip, while pure ZrS₃ and TiS₃ crystals had rounded tips, see Fig. 2 as well as Fig. S6 and S7. Based on the shapes of these needle-like crystals, it can be concluded that the fastest growth occurs in the b direction of 1D chains in the structure (Fig. 1b). According to the Burton–Cabrera–Frank (BCF) theory of crystal growth mechanics,⁴⁰ the surface of a growing crystal needs an atomic kink or an open step to promote further growth. For a Zr_1−xTi_xS₃ solid solution crystal, particularly when the Ti/Zr ratio is about 1 : 1, this kink forms naturally due to the presence of two types of atoms with the same number of valence electrons but differing atomic radii (0.160 nm for Zr and 0.147 nm for Ti). This difference in atomic radii significantly accelerates growth along the b direction, giving the crystals their sword-like shapes. The ‘sword’ edges could be formed by the planes with high-h (h11) Miller indices, where h > 3. These planes form because of the large discrepancy between the growth rates along the b direction and at oblique angles to it. A simple evaluation of the crystal shapes indicates that the growth rate along the b direction should be at least three times higher for the Zr_1−xTi_xS₃ solid solutions compared to pristine ZrS₃ and TiS₃ under the same conditions (Fig. S8).

We found that the size of the crystals strongly depends on the Ti/Zr ratio in the resulting solid solution. At high Ti/Zr ratios, the crystals grow significantly larger, reaching widths greater than 5 or even 10 μm. In contrast, at lower Ti/Zr ratios, the width of a single ribbon is typically less than 2 μm. It is important to note that all the crystals discussed above and shown in Fig. 2 were synthesized at 600 °C, using comparable masses of alloy precursors, same temperature gradient, and synthesis time. To achieve crystals of the same size for each composition, the synthesis conditions should be individually adjusted for each case.

All Zr_1−xTi_xS₃ crystals are reasonably stable in ambient conditions, and their degradation becomes noticeable only after weeks of storage in air. SEM images of samples after long-term storage in air reveals the formation of particles with characteristic shapes of anatase platelets⁴¹ on the surface of Zr_1−xTi_xS₃ crystals (Fig. S9), which also correlates with the increased oxygen content in EDX spectra (Fig. S10). In order to ensure that we analyzed pure solid solutions rather than samples containing oxidation products, all the materials characterization was performed on freshly prepared Zr_1−xTi_xS₃ crystals.

We studied the effect of chemical composition of solid solutions on their bond vibrations. Fig. 3a shows Raman spectra of all obtained compositions of Zr_1−xTi_xS₃ solid solutions, as well as the spectra of pristine ZrS₃ and TiS₃. For the Raman peaks of Zr_1−xTi_xS₃ solid solutions we used the same labelling approach as in ref. 42 for ZrS₃ and ZrSe₃. We observed a nearly linear change in the position of the A³_g peak with the increasing Ti content, from 154 cm⁻¹ in pristine ZrS₃ to 179 cm⁻¹ in TiS₃, due to the almost twofold difference in atomic masses of Zr and Ti (Fig. 3b). The vibration scheme for this peak is shown in Fig. 3c.

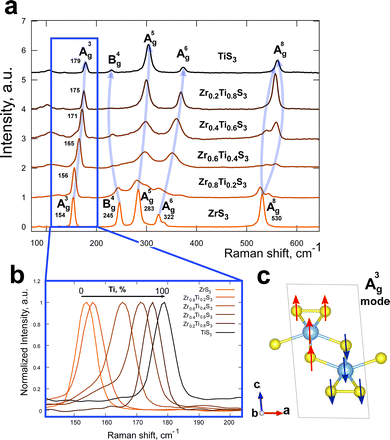Fig. 3 (a) Raman spectra of Zr_1−xTi_xS₃ crystals with (b) the A³_g peak position depending on the Ti/Zr ratio in a solid solution and (c) graphical representation of the A³_g vibration mode.

We found a different trend for the B⁴_g vibration mode, which is observed at 245 cm⁻¹ for ZrS₃. This band was not previously discussed in studies that employed a green 532 nm laser as the excitation source, where the B⁴_g peak was reported to have very low intensity.^42–44 Here, with a 780 nm laser, the B⁴_g mode band is very prominent in ZrS₃ and has a lower intensity in TiS₃. We also note that its intensity inversely correlates with the amount of Ti in the solid solutions, with the lowest intensity observed in Zr_0.2Ti_0.8S₃. The position of the B⁴_g band changes differently compared to the A³_g band, being smallest in Zr_0.2Ti_0.8S₃ and largest in ZrS₃ (230 and 245 cm⁻¹ respectively).

An interesting observation was made for the highest-frequency band A⁸_g located at 530 cm⁻¹ in ZrS₃. This band splits in all studied solid solution crystals, indicating the formation of new vibration modes in the Zr_1−xTi_xS₃ system. Finally, the positions of the A⁵_g and A⁶_g bands shift from lower to higher wavenumbers with the increasing Ti content.

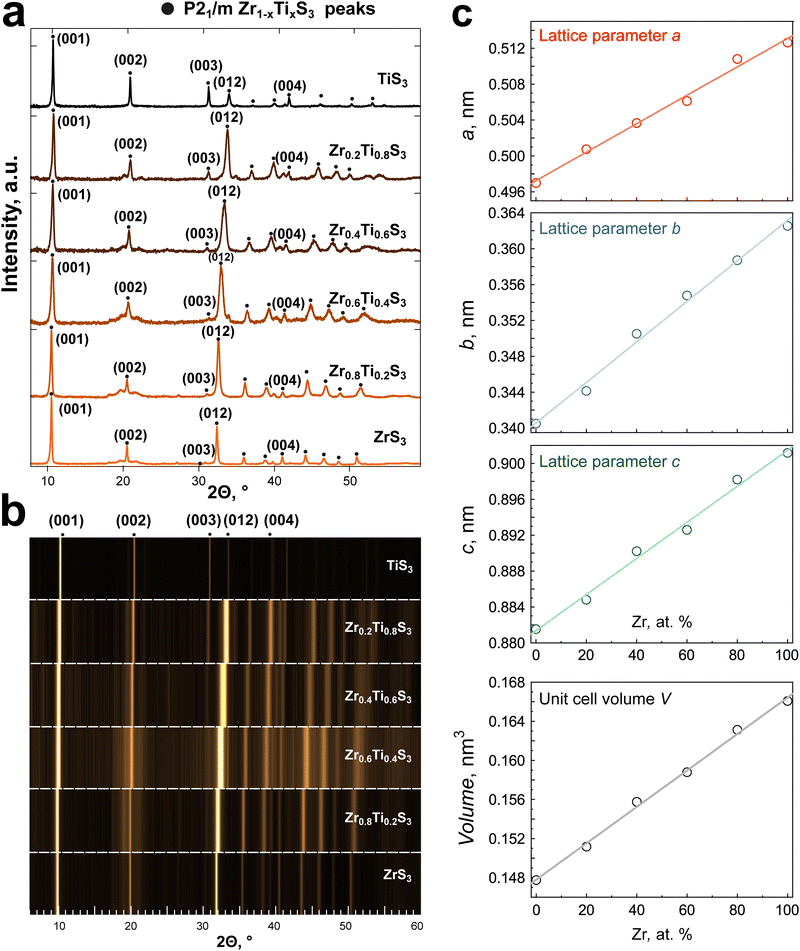
The structural parameters of the Zr_1−xTi_xS₃ solid solutions were identified using X-ray diffraction (XRD) analysis. The XRD patterns for all synthesized compounds are presented in Fig. 4, while the corresponding lattice parameters are summarized in Table S1. All diffractograms display very similar patterns, with the most intense reflections coming from the (001) and (012) planes (Fig. 4a). The XRD patterns exhibit texture due to the needle-like shape of the crystals. Starting from 2Θ = 30°, we observe a gradual shift of the peaks that linearly correlates with the Ti/Zr ratio. The dependence is even more prominent in the waterfall presentation of the XRD data in Fig. 4b. We did not detect any additional superstructure peaks, and the a, b, and c lattice parameters, as well as the unit cell volume show a clear linear dependence on the Zr content (Fig. 4c), in agreement with the Vegard's law.⁴⁵ No correlation was found between the angle β and the composition. The gradual shift in lattice parameters is in agreement with the formation of a substitutional solid solution at any given metal ratio.

Fig. 4 (a) XRD patterns for all Zr_1−xTi_xS₃ solid solution compositions measured with Cu Kα radiation. (b) Waterfall chart showing gradual shift of XRD peaks with the change of composition of solid solutions. (c) Lattice parameters and cell volumes for all Zr_1−xTi_xS₃ crystals showing linear dependences on the Zr content as expected for substitutional solid solutions.

Finally, we performed diffuse reflectance spectroscopy of Zr_1−xTi_xS₃ solid solutions and calculated their optical bandgaps using the conventional Kubelka–Munk function and the Tauc plot approximation for the linear parts of the spectra (Fig. 5a). We note in passing that TMTC compounds are known for rich excitonic physics,^37,46–48 but in this study we specifically focused on the absorption edge energies of Zr_1−xTi_xS₃ solid solutions to determine their optical bandgaps. We obtained a close to linear fit of the bandgap values for the investigated Zr_1−xTi_xS₃ materials with the composition varying from TiS₃ to ZrS₃, as shown in Fig. 5b. The optical bandgap of Zr_1−xTi_xS₃ solid solutions ranges from 1 to 2 eV. All these values fall within the optimal range for many optoelectronic applications.³⁰ The electronic bandgaps of these compounds should be higher by the values of the corresponding exciton binding energies. While not currently known for Zr_1−xTi_xS₃ (0 < x < 1), they are likely comparable to TiS₃, for which the exciton binding energy was experimentally shown to be about 0.13 eV.⁴⁷

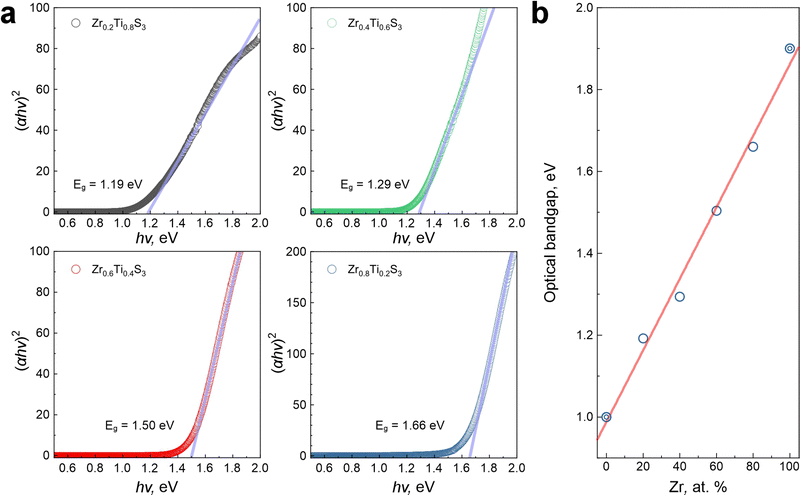Fig. 5 (a) Kubelka–Munk functions and Tauc plots for the diffuse reflectance spectra measured for Zr_1−xTi_xS₃ solid solution powders. (b) Linear fit of Zr_1−xTi_xS₃ (0 ≤ x ≤ 1) bandgap values including literature data (bullseye circles) for pristine ZrS₃ (ref. 12) and TiS₃ (ref. 31).

The ease of exfoliation of TMTC materials through simple ultrasonic treatment in various media allows for the production of ready-to-use inks suitable for slot-die,²⁹ inkjet,²² and other printing techniques, opening up numerous potential applications for Zr_1−xTi_xS₃ solid solutions. We also note that while it is also possible to modulate bandgaps of TMTCs by varying the chalcogen ratio in solid solutions like ZrS_3−xSe_x,^2,49,50 and ZrTe_3−xSe_x,⁵¹ the use of toxic chalcogens for this purpose, such as Se and Te, is less practical than the more environmentally friendly Ti/Zr substitution.

Conclusions

A full range of Zr_1−xTi_xS₃ solid solutions with x = 0.2 step was successfully synthesized using chemical vapor transport reactions between Zr_1−xTi_x alloys and sulfur vapor in sealed quartz ampoules at 600 °C. The structure and composition of solid solutions were confirmed through XRD, EDX, and Raman measurements. In particular, EDX analysis confirmed uniform distribution of Ti, Zr, and S within the crystals. In line with the Vegard's law, the refined lattice parameters a, b and c of Zr_1−xTi_xS₃ crystals display a linear dependence on the Zr content, which is consistent with the formation of substitutional solid solutions.

Our study demonstrates the ability to control the optical bandgap of Zr_1−xTi_xS₃ solid solutions by varying the metal ratio in the precursor alloy used for synthesis. The lowest bandgap value of 1.19 eV was determined for Zr_0.2Ti_0.8S₃, while the highest was 1.65 eV for Zr_0.8Ti_0.2S₃. Considering the known bandgaps of TiS₃ and ZrS₃ of about 1 and 2 eV, respectively, the resulting dependence of the bandgap of Zr_1−xTi_xS₃ on the Zr content is nearly linear, suggesting a straightforward preparation of solid solutions with desired bandgaps in the 1–2 eV range while maintaining the same ZrSe₃-type structure as in pristine TiS₃ and ZrS₃. The study demonstrates a simple and practical route for bandgap engineering in TMTC materials in the technologically important 1–2 eV range, suggesting their relevance to photovoltaics, light-emitting devices and photodetectors for telecommunications, integrated photonics, biomedical imaging, and many other optoelectronic applications.

Experimental

Synthesis of precursor alloys

Zr_1−xTi_x alloys were produced by co-melting of pure Ti and Zr metals using a high-vacuum arc-melting furnace. Titanium and zirconium were mixed in 20/80, 40/60, 60/40, and 80/20 molar ratios, and the chemical compositions of the resulting Zr_1−xTi_x alloys were confirmed by EDX, as shown in Table S2.

Synthesis of Zr_1−xTi_xS₃ solid solutions

The Zr_1−xTi_x alloys were ground into coarse particles and sealed under vacuum in separate quartz tubes with elemental sulfur. In a typical synthesis, we used 300–400 mg of a Zr_1−xTi_x alloy and a calculated amount of sulfur for obtaining stoichiometric Zr_1−xTi_xS₃ solid solutions. All solid solution crystals were synthesized at 600 °C in a tube furnace (Lenton LHC 12/750). The precursor materials were located directly in the center of the furnace (Fig. 1c), while the other side of the ampoule was kept a few centimeters away from the hot zone, forming a small temperature gradient along the ampoule. For the synthesis of TiS₃ and ZrS₃ crystals, we also prepared similar quartz tubes, in which sulfur was sealed with Ti or Zr powders, respectively. TiS₃ was synthesized at 500 °C while ZrS₃ was obtained at 800 °C. The produced crystals were then dispersed in isopropyl alcohol (10 mg mL⁻¹) and treated in an ultrasonic bath for 1.5 h to get stable dispersions. These dispersions were then printed with a slot-die Ossila printer on glass slides to test the ink deposition and prepare samples for optical measurements. The resulting samples are shown in the series of optical photographs in Fig. 1d.

Characterization methods

SEM imaging was performed using a Tescan Vega 3 scanning electron microscope with an integrated AZtec EDX module from Oxford Instruments. Raman spectroscopy was performed using a Thermo DXR Raman microscope with a 780 nm solid-state laser. XRD patterns were recorded using a PANalytical X'Pert instrument with Cu Kα radiation. Crystallographic data from the powder X-ray diffraction patterns were obtained using Le Bail profile fitting performed with BGMN package included within Profex software.⁵² Diffuse reflectance spectra were measured using a Cary 5000 UV-visible spectrometer.

Author contributions

Dmitry S. Muratov: conceptualization, data curation, formal analysis, investigation, methodology, visualization, writing – original draft, review and editing. Ettore Bianco: investigation. Dmitry Karpenkov: data curation, investigation, methodology. Alberto Castellero: resources, methodology. Alexey Lipatov: data curation, formal analysis, investigation, methodology, visualization, writing – original draft, review and editing. Valter Maurino: formal analysis, funding acquisition, project administration, resources, writing – review & editing. Alexander Sinitskii: conceptualization, data curation, formal analysis, funding acquisition, investigation, project administration, writing – original draft, review and editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article or included in SI, any additional data are available on request from the authors.

Refined lattice parameters, EDX spectra and SEM images of crystals and crystal shape description. See DOI: https://doi.org/10.1039/d5tc02480c

Acknowledgements

The authors acknowledge support from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP: D13C22003520001). The work was also supported by the National Science Foundation through awards OIA-2044049 (synthesis of solid solutions) and OSI-2329159 (materials characterization). DSM thanks Vladislav Vanyushin for his contribution to the development of the synthetic approach used in this work.³⁹

References

1. S. Furuseth, L. Brattås, A. Kjekshus, A. F. Andresen and P. Fischer, Acta Chem. Scand., Ser. A, 1975, 29, 623–631.
2. L. Brattas and A. Kjekshus, Acta Chem. Scand., 1972, 26, 3441–3449.
3. M. D. Randle, A. Lipatov, I. Mansaray, J. E. Han, A. Sinitskii and J. P. Bird, Appl. Phys. Lett., 2021, 118, 210502.
4. A. A. Balandin, F. Kargar, T. T. Salguero and R. K. Lake, Mater. Today, 2022, 55, 74–91.
5. M. Chen, L. Li, M. Xu, W. Li, L. Zheng and X. Wang, Research, 2023, 6, 66.
6. S. Ghosh, S. Rumyantsev and A. A. Balandin, Appl. Phys. Rev., 2024, 11, 21405.
7. A. V. Frolov, A. P. Orlov, F. Gay, A. A. Sinchenko and P. Monceau, Appl. Phys. Lett., 2021, 118, 213102.
8. M. Randle, A. Lipatov, A. Kumar, C.-P. Kwan, J. Nathawat, B. Barut, S. Yin, K. He, N. Arabchigavkani, R. Dixit, T. Komesu, J. Avila, M. C. Asensio, P. A. Dowben, A. Sinitskii, U. Singisetti and J. P. Bird, ACS Nano, 2019, 13, 803–811.
9. I. G. Gorlova, S. G. Zybtsev and V. Y. Pokrovskii, JETP Lett., 2014, 100, 256–261.
10. J. Dai and X. C. Zeng, Angew. Chem., Int. Ed., 2015, 54, 7572–7576.
11. J. O. Island, M. Barawi, R. Biele, A. Almazán, J. M. Clamagirand, J. R. Ares, C. Sánchez, H. S. J. van der Zant, J. V. Álvarez, R. D’Agosta, I. J. Ferrer and A. Castellanos-Gomez, Adv. Mater., 2015, 27, 2595–2601.
12. H. Yi, S. J. Gilbert, A. Lipatov, A. Sinitskii, J. Avila, J. Abourahma, T. Komesu, M. C. Asensio and P. A. Dowben, J. Phys. Condens. Matter, 2020, 32, 29LT01.
13. M. A. Stolyarov, G. Liu, M. A. Bloodgood, E. Aytan, C. Jiang, R. Samnakay, T. T. Salguero, D. L. Nika, S. L. Rumyantsev, M. S. Shur, K. N. Bozhilov and A. A. Balandin, Nanoscale, 2016, 8, 15774–15782.
14. A. Geremew, M. A. Bloodgood, E. Aytan, B. W. K. Woo, S. R. Corber, G. Liu, K. Bozhilov, T. T. Salguero, S. Rumyantsev, M. P. Rao and A. A. Balandin, IEEE Electron Device Lett., 2018, 39, 735–738.
15. J. O. Island, A. J. Molina-Mendoza, M. Barawi, R. Biele, E. Flores, J. M. Clamagirand, J. R. Ares, C. Sánchez, H. S. J. van der Zant, R. D’Agosta, I. J. Ferrer and A. Castellanos-Gomez, 2D Mater., 2017, 4, 022003.
16. J. O. Island, M. Buscema, M. Barawi, J. M. Clamagirand, J. R. Ares, C. Sánchez, I. J. Ferrer, G. A. Steele, H. S. J. van der Zant and A. Castellanos-Gomez, Adv. Opt. Mater., 2014, 2, 641–645.
17. A. Lipatov, P. M. Wilson, M. Shekhirev, J. D. Teeter, R. Netusil and A. Sinitskii, Nanoscale, 2015, 7, 12291–12296.
18. X. Wang, K. Wu, M. Blei, Y. Wang, L. Pan, K. Zhao, C. Shan, M. Lei, Y. Cui, B. Chen, D. Wright, W. Hu, S. Tongay and Z. Wei, Adv. Electron. Mater., 2019, 5, 1900419.
19. S. Yang, M. Wu, W. Shen, L. Huang, S. Tongay, K. Wu, B. Wei, Y. Qin, Z. Wang, C. Jiang and C. Hu, ACS Appl. Mater. Interfaces, 2019, 11, 3342–3350.
20. S. J. Gilbert, H. Yi, J. S. Chen, A. J. Yost, A. Dhingra, J. Abourahma, A. Lipatov, J. Avila, T. Komesu, A. Sinitskii, M. C. Asensio and P. A. Dowben, ACS Appl. Mater. Interfaces, 2020, 12, 40525–40531.
21. A. Lipatov, J. Abourahma, G. Viswan, K. Acharya, T. R. Paudel, M. J. Loes, S. Bagheri, A. T. N’Diaye, E. Mishra, T. K. Ekanayaka, M. Zaz, J. Rodenburg, A. Dhingra, R. Streubel, P. A. Dowben and A. Sinitskii, J. Mater. Chem. C, 2023, 11, 9425–9437.
22. S. Baraghani, J. Abourahma, Z. Barani, A. Mohammadzadeh, S. Sudhindra, A. Lipatov, A. Sinitskii, F. Kargar and A. A. Balandin, ACS Appl. Mater. Interfaces, 2021, 13, 47033–47042.
23. C. Wang, C. Zheng and G. Gao, J. Phys. Chem. C, 2020, 124, 6536–6543.
24. N. V. Morozova, I. V. Korobeinikov, K. V. Kurochka, A. N. Titov and S. V. Ovsyannikov, J. Phys. Chem. C, 2018, 122, 14362–14372.
25. N. Rafiefard, A. Iraji Zad, A. Esfandiar, P. Sasanpour, S. Fardindoost, Y. Zou, S. J. Haigh and S. H. H. Shokouh, Microchim. Acta, 2020, 187, 117.
26. V. V. Sysoev, A. V. Lashkov, A. Lipatov, I. A. Plugin, M. Bruns, D. Fuchs, A. S. Varezhnikov, M. Adib, M. Sommer and A. Sinitskii, Sensors, 2022, 22, 9815.
27. M. J. Loes, S. Bagheri, N. S. Vorobeva, J. Abourahma and A. Sinitskii, ACS Appl. Nano Mater., 2023, 6, 9226–9235.
28. C. C. Mayorga-Martinez, Z. Sofer, J. Luxa, Š. Huber, D. Sedmidubský, P. Brázda, L. Palatinus, M. Mikulics, P. Lazar, R. Medlín and M. Pumera, ACS Nano, 2018, 12, 464–473.
29. D. S. Muratov, A. R. Ishteev, D. A. Lypenko, V. O. Vanyushin, P. Gostishev, S. Perova, D. S. Saranin, D. Rossi, M. Auf der Maur, G. Volonakis, F. Giustino, P. O. Å. Persson, D. V. Kuznetsov, A. Sinitskii and A. Di Carlo, ACS Appl. Mater. Interfaces, 2019, 11, 48021–48028.
30. B. R. Sutherland, Joule, 2020, 4, 984–985.
31. H. Yi, T. Komesu, S. Gilbert, G. Hao, A. J. Yost, A. Lipatov, A. Sinitskii, J. Avila, C. Chen, M. C. Asensio and P. A. Dowben, Appl. Phys. Lett., 2018, 112, 52102.
32. E. Finkman and B. Fisher, Solid State Commun., 1984, 50, 25–28.
33. I. J. Ferrer, J. R. Ares, J. M. Clamagirand, M. Barawi and C. Sánchez, Thin Solid Films, 2013, 535, 398–401.
34. H. G. Grimmeiss, A. Rabenau, H. Hahn and P. Ness, Z. Phys. Chem., Abt. A, 1961, 65, 776–783.
35. S. Kurita, J. L. Staehli, M. Guzzi and F. Lévy, Phys. B, 1981, 105, 169–173.
36. K. Sieber, B. Fotouhi and O. Gorochov, Mater. Res. Bull., 1983, 18, 1477–1484.
37. P. Gard, C. Sourisseau and O. Gorochov, Phys. Status Solidi B, 1987, 144, 885–901.
38. P. Gard, F. Cruege, C. Sourisseau and O. Gorochov, J. Raman Spectrosc., 1986, 17, 283–288.
39. D. S. Muratov, V. O. Vanyushin, N. S. Vorobeva, P. Jukova, A. Lipatov, E. A. Kolesnikov, D. Karpenkov, D. V. Kuznetsov and A. Sinitskii, J. Alloys Compd., 2020, 815, 152316.
40. W. K. Burton, N. Cabrera and F. C. Frank, Nature, 1949, 163, 398–399.
41. F. Pellegrino, E. Ortel, J. Mielke, R. Schmidt, V. Maurino and V.-D. Hodoroaba, Adv. Eng. Mater., 2022, 24, 2101347.
42. K. Osada, S. Bae, M. Tanaka, H. Raebiger, K. Shudo and T. Suzuki, J. Phys. Chem. C, 2016, 120, 4653–4659.
43. A. Zwick, M. A. Renucci and A. Kjekshus, J. Phys. C-Solid State Phys., 1980, 13, 5603–5614.
44. J. Y. Harbec, C. Deville Cavellin and S. Jandl, Phys. Status Solidi, 1979, 96, K117–K120.
45. L. Vegard, Z. Phys, 1921, 5, 17–26.
46. K. N. Boldyrev, E. V. Mostovshchikova, A. N. Titov, V. Y. Pokrovskii and I. G. Gorlova, JETP Lett., 2024, 120, 565–572.
47. A. J. Molina-Mendoza, M. Barawi, R. Biele, E. Flores, J. R. Ares, C. Sánchez, G. Rubio-Bollinger, N. Agraït, R. D’Agosta, I. J. Ferrer and A. Castellanos-Gomez, Adv. Electron. Mater., 2015, 1, 1500126.
48. Q. Cui, A. Lipatov, J. S. Wilt, M. Z. Bellus, X. C. Zeng, J. Wu, A. Sinitskii and H. Zhao, ACS Appl. Mater. Interfaces, 2016, 8, 18334–18338.
49. A. Zwick, G. Landa, R. Carles, M. A. Renucci and A. Kjekshus, Solid State Commun., 1983, 45, 889–893.
50. J. Deslandes and S. Jandl, Phys. Rev. B: Condens. Matter. Mater. Phys., 1984, 29, 2088–2090.
51. X. Zhu, W. Ning, L. Li, L. Ling, R. Zhang, J. Zhang, K. Wang, Y. Liu, L. Pi, Y. Ma, H. Du, M. Tian, Y. Sun, C. Petrovic and Y. Zhang, Sci. Rep., 2016, 6, 26974.
52. N. Doebelin and R. Kleeberg, J. Appl. Crystallogr., 2015, 48, 1573–1580.

---