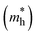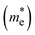Open Access Article
Open Access ArticleTuning the charge transfer and band shape of donor–acceptor covalent organic frameworks for optoelectronics†
Arnau
Garcia-Duran
 and
Maria
Fumanal
and
Maria
Fumanal
 *
*
Departament de Ciència de Materials i Química Física and IQTCUB, Facultat de Química, Universitat de Barcelona, Martí i Franquès 1, E-08028 Barcelona, Spain. E-mail: mfumanal@ub.edu
First published on 8th July 2025
Abstract
Donor–acceptor (D–A) covalent organic frameworks (COFs) have gained great attention in the fields of optoelectronics due to their ability to promote charge transfer (CT) and charge transport, leading to long-lived charge carriers and thus better device performances. The modularity of these materials makes them ideal for computational molecular design based on electronic structure calculations, able to predict their excited state and photoconductive properties in silico. However, the characterization of CT transitions in D–A COFs inherits the same difficulties as their analogous molecular systems. This poses a challenge for standard cost-effective electronic structure methods, whose reliability needs to be carefully assessed. Moreover, strong CT is usually associated with localized states, whereas band dispersion is ascribed to delocalized states. Thus, whether the CT and the in-plane photoconductivity can be enhanced simultaneously still needs to be addressed. In this work, we propose 12 chemical modifications for two families of 1,3,6,8-tetraphenylpyrene (Py) 2D-COFs with potential for light-induced CT and highly dispersive bands. Based on DFT/TD-DFT calculations, we characterize the low-lying excited state properties of the 26 monolayers and expose the limitations of the most common approximations to provide reliable data. Ultimately, we analyze the CT versus band shape correlation and identify two possible candidates with improved features for optoelectronic applications.
Introduction
Covalent organic frameworks (COFs) are a versatile class of porous crystalline materials that have been exploited in a wide range of applications, from gas adsorption1,2 to catalysis3,4 and energy storage,5,6 among others. COFs are composed of organic molecules covalently bonded through reticular chemistry, usually forming well-organized extended two-dimensional (2D) networks, which also endowed them with great attention in the fields of electronics7,8 and optoelectronics.9,10From the molecular-design perspective, the modular nature of COFs offers the possibility to control their optoelectronic properties by using different building blocks (donors, acceptors, linkers, etc.)11,12 and topologies (hexagonal, rhombic, Kagome, etc.).13,14 The performance of COF materials for photocatalysis or photovoltaics for instance, is directly associated with the lifetime of the photo-generated charge carriers, which can be typically enhanced using charge transfer (CT) donor–acceptor (D–A) pairs.15–18 In addition, 2D-COFs have the ability to trigger both in-plane π-conjugation as well as out-of-plane π–π-stacking interactions and, thus, favorable charge transport pathways that promote charge separation.19,20 However, only certain 2D topologies21 and π-stacking arrangements22 are able to optimize these charge transport pathways.
The versatile modularity of COFs causes an almost unlimited number of potential 2D-COF structures that can be synthesized, which makes the trial-and-error strategy unfeasible. In this context, computational modeling provides an attractive alternative route to accelerate the discovery of new COF structures with target properties.23–25 To this end, accurately predicting the excited state and photoconductive properties of COFs in silico is crucial. Nevertheless, COFs (together with metal–organic frameworks or MOFs) are uniquely positioned between a molecular and periodic material and thus may pose a challenge for the cost-effective electronic structure characterization of their excited states.26–28 On the one hand, DFT/TD-DFT approaches are commonly applied owing to their cost-accuracy prediction.29 However, the CT excited state prediction of D–A COF materials inherits the same difficulties than their partner D–A molecular systems and will strongly depend on the charge localization features of the DFT functional of choice.30–32 On the other hand, the band structure obtained at DFT level is typically sufficiently accurate and it is commonly applied to evaluate the effective mass values of 2D COFs.33–35
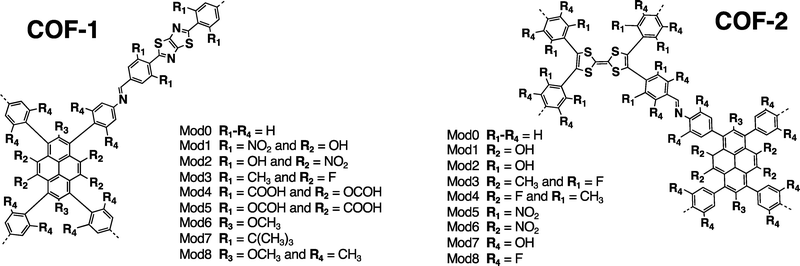
This work focuses on two families of 1,3,6,8-tetraphenylpyrene (Py) 2D-COFs with promising features for in-plane CT and photoconductive properties, named COF-1 and COF-2. (see Fig. 1). These COFs were selected from the literature for three reasons. First, they have already been synthesized and thus, their synthetic routes are available. Second, they hold ligands whose donor and acceptor character can be tuned at the molecular level. Finally, both COFs have an oblique/rectangular 2D topology, which have been reported as promising for the design of monolayers with in-plane highly dispersive bands.21 Through DFT/TD-DFT calculations, we characterize the ground and first excited state of 26 D–A COF monolayers, 13 for each family, and assess the reliability of the most common DFT approximations to predict the CT properties. The approximations considered are (i) reduction of the dimensionality to a cluster model, (ii) upgrading the DFT functional to a long-range corrected method, and (iii) optimizing the excited state geometry. Then, we evaluate the electron and hole effective mass values from the conduction and valence band minimum and maximum, respectively. Finally, we analyze the correlation between the CT and band shape and identify two possible candidates with promising features for improved optoelectronic performance.
 | ||
| Fig. 1 Molecular structure and unit cell of COF-1 (left) and COF-2 (right). Hydrogens omitted for clarity. | ||
Methods
COF structures
As mentioned in the introduction, two experimentally reported COF structures (COF-1 and COF-2) were chosen due to their synthetic availability, their tunable D–A character and their four-arm topology, whose symmetry promotes dispersive bands and thus potential in-plane photoconductivity.21 COF-1 monolayers expand as an oblique lattice built from electron-rich Py and electron-deficient thiazolo-[5,4-d]thiazole (Tz) ligands connected via an imine linker (Fig. 1).15,36 Thus, it is expected a significant Py-to-Tz CT character in its original form. COF-2 monolayers expand as a rectangular lattice built from the same Py ligand and the electron-richer tetrathiafulvalene (TTF) ligand, also connected via imine linkers (Fig. 1).37,38 In this way, the Py ligand is expected to be the donor in COF-1, while it is expected to be a poor acceptor in COF-2. The TTF-to-Py CT character is expected to improve by tuning the electronegativity of the ligands via in silico chemical modifications.12 chemical modifications were performed to these structures in silico aiming at tuning the D–A character and the in-plane band dispersion. 8 modifications consist in adding electron-withdrawing groups (–F, –COOH, –NO2) and/or electron-donating groups (–CH3, –OCHO, –OH) to the ligands (Mod1 to Mod8, see Fig. 2). 3 modifications consist in chemically changing the ligands by substituting some heteroatoms (Mod9 to Mod11). Finally, 1 modification consists in changing the imine linker to amide, (Mod12, see Table 1 and Fig. S1, ESI†). This modification is proposed based on the ability of this linker to tune the CT properties of other Py-based COFs.39
| COF-1 | COF-2 | |
|---|---|---|
| Mod9 | Pyrene → triazapyrene | Pyrene → triazapyrene |
| Mod10 | Phenyls attached to Tz → pyrazines | Phenyls attached to TTF → pyrazines |
| Mod11 | Tz → pyrrolo[3,2-b]pyrrole | Mod3 + TTF → naphtalene |
| Mod12 | Imine linker → amide | Imine linker → amide |
Geometry optimization
Optimization of the cell parameters and crystal coordinates of the 13 COF-1 and COF-2 monolayers was performed at the Γ-point in 2D periodic boundary conditions with DFT using the PBE functional40 including Grimme D3BJ dispersion correction41 as implemented in the CP2K 9.1 program.42,43 In all calculations, the GTH pseudopotential44 was used with a density cutoff of 400 Ry and DZVP-MOLOPT basis set.45 This set up has been shown to provide reliable cell and crystal structures of COFs23,46 and MOFs.47,48 The COF monolayers were oriented parallel to the x–y plane and separated by a fixed vacuum spacing of 25 Å in the z-direction. The optimized cell parameters are provided in Table S1 of ESI.†Excited state characterization
The lowest excited state singlet (S1) was computed for the optimized COF monolayers in periodic boundary conditions with linear-response TD-DFT using the truncated PBE0 functional49 and the Tamm–Dancoff approximation (TDA) as implemented in CP2K 9.1.42,43 The auxiliary density matrix method (ADMM)50 was used to reduce the computational cost together with the pFIT3 auxiliary basis set (3 Gaussian exponents per valence orbital, including polarization d-functions). The highest occupied crystal orbital (HOCO), lowest unoccupied crystal orbital (LUCO), band gap, S1 energies, and oscillator strengths are collected in Table S2 of ESI.†TDDFT/TDA calculations were also performed for the isolated D–A pairs with PBE049 and ωb97XD51 functionals using def2-SVP basis set as implemented in Gaussian.52 The calculations of the isolated dimers were done at (1st) the optimized geometry extracted from the 2D periodic structure, (2nd) the optimized geometry in gas phase and (3rd) the optimized geometry of the S1 state in gas phase. For the (1st) step, hydrogen atoms were added to saturate the 0D structure. For the (2nd) and (3rd) steps, the position of the atoms at the edge of both ligands was fixed to maintain the same relative disposition than in the 2D periodic structure.
For each excited state evaluation, the local character associated to the lowest excited state singlet is calculated as the weighted average of the spatial overlap between the Kohn–Sham occupied and virtual orbitals involved in the excitation as:53–58
 | (1) |
 | (2) |
Coefficients below |0.05| were not considered. The CT character of the excited state is evaluated as 1 − Λ.
Effective mass calculations
The mobility of the charge carriers μ is inversely related to the effective mass, which can be approximated from the curvature of the band structure. Band structure calculations were performed with PBE0 using FHI-AIMS version 210226.59 The “light/Tier1” numerical atom-centered orbital (NAO) basis set was used in all cases.60,61 The band structure was computed using a Monkhorst–Pack scheme with a x–y k-point grid of 3 × 3 to sample the 2D Brillouin zone. The dispersion of the conduction band minima (CBM) and valence band maxima (VBM) was then evaluated as the inverse of the effective mass: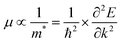 | (3) |
The data near the VBM and CBM was fitted to a parabola to obtain the curvature and therefore, the effective mass values. All high-symmetry points of the band structure path were considered to compute the effective mass. From the VBM or CBM, the forward and backward effective masses were computed, and the smallest values were considered the most favorable hole and electron photoconductive pathways, respectively.
Results and discussion
Charge transfer of the D–A COF monolayers
As mentioned in the introduction, the performance of a COF material for photocatalysis or photovoltaics will depend on its ability to generate long-lived charge carriers, which can be promoted in D–A CT states. Following Kasha's rules,62 we assume that photoexcited states will decay towards the lowest excited singlet (S1). The computed CT values (1 − Λ) associated with the lowest singlet (S1) excited state of the D–A COF monolayers are collected in Table 2 and Table 3 for the two non-substituted structures (Mod0) of COF-1 and COF-2 and their 12 in silico chemical modifications (Mod1-to-Mod12) as evaluated with truncated PBE0 implemented in CP2K 9.1. CT values from 0 to 0.5 indicate mostly local character and thus higher chances of fast electron–hole recombination, while values from 0.5 to 1 indicate mostly CT character and, therefore, longer charge carrier's lifetimes. The CT values expand from 0.21 to 0.77 in the case of COF-1 and from 0.27 to 0.92 in the case of COF-2, therefore covering all possible local and CT situations. Most COF-1 (9 out of 13) show a CT value below 0.5, whereas all COF-2 monolayers have a CT component above 0.5 except Mod11, for which the TTF ligand has been modified to naphthalene. This suggests that the CT character is mostly determined by the chemical nature of the D–A combination. The PBE0 calculations predict that three monolayers of COF-1 will show larger CT than the original structure, which correspond to Mod1, Mod10 and Mod11, and four monolayers of the COF-2 family will have larger CT: the Mod4, Mod6, Mod9 and Mod12. and
and  , in electron rest mass (m0 units), computed at the VBM and CBM, respectively, with PBE0. Corrected CT values as computed for the isolated D–A pairs with ωB97XD at the optimized S1 geometry
, in electron rest mass (m0 units), computed at the VBM and CBM, respectively, with PBE0. Corrected CT values as computed for the isolated D–A pairs with ωB97XD at the optimized S1 geometry
| PBE0 | ωB97XD | ||||||
|---|---|---|---|---|---|---|---|
| CT (1 − Λ) | CT component | Λ | Local component | Corrected CT | |||
| a Note that the Tz ligand has changed to pyrrolo[3,2-b]pyrrole. b The S1 excited state could not be optimized. | |||||||
| Mod0 | 0.53 | Py-to-Tz | 0.47 | Delocalized | 0.90 | 1.01 | 0.79 |
| Mod1 | 0.77 | Py-to-Tz | 0.23 | Local in Py | 24.08 | 5.28 | 0.59 |
| Mod2 | 0.39 | Tz-to-Py | 0.61 | Delocalized | 13.36 | 8.58 | 0.37 |
| Mod3 | 0.21 | Py-to-Tz | 0.79 | Delocalized | 4.84 | 2.20 | 0.15 |
| Mod4 | 0.35 | Py-to-Tz | 0.65 | Local in Py | 2.68 | 1.71 | 0.18 |
| Mod5 | 0.36 | Py-to-Tz | 0.64 | Delocalized | 1.43 | 0.79 | 0.28 |
| Mod6 | 0.49 | Py-to-Tz | 0.51 | Delocalized | 1.34 | 4.15 | 0.79 |
| Mod7 | 0.27 | Py-to-Tz | 0.73 | Local in Py | 9.55 | 1.02 | 0.17 |
| Mod8 | 0.33 | Py-to-Tz | 0.67 | Local in Tz | 1.37 | 2.00 | 0.60 |
| Mod9 | 0.34 | Py-to-Tz | 0.66 | Delocalized | 0.56 | 0.43 | 0.27 |
| Mod10 | 0.64 | Py-to-Tz | 0.36 | Delocalized | 1.01 | 2.28 | 0.80 |
| Mod11 | 0.77 | Py-to-Tza | 0.23 | Delocalized | 8.64 | 1.70 | —b |
| Mod12 | 0.37 | Tz-to-Py | 0.63 | Delocalized | 2.26 | 1.18 | 0.14 |
 and
and  , in electron rest mass (m0 units), computed at the VBM and CBM, respectively, with PBE0. Corrected CT values as computed for the isolated D–A pairs with ωB97XD at the optimized S1 geometry
, in electron rest mass (m0 units), computed at the VBM and CBM, respectively, with PBE0. Corrected CT values as computed for the isolated D–A pairs with ωB97XD at the optimized S1 geometry
| PBE0 | ωB97XD | ||||||
|---|---|---|---|---|---|---|---|
| CT (1 − Λ) | CT component | Λ | Local component | Corrected CT | |||
| a Note that the TTF ligand has changed to naphtalene. | |||||||
| Mod0 | 0.62 | TTF-to-Py | 0.38 | Local in TTF | 4.64 | 0.93 | 0.53 |
| Mod1 | 0.62 | TTF-to-Py | 0.38 | Local in TTF | 2.11 | 6.17 | 0.57 |
| Mod2 | 0.69 | TTF-to-Py | 0.31 | Local in TTF | 11.02 | 4.90 | 0.60 |
| Mod3 | 0.62 | TTF-to-Py | 0.38 | Local in TTF | 5.81 | 1.99 | 0.57 |
| Mod4 | 0.81 | TTF-to-Py | 0.19 | — | 70.78 | 6.67 | 0.56 |
| Mod5 | 0.63 | TTF-to-Py | 0.37 | Local in TTF | 6.81 | 2.00 | 0.86 |
| Mod6 | 0.90 | TTF-to-Py | 0.10 | — | 22.41 | 12.43 | 0.55 |
| Mod7 | 0.62 | TTF-to-Py | 0.38 | Local in TTF | 5.78 | 1.08 | 0.57 |
| Mod8 | 0.58 | TTF-to-Py | 0.42 | Local in TTF | 2.35 | 1.48 | 0.53 |
| Mod9 | 0.73 | TTF-to-Py | 0.27 | Local in TTF | 6.44 | 6.41 | 0.53 |
| Mod10 | 0.52 | TTF-to-Py | 0.48 | Delocalized | 1.74 | 1.94 | 0.58 |
| Mod11 | 0.27 | Py-to-TTFa | 0.73 | Delocalized | 2.68 | 0.80 | 0.19 |
| Mod12 | 0.92 | TTF-to-Py | 0.08 | — | 94.33 | 66.97 | 0.58 |
The characterization of the CT in the excited state can be made based on the occupied-virtual orbital contributions to the S1 state. These are collected in Tables S3 and S4 of ESI† for COF-1 and COF-2 monolayers, respectively. Remarkably, the major contribution to the S1 state for all COF-2 monolayers is the HOCO-to-LUCO transition, while for the COF-1 monolayers, this is the case only in half of the systems. This shows that, depending on the material, the lowest energy excitation does not necessarily correspond to the HOCO-to-LUCO transition but to a more complex electronic transition from lower to higher energy crystal orbitals whose exciton binding energy compensates a slightly larger orbital energy gap. Indeed, most COF-1 monolayers exhibit a remarkably small energy gap (<0.1 eV) between the LUCO and LUCO+1, whereas only Mod5 of COF-2 fulfills this condition. As a consequence, Mod5 of COF-2 exhibits a strongly mixed HOCO-to-LUCO and HOCO-to-LUCO+1 character (Table S4, ESI†).
Based on the crystal orbitals mainly involved in the one-electron contributions to the S1 state, it is possible to classify the local and CT component (Fig. S2, S3 (ESI†) and Tables 2, 3). The CT character of most COF-1 monolayers corresponds to Py-to-Tz except for Mod2 and Mod12 for which the CT component originates in a Tz-to-Py contribution (although the global character of the S1 state is still mainly local). In Mod2, the change in CT character originates in the addition of electron-withdrawing (–NO2) and electron-donating (–OH) substituents to the Py and Tz ligands, respectively. In Mod12, the change in CT character originates in the linker substitution from imine to amide. This highlights the importance of the linkage in the CT properties, in agreement with what has been observed in previous work.39 In the case of the COF-2 monolayers, TTF is significantly more donor than Py and consequently, the CT component is TTF-to-Py in all cases except when chemically modifying the TTF ligand to naphthalene in Mod11, in which case the CT polarization changes.
There are two different approaches to enhance the local component of the S1 state. On the one hand, delocalized occupied and/or virtual orbitals will result in one-electron transitions with a reduced CT component, thus enhancing the local component of the excitation. This is the case for most COF-1 monolayers, which exhibit a delocalized “local” component (Table 2). An example of the delocalized nature of the crystal orbitals of COF-1 is shown in Fig. 3a. On the other hand, one-electron transitions between localized crystal orbitals in the same ligand will also result in a small CT and a large local component. This is the case for Mod1, Mod4, and Mod7 of COF-1, which show a localized HOCO in the Py ligand, and for Mod8 of COF-1, which shows a LUCO strongly localized in the Tz (Fig. S2, ESI†). Similarly, the TTF-localized nature of the HOCO in most COF-2 monolayers (Fig. 3b) originates both the CT and local components, except in the case of Mod10 and Mod11, for which partial delocalization of the frontier crystal orbitals results in a diminution of the CT character (Fig. S3, ESI†).
Ultimately, the CT and localization features of the S1 state in D–A 2D-COF strongly depend on the relative disposition of the frontier molecular orbitals of the constituent D and A units in a similar way than in D–A dimers63 or in 1D D–A copolymers (Fig. 4).64,65 In Tables S5 and S6 (ESI†) are collected the PBE0 HOMO and LUMO energies of the isolated D and A monomers of each COF monolayer together with the relative HOMO and LUMO energy differences. The correlation between the resulting local and CT orbital energy gaps of the isolated monomers with the CT values of the 2D monolayer is shown in Fig. 5. Those D–A combinations with smaller local orbital gaps tend to result in smaller CT values, whereas those D–A combinations with smaller CT orbital gaps tend to provide larger CT values. Remarkably, COF-1 and COF-2 give rise to two parallel correlations between the orbital gaps and the CT values separated by a factor of 0.3 in the CT magnitude, as seen in Fig. 5. We ascribe this to the different (de)localization features of the frontier crystal orbitals (Fig. 3), which tend to result in systematically smaller CT values for COF-1 (delocalized) than for COF-2 (localized orbitals) monolayers.
 | ||
| Fig. 4 Schematic representation of the relative disposition of the HOMO and LUMO frontier molecular energies of a given D–A pair promoting CT or local contributions in the low-lying excited state. | ||
Charge transfer of the D–A isolated dimers
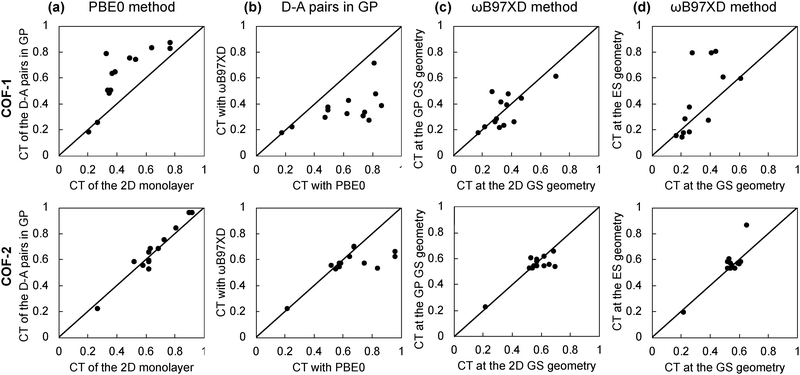
Global hybrid functionals such as PBE0 are not able to fully recover the 1/r dependence of the electron–hole interaction and, thus, tend to overstabilize the CT with respect to the local contributions, especially in long-range CT interactions such as the ones found in D–A pairs. In contrast, the coulomb potential is split into a long-range and a short-range local potential term in range-separated hybrid functionals such as ωB97XD, which has been shown to provide an accurate description of long-range CT interactions.63–67 Herein, we compare the CT values obtained with truncated PBE0 for the 2D monolayers with the CT values computed in the gas phase for the isolated D–A pairs, both with PBE0 and ωB97XD methods. We first compare the CT values at the geometry optimized for the 2D monolayers, then reoptimize the coordinates of the isolated D–A pairs in the gas phase, and, finally, optimize the excited state geometry and reevaluate the CT character. In this way, we assess (1st) the effect of the 2D periodicity, (2nd) the limitations of the PBE0 approximation, and (3rd) the effect of the relaxation of the excited state geometry. Tables S7 and S8 (ESI†) collect the CT values obtained in each case, and Fig. 6 shows the case-to-case correlations for COF-1 and COF-2.The correlation between the CT values obtained for the extended 2D monolayer and the isolated D–A pairs in gas phase is shown in Fig. 6a. COF-2 shows a perfect agreement between the 2D and isolated CT values. However, COF-1 shows a small deviation toward larger CT values for the isolated dimers. This is ascribed to the fact that COF-2 has mostly local crystal orbitals, whereas COF-1 has significantly delocalized crystal orbitals (Fig. 3) which reduces the overall CT values as explained above. In this way, the isolated D–A pairs fairly represent the CT properties of the COF-2 monolayers, whereas this is not the case for COF-1, which would require a larger-size 0D cluster model or considering point charge embedding schemes68,69 for the correct characterization of its excited state CT properties.
Fig. 6b shows the correlation between the CT values of the isolated D–A pairs computed with PBE0 and ωB97XD functional. In the case of COF-2, PBE0 and ωB97XD predict the same CT values up to CT values of 0.7. Above 0.7, PBE0 tends to overestimate the CT values. In the case of COF-1, PBE0 and ωB97XD methods predict the same CT values up to CT values of 0.3. Above 0.3, PBE0 overestimates the CT values. This highlights the difficulties of PBE0 in correctly predicting the CT when local and non-local excitations compete, especially in cases with strong delocalization features, such as in COF-1. In those cases, a range-separated hybrid functional such as ωB97XD is needed.
Comparison between the CT values computed with ωB97XD at the 2D and 0D optimized geometries show no systematic deviations towards smaller or larger values (Fig. 6c). Similarly, optimization of the excited state geometry does not significantly perturb the CT values in the case of COF-2 (Fig. 6d). However, the optimization of the excited state geometry in some COF-1 dimers results in significantly larger CT values (Fig. 6d). This is the case of Mod0, Mod6 and Mod10 of COF-1 dimers, for which the CT increases from 0.3-0.4 at the GS geometry to 0.8 at the ES geometry. The MO involved in the one-electron transitions with the largest coefficients in the S1 state are depicted in Fig. S4–S6 (ESI†). These show that there is a significant spatial redistribution of the electron and hole densities upon excited state relaxation for these systems. Indeed, the prediction of whether these systems have a low-lying excited state with mostly local (CT < 0.5) or non-local (CT > 0.5) character entirely relies on considering the excited state optimized geometry.
Altogether, the results on the isolated D–A pairs of the COF-1 and COF-2 monolayers indicate that (i) larger cluster models beyond the D–A pair may be needed depending on the (de)localization features of the COF monolayer, (ii) range-separated hybrid functionals such as ωB97XD are required to accurately characterize the CT character and avoid CT overestimation in those cases with competing local and non-local excitations and (iii) the relaxation of the excited state towards its minimum energy geometry may be crucial to predict the correct CT behavior in some particular cases. This highlights the difficulties of standard methods, such as PBE0 evaluated at the GS geometry, to accurately predict the CT character and the importance of establishing reliable computational protocols for its fair evaluation. Considering our best estimate of the CT values (obtained with ωB97XD at the S1 optimized geometries, also collected in Tables 2 and 3), Mod10 of COF-1 will present slightly enhanced CT with respect to the original Mod0 (CT of 0.8 versus 0.79), and Mod5 of COF-2 will show a significant promotion of the CT in comparison to the Mod0 analogous (CT of 0.86 versus 0.53). Therefore, Mod5 of COF-2 is identified as a promising candidate with significantly improved CT for enhanced charge carriers lifetimes.
Effective mass values of D–A COF monolayers
The photoconductive properties of the 2D-COF monolayers have been evaluated in the context of a band transport model.70 The band structure of the 2D monolayers computed at PBE0 level are collected in Fig. S7 and S8 of ESI.† The smallest effective mass obtained at the VBM and CBM have been assigned to the hole and electron
and electron  effective mass, respectively. The values, given in electron mass units (m0), are collected in Tables 2 and 3 for COF-1 and COF-2 monolayers, respectively. On the one hand, the results show that the experimentally reported material of COF-1, Mod0, displays small effective mass values (∼1 m0) for both the electron and the hole. On the other hand, the Mod0 of COF-2 shows a small effective mass for the electron (∼1 m0), but a four times larger value for the hole (∼4 m0). This is ascribed to the fact that both the HOCO and LUCO of COF-1, as well as the LUCO of COF-2, are well delocalized crystal orbitals, while the HOCO of COF-2 is strongly localized in the TTF units (see Fig. 3).
effective mass, respectively. The values, given in electron mass units (m0), are collected in Tables 2 and 3 for COF-1 and COF-2 monolayers, respectively. On the one hand, the results show that the experimentally reported material of COF-1, Mod0, displays small effective mass values (∼1 m0) for both the electron and the hole. On the other hand, the Mod0 of COF-2 shows a small effective mass for the electron (∼1 m0), but a four times larger value for the hole (∼4 m0). This is ascribed to the fact that both the HOCO and LUCO of COF-1, as well as the LUCO of COF-2, are well delocalized crystal orbitals, while the HOCO of COF-2 is strongly localized in the TTF units (see Fig. 3).
The 12 chemical modifications applied to the COF-1 and COF-2 monolayers significantly modulate the hole and electron effective mass values. For both COF-1 and COF-2 monolayers, all Mod1-12 display larger effective mass values, except in the case of Mod9 for COF-1, and Mod11 for COF-2. Remarkably, the imine-to-amide substitution of the linkage in Mod12 of COF-2 drastically increases the effective mass values up to >50 m0 values. This illustrates the profound impact of the linkage in the electronic structure of COF-2, in line with what has been observed in other systems.71 In contrast, the proposed Mod9 of COF-1 improves both the hole and electron mobilities by a factor of 2 (∼0.5 m0), which will potentially enhance the photoconductive properties with respect to the original Mod0. Therefore, Mod9 of COF-1 is identified as a promising candidate with potentially improved in-plane photoconductivity for optoelectronics. The question of whether the CT and band dispersion can be enhanced simultaneously is discussed in the following.
CT versus effective mass values of D–A COF monolayers
The improved CT and charge carriers mobilities in semiconductor materials are meant to reduce charge recombination and thus improve the light-to-electric or light-to-chemical energy conversion. Whether they can be optimized simultaneously in a single monolayer needs to be assessed since significant CT is mostly associated with local states, whereas band dispersion, and thus higher charge carriers mobilities, are associated with delocalized states. To address this question, we map the CT and effective mass values obtained for the Mod0-12 monolayers of COF-1 and COF-2 in Fig. 7a and b, respectively. In the case of the COF-1 monolayers (Fig. 7a), Mod9 reduces by a factor of two the sum of the effective mass values with respect to Mod0 (from ∼2 m0 to ∼1 m0) but strongly penalizes the CT value (from 0.8 to 0.2). In contrast, Mod5 also shows reduced CT character but does not significantly improve the charge carriers mobilities (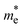 is reduced from 1 m0 to 0.8 m0, but
is reduced from 1 m0 to 0.8 m0, but  slightly increases from 1 m0 to 1.4 m0). In the case of COF-2 (Fig. 7b), Mod5 enhances the CT from 0.5 to 0.9, considering Mod0 as the reference, at the cost of increasing the effective mass values. In contrast, Mod11 reduces the effective mass values at the cost of reducing the CT to 0.2. However, there are two remarkable cases, Mod8 and Mod10, that improve the effective mass metric with respect to Mod0 without penalizing the CT value. Thus, overall, Mod8 and Mod10 of COF-2 display better CT and charge mobility features than the original Mod0. These results indicate that, although the promotion of the CT may be detrimental for the effective mass values and vice versa, there is not a direct correlation between the two properties, and, in principle, a targeted chemical design of COF monolayers can lead to novel materials with improved both CT and photoconductive features.
slightly increases from 1 m0 to 1.4 m0). In the case of COF-2 (Fig. 7b), Mod5 enhances the CT from 0.5 to 0.9, considering Mod0 as the reference, at the cost of increasing the effective mass values. In contrast, Mod11 reduces the effective mass values at the cost of reducing the CT to 0.2. However, there are two remarkable cases, Mod8 and Mod10, that improve the effective mass metric with respect to Mod0 without penalizing the CT value. Thus, overall, Mod8 and Mod10 of COF-2 display better CT and charge mobility features than the original Mod0. These results indicate that, although the promotion of the CT may be detrimental for the effective mass values and vice versa, there is not a direct correlation between the two properties, and, in principle, a targeted chemical design of COF monolayers can lead to novel materials with improved both CT and photoconductive features.
To identify the origin of the improvement of the band dispersion, we mapped the effective mass values with respect to the character of the local component of the S1 excitation, either delocalized or local (Fig. 7c). It can be seen that relatively low effective mass values (<3 m0) can only be obtained when the local component is delocalized. This agrees with the fact that band dispersion and orbital delocalization stem together. Two typical molecular design strategies to promote charge and/or state delocalization in D–A pairs include ensuring certain coplanarity and a close energy matching between either the HOMOs or the LUMOs of the molecular building blocks. In Fig. S9 of ESI,† these two features are mapped with respect to the  and
and  values. In general, more coplanar structures give rise to the lowest
values. In general, more coplanar structures give rise to the lowest  and
and 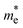 values. In contrast, the correlation with the D–A orbital energy differences is less pronounced. Further investigations with larger datasets of D–A COF monolayers are necessary to establish a comprehensive correlation between the properties of the 2D COF and those of the constituent building blocks, as well as their arrangement. Moreover, how the ligand size, and thus the pore size, may affect the CT and the effective mass values in D–A COF monolayers still needs to be assessed in a more diverse dataset of systems.
values. In contrast, the correlation with the D–A orbital energy differences is less pronounced. Further investigations with larger datasets of D–A COF monolayers are necessary to establish a comprehensive correlation between the properties of the 2D COF and those of the constituent building blocks, as well as their arrangement. Moreover, how the ligand size, and thus the pore size, may affect the CT and the effective mass values in D–A COF monolayers still needs to be assessed in a more diverse dataset of systems.
Conclusions
In this work, we have evaluated the CT and effective mass values of 26 D–A COF monolayers through DFT/TDDFT and band structure calculations. These 26 structures were generated via in silico chemical modification of 2 experimentally reported 2D Py-COFs, named COF-1 and COF-2. On the one hand, our results show that DFT/TDDFT calculations with PBE0 functional suffer from the same prediction bias as in 0D and 1D D–A systems. Namely, an overestimation of the CT character. Consequently, range-corrected functionals such as ωB97XD are required. Moreover, our results indicate that larger cluster models beyond the minimal D–A pair may be needed to evaluate the CT in COF monolayers with significantly delocalized crystal orbitals. Similarly, our results show that the optimization of the excited state may be required in some cases. These approximations should be considered for the accurate prediction of light-induced CT properties in these materials. On the other hand, we have calculated the effective mass values of the 26 monolayers at the VBM and CBM based on the band transport model, which provided an estimate of the hole and electron mobilities. Our results show that small effective mass values are obtained in systems with more delocalized crystal orbitals, whereas local states are detrimental for photoconductivity. Ultimately, we analyzed the correlation between the CT and effective mass values. In some cases, enhancing the CT is shown to be detrimental to the band dispersion. However, there is no direct correlation between the two properties. Therefore, it is, to some extent, possible to improve the CT and band dispersion simultaneously. This is the case of Mod8 and Mod10 of COF-2, which show reduced effective mass values with respect to the experimentally reported Mod0 without penalizing the CT character. Based on our calculations, we identify two possible candidates with either significantly enhanced CT or lower effective mass values than the originally reported materials. On the one side, Mod9 of COF-1 reduces both electron and hole effective mass values from ∼1 m0 to ∼0.5 m0, therefore significantly improving the in-plane band dispersion metric. On the other side, Mod5 of COF-2 significantly promotes the CT character from 0.5 to 0.8, therefore potentially extending the charge carriers lifetimes. Mod9 of COF-1 consists of three aza-substitutions in the Py ligand of the original COF, whereas Mod5 of COF-2 consists of the addition of -NO2 groups to the phenyl rings attached to the TTF. Altogether, our results show that aza-substitutions, the addition of functional groups, and the substitution of the linkage can improve, worsen, or leave unaltered the CT character and/or the band shape of the COF material, depending on the 2D-COF family in which they are applied. This highlights the difficulty of making simple general rules for the molecular design of 2D-COF with improved properties and points towards the use of automatized screening protocols and the development of artificial intelligence algorithms for the discovery of novel candidates. Future work devoted to the generation, characterization and computational screening of large datasets of chemically diverse D–A monolayers is envisioned to identify more materials with improved optoelectronic features and to enrich the library of systems for the development of comprehensive artificial intelligence algorithms.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article is available in the Zenodo repository https://doi.org/10.5281/zenodo.15130360. The database collects all the computations reported in this work. Supporting data has also been included in the ESI.†Acknowledgements
M. F. acknowledges financial support from the Ministerio de Ciencia, Innovación y Universidades and Agencia Estatal de Investigación MICIU/AEI/10.13039/501100011033 and the European Union NextGenerationEU/PRTR for the Ramón y Cajal research contract (RYC2021-030924-I), the CNS2023-144632 and PID2022-140460NA-I00 project funding, and the Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the IQTCUB, as well as the Generalitat de Catalunya for the 2021SGR00354 grant. A. G. and M. F. thank the University of Barcelona and IQTCUB for the computational resources.References
- H. Fan, A. Mundstock, A. Feldhoff, A. Knebel, J. Gu, H. Meng and J. Caro, Covalent organic framework–covalent organic framework bilayer membranes for highly selective gas separation, J. Am. Chem. Soc., 2018, 140, 10094–10098 CrossRef CAS PubMed.
- Y. Ying, M. Tong, S. Ning, S. K. Ravi, S. B. Peh, S. C. Tan, S. J. Pennycook and D. Zhao, Ultrathin two-dimensional membranes assembled by ionic covalent organic nanosheets with reduced apertures for gas separation, J. Am. Chem. Soc., 2020, 142, 4472–4480 CrossRef CAS PubMed.
- J. Guo and D. Jiang, Covalent organic frameworks for heterogeneous catalysis: Principle, current status, and challenges, ACS Cent. Sci., 2020, 6, 869–879 CrossRef CAS PubMed.
- M. E. G. Carmo, L. Spies, G. N. Silva, O. F. Lopes, T. Bein, J. Schneider and A. O. T. Patrocinio, From conventional inorganic semiconductors to covalent organic frameworks: Advances and opportunities in heterogeneous photocatalytic CO2 reduction, J. Mater. Chem. A, 2023, 11, 13815–13843 RSC.
- D. Wang, T. Qiu, W. Guo, Z. Liang, H. Tabassum, D. Xia and R. Zou, Covalent Organic Framework-Based Materials for Energy Applications, Energy Environ. Sci., 2021, 14, 688–728 RSC.
- Z. Zhou, Y. Xiao, J. Tian, N. Nan, R. Song and J. Li, Recent advances in metal-free covalent organic frameworks for photocatalytic applications in energy and environmental fields, J. Mater. Chem. A, 2023, 11, 3245–3261 RSC.
- Y. Yang and K. Börjesson, Electroactive covalent organic frameworks: a new choice for organic electronics, Trends Chem., 2022, 4, 60–65 CrossRef CAS.
- M. Souto and D. F. Perepichka, Electrically conductive covalent organic frameworks: bridging the fields of organic metals and 2D materials, J. Mater. Chem. C, 2021, 9, 10668–10676 RSC.
- N. Keller and T. Bein, Optoelectronic processes in covalent organic frameworks, Chem. Soc. Rev., 2021, 50, 1813–1845 RSC.
- A. K. Mandal, J. Mahmood and J.-B. Baek, Two-Dimensional Covalent Organic Frameworks for Optoelectronics and Energy Storage, ChemNanoMat, 2017, 3, 373–391 CrossRef CAS.
- M. Shao, Y. Liu and Y. Guo, Customizable 2D Covalent Organic Frameworks for Optoelectronic Applications, Chin. J. Chem., 2023, 41, 1260–1285 CrossRef CAS.
- J. Zhao, J. Ren, G. Zhang, Z. Zhao, S. Liu, W. Zhang and L. Chen, Donor-Acceptor Type Covalent Organic Frameworks, Chemistry, 2021, 27, 10781–10797 CrossRef CAS PubMed.
- Z.-F. Pang, T.-Y. Zhou, R.-R. Liang, Q. Y. Qi and X. Zhao, Regulating the topology of 2D covalent organic frameworks by the rational introduction of substituents, Chem. Sci., 2017, 8, 3866–3870 RSC.
- Z. F. Pang, S. Q. Xu, T. Y. Zhou, R. R. Liang, T. G. Zhan and X. Zhao, Construction of covalent organic frameworks bearing three different kinds of pores through the heterostructural mixed linker strategy, J. Am. Chem. Soc., 2016, 138, 4710–4713 CrossRef CAS PubMed.
- W. Q. Li, X. F. Huang, T. W. Zeng, Y. H. A. Liu, W. B. Hu, H. Yang, Y. B. Zhang and K. Wen, Thiazolo[5,4-d]thiazole-Based Donor–Acceptor Covalent Organic Framework for Sunlight-Driven Hydrogen Evolution, Angew. Chem., Int. Ed., 2021, 60, 1869–1874 CrossRef CAS PubMed.
- W. Chen, L. Wang, D. Mo, F. He, Z. Wen, X. Wu, H. Xu and L. Chen, Modulating Benzothiadiazole-Based Covalent Organic Frameworks via Halogenation for Enhanced Photocatalytic Water Splitting, Angew. Chem., Int. Ed., 2020, 59, 16902–16909 CrossRef CAS PubMed.
- G.-B. Wang, F.-C. Zhu, Q.-Q. Lin, J.-L. Kan, K.-H. Xie, S. Li, Y. Geng and Y.-B. Dong, Rational design of benzodifuran-functionalized donor-acceptor covalent organic frameworks for photocatalytic hydrogen evolution from water, Chem. Commun., 2021, 57, 4464–4467 RSC.
- Z. Li, Z. Zhang, R. Nie, C. Li, Q. Sun, W. Shi, W. Chu, Y. Long, H. Li and X. Liu, Construction of Stable Donor–Acceptor Type Covalent Organic Frameworks as Functional Platform for Effective Perovskite Solar Cell Enhancement, Adv. Funct. Mater., 2022, 2112553 CrossRef CAS.
- L. Chen, K. Furukawa, J. Gao, A. Nagai, T. Nakamura, Y. P. Dong and D. L. Jiang, Photoelectric Covalent Organic Frameworks: Converting Open Lattices into Ordered Donor-Acceptor Heterojunctions, J. Am. Chem. Soc., 2014, 136, 9806–9809 CrossRef CAS PubMed.
- G. Bian, J. Yin and J. Zhu, Recent Advances on Conductive 2D Covalent Organic Frameworks, Small, 2021, 17, 2006043 CrossRef CAS PubMed.
- S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J. L. Bredas, Electronic Structure of Two-Dimensional π-Conjugated Covalent Organic Frameworks, Chem. Mater., 2019, 31, 3051–3065 CrossRef CAS.
- M. Dogru and T. Bein, On the road towards electroactive covalent organic frameworks, Chem. Commun., 2014, 50, 5531–5546 RSC.
- B. Mourino, K. M. Jablonka, A. Ortega-Guerrero and B. Smit, In Search of Covalent Organic Framework Photocatalysts: A DFT-Based Screening Approach, Adv. Funct. Mater., 2023, 33, 2301594 CrossRef CAS.
- K. S. Deeg, D. Damasceno Borges, D. Ongari, N. Rampal, L. Talirz, A. V. Yakutovich, J. M. Huck and B. Smit, In Silico Discovery of Covalent Organic Frameworks for Carbon Capture, ACS Appl. Mater. Interfaces, 2020, 12, 21559–21568 CrossRef CAS PubMed.
- Y. Lan, M. Tong, Q. Yang and C. Zhong, Computational screening of covalent organic frameworks for the capture of radioactive iodine and methyl iodide, CrystEngComm, 2017, 19, 4920–4926 RSC.
- J. L. Mancuso, A. M. Kroz, K. N. Le and C. H. Hendon, Electronic Structure Modeling of Metal–Organic Frameworks, Chem. Rev., 2020, 120, 8641–8715 CrossRef CAS PubMed.
- V. Bernales, M. A. Ortuño, D. G. Truhlar, C. J. Cramer and L. Gagliardi, Computational Design of Functionalized Metal–Organic Framework Nodes for Catalysis, ACS Cent. Sci., 2018, 4, 5–19 CrossRef CAS PubMed.
- M. Fumanal, C. Corminboeuf, B. Smit and I. Tavernelli, Optical absorption properties of metal–organic frameworks: solid state versus molecular perspective, Phys. Chem. Chem. Phys., 2020, 22, 19512–19521 RSC.
- A.-S. Hehn, B. Sertcan, F. Belleflamme, S. K. Chulkov, M. B. Watkins and J. Hutter, Excited-State Properties for Extended Systems: Efficient Hybrid Density Functional Methods, J. Chem. Theory Comput., 2022, 18, 4186–4202 CrossRef CAS PubMed.
- C. Adamo and D. Jacquemin, The calculations of excited-state properties with Time-Dependent Density Functional Theory, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- S. Grimme and M. Parac, Substantial Errors from Time-Dependent Density Functional Theory for the Calculation of Excited States of Large Π Systems, Chem. Phys. Chem., 2003, 4, 292–295 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- D. Blätte, F. Ortmann and T. Bein, Photons, Excitons, and Electrons in Covalent Organic Frameworks, J. Am. Chem. Soc., 2024, 146, 32161–32205 CrossRef PubMed.
- M. Martinez-Abadia, K. Strutynski, C. T. Stoppiello, B. Lerma Berlanga, C. Marti-Gastaldo, A. N. Khlobystov, A. Saeki, M. Melle-Franco and A. Mateo-Alonso, Understanding charge transport in wavy 2D covalent organic frameworks, Nanoscale, 2021, 13, 6829–6833 RSC.
- K. Strutyński, A. Mateo-Alonso, M. Melle-Franco and M. Clar, Rules the Electronic Properties of 2D π-Conjugated Frameworks: Mind the Gap, Chem. – Eur. J, 2020, 26, 6569–6575 CrossRef PubMed.
- D. Bessinger, K. Mugli, M. Beets, F. Auras and T. Bein, Fast-Switching Vis-IR Electrochromic Covalent Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 7351–7357 CrossRef CAS PubMed.
- H. Ding, Y. Li, H. Hu, Y. Sun, J. Wang, C. Wang, C. Wang, G. Zhang, B. Wang, W. Xu and D. Zhang, A Tetrathiafulvalene-Based Electroactive Covalent Organic Framework, Chem. – Eur. J., 2014, 20, 14614–14618 CrossRef CAS PubMed.
- S. Jin, T. Sakurai, T. Kowalczyk, S. Dalapati, F. Xu, H. Wei, X. Chen, J. Gao, S. Seki, S. Irle and D. Jiang, Two-dimensional Tetrathiafulvalene Covalent Organic Frameworks: Towards Latticed Conductive Organic Salts, Chem. – Eur. J., 2014, 20, 14608–14613 CrossRef CAS PubMed.
- J. Kang, J. Hang, B. Chen, L. Chen, P. Zhao, Y. Xu, Y. Luo and C. Xia, Amide linkages in pyrene-based covalent organic frameworks toward efficient photocatalytic reduction of uranyl, ACS Appl. Mater. Interfaces, 2022, 14, 57225–57234 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, CP2K: Atomistic Simulations of Condensed Matter Systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- T. D. Kuhne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schutt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Muller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An Electronic Structure and Molecular Dynamics Software Package - Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152(19), 194103–194147 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- D. Ongari, A. V. Yakutovich, L. Talirz and B. Smit, Building a Consistent and Reproducible Database for Adsorption Evaluation in Covalent–Organic Frameworks, ACS Cent. Sci., 2019, 5, 1663–1675 CrossRef CAS PubMed.
- M. Fumanal, G. Capano, S. Barthel, B. Smit and I. Tavernelli, Energy-Based Descriptors for Photo-Catalytically Active Metal–Organic Framework Discovery, J. Mater. Chem. A, 2020, 8, 4473–4482 RSC.
- M. Fumanal, A. Ortega-Guerrero, K. M. Jablonka, B. Smit and I. Tavernelli, Charge Separation and Charge Carrier Mobility in Photocatalytic Metal-Organic Frameworks, Adv. Funct. Mater., 2020, 30, 2003792 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- M. Guidon, J. Hutter and J. VandeVondele, Auxiliary Density Matrix Methods for Hartree−Fock Exchange Calculations, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. J. Frisch, Gaussian16, rev. B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation Energies in Density Functional Theory: An Evaluation and a Diagnostic Test, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- M. J. G. Peach, R. Le Sueur, K. Ruud, M. Guillaume and D. J. Tozer, TDDFT Diagnostic Testing and Functional Assessment for Triazene Chromophores, Phys. Chem. Chem. Phys., 2009, 11, 4465–4470 RSC.
- M. J. G. Peach and D. J. Tozer, Overcoming Low Orbital Overlap and Triplet Instability Problems in TDDFT, J. Phys. Chem. A, 2012, 116, 9783–9789 CrossRef CAS PubMed.
- A. A. Taka, J. M. Herbert and L. M. McCaslin, Ground state orbital analysis predicts S1 charge transfer in donor–acceptor materials, J. Phys. Chem. Lett., 2023, 14, 11063–11068 CrossRef PubMed.
- J. M. Herbert, Visualizing and characterizing excited states from time-dependent density functional theory, Phys. Chem. Chem. Phys., 2024, 26, 3755–3794 RSC.
- J. M. Herbert and A. Mandal, Importance of Orbital Invariance in Quantifying Electron–Hole Separation and Exciton Size, J. Chem. Theory Comput., 2024, 20, 9446–9463 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Ab Initio Molecular Simulations with Numeric Atom-Centered Orbitals, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- V. Havu, P. Blum, P. Havu and M. Scheffler, Efficient O(N) Integration for All-Electron Electronic Structure Calculation Using Numeric Basis Functions, J. Comput. Phys., 2009, 228, 8367–8379 CrossRef CAS.
- I. Y. Zhang, X. Ren, P. Rinke, V. Blum and M. Scheffler, Numeric Atom-Centered-Orbital Basis Sets with Valence-Correlation Consistency from H to Ar, New J. Phys., 2013, 15, 123033 CrossRef.
- M. Kasha, Characterization of Electronic Transitions in Complex Molecules, Discuss. Faraday Soc., 1950, 9, 14–19 RSC.
- Y. Zhu, S. Vela, H. Meng, C. Corminboeuf and M. Fumanal, Donor–Acceptor–Donor “Hot Exciton” Triads for High Reverse Intersystem Crossing in OLEDs, Adv. Opt. Mater., 2022, 10, 2200509 CrossRef CAS.
- J. T. Blaskovits, M. Fumanal, S. Vela and C. Corminboeuf, Designing Molecular Architectures for Singlet Fission, Chem. Mater., 2020, 32, 6515–6524 CrossRef CAS.
- J. T. Blaskovits, M. Fumanal, S. Vela, R. Fabregat and C. Corminboeuf, Identifying the Trade-off between Intramolecular Singlet Fission Requirements in Donor–Acceptor Copolymers, Chem. Mater., 2021, 33, 2567–2575 CrossRef CAS.
- U. Salzner and A. Aydin, Improved Prediction of Properties of π-Conjugated Oligomers with Range-Separated Hybrid Density Functionals, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef CAS PubMed.
- D. Mester and M. Kállay, Charge-Transfer Excitations within Density Functional Theory: How Accurate Are the Most Recommended Approaches?, J. Chem. Theory Comput., 2022, 18, 1646–1662 CrossRef CAS PubMed.
- A. Sidat, M. Ingham, M. Rivera, A. J. Misquitta and R. Crespo-Otero, J. Chem. Phys., 2023, 159, 244108 CrossRef CAS PubMed.
- M. Ingham, M. Bradly and R. Crespo-Otero, Describing Excited States of Covalently Connected Crystals with Cluster and Embedded Cluster Approaches: Challenges and Solutions, Chemrxiv, 2025, preprint DOI:10.26434/chemrxiv-2025-spfvh.
- H. Oberhofer, K. Reuter and J. Blumberger, Charge Transport in Molecular Semiconductors, Chem. Rev., 2017, 117, 10319–10357 CrossRef CAS PubMed.
- S. Yang, H. Lv, H. Zhong, D. Yuan, X. Wang and R. Wang, Transformation of Covalent Organic Frameworks fromN-Acylhydrazone to Oxadiazole Linkages for Smooth ElectronTransfer in Photocatalysis, Angew. Chem., 2022, 134, e202115655 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Section S1: molecular structure of the Mod9–Mod12 monolayers. Section S2: optimized cell parameters. Section S3: HOCO, LUCO, band gap and S1 energies of the 26 monolayers. Section S4: characterization of the orbital contributions to the S1 state. Section S5: HOMO and LUMO energies of the constituent D and A monomers. Section S6: CT values of the isolated D–A pairs at PBE0 and ωB97XD level. Section S7: orbital contributions to the optimized S1 state of the Mod0, Mod6 and Mod10 of COF-1 D–A dimers. Section 8: band structure of the 26 monolayers. Section S9: correlation between the effective mass values and the dihedral and orbital energy differences of the D and A building blocks. All data, structures, inputs and outputs, are available in the Zenodo online repository https://doi.org/10.5281/zenodo.15130360. See DOI: https://doi.org/10.1039/d5tc01966d |
| This journal is © The Royal Society of Chemistry 2025 |