Open Access Article
Open Access ArticleDouble-hybrid density functionals applied to a large set of INVEST systems: validating the (SOS1-)PBE-DH-INVEST expressions†
P.
Maiz-Pastor
,
A. J.
Pérez-Jiménez
 and
J. C.
Sancho-García
and
J. C.
Sancho-García
 *
*
Department of Physical Chemistry, University of Alicante, E-03080 Alicante, Spain. E-mail: jc.sancho@ua.es
First published on 5th June 2025
Abstract
We thoroughly assess here the recently developed PBE-DH-INVEST expression and its SOS1-PBE-DH-INVEST variant, both belonging to the family of double-hybrid (DH) density functionals, against the NAH159 dataset of organic molecules displaying a very low (positive or even negative) energy gap, ΔEST, between the lowest-energy excited-state of singlet (S1) and triplet (T1) multiplicity. The NAH159 dataset comprises a large set of substituted derivatives of azulene, azupyrene, isopyrene, heptalene, cyclazine (or monoazaphenalene), pentazine (or pentaazaphenalene), and heptazine (or heptaazaphenalene) systems, thus covering most of the chemical templates so far discovered displaying ΔEST < 0 values. The performance of any model able to deliver correct ΔEST values, both in sign and magnitude, is critical for further studies in OLEDs and related applications. Given the robustness and accuracy of the results obtained by the (SOS1-)PBE-DH-INVEST functionals, together with their moderate basis set dependence, we can recommend them as an alternative to more costly wavefunction-based methods or other DH density functionals.
1 Introduction
INVEST (INVErted Singlet–Triplet excited-state energies) systems are those defined as molecules violating the (natural) order of the energy of (at least one of) their singlet and triplet molecular pairs, in the sense that a singlet electronic state can be found lower in energy than the associated triplet electronic state, thus violating the extension of Hund's rules to molecules. In the context of excited-state energies relevant to photophysics and organic light-emitting diodes (OLEDs), to which this study pertains, that violation mostly applies to the lowest-energy singlet–triplet pair, and thus implies that the singlet (S1 ← S0) excitation energy might become lower than the triplet (T1 ← S0) excitation energy, thus leading to a negative singlet–triplet energy difference (or gap) ΔEST < 0 after subtracting the values E(S1 ← S0) − E(T1 ← S0). Hence, a negative ΔEST value contradicts the positive (and large) values typically found for the singlet–triplet excited-states gap in conjugated chromophores, oligomers, and polymers,1,2 but as we will see next it is far from being just a theoretical anomaly or a physical curiosity.Although the possibility of having a singlet–triplet inversion leading to ΔEST < 0 values was experimentally3,4 and theoretically5,6 predicted time ago, already in the 80s, it has been recently invigorated by some modern yet challenging discoveries at both levels too. First of all, not only the original set of the very few molecules historically investigated (e.g. cycl[3.3.3]azine, or simply cyclazine, or 1,4,7-triazacycl[3.3.3]azine) are also shown to behave so particularly in modern experimental studies, but there has also been the corresponding confirmation along the last years for many other derivatives,7–17 both in solution and thin-film environments. Therefore, these systems are also receiving now a large interest18,19 for practical applications, thus constituting a new platform for further advances in photophysics [e.g. organic light emitting diodes (OLEDs)] or photocatalysis. For the former, the barrierless energy recovery of the (dark) triplet excitons could foster the performance of OLEDs upon increasing the internal quantum efficiency,20 while for the latter the larger singlet excitation lifetimes could compensate other energy losses during the photocatalytic process.21
Regarding the computational studies performed so far, the application of theoretical calculations has allowed to first isolate, and then understand, the quantum-chemical origin of that phenomenon,22–25 as well as to screen/predict possible candidates based on a larger variety of molecular scaffolds,26–37 which is also fostering the corresponding experimental search. The correct prediction of ΔEST < 0 values should of course rely on the correct prediction of the individual excitation energies S1 ← S0 and T1 ← S0, hopefully avoiding any error cancellation. As simple as it seems, the pronounced stabilization of the S1 state in these systems, with respect to the corresponding T1 state, is driven by electron correlation effects beyond single-particle excitations.22,23 This fact precludes the blind use of time-dependent density functional theory (TD-DFT), independently of the underlying exchange–correlation functional chosen, and prompts for the use of wavefunction-based methods introducing n-tuple particle excitations.38–52 However, it is also well-known that these latter excitations unfavorably scale with the system size, thus hindering the application to large (real-world) systems or its use in massive (low-cost) high-throughput screenings.
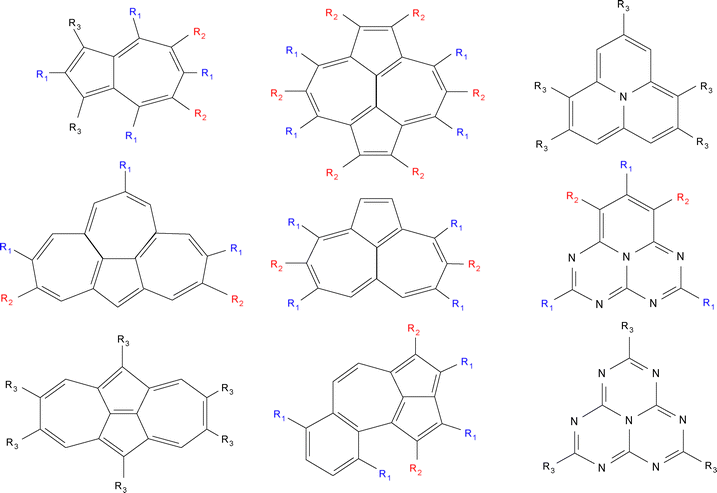
On the other hand, a set of recent studies has popularized the use of Double-Hybrid (DH) density functionals for this issue,53–57 which goes beyond standard TD-DFT applications, thanks to their capacity to introduce double excitations to electronic states of any multiplicity. The accuracy of these methods critically depends on their specific formulation, and more particularly to the weight given to correlation effects beyond single-particle excitations53 in analogy with wavefunction-based methods. Very recently, with the lessons gained so far for the optimal formulation of a DH functional able to correctly deliver ΔEST < 0 values, the so-called PBE-DH-INVEST functional was developed by some of us ref. 58. The original goal behind developing a tailored DH density functional was to provide a systematic and as low as possible error with respect to wavefunction-based reference results, upon calculations performed on a set of (mostly) triangle-shaped molecules. Given these antecedents, we will thus systematically assess here the accuracy of PBE-DH-INVEST on a significantly more extended dataset of molecules (i.e., the NAH159 set32 of compounds shown in Fig. S1, see the ESI,† for the detailed list) for the individual S1 ← S0 and T1 ← S0 excitation energies and the corresponding ΔEST values. We will complementarily check the basis set dependence of the model and the performance of the spin-scaled SOS1-PBE-DH-INVEST version, based again on a non-empirical derivation reached before for DH density functionals.59
2 Theoretical and computational details
A DH density functional60,61 represents a step further with respect to the very popular hybrid functionals, for which the EXact-eXchange (EXX) is coupled to an exchange functional (Ex[ρ]) by a parameter ax. Complementarily to this, in the case of double-hybrid expressions the correlation contribution is also splitted between the correlation functional (Ec[ρ]) and a wavefunction-based correlation component by a parameter ac. For the sake of having a computational cost as low as possible, the latter correlation component is that offered by a perturbation treatment at second-order. Following this simple yet effective philosophy, many DH density functionals do exist now in literature, like those related to the pioneering B2-PLYP expression,62 the DSD-based family of expressions,63 or the non-empirical expressions64 such as PBE0-DH65 or PBE-QIDH,66 to name just a few of the existing ones.2.1 The PBE-DH-INVEST expression
The recently derived PBE-DH-INVEST functional follows the aforesaid general expression for a DH density functional, where the values of the coefficients ax and ac are chosen (vide infra) to better represent the INVEST systems under consideration here: | (1) |
 and the 2nd order Perturbation Theory (PT2) contribution,
and the 2nd order Perturbation Theory (PT2) contribution, 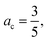 and are: (i) based on the relationship ac = ax3 used for deriving65,66 non-empirical double-hybrid functionals; and (ii) originally derived very recently58 as a compromise to obtain accurate values for INVEST systems, yet keeping an affordable computational cost. The wavefunction-based terms entering into eqn (1) are given by the well-known (for the example of a restricted calculation) first-principles expressions:
and are: (i) based on the relationship ac = ax3 used for deriving65,66 non-empirical double-hybrid functionals; and (ii) originally derived very recently58 as a compromise to obtain accurate values for INVEST systems, yet keeping an affordable computational cost. The wavefunction-based terms entering into eqn (1) are given by the well-known (for the example of a restricted calculation) first-principles expressions: | (2) |
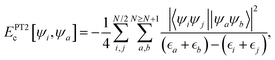 | (3) |
 and
and  , respectively. The parameter-free exchange, Ex[ρ], and correlation, Ec[ρ], functionals of eqn (1) are those given by the Perdew–Burke–Ernzerhof (PBE) model,67 which is also in agreement with the philosophy of minimally empirical double-hybrid functionals.
, respectively. The parameter-free exchange, Ex[ρ], and correlation, Ec[ρ], functionals of eqn (1) are those given by the Perdew–Burke–Ernzerhof (PBE) model,67 which is also in agreement with the philosophy of minimally empirical double-hybrid functionals.
2.2 The SOS1-PBE-DH-INVEST expression
On the other hand, the PT2 term of eqn (1) can be decomposed into same-spin and opposite-spin correlation contributions,68 scaled by the corresponding coefficients css and cos:| EPT2c = cssEss–PT2c + cosEos–PT2c. | (4) |
2.3 Extension to excited states
Importantly, the extension71,72 to calculate the excitation energies S1 ← S0 and T1 ← S0 (indistinctly called Ω in the following) by DH expressions relies on a correction, termed Δ(D), to the standard excitation energies calculated at the TD-DFT level (denoted as Ω′ in the following) given by:| Ω = Ω′ + acΔ(D), | (5) |
The extension to excited states of the SOS1-PBE-DH-INVEST functional follows the implementation74,75 for which the SOS1-based excitation energies are given by Ω = Ω′ + Δ(SOS1-D). That implementation is based on an energy correction to the total configuration interaction singles (CIS) energy of an excited state:
Ec = 〈ΦCIS|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |Û2Φ0〉 + 〈ΦCIS| |Û2Φ0〉 + 〈ΦCIS|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) | |![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2Û1|Φ0〉, 2Û1|Φ0〉, | (6) |
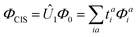 is the CIS determinant with tai single-excitation amplitudes and Φai singly-excited determinant, Û1 and Û2 are operators generating the singly and doubly excited wave functions from Φ0, respectively,
is the CIS determinant with tai single-excitation amplitudes and Φai singly-excited determinant, Û1 and Û2 are operators generating the singly and doubly excited wave functions from Φ0, respectively, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is a perturbation potential, and
is a perturbation potential, and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 is an operator generating the double excitation of two CIS-inactive electrons. The first and second terms above are known as the “direct” and “indirect” terms, respectively. The scaling into same- and opposite-spin components leads to:
2 is an operator generating the double excitation of two CIS-inactive electrons. The first and second terms above are known as the “direct” and “indirect” terms, respectively. The scaling into same- and opposite-spin components leads to:Ec = 〈ΦCIS|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |(cosUÛos2 + cssUÛss2)Φ0〉 + 〈ΦCIS| |(cosUÛos2 + cssUÛss2)Φ0〉 + 〈ΦCIS|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |(cosT |(cosT![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) os2 + cssT os2 + cssT![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ss2)Û1|Φ0〉. ss2)Û1|Φ0〉. | (7) |
2.4 Computational details
The geometries of all the compounds are those optimized at the ωB97X-D/aug-cc-pVTZ level in ref. 32. All the calculations reported here are done with the ORCA 5.0.3 release76 employing the sufficiently large aug-cc-pVTZ basis set,77 if not otherwise stated, which also allowed us to compare them with previously available results in the literature at the LR-CC2 level using the same basis set. The complementary calculations done here with the def2-TZVP basis set,78 for some selected compounds, did not bring any meaningful difference, confirming the minor influence of the basis set size beyond a ξ-triple basis set for a DH density functional. On the other hand, we will also assess the influence of reducing the basis set size comparing the results obtained using the aug-cc-pVDZ with those using the aug-cc-pVTZ basis set.We will also use the Tamm–Dancoff Approximation79 (or TDA in the following) to compute the Ω′ values, given its importance for practical calculations and seen its reduced computational cost with respect to the full solution of the TD-DFT equations. This is of interest since: (i) TDA is the default option in some computational packages; (ii) TDA is the most accepted option to excited-state studies of large chromophores;80–82 and (iii) simplified treatments based on TDA start to be available in the literature,83 further reducing the computational cost for excited state calculations of large samples of compounds. Furthermore, the set of optimal (ax, ac) pair of values for the PBE-DH-INVEST model were originally derived using TDA, and its use without that option might lead to some inconsistencies.
2.5 Choice of the NAH159 dataset
The NAH159 dataset (see Fig. 1 again) was originally32 compiled by Garner et al., and comprises a large set of substituted derivatives of triangle-shaped (e.g. cyclazine, pentazine, and heptazine) as well as non-alternant hydrocarbon systems. The set was later used47 by Mewes et al. to cross-check the performance of ΔDFT and ROKS methods and by Odoh et al. to assess84 the impact of ground-state geometries for vertical excitation energies. More specifically, the dataset comprises azulene, azupyrene, isopyrene, cyclopenta[e,f]heptalene, azuleno[2,1,8-k,i,a]heptalene, benzo[f]cyclopenta[c,d]azulene, cyclazine or monoazaphenalene, pentazine or pentaazaphenalene, and heptazine or heptaazaphenalene derivatives. Due to the structural diversity and relatively large number of systems included, it is believed to constitute and excellent dataset for assessing other computational methods.Mewes et al. obtained LR-CC2/aug-cc-pVTZ values for all the systems of the dataset, which compared favourably against other highly accurate, yet more costly methods, like Mk-MR-CCSD(T), and also against theoretically best estimates45 by Loos et al. The ΔEST values are between 0.39 and −0.32 eV, thus spanning a relatively large range of values, with ΔELR-CC2ST > 0 for 40 systems and ΔELR-CC2ST < 0 for the rest. Therefore, for all the reasons exposed above, these LR-CC2/aug-cc-pVTZ values will serve as reference to compare those calculated with (SOS1-)PBE-DH-INVEST, thus allowing us to analyze in detail their performance for ΔEST values of positive and negative sign.
2.6 Statistical analysis
The ‘mean-signed deviation’ (MSD), ‘mean absolute deviation’ (MAD), and the ‘root mean-squared deviation’ (RMSD) will be used to quantitatively compare the PBE-DH-INVEST with the LR-CC2 results. Recall that both set of calculations use the same aug-cc-pVTZ basis set and are performed at the same (ground-state) geometries. More specifically, they will be calculated as ,
,  , and
, and  respectively, with n being the number of excitation energies (S1 ← S0 or T1 ← S0) or the ΔEST values, with xi = ΩPBE-DH-INVEST − ΩLR-CC2, in the former case, or xi = ΔEPBE-DH-INVESTST − ΔELR-CC2ST in the latter. According to some recent recommendation for optimal statistical analysis,85 we will also consider the ΔEerr value, which is the difference between the most positive and the most negative deviation of the results with respect to the LR-CC2 values, as well as the kurtosis value, which for a normal distribution should follow
respectively, with n being the number of excitation energies (S1 ← S0 or T1 ← S0) or the ΔEST values, with xi = ΩPBE-DH-INVEST − ΩLR-CC2, in the former case, or xi = ΔEPBE-DH-INVESTST − ΔELR-CC2ST in the latter. According to some recent recommendation for optimal statistical analysis,85 we will also consider the ΔEerr value, which is the difference between the most positive and the most negative deviation of the results with respect to the LR-CC2 values, as well as the kurtosis value, which for a normal distribution should follow  thus indicating minor systematic errors. The corresponding values for the PBE-DH-INVEST and SOS1-PBE-DH-INVEST methods are gathered in Table 1. For the sake of completeness, we will also show (vide infra) the values for the (hybrid) PBE-DH-INVEST(SCF) calculations, to clearly disentangle the role played by double excitations.
thus indicating minor systematic errors. The corresponding values for the PBE-DH-INVEST and SOS1-PBE-DH-INVEST methods are gathered in Table 1. For the sake of completeness, we will also show (vide infra) the values for the (hybrid) PBE-DH-INVEST(SCF) calculations, to clearly disentangle the role played by double excitations.
| Basis set | Method | MSD | MAD | RMSD | Δ err | Kurtosis |
|---|---|---|---|---|---|---|
| aug-cc-pVTZ | ||||||
| PBE-DH-INVEST(SCF) | ||||||
| S1 ← S0 | 0.768 | 0.768 | 0.813 | 1.136 | 0.94 | |
| T1 ← S0 | 0.184 | 0.232 | 0.300 | 1.339 | 0.77 | |
| ΔEST | 0.584 | 0.584 | 0.610 | 0.910 | 0.96 | |
| PBE-DH-INVEST | ||||||
| S1 ← S0 | 0.107 | 0.107 | 0.115 | 0.179 | 0.93 | |
| T1 ← S0 | 0.092 | 0.099 | 0.114 | 0.373 | 0.87 | |
| ΔEST | 0.015 | 0.038 | 0.050 | 0.308 | 0.76 | |
| aug-cc-pVDZ | ||||||
| PBE-DH-INVEST(SCF) | ||||||
| S1 ← S0 | 0.761 | 0.761 | 0.803 | 1.102 | 0.95 | |
| T1 ← S0 | 0.182 | 0.230 | 0.296 | 1.330 | 0.78 | |
| ΔEST | 0.578 | 0.578 | 0.603 | 0.906 | 0.96 | |
| PBE-DH-INVEST | ||||||
| S1 ← S0 | 0.116 | 0.116 | 0.122 | 0.190 | 0.95 | |
| T1 ← S0 | 0.098 | 0.103 | 0.117 | 0.368 | 0.88 | |
| ΔEST | 0.018 | 0.039 | 0.050 | 0.297 | 0.78 | |
| SOS1-PBE-DH-INVEST | ||||||
| S1 ← S0 | 0.162 | 0.162 | 0.176 | 0.302 | 0.92 | |
| T1 ← S0 | 0.211 | 0.211 | 0.231 | 0.418 | 0.92 | |
| ΔEST | −0.049 | 0.058 | 0.073 | 0.282 | 0.79 | |
3 Results and discussion
3.1 Assessment of the PBE-DH-INVEST model
First of all, we will compare in the following the values (see the ESI†) obtained by the PBE-DH-INVEST model for the S1 ← S0, T1 ← S0, and ΔEST energies with respect to the LR-CC2 results (see Fig. 2). Furthermore, to clearly disentangle the prominent effect played by the Δ(D)-based correction for the final excitation energies, see eqn (5), we will also include the Ω′ values in the figures and the accompanying discussion. Recall that Ω′ are the excitation energies obtained with a standard TD-DFT treatment discarding the EPT2c[ψi, ψa] term in eqn (1), which thus translates to neglecting that Δ(D)-based correction in the final excitation values. The values obtained with this approximation are termed as PBE-DH-INVEST(SCF), to emphasize that they are obtained after a self-consistent-field (SCF) typical of a hybrid expression, with an exact-exchange weight as high as and do not consequently include the effect of the double excitations at all.
and do not consequently include the effect of the double excitations at all.
Inspecting Fig. 2 we can easily see how the S1 ← S0 excitation energies are strongly overestimated by the hybrid PBE-DH-INVEST(SCF) method, and how the deviations progressively increase with the value of the excitation energies. For instance, while the difference between PBE-DH-INVEST(SCF) and LR-CC2 is 0.46 eV for the lowest S1 ← S0 excitation energy of the dataset (1.361 vs. 0.897 eV, respectively), that difference increases to 1.45 eV for the highest S1 ← S0 excitation energy (5.437 vs. 3.989 eV, respectively). Fitting the PBE-DH-INVEST(SCF) data by a linear regression, we obtain Ω′(S1) = 0.143 + 1.30ΩLR-CC2 and a squared correlation coefficient r2 = 0.9814, with a considerably high value obtained for the slope in agreement with the large deviations found. On the other hand, the PBE-DH-INVEST method shows a very robust performance, practically matching the LR-CC2 reference values for all the range of values, with minimal differences irrespective of the molecules and their excitation energies. Going into more detail, the LR-CC2 values are slightly but almost systematically overestimated by PBE-DH-INVEST, that overestimation ranging from 0.01 to 0.19 eV, with an average value of 0.11 eV. The fitting now for the PBE-DH-INVEST values gives Ω(S1) = 0.061 + 1.02ΩLR-CC2, with r2 = 0.9984, with a slope close to the value of 1.0 for a perfect correlation between the PBE-DH-INVEST and LR-CC2 methods.
Analyzing now the T1 ← S0 excitation energies (see again Fig. 2) we observe a similar but much more attenuated performance compared with the S1 ← S0 excitation energies, with less deviations between the PBE-DH-INVEST(SCF) and PBE-DH-INVEST values. The LR-CC2 values are now under- or overestimated by both methods, although the general trend is again an overestimation, slightly more marked for the PBE-DH-INVEST(SCF) model. Fitting the PBE-DH-INVEST(SCF) data by a linear regression, we obtain Ω′(T1) = −0.226 + 1.19ΩLR-CC2, with r2 = 0.9724. Doing the same with the PBE-DH-INVEST data, the result is now Ω(T1) = 0.035 + 1.03ΩLR-CC2, with r2 = 0.9959. The fitting shows again the robust performance of the PBE-DH-INVEST model for the whole set of molecules, with a similar slope calculated for both S1 ← S0 and T1 ← S0 excitation energies (i.e., 1.02 vs. 1.03) and a very high correlation coefficient r2 (0.998 vs. 0.996) for both cases. Generally speaking, the role of double excitations introduced by the PBE-DH-INVEST model is the reason for their greater performance (vide infra) for both S1 ← S0 and T1 ← S0 excitation energies.
The performance of PBE-DH-INVEST(SCF) and PBE-DH-INVEST models for the ΔEST values is also presented in Fig. 2. The values are more scattered and largely overestimated by using the hybrid PBE-DH-INVEST(SCF) functional, since double corrections are not introduced at this level, as it is also evidenced by the linear fitting done: ΔEPBE-DH-INVEST(SCF)ST = 0.613 + 1.43ΔELR-CC2ST, r2 = 0.7326. On the other hand, the ΔEST values are again robustly calculated by PBE-DH-INVEST and fitted to the expression ΔEPBE-DH-INVESTST = 0.018 + 1.05ΔELR-CC2ST, r2 = 0.9375. Note the low slopes (1.02–1.05) obtained for the S1 ← S0, T1 ← S0, and ΔEST fittings, which are behind the good results systematically obtained. Indeed, the ΔEST deviations between the LR-CC2 and the PBE-DH-INVEST oscillate between −0.21 and 0.11 eV, showing the great performance of the PBE-DH-INVEST values.
Not surprisingly, the MSD, MAD, and RMSD errors at the PBE-DH-INVEST(SCF) level are considerably higher, see Table 1, than the values for the PBE-DH-INVEST once the double corrections are introduced in the latter case for both the S1 ← S0 and T1 ← S0 excitation energies. The values at the former level are unreliable for making any robust prediction for this kind of systems, as a consequence of the poor performance of the PBE-DH-INVEST(SCF) method shown in Fig. 2, which would be shared by standard TD-DFT treatments employing a hybrid functional. Strikingly, the error for the T1 ← S0 excitation energies are largely reduced with respect to the S1 ← S0 values (e.g. compare a MAD value of 0.77 eV for the former with respect to 0.23 eV for the latter) which reflects the triplet instability problem86 typical of TD-DFT calculations. The use of the Tamm–Dancoff approximation helps to reduce the error affecting the T1 ← S0 excitation energies,87–89 which is known to markedly depend on the ax value (i.e., the greater the ax values is, the larger the influence of the Tamm–Dancoff approximation for the T1 ← S0 excitation energies). Following the error metrics commented before, we can also calculate the difference between the more positive and the more negative deviation of the results with respect to the LR-CC2 values, or Δerr in the following, which amounts to values as high as 1.14, 1.34, and 0.91 eV for the S1 ← S0, T1 ← S0, and ΔEST results, respectively. This Δerr range also remarks once again the unreliability of the PBE-DH-INVEST(SCF) calculations.
Interestingly, the values of the MSD errors from the PBE-DH-INVEST calculations are as low as 0.1 eV, for both the S1 ← S0 and T1 ← S0 excitation energies, and of the same size which translates to an even lower (and thus very competitive) MSD value of less than 0.02 eV for the corresponding ΔEST. This also explains the low values, of only 0.04 and 0.05 eV respectively, for the MAD and RMSD errors. The Δerr values are 0.18, 0.37, and 0.31 eV for the S1 ← S0, T1 ← S0, and ΔEST results, respectively, and thus are also considerably reduced with respect to the previous PBE-DH-INVEST(SCF) values. These error metrics clearly emphasize the key role played by the double excitations to bring the results much closer to the reference LR-CC2 ones. That influence will be analyzed in more detail in the next section. Additionally, the ΔEST values closely follow a normal distribution, according to a kurtosis value around 0.8, with a larger kurtosis value for S1 ← S0 and T1 ← S0 excitation energies indicating a distribution with a more flattened peak and shorter tail (i.e., a platykurtic distribution).
We discuss next the case when the PBE-DH-INVEST ΔEST value differs in sign with respect to that calculated by LR-CC2. A false negative, when ΔELR-CC2ST > 0 but ΔEPBE-DH-INVESTST < 0, only occurs for molecule 132. On the other hand, false positives, when ΔELR-CC2ST < 0 but ΔEPBE-DH-INVESTST > 0, happens for several molecules, namely 3, 5, 7, 8, 10, 30, 40, 100, 102, 103, 104, 133, and 153. Therefore, in just 14 out of the 159 systems (8.8% of the cases) there is a wrong prediction of the ΔEST sign. However, we also note that for these cases the absolute value of ΔELR-CC2ST is quite small, 0.01 < |ΔELR-CC2ST (in![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV)| < 0.06, and of the same size than the MAD or RMSD values. Therefore, a minimal deviation between the two methods could reverse the sign. Hence, for future uses of PBE-DH-INVEST in e.g. massive and blind screenings of candidate molecules, we always recommend to impose some thresholds (e.g. ΔEPBE-DH-INVESTST < 0.05 eV) to not completely discard possible INVEST systems.
eV)| < 0.06, and of the same size than the MAD or RMSD values. Therefore, a minimal deviation between the two methods could reverse the sign. Hence, for future uses of PBE-DH-INVEST in e.g. massive and blind screenings of candidate molecules, we always recommend to impose some thresholds (e.g. ΔEPBE-DH-INVESTST < 0.05 eV) to not completely discard possible INVEST systems.
3.2 Comparison with related models
We would also like to compare the performance of the PBE-DH-INVEST model with respect to other methods and results available in the literature. First of all, we note that the ratio satisfied by the PBE-DH-INVEST model, without any parameterization, is very close to the one recently disclosed90 after independently optimizing both coefficients for a similar DH density functional, and thus relaxing the condition ac = ax3 typical of minimally empirical double-hybrid density functionals. The authors searched the best performance of a DH density functional with the expression given by eqn (1) employing also the PBE exchange and correlation functionals, which led to final values of ax = 0.75 and ac = 0.55, and thus to a corresponding ratio of
satisfied by the PBE-DH-INVEST model, without any parameterization, is very close to the one recently disclosed90 after independently optimizing both coefficients for a similar DH density functional, and thus relaxing the condition ac = ax3 typical of minimally empirical double-hybrid density functionals. The authors searched the best performance of a DH density functional with the expression given by eqn (1) employing also the PBE exchange and correlation functionals, which led to final values of ax = 0.75 and ac = 0.55, and thus to a corresponding ratio of 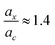 too. However, those authors employed (a limited set of) triangle-shaped molecules and a smaller (aug-cc-pVDZ) basis set. It is thus quite satisfying to note the excellent performance of the non-parameterized PBE-DH-INVEST model for a much larger (i.e., 159 vs. 12 molecules) dataset.
too. However, those authors employed (a limited set of) triangle-shaped molecules and a smaller (aug-cc-pVDZ) basis set. It is thus quite satisfying to note the excellent performance of the non-parameterized PBE-DH-INVEST model for a much larger (i.e., 159 vs. 12 molecules) dataset.
The ΔSCF method has also been applied before to the NAH159 dataset,47 correctly predicting the ΔEST sign in 83% of cases using the PBE0 functional and the smaller def2-SVP basis set. However, this method is known to largely depend on: (i) the window or molecular orbitals selected; in fact when the HOMO and LUMO orbitals are used (instead of the set HOMO−1, HOMO, LUMO, LUMO+1) to build all the involved electronic states, the percentage of correct predictions reduces from 83% to 77%; and (ii) the underlying exchange–correlation functional used, with large differences between them depending on the ax value; i.e., the authors tested PBE (ax = 0), PBE0 (ax = 1/4), PBE38 (ax = 0.38), and PBE50 (ax = 1/2). The best results were obtained at the PBE0/def2-SVP level with the HOMO−1, HOMO, LUMO, LUMO+1 window of orbitals: MSD, MAD, and RMSD values (all in eV) of 0.002, 0.056, and 0.063 for ΔEST, and thus slightly larger than the best results obtained here with the PBE-DH-INVEST double-hybrid functional.
3.3 Oscillator strength values
We also inspected the oscillator strength values, fosc, necessarily calculated at the PBE-DH-INVEST(SCF) level according to the existing implementations, and tried to correlate them with the ΔEST values (see Fig. 3). As it was expected from the poor overlap between the orbitals (e.g. HOMO and LUMO) involved in the formation of the S1 state, typical of these systems,91,92 the fosc values are relatively low for all them (see the ESI†) and even a large percentage of molecules show dark S1 states, with vanishing oscillator strengths. | ||
| Fig. 3 Correlation between the oscillator strength values (fosc) and the ΔEST energies (in eV) of the molecules composing the NAH159 dataset. | ||
Only a few systems (molecules numbered as 63, 156, and 157) show fosc > 0.05 while concomitantly having ΔEST < 0 values. These molecules are dimethylamine-substituted heptazine, triamine-substituted pentazine, and trimethylamine-substituted pentazine, see Fig. 5. On the other hand, Fig. 6 shows the pair of molecules (diamine-substituted pentazine and dimethylamine-substituted pentazine) holding the largest fosc values (fosc > 0.10) from all the NAH159 dataset but in this case for ΔEST > 0 values. These results show how the introduction of electroactive amine-based substituents might be a good strategy to increase the fosc values, together with low ΔEST values (independently of its sign). The exploration of other cores and/or substituents might lead to increased fosc values, which is the subject of current investigations, as recently exemplified by the design of INVEST molecules with conjugated branches as substituents,93 to have an appreciable emission of light. In this regard, the PBE-DH-INVEST model might be also considered as a good alternative to perform further screenings of the chemical space of candidate molecules.
3.4 The influence of double excitations
We now apply eqn (5) to both S1 ← S0 and T1 ← S0 excitation energies calculated by the PBE-DH-INVEST model, that is: | (8) |
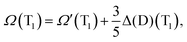 | (9) |
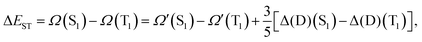 | (10) |
| ΔEPBE-DH-INVESTST = ΔEPBE-DH-INVEST(SCF)ST + Δ[Δ(D)], | (11) |
Additionally, an alternative formulation is often found in the literature, where ΔEST ≈ 2K, with K being the exchange integral (ϕiϕa|ϕjϕb) between the corresponding orbitals from a single-excitation (e.g. Configuration Interaction Singles or CIS) picture.22 The corresponding extension to TD-DFT involves an additional term based on the exchange–correlation kernel,94 but always leads to ΔEST > 0 in practical calculations. If a wavefunction-based correlation treatment is instead invoked, the extension is often simplified to ΔEST ≈ 2K + ΔEc, with the ΔEc contribution arising from e.g. the n-tuple excitations introduced by the particular method selected.24 In this context, the advantage of using of a DH density functional is the affordable computation of single and double excitations, thanks to the decomposition made in eqn (11) and shown in Fig. 4, thus allowing to merge the lessons gained so far from both DFT-based and wavefunction-based studies of INVEST systems.
3.5 Exploring the reduction in computational cost
Furthermore, to clearly illustrate the reduction in computational time going from the aug-cc-pVTZ to the aug-cc-pVDZ basis set, we have considered the total time required for running the calculations on the whole NAH159 dataset employing the same technical details and the same number of cores for both basis sets. The total time needed is drastically reduced going from about 1560 to about 340 hours when the aug-cc-pVDZ is used instead of the aug-cc-pVTZ one, thus representing just a 22% of the time needed for the larger one (see the ESI† for further details including the relative time for each of the molecules of the NAH159 dataset).
4 Conclusions
This study explores the possibility of using a recently developed double-hybrid density functional (PBE-DH-INVEST) as a computationally viable method to accurate predict singlet–triplet energy gaps (ΔEST) of INVEST molecules (i.e., those molecules for which the singlet–singlet S1 ← S0 excitation energy lies lower than the corresponding singlet–triplet T1 ← S0 one) For that purpose, we applied the method to the NAH159 dataset of organic molecules containing very popular scaffolds for these INVEST systems, such as cyclazine, pentazine, and heptazine, as well as non-alternant hydrocarbons of various types. The large sample of 159 molecules thus differ not only in their molecular core but also on the number and position of electron-donating and electron-withdrawing substituents. Since the PBE-DH-INVEST method goes beyond a single-reference (standard) TD-DFT treatment for excited states, we have systematically quantified and confirmed the importance of the double excitations introduced by the double-hybrid expression, which is known to play a key role for INVEST systems. Overall, the method shows a very robust performance with respect to reference results previously computed at the LR-CC2 level, as well as a small basis set dependence after comparing results with the aug-cc-pVDZ and aug-cc-pVTZ basis sets. We have also explored the SOS1-PBE-DH-INVEST variant, with a slightly worse performance with respect to the pristine PBE-DH-INVEST form. These features seem to confirm the accuracy and robustness of this model chemistry (i.e., PBE-DH-INVEST/aug-cc-pVDZ) for e.g. exploratory calculations, high-throughput screenings or machine-learned applications at a very affordable computational cost.Data availability
The data that supports the findings of this study are available within the article and its ESI† or are available from the corresponding authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work in Alicante is supported by grant PID2023-152372NB-I00 funded by MICIU/AEI/10.13039/501100011033 and by FEDER, UE. We gratefully acknowledge Jan-Michael Mewes (U. Bonn, Germany) for providing the raw data of the LR-CC2/aug-cc-pVTZ calculations.References
- A. Köhler and D. Beljonne, The singlet–triplet exchange energy in conjugated polymers, Adv. Funct. Mater., 2004, 14, 11–18 CrossRef.
- J. Gierschner, J. Cornil and H.-J. Egelhaaf, Optical bandgaps of π -conjugated organic materials at the polymer limit: experiment and theory, Adv. Mater., 2007, 19, 173–191 CrossRef CAS.
- W. Leupin and J. Wirz, Low-lying electronically excited states of cycl[3.3.3]azine, a bridged 12π -perimeter, J. Am. Chem. Soc., 1980, 102, 6068–6075 CrossRef CAS.
- W. Leupin, D. Magde, G. Persy and J. Wirz, 1,4,7-Triazacycl[3.3.3]azine: basicity, photoelectron spectrum, photophysical properties, J. Am. Chem. Soc., 1986, 108, 17–22 CrossRef CAS.
- A. Toyota and T. Nakajima, Violation of Hund's multiplicity rule in the lowest excited singlet–triplet pairs of cyclic bicalicene and its higher homologues, J. Chem. Soc., Perkin Trans. 2, 1986, 1731–1734 RSC.
- A. Toyota, Violation of Hund's rule in the lowest excited singlet–triplet pairs of dicyclohepta[cd,gh] pentalene and dicyclopenta[ef,kl]heptalene, Theor. Chim. Acta, 1988, 74, 209–217 CrossRef CAS.
- N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-I. Nakayama and S. Maeda, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nature, 2022, 609, 502–506 CrossRef CAS PubMed.
- J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, X. Li, Y. Wang and Q. Guo, Down-conversion-induced delayed fluorescence via an inverted singlet–triplet channel, Dyes Pigm., 2022, 203, 110366 CrossRef CAS.
- D. Blasco, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Gold(I)-containing light-emitting molecules with an inverted singlet–triplet gap, Chem. Sci., 2023, 14, 3873–3880 RSC.
- Y. Lee, J. Kim, S. Lee, E. Sim and J.-I. Hong, Electron donor-acceptor type delayed fluorescence emitters with inverted singlet and triplet excited states, Chem. Eng. J., 2023, 476, 146659 CrossRef CAS.
- X. Wang, A. Wang, M. Zhao and N. Marom, Inverted Lowest Singlet and Triplet Excitation Energy Ordering of Graphitic Carbon Nitride Flakes, J. Phys. Chem. Lett., 2023, 14, 10910–10919 CrossRef CAS PubMed.
- A. Actis, M. Melchionna, G. Filippini, P. Fornasiero, M. Prato, M. Chiesa and E. Salvadori, Singlet–Triplet Energy Inversion in Carbon Nitride Photocatalysts, Angew. Chem., Int. Ed., 2023, 62, e202313540 CrossRef CAS PubMed.
- Y. Tsuchiya, K. Mizukoshi, M. Saigo, T. Ryu, K. Miyata, K. Onda and C. Adachi, Luminescence mechanism analysis of a TADF molecule showing peculiar thermal behavior, Faraday Discuss., 2024, 250, 233–250 RSC.
- D. Blasco, R. T. Nasibullin, R. R. Valiev, M. Monge, J. M. López-de Luzuriaga and D. Sundholm, Experimental and computational studies of the optical properties of 2,5,8-tris(phenylthiolato)heptazine with an inverted singlet–triplet gap, Phys. Chem. Chem. Phys., 2024, 26, 5922–5931 RSC.
- R. Okumura, H. Tanaka, K. Shizu, S. Fukushima, Y. Yasuda and H. Kaji, Development of an Organic Emitter Exhibiting Reverse Intersystem Crossing Faster than Intersystem Crossing, Angew. Chem., Int. Ed., 2024, 63, e202409670 CrossRef CAS PubMed.
- K. D. Wilson, W. H. Styers, S. A. Wood, R. C. Woods, R. J. McMahon, Z. Liu, Y. Yang and E. Garand, Spectroscopic Quantification of the Inverted Singlet–Triplet Gap in Pentaazaphenalene, J. Am. Chem. Soc., 2024, 146, 15688–15692 CrossRef CAS PubMed.
- Y. Kusakabe, K. Shizu, H. Tanaka, K. Tanaka and H. Kaji, An inverted singlet–triplet excited state in a pentaazaphenalene derivative (5AP-N(C12)2), Appl. Phys. Express, 2024, 17, 061001 CrossRef CAS.
- T. Won, K.-I. Nakayama and N. Aizawa, Inverted singlet–triplet emitters for organic light-emitting diodes, Chem. Phys. Rev., 2023, 4, 021310 CrossRef CAS.
- R. Su and Z. Huang, A Series of Singlet–Triplet InVerted TADF Fluorescent Probes with High Stability, Low Molecular Weight, and Synthesis Accessibility, Adv. Theory Simul., 2023, 6, 2200863 CrossRef CAS.
- K. Shizu and H. Kaji, Quantitative prediction of rate constants and its application to organic emitters, Nat. Commun., 2024, 15, 4723 CrossRef CAS PubMed.
- J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, Singlet–triplet inversion in heptazine and in polymeric carbon nitrides, J. Phys. Chem. A, 2019, 123, 8099–8108 CrossRef CAS PubMed.
- P. de Silva, Inverted singlet–triplet gaps and their relevance to thermally activated delayed fluorescence, J. Phys. Chem. Lett., 2019, 10, 5674–5679 CrossRef CAS PubMed.
- G. Ricci, E. San-Fabián, Y. Olivier and J.-C. Sancho-Garca, Singlet–triplet excited-state inversion in heptazine and related molecules: assessment of TD-DFT and ab initio methods, ChemPhysChem, 2021, 22, 553–560 CrossRef CAS PubMed.
- M. E. Sandoval-Salinas, G. Ricci, A. Pérez-Jiménez, D. Casanova, Y. Olivier and J.-C. Sancho-Garcia, Correlation vs. exchange competition drives the singlet–triplet excited-state inversion in non-alternant hydrocarbons, Phys. Chem. Chem. Phys., 2023, 25, 26417–26428 RSC.
- D. Drwal, M. Matousek, P. Golub, A. Tucholska, M. Hapka, J. Brabec, L. Veis and K. Pernal, Role of Spin Polarization and Dynamic Correlation in Singlet–Triplet Gap Inversion of Heptazine Derivatives, J. Chem. Theory Comput., 2023, 19, 7606–7616 CrossRef CAS PubMed.
- R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4, 1654–1682 CrossRef CAS.
- J. Terence Blaskovits, M. H. Garner and C. Corminboeuf, Symmetry-Induced Singlet–Triplet Inversions in Non-Alternant Hydrocarbons, Angew. Chem., 2023, 135, e202218156 CrossRef.
- O. H. Omar, X. Xie, A. Troisi and D. Padula, Identification of Unknown Inverted Singlet–Triplet Cores by High-Throughput Virtual Screening, J. Am. Chem. Soc., 2023, 145, 19790–19799 CrossRef CAS PubMed.
- M. H. Garner, J. T. Blaskovits and C. Corminboeuf, Double-bond delocalization in non-alternant hydrocarbons induces inverted singlet–triplet gaps, Chem. Sci., 2023, 14, 10458–10466 RSC.
- Y.-J. Pu, D. Valverde, J. C. Sancho-Garca and Y. Olivier, Computational Design of Multiple Resonance-Type BN Molecules for Inverted Singlet and Triplet Excited States, J. Phys. Chem. A, 2023, 127, 10189–10196 CrossRef CAS PubMed.
- R. Pollice, B. Ding and A. Aspuru-Guzik, Rational design of organic molecules with inverted gaps between the first excited singlet and triplet, Matter, 2024, 7, 1161–1186 CrossRef CAS.
- M. H. Garner, J. T. Blaskovits and C. Corminboeuf, Enhanced inverted singlet–triplet gaps in azaphenalenes and non-alternant hydrocarbons, Chem. Commun., 2024, 60, 2070–2073 RSC.
- J. T. Blaskovits, C. Corminboeuf and M. H. Garner, Singlet–Triplet Inversions in Through-Bond Charge-Transfer States, J. Phys. Chem. Lett., 2024, 15, 10062–10067 CrossRef CAS PubMed.
- K. Jorner, R. Pollice, C. Lavigne and A. Aspuru-Guzik, Ultrafast Computational Screening of Molecules with Inverted Singlet–Triplet Energy Gaps Using the Pariser–Parr–Pople Semiempirical Quantum Chemistry Method, J. Phys. Chem. A, 2024, 128, 2445–2456 CrossRef CAS PubMed.
- A. Nigam, R. Pollice, P. Friederich and A. Aspuru-Guzik, Artificial design of organic emitters via a genetic algorithm enhanced by a deep neural network, Chem. Sci., 2024, 15, 2618–2639 RSC.
- A. Majumdar and R. Ramakrishnan, Resilience of Hund's rule in the chemical space of small organic molecules, Phys. Chem. Chem. Phys., 2024, 26, 14505–14513 RSC.
- L. Barneschi, L. Rotondi and D. Padula, Molecular Geometry Impact on Deep Learning Predictions of Inverted Singlet–Triplet Gaps, J. Phys. Chem. A, 2024, 128, 2417–2426 CrossRef CAS PubMed.
- J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J.-C. Sancho-Garcia, Negative singlet–triplet excitation energy gap in triangle-shaped molecular emitters for efficient triplet harvesting, J. Phys. Chem. A, 2021, 125, 513–522 CrossRef CAS PubMed.
- K. Bhattacharyya, Can TDDFT render the electronic excited states ordering of Azine derivative? A closer investigation with DLPNO-STEOM-CCSD, Chem. Phys. Lett., 2021, 779, 138827 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Are Heptazine-Based Organic Light-Emitting Diode Chromophores Thermally Activated Delayed Fluorescence or Inverted Singlet–Triplet Systems?, J. Phys. Chem. Lett., 2021, 12, 6852–6860 CrossRef CAS PubMed.
- S. Pios, X. Huang, A. L. Sobolewski and W. Domcke, Triangular boron carbon nitrides: an unexplored family of chromophores with unique properties for photocatalysis and optoelectronics, Phys. Chem. Chem. Phys., 2021, 23, 12968–12975 RSC.
- L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet–triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24, 18713–18721 RSC.
- A. L. Sobolewski and W. Domcke, Excited-state singlet–triplet inversion in hexagonal aromatic and heteroaromatic compounds, Phys. Chem. Chem. Phys., 2023, 25, 21875–21882 RSC.
- E. Monino and P.-F. Loos, Connections and performances of Green's function methods for charged and neutral excitations, J. Chem. Phys., 2023, 159, 034105 CrossRef CAS PubMed.
- P.-F. Loos, F. Lipparini and D. Jacquemin, Heptazine, Cyclazine, and Related Compounds: Chemically-Accurate Estimates of the Inverted Singlet–Triplet Gap, J. Phys. Chem. Lett., 2023, 14, 11069–11075 CrossRef CAS PubMed.
- A. E. Izu, J. M. Matxain and D. Casanova, Reverse intersystem crossing mechanisms in doped triangulenes, Phys. Chem. Chem. Phys., 2024, 26, 11459–11468 RSC.
- L. Kunze, T. Froitzheim, A. Hansen, S. Grimme and J.-M. Mewes, ΔDFT Predicts Inverted Singlet–Triplet Gaps with Chemical Accuracy at a Fraction of the Cost of Wave Function-Based Approaches, J. Phys. Chem. Lett., 2024, 15, 8065–8077 CrossRef CAS PubMed.
- P. S. Sanyam and A. Mondal, Rational Design of Organic Emitters with Inverted Singlet–Triplet Gaps for Enhanced Exciton Management, J. Phys. Chem. A, 2024, 128, 7114–7123 CrossRef PubMed.
- R. Toews and A. Köhn, Cyclohepta[def]fluorene as a bistable molecule: first principles studies on its electronic structure and the effects of benzo-extension, substitution and solvation, Phys. Chem. Chem. Phys., 2024, 26, 20462–20469 RSC.
- M. Bedogni, D. Giavazzi, F. Di Maiolo and A. Painelli, Shining Light on Inverted Singlet–Triplet Emitters, J. Chem. Theory Comput., 2023, 20, 902–913 CrossRef PubMed.
- M. Bedogni and F. Di Maiolo, Singlet–Triplet Inversion in Triangular Boron Carbon Nitrides, J. Chem. Theory Comput., 2024, 20, 8634–8643 CrossRef CAS PubMed.
- S. Chanda and S. Sen, Benchmark computations of nearly degenerate singlet and triplet states of N-heterocyclic chromophores. I. Wavefunction-based methods, J. Chem. Phys., 2024, 161, 174117 CrossRef CAS PubMed.
- J. C. Sancho-Garcia, E. Bremond, G. Ricci, Á. Pérez-Jiménez, Y. Olivier and C. Adamo, Violation of Hund's rule in molecules: Predicting the excited-state energy inversion by TD-DFT with double-hybrid methods, J. Chem. Phys., 2022, 156, 034105 CrossRef CAS PubMed.
- M. Kondo, Singlet–triplet energy gap of multiresonant molecular systems: a double hybrid time-dependent density functional theory study, Chem. Phys. Lett., 2022, 804, 139895 CrossRef CAS.
- M. Alipour and T. Izadkhast, Do any types of double-hybrid models render the correct order of excited state energies in inverted singlet–triplet emitters?, J. Chem. Phys., 2022, 156, 064302 CrossRef CAS PubMed.
- K. Curtis, O. Adeyiga, O. Suleiman and S. O. Odoh, Building on the strengths of a double-hybrid density functional for excitation energies and inverted singlet–triplet energy gaps, J. Chem. Phys., 2023, 158, 024116 CrossRef CAS PubMed.
- S. Chanda, S. Saha and S. Sen, Benchmark Computations of Nearly Degenerate Singlet and Triplet states of N-heterocyclic Chromophores: II. Density-based Methods, J. Chem. Phys., 2025, 162, 024111 CrossRef CAS PubMed.
- A. Derradji, D. Valverde, É. Brémond, Á. J. Pérez-Jiménez, Y. Olivier and J. C. Sancho-Garca, Searching the Best Double-Hybrid Density Functional to Correctly Predict the Singlet–Triplet Excited-State Inversion in Organic Systems, J. Phys. Chem. C, 2024, 128, 18313–18327 CrossRef CAS.
- É. Brémond, M. Savarese, J. C. Sancho-Garca, Á. J. Pérez-Jiménez and C. Adamo, Quadratic integrand double-hybrid made spin-component-scaled, J. Chem. Phys., 2016, 144, 031101, DOI:10.1063/1.4890314.
- L. Goerigk and S. Grimme, Double-hybrid density functionals, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 576–600 CAS.
- J.-C. Sancho-Garcia, E. Brémond, A. Pérez-Jiménez, I. Ciofini and C. Adamo, Non-empirical double-hybrid density functionals as reliable tools for electronic structure calculations, Electron. Struct., 2022, 4, 043001 CrossRef CAS.
- S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- S. Kozuch and J. M. Martin, Spin-component-scaled double hybrids: an extensive search for the best fifth-rung functionals blending DFT and perturbation theory, J. Comput. Chem., 2013, 34, 2327–2344 CrossRef CAS PubMed.
- E. Bremond, I. Ciofini, J. C. Sancho-Garca and C. Adamo, Nonempirical double-hybrid functionals: An effective tool for chemists, Acc. Chem. Res., 2016, 49, 1503–1513 CrossRef CAS PubMed.
- E. Brémond and C. Adamo, Seeking for parameter-free double-hybrid functionals: the PBE0-DH model, J. Chem. Phys., 2011, 135, 024106 CrossRef PubMed.
- É. Brémond, J. C. Sancho-Garca, Á. J. Pérez-Jiménez and C. Adamo, Communication: double-hybrid functionals from adiabatic-connection: the QIDH model, J. Chem. Phys., 2014, 141, 031101 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, Improved second-order Møller-Plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- Y. Jung, R. C. Lochan, A. D. Dutoi and M. Head-Gordon, Scaled opposite-spin second order Møller–Plesset correlation energy: an economical electronic structure method, J. Chem. Phys., 2004, 121, 9793–9802 CrossRef CAS PubMed.
- N. O. Winter and C. Hättig, Scaled opposite-spin CC2 for ground and excited states with fourth order scaling computational costs, J. Chem. Phys., 2011, 134, 184101, DOI:10.1063/1.3584177.
- S. Grimme and F. Neese, Double-hybrid density functional theory for excited electronic states of molecules, J. Chem. Phys., 2007, 127, 154116 CrossRef PubMed.
- A. Ottochian, C. Morgillo, I. Ciofini, M. J. Frisch, G. Scalmani and C. Adamo, Double hybrids and time-dependent density functional theory: an implementation and benchmark on charge transfer excited states, J. Comput. Chem., 2020, 41, 1242–1251 CrossRef CAS PubMed.
- M. Head-Gordon, R. J. Rico, M. Oumi and T. J. Lee, A doubles correction to electronic excited states from configuration interaction in the space of single substitutions, Chem. Phys. Lett., 1994, 219, 21–29 CrossRef CAS.
- T. Schwabe and L. Goerigk, Time-dependent double-hybrid density functionals with spin-component and spin-opposite scaling, J. Chem. Theory Comput., 2017, 13, 4307–4323 CrossRef CAS PubMed.
- M. Casanova-Páez and L. Goerigk, Time-dependent long-range-corrected double-hybrid density functionals with spin-component and spin-opposite scaling: a comprehensive analysis of singlet–singlet and singlet–triplet excitation energies, J. Chem. Theory Comput., 2021, 17, 5165–5186 CrossRef PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108, DOI:10.1063/5.0004608.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm-Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- S. Grimme, A simplified Tamm-Dancoff density functional approach for the electronic excitation spectra of very large molecules, J. Chem. Phys., 2013, 138, 244104, DOI:10.1063/1.4811331.
- A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, Is the Tamm-Dancoff approximation reliable for the calculation of absorption and fluorescence band shapes?, J. Chem. Theory Comput., 2013, 9, 4517–4525 CrossRef CAS PubMed.
- T. Risthaus, A. Hansen and S. Grimme, Excited states using the simplified Tamm-Dancoff-Approach for range-separated hybrid density functionals: Development and application, Phys. Chem. Chem. Phys., 2014, 16, 14408–14419 RSC.
- M. de Wergifosse and S. Grimme, The eXact integral simplified time-dependent density functional theory (XsTD-DFT), J. Chem. Phys., 2024, 160, 204110, DOI:10.1063/5.0206380.
- G. Odonkor and S. O. Odoh, Impact of Structure on Excitation Energies and S1–T1 Energy Gaps of Asymmetrical Systems of Interest for Inverted Singlet–Triplet Gaps, J. Comput. Chem., 2025, 46, e70090 CrossRef CAS PubMed.
- A. Karton and M. T. De Oliveira, Good Practices in Database Generation for Benchmarking Density Functional Theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e1737 Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Stability analysis for solutions of the closed shell Kohn-Sham equation, J. Chem. Phys., 1996, 104, 9047–9052 CrossRef CAS.
- M. J. Peach, M. J. Williamson and D. J. Tozer, Influence of triplet instabilities in TD-DFT, J. Chem. Theory Comput., 2011, 7, 3578–3585 CrossRef CAS PubMed.
- M. J. Peach and D. J. Tozer, Overcoming low orbital overlap and triplet instability problems in TDDFT, J. Phys. Chem. A, 2012, 116, 9783–9789 CrossRef CAS PubMed.
- M. J. Peach, N. Warner and D. J. Tozer, On the triplet instability in TDDFT, Mol. Phys., 2013, 111, 1271–1274 CrossRef CAS.
- A. Majumdar and R. Ramakrishnan, Leveraging the Bias-Variance Tradeoff in Quantum Chemistry for Accurate Negative Singlet–Triplet Gap Predictions: A Case for Double-Hybrid DFT, arXiv, 2025, preprint, arXiv:2502.09330 DOI:10.48550/arXiv.2502.09330.
- G. Ricci, J.-C. Sancho-Garca and Y. Olivier, Establishing design strategies for emissive materials with an inverted singlet–triplet energy gap (INVEST): a computational perspective on how symmetry rules the interplay between triplet harvesting and light emission, J. Mater. Chem. C, 2022, 10, 12680–12698 RSC.
- Y. Olivier, B. Yurash, L. Muccioli, G. D’Avino, O. Mikhnenko, J.-C. Sancho-Garcia, C. Adachi, T.-Q. Nguyen and D. Beljonne, Nature of the singlet and triplet excitations mediating thermally activated delayed fluorescence, Phys. Rev. Mater., 2017, 1, 075602 CrossRef.
- H. Kim, G. D. Scholes and S. K. Min, Extension of molecules with an inverted singlet–triplet gap with conjugated branches to alter the oscillator strength, Phys. Chem. Chem. Phys., 2024, 26, 5508–5516 RSC.
- M. Moral, L. Muccioli, W.-J. Son, Y. Olivier and J.-C. Sancho-Garcia, Theoretical rationalization of the singlet–triplet gap in OLEDs materials: impact of charge-transfer character, J. Chem. Theory Comput., 2015, 11, 168–177 CrossRef CAS PubMed.
- Y.-Y. Chuang and S.-M. Chen, Infinite basis set extrapolation for double hybrid density functional theory 1: effect of applying various extrapolation functions, J. Comput. Chem., 2011, 32, 1671–1679 CrossRef CAS PubMed.
- D. Traore, E. Giner and J. Toulouse, Basis-set correction based on density–functional theory: linear-response formalism for excited-state energies, J. Chem. Phys., 2023, 158, 234107, DOI:10.1063/5.0156317.
- Y. Jung, Y. Shao and M. Head-Gordon, Fast evaluation of scaled opposite spin second-order Møller–Plesset correlation energies using auxiliary basis expansions and exploiting sparsity, J. Comput. Chem., 2007, 28, 1953–1964 CrossRef CAS PubMed.
- H. Ji, Y. Shao, W. A. Goddard and Y. Jung, Analytic derivatives of quartic-scaling doubly hybrid XYGJ-OS functional: theory, implementation, and benchmark comparison with M06-2X and MP2 geometries for nonbonded complexes, J. Chem. Theory Comput., 2013, 9, 1971–1976 CrossRef CAS PubMed.
- C. Song and T. J. Martnez, Atomic orbital-based SOS-MP2 with tensor hypercontraction. I. GPU-based tensor construction and exploiting sparsity, J. Chem. Phys., 2016, 144, 174111, DOI:10.1063/1.4948438.
- L. A. Martínez-Martínez and C. Amador-Bedolla, Gpu algorithm for the scaled opposite-spin (SOS)MP2 energy evaluation, J. Mex. Chem. Soc., 2017, 61, 60–66 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: We include all the raw data used for the statistics and figures: (i) the detailed list of all the molecules comprising the NAH159 dataset; (ii) the individual values for the S1 ← S0 and T1 ← S0 excitation energies at the LR-CC2, PBE-DH-INVEST(SCF), PBE-DH-INVEST, and SOS1-PBE-DH-INVEST levels, with both the aug-cc-pVDZ and aug-cc-pVTZ basis sets for the PBE-DH-INVEST case; (iii) the oscillator strength values with both the aug-cc-pVDZ and aug-cc-pVTZ basis sets; (iv) the total time needed for each of the NAH159 molecules at the PBE-DH-INVEST level with both the aug-cc-pVDZ and aug-cc-pVTZ basis sets, as well as the corresponding relative time; (v) technical details of the CPUs used for the calculations; (vi) an example input file for the (SOS1-)PBE-DH-INVEST calculations. See DOI: https://doi.org/10.1039/d5tc01799h |
| This journal is © The Royal Society of Chemistry 2025 |