Subtle conformational variations induce distinct optical and electron transport properties in naphthalenediimide-based solids

Abstract

Semiconductor layer homogeneity and uniform crystallinity are essential for ensuring reliable and reproducible performance in organic electronic devices such as OFETs, OLEDs, and organic solar cells. However, in solution-processed organic semiconductors—particularly those based on small molecules—the occurrence of polymorphic domains significantly undermines their reliability. In OFETs, in particular, such film inhomogeneities lead to large variations in device parameters. These polymorphic domains arise due to barrierless and competing crystallization pathways, a challenge that must be addressed to achieve consistent device performance. Rigid molecular systems are especially prone to such polymorphism, as their conformational rigidity combined with multiple non-covalent interaction modes can lead to structurally distinct yet energetically similar packing motifs. In this study, we explore the formation and implications of polymorphic forms in a rigid, end-group-substituted naphthalenediimide (NDI)-based n-type molecular semiconductor. To maintain structural rigidity and hence enhanced charge transport, picolyl end groups were employed. We isolated three distinct crystalline polymorphs—P-NDI, B-NDI, and R-NDI—each displaying unique colors and optical characteristics. Single-crystal X-ray diffraction (SCXRD) analysis revealed that these are conformational polymorphs, differing primarily in the torsional angle around the bridging carbon, which was calculated to be 62°, 99°, and 134° for P-, R-, and B-NDI, respectively. These subtle conformational differences significantly influenced the nature and strength of intermolecular interactions. Among the polymorphs, P-NDI exhibited a shorter centroid-to-centroid distance, a moderate π–π overlap, along with a high LUMO orbital overlap integral, and a large excimer-to-monomer emission ratio in its crystalline state. Despite promising charge transport properties, experimental OFET fabrication was limited by the poor solubility of these polymorphs in common organic solvents. This manuscript details the comprehensive structure–optical property–charge transport relationships of these polymorphs and highlights the need for design strategies that address polymorphic behavior in rigid small-molecule semiconductors.

---

1. Introduction

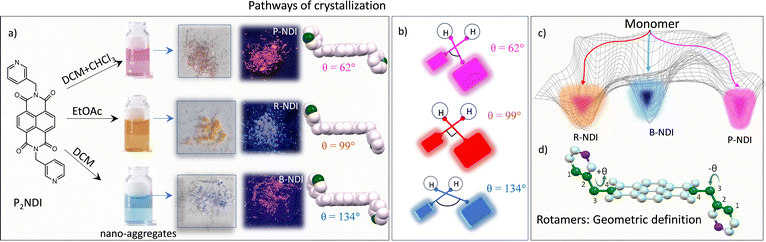
Organic semiconductor-based electronic devices have attracted considerable attention due to their unique advantages, including low cost, mechanical flexibility, and lightweight nature.^1–5 Among these, the development of efficient n-type (electron-transporting) and p-type (hole-transporting) semiconductors has been a major research focus, especially in the context of π-conjugated molecular materials.⁶ However, n-type organic semiconductors (OSCs) have generally lagged behind their p-type counterparts in terms of charge carrier mobility (μ), limiting their broader applications in devices such as organic field-effect transistors (OFETs), organic light-emitting diodes (OLEDs), organic photovoltaics (OPVs), and thermoelectrics.⁷ For high-performance n-type OSCs, a rigid and planar molecular backbone with extended π-conjugation is crucial, as it enables efficient intermolecular π–π stacking and facilitates charge carrier transport in the solid state or self-assembled aggregates.^8,9 Naphthalenediimide (NDI) derivatives, particularly symmetrically disubstituted variants, have emerged as promising n-type semiconductor building blocks due to their high electron affinity (EA), robust π–π interactions, and versatile functionalization at both the aromatic core and side chains.¹⁰ Theoretical evaluation of charge transport in such systems can be performed using computational models that estimate charge hopping rates across π-stacked molecular arrays.^11–13 While advanced charge transport models can be computationally intensive and less suited for rapid screening, the Marcus hopping model provides a balance between accuracy and efficiency for estimating mobility in OSCs.^14–16 According to this model, charge transfer is primarily governed by two key parameters: the reorganization energy (λ), which reflects the free energy cost of structural relaxation during charge transfer, and the charge transfer integral (J), determined by the degree of orbital overlap between adjacent molecules.¹⁷ It has been well-documented that even subtle changes in side chains of NDI derivatives can significantly alter molecular packing and material properties.¹⁸ Flexible alkyl side chains, for instance, often exhibit conformational variability, leading to polymorphism and reversible phase transitions between crystalline and mesophase states, which in turn impact device performance.^19–22 Moreover, the emergence of additional polymorphs has been observed when such materials are processed into thin films for OFET fabrication.^23–25 While rigid molecular structures can minimize reorganization losses and enhance charge transport efficiency, they often introduce the risk of polymorphism, which adversely affects device uniformity and reproducibility.^26–29 Different polymorphs typically exhibit distinct physical characteristics—including crystal habit, melting point, solubility, and electronic, optical, and mechanical properties—which can result in inconsistent device behavior.³⁰ The formation of multiple domains within the active layer contributes to variability in performance, reduced reproducibility, and limited device longevity. Thus, managing polymorphism is a critical aspect of materials design for OFETs and emerging organic electronic applications. In light of these considerations, we sought to reduce conformational flexibility while retaining favorable charge transport characteristics by designing molecules based on a rigid NDI core covalently linked to a picolyl ring—a secondary electron-hopping moiety. The nitrogen atom in the picolyl group was expected to contribute to improved molecular stacking and enhanced electronic interactions. To simultaneously improve solubility and processing ability and to introduce slight flexibility that might assist in crystallization, a methylene (–CH₂–) spacer was introduced between the NDI core and the pyridyl unit. This sp³-hybridized carbon effectively limits conjugation between the two π-systems but enables rotational freedom, thereby introducing the possibility of thermally induced conformational isomerism. Following synthesis in dry dimethylformamide (DMF) at 156 °C and subsequent purification, multi-colored crystalline compounds were obtained. Single-crystal X-ray diffraction (SCXRD) revealed the presence of three distinct conformational polymorphs—blue (B-NDI), pink (P-NDI), and red (R-NDI) crystals—each corresponding to a specific rotamer.³¹ These polymorphs differed not only in appearance but also in optical and charge transport properties. Additionally, the compounds exhibited limited solubility and domain boundary formation within crystals and films, indicative of complex crystallization behavior. The presence of both crystalline and film-state polymorphs in this rigid molecular system underscores the challenges and opportunities in designing high-performance n-type OSCs with tailored structural and electronic characteristics.

2. Results and discussion

2.1. Molecular features, pathways of crystallization and thermal properties of various polymorphs

B-NDI and P-NDI crystals were obtained as long, needle-like structures, while R-NDI exhibited a flat, plate-like morphology (Fig. S11). These polymorphs were obtained during either the purification or recrystallization steps. The crystallization pathways for each rotamer appeared to differ, as a strong correlation was observed between the choice of solvent and the resulting crystal form. The distinct colors of the polymorphs facilitated straightforward visual isolation and subsequent characterization. Interestingly, certain solvents—such as dichloromethane (DCM), chloroform (Chl), ethyl acetate (EA), and methanol—produced mixtures containing multiple crystal types from the same solution (Table S1, Fig. S4). In this study, we focus on three representative crystal samples obtained from ethyl acetate, DCM, and a 1: 2 (v/v) DCM: Chl mixture (Fig. 1a–c). Single crystals suitable for X-ray diffraction were analyzed to determine their molecular structures, geometries, and packing arrangements (CCDC numbers: 2447749–2447752). SCXRD analysis revealed distinct variations in molecular geometry and unit cell parameters across the three forms. Notably, none of the polymorphs could be converted into another form via thermal annealing (from room temperature up to 200 °C) or by exposure to common organic solvents, suggesting high activation barriers for interconversion and restricted bond rotation (Fig. 1c). Crystallographically, P-NDI and R-NDI belong to the triclinic system (space group P1̄), whereas B-NDI crystallizes in the monoclinic system (I2/a space group). Substantial differences were observed in unit cell dimensions, volumes, and molecular packing motifs (Table 1), underscoring the structural uniqueness of each rotameric form.

Fig. 1 (a) Chemical structure and pathways of crystallization yielding P, R, and B- NDI from precursor P₂NDI. Photographs of the corresponding nano-aggregates in solutions and resultant crystals under daylight (left panel) and under UV (375nm) irradiation (right panel). Schematic representation of the (b) geometry of rotamers and (c) plausible energetic pathways of crystallization to yield polymorphs from the monomer. (d) Geometric definition of rotamers.

Table 1 Parameters extracted from SCXRD analysis for the three polymorphic forms of NDI

	P-NDI	R-NDI	B-NDI
Crystal system	Triclinic	Triclinic	Monoclinic
Space group	P1̄	P1̄	I2/a
a (Å)	4.4824(3)	6.9207(3)	14.8011(4)
b (Å)	10.8989(5)	8.4747(5)	4.7503(1)
c (Å)	10.9310(7)	11.6077(4)	28.0666(8)
α (°)	112.564(5)	79.498(4)	90
β (°)	97.404(5)	83.100(4)	102.016(3)
γ (°)	95.958(4)	72.172(5)	90
V (Å^3)	482.13(5)	635.75(6)	1930.12(9)
Z	1	1	4
D (g cm^−3)	1.544	1.171	1.543
R 1 (%)	4.71	7.47	3.50
Temperature	100 K	293 K	293 K

---

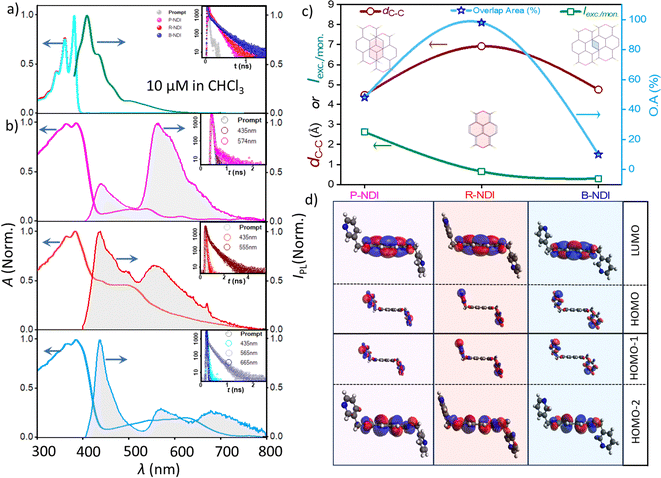
A detailed single-crystal X-ray diffraction (SCXRD) analysis was performed to investigate the geometry and molecular packing of the polymorphic NDI derivatives, aiming to understand their distinct optical and charge transport characteristics in the solid state. In organic semiconductors, the spatial arrangement of nearest-neighbor molecular pairs plays a critical role in determining charge hopping efficiency. All three NDI polymorphs exhibited a chair-like molecular conformation, with the pyridyl nitrogen atoms oriented diagonally across the molecular plane. However, significant structural variations were observed among the monomers extracted from the pink, blue, and red crystalline forms. A key distinction lay in the torsional angle (θ), defined as the C–C–C–N dihedral connecting the NDI core and the picolyl unit (see Fig. 1d). This angle, which dictates the spatial orientation of the pyridyl group, varied markedly between the polymorphs: 62° for P-NDI, 99° for R-NDI, and 134° for B-NDI. Such variations directly influence supramolecular packing, as the pyridyl nitrogen is a potential nucleation site for non-covalent interactions. Consequently, these conformational differences are expected to have pronounced effects on both optical and charge transport properties.³² Analysis of intermolecular interactions revealed notable differences in packing motifs. Both P-NDI and B-NDI formed slipped face-to-face π-stacked dimers, with an average π–π stacking distance of ∼3.3 Å (calculated between adjacent molecules along the stacking axis). These structures also displayed co-facial overlap between the secondary aromatic moieties (i.e., the picolyl units), indicating potential secondary charge-hopping pathways. In contrast, R-NDI adopted a nearly ideal face-to-face π-stacked geometry but with no lateral offset and a significantly larger π–π separation of ∼6.91 Å. Here, edge-to-face C–H⋯π interactions between terminal pyridyl rings stabilized a one-dimensional brickwork-type stacking motif. Across all polymorphs, diverse non-covalent interactions—including C–H⋯π, C–H⋯C–H, C–H⋯O, and C–H⋯N—were identified to varying extents, contributing to the overall stabilization of their respective packing arrangements (Fig. 2). Given that even subtle changes in molecular organization can profoundly impact charge transport and photophysical properties, these structural insights highlight the importance of conformational control in designing high-performance organic semiconductors.

Fig. 2 Detailed X-ray crystal structure analysis of three polymorphs under study. View along the molecular short axis indicating (a) the π–π stacking along the perpendicular axis to the NDI plane, (b) molecular packing along the expanded columns and (c) molecules in a unit cell.

Attenuated total reflectance Fourier transform infrared (ATR-FTIR) spectroscopy was employed to investigate the influence of intermolecular non-covalent interactions on vibrational modes in the polymorphic NDI crystals. Key vibrational frequencies corresponding to relevant functional groups are summarized in Table S5. Notable variations were observed in the aromatic C–H, alkyl (sp³ C–H), and imide vibrational regions, with selected characteristic bands presented in Fig. S12. The C–H stretching region (2800–3000 cm⁻¹) revealed distinguishable differences in both alkyl and aromatic vibrational modes, indicative of altered molecular environments. Furthermore, bending vibrations—including aromatic C–H in-plane and out-of-plane modes, and alkyl C–H bending—provided insight into the extent and nature of intermolecular interactions such as C–H⋯π, C–H⋯C–H, C–H⋯O, and C–H⋯N contacts among the polymorphs. In contrast, vibrational bands associated with the aromatic C=C stretch (1560–1600 cm⁻¹), out-of-plane aromatic C–H bending (740–780 cm⁻¹), carbonyl (C=O) stretching (1640–1700 cm⁻¹), and C–N stretching (∼1320 cm⁻¹) exhibited minimal shifts, confirming the structural rigidity of the core NDI framework across all polymorphs. Minor spectral differences in these regions likely stem from variations in supramolecular packing.³³

Thermal properties of the polymorphs were evaluated using thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). All three polymorphs demonstrated excellent thermal stability, with decomposition onset temperatures exceeding 380 °C, attributable to the robust, π-conjugated aromatic backbone and the inherent stability of the NDI core.³⁴ Subtle differences were noted in the TGA profiles of B-NDI and P-NDI, including variation in decomposition temperature and total weight loss, suggesting polymorph-dependent thermal degradation mechanisms likely influenced by intermolecular interactions. Notably, the red (R-NDI) powder showed an early weight loss (∼4%) starting at ∼153 °C, consistent with the boiling point of DMF, indicating solvent inclusion in this form. DSC thermograms of P-NDI and B-NDI exhibited sharp, single endothermic peaks at ∼325 °C, corresponding to their melting points, with no additional transitions, suggesting thermodynamic stability and phase purity. In contrast, R-NDI displayed a small endothermic event at 302 °C prior to its melting at 338 °C, indicating a polymorphic transition possibly associated with DMF loss (Fig. S9, Table S4). Powder X-ray diffraction (PXRD) patterns further confirmed the uniqueness of each polymorph, with distinct diffraction profiles reflecting differences in molecular packing (Fig. S10).

2.2. Optical properties

Steady-state UV-vis absorption and photoluminescence (PL) studies were performed on all three NDI polymorphs in both dilute solution (monomeric) and solid/crystalline states to investigate the optical consequences of polymorphism. In chloroform solution (10 μM), all samples exhibited nearly identical and well-resolved absorption bands at 380 nm (0-0), 360 nm (0-1), and 342 nm (0–2), corresponding to (HOMO−2) → LUMO π–π* transitions (Fig. 3d). Among these, the 0–0 transition was the most intense, a typical feature of rigid aromatic systems with minimal geometric relaxation upon photoexcitation. Furthermore, the solution-phase spectra were largely insensitive to solvent polarity, and the PL quantum yields were extremely low (<0.2%), accompanied by short lifetimes (∼0.8–1.2 ns), indicating dominant non-radiative decay pathways, as expected for such systems. The intensity ratio of the 0-0 to 0-1 transitions (A_0-0/A_0-1) was 1.3 in all monomeric samples, which served as a reference benchmark for evaluating aggregated-state optical behavior.³⁵ In contrast, solid-state UV-vis absorption and PL spectra revealed distinct features for each polymorph, diverging significantly from their monomeric counterparts. UV-vis diffuse reflectance spectra (200–800 nm) were recorded using a Shimadzu UV-2600 spectrophotometer, with BaSO₄ as the reflectance standard. The Kubelka–Munk function, F(R) = (1−R)²/2R, was applied to convert reflectance (R) into apparent absorption. In the solid-state spectra, vibronic progressions were notably absent (Fig. 3b), indicating the presence of intermolecular interactions. Additionally, weak lower-energy absorption bands (450–700 nm) emerged, which are attributed to electronic transitions between new states formed by intermolecular coupling, accounting for the distinct coloration of each polymorph. Slight redshifts in band edges (to ∼420 nm) were observed without significant shifts in absorption maxima. The A_0-0/A_0-1 ratios decreased in the solid state, with values of 1.00 (P-NDI), 1.05 (R-NDI), and 1.04 (B-NDI), relative to the monomeric state value of 1.3. PL emission spectra in the solid state exhibited both monomer-like and excimer-like emission bands, with the monomeric band near 435 nm and a broad excimer-related emission between 555 and 575 nm. Although the IUPAC definition of an excimer refers to chromophores in the monomeric state and the electronically excited dimer that lacks interactions in the ground state, the context is slightly different in the molecular aggregate. The observed emission originates from an excimer-like state known in the literature,³⁵ which describes that the excitonically coupled chromophores often relax into a lower-energy, localized ‘excimer-like’ configuration. The broad, strongly red-shifted emission profile further supports this assignment, indicating an excited state characterized by significant structural relaxation and enhanced intermolecular stabilization within the aggregate. Polymorphs differed significantly in the extent of π–π interactions. P-NDI, which displayed the most intense excimer band, featured a moderate π-overlap area³⁶ (OA) of 48% and the smallest centroid-to-centroid distance (d_C–C) of 4.48 Å. Despite minimal slippage, R-NDI showed the weakest excimer features due to its larger interplanar distance (6.91 Å), limiting effective π surface overlap. In contrast, B-NDI, with greater molecular slippage, exhibited broader and weaker excimer emission along with a more pronounced monomeric peak. To further confirm the emissive state with excimer character, the lifetime decay of both the monomeric and excimer bands was measured, revealing an increased lifetime of the latter (as shown in the inset of Fig. 3a and b). These observations, summarized in Fig. 3c, highlight the critical role of supramolecular arrangement and π–π stacking geometry in governing excimer formation.

Fig. 3 (a) Normalized UV-vis absorption and emission spectra of the monomers in 10 μM chloroform solutions. (b) Normalized UV-vis absorption and emission of crystalline solid samples. Inset shows the PL decay profile of the crystalline samples. (c) Summarized parameters: centroid-to-centroid distance (d_c-c), percentage of the overlap area (OA%) and the excimer to monomer PL intensity ratio in three polymorphs. (d) Frontier molecular orbitals involved in the optical transitions for each form.

2.3. Interaction energy analysis, charge transfer integral and electron mobility estimation

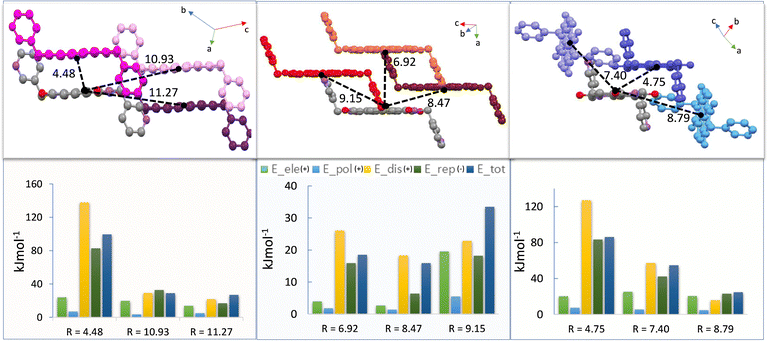
Intrinsic charge transport in molecular solids is fundamentally governed by the transfer integrals, which are, in turn, determined by the extent of molecular orbital overlap between neighbouring molecules. Since this overlap is directly influenced by intermolecular interactions, a comprehensive understanding of the non-covalent interactions that dictate supramolecular arrangements is essential, particularly when correlating with charge transport properties. To this end, a detailed computational analysis was performed to quantify the various interaction energies present in the crystalline phases of the NDI polymorphs. For each polymorph, intermolecular interaction energies were calculated using distinct molecular dimers formed around a reference molecule (M) and its immediate neighbours (denoted D1, D2, D3, etc.), along all crystallographic directions. These dimers were selected based on the presence of significant short contacts. The face-to-face π-stacked dimer (co-facial arrangement) was assigned as D1, with other relevant interacting pairs labelled accordingly. Energy decomposition analyses were carried out using density functional theory (B3LYP/6-31G(d,p)) to estimate individual contributions from electrostatic, polarization, dispersion, and exchange–repulsion interactions, as well as the total interaction energy.^37,38

Among these interactions, dispersion forces were found to be the dominant stabilizing factor across all polymorphs, highlighting their critical role in facilitating charge hopping through π–π stacking. Electrostatic interactions also contributed favorably, while polarization energy had minimal impact. Conversely, exchange-repulsion energy was destabilizing and often reduced the net interaction energy, underscoring the delicate balance required for optimal packing. P-NDI exhibited the highest total interaction energy (99.5 kJ mol⁻¹) among all dimers, with a centroid-to-centroid (d_c–c) distance of 4.5 Å. This strong stabilization was primarily driven by a substantial dispersion component (137.8 kJ mol⁻¹), although offset by significant repulsion energy (−82.7 kJ mol⁻¹). This observation indicates the crucial role of slipped face-to-face π–π stacking in achieving both structural stability and high charge transport efficiency. In R-NDI, interaction energies were comparatively lower. An unusual trend was observed: the total lattice energy of the closest dimer was 18.5 kJ mol⁻¹, which decreased to 15.9 kJ mol⁻¹ and then increased to 33.5 kJ mol⁻¹ with increasing d_c–c. This non-monotonic behavior suggests that even dimers with larger separations can contribute meaningfully to lattice stabilization, likely due to combined electrostatic and dispersion effects. The presence of ∼1.12 DMF molecules per unit cell (∼45 electrons) likely perturbed the local interaction environment, modifying the effective interactions between adjacent NDI units. For B-NDI, the molecules adopt a sandwich herringbone packing, with the most significant contribution to lattice energy arising from a slipped π–π stacked dimer. The interaction energy was notably high due to strong dispersion forces (127.1 kJ mol⁻¹). While longer d_C–C distances typically reduced energy contributions, a unique dimer arrangement in B-NDI retained significant interaction energy (54.7 kJ mol⁻¹) even at a separation of 7.40 Å (Fig. 4). This highlights how specific molecular orientations, despite larger separations, can still facilitate charge transport via efficient packing. Overall, these results emphasize that the nature and geometry of intermolecular interactions play a pivotal role in modulating charge transport.³⁹ Subtle variations in stacking motifs and interaction types across polymorphs lead to pronounced differences in transfer integrals, thereby influencing the electronic performance of the NDI-based molecular solids.

Fig. 4 Illustration of electrostatic energy (E_ele), polarization energy (E_pol), dispersion energy (E_dis) and repulsion energy (E_rep) contributing to the total energy (E_total) of all nearby dimers in P, R, and B-NDI (R = centroid-to-centroid distance). (+) and (–) signs in the parentheses indicate stabilization/destabilization respectively.

The charge transfer integrals (J) for the NDI polymorphs were calculated using the same dimeric configurations employed in the interaction energy analysis. As J reflects the degree of molecular orbital overlap between neighboring molecules, it is highly sensitive to the relative orientation and spatial arrangement of the charge transport centers within the crystal lattice. Specifically, electron transport correlates with the LUMO orbital overlap, while hole transport depends on HOMO orbital interactions. To evaluate these integrals, the dimer projection (DIPRO) method proposed by Baumeier et al.⁴⁰ was employed. Calculations were performed at the B3LYP-D3/6-31 + G* level of theory, incorporating the effects of electronic polarization for a more realistic estimation of charge transport parameters.

Significant variation in charge transfer integrals was observed across the polymorphs. These differences were rationalized by considering centroid-to-centroid distances, interplanar separations, and orbital overlap characteristics. P-NDI displayed the highest hole (16.31 meV) and electron (88.27 meV) transfer integrals, corresponding to a favorable stacking geometry with a plane-to-plane distance of 3.4 Å and centroid-to-centroid distance of 4.5 Å. The efficient π–π stacking and substantial LUMO overlap (Fig. S6) in P-NDI contributed to its enhanced electron transport. The stacking motif resembled a brickwork pattern with slight molecular slipping, supporting extended dispersive interactions and promoting long-range charge delocalization. As expected, charge transfer integrals decreased monotonically with increasing intermolecular distance due to reduced orbital overlap. In R-NDI, the values varied notably among different dimers, highlighting the anisotropic nature of molecular packing and orbital alignment. For dimer I, hole and electron transfer integrals were relatively low (J_h = 0.42 meV, J_e = 1.69 meV), attributed to poor orbital overlap stemming from large intermolecular separation. In contrast, dimer II, with a centroid-to-centroid distance of 8.5 Å and a plane-to-plane distance of 2.7 Å, yielded a significantly higher electron transfer integral (J_e = 42.58 meV), although hole transfer integral remained negligible (J_h = 0.17 meV). This suggests that a low interplanar distance, despite large centroid separation, can still support efficient electron transport due to favorable electronic coupling. Dimer III, with a larger interplanar separation (4.1 Å), showed low transfer integrals (J_h = 1.81 meV, J_e = 8.64 meV), confirming the critical role of spatial proximity and orientation. B-NDI exhibited better transport properties than R-NDI, though slightly inferior to P-NDI. Dimer I (d_C–C = 4.7 Å; plane-to-plane = 3.3 Å) had J_h = 5.13 meV and J_e = 63.07 meV, reflecting moderate π–π overlap. In dimer II (d_C–C = 7.4 Å), various non-covalent interactions, including C–H⋯π, C–H⋯O, and C–H⋯N hydrogen bonds, contributed to electrostatically guided stacking, thereby enhancing the LUMO overlap and resulting in appreciable electron transfer despite the extended centroid separation (Fig. 5). This detailed analysis reveals that intermolecular interactions in molecular crystals are highly anisotropic, and electronic transport is strongly direction-dependent. Even slight variations in molecular conformation or packing can lead to drastic differences in charge carrier mobility.

Fig. 5 (a) Illustration of various charge hoping (transport) pathways of the representative polymorphs and (b) their hole and electron transfer integrals, respectively.

To further elucidate the intrinsic electron mobility of the solid forms of the molecule, the inner-sphere reorganization energy (λ) was computed using the four-point energy method within the Marcus–Hush formalism (Fig. S8). This parameter quantifies the free energetic cost associated with the geometric reorganization that occurs when a charge (electron or hole) is transferred—i.e., the energy required for a molecule to reorganize from its neutral geometry to the geometry of its charged state. The calculations revealed that the electron reorganization energy (λ_e) was 376.3 meV, which was lower than the hole reorganization energy (λ_h) of 405.4 meV. According to Marcus–Hush theory, the charge transfer rate constant (k) is inversely proportional to the reorganization energy (λ) and directly proportional to the charge transfer integral (J). The mathematical relationship among these parameters is provided in the SI. Given the lower λ_e and higher J_e compared to λ_h and J_h, respectively, the molecule incurs a lower energetic penalty for electron transfer, which in turn leads to enhanced electron mobility (μ_e). The electron-mobility anisotropy was calculated to understand the relative magnitude of electronic couplings in various types of charge-hopping pathways and molecular-packing motifs in these polymorphs. From the predicted electron-mobility anisotropic curve, the highest values were obtained when the orientation was along dimer D1 (where the angle is 0°) as shown in Fig. 6. Recognizing the significant theoretical electron mobility of our n-type semiconductor molecule, we tried to fabricate OFET devices using these molecules. However, the compounds were poorly soluble in chloroform or other organic solvents. Hence, we had very poor-quality films with large crystalline domains and inhomogeneous layers on substrates. Device parameters thus obtained were with poor reproducibility and inferior reliability; we haven't included them in the current manuscript. A comprehensive comparison evaluating the performance against both theoretical predictions and experimental observations of electron mobility in a range of NDI derivatives from the literature is summarized in Table S2 to understand the importance of structural engineering for efficient n- channel OFETs.

Fig. 6 Calculated angle resolved anisotropic electron mobility (μ_e) in cm² V⁻¹ s⁻¹ for P-NDI, R-NDI and B-NDI (pink, red and blue circles respectively).

3. Conclusion

In this study, we investigated the formation of polycrystalline polymorphs in an n-type molecular semiconductor derived from a rigid picolyl end-substituted naphthalenediimide (NDI). The isolation of three distinct crystal forms—P-NDI, B-NDI, and R-NDI—was achieved by leveraging competing crystallization pathways and multiple local energy minima. These forms displayed microstructural heterogeneity, endowing them with unique colors and optical properties. All polymorphs adopted a chair-like molecular conformation, with pyridyl nitrogen atoms oriented diagonally opposite to each other. The torsional angle relative to the bridging carbon was a key parameter, measured at 62°, 99°, and 134° for P-, R-, and B-NDI, respectively. Various intermolecular interactions—including C–H⋯π, C–H⋯C–H, C–H⋯O, and C–H⋯N—were present to varying extents across the polymorphs, reinforcing their supramolecular assemblies. ATR-FTIR analysis revealed notable shifts in aromatic and alkyl (sp³) C–H vibrational frequencies as well as in imide moieties. All polymorphs demonstrated high thermal stability, with decomposition onset temperatures above 380 °C. However, subtle differences in TGA profiles, such as variations in weight loss percentages and decomposition temperatures, indicated distinct degradation mechanisms likely linked to their differing intermolecular interactions. Consistent with expectations, the absorption and emission spectra varied among P-, R-, and B-NDI. A thorough computational analysis of the intermolecular interactions and supramolecular packing showed that P-NDI exhibited the highest stabilizing energy, correlating with enhanced electron transport characteristics, as evidenced by higher electron transfer integrals (J). Despite promising charge transport, experimental organic field-effect transistor (OFET) fabrication was hindered by the polymorph's poor solubility in common organic solvents. The resulting poor-quality films, characterized by large crystalline domains and inhomogeneous layers, clearly demonstrate how semiconductor domain structure and molecular packing profoundly impact solid-state charge carrier transport. Nevertheless, our robust computational insights offer a valuable foundation for understanding structure–property relationships in NDI polymorphism, guiding future materials design and experimental exploration. This work ultimately reveals the formation of polymorphic rotamers in rigid end-group NDI derivatives and underscores their significant influence on both optical and electronic transport properties.

Author contributions

Conceptualization: R. K. V.; methodology: J. J., R. K. V. and I. G.; investigation: J. J., I. G., A. K. K. T.; supervision: R. K. V.; writing – original draft: J. J.; writing – review and editing: J. J. and R. K. V.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Data availability

The data supporting this article have been included as part of the SI.

Detailed experimental and anlytical data is provided in the supporing information file. See DOI: https://doi.org/10.1039/d5tc01728a

CCDC 2447749–2447752 contain the supplementary crystallographic data for this paper.^41–44

Acknowledgements

JJP and IG thank UGC, India, for the fellowship. JJ acknowledges Dr. Chhotan Mandal for the help in solving a single crystal structure. This work was supported by the DBT grant BT/PR44972/NNT/28/1810/2021. The authors acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for providing some experimental facilities. Beamtime was allocated for proposal(s) (Project No. I-20240653). Financial support by the Department of Science & Technology, Government of India (DST), provided within the framework of the India@Desy collaboration, is acknowledged.

References

1. J. Lee, S. A. Park, S. U. Ryu, D. Chung, T. Park and S. Y. Son, J. Mater. Chem. A, 2020, 8, 21455–21473.
2. M. Waldrip, Y. Yu, D. Dremann, T. Losi, B. Willner, M. Caironi, I. McCulloch and O. D. Jurchescu, Adv. Mater., 2024, 36, 2410442.
3. H. Liu, D. Liu, J. Yang, H. Gao and Y. Wu, Small, 2023, 19, 2206938.
4. Y. Zhang, Y. Wang, C. Gao, Z. Ni, X. Zhang, W. Hu and H. Dong, Chem. Soc. Rev., 2023, 52, 1331–1381.
5. R. González-Núñez, M. J. Alonso-Navarro, F. Suárez-Blas, E. Gala, M. M. Ramos, J. L. Segura and R. P. Ortiz, Mater. Chem. Front., 2024, 8, 1981–1992.
6. J. Dhar, U. Salzner and S. Patil, J. Mater. Chem. C, 2017, 5, 7404–7430.
7. V. M. Abbinante, M. Zambra, G. García-Espejo, C. Pipitone, F. Giannici, S. Milita, A. Guagliardi and N. Masciocchi, Chem. – Eur. J., 2023, 29, e202203441.
8. T. Okamoto, S. Kumagai, E. Fukuzaki, H. Ishii, G. Watanabe, N. Niitsu, T. Annaka, M. Yamagishi, Y. Tani and H. Sugiura, Sci. Adv., 2020, 6, eaaz0632.
9. S. Griggs, A. Marks, H. Bristow and I. McCulloch, J. Mater. Chem. C, 2021, 9, 8099–8128.
10. S. V. Bhosale, M. Al Kobaisi, R. W. Jadhav, P. P. Morajkar, L. A. Jones and S. George, Chem. Soc. Rev., 2021, 50, 9845–9998.
11. (a) Y. Olivier, V. Lemaur, J.-L. Brédas and J. Cornil, J. Phys. Chem. A, 2006, 110, 6356–6364; (b) M. V. Vener, O. G. Kharlanov and A. Y. Sosorev, Int. J. Mol. Sci., 2022, 23, 13305; (c) M. V. Vener, O. D. Parashchuk, O. G. Kharlanov, D. R. Maslennikov, D. I. Dominskiy, I. Y. Chernyshov, D. Y. Paraschuk and A. Y. Sosorev, Adv. Electron. Mater., 2021, 7, 2001281.
12. W.-Q. Deng, L. Sun, J.-D. Huang, S. Chai, S.-H. Wen and K.-L. Han, Nat. Protoc., 2015, 10, 632–642.
13. J. M. Toldo, M. T. Do Casal, E. Ventura, S. A. Do Monte and M. Barbatti, Phys. Chem. Chem. Phys., 2023, 25, 8293–8316.
14. D. L. Cheung and A. Troisi, Phys. Chem. Chem. Phys., 2008, 10, 5941–5952.
15. Y. Jiang, X. Zhong, W. Shi, Q. Peng, H. Geng, Y. Zhao and Z. Shuai, Nanoscale Horiz., 2016, 1, 53–59.
16. A. Y. Sosorev, Mater. Des., 2020, 192, 108730.
17. A. Mandal, CrystEngComm, 2022, 24, 2072–2080.
18. S. Milita, F. Liscio, L. Cowen, M. Cavallini, B. A. Drain, T. Degousée, S. Luong, O. Fenwick, A. Guagliardi and B. C. Schroeder, J. Mater. Chem. C, 2020, 8, 3097–3112.
19. I. Giri and R. K. Vijayaraghavan, Small, 2025, 2502456.
20. M. Dharmarwardana, R. P. Welch, S. Kwon, V. K. Nguyen, G. T. McCandless, M. A. Omary and J. J. Gassensmith, Chem. Commun., 2017, 53, 9890–9893.
21. T. He, M. Stolte, C. Burschka, N. H. Hansen, T. Musiol, D. Kälblein, J. Pflaum, X. Tao, J. Brill and F. Würthner, Nat. Commun., 2015, 6, 5954.
22. M. Diebold, E. Christ, L. Biniek, L. Karmazin, B. Heinrich, C. Contal, S. Ghosh, P. J. Mesini and M. Brinkmann, J. Mater. Chem. C, 2019, 7, 13120–13129.
23. X. Jiao, S. Maniam, S. J. Langford and C. R. McNeill, Phys. Rev. Mater., 2019, 3, 013606.
24. I. de Oliveira Martins, F. Marin, E. Modena and L. Maini, Faraday Discuss., 2022, 235, 490–507.
25. C. Karunasena, J. R. Thurston, T. P. Chaney, H. Li, C. Risko, V. Coropceanu, M. F. Toney and J. L. Brédas, Adv. Funct. Mater., 2025, 2422156.
26. S. M. Swick, W. Zhu, M. Matta, T. J. Aldrich, A. Harbuzaru, J. T. Lopez Navarrete, R. Ponce Ortiz, K. L. Kohlstedt, G. C. Schatz and A. Facchetti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E8341–E8348.
27. Y. Shi, Y. Chang, K. Lu, Z. Chen, J. Zhang, Y. Yan, D. Qiu, Y. Liu, M. A. Adil and W. Ma, Nat. Commun., 2022, 13, 3256.
28. W. Shi, Q. Han, Y. Zhu, Y. Xia, T. He, S. Wang, L. Li, W. Ma, G. Long and G. Li, Natl. Sci. Rev., 2025, 12, nwae409.
29. V. M. Abbinante, G. García-Espejo, G. Calabrese, S. Milita, L. Barba, D. Marini, C. Pipitone, F. Giannici, A. Guagliardi and N. Masciocchi, J. Mater. Chem. C, 2021, 9, 10875–10888.
30. H. Chung and Y. Diao, J. Mater. Chem. C, 2016, 4, 3915–3933.
31. J. P. Brog, C. L. Chanez, A. Crochet and K. M. Fromm, RSC Adv., 2013, 3, 16905–16931.
32. A. Haque, K. M. Alenezi, M. S. Khan, W.-Y. Wong and P. R. Raithby, Chem. Soc. Rev., 2023, 52, 454–472.
33. D. Chlebosz, W. Goldeman, K. Janus, M. Szuster and A. Kiersnowski, Molecules, 2023, 28, 2940.
34. I. Giri, S. Chhetri, J. P. John, M. Mondal, A. B. Dey and R. K. Vijayaraghavan, Chem. Sci., 2024, 15, 9630–9640.
35. (a) S. Chhetri, I. Giri, T. Pal, S. Sao, P. Lakar, A. B. Dey, D. Chaudhuri and R. K. Vijayaraghavan, J. Phys. Chem. C, 2024, 128, 8812–8820; (b) D. Chaudhuri, Org. Mater., 2021, 3, 455–468; (c) G. Johannes, L. Lüer, B. M. Medina, D. Oelkrug and H. J. Egelhaaf, J. Phys. Chem. Lett., 2013, 4, 2686–2697.
36. Y. Ge, Y. Wen, H. Liu, T. Lu, Y. Yu, X. Zhang, B. Li, S.-T. Zhang, W. Li and B. Yang, J. Mater. Chem. C, 2020, 8, 11830–11838.
37. K. J. Kalita, I. Giri and R. K. Vijayaraghavan, RSC Adv., 2021, 11, 33703–33713.
38. X. Chen, H. Sakurai, H. Wang, S. Gao, H.-D. Bi and F.-Q. Bai, Phys. Chem. Chem. Phys., 2021, 23, 4681–4689.
39. K. Carter-Fenk and J. M. Herbert, Phys. Chem. Chem. Phys., 2020, 22, 24870–24886.
40. E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882–9886.
41. P. Jesslyn, I. Giri, K. T. Amjed Khader and R. K. Vijayaraghavan, CCDC 2447749: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2n52nl.
42. P. Jesslyn, I. Giri, K. T. Amjed Khader and R. K. Vijayaraghavan, CCDC 2447750: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2n52pm.
43. P. Jesslyn, I. Giri, K. T. Amjed Khader and R. K. Vijayaraghavan, CCDC 2447751: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2n52qn.
44. P. Jesslyn, I. Giri, K. T. Amjed Khader and R. K. Vijayaraghavan, CCDC 2447752: Experimental Crystal Structure Determination, 2025,  DOI:10.5517/ccdc.csd.cc2n52rp.

---