 Open Access Article
Open Access ArticleFirst-principles understanding of hole mobility and intrinsic transport mechanisms in Sn(II) oxides†
Romain
Claes
 ab,
David O.
Scanlon
ab,
David O.
Scanlon
 a,
Gian-Marco
Rignanese
a,
Gian-Marco
Rignanese
 bcd and
Geoffroy
Hautier
bcd and
Geoffroy
Hautier
 *e
*e
aSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
bEuropean Theoretical Spectroscopy Facility, Institute of Condensed Matter and Nanosciences, UCLouvain, Chemin des Étoiles 8, B-1348 Louvain-la-Neuve, Belgium
cWEL Research Institute, avenue Pasteur, 6, 1300 Wavre, Belgium
dSchool of Materials Science and Engineering, Northwestern Polytechnical University, No. 127 Youyi West Road, Xi’an 710072, Shaanxi, P. R. China
eThayer School of Engineering, Dartmouth College, Hanover, New Hampshire 03755, USA. E-mail: geoffroy.hautier@dartmouth.edu
First published on 10th June 2025
Abstract
Transparent conducting oxides (TCOs) have attracted considerable attention due to their applications in electronic devices, ranging from solar cells to flat panel displays and touch screens. While n-type TCOs, such as indium tin oxide (ITO) and tin dioxide (SnO2), have been extensively studied and widely adopted, the development of p-type TCOs remains an important challenge due to several factors, including their low carrier mobilities which arise from the flat valence bands of metal oxides. In this work, we employ first-principles calculations to investigate the transport properties of the binary Sn(II) oxide SnO and four promising ternary Sn(II) oxides: TiSnO3, K2Sn2O3 (in both cubic and rhombohedral phases), and Rb2Sn2O3. Our results show that the studied ternary Sn(II) oxides exhibit carrier mobilities comparable to state-of-the-art n-type TCOs, with band gaps ranging between 2 and 3 eV. The computational methodology, which provides an exact treatment of the Boltzmann transport equation, yields excellent agreement with experimental mobility values for SnO, suggesting that experimental measurements for the ternary compounds may also follow closely our predictions. In addition, we highlight the importance of effective masses for carrier lifetimes and the number of scattering channels involved, using a new decoupling approach for the scattering rates. Finally, we reveal that in SnO, high-frequency phonon modes involving oxygen motion dominate electron–phonon interactions, while in ternary compounds, vibrational modes involving the third atomic species are also of crucial importance. These findings could offer new perspectives on mitigating these specific vibrations to reduce electron–phonon scattering and enhance transport properties in oxide semiconductors.
1 Introduction
Transparent conductive oxides (TCOs) have garnered significant attention due to their vast potential for application in various electronic devices, including solar cells, flat panel displays, and touch screens.1–3 They have also been proposed for use in complementary metal–oxide–semiconductors (CMOS) or field-effect transistors (FETs).4–6 While n-type TCOs such as indium tin oxide (ITO), gallium oxide (Ga2O3) or tin dioxide (SnO2) have been extensively investigated and widely adopted,1,7–11 developing p-type TCOs has proven to be a challenging task.12,13 This is primarily due to their low carrier mobilities, which are one order of magnitude lower than those of their n-type counterparts. The underlying reason lies in the typically flat valence bands of metal oxides, which are dominated by localised p-orbitals of oxygen atoms. One way to mitigate this is by strong hybridisation of the O 2p orbital with, for instance, the Cu 3d10 orbital, as observed in Cu2O.12–15 This led to the “chemical modulation of the valence band” approach which saw a range of delafossite oxides studied. These materials were p-type in nature, however, they all displayed deep defect levels and ultimately poor conductivity.16–21 Sn(II) oxides also exhibit a departure from typical oxides in that the top of the valence bands also possesses a metallic character owing to the presence of lone pairs on tin atoms.22 However, it has been also demonstrated by Ha et al.23 that the presence of Sn(II) alone does not guarantee a low effective mass; the crystalline structure also plays an important role. Indeed, the angle formed by the Sn–O–Sn bonds within the crystal structure has a strong influence on the effective mass of these oxides: when this angle approaches 180°, it promotes orbital overlap, leading to lower effective masses.In this work, we use first-principles calculations to investigate the transport properties of the prototypical binary tin oxide SnO as well as four identified promising ternary compounds: TiSnO3, K2Sn2O3 (in the cubic (c) and rhombohedral (r) phases) and r-Rb2Sn2O3. These ternary tin oxides have already been identified as potential TCO candidates based on effective mass calculations23,24 or, more recently, through the use of phenomenological mobility models25–27 but without using a fully first-principles approach such as in the present study. Our computations, which rely on the iterative solution of the Boltzmann transport equation, allow us to delve deeper into the understanding of the differences between these materials, thereby assessing their significant potential. The relative importance of the electron–phonon (e–ph) coupling is also assessed using a new decomposition method of the scattering rates and a detailed analysis of the phonon modes involved.
2 Computational methodology
2.1 Computational details
The band structures shown in this work were computed using VASP28,29 at the PBE0 level30 allowing a better evaluation of the band gap than with semi-local exchange–correlation (XC) functionals. In contrast, the transport calculations presented in this study were performed using Abinit31,32 at the generalised-gradient approximation (GGA) level, employing the PBE (for SnO) or PBEsol functional (for the ternary tin oxides).30,33 This difference in terms of XC functional is justified by the absence of band gap in SnO with PBEsol, making the mobility calculation less accurate. The complexity and cost of the density functional perturbation theory (DFPT) methodology employed in this work prevent the use of higher-level XC functionals, such as hybrid functionals. We do not expect significant discrepancies, as the effective masses computed with GGA remains in the range of those obtained with higher level of theory for the Sn(II) oxides studied here, as shown in Table 2.Abinit employs a fully first-principles approach to compute phonon-limited mobilities by iteratively solving the Boltzmann transport equation (IBTE).34–37 The methodology employed in Abinit, which is comprehensively outlined in ref. 34 and 35, allows us to achieve performance levels comparable to Wannier-based packages, eliminating the necessity of using Wannier functions altogether. In this work, convergence is assumed to be reached when the mobilities of three consecutive grids differ by no more than 5%. The converged IBTE mobilities were obtained with k-meshes (for the electronic part) of 128 × 128 × 96 for SnO, 130 × 130 × 130 for c-K2Sn2O3, 156 × 156 × 156 for r-K2Sn2O3, 144 × 144 × 144 for Rb2Sn2O3 and 110 × 110 × 110 for TiSnO3. On the other hand, DFPT scattering potentials and interatomic force constants also needed for the computation of the mobility were obtained by interpolation starting from a coarse q-mesh of 8 × 8 × 6 for SnO, 6 × 6 × 6 for c-K2Sn2O3, r-K2Sn2O3, and Rb2Sn2O3 and 5 × 5 × 5 for TiSnO3. The latter originate from the phonon database of Petretto et al.38 All the mobility and scattering potential calculations were performed with the inclusion of dynamical quadrupoles (Q*). It has been shown that the integration of Q*, the next order of correction to dynamical dipoles, in the computation of the mobility is essential to obtain accurate results.34,36 As the computation of Q* is still limited to norm-conserving pseudopotentials without non-linear core corrections (NLCC), a slight deviation in mobility can be expected but it is several orders of magnitude smaller compared to performing calculations without Q*.
2.2 Decomposition of the scattering rates
One of the aims of this work is to gain a better understanding of the importance of e–ph coupling and the influence of the effective mass on the lifetime. To this end, an analysis of the scattering rates was carried out. While, the IBTE method provides an exact solution of the BTE and is used to determine the phonon-limited hole mobility in our systems, it does not directly give access to these scattering rates. Therefore, we had to take a step back in terms of accuracy and analyse the scattering rates obtained from the self-energy relaxation time approximation (SERTA). In the Boltzmann transport formalism under the SERTA, the hole mobility is given by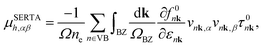 | (1) |
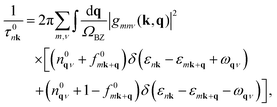 | (2) |
 | (3) |
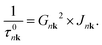 | (4) |
To enable this factorisation to be carried out computationally, it is only necessary to perform a conventional calculation of the scattering rates under the SERTA and another where all the matrix elements are set to 1. The latter gives us a direct access to the J parameter whereas the G2 parameter is obtained by dividing the scattering rates calculated conventionally by Jnk.
3 Results
3.1 Crystal and electronic structures
Among the various Sn(II) oxides, the conventional SnO has been extensively studied both theoretically and experimentally. It possesses a tetragonal crystalline structure with a distinguishing layered arrangement as shown in Fig. 1(a). The presence of a lone pair on the tin atom results in different stacking patterns compared to SnO2. In the case of SnO, the Sn–O–Sn layers are stacked along the c-axis, exhibiting relatively weak van der Waals (vdW) interactions.40 The structural properties of SnO obtained with GGA PBE and PBE0 are in good agreement with the experimental results,40–43 as shown in Table 1 but also with the numerous computational data obtained with various techniques.25,44–49 The use of vdW corrections has been shown to significantly improve structural agreement with experimental data in the case of SnO44,49 (and more generally in layered materials). However, in the case of SnO, these corrections tend to underestimate the band gap with PBE, resulting in a semi-metallic behaviour. The lack of a band gap is detrimental to the study of the transport properties of SnO and therefore PBE with vdW cannot be used. Our PBE values for the effective masses – one of the key parameters in carrier transport calculations – lie between the values obtained using PBE0 (with and without vdW corrections), see Table 2. We expect our transport results to be relatively unaffected by the choice of the XC functional in SnO. Nevertheless, the use of a hybrid functional remains needed to obtain accurate band gaps. In the case of SnO, a direct band gap of 3.29 eV is obtained with PBE0 without vdW corrections, in agreement with other experimental studies ranging from 2.5 to 3.3 eV,5,50–53 as shown in Fig. 2. | ||
| Fig. 1 Crystal structures of (a) SnO, (b) c-K2Sn2O3, (c) Rb2Sn2O3 and (d) TiSnO3. r-K2Sn2O3 has the same rhombohedral structure as Rb2Sn2O3 and is therefore not shown here. Sn atoms are in dark green, O atoms in red, K atoms in blue, Rb atoms in light green and Ti atoms in orange. The different crystal structures are plotted using VESTA.54 | ||
| Materials | Space group | Sn–O–Sn (°) | a (Å) | c (Å) | ||||
|---|---|---|---|---|---|---|---|---|
| PBE(sol) | PBE0 | Exp. | PBE(sol) | PBE0 | Exp. | |||
| a In the case of SnO, PBE was used instead of PBEsol. b PBE0 with vdW correction. | ||||||||
| SnO | P4/nmm | 117.8 | 3.88a | 3.80 | 3.8042,43 | 5.06a | 4.98 | 4.8443 |
| 3.79b | 4.82b | |||||||
| c-K2Sn2O3 |
I21![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
167.6 | 8.32 | 8.41 | 8.4157 | 8.32 | 8.41 | 8.4157 |
| r-K2Sn2O3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
180 | 6.04 | 6.03 | 6.0057 | 14.07 | 14.34 | 14.3457 |
| r-Rb2Sn2O3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
180 | 6.13 | 6.13 | 6.0957 | 14.86 | 15.22 | 15.1057 |
| TiSnO3 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
— | 5.08 | 5.07 | 5.0756 | 20.83 | 22.04 | 20.6956 |
| 5.06b | 20.23b | |||||||
| Materials | μ h (cm2 V−1 s−1) | |||||
|---|---|---|---|---|---|---|
| Intralayer | Interlayer | Intralayer | Interlayer | |||
| PBEsol | PBE0 | PBEsol | PBE0 | |||
| a In the case of SnO, PBE was used instead of PBEsol. b PBE0 with vdW correction. | ||||||
| SnO | 2.32a | 2.19 | 0.58a | 0.47 | 11.0 | 40.8 |
| 2.09b | 0.66b | |||||
| c-K2Sn2O3 | 0.23 | 0.23 | — | — | 346.8 | — |
| r-K2Sn2O3 | 0.19 | 0.21 | 0.43 | 0.29 | 316.5 | 181.7 |
| r-Rb2Sn2O3 | 0.20 | 0.24 | 0.32 | 0.28 | 281.4 | 182.6 |
| TiSnO3 | 0.41 | 0.44 | 0.66 | 0.46 | 171.7 | 98.6 |
| 0.34b | 0.55b | |||||
 | ||
| Fig. 2 Band structures of (a) SnO, (b) c-K2Sn2O3, (c) r-K2Sn2O3, (d) Rb2Sn2O3 and (e) TiSnO3 computed using hybrid DFT (PBE0). (f) Band–band optical absorption for the different Sn(II) oxides. | ||
The other ternary tin oxides investigated in this study share a similar layered structure to SnO, except for c-K2Sn2O3, as seen in Fig. 1. Notably, K2Sn2O3 is slightly more stable in its cubic phase rather than the rhombohedral phase which is described experimentally as the high-temperature phase.55 Besides, the phonon dispersion curve of r-K2Sn2O3 presents imaginary frequencies, a sign of dynamical instability (see ESI†). On the other hand, Rb2Sn2O3 favours the rhombohedral configuration. Nevertheless, even in the cubic phase, the lone pairs of tin atoms tend to avoid each other within a three-dimensional Sn–O–Sn network. Finally, the rhombohedral structure of TiSnO3 is slightly different than those of r-K2Sn2O3 and Rb2Sn2O3 as edge-sharing TiO6 octahedra are present instead of hexagonal planar geometry between K/Rb and O. The structural properties of the ternary tin oxides are summarised in Table 1, where good agreement is also found with experimental literature55–59 and other theoretical works.23,27,60 For K2Sn2O3 and Rb2Sn2O3, the PBE0 functional shows very close agreement with experimental results. However, this is less true for TiSnO3, where PBE0 significantly overestimates the c-axis, resulting in a larger interlayer spacing. Applying vdW corrections, as was done for SnO, brings the results closer to experimental values, though some discrepancies remain. Our PBEsol results fall between the two PBE0 calculations, with and without vdW corrections and are closer to the experimental measurements. As in the case of SnO, we have chosen not to use vdW corrections for the transport calculations, as they do not lead to significant changes in the conductivity effective masses, as seen in Table 2.
The band structures and optical properties of the different ternary oxides computed with PBE0 are shown in Fig. 2. The band gaps of r-K2Sn2O3 and Rb2Sn2O3 are relatively small with values close to 2 eV (2.355 and 2.365 eV, respectively). For c-K2Sn2O3, an indirect band gap of 2.504 eV is found whereas TiSnO3 presents the highest band gap of the ternary oxides with an indirect band gap of 2.433 computed with PBE0 and vdW corrections (3.369 eV without), slightly higher than experimental results of 1.90 eV.61 For the sake of completeness, the band gaps have also been calculated using the HSE06 XC functional. They are provided in the ESI.†
3.2 Transport
 | ||
| Fig. 3 IBTE hole drift mobility of SnO against temperature. Using a constant Hall factor of 1.7725 for the range of temperature, the approximate Hall mobility is also shown and compared with experimental results from ref. 64. | ||
On the other hand, thin films results range from 1 to 21 cm2 V−1 s−1 using different deposition methods.5,52,65–70 The high volatility of Sn during the growth of thin films leads to the formation of Sn vacancies, resulting in an increased carrier concentration and unintentional doping of the SnO thin films.66 This can explain the slightly lower experimental results observed for thin films compared to bulk samples. However, through precise modulation of the kinetic and thermodynamic conditions during the film growth process, it becomes possible to effectively minimise ionised-impurity and grain boundary scattering. This optimisation strategy contributes to the achievement of the highest thin film mobility value reported of 21 cm2 V−1 s−1 obtained by Minohara et al.66 with a low carrier concentration of 7 × 1016 cm−3. Our mobility results are also in agreement with a previous computational work performed by Hu et al.25 where a mobility of 7.4 and 60.0 cm2 V−1 s−1 is found using two empirical models for polar optical and acoustic deformation scattering.
Fig. 4 demonstrates that the linewidths of SnO, and therefore the scattering rates (as linewidth is proportional to 1/τ), closely follow the behaviour of the G2 parameter (see eqn (4)), which is directly linked to the strength of the e–ph coupling. Specifically, we observe a first plateau in the scattering times up to 50 meV, followed by a substantial increase and a second plateau. Given the lack of any significant changes in the electronic structure at these energies, the sudden rise in scattering times can be attributed to the activation of new important phonon-mediated scattering channels with energies around 50 meV. The function  (reported in grey in Fig. 4), which gives access to the hole mobility once integrated, shows the energy states participating in the hole transport and their relative importance. Even if the peak of this curve (at 34 meV) is reached before the sudden increase, the tail largely encompasses it, demonstrating the importance of these high-frequency modes for the hole mobility in SnO. Another way to show the importance of high-frequency phonons is to look at the temperature dependence of the mobility. As shown in Fig. S2 (ESI†), an important temperature-dependence change is observed around 100 K when higher energy vibrational modes are thermally activated.
(reported in grey in Fig. 4), which gives access to the hole mobility once integrated, shows the energy states participating in the hole transport and their relative importance. Even if the peak of this curve (at 34 meV) is reached before the sudden increase, the tail largely encompasses it, demonstrating the importance of these high-frequency modes for the hole mobility in SnO. Another way to show the importance of high-frequency phonons is to look at the temperature dependence of the mobility. As shown in Fig. S2 (ESI†), an important temperature-dependence change is observed around 100 K when higher energy vibrational modes are thermally activated.
A comprehensive view of the phonon properties of SnO is shown in Fig. 5: panel (a) displays the phonon band structure, while panel (b) shows the projected density of states (PDOS) for this structure. Finally, panel (c) presents the spectral decomposition of the scattering rates at two distinct energies (34 and 64 meV) corresponding to the first and second plateau of Fig. 4. Notably, this decomposition highlights and confirms the crucial role played by high-energy phonon modes in the scattering rate of SnO. However, these modes, mainly associated with oxygen motion (as indicated in the PDOS), can only participate to the transport when the transition fnk to fmk+q requires a high-frequency phonon ωqν of ∼50 meV as schematised in Fig. S3(a) (ESI†). Within the first plateau (around 34 meV for instance), the only scattering processes involving these states and these high-frequency phonons can only be out-of-state transitions by phonon emission or in-state transitions by phonon absorption. Other types of transitions are not possible as the state fmk+q does not exist (i.e., the electronic state would be in the band gap). In the case of SnO, the out-of-state emissions are favoured as the states that can perform this type of transition are closer to the top of the valence band. This is also induced by the decreasing shape of the curve of the J parameter shown in Fig. 4. This can be demonstrated by using a simple model based on a single parabolic band and a phonon following the Einstein model as seen in Fig. S3(b) (ESI†). We observe a decreasing behaviour of J with energy in the case of a transition due to the emission of a phonon and an increasing behaviour when an absorption take place.On the other hand, an initial state close in energy to the second plateau (at 64 meV for example) allows all the different transitions with these phonons. This is also expressed by the much larger area under the curve in Fig. 5(c) for the latter. With this first-principles study, we reaffirm the significance of these high-frequency phonon modes, complementing previous findings based on phenomenological models25 with a more in-depth analysis.
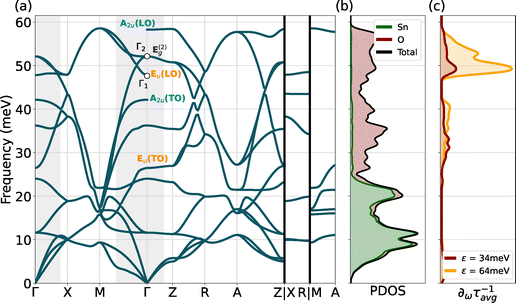 | ||
| Fig. 5 (a) SnO phonon dispersion computed using the PBEsol functional. The Eu (TO and LO) and A2u (TO and LO) are highlighted in orange and teal, respectively. The grey areas around Γ show the regions relevant (due to energy conservation) for the scattering, as expressed in eqn (2). (b) Phonon projected density of state (PDOS) with the contribution of Sn and O in green and red, respectively. (c) Spectral decomposition of the hole scattering rates at two different band energy level corresponding to the two plateaus of Fig. 4 (34 meV in red and 64 meV in orange). | ||
The other important parameter to look at during a transition between two states is the conservation of momentum. The light grey regions in the dispersion curve (Fig. 5(a)) correspond to the areas where intravalley scattering is relevant. This means that the only q vectors available for a transition that respect the conservation of the momentum are in the light grey area. For instance, this implies that acoustic modes with a large e–ph coupling at q = M as identified by Chen et al.71 do not participate in the hole transport. Indeed, due to a rather curvy band at the Γ-point of SnO, a transition involving a momentum transfer of q = M is forbidden. In short, the phonon modes that scatter the hole the most in SnO are high-frequency modes with small q (i.e., close to Γ) that predominantly involve intralayer vibrations of oxygen. Fig. 6(a) and (d) illustrate these modes at two different locations at Γ, corresponding respectively to an optical longitudinal (LO) Eu mode (Γ1 in Fig. 5), where the oxygen atoms move in phase, and an optical degenerate Eg mode (Γ2 in Fig. 5), with oxygen atoms moving out-of-phase (the two degenerate Eg modes have the same atomic displacements pattern but in the two different intralayer directions).
 | ||
| Fig. 6 (a) and (d) Atomic displacements corresponding to the LO Eu mode (Γ1 in Fig. 5) and the degenerate Eg modes (Γ2 in Fig. 5), respectively. The two degenerate Eg modes showing the same atomic displacements but in the two different intralayer directions. (b) and (e) Present the projected Crystal Orbital Hamiltonian Populations (COHP) for the two corresponding vibrational modes (in red) as well as the pristine SnO (in blue). The interaction between O2p and O2p is highlighted. Here, the –COHP is plotted in order to have the bonding levels to go to the right and the anti-bonding levels to the left. (c) and (f) Show the DOS corresponding to the two modes and pristine SnO with a focus on the O2p contribution. | ||
A crystal orbital Hamilton population (COHP) analysis (Fig. 6(b) and (c)) with distorted structures due to these two phonons is carried out using an amplitude of 0.5 Å for the largest atomic displacement. The Γ1 mode does not seem to affect the electronic structure considerably, whereas the Γ2 mode tends to strongly destabilise the VBM. While increased mixing between the Sn5s–O2p and Sn5p orbitals could have increased the s-character of the VBM and caused destabilisation, in this case, the destabilisation mostly results from the interaction between the O2p orbitals of two neighboring oxygen atoms. The two states being similar in energy, this hybridisation is favoured. However, this interaction is only possible when the oxygen atoms move out-of-phase, bringing them closer together and enabling this important hybridisation.
The hole mobilities results for the ternary oxides are summarised in Table 2. The mobility obtained are much higher than those obtained for SnO, with c-K2Sn2O3 presenting the higher value with 347 cm2 V−1 s−1. We note that the results for r-K2Sn2O3 should be considered with caution due to the presence of imaginary phonon frequencies. Overall, the hole mobilities obtained using the IBTE methodology mainly follows the trend of the effective masses except for TiSnO3. Indeed, with a larger effective mass than SnO in the interlayer direction, one might expect a lower mobility in this direction compared with the value obtained for SnO. In fact, this is what is obtained using simple phenomenological models.26,27 These simple approaches, however, based on the Fröhlich73 or Vogl models74 do not fully take into account the anisotropy and particularly in this case the effective masses in the other directions. In the Boltzmann transport formalism and the relaxation-time approximation (RTA), the curvature of the bands plays a crucial role not only in determining velocities in eqn (1) but also indirectly influences the number of states participating to transport. A higher effective mass corresponds to a flatter band structure, which in turn provides a larger number of available states and scattering channels for the carriers. This can be seen as the parameter J, obtained from eqn (2) and shown in Fig. 7(c). The importance of this J parameter is largely underestimated in the models. Consequently, materials exhibiting an excellent effective mass in one direction but poor effective masses in the other two directions, such as SnO, might exhibit lower mobility in that favourable direction compared to materials, such as TiSnO3 with a higher effective mass in the same direction but excellent low effective masses in the other two directions.
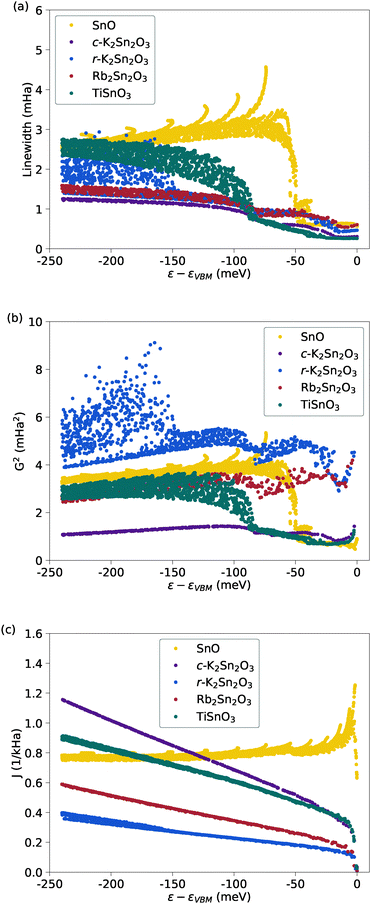 | ||
| Fig. 7 (a) Hole linewidths, (b) G2 parameters and (c) J parameters with SnO in yellow, c-K2Sn2O3 in purple, r-K2Sn2O3 in blue, Rb2Sn2O3 in red and TiSnO3 in green. | ||
Generally speaking, the parameter J is directly related to the DOS (or Seebeck) effective mass which takes into account both the effective mass and the valley degeneracy.75 In fact, J is very low for r-K2Sn2O3 and Rb2Sn2O3 due to their low effective mass, whereas it is slightly higher for TiSnO3 for the same reason. Among the ternary oxides, c-K2Sn2O3 exhibits the highest value for J, primarily due to the presence of multiple pockets resulting from its VBM at the high symmetry point H, as shown in Fig. S4 (ESI†). This larger number of valleys, in contrast to the classic single valley at Γ observed in the other studied materials, leads to an increased number of available states facilitating new intervalley transitions. Finally, the shape of the curves of the various ternary oxides is also very different from SnO. This is probably linked to the larger number of transitions made by absorption of a phonon and not emission as shown in Fig. S3(b) (ESI†), which is the opposite of what happens in SnO.
However, this high number of possible transitions in c-K2Sn2O3 is counterbalanced by the low strength of e–ph coupling (G2) leading to very low scattering rates close to the VBM, as shown in Fig. 7(a) and (b). In comparison with SnO, the ternary oxides do not present such an abrupt increase of this G2 parameter close to the VBM. An important rise is observed for TiSnO3, similarly to SnO, but it only occurs after 90 meV where the electronic states do no longer participate greatly to transport. By analysing the linewidths, it can be seen that the lowest values are observed for TiSnO3 and c-K2Sn2O3, while the highest values are found for r-K2Sn2O3 and Rb2Sn2O3 within the energy range relevant for transport. This pattern aligns with the trend observed in the G2 parameter related to the e–ph coupling. However, it is noteworthy that these linewidths remain considerably lower than those exhibited by SnO after the important increase. This implies that in SnO the high scattering rates are due to both an important e–ph coupling and an important number of states allowing the different transitions to happen. In other words, the tendency for a large J parameter to be linked to a small G2 parameter as observed in the different ternary oxides, does not apply in the case of SnO.
To analyse the phonon modes that exhibit the strongest coupling with electrons and compare them with SnO, we performed a spectral decomposition of the scattering rates for the four ternary oxides at 300 K. The analysis is performed at an energy value specifically chosen to correspond to the energy for which the maximum number of states participate in transport, as shown in Fig. S5 (ESI†). The results are shown in the ESI† (Fig. S6, S7, S8, and S9 for c-K2Sn2O3, r-K2Sn2O3, Rb2Sn2O3 and TiSnO3, respectively). The most noticeable observation is that the modes with the strongest hole coupling are consistently associated with a significant displacement of the third atom, namely Rb, K, or Ti, in addition to oxygen, as depicted in panel (b) of these figures. Another interesting finding is that the tin displacement in these modes is small, which is also in line with the results observed in SnO. In the rhombohedral materials, the large displacement of the third atom can be either in the direction perpendicular to the layers or in the layers and exhibits a similar pattern across all three compounds. These vibrational modes exhibit an LO–TO splitting and belong to either Eu or A2u symmetry. However, TiSnO3 also possesses rather important high-frequency phonon modes, in contrast with r-K2Sn2O3 and Rb2Sn2O3 but in a similar way to SnO. Being very high in frequency, they do not allow a large number of transitions, which limits their impact at room temperature. Nevertheless, we can expect them to play a crucial role as the temperature rise. Finally, in the case of c-K2Sn2O3, the T (LO) mode just below 18 meV, associated with perpendicular displacement of the two distinct K atoms, is responsible for just under half of the scattering of the holes. In comparison to SnO, the high-frequency modes associated with oxygen motions do not play the main role in the ternary oxides at room temperature. This can be attributed to their too high frequencies, which are already barely accessible in SnO at 300 K, leading to a restricted number of electronic transitions.
For the moment, these ternary tin oxides remain challenging to synthesise, with only a few studies reporting successful samples. Theoretically, their stability regions have been shown to be very narrow, primarily due to the lower stability of Sn(II) compared to Sn4+. Nevertheless, TiSnO3 has been successfully synthesised recently,56 and K2Sn2O3 has also been reported to be synthesised via the in situ reduction of K2Sn3O7.76 These recent advancements could open new avenues for the synthesis of tin(II) oxides, allowing experimental confirmation of our theoretical insights.
4 Conclusion
In this work, we present the computationally predicted hole mobility of SnO as well as that of different ternary Sn(II) oxides, assessing their potential as promising new candidates in the TCO field, with mobilities comparable to state-of-the-art n-type materials and band gap between 2 and 3 eV. The computational methodology employed in this study for the transport properties, which is based on an exact treatment of the BTE, has demonstrated excellent agreement with experimental results for SnO. We are therefore confident that experimental measurements on the ternary oxides could also align closely with our predicted mobility values.Our theoretical work also demonstrates the use of a new decoupling methodology of the scattering rates that provides significant insights into the e–ph scattering behaviour in these oxides. We highlighted the important role of effective mass on the lifetime of the studied compounds, something that is not always taken into account in simple models. One such example is SnO, which exhibits two very poor transport directions primarily attributed to a high effective mass in these directions. Consequently, the direction in which SnO demonstrates a more favourable effective mass is directly impacted, influenced by the large number of scattering channels provided by a flat band.
We also show that in SnO, e–ph scattering is predominantly dominated by high-frequency modes involving oxygen motion, which are also associated with significant destabilisation of the VBM. In the ternary compounds, it appears that the third atom plays a direct role in carrier scattering, with a limited number of phonon modes participating. These new insights into the scattering behaviour of these oxides could help to mitigate e–ph scattering, potentially enhancing the transport properties of this class of materials.
Conflicts of interest
The authors declare no competing interests.Data availability
The data supporting this article are included either directly in the main text or in the ESI.†Acknowledgements
This work was supported by the PRAETORIAN project, funded by UK Research and Innovation (UKRI) under the UK government's Horizon Europe funding guarantee (EP/Y019504/1) and the Communauté Française de Belgique, grant ARC 18/23-093. The computations done in this work were performed using the University of Birminghams BlueBEAR HPC service, the Baskerville Tier 2 HPC service (https://www.baskerville.ac.uk/; funded by the EPSRC and UKRI through the World Class Labs scheme (EP/T022221/1) and the Digital Research Infrastructure programme (EP/W032244/1)), the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick (funded by EPSRC Grant EP/T022108/1 and the HPC Midlands+ consortium), the Consortium des Équipements de Calcul Intensif, funded by the F.R.S.- FNRS under grant no. 2.5020.11 and by the Walloon Region. The present research also benefited from computational resources made available on the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles, infrastructure funded by the Walloon Region under grant no. 1117545. Through our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/L000202, EP/R029431, EP/T022213), this work also used ARCHER2 UK National Supercomputing Services. We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1). GH aknowledges supports by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Contract No. DE-AC02-05-CH11231 (Materials Project program KC23MP). GMR acknowledges financial support from the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS).References
- K. Ellmer, Past achievements and future challenges in the development of optically transparent electrodes, Nat. Photonics, 2012, 6(12), 809–817, DOI:10.1038/nphoton.2012.282.
- S. M. Rozati and S. A. M. Ziabari, A review of various single layer, bilayer, and multilayer TCO materials and their applications, Mater. Chem. Phys., 2022, 292, 126789, DOI:10.1016/j.matchemphys.2022.126789.
- H. Liu, V. Avrutin, N. Izyumskaya, U. Özgür and H. Morkoç, Transparent conducting oxides for electrode applications in light emitting and absorbing devices, Superlattices Microstruct., 2010, 48(5), 458–484, DOI:10.1016/j.spmi.2010.08.011.
- S. Salahuddin, K. Ni and S. Datta, The era of hyper-scaling in electronics, Nat. Electron., 2018, 1(8), 442–450, DOI:10.1038/s41928-018-0117-x.
- Y. Ogo, H. Hiramatsu, K. Nomura, H. Yanagi, T. Kamiya, M. Hirano and H. Hosono, p-channel thin-film transistor using p-type oxide semiconductor, SnO, Appl. Phys. Lett., 2008, 93(3), 032113, DOI:10.1063/1.2964197.
- H. Zhou, K. Maize, G. Qiu, A. Shakouri and P. D. Ye, β-Ga2O3 on insulator field-effect transistors with drain currents exceeding 1.5a/mm and their self-heating effect, Appl. Phys. Lett., 2017, 111(9), 092102, DOI:10.1063/1.5000735.
- N. Suzuki, S. Ohira, M. Tanaka, T. Sugawara, K. Nakajima and T. Shishido, Fabrication and characterization of transparent conductive Sn-doped β-Ga2O3 single crystal, Phys. Status Solidi C, 2007, 4(7), 2310–2313, DOI:10.1002/pssc.200674884.
- S. Ohira, N. Suzuki, N. Arai, M. Tanaka, T. Sugawara, K. Nakajima and T. Shishido, Characterization of transparent and conducting Sn-doped β-Ga2O3 single crystal after annealing, Thin Solid Films, 2008, 516(17), 5763–5767, DOI:10.1016/j.tsf.2007.10.083.
- T. Minami, Transparent conducting oxide semiconductors for transparent electrodes, Semicond. Sci. Technol., 2005, 20(4), S35–S44, DOI:10.1088/0268-1242/20/4/004.
- M. Fukumoto, S. Nakao, K. Shigematsu, D. Ogawa, K. Morikawa, Y. Hirose and T. Hasegawa, High mobility approaching the intrinsic limit in Ta-doped SnO2 films epitaxially grown on TiO2 (001) substrates, Sci. Rep., 2020, 10(1), 6844, DOI:10.1038/s41598-020-63800-3.
- B. A. D. Williamson, T. J. Featherstone, S. S. Sathasivam, J. E. N. Swallow, H. Shiel, L. A. H. Jones, M. J. Smiles, A. Regoutz, T.-L. Lee, X. Xia, C. Blackman, P. K. Thakur, C. J. Carmalt, I. P. Parkin, T. D. Veal and D. O. Scanlon, Resonant Ta Doping for Enhanced Mobility in Transparent Conducting SnO2, Chem. Mater., 2020, 32(5), 1964–1973, DOI:10.1021/acs.chemmater.9b04845.
- J. Willis and D. O. Scanlon, Latest directions in p-type transparent conductor design, J. Mater. Chem. C, 2021, 9(36), 11995–12009, 10.1039/d1tc02547c.
- K. H. L. Zhang, K. Xi, M. G. Blamire and R. G. Egdell, P-type transparent conducting oxides, J. Phys.: Condens. Matter, 2016, 28(38), 383002, DOI:10.1088/0953-8984/28/38/383002.
- D. O. Scanlon, B. J. Morgan, G. W. Watson and A. Walsh, Acceptor Levels in p-type Cu2O: Rationalizing Theory and Experiment, Phys. Rev. Lett., 2009, 103(9), 096405, DOI:10.1103/physrevlett.103.096405.
- D. O. Scanlon and G. W. Watson, Undoped n-type Cu2O: Fact or Fiction?, J. Phys. Chem. Lett., 2010, 1(17), 2582–2585, DOI:10.1021/jz100962n.
- D. O. Scanlon, A. Walsh, B. J. Morgan, G. W. Watson, D. J. Payne and R. G. Egdell, Effect of Cr substitution on the electronic structure of CuAl(1−x)Cr(x)O2, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 79(3), 035101, DOI:10.1103/physrevb.79.035101.
- D. O. Scanlon, A. Walsh and G. W. Watson, Understanding the p-Type Conduction Properties of the Transparent Conducting Oxide CuBO2: A Density Functional Theory Analysis, Chem. Mater., 2009, 21(19), 4568–4576, DOI:10.1021/cm9015113.
- D. O. Scanlon and G. W. Watson, Conductivity Limits in CuAlO2 from Screened-Hybrid Density Functional Theory, J. Phys. Chem. Lett., 2010, 1(21), 3195–3199, DOI:10.1021/jz1011725.
- D. O. Scanlon, K. G. Godinho, B. J. Morgan and G. W. Watson, Understanding conductivity anomalies in Cu(I)-based delafossite transparent conducting oxides: Theoretical insights, J. Chem. Phys., 2010, 132(2), 024707, DOI:10.1063/1.3290815.
- D. O. Scanlon and G. W. Watson, Understanding the p-type defect chemistry of CuCrO2, J. Mater. Chem., 2011, 21(11), 3655, 10.1039/c0jm03852k.
- D. O. Scanlon, J. Buckeridge, C. R. A. Catlow and G. W. Watson, Understanding doping anomalies in degenerate p-type semiconductor LaCuOSe, J. Mater. Chem. C, 2014, 2(17), 3429–3438, 10.1039/c4tc00096j.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Stereochemistry of post-transition metal oxides: revision of the classical lone pair model, Chem. Soc. Rev., 2011, 40(9), 4455, 10.1039/c1cs15098g.
- V. A. Ha, F. Ricci, G. M. Rignanese and G. Hautier, Structural design principles for low hole effective mass s-orbital-based p-type oxides, J. Mater. Chem. C, 2017, 5(23), 5772–5779, 10.1039/c7tc00528h.
- G. Hautier, A. Miglio, G. Ceder, G. M. Rignanese and X. Gonze, Identification and design principles of low hole effective mass p-type transparent conducting oxides, Nat. Commun., 2013, 4(1), 1–7, DOI:10.1038/ncomms3292.
- Y. Hu, J. Hwang, Y. Lee, P. Conlin, D. G. Schlom, S. Datta and K. Cho, First principles calculations of intrinsic mobilities in tin-based oxide semiconductors SnO, SnO2, and Ta2SnO6, J. Appl. Phys., 2019, 126(18), 185701, DOI:10.1063/1.5109265.
- Y. Hu, X. Yao, D. G. Schlom, S. Datta and K. Cho, First Principles Design of High Hole Mobility p-Type Sn–O–X Ternary Oxides: Valence Orbital Engineering of Sn2+ in Sn2+–O–X by Selection of Appropriate Elements X, Chem. Mater., 2020, 33(1), 212–225, DOI:10.1021/acs.chemmater.0c03495.
- Y. Hu, D. Schlom, S. Datta and K. Cho, Ilmenite and amorphous SnTiO3 as p-type oxide semiconductors, J. Mater. Chem. C, 2023, 11(14), 4830–4836, 10.1039/d2tc04937f.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269, DOI:10.1103/physrevb.49.14251.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/physrevlett.77.3865.
- X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J. M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Charraud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Geneste, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A. L. Marques, A. Martin, C. Martins, H. P. C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. Setten, B. V. Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, The Abinitproject: Impact, environment and recent developments, Comput. Phys. Commun., 2020, 248, 107042, DOI:10.1016/j.cpc.2019.107042.
- A. H. Romero, D. C. Allan, B. Amadon, G. Antonius, T. Applencourt, L. Baguet, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, F. Bruneval, G. Brunin, D. Caliste, M. Côté, J. Denier, C. Dreyer, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, F. Jollet, G. Jomard, A. Martin, H. P. C. Miranda, F. Naccarato, G. Petretto, N. A. Pike, V. Planes, S. Prokhorenko, T. Rangel, F. Ricci, G.-M. Rignanese, M. Royo, M. Stengel, M. Torrent, M. J. Setten, B. V. Troeye, M. J. Verstraete, J. Wiktor, J. W. Zwanziger and X. Gonze, ABINIT: Overview and focus on selected capabilities, J. Chem. Phys., 2020, 152(12), 124102, DOI:10.1063/1.5144261.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100(13), 136406, DOI:10.1103/physrevlett.100.136406.
- G. Brunin, H. P. C. Miranda, M. Giantomassi, M. Royo, M. Stengel, M. J. Verstraete, X. Gonze, G.-M. Rignanese and G. Hautier, Phonon-limited electron mobility in Si, GaAs, and GaP with exact treatment of dynamical quadrupoles, Phys. Rev. B, 2020, 102(9), 094308, DOI:10.1103/PhysRevB.102.094308.
- R. Claes, G. Brunin, M. Giantomassi, G. M. Rignanese and G. Hautier, Assessing the quality of relaxation-time approximations with fully automated computations of phonon-limited mobilities, Phys. Rev. B, 2022, 106(9), 094302, DOI:10.1103/PhysRevB.106.094302.
- G. Brunin, H. P. C. Miranda, M. Giantomassi, M. Royo, M. Stengel, M. J. Verstraete, X. Gonze, G.-M. Rignanese and G. Hautier, Electron-phonon beyond Fröhlich: dynamical quadrupoles in polar and covalent solids, Phys. Rev. Lett., 2020, 125(13), 136601, DOI:10.1103/PhysRevLett.125.136601.
- R. Claes, S. Poncé, G. M. Rignanese and G. Hautier, Phonon-limited electronic transport through first principles, Nat. Rev. Phys., 2025, 7(2), 73–90, DOI:10.1038/s42254-024-00795-0.
- G. Petretto, S. Dwaraknath, H. P. C. Miranda, D. Winston, M. Giantomassi, M. J. Setten, X. Gonze, K. A. Persson, G. Hautier and G.-M. Rignanese, High-throughput density-functional perturbation theory phonons for inorganic materials, Sci. Data, 2018, 5(1), 1–12, DOI:10.1038/sdata.2018.65.
- F. Giustino, Electron-phonon interactions from first principles, Rev. Mod. Phys., 2017, 89(1), 015003, DOI:10.1103/RevModPhys.89.015003.
- F. Izumi, Pattern-fitting structure refinement of tin (II) oxide, J. Solid State Chem., 1981, 38(3), 381–385, DOI:10.1016/0022-4596(81)90068-2.
- H. Giefers, F. Porsch and G. Wortmann, High-pressure EXAFS and XRD investigation of unit cell parameters of SnO, Phys. Scr., 2005, 2005(T115), 538, DOI:10.1238/Physica.Topical.115a00538.
- X. Wang, F. Zhang, I. Loa, K. Syassen, M. Hanfland and Y. L. Mathis, Structural properties, infrared reflectivity, and Raman modes of SnO at high pressure, Phys. Status Solidi B, 2004, 241(14), 3168–3178, DOI:10.1002/pssb.200405231.
- W. J. Moore Jr and L. Pauling, The crystal structures of the tetragonal monoxides of lead, tin, palladium, and platinum, J. Am. Chem. Soc., 1941, 63(5), 1392–1394, DOI:10.1021/ja01850a074.
- J. P. Allen, D. O. Scanlon, S. C. Parker and G. W. Watson, Tin Monoxide: Structural Prediction from First Principles Calculations with van der Waals Corrections, J. Phys. Chem. C, 2011, 115(40), 19916–19924, DOI:10.1021/jp205148y.
- E. P. Blancá, A. Svane, N. Christensen, C. Rodriguez, O. Cappannini and M. Moreno, Calculated static and dynamic properties of β-Sn and Sn-O compounds, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48(21), 15712, DOI:10.1103/PhysRevB.48.15712.
- Q. J. Liu, Z. T. Liu and L. P. Feng, First-principles calculations of structural, electronic and optical properties of tetragonal SnO2 and SnO, Comput. Mater. Sci., 2010, 47(4), 1016–1022, DOI:10.1016/j.commatsci.2009.11.038.
- Y. W. Li, Y. Li, T. Cui, L. J. Zhang, Y. M. Ma and G. T. Zou, The pressure-induced phase transition in SnO: a first-principles study, J. Phys.: Condens. Matter, 2007, 19(42), 425230, DOI:10.1088/0953-8984/19/42/425230.
- J. B. Varley, A. Schleife, A. Janotti and C. G. V. Walle, Ambipolar doping in SnO, Appl. Phys. Lett., 2013, 103(8), 082118, DOI:10.1063/1.4819068.
- J. P. Allen, D. O. Scanlon, L. F. J. Piper and G. W. Watson, Understanding the defect chemistry of tin monoxide, J. Mater. Chem. C, 2013, 1(48), 8194, 10.1039/c3tc31863j.
- R. Sivaramasubramaniam, M. R. Muhamad and S. Radhakrishna, Optical Properties of Annealed Tin(II) Oxide in Different Ambients, Phys. Status Solidi A, 1993, 136(1), 215–222, DOI:10.1002/pssa.2211360126.
- J. Geurts, S. Rau, W. Richter and F. J. Schmitte, SnO films and their oxidation to SnO2: Raman scattering, IR reflectivity and X-ray diffraction studies, Thin Solid Films, 1984, 121(3), 217–225, DOI:10.1016/0040-6090(84)90303-1.
- L. Y. Liang, Z. M. Liu, H. T. Cao and X. Q. Pan, Microstructural, Optical, and Electrical Properties of SnO Thin Films Prepared on Quartz via a Two-Step Method, ACS Appl. Mater. Interfaces, 2010, 2(4), 1060–1065, DOI:10.1021/am900838z.
- N. F. Quackenbush, J. P. Allen, D. O. Scanlon, S. Sallis, J. A. Hewlett, A. S. Nandur, B. Chen, K. E. Smith, C. Weiland, D. A. Fischer, J. C. Woicik, B. E. White, G. W. Watson and L. F. J. Piper, Origin of the Bipolar Doping Behavior of SnO from X-ray Spectroscopy and Density Functional Theory, Chem. Mater., 2013, 25(15), 3114–3123, DOI:10.1021/cm401343a.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276, DOI:10.1107/s0021889811038970.
- R. M. Braun and R. Hoppe, The first oxostannate (II): K2Sn2O3, Angew. Chem., Int. Ed. Engl., 1978, 17(6), 449–450, DOI:10.1002/anie.197804491.
- L. Diehl, S. Bette, F. Pielnhofer, S. Betzler, I. Moudrakovski, G. A. Ozin, R. Dinnebier and B. V. Lotsch, Structure-Directing Lone Pairs: Synthesis and Structural Characterization of SnTiO3, Chem. Mater., 2018, 30(24), 8932–8938, DOI:10.1021/acs.chemmater.8b04261.
- R. Hoppe and B. Nowitzki, Oxydationsprodukte intermetallischer Phasen. III. Tieftemperaturformen von K2Sn2O3 und Rb2Sn2O3 und eine Notiz über K2Ge2O3, Z. Anorg. Allg. Chem., 1984, 509(2), 145–152, DOI:10.1002/zaac.19845090215.
- R. Braun and R. Hoppe, Über Oxostannate (II). I. Zur Kenntnis von K2Sn2O3, Z. Anorg. Allg. Chem., 1981, 478(7), 7–12, DOI:10.1002/zaac.19814780702.
- R. Braun and R. Hoppe, Über Oxostannate (II). III. K2Sn2O3, Rb2Sn2O3 und Cs2Sn2O3–ein Vergleich, Z. Anorg. Allg. Chem., 1982, 485(1), 15–22, DOI:10.1002/zaac.19824850103.
- F. Pielnhofer, L. Diehl, A. Jiménez-Solano, A. Bussmann-Holder, J. C. Schön and B. V. Lotsch, Examination of possible high-pressure candidates of SnTiO3: The search for novel ferroelectric materials, APL Mater., 2021, 9(2), 021103, DOI:10.1063/5.0029968.
- L. Diehl, D. H. Fabini, N. M. Vargas-Barbosa, A. Jiménez-Solano, T. Block, V. Duppel, I. Moudrakovski, K. Küster, R. Pöttgen and B. V. Lotsch, Interplay between Valence Band Tuning and Redox Stability in SnTiO3: Implications for Directed Design of Photocatalysts, Chem. Mater., 2021, 33(8), 2824–2836, DOI:10.1021/acs.chemmater.0c04886.
- J. Y. Kim, B. Bae and E. J. Yun, Effects of Post-Annealing on the Electrical Properties of Sputter-Deposited SnO Thin-Film Transistors, Sci. Adv. Mater., 2016, 8(2), 272–277, DOI:10.1166/sam.2016.2478.
- S. Poncé, F. Macheda, E. R. Margine, N. Marzari, N. Bonini and F. Giustino, First-principles predictions of Hall and drift mobilities in semiconductors, Phys. Rev. Res., 2021, 3(4), 043022, DOI:10.1103/PhysRevResearch.3.043022.
- S. A. Miller, P. Gorai, U. Aydemir, T. O. Mason, V. Stevanović, E. S. Toberer and G. J. Snyder, SnO as a potential oxide thermoelectric candidate, J. Mater. Chem. C, 2017, 5(34), 8854–8861, 10.1039/c7tc01623a.
- A. B. Mei, L. Miao, M. J. Wahila, G. Khalsa, Z. Wang, M. Barone, N. J. Schreiber, L. E. Noskin, H. Paik, T. E. Tiwald, Q. Zheng, R. T. Haasch, D. G. Sangiovanni, L. F. J. Piper and D. G. Schlom, Adsorption-controlled growth and properties of epitaxial SnO films, Phys. Rev. Mater., 2019, 3(10), 105202, DOI:10.1103/physrevmaterials.3.105202.
- M. Minohara, A. Samizo, N. Kikuchi, K. K. Bando, Y. Yoshida and Y. Aiura, Tailoring the Hole Mobility in SnO Films by Modulating the Growth Thermodynamics and Kinetics, J. Phys. Chem. C, 2019, 124(2), 1755–1760, DOI:10.1021/acs.jpcc.9b11616.
- M. Minohara, N. Kikuchi, Y. Yoshida, H. Kumigashira and Y. Aiura, Improvement of the hole mobility of SnO epitaxial films grown by pulsed laser deposition, J. Mater. Chem. C, 2019, 7(21), 6332–6336, 10.1039/c9tc01297d.
- M. Budde, P. Mazzolini, J. Feldl, C. Golz, T. Nagata, S. Ueda, G. Hoffmann, F. Hatami, W. T. Masselink, M. Ramsteiner and O. Bierwagen, Plasma-assisted molecular beam epitaxy of SnO(001) films: Metastability, hole transport properties, Seebeck coefficient, and effective hole mass, Phys. Rev. Mater., 2020, 4(12), 124602, DOI:10.1103/physrevmaterials.4.124602.
- Y. Pei, W. Liu, J. Shi, Z. Chen and G. Wang, Fabrication and Characterization of p-Type SnO Thin Film with High c-Axis Preferred Orientation, J. Electron. Mater., 2016, 45(11), 5967–5973, DOI:10.1007/s11664-016-4816-7.
- J. A. Caraveo-Frescas, P. K. Nayak, H. A. Al-Jawhari, D. B. Granato, U. Schwingenschlögl and H. N. Alshareef, Record Mobility in Transparent p-Type Tin Monoxide Films and Devices by Phase Engineering, ACS Nano, 2013, 7(6), 5160–5167, DOI:10.1021/nn400852r.
- P. J. Chen and H. T. Jeng, Phase diagram of the layered oxide SnO: GW and electron-phonon studies, Sci. Rep., 2015, 5(1), 16359, DOI:10.1038/srep16359.
- P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, Crystal Orbital Bond Index: Covalent Bond Orders in Solids, J. Phys. Chem. C, 2021, 125(14), 7959–7970, DOI:10.1021/acs.jpcc.1c00718.
- H. Fröhlich, Electrons in lattice fields, Adv. Phys., 1954, 3(11), 325–361, DOI:10.1080/00018735400101213.
- P. Vogl, Microscopic theory of electron-phonon interaction in insulators or semiconductors, Phys. Rev. B, 1976, 13(2), 694–704, DOI:10.1103/physrevb.13.694.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, Effective mass and Fermi surface complexity factor from ab initio band structure calculations, npj Comput. Mater., 2017, 3(1), 1–7, DOI:10.1038/s41524-017-0013-3.
- R. D. McAuliffe, Materials discovery using in situ reduction and X-ray diffraction, University of Illinois at Urbana-Champaign, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc01708d |
| This journal is © The Royal Society of Chemistry 2025 |





