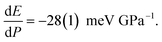Metallophilicity-assisted piezochromism in a rhodium(I) dicarbonyl Schiff-base complex: structural, energetic, electronic and spectroscopic investigations under high pressure

Abstract

For the development of piezochromic materials, it is critical to understand their structure–property relationships under high-pressure (HP). In this contribution, we report the experimental HP behaviour of a luminescent and nearly square-planar rhodium(I) dicarbonyl Schiff-base complex (Rh-4-Br) in the solid state, complemented by theoretical calculations. The crystal structure of Rh-4-Br is primarily governed by Rh⋯Rh metallophilic and C–H⋯O hydrogen-bond-type interactions. Both interaction types show notable structural, electronic, and energetic sensitivities to elevated pressures. HP single-crystal X-ray diffraction studies conducted between ambient pressure and ∼10.5 GPa revealed metallophilic interaction enhancement with the Rh⋯Rh distance shortening by ∼0.60 Å. HP-induced structural changes additionally affected the electronic properties. For instance, the electron density (ϱ(r_BCP)) at the Rh⋯Rh interaction bond critical point (BCP) increased by 0.155 e Å⁻³, whereas a higher delocalization index (δ) and ratio of 1 < |V(r_BCP)|/G(r_BCP) < 2 (V & G – local potential & kinetic energy densities) indicated partial covalency of this interaction at the highest pressures. Strengthening of the metallophilic interaction under HP influences molecular orbitals contributing to the lowest-energy electronic transitions. Consequently, a reversible piezochromism (yellow-to-orange-to-red) under compression–decompression cycles with a bathochromic shift of ∼75 nm (in the range up to 7 GPa) and Raman blue-shift of the ν_Rh⋯Rh band by ∼19 cm⁻¹ (in the range up to 5.4 GPa) were observed. These findings align closely with the results of periodic density functional theory modelling under isotropic external pressures.

---

1. Introduction

Over the past decade, there has been a growing interest in developing transition-metal based luminescent materials due to their diverse applications in light-emitting diodes (LEDs), electroluminescent devices, photo-switches, photoluminescent sensing and imaging.¹ Self-assembled entities of these complexes often exhibit distinct and sometimes enhanced photophysical properties compared to their individual molecular components in solution.² These molecular self-assemblies are primarily driven by intermolecular interactions, such as π⋯π stacking, sigma-hole interactions, hydrogen-bonds, and/or metallophilic interactions.³ Metallophilic interactions are commonly observed in transition-metal complexes with closed-shell d¹⁰ or pseudo-closed-shell d⁸ metallic centres. These are metal⋯metal interactions, which can be either homometallic or heterometallic, with a weak yet attractive nature and the interaction distances are typically shorter than the sum of the van der Waals radii of the interacting metal centers.⁴ Despite their prominent significance, the exact nature and strength of metallophilic interactions still remain obscure.⁵ While molecular orbital (MO) analysis and energy decomposition analysis (EDA) usually suggest favourable electrostatic and weakly covalent orbital interactions, recent studies have highlighted the role of strong Pauli repulsion and repulsive MO interactions due to relativistic effects.⁶ The first identified and most extensively studied subclass of metallophilic interactions are the aurophilic interactions (Au^I⋯Au^I).⁷ In some cases, the interaction energy of such interactions has been estimated to be comparable to that of moderate hydrogen-bonds,⁸ whereas in other gas-phase calculations this has been found to be nearly negligible,⁹ marking its ambiguity as a structure-directing synthon. Analogous investigations were also extended to other metallic centres, such as Ag^I, Cu^I, Rh^I, Pt^II, Pd^II, Hg^II and Ni^II.^4c,10

Metallophilic interactions, when present, play a crucial role in shaping the spectroscopic properties of transition-metal complexes.¹¹ Due to their relatively weak nature, these interactions can be readily modified by external stimuli, such as pressure, temperature, pH, or light.¹² Pressure is particularly useful for exploring structure–property relationships, as it may induce gradual geometrical changes in a crystal structure resulting in modifications of the crystal packing and intermolecular interactions, which can be further correlated with the corresponding spectroscopic behaviour.¹³ For instance, in piezochromic materials, the emission colour and other optical properties can be modulated by applying hydrostatic or non-hydrostatic pressure. Non-hydrostatic methods, such as grinding, pressing, or stretching, however often lead to microfractures, structural deformations, or phase transitions in materials, which complicate controlled studies of structural changes under pressure.¹⁴ In contrast, hydrostatic pressure, typically applied using a diamond-anvil cell (DAC), provides a more precise and controlled platform for systematic investigations.¹⁵

Square-planar geometries in transition-metal complexes with d⁸ and/or d¹⁰ metal centres often facilitate the formation of almost linear metal⋯metal chains due to a combination of dispersion forces, relativistic effects and orbital overlap, particularly involving the d_z² and p_z orbitals of the interacting metal centres. In contrast, more significantly distorted square-planar geometries often yield discrete molecular dimers with metal⋯metal contacts, involving also other types of interactions.¹⁶ Pressure-induced structural changes affecting these interactions can lead to significant variations in corresponding photoluminescent properties.¹⁷ While transition-metal complexes involving Au^I, Pt^II, and Pd^II metal centres have commonly been investigated in this context, case studies involving (nearly) square-planar Rh^I coordination compounds remain limited, thus their luminescent properties are largely unexplored. Our interest in the potential drug and electronic applications of salicylidene group 7 and 9 complexes¹⁸ resulted in our recent report of a nearly square planar rhodium(I) complex (Rh-4-Br), featuring a monocharged bidentate ligand, namely (N,O)-salicylidene p-bromoaniline, and two carbonyl ligands coordinated to the Rh^I metal centre.^16g In the solid state, this complex forms discrete molecular dimers with strong Rh⋯Rh metallophilic interactions and exhibit light-yellow luminescence ((λ_em)_max = 566 nm) under ambient conditions. These Rh⋯Rh interactions appeared to play a major role in the photoexcitation process. Hence, in the current work, we examine the relationship between the HP evolution of metallophilic interactions and the luminescent properties of Rh-4-Br. To this end, we have structurally investigated Rh-4-Br single crystals under hydrostatic pressures ranging from 0.00(5) to 10.45(5) GPa, and complemented these results by high-pressure (HP) luminescence and Raman spectroscopic analyses as well as by theoretical computations, in an attempt to provide a comprehensive understanding of structural factors governing these principles.

2. Results and discussion

2.1. Crystal structure description at ambient conditions

Rh-4-Br crystallises in the monoclinic P2₁/n space group with one molecule in the asymmetric unit (Fig. 1(a), Table S1 in ESI†). The complex consists of two carbonyl (C≡O) and one (N,O)-salicylidene p-bromoaniline (SPA) ligands covalently bonded to the Rh centre through electron-donating N, O and C atoms. The Rh^I coordination sphere adopts a distorted square-planar geometry, with the CO ligands and Rh atom positioned slightly out of the plane defined by the N1, C9, C3, and O3 atoms (Fig. S1a, ESI†). Additionally, the 4-bromophenyl ring in the SPA ligand is rotated by ∼49° (referred to as φ) relative to the remaining molecular framework (Fig. S1b, ESI†).

Fig. 1 (a) The asymmetric unit of Rh-4-Br with atomic thermal motion represented as ellipsoids at the 50% probability level for non-hydrogen atoms. For clarity only non-hydrogen atoms are labelled. (b) The most significant molecular dimers (dimer A–D) constituting the crystal packing of Rh-4-Br. The reference (x, y, z) molecule is shown with elemental colours, while neighbouring symmetry-generated molecules in different uniform colours.

The energetic ranking of molecular dimers (Table S6, ESI†) revealed that dimer A is best stabilised with a total interaction energy (E_int) of −87.8 kJ mol⁻¹ (Fig. 1(b) and Fig. S2a, ESI†). This dimer is composed of two centre-of-symmetry-related molecules held by the metallophilic Rh1⋯Rh1 (d_Rh⋯Rh = 3.4571(4) Å) interaction and several centrosymmetric C15–H15⋯O3 hydrogen-bond-type (HB) interactions. Energy decomposition analysis indicates that dimer A is equally stabilised by electrostatic (−78.1 kJ mol⁻¹) and dispersive (−73.3 kJ mol⁻¹) contributions. The electrostatic stabilisation arises from both the HBs and Rh⋯Rh interactions, while the dispersive component is primarily attributed to the metallophilic interactions, highlighting their critical role in stabilising the crystal packing of Rh-4-Br. These Rh⋯Rh interactions further propagate along [128̄] or [12̄8̄] crystallographic directions (Fig. S2c, ESI†). The second most significant dimer motif, dimer B, is characterised by E_int of −37.5 kJ mol⁻¹, which is less than half of that of dimer A. This dimer also exhibits inversion symmetry and is stabilised by a pair of C12–H12⋯O1 HBs (Fig. 1(b) and Fig. S2b, ESI†). For these and two other notable molecular dimers, dimer C and dimer D (Fig. 1(b) and Fig. S3, ESI†), the primary component of interatomic interaction vectors is oriented along the crystallographic Z axis.

Additionally, six other molecular dimers are present within the molecular shell of 3.80 Å (Table S6, ESI†), though they have minor contributions to stabilising the Rh-4-Br crystal structure, as reflected by their E_int values being lower than −20 kJ mol⁻¹. The primary components of the interatomic interaction vectors for these dimers are mostly oriented along other crystallographic directions (ESI†). Overall, the crystal packing of Rh-4-Br exhibits significant anisotropy in intermolecular interactions at ambient conditions. This anisotropic packing suggests that the crystal may exhibit variable compressibility along different crystallographic axes when subjected to external pressure, which could have important implications for the mechanical and physical properties of Rh-4-Br.

2.2. Crystal-structure description at high-pressure

Rh-4-Br was subjected to HP single-crystal X-ray diffraction (HP-SCXRD) experiments, conducted from 0.00(5) up to 10.45(5) GPa (referred to as exp1) at the ID15B high-pressure beamline of the European Synchrotron Radiation Facility (ESRF), and from 0.00(5) up to 5.71(5) GPa (referred to as exp2) using an in-house diffractometer with Mo-K_α X-ray source (Section S1 and Tables S3, S4, ESI†). Additionally, theoretical HP optimisations were performed using isotropic external pressures ranging from 0 to 11 GPa (referred to as theor) (Section S2 and Table S5, ESI†). For all three data sets the unit-cell volume evolution with pressure is monotonic and does not show any particular discontinuities. Thus, it allowed to obtain a smooth fit of the 3rd-order Birch–Murnaghan equation of state (EOS)¹⁹ using the EOSFIT7-GUI software²⁰ within the whole pressure range for all considered data sets (Fig. 2(a)). Also, this monotonic evolution of the volume rules out the possibility of any phase transitions in Rh-4-Br under HP. The exp1 set revealed ∼29% overall reduction in the unit-cell volume. The fitting parameters, B₀ = 8(1) GPa (bulk modulus) and (1st pressure derivative of B₀), align well with the values previously reported for rather soft molecular crystals.²¹ Meanwhile, exp2, which is limited to a maximum pressure of 5.71(5) GPa, showed a reduction of ∼22% in the unit-cell volume, which is comparable to that in exp1 at a similar pressure range. The EOS fitting parameters, B₀ = 7(1) GPa and , are in good agreement with exp1. This suggests a coherent response of Rh-4-Br to pressure regardless of the different pressure-transmitting medium used. To further validate these experimental findings, EOS of the theor dataset was also analysed. It showed a reduction of ∼28% in unit cell volume up to 11 GPa, with the fitting parameters B₀ = 7(1) GPa and 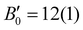. This demonstrates a good agreement with the experimental results. All the three datasets exhibited similar evolution behaviour in the unit-cell volume and EOS parameters up to ∼5.7 GPa (pressure limit of exp2). Minor discrepancies between the experimental and theoretical EOS could be attributed to temperature effects not accounted for in theoretical calculations.

Fig. 2 (a) Evolution of the unit-cell volume fitted as a function of pressure with 3rd-order Birch–Murnaghan equation of state (EOS) for exp1, exp2 and theor data sets (small circles – data points, line – EOS fitted curve). V₀ – initial volume, B₀ – bulk modulus and – 1st pressure derivative of B₀. (b) Relative variation of unit-cell dimensions as a function of pressure. Lines connecting the data points are included as a visual guide, error bars are smaller than the symbols used.

The relative changes in the unit-cell parameters as a function of pressure revealed distinct compressibilities along different crystallographic axes, suggesting that anisotropy in intermolecular interactions induces anisotropic strain under pressure (Fig. 2(b)). All three unit-cell dimensions decreased with increasing pressure, with the c parameter exhibiting the highest compressibility, followed by b and then a. Relative compressibility values (ΔX/X, where ΔX = X(P_max) − X_0 GPa, X_0 GPa – parameter for 0 GPa and X = a, b or c) were calculated for each unit-cell parameter. As expected, along the Z direction, closest to the averaged direction of metallophilic interactions, showed the highest values of 19% for exp1, 18% for exp2 and 15% for the theor data sets. This was followed by the Y direction, with compressibility values of 8% for exp1, 9% for exp2, and 5% for theor, thus indicating more pronounced strain along the Z direction compared to Y. The X direction exhibited the least compressibility, with values of 6% for both exp1 and exp2, and 5% for theor, highlighting greater rigidity in this direction. Notably, exp2 displayed minor fluctuations in the unit-cell dimensions, particularly at 2.06(5) GPa, but these variations balanced out and resulted in a smooth overall evolution of the unit-cell volume. A comparison of exp1 and theor data with exp2 revealed higher compressibility during the initial phase of pressure increase (up to ∼6 GPa), followed by a slower compression rate. Despite some differences, the experimental and theoretical datasets showed good agreement in compressibility trends. The relative change in the monoclinic angle (β/β₀) also decreased with increased pressure, though the rate of decrease was very gradual (Fig. S7, ESI†).

To gain deeper insights into the HP behaviour for Rh-4-Br, the principal axes of compression and the associated compressibility values were determined using the PASCAL (principal axis strain calculator) web tool (Table 1).²² The first principal axis of compression (X₁) predominantly aligns with the crystallographic Z direction, exhibiting compressibility values (K₁) of 12.4(1) TPa⁻¹ and 10.6(1) TPa⁻¹ for the exp1 and theor datasets, respectively. The 2nd (X₂) and 3rd (X₃) axes are approximately oriented along the [010] and [100] crystallographic directions, with compressibility values less than half of K₁. In contrast, exp2 shows slightly higher K_i (i = 1, 2, 3) values, likely due to differing pressure limits and noticeable non-monotonic fluctuations in the unit-cell parameters, reflecting relatively lower data quality. The corresponding compressibility indicatrix plots display similar shapes across all datasets, with exclusively positive compressibility values in all directions (Fig. S8, ESI†). Additionally, multi-temperature SCXRD experiments were conducted on Rh-4-Br over a 100–300 K temperature range (Section S1 and Table S2, ESI†). The expansivity indicatrix plot, along with the evolution of unit-cell parameters, reveals only minor thermal changes in the crystal structure (Table S7, ESI†), in contrast to the significant variations observed under HP.

Table 1 Principal axes of compression (X_i) and their corresponding compressibility values (K_i), along with the estimated standard deviations, are reported for three data sets: exp1 (1st row), exp2 (2nd row), theor (3rd row)

Principal axis no., i	Compressibility, Ki/TPa^−1	Components of Xi along the crystallographic axes/TPa^−1
		X	Y	Z
1	12.4(1)	−0.0309	0.0	0.9995
	22(1)	0.0189	0.0	0.9998
	10.6(1)	−0.1384	0.0	0.9904
2	5.2(1)	0.0	1.0	0.0
	8(2)	0.0	1.0	0.0
	4.5(2)	0.0	1.0	0.0
3	3.1(1)	0.9719	0.0	0.2354
	6(2)	0.9782	0.0	0.2078
	3.11(4)	0.9565	0.0	0.2916

---

The molecular geometry of Rh-4-Br also underwent significant HP-induced modifications. Specifically, the angle φ between the plane of the 4-bromophenyl ring in the SPA ligand and the plane of the rest of the molecule decreases (∼16°) as pressure increases (Fig. S9, ESI†). This observation suggests a tendency for the molecule to adopt a more planar conformation at higher pressures (ESI†).

2.3. Variation of intermolecular interactions with pressure

Intermolecular interactions are highly sensitive to external pressure, often leading to significant modifications, or even structural rearrangements that affect materials’ properties under extreme conditions.²³ Thus, the evolution of Rh⋯Rh metallophilic and C–H⋯O HB interactions within dimer A has been systematically analysed as a function of pressure. The interatomic distance between Rh atoms clearly decreases with increasing pressure (Fig. 3(a)). In exp1, the Rh⋯Rh distance shortens from 3.4717(16) Å at 0.00(5) GPa to 2.8718(17) Å at 10.45(5) GPa, indicating progressively stronger metallophilic interactions under HP by ∼17% contraction of the interaction. Notably, at ∼9 GPa the interatomic distance approaches the sum of the covalent radii of Rh atoms (2.90 Å), suggesting the potential formation of a partially covalent bond. In theor, a similar trend is observed, with the Rh⋯Rh distance decreasing from 3.385 Å at 0 GPa to 2.770 Å at 11 GPa (∼18% contraction). However, in this dataset, the interatomic distance falls below the sum of the covalent radii as early as 6 GPa. This discrepancy could be attributed to the slight underestimation of the theoretically calculated Rh⋯Rh distances compared to the experimental values from exp1, particularly at pressures above 5 GPa. It should be noted here that theoretical approaches, especially when modelled molecular systems contain heavy atoms and additionally external factors such as pressure, are concerned, still have significant limitations. The shortcomings of computational models used may lead to some artefacts in the optimised geometries (especially near borderlines of various approximations, or when multiple local energy minima are closely spaced). Naturally, the experimental structural models are not ideal either, mainly due to the challenges associated with high-pressure data collection. Thus, one needs to be careful to not overinterpret the obtained results. In the case of exp2 the limit of the Rh⋯Rh covalent radii is not reached due to the limited pressure achieved during in-house measurements (Rh⋯Rh distance decreases from 3.4626(16) Å at 0.00(5) GPa to 3.018(12) Å at 5.71(5) GPa; ∼13% contraction).

Fig. 3 Evolution of (a) Rh⋯Rh interatomic distances and (b) the energy difference parameter (ΔE) for dimer A, as a function of pressure.

A similar trend is observed for the C–H⋯O interactions, where the interatomic distance also decreases with elevated pressure, while the HB angle deviates further from linearity (Fig. S10, ESI†). In exp1, the C–H⋯O interaction distance becomes reduced from 2.26 Å at 0.00(5) GPa to 1.97 Å at 10.45(5) GPa (∼13% contraction). Concurrently, the interaction angle decreases from 170 to 142°. Similarly, in theor, the distance shortens from 2.13 Å at 0 GPa to 1.85 Å at 11 GPa (∼13% contraction), with a slightly higher angle of 149° at the highest pressure. This behaviour is also consistently observed in the exp2 dataset. Given the quality of the data and the applied pressure range, subsequent analyses are focused exclusively on the exp1 and theor datasets.

The evolution of intermolecular interaction energies of individual dimers were analysed as a function of pressure using CRYSTALEXPLORER. The extent of stabilisation or destabilisation at each pressure point x was quantified using the energy difference parameter ΔE = E(x) −E(0). The ΔE versus pressure plot (Fig. 3(b) and Fig. S11, ESI†) reveals that dimer A undergoes the most significant change in E_int under pressure, with ΔE reaching −26.8 kJ mol⁻¹ for the exp1, and −17 kJ mol⁻¹ for the theor data sets. Both data sets show an initial decrease in ΔE up to ∼7 GPa, followed by an increase, although the theoretical data exhibit some fluctuations. This trend may suggest that attractive forces dominate at lower pressures, while repulsive forces become increasingly significant at higher pressures due to the close proximity of the molecules. In turn, other dimers exhibit much smaller variations in ΔE (<6 kJ mol⁻¹) compared to dimer A (ESI†).

The effect of temperature on these intermolecular interactions is minimal (Fig. S12, ESI†). The Rh⋯Rh distance decreases slightly from 3.4618(4) Å at 300 K to 3.3676(2) Å at 100 K (∼3% contraction). Similarly, the C–H⋯O distance decreases marginally, while the HB angle shows negligible non-monotonic deviations from its initial value.

Under increasing pressure, other non-covalent interactions within the crystal packing also significantly shorten, and new interactions emerge as molecules are drawn closer in space, which is well illustrated as more intense and numerous red spots are observed under elevated pressure on the respective Hirshfeld surfaces²⁴ (Fig. S13, ESI†). Correspondingly, the Hirshfeld fingerprint plots show notable shape changes, shifting towards the lower d_e–d_i region at higher pressures due to the compression of contacts.

2.4. Variation of charge density properties at BCPs with pressure

To explore the electronic characteristics of individual interactions and their modifications under HP, the Rh⋯Rh metallophilic and C–H⋯O HB interactions within dimer A were analysed using the Bader's quantum theory of atoms in molecules (QTAIM) methodology based on the theoretical wavefunction and electron density distribution generated at the DFT(PBE0)/LANL2DZ level of theory (DFT – density functional theory; ESI†). The analyses focused on key local electronic properties, such as the electron density (ϱ) and its Laplacian (∇²ϱ) at the BCPs, as well as energetic descriptors, like the ratio of the local potential energy density to the local kinetic energy density (|V|/G) at BCPs of these interactions. Furthermore, the delocalization index (δ) was employed to characterise these interactions, providing a quantitative measure of the number of electron pairs shared between two atoms.²⁵ The δ offers critical insights into the degree of covalent bonding in an interaction. Changes in ϱ, ∇²ϱ, |V|/G and δ for the Rh⋯Rh metallophilic interaction under pressure are presented in Fig. 4 and Tables S8, S9 (ESI†). These parameters reveal strengthening of the Rh⋯Rh interaction with increasing pressure, as evidenced by the steady rise in ϱ at BCP. In the case of experimental geometries, ϱ increases from 0.080 e Å⁻³ at 0.00(5) GPa to 0.235 e Å⁻³ at 10.45(5) GPa (Δϱ of 0.155 e Å⁻³). Theoretical data in general exhibit a similar trend, with ϱ increasing from 0.091 e Å⁻³ at 0 GPa to 0.281 e Å⁻³ at 11 GPa (Δϱ = 0.189 e Å⁻³), demonstrating good agreement with experimental results. It should be noted, however, that again the observed changes in the electron density distribution along with the pressure increase are less smooth for the theoretical geometries than those derived for the experimental structures. The more sudden inflection/change in slope in the metal⋯metal distances around 1.5 GPa and 4.5 GPa noted earlier (Fig. 3(a)) translate into sharper changes in electronic properties at these pressure points, as can be seen in Fig. 4. Nevertheless, based on the obtained results and theoretical calculations for dimer A, as well considering different methods’ limitations, no binding conclusions can be drawn here.

Fig. 4 (a) Electron density – ϱ(r_BCP), (b) Laplacian of ϱ − ∇²ϱ(r_BCP), (c) |V(r_BCP)|/G(r_BCP), and (d) delocalisation index (δ) at BCP as a function of pressure for the Rh⋯Rh interaction. In panel (c) the |V|/G = 1 limit is shown as a black dashed line.

As expected, the increase in ϱ is accompanied by a proportional rise in ∇²ϱ at BCP. Experimentally, ∇²ϱ increases by 1.696 e Å⁻⁵, while the theoretical dataset shows a corresponding change of 2.018 e Å⁻⁵. Interestingly, the |V|/G parameter indicates a transition of the Rh⋯Rh interaction from non-covalent to partially covalent character. Experimentally, |V|/G begins at 0.918 at 0.00(5) GPa, surpasses the threshold of 1.0 (where potential energy density dominates over kinetic energy density) at 2.03(5) GPa,²⁶ and reaches 1.176 at 10.45(5) GPa (Δ(|V|/G) = 0.258). This indicates the emergence of partial covalency beyond 2.03(5) GPa, with increasing covalent character as pressure rises further. The theoretical dataset mirrors a similar trend, with |V|/G increasing from 0.929 at 0 GPa to 1.228 at 11 GPa (Δ(|V|/G) = 0.299), and the transition to partial covalency occurring at ∼3 GPa. The δ parameter also provides evidence for increasing covalent degree in the Rh⋯Rh interaction. Experimentally, δ rises from 0.116 at 0.00(5) GPa to 0.263 at 10.45(5) GPa (Δδ = 0.147), while theoretically, it increases from 0.126 at 0 GPa to 0.290 at 11 GPa (Δδ = 0.164). Overall, topological analysis not only underscores the progressive strengthening of the Rh⋯Rh metallophilic interaction under HP but also highlights its transition from non-covalent to partially covalent character beyond 2–3 GPa. Structural studies revealed that the Rh⋯Rh distance falls below the sum of the covalent radii above 8.72(5) GPa experimentally and 6 GPa theoretically. This finding suggests that relying solely on structural distances is insufficient for accurately characterising the covalent nature of intermolecular interactions.

The topological analysis was also extended to the C–H⋯O interaction (Fig. S14 and Tables S8, S9, ESI†). Based on the charge-density parameters, at the lowest pressure, this interaction is stronger than the Rh⋯Rh interaction, with ϱ values of 0.092 e Å⁻³ (experimental geometry) and 0.126 e Å⁻³ (theoretical geometry). By 10.45(5) GPa, experimental ϱ increases to 0.189 e Å⁻³ (Δϱ = 0.097 e Å⁻³), while the theoretical ϱ reaches 0.244 e Å⁻³ (Δϱ = 0.118 e Å⁻³) at 11 GPa. However, these values remain lower than those for Rh⋯Rh at the corresponding pressures. This reversal in significance occurs above 4.55(5) GPa experimentally and above 6 GPa theoretically. Similarly, ∇²ϱ for C–H⋯O increases with pressure, with Δ(∇²ϱ) values of 1.405 e Å⁻⁵ (experimental) and 1.582 e Å⁻⁵ (theoretical). Despite higher initial ϱ values, |V|/G for C–H⋯O remains lower than for Rh⋯Rh interaction due to greater G component, which depletes electron density. Experimentally, |V|/G for C–H⋯O increases to 0.957 (Δ(|V|/G) = 0.132), while the theoretical values reach 1.012 (Δ(|V|/G) = 0.130), indicating comparatively weaker covalency at higher pressures. Similarly, δ for C–H⋯O increases experimentally from 0.048 to 0.073 (Δδ = 0.025) and theoretically from 0.061 to 0.091 (Δδ = 0.030) over the studied pressure range. Notably, δ for C–H⋯O at the highest pressure remains lower or comparable to δ for Rh⋯Rh at the lowest pressure, highlighting the lower covalency of C–H⋯O under HP. Moreover, all the changes (Δy) in the analysed parameters (y = ϱ, ∇²ϱ, |V|/G or δ) for the C–H⋯O interaction, are considerably smaller than those for the Rh⋯Rh contact. This indicates that the Rh⋯Rh metallophilic interaction is far more sensitive to pressure than the C–H⋯O HB, with the observed changes in the crystal packing properties under HP being predominantly driven by the metallophilic interactions.

The non-covalent interactions within dimer A were also visualised using 3-dimensional non-covalent interaction (NCI) surfaces and 2-dimensional reduced density gradient (RDG) scatter plots²⁷ (Fig. S15 and S16, ESI†). The transition of both Rh⋯Rh and C–H⋯O interactions from moderate to stronger interactions under HP were effectively captured with this colour code representation (see ESI† for more details).

2.5. Electronic transitions and piezochromism

Our previous study demonstrated that the luminescence of Rh-4-Br primarily arises from the lowest-energy singlet–singlet (S₀ → S₁) electronic transition.^16g This transition is a combination of π → π* excitation, metal-to-ligand charge transfer and metal-to-metal bond charge transfer. Time-dependent DFT (TDDFT) calculations performed at the DFT(PBE0)/LANL2DZ level of theory reveal that this electronic transition occurs at ∼400 nm and involves multiple molecular orbitals (Table S10, ESI†), the detailed composition of which depends to some extent on the applied level of theory.²⁸ This is in close agreement with the absorption peak observed experimentally from the powdered Rh-4-Br sample (Fig. S17, ESI†). It should also be stressed that the calculations were performed for dimer A, which served only as a simplified model system. Nevertheless, it is worth noting that the involved occupied MOs exhibit anti-bonding character between the Rh atoms, whereas the respective unoccupied MOs display bonding character (Fig. S18, ESI†). A similar but more intense S₀ → S₃ electronic transition is also seen at ∼370 nm, involving the same kinds of MOs, while the lowest singlet–triplet (S₀ → T₁) electronic transition seems to be significantly red-shifted. Since MOs involved in these electronic transitions have substantial contributions from the Rh atoms, it is anticipated that the strengthening of the metallophilic interaction under HP will alter the positioning of these MOs. Consequently, this modification is likely to narrow down the HOMO–LUMO gap (HOMO & LUMO – highest occupied & lowest unoccupied MO), affecting the absorption and emission properties of Rh-4-Br. To validate this hypothesis, TDDFT calculations were performed on dimer A extracted from the crystal structures determined at different pressures (ESI†). For the experimental dataset, the calculated HOMO–LUMO gap decreases monotonically from 3.94 eV at 0.00(5) GPa to 3.43 eV at 10.45(5) GPa, indicating a gap narrowing of 0.51 eV (Fig. S19, ESI†). This reduction is primarily driven by the energetic destabilisation of the HOMO under pressure, which outweighs the stabilisation of the LUMO. Note that such results were also observed, for example, for gold(I) complexes subjected to high-pressure studies.²⁹ As anticipated, this narrowing of the energy gap leads to changes in the theoretically calculated UV-Vis absorption spectra, showing a red-shift toward longer wavelengths across all three sets of peaks observed (Fig. S20, ESI†). Although minor fluctuations are observed in the relative positions and intensities of peaks at successive pressure points, an overall red shift is clearly visible. Additionally, MOs undergo significant changes in shape and relative contributions to individual electronic transitions, showing more plausible overlap between Rh atoms at higher pressures (Fig. S21 and Table S11, ESI†). Similarly, a comparable narrowing of the HOMO–LUMO gap by 0.50 eV (from 3.84 eV at 0 GPa to 3.34 eV at 11 GPa) is observed in the theoretical dataset (Fig. S19, ESI†). The reduction in the HOMO–LUMO gap and the red-shift of absorption peaks under HP results in the piezochromic effect observed for Rh-4-Br single crystals. The crystal changes its colour from light yellow to orange to red as pressure increases from 0.00(5) GPa to 6.42(5) GPa (Fig. 5), which is reversible under decompression.

Fig. 5 Optical microscopy images of the Rh-4-Br single crystal illustrate its piezochromic behaviour. The corresponding pressure values (with e.s.d.s. of 0.05 GPa) are indicated in each image. Images labelled with the suffixes “_c” and “_d” correspond to those captured during the compression and decompression processes, respectively. The small ruby sphere used for in situ pressure estimation is visible in the top left corner of the pressure chamber. Note that, fractures were observed in the crystal at higher pressures which is mainly due to the size of the crystal and to some extent could be caused by PTM behaviour at highest pressures (Section S1.3.4, ESI†).

The HP luminescence spectra of Rh-4-Br align well with the changes observed in its optical colour and absorption spectra, with the emission displaying a red-shift as pressure increases. The spectrum contained a few peaks, which was difficult to resolve, so the position of maximum of the strongest emission band, (λ_em)_max was analysed. Under ambient conditions, (λ_em)_max was reported at 566 nm (2.19 eV).^16g Once a crystal was placed in the Merrill-Bassett DAC (MB-DAC) and a small pressure of 0.63(5) GPa was applied, a red-shift of (λ_em)_max to 580 nm (2.14 eV) was already observed (Fig. 6(a), Fig. S22 and Table S12, ESI†), along with a ∼4-fold decrease in emission intensity compared to measurements outside the DAC. A non-homogeneous emission profile was measured across the crystal surface. Despite these challenges, luminescence spectra were consistently recorded at high-intensity region on the crystal surface. As pressure increased, the peak shifted down to 1.94(2) eV ((λ_em)_max = 640 nm) at 6.93(5) GPa (a bathochromic shift of ∼75 nm; with respect to the value reported earlier at ambient conditions). Linear approximation of the changes in the range up to 7 GPa gives the pressure coefficient (slope of the fitted straight line)

. The emission spectra showed reversibility upon decompression, with all spectrum features returning to their initial value. Unlike some previous reports, emission intensity exhibited a non-monotonic behaviour, likely due to weak luminescence within MB-DAC at higher pressures, non-homogeneous crystal response and potential pressure-induced defects. At 0.63(5) GPa, a shoulder peak observed at ∼602 nm (∼2.05 eV) alongside the main peak at 580 nm, becomes more prominent and red-shifted to ∼680 nm (∼1.82 eV) at 6.93(5) GPa. Above 5 GPa its emission intensity weakened significantly. This could suggest that a potential emissive excited state becomes accessible at lower pressures and then subsequently quenches at higher pressures (and is also reversible on decompression). Linking with the changes observed in the topological parameters, this behaviour may be attributed to a pressure-stabilised more metallophilic in the native excited state, associated with a change of the Rh⋯Rh interaction parameters at ∼2 GPa. The quenching observed at ∼4.2 GPa could result from enhanced intermolecular metal⋯metal orbital overlap, which activates non-radiative decay pathways.

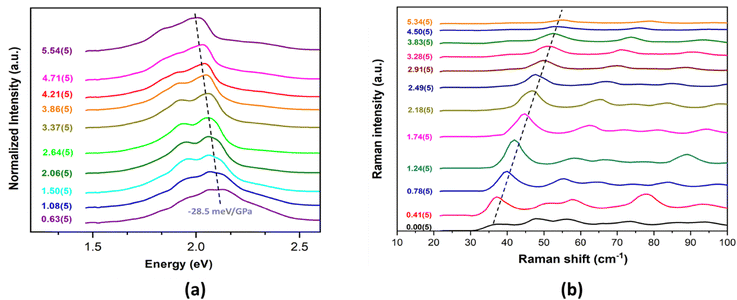Fig. 6 (a) HP luminescence spectra of Rh-4-Br at selected pressure points (see ESI† for more information, Fig. S22 and Table S12), and (b) HP Raman spectra recorded during compression process, black dashed lines indicating the progressive shift in peak maxima.

Additionally, Raman spectroscopy is a well-established experimental probe for investigating the HP evolution of inter- and intramolecular interactions.³⁰ In Rh-4-Br, reversible modifications in Rh⋯Rh metallophilic interactions during a compression–decompression cycle were traced using HP Raman spectroscopy. At ambient conditions, the Rh⋯Rh stretching mode (ν_Rh⋯Rh) observed at ∼36 cm⁻¹, is a characteristic low-frequency band for metallophilic interactions (Fig. S23a, ESI†). Structural and electronic analyses previously confirmed an enhanced Rh⋯Rh interaction at HP, corroborated with the HP Raman spectra showing a linear blue shift of ν_Rh⋯Rh from ∼37 cm⁻¹ at 0.00(5) GPa to ∼55 cm⁻¹ at 5.34(5) GPa, with an overall wavenumber change of Δν ∼ 19 cm⁻¹ with respect to ambient conditions (Fig. 6(b)). The Raman intensity of the ν_Rh⋯Rh peak exhibits a non-monotonic trend, initially increases up to 1.74(5) GPa and decreases later on with potential attenuation at the highest pressures. This behaviour may reflect non-monotonic polarizability changes of the Rh⋯Rh contact under pressure. However, a definitive conclusion is challenging due to various other factors that could influence Raman intensity and peak broadening, including anharmonic effects, phonon–phonon interactions, optical path distortions, and sample deformation at extreme conditions. Importantly, the blue shift and intensity changes are fully reversible upon decompression (Fig. S23b, ESI†).

3. Conclusions

This study explores the HP behaviour of a nearly square-planar transition-metal salicylidene complex Rh-4-Br in the crystalline state, where the crystal packing is predominantly driven by the Rh⋯Rh metallophilic and C–H⋯O HB interactions. These interactions exhibit pronounced structural, electronic, and energetic sensitivities under HP conditions. Interestingly, HP-SCXRD studies reveal that the Rh⋯Rh distance falls below the sum of the covalent radii at ∼9 GPa, suggesting the potential formation of a partial covalent bond. This observation is supported by electronic analysis performed within the QTAIM framework, where the evolution in the |V|/G parameter at BCP indicated partial covalency in Rh⋯Rh at ∼2.03(5) GPa. These findings underscore the importance of integrating structural and electronic analyses for an accurate description of intermolecular interactions. In addition, the Rh⋯Rh metallophilic interaction demonstrates greater sensitivity to pressure compared to C–H⋯O HBs, as evidenced by relative evolution in their local electronic and energetic parameters. Single-crystals of Rh-4-Br also exhibit reversible piezochromism, with the colour transitioning from light yellow to orange to red, accompanied with a bathochromic shift of ∼75 nm in (λ_em)_max between ambient and 6.93(5) GPa. These reversible optical changes are attributed to pressure-induced modifications in the metallophilic interactions, which alter the emissive states and narrow down the HOMO–LUMO gap. Reversible modifications of the Rh⋯Rh interaction were further traced with the aid of HP Raman spectroscopy which showed that the ν_Rh⋯Rh stretching mode exhibits a blue shift of ∼19 cm⁻¹ between ambient pressure and 5.34(5) GPa. The Raman intensity initially increases and then decreases, likely reflecting changes in the polarizability of the Rh⋯Rh interaction under pressure, however, a concrete conclusion is challenging. These experimental results are corroborated by theoretical HP periodic calculations, which align closely with the experimental findings and effectively capture the structural, electronic, energetic, and optical changes induced by pressure. Such theoretical approaches could provide deeper insights into the physical-electronic properties and are invaluable when experimental data are limited.

This study highlights the potential of metallophilic interactions as structural synthons for the development of piezochromic materials. Transition metal complexes with (nearly) square-planar geometries around d⁸ or d¹⁰ metallic centres are particularly promising, as they facilitate strong metallophilic interactions. These interactions enable precise tuning of structural, energetic, electronic, and optical properties under external pressure, establishing robust structure–property correlations. The reversible behaviour of these properties under compression–decompression cycles makes such materials promising candidates for pressure switches, sensors and optoelectronic applications. Further studies focusing on the HP behaviour of square-planar Rh^I complexes forming metal⋯metal chains rather than molecular dimers are underway, which may further expand the understanding and utility of these systems.

Author contributions

Conceptualization – V. V.-S., A. R., A. B., K. N. J., data curation – V. V.-S., P. B., K. P., D. P., K. P. K., P. Ł. R. K., formal analysis – V. V.-S., P. B., K. P., K. P. K., P. Ł., R. K., K. N. J., funding acquisition – A. B., K. N. J., investigation – V. V.-S., L. B. (synthesis), K. P. K. (spectroscopy), P. Ł. (spectroscopy), R. K. (crystallography, spectroscopy), K. N. J., methodology – V. V.-S., L. B., D. P., K. P. K., A. R., A. B., K. N. J., project administration – A. B., K. N. J., resources – K. P. K., R. K., A. B., K. N. J., supervision – R. K., D. V. K., A. B., K. N. J., validation – V. V.-S., D. P., K. P. K., P. Ł., R. K., A. B., K. N. J., visualization – V. V.-S., writing (original draft) – V. V.-S., writing (review & editing) – V. V.-S., D. P., K. P. K., R. K., A. B., K. N. J.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the ESI.† In accordance with the open access (OA) policy, the raw and processed data are deposited in the UW Research Data Repository under the following DOI: 10.58132/JXY8GL.

Acknowledgements

V. V.-S., P. B., K. P. and K. N. J. acknowledge the National Science Centre (Poland) (SONATA BIS programme, grant no. 2020/38/E/ST4/00400) for financial support. Financial assistance from the South African National Research Foundation (SA-NSF, South Africa) (grants no. 116180, 137759, 107802, 111698) and Sasol Ltd is gratefully acknowledged. The grant holders acknowledge that opinions, findings and conclusions or recommendations expressed in any publication generated by the SA-NRF-supported research are those of the authors, and that the SA-NRF accepts no liability whatsoever in this regard. We acknowledge the European Synchrotron Radiation Facility (ESRF; France) for provision of synchrotron radiation facilities under proposal no. CH-6469 (ID15b beamtime). Access to ESRF was also made available by the Ministry of Science and Higher Education (Poland) (grant no. 2021/WK/11). We gratefully acknowledge high-performance computing infrastructure of Wrocław Centre for Networking and Supercomputing (WCSS; Poland) and PLGrid (HPC Center, ACK Cyfronet AGH; Poland) for providing computer facilities and support within computational grants no. 285 and PLG/2024/016920, respectively. We are grateful to M. Hanfland (Grenoble, France) for his assistance during the high-pressure measurements at ESRF. Finally, we extend our gratitude to M. Vincent and S. Sajeev (Warsaw, Poland) for their assistance with high-pressure Raman measurements.

References

1. (a) J. Slinker, D. Bernards, P. L. Houston, H. D. Abruña, S. Bernhard and G. G. Malliaras, Chem. Commun., 2003, 2392–2399; (b) F. L. Thorp-Greenwood, R. G. Balasingham and M. P. Coogan, J. Organomet. Chem., 2012, 714, 12–21; (c) V. Sathish, A. Ramdass, M. Velayudham, K.-L. Lu, P. Thanasekaran and S. Rajagopal, Dalton Trans., 2017, 46, 16738–16769; (d) C. Wang, F. Yang and Y. Gao, Nanoscale Adv., 2020, 2, 4323–4340; (e) D. Gupta, A. K. Gaur, H. Kumar, S. Singh and S. Venkataramani, ChemPhotoChem, 2023, 7, e202300068.
2. (a) V. Sathish, A. Ramdass, P. Thanasekaran, K.-L. Lu and S. Rajagopal, J. Photochem. Photobiol., C, 2015, 23, 25–44; (b) P. Alam, C. Climent, P. Alemany and I. R. Laskar, J. Photochem. Photobiol., C, 2019, 41, 100317; (c) S.-Y. Yang, Y. Chen, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Chem. Soc. Rev., 2024, 53, 5366–5393.
3. (a) M. J. Katz, K. Sakai and D. B. Leznoff, Chem. Soc. Rev., 2008, 37, 1884; (b) T. Hajiashrafi, R. Zekriazadeh, K. J. Flanagan, F. Kia, A. Bauzá, A. Frontera and M. O. Senge, Acta Crystallogr., Sect. C: Struct. Chem., 2019, 75, 178–188; (c) A. Bauzá, I. Alkorta, J. Elguero, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2020, 59, 17482–17487; (d) X. Zhao, J. Gong, Z. Li, H. H. Y. Sung, I. D. Williams, J. W. Y. Lam, Z. Zhao, B. Z. Tang, W. Wong and L. Xu, Aggregate, 2024, e686; (e) M. Karmakar, R. M. Gomila, A. Frontera and S. Chattopadhyay, Cryst. Growth Des., 2024, 24, 5990–6000.
4. (a) P. Pyykkö, Chem. Rev., 1997, 97, 597–636; (b) S. Sculfort and P. Braunstein, Chem. Soc. Rev., 2011, 40, 2741; (c) S. Raju, H. B. Singh and R. J. Butcher, Dalton Trans., 2020, 49, 9099–9117.
5. (a) P. Pyykkö and Y. Zhao, Angew. Chem., Int. Ed. Engl., 1991, 30, 604–605; (b) E. Hupf, R. Kather, M. Vogt, E. Lork, S. Mebs and J. Beckmann, Inorg. Chem., 2016, 55, 11513–11521; (c) A. S. Novikov, Inorg. Chim. Acta, 2018, 483, 21–25; (d) R. Donamaría, V. Lippolis, J. M. López-de-Luzuriaga, M. Monge, M. Nieddu and M. E. Olmos, Chem. – Eur. J., 2018, 24, 13740–13743; (e) L. De Azevedo Santos, T. Wagner, K. Visscher, J. Nitsch, F. M. Bickelhaupt and C. Fonseca Guerra, Phys. Chem. Chem. Phys., 2024, 26, 20928–20936.
6. (a) L. Magnko, M. Schweizer, G. Rauhut, M. Schütz, H. Stoll and H.-J. Werner, Phys. Chem. Chem. Phys., 2002, 4, 1006–1013; (b) R. Echeverría, J. M. López-de-Luzuriaga, M. Monge and M. E. Olmos, Chem. Sci., 2015, 6, 2022–2026; (c) M. B. Brands, J. Nitsch and C. F. Guerra, Inorg. Chem., 2018, 57, 2603–2608; (d) Q. Zheng, S. Borsley, G. S. Nichol, F. Duarte and S. L. Cockroft, Angew. Chem., Int. Ed., 2019, 131, 12747–12753; (e) Q. Wan, J. Yang, W.-P. To and C.-M. Che, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019265118.
7. (a) F. Scherbaum, A. Grohmann, B. Huber, C. Krüger and H. Schmidbaur, Angew. Chem., Int. Ed. Engl., 1988, 27, 1544–1546; (b) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931; (c) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412; (d) N. Mirzadeh, S. H. Privér, A. J. Blake, H. Schmidbaur and S. K. Bhargava, Chem. Rev., 2020, 120, 7551–7591; (e) T. P. Seifert, V. R. Naina, T. J. Feuerstein, N. D. Knöfel and P. W. Roesky, Nanoscale, 2020, 12, 20065–20088.
8. (a) D. E. Harwell, M. D. Mortimer, C. B. Knobler, F. A. L. Anet and M. F. Hawthorne, J. Am. Chem. Soc., 1996, 118, 2679–2685; (b) R. E. Bachman, M. S. Fioritto, S. K. Fetics and T. M. Cocker, J. Am. Chem. Soc., 2001, 123, 5376–5377; (c) A. Codina, E. J. Fernández, P. G. Jones, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, J. Pérez and M. A. Rodríguez, J. Am. Chem. Soc., 2002, 124, 6781–6786; (d) E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1636.
9. (a) M. Andrejić and R. A. Mata, Phys. Chem. Chem. Phys., 2013, 15, 18115; (b) A. Wuttke, M. Feldt and R. A. Mata, J. Phys. Chem. A, 2018, 122, 6918–6925.
10. (a) E. Laurila, R. Tatikonda, L. Oresmaa, P. Hirva and M. Haukka, CrystEngComm, 2012, 14, 8401; (b) H. Schmidbaur and A. Schier, Angew. Chem., Int. Ed., 2015, 54, 746–784; (c) E. V. Andrusenko, E. V. Kabin, A. S. Novikov, N. A. Bokach, G. L. Starova and V. Yu. Kukushkin, New J. Chem., 2017, 41, 316–325; (d) N. V. S. Harisomayajula, S. Makovetskyi and Y. Tsai, Chem. – Eur. J., 2019, 25, 8936–8954; (e) Y. Makino, M. Yoshida, S. Hayashi, T. Sasaki, S. Takamizawa, A. Kobayashi and M. Kato, Dalton Trans., 2023, 52, 8864–8872.
11. (a) A. Aliprandi, D. Genovese, M. Mauro and L. De Cola, Chem. Lett., 2015, 44, 1152–1169; (b) R. Donamaría, V. Lippolis, J. M. López-de-Luzuriaga, M. Monge, M. Nieddu and M. E. Olmos, Inorg. Chem., 2018, 57, 11099–11112; (c) M. J. Bryant, S. Fuertes, L. E. Hatcher, L. H. Thomas and P. R. Raithby, Faraday Discuss., 2023, 244, 411–433.
12. (a) J. Lima and L. Rodríguez, Inorganics, 2014, 3, 1–18; (b) C. Jobbágy, P. Baranyai, G. Marsi, B. Rácz, L. Li, P. Naumov and A. Deák, J. Mater. Chem. C, 2016, 4, 10253–10264; (c) M. Gil-Moles, M. C. Gimeno, J. M. López-de-Luzuriaga, M. Monge and M. E. Olmos, Dalton Trans., 2019, 48, 5149–5155; (d) S. Moreno, N. Casati, M. Rodríguez-Castillo, M. Monge, M. E. Olmos and J. M. López-de-Luzuriaga, Inorg. Chem., 2023, 62, 10307–10316.
13. (a) Y. Dong, B. Xu, J. Zhang, X. Tan, L. Wang, J. Chen, H. Lv, S. Wen, B. Li, L. Ye, B. Zou and W. Tian, Angew. Chem., Int. Ed., 2012, 51, 10782–10785; (b) C. Feng, K. Wang, Y. Xu, L. Liu, B. Zou and P. Lu, Chem. Commun., 2016, 52, 3836–3839; (c) Z. Fu, K. Wang and B. Zou, Chin. Chem. Lett., 2019, 30, 1883–1894; (d) D. Tchoń, D. Bowskill, I. Sugden, P. Piotrowski and A. Makal, J. Mater. Chem. C, 2021, 9, 2491–2503.
14. (a) K. Nagura, S. Saito, H. Yusa, H. Yamawaki, H. Fujihisa, H. Sato, Y. Shimoikeda and S. Yamaguchi, J. Am. Chem. Soc., 2013, 135, 10322–10325; (b) S. Yagai, T. Seki, H. Aonuma, K. Kawaguchi, T. Karatsu, T. Okura, A. Sakon, H. Uekusa and H. Ito, Chem. Mater., 2016, 28, 234–241; (c) T. Seki and H. Ito, Chem. – Eur. J., 2016, 22, 4322–4329; (d) S. Li, M. Wu, Y. Kang, H.-W. Zheng, X.-J. Zheng, D.-C. Fang and L.-P. Jin, Inorg. Chem., 2019, 58, 4626–4633; (e) Y. Hirai, ACS Appl. Opt. Mater., 2024, 2, 1025–1045.
15. (a) A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, ACS Cent. Sci., 2016, 2, 201–209; (b) A. Katrusiak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 918–926; (c) J. Guan, C. Zhang, D. Gao, X. Tang, X. Dong, X. Lin, Y. Wang, X. Wang, L. Wang, H. H. Lee, J. Xu, H. Zheng, K. Li and H. Mao, Mater. Chem. Front., 2019, 3, 1510–1517; (d) H. Cui, T. Tsumuraya, H. H.-M. Yeung, C. S. Coates, M. R. Warren and R. Kato, Molecules, 2019, 24, 1843.
16. (a) E. Frasson, C. Panattoni and R. Zannetti, Acta Crystallogr., 1959, 12, 1027–1031; (b) T. W. Thomas and A. E. Underhill, Chem. Soc. Rev., 1972, 1, 99–120; (c) M. Mégnamisi-Bélombé, J. Solid State Chem., 1979, 27, 389–396; (d) V. W.-W. Yam and K. M.-C. Wong, Chem. Commun., 2011, 47, 11579; (e) V. W.-W. Yam, V. K.-M. Au and S. Y.-L. Leung, Chem. Rev., 2015, 115, 7589–7728; (f) V. Sivchik, A. Kochetov, T. Eskelinen, K. S. Kisel, A. I. Solomatina, E. V. Grachova, S. P. Tunik, P. Hirva and I. O. Koshevoy, Chem. – Eur. J., 2021, 27, 1787–1794; (g) P. Łaski, L. Bosman, J. Drapała, R. Kamiński, D. Szarejko, P. Borowski, A. Roodt, R. Henning, A. Brink and K. N. Jarzembska, J. Phys. Chem. Lett., 2024, 15, 10301–10306.
17. (a) F. Baril-Robert, M. A. Radtke and C. Reber, J. Phys. Chem. C, 2012, 116, 2192–2197; (b) D. Paliwoda, P. Wawrzyniak and A. Katrusiak, J. Phys. Chem. Lett., 2014, 5, 2182–2188; (c) K. N. Jarzembska, R. Kamiński, K. F. Dziubek, M. Citroni, D. Paliwoda, K. Durka, S. Fanetti and R. Bini, Inorg. Chem., 2018, 57, 8509–8520; (d) S. Racioppi, M. Andrzejewski, V. Colombo, A. Sironi and P. Macchi, Inorg. Chem., 2020, 59, 2223–2227; (e) Z. Lu, C. M. Archambault, S. Li, U. Syed, S. Wang, A. Kumar, G. Shen, Z. Liu, M. A. Omary and H. Yan, J. Phys. Chem. Lett., 2023, 14, 508–515.
18. (a) P. P. Mokolokolo, A. Brink, A. Roodt and M. Schutte-Smith, J. Coord. Chem., 2020, 73, 2740–2762; (b) F. J. F. Jacobs, G. J. S. Venter, E. Fourie, R. E. Kroon and A. Brink, RSC Adv., 2021, 11, 24443–24455; (c) H. Van Dyk, F. J. F. Jacobs, R. E. Kroon, T. J. Makhafola and A. Brink, J. Mol. Struct., 2023, 1276, 134737; (d) E. Mfotie Njoya, H. Van Dyk, J. Nambooze, C. I. Chukwuma, A. Brink and T. J. Makhafola, Eur. J. Pharmacol., 2024, 985, 177129.
19. R. J. Angel, Rev. Mineral. Geochem., 2000, 39, 85–104.
20. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, J. Appl. Crystallogr., 2016, 49, 1377–1382.
21. (a) C. Slebodnick, J. Zhao, R. Angel, B. E. Hanson, Y. Song, Z. Liu and R. J. Hemley, Inorg. Chem., 2004, 43, 5245–5252; (b) P. J. Byrne, P. J. Richardson, J. Chang, A. F. Kusmartseva, D. R. Allan, A. C. Jones, K. V. Kamenev, P. A. Tasker and S. Parsons, Chem. – Eur. J., 2012, 18, 7738–7748; (c) S. R. Madsen, J. Overgaard, D. Stalke and B. B. Iversen, Dalton Trans., 2015, 44, 9038–9043.
22. (a) M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329; (b) M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, J. Open Source Softw., 2023, 8, 5556.
23. (a) E. V. Boldyreva, Cryst. Eng., 2003, 6, 235–254; (b) E. V. Boldyreva, J. Mol. Struct., 2003, 647, 159–179; (c) E. C. Spencer, R. J. Angel, N. L. Ross, B. E. Hanson and J. A. K. Howard, J. Am. Chem. Soc., 2009, 131, 4022–4026; (d) J. Bąkowicz and I. Turowska-Tyrk, CrystEngComm, 2016, 18, 8898–8905; (e) I. E. Collings and M. Hanfland, Molecules, 2019, 24, 1759; (f) V. Vijayakumar-Syamala, E. Aubert, M. Deutsch, E. Wenger, A. Dhaka, M. Fourmigué, M. Nespolo and E. Espinosa, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2022, 78, 436–449.
24. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
25. D. Hugas, L. Guillaumes, M. Duran and S. Simon, Comput. Theor. Chem., 2012, 998, 113–119.
26. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
27. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
28. (a) L. Petit, P. Maldivi and C. Adamo, J. Chem. Theory Comput., 2005, 1, 953–962; (b) A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
29. (a) F. Baril-Robert, M. A. Radtke and C. Reber, J. Phys. Chem. C, 2012, 116, 2192–2197; (b) R. J. Roberts, N. Bélanger-Desmarais, C. Reber and D. B. Leznoff, Chem. Commun., 2014, 50, 3148–3150; (c) A. J. Blake, R. Donamaría, V. Lippolis, J. M. López-de-Luzuriaga, M. Monge, M. E. Olmos, A. Seal and J. A. Weinstein, Inorg. Chem., 2019, 58, 4954–4961.
30. (a) S. Mosca, A. Milani, M. Peña-Álvarez, S. Yamaguchi, V. Hernández, M. C. Ruiz Delgado and C. Castiglioni, J. Phys. Chem. C, 2018, 122, 17537–17543; (b) A. K. Mishra, C. Murli, K. K. Pandey, T. Sakuntala, H. K. Poswal and A. K. Verma, J. Phys. Chem. B, 2020, 124, 373–379.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2427930–2427957, 2428057–2428064 and 2428186. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc00925a

---