 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Giant thermally induced band-gap renormalization in anharmonic silver chalcohalide antiperovskites†
Pol
Benítez
 *ab,
Siyu
Chen
*ab,
Siyu
Chen
 cd,
Ruoshi
Jiang
cd,
Ruoshi
Jiang
 c,
Cibrán
López
c,
Cibrán
López
 ab,
Josep-Lluís
Tamarit
ab,
Josep-Lluís
Tamarit
 ab,
Jorge
Íñiguez-González
ab,
Jorge
Íñiguez-González
 ef,
Edgardo
Saucedo
ef,
Edgardo
Saucedo
 bg,
Bartomeu
Monserrat
bg,
Bartomeu
Monserrat
 cd and
Claudio
Cazorla
cd and
Claudio
Cazorla
 *ab
*ab
aGroup of Characterization of Materials, Departament de Física, Universitat Politècnica de Catalunya, Campus Diagonal Besòs, Av. Eduard Maristany 10–14, 08019 Barcelona, Spain. E-mail: pol.benitez@upc.edu; claudio.cazorla@upc.edu
bResearch Center in Multiscale Science and Engineering, Universitat Politècnica de Catalunya, Campus Diagonal-Besòs, Av. Eduard Maristany 10–14, 08019 Barcelona, Spain
cDepartment of Materials Science and Metallurgy, University of Cambridge, Cambridge, CB30FS, UK
dCavendish Laboratory, University of Cambridge, Cambridge, CB30HE, UK
eMaterials Research and Technology Department, Luxembourg Institute of Science and Technology (LIST), Avenue des Hauts-Fourneaux 5, L-4362 Esch/Alzette, Luxembourg
fDepartment of Physics and Materials Science, University of Luxembourg, 41 Rue du Brill, L-4422 Belvaux, Luxembourg
gMicro and Nanotechnologies Group, Emerging Thin Film Photovoltaics Lab, Departament dEnginyeria Electrònica, Universitat Politècnica de Catalunya, Campus Diagonal Besòs, Av. Eduard Maristany 10–14, 08019 Barcelona, Spain
First published on 14th April 2025
Abstract
Silver chalcohalide antiperovskites (CAP), Ag3XY (X = S, Se; Y = Br, I), are a family of highly anharmonic inorganic compounds with great potential for energy applications. However, a substantial and unresolved discrepancy exists between the optoelectronic properties predicted by theoretical first-principles methods and those measured experimentally at room temperature, hindering the fundamental understanding and rational engineering of CAP. In this work, we employ density functional theory, tight-binding calculations, and anharmonic Fröhlich theory to investigate the optoelectronic properties of CAP at finite temperatures. Near room temperature, we observe a giant band-gap (Eg) reduction of approximately 20–60% relative to the value calculated at T = 0 K, bringing the estimated Eg into excellent agreement with experimental measurements. This relative T-induced band-gap renormalization is roughly twice the largest value previously reported in the literature for similar temperature ranges. Low-energy optical polar phonon modes, which break inversion symmetry and enhance the overlap between silver and chalcogen s electronic orbitals in the conduction band, are identified as the primary drivers of this significant Eg reduction. Furthermore, when temperature effects are considered, the optical absorption coefficient of CAP increases by nearly an order of magnitude in the visible light spectrum. These findings not only bridge a critical gap between theory and experiment but also pave the way for future technologies where temperature, electric fields, and light dynamically modulate optoelectronic properties, establishing CAP as a versatile platform for energy and photonic applications.
Introduction
Electron–phonon coupling (EPC), arising from the interactions between electrons and lattice vibrations, is ubiquitous in materials and is responsible for a wide range of condensed matter physical effects.1–4 For example, EPC plays a crucial role in the temperature (T) dependence of electrical resistivity in metals, carrier mobility in semiconductors, optical absorption in indirect band gap semiconductors, and the onset of conventional superconductivity. Additionally, EPC enables the thermalization of hot carriers, influences the phonon dispersion in metals, and determines the T-dependence of electronic energy bands in solids.5,6Likewise, the band gap (Eg) of semiconducting and dielectric materials can be significantly affected by EPC, typically decreasing with increasing temperature (the so-called Varshni effect7). This common Eg behavior can be explained by the Allen–Heine–Cardona perturbative theory, which attributes it to a larger T-induced energy increase in the valence band compared to the conduction band due to a greater sensitivity to phonon population variations (i.e., larger second-order electron–phonon coupling constants).8–10 Representative examples of this thermal Eg dependence include diamond, which exhibits a ∼5% band-gap reduction at around 1000 K;11,12 antimony sulfide (Sb2S3), which shows a Eg reduction of 200 meV in the temperature range of 10 ≤ T ≤ 300 K;13 MgO, which displays a band-gap reduction of ∼15% in the temperature interval 0 ≤ T ≤ 1500 K;14 SrTiO3, which exhibits a ∼15% band-gap reduction from 300 to 1000 K;15 and molecular crystals, which display record band-gap reductions of 15–20% at low temperatures.16 Anomalous band-gap thermal behaviour, in which Eg increases with increasing temperature, has also been observed in a variety of materials such as black phosphorus,17 halide perovskites,18 and chalcopyrite19 and hydride12 compounds.
Highly anharmonic silver chalcohalide antiperovskites (CAP)20 with chemical formula Ag3XY (X = S, Se; Y = Br, I) are structurally similar to lead halide perovskites (e.g., CsPbI3), with the “anti” designation indicating the exchange of anions and cations compared to the typical ionic perovskite arrangement. Analogous to lead halide perovskites, CAP are highly promising materials for energy and optoelectronic applications,21–26 offering low toxicity due to their lead-free composition.27,28 The two most extensively studied CAP compounds, Ag3SBr and Ag3SI, possess experimentally determined band gaps of approximately 1.0 eV,29,30 making them favorable for photovoltaic applications. These materials have also been recognized as high temperature superionic conductors.21,22 Additionally, CAP have been investigated as potential thermoelectric materials25,26 owing to their substantial vibrational anharmonicity and unique charge transport properties.23,24
Intriguingly, for both Ag3SBr and Ag3SI, there is an enormous disagreement between the Eg predicted by first-principles methods (at T = 0 K, under static lattice conditions) and those measured experimentally at room temperature. In particular, high-level density functional theory (DFT) calculations employing hybrid functionals and including spin–orbit coupling (SOC) effects estimate the band gap of these two archetypal CAP to be 1.8 and 1.4 eV, respectively.29–31 The Eg discrepancies between theory and measurements amount to 60–80% of the experimental values (i.e., differences of 0.5–0.8 eV), which are unusually large and call for a careful inspection of the factors causing them.
In this study, we assessed the influence of EPC effects on the Eg and optical absorption spectra of CAP using first-principles DFT methods, tight-binding calculations, and anharmonic Fröhlich theory. Near room temperature, our computational investigations revealed a giant Eg reduction of 20–60% relative to the value calculated at T = 0 K, bringing the estimated band gap into excellent agreement with the experimental values. Low-energy optical polar phonons, which cause large symmetry-breaking structural distortions and promote the overlap between silver and chalcogen s electronic orbitals in the conduction band, were identified to be the primary mechanism driving this substantial T-induced band-gap reduction. Furthermore, at finite temperatures the optical absorption spectra of CAP were significantly enhanced, in some cases by nearly an order of magnitude. The polar nature of the phonons causing these effects opens up new technological possibilities, where the optoelectronic properties of materials could be effectively manipulated by external electric fields and light.
Results
The room-temperature phase of both Ag3SI and Ag3SBr have been experimentally identified as cubic with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.30,32–34 This phase is characterized by a five-atom unit cell: a chalcogen atom at the center of the cube, halide atoms in each vertex, and silver atoms at the center of each face (Fig. 1a and b). Phonon calculations of this phase within the harmonic approximation (T = 0 K) reveal imaginary phonon branches, thus indicating dynamical instability. However, when phonons are calculated fully accounting for anharmonic effects at finite-T conditions, the resulting phonon spectrum is well-behaved with no signs of instability (Fig. 1c).20 Thus, the cubic Pm
m.30,32–34 This phase is characterized by a five-atom unit cell: a chalcogen atom at the center of the cube, halide atoms in each vertex, and silver atoms at the center of each face (Fig. 1a and b). Phonon calculations of this phase within the harmonic approximation (T = 0 K) reveal imaginary phonon branches, thus indicating dynamical instability. However, when phonons are calculated fully accounting for anharmonic effects at finite-T conditions, the resulting phonon spectrum is well-behaved with no signs of instability (Fig. 1c).20 Thus, the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase was considered throughout this work for all CAP.
m phase was considered throughout this work for all CAP.
 | ||
Fig. 1 General physical properties of the archetypal CAP Ag3SBr. (a) The cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase experimentally observed at room temperature. (b) Experimental diffractogram of Ag3SBr30 compared with the theoretical one estimated for the cubic Pm m phase experimentally observed at room temperature. (b) Experimental diffractogram of Ag3SBr30 compared with the theoretical one estimated for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. (c) Vibrational phonon spectrum (left) and phonon density of states (right) calculated within the harmonic approximation for the cubic Pm m phase. (c) Vibrational phonon spectrum (left) and phonon density of states (right) calculated within the harmonic approximation for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase of Ag3SBr at T = 0 K (black lines) and at T = 200 K (red lines) fully considering anharmonic effects. (d) Electronic band structure (left) and density of states (right) of Ag3SBr calculated with the hybrid functional HSEsol.35 Red and blue lines (dots) represent valence (top of the valence) and conduction (bottom of the conduction) bands, respectively. m phase of Ag3SBr at T = 0 K (black lines) and at T = 200 K (red lines) fully considering anharmonic effects. (d) Electronic band structure (left) and density of states (right) of Ag3SBr calculated with the hybrid functional HSEsol.35 Red and blue lines (dots) represent valence (top of the valence) and conduction (bottom of the conduction) bands, respectively. | ||
As discussed in the Introduction, the discrepancies between the experimentally measured (at T = 300 K) and theoretically determined (at T = 0 K) band gaps of Ag3SBr and Ag3SI are tremendously large (i.e., 60–80% of the experimental values). Therefore, we investigated their potential causes by assessing the impact of electron–phonon coupling (EPC) and temperature on the band gap of CAP.
Band gap renormalization due to electron–phonon interactions is typically estimated using two main approaches: density functional perturbation theory (DFPT)1 and finite-differences.2 In DFPT, electron–phonon interactions are treated as a perturbation, with band energy variations (and consequently, band gap shifts) derived from the Fan-Migdal and Debye–Waller self-energies, as described by Allen and Heine.36 A key advantage of DFPT is its computational efficiency, as it does not require the use of supercells. This method has been widely employed in band gap renormalization studies37 and is implemented in popular ab initio codes such as EPW.38
Finite-differences approaches, on the other hand, are computationally more demanding, requiring supercells to reproduce phonons in real space and dynamical simulations to correctly sample the electronic response to ionic fluctuations. However, they offer distinct advantages over DFPT. One key benefit is their flexibility, as they can be applied with any underlying electronic structure method. Additionally, finite-differences methods naturally incorporate terms beyond the lowest order in the electron–phonon interaction, making them particularly useful for capturing higher-order effects.18 Readers seeking a more comprehensive discussion of DFPT and finite-differences methods are referred to the review articles,1,2 which extensively cover these techniques.
In this study, we employ the finite-differences approach to estimate temperature-renormalized band gaps, as CAP materials exhibit strong anharmonicity.20 Consequently, renormalizing their electronic band energies at the harmonic level would be inadequate. Moreover, since accurate CAP band gap predictions require the use of hybrid functionals and spin–orbit coupling, the finite-differences approach emerges as the most practical and reliable choice.
In particular, we performed first-principles calculations and ab initio molecular dynamics (AIMD) simulations based on DFT (Methods). Additionally, to capture long-range EPC effects, we employed anharmonic Fröhlich theory39–42 considering long-range dipole–dipole interactions and T-renormalized phonons (Methods). Furthermore, the optical absorption spectra of all CAP were assessed at T ≠ 0 K conditions and the main EPC mechanisms underlying the Eg discrepancies were identified with the help of a tight-binding model.
EPC band-gap renormalization in CAP
The T-renormalized band gap of CAP was calculated as follows:| Eg(T) = Eg(0) + ΔEg(T), | (1) |
| ΔEg(T) = ΔESg(T) + ΔELg(T). | (2) |
The short-wavelength phonon correction was estimated through AIMD simulations using a supercell (Methods), where the band-gap value was averaged over multiple generated configurations, as described in ref. 39:
 | (3) |
In polar materials, there is an additional contribution to the band-gap renormalization stemming from long-range Fröhlich coupling that is not fully captured by the finite size of the supercells employed in the AIMD simulations.39–43 This long-wavelength phonon band-gap correction can be expressed as follows:
 | (4) |
For a 3D polar material, the T-induced energy level shifts appearing in eqn (4) can be computed as follows:39
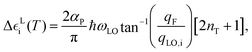 | (5) |
 , m* being the charge carrier effective mass and ħωi the state energy. The term nT is the Bose–Einstein occupation number corresponding to the average LO vibrational frequency, and the polaron constant can be computed as follows:39
, m* being the charge carrier effective mass and ħωi the state energy. The term nT is the Bose–Einstein occupation number corresponding to the average LO vibrational frequency, and the polaron constant can be computed as follows:39 | (6) |
Fig. 2a presents the anharmonic phonon spectrum calculated for Ag3SBr under finite-temperature conditions, accounting for long-range dipole–dipole interactions (i.e., including non-analytical corrections), which result in LO–TO splitting near the reciprocal space point Γ. Fig. 2b shows the corresponding short- and long-wavelength phonon band-gap corrections expressed as a function of temperature, which are always negative. Since in this study the ΔELg correction term has been calculated using the material's anharmonic phonon spectrum, we refer to this method as anharmonic Fröhlich theory (Methods).
 | ||
| Fig. 2 Anharmonic phonon spectrum and thermal band-gap corrections estimated for the archetypal CAP Ag3SBr. (a) Anharmonic phonon spectrum obtained at T = 200 K neglecting (black solid lines) and considering (red dashed lines) non-analytical corrections (NAC). (b) Short- and long-wavelength phonon band-gap corrections, ΔESg and ΔELg, respectively, expressed as a function of temperature (excluding quantum nuclear effects). The short-range correction term was evaluated at several temperature points (blue circles and error bars); as a guide to the eye, the ΔESg data points were fitted to an arbitrary polynomial function (blue dashed line). Calculations were performed at the HSEsol + SOC level.35 | ||
In Fig. 2b, it is observed that near room temperature the ΔESg correction is dominant and significantly larger than ΔELg, approximately six times greater in the absolute value. Notably, at T = 400 K, the total band-gap correction for Ag3SBr amounts to 0.7 eV, which is of giant proportions, representing roughly 40% of the Eg value calculated at zero temperature (excluding quantum nuclear effects).
Fig. 3 shows the relative band-gap variation, referenced to the value calculated at zero temperature and expressed as a function of temperature, for the four CAP compounds Ag3SBr, Ag3SI, Ag3SeBr and Ag3SeI. In all cases, the band gap significantly decreases as the temperature increases (Table 1). The relative T-induced Eg reduction is largest for Ag3SeBr and smallest for Ag3SI. In particular, near room temperature, the band gap of Ag3SBr and Ag3SI is reduced by 39% and 29% while those of Ag3SeBr and Ag3SeI decrease by 56% and 38%, respectively (Fig. 3). As shown in Table 1, the agreement between the experimental and theoretical Eg values for Ag3SBr and Ag3SI improves as the temperature increases. In Ag3SeBr and Ag3SeI, the liquid phase is stabilized over the crystal phase at moderate temperatures (Fig. 3c and d); thus no band gaps were estimated for these two compounds under T > 400 K conditions.
 | ||
| Fig. 3 Temperature-induced relative band-gap variation in CAP. Percentages are referenced to the band gap calculated at T = 0 K conditions (excluding quantum nuclear effects), namely, ΔEg(T) = Eg(T) − Eg(0), for (a) Ag3SBr, (b) Ag3SI, (c) Ag3SeBr, and (d) Ag3SeI. Error bars indicate numerical uncertainties and dashed lines are a guide to the eye. Shaded areas indicate regions of thermodynamic stability of the liquid phase (theory). Calculations were performed at the HSEsol + SOC level.35 | ||
| CAP | E 0Kg [eV] | E 200Kg [eV] | ΔESg [meV] | ΔELg [meV] | E 400Kg [eV] | ΔESg [meV] | ΔELg [meV] | E 600Kg [eV] | ΔESg [meV] | ΔELg [meV] | E expg [eV] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ag3SBr | 1.8 | 1.3 ± 0.1 | −440 | −42 | 1.1 ± 0.1 | −570 | −108 | 0.9 ± 0.2 | −680 | −175 | 1.0 |
| Ag3SI | 1.4 | 1.1 ± 0.1 | −260 | −29 | 1.0 ± 0.1 | −290 | −75 | 0.8 ± 0.1 | −490 | −122 | 0.9 |
| Ag3SeBr | 1.6 | 0.9 ± 0.1 | −630 | −42 | 0.7 ± 0.1 | −770 | −105 | Liquid | — | — | — |
| Ag3SeI | 1.3 | 0.9 ± 0.1 | −370 | −37 | 0.8 ± 0.2 | −400 | −90 | Liquid | — | — | — |
Notably, our theoretical Eg results obtained at T = 400 K are fully consistent with the available experimental data obtained at room temperature. This excellent agreement near ambient conditions strongly suggests that the neglect of EPC effects is the main reason for the huge theoretical–experimental Eg discrepancies discussed in the Introduction. The T-induced relative band-gap renormalization found in CAP are of giant proportions, ranging from 20 to 60% near room temperature, setting a new record previously held by molecular crystals, which exhibited a 15 to 20% band-gap renormalization for similar temperature ranges.16
Table 1 also presents the value of the ΔESg and ΔELg correction terms estimated for each CAP at three different temperatures. In all cases, both the short- and long-wavelength phonon corrections are negative, with the former term considerably surpassing the latter in absolute value. For example, at T = 400 K, the short-range band-gap corrections are seven and four times larger than the long-range ones calculated for Ag3SeBr and Ag3SI, respectively. As the temperature is raised, the size of the two band-gap correction terms increases in absolute value, with |ΔELg| exhibiting the largest relative enhancement (e.g., approximately a 320% relative increase for Ag3SBr from 200 to 600 K).
To provide further insights into the impact of thermal effects on the electronic band structure of CAP, we also examined how band morphology evolves with temperature. Since band-gap renormalization in this study is assessed using the finite-differences approach based on AIMD simulations, it is convenient to unfold the energy bands calculated for the supercell into the reciprocal space of the primitive unit cell.44 This was done using the Easyunfold software,45 focusing on the representative CAP compound Ag3SBr (Fig. S1, ESI†).
Specifically, we analyzed five uncorrelated supercell snapshots extracted from a long AIMD trajectory (∼100 ps) at T = 200 K. For this particular case, the PBEsol exchange–correlation functional was employed due to the very high computational cost of performing hybrid functional calculations on supercells. Reassuringly, we verified that the band structures obtained using semilocal and hybrid functionals are practically equivalent in morphology (Fig. S2, ESI†).
Our results indicate that thermal effects lead to a downward shift of the conduction band minimum, which remains located at the Γ point, which is consistent with the band-gap trends observed in the corresponding electronic density of states. However, the ionic disorder induced by lattice vibrations causes a noticeable flattening of the valence band near its top. As a result, the valence band maximum becomes poorly defined, unlike in the static case (Fig. S1, ESI†). The consistency of results across the five ionically disordered configurations suggests that this small sampling is sufficient to capture the key temperature-induced changes in band morphology.
Thermal effects on the optical absorption coefficient of CAP
Following a similar approach to that used for the calculation of T-renormalized band gaps (i.e., performing AIMD simulations with a supercell and averaging the quantity of interest over several of the generated configurations), we determined the frequency-dependent complex dielectric tensor of CAP under T ≠ 0 K conditions (Methods and Supplementary methods, ESI†), employing linear response theory. From the average dielectric tensor, we computed several macroscopic optical properties like the optical absorption coefficient, α(ω), refractive index, and reflectivity.46Fig. 4 shows the optical absorption spectra estimated for CAP as a function of incident light wavelength and temperature. It is found that α is significantly enhanced under increasing temperature, in some cases by as much as an order of magnitude. Similarly to the band gap, the T-induced optical absorption variations are the largest for Ag3SeBr (for which α ∼ 103–105 cm−1 at zero temperature and ∼104–106 cm−1 at 200 K) and smallest for Ag3SI (for which α ∼ 103–105 cm−1 at any temperature). It is also noted that the most significant optical absorption changes generally occur at low temperatures, that is, within the 0 ≤ T ≤ 200 K interval. These T-induced α trends align well with the remarkably large influence of the EPC on the band gap, underscoring the critical role of thermal renormalization effects on the optoelectronic properties of CAP.
 | ||
| Fig. 4 Optical absorption coefficient (α) of CAP calculated at different temperatures as a function of photon energy. (a) Ag3SBr, (b) Ag3SI, (c) Ag3SeBr, and (d) Ag3SeI. Solid lines represent the estimated average values and statistical errors are indicated with shaded thick curves. The rainbow-colored region denotes photons with energy in the visible spectrum. Calculations were performed at the HSEsol + SOC level.35 | ||
Unfortunately, we cannot directly compare our theoretical α(ω) results with experimental data, as such data are not available in the literature. Notably, Caño et al.30 measured the optical absorption coefficient of CAP films scaled by their layer thickness, d, specifically, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) ≡ α·d. However, since the thickness of the synthesized CAP films was not determined in work,30 we cannot access the physical quantity of interest. In this regard, performing new optoelectronic experiments on CAP films across a broad range of temperatures, including the low-T regime, would be highly desirable.
≡ α·d. However, since the thickness of the synthesized CAP films was not determined in work,30 we cannot access the physical quantity of interest. In this regard, performing new optoelectronic experiments on CAP films across a broad range of temperatures, including the low-T regime, would be highly desirable.
EPC mechanisms in CAP
We have already shown that temperature and EPC effects are essential for understanding the thermal evolution of the optoelectronic properties of CAP and for achieving a consistent agreement between first-principles calculations and room-temperature experiments. Next, we focus on unraveling the primary ionic–electronic mechanisms underlying these key temperature and EPC effects.As shown in Fig. 5a, the influence of each of the fifteen Γ phonon modes on the band gap of Ag3SBr was analysed by monitoring the change in Eg driven by frozen-phonon eigenmode distortions of increasing amplitude, u. The Γ phonons were classified into acoustic (A), optical polar (P) and optical nonpolar (NP), where the P phonons break the inversion symmetry of the centrosymmetric cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. It was found that Eg is unresponsive to acoustic phonon distortions, as expected, while optical P phonons produce the largest band-gap variations. As the amplitude of the optical phonon distortions increases, Eg systematically decreases in both the P and NP cases.
m phase. It was found that Eg is unresponsive to acoustic phonon distortions, as expected, while optical P phonons produce the largest band-gap variations. As the amplitude of the optical phonon distortions increases, Eg systematically decreases in both the P and NP cases.
 | ||
Fig. 5 Phonon-induced band-gap variation estimated for the archetypal CAP Ag3SBr. (a) Band gap as a function of the lattice distortion amplitude u for acoustic, polar optical (P) and non-polar optical (NP) Γ phonons. (b) Derivative of the band gap with respect to the phonon distortion amplitude calculated at u0 = 0.4 Å and expressed as a function of the phonon energy. The eigenmode of the optical polar Γ phonon rendering the largest band-gap derivative in absolute value is sketched: Ag, S and Br atoms are represented with grey, yellow and brown spheres, respectively. Calculations were performed at the HSEsol + SOC level.35 (c) Γ phonon-induced relative bond length distortions in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase for a distortion amplitude of 0.4 Å. m phase for a distortion amplitude of 0.4 Å. | ||
Fig. 5b shows the value of the derivative of the band gap with respect to the phonon distortion amplitude, u, expressed as a function of the phonon eigenmode energy (as obtained from T-renormalised phonon calculations, Methods). We found that low-energy polar phonon modes (∼10 meV) cause the most significant band-gap reductions, followed by high-energy lattice vibrations of the same type (∼200 meV). At room temperature, phonon excitations with the lowest energy host the highest populations and, consequently, represent the most characteristic lattice vibrations in the crystal. Therefore, based on the results shown in Fig. 3 and 5, we conclude that low-energy polar phonon modes are primarily responsible for the substantial temperature-induced Eg reduction reported in this study for CAP compounds.
The eigenmode of the optical P phonon with the lowest energy is represented in Fig. 5b. As observed therein, this frozen-phonon lattice distortion reduces the distance between the central sulfur atom and one adjacent silver atom (Ag2), while increasing the other two S–Ag1 and S–Ag3 bond lengths, compared to the undistorted cubic unit cell. Fig. 5c summarizes the relative bond length variation, in absolute value, for all pairs of atoms resulting from each of the fifteen Γ phonon modes calculated for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. As shown therein, the optical P phonons produce the largest S–Ag distance changes (up to 20%), while the optical NP phonons cause the largest Br–Ag bond length variations (up to 12%). The Br–Ag bond lengths are also appreciably impacted by the optical P phonons (5–10%). This general behaviour is reminiscent of that observed for optical polar phonons in model perovskite oxides like BaTiO3 (with atomic substitutions Ag ↔ O, S ↔ Ti and Br ↔ Ba).47,48
m phase. As shown therein, the optical P phonons produce the largest S–Ag distance changes (up to 20%), while the optical NP phonons cause the largest Br–Ag bond length variations (up to 12%). The Br–Ag bond lengths are also appreciably impacted by the optical P phonons (5–10%). This general behaviour is reminiscent of that observed for optical polar phonons in model perovskite oxides like BaTiO3 (with atomic substitutions Ag ↔ O, S ↔ Ti and Br ↔ Ba).47,48
After identifying the phonon modes that underpin the giant T-induced band-gap reduction reported in this study for CAP, specifically low-energy optical P modes, we further analyse the induced changes in the electronic band structure. Fig. 6a shows the electronic density of states calculated for the archetypal compound Ag3SBr (equilibrium geometry). It is observed that the top of the valence band (VB) is dominated by highly hybridized silver d and chalcohalide p electronic orbitals, while the bottom of the conduction band (CB) is dominated by isotropic and more delocalized S and Ag s orbitals. The electronic band structure in Fig. 6b shows that the VB corresponds to the high-symmetry reciprocal space point M (1/2,1/2,0), while the CB to the center of the Brillouin zone, Γ (0,0,0); thus the band gap of Ag3SBr is indirect (we have checked that the same conclusion applies to the rest of CAP compounds analyzed in this study).
 | ||
Fig. 6 Electronic band structure properties of the archetypal CAP Ag3SBr. (a) Electronic density of states calculated for the equilibrium cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. Calculations were performed at the HSEsol + SOC level.35 (b) Electronic band structure calculated for the equilibrium and phonon distorted (i.e., considering the lowest-energy Γ optical P mode with amplitude u0 = 0.4 Å) cubic Pm m phase. Calculations were performed at the HSEsol + SOC level.35 (b) Electronic band structure calculated for the equilibrium and phonon distorted (i.e., considering the lowest-energy Γ optical P mode with amplitude u0 = 0.4 Å) cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase; in both cases, the energy bands are referred to a same energy origin, a deep core electronic level that remains unaffected by the distortion (Methods). (c) and (d) The conduction band near its minimum at Γ computed with a TB model for silver and sulfur atoms (Methods); solid and dashed lines correspond to the equilibrium and distorted structures, respectively. (e) Sketch illustrating the mechanism of band-gap closure induced by low-energy polar soft phonon modes in CAP. Upon phonon distortion, the hybridization of silver and sulfur s electrons in the conduction band is enhanced, lowering (increasing) the energy of the corresponding bonding σ (antibonding σ*) state. m phase; in both cases, the energy bands are referred to a same energy origin, a deep core electronic level that remains unaffected by the distortion (Methods). (c) and (d) The conduction band near its minimum at Γ computed with a TB model for silver and sulfur atoms (Methods); solid and dashed lines correspond to the equilibrium and distorted structures, respectively. (e) Sketch illustrating the mechanism of band-gap closure induced by low-energy polar soft phonon modes in CAP. Upon phonon distortion, the hybridization of silver and sulfur s electrons in the conduction band is enhanced, lowering (increasing) the energy of the corresponding bonding σ (antibonding σ*) state. | ||
The effects on the electronic band structure resulting from a frozen-phonon lattice distortion corresponding to the lowest-energy optical P eigenmode (u0 = 0.4 Å) are twofold (Fig. 6b). First, due to the breaking of phonon-induced inversion symmetry, the energy band degeneracy at the reciprocal space point M is lifted. However, the band gap of the system is unaffected by this energy degeneracy lifting effect since the VB remains practically invariant. Second, the CB edge experiences a significant decrease in energy and, as a consequence, the band gap of the system is reduced by approximately 30%. Therefore, we may conclude that the giant T-induced Eg reduction reported in this study for CAP is primarily caused by low-energy polar phonon modes that induce a pronounced CB energy decrease.
To better understand the electronic origins of the optical P phonon-induced CB energy lowering, we constructed a tight-binding (TB) model based on Wannier functions that accurately reproduces our DFT band structure results (Methods and Fig. S3, ESI†). Specifically, the TB model consists of s, p, and d orbitals for the five atoms in the unit cell, resulting in a total of 45 distinct Wannier orbitals. Consistently, the TB model reproduces the dominant Ag and S s character of the CB and its energy lowering under the polar lattice distortion of interest (Fig. 6c and d).
According to this TB model, the impact of the frozen-phonon distortion on the Ag and S s conduction orbitals is twofold. First, the difference in their kinetic energies, corresponding to the diagonal Hamiltonian matrix elements difference |〈Ag s|H|Ag s〉 − 〈S s|H|S s〉|, decreases (Fig. S3, ESI†). And second, the hopping s term involving the Ag2 and S atoms, represented by the off-diagonal Hamiltonian matrix element 〈Ag2 s|H|S s〉, increases (Fig. S3, ESI†). The general physical interpretation that follows from these TB results is that the polar frozen-phonon distortion enhances the hybridization of Ag2 and S s conduction orbitals, which lowers and increases the energy of the corresponding bonding (σ) and antibonding (σ*) states, respectively. Consequently, the CB, which is dominated by the Ag2-S σ interaction, is lowered. The revealed EPC mechanism, which overall produces a band-gap reduction, is schematically represented in Fig. 6e.
Discussion
Thermal expansion is another physical mechanism that can influence the band gap of materials,40 but it was not explicitly considered in this study due to its high computational cost. However, we performed a series of tests in which we arbitrarily increased and decreased the unit cell volume of Ag3SBr and estimated the corresponding relative Eg variation (Fig. S4 and Table S1, ESI†). We found that, when the volume of the system increases by a reasonable ∼1%, as might occur due to thermal expansion near room temperature, the band gap decreases by only ∼40 meV (i.e., an order of magnitude smaller change than short-wavelength phonon corrections, Table 1). Additionally, thermal expansion likely contributes to the softening of optical P modes, increasing their population and consequently enhancing the Eg reduction due to EPC. Therefore, while thermal expansion effects were omitted in our calculations, the reported results likely represent a lower bound of the actual effect, and our conclusions for CAP compounds remain robust and accurate.One may wonder whether, in addition to silver chalcohalide antiperovskites, there exist other families of materials exhibiting similarly large T-renormalization effects on the band gap and optical absorption coefficient. As discussed in previous sections, the polar nature of low-energy optical phonons appears to be essential in this regard. Consequently, a tentative set of necessary conditions for identifying potential materials that display similar T-induced effects on the optoelectronic properties may include dielectric materials exhibiting (1) centrosymmetric crystalline phases, (2) low-energy or even imaginary optical polar phonons, and (3) highly hybridized and delocalized electronic orbitals near the Fermi energy level. The availability of large DFT calculations and phonon databases may enable high-throughput material screening of such a kind.49,50
Ferroelectric oxide perovskites, exemplified by the archetypal compounds SrTiO3 (STO) and BaTiO3 (BTO), appear to satisfy the set of necessary conditions outlined above. Notably, a significant band-gap modulation has been reported for STO under biaxial strain conditions, although this phenomenon arises from different physical mechanisms than those identified in this study for CAP compounds (i.e., energy degeneracy lifting due to symmetry breaking).51 Moreover, the experimental room-temperature band gap of BTO (≈3.2 eV52) shows substantial disagreement with zero-temperature theoretical estimates obtained with hybrid functionals (≈4.0 eV53), highlighting an experiment–theory inconsistency similar to that described for Ag3SBr and Ag3SI in the Introduction. Additionally, the band gap of the multiferroic oxide perovskite BiFeO3 exhibits a remarkable temperature-dependent shrinkage, decreasing by approximately 50% within the temperature range 300 ≤ T ≤ 1200 K,54 likely influenced by the magnetic degrees of freedom.55 These findings suggest that the temperature effects and EPC mechanisms identified in this study for CAP compounds may have broader relevance, potentially extending to other well-known families of functional materials. Theoretical investigations exploring this possibility are currently underway.
The polar nature of the optical phonon modes, which cause the significant T-induced reduction in the Eg of CAP, opens up exciting technological possibilities. Similar to how an electric field can stabilize a polar phase with ferroelectric polarization over a paraelectric state at constant temperature through a phase transformation,56 it is likely that polar optical phonons in CAP can also be stimulated using external electric fields. This possibility implies that the optoelectronic properties of CAP could be effectively tuned by applying an electric field rather than altering the temperature, providing a more practical approach for the development of advanced optical devices and other technological applications. Experimental validation of this hypothesis would be highly valuable.
Finally, advances in light sources and time-resolved spectroscopy have made it possible to excite specific atomic vibrations in solids and to observe the resulting changes in their electronic and electron–phonon coupling properties.57–59 These developments also suggest the possibility of tuning the optoelectronic properties of CAP, as well as of similar materials like oxide perovskites,60–62 through specific phonon excitations using optical means such as lasers. This approach may simplify the design and manufacture of practical setups by eliminating the need for electrode deposition. Therefore, the results presented in this work are significant not only from a fundamental perspective but also for envisioning potential technological applications in which the optical and electronic properties of materials could be effectively tuned by external fields and photoexcitation.
Conclusions
In this study, we have explored the temperature effects on the band gap of silver chalcohalide antiperovskites (CAP), specifically Ag3XY compounds (X = S, Se; Y = Br, I), which are promising for energy and photonic applications due to their lead-free composition, high ionic conductivity, and optoelectronic properties. The key findings of our research are summarized as follows. A giant reduction in the band gap of CAP materials has been disclosed at room temperature, ranging from 20% to 60% relative to their values calculated at zero temperature (neglecting zero-point corrections). This large band-gap renormalization brings theoretical predictions closer to experimental results, resolving previous discrepancies.The significant Eg reduction is attributed to strong electron–phonon coupling driven by low-energy polar phonon modes, which distorts the lattice symmetry, increases the overlap between silver and chalcogen s orbitals in the conduction band, and lowers the reference energy of the resulting bonding state. With increasing temperature, the optical absorption coefficient of CAP materials also rises, enhancing their response to visible light by nearly an order of magnitude and highlighting their potential for optoelectronic applications.
This research demonstrates that CAP compounds exhibit giant band-gap renormalization primarily due to temperature and electron–phonon coupling effects, suggesting that they could be tailored for specific applications through thermal, electric field, and/or optical control. These fundamental findings open possibilities for the design of innovative optoelectronic devices and establish a foundation for exploring similar effects in other dielectric materials with strong electron–phonon coupling.
Methods
Zero-temperature first-principles calculations
The DFT calculations63–65 were performed using the semilocal PBEsol approximation,66 considering the following electronic states as valences: Ag 5s–4d, S 3s–3p, Se 4s–4p, Br 4s–4p, I 5s–5p. Wave functions were represented in a plane-wave basis set truncated at 650 eV. Using these parameters and a dense k-point grid of 8 × 8 × 8 for reciprocal-space Brillouin zone (BZ) sampling, we obtained zero-temperature energies converged to within 0.5 meV per formula unit. For the geometry relaxations, a force tolerance of 0.005 eV Å−1 was imposed on all the atoms. The optoelectronic properties were estimated using hybrid functionals35 (Fig. S5 and Supplementary methods, ESI†) and considering spin–orbit coupling (SOC) effects, a computational approach named HSEsol + SOC here. In this case, to make the calculations feasible, the energy cutoff and k-point grid were slightly reduced to 550 eV and 6 × 6 × 6, respectively. Quantum nuclear effects65 were disregarded throughout this work, as well as the likely presence of weak excitons.67,68All-electron DFT calculations were also performed with the WIEN2k package69 using the local-density approximation (LDA)70 to the exchange correlation energy along using the linearized augmented plane wave method (FP-LAPW).71,72 The technical parameters for these calculations were a 10 × 10 × 10 k-point grid and a muffin-tin radius equal to RMT = 7.0/Kmax, where Kmax represents the plane-wave cutoff. Localized energy-resolved Wannier states73 were then obtained for the tight-binding calculations74–76 considering the relevant Hilbert space in the interval −10 ≤ E ≤ 20 eV around the Fermi energy.
Finite-temperature first-principles simulations
Ab initio molecular dynamics (AIMD) simulations were performed in the canonical (N, V, T) ensemble, neglecting thermal expansion effects and employing a large simulation cell containing 320 atoms with periodic boundary conditions applied along the three Cartesian directions. The temperature in the AIMD simulations was kept fluctuating around a set-point value by using Nose–Hoover thermostats. Newton's equations of motion were integrated using the standard Verlet's algorithm with a time step of 1.5 × 10−3 ps. Γ-Point sampling for reciprocal-space integration was employed in the AIMD simulations, which spanned approximately 100 ps. These calculations were performed with the semilocal PBEsol exchange–correlation functional.66Harmonic phonon calculations
The second-order interatomic force constant matrix of all CAP and resulting harmonic phonon spectrum were calculated using the finite-differences method as is implemented in the PhonoPy software.77 Large supercells (i.e., 4 × 4 × 4 for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m supercell containing 320 atoms) and a dense k-point grid of 3 × 3 × 3 for BZ sampling were employed for the phonon calculations of targeted structures. Several numerical tests were conducted that demonstrated the adequacy of the selected k-point grid. These calculations were performed with the semilocal PBEsol exchange–correlation functional.66
m supercell containing 320 atoms) and a dense k-point grid of 3 × 3 × 3 for BZ sampling were employed for the phonon calculations of targeted structures. Several numerical tests were conducted that demonstrated the adequacy of the selected k-point grid. These calculations were performed with the semilocal PBEsol exchange–correlation functional.66
Anharmonic phonon calculations
The DynaPhoPy code78 was used to calculate the anharmonic lattice dynamics (i.e., T-renormalized phonons) of CAP in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase from ab initio molecular dynamics (AIMD) simulations. A reduced 2 × 2 × 2 supercell and 4 × 4 × 4 k-point grid for BZ sampling were employed in the AIMD simulations to maintain high numerical accuracy (Supplementary methods and work, ESI,† (ref. 20)).
m phase from ab initio molecular dynamics (AIMD) simulations. A reduced 2 × 2 × 2 supercell and 4 × 4 × 4 k-point grid for BZ sampling were employed in the AIMD simulations to maintain high numerical accuracy (Supplementary methods and work, ESI,† (ref. 20)).
A normal-mode decomposition technique was employed in which the atomic velocities vjl(t) (j and l represent particle and Cartesian direction indexes) generated during fixed-temperature AIMD simulation runs were expressed as follows:
 | (7) |
The Fourier transform of the autocorrelation function of vqs was then calculated, yielding the following power spectrum:
 | (8) |
Finally, this power spectrum was approximated by a Lorentzian function of the following form:
 | (9) |
Short-wavelength phonon band-gap correction
The electron–phonon correction to the band gap due to the short-range phonon modes was computed as the difference between the band gap at zero temperature for the static structure and the average band gap obtained from AIMD simulations performed with a supercell, namely | (10) |
These calculations were performed using the hybrid HSEsol exchange–correlation functional35 and considering spin–orbit coupling effects (HSEsol + SOC). Due to the high computational expense involved, the AIMD calculations were performed using a supercell containing 40 atoms and a k-point mesh of a single point. The total number of configurations used for the average was N = 10 for each material and temperature. These values were found to be appropriate for obtaining band-gap results accurate to within 0.1 eV (Supplementary methods, ESI†).
Long-wavelength phonon band-gap correction
The electron–phonon correction to the band gap due to long-range phonon modes was computed using the Fröhlich equation for a three-dimensional polar material.39–42 This correction was determined as the difference in the shifts of the conduction and valence bands, as given in eqn (4), where the shift of each band was computed using the expression in eqn (5). The physical quantities entering this latter expression were determined with DFT methods; the electron and hole effective masses were computed using the parabolic approximation at the maximum of the valence band and the minimum of the conduction band, respectively. For the LO phonon frequency, we used an effective value computed as the average of the three corresponding modes, as done in ref. 43. Temperature-induced anharmonic effects were fully taken into account for the calculation of these LO phonon frequencies, using the renormalized phonon frequencies obtained at T = 200 K. Due the superionic behavior of these materials at higher temperatures, the renormalized phonon dispersions calculated at T ≥ 200 K conditions presented imaginary frequencies,20 and hence were not considered in this study.The high-frequency and static dielectric constants calculated for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase were unusually large in static calculations, since this phase is not vibrationally stable at T = 0 K. Thus, the dielectric constants were recomputed as functions of temperature (using the same approach as we applied to the band gap and dielectric tensor) to capture thermal effects. In view of their weak temperature dependence, and for simplicity, the dielectric constants obtained at T = 200 K were employed throughout this work. We also considered the anisotropy of the dielectric tensor using the following formula:
m phase were unusually large in static calculations, since this phase is not vibrationally stable at T = 0 K. Thus, the dielectric constants were recomputed as functions of temperature (using the same approach as we applied to the band gap and dielectric tensor) to capture thermal effects. In view of their weak temperature dependence, and for simplicity, the dielectric constants obtained at T = 200 K were employed throughout this work. We also considered the anisotropy of the dielectric tensor using the following formula:
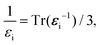 | (11) |
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by MICIN/AEI/10.13039/501100011033 and ERDF/EU under the grants TED2021-130265B-C22, TED2021-130265B-C21, PID2023-146623NB-I00, PID2023-147469NB-C21 and RYC2018-024947-I and by the Generalitat de Catalunya under the grants 2021SGR-00343, 2021SGR-01519 and 2021SGR-01411. Computational support was provided by the Red Española de Supercomputación under the grants FI-2024-1-0005, FI-2024-2-0003 and FI-2024-3-0004. This work is part of the Maria de Maeztu Units of Excellence Programme CEX2023-001300-M funded by MCIN/AEI (10.13039/501100011033). P. B. acknowledges support from the predoctoral program AGAUR-FI ajuts (2024 FI-1 00070) Joan Oró, which is backed by the Secretariat of Universities and Research of the Department of Research and Universities of the Generalitat of Catalonia, as well as the European Social Plus Fund. C. L. acknowledges support from the Spanish Ministry of Science, Innovation and Universities under an FPU grant. E. S. and J.-Ll.T. are grateful to the ICREA Academia program. Work at LIST was supported by the Luxembourg National Research Fund through grant C21/MS/15799044/FERRODYNAMICS. This project received funding from the European Union's H2020 European Research Council under the grant agreement number 866018 (SENSATE). S. C. and B. M. are supported by a EPSRC grant [EP/V062654/1] and R. J. and B. M. are supported by a UKRI Future Leaders Fellowship [MR/V023926/1]. B. M. also acknowledges support from the Gianna Angelopoulos Programme for Science, Technology, and Innovation, and from the Winton Programme for the Physics of Sustainability.References
- F. Giustino, Electron-phonon interactions from first principles, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- B. Monserrat, Electron-phonon coupling from finite differences, J. Phys.: Condens. Matter, 2018, 30, 083001 CrossRef PubMed.
- Z. Lin, L. V. Zhigilei and V. Celli, Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 075133 CrossRef.
- K.-P. Bohnen, R. Heid and B. Renker, Phonon dispersion and electron-phonon coupling in MgB2 and AlB2, Phys. Rev. Lett., 2001, 86, 5771 CrossRef CAS PubMed.
- B. Monserrat, J.-S. Park and A. Walsh, Role of electron-phonon coupling and thermal expansion on band gaps, carrier mobility, and interfacial offsets in kesterite thin-film solar cells, Appl. Phys. Lett., 2018, 112, 193903 CrossRef.
- B. Monserrat and D. Vanderbilt, Temperature dependence of the bulk Rashba splitting in the bismuth tellurohalides, Phys. Rev. Mater., 2017, 1, 054201 CrossRef.
- Y. P. Varshni, Temperature dependence of the energy gap in semiconductors, Physica, 1967, 34, 149 CrossRef CAS.
- K. P. O'Donnell and X. Chen, Temperature dependence of semiconductor band gaps, Appl. Phys. Lett., 1991, 58, 2924 CrossRef.
- S. Poncé, Y. Gillet, J. L. Janssen, A. Marini, M. Verstraete and X. Gonze, Temperature dependence of the electronic structure of semiconductors and insulators, J. Chem. Phys., 2015, 143, 102813 CrossRef PubMed.
- J. Park, W. A. Saidi, B. Chorpening and Y. Duan, Applicability of Allen-Heine-Cardona theory on MOx metal oxides and ABO3 perovskites: Toward high-temperature optoelectronic applications, Chem. Mater., 2022, 34, 6108 CrossRef CAS.
- F. Giustino, S. G. Louie and M. L. Cohen, Electron-phonon renormalization of the direct band gap of diamond, Phys. Rev. Lett., 2010, 105, 265501 CrossRef PubMed.
- B. Monserrat, N. D. Drummond and R. J. Needs, Anharmonic vibrational properties in periodic systems: energy, electron-phonon coupling, and stress, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 87, 144302 CrossRef.
- Y. Liu, B. Monserrat and J. Wiktor, Strong electron-phonon coupling and bipolarons in Sb2S3, Phys. Rev. Mater., 2023, 7, 085401 CrossRef CAS.
- Y. Zhang, Z. Wang, J. Xi and J. Yang, Temperature-dependent band gaps in several semiconductors: from the role of electron-phonon renormalization, J. Phys.: Condens. Matter, 2020, 32, 475503 CrossRef CAS PubMed.
- Y.-N. Wu, W. A. Saidi, J. K. Wuenschell, T. Tadano, P. Ohodnicki, B. Chorpening and Y. Duan, Anharmonicity explains temperature renormalization effects of the band gap in SrTiO3, J. Phys. Chem. Lett., 2020, 11, 2518 CrossRef CAS PubMed.
- B. Monserrat, E. A. Engel and R. J. Needs, Giant electron-phonon interactions in molecular crystals and the importance of nonquadratic coupling, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 140302 CrossRef.
- C. E. P. Villegas, A. R. Rocha and A. Marini, Anomalous temperature dependence of the band gap in black phosphorus, Nano Lett., 2016, 16, 5095 CrossRef CAS PubMed.
- W. A. Saidi, S. Poncé and B. Monserrat, Temperature dependence of the energy levels of methylammonium lead iodide perovskite from first-principles, J. Phys. Chem. Lett., 2016, 7, 5247 CrossRef CAS PubMed.
- L. Artus and Y. Bertrand, Anomalous temperature dependence of fundamental gap of AgGaS2 and AgGaSe2 chalcopyrite compounds, Solid State Commun., 1987, 61, 733 CrossRef CAS.
- P. Benítez, C. López, C. Liu, I. Caño, J.-L. Tamarit, E. Saucedo and C. Cazorla, Crystal structure prediction and phase stability in highly anharmonic silver-based chalcohalide anti-perovskites, PRX Energy, 2025, 4, 023002 CrossRef.
- T. Takahashi and O. Yamamoto, The Ag/Ag3SI/I2 solid-electrolyte cell, Electrochim. Acta, 1966, 11, 779 CrossRef CAS.
- S. Hull, Superionics: crystal structures and conduction processes, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS.
- K. Wakamura, F. Miura, A. Kojima and T. Kanashiro, Observation of anomalously increasing phonon damping constant in the β phase of the fast-ionic conductor Ag3SI, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 41, 2758 CrossRef CAS PubMed.
- T. Sakuma, Treatment of anharmonic thermal vibration by using transformation of scattering vector, J. Phys. Soc. Jpn., 1985, 54, 4188 CrossRef CAS.
- J. Kawamura, M. Shimoji and H. Hoshino, The ionic conductivity and thermoelectric power of the superionic conductor Ag3SBr, J. Phys. Soc. Jpn., 1981, 50, 194 CrossRef CAS.
- A. Magistris, E. Pezzati and C. Sinistri, Thermoelectric properties of high-conductivity solid electrolytes, Z. Naturforsch., 1972, 27a, 1379 CrossRef.
- F. Palazon, Metal chalcohalides: Next generation photovoltaic materials?, Sol. RRL, 2022, 6, 2100829 CrossRef CAS.
- U. V. Ghorpade, M. P. Suryawanshi, M. A. Green, T. Wu, X. Hao and K. M. Ryan, Emerging chalcohalide materials for energy applications, Chem. Rev., 2023, 123, 327 CrossRef CAS PubMed.
- L. Sebastiá-Luna, N. Rodkey, A. S. Mirza, S. Mertens, S. Lal, A. Melchor, G. Carranza, J. Calbo, M. Righetto, M. Sessolo, L. M. Herz, K. Vandewal, E. Ortí, M. Morales-Masis, H. J. Bolink and F. Palazon, Chalcohalide antiperovskite thin films with visible light absorption and high charge-carrier mobility processed by solvent-free and low-temperature methods, Chem. Mater., 2023, 35, 6482 CrossRef.
- I. Caño, J. W. Turnley, P. Benítez, C. López-Álvarez, J.-M. Asensi, D. Payno, J. Puigdollers, M. Placidi, C. Cazorla, R. Agrawal and E. Saucedo, Novel synthesis of semiconductor chalcohalide anti-perovskites by low-temperature molecular precursor ink deposition methodologies, J. Mater. Chem. C, 2024, 12, 3154 RSC.
- Z. Liu, R. Mi, G. Ji, Y. Liu, P. Fu, S. Hu, B. Xia and Z. Xiao, Bandgap engineering and thermodynamic stability of oxyhalide and chalcohalide antiperovskites, Ceram. Int., 2021, 47, 32634 CrossRef CAS.
- T. Sakuma and S. Hoshino, The phase transition and the structures of superionic conductor Ag3SBr, J. Phys. Soc. Jpn., 1980, 49, 678 CrossRef CAS.
- S. Hoshino, H. Fujishita, M. Takashige and T. Sakuma, Phase transition of Ag3 SX (X= I, Br), Solid State Ionics, 1981, 3, 35 CrossRef.
- N. Cho, S. Kikkawa, F. Kanamaru and A. Yoshiasa, Structural refinement of Ag3SI by single crystal X-ray diffraction method, Solid State Ionics, 1994, 68, 57 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- P. B. Allen and V. Heine, Theory of the temperature dependence of electronic band structures, J. Phys. C: Solid State Phys., 1976, 9, 2305 CrossRef CAS.
- E. Cannuccia and A. Marini, Effect of the quantum zero-point atomic motion on the optical and electronic properties of ciamond and trans-polyacetylene, Phys. Rev. Lett., 2011, 107, 255501 CrossRef PubMed.
- H. Lee, S. Poncé and K. Bushick, et al., Electron-phonon physics from first principles using the EPW code, npj Comput. Mater., 2023, 9, 156 CrossRef CAS.
- M. Zacharias, M. Scheffler and C. Carbogno, Fully anharmonic nonperturbative theory of vibronically renormalized electronic band structures, Phys. Rev. B, 2020, 102, 045126 CrossRef CAS.
- S. Chen, I. J. Parker and B. Monserrat, Temperature effects in topological insulators of transition metal dichalcogenide monolayers, Phys. Rev. B, 2024, 109, 155125 CrossRef CAS.
- S. Poncé, Y. Gillet, J. L. Janssen, A. Marini, M. Verstraete and X. Gonze, Temperature dependence of the electronic structure of semiconductors and insulators, J. Chem. Phys., 2015, 143, 102813 CrossRef PubMed.
- M. Zacharias and F. Giustino, Theory of the special displacement method for electronic structure calculations at finite temperature, Phys. Rev. Res., 2020, 2, 013357 CrossRef CAS.
- P. M. Melo, J. C. Abreu, B. Guster, M. Giantomassi, Z. Zanolli, X. Gonze and M. J. Verstraete, High-throughput analysis of Fröhlich-type polaron models, npj Comput. Mater., 2023, 9, 147 CrossRef.
- V. Popescu and A. Zunger, Extracting E versus k effective band structure from supercell calculations on alloys and impurities, Phys. Rev. Res., 2012, 85, 085201 CrossRef.
- B. Zhu, S. R. Kavanagh and D. Scanlon, easyunfold: A Python package for unfolding electronic band structures, J. Open Source Softw., 2024, 9, 5974 CrossRef.
- V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- R. E. Cohen, Origin of ferroelectricity in perovskite oxides, Nature, 1992, 358, 136 CrossRef CAS.
- W. Zhong, D. Vanderbilt and K. M. Rabe, Phase transitions in BaTiO3 from first principles, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 73, 1861 CAS.
- A. Jain, S. P. Ong and G. Hautier, et al., The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- https://github.com/atztogo/phonondb .
- R. F. Berger, C. J. Fennier and J. B. Neaton, Band gap and edge engineering via ferroic distortion and anisotropic strain: The case of SrTiO3, Phys. Rev. Lett., 2011, 107, 146804 CrossRef PubMed.
- S. H. Wemple, Polarization fluctuations and the optical-absorption edge in BaTiO3, Phys. Rev. B, 1970, 2, 2679 CrossRef.
- R. A. Evarestov and A. V. Bandura, First-principles calculations on the four phases of BaTiO3, J. Comput. Chem., 2012, 33, 1123 CrossRef CAS PubMed.
- M. C. Weber, M. Guennou, C. Toulouse, M. Cazayous, Y. Gillet, X. Gonze and J. Kreisel, Temperature evolution of the band gap in BiFeO3 traced by resonant Raman scattering, Phys. Rev. B, 2016, 93, 125204 CrossRef.
- C. Cazorla and J. Íñiguez-González, Insights into the phase diagram of bismuth ferrite from quasiharmonic free-energy calculations, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 214430 CrossRef.
- C. Cazorla and J. Íñiguez-González, Giant direct and inverse electrocaloric effects in multiferroic thin films, Phys. Rev. B, 2018, 98, 174105 CrossRef CAS.
- D. Kennes, E. Wilner and D. Reichman, et al., Transient superconductivity from electronic squeezing of optically pumped phonons, Nat. Phys., 2017, 13, 479 Search PubMed.
- T. Dekorsky, W. Kütt, T. Pfeifer and H. Kurz, Coherent control of LO-phonon dynamics in opaque semiconductors by femtosecond laser pulses, Europhys. Lett., 1993, 23, 223 CrossRef.
- E. Pomarico, M. Mitrano and H. Bromberger, et al., Enhanced electron-phonon coupling in graphene with periodically distorted lattice, Phys. Rev. B, 2017, 95, 024304 CrossRef.
- Y. Qi, S. Liu, A. M. Lindenberg and A. M. Rappe, Ultrafast electric field pulse control of giant temperature change in ferroelectrics, Phys. Rev. Lett., 2018, 120, 055901 CrossRef CAS PubMed.
- B. Peng, Y. Hu, S. Murakami, T. Zhang and B. Monserrat, Topological phonons in oxide perovskites controlled by light, Sci. Adv., 2020, 6, eabd1618 CrossRef CAS PubMed.
- R. Rurali, C. Escorihuela-Sayalero, J.-L. Tamari, J. Íñiguez-González and C. Cazorla, Giant photocaloric effects across a vast temperature range in ferroelectric perovskites, Phys. Rev. Lett., 2024, 133, 116401 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- C. Cazorla and J. Boronat, Simulation and understanding of atomic and molecular quantum crystals, Rev. Mod. Phys., 2017, 89, 035003 CrossRef.
- J. P. Perdew, A. Ruzsinszky and G. I. Csonka, et al., Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. Y. Yu and M. Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Springer, 2010 Search PubMed.
- C. Liu, I. Errea and C. Ding, et al., Excitonic insulator to superconductor phase transition in ultra-compressed helium, Nat. Commun., 2023, 14, 4458 CrossRef CAS PubMed.
- P. Blaha, S. Karlheinz, T. Fabien, R. Laskowski, M. Georg and D. M. Laurence, WIEN2k: An APW + lo program for calculating the properties of solids, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B, 1992, 45, 13244 CrossRef PubMed.
- J. S. David, Planewaves, pseudopotentials and the LAPW method, Springer, New York, NY, 2006 Search PubMed.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Full-potential, linearized augmented plane wave programs for crystalline systems, Comput. Phys. Commun., 1990, 59, 399 CrossRef CAS.
- N. Marzari and D. Vanderbilt, Maximally localized generalized Wannier functions for composite energy bands, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 56, 12847 CrossRef CAS.
- K. Wei, H. Rosner, W. E. Pickett and R. T. Scalettar, Insulating ferromagnetism in La4Ba2Cu2O10: An ab initio Wannier function analysis, Phys. Rev. Lett., 2002, 89, 167204 CrossRef PubMed.
- Y. Wei-Guo, D. Volja and K. Wei, Orbital ordering in LaMnO3: Electron-electron versus electron-lattice interactions, Phys. Rev. Lett., 2006, 96, 116405 CrossRef PubMed.
- J. Ruoshi, Z.-J. Lang, T. Berlijn and W. Ku, Variation of carrier density in semimetals via short-range correlation: A case study with nickelate NdNiO2, Phys. Rev. B, 2023, 108, 155126 CrossRef.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- A. Carreras, A. Togo and I. Tanaka, DynaPhoPy: A code for extracting phonon quasiparticles from molecular dynamics simulations, Comput. Phys. Commun., 2017, 221, 221 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00863h |
| This journal is © The Royal Society of Chemistry 2025 |
