2D elastic fluorinated donor–acceptor type π-conjugated molecular crystals and their optical crystal–polymer hybrid films

Abstract

Robust and mechanically deformable organic molecular crystals present a promising alternative to conventional inorganic and polymeric solids as flexible materials. Here, we report the design of elastic crystals based on asymmetric fluorinated donor–acceptor–donor molecular structures involving 2D planes of heteroatom interactions and pitched π-stacking arrangements. 4,7-Bis(2-thienyl)-5,6-difluoro-2,1,3-benzothiadiazole in crystals exhibited a planar structure with minimized torsion angles (within 2.04°) due to intramolecular heteroatom interactions and hydrogen bonds between the fluorinated benzothiadiazole acceptor and thiophene donor groups. The crystal also formed a two-dimensional noncovalent network along the ac-axis, stabilized by F–H hydrogen bonds between the fluorinated benzothiadiazole-thiophene units and CH–π interactions between thiophene moieties. Furthermore, introducing heteroatoms along the molecular short-axis leads to the formation of pitched π-stack structures. These crystals show macroscopic elasticity for applying stress in each (100) and (001) plane, respectively; thus, the material has 2D elasticity. Micro- and nano-indentation tests revealed that the mechanical robustness (elasticity and hardness) of the crystal surpasses that of common polymeric solids. In addition to their mechanical properties, the crystal exhibited yellow-photoluminescence due to charge-transfer interaction (a maximum emission wavelength of 563 nm). This design of donor–acceptor–donor promotes inter- and intra-molecular charge-transfer interactions. The 2D elastic crystals were easily hybridized with polyimide films and exhibited 3D active optical waveguide properties. This molecular-supramolecular strategy for tuning the mechanical and optical properties provides new opportunities for the engineering of crystal functionalities.

---

Introduction

Robust and mechanically deformable organic materials, also known as flexible organic materials, have potential applications in actuators,^1–4 sensors,^5–7 and optoelectronic devices.^8–11 Flexible materials composed of inorganic or polymeric solids are often organized in less-anisotropic alignment, disordered arrangements, and/or less densely packed structures. In contrast, organic molecular crystals consist of three-dimensional ordered and anisotropic directional molecular arrays, which lead to unique properties in photonics and electronics;^12–20 however, such materials are mechanically weak and have less flexibility. On the other hand, the diversity of molecular structures in organic chemistry makes it possible to control their supramolecular alignments derived from molecular structures having specific monomer functions in various functional self-assembled materials. By understanding the relationship between the molecular structure and arrangement, flexible (elastic) molecular crystals have been developed through molecular design.^21–28

Highly planar π-conjugated molecules offer a narrow HOMO–LUMO energy gap due to the delocalization of π-electrons across the main structure. The crystal structures of such molecules exhibit herringbone or brick-like arrangements due to CH–π and π–π interactions between neighboring molecules (Fig. 1).^29–34 In our previous work, we designed molecular stacking structures based on π–π interactions driven by a partial repulsive interaction (δ⁻–δ⁻) to develop the first flexible, elastic, molecular crystals of π-conjugated molecules.^35–38 Pitched π-stacking structures, exemplified by rubrene crystals—one of the most prominent molecular semiconductors—are known for supporting high carrier mobility, a key advantage of π–π interactions. According to the strategy for elastic π-conjugated molecular crystals, 1,4-bis(2-thienyl)-2,3,5,6-tetrafluorobenzene (BTFB) crystals have been designed and synthesized.³⁸ The crystal structure exhibited high planarity due to intramolecular H–F hydrogen bonds and S–F dipole–dipole interactions; thus, pitched π-stacked structures and H–F hydrogen bonds along the short-axis direction are shown. This crystal structure is key to high elasticity in response to mechanical stress on the (001) plane. However, this crystal is limited to one-dimensional elasticity, and its robustness is inferior to that of polymer materials. To address this issue, we focused on the symmetry of the molecular structure. A decrease in molecular symmetry induces disorder in the intramolecular rotation units. Therefore, we replaced the central benzene unit of BTFB, a C_2v group, with an asymmetric skeleton, hoping to control the molecular arrangement and mechanical properties by inducing hydrogen–nitrogen competition in intramolecular and intermolecular interactions.

Fig. 1 Chemical structures of BTFB, BTT, and BTFT, respectively.

In this study, we developed 2D elastic and yellow-photoluminescent crystals through the following design strategies: (1) asymmetric donor–acceptor–donor (DAD) π-conjugated structures, (2) control over a two-dimensional network through heteroatom interactions, and (3) “pitched π-stack” structures by minimizing CH interactions via the introduction of heteroatoms along the short-axis direction. As an asymmetric skeleton, fluorinated benzothiadiazole was expected to inhibit the intramolecular interaction with thiophene and the successive hydrogen bonds. DAD structures composed of fluorinated benzothiadiazole (A) and thiophene (D) are expected to exhibit a lower energy absorption band due to intramolecular charge-transfer (CT) interactions, as well as facilitate the formation of pitched π-stacked structures via intermolecular interactions. Here, we demonstrate DAD-type elastic crystals by designing 4,7-bis(2-thienyl)-5,6-difluoro-2,1,3-benzothiadiazole (BTFT). Additionally, we investigate the relationship between the molecular structure, crystal structure, and their corresponding mechanical and optical properties by comparing BTFT crystals with those of BTFB and 4,7-bis(2-thienyl)-2,1,3-benzothiadiazole (BTT).^39,40

Results and discussion

BTFT was synthesized by Stille cross-coupling of 4,7-dibromo-5,6-difluoro-2,1,3-benzothiadiazole with tri-n-butyl(2-thienyl)tin in toluene using Pd(PPh₃)₄ as a catalyst for 24 hours in 23% yield (Fig. S1, ESI†). The molecular structure of BTFT was characterized by ¹H NMR and ¹³C NMR spectroscopic measurements (Fig. S2 and S3, ESI†). Crystallization of BTFT was performed by vapor diffusion of a chloroform solution containing BTFT with n-hexane in a sample tube (Fig. 2a), yielding good-quality orange needle-like crystals (Fig. 2b). The crystals show yellow-PL under UV irradiation (Fig. 2c).

Fig. 2 Crystallization and crystals of BTFT. (a) Illustration of the vapor diffusion crystallization process using chloroform and n-hexane. (b) A microscopy image of BTFT crystals under ambient light. (c) A fluorescent microscopy image of BTFT crystals under UV irradiation.

The single-crystal X-ray diffraction data are summarized in Table 1. BTFT crystals were analyzed in the monoclinic system with Z′ = 4, space group P2₁/c (CCDC dep. no. 2424463†), and the thienyl unit is disordered (Fig. S8, ESI†). Within the molecule, several intermolecular distances—F–H (2.28 Å), N–H (2.40 Å), F–S (2.70 Å), and N–S (2.83 Å)—are shorter than the corresponding van der Waals radii (d_FH = r_F + r_H = 2.67 Å, d_NH = r_N + r_H = 2.75 Å, d_FS = r_F + r_S = 3.27 Å, and d_NS = r_N + r_S = 3.35 Å) (Fig. 3a). The maximum torsion angle between the benzene and thiophene units is 2.04°, indicating a highly planar molecular structure. These results suggest the presence of intramolecular F–H, N–H, F–S, and N–S interactions, which contribute to its overall planarity. The molecules show π–π stacking in an intermolecular plane (center-to-center distance, 4.78 Å) along the b-axis (Fig. 3b). Additionally, intermolecular F–H interactions (2.60 Å) between the fluorinated benzothiadiazole and thiophene units, as well as C–H interactions (2.81 Å) between thiophenes, establish a two-dimensional noncovalent network via CH–F hydrogen bonds along the a-axis and CH–π interactions between thiophenes along the c-axis (Fig. 3c). Thus, by designing an alternating thiophene–fluorinated benzothiadiazole–thiophene structure, it was possible to achieve molecular planarity through intramolecular interactions and to achieve a pitched π-stacking structure through intermolecular interactions. The low symmetry of the fluorinated benzothiadiazole backbone also facilitates anisotropic intermolecular interactions. In the structures of the BTT and BTFB crystals, intramolecular interactions include N–S (2.95 Å) and N–H (2.46 Å) of BTT and F–H (2.23 Å) and F–S (2.74 Å) of BTFB, respectively (Fig. S9 and S10, ESI†). The maximum torsion angles of both BTT and BTFB molecules were 15.94° and 6.48°, respectively, which indicate a highly planar molecular structure. The intermolecular interactions in both BTT and BTFB crystals show both π–π stacking between molecular planes along the b-axis and CH–π contacts between thienyl–thienyl terminals along the c-axis (Fig. S9 and S10, ESI†). On the other hand, in the intermolecular interactions along the a-axis, hydrogen bonds were formed between F–H in the BTFB crystal; however, no atomic short contact was observed in the BTT crystal (Fig. S9, ESI†).

Table 1 Summary of crystallographic data

	BTFT	BTT	BTFB
a R 1 = Σ||Fo| − |Fc||/Σ|Fo|[β] wR2 = {Σ[w(Fo^2 − Fc^2)^2]/Σ[w(Fo^2)^2]}^1/2.
Empirical formula	C14H6F2N2S3	C14H8N2S3	C14H6F4S2
Formula weight	336.39	300.40	314.32
Temperature [K]	103	93	103
Crystal system	monoclinic	monoclinic	monoclinic
Space group	P21/c	P21/n	P21/n
a [Å]	15.7783(9)	13.6321(4)	6.3133(3)
b [Å]	4.7778(2)	5.2997(2)	5.0761(4)
c [Å]	17.6686(9)	18.5171(6)	18.6666(5)
α [°]	90	90	90
β [°]	104.731(5)	111.118(4)	90.463(3)
γ [°]	90	90	90
V [Å^3]	1288.18(11)	1247.94(8)	598.19(4)
Z	4	4	4
ρ calcd [g cm^−3]	1.734	1.599	1.745
Goodness-of-fit on F^2	1.054	1.067	1.086
R 1 [I ≧ 2σ(I)]^a	0.0674	0.0328	0.0384
wR 2 (for all data)	0.1482	0.0698	0.0905

---

Fig. 3 Crystal structure of the BTFT crystal measured by single-crystal X-ray analysis. (a) Molecular structure, top and side views, respectively. (b) Pitched-π stacked structure, slip-stacking, J-aggregate, focused on π–π stacking of three BTFT molecules. The length of π–π and slipping are shown in the inset. (c) Molecular arrangement in the crystal of BTFT projected on the representative crystal facets.

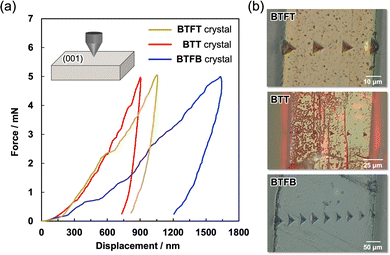
The BTFT crystal shows 2D elastic bending flexibility. Thus, we performed bending tests by applying load on both the (100) plane (Fig. 4a) and the (001) plane (Fig. 4b), respectively, resulting in bending deformation under stress and relaxation along both the c-axis and a-axis. On the other hand, BTFB and BTT crystals showed 1D elastic deformation along the c-axis direction (Fig. S11 and S12, ESI†). To investigate the macroscopic deformation of flexible materials, the measurements of stress (σ), strain (ε), mean elastic modulus (E_ave), and mean elastic limit (S_lim) were performed via indentation tests of BTFT, BTT, and BTFB crystals (Fig. S13, ESI†).⁴¹E_ave is the resistance to macroscopic elastic deformation, i.e., the material's robustness. Indentation was performed along the c-axis direction of each crystal, resulting in elastic deformation with E_ave = 1.168 GPa for BTFT, E_ave = 0.757 GPa for BTT, and E_ave = 0.306 GPa for the BTFB crystals (Fig. S14 and Table S1, ESI†). The S_lim values along the c-axis were 4.29% for BTFT, 1.54% for BTT, and 3.00% for BTFB crystals. The elastic modulus of the PET resin and polystyrene resin measured with the same apparatus was E_ave = 0.572 GPa, and E_ave = 0.349 GPa, respectively (Fig. S15 and Table S2, ESI†); thus, these results indicate that BTFT and BTT crystals are capable of undergoing more robust mechanical deformation like the polymeric materials and that BTFT crystals can undergo the most significant deformation. On the other hand, indentation tests along the a-axis direction of each crystal showed that the BTFT crystal exhibited macroscopic elastic deformation, with an elastic modulus of E_ave = 0.406 GPa (Fig. S16 and Table S3, ESI†). The BTT and BTFB crystals fractured immediately when indentation was applied, estimating elastic moduli of E_ave = 0.526 GPa and E_ave = 0.374 GPa, respectively. The S_lim values along the c-axis were 7.50% for BTFT, 2.40% for BTT, and 3.27% for BTFB crystals. The results of the BTFT and BTT crystals show high E_ave in the elastic direction, and the BTFT crystals have two bending directions with good elastic deformation. Thus, it was suggested that reducing the molecular symmetry makes it possible to adjust the intermolecular interactions and molecular arrangement, which will significantly contribute to controlling the mechanical properties of the crystal.

Fig. 4 Mechanical deformation of the BTFT crystal. (a) Applied stress with loading on the (100) face. (b) Applied stress with loading on the (001) face.

Furthermore, to investigate the effect of temperature on the mechanical properties of BTFT crystals, the elastic modulus was evaluated under high-temperature conditions (Fig. S13, ESI†). A soldering iron was placed near the fixed BTFT crystals, and macroindentation tests along the c-axis direction were performed at least three times at heater temperatures of 30 °C, 50 °C, 100 °C, 150 °C, 200 °C, and 250 °C (Fig. S17 and Table S4, ESI†). As a result, the elastic modulus of BTFT crystals decreased from 1.168 GPa to 0.433 GPa in the temperature range of 30 °C to 100 °C. Young's modulus remained constant in the temperature range from 100 °C to 250 °C, although there was some variation in the modulus from room temperature to 100 °C. This suggests that the elastic modulus of BTFT crystals decreases with heating. The DSC results indicate that the crystals exhibit endothermic peaks with melting point (T_m) at 216 °C and crystallization exothermic peaks (T_c) at 171 °C, respectively. No phase transition is observed in this temperature range, suggesting that the effect on mechanical properties is due to temperature-dependent lattice deformation.

To investigate the relationship between the mechanical properties and the structure of the BTFT crystal, energy framework calculations (HF/3-21G) were carried out using Crystal Explorer. The simulation results showed that the total pair energy (E_Tot) of the intermolecular interactions was dominated by π–π interactions (E_Tot = −61.5 kJ mol⁻¹) (Fig. 5a). The two π-stacked columns were mainly bonded by F–H interactions (E_Tot = −17.6 kJ mol⁻¹), London dispersion forces (E_Tot = −13.7 kJ mol⁻¹), and CH–π interactions (E_Tot = −9.3 kJ mol⁻¹), forming a non-covalent network that extended to the ac plane. In the BTT and BTFB crystals, the π–π interactions were dominant, as in the BTFT crystals (E_Tot = −48.3 kJ mol⁻¹) (Fig. 5b). In BTT crystals, the two π-stacked rows were mainly bonded by London dispersion forces (E_Tot = −25.8 kJ mol⁻¹) and CH–π interactions (E_Tot = −11.0 kJ mol⁻¹, −12.1 kJ mol⁻¹). In the BTTF crystals, the two π-stacked rows were mainly bonded by F–H interactions (E_Tot = –18.8 kJ mol⁻¹) and CH–π interactions (E_Tot = –9.2 kJ mol⁻¹), and both the BTT and BTTF crystals formed relatively weak non-covalent networks on the ac-plane.

Fig. 5 Energy framework calculation results for (a) BTFT, (b) BTT, and (c) BTFB crystals, respectively. Each interaction energy is displayed along the b-axis for π-stacked molecules and in the ac-plane.

It has already been reported that the intermolecular interaction forces between orthogonally arranged molecules play an essential role in accessing elastic deformation on two planes.^23,42 The BTFT, BTT, and BTFB crystals exhibited elastic deformation in response to mechanical stress on the (001) plane, forming C–π interactions or London dispersion forces along the c-axis corresponding to the loading direction (E_Tot = −9.2 kJ mol⁻¹ ∼ −14.2 kJ mol⁻¹). Therefore, we focused on the intermolecular interactions along the a-axis perpendicular to the c-axis. In the BTFT and BTT crystals, weak interactions (E_Tot = −7.4 kJ mol⁻¹, −11.6 kJ mol⁻¹) and strong interactions (E_Tot = −17.6 kJ mol⁻¹, −25.8 kJ mol⁻¹) were alternately arranged along the a-axis. This is due to the asymmetric structure of the benzothiadiazole skeleton. On the other hand, in the BTFB crystal, strong interactions between CH–F (E_Tot = −18.8 kJ mol⁻¹) were continuously formed. Comparing the total interaction energy along the a-axis, the BTFT crystal shows −24.6 kJ mol⁻¹, the BTT crystal shows −32.4 kJ mol⁻¹, and the BTFB crystal shows −37.6 kJ mol⁻¹, revealing that the BTFT crystal, which has an asymmetric structure and is mediated by F–H hydrogen bonds, had the lowest value.

From the above results, it can be inferred that the BTFT, BTT, and BTFB crystals formed attractive intermolecular interactions along the c-axis and a-axis. The molecular design significantly affected the interactions along the a-axis, and the total interaction energy of the BTFT crystal was the lowest. These results suggest that adjusting the crystal hardness by attractive intermolecular interactions along the loading direction is essential for accessing the two bending planes. In addition, mechanical stress along the a-axis caused a fracture in the BTT crystal and vertical cracking in the BTFB crystal (Fig. S11 and S12, ESI†). This indicates that the adjustment of strong and weak E_Tot by CH–F hydrogen bonds and alternating arrangements significantly contributes to the flexibility of the molecular crystal.

To further investigate the mechanical properties of the BTFT, BTT, and BTFB crystals, elastic modulus E_IT and the hardness H_IT of each crystal were measured using the nanoindentation method (Table 2). The indentation test of each single crystal using a Berkovich indenter was performed on the (001) plane at least 3 times. Fig. 6a and b display the load–displacement curves and indentation marks on the crystal surfaces of each crystal. The measurement results showed that the E_IT and H_IT of the BTFT crystal were 7.836 GPa and 0.215 GPa, respectively, under a load of 5.0 mN. When compared with the BTT crystal (E_IT = 8.811 GPa and H_IT = 0.275 GPa) and BTFB crystal (E_IT = 2.476 GPa and H_IT = 0.101 GPa), both the elastic modulus and hardness are higher in the order of the BTT crystal, the BTFT crystal, and the BTFB crystal. In addition, the BTFB crystals were found to exhibit extremely low values. Nanoindentation is a measurement method that involves the three-dimensional destruction of materials by pressing an indenter into them. Therefore, it can be predicted that the elastic modulus and hardness of molecular crystals are affected by the smallest E_Tot among the intermolecular interactions that primarily contribute to the formation of the structure. In fact, among the main contributing interactions in the crystals compared in this study, π–π interactions, CH–F interactions, and CH–π interactions, the smallest E_Tot was E_Tot = −7.4 kJ mol⁻¹ in the BTFT crystal, E_Tot = −11.1 kJ mol⁻¹ in the BTT crystal, and E_Tot = −6.2 kJ mol⁻¹ in the BTFB crystal, suggesting that the intermolecular interaction with the smallest E_Tot affects the elastic modulus and hardness of the crystal.

Table 2 Instrumented indentation modulus (E_IT) and instrumented indentation hardness (H_IT) values determined via nanoindentation tests on the (001) faces of the crystals

Crystals	E IT (GPa)	H IT (GPa)
BTFT	7.836 ± 0.421	0.215 ± 0.009
BTT	8.811 ± 0.863	0.275 ± 0.037
BTFB	2.476 ± 0.308	0.101 ± 0.006

---

Fig. 6 Nanoindentation studies on the BTFT, BTT, and BTFB crystals, respectively. (a) Representative load–depth (P–h) curves measured at 5 mN on the (001) face. (b) Microscopy images of the crystal face after the indentation.

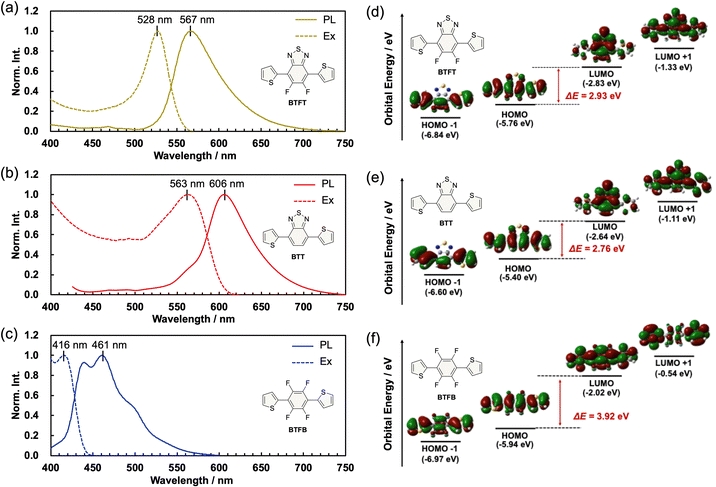
Fig. 7 displays the optical properties and the calculated electron distribution of the molecules. The crystals show photoluminescence under UV irradiation (Fig. 7a). The PL spectra of the crystals showed that the maximum wavelengths of photoluminescence (λ^PL) are 567 nm for the BTFT crystal, 606 nm for the BTT crystal, and 461 nm for the BTFB crystal, respectively. Compared to the BTFB crystal, the BTT and BTFT crystals showed lower energy photoluminescence, indicating charge transfer interaction due to the DA-type molecular structure consisting of benzothiadiazole A and thiophene D. On the other hand, λ^PL of the BTFB crystal shows higher energy photoluminescence than the BTT crystals despite a similar structure. This is probably due to the cancellation of the transition dipole by the substituted fluorine atoms. The photoluminescence quantum yields Φ^PL were 0.27 for BTFT, 0.07 for BTT, and 0.17 for BTFB crystals. Thus, the BTFT crystal exhibits a lower energy photoluminescence than the BTFB crystal despite the highest photoluminescence quantum yield among the compared crystals due to its DA-type molecular structure design and its aggregated state.

Fig. 7 PL spectra (solid line) and excitation spectra (dotted line) of (a) BTFT, (b) BTT, and (c) BTFB in crystals. Electron cloud distribution of (d) BTFT, (e) BTT, and (f) BTFB monomers. HOMO−1, HOMO, LUMO, LUMO+1, isovalue: 0.02.

In organic optoelectronics, hybridization with flexible substrates is essential.^43,44 A BTFT crystal exhibiting 2D elasticity was fixed to a polyimide film tape with excellent flexibility (tensile strength: 0.428 kg mm⁻¹)⁴⁵ and optical transparency in the near-infrared region to fabricate a crystal–polymer hybrid (Fig. 8a). When the crystal was deformed into an arch shape, it showed a similar arch-shaped deformation without breaking (Video S1, ESI†). The jig was rotated to the left and right in opposite directions, and the tape was slowly twisted. As a result, it was observed that the crystal showed a bending deformation with a strong inclination (Videos S2 and S3, ESI†). In this case, the BTFT crystal was observed before and after the test, and no cracks or fractures were found in the crystal (Fig. 8b). These results reveal that the BTFT crystal exhibits excellent 3D deformation without breaking when subjected to loads from multiple directions (Fig. S18, ESI†). On the one hand, in a similar test performed on a BTT crystal as a comparison, the crystal was cleaved in multiple places, and no sign of 3D deformation was observed (Fig. S19, ESI†). Next, the waveguiding properties of the BTFT crystal were observed by irradiating light. The BTFT crystal-polyimide hybrid film was fixed in a straight and coil-like bend of 360° (Fig. 8c). When the center of the crystal was irradiated with excitation light, the emission at the irradiated site and the crystal end was observed, and the fluorescence spectrum was measured (Fig. 8c–e). Although there has been much research into flexible organic crystal-based optical waveguides,^46–51 in the case of crystal–polymer hybrids, it is expected that the optical signal at the end may not be observed due to light diffusion. For the BTFT crystal fixed on the straight film tape, the emission was observed at the irradiated site and terminal end of the crystal (Fig. 8d). The emission spectrum showed a maximum fluorescence wavelength of 553.9 nm at the irradiated site and 568.9 nm at the crystal end (Fig. 8f). The apparent red-shift of the emission band is due to the fluorescence reabsorption within the crystal. In addition, for the crystal bent on the film at 360° like a coil while tilting, the emissions were observed only at the irradiated site and one end of the crystal (Fig. 8e). The emission spectrum showed a maximum fluorescence wavelength of 547.3 nm at the irradiated site and 594.6 nm at the crystal end (Fig. 8g). Therefore, we found that the crystal deformation can be spatially controlled using a polyimide film and that the BTFT crystal can be deformed in two dimensions. In addition, it was shown that BTFT crystals maintain their optical waveguiding properties not only in a linear state but also when deformed in three dimensions.

Fig. 8 Demonstration of flexible crystal-polymer hybrid optical waveguide. (a) Illustration of the flexible molecular crystal and polyimide film hybrid. (b) The BTFT crystal–polyimide film hybrid before and after applying mechanical stress. (i) Photograph of a crystal–polymer hybrid under UV irradiation. (ii) Mechanical deformation. (iii) State of a crystal under UV irradiation after mechanical stress. (c) Photograph of the original and rolled hybrids under spot UV irradiation. (d) Optical waveguiding characteristic of the hybrid. (e) Optical waveguiding characteristic of the rolled hybrid. (f) The PL spectra of the hybrid measured with a fiber probe. Blue: Excited position. Red: Waveguiding output. (g) PL spectra of the rolled hybrid measured with a fiber probe. Blue: Excited position. Red: Waveguiding output.

Experimental

Chemicals

Reagents of 1,4-dibromotetrafluorobenzene, 4,7-dibromo-2,1,3-benzothiadiazole, 4,7-dibromo-5,6-difluoro-2,1,3-benzothiadiazole, and tributyl(2-thienyl)tin were purchased from Tokyo Chemical Industry (TCI inc.). The palladium catalyst, Pd(PPh₃)₄, was purchased from Sigma-Aldrich. The compounds, 4,7-bis(2-thienyl)-2,1,3-benzothiadiazole and 1,4-bis(2-thienyl)-2,3,5,6-tetrafluorobenzene, were prepared by Stille cross-coupling reaction according to the previous reports.^38–40 Insulation polyimide tape (B0BF4VBKWX) was used as received.

General methods

Unless otherwise noted, all the experiments were conducted at room temperature (25 ± 3 °C). Liquid-state ¹H (400 MHz) and ¹³C (100 MHz) nuclear magnetic resonance (NMR) spectra were recorded on a JEOL ECZ400S. Optical microscopy and fluorescence images were obtained using a SHIMADZU moticam 1080BMH with WUBEN E19 UV 365 nm. The optical microscope used was a STZ-171-TP/TLED made by Shimadzu Corporation. The photographs of the observation results were taken using a moticam 1080BMH made by Shimadzu Corporation. The digital microscope used was a VHX-S8000 made by KEYENCE, and its observation system was a VHX-S750 made by KEYENCE. X-ray crystal analysis data were collected using Rigaku/XtaLAB Synergy-S/Cu (CuKαλ = 0.7107 Å) diffractometers. The single-crystal X-ray measurement was performed at 103 K for the BTFT and BTFB crystals and at 93 K for the BTT crystal. The structures were solved by direct methods (SHELXT) and refined through full-matrix least-squares techniques on F2 using SHELXL and OLEX2 crystallographic software packages. The nanoindentation test was performed using Hit300, and at least three tests were performed for each crystal. A soldering iron made by Taiyo Electric Co., Ltd (RX-802AS) was used. A micro-indentation tester was used to measure static mechanical properties. Differential scanning calorimetry (DSC) was performed using a Shimadzu DSC-60 plus differential scanning calorimeter with heating from room temperature to 0 °C–250 °C at 20 °C min⁻¹ in nitrogen. Absorption spectra were obtained on a V-650 (JASCO Corp.). PL and excitation spectra were measured on a JASCO model FP-8500 spectrophotometer. The photoluminescence quantum yield was measured using the Quantaurus-QY Plus UV-NIR absolute PL quantum yield measurement device C13534 (Hamamatsu Photonics). The optical waveguide characteristics of the hybrid, such as emission from the crystal end, were measured by analyzing the system (405 nm UV laser OptoSigma LDU33-405-3.5, OceanOptics a USB400, and a R400-7-UV-VIS probe). The excitation laser focused on the microrod with an objective (10×, NA = 0.3). The collected emission was then guided to a spectrometer (OcianOptics) and recorded using a CCD (OptoSigma, HC-MV90). The detector was fixed to the crystal end and the laser excitation position.

Theoretical calculation

DFT calculation was performed using the Gaussian 03 suite of programs by optimization using the B3LYP/6-31G(d) methods, respectively. The orbital diagrams were generated by using the GaussView program. Energy frameworks were generated by using the CrystalExplorer and HF/3-21G method.

Synthesis

Tributyl(2-thienyl)tin (123 mg, 0.33 mmol) was dissolved in toluene (2 mL) and added in a 10 mL two-necked flask containing a solution of 4,7-dibromo-5,6-difluoro-2,1,3-benzothiadiazole (50 mg, 0.15 mmol) and Pd(PPh₃)₄ (35 mg, 0.03 mmol) under argon. Then, the reaction mixture was stirred at 100 °C for 24 hours. The progress of the reaction was monitored by TLC (SiO₂, n-hexane). The reaction mixture was then cooled to room temperature and concentrated under reduced pressure. When this reaction mixture was confirmed by TLC (SiO₂, n-hexane), five spots of R_f values 0.86, 0.38, 0.34, 0.31, and 0.00 were confirmed. Therefore, the product was purified through column chromatography (SiO₂, n-hexane). When the position of the spot was confirmed by TLC (SiO₂, n-hexane), three spots of R_f values 0.38, 0.34, and 0.31 were confirmed. The excess solvent was removed under reduced pressure, followed by recrystallization from hexane. Finally, a yellow-colored needle-liked compound (BTFT) was obtained, which yielded 12 mg (0.04 mmol, 23%). T_m = 216.3 °C, T_c = 171.5 °C. ¹H NMR (400 MHz, CDCl₃): δ (ppm) 8.29 (d, J = 3.2 Hz, 2H), 7.62 (dd, J = 4.8 Hz, 2H), 7.28 (d, J = 4.8 Hz, 2H); ¹³C NMR (100 MHz, CDCl₃): δ (ppm): 151.4, 149.1, 131.7, 131.1, 129.1, 127.6, 112.0.

Conclusions

4,7-Bis(2-thienyl)-5,6-difluoro-2,1,3-benzothiadiazole (BTFT) crystals exhibited yellow-PL and two-dimensional elasticity. The asymmetric and highly planar molecular structure in the crystal has been attributed to intramolecular H–F hydrogen bonding and S–F dipole–dipole interactions. Intermolecular H–F hydrogen bonds and CH–π interactions formed a non-covalent network along the a- and c-axes, while a pitched π-stacked structure was formed along the b-axis. The BTFT crystal was elastically deformable along the a- and c-axes due to such crystal packing. Compared to the corresponding molecular structures, 4,7-bis(2-thienyl)-2,1,3-benzothiadiazole (BTT) and 1,4-bis(2-thienyl)-2,3,5,6-tetrafluorobenzene (BTFB), these crystals were also dominated by π-stacking with a relatively weak non-covalent network extending along the ac plane, resulting in one-dimensional elasticity. However, in contrast, the BTFT crystal was alternately aligned via CH–F and thiadiazole intermolecular contacts, forming selective interactions along the loading direction of the (100) plane. This suggests that the mechanical properties of the molecular crystals can be controlled by tuning the intermolecular interactions with minimal E_Tot along the direction of mechanical stress. Furthermore, the crystals exhibited highly efficient yellow emission with λ^PL = 563 nm and Φ^PL = 0.27 due to the design of DA-type π-conjugated molecules. The 2D elastic crystal was easily hybridized with the non-emissive polymer film, exhibiting 3D active optical waveguide properties. This design strategy is useful for the systematic order-made synthesis of multi-functional organic crystals.

Author contributions

KY performed all experiments and wrote the paper. TM performed single-crystal X-ray analysis, supported the optical measurements, and checked the manuscript. SH supervised this research and wrote the paper.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for BTFT have been deposited at the CCDC under 2424463 and can be obtained from https://www.ccdc.cam.ac.uk/structures/Search?Compound=5,6-difluoro-4,7-bis(thiophen-2-yl)-2,1,3-benzothiadiazole&Author=Keigo%20Yano&DatabaseToSearch=Published.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. H. acknowledges the JST FOREST Program (no. JPMJFR211W) and a KAKENHI Grant-in-Aid for Scientific Research B (no. 24K01574) from the Japan Society for the Promotion of Science (JSPS). T. M. acknowledges a KAKENHI Grant-in-Aid for Young Scientific Research (no. 22K14671) from JSPS and a Scientific Research Grant from the “Iketani Science and Technology Foundation”. The authors acknowledge Prof. Dr Akitaka Ito at Kochi University of Technology for measurements of evaluation of absolute quantum yield, Φ_PL.

Notes and references

1. C. L. Van Oosten, C. W. Bastiaansen and D. J. Broer, Nat. Mater., 2009, 8, 677–682.
2. S. C. Sahoo, M. K. Panda, N. K. Nath and P. Naumov, J. Am. Chem. Soc., 2013, 135, 12241–12251.
3. X. Pang, J.-A. Lv, C. Zhu, L. Qin and Y. Yu, Adv. Mater., 2019, 31, 1904224.
4. S. Petsch, R. Rix, B. Khatri, S. Shuhladen, P. Muller, R. Zentel and H. Zappe, Sens. Actuators, A, 2015, 231, 44–51.
5. S. Yuvaraja, A. Nawaz, Q. Liu, D. Dubal, S. G. Surya, K. N. Salama and P. Sonar, Chem. Soc. Rev., 2020, 49, 3423–3460.
6. Z. Ren, J. Yang, D. Qi, P. Sonar, L. Liu, Z. Lou, G. Shen and Z. Wei, Adv. Mater. Technol., 2021, 6, 2000889.
7. S. Yousuf, J. M. Halabi, I. Tahir, E. Ahmed, R. Rezgui, L. Li, P. Laws, M. Daqaq and P. Naumov, Angew. Chem., Int. Ed., 2023, 135, e202217329.
8. H. Lee, Z. Jiang, T. Yokota, K. Fukuda, S. Park and T. Someya, Mater. Sci. Eng., 2021, 146, 100631.
9. R. Su, S. H. Park, X. Ouyang, S. I. Ahn and M. C. Mcalpine, Sci. Adv., 2022, 8, eabl8798.
10. J. Song, H. Liu, Z. Zhao, P. Lin and F. Yan, Adv. Mater., 2024, 36, 2300034.
11. A. Takemoto, T. Araki, K. Nishimura, M. Akiyama, T. Uemura, K. Kiriyama, J. M. Koot, Y. Kasai, N. Kurihira, S. Osaki, S. Wakida, J. M. J. D. Toonder and T. Sekitani, Adv. Sci., 2023, 10, 2204746.
12. S. J. Yoon, J. W. Chung, J. Gierschner, K. S. Kim, M. G. Choi, D. Kim and S. Y. Park, J. Am. Chem. Soc., 2010, 132, 13675–13683.
13. C. Zhang, Y. S. Zhao and J. Yao, Phys. Chem. Chem. Phys., 2011, 13, 9060–9073.
14. M. Saito, H. Shinokubo and H. Sakurai, Mater. Chem. Front., 2018, 2, 635–661.
15. H. Omachi, Y. Segawa and K. Itami, Acc. Chem. Res., 2012, 45, 1378–1389.
16. M. Rivera, L. Stojanovic and R. C. Otero, J. Phys. Chem. A, 2021, 125, 1012–1024.
17. Z. Shuai and Q. Peng, Phys. Rep., 2014, 537, 123–156.
18. H.-H. Fang, J. Yang, J. Feng, T. Yamao, S. Hotta and H.-B. Sun, Laser Photonics Rev., 2014, 8, 687–715.
19. J. Gierschner, S. Varghese and S. Y. Park, Adv. Opt. Mater., 2016, 4, 348–364.
20. S. Wengert, G. Csanyi, K. Reuter and J. T. Margraf, Chem. Sci., 2012, 12, 4536–4546.
21. S. Ghosh and M. K. Mishra, Cryst. Growth Des., 2021, 21, 2566–2580.
22. C. M. Reddy, M. T. Kirchner, R. C. Gundakaram, K. A. Padmanabhan and G. R. Desiraju, Chem. – Eur. J., 2006, 12, 2222–2234.
23. S. Mondal, C. M. Reddy and S. Saha, Chem. Sci., 2024, 15, 23578–23587.
24. S. Saha and G. R. Desiraju, J. Am. Chem. Soc., 2017, 139, 1975–1983.
25. J. Peng, J. Zhao, K. Ye, H. Gao, J. Sun and R. Lu, Chem. – Asian J., 2018, 13, 1719–1724.
26. S. Chen, M. P. Zhuo, X. D. Wang, G. Q. Wei and L. S. Liao, PhotoniX, 2021, 2, 1–24.
27. S. Hayashi, Polym. J., 2019, 51, 813–823.
28. T. Seki, N. Hoshino, Y. Suzuki and S. Hayashi, CrystEngComm, 2021, 23, 5686–5696.
29. D. J. Gundlach, Y. Y. Lin, T. N. Jackson, S. F. Nelson and D. G. Schlom, IEEE Electron Device Lett., 1997, 18, 87–89.
30. J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, J. Am. Chem. Soc., 2001, 123, 9482–9483.
31. C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651–669.
32. G. R. Desiraju and A. Gavezzotti, J. Chem. Soc., Chem. Commun., 1989, 621–623.
33. Z.-F. Yao, J.-Y. Wang and J. Pei, Cryst. Growth Des., 2018, 18, 7–15.
34. S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274.
35. S. Hayashi, Symmetry, 2020, 12, 2022.
36. S. Hayashi and T. Koizumi, Angew. Chem., Int. Ed., 2016, 55, 2701–2704.
37. S. Hayashi, F. Ishiwari, T. Fukushima, S. Mikage, Y. Imamura, M. Tashiro and M. Katouda, Angew. Chem., Int. Ed., 2020, 59, 16195–16201.
38. S. Hayashi, A. Asano, N. Kamiya, Y. Yokomori, T. Maeda and T. Koizumi, Sci. Rep., 2017, 7, 9453.
39. S. E. Tan, F. H. Anuar, S. Rahman and M. S. Sarjadi, ChemistrySelect, 2019, 23, 936–940.
40. K. Ranjith, S. K. Swathi, A. Malavika and P. C. Ramamurthy, Sol. Energy Mater. Sol. Cells, 2012, 105, 263–271.
41. N. Hoshino and T. Akutagawa, CrystEngComm, 2022, 24, 5234–5237.
42. S. Saha and G. R. Desiraju, J. Am. Chem. Soc., 2017, 139, 1975–1983.
43. K. Maruyama, K. Sawabe, T. Sakanoue, J. Li, W. Takahashi, S. Hotta, Y. Iwasa and T. Takenobu, Sci. Rep., 2015, 5, 10221.
44. X. Yang, L. Lan, X. Pan, Q. Di, X. Liu, L. Li, P. Naumov and H. Zhang, Nat. Commun., 2023, 14, 2287.
45. https://www.protapes.com/wp-content/uploads/2022/12/Pro-950.pdf .
46. L. Lan, X. Yang, B. Tang, X. Yu, X. Liu, L. Li, P. Naumov and H. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202200196.
47. T. Matsuo, H. Tanikubo and S. Hayashi, Adv. Opt. Mater., 2024, 13, 2401119.
48. S. Hayashi, S. Yamamoto, D. Takeuchi, Y. Ie and K. Takagi, Angew. Chem., Int. Ed., 2018, 57, 17002–17008.
49. H. Liu, Z. Lu, Z. Zhang, Y. Wang and H. Zhang, Angew. Chem., Int. Ed., 2018, 57, 8448–8452.
50. T. Matsuo, K. Ikeda and S. Hayashi, Aggregate, 2023, 4, e378.
51. K. Ikeda, T. Matsuo and S. Hayashi, Bull. Chem. Soc. Jpn., 2024, 4, uoae115.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2424463. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc00790a

---