Iodide substituted halide-rich lithium argyrodite solid electrolytes with improved performance for all solid-state batteries

Abstract

Halogen substitution has been a widely accepted strategy to boost ionic conductivity of lithium argyrodites. Mixed halide argyrodites containing Cl and Br have been shown to be promising candidates as solid electrolytes, featuring high room temperature ionic conductivities >10 mS cm⁻¹. This study focuses on the less explored halide-rich Cl–I mixed halide argyrodites as solid-state electrolytes, comparing them to their Cl–Br analogues. DFT calculations reveal that Cl–I argyrodites possess enhanced phase stability and electrode compatibility. Despite differences in the type of halogen used, Cl–I and Cl–Br argyrodites exhibit similar ionic conductivities at equivalent Cl/X (X = Br, I) ratios. AIMD simulations of Li_5.5PS_4.5Cl_1.5−xI_x systems identify an optimal I and Cl content of 0.75 each, yielding a maximum conductivity of 23.5 mS cm⁻¹, attributed to enlarged Li⁺ migration channels.

---

1. Introduction

Over the past decade, there has been a growing interest in electric vehicles powered by lithium-ion batteries, due to their immense potential in reduction of “well-to-wheel” greenhouse emissions. Typically, liquid electrolytes have been a popular choice in commercial lithium-ion batteries as they exhibit fast Li⁺ ion conduction (10⁻²–10⁻¹ S cm⁻¹ at room temperature). However, utilization of liquid electrolytes poses safety concerns due to their thermal instability, volatility, flammability, and Li dendrite formation. Solid state electrolyte (SSE) batteries, besides their promise to enable the use of Li metal and increase energy density, can provide a noticeable advantage over conventional liquid batteries with regards to safety and in recent years have begun to outperform conventional liquid batteries.^1–6

One of the most notable compound groups for applications in SSEs are sulfide-based lithium argyrodites which have shown great progress in recent years through the discovery of compounds featuring very high ionic conductivities. By making use of various cationic and anionic substitution strategies, several compounds have been discovered with ionic conductivities in the range of 10⁻⁴–10⁻² S cm⁻¹.⁷ Amongst all other strategies, halogen substituted lithium argyrodites, i.e. Li_7−yPS_6−yX_y (X = Cl, Br, I) have been more popular. This is due to the resulting lithium vacancies generated when halogens are added and the S⁻²/X⁻ anionic site disorder, which occurs in argyrodites substituted with Cl and Br anions, where the halogens, to some degree, swap their 4a crystallographic positions with 4d sites of S⁻² ions, due to being similar in size. This shift results in a modification of the energy landscape for Li⁺ ions, which results in better transport kinetics. Such a phenomenon is absent in the case of I⁻ anions as they only occupy 4a crystallographic positions in the structure.⁸ Previous experimental studies have reported an ionic conductivity value of 1.9 mS cm⁻¹ for Li₆PS₅Cl and 0.7 mS cm⁻¹ for Li₆PS₅Br. However, depending on the synthetic method used, the ionic conductivity could be increased to ∼3.1 mS cm⁻¹ for both Li₆PS₅Cl and Li₆PS₅Br.^9,10

Based on the halogen substitution strategy to generate lithium vacancies, excess halogen substituted or halide-rich argyrodites of the type Li_6−xPS_5−xX_1+x (0 < x < 0.5) have also been studied. Out of all the compounds, Li_5.5PS_4.5Cl_1.5 exhibited the best performance, reaching an experimental ionic conductivity value of 12 mS cm⁻¹. Synthesizing a pure crystalline phase of Li_6−xPS_5−xX_1+x (X = Br, I) proved to be difficult due to the large anionic size and the formation of LiX (X = Br, I) phase which negatively affected ionic conductivity.¹¹ Yu et al. were able to create a stable Li_5.5PS_4.5Br_1.5 phase, which exhibited an ionic conductivity of 4.35 mS cm⁻¹.¹² Zhang et al. were able to synthesize a stable Li_5.5PS_4.5I_1.5, which had an ionic conductivity of 0.31 mS cm⁻¹.¹³ Other literature studies on similar single halogen substitution strategies involve an addition of other elements such as Si, Ge, Sb, or Se for boosting conductivity via vacancy generation, change in anionic polarizability etc.^14–16

Mixed halide rich argyrodites have gained significant popularity in recent years, with argyrodites containing 2 or more halogens substituted in the structure which have yielded ionic conductivity values greater than 10 mS cm⁻¹. Experimental and computational studies done on Li_6−xPS_5−xClBr_x showed that Li_5.3PS_4.3ClBr_0.7 was the best choice amongst other candidates in the family, with an ionic conductivity of 24 mS cm⁻¹ at room temperature with a low lithium ion migration barrier.¹⁷ Li et al. conducted a thorough exploration of the Li_5.5PS_4.5Cl_1.5−xBr_x chemical space, establishing the role of configurational entropy in boosting ionic conductivity of these systems, and discovering a novel Li_5.5PS_4.5Cl_0.8Br_0.7 phase exhibiting a bulk ionic conductivity of 22.7 mS cm⁻¹.¹⁸ There have been limited experimental studies on Cl–I mixed halide rich compositions. Most notably, Li_5.4PS_4.4Cl_1.4I_0.2 and Li_5.6PS_4.6Cl_1.3I_0.1 with an ionic conductivity of 16.43 and 10.45 mS cm⁻¹ respectively.^19,20

Although mixed halide substitution strategies show a lot of promise, there exist a few unanswered questions which demand exploration. In this work, we focus on the less explored Cl–I mixed halide argyrodite chemical space, to evaluate and compare their performance with the widely explored Cl–Br chemical space. In the first section, ground state calculations revealed that Cl–I mixed argyrodites exhibited a better overall stability than their Cl–Br analogues due to their low energy phase equilibrium compounds and lower charge per unit volume leading to lower electrostatic repulsions in the structure. Furthermore, interface reaction energy calculations show that Cl–I mixed compounds have a slight edge in terms of compatibility with commercial electrodes. AIMD simulations showed that despite having different halogens altogether, both Cl–I and Cl–Br mixed argyrodites exhibited similar ionic conductivity, if the composition ratios of Cl/Br and Cl/I are the same. Lastly, AIMD simulations were conducted to understand the effect of varying I/Cl ratios on ionic conductivity for Li_5.5PS_4.5Cl_1.5−xI_x systems. The maximum ionic conductivity of 23.5 mS cm⁻¹ was achieved for x = 0.75, due to this composition having the maximum average Li Voronoi polyhedron volume, indicating wide migration channels. To this end, these results may be used to complement experimental work, to provide a sense of direction to researchers working on screening different formulations of these mixed halide rich Cl–I argyrodites.

2. Computational details

2.1 Density functional theory (DFT) calculations

All the calculations were carried out within the DFT framework, implemented in Vienna Ab Initio Simulation Package (VASP).²¹ The projector augmented-wave pseudopotentials were used to describe the interaction between ions and electrons, and the exchange–correlation effects were treated using the Perdew–Burke–Ernzerhof (PBE) functional under the generalized gradient approximation (GGA).²² The initial structure for Li₆PS₅Cl, used as the basis of this work was sourced from the ICSD (collection code 418490).²³ Stable structure for excess Li₆PS₅ClX_y (X = Cl, Br, I; 0 < y < 0.5) was determined by halogen substitution of 4d sulfur sites, and rigorous enumeration using pymatgen.²⁴ Structural optimization for all the systems was performed using Monkhorst–Pack grid k-points of 4 × 4 × 4 and an energy cut-off of 520 eV. All the optimized 1 × 1 × 1 argyrodite structures had a lattice parameter ∼10 Å, which is a moderate system size for AIMD calculations.²⁵

2.2 Ab initio molecular dynamics (AIMD) simulations

AIMD calculations were then performed with a time-step of 2 fs. For each species, the structure underwent five different AIMD calculations, where the diffusivity would be determined at four different temperatures, in intervals of 100, from 600 K to 1000 K. The simulations were run for a total of 110 ps using NVT ensemble with a single Γ-center k-point grid, with the initial. The lithium-ion diffusivity in the structures was determined by computing the total mean squared displacement of lithium ion during AIMD simulations over 100 ps, after initially equilibrating the system for 10 ps. The mean square displacement (MSD) over time was used to calculate the diffusion coefficient (D) as shown in eqn (1).The dimension of diffusion is represented by d, the total number of diffusion ions is denoted by N, and r_i(t) signifies the displacement of the i-th ion at time t. The ionic conductivity of the system was determined using the Nernst–Einstein relation given in eqn (2).The ionic conductivity is represented by σ, volume of the system is given by V, k is the Boltzmann constant, T is the temperature of the AIMD calculation, q is the charge of the mobile ion species and lastly, D is the diffusivity value obtained from AIMD simulations. The room temperature ionic conductivity and activation barrier were obtained by fitting the diffusivity data to Arrhenius law and extrapolation at 300 K.²⁶

2.3 Electrode interface compatibility

To understand possible degradation causing side-reactions at the interface with common cathode materials, a pseudo binary model was employed. To assess the phase equilibria, the calculation of the energy minimum was performed using the reaction energy (ΔE_D). The determination of ΔE_D involved comparing the energy of relevant phases within their compositional space. By utilizing the grand potential phase diagram, the phase equilibria C_eq (C, μ_M) of a specific phase with composition C in equilibrium with the chemical potential μ_M of element M can be identified. The reaction energy is determined using eqn (3).The first term in the RHS denotes the energy of phase equilibria for the composition in the bracket, x is the molar fraction of the electrolyte, E(electrolyte/cathode), denote the energies of the electrolyte/cathode material respectively.²⁷ The energies of common cathode materials were sourced from materials project and these calculations were facilitated by pymatgen.²⁴

3. Results and discussion

3.1 Comparison of Br and I substituted structures

The lithium atoms in the initial structure referenced from ICSD, populated the 48 h sites. Stoichiometric Li₆PS₅Cl was obtained by iteratively removing Li atoms from the reference structure via rigorous enumeration and coulomb energy calculations using pymatgen.²⁴ The resulting structure with an occupancy of 0.5 for 48 h sites is shown in Fig. 1(a).

Fig. 1 (a) Schematic of reference structure for Li₆PS₅Cl from ICSD with adjusted occupancies (b) Composition vs. E_hull and formation energy for all halogen substituted argyrodites (c) Band structure of Li_5.5PS_4.5ClBr_0.5 (d) Band Structure of Li_5.5PS_4.5ClI_0.5.

To keep the computational costs reasonable, 4a/4d antisite site disorder between Cl⁻ and S²⁻ ions have been avoided. Halogen substitutions were carried out on 4d sites containing S²⁻ ions, with Cl, Br and I atoms with rigorous enumeration. These structures were optimized using DFT and the structures with minimum energy was considered for further analysis and AIMD simulations. It was found that both Br and I atoms preferred 4a sites over 4d sites, with the difference in energy being 0.14 eV per atom and 0.35 eV per atom for Br and I respectively. This site selectivity is due to the higher ionic radius of Br⁻ and I⁻ ions, as compared to S⁻² and Cl⁻ ions.

The variation in Energy above convex hull (E_hull) and formation energy with respect to halogen composition in shown in Fig. 1(b). Although perfectly stable compounds are on the convex hull, with energy above hull equal to 0, we consider a threshold value of 40 meV per atom for determining stable argyrodite configurations. This is because most of the compounds in ICSD were determined to have E_hull < 36, which means that some of these compounds could be stabilized via entropic effects.^28,29 The obtained energy above hull (E_hull) value of 24 meV for Li₆PS₅Cl is in good agreement with the literature value of 21 meV.²⁵ We observe that for pure Cl substitution case the E_hull increases to 28 meV for Li_5.5PS_4.5Cl_1.5. However, we observe that addition of Br leads to a slight decrease in E_hull and addition of I results in a decrease in E_hull resulting in the most phase stable configurations, with Li_5.5PS_4.5ClI_0.5 being the most phase stable compounds out of all with E_hull value of 18 meV. This implies that the addition of small amounts of larger halogens such as Br and especially I result in the formation of stable configurations. The phase decomposition products for all argyrodites were Li₃PS₄, Li₂S and LiX (X = Cl, Br, I). Therefore, in this case E_hull = E_f(argyrodite) − (aE_f(Li₃PS₄) + bE_f(Li₂S) + cE_f(LiX)), where E_f denotes formation energy and a, b, c are constants. As documented in the Materials Project,³⁰ the formation energy for LiX follows the order of LiCl > LiBr > LiI (E_LiCl = −2.03 eV per atom, E_LiBr = −1.83 eV per atom, E_LiI = −1.39 eV per atom). Despite Li–Cl and Li–Br interactions being energetically more favorable for the argyrodites than Li–I interactions, as evidenced by slightly lower formation energies for I-substituted systems, the resulting E_hull value was still lower than their Cl and Br-substituted counterparts. To better understand this phenomenon, Bader charge calculations were conducted for all halides with a total halogen content of 1.5, to determine the average Bader charge and Bader charge per unit volume as documented in Table 1.

Table 1 Bader charge and Bader charge per unit volume for Cl, Br and I anions in argyrodites with total halogen content = 15

Material	QCl (|e|)	QCl (|e| Å^−3)	QBr (|e|)	QBr(|e| Å^−3)	QI (|e|)	QI (|e| Å^−3)
Li5.5PS4.5Cl1.5	−0.898	−0.0232	—	—	—	—
Li5.5PS4.5ClBr0.5	−0.897	−0.0231	−0.889	−0.0202	—	—
Li5.5PS4.5ClI0.5	−0.897	−0.0231	—	—	−0.857	−0.0163

---

An increase in halogen content would lead to an increase in electrostatic repulsion in the anionic sublattice which could affect the stability of the system. A lower Bader charge for Li_5.5PS_4.5ClI_0.5 as compared to Li_5.5PS_4.5Cl_1.5 and Li_5.5PS_4.5ClBr_0.5 indicated a lower charge polarization in this system. This resulted in a lower charge per unit volume for Li_5.5PS_4.5ClI_0.5 systems which caused the decrease of overall electrostatic repulsion in the anionic sublattice of these systems. As a result of this phenomenon, despite Li–Cl and Li–Br interactions being much stronger than Li–I interactions, the formation energy for I-substituted systems did not decrease significantly. This phenomenon combined with lower energy phase decomposition products, resulted in a higher phase stability of I-substituted systems as compared to Cl and Br-substituted systems.

Band structures were determined as shown in Fig. 1(c) and (d) for Li_5.5PS_4.5ClBr_0.5 and Li_5.5PS_4.5ClI_0.5, respectively. Band structures for all other compounds of study are shown in Fig. S1 in the ESI.† The bandgap for Li_5.5PS_4.5ClBr_0.5 was 2.19 eV, which was lower than the value of 2.32 eV for Li_5.5PS_4.5ClI_0.5. A larger bandgap is desirable for application in solid-state batteries, as it prevents leakage of electrons and increases dendrite formation resistance, resulting in an increased stability. Overall, all compounds exhibited poor electronic conductivity and were sufficiently insulating for application as solid-state electrolytes, with Li_5.5PS_4.5ClI_0.5 being the best candidate amongst all of them.

The electrode compatibility of all compounds with common cathodes like LiCoO₂, LiFePO₄ or sulfur (S) with their lithiated/delithiated configurations were studied to determine the practical applicability of these materials as solid electrolytes. All detailed results for have been provided in Tables S2–S4 (ESI†).

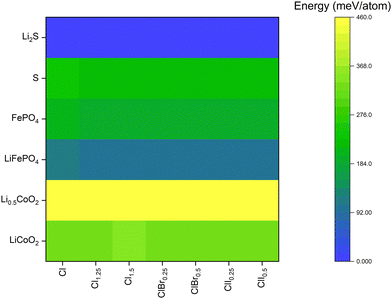
The reaction energy for each argyrodite composition with respective cathode materials has been shown in Fig. 2. In the case of LiCoO₂ and Li_0.5CoO₂, the interfacial reaction energy is quite high, which makes argyrodites an unsuitable class of materials for this type of cathode. Furthermore, the delithiated variant Li_0.5CoO₂, showed much higher reaction energies, which implied that the cathode would become even more susceptible to degradation during the beginning of discharge and end of charge cycles. The general trend that was observed was that reaction energy increased with an increase in halogen content in the system. However, for all systems, I-substituted compounds performed slightly better as the reaction products included LiX (X = Cl, Br, I), and as discussed before, due to LiI having the lowest formation energy, the energy of reaction for I-substituted compounds was slightly lower.

Fig. 2 Heatmap of interfacial reaction energy between cathodes and argyrodites.

In the case of LiFePO₄/FePO₄, the reaction energy was much lower, making LiFePO₄ a better cathode material than LiCoO₂. Similar trend of delithiated FePO₄ having higher reaction energy than LiFePO₄ was observed, but the overall reaction energies were still much lower than LiCoO₂. In these systems, however, an increased halogen content showed a lower reaction energy. This could be due to the lower concentration of sulfur in these systems, due to Fe having a high affinity for S atoms. Amongst Cl, Br and I rich halogen compounds, I-substituted compounds had a better edge due to LiI formation with LiFePO₄ and I₂ formation with FePO₄, both having lower formation energies than LiCl/LiBr.

For S cathodes, the reaction energies were higher than LiFePO₄ but were in the range of FePO₄. However, the lithiated variant Li₂S showed no interfacial reaction with any argyrodite, thereby making argyrodites an excellent material of choice for batteries with S cathodes. In this case however, Cl-rich argyrodites performed slightly better than Br and I-substituted argyrodites due to the formation of low energy side products such as SCl, SBr and I₂. However, both Br and I-substituted compounds exhibited similar performance with the S electrode.

Overall, the ground state calculations highlighted an increased phase stability and slightly better electrode compatibility for Cl–I mixed halide systems as compared to their Cl–Br analogues, for the same I/Cl and Br/Cl ratios. Furthermore, for a deeper comparison of both material classes, AIMD simulations were conducted to ascertain the Li⁺ ion transport characteristics in these systems.

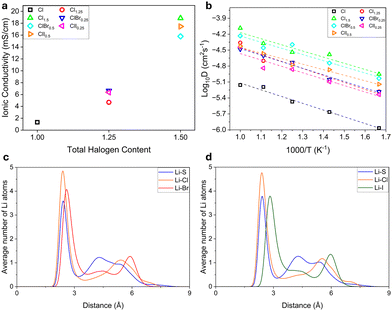
The log plot of diffusivity vs. temperature and ionic conductivities vs. total halogen mole fraction is shown in Fig. 3a and b, respectively. The AIMD simulations showed that the ionic conductivity of Li₆PS₅Cl, Li_5.75PS_4.75Cl_1.25 and Li_5.5PS_4.5Cl_1.5 was 1.33 mS cm⁻¹, 4.69 mS cm⁻¹, and 18.86 mS cm⁻¹, respectively. We obtained a good fit for the experimental conductivity for Li₆PS₆Cl and Li_5.75PS_4.75Cl_1.25 obtained by Adeli et al., which was 2.5 mS cm⁻¹ and 4.2 mS cm⁻¹ respectively.¹¹ The predicted ionic conductivity for Li_5.5PS_4.5Cl_1.5 was slightly higher than the literature value of 12 mS cm⁻¹, however, both were in the order of 10 mS cm⁻¹. There are multiple factors that could have resulted in this difference. Firstly, Li⁺ ionic conductivity was determined from diffusivity at high temperatures using Arrhenius law, which could cause the resulting variation. Secondly, in the experimental structure, Cl⁻ ions have shown to occupy both 4a and 4c sites, whereas, we have only considered 4a sites, based on the reference ICSD structure. Moreover, 4a/4d site disorder has not been considered in this work due to simplicity. These slight structural variations could also result in discrepancies in ionic conductivity. Lastly, synthesis methods, macroscopic conditions and different time scales of measurements could also result in the resulting difference. For the mixed halide system, we compare the AIMD results with the available data for Li_5.5PS_4.5ClBr_0.5. The calculated conductivity of 15.79 mS cm⁻¹ was in good agreement with the experimental conductivity of 17 mS cm⁻¹.

Fig. 3 (a) Plot of ionic conductivity vs. total halogen mole fractions, with all compositions categorized based on total halogen content. (b) Plot of calculated diffusivities for temperatures 600–1000 K for different halogen compositions (c) Radial distribution of Li atoms around all anions in Li_5.5PS_4.5ClBr_0.5 (d) Radial distribution of Li atoms around all anions in Li_5.5PS_4.5ClI_0.5.

To further understand the effect of change in Li transport behavior by the addition of larger halogens in the structure, the radial distribution of Li atoms around anions at 600 K, was plotted for Li_5.5PS_4.5ClBr_0.5 and Li_5.5PS_4.5ClI_0.5, as shown in Fig. 3(c) and (d) respectively. Although average Li clustering was highest around Cl⁻ ions, the peaks for Br⁻ and I⁻ showed significant clustering of Li around these ions showing high Li–Br and Li–I interactions. An increase in concentration of Br and I would further increase these interactions, resulting in sluggish diffusion kinetics.³¹ Li_5.5PS_4.5ClBr_0.5 showed a slightly lower ionic conductivity than Li_5.5PS_4.5ClI_0.5 as both systems had polarizable ions and the latter had a smaller RDF peak for I⁻ ions which implied lesser Li–I interactions as compared to Li–Br interactions in Li_5.5PS_4.5ClBr_0.5. However, it is to be noted that irrespective of the type of halogen, all argyrodites with total halogen content = 1.5 exhibited ionic conductivities in the order of 10 mS cm⁻¹ which makes them perfectly suitable for application as solid electrolytes. Despite the small difference in ionic conductivities of Li_5.5PS_4.5ClBr_0.5 and Li_5.5PS_4.5ClI_0.5, it was not significant enough to claim that Cl–I mixed argyrodites outperformed Cl–Br systems in terms of ionic transport. However, due to Cl–Br and Cl–I systems showing very similar ionic conductivities for similar Br/Cl and I/Cl ratios, we can expect these systems to exhibit similar ionic conductivities despite having different halogens, if their element ratios with respect to Cl in the system and total halogen content were the same.

3.2 Effect of I/Cl ratios on ionic transport in Li_5.5PS_4.5Cl_1.5−xI_x

AIMD simulations were performed to gain a deeper understanding of ionic transport in Cl–I mixed argyrodites, while keeping the total halogen content constant, at 1.5. Fig. 4(a) and (c) show the variation of ionic conductivity and activation energy with x in Li_5.5PS_4.5Cl_1.5−xI_x and the calculated diffusivities for temperatures in the range of 600–1000 K. The ionic conductivity shows an initial increasing trend, with the ionic conductivity maximizing at 23.5 mS cm⁻¹ for the I/Cl ratio (x = 0.75), followed by a decreasing trend. In the previous section, we showed that Cl–Br and Cl–I mixed halide argyrodites would show very similar transport properties for the same atomic ratios. Comparing the ionic conductivity trend obtained for these systems with the experimental results of Li et al. for the Li_5.5PS_4.5Cl_1.5−xBr_x system, show a similar increasing–decreasing trend, with the maximum ionic conductivity obtained at a near equiatomic composition (x = 0.7).¹⁸ Furthermore, the range of ionic conductivity values obtained through our AIMD simulations for these Cl–I systems is also in the range of bulk ionic conductivity measurements through PFG NMR for Cl–Br systems, with the maximum value being >20 mS cm⁻¹.¹⁸ Although there is no literature on the exact I/Cl ratios chosen in this work, our AIMD results are in good agreement with the experimental results for Li_5.4PS_4.4Cl_1.4I_0.2 exhibiting an ionic conductivity of 16.43 mS cm⁻¹ for a pellet-sintered sample and Li_5.6PS_4.6Cl_1.3I_0.1 with an ionic conductivity of 10.45 mS cm⁻¹, by accurately capturing the range of ionic conductivities which is >10 mS cm⁻¹. Increasing I content in the structure also resulted in a decrease followed by an increase in activation barrier for ionic transport, minimizing at 0.18 eV for the equiatomic composition.

Fig. 4 (a) Variation Ionic conductivity and Activation barrier for increasing I/Cl ratios (b) Comparison of variation of average volume of Li Voronoi polyhedron and ionic conductivity with increasing I/Cl ratios (c) Plot of calculated diffusivities at for 600–1000 K (d) Schematic of enlarged Li polyhedron in Li_5.5PS_4.5Cl_1.25I_0.25. Distribution of Li polyhedra volume in (e) Li_5.5PS_4.5Cl_1.5, (f) Li_5.5PS_4.5Cl_0.75I_0.75 and (g) Li_5.5PS_4.5I_1.5.

Voronoi method was used to determine the Li⁺ coordination polyhedron, to understand the structure–property relationship governing ionic conductivity in these systems. A larger polyhedron volume would indicate wider migration channels for the Li⁺ ion to move through the lattice, resulting in a lower activation barrier, boosting ionic conductivity. Fig. 4(b) shows the variation of the average volume of Li⁺ ion coordination polyhedron and ionic conductivity with varying I/Cl ratios. The average volume shows an increasing–decreasing trend, like ionic conductivity, maximizing for the equiatomic Cl–I composition at 9.39 ų. The structures undergo lattice expansion due to the addition of I atoms into the structure, which is the main cause of this volume increase, which explains the increasing trend and widening of the migration channels. However, for x > 0.75, the addition of I into the structure resulted in a decrease in average polyhedron volume which is unexpected, as substitution of smaller Cl atoms with larger I atoms would result in lattice expansion. To understand this phenomenon, each Li⁺ coordination polyhedron was analyzed separately to highlight the effect of local disorder due to structural mismatch caused by mixed halide substitution. Fig. 4(d) shows a schematic of a Li⁺ coordination polyhedron in Li_5.5PS_4.5Cl_1.25I_0.25 and Fig. 4(e)–(g) show individual histograms capturing the overall polyhedron volume distribution for Li_5.5PS_4.5Cl_1.5, Li_5.5PS_4.5Cl_0.75I_0.75 and Li_5.5PS_4.5I_1.5. Histograms for other compositions are available in the Fig. S2 of ESI.† Due to an increased concentration of Li vacancies for this composition, instead of forming a standard 4-atom coordinated tetrahedral polyhedron, certain Li sites form a larger distorted 5-atom coordinated polyhedron. These polyhedra contribute the most to ionic conductivity due to having much larger volumes and skewed the results shown in Fig. 4b, causing an increasing-decreasing trend. Till x = 0.75, addition of I resulted in overall increase in polyhedron volumes, including the 5-atom coordinated one, as marked in Fig. 4d, however a further increase in I concentration resulted in reversion of some of the 5-atom coordinated polyhedra back to a 4-atom coordinated configuration, significantly reducing the width of migration channel, thereby lowering the average Li⁺ polyhedron volume. For x = 1.5, all the 5-atom coordinated polyhedra reverted back to 4 atom coordination, resulting in the lowest ionic conductivity out of all the systems, at 4.3 mS cm⁻¹.

Overall, for Cl–I systems, these results indicate a strong dependency of ionic conductivity on local coordination environments of Li⁺ ions, where a faster conduction is facilitated by wider migration channels and the presence of 5-atom coordinated Li⁺ ions. Li et al. discussed the role of site configurational entropy for the increasing-decreasing trend observed in the case of Li_5.5PS_4.5Cl_1.5−xBr_x systems, as entropy maximizes for a near equiatomic composition. However, that discussion is beyond the scope of this work, as anti-site disorder was avoided for simplification of systems in this study, which contributes significantly to site configurational entropy.

Conclusions

In this study, we investigated the transport properties of mixed halide argyrodites, with a focus on Cl–I halide rich compositions through first-principles calculations. The results revealed that Cl–I systems offer better phase stability, and have a slightly better compatibility with commercial electrodes, than Cl–Br systems. Additionally, Cl–I and Cl–Br systems exhibited similar ionic conductivities at room temperature, if the I/Cl and Br/Cl ratios for the compositions were the same. AIMD simulations for different I/Cl ratios revealed a novel composition Li_5.5PS_4.5Cl_0.75I_0.75 which exhibited an ionic conductivity of 23.5 mS cm⁻¹ at 300 K with a low activation barrier of 0.18 eV. Overall, the ionic conductivity for the Li_5.5PS_4.5Cl_1.5−xI_x (x = [0–1.5]) systems showed an increasing–decreasing trend. The major reason behind this was the widening of migration channels due to substitution of smaller Cl atoms with larger I atoms and reversion of 5-atom coordinated Li⁺ coordination polyhedra to 4-atom coordinated configurations.

Author contributions

Adwitiya Rao performed DFT and AIMD calculations, conducted the analysis, and prepared the manuscript. Jacob Rempel contributed to DFT and AIMD calculations. Ming Jiang, Parvin Adeli, Chae-Ho Yim, and Mohamed Houache contributed to the discussion and development of this work. Yaser Abu-Lebdeh and Chandra Veer Singh initiated this research project and contributed to the ideation, discussion, and funding of this work.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research project has been funded by the University of Toronto and the National Research Council of Canada (RGPIN-2018-04642). The authors are grateful to the Natural Sciences and Engineering Research Council of Canada (NSERC), the Canadian Foundation for Innovation, and the Ontario Research Fund. This work was supported in part by a contribution from the National Research Council of Canada (NRC) through the NRC/University of Toronto Collaboration Centre in Green Energy Materials (CC-GEM).

References

1. J. Speirs, M. Contestabile, Y. Houari and R. Gross, Renewable Sustainable Energy Rev., 2014, 35, 183–193.
2. N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686.
3. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162.
4. X. Yang, X. Gao, C. Zhao, Q. Sun, Y. Zhao, K. Adair, J. Luo, X. Lin, J. Liang, H. Huang, L. Zhang, S. Lu, R. Li and X. Sun, Energy Storage Mater., 2020, 27, 198–204.
5. J. Wu, S. Liu, F. Han, X. Yao and C. Wang, Adv. Mater., 2021, 33(6), 2000751.
6. Q. Jia, Z. Yao, J. Xiang, J. Shi, Y. Zhou, J. Huang, H. Zhang, X. Zhang, Y. Yang and J. Tu, Adv. Funct. Mater., 2025, 2426053.
7. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030.
8. C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858.
9. R. P. Rao and S. Adams, Phys. Status Solidi A, 2011, 208, 1804–1807.
10. P. R. Rayavarapu, N. Sharma, V. K. Peterson and S. Adams, J. Solid State Electrochem., 2012, 16, 1807–1813.
11. P. Adeli, J. D. Bazak, K. H. Park, I. Kochetkov, A. Huq, G. R. Goward and L. F. Nazar, Angew. Chem., Int. Ed., 2019, 58, 8681–8686.
12. C. Yu, Y. Li, W. Li, K. R. Adair, F. Zhao, M. Willans, J. Liang, Y. Zhao, C. Wang, S. Deng, R. Li, H. Huang, S. Lu, T.-K. Sham, Y. Huang and X. Sun, Energy Storage Mater., 2020, 30, 238–249.
13. Z. Zhang, C. Yu, R. Xu, L. Peng, H. Ren, J. Zhang, L. Zhang, S. Cheng and J. Xie, Scr. Mater., 2022, 210, 114475.
14. M. Jiang, Z.-W. Chen, A. Rao, L.-X. Chen, X.-T. Zu and C. V. Singh, J. Mater. Chem. C, 2022, 10, 18294–18302.
15. L. Zhou, N. Minafra, W. G. Zeier and L. F. Nazar, Acc. Chem. Res., 2021, 54, 2717–2728.
16. H. Schneider, H. Du, T. Kelley, K. Leitner, J. ter Maat, C. Scordilis-Kelley, R. Sanchez-Carrera, I. Kovalev, A. Mudalige, J. Kulisch, M. M. Safont-Sempere, P. Hartmann, T. Weiβ, L. Schneider and B. Hinrichsen, J. Power Sources, 2017, 366, 151–160.
17. S. V. Patel, S. Banerjee, H. Liu, P. Wang, P.-H. Chien, X. Feng, J. Liu, S. P. Ong and Y.-Y. Hu, Chem. Mater., 2021, 33, 1435–1443.
18. S. Li, J. Lin, M. Schaller, S. Indris, X. Zhang, T. Brezesinski, C. Nan, S. Wang and F. Strauss, Angew. Chem., Int. Ed., 2023, 62(50), e202314155.
19. H. Yan, R. Song, R. Xu, S. Li, Q. Lin, X. Yan, Z. Wang, C. Yu and L. Zhang, J. Energy Chem., 2023, 86, 499–509.
20. G. Liu, J. Zhang, J. Yang, J. Chen, X. Xiao and X. Yao, J. Energy Chem., 2025, 100, 50–58.
21. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
23. D. Zagorac, H. Müller, S. Ruehl, J. Zagorac and S. Rehme, J. Appl. Crystallogr., 2019, 52, 918–925.
24. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
25. Z. Deng, Z. Zhu, I.-H. Chu and S. P. Ong, Chem. Mater., 2017, 29, 281–288.
26. Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17.
27. S. P. Ong, L. Wang, B. Kang and G. Ceder, Chem. Mater., 2008, 20, 1798–1807.
28. W. Li, R. Jacobs and D. Morgan, Comput. Mater. Sci., 2018, 150, 454–463.
29. O. I. Malyi, K. V. Sopiha and C. Persson, ACS Appl. Mater. Interfaces, 2019, 11, 24876–24884.
30. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
31. M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00529a

---